Abstract
We explored the underlying mechanisms of differentiation, dedifferentiation, reprogramming and transdifferentiation (cell type switchings) from landscape and flux perspectives. Lineage reprogramming is a new regenerative method to convert a matured cell into another cell including direct transdifferentiation without undergoing a pluripotent cell state and indirect transdifferentiation with an initial dedifferentiation-reversion (reprogramming) to a pluripotent cell state. Each cell type is quantified by a distinct valley on the potential landscape with higher probability. We investigated three driving forces for cell fate decision making: stochastic fluctuations, gene regulation and induction, which can lead to cell type switchings. We showed that under the driving forces the direct transdifferentiation process proceeds from a differentiated cell valley to another differentiated cell valley through either a distinct stable intermediate state or a certain series of unstable indeterminate states. The dedifferentiation process proceeds through a pluripotent cell state. Barrier height and the corresponding escape time from the valley on the landscape can be used to quantify the stability and efficiency of cell type switchings. We also uncovered the mechanisms of the underlying processes by quantifying the dominant biological paths of cell type switchings on the potential landscape. The dynamics of cell type switchings are determined by both landscape gradient and flux. The flux can lead to the deviations of the dominant biological paths for cell type switchings from the naively expected landscape gradient path. As a result, the corresponding dominant paths of cell type switchings are irreversible. We also classified the mechanisms of cell fate development from our landscape theory: super-critical pitchfork bifurcation, sub-critical pitchfork bifurcation, sub-critical pitchfork with two saddle-node bifurcation, and saddle-node bifurcation. Our model showed good agreements with the experiments. It provides a general framework to explore the mechanisms of differentiation, dedifferentiation, reprogramming and transdifferentiation.
Introduction
A pluripotent undifferentiated cell can differentiate into types of differentiated cells. Each cell type has a specific regulated gene expression. Cellular differentiation is determined by the underlying gene regulatory network during the process of development, which leads the primary cell into its ultimate fate-a particular phenotype. Induced pluripotent stem (iPS) cells provide the opportunity to obtain pluripotent stem cells which potentially have therapeutic uses [1], [2]. Recently many studies have been reported that one type of cells can be converted to another type of functional cells directly [3]–[7]. This is a big step forward in the cell biology since there is no need to create iPS cells first for cell type switching, skipping many intermediate steps. This direct reprogramming technology is called the lineage reprogramming. Thus an adult cell can be reprogrammed directly to new cells as lineage switching. The lineage switching through direct transdifferentiation without going through the iPS state might be applied to regenerative medicine with less risk of cancer. However, it is still challenging to quantify the mechanisms of the differentiation, dedifferentiation, reprogramming and transdifferentiation [3]–[11].
The concept of “epigenetic landscape” was first introduced by Waddington in 1940s [12] The quantifications of the Waddington potential landscape for the process of cell differentiation have been explored recently [13]–[17]. Different valleys represent different cell phenotypes (cell fates) on the cell development potential landscape [13]–[17]. Waddington visualized the undifferentiated state as the local maximum and differentiated states as the local minimum on the landscape [12]. In our landscape picture, the undifferentiated state and differentiated state are both local minima in certain regions of the landscape. Undifferentiated state has relatively low expressions of differentiation mark genes while differentiated state has at least one high expressions of differentiation mark genes. In addition, Waddington believed the differentiation is a downhill process driven by the funneled landscape gradient. In our picture, the differentiation can occur with several different mechanisms, through funneled landscape, through stochastic fluctuations and the probability fluxes even when the landscape is not funneled towards the differentiated states, and through induction.
For development and differentiation system, we represent a cell as a chemical system having given genomic makeup, with each and every possible phenotype as a potential “state” [18], [19]. This is very much analogous to the notion of a polypeptide, as a chemical molecule, can have many different possible “conformational states”, although each individual protein molecule has only a particular state at a given moment in time. This chemical definition of “the system” is important. Imagine that proteins are defined only through biological functions; then different conformations of a polypeptide will be considered as “different molecules.” Then the notion of spontaneous conformational change would not make sense. Indeed, there are still cell biologists who think different cells from the same person as different cells; rather than as a “same chemical system in different states” [18], [19]. The process of the cell development can be viewed as the system moving from one valley (primary or stem cell phenotype) through bifurcation to another valley (differentiated cell phenotype) on the potential landscape. And the transdifferentiation process can be viewed as the system escaping from one stable differentiated valley to another differentiated valley through certain paths on the potential landscape shown in Figure 1(A). The differentiated cells ( ) can switch to another lineage cell type (
) can switch to another lineage cell type (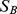 ) through an explicit pluripotent stable state (
) through an explicit pluripotent stable state (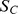 ). Indirect transdifferentiation mechanism which requires an initial dedifferentiation step
). Indirect transdifferentiation mechanism which requires an initial dedifferentiation step 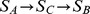 shown in Figure 1(A). It illustrates a differentiated cell (
shown in Figure 1(A). It illustrates a differentiated cell (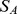 ) reprogrammed back to a pluripotent state (
) reprogrammed back to a pluripotent state (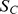 ) with less differentiated, and then can be re-differentiated to another type of differentiated cell (
) with less differentiated, and then can be re-differentiated to another type of differentiated cell (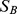 ) [3], [5], [6]. This is a possible strategy of pluripotent lineage reprogramming while the enhancement of efficiency is required. The underlying process is a transdifferentiation involving a stepwise dedifferentiation. In addition to indirect transdifferentiation, there is another lineage reprogramming approach: the direct transdifferentiation mechanism as
) [3], [5], [6]. This is a possible strategy of pluripotent lineage reprogramming while the enhancement of efficiency is required. The underlying process is a transdifferentiation involving a stepwise dedifferentiation. In addition to indirect transdifferentiation, there is another lineage reprogramming approach: the direct transdifferentiation mechanism as  shown in Figure 1(A). Direct transdifferentiation is a mechanism of converting one type of differentiated cells to another type of differentiated cells without undergoing through a pluripotent state or progenitor cell type. The differentiated cells (
shown in Figure 1(A). Direct transdifferentiation is a mechanism of converting one type of differentiated cells to another type of differentiated cells without undergoing through a pluripotent state or progenitor cell type. The differentiated cells (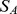 ) down regulate their own cell-specific genes (
) down regulate their own cell-specific genes (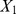 ) and activate the target cell-specific genes (
) and activate the target cell-specific genes (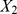 ), thus they can switch to another lineage cell type (
), thus they can switch to another lineage cell type (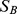 ) through an explicit intermediate stable state (
) through an explicit intermediate stable state (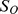 ) or a series of indeterminate states [3]–[5], [8], [9]. In our study, the intermediate state is defined as an intermediate stable state with low or medium pluripotency and having very low expressions of the differentiation mark genes, while a series of indeterminate states are defined as a series of unstable states with low or medium pluripotency and very low expressions of differentiation mark genes in the course of lineage switching. Sridharan et al [20] showed that partially reprogrammed cells as an intermediate stage of the reprogramming process can switch to the completely reprogrammed iPS state. Thus the states of partially reprogrammed cells may exist along the paths from a differentiated state
) or a series of indeterminate states [3]–[5], [8], [9]. In our study, the intermediate state is defined as an intermediate stable state with low or medium pluripotency and having very low expressions of the differentiation mark genes, while a series of indeterminate states are defined as a series of unstable states with low or medium pluripotency and very low expressions of differentiation mark genes in the course of lineage switching. Sridharan et al [20] showed that partially reprogrammed cells as an intermediate stage of the reprogramming process can switch to the completely reprogrammed iPS state. Thus the states of partially reprogrammed cells may exist along the paths from a differentiated state 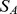 or
or 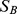 to iPS state
to iPS state 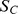 . The research by Mikkelsen [21] showed that partially reprogrammed cells can be trapped at a common intermediate state. Thus the states of partially reprogrammed cells may exist along the paths from a differentiated state
. The research by Mikkelsen [21] showed that partially reprogrammed cells can be trapped at a common intermediate state. Thus the states of partially reprogrammed cells may exist along the paths from a differentiated state 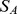 to another differentiated state
to another differentiated state 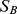 through an intermediate
through an intermediate 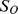 or indeterminate states. These intermediate state and indeterminate states may have certain expressions of stem cell marker genes and thus can be viewed as partially reprogrammed cells. This is supported by the observation that fibroblast cells specific genes are efficiently silenced and the embryonic reprogramming is not fully induced in partially reprogrammed cells [20]. We believe that different experimental and environmental conditions can lead to quite different results and change the topological structure of the potential landscape [20], [21]. The partially reprogrammed cells may be trapped in certain regions in the gene expression space.
or indeterminate states. These intermediate state and indeterminate states may have certain expressions of stem cell marker genes and thus can be viewed as partially reprogrammed cells. This is supported by the observation that fibroblast cells specific genes are efficiently silenced and the embryonic reprogramming is not fully induced in partially reprogrammed cells [20]. We believe that different experimental and environmental conditions can lead to quite different results and change the topological structure of the potential landscape [20], [21]. The partially reprogrammed cells may be trapped in certain regions in the gene expression space.
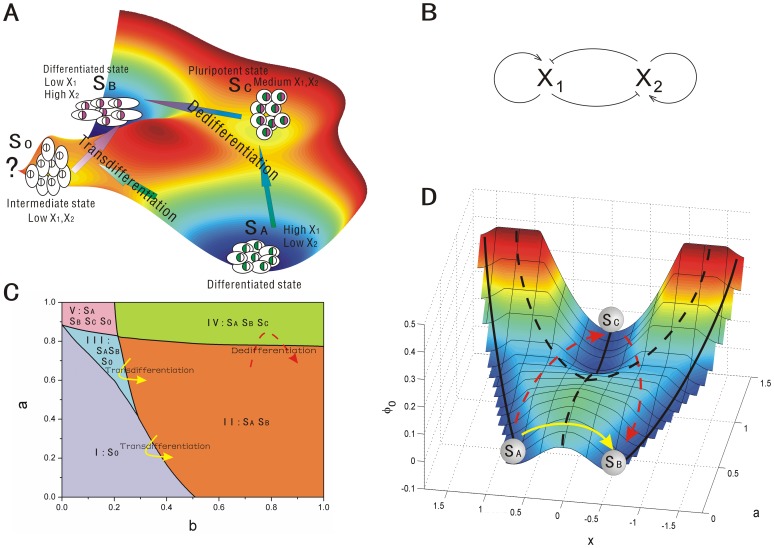
Figure 1. The scheme, phase diagram and intrinsic potential landscape of cell type switchings.
A: The scheme of dedifferentiation (including reprogramming and differentiation) and transdifferentiation. B: A model for the gene circuit for cell development. C: The phase diagram for the gene circuit with 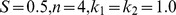 . D: The cell fate landscape
. D: The cell fate landscape 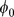 obtained from the Hamilton-Jacobi equation versus
obtained from the Hamilton-Jacobi equation versus  and
and  , and the phase diagram was drawn on the intrinsic potential landscape with stable states represented by black solid lines and unstable states represented by black dash line. The red dash lines represent the dedifferentiation(reprogramming) and redifferentiation process while the yellow solid lines represents the transdifferentiation process. (
, and the phase diagram was drawn on the intrinsic potential landscape with stable states represented by black solid lines and unstable states represented by black dash line. The red dash lines represent the dedifferentiation(reprogramming) and redifferentiation process while the yellow solid lines represents the transdifferentiation process. (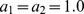 ,
,  ,
, 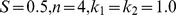 .)
.)
In this study, we term direct transdifferentiation as transdifferentiation and indirect transdifferentiation requiring an initial dedifferentiation or reprogramming step as dedifferentiation. The goal of regenerative medicine can potentially be realized through the processes of differentiation, dedifferentiation, reprogramming and transdifferentiation [4]. Here we use cell type switchings short for the terms “differentiation, dedifferentiation, reprogramming, and transdifferentiation”. Recent advances have shown that there are three possible driving forces for cell type switchings: (1) Stochastic Fluctuations. Cells choose their pathways of differentiation stochastically in the process of development without apparent regards to environment or history [22]. Some studies in cell development reveal that intrinsic stochasticity is an important mechanism for development [22]. The extrinsic fluctuations are also expected to play a role in cell development. Thus the fluctuations can be a driving force for the processes of cell type switchings. (2) Gene Regulation. cell type switchings can be achieved by the change of regulation strengths of their lineage specific genes in many studies [6], [8], [9], [14], [15]. (3) Induction. Lineage specific cells can be reprogrammed to a pluripotent state through over-expressions of some defined transcription factors [23], [24]. Transfection of certain cell specific genes into the primary cells, and over-expressions of the target lineage specific genes as well as certain stem cell-associated genes can induce the processes of cell type switchings.
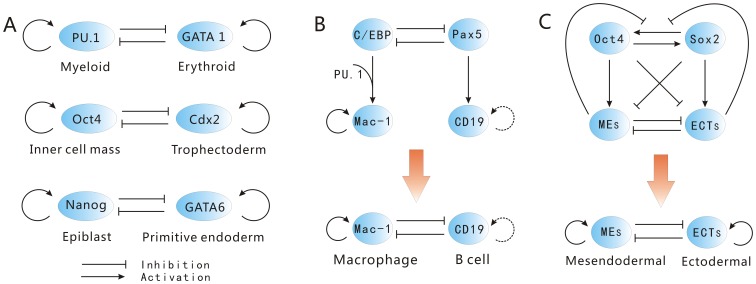
Given the three driving forces for cell fate decision making, it is still challenging on how to quantify the processes of cell type switchings on the landscape, and how to connect them to experiments. These processes of cell type switchings are controlled by their underlying gene regulatory network. The lineage-specific transcription factors play a critical role in the processes of cell type switchings. In this study, we explored a simple cell differentiation network module with autoregulation and mutual antagonism between transcription factors (lineage-specific genes) [15], [17], which exists in many cell differentiation processes, shown in Figure 1(B). The lineage-specific genes can strongly instruct the cellular lineage choice. The circuit is composed of a pair of self activating autoregulation and mutual inhibiting cross-antagonism cell-specific genes 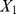 and
and 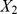 [15], [17]. In iPSC or ESC (embryonic stem cell), pluripotent genes are often highly expressed, and most lineage related genes are off. However, there are examples of gene regulatory circuits with the same architecture in our study which control binary decisions at branch points of cell differentiation in multi-potent cells. Such mutual antagonism gene circuit modules (where the self activation can also be indirect) in binary branch points of cell lineage commitment can often be found. A lot of studies have explored the primed multipotent common myeloid progenitor (CMP) can differentiate to either myeloid cell or erythroid cell in blood cell formation by mutual antagonism interaction of transcription factor gene
[15], [17]. In iPSC or ESC (embryonic stem cell), pluripotent genes are often highly expressed, and most lineage related genes are off. However, there are examples of gene regulatory circuits with the same architecture in our study which control binary decisions at branch points of cell differentiation in multi-potent cells. Such mutual antagonism gene circuit modules (where the self activation can also be indirect) in binary branch points of cell lineage commitment can often be found. A lot of studies have explored the primed multipotent common myeloid progenitor (CMP) can differentiate to either myeloid cell or erythroid cell in blood cell formation by mutual antagonism interaction of transcription factor gene 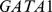 and
and 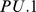 shown in Figure 2(A)
[25], [26].
shown in Figure 2(A)
[25], [26]. 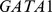 and
and 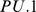 are both self-activated. In the genetic regulation of the inner cell mass/trophectoderm lineage decision,
are both self-activated. In the genetic regulation of the inner cell mass/trophectoderm lineage decision, 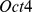 represses expression of
represses expression of 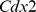 , and
, and 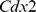 represses expression of
represses expression of 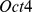 to allow the segregation of inner cell mass and trophectoderm lineages [27], [28].
to allow the segregation of inner cell mass and trophectoderm lineages [27], [28]. 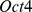 and
and 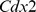 are mutual inhibited and self-activated [27], [28] shown in Figure 2(A). In the genetic regulation of the epiblast/primitive endoderm lineage decision, antagonism between Nanog and Gata6 results in segregation of primitive endoderm and epiblast within the inner cell mass [27], [29], [30] shown in Figure 2(A).
are mutual inhibited and self-activated [27], [28] shown in Figure 2(A). In the genetic regulation of the epiblast/primitive endoderm lineage decision, antagonism between Nanog and Gata6 results in segregation of primitive endoderm and epiblast within the inner cell mass [27], [29], [30] shown in Figure 2(A). 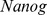 and
and 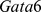 are also both self-activated [30]. These three circuits all can be viewed as
are also both self-activated [30]. These three circuits all can be viewed as 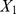 and
and 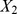 in our network.
in our network.
Figure 2. The gene circuits of mutual antagonism and self activation.
A: The interaction of 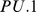 and
and 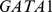 in determining myeloid cell or erythroid cell,
in determining myeloid cell or erythroid cell, 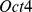 and
and 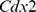 in determining inner cell mass or trophectoderm,
in determining inner cell mass or trophectoderm, 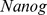 and
and 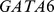 in determining epiblast or primitive endoderm. B: Scheme for the gene circuit of B cell to macrophage conversion. The dashed lines indicate uncertainty. C: Scheme for the gene circuit in determining mesendodermal and ectodermal.
in determining epiblast or primitive endoderm. B: Scheme for the gene circuit of B cell to macrophage conversion. The dashed lines indicate uncertainty. C: Scheme for the gene circuit in determining mesendodermal and ectodermal.
We will study this key network module to uncover the underlying functional mechanisms of cell type switchings. The phase diagram in Figure 1(C) suggests that the system can have five different phase regions, each of which has different underlying landscapes with different distribution of valleys. Furthermore, we show how stochastic fluctuation, gene regulation and induction induce the cell type switchings. The potential landscape and flux both direct the processes of cell type switchings. Probability flux provide a curling force breaking the detailed balance and lead the biological paths of cell type switchings to be deviated from the paths obtained by steepest descent gradient of the landscape. The forward and backward paths of cell type switchings are irreversible, without passing through the saddle point. Furthermore, the flux can become the main driving force for cell type switching when the landscape is not biased towards the specific processes [16], [31]. Barrier height and dynamic transition speed are used to quantify the global stability of the landscape topography. The stability here represents the ability for a cell to stay at a certain cell type state against certain fluctuations. In practice, the fluctuations in some cases maybe small but never zero. We uncover and classify four mechanisms of cell type switchings: super-critical pitchfork bifurcation, sub-critical pitchfork bifurcation, sub-critical pitchfork with two saddle-node bifurcation, and saddle-node bifurcation.
Results and Discussions
I. The model of cell fate network
We start with gene circuit module for typical differentiation. The gene regulatory circuit for cell fate decision has two mutual repression and self-activation lineage-specific transcription factors: 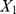 and
and 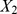 shown in Figure 1(B). It is more complete to consider three or more gene system. But the challenge is that a network with more genes requires more parameters to describe and therefore much bigger search space to explore exhaustively for uncovering the underlying mechanisms. Furthermore, with more genes, it is more difficult to visualize the results. The two gene system we considered is the simplest to exhaustively and effectively explore the underlying mechanism in parameter space [15]–[17], [25]. We would like to use this model to explore the basic underlying mechanisms. The dynamics of this circuit is described by a set of two-variable ordinary differential equations below, with the rate of expression change for these two genes:
shown in Figure 1(B). It is more complete to consider three or more gene system. But the challenge is that a network with more genes requires more parameters to describe and therefore much bigger search space to explore exhaustively for uncovering the underlying mechanisms. Furthermore, with more genes, it is more difficult to visualize the results. The two gene system we considered is the simplest to exhaustively and effectively explore the underlying mechanism in parameter space [15]–[17], [25]. We would like to use this model to explore the basic underlying mechanisms. The dynamics of this circuit is described by a set of two-variable ordinary differential equations below, with the rate of expression change for these two genes:
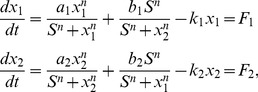 |
(1) |
where 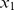 and
and 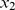 are the time-dependent expressions of the two cell-specific transcription factors
are the time-dependent expressions of the two cell-specific transcription factors 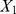 and
and 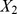 [15], [17], [25]. Parameter
[15], [17], [25]. Parameter 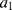 and
and 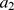 are the self activation strength of the transcription factors
are the self activation strength of the transcription factors 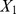 and
and 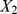 respectively.
respectively. 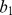 and
and 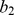 are the strength of the mutual repression for transcription factors
are the strength of the mutual repression for transcription factors 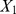 and
and 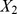 respectively.
respectively. 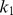 and
and 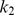 are the first-order degradation rate for
are the first-order degradation rate for 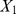 and
and 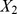 respectively [15], [17], [25].
respectively [15], [17], [25]. 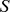 represents the threshold (inflection point) of the sigmoidal functions, i.e., the minimum concentration needed for appreciable changes, and
represents the threshold (inflection point) of the sigmoidal functions, i.e., the minimum concentration needed for appreciable changes, and  is the Hill coefficient which represents the cooperativity of the regulatory binding and determines the steepness of the sigmoidal function. For simplicity, we do not include studies of all the different parameters of
is the Hill coefficient which represents the cooperativity of the regulatory binding and determines the steepness of the sigmoidal function. For simplicity, we do not include studies of all the different parameters of  and
and  in the main text. We included the studies in the supporting information. We show the phase diagrams for varying these parameters in Figure S1 in File S1. We can see varying these parameters can also lead to bi-stable states or tri-stable states and also the phase transitions. In the main text, the parameters for Hill function and degradation rate for
in the main text. We included the studies in the supporting information. We show the phase diagrams for varying these parameters in Figure S1 in File S1. We can see varying these parameters can also lead to bi-stable states or tri-stable states and also the phase transitions. In the main text, the parameters for Hill function and degradation rate for 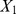 and
and 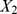 are specified as:
are specified as: 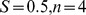 , and
, and 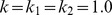 [15]–[17], [25]. In this section, we assume the symmetric situation
[15]–[17], [25]. In this section, we assume the symmetric situation 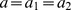 and
and 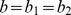 . Although the values of parameters can be different in organisms under different circumstance, the mathematical model here describes a simple yet representative motif gene circuit, and these values (
. Although the values of parameters can be different in organisms under different circumstance, the mathematical model here describes a simple yet representative motif gene circuit, and these values (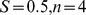 ,
,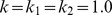 ) are used in many previous studies [15]–[17], [25].
) are used in many previous studies [15]–[17], [25].
1. The phase of cell fate network
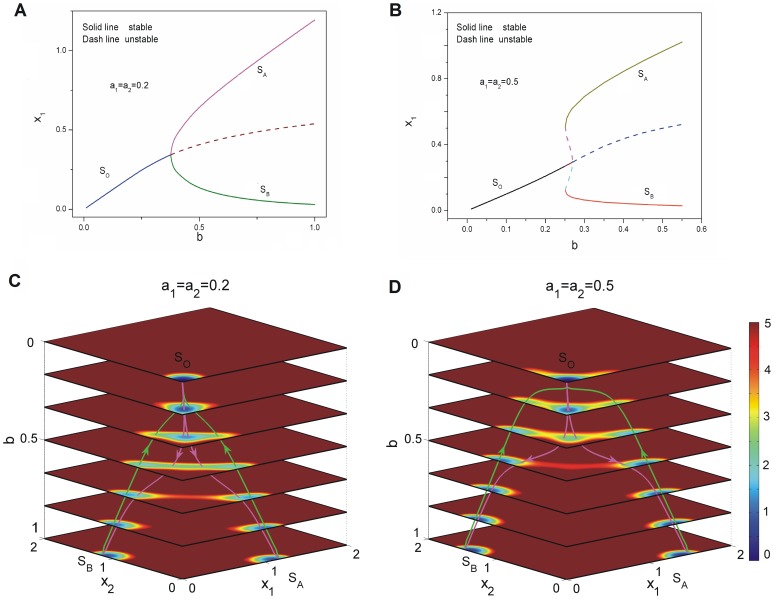
To explore the dynamics under different conditions mimicking by different choice of parameters, we showed the phase diagram in Figure 1(C). If we can keep the mutual repression strength 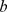 fixed and the self activation
fixed and the self activation  at various levels mimicking the actual developmental process where expression levels of transcription factor change [15](e.g. The expression level of transcription factor
at various levels mimicking the actual developmental process where expression levels of transcription factor change [15](e.g. The expression level of transcription factor 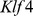 can be viewed as the effective self activation
can be viewed as the effective self activation  at various levels mimicking the actual developmental process [32]. Because
at various levels mimicking the actual developmental process [32]. Because 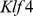 is not required for the maintenance of undifferentiated state of ES cells [32]. Furthermore, the expression level of
is not required for the maintenance of undifferentiated state of ES cells [32]. Furthermore, the expression level of 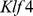 decreases gradually after induced differentiation [32].), the cells are attracted to different differentiated and undifferentiated states. There are five regions in the parameter phase space in Figure 1(C). Region I with lower self activation
decreases gradually after induced differentiation [32].), the cells are attracted to different differentiated and undifferentiated states. There are five regions in the parameter phase space in Figure 1(C). Region I with lower self activation  and mutual repression
and mutual repression 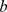 has only one stable state
has only one stable state 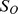 with lower equal levels of the expressions of two lineage specific genes
with lower equal levels of the expressions of two lineage specific genes  and
and 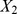 shown in Figure 1(A). This is an intermediate state phase with lower lineage specific genes in the process of transdifferentiation [4]. Region II with higher mutual repression
shown in Figure 1(A). This is an intermediate state phase with lower lineage specific genes in the process of transdifferentiation [4]. Region II with higher mutual repression 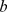 and lower self activation
and lower self activation  has two stable states shown in Figure 1(A):
has two stable states shown in Figure 1(A): 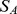 which represents the differentiated state with higher expression of
which represents the differentiated state with higher expression of 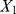 and lower expression of
and lower expression of 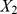 ,
, 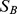 which represents another differentiated state with lower expression of
which represents another differentiated state with lower expression of 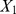 and higher expression of
and higher expression of 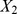 . Region III with lower mutual repression
. Region III with lower mutual repression 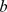 and relative higher self activation
and relative higher self activation  has three states:
has three states: 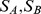 and
and 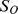 . Region IV with higher mutual repression
. Region IV with higher mutual repression 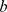 and self activation
and self activation  has three states:
has three states: 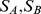 and
and 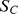 which represents a pluripotent state with medium equal expressions of
which represents a pluripotent state with medium equal expressions of 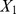 and
and 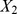 in the process of dedifferentiation which can also be viewed as the process of reprogramming. Region V with lower mutual repression
in the process of dedifferentiation which can also be viewed as the process of reprogramming. Region V with lower mutual repression 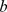 and higher self activation
and higher self activation  has all the four stable states:
has all the four stable states: 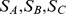 and
and 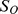 .
.
By changing the parameters of self activation  and mutual repression
and mutual repression 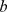 , we can induce the initial differentiated cell to another differentiated cell in region II through the region III or region I by transdifferentiation (the yellow solid line), or through the region IV by dedifferentiation (the red dash line). In regions II, III, IV and V, there also exist tansdifferentiation within each. We will explore the dynamics of gene regulatory network for cell fate decision making process resulted from three driving force of stochastic fluctuations, gene regulation and induction through the instructive changes in details via the corresponding landscape topography for cell development.
, we can induce the initial differentiated cell to another differentiated cell in region II through the region III or region I by transdifferentiation (the yellow solid line), or through the region IV by dedifferentiation (the red dash line). In regions II, III, IV and V, there also exist tansdifferentiation within each. We will explore the dynamics of gene regulatory network for cell fate decision making process resulted from three driving force of stochastic fluctuations, gene regulation and induction through the instructive changes in details via the corresponding landscape topography for cell development.
2. Super-critical and sub-critical pitchfork bifurcation versus saddle-node bifurcation in cell fate network
We explored the bifurcation for cell fate decision network for different conditions. When mutual repression regulation parameters 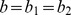 increase with small self activation regulation
increase with small self activation regulation  , the phase diagram has a super-critical pitchfork bifurcation which is a second order phase transition [33], [34] shown in Figure 3(A). The solid lines represent stable fixed points while the dash lines represent unstable fixed points. We can see a stable state
, the phase diagram has a super-critical pitchfork bifurcation which is a second order phase transition [33], [34] shown in Figure 3(A). The solid lines represent stable fixed points while the dash lines represent unstable fixed points. We can see a stable state 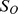 becomes an unstable state and splits into a pair of new stable states
becomes an unstable state and splits into a pair of new stable states 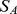 and
and 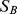 at the critical point [33], [35]. As the self activation regulation strength
at the critical point [33], [35]. As the self activation regulation strength  increases, the phase diagram changes to a new form of sub-critical pitchfork with two saddle-node bifurcation which is a first order phase transition shown in Figure 3(B) as
increases, the phase diagram changes to a new form of sub-critical pitchfork with two saddle-node bifurcation which is a first order phase transition shown in Figure 3(B) as 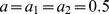 . The initial state
. The initial state 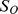 is mono stable at lower mutual repression
is mono stable at lower mutual repression 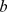 , then a pair of new stable states
, then a pair of new stable states 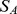 and
and 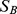 (two saddle-node bifurcations) emerge at somewhere far away from the initial state
(two saddle-node bifurcations) emerge at somewhere far away from the initial state 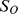 as mutual repression
as mutual repression 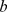 increases. After the critical point of sub-critical pitchfork, the center initial stable state
increases. After the critical point of sub-critical pitchfork, the center initial stable state 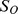 at the center becomes unstable, only the two new stable states
at the center becomes unstable, only the two new stable states 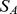 and
and 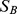 are left in the phase space. Super-critical pitchfork bifurcation represents a type of “second-order transition” in physics [36]. The difference between super-critical pitchfork bifurcation and sub-critical pitchfork bifurcation is that: super-critical pitchfork bifurcation represents one stable equilibrium splits into two stable equilibrium and a unstable equilibrium while sub-critical pitchfork bifurcation represents two unstable equilibrium and a stable equilibrium merge into an unstable equilibrium. Thus super-critical pitchfork bifurcation differs from the sub-critical one in that two new stable equilibrium
are left in the phase space. Super-critical pitchfork bifurcation represents a type of “second-order transition” in physics [36]. The difference between super-critical pitchfork bifurcation and sub-critical pitchfork bifurcation is that: super-critical pitchfork bifurcation represents one stable equilibrium splits into two stable equilibrium and a unstable equilibrium while sub-critical pitchfork bifurcation represents two unstable equilibrium and a stable equilibrium merge into an unstable equilibrium. Thus super-critical pitchfork bifurcation differs from the sub-critical one in that two new stable equilibrium 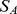 and
and 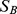 , when they appear, already have a significant distance away from the middle stable equilibrium
, when they appear, already have a significant distance away from the middle stable equilibrium 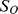 . But the two stable fixed points and the two unstable fixed points in sub-critical pitchfork with two saddle-node bifurcations are both symmetric in
. But the two stable fixed points and the two unstable fixed points in sub-critical pitchfork with two saddle-node bifurcations are both symmetric in 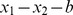 three dimensional space, while they are not symmetric in
three dimensional space, while they are not symmetric in 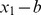 two dimensional space shown in Figure 3(B). These two bifurcations shown in Figure 3(A) and (B) are similar to the picture described in Waddington's epigenetic landscape [12].
two dimensional space shown in Figure 3(B). These two bifurcations shown in Figure 3(A) and (B) are similar to the picture described in Waddington's epigenetic landscape [12].
Figure 3. The dynamics of super-critical and sub-critical bifurcations for cell type switchings.
A: The phase diagram for changing the parameter 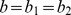 with
with  . B: The phase diagram for changing the parameter
. B: The phase diagram for changing the parameter 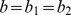 with
with 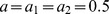 . C: The quantified dedifferentiation and differentiation landscape and pathways for continuous changing parameter
. C: The quantified dedifferentiation and differentiation landscape and pathways for continuous changing parameter 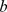 with
with 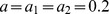 . D: The quantified dedifferentiation and differentiation landscape and pathways for continuous changing parameter
. D: The quantified dedifferentiation and differentiation landscape and pathways for continuous changing parameter 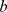 with
with 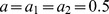 .
.
The phase diagrams shown in Figure 4(A), Figure 5(A) and Figure 6(A) are saddle-node bifurcations. A saddle-node bifurcation denotes a collision and disappearance of two equilibria rather than a pitchfork bifurcation [33], [35]. The saddle-node bifurcation is a first order phase transition [33], [34]. We can see that the initial valley 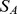 does not split into new valleys as the description of Waddingtons epigenetic landscape (a pitchfork bifurcation) [35]. New valleys
does not split into new valleys as the description of Waddingtons epigenetic landscape (a pitchfork bifurcation) [35]. New valleys 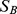 and
and 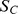 or
or 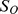 are born at somewhere far from the existing valley
are born at somewhere far from the existing valley 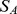 in the state space. It is anther way of creating or eliminating the valleys from the potential landscape besides a pitchfork bifurcation [35]. The cell moves to the new valley
in the state space. It is anther way of creating or eliminating the valleys from the potential landscape besides a pitchfork bifurcation [35]. The cell moves to the new valley 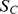 or
or 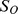 and
and 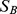 in sequence under fluctuations since its own valley disappears in another saddle-node bifurcation. We have already explored another form of bifurcation for cell fate network as self activation
in sequence under fluctuations since its own valley disappears in another saddle-node bifurcation. We have already explored another form of bifurcation for cell fate network as self activation  decreasing with
decreasing with  in our previous study [15], [17]. The phase diagram was drawn on the intrinsic potential landscape as the black lines in Figure 1(D) which is a sub-critical pitchfork [33], [34] at the phase transition point (
in our previous study [15], [17]. The phase diagram was drawn on the intrinsic potential landscape as the black lines in Figure 1(D) which is a sub-critical pitchfork [33], [34] at the phase transition point ( ).
).
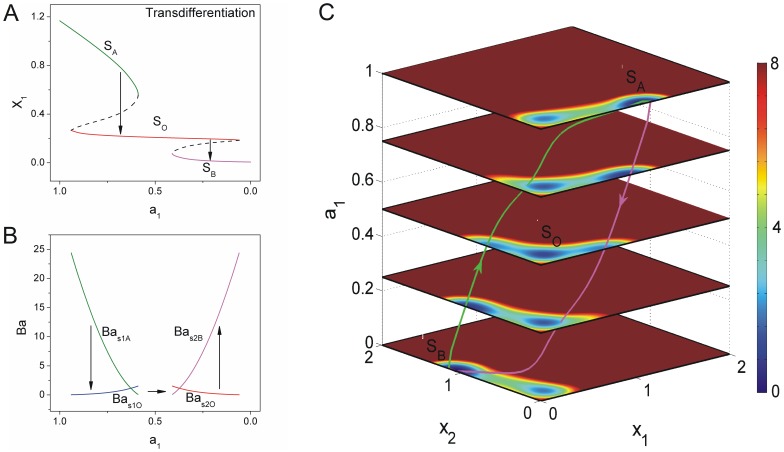
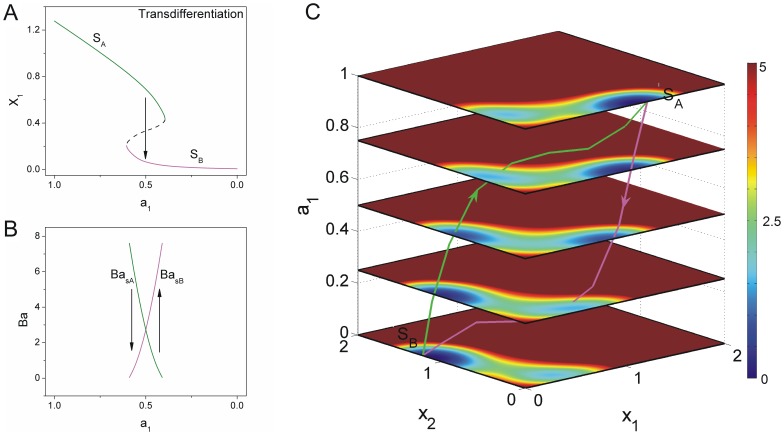
Figure 4. The dynamics of transdifferentiation undergoing an intermediate state.
A: The phase diagram for decreasing  induced the differentiated state
induced the differentiated state  to the other differentiated state
to the other differentiated state 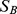 through the intermediate state
through the intermediate state 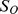 . (
. (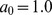 ,
, 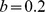 ) B: The barrier heights of the population landscape versus the parameter
) B: The barrier heights of the population landscape versus the parameter 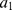 . C: The quantified transdifferentiation landscape and pathways for continuous changing parameter
. C: The quantified transdifferentiation landscape and pathways for continuous changing parameter 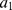 .
.
Figure 5. The dynamics of transdifferentiation undergoing a series of unstable states.
A: The phase diagram for decreasing 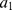 induced the differentiated state
induced the differentiated state 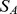 to the other differentiated state
to the other differentiated state 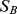 . (
. (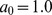 ,
, 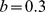 ) B: The barrier heights of the population landscape versus the parameter
) B: The barrier heights of the population landscape versus the parameter 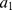 . C: The quantified transdifferentiation landscape and pathways for continuous changing parameter
. C: The quantified transdifferentiation landscape and pathways for continuous changing parameter 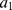 .
.
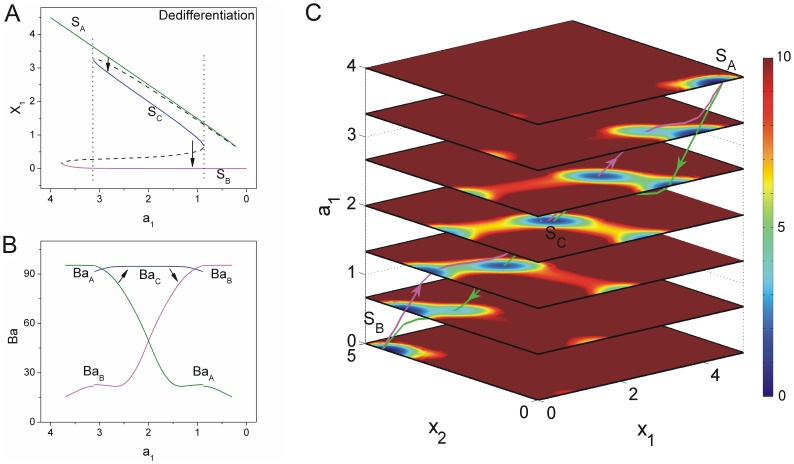
Figure 6. The dynamics of dedifferentiation undergoing a pluripotent state.
A: The phase diagram for decreasing 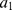 induced the differentiated state
induced the differentiated state 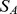 to the other differentiated state
to the other differentiated state 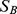 through the pluripotent state
through the pluripotent state 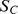 . (
. (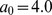 ,
, 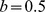 ) B: The barrier heights of the population landscape versus the parameter
) B: The barrier heights of the population landscape versus the parameter 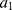 . C: The quantified dedifferentiation landscape and pathways for continuous changing parameter
. C: The quantified dedifferentiation landscape and pathways for continuous changing parameter 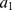 .
.
We would like to explore these mentioned non-equilibrium phase transition under fluctuations and gene regulation. We might monitor the expressions of the differentiation marker genes in time and obtain the correlation functions. The singularity of the self-correlation function indicates the first order phase transition (saddle-node bifurcation) and the continuity of that shows the second order phase transition [33], [34]. Thus we might distinguish these mechanisms of cell type switchings. We will explore these mechanisms of four bifurcations through our potential landscape theory in details below.
3. Intrinsic potential landscape
We obtained the intrinsic potential landscape 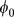 (see the section of Methods) with Lyapunov properties to quantify the global stability by solving the zero fluctuation limit Hamilton-Jacobi equation and the associated intrinsic flux velocity in the zero noise limit [37]. The population potential landscape of cell development can be obtained through the exploration of the underlying probability dynamics, by solving the Fokker-Planck diffusion equation (see the section of Methods) [15]. The population potential landscape
(see the section of Methods) with Lyapunov properties to quantify the global stability by solving the zero fluctuation limit Hamilton-Jacobi equation and the associated intrinsic flux velocity in the zero noise limit [37]. The population potential landscape of cell development can be obtained through the exploration of the underlying probability dynamics, by solving the Fokker-Planck diffusion equation (see the section of Methods) [15]. The population potential landscape 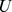 is related to steady state probability distribution
is related to steady state probability distribution 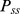 through
through 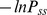 under fluctuations. The intrinsic potential landscape is quantified at the zero noise limit while the population potential landscape is quantified under finite fluctuations. Both show the global properties of the cell developmental process. Although intrinsic potential landscape gives less information (only at zero noise limit) about the network than population potential landscape, it can be used to quantify the global stability due to its nature of being a Lyapunov function [37]. We can illustrate two-dimensional potential landscape (the coordinates
under fluctuations. The intrinsic potential landscape is quantified at the zero noise limit while the population potential landscape is quantified under finite fluctuations. Both show the global properties of the cell developmental process. Although intrinsic potential landscape gives less information (only at zero noise limit) about the network than population potential landscape, it can be used to quantify the global stability due to its nature of being a Lyapunov function [37]. We can illustrate two-dimensional potential landscape (the coordinates 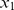 and
and 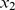 ) to one dimension. One dimensional cross section coordinate
) to one dimension. One dimensional cross section coordinate  links
links 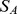 side minimum through
side minimum through 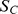 middle minimum to
middle minimum to 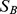 side minimum.
side minimum.  represents the gene expression levels,
represents the gene expression levels, 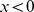 shows gene
shows gene 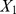 is dominant while
is dominant while 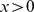 shows
shows 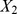 is dominant. If the self activation strength
is dominant. If the self activation strength  decreases relatively slowly, relative to gene regulation in development, the potential landscape can be viewed as a succession of one dimensional potential slice. Figure 1(D) shows the intrinsic potential landscape for normal cell differentiation development process from pluripotent state (
decreases relatively slowly, relative to gene regulation in development, the potential landscape can be viewed as a succession of one dimensional potential slice. Figure 1(D) shows the intrinsic potential landscape for normal cell differentiation development process from pluripotent state (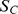 ) to differentiated states (
) to differentiated states (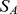 and
and 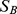 ) and the pluripotent reprogramming process from differentiated states (
) and the pluripotent reprogramming process from differentiated states (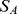 and
and 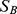 ) to pluripotent state (
) to pluripotent state (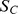 ). We can see the intrinsic potential landscape
). We can see the intrinsic potential landscape 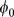 can be used to quantify the Waddington's picture and has almost the same shape with the population potential landscape [15].
can be used to quantify the Waddington's picture and has almost the same shape with the population potential landscape [15].
The red dash lines and the yellow solid line shown in Figure 1(D) schematically described the lineage reprogramming process: dedifferentiation and transdifferentiation, respectively. The dedifferentiation process shows that differentiated state 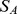 follows a step backward to a pluripotent state
follows a step backward to a pluripotent state 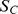 and then is induced to re-differentiate to another differentiated state
and then is induced to re-differentiate to another differentiated state 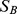 . While the transdifferentiation process shows that differentiated state
. While the transdifferentiation process shows that differentiated state 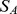 converts directly to another differentiated state
converts directly to another differentiated state 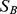 through certain intermediate stable state or not. Much work has been done on lineage reprogramming and progress has been made in manipulating the key regulator gene to convert cell lineages [3]–[6], [8], [9]. The understanding of the underlying mechanism is still challenging. We will discuss the possible mechanisms of these lineage reprogramming process in detail using this simple gene regulatory circuit.
through certain intermediate stable state or not. Much work has been done on lineage reprogramming and progress has been made in manipulating the key regulator gene to convert cell lineages [3]–[6], [8], [9]. The understanding of the underlying mechanism is still challenging. We will discuss the possible mechanisms of these lineage reprogramming process in detail using this simple gene regulatory circuit.
We can see that when self activation 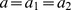 is strong with higher mutual repression
is strong with higher mutual repression 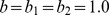 , the valley of the central pluripotent state
, the valley of the central pluripotent state 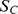 is much deeper and the system is attracted to this valley shown in Figure 1(D). As the strength of self activation
is much deeper and the system is attracted to this valley shown in Figure 1(D). As the strength of self activation  decreases, the valleys of side differentiated attractors
decreases, the valleys of side differentiated attractors 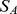 and
and 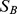 become deeper while the central pluripotent state
become deeper while the central pluripotent state 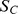 becomes weaker. When the strength of self activation
becomes weaker. When the strength of self activation  approaching to zero, the central state
approaching to zero, the central state 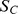 becomes a ridge and therefore it is not stable while the side states
becomes a ridge and therefore it is not stable while the side states 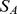 and
and 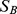 become stable. This result of intrinsic potential landscape with global Lyapunov property of global stability shows the similar mechanism with the result obtained from exploring the population potential landscape [15]–[17].
become stable. This result of intrinsic potential landscape with global Lyapunov property of global stability shows the similar mechanism with the result obtained from exploring the population potential landscape [15]–[17].
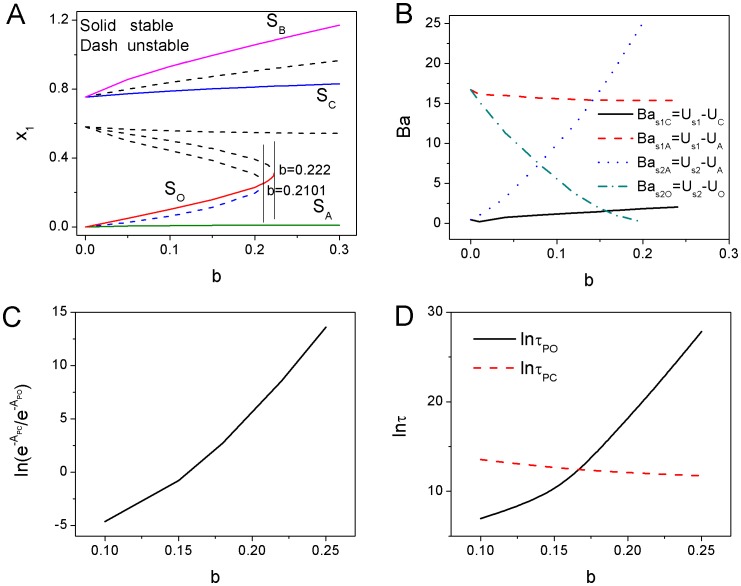
In order to quantify the stability of each state from the potential landscape topography, we can apply barrier height to measure the relative weights between different stable states. We showed barrier height of intrinsic potential landscape versus the strength of self activation  in Figure 7A. We set
in Figure 7A. We set 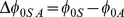 and
and 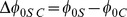 , where
, where 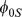 is the value of the intrinsic potential landscape at the saddle point between state
is the value of the intrinsic potential landscape at the saddle point between state 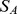 and state
and state 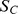 ,
, 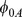 represents the minimum value of the intrinsic potential landscape at differentiated state
represents the minimum value of the intrinsic potential landscape at differentiated state 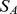 while
while 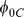 represents the value of that at pluripotent state
represents the value of that at pluripotent state 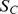 . Barrier height
. Barrier height 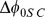 decreases as
decreases as  decreases, and state
decreases, and state 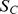 vanished after the phase transition critical point
vanished after the phase transition critical point 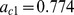 , where the system transits from three stable states (
, where the system transits from three stable states (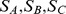 ) to two stable states (
) to two stable states (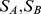 ). It implies that the attraction of state
). It implies that the attraction of state 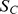 becomes shallower. Barrier height of
becomes shallower. Barrier height of 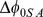 increases first, then decreases. It shows that the attraction of the differentiated state
increases first, then decreases. It shows that the attraction of the differentiated state 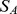 (
(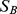 ) becomes deeper first, then becomes weaker after another critical point around
) becomes deeper first, then becomes weaker after another critical point around 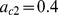 . So differentiated states
. So differentiated states 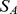 and
and 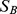 at
at 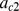 are more stable. Figure 7B shows the intrinsic potential barrier height
are more stable. Figure 7B shows the intrinsic potential barrier height 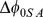 has positive correlation with the population potential barrier height
has positive correlation with the population potential barrier height 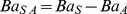 under the diffusion coefficient
under the diffusion coefficient 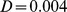 and
and 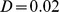 , where
, where 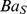 is the value of the population potential landscape at the saddle point between state
is the value of the population potential landscape at the saddle point between state 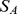 and state
and state 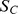 ,
, 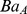 represents the minimum value of the population potential landscape at the differentiated state
represents the minimum value of the population potential landscape at the differentiated state 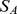 . The mean first passage time (MFPT) is useful to characterize the global stability if stochastic fluctuations are the dominant source of noise since it measures how the system can globally communicate from one state to another. The intrinsic barrier height
. The mean first passage time (MFPT) is useful to characterize the global stability if stochastic fluctuations are the dominant source of noise since it measures how the system can globally communicate from one state to another. The intrinsic barrier height 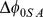 and the corresponding MFPT have the correlation of
and the corresponding MFPT have the correlation of 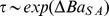 shown in Figure 7(C) with diffusion coefficient
shown in Figure 7(C) with diffusion coefficient 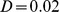 .
.
Figure 7. The barrier height, escape time and dissipation rate for different self activation strength  with mutual repression strength
with mutual repression strength 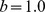 under fluctuations.
under fluctuations.
A: The intrinsic barrier height 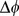 versus
versus  . B: The intrinsic barrier height
. B: The intrinsic barrier height 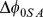 versus the population barrier height
versus the population barrier height 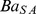 in
in 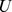 for
for 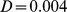 and
and 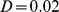 . C: The escape time
. C: The escape time 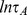 from the valley
from the valley 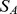 versus the intrinsic barrier height
versus the intrinsic barrier height 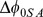 . D: The dissipation rate versus the decreasing parameter
. D: The dissipation rate versus the decreasing parameter  .
.
A cell is a non-equilibrium open system with exchanges of energy and information from the outside environment. This leads to dissipation which is determined by both potential landscape and flux. The dissipation can give another global physical characterization of the non-equilibrium system. Non-equilibrium system dissipates both energy and entropy in steady state, where the entropy production rate is equal to heat dissipation rate. The heat dissipation rate is formulated as 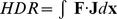 [13], [37]–[40], which increases first then decreases as self activation
[13], [37]–[40], which increases first then decreases as self activation  decreases as shown in Figure 7(D). This indicates that larger area of the dominant probability flux leads to more heat dissipation because the system needs to consume more energy [37]. The system consumes more energy in the process of the development with three dominant states while the system consumes less at the beginning of cell development and at the end of cell development with less states. The heat dissipation rate provides a global characterization of cell development. It is intimately related to the robustness of the underlying network.
decreases as shown in Figure 7(D). This indicates that larger area of the dominant probability flux leads to more heat dissipation because the system needs to consume more energy [37]. The system consumes more energy in the process of the development with three dominant states while the system consumes less at the beginning of cell development and at the end of cell development with less states. The heat dissipation rate provides a global characterization of cell development. It is intimately related to the robustness of the underlying network.
II. The mechanisms of cell type switchings
1. Stochastic Fluctuations. The cell type switchings at a given stage of development with different symmetric self activation  at fixed mutual repression
at fixed mutual repression 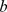
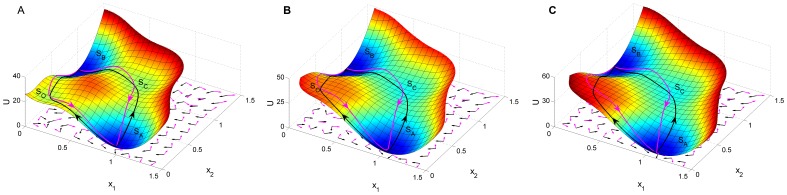
The stochastic or inductive cell development can often be influenced by the external environment. We showed the paths of state transitions in cell development on the intrinsic potential landscapes for different self activation  with fixed mutual repression
with fixed mutual repression 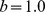 due to stochastic fluctuations shown in Figure 8. We can see the green lines represent the reprogramming or dedifferentiation paths from differentiated state
due to stochastic fluctuations shown in Figure 8. We can see the green lines represent the reprogramming or dedifferentiation paths from differentiated state  or
or  to pluripotent state
to pluripotent state  while the red lines represent the differentiation paths from pluripotent state
while the red lines represent the differentiation paths from pluripotent state 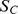 to differentiated state
to differentiated state 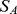 or
or 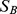 shown in Figure 8(A)(B) when self activation
shown in Figure 8(A)(B) when self activation  is relative stronger and the system has three stable states. Its worth pointing out that a green path from differentiated state
is relative stronger and the system has three stable states. Its worth pointing out that a green path from differentiated state 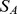 to pluripotent state
to pluripotent state 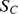 connected to a red path from pluripotent state
connected to a red path from pluripotent state 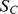 to another differentiated state
to another differentiated state 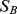 can provide a possible mechanism of the process of dedifferentiation first and then redifferentiation shown in Figure 8(A)(B). We also showed that both the green and the red lines represent the transdifferentiation paths from one differentiated state to another differentiated state shown in Figure 8(C)(D) when self activation
can provide a possible mechanism of the process of dedifferentiation first and then redifferentiation shown in Figure 8(A)(B). We also showed that both the green and the red lines represent the transdifferentiation paths from one differentiated state to another differentiated state shown in Figure 8(C)(D) when self activation  is relative weaker and the system has only two stable states, just as a toggle switch. The intrinsic flux velocity (
is relative weaker and the system has only two stable states, just as a toggle switch. The intrinsic flux velocity (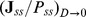 ) represented by purple arrows are perpendicular to the negative gradient of intrinsic potential (
) represented by purple arrows are perpendicular to the negative gradient of intrinsic potential (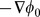 ) represented by the white arrows in Figure 8 (see the section of Methods).
) represented by the white arrows in Figure 8 (see the section of Methods).
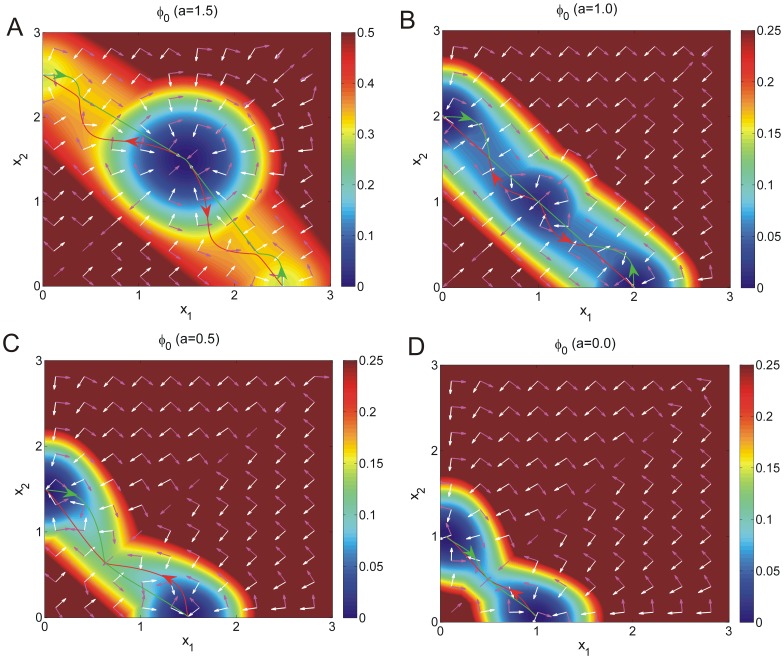
Figure 8. The paths of cell type switchings with different self activation strength  .
.
The paths of differentiation (A,B), dedifferentiation (A,B) and transdifferentiation (C,D) for different  in zero-limit fluctuations on the intrinsic potential
in zero-limit fluctuations on the intrinsic potential  . Purple arrows represent the intrinsic flux velocity (
. Purple arrows represent the intrinsic flux velocity (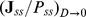 ) while the white arrows represent the negative gradient of intrinsic potential (
) while the white arrows represent the negative gradient of intrinsic potential (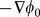 )).
)).
The cell type switchings processes at a given stage of development with symmetric changing mutual repression 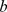 while fixing self activation
while fixing self activation 
We considered the potential landscape changing under fluctuations with varying mutual repression parameter 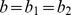 at a given state with fixed self activation
at a given state with fixed self activation 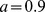 . Figure 9(A) shows the phase diagram for changing mutual repression strength
. Figure 9(A) shows the phase diagram for changing mutual repression strength 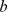 . We can see that when mutual repression strength
. We can see that when mutual repression strength 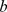 decreases below
decreases below 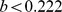 , a new stable state
, a new stable state 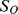 emerges. This is an intermediate stable state between differentiated states
emerges. This is an intermediate stable state between differentiated states 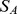 and
and 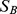 . There are lower expressions of gene
. There are lower expressions of gene 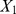 and
and 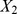 in state
in state  . Dashed lines represent the saddle point between stable states. As mutual repression
. Dashed lines represent the saddle point between stable states. As mutual repression 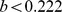 , the system has all four states
, the system has all four states 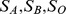 and
and 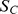 . The fluctuations in the system can enable stochastic switching among the stable states. Note that smaller mutual repression strength
. The fluctuations in the system can enable stochastic switching among the stable states. Note that smaller mutual repression strength 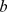 here represents larger repression effect since the parameter
here represents larger repression effect since the parameter  is in the numerator of an inhibition term with a positive sign. Smaller
is in the numerator of an inhibition term with a positive sign. Smaller 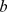 , that is larger repression, leads the system towards intermediate state
, that is larger repression, leads the system towards intermediate state 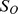 , while larger
, while larger 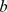 which represents smaller repression effect leads the system towards pluripotent state
which represents smaller repression effect leads the system towards pluripotent state 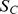 .
.
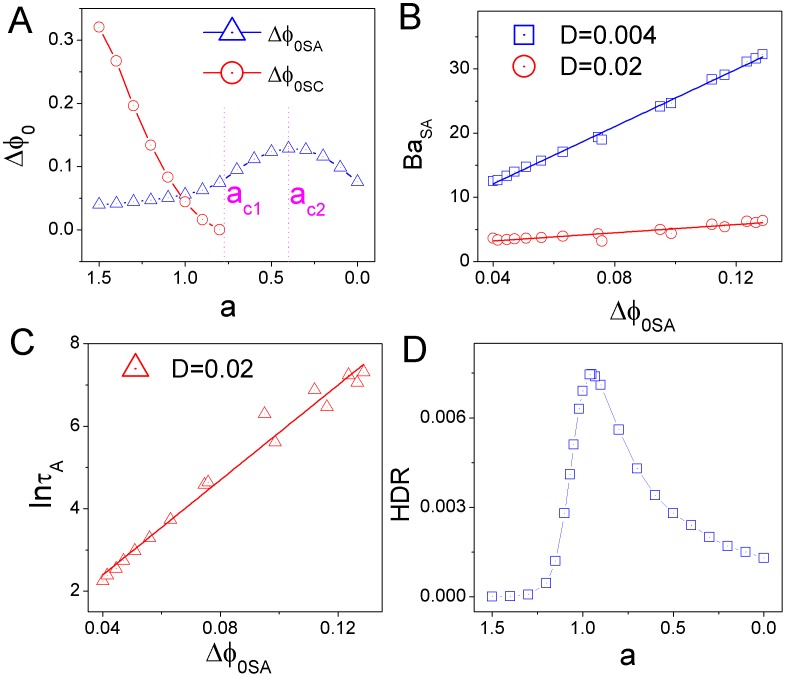
Figure 9. The phase diagram, barrier height, probability of the dominant path and mean first passaging time for different mutual repression strength 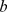 .
.
A: The phase diagram for changing mutual repression strength 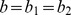 with
with 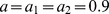 . B: The barrier heights versus the parameter
. B: The barrier heights versus the parameter 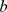 . C: The probability of the dominant path through the progenitor cell state
. C: The probability of the dominant path through the progenitor cell state 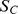 divided that of the path through the intermediate state
divided that of the path through the intermediate state 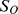 versus the inhibition strength
versus the inhibition strength 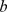 . D: The mean first passaging time through the two paths versus the inhibition strength
. D: The mean first passaging time through the two paths versus the inhibition strength 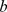 .
.
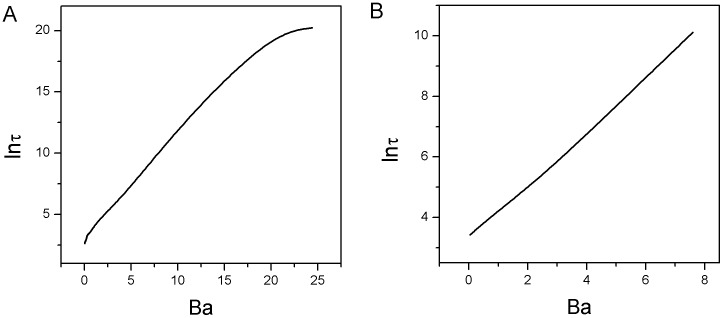
Any given cell may take a completely different route back to their pluripotent state in principle. Certain sequence of stages can emerge in the process of cell type switchings [4]. In experiments, if there are several pathways, one can collect the statistics and find out the relative probabilities of each path, giving the quantification of the path weights. In modeling, path integral weights are calculated by the action of the system analogous to the classical mechanical systems which determine the likelihood of one path versus the other. We often used the dominant paths with the largest weights to represent the major pathways. We showed four dominant biological paths on the corresponding population landscape with different mutual repression strength 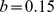 (A),
(A), 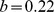 (B),
(B), 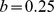 (C) in Figure 10. These processes are fluctuation or induction induced transition. The purple lines represent the paths from state
(C) in Figure 10. These processes are fluctuation or induction induced transition. The purple lines represent the paths from state  to state
to state 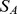 while the black lines represent the paths from state
while the black lines represent the paths from state 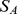 to state
to state 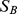 [15], [37]. We can see there are two dominant paths with the same color for transdifferentiation from a certain differentiated state to another differentiated state in each sub figures, one path is through intermediate state
[15], [37]. We can see there are two dominant paths with the same color for transdifferentiation from a certain differentiated state to another differentiated state in each sub figures, one path is through intermediate state 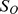 while the other path is through pluripotent state
while the other path is through pluripotent state 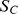 . We also found the two different colored development paths between each two states follow quite different routes. It is irreversible between the forward dedifferentiation and the backward dedifferentiation paths through the pluripotent state
. We also found the two different colored development paths between each two states follow quite different routes. It is irreversible between the forward dedifferentiation and the backward dedifferentiation paths through the pluripotent state 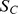 , and between the two transdifferentiation paths through intermediate state
, and between the two transdifferentiation paths through intermediate state 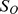 or without an explicit intermediate state. This illustrates the irreversibility of the developmental paths which can be verified from the ongoing and future dynamical experiments.
or without an explicit intermediate state. This illustrates the irreversibility of the developmental paths which can be verified from the ongoing and future dynamical experiments.
Figure 10. The flux on the population potential landscape.
The flux on the population potential landscape with 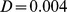 . Purple arrows represent the flux (
. Purple arrows represent the flux (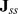 ) while the black arrows represent the negative gradient of population potential landscape (
) while the black arrows represent the negative gradient of population potential landscape (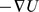 )) for
)) for 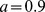 ,
, 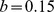 (A),
(A), 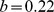 (B),
(B), 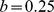 (C). The black lines represent the pathways from state
(C). The black lines represent the pathways from state  to state
to state  while the purple lines represent the pathways from state
while the purple lines represent the pathways from state 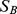 to state
to state 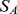 .
.
The path weight represents the probability of each route for cell type switchings. It can be used to predict the probability of different routes for cell type switchings. The path probability can be obtained by the action 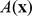 for cell development (See methods for details). We labeled
for cell development (See methods for details). We labeled 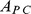 as the action of the path through state
as the action of the path through state 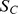 , and
, and 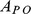 as the action of the path through state
as the action of the path through state 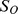 . Figure 9(C) showed the logarithm of dedifferentiation path probability through state
. Figure 9(C) showed the logarithm of dedifferentiation path probability through state 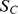 divided that of transdifferentiation through state
divided that of transdifferentiation through state 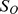 decreases as mutual repression strength
decreases as mutual repression strength 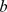 becomes weaker. This showed that the dedifferentiation path probability through state
becomes weaker. This showed that the dedifferentiation path probability through state 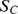 decreases or the transdifferentiation path probability through state
decreases or the transdifferentiation path probability through state 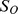 increases as mutual repression strength becomes weaker.
increases as mutual repression strength becomes weaker.
The purple arrows represent the direction of the probability flux 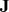 while the black arrows represent the direction of the negative gradient of population potential landscape
while the black arrows represent the direction of the negative gradient of population potential landscape 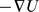 shown in Figure 10. We can see the flux is almost perpendicular to the negative gradient of the population potential landscape [13], [37]. The dynamics of transdifferentiation and dedifferentiation processes are determined by both gradient landscape and probability flux. Probability flux provides a curling force breaking the detailed balance, and leads the system to stay at the non-equilibrium state. The gradient force attracts the system into stable valleys. The potential landscape and flux both direct the processes of cell type switching. Flux can lead a system to move on even a relatively flat landscape, e.g., the limit cycle attractor, thus “flux-directed differentiation” and “down-hill-directed differentiation (Waddington)” both can occur in cell development. “down-hill-directed differentiation (Waddington)” leads to the exponential waiting of barrier crossing while “flux-directed differentiation” gives a much more precise timing. Flux also can lead the biological paths of cell type switchings to be deviated from the paths obtained by steepest descent gradient, and the corresponding paths of cell type switchings are irreversible. We would like to point out additional flux can emerge from epigenetics of slow (non-adiabatic) transcription and translation regulations [41] often encountered in eukaryotic cells. The flux generated by the slow time scales can lead to the new mechanism of differentiation and reprogramming [31], [42]. The competition of barrier crossing and slow binding can lead to optimal speed of cell type switching. [31], [42], [43].
shown in Figure 10. We can see the flux is almost perpendicular to the negative gradient of the population potential landscape [13], [37]. The dynamics of transdifferentiation and dedifferentiation processes are determined by both gradient landscape and probability flux. Probability flux provides a curling force breaking the detailed balance, and leads the system to stay at the non-equilibrium state. The gradient force attracts the system into stable valleys. The potential landscape and flux both direct the processes of cell type switching. Flux can lead a system to move on even a relatively flat landscape, e.g., the limit cycle attractor, thus “flux-directed differentiation” and “down-hill-directed differentiation (Waddington)” both can occur in cell development. “down-hill-directed differentiation (Waddington)” leads to the exponential waiting of barrier crossing while “flux-directed differentiation” gives a much more precise timing. Flux also can lead the biological paths of cell type switchings to be deviated from the paths obtained by steepest descent gradient, and the corresponding paths of cell type switchings are irreversible. We would like to point out additional flux can emerge from epigenetics of slow (non-adiabatic) transcription and translation regulations [41] often encountered in eukaryotic cells. The flux generated by the slow time scales can lead to the new mechanism of differentiation and reprogramming [31], [42]. The competition of barrier crossing and slow binding can lead to optimal speed of cell type switching. [31], [42], [43].
It is worth noting that even though state 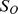 disappears in Figure 10(C), there still exist transdifferentiation paths through a series of indeterminate states near
disappears in Figure 10(C), there still exist transdifferentiation paths through a series of indeterminate states near  position. This provides the possible mechanism of two ways of lineage reprogramming. We labeled the saddle point between state
position. This provides the possible mechanism of two ways of lineage reprogramming. We labeled the saddle point between state 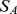 and state
and state 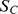 as
as 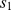 while the saddle point between state
while the saddle point between state 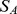 and state
and state 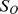 as
as 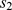 . In Figure 9(B), we can see barrier height
. In Figure 9(B), we can see barrier height 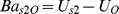 measuring the stability of intermediate state
measuring the stability of intermediate state 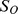 increases and barrier height
increases and barrier height 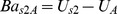 measuring the degree of difficulty for transition from state
measuring the degree of difficulty for transition from state 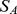 to state
to state 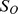 decreases dramaticlly as mutual repression strength
decreases dramaticlly as mutual repression strength 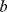 decreases, where
decreases, where 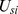 is the potential value at saddle point
is the potential value at saddle point 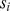 and
and 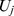 is the minimum potential value at valley
is the minimum potential value at valley 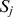 . This implies that state
. This implies that state 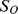 becomes more stable and robust as
becomes more stable and robust as 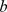 decreases.
decreases.
We also can explore MFPT by 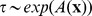 [44]. Importantly, MFPT is also useful to characterize stability of the network for changing the regulations represented by the self activation
[44]. Importantly, MFPT is also useful to characterize stability of the network for changing the regulations represented by the self activation  and mutual repression
and mutual repression 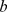 under a small but fixed fluctuations (during the regulation changes or induction) mimicking the real environments. Figure 9(D) showed MFPT along dedifferentiation and transdifferentiation paths versus mutual repression strength
under a small but fixed fluctuations (during the regulation changes or induction) mimicking the real environments. Figure 9(D) showed MFPT along dedifferentiation and transdifferentiation paths versus mutual repression strength 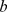 . We can see that the transdifferentiation path through state
. We can see that the transdifferentiation path through state 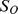 becomes more preferred than dedifferentiation path through state
becomes more preferred than dedifferentiation path through state 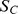 , and MFPT becomes shorter for transdifferentiation path through state
, and MFPT becomes shorter for transdifferentiation path through state 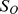 as mutual repression strength decreases. In other words, transdifferentiation process is easier (harder) and the dedifferentiation process is harder (easier) when mutual repression is weaker (stronger).
as mutual repression strength decreases. In other words, transdifferentiation process is easier (harder) and the dedifferentiation process is harder (easier) when mutual repression is weaker (stronger).
2. Gene Regulation. Decreasing self activation 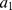 and increasing self activation
and increasing self activation 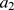 induce the transdifferentiation process from state
induce the transdifferentiation process from state 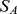 to state
to state 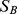 with lower mutual repression strength
with lower mutual repression strength 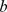
The instructive change of landscape via varying regulation strengths is another important mechanism in action for cell development. Down regulating the lineage specific gene for initial primary differentiated cell and up regulating the lineage specific gene for final target differentiated cell can induce transdifferentiation or dedifferentiation. We explored this mechanism below with changes in decreasing self activation 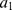 for gene
for gene 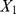 and increasing self activation
and increasing self activation 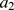 for gene
for gene 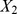 .
.
Self activation strength can be set for describing the time evolution of the self activation regulation parameters as: 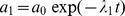 [25] which continuously decreases in time (down-regulates cell specific gene
[25] which continuously decreases in time (down-regulates cell specific gene 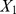 for differentiated state
for differentiated state 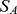 ) and another self activation regulation strength
) and another self activation regulation strength 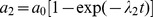 which continuously increases in time (up-regulates cell specific gene
which continuously increases in time (up-regulates cell specific gene 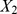 for target differentiated state
for target differentiated state 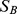 ) in cell developmental process due to the influences of the regulations of other genes.
) in cell developmental process due to the influences of the regulations of other genes.  and
and 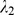 are the rates for the decrease of self activations
are the rates for the decrease of self activations 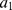 and
and 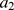 . We assumed the same value of
. We assumed the same value of 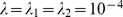 for simplicity for the latter calculations. At this value of
for simplicity for the latter calculations. At this value of 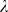 , self activation strength
, self activation strength 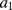 and
and 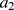 decrease relatively slowly compared with regulation dynamics of gene
decrease relatively slowly compared with regulation dynamics of gene 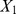 and
and 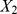 . Thus the dynamics is a slow non-equilibrium relaxation process.
. Thus the dynamics is a slow non-equilibrium relaxation process. 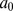 is the scaled value of self activation
is the scaled value of self activation 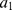 and
and 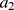 [25].
[25].
We explored the transdifferentiation mechanism below with decreasing self activation 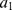 and increasing self activation
and increasing self activation 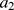 with lower mutual repression strength
with lower mutual repression strength 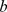 . Figure 4(A) shows the saddle-node bifurcation phase diagram for decreasing self activation strength
. Figure 4(A) shows the saddle-node bifurcation phase diagram for decreasing self activation strength 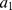 with lower
with lower 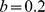 and smaller
and smaller 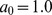 . Figure 4(B) shows barrier height versus decreasing self activation
. Figure 4(B) shows barrier height versus decreasing self activation 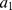 with
with 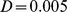 . We defined the saddle point between state
. We defined the saddle point between state 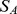 and state
and state 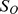 as
as 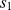 , and the saddle point between state
, and the saddle point between state 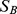 and state
and state 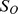 as
as 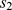 . Barrier height is defined as:
. Barrier height is defined as: 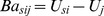 , where
, where 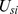 is the potential value of the
is the potential value of the  saddle point, and
saddle point, and 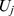 is the minimum at valley
is the minimum at valley 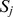 . Barrier height can quantify the degree of global robust and stability at a valley. We can see the cell stays at the monostable differentiated state
. Barrier height can quantify the degree of global robust and stability at a valley. We can see the cell stays at the monostable differentiated state 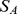 at the beginning of the transdifferentiation. As self activation
at the beginning of the transdifferentiation. As self activation 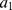 decreases, an intermediate state
decreases, an intermediate state 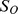 emerges. Valley
emerges. Valley 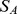 is much deeper than valley
is much deeper than valley 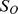 due to barrier height
due to barrier height 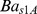 of valley
of valley 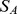 being higher than that of
being higher than that of 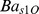 . It means the differentiated state
. It means the differentiated state 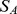 is more preferred and more attractive than intermediate state
is more preferred and more attractive than intermediate state 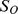 . The system is preferred to stay at state
. The system is preferred to stay at state 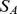 with gene
with gene 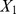 being dominant. As self activation strength
being dominant. As self activation strength 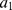 becomes weaker and self activation
becomes weaker and self activation 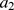 becomes stronger, the valley of state
becomes stronger, the valley of state 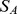 becomes shallower while the valley of state
becomes shallower while the valley of state 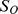 becomes deeper. Then, the valley of state
becomes deeper. Then, the valley of state 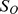 is more attractive than that of state
is more attractive than that of state 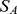 since barrier height
since barrier height 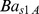 is lower than barrier height
is lower than barrier height 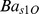 , and gene
, and gene 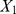 and
and 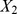 are both at lower expressions. After state
are both at lower expressions. After state 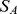 disappears, the cell is driven into intermediate state
disappears, the cell is driven into intermediate state 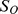 . As self activation strength
. As self activation strength 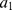 decreases further, the other differentiated state
decreases further, the other differentiated state 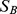 emerges, and barrier height
emerges, and barrier height 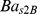 becomes higher than barrier height
becomes higher than barrier height 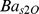 . Finally, the cell is forced into state
. Finally, the cell is forced into state 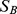 . This process interprets the mechanism of transdifferentiation from state
. This process interprets the mechanism of transdifferentiation from state 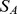 to state
to state 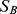 through an intermediate state
through an intermediate state 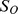 .
.
The above results showed the dynamics at certain stage of transdifferentiation. We can also explore the continuous dynamics controlled by the set of equations below:
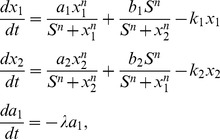 |
(2) |
where 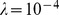 and
and 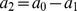 . The continuous time dynamics of down-regulating gene
. The continuous time dynamics of down-regulating gene 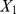 and up-regulating gene
and up-regulating gene 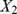 is shown in Figure 4(C) with
is shown in Figure 4(C) with 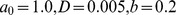 using Eq.2. We obtained the transdifferentiation paths on the four dimensional potential landscape. The purple path is from state
using Eq.2. We obtained the transdifferentiation paths on the four dimensional potential landscape. The purple path is from state 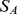 to state
to state 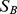 while the green path is the reverse transition both through intermediate state
while the green path is the reverse transition both through intermediate state 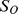 . It implies that the system with small mutual repression strength
. It implies that the system with small mutual repression strength  (large inhibition) prefers the transdifferentiation path through intermediate state
(large inhibition) prefers the transdifferentiation path through intermediate state 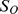 . Although transdifferentiation process does not seem to occur naturally, it has been observed in many experiments. For example, the exocrine cells in adult mice can transdifferentiate into
. Although transdifferentiation process does not seem to occur naturally, it has been observed in many experiments. For example, the exocrine cells in adult mice can transdifferentiate into 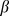 -cells using defined factors for direct reprogramming without passing through a pluripotent state but through an unnatural intermediate state [4], [8], [9].
-cells using defined factors for direct reprogramming without passing through a pluripotent state but through an unnatural intermediate state [4], [8], [9].
Figure 5(A) shows the phase diagram of saddle-node bifurcation under 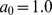 and mutual repression
and mutual repression 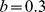 . Figure 5(B) shows barrier height versus self activation
. Figure 5(B) shows barrier height versus self activation 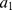 with
with  . We defined barrier height as
. We defined barrier height as 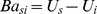 , where
, where 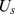 is the potential value of saddle point
is the potential value of saddle point  between state
between state  and state
and state  , and
, and 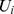 is the potential value at state
is the potential value at state 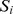 . Figure 5(C) shows the paths and the landscape for continuous dynamics using Eq.2 with
. Figure 5(C) shows the paths and the landscape for continuous dynamics using Eq.2 with 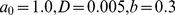 . We can see the cell stays at differentiated state
. We can see the cell stays at differentiated state 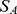 with higher barrier height
with higher barrier height 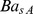 at first, then the landscape valley tilts the cell from state
at first, then the landscape valley tilts the cell from state 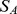 to state
to state 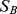 , barrier height
, barrier height 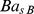 becomes higher than barrier
becomes higher than barrier 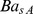 and the valley of state
and the valley of state 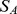 eventually disappears. Finally, valley
eventually disappears. Finally, valley 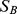 becomes deeper. The weights of these two valleys exchange at the end of transdifferentiation process [35]. This process interprets the mechanism of transdifferentiation from state
becomes deeper. The weights of these two valleys exchange at the end of transdifferentiation process [35]. This process interprets the mechanism of transdifferentiation from state 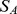 to state
to state 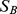 directly without through a specific intermediate state but through a series of indeterminate states. This result can be used to explain the mechanism that the enforced expressions of
directly without through a specific intermediate state but through a series of indeterminate states. This result can be used to explain the mechanism that the enforced expressions of 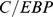 with endogenous
with endogenous  can reprogram B cell into macrophages [4], [5]. B cell specific marker is
can reprogram B cell into macrophages [4], [5]. B cell specific marker is 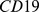 while the macrophage specific genes is
while the macrophage specific genes is 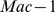 . The gene regulatory circuit is shown in Figure 2(B). B cell commitment factor
. The gene regulatory circuit is shown in Figure 2(B). B cell commitment factor 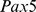 can up-regulate many B cell specific genes (such as
can up-regulate many B cell specific genes (such as 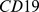 ). The macrophage commitment factor
). The macrophage commitment factor 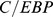 can up-regulate many macrophage cell specific genes (such as
can up-regulate many macrophage cell specific genes (such as 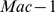 ) and down-regulate B cell specific genes (such as
) and down-regulate B cell specific genes (such as 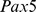 ) [4], [5]. Transcription factor
) [4], [5]. Transcription factor 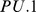 is needed in the process of transdifferentiation. The gene
is needed in the process of transdifferentiation. The gene 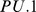 has the property of auto-activation. Mikkola's work indicated that
has the property of auto-activation. Mikkola's work indicated that 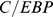 and
and 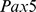 act in mutual antagonisms [5], [45]. The dashed lines for the auto-activation indicate uncertainty in Figure 2(B). Thus we can reduce the gene regulatory circuit in to two markers of
act in mutual antagonisms [5], [45]. The dashed lines for the auto-activation indicate uncertainty in Figure 2(B). Thus we can reduce the gene regulatory circuit in to two markers of 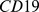 and
and 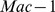 similar as our mutual antagonistic and self activation
similar as our mutual antagonistic and self activation 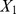 and
and 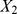 [4], [5].
[4], [5]. 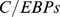 inhibit B cell commitment transcription factor (B cell-specific genes) which down-regulates B cell marker
inhibit B cell commitment transcription factor (B cell-specific genes) which down-regulates B cell marker 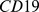 (
(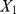 ) in B cell, and co-activate macrophage specific genes which up-regulates its target marker
) in B cell, and co-activate macrophage specific genes which up-regulates its target marker 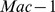 (
(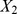 ) in macrophages. B cells pass through a series of indeterminate states with lower expressions of B cell-specific genes
) in macrophages. B cells pass through a series of indeterminate states with lower expressions of B cell-specific genes 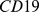 (
(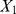 ) and macrophage-specific genes
) and macrophage-specific genes 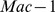 (
(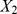 ), which does not seem to undergo an initial dedifferentiation [4], [5].
), which does not seem to undergo an initial dedifferentiation [4], [5].
Figure 11(A)(B) show the logarithms of MFPT versus barrier heights using the same parameters in Figure 4(B) and Figure 5(B) respectively. We can see the time spent from one state to another and barrier height have the relationship as: 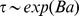 . It implies that the harder the system is out from one valley with higher barrier height, the longer the escape time is.
. It implies that the harder the system is out from one valley with higher barrier height, the longer the escape time is.
Figure 11. Mean first passage time versus barrier height with different mutual repression strength 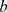 .
.
A: The logarithm of the mean first passage time (MFPT) versus the barrier heights according to Figure 4(B). B: The logarithm of the mean first passage time (MFPT) versus the barrier heights according to Figure 5(B).
We also explored the behavior for the system when regulation is not symmetrical, not only for the case when self-activation strength 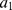 is not equal to self-activation strength
is not equal to self-activation strength 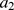 , but also for the case when self-activation strength
, but also for the case when self-activation strength 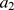 is not changing synchronously with self-activation strength
is not changing synchronously with self-activation strength 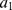 . In Figure S2 in File S1, we showed the potential landscape of continuous dynamics with self-activation strength
. In Figure S2 in File S1, we showed the potential landscape of continuous dynamics with self-activation strength 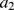 set as a constant (
set as a constant (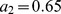 ) while the self-activation strength
) while the self-activation strength 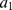 continuously decreases. The other parameters are diffusion coefficient
continuously decreases. The other parameters are diffusion coefficient 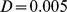 , mutual inhibition strength
, mutual inhibition strength 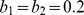 . We can see the cell may stay at differentiated state
. We can see the cell may stay at differentiated state  at first since the basin of differentiated state
at first since the basin of differentiated state  is lower than differentiated state
is lower than differentiated state 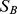 when self-activation strength
when self-activation strength 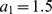 , then the landscape basin tilts the cell from the differentiated state
, then the landscape basin tilts the cell from the differentiated state 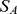 to the intermediate state
to the intermediate state 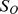 , and the basin of state
, and the basin of state 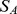 eventually disappears. Finally, the basin
eventually disappears. Finally, the basin 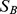 becomes deeper, and the system shifts from the intermediate state
becomes deeper, and the system shifts from the intermediate state 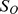 to the differentiated state
to the differentiated state 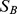 . The green path is from state
. The green path is from state  to state
to state  while the purple path is the reverse transition from state
while the purple path is the reverse transition from state  to state
to state  both through the intermediate state
both through the intermediate state 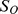 . In Figure S3 in File S1, we showed the potential landscape of continuous dynamics with self-activation strength
. In Figure S3 in File S1, we showed the potential landscape of continuous dynamics with self-activation strength 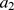 set as a constant (
set as a constant (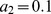 ) while the self-activation strength
) while the self-activation strength 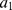 continuously decreases. The other parameters are diffusion coefficient
continuously decreases. The other parameters are diffusion coefficient 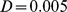 , mutual inhibition strength
, mutual inhibition strength 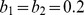 . We can see the cell may stay at differentiated state
. We can see the cell may stay at differentiated state  at first when self-activation strength
at first when self-activation strength 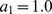 , then the cell shifts from the differentiated state
, then the cell shifts from the differentiated state 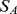 to the intermediate state
to the intermediate state 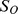 , and eventually the basin of state
, and eventually the basin of state 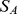 disappears. The green path is from state
disappears. The green path is from state 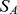 to state
to state 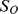 while the purple path is the reverse transition from state
while the purple path is the reverse transition from state 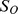 to state
to state 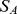 . Here, intermediate state
. Here, intermediate state 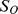 may represent the partially reprogrammed cells.
may represent the partially reprogrammed cells.
Decreasing self activation 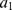 and increasing self activation
and increasing self activation 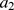 induce dedifferentiation process from state
induce dedifferentiation process from state  to state
to state  with higher mutual repression strength
with higher mutual repression strength 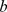
We assumed self activation 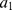 and
and 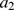 at relatively higher average scaled values with
at relatively higher average scaled values with 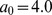 and relative larger mutual repression strength
and relative larger mutual repression strength 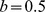 to induce the initial cell undergoing through a balanced pluripotent state [24]. Figure 6(A) showed the saddle-node bifurcation phase diagram for decreasing self activation strength
to induce the initial cell undergoing through a balanced pluripotent state [24]. Figure 6(A) showed the saddle-node bifurcation phase diagram for decreasing self activation strength 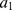 with
with 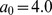 at different time. Figure 6(B) showed the barrier height versus the parameter
at different time. Figure 6(B) showed the barrier height versus the parameter 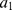 with
with 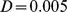 . We defined the barrier height as
. We defined the barrier height as 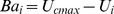 , where
, where  is a constant relative maximum value of population potential landscape and
is a constant relative maximum value of population potential landscape and  is the minimum value of population potential at valley
is the minimum value of population potential at valley 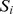 . We can see the system begins with a monostable differentiated state
. We can see the system begins with a monostable differentiated state 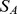 with higher expression of cell-specific gene
with higher expression of cell-specific gene 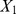 and lower expression of cell-specific gene
and lower expression of cell-specific gene 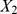 . As parameter
. As parameter 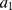 decreases, a saddle node bifurcation emerges, giving rise to another differentiated state
decreases, a saddle node bifurcation emerges, giving rise to another differentiated state 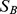 with lower expression of cell-specific gene
with lower expression of cell-specific gene 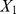 and higher expression of cell-specific gene
and higher expression of cell-specific gene 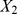 . Initially, barrier height
. Initially, barrier height  of valley
of valley  is much higher than that of valley
is much higher than that of valley  , thus valley
, thus valley  is much more stable than valley
is much more stable than valley  . So the system prefers to stay at differentiated state
. So the system prefers to stay at differentiated state  . As
. As 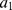 becomes weaker and the corresponding
becomes weaker and the corresponding  becomes stronger, two self activations
becomes stronger, two self activations 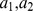 for two cell specific mutually exclusive genes
for two cell specific mutually exclusive genes 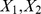 are over-expressing balanced (relative higher expression), another stable pluripotent state
are over-expressing balanced (relative higher expression), another stable pluripotent state 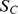 with medium expressions of gene
with medium expressions of gene 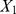 and
and 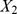 emerges, and the potential landscape has three valleys. Valley
emerges, and the potential landscape has three valleys. Valley 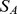 quantified by barrier height
quantified by barrier height 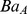 is deeper than valley
is deeper than valley 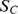 and valley
and valley 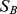 quantified by barrier height
quantified by barrier height 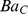 and
and 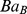 at the beginning of valley
at the beginning of valley 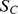 emerging. As self activation
emerging. As self activation 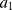 decreases and
decreases and 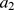 increases further, valley
increases further, valley 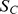 and valley
and valley 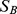 become deeper while valley
become deeper while valley 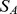 becomes shallower. Barrier height
becomes shallower. Barrier height 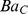 is higher than
is higher than 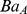 and
and 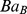 at
at 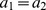 . Therefore, the system with differentiated state
. Therefore, the system with differentiated state 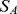 shifts to under pluripotent state
shifts to under pluripotent state 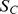 as a process of dedifferentiation. A recent experimental studies [24] proposed a model for the coupled pluripotency module (self-activation of
as a process of dedifferentiation. A recent experimental studies [24] proposed a model for the coupled pluripotency module (self-activation of 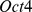 and
and 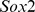 ) and for the differentiation module with mutual antagonism between the
) and for the differentiation module with mutual antagonism between the  (mesendodermal) and
(mesendodermal) and  (ectodermal) shown in Figure 2(C).
(ectodermal) shown in Figure 2(C).  inhibit the activation between
inhibit the activation between 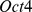 and
and 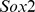 , then
, then  can only activates gene
can only activates gene  , and inhibits gene
, and inhibits gene  [24]. This process can be viewed as
[24]. This process can be viewed as  have the effect of self activation. Thus, this module can be reduced to two mutual antagonism gene
have the effect of self activation. Thus, this module can be reduced to two mutual antagonism gene  and
and  with indirect self activation as our gene regulatory circuit of
with indirect self activation as our gene regulatory circuit of 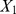 and
and 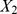 shown in Figure 2(C). It implies that higher self activation strength
shown in Figure 2(C). It implies that higher self activation strength 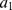 and
and 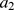 being balanced can lead the differentiated cell back towards the pluripotent cell. As self activation
being balanced can lead the differentiated cell back towards the pluripotent cell. As self activation 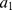 keeps on decreasing and
keeps on decreasing and 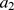 keeps on increasing, the
valley of the other differentiated cell state
keeps on increasing, the
valley of the other differentiated cell state 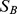 becomes deeper than that of pluripotent cell state due to barrier height
becomes deeper than that of pluripotent cell state due to barrier height 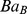 being higher than
being higher than 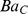 and
and 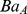 . Eventually, the valleys of
. Eventually, the valleys of 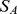 and
and 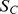 disappear at their saddle-node bifurcation [35]. Thus the cell leaves the pluripotent cell state
disappear at their saddle-node bifurcation [35]. Thus the cell leaves the pluripotent cell state 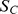 and is forced to enter into the other differentiated cell state
and is forced to enter into the other differentiated cell state 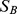 . The results showed the mechanism of dedifferentiation and redifferentiation. This mechanism can be used to explain many studies of cell dedifferentiation process during tissue regeneration both in vitro and in vivo [6]. For example,
. The results showed the mechanism of dedifferentiation and redifferentiation. This mechanism can be used to explain many studies of cell dedifferentiation process during tissue regeneration both in vitro and in vivo [6]. For example, 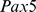 is essential for initiating B cell commitment and is continuously required to maintain B cell lineage commitment [6], [7], [45].
is essential for initiating B cell commitment and is continuously required to maintain B cell lineage commitment [6], [7], [45]. 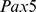 deletion can convert committed B cells into hematopoietic progenitors with pluripotency [6], [7], [45]. It is partly similar as the circuit in Figure 2(B) if we substitute
deletion can convert committed B cells into hematopoietic progenitors with pluripotency [6], [7], [45]. It is partly similar as the circuit in Figure 2(B) if we substitute 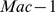 into other lineage specific genes.
into other lineage specific genes. 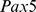 deletion means down-regulating the B cell specific genes (such as BCs) as the effect of self activation
deletion means down-regulating the B cell specific genes (such as BCs) as the effect of self activation 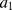 . This gene regulation can lead B cells (
. This gene regulation can lead B cells (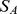 ) to dedifferentiate to hematopoietic progenitors (
) to dedifferentiate to hematopoietic progenitors (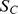 ). Then these cells can re-differentiate to T cell, macrophage or granulocyte (
). Then these cells can re-differentiate to T cell, macrophage or granulocyte (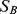 ) under appropriate culture conditions, such as the T-cell-deficient circumstance to reconstitute T cell development [6], [7]. The appropriate culture conditions can be achieved by up-regulating the target cell genes as the effect of another self activation
) under appropriate culture conditions, such as the T-cell-deficient circumstance to reconstitute T cell development [6], [7]. The appropriate culture conditions can be achieved by up-regulating the target cell genes as the effect of another self activation 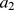 .
.
The population potential landscape at different developmental stage of decreasing self activation parameter 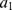 after the relaxation process to a steady state among
after the relaxation process to a steady state among 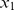 and
and 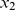 is shown in Figure 6(C) using Eq.2. The green line represents the dedifferentiated path from differentiated state
is shown in Figure 6(C) using Eq.2. The green line represents the dedifferentiated path from differentiated state 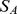 to another differentiated state
to another differentiated state 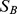 through pluripotent state
through pluripotent state 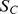 . The purple line represents the backwards dedifferentiated path from differentiated state
. The purple line represents the backwards dedifferentiated path from differentiated state 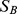 to another differentiated state
to another differentiated state 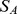 also through pluripotent state
also through pluripotent state 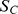 . We can see the irreversible paths on the four dimensional population potential landscape due to non-zero flux. The dedifferentiated landscape and the paths can be quantitatively described for predictions.
. We can see the irreversible paths on the four dimensional population potential landscape due to non-zero flux. The dedifferentiated landscape and the paths can be quantitatively described for predictions.
Decreasing mutual repression strength 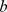 induces differentiation and dedifferentiation process from state
induces differentiation and dedifferentiation process from state 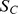 to state
to state 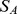 (
(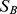 ) with certain self activation
) with certain self activation 
Figure 3(A) shows the phase diagram of super-critical pitchfork bifurcation under self activation 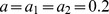 while changing mutual repression strength
while changing mutual repression strength 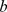 . We can see the potential landscape of continuous dynamics shown in Figure 3(C) using Eq.2 with
. We can see the potential landscape of continuous dynamics shown in Figure 3(C) using Eq.2 with 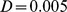 , self activation
, self activation 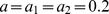 and decreasing mutual repression
and decreasing mutual repression 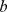 is similar to Waddington's epigenetic landscape [12], [35]. A cell valley can form from an undifferentiation state around
is similar to Waddington's epigenetic landscape [12], [35]. A cell valley can form from an undifferentiation state around  .
.  can be viewed as a stem cell state with lower expressions of differentiation gene markers while
can be viewed as a stem cell state with lower expressions of differentiation gene markers while 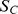 can be viewed as the stem cell with medium expressions of the stem cell markers [17], [46]. When decreasing mutual repression strength
can be viewed as the stem cell with medium expressions of the stem cell markers [17], [46]. When decreasing mutual repression strength 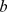 , the initial valley splits into two other valleys and the initial valley becomes a ridge [35]. The cell will choose one valley as its fate. Figure 3(B) also shows the phase diagram of another form of sub-critical pitchfork with two saddle-node bifurcation under larger self activation strength
, the initial valley splits into two other valleys and the initial valley becomes a ridge [35]. The cell will choose one valley as its fate. Figure 3(B) also shows the phase diagram of another form of sub-critical pitchfork with two saddle-node bifurcation under larger self activation strength 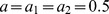 when increasing mutual repression
when increasing mutual repression 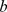 . The continuous potential landscape shown in Figure 3(D) using Eq.2 with
. The continuous potential landscape shown in Figure 3(D) using Eq.2 with 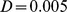 , self activation
, self activation 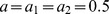 and decreasing mutual repression
and decreasing mutual repression  is also similar to Waddington's epigenetic landscape [12], [35] except the surrounding of the critical point. Around the critical point, there coexist three stable states
is also similar to Waddington's epigenetic landscape [12], [35] except the surrounding of the critical point. Around the critical point, there coexist three stable states 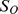 ,
, 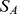 and
and 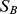 . We also quantified the paths on the potential landscapes. The purple lines represent the differentiation paths from undifferentiation state to differentiation state while the green lines represent the dedifferentiation or reprogramming paths. We can see the paths are irreversible even in the pitchfork bifurcation due to the existence of flux. This mechanism can describe the autonomous cell fate specification [47]. Stem cells must fulfill two tasks of self-renewal and generation of differentiated cells. In symmetric cell division, each stem cell can divide to generate either two daughter stem cells or two differentiated cells symmetrically while in asymmetric cell division, each stem cell splits to one daughter stem cell and one daughter differentiated cell [48]. The pitchfork bifurcation in this study can represent an asymmetry event that a polarized mother stem cell splits into two daughter cell
. We also quantified the paths on the potential landscapes. The purple lines represent the differentiation paths from undifferentiation state to differentiation state while the green lines represent the dedifferentiation or reprogramming paths. We can see the paths are irreversible even in the pitchfork bifurcation due to the existence of flux. This mechanism can describe the autonomous cell fate specification [47]. Stem cells must fulfill two tasks of self-renewal and generation of differentiated cells. In symmetric cell division, each stem cell can divide to generate either two daughter stem cells or two differentiated cells symmetrically while in asymmetric cell division, each stem cell splits to one daughter stem cell and one daughter differentiated cell [48]. The pitchfork bifurcation in this study can represent an asymmetry event that a polarized mother stem cell splits into two daughter cell 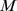 or
or 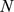 with different expressions of
with different expressions of 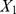 or
or 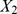 . If daughter cell
. If daughter cell 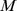 with a very low value of
with a very low value of 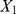 or
or 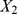 , it might fall into differentiated state, while daughter cell
, it might fall into differentiated state, while daughter cell 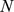 with relative higher expression of
with relative higher expression of 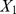 or
or 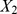 still stays at the pluripotent state [35], [48]. The asymmetric cell division usually occurs early in embryogenesis [35], [47].
still stays at the pluripotent state [35], [48]. The asymmetric cell division usually occurs early in embryogenesis [35], [47].
3. Induction of over expression
Cell fate is influenced by inductive stimulus from a group of surrounding cells [23], [35]. Over-expressions of defined transcription factors can induce one cell type to another cell type which does not depend on gene regulations. This has been achieved in practice using over expression of stem cell marker transcription factors. In our previous gene circuit studies of cell fate decision making for stem cell differentiation and development [15], [17], the two genes in the network are both differentiation markers. The idea is that the specific differentiation markers when imbalanced will give differentiation of one cell fate or the other (two side basins 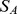 and
and 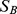 ). A more balanced differentiation marker setup (between the two) will lead to iPS stem cell state (center basin
). A more balanced differentiation marker setup (between the two) will lead to iPS stem cell state (center basin 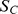 ). Our theoretical work [15], [17] has predicted the possibility of the seasaw mechanism (balance or imbalance) of reprogramming. That is over-expressing both the concentrations of differentiation marker genes in a balanced way can induce and force differentiated cells into iPS stem cells or pluripotent cells [15], [17].
). Our theoretical work [15], [17] has predicted the possibility of the seasaw mechanism (balance or imbalance) of reprogramming. That is over-expressing both the concentrations of differentiation marker genes in a balanced way can induce and force differentiated cells into iPS stem cells or pluripotent cells [15], [17].
The two mutually exclusive differentiation markers  (
( ) and
) and  (
(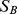 ) shown in Figure 2(C) with balanced over-expressions of key transcription linage specific factors can induce the lineage cell into pluripotent state (
) shown in Figure 2(C) with balanced over-expressions of key transcription linage specific factors can induce the lineage cell into pluripotent state (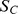 ) instead of the stem cell markers
) instead of the stem cell markers  and
and  for pluripotency of reprogramming as a “seesaw model” [24]. Our theoretical work [15], [17] has already predicted this possibility of expressing differentiation markers for reprogramming and the seasaw mechanism suggested in their work [24].
for pluripotency of reprogramming as a “seesaw model” [24]. Our theoretical work [15], [17] has already predicted this possibility of expressing differentiation markers for reprogramming and the seasaw mechanism suggested in their work [24].
Significant efforts have been made towards the experimental converting fibroblasts (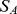 ) to cardiomyocytes (
) to cardiomyocytes (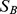 ) by induction of over-expressing key genes. It is reported that direct transdifferentiation can be achieved by over-expressing gene
) by induction of over-expressing key genes. It is reported that direct transdifferentiation can be achieved by over-expressing gene 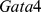 ,
, 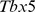 and
and 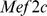 from fibroblasts (
from fibroblasts (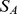 ) to cardiomyocytes (
) to cardiomyocytes (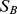 ) [11].
) [11]. 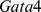 ,
, 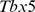 and
and 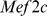 are core transcription factors during early heart development and can co-activate other cardiac gene expression [11]. So
are core transcription factors during early heart development and can co-activate other cardiac gene expression [11]. So 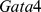 ,
, 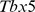 and
and 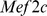 can be viewed as cardiomyocyte cell specific gene
can be viewed as cardiomyocyte cell specific gene 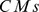 which have self activation. Over-expressing gene
which have self activation. Over-expressing gene 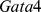 ,
, 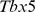 and
and 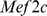 (
(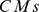 ) can transdifferentiate fibroblasts to cardiomyocytes not through a pluripotent state [11]. Another experiment showed that the indirect transdifferentiation can be achieved with an initial dedifferentiation from fibroblasts (
) can transdifferentiate fibroblasts to cardiomyocytes not through a pluripotent state [11]. Another experiment showed that the indirect transdifferentiation can be achieved with an initial dedifferentiation from fibroblasts (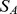 ) through pluripotent precursor-Cardiac progenitor (
) through pluripotent precursor-Cardiac progenitor (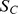 ) by over-expressing some stem cell markers
) by over-expressing some stem cell markers 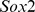 ,
,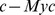 ,
,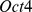 and
and 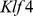 , and then be induced to cardiomyocytes (
, and then be induced to cardiomyocytes (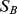 ) [10].
) [10].
Conclusions
In this study, we applied our potential and flux framework to explore the mechanisms of cell developmental processes of differentiation, dedifferentiation, reprogramming and transdifferentiation. The potential landscape of two gene regulatory circuit shows that the system has four stable valleys at specific regulation regions, two differentiated state 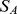 and
and 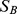 , one pluripotent state
, one pluripotent state 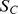 , and an intermediate state
, and an intermediate state 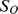 . Our work provides a quantitative basis for explaining the mechanisms of the transition among the four states. Barrier height based on the population potential landscape or the intrinsic potential landscape can quantify the stability of the attractors and the efficiency of switching among the attractors. We can acquire the dynamical transition rate of the system from one valley of attraction to another by MFPT for escape and the dominant paths for dedifferentiation and transdifferentiation via the path integral method. We can see the paths of cell type switchings are irreversible due to non-zero probability flux.
. Our work provides a quantitative basis for explaining the mechanisms of the transition among the four states. Barrier height based on the population potential landscape or the intrinsic potential landscape can quantify the stability of the attractors and the efficiency of switching among the attractors. We can acquire the dynamical transition rate of the system from one valley of attraction to another by MFPT for escape and the dominant paths for dedifferentiation and transdifferentiation via the path integral method. We can see the paths of cell type switchings are irreversible due to non-zero probability flux.
In this study, we have discussed three driving forces: stochastic fluctuations, gene regulation and induction, which can lead to cell type switchings. The cell type switching driven by stochastic fluctuations is a spontaneous transition, gene regulation is much like a non-autonomous varying of time-dependent landscape, and induction is a condition of initial value re-setting process with no apparent paths. The fluctuations maybe small in some cases but never zero. When exploring the stochasticity, we used fixed set of the values of self activation and mutual repression regulation parameters  and
and 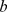 . We not only discussed the possibility of cell type switching through stochastic dynamics but also other two mechanisms including the induction and regulation changes. We also explored the different dynamics with different sets of the parameter
. We not only discussed the possibility of cell type switching through stochastic dynamics but also other two mechanisms including the induction and regulation changes. We also explored the different dynamics with different sets of the parameter  and
and 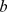 . For gene regulation, we varied the parameters
. For gene regulation, we varied the parameters  and
and 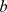 for regulating the cell type switchings. For induction, we did not change any parameters. Instead, we just gave the cell an initial set (condition) with over-expression of its lineage specific gene. We quantitatively investigated the mechanism of cell type switching through the induction without the change of the underlying landscape and through the changes in regulations leading to the changes of the underlying landscape topography. Furthermore, these two types of cell type switchings driven by gene regulation and induction are not spontaneous transitions only due to fluctuations, but a controlled process under either the changes in regulations with regulation-dependent potential landscape or the induction with fixed potential landscape.
for regulating the cell type switchings. For induction, we did not change any parameters. Instead, we just gave the cell an initial set (condition) with over-expression of its lineage specific gene. We quantitatively investigated the mechanism of cell type switching through the induction without the change of the underlying landscape and through the changes in regulations leading to the changes of the underlying landscape topography. Furthermore, these two types of cell type switchings driven by gene regulation and induction are not spontaneous transitions only due to fluctuations, but a controlled process under either the changes in regulations with regulation-dependent potential landscape or the induction with fixed potential landscape.
We found that the topography of the global potential landscapes is strongly correlated to the self activation strength and the mutual repression strength of the transcription factors. Dedifferentiation can be induced by the core regulators of pluripotent genes using in iPS or the synergistic effect of lineage specifiers in specification of differentiated cells. We can adjust two self activation strength 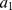 and
and 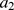 to be relative larger to force the differentiated cell to a pluripotent cell with higher inhibition strength
to be relative larger to force the differentiated cell to a pluripotent cell with higher inhibition strength 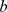 , and then re-differentiate the pluripotent cell to our target differentiated cell type [24]. This process can be viewed as an initial epigenetic activation phase representing the redifferentiation after a temporal overexpression of pluripotent reprogramming factors to a pluripotent state [4], [24], [49]. Somatic cells can be transdifferentiated by temporal over-expressions of pluripotent reprogramming transcription factors. Transdifferentiation can be induced by down regulating the lineage specific marker gene (
, and then re-differentiate the pluripotent cell to our target differentiated cell type [24]. This process can be viewed as an initial epigenetic activation phase representing the redifferentiation after a temporal overexpression of pluripotent reprogramming factors to a pluripotent state [4], [24], [49]. Somatic cells can be transdifferentiated by temporal over-expressions of pluripotent reprogramming transcription factors. Transdifferentiation can be induced by down regulating the lineage specific marker gene (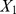 ) of the original differentiated cell (decreasing self activation
) of the original differentiated cell (decreasing self activation 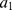 ) while activating another lineage specific marker gene (
) while activating another lineage specific marker gene (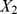 ) of the final differentiated cell (increasing self activation
) of the final differentiated cell (increasing self activation 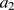 ) at relative lower inhibition strength
) at relative lower inhibition strength 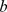 , through an intermediate state or a series of indeterminate states. This process can be viewed as lineage-instructive transcription representing the induction of lineage specific gene for the target differentiated cells [4], [49]. This gives us a new understanding that the topography of underlying potential landscapes in cell development dynamics determines the feasibility and efficiency of cell type switchings.
, through an intermediate state or a series of indeterminate states. This process can be viewed as lineage-instructive transcription representing the induction of lineage specific gene for the target differentiated cells [4], [49]. This gives us a new understanding that the topography of underlying potential landscapes in cell development dynamics determines the feasibility and efficiency of cell type switchings.
We also classified the mechanisms of pitchfork bifurcations depicted Waddington's epigenetic development landscape including super-critical pitchfork bifurcation, sub-critical pitchfork bifurcation, sub-critical pitchfork with two saddle-node bifurcation, and saddle-node bifurcation depicted the transdifferentiation landscape [35]. We uncovered a pitchfork bifurcation of Waddington's epigenetic landscape and the irreversible paths (caused by the non-equilibrium flux) between differentiation and reprogramming. We also uncovered the saddle-node bifurcation landscape. Saddle-node bifurcation can give the explanation of possible mechanisms of dedifferentiation and transdifferentiation processes and can further explain the irreversibility of the paths for differentiation, dedifferentiation, reprogramming and transdifferentiation processes as hysteresis loop even without the presence of the non-equilibrium flux. We noticed a special kind of sub-critical pitchfork with two saddle-node bifurcations also shares the certain features with saddle-node bifurcation (hysteresis loop) and certain features of pitchfork bifurcation (Waddington's landscape).
Importantly, we uncovered some novel mechanisms as a starting point to decipher the mysterious code of the cell type switchings. Our theory can be used to guide the designs of the differentiation, dedifferentiation, reprogramming and transdifferentiation processes.
Methods
Quantifying non-equilibrium potential landscape, flux, non-equilibrium thermodynamics and the paths
Fluctuations exist widely in biological systems [13], [50]–[55]. The dynamics in noisy fluctuating environments can be formulated as: 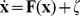 .
. 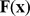 is the deterministic force, where
is the deterministic force, where  is the vector representing different concentrations in state space.
is the vector representing different concentrations in state space.  is Gaussian noise term and its autocorrelation function is
is Gaussian noise term and its autocorrelation function is 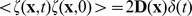 , where
, where 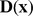 is diffusion coefficient matrix. We set
is diffusion coefficient matrix. We set 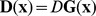 , where
, where 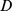 is the diffusion coefficient representing the level of noise strength while
is the diffusion coefficient representing the level of noise strength while 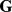 is the scaled diffusion matrix described the anisotropy phenomenon. We can explore the corresponding Fokker-Planck diffusion equation [56], [57] for probability distribution
is the scaled diffusion matrix described the anisotropy phenomenon. We can explore the corresponding Fokker-Planck diffusion equation [56], [57] for probability distribution 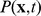 :
: 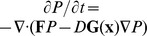 . In this study, we set
. In this study, we set 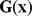 as a unit matrix for simplicity. The probability flux
as a unit matrix for simplicity. The probability flux 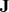 is defined as:
is defined as: 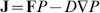 . In steady state, the force decomposition is shown as:
. In steady state, the force decomposition is shown as: 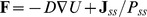 [13], [50], [51].
[13], [50], [51].
We obtained the Lyapunov function  as the intrinsic potential from the zero fluctuation limit Hamilton-Jacobi equation(HJE) [37], [58]:
as the intrinsic potential from the zero fluctuation limit Hamilton-Jacobi equation(HJE) [37], [58]: 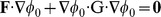 by a numerical method - level set method using the Mitchell's level-set toolbox [59]. The force decomposition in zero fluctuation limit is shown as:
by a numerical method - level set method using the Mitchell's level-set toolbox [59]. The force decomposition in zero fluctuation limit is shown as: 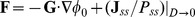 . From the Hamilton-Jacobian equation above, we can obtain
. From the Hamilton-Jacobian equation above, we can obtain 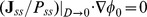 [37], [51], [60], [61]. We also can obtain the mean first passage time from the following equation [56]:
[37], [51], [60], [61]. We also can obtain the mean first passage time from the following equation [56]: 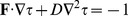 .
.  represents the mean first passage time from state
represents the mean first passage time from state  to state
to state  .
.
The path integral approach we used is shown as below. The path probability starts from initial state 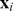 at
at  , and end at the final state of
, and end at the final state of  at time
at time  . The path integral formula is shown as [15], [44]
. The path integral formula is shown as [15], [44]
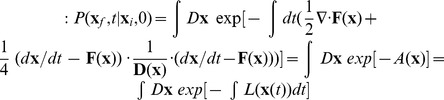 , where
, where 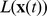 is the Lagrangian and
is the Lagrangian and 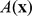 is the action for each path [15], [44]. The path integral over
is the action for each path [15], [44]. The path integral over 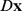 represents the sum over all possible paths connecting
represents the sum over all possible paths connecting 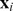 at time
at time 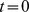 to
to 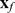 at time
at time  . The exponent factor gives the weight of each specific trajectory path. The probability from initial state to the final state is equal to the sum of all possible paths with different weights. Every dynamical path doesn't contribute to the same weight and each path is exponentially weighted. Therefore, the path integrals can be approximated with a set of dominant paths while the other subleading path weights can be neglected for their relative small values. We can find the dominant paths with the optimal weights through minimization of the action
. The exponent factor gives the weight of each specific trajectory path. The probability from initial state to the final state is equal to the sum of all possible paths with different weights. Every dynamical path doesn't contribute to the same weight and each path is exponentially weighted. Therefore, the path integrals can be approximated with a set of dominant paths while the other subleading path weights can be neglected for their relative small values. We can find the dominant paths with the optimal weights through minimization of the action 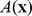 or Lagrangian
or Lagrangian 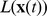 . Thus, we can identify the optimal paths which give more contribution to the weight as biological paths or cell type switching pathways in our study.
. Thus, we can identify the optimal paths which give more contribution to the weight as biological paths or cell type switching pathways in our study.
Supporting Information
Supporting figures. Figure S1, A: The phase diagram for varying parameter  with
with 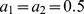 ,
, 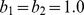 ,
, 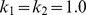 and
and 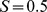 . B: The phase diagram for varying parameter
. B: The phase diagram for varying parameter 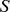 with
with 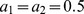 ,
, 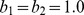 ,
, 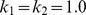 and
and 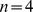 . Figure S2, The quantified transdifferentiation landscape and pathways for continuous changing parameter
. Figure S2, The quantified transdifferentiation landscape and pathways for continuous changing parameter 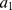 and constant
and constant 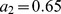 . (
. (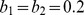 ,
, 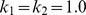 ,
, 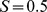 and
and 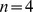 ). Figure S3, The quantified transdifferentiation landscape and pathways for continuous changing parameter
). Figure S3, The quantified transdifferentiation landscape and pathways for continuous changing parameter 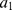 and constant
and constant 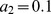 .(
.(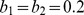 ,
, 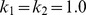 ,
, 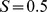 and
and 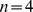 ).
).
(DOC)
Data Availability
The authors confirm that all data underlying the findings are fully available without restriction. Relevant data are included within the paper.
Funding Statement
This work is supported in part by Natural Science Foundation of China (NSFC Grant Nos. 21190040, 91227114, 11174105, and 11305176, 973 project 2010CB933600) and National Science Foundation (NSFMCB-0947767). NSFC website is: www.nsfc.gov.cn. NSF website: www.nsf.gov. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Takahashi K, Yamanaka S (2006) Induction of pluripotent stem cells from mouse embryonic and adult fibmblast cultures by defined factors. Cell 126: 663–676. [DOI] [PubMed] [Google Scholar]
- 2. Takahashi K, Tanabe K, Ohnuki M (2007) Induction of pluripotent stem cells from adult human fibroblasts by defined factors. Cell 131: 861–872. [DOI] [PubMed] [Google Scholar]
- 3. Vierbuchen T, Ostermeier A, Pang ZP, Kokubu Y, Sudhof TC, et al. (2010) Direct conversion of fibroblasts to functional neurons by defined factors. Nature 463: 1035–1041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Jopling C, Boue S, Belmonte JC (2011) Dedifferentiation, transdifferentiation and reprogramming: three routes to regeneration. Nat Rev Mol Cell Bio 12: 79–89. [DOI] [PubMed] [Google Scholar]
- 5. Xie HF, Ye M, Feng R, Graf T (2004) Stepwise reprogramming of b cells into macrophages. Cell 117: 663–676. [DOI] [PubMed] [Google Scholar]
- 6. Cobaleda C, Jochum W, Busslinger M (2007) Conversion of mature b cells into t cells by dedifferentiation to uncommitted progenitors. Nature 449: 473–477. [DOI] [PubMed] [Google Scholar]
- 7. Graf T, Enver T (2009) Forcing cells to change lineages. Nature 462: 587–594. [DOI] [PubMed] [Google Scholar]
- 8. Zhou Q, Melton DA (2008) Extreme makeover: Converting one cell into another. Cell Stem Cell 3: 382–388. [DOI] [PubMed] [Google Scholar]
- 9. Zhou Q, Brown J, Kanarek A, Rajagopal J, Melton DA (2008) In vivo reprogramming of adult pancreatic exocrine cells to beta-cells. Nature 455: 627–632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Efe JA, Hilcove S, Kim J, Zhou HY, Ouyang K, et al. (2011) Conversion of mouse fibroblasts into cardiomyocytes using a direct reprogramming strategy. Nat Cell Biol 13: 215–222. [DOI] [PubMed] [Google Scholar]
- 11. Ieda M, Fu JD, Delgado-Olguin P, Vedantham V, Hayashi Y, et al. (2010) Direct reprogramming of fibroblasts into functional cardiomyocytes by defined factors. Cell 142: 375–386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Waddington CH (1957) The Strategy of the Genes. London, UK: Volume George Allen and Unwin.
- 13. Wang J, Xu L, Wang EK (2008) Potential landscape and flux framework of nonequilibrium networks: Robustness, dissipation, and coherence of biochemical oscillations. Proc Natl Acad Sci USA 105: 12271–12276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Li C, Wang J (2013) Quantifying cell fate decisions for differentiation and reprogramming of a human stem cell network: Landscape and biological paths. PLoS Comput Biol 9: e1003165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Wang J, Zhang K, Xu L, Wang EK (2011) Quantifying the waddington landscape and biological paths for development and differentiation. Proc Natl Acad Sci USA 108: 8257–8262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Feng H, Wang J (2012) A new mechanism of stem cell differentiation through slow binding/unbinding of regulators to genes. Sci Rep 2: 550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Wang J, Xu L, Wang EK, Huang S (2010) The potential landscape of genetic circuits imposes the arrow of time in stem cell differentiation. Biophys J 99: 29–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Qian H (2010) Cellular biology in terms of stochastic nonlinear biochemical dynamics: Emergent properties, isogenetic variations and chemical system inheritability. J Stat Phys 141: 990–1013. [Google Scholar]
- 19. Qian H (2012) Cooperativity in cellular biochemical processes: Noise-enhanced sensitivity, fluctuating enzyme, bistability with nonlinear feedback, and other mechanisms for sigmoidal responses. Annual Review of Biophysics 41: 179–204. [DOI] [PubMed] [Google Scholar]
- 20. Sridharan R, Tchieu J, Mason MJ, Yachechko R, Kuoy E, et al. (2009) Role of the murine reprogramming factors in the induction of pluripotency. Cell 136: 364–377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Mikkelsen TS, Hanna J, Zhang X, Ku M, Wernig M, et al. (2008) Dissecting direct reprogramming through integrative genomic analysis. Nature 454: 49–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Losick R, Desplan C (2008) Stochasticity and cell fate. Science 320: 65–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Amabile G, Meissner A (2009) Induced pluripotent stem cells: current progress and potential for regenerative medicine. Trends Mol Med 15: 59–68. [DOI] [PubMed] [Google Scholar]
- 24. Shu J, Wu C, Wu YT, Li Z, Shao S, et al. (2013) Induction of pluripotency in mouse somatic cells with lineage specifiers. Cell 153: 963–975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Huang S, Guo YP, May G, Enver T (2007) Bifurcation dynamics of cell fate decision in bipotent progenitor cells. Dev Biol 305: 695–713. [DOI] [PubMed] [Google Scholar]
- 26. Huang S (2009) Reprogramming cell fates: reconciling rarity with robustness. BioEssays 31: 546–560. [DOI] [PubMed] [Google Scholar]
- 27. Ralston A, Rossant J (2005) Genetic regulation of stem cell origins in the mouse embryo. Clin Genet 68: 106–112. [DOI] [PubMed] [Google Scholar]
- 28. Niwa H, Toyooka Y, Shimosato D, Strumpf D, Takahashi K, et al. (2005) Interaction between oct3/4 and cdx2 determines trophectoderm differentiation. Cell 123: 917–929. [DOI] [PubMed] [Google Scholar]
- 29. Orkin SH, Zon LI (2008) Hematopoiesis: an evolving paradigm for stem cell biology. Cell 132: 631–644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Chickarmane V, Peterson C (2008) A computational model for understanding stem cell, trophectoderm and endoderm lineage determination. PLOS ONE 3: e3478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Li CH, Wang J (2013) Quantifying waddington landscapes and paths of non-adiabatic cell fate decisions for differentiation, reprogramming and transdifferentiation. J R Soc Interface 10: 20130787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Jiang J, Chan Y, Loh Y, Cai J, Tong G (2008) A core klf circuitry regulates self-renewal of embryonic stem cells. Nat Cell Biol 10: 353–360. [DOI] [PubMed] [Google Scholar]
- 33.Guckenheimer J, Holmes P (1990) Nonlinear oscillations, dynamical systems, and bifurcations of vector fields. Applied mathematical sciences. Springer-Verlag.
- 34.Nicolis G, Prigogine I (1977) Self-organization in nonequilibrium systems: from dissipative structures to order through fluctuations. A Wiley-Interscience Publication. Wiley.
- 35. Ferrell JE (2012) Bistability, bifurcations, and waddingtons epigenetic landscape. Curr Biol 22: 458–466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ao P, Qian H, Tu YH, Wang J (2013) A theory of mesoscopic phenomena: Time scales, emergent unpredictability, symmetry breaking and dynamics across different levels. Available: http://arxivorg/abs/13105585.
- 37. Zhang F, Xu L, Zhang K, Wang EK, Wang J (2012) The potential and flux landscape theory of evolution. J Chem Phys 137: 065102. [DOI] [PubMed] [Google Scholar]
- 38. Qian H (2006) Open-system nonequilibrium steady-state: Statistical thermodynamics, fluctuations and chemical oscillations. J Phys Chem B 110: 15063–15074. [DOI] [PubMed] [Google Scholar]
- 39. Ge H, Qian H (2010) Physical origins of entropy production, free energy dissipation, and their mathematical representations. Phys Rev E 81: 051133. [DOI] [PubMed] [Google Scholar]
- 40. Qian H (2009) Entropy demystified: The “thermo”-dynamics of stochastically fluctuating systems. Method Enzymol 467: 111–134. [DOI] [PubMed] [Google Scholar]
- 41. Zhang K, Sasai M, Wang J (2013) Eddy current and coupled landscapes for nonadiabatic, nonequilibrium dynamics of complex systems. Proc Natl Acad Sci USA 110: 14930–14935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Feng HD, Han B, Wang J (2012) Landscape and global stability of nonadiabatic and adiabatic oscillations in a gene network. Biophys J 102: 1001–1010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Feng HD, Han B, Wang J (2011) Adiabatic and non-adiabatic non-equilibrium stochastic dynamics of single regulating genes. J Phys Chem B 115: 1254–1261. [DOI] [PubMed] [Google Scholar]
- 44. Wang J, Zhang K, Wang EK (2010) Kinetic paths, time scale, and underlying landscapes: A path integral framework to study global natures of nonequilibrium systems and networks. J Chem Phys 133: 125103. [DOI] [PubMed] [Google Scholar]
- 45. Mikkola I, Heavey B, Horcher M, Busslinger M (2002) Reversion of b cell commitment upon loss of pax5 expression. Science 297: 110–113. [DOI] [PubMed] [Google Scholar]
- 46. Liu R, Aihara K, Chen L (2013) Dynamical network biomarkers for identifying critical transitions and their driving networks of biologic processes. Quant Biol 1: 105–114. [Google Scholar]
- 47. Xiong W, Ferrell JE (2003) A positive-feedback-based bistable ‘memory module’ that governs a cell fate decision. Nature 426: 460–465. [DOI] [PubMed] [Google Scholar]
- 48. Morrison SJ, Kimble J (2006) Asymmetric and symmetric stem-cell divisions in development and cancer. Nature 441: 1068–1074. [DOI] [PubMed] [Google Scholar]
- 49. Pournasr B, Khaloughi K, Salekdeh GH, Totonchi M, Shahbazi E, et al. (2011) Concise review: Alchemy of biology: Generating desired cell types from abundant and accessible cells. Stem Cells 29: 1933–1941. [DOI] [PubMed] [Google Scholar]
- 50. Li CH, Wang EK, Wang J (2012) Potential flux landscapes determine the global stability of a lorenz chaotic attractor under intrinsic fluctuations. J Chem Phys 136: 194108. [DOI] [PubMed] [Google Scholar]
- 51. Xu L, Zhang F, Wang EK, Wang J (2013) The potential and flux landscape, lyapunov function and non-equilibrium thermodynamics for dynamic systems and networks with an application to signal-induced ca 2+ oscillation. Nonlinearity 26: 69. [Google Scholar]
- 52. Zheng L, Chen M, Nie Q (2012) External noise control in inherently stochastic biological systems. J Math Phys 53: 115616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Miller CA, Beard DA (2008) The effects of reversibility and noise on stochastic phosphorylation cycles and cascades. Biophys J 95: 2183–2192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Pujato M, MacCarthy T, Fiser AF, Bergman A (2013) The underlying molecular and network level mechanisms in the evolution of robustness in gene regulatory networks. PLoS Comput Biol 9: e1002865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Balzsi G, van Oudenaarden A, Collins JJ (2011) Cellular decision making and biological noise: from microbes to mammals. Cell 144: 910–925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Van Kampen NG (2007) Stochastic processes in physics and chemistry. Amsterdam: Elsevier.
- 57. Gillespie DT (1977) Exact stochastic simulation of coupled chemical reactions. J Phys Chem 81: 2340–2361. [Google Scholar]
- 58. Hu G (1986) Lyapunov function and stationary probability distributions. Zeit Phys B: Condens Matter 65: 103–106. [Google Scholar]
- 59. Mitchell IM (2008) The flexible, extensible and effcient toolbox of level set methods. J Sci Comput 35: 300–329. [Google Scholar]
- 60.Graham R (1989) Macroscopic potentials, bifurcations and noise in dissipative systems. In: Moss F, McClintock P, editors, Noise in Nonlinear Dynamical Systems Vol.1, Cambridge University Press. pp. 225–278. [Google Scholar]
- 61.Haken H (1987) Advanced synergetics: instability hierarchies of self-organizing systems and devices. Berlin: Springer. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting figures. Figure S1, A: The phase diagram for varying parameter  with
with 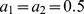 ,
, 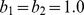 ,
, 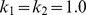 and
and 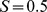 . B: The phase diagram for varying parameter
. B: The phase diagram for varying parameter 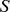 with
with 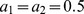 ,
, 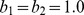 ,
, 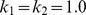 and
and 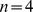 . Figure S2, The quantified transdifferentiation landscape and pathways for continuous changing parameter
. Figure S2, The quantified transdifferentiation landscape and pathways for continuous changing parameter 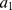 and constant
and constant 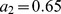 . (
. (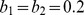 ,
, 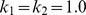 ,
, 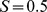 and
and 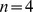 ). Figure S3, The quantified transdifferentiation landscape and pathways for continuous changing parameter
). Figure S3, The quantified transdifferentiation landscape and pathways for continuous changing parameter 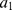 and constant
and constant 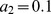 .(
.(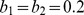 ,
, 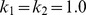 ,
, 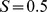 and
and 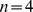 ).
).
(DOC)
Data Availability Statement
The authors confirm that all data underlying the findings are fully available without restriction. Relevant data are included within the paper.