Abstract
Aims/hypothesis
Little is known about the performance of surrogates in assessing changes in insulin sensitivity over time. This report compared updated HOMA of insulin sensitivity (HOMA2-%S) and the Matsuda index from OGTTs with minimal model-based estimates of insulin sensitivity (SI) from frequently sampled IVGTTs (FSIGTs) in longitudinal settings and cross-sectional settings.
Methods
Two longitudinal studies were used: one a natural observational study in which 338 individuals were followed for a median of 4 years; one a clinical treatment study in which 97 individuals received pioglitazone treatment and were followed for 1 year. Pairs of OGTTs and FSIGTs were performed at baseline and follow-up. Correlations were computed. Impact of measurement uncertainty was investigated through simulation studies.
Results
Correlations between HOMA2-%S and SI from baseline or follow-up data were in the range reported previously (0.61-0.69). By contrast, correlations for changes over time were only 0.35-0.39. The corresponding correlations between the Matsuda index and SI were 0.66-0.72 for cross-sectional data and 0.40-0.48 for longitudinal change. Correlations for changes were significantly lower than the cross-sectional correlations in both studies (p<0.03). Simulation results demonstrated that the reduced correlations for change were not explained by error propagation, supporting a real limitation of surrogates to fully capture longitudinal changes in insulin sensitivity.
Conclusions/interpretation
HOMA and Matsuda indices derived from cross-sectional data should be used cautiously in assessing longitudinal changes in insulin sensitivity.
Keywords: Homeostasis models, Insulin sensitivity surrogates, Intravenous glucose tolerance test, Longitudinal change, Oral glucose tolerance test
Introduction
Insulin sensitivity is generally measured by euglycaemic–hyperinsulinaemic glucose clamp [1], insulin suppression test [2], or minimal model analysis of glucose and insulin patterns from the frequently sampled IVGTT (FSIGT) [3]. Due to the complexities and expense of these tests, a wide variety of surrogate measures have been proposed and used in large-scale studies. These surrogate measures generally use glucose and insulin levels in the fasting state or following an oral glucose challenge to estimate insulin sensitivity. Most surrogates were derived empirically and then validated against measures from more accurate but complex tests using cross-sectional correlations. Whether surrogates validated in this way remain robust in other research settings has not been fully addressed. Genetic studies have demonstrated different genetic contributions to insulin resistance between direct and surrogates measures [4, 5]. In this report, we compare the longitudinal performance of two commonly used surrogates, updated HOMA of insulin sensitivity (HOMA2-%S) [6, 7] and the Matsuda index [8], with minimal model-based estimates of insulin sensitivity (SI) from FSIGTs using data from two independent longitudinal studies. We used HOMA2-%S as recommended by the developers of HOMA for comparison between HOMA and other approaches to estimate insulin sensitivity. Since measurement uncertainty (error) presents in both surrogates and the more complex measures, measurement errors will attenuate correlation coefficient estimates. We conducted simulation studies to investigate the impact of error propagation on the differences in correlation coefficients between longitudinal and cross-sectional settings.
Methods
Participants
Data from two longitudinal studies were used, one under natural observation (BetaGene) [9] and one in response to treatment (PIPOD) [10]. Briefly, the BetaGene study included Mexican-American adults who were women with recent gestational diabetes mellitus (GDM) and their siblings and/or cousins, or women with normal glucose levels in pregnancy. Data from 338 individuals who had an OGTT and FSIGT at baseline and a median of 4.1 years later were used for this report. The PIPOD study included women with prior GDM who were treated with open label pioglitazone. Data from 97 women who had an OGTT and FSIGT at baseline and 1 year later were included in this report. Insulin-modified FSIGTs were performed in the BetaGene study, and tolbutamide-modified FSIGTs were performed in the PIPOD study. All participants gave written informed consent for participation in the studies, which were approved by the institutional review boards of participating institutions.
Data analysis
FSIGT results were analysed using the MINMOD program to estimate SI [11]. HOMA2-%S was calculated using the updated version of the HOMA calculator [6] (www.dtu.ox.ac.uk/homacalculator/index.php) using fasting glucose and insulin from OGTTs. The Matsuda index of insulin sensitivity was calculated as described previously [8].
Correlation coefficients between surrogates and SI were reported from the Pearson coefficients calculated on natural log-transformed data for cross-sectional correlations, and changes in natural log-transformed data for longitudinal correlations. The equality of the baseline correlation to the longitudinal correlation for each pair of insulin sensitivity measures was tested using Fisher’s z test. In addition, changes in surrogates and SI were dichotomised as increasing values vs no change or falling values over time, and Kappa coefficients were calculated.
Measurement uncertainty was expressed as the proportion of total variance that was accounted for by the within-subject repeated measures variance, estimated from FSIGTs performed 3 months apart without any interventions. These measurements were made in a separate cohort of 109 Hispanic women [12] with similar characteristics to those of the BetaGene and PIPOD samples. The estimated measurement errors were 28% for log(HOMA2-%S) and 15% for log(SI). Measurement error for the Matsuda index was not calculated because OGTTs were not performed at 3 month intervals in the separate cohort. Means and SDs of baseline log(HOMA2-%S) and log(SI), and changes in log(HOMA2-%S) and log(SI) from the BetaGene cohort were used to generate the bivariate normal data for both baseline and change, assuming various true correlations for baseline and change in the simulations studies. Random measurement errors of 28% for log(HOMA2-%S) and 15% for log(SI) were then added to both baseline and follow-up in the simulated data. Sample size for the simulated data was set at 340 to mimic the size of the BetaGene cohort and repeated 1,000 times. Pearson correlations were calculated from each of the simulated data sets and averaged across the 1,000 replications. Calculated average correlations from the simulated data were compared with the correlations from the BetaGene cohort. SAS version 9.2 (SAS Institute, Cary, NC, USA) was used for all statistical analyses and simulations. A p value of <0.05 was considered statistically significant.
Results
The BetaGene sample included both males and females with wider age (18-66 vs 25-54 years) and BMI (17.1-52.9 vs 21.3-47.8 kg/m2) ranges compared with PIPOD (see electronic supplementary material [ESM] text and ESM Table 1). The PIPOD sample was slightly more obese and had worse average glucose and insulin sensitivity compared with the BetaGene sample. Baseline and changes in all three insulin sensitivity indices covered wide ranges; median changes in all three indices were negative in the BetaGene sample but positive in the PIPOD sample, consistent with the different study designs.
Cross-sectional and longitudinal correlations
At baseline, the cross-sectional correlations between SI and HOMA2-%S were 0.69 for BetaGene and 0.61 for PIPOD; the correlations between SI and Matsuda were 0.71 for BetaGene and 0.66 for PIPOD. Correlations of similar magnitude and direction were obtained using cross-sectional data at follow-up (Table 1). However, correlations calculated using changes in insulin sensitivity were 27-49% lower than the analogous correlations made with cross-sectional correlations (Table 1). For SI vs HOMA2-%S, correlations for change were 0.35 for BetaGene and 0.39 for PIPOD, which were significantly lower than the baseline correlations of 0.69 for BetaGene (p<0.0001) and 0.61 for PIPOD (p=0.02). Likewise, correlations for change between SI and Matsuda index were 0.40 for BetaGene and 0.48 for PIPOD, which were significantly lower than the baseline correlations of 0.71 for BetaGene (p<0.0001) and 0.66 for PIPOD (p=0.03). Scatter plots of baseline and change data appear in Fig. 1. Kappa coefficients, which assess agreement for dichotomised changes between surrogates and SI (increasing vs no change or falling; 1.0 = perfect concordance) were also low, in the range 0.17-0.32 (Table 1).
Table 1.
Cross-sectional and longitudinal correlations between FSIGT SI and surrogate measuresa
| Surrogate measure vs FSIGT SI | BetaGene (n=338)
|
PIPOD (n=97)
|
||||||
|---|---|---|---|---|---|---|---|---|
| Cross-sectional
|
Longitudinal change
|
Cross-sectional
|
Longitudinal change
|
|||||
| Baseline | Follow-up | Correlation coefficient | Kappa coefficient | Baseline | Follow-up | Correlation coefficient | Kappa coefficient | |
| HOMA2-%S | 0.69 | 0.69 | 0.35 | 0.17 | 0.61 | 0.64 | 0.39 | 0.23 |
| Matsuda index | 0.71 | 0.72 | 0.40 | 0.25 | 0.66 | 0.69 | 0.48 | 0.32 |
Correlation coefficients were the Pearson coefficients calculated on natural log-transformed data (cross-sectional) and change in natural log-transformed data (longitudinal change). Kappa coefficients were calculated by dichotomising changes as increasing values vs no change or falling values over time
Fig. 1.
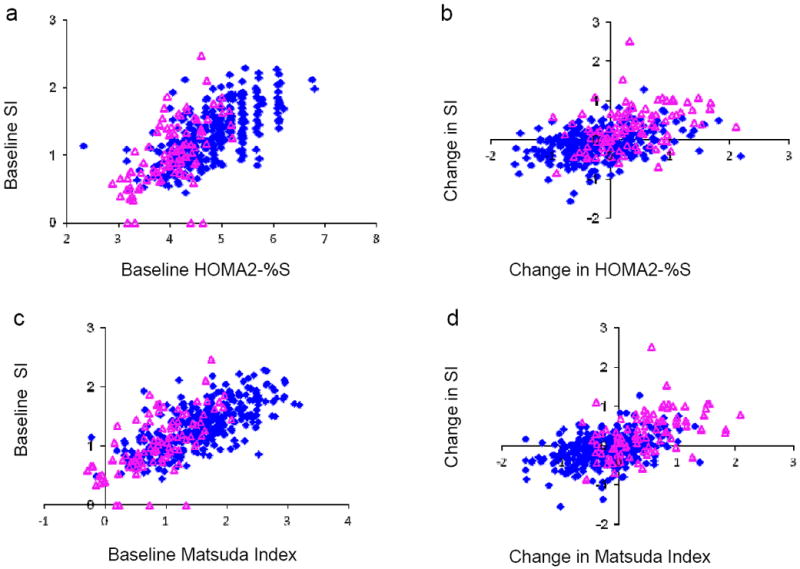
Scatter plots of baseline FSIGT SI and change in SI vs HOMA2-%S (a, b), and in SI vs Matsuda index (c, d) for data from the BetaGene (blue diamond, n=338) and PIPOD (pink triangle, n=97) studies. Data were in natural log scale for baseline and change in natural log scale for change
Were reduced correlations explained by the measurement error?
Details of simulations to address this question appear in ESM text and ESM Table 2. Briefly, measurement errors of 15% for log(SI) and 28% for log(HOMA2-%S) should have caused the correlation coefficient between changes in these two variables to fall from baseline only slightly, i.e. from 0.69 to 0.56 in the BetaGene study. In fact, the observed reduction was much larger, from 0.69 to 0.35 (Table 1). This finding indicates that the lower correlation coefficient for change compared with that at baseline was not explained by propagation of measurement error alone.
Discussion
Using data from two independent longitudinal studies we showed that HOMA2-%S and the Matsuda index had much lower correlations with FSIGT SI when assessing longitudinal changes in insulin sensitivity than in cross-sectional settings. The results were consistent whether insulin-modified or tolbutamide-modified FSIGTs were used. Agreement between surrogates and SI assessed on the dichotomous scale of change was also low. The reduced correlations were not explained by measurement uncertainty, suggesting true lower validity of the surrogates against FSIGT-derived insulin sensitivity in longitudinal settings.
We are aware of two previous follow-up studies, both relatively small and of short duration, that examined change in QUICKI and change in insulin sensitivity by euglycaemic–hyperinsulinaemic clamps in patients with type 2 diabetes [13] or hypertension [14]. They concluded that QUICKI is useful; close examination of their results, however, indicates that the mean change was much less in QUICKI than in the clamp insulin sensitivity (8% vs 38%) [13], and the correlation between QUICKI and the clamp was considerably less for change than for baseline (r=0.42 vs 0.60 [13] and r=0.61 vs 0.82 [14]). Thus, these data appear to support our conclusion that surrogates may perform relatively poorly for change in contrast to their generally good performance in cross-sectional studies. Surrogates have not been shown to be superior to simple measures of fasting glucose and insulin in cross-sectional settings [15-17], and their performance may be race- and sex-dependent [17].
The strengths of this study were (a) its use of two independent, relatively large and long-term follow-up studies, one with natural observation and one with an insulin-sensitising drug, and (b) the evaluation of the impact of measurement uncertainty. Variability was large in all measures, whether considered cross-sectionally or as change; thus, the impact of data range restriction on the correlation is minimal. Limitations were the inclusion of only two surrogates and the inclusion of only Mexican-American study participants. Our results need to be confirmed for other ethnic groups. The performance of other indices under longitudinal settings should also be the subject of investigation.
In conclusion, our results suggest that HOMA and the Matsuda index may capture different components of changes in insulin sensitivity compared with SI. It remains to be determined which, if either, of these measures is a better indicator of important biological variables. Until that is known, we suggest caution in applying surrogate measures to studies with longitudinal designs.
Supplementary Material
Acknowledgments
The authors thank the staff and participants of the BetaGene and PIPOD studies.
Funding
This work was supported by National Institutes of Health/National Institute of Diabetes and Digestive and Kidney Diseases grant DK-061628; a Distinguished Clinical Scientist Award and award 7-09-CT from the American Diabetes Association; National Institutes of Health/National Center for Advancing Translational Sciences grant UL1-TR000130; and Kaiser Permanente Southern California Direct Community Benefit funds.
Abbreviations
- FSIGT
Frequently sampled IVGTT
- GDM
Gestational diabetes mellitus
- HOMA2-%S
Updated HOMA of insulin sensitivity
- SI
Minimal model-based estimates of insulin sensitivity
Footnotes
Contribution statement
AHX contributed to the conception and design of the study, to data acquisition, analysis and interpretation, and drafted the article. RMW and TAB contributed to data acquisition and interpretation, and revised the manuscript critically for important intellectual content. All authors approved the final version to be published.
Duality of interest
The authors declare that there is no duality of interest associated with this manuscript.
References
- 1.DeFronzo RA, Tobin JD, Andres R. Glucose clamp technique: a method for quantifying insulin secretion and resistance. Am J Physiol. 1979;237:E214–223. doi: 10.1152/ajpendo.1979.237.3.E214. [DOI] [PubMed] [Google Scholar]
- 2.Shen SW, Reaven GM, Farquhar JW. Comparison of impedance to insulin-mediated glucose uptake in normal subjects and in subjects with latent diabetes. J Clin Invest. 1970;49:2151–2160. doi: 10.1172/JCI106433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bergman RN, Ider YZ, Bowden CR, Cobelli C. Quantitative estimation of insulin sensitivity. Am J Physiol. 1979;236:E667–E677. doi: 10.1152/ajpendo.1979.236.6.E667. [DOI] [PubMed] [Google Scholar]
- 4.Bergman RN, Zaccaro DJ, Watanabe RM, et al. Minimal model-based insulin sensitivity has greater heritability and a different genetic basis than homeostasis model assessment or fasting insulin. Diabetes. 2003;52:2168–2174. doi: 10.2337/diabetes.52.8.2168. [DOI] [PubMed] [Google Scholar]
- 5.Ingelsson E, Langenberg C, Hivert MF, et al. Detailed physiologic characterization reveals diverse mechanisms for novel genetic loci regulating glucose and insulin metabolism in humans. Diabetes. 2010;59:1266–1275. doi: 10.2337/db09-1568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Levy JC, Matthews DR, Hermans MP. Correct homeostasis model assessment (HOMA) evaluation uses the computer program. Diabetes Care. 1998;21:2191–2192. doi: 10.2337/diacare.21.12.2191. [DOI] [PubMed] [Google Scholar]
- 7.Wallace TM, Levy JC, Matthews DR. Use and abuse of HOMA modeling. Diabetes Care. 2004;27:1487–1495. doi: 10.2337/diacare.27.6.1487. [DOI] [PubMed] [Google Scholar]
- 8.Matsuda M, DeFronzo RA. Insulin sensitivity indices obtained from oral glucose tolerance testing: comparison with the euglycemic insulin clamp. Diabetes Care. 1999;22:1462–1470. doi: 10.2337/diacare.22.9.1462. [DOI] [PubMed] [Google Scholar]
- 9.Watanabe RM, Allayee H, Xiang AH, et al. Transcription factor 7-like 2 (TCF7L2) is associated with gestational diabetes mellitus and interacts with adiposity to alter insulin secretion in Mexican Americans. Diabetes. 2007;56:1481–1485. doi: 10.2337/db06-1682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Xiang AH, Peters RK, Kjos SL, et al. Effect of pioglitazone on pancreatic beta-cell function and diabetes risk in Hispanic women with prior gestational diabetes. Diabetes. 2006;55:517–522. doi: 10.2337/diabetes.55.02.06.db05-1066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bergman RN. Toward physiological understanding of glucose tolerance. Minimal model approach. Diabetes. 1989;38:1512–1527. doi: 10.2337/diab.38.12.1512. [DOI] [PubMed] [Google Scholar]
- 12.Buchanan TA, Xiang AH, Peters RK, et al. Preservation of pancreatic B cell function and prevention of type 2 diabetes by pharmacological treatment of insulin resistance in high-risk Hispanic women. Diabetes. 2002;51:2769–2803. doi: 10.2337/diabetes.51.9.2796. [DOI] [PubMed] [Google Scholar]
- 13.Katsuki A, Sumida Y, Gabazza EC, et al. QUICKI is useful for following improvements in insulin sensitivity after therapy in patients with type 2 diabetes mellitus. J Clin Endocrinol Metab. 2002;87:2906–2908. doi: 10.1210/jcem.87.6.8592. [DOI] [PubMed] [Google Scholar]
- 14.Chen H, Sullivan G, Yue LQ, Katz A, Quon MJ. QUICKI is a useful index of insulin sensitivity in subjects with hypertension. Am J Physiol Endocrinol Metab. 2003;284:E804–812. doi: 10.1152/ajpendo.00330.2002. [DOI] [PubMed] [Google Scholar]
- 15.Lorenzo C, Haffner SM, Stancakova A, Laakso M. Relation of direct and surrogate measures of insulin resistance to cardiovascular risk factors in nondiabetic Finnish offspring of type 2 diabetic individuals. J Clin Endocrinol Metab. 2010;95:5082–5090. doi: 10.1210/jc.2010-1144. [DOI] [PubMed] [Google Scholar]
- 16.Buchanan TA, Watanabe RM, Xiang AH. Limitations in surrogate measures of insulin resistance. J Clin Endocrinol Metab. 2010;95:4874–4876. doi: 10.1210/jc.2010-2167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Pisprasert V, Ingram KH, Lopez-Davila MF, Munoz AJ, Garvey WT. Limitations in the use of indices using glucose and insulin levels to predict insulin sensitivity: impact of race and gender and superiority of the indices derived from oral glucose tolerance test in African Americans. Diabetes Care. 2013;36:845–853. doi: 10.2337/dc12-0840. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


