The Dynamical Balance of the Brain at Rest

Abstract

We review evidence that spontaneous, i.e. not stimulus- or task-driven, activity in the brain is not noise, but orderly organized at the level of large scale systems in a series of functional networks that maintain at all times a high level of coherence. These networks of spontaneous activity correlation or resting state networks (RSN) are closely related to the underlying anatomical connectivity, but their topography is also gated by the history of prior task activation. Network coherence does not depend on covert cognitive activity, but its strength and integrity relates to behavioral performance. Some RSN are functionally organized as dynamically competing systems both at rest and during tasks. Computational studies show that one of such dynamics, the anti-correlation between networks, depends on noise driven transitions between different multi-stable cluster synchronization states. These multi-stable states emerge because of transmission delays between regions that are modeled as coupled oscillators systems. Large-scale systems dynamics are useful for keeping different functional sub-networks in a state of heightened competition, which can be stabilized and fired by even small modulations of either sensory or internal signals.

Introduction

Traditional accounts of brain function {Hubel and Wiesel 1968; Barlow 1990} emphasize the role of feedforward information processing in generating from the ‘ground up’ sensory, cognitive, and motor representations that implement behavior. For instance, identifying and reaching for a common object, an apple, involves the creation of a sensory representation of that object, as compared to other objects present in the visual scene; the sensory evidence for the relevant object is fed forward continuously until some threshold for recognition or action is reached. While feed forward sensory analysis can be also modulated by endogenous signals like attention, familiarity, and reward, a central tenet of this view is that any spontaneous or intrinsic activity reflects noise. Internal noise is critical as it produces random fluctuations of spike rate affecting forward transmission of information. Such feedforward ‘sensory-motor’ models have been successful in linking activity recorded from single neurons to perceptual decisions {Newsome and others 1989; Shadlen and others 1996; Shadlen and Newsome 1996}.

However, a different class of models suggests that the brain is not a passive ‘sensory-motor’ analyzer driven by sensory information, but that it actively generates and maintains predictions (priors) about forthcoming sensory stimuli, cognitive states and actions {Llinas and others 1998; Varela and others 2001; Engel and others 2001; Friston 2002}. This class of models emphasize the role of spontaneous activity in maintaining active representations that are modulated rather than determined by sensory information. Accordingly, spontaneous activity should not be random (as often implied by its dismissal as mere “noise”), but organized into structured spatio-temporal profiles that reflect the functional architecture of the brain, possibly encode traces of previous behavior, or even predict future decisions.

Experimental and theoretical evidences reveal that the spontaneous ongoing activity of local cortical circuits result from a global balance between excitatory and inhibitory synaptic currents. Experimental observations in vitro {Shu and others 2003} as well as in vivo {Haider and others 2006} demonstrate an ongoing temporal evolution between excitation and inhibition, which exhibits remarkable proportionality within and across neurons in active local networks. Theoretical studies {Amit and Brunel 1997; Brunel and Wang 2001} indicates that this global balance between excitation and inhibition is ideal for sustaining a stable spontaneous state, and especially for allowing rapid transitions between relatively stable network states. One classic example is attention: a balanced network is particularly suitable for implementing biased competition {Rolls and Deco 2002; Deco and Rolls 2005}, a mechanism to amplify the rate of modulation induced by sensory bottom-up or attentional top-down biases.

At the level of global cortical circuits, it would be relevant if large-scale networks of cortical and subcortical areas would also show a similar dynamic balance, as this arrangement would also facilitate rapid transitions between global network states associated with cognitive functions. Specifically, it would be particularly relevant to find cortical networks that are in dynamic equilibrium or competition with each other.

In the mammalian forebrain neuronal networks in demonstrate rhythmic synchronization in several distinct frequency bands ranging from approximately 0.05 Hz to 500 Hz {Buzsaki and Draguhn 2004}. Rhythmic synchronization in specific frequency bands, as theta, beta, or gamma, result in alternating periods of network inhibition and excitation {Buzsaki and others 2003; Hasenstaub and others 2005; Kopell and others 2000}. These rhythmic and synchronized changes in excitability may have important consequences for neuronal communication. Two groups of neurons may communicate most effectively when their excitability fluctuations are coordinated in time, i.e. when they are coherent, and control of cortical coherence has been proposed as a mechanism for large-scale (distant) communication {Fries 2005}.

Task-induced changes in synchronization or coherence have been reported at level of individual regions during sensory integration {Gray and others 1989; Roelfsema and others 1997}, selective attention {Fries and others 2001; Womelsdorf and others 2006}, working memory {Howard and others 2003; Pesaran and others 2002}, and motor control {Crone and others 1998}; and, between distant cortical regions during object recognition {Varela and others 2001}, working memory {Jones and Wilson 2005}, long-term memory encoding {Fell and others 2001}, visual attention {Gregoriou and others 2009}, and sensory-motor integration {Roelfsema and others 1997}. While task-specific neuronal synchronization or coherence is well-established, less is known about the role of spontaneous or intrinsic activity, i.e. activity not driven by stimuli or tasks. An increasing number of experimental studies are characterized the dynamics of spontaneous activity at rest, i.e. intrinsic, and not stimuli- or task-evoked, with a variety of different methods including EEG {Creutzfeldt and others 1966}; optical imaging {Arieli and others 1996; Kenet and others 2003}, single unit {Engel and others 2001}, and fMRI {Biswal and others 1995; Fox and Raichle 2007}.

Here we review evidence primarily from fMRI studies about the existence of distinct oscillating networks of spontaneous activity, i.e. not stimulus- or task-driven, at rest, or resting state networks (RSN). We show that although RSN strongly reflect the underlying anatomical circuitries, they are also influenced by prior history of network co-activation during active behavior. This functional gating may allow for the retention of prior information, and may influence future task-dependent network recruitment and related behavioral output.

Some RSN may be functionally organized as dynamically competing systems both at rest and during different task conditions. Computational analyses indicate one of such dynamic states, anti-correlation between two networks, can be modeled based on the level of synchronization between different brain areas without the use of long range inhibition. The anti-correlation patterns emerges as the result of noise driven transitions between different multi-stable cluster synchronization states. This multi-stable state emerges in coupled oscillators systems because of transmission delays between regions. This result highlights the relevance of space-time structures for network dynamics, with the spatial component captured by the anatomical connectivity, and the temporal component by the transmission delays. We believe that this and other forms of large-scale dynamics are useful for keeping different functional sub-networks in a state of heightened competition, such that even small modulations of either sensory or internal signals can lead to the stabilization of one or another sub-network, and the generation of task-specific evoked activity. Metaphorically speaking, the resting state is like a tennis player waiting for the service of his opponent. The player is not static, but continues to move with small lateral jumps left and right to be able to react more promptly to a fast ball.

Experimental Evidences of the Resting State Dynamics

fMRI resting state networks (RSN)

fMRI measures local changes in magnetic susceptibility (so called, blood oxygen level dependent, BOLD signal) caused by variations in the capillary concentration of deoxyhemoglobin due to blood flow and blood volume increases in response to neuronal activation. Even at rest, i.e. in the absence of stimuli or task, the spontaneous (intrinsic, not task-evoked) BOLD signal is characterized by slow fluctuations (<0.1 Hz). It was noted more than a decade ago that spontaneous BOLD signal fluctuations are temporally correlated (or coherent) between brain regions of similar functionality {Biswal and others 1996; Hampson and others 2002; De Luca and others 2005; Fox and others 2005} (see {Vincent and others 2007; Greicius and others 2009; Skudlarski and others 2008} for a review). Figure 1 shows the basic phenomenology. The time course of the BOLD signal extracted from the left central sulcus (primary motor cortex, M1) is significantly correlated with time courses from other regions including primary sensory cortex (S1), second sensory cortex (S2), SMA, ventral premotor cortex (vPM), putamen, thalamus (thal), and cerebellum, all regions commonly recruited during motor actions. So regions that activate jointly seem to maintain a high level of spontaneous correlation at rest. The inset shows the high correlation over about 30 minutes between signal time courses in central sulcus and SMA. Regions showing high correlation are rest are said to be ‘functionally’ connected; accordingly, this novel method of analysis of fMRI time series has been labeled either functional connectivity-by-MRI (fcMRI) or resting state-fMRI (rs-fMRI); finally, the ensuing networks of correlation are said to constitute a resting state network (RSN).

Figure 1.

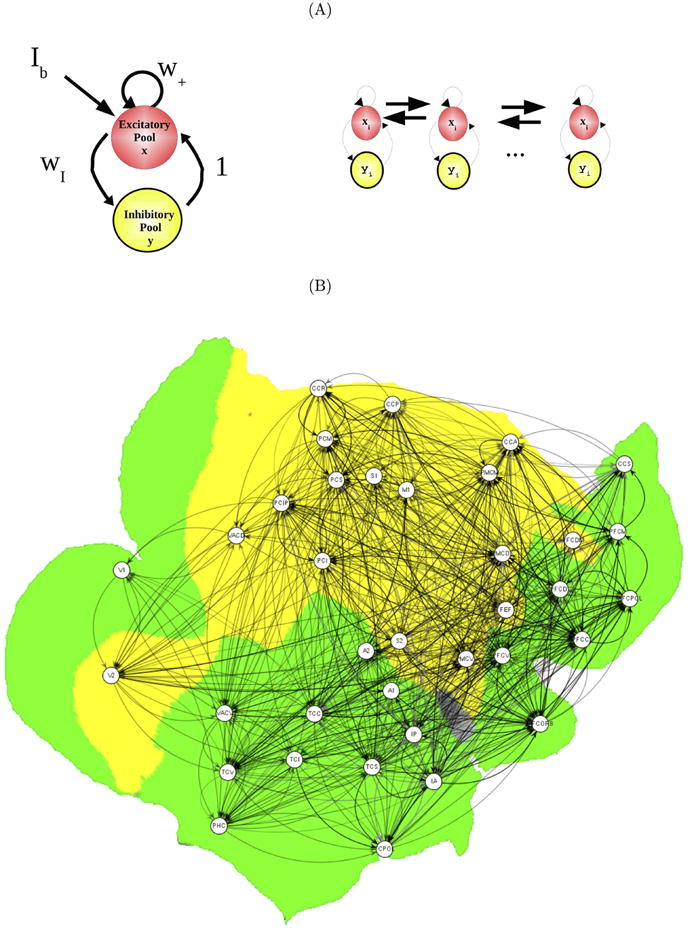
(A) (left) Basic Wilson-Cowan computational module for each node. Excitatory pools are connected with a inhibitory pool. (right) Network architecture built up by Wilson-Cowan units coupled through the excitatory pools. (B) Anatomical plot of the CoCoMac structural connectivity matrix. The colours show the two extracted communities. The green cluster consists mostly of visual areas (with the exception of V2) as well as prefrontal areas. The yellow cluster consists mainly of sensorimotor and premotor areas.

We can repeat this basic experiment over in different cortical regions, and different RSN will be identified. For example, figure 3A (blue regions) shows another network (dorsal attention network, DAN) obtained by calculating a correlation map between a time course extracted at rest from the posterior medial intraparietal sulcus (pIPS), a retinotopic area involved in the control of spatial attention and eye movements, and the rest of the brain. Significant correlation is seen in the homologous region in the right hemisphere, left and right frontal regions corresponding to the frontal eye field (FEF), other regions in the intraparietal sulcus corresponding to areas V3A and V7, and occipital regions like the MT+ complex involved in motion processing. This cortical network is commonly recruited during tasks that require either covert or overt (eye movement) shifts of spatial attention, but also in many other tasks involving the selection/processing of stimuli and actions (eye, arm). Interestingly, this network appears to be anti-correlated at rest with another large scale cortical network, the default-mode network (DMN)(figure 3A orange regions), which has been implicated in the control of internal functions (e.g. episodic memory). The DMN includes the angular gyrus (AG), superior frontal sulcus (SFS), anterior temporal (aTp, medial prefrontal cortex, posterior cingulate, and hippocampus. Note in the inset time series of the BOLD signal from pIPS (DAN) and AG (DMN) over 5 minutes of recordings, and the anti-correlation of the two signals. This raises the possibility that some RSN are functionally organized as dynamically opposing systems (see below).

Figure 3.

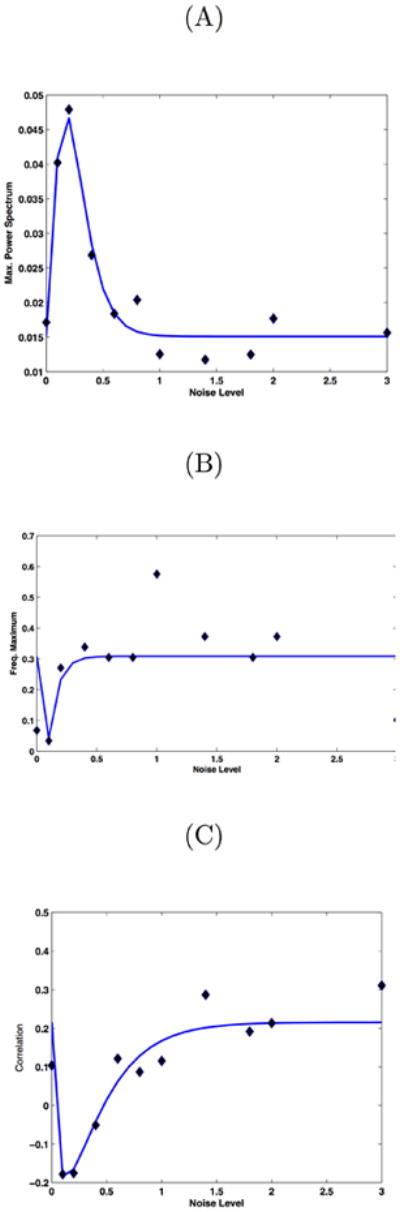
(A): Maximum of the power spectrum peak of the signal given by differences between the level of synchronization between both communities versus the noise level (variance). (B): Maximum in the power spectrum of the signal given by differences between the level of synchronization between both communities versus the noise level. (C): Correlation between the level of synchronization between both communities versus the noise level. Note the stochastic resonance effect that for the same level of fluctuations reveals the optimal emergence of 0.1 Hz global slow oscillations and the emergence of anticorrelated spatio temporal patterns for both communities. Points (diamonds) corresponds to numerical simulations, whereas the line corresponds to a nonlinear least-squared fitting using an alpha-function.

How many RSN are simultaneously oscillating at rest in the human brain? The answer to this question partly depends on some technical details like the MRI scanner field strength and the size of the voxels used to measure the BOLD signal. In general, higher field strength and smaller voxels will lead to a higher number of more spatially localized networks. With these caveats in mind, using a standard scanner (1.5 or 3.0 Tesla) and typical resolution for human studies (3-4 mm), several groups have reported between 6 and 10 reliable RSN including somato-motor, visual occipital and auditory temporal, and several associative networks covering fronto-temporal-parietal cortices (dorsal attention, default, language, and control) {Fox and others 2006; Fox and others 2005; Hampson and others 2006; Dosenbach and others 2007; Cordes and others 2002; De Luca and others 2005; Damoiseaux and others 2006; Mantini and others 2007}. Figure 2 shows a mapping of these different networks onto the same atlas brain which cover about 66% of the total brain volume. More recent approaches are trying to parse out in a data-driven the exact functional parcellation of the resting state functional connectivity matrix {Cohen and others 2008}.

Figure 2.

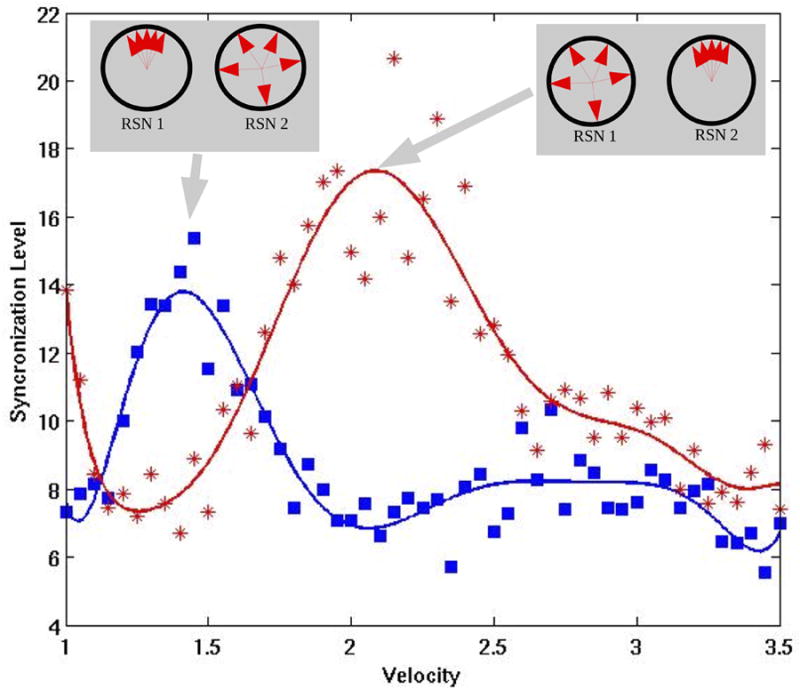
Level of synchronization in each of the two extracted communities as a function of the transmission velocity v. The synchronization level is relatively low for most of the v. There are two regions that show elevated levels of synchronization that correspond to the increase of synchronization in either one of the community clusters: The left bump corresponds to one of the communities and the right bump to the other community. In the working point P between the two synchronization bumps (v=1.65 m/s), the system is expected to show alternates of maximal cluster synchronization in one or the other community because of the underlying fluctuations.

What is the origin of RSN? Based on their topography, it is now well accepted that RSN resemble both functional networks, i.e. regions activated during behavioral tasks {Biswal and others 1996; Hampson and others 2002; De Luca and others 2005; Fox and others 2005} as well as anatomical networks, i.e. regions connected by anatomical pathways {Vincent and others 2007; Greicius and others 2009; Skudlarski and others 2008}. Let's consider anatomical and functional variables separately.

RSN and anatomical connectivity

Anatomical and fMRI connectivity are strongly related, and this is hardly surprising. Both resting state correlation and task-driven responses must involve connections between brain regions. This point is best exemplified by Vincent et al who scanned anesthetized monkeys and found that the pattern of fMRI connectivity obtained by seeding area LIP in posterior parietal cortex closely corresponds to the topography/strength of anatomical connections to/from LIP including regions in prefrontal cortex (FEF) and superior temporal sulcus {Vincent and others 2007}. Similar observations have been obtained in humans by comparing fMRI connectivity with diffusion tensor imaging, a different MR technique that allows fiber tracking of major white matter bundles {Greicius and others 2009; Skudlarski and others 2008; van den Heuvel and others 2009}. Figure 3A compares maps of fMRI correlation between regions of the DAN and DMN in both macaque and humans. Note the similarity between the two maps overall suggestive of the presence of similar functional systems maintained through evolution.

However, the topography of RSN is not identical to anatomical connectivity. In fact some regions can show strong fMRI correlation in the absence of direct anatomical connections. Again in the Vincent et al. study, the peripheral representations of primary visual cortex in each hemisphere showed strong resting fMRI correlation while we know that peripheral V1 representations are not directly connected. It is therefore likely that fcMRI maps reflect not only direct, but also indirect anatomical connections, either through other cortical or subcortical regions.

Interestingly, there are also cases in which fcMRI is not seen when direct anatomical pathways are in place. For instance, motion specific area MT+ shows strong functional correlation with regions in the IPS, but not with visual areas V1-V2 despite being strongly connected with both sets of areas (Figure 3A). Therefore the fMRI correlation signal may reflect some form of functional gating of the anatomical pathway. This gating may reflect a temporal mechanism like presence of synchronized oscillations in spontaneous activity and/or more structural synaptic plasticity of the kind implemented in Hebbian models {Hebb 1949}. It is unknown if the presence of correlation at rest between two regions also impacts synaptic efficiency as expressed in magnitude of activation in the course of a task.

One of the main goals for the future is to explore in a systematic fashion the functional-anatomical architecture of these large-scale networks, in conjunction with computational methods to quantitatively describes the rules underlying their interaction at the global level. Several recent studies have begun to investigate this issue. For example, a recent study that used computational methods to compare anatomical and fMRI connectivity concluded that ‘inferences of structural connectivity from functional connectivity are impractical’, although indirect connections and interregional distance accounted for some of the variance in functional connectivity. Therefore, the large-scale anatomical structure of the human cerebral cortex may constrain but not entirely account for the observed global functional connectivity {Honey and others 2009}.

Influence of task-evoked activation on RSN

One of the most striking observations about RSN is that their topography closely resembles the pattern of task-evoked activation of the same regions during a task. A sensible hypothesis is that the topography of RSN may be sculpted by the history of co-activation between regions belonging to a ‘functional’ network. For instance, if regions of the brain involved in attention selection and generation of eye movements work together many hours a day while we explore the environment, then even at rest these areas may continue to communicate. Patterns of neuronal activity during behavior may entrain patterns of coherence at rest. In non-linear dynamics terms, different RSN represent sets of ‘attractor’ states developed through repetitive activation of the same oscillatory mechanisms, and maintained by intrinsic dynamics at rest. If this hypothesis is correct, then the particular ensemble of RSN commonly observed in the adult brain (visual, auditory, somato-motor, default, dorsal attention, etc.) should include sets of functional areas that tend to activate jointly in most tasks. Conversely, there may well be regions that do not cluster in a network. These regions may be important for control of functions across multiple domains, and they would be expected to flexibly interact for short periods of time with different more domain specific networks. A possible example include the right temporo-parietal junction, a region we suspect is important for shifting between different tasks/networks {Corbetta and others 2008}, and that appears to have limited connectivity with other RSN {Dosenbach and others 2007}.

The evidence supporting this hypothesis is circumstantial at best this point. Similarity in topography between RSN and task-evoked activity suggests but does not demonstrate a causal link. A potentially more specific link may be provided by similarities in network dynamics during active behavior and at rest. As earlier indicated (DAN) and default-mode network (DMN) are anti-correlated at rest. Sometimes referred to as ‘task-positive’ or ‘task-negative’ networks, these two networks are activated in opposite direction by most tasks. Any goal-driven task involving an interaction with the environment (looking, deciding, reaching, etc) strongly activate the DAN while deactivating the DMN {Shulman and others 1997}. Conversely, tasks that involve internal processes, like remembering personal events strongly activate parts of the default-mode network while deactivating the dorsal attention network {Sestieri and others 2009}. Figure 3B shows a task in which subjects search for a coherently moving frame of motion among randomly moving dots. The DAN show strong sustained activations (see map and time course from posterior IPS). In contrast regions in the DMN show strong deactivation (see map and time course from angular gyrus, AG) {Shulman and others 2003}. Interestingly, the degree of deactivation is predictive of performance on the motion task suggestive of a competitive interaction between DAN and DMN {Shulman and others 2007}. It is interesting that this competitive interaction clearly observed during active behavior may also be present in the pattern of spontaneous or intrinsic anti-correlation (see time course from figure 3A showing anti-correlation at rest between pIPS and AG). This relationship would be significant as both networks are involved in control, i.e. must be rapidly deployed as function of behavioral conditions, but are specialized for very different functions, attention to the environment (DAN) or to internal processes (DMN). Such competitive relationship may have developed in the course of evolution, and/or during development, perhaps because of anatomical convergence, hence potential bottlenecks in processing, or because of shared neuro-modulatory influences potentially affecting available processing resources. As later discussed in the computational section this is a highly sensible way to set up a system to afford rapid engagement whenever necessary. It is importance to underscore that the presence of anti-correlation in spontaneous activity between DAN and DMN is not seen with all analyses¹, although its occurrence may be expected on computational grounds based on the underlying anatomical connectivity {Honey and others 2007}.

Finally, the most direct evidence that RSN are shaped by the history of co-activation comes from a recent study showing that the pattern of resting covariance between two RSN, DAN and visual, is specifically changed by acquisition of a new skill. Healthy subjects learned a difficult shape identification task in the left lower quadrant of the visual field. After training learning-specific evoked modulations were observed in the trained quadrant of visual cortex. Critically, there was a significant change post-training in the pattern of spontaneous correlation between DAN and trained visual cortex, which correlated with the degree of acquired competence {Lewis and others 2009}. This experiment shows directly for the first time that entraining a new pattern of task-driven activation leads to the development of a new RSN.

Influence of RSN on task-evoked activation

The other side of the coin is whether RSN, once organized, constrain task-driven activation. In other words, does the ongoing functional organization of spontaneous activity plays a role in determining the pattern of task-driven neuronal activation?

The best available evidence indicates that fMRI RSN in the adult human brain are stationary; that their global topography is not dramatically altered by extreme manipulations of behavioral state; and, that they do not reflect ongoing covert cognitive activity. For instance, no striking global difference is observed going from resting with eyes closed, to eyes open, to fixating {Fox and others 2005}, even if the strength of correlation between specific regions is affected {Golland and others 2007}. RSN topography is also generally preserved by more dramatic manipulations like anesthesia even down to the level of EEG burst suppression {Vincent and others 2007} which eliminates the possibility of ongoing covert cognitive activity, or sleep {Larson-Prior and others 2009}. This relative independence from behavioral states may suggest that RSN reflect a physiological marker of connectional anatomy, perhaps underlying some fundamental ‘house-keeping’ or maintenance process (e.g. synaptic turn-over) {Marder and Goaillard 2006}. However, other data suggest a more direct and functional link between task-evoked and spontaneous activity. Optical imaging studies in cat's visual cortex show that the variability of stimulus-evoked activity is accounted in large part by variation of spontaneous activity {Arieli and others 1996} A similar effect has been reported in human motor cortex where fMRI spontaneous activity accounts for about 70% of trial-to-trial variability of motor evoked response {Fox and others 2007}. Ongoing activity in motor cortex has been also associated with trial-to-trial variability in behavioral performance {Fox and others 2007}. One interpretation of these findings is that task-evoked activity, and by extrapolation behavior, simply reflects modulations of ongoing activity. RSN may then represent dynamic functional states whose flexible combination determines the organization of behaviorally relevant task-networks. However, flexible behavior would seem to require a larger combination of network states than those afforded by RSN or their combination. A more fundamental problem is that the apparent stationarity of RSN, and apparent link with task-evoked activity, may be just an artifact of the slow neuro-vascular coupling. A fundamental next step is therefore a comparison of slow (fMRI) and fast (neuronal) dynamics measured under comparable behavioral conditions and ideally in the same individual.

Neurophysiology of RSNs

It is now well accepted that stimulus-induced changes of the BOLD signal underlie mass action changes in local field potential (LFP) and multi-unit spike rate of neuronal populations included in the recorded fMRI voxel {Logothetis and others 2001; Logothetis 2008}. At least in visual cortex, where most studies have been conducted, the BOLD signal is more closely related to LFP than spikes. This is extensively discussed in recent papers {Logothetis 2008; Goense and Logothetis 2008}, and will not be further reviewed here. Much less is known about the neural basis of spontaneous BOLD signal fluctuations. In 2008, two studies recorded electrocorticography (EcoG), either with grid arrays or deep electrodes, in patients undergoing monitoring of cortical activity for treatment of epilepsy. Nir et al reported positive inter-hemispheric correlation between left and right homologous regions in auditory cortex, a characteristic feature of BOLD RSN, of the band limited power (BLP) in the gamma band (but also in other bands) and multi-unit activity {Nir and others 2008b}. He et al reported a relationship between the spatial topography of BOLD correlation in the somatomotor network and slow cortical potentials (0.1-4 Hz), as well as gamma BLP. Interestingly, while the correlation with slow potentials was independent of whether the subject was awake, or asleep (slow wave and REM), the correlation with BLP gamma was strong only in the awake state and during REM sleep {He and others 2008}. Interestingly, in both experiment the correlation had a 1/f distribution with correlation stronger at lower frequencies (<0.1 Hz). A recent MEG study also found correlates of fMRI RSN (DAN,DMN) with a 1/f distribution of the inter-regional power correlation, with more defined cortical topography at slow (theta, alpha, beta) than high (gamma) frequencies {De Pasquale and others 2010}

A different approach using simultaneous fMRI and EEG recordings has been used to study the electrophysiological correlates of RSN. Two studies have reported a link between DAN and DMN and alpha/beta power changes {Laufs and others 2003; Mantini and others 2007}. Interestingly, even in this case although the fMRI RSN appeared independent (see footnote 1), the EEG analysis showed a positive association of alpha/beta power with DMN, but a negative relationship with DAN. This fMRI/EEG association is consistent with the well-known alpha desynchronization observed during focusing of attention to the environment {Klimesch and others 1998; Sauseng and others 2005}. It is interesting that over time in a state of rest relative power increases in the alpha/beta band correspond to stronger correlation with the ‘internally-directed’ DMN, specialized for controlling internal functions, whereas relative power decreases correspond to a stronger correlation with the ‘externally’ directed DAN. This interpretation is consistent with the hypothesis that the dynamics in these two networks are competitive both at rest and during behavior.

Functions of RSNs

We consider in this last section RSN's putative function and behavioral relevance, on which we have already commented in previous sections. Here, we briefly summarize the main points.

The first hypothesis is that RSN reflect a physiological marker of anatomical connectivity. One possibility under this hypothesis is synaptic turn-over, an energy dependent process well investigated in rodents and crustacean {Marsden}. This is a fundamentally structural and stationary signal unrelated to moment-by-moment information processing, and its extreme version, this hypothesis predicts no correlation with behavioral performance.

However, if we emphasize the observation that RSN topography and strength also relates to the history of network activation (Fire-Wire hypothesis), and potentially to the synaptic efficiency of certain circuits, then some behavioral correlation with established abilities, or with new learning may be expected. Significant correlations of RSN strength with cognitive abilities {Hampson and others 2006}, neurological deficits {He and others 2007}, and recently acquired skills {Lewis and others 2009; Tambini and others 2010} have been reported. The third hypothesis is that RSN reflect a functional spatial and temporal network-wide landscape that facilitates large-scale communication. There are only a few electrophysiological studies on RSN, but they seem to find a consistent relationship with slow cortical potentials, and correlation of the band limited power at slow frequencies (1/f distribution). For theoretical reasons, related to cortical distance and cortical wiring {Buzsaki and Draguhn 2004}, slow cortical fluctuations of excitability may have a role more in large-scale (inter-area) communication. This idea is based on the notion that there may well be a relationship between slow and fast rhythms in the cortex with slow rhythms providing windows of excitability for fast rhythms, neuronal synchrony, and increases in spike rate during tasks. The relationship between BOLD RSN and slow and fast cortical rhythms is being directly explored by a team of scientists in Europe and USA (www.brainsynch.org). One relationship found experimentally in electrophysiological studies is between high gamma synchrony and theta phase {Canolty and others 2006}, and ultra-slow and fast EEG rhythms {Vanhatalo and others 2005}. This hypothesis predicts a positive correlation between RSN or their electrophysiological correlates and on-line (trial-to-trial) behavioral performance {Fox and others 2007; Monto and others 2008}.

The final hypothesis is that RSN code information prospectively. In other words do they play a role in representing expected features of an object, a selected location, a cognitive state, or a prospective action? As RSN are made of spontaneous activity clearly this kind of coding must reflect prior exposure to that particular behavior. The difference as compared to the previous hypothesis is that RSN do not represent only windows for communication but maintain some of the representations that makes an individual (experiences, body and cognitive states). These patterns represent functional-structural ‘priors’ that will constrain task-evoked activity by facilitating states that are more strongly represented in the spontaneous activity. Possible examples would be the relative sensitivity to collinear objects in the visual world or the characteristic tri-modal spatial distribution of saccadic eye movements in the dark.

Resting State as Noise Driven Transitions Between Multistable State}

Under resting state conditions, the brain shows a global dynamics that can only emerges due to its intrinsic characteristics, as it is uncontaminated from tasks and stimuli influence. These intrinsic characteristics are given by the underlying neuroanatomical connectivity matrix, by the temporal delays in the communications between different brain areas, and also by the general level of fluctuations present in the brain. In fact, recent theoretical models {Honey and others 2007; Ghosh and others 2008a} have shown the relevance of the characteristic “small-world” structure of the underlying connectivity matrix between different brain area, using realistic neuroanatomical information on the macaque cortex (CoCoMac; see Kötter 2004}), as well as between regions of human cortex {Honey and others 2009}. In particular, Ghosh {2008a} proposed that the space-time structure of coupling and time delays in the presence of noise defines a dynamic framework for the emergence of the resting brain fluctuations. In that study, fluctuations destabilize the groundstate, producing excursion in the dynamical repertoire of the global brain network that results in oscillations that are structured in the experimentally observed resting state subnetworks.

Another possible scenario {Deco and others 2009} considers that resting state ultra-slow oscillations and in particular the emergence of anti-correlated sub-networks result from fluctuations driven transitions between multi-stable states. In this scenario, multi-stable cluster synchronization states appear in coupled oscillators systems because of the delay of transmission times underwriting the importance of the space-time structure of couplings in networks (see also {Ghosh and others 2008b}), where the anatomical connectivity captures the spatial component and the transmission time delays the temporal component thereof. Figure 1 shows the main elements of these scenario. This scenario considers explicitly the specific link between local neuronal communication and global cortical dynamics, and in particular the interaction between fast local dynamics in the gamma range (40 Hz) and the ultra-slow 0.1 Hz oscillations at the global level. For this, a very simple neurodynamic model for each node is assumed, namely a Wilson-Cowan model that captures node's dynamics by a mean-field-like rate model expressing the coupling between excitatory and inhibitory neurons. In particular, this Wilson-Cowan model is tuned such that each independent node, if disconnected, is silent (low activity regime); but because their working point is very near to a Hopf bifurcation, when coupled, each node starts to oscillate. In particular, one chooses a working point such that the oscillation of each node arising from coupling was in the gamma-band-range of 40 Hz. In this way, keeping the single node dynamics as simple as possible, allows us to focus on the emergence of a complex collective brain dynamic due to the intrinsic properties mentioned above. Furthermore, by considering simple 40 Hz fast oscillations at the single node dynamics, we are able to investigate one potential link between fast local dynamics and slow global fluctuations {Nir and others 2008a; He and others 2008; Monto and others 2008}.

Figure 1A shows the schematic of intrinsic connectivity of each node. The network dynamics is obtained by coupling the single Wilson-Cowan modules through the excitatory pools by using a realistics neuroanatomical connectivity matrix C_ij and delays T_ij,

\begin{eqnarray}

\label{eqnet} \tau \frac{\partial x_i(t)}{\partial t}

& = & -x_i(t) + \phi(I_b+ \sum_j \alpha C_{ji} x_j(t-T_{ji}) - y_i(t)) + \nu_i(t)

\end{eqnarray}

\begin{equation}

\label{eqnet2} \tau′ \frac{\partial y_i(t)}{\partial t} = -y_i(t) + \phi(w_I x_i(t)) + \nu_i(t)

\end{equation}

where the nonlinearity

\begin{equation}

\phi(x) = \frac{c}{1 - \exp{-a(x-b)}}

\end{equation}

is the response function (transforming current into discharge rates) for a spiking neuron with deterministic input, time membrane constant tau. In last equations, C_ii=w₊/alpha, being alpha a parameter regulating globally the coupling strength. In all simulations alpha =0.007, a=0.1, b=40, c=100, tau=1, tau′=0.2$, w_I=1.5, I_b=10 and w₊=1.4. The neuroanatomical connectivity matrix C_ij corresponds to the connectivity matrix of the primate brain based on the CoCoMac neuroinformatics tool {Kötter 2004} (Figure 1B). Kötter und Wanke proposed a coarse parcellation of cerebral cortex into 38 regions, which deliberately reflected broad and rather uncontroversial divisions so that a rough mapping of the human brain appeared feasible {Kötter and Wanke 2005}. Connectivity data from tracer studies collated in CoCoMac were transformed to the regional map using the ORT procedure as described by Stephan {Stephan and others 2000}. In addition, the centre coordinates of the 38 cortical areas were calculated and their distances obtained from the geometry defined in the AAL cortical surface template of a human hemisphere {Tzourio-Mazoyer and others 2002}. Assuming a uniform velocity of transmission v one can derive approximate delays T_ij. The velocity v is adjusted such that cluster synchronization emerges (Figure 1C). In order, to find clusters that are more prone to synchronize, first a division of the network in clusters or communities is identified using a modularity algorithm {Leicht and Newman 2008}. The community structure is given by a group of nodes that have a high density of connections within them, but a lower density of connections between groups. We found that the network can be subdivided in two communities (shown in Figure 1B in two different colours). In fact, these two communities are highly similar to the ones found in {Honey and others 2007}.

Now, the level of cluster synchronization in each community as a function of the velocity of transmission v can be studied. Two hundred forty seconds of the whole network dynamics were simulated. Figure 2 shows the level of synchronization in each of the two extracted communities (the figure plots the maximum of the Kuramoto indices defined in {Deco and others 2009}). The figure shows that the synchronization level is relatively low for most of the v. However, there are two regions that show elevated levels of synchronization that correspond to the increase of synchronization in either one of the community clusters: The left bump corresponds to one of the communities and the right bump to the other community. In the working point P between the two synchronization bumps (v=1.65 m/s), the system is expected to show alternates of maximal cluster synchronization in one or the other community because of the underlying fluctuations. Consequently, fixing the transmission velocity according the working point P, one can now study the optimal level of noise such that the system is optimally driven between the two multistable states of elevated synchronization in one or the other community. The goal is to find an optimal level of noise such that the signal reflecting the level of synchronization in the two communities shows resting state characteristics, i.e. ultra-slow oscillation and anticorrelation. For that, again 240s. of simulations for different levels of noise are simulated. Figure 3A plots the dependence of the maximum of the power spectrum peak of the signal given by differences between the level of synchronization between both communities versus the noise level (variance of the stochastic fluctuations). This gives us a measure of the level of fluctuation that has a maximum effect on the emergence of global oscillations. Note, that the level of synchronization is correlated with the associated BOLD-signal, as we will show in the next section. In all plots, points (diamonds) correspond to numerical simulation results, whereas the lines correspond to a nonlinear least-squared fitting using an alpha-function. As the figure shows, there is a stochastic resonance effect, i.e. there is a specified level of noise for which the optimum is reached. Lower or higher levels of noise attenuate the global 0.1 Hz oscillations. Figure 3B plots the dependence of the location (in frequency domain) of the maximum in the power spectrum of the signal given by differences between the level of synchronization between both communities versus the noise level. This measure specifies the position of the maximum of the global oscillation. The figure shows again a stochastic resonance effect for the same level of noise. Furthermore, at this optimal level of noise, the maximum of the spectrum is given by 0.1 Hz global slow oscillations. Finally, figure 3C plots the level of correlation between the levels of synchronization between both communities versus the noise level. Stochastic resonance at the same level of noise reveals a maximum of the anti-correlation between the two sub-networks, consistent with the experimental data. It is important to remark, not only the essential role of fluctuations, as documented by the presence of a stochastic resonance effect, but also the fact that the optimum level of fluctuations is given simultaneously for the emergence of 0.1 Hz global slow oscillations and the emergence of anti-correlated spatio-temporal patterns for both communities.

Fast and Slow Oscillations

In the last section, we demonstrated that for an optimal level of noise associated with a stochastic phenomenon, a cortical network of oscillators is able to show slow transitions between patterns of synchronization that were anti-correlated at less than 0.1 Hz across the sets in line with a wide range of recent experimental observations. In this section, we show that at that optimal point, the associated BOLD-signal also shows the same sub-networks of anti-correlated ultra-slow oscillating activity.

Figure 4A (left) shows that the optimal working point can reproduce the typical collective brain dynamics found at rest conditions. The black and red curves, respectively, plot the level of synchronization for each of the two communities. The blue curve indicates the differences between the level of synchronization in the two clusters. (The results to relative variations with respect to the mean (i.e. z = (z-<z>)/<z>). The right panel of figure 4A shows the power spectrum of the signal given by differences between the level of synchronization between both communities.

Figure 4.

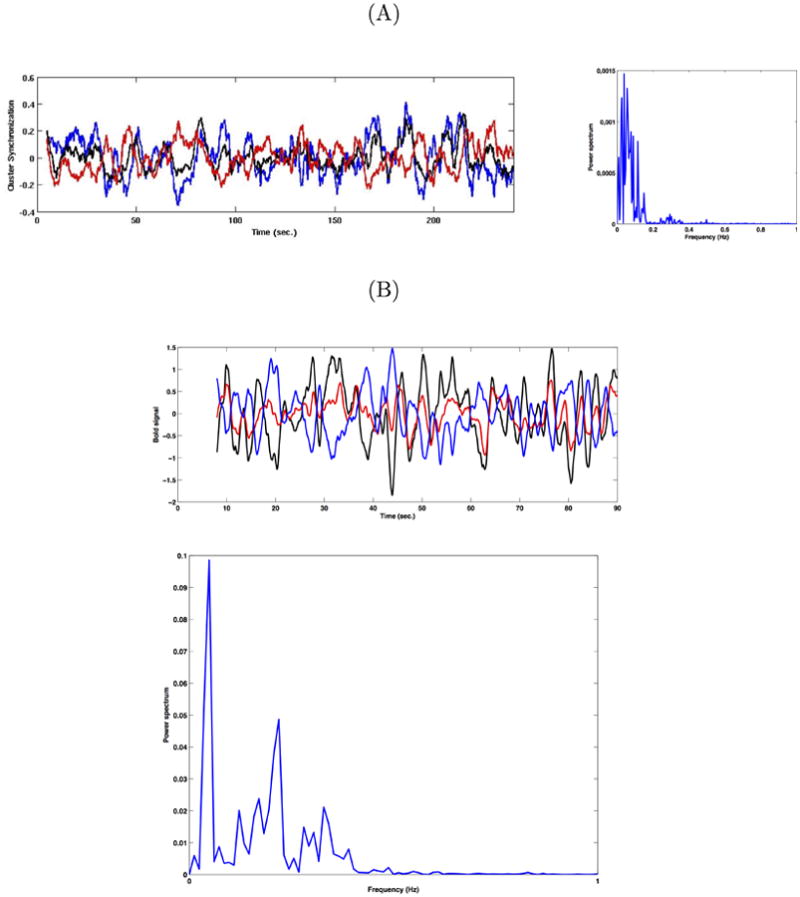
(A) Left: Level of synchronization for each of the two individual communities(community 1: black, community 2: red, difference: blue). Right: Power spectrum of the signal given by differences between the level of synchronization between both communities. (B) Left: BOLD signal for each of the two single communities (community 1: black, community 2: red, difference: blue). Right: Power spectrum of the BOLD signal given by the differences between the level of BOLD signal between both communities.

Figure 4B plots the same activity, but now as evidenced by fMRI, i.e. by plotting the associated BOLD-signal to each of both communities. The BOLD-signal was calculated using the Balloon-Windkessel hemodynamic model of Friston et al. {Friston and others (2003)}, which specifies the coupling of perfusion to the BOLD signal, with a dynamical model of the transduction of neural activity into perfusion changes. Figure 4B (left) plots the BOLD signal calculated from the model at the optimal working point P. The figure shows that the model can reproduce both the slow 0.1 Hz oscillations and the anti-correlation of the BOLD signals of both communities. The black and red curves plot respectively the BOLD signal for each of the two single communities. The right panel of figure 4B shows the power spectrum of the BOLD signal given by the differences between the level of BOLD signal in the two communities. The fact that synchronization predicts BOLD activity is not trivial. This is because the drive to the hemodynamic responses reflects mean population activity, not its synchronization. These results therefore mean that there is a coupling between the degree of synchronization and neural activity that is manifest in elevated BOLD signals. This coupling has been studied in the context of evoked responses {Chawla and others 2000} and in terms of endogenous fluctuations {Chawla and others 1999}. These analyses of simulated spike trends and local field potentials show that in nearly every domain of parameter space, mean activity and synchronization are tightly coupled allowing us to conclude that indices of brain activity that are based purely upon synaptic activity (e.g. functional magnetic resonance imaging) may also be sensitive to changes in synchronous coupling. Thus, our simulations explain why BOLD might be particularly sensitive to slow fluctuations in fast synchronised dynamics.

Conclusion

In this paper, we discussed the experimental evidence characterizing the intrinsic ongoing dynamics of the brain under resting conditions. Many points are worthwhiles to stress: 1) Functional neuroimaging and electrophysiological studies evidence a dynamic baseline of intrinsic (not stimulus- or task-evoked) brain activity during resting wakefulness; 2) This baseline is characterized by slow (<0.1 Hz) fluctuations of functional imaging signals that are topographically organized in discrete brain networks, and by much faster electrical oscillations; 3) The blood oxygenation level-dependent signal fluctuations associated with each network are correlated with the EEG power variations of faster rythms rhythms (including gamma); 4) The extracted networks show a degree of anti-correlation.

From a theoretical point of view, we discussed different scenarios from which these highly structured intrinsic ongoing activities could emerges. In particular, we believe that the “small world”-like type of underlying neuroanatomical connectivity matrix, the delays and in particular the noise play a crutial role. The underlying mechanisms seems to be associated with a stochastic resonance phenomenon by which noise driven transitions between cluster synchronization shows both the ultra-slow and anti-correlation characteristics of the ongoing oscillations.

Our current hypothesis is that these resting state networks represent a finite set of spatiotemporal basis function (or dynamical modes) from which task-networks are then dynamically assembled and modulated during different behavioral states. One form of modulation would be the combination of different networks to mediate behavior, which is apparent in this study. In particular, in the abscence of task and stimulation, the underlying system seems to be optimally tuned for sustaining all the basic dynamical modes activated in a regular and equilibrated way. This fact, may give the network a maximal sensitivity to the system to react as efficient as possible, when a concrete task or stimulation has to be processed.