Dectecting disease variants in case-parent trio studies using the Bioconductor software package trio

Abstract

Case-parent trio studies are commonly employed in genetics to detect variants underlying common complex disease risk. Both commercial and freely available software suites for genetic data analysis usually contain methods for case-parent trio designs. A user might, however, experience limitations with these packages, which can include missing functionality to extend the software if a desired analysis has not been implemented, and the inability to programmatically capture all the software versions used for low-level processing and high-level inference of genomic data, a critical consideration in particular for high-throughput experiments. Here, we present a software vignette (i.e., a manual with step by step instructions and examples to demonstrate software functionality) for reproducible genome-wide analyses of case-parent trio data using the open source Bioconductor package trio. The workflow for the practitioner uses data from previous genetic trio studies to illustrate functions for marginal association tests, assessment of parent-of-origin effects, power and sample size calculations, and functions to detect gene-gene and gene-environment interactions associated with disease.

Introduction

Case-parent trio studies, considering diseased children and their parents, are a popular alternative to population-based case-control studies composed of unrelated individuals for detecting variants underlying common complex disease risk, in part because case-parent trio designs guard against population stratification and the resulting type I error inflation commonly observed in population based studies (Spielman and Ewens, 1996; Laird and Lange, 2006). Software suites for genetic data analysis usually contain methods for case-parent trio designs, including commercially available packages such as GoldenHelix (http://www.goldenhelix.com), and freely available software environments such as PLINK (Purcell et al., 2007, http://pngu.mgh.harvard.edu/~purcell/plink/). PLINK, arguably the most commonly used software suite in the field, is an extremely powerful environment to carry out genetic association analyses, and in addition to a multitude of statistical approaches for population based studies, has a built-in module to carry out the allelic transmission disequilibrium test introduced by Spielman et al. (1993) to assess the marginal SNP effects on the phenotype in case-parent trio studies.

Here, we present a vignette specifically for comprehensive genome-wide analyses of case-parent trio data, using the software package trio written in the open source statistical environment R (http://cran.r-project.org/). The workflow shown here for the practitioner includes functions for marginal association tests, assessment of parent-of-origin effects, power and sample size calculations, and functions to detect gene-gene and gene-environment interactions associated with disease. We hope this vignette can also serve as a template for good statistical practice to carry out reproducible analyses, a critical consideration in particular for high-throughput experiments (Baggerly and Coombes, 2011; Peng, 2011). The trio package is freely available from the Biocon-ductor repository (http://www.bioconductor.org/) and available as open source code and binary (compiled) code for all common operating systems.

For illustration, we use the case-parent trios from the International Cleft Consortium, genotyped on the Illumina Human610 Beadarray and later imputed against the whole genomes of the HapMap3 consortium (e.g., Beaty et al., 2010, 2011; Taub et al., 2012; Murray et al., 2012; Beaty et al., 2013). These case-parent trios were ascertained through a child with an isolated, non-syndromic oral cleft (cleft lip, cleft lip with cleft palate, or cleft palate). DNA samples of about 2,500 case-parent trios recruited from several countries were genotyped at the Center of Inherited Disease Research (CIDR, http://www.cidr.jhmi.edu/) using the Illumina Human610-Quad Beadchip. The observed probe intensities were processed using Illumina BeadStudio, and genotype calls at ~600,000 polymorphic markers were released after initial quality control (for details, see Beaty et al., 2010). These data are now available via dbGAP (http://www.ncbi.nlm.nih.gov/gap). To illustrate the utility of the R functions in the trio package we particularly focus on 32,280 autosomal SNPs from chromosome 8, which contains regions of particular interest (see Beaty et al., 2011; Murray et al., 2012) in 1925 case-parent trios with an oral cleft proband, and genotype data from 297 case-parent trios and 111 SNPs from genes coding for fibroblast growth factors and their receptors (FGF/FGFR genes) previously analyzed, e.g., by Wang et al. (2013). In addition, we demonstrate how trio builds on the Bioconductor package VariantAnnotation to import data from vcf files, to also provide functionality for the analysis of sequencing data.

1 Reading and Manipulating Data

Trio data are most commonly and conveniently encoded via ped files, which can be imported into an R session using the function read.pedfile() from the trio package. The first six columns of these ped files typically contain information about the individuals (in order: family ID, personal ID, father’s ID, mother’s ID, sex of the individual, and affection status) and in the following columns the data for each variant, where two consecutive columns specify the alleles at each locus. The function read.pedfile() accepts and automatically interprets all conventional allele codes (numeric as 1, 2 and possibly also 3, 4, or alphabetic as A and B, or encoded as nucleotides A, T, C, and G), reads SNP identifiers such as rs-numbers if available, and stores the data in a data frame. As an example, the oral cleft data from chromosome 8 can be read into R by

  > pedChr8 <- read.pedfile(“chr8.ped”)

which stores the object pedChr8 in the following format:

 > head(pedChr8[,1:8])
    famid      pid      fatid    motid  sex  affected  rs11780869.1  rs11780869.2
 1  11004  11004_1  11004_3  11004_2    1       2            4            4
 2  11004  11004_2        0        0    2       1            4            4
 3  11004  11004_3        0        0    1       1            4            4
 4  11007  11007_1  11007_3 1  1007_2    1       2            4            4
 5  11007  11007_2        0        0    2       1            0            0
 6  11007  11007_3        0        0    1       1            4            4

The SNP data can also conveniently be stored in genotype matrix format, which for example is necessary for all transmission disequilibrium test functions. In this format, each SNP is represented by one matrix column, where the genotypes are coded as the number of minor alleles, and each block of three consecutive rows comprise the genotypes of a trio’s father, mother, and offspring (in this order). This is conveniently achieved by setting the option p2g = TRUE (ped format to genotype format) in the read.pedfile() function.

 > matChr8 <- read.pedfile(“chr8.ped”, p2g = TRUE)

which stores the object matChr8 in the following format:

 > head(matChr8[,1:4])
         rs11780869   rs3008282   rs2003497   rs12676364
 11004_3         0          1          1            0
 11004_2         0          1          1            0
 11004_1         0          1          1            0
 11007_3         0          1          1            0
 11007_2       NA        NA        NA          NA
 11007_1         0          1          2            0

As default, the minor allele at a SNP is the less frequent allele among the parents in the data set. Alternatively, the function ped2geno() can be applied to the R object pedChr8, to transform pedChr8 into genotype matrix format.

Similarly, a matrix in genotype format can be generated from sequencing data with variant information stored in variant call format (vcf) files, by applying the trio function vcf2geno(). After reading the vcf files with the standard Bioconductor function readVcf() function from the VariantAnnotation package, the matrix in genotype format is obtained by

 > matGeno <- vcfgeno(vcf, ped)

where vcf is the R object obtained from readVcf(), and ped is a data frame in ped format, which only contains the family structure information. By default, the sample names in the vcf files are matched with the personal IDs (and hence, they must be identical), but other options for example based on the row names of the ped object can also be used.

After a matrix in genotype format is generated either with ped2geno() or vcf2geno(), basic data manipulations can be carried out, such as ordering SNPs by their genomic position, which is easily done using the function orderSNPs().

 > matChr8 <- orderSNPs(matChr8, map)

Here, the data frame map consists of columns specifying the SNP name, position, and chromosome (only needed if more than one chromosome is considered), readily available from any annotation file or package. For user convenience, there are specific functions to remove entire case-parent trios (e.g., those with a high percentage of missing data, indicating sample quality issues) and SNPs (e.g., those with very low minor allele frequencies) from the analysis. For example, the line

 > matChr8 <- removeTrios(matChr8, perc.na = 0.2)

removes all trios with at least 20% missing genotype information, and the line

 > matChr8 <- removeSNPs(matChr8, maf = 0.05, perc.na = 0.1)

removes all SNPs with minor allele frequency below 5% or more than 10% missing values.

2 Marginal Association Tests

2.1 Transmission Disequilibrium Tests

Transmission disequilibrium tests (TDTs) are the procedure of choice for testing association of individual SNPs with disease in case-parent trio designs, and either consider alleles (Spielman et al., 1993) or genotypes (Self et al., 1991; Schaid, 1996) as units in the analysis. Both the allelic and genotyopic TDTs (aTDT and gTDT) are available in trio. This package is the first to use the closed-form solutions of the gTDTs derived by Schwender et al. (2012), providing for the first time gTDTs scalable on a genome-wide level. Score tests for the parameter of interest based on the underlying conditional regression of the gTDTs are also available, but for brevity are not discussed here (see Schwender et al., 2012).

The aTDT is applied to all 28,585 markers using the function allelicTDT(), and the five most significant SNPs are displayed.

 > outTDT <- allelicTDT(matChr8)
 > outTDT
      Allelic TDT
 Top 5 SNPs:
           Statistic    p-value
 rs987525     68.26   < 2.2e-16
 rs1519847    52.36   4.612e-13
 rs882083     49.29   2.213e-12
 rs12542837   49.22   2.289e-12
 rs1519841    46.92   7.406e-12

The default is to show the five most significant findings, which can be altered with the top argument, for example showing the ten most significant findings with

 > print(outTDT, top = 10)

An object with all results suitable for export into spread sheet format can be generated by setting top to a non-positive number, e.g.

 > allTDT <- print(outTDT, top = 0)

In this case, the SNPs are not ordered by significance, but are returned in the same order as stored in the data object matChr8.

In contrast to the aTDT which only provides test statistics and p-values, the gTDT additionally allows to specify genetic models, and also returns parameter estimates and standard errors. These statistics are required for example in meta-analyses in which information from different experiments are combined, and often additional risk loci can be identified due to the increase in power (see for example Ludwig et al. (2012) for a meta-analysis of a case parent trio and a case-control study). Here, the gTDT is applied to all SNPs in the object matChr8 by calls to the function colTDT(), with an assumed additive model as default.

 > outgTDT <- colTDT(matChr8)

For dominant or recessive models the argument model can be used, and any unambiguous substring can be given, e.g.

 > outgTDTrec <- colTDT(matChr8, model = “rec”)

carries out a recessive gTDT to all SNPs in the object matChr8. If just a single SNP should be tested, the function tdt() can also be used. For each marker, these functions compute and return the slope parameter in the conditional logistic regression under the specified genetic model and its estimated standard error, the odds ratio with its 95% confidence interval, the test statistic, the corresponding (unadjusted) p-value based on a ${\chi }_1^2$ null distribution, and the effective number of trios used in the maximization of the log-likelihood (i.e., the number of trios with at least one heterozygous parent in the additive model, etc). By default, objects created by calls to colTDT() return the 5 most significant results.

 > outgTDT
         Genotypic TDT Based on 3 Pseudo Controls
 Model Type: Additive
 Top 5 SNPs:
            Coef   OR  Lower  Upper    SE   Statistic   p-Value  Trios
 rs987525   0.577  1.78   1.55  2.05  0.0709     66.4   3.68e-16   709
 rs1519847  0.443  1.56   1.38  1.76  0.0618     51.5   7.11e-13   868
 rs12542837 0.429  1.54   1.36  1.73  0.0616     48.5   3.35e-12   873
 rs882083   0.449  1.57   1.38  1.78  0.0646     48.5   3.36e-12   805
 rs1519841  0.418  1.52   1.35  1.71  0.0614     46.2   1.05e-11   878

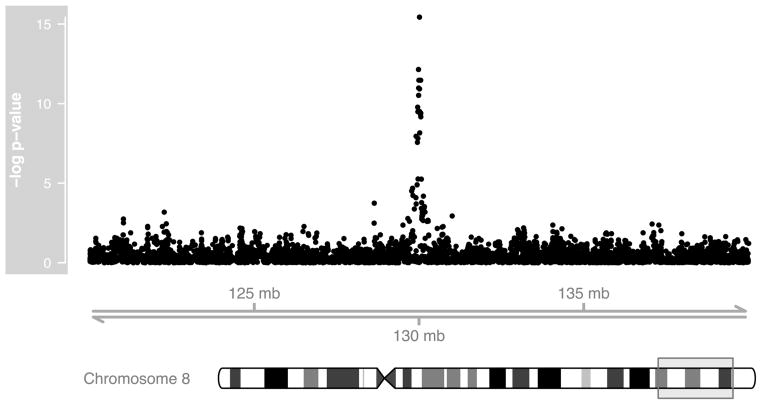
As before, the number of marker results in the output can be modified with the top argument in the print() function. Also, the findings from such an analysis can be displayed by interfacing them with other R packages such as Gviz (Figure 1).

Figure 1.

Results (–log₁₀ p-values, y-axis) from the genotypic TDTs under an additive genetic model are shown as a function of genomic location (x-axis) for a subset of SNPs on chromosome 8. The specific region shown in detail is indicated by a rectangle on the cytoband.

In practice, the true underlying disease model is not known, which led to the suggestion of using the maximum of the three gTDT statistics (additive, dominant, recessive) as the actual test statistic, since specifying an incorrect genetic model may lead to a substantial loss of power (Freidlin et al., 2002). The null distribution of the maximum over these three (highly) correlated test statistics is unknown however, and permutation tests have to be applied to determine statistical significance. While this procedure is generally not scalable on a genome-wide level, case-parent trio design can again be exploited to make a genome-wide determination of p-values based on a sufficient number of permutations feasible (Schwender et al., 2012). In our trio package, this MAX test can be carried out by a call to the functions colTDTmaxTest().

2.2 Sample Size and Power

The closed-form solution for the gTDT also enables an exact analytic calculation of sample size and power of this test (Neumann et al., 2014), and we implemented the procedures for instantaneous sample size and power determinations for the allelic TDT, the gTDTs, and the score tests in the function trio.power(). For a relative risk specified by the argument RR (default RR = 1.5) and a type I error specified by the argument alpha (default alpha = 5 * 10^-8, the value commonly used for genome-wide significance), the power is calculated if the sample size n is specified, or the sample size is calculated if the power beta is given. For minor allele frequencies of 0.1 and 0.2, a desired power of β = 0.8, and the default values of RR and alpha, the sample sizes required for the statistical tests mentioned above (under additive or dominant models) are close to the number of trios available in our oral cleft study.

 > trio.power(maf = c(0.1, 0.2), beta = 0.8, model = c(“add”, “dom”))
      Trio studies sample size calculation
   Test         Model  MAF alpha   RR  beta  Trios
 1 gTDT       additive  0.1   5e-08   1.5   0.8  2524
 2 gTDT       additive  0.2   5e-08   1.5   0.8  1607
 3 gTDT      dominant  0.1   5e-08   1.5   0.8  2771
 4 gTDT      dominant  0.2   5e-08   1.5   0.8  1950
 5 Score       additive  0.1   5e-08   1.5   0.8  2505
 6 Score       additive  0.2   5e-08   1.5   0.8  1596
 7 Score      dominant  0.1   5e-08   1.5   0.8  2749
 8 Score      dominant  0.2   5e-08   1.5   0.8  1935
 9  aTDT  multiplicative  0.1   5e-08   1.5   0.8  2505
 10  aTDT  multiplicative  0.2   5e-08   1.5   0.8  1596

2.3 Parent-of-Origin Effects

Parent-of-origin effects are particularly important to consider when studying birth defects such as oral clefts, because the maternal genotype controls also the in utero environment of the developing fetus, and separating maternal genotypic effects from imprinting effects remains an important question (Wilkins and Haig, 2003; Weinberg and Umbach, 2005). The Transmission Asymmetry Test (TAT; Weinberg et al., 1998) and the Parent-of-Origin Likelihood Ratio Test (PO-LRT; Weinberg, 1999b) are implemented in trio as functions colTAT() and colPOlrt(), respectively, to provide methods for assessment of parent-of-origin-effects. For the latter we receive the following output.

 > poOut <- colPOlrt(matChr8)
 > poOut
         Parent-Of-Origin Likelihood Ratio Test
 Top 5 SNPs:
          LL (with) LL (without)  Statistic   P-Value
 rs4921798   -191.4       -201.5    20.19  7.026e-06
 rs13259591   -379.7      -389.6   19.76  8.770e-06
 rs4311638   -604.7       -614.6   19.69  9.100e-06
 rs2570683   -613.1       -621.5   16.65  4.487e-05
 rs1460172   -522.4       -530.2   15.64  7.645e-05

As before, by default the results from the top 5 markers are shown, including the values of the maximized log-likelihoods for logistic regression models with and without a term for the parent-of-origin effect, the likelihood ratio test statistics, and their corresponding p-values.

For the TAT, similar to the allelic TDT, the test statistics and corresponding p-values are computed for each SNP. Originally, matings between two heterozygotes were excluded because transmission can be ambiguous, however, in some implementation such as PLINK (Purcell et al., 2007) these ambiguous transmissions are counted as 0.5 for both mother and father. The function colTAT() provides an argument bothHet to govern the contribution of the heterozygotes to the test statistic, with bothHet = 0 as default, leading to the original TAT.

3 Gene-Environment Interactions

3.1 Gene-Environment Tests with Binary E

An additional feature of the gTDT compared to the allelic TDT is that the model can be readily extended to test for gene-gene and gene-environment interactions, by simply including interaction terms in the conditional logistic regression model. For gene-environment tests, these conditional logistic regression models include one term for the SNP main effect and one term for the gene-environment interaction (the model does not contain a term for the environmental variable itself, since its value is always identical within a trio which constitutes the grouping factor, and thus the main environmental effect is not identifiable; Maestri et al., 1997; Schaid, 1999).

In the vast majority of analyses the environmental factor is binary (for example given as indicator of maternal smoking or alcohol consumption, exposure to a pollutant, etc), and in that instance the test statistic for the gene-environment interaction term in the gTDT has again a known closed-form solution (Schwender et al., 2012), also implemented in trio. For example, testing for differences in genetic effects between males and females, we can invoke the colGxE function

 > outGxE <- colGxE(matChr8, gender)

assuming the children’s records for gender in the object gender are in the same order as the trios in matChr8. Otherwise the trio / family IDs corresponding to the entries in gender can be specified using the argument famid.

As in colTDT(), an additive mode of inheritance is assumed as default, but other genetic models can also be selected by specifying the argument model. The function colGxE() computes the parameter estimates, estimated standard errors, odds ratios, 95% confidence intervals, test statistics, and the (unadjusted) p-values for both the SNP main effects and the gene-environment interaction terms. In addition, similar to the marginal calculations, the effective number of trios contributing to the likelihoods are determined, as well as the odds ratios for the exposed cases with the corresponding 95% confidence intervals (assuming addGandE = TRUE is used as an argument in the function, which is the default). Further, the 2 degrees of freedom Wald and likelihood ratio tests simultaneously assessing the SNP main effect and the interaction with the environment are carried out by default for each marker, as well as a 1 degree of freedom likelihood ratio test assessing the interaction term alone.

For our example, the default output for outGxE is displayed in the supplementary materials. As before, the default is to show statistics for the five most significant gene-environment interactions determined by the p-values of the 1 degree of freedom GxE Wald test. The function getGxEstats() can be applied to the output of colGxE() to obtain these statistics for all gene-environment interactions, either unsorted or ordered by the p-values of one of the performed tests. In our example, none of the markers on chromosome 8 shows a genome-wide significant difference between males and females (nor was this the case for any marker on any other chromosome, see the supplementary material in Schwender et al., 2012, for details).

3.2 Gauderman’s 2-step Procedure

Additional power to detect gene-environment interactions can be obtained by using the two-step procedure proposed by Gauderman et al. (2010). In the first step, a logistic regression is used for each marker with the binary environmental factor as a dependent variable, and the sum over the genotype codings for the respective parents as an independent variable. In the second step, the same gTDT as described above is used to test for gene-environment interactions only for those markers achieving a p-value smaller than a pre-determined significance level (α₁) in step one. The gain in power stems from the two test statistics for each marker being (asymptotically) independent, and thus, fewer markers are investigated in step 2. If in the function colGxE() the argument alpha1 is set to a value between 0 and 1, Gauderman’s 2-step procedure with a step 1 significance level of α₁ is carried out. In colGxE(), a ${\chi }_1^2$-distribution is employed as asymptotic null distribution to determine the p-values. If this is a concern, the function colGxEperm() can be used instead to calculate p-values based on a permutation null distribution.

4 Epistatic Interactions

4.1 Pairwise Interactions

Interactions between specific pairs of SNPs via a gTDT can be tested using the function tdtGxG(), all pairs of SNPs comprised by a matrix in genotype format can be tested using the function colGxG(). By default (argument test=“epistatic”) the 4 degrees of freedom likelihood ratio test proposed by Cordell (2002) for epistatic interactions is applied, comparing the likelihoods of conditional logistic regression models with and without four terms encoding the interaction (two orthogonal vectors coding each bi-allelic marker). Alternative approaches include a conditional logistic regression (”screening”) model with only one term for the interaction (test = “screen”), a model containing additional terms for the two main effects (test = “full”), and a likelihood ratio test comparing the likelihoods of the full model with the reduced model (main effects, no interaction; test = “lrt”). A faster implementation for the screening model is also available (fastGxG()). As before, by default an additive genetic model is assumed for all SNPs, with alternatives available (model = “dominant” and model = “recessive”, for dominant and recessive models, respectively).

Commonly, only interactions from different specific regions are of interest, for example epistatic interactions between markers from separate candidate genes. The argument genes in colGxG() and fastGxG() provides a convenient approach to carry out this task. For example, if we consider the FGF and FGFR gene family data analyzed by Wang et al. (2013) and store these data in the matrix matFGF in genotype format, then interactions between SNPs from different FGF genes can be tested by constructing a vector genes using an object with the gene names, and specifying the number of SNPs in the respective genes. In this example this yields 5,322 pairwise interactions to be tested, for example using Cordell’s 4 degrees of freedom test for epistatic interactions

 > outGxG <- colGxG(matFGF, genes = genes)

The default output contains the values of the log-likelihoods, the test statistics, the miminal p-values, and the gene names for the five most significant interactions.

 > outGxG
       Genotypic TDT for Epistatic Interactions (Using 15 Pseudo Controls)
  Top 5 SNP Interactions (Likelihood Ratio Test):
                      LL (with IAs)  LL (w/o IAs)  Statistic   P-Value  Genes
  rs2043278 : rs12870202       -638.7       -650.6    23.85  8.544e-05   18:9
  rs1482679 : rs3934591        -630.3       -639.2    17.74  0.001385  10:18
  rs4733930 : rs2981427        -667.9       -675.9    15.97  0.003055  R1:R2
  rs6887323 : rs1893047        -554.7       -562.2    15.14  0.004429   18:3
  rs1384449 : rs2981430        -673.6       -680.8    14.34  0.006292  10:R2

Alternatively, the fast screening test described above runs about two orders of magnitude faster:

 > outGxGfast <- fastGxG(matFGF, genes = genes)

The difference in computing time is due to the much higher complexity of the Cordell test where conditional logistic regression models with four and eight parameters are numerically fitted using an iterative procedure, while in the screening test the likelihood is first converted to a form which is much easier to maximize than the standard expression for the likelihood (see the supplementary material to Schwender et al., 2012), since maximization only applies to one parameter.

4.2 Higher-order Interactions

Trio Logic Regression

Detecting higher-order SNP interactions is foremost a high-dimensional search problem, and for case-parent trios in particular few such approaches exist. Trio logic regression (Li et al., 2010), an adaptation of logic regression (Ruczinski et al., 2003) to case-parent trio data implemented in the trio package is one such method. The algorithm considers all possible interactions of SNPs (encoded as two binary variables in dominant and recessive coding) by using a stochastic search algorithm (simulated annealing; Koza, 1993) to directly search for a Boolean combination of these binary (“logic”) terms. Trio logic regression can be carried out using the function trioLR() in the trio package. We describe this more specialized procedure and present R code in the Supplementary Materials (Section 3.1).

Trio Feature Selection

Since trioLR() is based on a stochastic search algorithm, repeated applications of the algorithm to the same data often yield different and competing models, for example consisting of different SNPs from the same LD block. To stabilize the search for interactions and to quantify the importance of these interactions on disease risk, Schwender et al. (2011) proposed a method called trio Feature Selection (trioFS). In this resampling-based procedure, trio logic regression is applied to several bootstrap or subsamples of the data, and the out-of-bag trios in each iteration are used to determine the importance of the detected interactions, and to rank these interactions by their influence on disease risk. We describe this procedure and present R code in detail in the Supplementary Materials (Section 3.2).

Discussion

In this manuscript, we presented a software vignette for genome-wide analyses of case-parent trio data using the open source Bioconductor package trio, which includes functionality for marginal association tests, assessment of parent-of-origin effects, power and sample size calculations, and functions to detect gene-gene and gene-environment interactions. This approach allows for completely reproducible analyses and results also in conjunction with the Sweave environment (Leisch, 2002). In addition, the objects created by trio functions can easily be interfaced with other functionality provided by specialized packages such as Gviz for visualization (see Figure 1), or can be exported and made available for example as input into meta-analyses (see for example Lud-wig et al., 2012). All functions presented in this document are implemented in the Bioconductor package trio version 3.2.1 and later, available at http://www.bioconductor.org/. Some additional functionality not presented here is available in trio, as documented in the online manual at http://www.bioconductor.org/, and also available by calling

 > vignette(“trio”, package=“trio”)

One example for additional functionality is a method for efficient retrospective simulation of case parent trios where disease risk can also depend on complex gene-gene and gene-environment interactions (as described in Li et al., 2013). We also offer an implementation of the EM algorithm proposed by Weinberg (1999a) in the function colEMlrt(), based on a likelihood-based method including genetic information from incomplete trios, thereby not suffering from a loss of power and induced bias, compared to a complete case analysis (see Curtis and Sham, 1995).

Open source Bioconductor packages such as trio can readily be extended, and we plan to make updated software releases available to the community in the future. Additional functionality will for example include methods to test for epistatic interactions when markers are from the same haplotype block as proposed by Cordell and Clayton (2002), in addition to the ones currently available assuming unlinked markers (see Cordell, 2002). We also plan a major extension of the available functionality in the future by incorporating methods for copy number variant analyses, such as the MinimumDistance approach to detect de novo DNA copy number deletions associated with disease (Scharpf et al., 2012; Younkin et al., 2014).