High Speed All Optical Nyquist Signal Generation and Full-band Coherent Detection

Abstract

Spectrum efficient data transmission is of key interest for high capacity optical communication systems considering the limited available bandwidth. Transmission of the high speed signal with higher-order modulation formats within the Nyquist bandwidth using coherent detection brings attractive performance advantages. However, high speed Nyquist signal generation with high order modulation formats is challenging. Electrical Nyquist pulse generation is restricted by the limited sampling rate and processor capacities of digital-to-analog convertor devices, while the optical Nyquist signals can provide a much higher symbol rate using time domain multiplexing method. However, most optical Nyquist signals are based on direct detection with simple modulation formats. Here we report the first experimental demonstration of high speed all optical Nyquist signal generation based on Sinc-shaped pulse generation and time-division multiplexing with high level modulation format and full-band coherent detection. Our experiments demonstrate a highly flexible and compatible all optical high speed Nyquist signal generation and detection scheme for future fiber communication systems.

The bandwidth demand of the network data service continues to grow at around 30% to 60% per year, driven by more and more video streaming and proliferation of cloud computing, social media, and mobile data delivery in both long haul backbone and short haul optical networks¹,²,³,⁴,⁵,⁶,⁷,⁸,⁹,¹⁰. Considering the requirement of cost reduction per bit per Hz, higher-speed underlying optical transmission interfaces and higher spectrum efficiency technology is becoming more and more important. The technology options for transmission with higher bandwidth efficiency are being intensively studied, which comes in two major categories: reducing the signal spectrum bandwidth requirement or increasing the modulation levels¹¹,¹²,¹³,¹⁴,¹⁵,¹⁶,¹⁷,¹⁸,¹⁹,²⁰,²¹,²²,²³,²⁴,²⁵,²⁶. The former uses orthogonal multiplexing technologies based on optical or electrical waveform generation, known as the orthogonal-frequency-division-multiplexing (OFDM) in frequency domain or Nyquist pulse technology in time domain¹¹,¹²,¹³,¹⁴,¹⁵,¹⁶,¹⁷,¹⁸,¹⁹,²⁰,²¹; the latter uses multi-level advanced modulation formats enabled by coherent detection, such as QPSK, 16-QAM, 64-QAM and even higher order QAMs²²,²³,²⁴,²⁵,²⁶. Until now, OFDM with high-order modulation formats has been widely investigated, using both electrical and all optical OFDM signal generation¹²,¹³,¹⁴,¹⁵. Especially in Ref. [15], a 26 Tb/s line-rate super-channel transmission system utilizing all-optical OFDM has been demonstrated based on 16QAM and coherent detection. Compared with OFDM, Nyquist signal transmission has several unique advantages such as lower receiver complexity, lower receiver bandwidths and lower peak-to-average power ratios which give better performances under fiber nonlinear impairments¹⁶,¹⁷,¹⁸,¹⁹,²⁰,²¹,²⁷,²⁸. The high transmission capacity with high spectrum efficiency has also been demonstrated by the single-laser 32.5 Tbit/s Nyquist WDM transmission based on 12.5GBaud PDM-16QAM with 325 optical carriers in²⁷. However, most Nyquist pulse-shaping methods for each carrier reported are either too complex¹⁶ or restricted by the electronics speed because of the limited sampling rate and limited processor capacities¹⁷,¹⁸,¹⁹,²⁰,²¹,²²,²³,²⁴,²⁵,²⁶,²⁷.

Most recently, a novel all-optical method to produce Sinc-shaped Nyquist pulses of very high quality has been proposed based on the direct synthesis of a rectangular shaped and phase-locked frequency comb in²⁸. However, the full-band modulation, multiplexing and detection are not investigated in this work. Although Nyquist signal modulation, multiplexing and detection is similar to the optical time-division multiplexing (OTDM) in previous works²⁹,³⁰,³¹,³², some important features are not considered for Nyquist signals. When we look at the previous OTDM works, the most recent experiment has achieved a symbol rate of 1.28 Tbaud and a single-channel bit rate of 10.2 Tb/s with RZ 16-QAM modulation and coherent detection. However, the local oscillator (LO) is not free-run, and a precisely synchronized and complicated receiver is needed for channel multiplexing²⁹,³⁰. In order to detect the signal in each time division, a large number of receivers are needed in normal OTDM signal detection. In addition, the OTDM relies on short pulses occupying large bandwidth in the frequency domain which reduces the spectral efficiency²⁹,³⁰. The combination of Nyquist pulse generation and OTDM system is reported in³¹,³²,³³,³⁴. However, these works are mainly on the on-off keying or differential phase-shift keying. Higher-order modulation and coherent detection are not mentioned in these works. Again, the receivers in these works³¹,³²,³³,³⁴ are typical OTDM one with complicated channel demultiplexing setups. In addition, as analyzed in²⁸, the Nyquist pulses in³³,³⁴,³⁶ are not an optimal one but with very large roll-off factors (0.4 or even 0.5). In³⁶, the optical pulse-shaper yields the worst Sinc-approximation compared with digital and electrical method. Therefore, multiplexing using this kind of pulses results in a non-optimal use of bandwidth.

Therefore, in this paper, we report the first experimental demonstration of high speed all optical Nyquist signal generation based on Sinc-shaped pulse generation and time-division multiplexing with high level modulation format and coherent detection. A developed all optical Nyquist pulse generation method is proposed and demonstrated in our experiments based on the radio frequency driven Mach–Zehnder modulators (MZM) and band-pass optical filter, which is more flexible and compatible compared with previous works. High-order modulated Nyquist pulse with 32.5, 62.5, 75 and up to 125GBaud QPSK signals are multiplexed. Different with regular OTDM system with complicated demultiplexing setup, the generated and multiplexed Nyquist signals are detected as one full signal using a high speed digital coherent receiver. The Nyquist signals are sampled and off-line processed using digital signal processing algorithms. To the best of our knowledge, it is the highest baud rate Nyquist QPSK signal generation, coherent detection and digital processing record. Our experiments demonstrate a highly flexible and compatible all optical high speed Nyquist signal generation and detection scheme for future fiber communication systems.

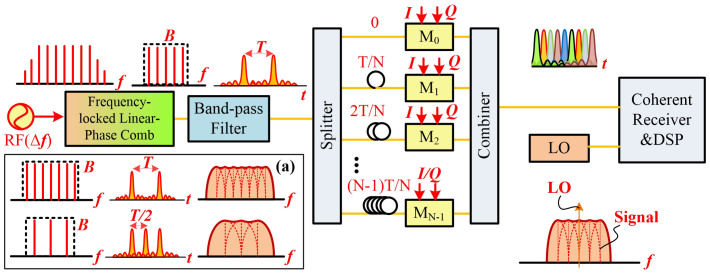
Fig. 1 shows the principle of the all optical Nyquist pulse generation, high-order formats modulation based on inphase and quadrature (I/Q) modulators, multiplexing and digital signal processing. The flexible Nyquist pulse is generated by using a frequency-locked, linear-phase comb source cascade with a tunable band-pass filter (BPF). The frequency-locked comb source can be realized by the radio frequency (RF) driven cascaded Mach–Zehnder modulators (MZM), of which each sub-carriers are with linear phase relation²⁸. The sub-carrier frequency spacing and the total bandwidth of the comb are tunable, which can be realized by adjusting the frequency of RF signal and the pass-band of the BPF. This method for all optical Nyquist pulse generation is developed from the previous work in²⁸. Different with the method in²⁸, we add one tunable BPF here. There are two main advantages by adding on BPF. First, the undesired side-bands can be greatly suppressed to reduce the crosstalk by using the BPF. The results in²⁸ show the power suppression of unwanted components is only 21–27 dB. However, the power suppression of unwanted higher-order sidebands can be larger than 40-dB by using the BPF. Second, one can easily adjust the time-division channel numbers by changing the pass-band bandwidth of BPF, without changing the bias and driven voltage which is quite sensitive and hard to matching each other as analyzed in²⁸. Assuming the N tone frequency-locked comb with central frequency f₀, carrier spacing of Δf, and equal amplitude E₀/N, then time-domain expression of the optical field of the comb can be expressed as

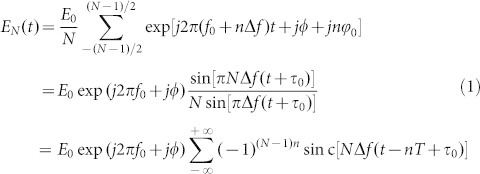Here T = 1/Δf, which is the pulse repetition period. We define a time delay τ₀, which satisfies ϕ₀ = 2πΔfτ₀.Therefore, for a N tone frequency-locked comb with linear phase and equal amplitude, the time domain optical signal is a periodic Sinc-shaped Nyquist pulse with period of T and zero-crossing pulse wide of 2T/N.

Figure 1. The principle.

All optical Nyquist pulse can be generated by a frequency-locked comb source cascaded with a band-pass filter. The high-order formats modulation is realized by inphase and quadrature (I and Q) signal modulation; Nyquist signal generation can be realized by time-domain multiplexing; Full-band signal coherent detection and digital signal processing can be realized by a common coherent detection setup.

Assuming the bandwidth of BPF is B, the tone number of the comb is N = B/Δf. Changing the bandwidth of the BPF or the comb carrier spacing can change the pulse width and also the repetition period as shown in inset (a) in Fig. 1. The periodic Sinc-shaped Nyquist pulse sequence is then split into N branches for independent modulation with accurate delay of t_n = nT/N + KT, here n = 0 ~ N-1 and K is any non-negative integer. The symbol duration for multiplexed Nyquist signal is T/N. After combination, a modulated Nyquist signal with baud rate of B or NΔf can be obtained. For the Nyquist pulse before modulation, the roll-off factor is practically zero with the rectangular comb spectrum. However, as analyzed in²⁸, since the modulation in time-domain corresponds to a convolution in frequency domain; the spectrum of the modulated Sinc-shaped pulses is given by the convolution of the frequency comb and the frequency representation of the modulating signal. Therefore, the spectrum of modulated Nyquist pulse is actually broadened after modulation and the spectrum roll-off or excess bandwidth is no longer zero.

It is worth noting that this actual excess bandwidth, as a ratio of the Nyquist frequency, does not depend on the roll-off factor of the unmodulated pulses, since the factor is zero before modulation. The Nyquist bandwidth of the signal is

The modulation baud rate for each pulse is Δf. Therefore, as shown in figure above, the effective bandwidth after modulation is B_effective = (N + 1) Δf. Thus, the effective excess bandwidth and effective frequency roll-off factor after modulation is

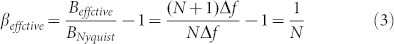Therefore, the effective roll-off factor (Note: Here the effective roll-off should be delimited from the general used roll-off factor for raised-cosine signals; We use the term “effective roll-off factor” to describe the excess bandwidth occupied by the Nyquist signal after modulation) or the excess bandwidth of modulated Nyquist signal is β_effctive = 1/N. The effective roll-off factor after modulation versus the tone number is shown in Fig. 2. We can see that, 0.2 and 0.1 effective roll-off factor after modulation can be obtained when the comb is with 5 or 10 tones. At the coherent receiver, one free-run continuous wave (CW) local oscillator (LO) laser working at the central frequency of the comb is used for coherent homodyne beating. As mentioned before, the full-band coherent receiver is simpler compared with the typical OTDM receiver reported in²⁹,³⁰,³¹,³²,³³,³⁴,³⁵. The simpler receiver setup mainly shows in two aspects: the reduced number of receivers and the free run LO. Instead of using a large number of receivers of smaller bandwidth, we propose to use one full-band receiver with wider bandwidth. The receiver size can be reduced and the structure can be simplified. It is easier for integration. On the other hand, as shown in²⁹,³⁰, in order to get the right time slot, the receiver-side LO should be strictly synchronized pulse source. It is hard to implement such synchronization in practical system. However, in our experiment, the LO is commercial available, free-run, CW ECL, which is quite easy for implementation. No strict synchronization pulse demultiplexing²⁹,³⁰,³¹,³²,³³,³⁴ or comb source LO³⁵ is used in the receiver side, while a full-band coherent detection and digital signal processing (DSP) is applied. The DSP is based on regular algorithms and subsystems, which is commonly used in coherent system³⁷,³⁸,³⁹,⁴⁰,⁴¹.

Figure 2. The effective roll-off factor after modulation versus the tone number.

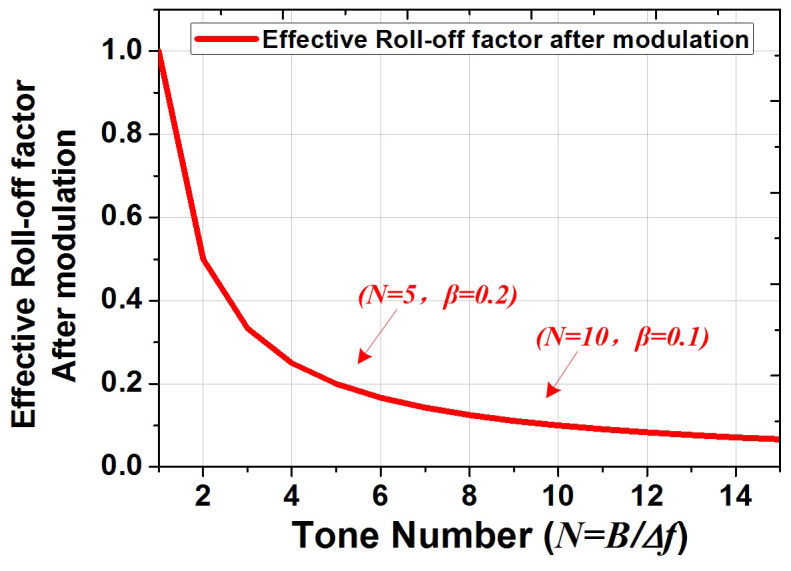
The effective roll-off factor (or the excess bandwidth) of modulated Nyquist signal is β = 1/N.

Results

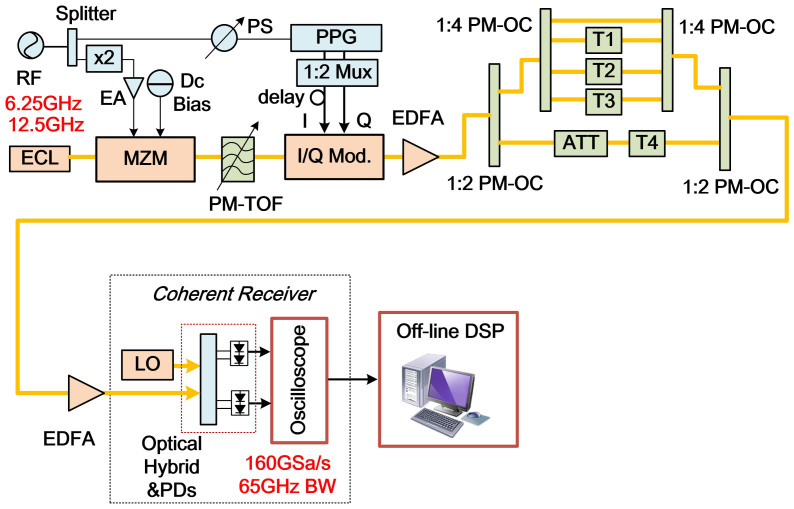
Here we present a proof-of-concept experimental setup for all-optical Nyquist pulse generation, signal modulation with high order modulation formats and full-band coherent detection with one receiver. As shown in Fig. 3, all-optical Nyquist QPSK signal are generated and coherent detected. One external cavity laser (ECL) is used as the light source with wavelength at 1549.50 nm, linewidth less than 100 kHz and output power of 14.5 dBm. One commercial MZM driven by the RF source is used for the frequency-locked comb generation. Here, we choose RF at 6.25 and 12.5 GHz with a 1:2 frequency doubler for the comb generation with 12.5 and 25-GHz carrier spacing, respectively. One electrical amplifier (EA) is used to boost the amplitude of the RF signal. It is worth noting that the voltage of the drive RF signal and the DC bias should be adjusted simultaneously and matching each other to obtain a flattened and linear phase multi-tones. In our case, we choose the driving voltage about 2V_pi and the DC bias about 0.52V_pi and V_pi is half-wave voltage of the modulator. One polarization-maintaining tunable optical filter (PM-TOF) is used to choose the comb tones. The PM-TOF is the commercial wavelength- and bandwidth-tunable optical band-pass filter (Alnair Lab, BVF-200). The filtering bandwidth is variable from 0.1 nm to 15 nm, and the center wavelength is tunable from 1525 nm to 1610 nm. It has an ideal flat-top response with sharp roll-off > 150 dB/nm and the out-of-band suppression is about 50 dB. It has negligible chromatic dispersion less than 0.1 ps/nm. The TOF does not compensate the phase relation since the linear phase can be easily achieved. However, we can use this filter to suppress the 2nd-order sidebands to equalize the power to achieve more flattened comb. The power difference of the generated 5-tone comb after the filter is less than 0.3 dB.

Figure 3. Experiment Setup of all-optical Nyquist QPSK signal generation and full-band signal coherent detection.

(RF: radio frequency; PS: phase shifter; PPG: programmable pulse generator; EA: electrical amplifier; ECL: external cavity laser; MZM: Mach–Zehnder modulator; I/Q Mod.: In-phase and quadrature modulator; PM-TOF: polarization-maintaining tunable optical filter; PM-OC: polarization-maintaining optical coupler; T1 ~ T4: tunable optical delay-line consists of fixed fiber jumper and manually tunable optical time delay; ATT: tunable attenuator; LO: local oscillator).

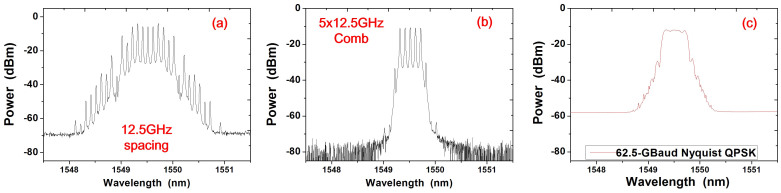
Fig. 4 (a) and (b) show the optical spectra of the generated optical comb with 12.5-GHz before and after the PM-TOF. The PM-TOF is with bandwidth of 62.5 GHz (5 × 12.5 GHz) in this case. Fig. 4(c) shows the optical spectrum of the Nyquist signal after modulation. We can see the full-band Nyquist signal with spectrum approaching rectangular shape. The excess bandwidth or roll-off factors are 0.2, since 5 peaks are used in this comb with 5 time division sub-channels.

Figure 4. Optical Spectra.

(a) and (b) show the generated optical comb with 12.5-GHz carrier spacing before and after the band-pass filter; (c) shows the generated optical comb after modulation. The resolution of figure 4 (a), (b) and (c) is 0.02 nm. The power difference of each tone in the comb is less than 0.3 dB.

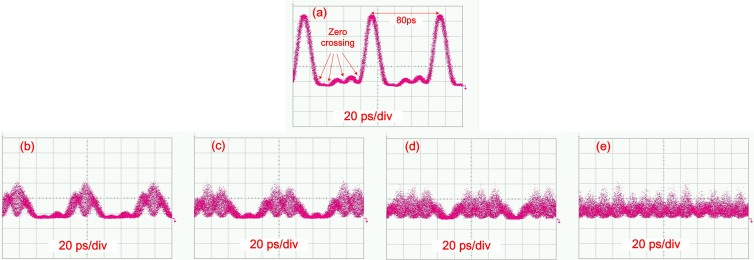
As analyzed in previous section, the Sinc-shaped Nyquist pulse can be generated after the PM-TOF. Fig. 5(a) shows the time domain waveform of the 5 × 12.5 GHz combs. We can see the Sinc-shaped Nyquist pulses obtained with four zero-crossing points between each Nyquist pulses and the pulse repeating period is 80 ps. For Nyquist signal modulation, we first directly modulate the Nyquist pulse and then multiplex these time-division channels by polarization-maintaining optical coupler (PM-OC) with polarization-maintaining tunable optical delay-line (PM-TDL, T₁ ~ T₄). Noting that in our experimental demonstration, each branch carries the same data sequence. Therefore, to ensure the orthogonality as well as the de-correlation between tributaries, the delay time should be long enough. In our experiment, the polarization maintaining (PM) tunable delay line consists of a fixed fiber delay lines (PM fiber jumpers, about 5 ns delay for per meter) and a manually tunable time delay module (0 ~ 300 ps tunable delay). For QPSK modulation, the 12.5GBaud binary in-phase (I) and quadrature (Q) data signals are generated by a programmable pulse generation (PPG) cascaded with a 2:1 multiplexer (Mux). The I/Q modulator is biased at the null point and driven at full swing to achieve zero-chirp 0 and π phase modulation. One electronic phase shifter (PS) is used for the PPG clock signal split from the same RF source for comb generation. It can synchronize the modulation I/Q signals and the Nyquist pulses, keeping the peak of the Nyquist pulses within the QPSK symbol durations.

Figure 5. Time-domain waveform and the multiplexing process of the 62.5GBaud Nyquist signal.

(a) is the Sinc-shaped Nyquist pulses of 5 × 12.5 GHz combs; (b) ~ (e) show the process of 62.5GBaud Nyquist QPSK signal multiplexing. There are 2, 3, 4, and 5 branches Nyquist signals in Figs. 5 (b), (c), (d) and (e), respectively. In the measurement, the pulse waveforms are measured after one EDFA and the input power of oscilloscope is keep at one fixed value for protection, thus the pulse amplitude shows weaker as more pulses added. The pulse amplitude of the figure 5 (a) is measured before modulation and multiplexing, thus the power is larger than other figures. Additional insertion loss is added after modulation and multiplexing.

In order to form a 5 channel Nyquist pulse time-division multiplexing, two pairs of 1:2 PM-OC and 1:4 PM-OC are used with four PM-TDL. Each Nyquist pulse branch is delayed long enough for decorrelation and the delayed time length is the integer multiples of the symbol duration (T/N, 16 ps for 62.5GBaud Nyquist signal). For the 5 × 12.5 GHz combs, T1 is 10 ns + 16 ps, T2 is 20 ns + 32 ps, T3 is 30 ns + 48 ps, and T4 is 40 ns + 64 ps. There is about 125 symbols delay between each branch for decorrelation. Using this transmitter setup, we generate 62.5-GBaud Nyquist QPSK signals of which the time-domain waveform is shown in Fig. 5. Symbol durations of 16 ps for the 62.5-GBaud Nyquist QPSK signals can be observed. Figs. 5(b), (c), (d) and (e) clearly show the time-domain multiplexing process of the 62.5GBaud Nyquist signal generation by 5 channel Nyquist pulse. There are 2, 3, 4, and 5 branches Nyquist signals in Figs. 5 (b), (c), (d) and (e), respectively. Since all the Nyquist pulse are multiplexed at the zero crossing points, orthogonal overlap in the time domain can be obtained without ISI. Therefore, the modulated Nyquist pulses with accurate time-division multiplexing show minimum ISI and maximum spectral efficiency. The pulses are not so symmetric for the measured waveform in Fig. 5. We believe the waveform shape asymmetry in these measured pulses is due to the overshoot problem caused by the optical sampling oscilloscope in pulse fall and rise. A high performance and larger bandwidth sampling oscilloscope designed for fast pulse signals would have better measurement performance.

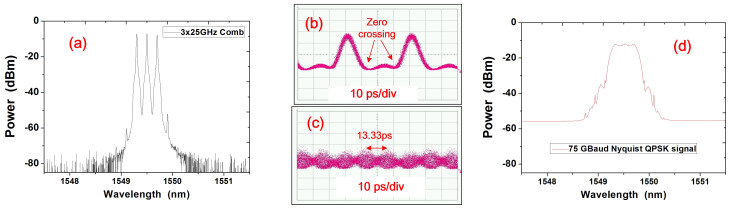
Higher baud rate Nyquist signal can be generated by using combs with more tones or larger carrier spacing. Here, we successfully generated 75 and 125-GBaud Nyquist QPSK signals by using the 25-GHz spaced combs. Using the RF source working at 12.5 GHz, we set the bandwidth of the BPF at 75 GHz to generate the 3 × 25-GHz comb as shown in Fig. 6(a). As analyzed in Section 2, the waveform of the Sinc-shaped Nyquist pulse is also changed. Fig. 6(b) shows the time-domain Nyquist pulse waveform of the 3 × 25-GHz comb. We find that there is two zero-crossing points between each Nyquist pulse. The pulse repeating period is 40-ps, which is only half of that of the 5 × 12.5-GHz comb. Therefore, only 3 delay-line branches are used here with time delay of the integer multiples of the symbol duration. For the 3 × 25 GHz combs, T1 and T2 are about 5 ns + 13.33 ps, 10 ns + 26.66 ps, respectively. There is also about 125 symbols delay between each branch for decorrelation. The waveform of the multiplexed 75-GBaud Nyquist QPSK signal is also shown in Fig. 6(c) with 13.33-ps symbol duration. The optical spectrum of the Nyquist pulse after signal modulation and multiplexing is shown in Fig. 6(d). The effective roll-off factor after modulation is 0.33, since only three-tone comb is used.

Figure 6. Optical spectra and the time-domain waveform of the 75-GBaud Nyquist signals.

(a) shows the optical spectrum of the Nyquist pulse of 3 × 25-GHz comb after the PM-TOF and before modulation (b) shows the time-domain Nyqusit pulse waveform of the 3 × 25-GHz comb; (c) shows the waveform of the multiplexed 75-GBaud Nyquist QPSK signal; (d) shows the modulated and multiplexed 75-GBaud Nyquist QPSK signal. The power difference of each tone in the comb is less than 0.3 dB. The resolution of (a) and (d) is 0.02 nm.

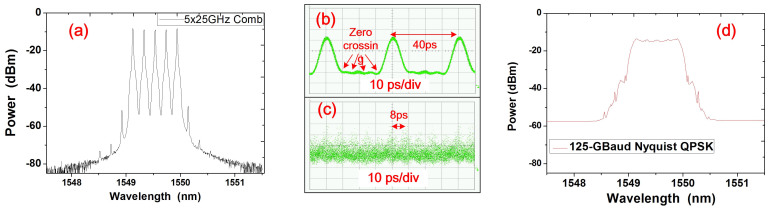
Besides the tunability of the Nyquist pulse generation using different radio frequencies as shown above, we also verify the flexibility of the pulse generation by changing the bandwidth of the BPF but keeping the same radio frequency. Using the same RF source at 12.5-GHz, we increase the bandwidth of PM-TOF to 125 GHz to generate the 5 × 25-GHz comb as shown in Fig. 7(a). Fig. 7(b) shows the time domain waveform of the generated 5 × 25-GHz comb. Compared with the 5 × 12.5-GHz comb, we find that the pulse repeating period is reduced to 40 ps. There are four zero-crossing points in each period. The waveform of the modulated and multiplexed 125-GBaud Nyquist signal is shown in Fig. 7(c). The symbol duration is 8 ps for the generated 125-GBaud Nyquist signal. For the 5 × 25 GHz combs, T1 ~ T4 are 5 ns + 8 ps, 10 ns + 16 ps, 15 ns + 24 ps and 20 ns + 32 ps, respectively. About 125 symbols delay are obtained between each branch for decorrelation. The optical spectrum of the modulated and multiplexed 125-GBaud Nyquist signal is shown in Fig. 7(d). The effective excess bandwidth or roll-off factor after modulation is also 0.2.

Figure 7. Optical spectra and the time-domain waveform of the 125-GBaud Nyquist signals.

(a) shows the optical spectrum of the Nyquist pulse of 5 × 25-GHz comb after the PM-TOF and before modulation (b) shows the time-domain Nyqusit pulse waveform of the 5 × 25-GHz comb; (c) shows the waveform of the multiplexed 125-GBaud Nyquist QPSK signal; (d) shows the modulated and multiplexed 125-GBaud Nyquist QPSK signal. The power difference of each tone in the comb is less than 0.3 dB. The resolution of (a) and (d) is 0.02 nm.

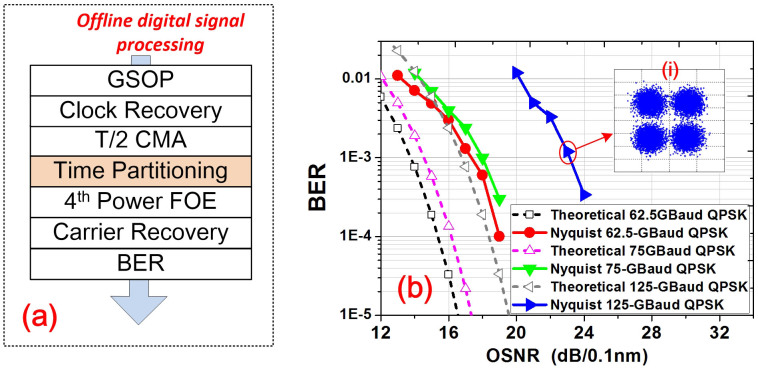
At the receiver side with full-band signal coherent detection, a free-running ECL with linewidth less than 100 kHz is utilized as LO as shown in Fig. 3. An optical 90° hybrid is used for phase-diversity coherent detection. The 3-dB bandwidth of the balanced detector is 50 GHz. The sampling and digitization (A/D) is realized by the high speed real-time digital oscilloscopes with 160-GSa/s sample rate and 65-GHz electrical bandwidth, which is wide enough for the 125-GBaud Nyquist signal. After the ADC, the off-line DSP is then applied for four channel 160-GSa/s sampled data sequence. The off-line DSP is shown in Fig. 8(a), which is similar to that used for regular coherent systems, including the compensation for I/Q imbalance, time recovery, linear equalization, frequency offset estimation (FOE) and carrier phase recovery (CPR)³⁷,³⁸,³⁹,⁴⁰,⁴¹. The data is first resampled to 2 samples per symbol, and then processed by the modified QPSK DSP blocks as shown in Fig. 3. Since the phase between the symbols in each tributary is unknown, we need to do the time partitioning after the classic linear equalizer constant-modulus algorithm (CMA), and before the FOE and CPR.

Figure 8. Off-line DSP blocks and Back-to-back bit-error-ratio results versus the OSNR.

(a) shows the off-line DSP blocks for the Nyquist QPSK signal recovery. (b) shows the back-to-back BER performance of the generated all-optical Nyquist 62.5, 75 and 125-GBaud QPSK signal versus the optical signal-noise-ratio (OSNR in 0.1 nm reference bandwidth) is measured compared with the theoretical values.

To measure the signal performance with full-band signal coherent detection, we test the back-to-back bit-error-ratio (BER) performance of the generated all-optical Nyquist 62.5, 75 and 125-GBaud QPSK signal versus the optical signal-noise-ratio (OSNR in 0.1 nm reference bandwidth). As shown in Fig. 8(b), compared with theoretical BER curve, there is 4-dB OSNR penalty for Nyquist 62.5 and 75-GBaud QPSK signals, and there is about 6-dB penalty for the 125-GBaud QPSK signal due to the inaccurate time delay. These theory curves are the limit of achieved BER performance (the best performance) for different Baud rate signals. We believe the discrepancy between theory and experiment results is due to two main reasons. The first one is the inaccurate time delays for signal multiplexing. Since the fixed PM fiber jumpers are commercial and non-adjustable, the PM manually tunable delay line is used for accurate pulse position adjusting. The resolution of this module is 0.05 mm in moving distance reading which is corresponding to 0.33-ps delay change. However, since the delay line is manually tunable, in the experiment we have to use the optical sampling oscilloscope for pulse orthogonal time-division multiplexing. Compared with programmable time delay line or integrated optics-delay, larger delay error exists for the manually tunable delay line. This time delay error reduces the pulse orthogonality in time domain and causes ISI. For this reason, the generated Nyquist signals are degraded by the ISI induced by time error in multiplexing. Second, we believe the bandwidth limitation of optoelectronic devices used in our system is another reason. The balanced PDs used in our experiment for coherent detection are with 50 GHz 3-dB bandwidth. This bandwidth limitation will cause additional penalty. We believe better performance can be achieved by integrated signal generation and modulation setup with wideband optoelectronic devices. Therefore, we report the first experimental demonstration of high speed all optical Nyquist signal generation based on Sinc-shaped pulse generation and time-division multiplexing with high level modulation format and full-band coherent detection.

Discussion

Here in this paper, we report the first experimental demonstration of high speed all optical Nyquist signal generation based on Sinc-shaped pulse generation and time-division multiplexing with high level modulation format and full-band signal coherent detection with one receiver. A simple all optical Nyquist pulse generation method is proposed and demonstrated based on the Mach–Zehnder modulators driven by the radio frequency cascaded with a band-pass optical filter. Nyquist pulse with 62.5, 75 and up to 125GBaud QPSK signals are generated and detected. One high speed coherent receiver with 160 GSa/s sample rate and 65-GHz analog bandwidth is used for the full-band signal. The effective roll-off factor of Nyquist QPSK signal of 0.2 after modulation is realized. To the best of our knowledge, 125Gbaud is the highest baud rate record for the all-optical Nyquist QPSK signal generation, and coherent detection by one receiver based on digital signal processing. The previous record baud rate for one coherent receiver for full-band signal detection is 107Gbaud in⁴²,⁴³ and 110GBaud in⁴⁴.

The flexibility of this method is also verified. Compared with previous work in²⁸, additional BPF is used for comb generation gives more tunability for different Nyquist pulses generation. As analyzed in this paper, the roll-off factor of the modulated Nyquist signal based on this method is determined by the number of the tones of the comb within the BPF bandwidth. Therefore, one simple approach to get smaller roll-off factor is to reduce the carrier spacing and increase the BPF bandwidth. For a fixed BPF bandwidth, reducing the carrier spacing means more branches of sub-channels used. Therefore, more modulators with lower data rate are needed.

Here, a full-band coherent detection shows the simply receiver side setup for signal recovering. Compared with the regular OTDM receivers, only a free-running LO is needed with a common coherent receiver setup. The Nyquist signal is detected as one full-band signal, without optical demultiplexing before detection.

Finally, using this method, we demonstrate a highly flexible and compatible all optical high speed Nyquist signal generation and detection scheme for future fiber communication systems. It enables high speed transmission with high spectrum efficiency and simple system setup.

Methods

Experimental measurement

All the transmitter and receiver optical and electrical devices are commercially available. The two laser sources in our experiment for signal modulation and homodyne beating are both working at 1549.50 nm with the output power of 14.5 dBm and the linewidth less than 100 kHz. The I/Q modulator is based on LiNbO3 waveguides with a modulation bandwidth of 27-GHz. The balanced PDs used in our experiment are from u2t with 50 GHz 3-dB bandwidth. At the receiver, the digital ADCs are working at 160 GSa/s with 65 GHz bandwidth as a real-time sampling scope (Lecroy, Labmaster 10–65 Zi). The sampled waveforms were stored and processed offline by using MATLAB in a computer. The optical spectra of the signals are all measured by a commercial optical spectrum analyzer (Yokogawa, AQ6370B). The time-domain waveforms of the Nyquist pulse and multiplexed signals are all measured by an optical sampling oscilloscope (Agilent 8611B) with 65 GHz bandwidth.

Comb Generation

In our experiment demonstration, we use one single MZM and one PM-TOF to generate the 5 tones comb with equal amplitude and linear phase. To realize the conditions given by above Eq. 2, we need to adjust the voltage of the RF driving signal and the DC bias for optimal output.

Using the same method in²⁸, we can expand the output of MZM by Bessel function. For zero-chirp MZ intensity modulator, assuming the RF driver signal voltages represented as aV_picos(2πΔft), and the DC bias voltages as bV_pi, then the output of the single MZM can be expanded by Jacobi–Anger expansion as

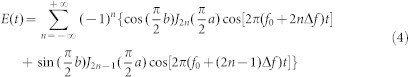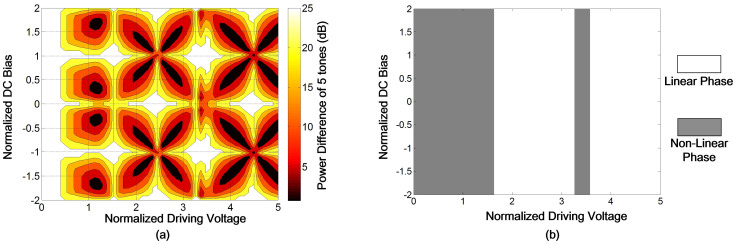
Here J_n is the n-th order Bessel function of the first kind, V_pi is the half-wave voltage of the modulator and a and b are the normalized driving voltage and DC bias. Therefore, two degrees of freedom, modulation and bias index can be used to equalize the amplitude and phase of each frequency tone of generated comb. To obtain the Sinc-shaped pulse, the comb should satisfy the equal amplitude and linear phase conditions given by above Eq. 1. From Eq. 4, we can see that the phase of each tone is dependent on the sign of the amplitude, either 0 or π. Therefore, assuming the phase of the center carrier is 0, the phase of the 5 tones can be {0, 0, 0, 0, 0} or {0, π, 0, π, 0}. The even tones should have the same phase. Using the Eq. 4, we can plot the power difference and also the phase relation of the 5-tone comb by varying the normalized amplitude and DC bias, as shown in the Fig. 9 below.

Figure 9. The power differences and the phase relation of the generated 5-tone comb by varying the normalized driving voltage and the DC bias.

(a) shows the power difference of the 5 tone-comb versus the normalized driving voltage and the DC bias; (b) shows the phase relation of 5 tones versus the driving voltage and DC bias.

From above Fig. 9, several conclusions can be made. First, there are several optimal zones with RF driving voltages and DC bias values (black zones in Fig. 9(a)) to achieve a flattened 5-tone comb generation with smallest power differences. The power difference is determined by both driving voltage and DC bias. Second, we find the linear phase relation of generated tones is only determined by the driving voltage. The linear phase relation of the 5 tones is easy to achieve by applying an appropriate driving voltage with a large tunable range. Third, the optimal zones in Fig. 9(a) and linear phase zones in Fig. 9(b) can both be satisfied, since there are several overlapping areas. However, we can see that, the area of optimal zones for flattened comb with smallest power difference is much smaller than that of the linear phase zones. Compared with the phase relation, the power difference is much more sensitive to the value of driving voltage and DC bias. Finally, since the linear-phase condition of the 5-tone comb is much easier to achieve, the equal power conditions can be relieved by using power equalizer devices, such as filters or wavelength selective switch (WSS). In our case, we choose the driving voltage about 2V_pi and the DC bias about 0.52 V_pi. The power differences of the generated 5-tone comb for the 5 × 12.5 GHz, 3 × 25 GHz, and 5 × 25 GHz comb after the filter are all less than 0.3 dB.

OSNR and offline BER measurement

The OSNR is measured by using the optical spectrum analyzer (Yokogawa, AQ6370B) and the ASE noise is measured within 0.1 nm. In our experiment, the signals are sampled and stored by using a real-time sampling scope (Lecroy Labmaster 10–65 Zi) with 160 GSa/s and the BER is measured by comparing with the original transmitted data pattern after the offline processing. The recording length is set longer enough for BER counting. The original transmitted data pattern is pseudo-random bit sequence with the length of 2¹⁵-1 for signal generation. In our experiment, the measured BER value is stable and without much fluctuations.

Theory BER Curves

From the basic digital communication theory⁴⁵, we have BER of QPSK signal for additive white Gaussian noise (AWGN) channel as

SNR_b is the signal-to-noise ratio per bit, known as E_b/N₀, the energy per bit per noise power spectral density.

Optical communication uses OSNR where the signal can be in one or two polarizations and the noise is summed over both polarizations. The noise is in a fixed bandwidth of 0.1 nm (~12.5 GHz)⁴⁶. Therefore, the definition of OSNR can be expressed as⁴⁶:

where P_S is the total average signal power summed over the two states of polarization, N_ASE is the spectral density of amplified spontaneous emission (ASE) in one polarization and the reference bandwidth B_ref is commonly taken to be 12.5 GHz, corresponding to a 0.1 nm resolution bandwidth of optical spectrum analyzers at 1550 nm carrier wavelength (193.4 THz carrier frequency). We have

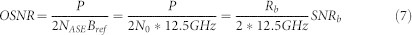where N₀ is the spectral density of AWGN in one polarization. N₀ and N_ASE are assumed to be equivalent. Therefore, we have the relation of SNR_b with OSNR as

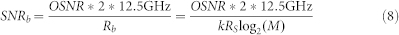where R_S is the symbol rate (Baud rate), M is the modulation order (M = 4 for QPSK signal), k is the polarization-multiplexing number (k = 1 in our case). Thus, substituting above Eq. 8 into Eq. 5, one obtains the following expression of the BER of QPSK

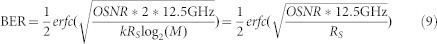The theory BER with OSNR curves in Fig. 8 (b) are obtained by above Eq.9.

Author Contributions

J.Z. developed the presented basic idea for the generation all optical Nyquist signal and full-band detection. J.Z. and J.Y. proposed the proof-of-concept set-up, carried out the experiments and analyzed the data. Y.F. and N.C. prepared the figures and reviewed the paper. All authors contributed to the writing of the manuscript.

Supplementary Material

Supplementary Information

Supplementary Material