The torque correlation length and stochastic twist dynamics of DNA

Abstract

We introduce a short correlation length for torque in twisting-stiff biomolecules, which is necessary for the physical property that torque fluctuations be finite in amplitude. We develop a nonequilibrium theory of dynamics of DNA twisting which predicts two crossover time scales for temporal torque correlations in single-molecule experiments. Bending fluctuations can be included, and at linear order we find that they do not affect the twist dynamics. However, twist fluctuations affect bending, and we predict the spatial inhomogeneity of twist, torque, and buckling arising in nonequilibrium “rotor-bead” experiments.

I. INTRODUCTION

Many statistical-mechanical properties of biopolymers are controlled by their bending persistence length. For example, DNA has a persistence length of A ≈ 50 nm, which controls its basic polymer elasticity [1–5]. However, recent single-molecule experiments [6] have revealed that DNA-binding proteins interact allosterically over shorter length scales of ≈ 5 nm along the DNA strand. These interactions are mechanical, and are thought to be due to correlated bends [6, 7]. This raises the questions of whether the twist degrees of freedom of DNA similarly possess a short correlation length below the 100 nm twist persistence length scale [8, 9], and what signature of such a length might appear in single-molecule DNA torque experiments [10, 11].

The canonical model for DNA twist [1, 2] suffers a basic defect. In this model, the local free energy density is proportional to the gradient of twist strain, squared, with a proportionality coefficient of twist persistence length, c₁. As a result, the model has the unphysical property that its static torque correlations are divergent (see Appendix A). To control this pathology, the free energy must regulate torque fluctuations; the simplest mechanism is for the DNA polymer to energetically favor spatially uniform torque [12] (see Appendix A). Thus, we add a gradient-squared term to the usual twist free energy:

$$\beta E=\frac{1}{2}{\int }_0^L[c_1{\left({\partial }_s\theta \right)}^2+c_2{\left({\partial }_s^2\theta \right)}^2]ds,$$ (1)

where the field θ(s) describes the twist angle distortion away from equilibrium as a function of contour length, s. The new term, proportional to c₂, controls fluctuations of torque, τ(s) = c₁∂_s , since $\langle {\mid {\partial }_s\theta \mid }^2\rangle ={\left(c_1{c}_2\right)}^{-\frac{1}{2}}$; as c₂ → 0 the short-range torque correlations diverge (see Appendix A). The inclusion of c₂ ≠ 0 in Eq. (1) also introduces a correlation length for torque fluctuations; correlations in ∂_sθ now decay exponentially over a new length scale, $\xi =\sqrt{c_2∕c_1}$.

To fully understand the implications of the correlation length ξ, we develop a theory for twist and torque dynamics, which are studied in single-molecule DNA experiments [10, 11, 13–17]. Twist dynamics of elastic filaments have been studied in the context of twirling and whirling [18–20], bacterial flagella [21], and some models of DNA [1, 22–24]. Less is known about these dynamics in single-molecule DNA twisting experiments, which are subject to thermal noise, have complicated boundary conditions, and may be driven out of equilibrium.

II. RESULTS

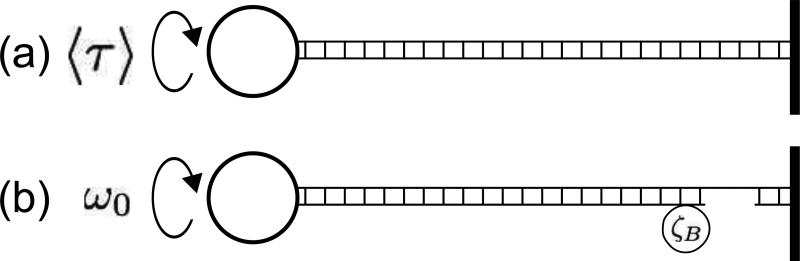
Two types of experiment are of particular interest. In the first, twist is controlled by manipulating a micron-sized particle attached to one end of DNA while the other end is immobilized [15–17] (Fig. 1(a)), leading to fixed twist with torque fluctuating around its thermal equilibrium average. In the second experiment, twist is continuously injected at one end of the DNA by rotating a micron-sized bead at frequency ω₀. Twist “leaks out” at the other end at a rate controlled by a “rotor” bead with relatively large viscous drag, ζ_B [10, 11] (Fig. 1(b)). This latter case generates a nonequilibrium steady state in which the DNA molecule dissipates torsional energy injected by the magnetic bead through the motion of the rotor bead against viscous drag.

FIG. 1.

(a) Schematic of the equilibrium experiment. A magnetic bead attached to the DNA molecule at the left end is rotated with a mean torque 〈τ〉, and the molecule is attached to a substrate at the right end to fix the twist. (b) Schematic of the nonequilibrium experiment. A magnetic bead attached to DNA at the left end is rotated at a constant angular velocity, ω₀, and the molecule is nicked so that it releases twist. Twist release is opposed by the viscous drag, ζ_B, of the “rotorbead,” which is attached to DNA to the left of the nick.

In the nonequilibrium case, the equation of motion for twist, θ(s, t), follows by balancing dissipative torque within the molecule against mechanical and stochastic torques [1, 20, 23, 25]:

$$\zeta \stackrel{.}{\theta }\left(s\right)=-\frac{\delta E}{\delta \theta }+f(s,t)=\frac{1}{2\beta }(c_1{\partial }_s^2\theta -c_2{\partial }_s^4\theta )+f(s,t).$$ (2)

The boundary conditions are surface terms obtained by integrating by parts before functional differentiation [26,

$$\begin{array}{cc}\hfill & {\theta \mid }_{s=0}={\omega }_{0}t\hfill \\ \hfill & {c_2{\partial }_s^2\theta \mid }_{s=0}={c_2{\partial }_s^2\theta \mid }_{s=L}=0\hfill \\ \hfill & {{\zeta }_B\stackrel{.}{\theta }\mid }_{s=L}={-\frac{1}{2\beta }[c_1{\partial }_s\theta -c_2{\partial }_s^3\theta ]\mid }_{s=L}.\hfill \end{array}$$ (3)

These conditions stipulate that i) twist at the driving end increases at the rate of bead rotation, ω₀; ii) DNA is clamped so that the torque approaches a constant at both ends [26] and the DNA is in instantaneous local equilibrium with the driving and rotor beads; and iii) mechanical torque at the rotor bead is dissipated by the bead's viscous drag. The third boundary condition mixes time and space derivatives, and requires careful attention. In steady state, twist evolves at the driving rate, ω₀, and the spatial dependence is found through a power series solution as:

$${\theta }_0(s,t)={\omega }_{0}t+\frac{\zeta \beta {\omega }_0}{c_1}\left\{-2\left(\frac{{\zeta }_B}{\zeta }+L\right)s+s^2+2{\xi }^2\left[e^s∕\xi \left(\tanh \left(\frac{L}{2\xi }\right)-1\right)-e^{-s∕\xi }\left(\tanh \left(\frac{L}{2\xi }\right)+1\right)+1\right]\right\},$$ (4)

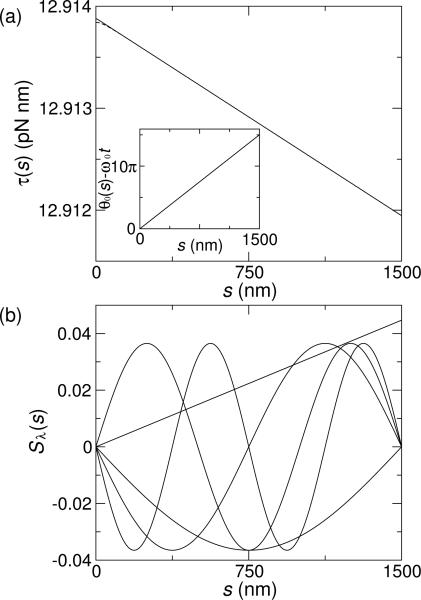
where ζ is the rotational drag of DNA and L is the length of the molecule. When c₂ = 0 (ξ = 0), twist dynamics are diffusive, and thus, the torque decreases linearly with distance, s, from the driving end. Estimating the parameters with values from single-molecule experiments [10] (see caption to Fig. 2), we find that the rotor bead sets the applied steady-state torque and dominates the dynamics since ${\zeta }_B\gg \zeta L$. Thus, the torque changes by less than 0.02% throughout the entire DNA molecule, justifying the assumption of constant torque in typical rotor-bead experiments [10, 11]. Fig. 2(a) and its inset, respectively, show the steady-state torque and twist.

FIG. 2.

Solution to Eq. (2) subject to the boundary conditions in Eq. (3). We estimate ζ ≈ 4πηd² with viscosity η ≈ 10^–3 Pa·s and DNA diameter d ≈ 1 nm, L ≈ 1500 nm, βζ_B ≈ 0:1 s, ω₀ ≈ 10π rad/s as in experiments [10], and c₁ ≈ 100 nm [8, 9]. We expect the correlation length to be small, ξ < c₁, so that the wormlike chain behavior is observed at large length scales [2–5]. (a) Steady-state torque in the molecule versus distance from driving end. The solid line shows c₂ = 1000 nm³ (ξ = 3.16 nm). Torque curves for other values of c₂ are nearly identical, with deviations near the boundaries only noticeable for large c₂ (dashed line shows c₂ = 10⁵ nm³). For large c₂, ξ is large and the torque clamp boundary condition is felt over a longer length scale. Inset: Time-independent part of the twist angle versus distance from driving end for c₂ = 1000 nm³. (b) First five spatial eigenmodes. The lowest mode is approximately linear in s, and arises from the non-zero mechanical torque at s = L. The remaining sinusoid-like modes are nearly identical to those of the equilibrium system. As mode number, k, increases, the number of times S_λ crosses zero increases.

In experiments, there are significant fluctuations about the steady-state [10, 11]. We therefore find the dynamical modes of the steady state by assuming separability, θ(s, t) − θ₀(s, t) = ψ(s, t) = T (t)S(s), and applying the boundary conditions in Eq. (3) [28]. The stochastic fluctuation ψ(s, t) is the sum of eigenfunctions, ψ_λ (s, t):

$${\psi }_{\lambda }(s,t)=(\sinh \left(\sqrt{{\gamma }_{+}^{\lambda }}s\right)-\frac{{\gamma }_{+}^{\lambda }\sinh \left(\sqrt{{\gamma }_{+}^{\lambda }}L\right)\sinh \left(\sqrt{{\gamma }_{-}^{\lambda }}s\right)}{{\gamma }_{-}^{\lambda }\sinh \left(\sqrt{{\gamma }_{-}^{\lambda }L}\right)})e^{-\frac{\lambda t}{2\beta \zeta }},$$ (5)

where ${\gamma }_{\pm }^{\lambda }=\frac{-1\pm \sqrt{1-4{\xi }^2\lambda ∕c_1}}{2{\xi }^2}$, and we have omitted the arbitrary normalization. The first five spatial eigenfunctions are plotted in Fig. 2(b). The eigenvalues, λ, are quantized by the dissipative boundary condition $\frac{{\zeta }_B}{\zeta }\lambda S_{\lambda }\left(L\right)={[c_1{\partial }_s{S}_{\lambda }-c_2{\partial }_s^3{S}_{\lambda }]\mid }_{s=L}$. The slowest mode, ${\lambda }_0\approx \frac{4c_1\zeta }{4{\zeta }_{B}L+9\zeta {\xi }^2+2\zeta L\xi \coth \left(\frac{L}{\xi }\right)}\approx \frac{c_1\zeta }{{\zeta }_{B}L}$, explicitly depends on the rotor bead drag. The remaining modes are nearly those of the free (equilibrium) molecule, ${\lambda }_k\approx c_1{\left(\frac{k\pi }{L}\right)}^2+c_2{\left(\frac{k\pi }{L}\right)}^4$, with integer k ≥ 1. Thus, fluctuations are composed of one mode, ψ₀, with relaxation time $T_0=\frac{2\beta \zeta }{{\lambda }_0}$ controlled by the boundary condition, and approximately the normal spectrum of modes of the free molecule, {ψ_{k≥ 1}}, with relaxation times $T_k=\frac{2\beta \zeta }{{\lambda }_k}$. Therefore, we assume completeness of the eigenfunctions in the domain defined by Eqs. (2)-(3).

However, due to the non-zero mechanical torque maintained at the end of the molecule, the operator, $\mathcal{L}=c_1{\partial }_s^2-c_2{\partial }_s^4$, is not self-adjoint with the boundary conditions in Eq. (3) (see Appendix B). Nonetheless, the eigenfunctions are orthogonal under the inner product:

$$(S_{\lambda },S_{{\lambda }^{\prime }})=\frac{{\int }_0^L{S}_{\lambda }\left(s\right)S_{{\lambda }^{\prime }}\left(s\right)w\left(s\right)ds}{{\int }_0^L{S}_{\lambda }^2\left(s\right)ds+\frac{{\zeta }_B}{\zeta }{S}_{\lambda }^2\left(L\right)}={\delta }_{\lambda {\lambda }^{\prime }},$$ (6)

where the weight $w\left(s\right)=1+\frac{{\zeta }_B}{\zeta }\delta (s-L)$ accounts for the boundary condition. Using Eq. (6), we can construct arbitrary twist perturbations, p(s) = ∑_λ(S_{λ, p})S_λ(s) and the Green's function,

$$G(s,s^{\prime },t)=\sum _{\lambda }\frac{S_{\lambda }\left(s\right)S_{\lambda }\left(s^{\prime }\right)e^{-\frac{\lambda t}{2\beta \zeta }}}{{\int }_0^L{S}_{\lambda }^2\left(s\right)ds+\frac{{\zeta }_B}{\zeta }{S}_{\lambda }^2\left(L\right)},$$ (7)

where $S_{\lambda }(s,t)={\int }_0^{L}G(s,s^{\prime },t)S_{\lambda }\left(s^{\prime }\right)w\left(s^{\prime }\right)d{s}^{\prime }$. This allows a full description of the fluctuations and correlations.

Using the eigenfunction expansion (see Appendix B), the energy can be written as:

$$\beta E=\frac{1}{2}\left(\sum _{\lambda }{a}_{\lambda }^2\lambda \left(\frac{{\zeta }_B}{\zeta }{S}_{\lambda }^2\left(L\right)+{\int }_0^L{S}_{\lambda }^2\left(s\right)ds\right)\right),$$ (8)

where a_λ is the amplitude of twist perturbations about the steady state. In Eq. (8), the energy explicitly includes a term for boundary torque. As expected, if ζ_B = 0, a non-zero mechanical torque cannot be balanced against dissipation, and we recover the equilibrium free energy. Eq. (8) is manifestly quadratic in the amplitude, a, leading to the fluctuation relation:

$$\langle a_{\lambda }{a}_{{\lambda }^{\prime }}\rangle =\frac{k_{B}T{\delta }_{\lambda {\lambda }^{\prime }}}{\lambda ({\int }_0^L{S}_{\lambda }^2\left(s\right)ds+\frac{{\zeta }_B}{\zeta }{S}_{\lambda }^2\left(L\right))},$$ (9)

which reduces to the equipartition theorem when ζ_B = 0.

Noise correlations are found by writing the evolution of twist as a series of Rouse-like modes, $\zeta {\stackrel{.}{a}}_{\lambda }=-\lambda a_{\lambda }+f_{\lambda }$ [25]. Using Eq. (6) and assuming delta-correlated noise, we find (see Appendix B):

$$\langle f(s,t)f(s^{\prime },0)\rangle =\frac{2k_{B}T\zeta \delta (s-s^{\prime })\delta \left(t\right)}{1+\frac{{\zeta }_B}{\zeta }\delta (s^{\prime }-L)}.$$ (10)

Noise correlations explicitly depend on the rotor bead, but are identical to equilibrium correlations for s ≠ L.

For further insights into twist dynamics, we construct the spatiotemporal torque correlation function from the Green's function and amplitudes, Eqs. (7) and (9):

$$C_{\tau }(s,s^{\prime },t)={\langle \left[{\partial }_s\theta \right]\mid }_{st}{[{\partial }_s,\theta ]\mid }_{s^{\prime },0}\rangle =\sum _{\lambda }\langle a_{\lambda }^2\rangle {\left[{\partial }_s{S}_{\lambda }\right]\mid }_s{\left[{\partial }_s{S}_{\lambda }\right]\mid }_{s^{\prime }}{e}^{-\frac{\lambda t}{2\beta \zeta }}$$ (11)

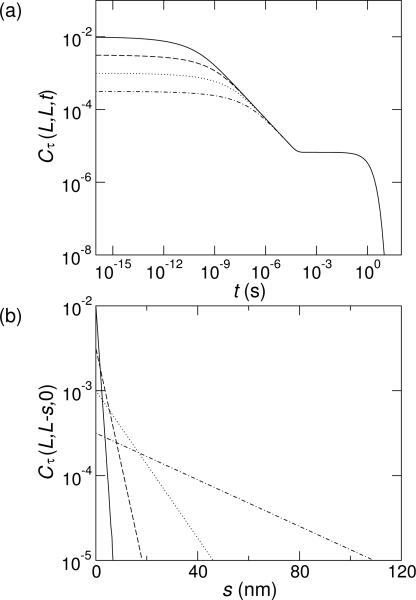
Temporal torque correlations (see Appendix C) at s = L have three scaling regimes:

$$C_{\tau }(L,L,t)\sim \{\begin{array}{cc}\frac{(1-\frac{1}{4}\Gamma (-\frac{1}{4})t^{\frac{1}{4}})}{\sqrt{c_1{c}_2}}\hfill & t<\frac{2\beta \zeta {\xi }^2}{c_1}\hfill \\ t^{-\frac{1}{2}}\hfill & \frac{2\beta \zeta {\xi }^2}{c_1}<t<\frac{2\beta \zeta L^2}{\pi c_1}=\frac{2\pi \beta \zeta }{{\lambda }_1}\hfill \\ e^{-\frac{c_{1}t}{2\beta {\zeta }_{B}L}}\hfill & t>\frac{2\beta \zeta L^2}{\pi c_1}=\frac{2\pi \beta \zeta }{{\lambda }_1}.\hfill \end{array}\phantom{\}}$$ (12)

At long times, t > 0.1 ms for our typical parameters, torque correlations are dominated by the rotor bead dynamics since its correlations decay exponentially on the slowest time scale, $T_0=\frac{2\beta \zeta }{{\lambda }_0}$. This implies that if ζ_B is decreased to obtain higher temporal resolution in experiments [10, 11, 17], C_τ(L, L, t) → 0 more rapidly. The crossover time, $\frac{2\beta \zeta L^2}{\pi c_1}$, is independent of ζ_B since ${\zeta }_B\gg \frac{\zeta L}{{\pi }^2}({\lambda }_0\ll {\lambda }_1)$. At earlier times, we observe near equilibrium dynamics. Many dynamical modes, with decay times $T_k\approx \frac{2\beta \zeta L^2}{c_1{\left(k\pi \right)}^2}$, contribute to torque correlations. This continuum of time scales crosses over at $k\approx \frac{L}{\pi \xi }$ to $T_k\approx \frac{2\beta \zeta L^4}{c_2{\left(k\pi \right)}^4}$, so that at short time scales, $t\lesssim 1$ ns, correlations approach a constant instead of diverging as t → 0, as they would for c₂ = 0. This constant is approximately the expected equilibrium fluctuation. It is also possible that torque correlations are cut off by internal molecular dissipation [29], which could be included in this model.

Eq. (12) is illustrated by Fig. 3(a), which shows C_τ(L, L, t) for several values of c₂. The correlation function shows that even though steady-state properties such as the torque and twist are insensitive to c₂ for small ξ, the dynamics strongly depend on the correlation length. This provides a direct way to experimentally measure ξ.

FIG. 3.

(a) The temporal correlation function, C_τ(L, L, t), has three regimes: approximately constant correlations, t^-1/2 decay, and exponential decay (Eq. (12)). C_τ(L, L, t) is plotted for ξ = 1 nm (solid line), ξ = 3.16 nm (dashed), ξ = 10 nm (dotted), and ξ = 31.6 nm (dash-dotted). (b) The spatial correlation function, C_τ(L, L – s, 0), decays exponentially. Lines show C_τ(L, L – s, 0) for the same values of ξ as in (a).

Spatial torque correlations provide additional means to measure ξ. These correlations decay exponentially with a characteristic length scale of ξ, following the expected behavior for equilibrium statistical mechanics:

$$C_{\tau }(L,L-s,0)\approx \frac{e^{-\frac{s}{\xi }}}{\sqrt{c_1{c}_2}}.$$ (13)

Fig. 3(b) demonstrates this behavior for several c₂.

The predictions of Eqs. (12) and (13) can be tested experimentally. Temporal torque correlations at s = L can be measured through the angular velocity of the rotor bead at different times. Spatial and temporal correlations in DNA could be measured through use of fluorescent labels. Fluorescence resonance energy transfer (FRET) could detect changes in the relative twist angle between nearby DNA-bound fluorescent proteins, providing a local estimate of torque within the molecule. Total internal reflection fluorescence (TIRF) experiments similar to those that probed DNA bending correlations [6] could test short-scale allosteric interactions between proteins that bind and twist DNA.

In the preceding analysis, we assumed that driving the molecular twist affects only the twist degrees of freedom. However, twist strain can be relieved by filament writhe, so twist and bend are topologically coupled [8, 20, 30–33]. Moreover, when the applied torque is large, the filament buckles [8, 34]. Following previous work [18, 20, 35, 36] (see Appendix D), we assume that the tension, F , across DNA is large (βAF > 1), so transverse bending fluctuations are small, and the linearized equations for twist and bend are:

$$2\beta \zeta {\partial }_t\theta =c_1{\partial }_s^2\theta -c_2{\partial }_s^4\theta +f\left(t\right)$$ (14)

$$2\beta {\zeta }_{\perp }{\partial }_{t}R=i\left(\left(c_2{\partial }_s^4\theta -c_1{\partial }_s^2\theta \right){\partial }_s^{2}R+(c_2{\partial }_s^3\theta -c_1{\partial }_s\theta ){\partial }_s^{3}R\right)-A{\partial }_s^{4}R+\beta F{\partial }_s^{2}R+g_x\left(t\right)+i{g}_y\left(t\right)$$ (15)

where $R={\overrightarrow{r}}_{\perp }\cdot \widehat{x}+i{\overrightarrow{r}}_{\perp }\cdot \widehat{y}$, ${\zeta }_{\perp }\approx \zeta ∕\ln (2L∕d)$ [20, 37] and $\overrightarrow{g}\left(t\right)$ is bending noise. The DNA ends are clamped so that R(0) = R(L) = 0 and ${{\partial }_{s}R\mid }_{s=0}={{\partial }_{s}R\mid }_{s=L}=0$ [26].

To linear order R, twist dynamics are from bending fluctuations. However, decoupled twist impacts bending fluctuations; this is manifested in the bending fluctuations and amplitudes, and consequently, the buckling transition. Solutions to Eq. (15) are described by the amplitudes (see Appendix D):

$$R_q\left(\omega \right)=\{\begin{array}{c}\frac{g_q\left(\omega \right)}{A{q}^4+\tau q^3+\beta F{q}^2-2i\beta {\zeta }_{\perp }\omega }\text{for equilibrium experiments}\left(\mathrm{Fig}.1\right(a\left)\right)\hfill \\ \frac{g_q\left(\omega \right)}{A{q}^4+2\beta ({\zeta }_B+\zeta (L-s_0)){\omega }_0{q}^3+\beta (F-2i\zeta {\omega }_0)q^2-2i\beta {\zeta }_{\perp }\omega }\text{for nonequilibrium experiments}\left(\mathrm{Fig}.1\right(b\left)\right).\hfill \end{array}\phantom{\}}$$ (16)

In the equilibrium system, the stochastic dynamic description recovers the classical buckling transition at zero frequency [8, 34]. In both cases, R_q is independent of both the twist persistence length, c₁, and the correlation length, ξ. Bending fluctuations in the driven system are described by local amplitudes; bending fluctuations, R(s), at s ≈ s₀ may be found by summing the local modes in Eq. (16). This approximation is valid in the high-force limit, since the characteristic buckling wavelength, $\sqrt{\frac{A}{\beta F}}$, is small (see Appendix D).

Eq. (16) implies that buckling is controlled by the local torque. This torque is large near the driven end of the molecule, and falls o linearly with distance. Thus, the largest bending fluctuations, occur near the rotating magnetic bead, and the imhomogeneity of fluctuations across the entire molecule increases as ζψ₀ increases. This instability is distinct from the twirling/whirling transition [18–20], but consistent with simulations showing that plectonemes are created near the driving end of a twisting polymer [24].

III. CONCLUSION

Our theory illustrates that boundary conditions uniquely regulate the dynamics of twisted elastic filaments such as DNA. Experiments have shown that the activity of topoisomerase IB, an enzyme which relaxes DNA supercoils, is sensitive to the viscous drag at the end of a microns-long DNA molecule [38]. We thus predict that the activity of enzymes modulating DNA twist will also sensitively depend on boundary conditions. Similarly, through the indirect effect of influencing bending fluctuations, the rate of DNA twisting might affect protein activity such as binding and unbinding. Such effects could be important in vivo for proteins that interact allosterically [6] or in situations where torsional stress is built up by DNA-distorting proteins such as RNA polymerase [39]. Additionally, it is possible that this type of effect could be observed in other condensed matter systems with dissipative boundary conditions.

We have shown that a short correlation length, ξ < c₁, in twisted elastic biofilaments strongly influences filament dynamics even when it does not affect steady-state properties. We developed a theory for DNA in single-molecule experiments, but the results also apply to other elastic filaments. The torque correlation length for DNA is analogous to the bending correlation length found in experiments [6, 7]. ξ could be related to the pitch of the double helix, a length scale that does not play a role in the basic wormlike chain theory. It manifests itself in experiments by regulating torque fluctuations. This could be biologically significant if torque correlations affect protein-DNA binding through allosteric interactions.

Appendix A: Equilibrium calculation of torque fluctuations

Equilibrium fluctuations and spatial correlations for a DNA molecule with the free energy

$$\beta E=\frac{1}{2}{\int }_0^L[c_1{\left({\partial }_s\theta \right)}^2+c_2{\left({\partial }_s^2\theta \right)}^2]ds$$ (A1)

can be calculated by diagonalizing the Hamiltonian:

$$\beta E=\frac{L}{2}\sum _q(c_1{q}^2+c_2{q}^4){\mid {\theta }_q\mid }^2.$$ (A2)

Following from the equipartition theorem and Parse-val's theorem (e.g., see [12, 25]), the torque fluctuations,

$$\langle {\mid \tau \left(s\right)\mid }^2\rangle =\langle {\mid c_1{\partial }_s\theta \mid }^2\rangle ,\text{are}:\langle {\mid \tau \left(s\right)\mid }^2\rangle =\frac{L}{2\pi }{\int }_{-\infty }^{\infty }\langle {\mid c_{1}q{\theta }_q\mid }^2\rangle dq=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }\frac{c_1}{c_1+c_2{q}^2}dq.$$ (A3)

Thus, torque fluctuations diverge if c₂ = 0; however, for c₂ ≠ 0, 〈τ(s)|² = c₁/ξ.

It is possible that additional mechanisms for controlling torque fluctuations exist, such as a cuto due to the finite size of DNA basepairs. However, the correlation length, ξ is expected to be of order several nm, similar to what has been found for the bending correlation length [6, 7]. This is a few tens of basepairs, so a continuum theory of twist is justified. Moreover, the proposed modification to the free energy, which assumes uniform torque is energetically favorable, is a simple mechanism that is motivated by classical field theory [12].

Appendix B: Eigenfunction expansion

The operator, $\mathcal{L}=c_1{\partial }_s^2-c_2{\partial }_s^4$ is not self-adjoint on the domain described by in Eqs. (2)-(3). Instead, we find:

$${\int }_0^L{S}_{\lambda }^{\ast }\mathcal{L}{S}_{{\lambda }^{\prime }}ds={\int }_0^L{S}_{{\lambda }^{\prime }}\mathcal{L}{S}_{\lambda }^{\ast }ds-(\lambda -{\lambda }^{\prime })\frac{{\zeta }_B}{\zeta }{S}_{\lambda }\left(L\right)S_{{\lambda }^{\prime }}\left(L\right).$$ (B1)

Note that this can also be written as:

$${\int }_0^L{S}_{\lambda }\mathcal{L}{S}_{{\lambda }^{\prime }}ds+\frac{{\zeta }_B}{\zeta }{S}_{\lambda }\left(L\right){\tau }_{{\lambda }^{\prime }}\left(L\right)={\int }_0^L{S}_{{\lambda }^{\prime }}\mathcal{L}{S}_{\lambda }ds+\frac{{\zeta }_B}{\zeta }{S}_{{\lambda }^{\prime }}\left(L\right){\tau }_{\lambda }\left(L\right),$$ (B2)

where ${\tau }_{\lambda }\left(L\right)={[c_1{\partial }_s{S}_{\lambda }-c_2{\partial }_s^3{S}_{\lambda }]\mid }_{s=L}$ is the mechanical torque at the end of the DNA. Thus, if τ_λ (L) = 0, the problem is homogeneous and $\mathcal{L}$ is self-adjoint.

As a result of Eqs. (B1)-(B2), when τ_λ (L) = 0, the eigenfunctions, S_λ (s), are not orthogonal if they are un- weighted. Their overlap is:

$${\int }_0^L{S}_{\lambda }\left(s\right)S_{{\lambda }^{\prime }}\left(s\right)ds=\{\begin{array}{cc}-\frac{{\zeta }_B}{\zeta }{S}_{\lambda }\left(L\right)S_{{\lambda }^{\prime }}\left(L\right)\hfill & \text{for}\lambda \ne {\lambda }^{\prime }\hfill \\ {\int }_0^L{S}_{\lambda }^2\left(s\right)ds\hfill & \text{for}\lambda ={\lambda }^{\prime },\hfill \end{array}\phantom{\}}$$ (B3)

where S_λ (L) ≠ 0 in general. However the eigenfunctions are orthogonal with respect to the weight $w\left(s\right)=1+\frac{{\zeta }_B}{\zeta }\delta (s-L)$, and thus we define the inner product as in Eq. (6). Then, assuming completeness, we can uniquely construct arbitrary perturbations $p\left(s\right)={\sum }_{\lambda }{p}_{\lambda }{S}_{\lambda }\left(s\right)={\sum }_{\lambda }(S_{\lambda },p)S_{\lambda }\left(s\right)$, including the delta function:

$$\delta (s-s^{\prime })=\sum _{\lambda }\frac{S_{\lambda }\left(s\right)S_{\lambda }\left(s^{\prime }\right)}{{\int }_0^L{S}_{\lambda }^2\left(s^{\prime }\right)d{s}^{\prime }+\frac{{\zeta }_B}{\zeta }{S}_{\lambda }^2\left(L\right)}.$$ (B4)

To find the derive the fluctuation relation (Eq. (9)), we first integrate the free energy (Eq. (A1)) by parts:

$$\beta E=\frac{1}{2}{\int }_0^L(-c_1{\partial }_s^2\theta +c_2{\partial }_s^4\theta )\theta \left(s\right)ds+\frac{1}{2}{\left[(c_1{\partial }_s\theta -c_2{\partial }_s^3\theta )\theta \left(s\right)\right]\mid }_{s=L}.$$ (B5)

Writing the twist as a sum of the spatial eigenfunctions, we have:

$$\beta E=\frac{1}{2}\sum _{\lambda {\lambda }^{\prime }}\left({\int }_0^L(-c_1{\partial }_s^2{S}_{\lambda }+c_2{\partial }_s^4{S}_{\lambda }){S_{\lambda }}^{\prime }\left(s\right)ds+{\left[(c_1{\partial }_s{S}_{\lambda }-c_2{\partial }_s^3{S}_{\lambda })S_{{\lambda }^{\prime }}\left(s\right)\right]\mid }_{s=L}\right).$$ (B6)

Rewriting the boundary term using the dissipative boundary condition in Eq. (3) and noting that $\mathcal{L}{S}_{\lambda }=\lambda S_{\lambda }$, and subsequently using Eq. (B3), we have: L

$$\begin{array}{cc}\hfill \beta E& =\frac{1}{2}\sum _{\lambda {\lambda }^{\prime }}{a}_{\lambda }{a}_{{\lambda }^{\prime }}\left(\lambda \frac{{\zeta }_B}{\zeta }{S}_{\lambda }\left(L\right)S_{{\lambda }^{\prime }}\left(L\right)+{\int }_0^L\lambda S_{\lambda }\left(s\right)S_{{\lambda }^{\prime }}\left(s\right)ds\right)\hfill \\ \hfill & =\frac{1}{2}\left(\sum _{\lambda {\lambda }^{\prime }}{a}_{\lambda }{a}_{{\lambda }^{\prime }}\left(\lambda \frac{{\zeta }_B}{\zeta }{S}_{\lambda }\left(L\right)S_{{\lambda }^{\prime }}\left(L\right)\right)-\frac{{\zeta }_B}{\zeta }\sum _{\lambda {\lambda }^{\prime },\lambda \ne {\lambda }^{\prime }}{a}_{\lambda }{a}_{{\lambda }^{\prime }}\lambda S_{\lambda }\left(L\right)S_{{\lambda }^{\prime }}\left(L\right)+\sum _{\lambda }{a}_{\lambda }^2\lambda {\int }_0^L{S}_{\lambda }^2\left(s\right)ds\right)\hfill \\ \hfill & =\frac{1}{2}\left(\sum _{\lambda }{a}_{\lambda }^2\lambda \left(\frac{{\zeta }_B}{\zeta }{S}_{\lambda }^2\left(L\right)+{\int }_0^L{S}_{\lambda }^2\left(s\right)ds\right)\right)\hfill \end{array}$$ (B7)

Thus, the energy is quadratic in the fluctuation amplitudes {a}, which are independent by construction. The fluctuation theorem (Eq. (9)) follows from performing the Gaussian integrals.

To find noise correlations, we write the time evolution of twist as a a series of Rouse-like modes, $\zeta {\stackrel{.}{a}}_{\lambda }=-\lambda a_{\lambda }+f_{\lambda }$. We then note that $\langle a_{\lambda }^2\rangle =\langle f_{\lambda }^2\rangle ∕\left(2\zeta \lambda \right)$ [12]. The final assumption necessary to produce Eq. (10) is the assumption that noise correlations decay much faster than any other characteristic time scale in the system – the noise is delta-correlated in time. Then, using the eigenfunction expansion, we arrive at Eq. (10).

Appendix C: Temporal correlation function

For a free DNA molecule fluctuating about its equilibrium state, the temporal torque correlation function, C_τ(s, s, t), is given by:

$$\begin{array}{cc}\hfill C_{\tau }(s,s,t)& =\frac{2}{L}{\int }_0^{\infty }\frac{\exp \left\{\frac{-{\left(\frac{k\pi }{L}\right)}^2(c_1+{\left(\frac{k\pi }{L}\right)}^2{c}_2)t}{2\beta \zeta }\right\}}{c_1+c_2{\left(\frac{k\pi }{L}\right)}^2}dk\hfill \\ \hfill & \approx \frac{2}{L}\left({\int }_0^{\frac{L}{\xi \pi }}\frac{e^{\frac{-c_1{\pi }^2}{2\beta \zeta L^2}}{k}^{2}t}{c_1}dk+{\int }_{\frac{L}{\xi \pi }}^{\infty }\frac{e^{\frac{-c_2{\pi }^4}{2\beta \zeta L^4}}{k}^{4}t}{c_2{\left(\frac{k\pi }{L}\right)}^2}dk\right).\hfill \end{array}$$ (C1)

The first term of the final expression in Eq. (C1) scales as $t^{-\frac{1}{2}}$ and the second term approaches ${\left(c_1{c}_2\right)}^{-\frac{1}{2}}$ as t → 0. This is the origin of the behavior of C_τ(L, L, t) in the nonequilibrium system (Eq. (12)). The additional late-time exponential decay of C_τ(L, L, t) arises from the slowest mode, which is present due to the rotor bead and the large separation of time scales between $T_0=\frac{2\beta \zeta }{{\lambda }_0}$ and $T_1=\frac{2\beta \zeta }{{\lambda }_1}(T_0\gg T_1)$.

Appendix D: Coupling to bending fluctuations

The dynamical equations for coupled twist and bend can be derived by balancing local forces and moments and considering geometrical constraints [18–20, 32, 33, 35, 36]. The twist strain, Ω(s) = ∂_sθ, and DNA contour spatial position, $\overrightarrow{r}\left(s\right)$, evolve as:

$$2\beta {\partial }_t\Omega =\frac{1}{\zeta }(c_1{\partial }_s^2\Omega -c_2{\partial }_s^4\Omega )+\frac{1}{{\zeta }_{\perp }}({\partial }_s\overrightarrow{r}\times {\partial }_s^2\overrightarrow{r}){\partial }_s{\partial }_t\overrightarrow{r}+f\left(t\right)$$ (D1)

$$2\beta ({\zeta }_{\parallel }\widehat{t}\widehat{t}+{\zeta }_{\perp }(\mathbf{I}-\widehat{t}\widehat{t})){\partial }_t\overrightarrow{r}={\partial }_s((c_1\Omega -c_2{\partial }_s^2\Omega )\left({\partial }_s\overrightarrow{r}\right)\times {\partial }_s^2\overrightarrow{r})-A{\partial }_s^4\overrightarrow{r}+\beta {\partial }_s\left(\Lambda \left(s\right){\partial }_s\overrightarrow{r}\right)+\overrightarrow{g}\left(t\right)$$ (D2)

where $\widehat{t}={\partial }_s\overrightarrow{r}$ is the local tangent vector, ζ_∥ and ζ_⊥ and are the drags on longitudinal and transverse bending fluctuations, respectively [37], ^(s) is the local line tension in the DNA molecule and enforces inextensibility $(\left({\partial }_t\widehat{t}\right)\cdot \widehat{t}=0)$ [18, 20, 35, 36], and $\overrightarrow{g}\left(t\right)$ is noise for the contour position. The cross-product terms arise from the interplay between twist and bend. Assuming that the externally applied tension, F , is large (βAF > 1) so that transverse bending fluctuations are small, we linearize Eqs. (D1)-(D2) in $R={\overrightarrow{r}}_{\perp }\cdot \widehat{x}+i{\overrightarrow{r}}_{\perp }\cdot \widehat{y}$ to obtain Eqs. (14)-(15).

Substituting the steady-state solution to Eq. (14) into Eq. (15), and introducing Δs = s−s₀, where s₀ is a fixed position, we write:

$$2{\zeta }_{\perp }{\partial }_{t}R=\beta (F-2i\zeta {\omega }_0){\partial }_s^{2}R+2i({\zeta }_B+\zeta (L-s_0)){\omega }_0{\partial }_s^{3}R-\frac{A}{\beta }{\partial }_s^{4}R+g\left(t\right)-2i\zeta {\omega }_0\Delta s{\partial }_s^{3}R,$$ (D3)

where g(t) = g_x(t) + ig_y(t). Choosing s₀ = 0, we solve around s ≈ s₀. Thus, we drop $\mathcal{O}\left(\Delta s\right)$ terms, which are small since ${\zeta }_B+\zeta (L-s_0)\gg \zeta \Delta s$. The real-space bending fluctuations near s₀ = 0 are then described by the local modes:

$$R_q\left(\omega \right)=\frac{g_q\left(\omega \right)}{A{q}^4+2\beta ({\zeta }_B+\zeta L){\omega }_0{q}^3+\beta (F-2i\zeta {\omega }_0)q^2-2i\beta {\zeta }_{\perp }\omega }.$$ (D4)

Similarly, to solve Eq. (D3) at the rotor bead end, we choose s₀ = L, and find that bending fluctuations for s ≈ L are described by the local modes:

$$R_q\left(\omega \right)=\frac{g_q\left(\omega \right)}{A{q}^4+2\beta {\zeta }_B{\omega }_0{q}^3+\beta (F-2i\zeta {\omega }_0)q^2-2i\beta {\zeta }_{\perp }\omega }.$$ (D5)

For arbitrary s, the solution to Eq. (D3), accurate to $\mathcal{O}\left(\Delta s\right)$, can be found by fixing s₀ and summing the local bending modes:

$${R\left(s\right)\mid }_{s\approx s_0}=\sum _q{R}_q(\omega ;s_0)e^{iqs}.$$ (D6)

These local modes are not the Fourier amplitudes for bending for the entire molecule. Instead, they describe bending fluctuations for positions near s₀. Thus, at each position, s ≈ s₀ within the molecule, bending fluctuations are comprised of components resembling equilibrium modes with a locally determined torque, τ(s₀) =2β(ζ_B + ζ(L − s₀))ψ₀. This leads the bottom line of Eq. (16). The complete solution is complicated, but, this systematic approximation provides physical insight into the character of bending fluctuations and the buckling transition. Similar to the case of the equilibrium system, a divergent R_q(ψ; s₀) indicates buckling.

This local approximation for studying the buckling transition is justified because we work in the high-force limit, so the characteristic buckling wavelength, $\sqrt{\frac{A}{\beta F}}$, is small [8, 34]. Even if ζ_B were small, this approximation would still be useful near the driving end of the molecule, since the buckling wavelength is small compared the length scale, L, over which the local torque varies significantly. Thus, $\mathcal{O}\left(\Delta s\right)$ terms are small over the length scale of interest.