Extending the distance range accessed with continuous wave EPR with Gd³⁺ spin probes at high magnetic fields

Abstract

Interspin distances between 0.8 nm and 2.0 nm can be measured through the dipolar broadening of the continuous wave (cw) EPR spectrum of nitroxide spin labels at X-band (9.4 GHz, 0.35 T). We introduce Gd³⁺ as a promising alternative spin label for distance measurements by cw EPR above 7 Tesla, where the |−1/2〉 to |1/2〉 transition narrows below 1 mT and becomes extremely sensitive to dipolar broadening. To estimate the distance limits of cw EPR with Gd³⁺, we have measured spectra of frozen solutions of GdCl₃ at 8.6 T (240 GHz) and 10 K at concentrations ranging from 50 mM to 0.1 mM, covering a range of average interspin distances. These experiments show substantial dipolar broadening at distances where line broadening cannot be observed with nitroxides at X-band. This data, and its agreement with calculated dipolar-broadened lineshapes, show Gd³⁺ to be sensitive to distances as long as ~3.8 nm. Further, the linewidth of a bis-Gd³⁺ complex with a flexible ~1.6 nm bridge is strongly broadened as compared to the mono-Gd³⁺ complex, demonstrating the potential for application to pairwise distances. Gd-DOTA-based chelates that can be functionalized to protein surfaces display linewidths narrower than aqueous GdCl₃, implying they should be even more sensitive to dipolar broadening. Therefore, we suggest that the combination of tailored Gd³⁺ labels and high magnetic fields can extend the longest interspin distances measurable by cw EPR from 2.0 nm to 3.8 nm. cw EPR data at 260 K demonstrate that the line broadening remains clear out to similar average interspin distances, offering Gd³⁺ probes as promising distance rulers at temperatures higher than possible with conventional pulsed EPR distance measurements.

1 Introduction

Measurements of nanometer length scales are vital to accessing the structure and organization of biomolecules and their assemblies. Distance measurements using electron paramagnetic resonance (EPR), generally applied at low magnetic fields (0.35 T), have become important for gaining sparse, nm-scale structural information of large or complex biological systems where other methods—such as X-ray crystallography or NMR—cannot be applied.^1,2 Spin labeling, almost exclusively carried out with nitroxide-based spin probes, allows EPR to target one or two specific sites in proteins, membranes, polyelectrolytes, and other biological systems for intra- or inter-molecular distance measurements.^3–6

In situations where electron spins are sufficiently close to each other, their dipolar coupling broadens the EPR lineshape beyond the intrinsic linewidth. Using nitroxides at a spectrometer frequency of ~10 GHz (X-band, ~0.35 T), distances between 0.8 nm and 2.0 nm can be quantified through extraction of the broadening function from the continuous wave (cw) EPR spectrum.^7–9 When distances become longer than 2.0 nm, the intrinsic linewidth of the nitroxide probe prevents observation of the dipolar broadening. Additionally, careful studies of short peptide chains have demonstrated that even this 2.0 nm estimate of the distance limit can be difficult to realize in practice, and the limits for reliable distance measurements may be closer to 1.8 nm.¹⁰ Nevertheless, the measurement of distances longer than ~2.0 nm with nitroxide spin labels necessitates pulsed dipolar spectroscopy (PDS), which isolates the spin–spin dipolar interaction to determine distances.^11–13 In ideal scenarios, pulsed EPR measurements can access distances and distributions as long as 6–8 nm, making them powerful methods.^14,15 However, despite recent advances demonstrating measurements of short distances on an immobilized protein in solution at room temperature,¹⁶ PDS measurements most often require temperatures below 100 K. Further, the effect of high local spin concentration can dramatically reduce the phase memory time of spins, as found in studies of proteins in lipid membrane systems, rendering PDS difficult in this biologically important environment.¹⁷ Thus, if the distance range of cw EPR-based measurements could be extended beyond 2.0 nm, it would offer an important alternative to pulsed EPR for measurements of longer distances relevant in structural biology. The potential advantages of cw EPR measurements include the ability to measure quickly, under milder experimental conditions, with high sensitivity, and in more complex biological environments, including lipid membrane systems. Most dramatically, at temperatures above the protein–glass transition temperature proteins begin to explore their natural conformational space.^18–20 Thus, the prospect of measuring distances beyond 2.0 nm above 200 K offers the opportunity to study the structure and dynamics of proteins in an environment more representative of ambient biological conditions, while also allowing for the possibility to trackmotion. Here we discuss the opportunities of utilizing cw EPR for long range distance measurements with an alternative family of spin probes based on Gd³⁺.

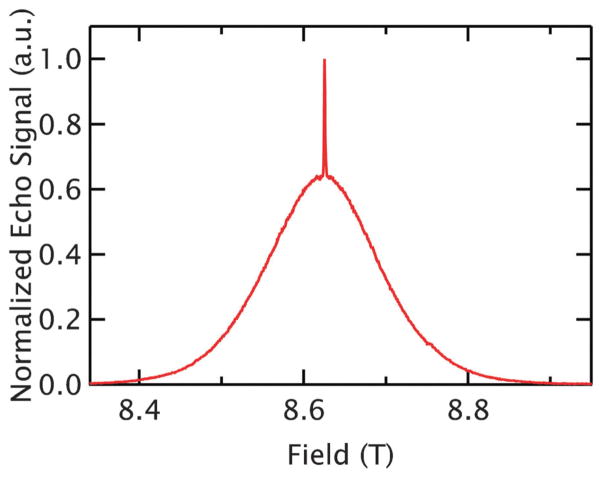
Gd³⁺ is a spin 7/2 ion with an isotropic g-value of ~1.992 that is commonly used with a variety of chelates as a contrast agent for magnetic resonance imaging (MRI). Itsmost propitious characteristic is the narrowness of the |−1/2〉→|1/2〉 transition at high magnetic fields.²¹ While all other transitions are broadened substantially by zero-field splitting, this central transition is an extremely sharp feature in the spectrum at 8.6 T, as shown in Fig. 1. Additionally, the magnetic moment of Gd³⁺ is 7× larger than that of the S = 1/2 nitroxide, yielding a stronger dipolar field and thus leading to longer-range dipolar interactions. Since Gd³⁺ is already commonly used in relaxometry, in imaging,²² and in lanthanide tags for paramagnetic NMR on biomolecules,^23,24 several chemical structures and strategies exist for labeling biological systems with Gd^3+.25,26 Recent work has found that the narrow central feature and isotropic g-value makes Gd³⁺ an exciting new probe for the PDS technique DEER (Double Electron-Electron Resonance) at high fields as it abolishes the orientational selectivity that can dramatically complicate high-field DEER analysis of nitroxides.²¹ DEER measurements using Gd³⁺ have been demonstrated at Q-band (35 GHz, 1.2 T) and W-band (94 GHz, 3.5 T), notably achieving distance measurements out to 6.0 nm on a protein.^27–29 Recently, distancemeasurements between Gd³⁺ and nitroxide spin labels have also been reported.^30,31

Fig. 1.

The Gd³⁺ spectrum at 240 GHz. The 5 K, echo-detected spectrum of GdCl₃ at r̄ = 3.8 nm (5 mM) shows the narrow |−1/2〉→|1/2〉 transition centered on the broad peak associated with the transitions of the other states.

In this work we use a concentration series of GdCl₃—which acts as a good model of potential Gd³⁺ spin labels in a system with a broad distance distribution—as a case study to explore the potential limits for cw EPR distance measurements. We show that the cw EPR spectra of frozen, random solutions of GdCl₃ in deuterated water–glycerol glass at 240 GHz and 10 K are sensitive to dipolar broadening at average interspin distances up to 5 nm. Calculations of the expected lineshape broadening for Gd³⁺ agree with the experiments in random solutions, confirming that broadening is visible at longer distances than with nitroxides. These measurements occurred in a random solution (and therefore a necessarily broad distance distribution), but the actual pairwise distance sensitivity (which is usually more relevant for biological systems) is estimated to be up to ~3.8 nm. Measurements of bis-Gd³⁺ complexes with a flexible bridge yielding ~1.6 nm inter-Gd³⁺ distances shows dramatic broadening consistent with that found for an isotropic GdCl₃ solution with comparable average interspin distances. This suggests cw EPR will be useful for measuring distances in systems with discrete distances. The trends and limits in both experimental and calculated broadening effects are found not to change at 260 K, introducing the exciting prospect of extending cw EPR distance measurements out to ~3.8 nm at much higher temperatures than are typically possible with PDS. In addition to dipolar broadening, a second contributor to the EPR lineshape was also encountered at high concentrations resulting from the large change in the refractive properties of these samples on resonance, an effect we call refractive broadening. This effect did not interfere with observation of dipolar broadening at long distances, and is irrelevant for the low spin probe concentrations typically used in biological distance measurements. However, it is discussed and analyzed in detail to provide a comprehensive understanding of EPR lineshape effects caused by Gd³⁺ dipolar broadening.

2 Spectroscopic properties of Gd³⁺

The Hamiltonian of a single Gd³⁺ ion is generally given by^32,33

$$H=g{\mu }_{\mathrm{B}}{B}_0{S}_Z+D\left[{S_{Z_{\mathrm{c}}}}^2-\frac{1}{3}(S(S+1))\right]+E\left[{S_{X_{\mathrm{c}}}}^2-{S_{Y_{\mathrm{c}}}}^2\right]$$ (1)

where μ_B is the Bohr magneton, B₀ is the applied magnetic field, g~1.992 is the isotropic g-value of Gd³⁺, the S_i’s and S_iC’s are the spin operators in the laboratory and zero-field frames respectively, while D and E are the axial and non-axial zero-field splitting (ZFS) parameters. Both ¹⁵⁵Gd and ¹⁵⁷Gd have nuclear magnetic moments and are present in appreciable amounts at natural abundance (~30% combined); although these isotopes will contribute to the Gd³⁺ lineshape through hyperfine coupling it is generally neglected as a small effect due to their small magnetic moments.³⁴ The first term of eqn (1) dominates at high fields and simply gives the eight Zeeman levels, yielding seven allowed EPR transitions. The second two terms account for the zero-field splitting which shifts the energy levels, spacing the allowed transitions by tens of mT from each other. Generally, the coordinating environment controls the strength of the ZFS, and more symmetric coordinating environments lead to smaller values of D. However, the central |−1/2〉 and |1/2〉 levels are not affected by the zero-field splitting to first order in perturbation theory.

The zero-field shifts of the non-central transitions depend on the strength of the zero-field interaction (expressed by the D and E values) and the orientation of the ZFS principal-axis frame with respect to the applied magnetic field.³³ In a randomly distributed frozen glass, both the orientation and magnitude of the Gd³⁺ ZFS are broadly distributed. This causes all the resonances—with the exception of the |−1/2〉 → |1/2〉 transition—to broaden substantially, leading to the nearly featureless, broad component of the Gd³⁺ echo-detected spectrum shown in Fig. 1.³³ Because the central line is affected starting at second order, its linewidth scales with D²/(g_eμ^B)²B₀ leading to a narrowing of this central line with increasing magnetic field.²⁸ Previous work has helped characterize the ZFS parameters and distributions in commonly used MRI contrast agents at fields up to 8.6 T.^33,35 Values of D/(g_eμ_B) on the order of 10–60 mT are commonly reported in the literature for Gd³⁺ chelates. At 8.6 T (240 GHz Larmor frequency), the central line reaches peak-to-peak widths as narrow as ~0.5 mT, which is shown to be sufficiently narrow to be sensitive to dipolar broadening of distant electron spins at ~3.8 nm.

3 Results

3.1 cw EPR concentration series of GdCl₃

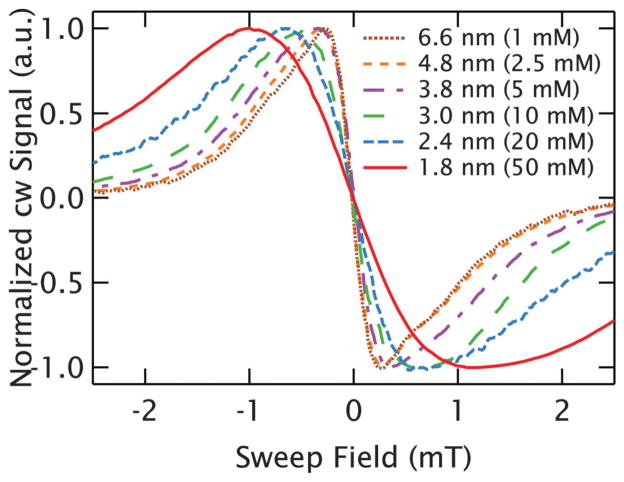
A concentration series of Gd³⁺ ions allows us to evaluate its capabilities as a cw EPR distance probe by observing the line-shape as the average interspin distance is varied. Due to the 1/r³ falloff of the dipolar interaction, we approximate the distance distribution with the average nearest-neighbor distance distribution. For the remaining discussion, we will refer to the average nearest-neighbor interspin distance rather than concentration, as in a random 3D solution these are related by $\overline{r}=0.554/c^{(\frac{1}{3})}$, where c is the concentration.³⁶ As the ions will be freely dissolved in solution, the actual nearest-neighbour interspin distances are broadly distributed about the average values. To probe the effects of dipolar broadening in Gd³⁺, the 240 GHz cw EPR spectra of different concentrations of GdCl₃ were measured at 10 K. The GdCl₃ was dissolved in a solution of D₂O and deuterated glycerol. The concentration was varied between 100 μM and 50 mM, resulting in average nearest-neighbor interspin distances ranging from 14.1 to 1.8 nm. Deuterated solvents were used to minimize broadening due to hyperfine interactions with the water ligands. The measurements show that as the average interspin distance increases, the central transition narrows for average nearest-neighbor distances up to r̄ ~ 4.8 nm (2.5 mM). It is important to note that in a random solution of a given concentration, the 1/r³ dependence of the dipolar interaction results in far stronger dipolar broadening from spin pairs separated by less than r̄ than for those separated by more than r̄. At distances beyond 4.8 nm(2.5 mM), the central linewidth ceases to change, as expected when the broadening due to the local dipolar field is substantially smaller than the intrinsic linewidth. Thus, for a more biologically relevant, narrow distribution in a doubly-labeled biomolecule, a somewhat shorter distance limit likely exists and will be addressed in calculations to be discussed. Fig. 2 demonstrates the narrowing of the central transition as a function of interspin distance in cw spectra at 10 K. Though not shown in Fig. 2 for the sake of clarity, the most dilute sample measured was 100 μM, which still showed a strong signal with a $\text{SNR}=V_{\mathrm{P}-\mathrm{P}}^{\text{signal}}/(2V_{\text{RMS}}^{\text{Noise}})\approx 80$.³⁷

Fig. 2.

Broadening of the central transition of Gd³⁺. cw EPR spectra of GdCl₃ at 10 K show evidence of dipolar broadening out to r̄ = 4.8 nm (2.5 mM). For longer interspin distances, the linewidths remain constant as the effects of dipolar broadening are too small to resolve on the intrinsic lineshape.

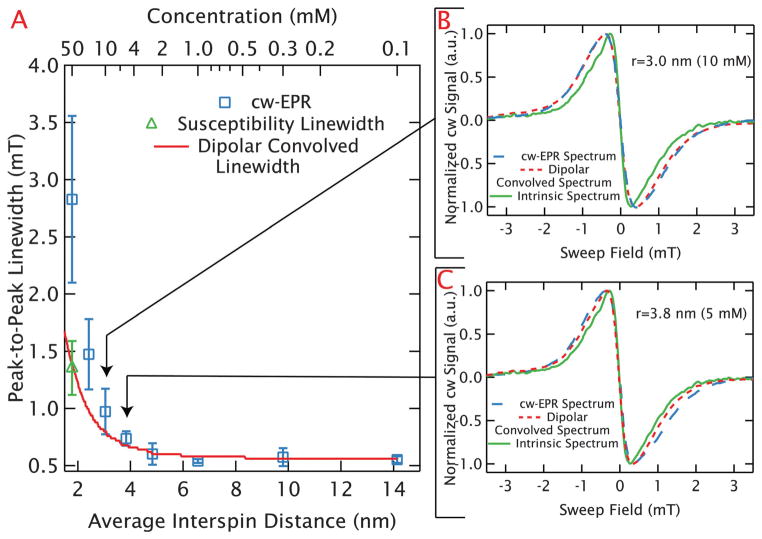
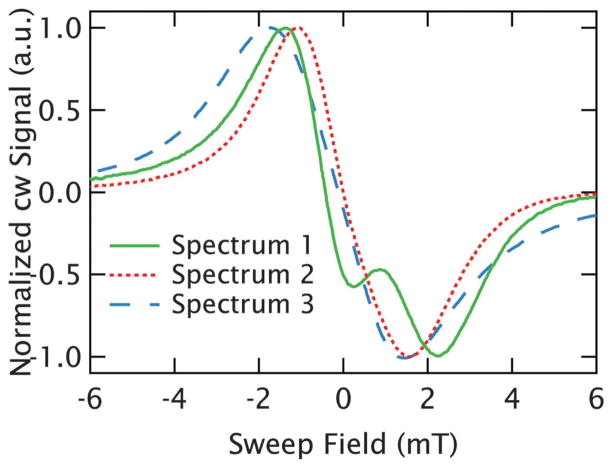
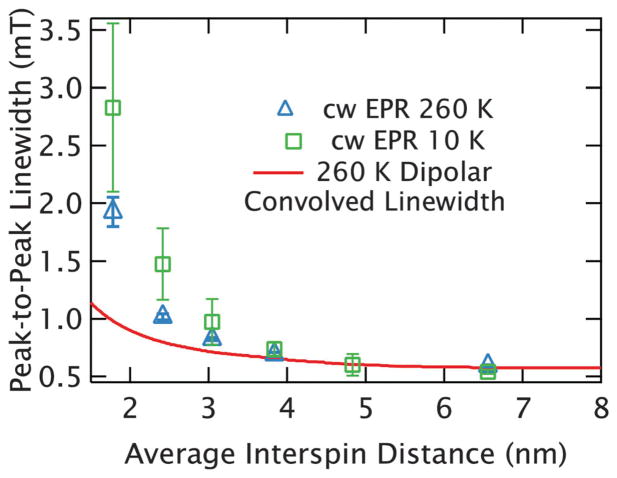
The broadening can be clearly visualized through the peak-to-peak linewidths of the spectra as plotted in blue square symbols in Fig. 3A. Multiple measurements were taken at each concentration as the quality of measurements improved with modifications of the sample holder to increase the sample cross-section, and adjustment of the loading procedures to improve the reproducibility of the sample positioning and flatness. Therefore, as described fully in the caption, each data point in Fig. 3 is an average determined from multiple measurements with an error bar that incorporates the sample-to-sample variations observed. Curiously, for samples with interspin distances at or below r̄ = 3.0 nm (10 mM) the sample shape and volume are found to measurably affect the lineshape, leading to a substantial scatter of linewidths at shorter interspin distances reflected in the large error bars in Fig. 3A. For example, the peak-to-peak linewidths of the r̄ = 1.8 nm (50 mM) samples ranged between 2.2 and 3.6 mT with widely varying lineshapes, several of which are shown in Fig. 4. We are able to identify that this variation is caused by refractive broadening, emerging when the change in a sample’s susceptibility on resonance is large enough to change its refractive properties. This effect becomes so dramatic at the highest concentrations (r̄ = 1.8 nm (50 mM)) that the spectrum of some samples no longer display a single peak, as can be seen in Fig. 4. However, lineshapes at longer interspin distances (r̄ > 3.0 nm or below ~10 mM) are found to be reproducible with different sample volumes and holders.

Fig. 3.

Distance limits of dipolar broadening in random solutions of GdCl₃. (A) The measured peak-to-peak linewidths are plotted in blue squares as a function of average interspin distance for random, frozen solutions of GdCl₃ at 10 K. The average values and error bars are determined from multiple measurements at each average nearest-neighbor distance. An uncertainty in the peak to peak linewidth for each experiment was estimated based on the resolution with which the peak could be determined (which depended largely on the sweep rates and noise). These uncertainties were used to carry out a weighted averaging of the measured linewidths to generate an average linewidth for each concentration. The error bar for each average linewidth was determined from the unbiased, weighted variance. The large error bars apparent at higher concentrations result from refractive broadening. The average best-fit value for the peak-to-peak linewidth after elimination of refractive broadening are shown with a green triangle for r̄ = 1.8 nm (50 mM). As with the experiments, the average value and error bar result from a weighted average and the unbiased, weighted variance respectively (based on uncertainties determined from the error landscape of the correction). The linewidths from the dipolar-convolved spectra are shown with the red line and agree well with the narrowest linewidths measured up to r̄ = 3.0 nm (10 mM). (B) and (C) Confirm this by demonstrating the narrowest experimental lineshape (blue, dashed line) and dipolar-convolved lineshape (red, dotted line) agree well at r̄ = 3.0 nm (10 mM) and r̄ = 3.8 nm (5 mM). Each plot includes the intrinsic linewidth (the experimental r̄ = 14.3 nm (100 μM) spectrum) as a solid green line.

Fig. 4.

Refractive broadening at high concentrations. Three different cw spectra of r̄ = 1.8 nm (50 mM) GdCl₃ using different sample holders and sample volumes are plotted. The lineshape inconsistency is evidence of the refractive broadening, which can even result in the extreme lineshapes of spectrum 1 (solid green line).

The same measurements were repeated at higher temperatures (~260 K) with identically prepared GdCl₃ solutions. The freezing temperature is expected to be ~230 K³⁸ for a non-deuterated sample with the large concentration of glycerol used in these samples (D-glycerol :D₂O 60 : 40 by volume, 65 : 35 by mass). Though deuteration of water raises the freezing temperature slightly, we can assume the effect of deuteration will remain small enough that the sample is in a state of a highly viscous fluid at 260 K. Following calculations in the literature,³⁹ we find the viscosity of our sample to be roughly 140× larger than that of water at 298 K. At 260 K the peak-to-peak linewidth again decreases with increasing interspin distances until reaching the intrinsic linewidth between r̄ = 3.8 nm and r̄ = 6.6nm as shown in Fig. 5. As will be discussed later, the central peak-to-peak linewidth was typically narrower than at 10 K, due to partially reduced dipolar broadening (which slightly reduces the distance limit at 260 K), but the overall trend was found to be comparable.

Fig. 5.

Dipolar broadening at high temperatures. 260 K, experimental linewidths are plotted in blue triangles, with average values of the 10 K measurements (from Fig. 3A) in green squares for comparison. The averages and error bars were calculated identically to Fig. 3A, except that for samples where only a single measurement was made, the error bars were estimated at ±2.5%. The 260 K measurements have routinely narrower linewidths that at 10 K, as is expected from the reduced dipolar broadening at high temperatures. This is demonstrated by comparison with the 260 K dipolar-convolved linewidths plotted as a solid, red line.

3.2 EPR linewidths of Gd³⁺ chelates

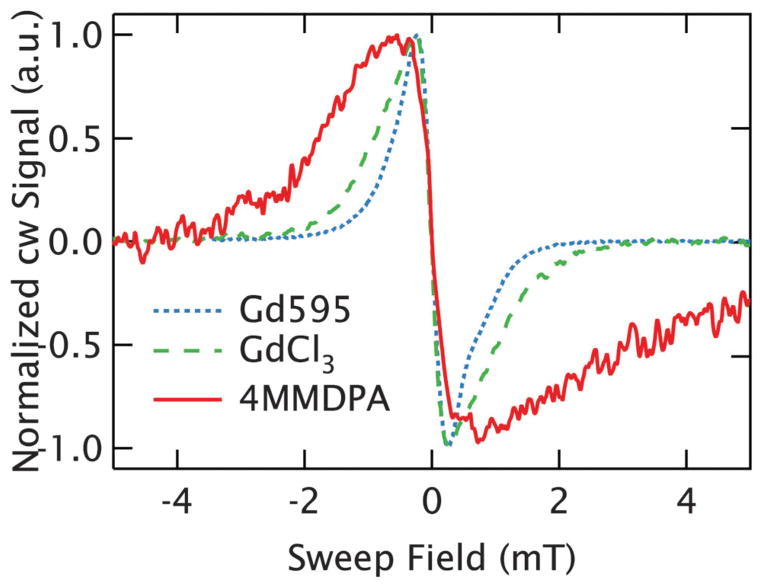
A brief investigation of Gd³⁺ chelating structures was undertaken to identify ligands compatible with spin labeling that also have a narrow line. These studies examined the peak-to-peak linewidth of the central transition at 240 GHz and 10 K. To ensure these measurements represented the intrinsic linewidth, a concentration of 1 mM (r̄ ~6.6 nm) was used as dipolar broadening was shown to be negligible at 1 mM in the GdCl₃ measurements. As reported above, GdCl₃ dissolved in solution, where the hydrated Gd³⁺ ion is coordinated by 9 water molecules, presents a narrow intrinsic linewidth of ~0.55 mT resulting from the relatively small ZFS compared to other Gd³⁺ chelates.³³ 4MMDPA,²⁵ a dipicolinic acid that chelates Gd³⁺ and can be functionalized to cysteine residues of proteins, shows a much broader intrinsic linewidth of ~1.3mT at a 1:1 Gd³⁺ : ligand ratio.^29,40 Because 4MMDPA has several stable ligation states, there is some contribution from Gd³⁺ bound to two 4MMDPA ligands (i.e. Gd³⁺–(4MMDPA)₂) as well as free Gd³⁺. The former contributes to the broadness of the experimental line, as it has a larger ZFS than the singly coordinated species, but is not expected to occur in spin-labeled proteins.^29,40 Alternatively, Gd595 is a Gd³⁺ chelating structure that embeds the high-spin ion in a highly symmetric environment and is similar to the coordinating complexes developed for spin-labeling of biomolecular structures.^28,41 This symmetric environment yields a small ZFS (D ~ 20 mT),²⁸ resulting in a peak-to-peak linewidth of 0.45 mT, making it the narrowest chelate studied so far. In Fig. 6, the cw EPR lineshapes at 240 GHz are shown for the 1 mM samples of each species. As Gd595 offers a linewidth narrower than GdCl₃ and thus is compatible with long-range distance measurements, we utilize bis-Gd³⁺ complexes based on Gd595 as a case study to observe the dipolar broadening in a system of spin-pairs.

Fig. 6.

Intrinsic linewidth of Gd³⁺ chelates. The cw EPR spectra compare the central transition of Gd³⁺ at 1 mM (r̄ = 6.6 nm) in three different coordinating environments. Gd595 is plotted as a dotted blue line, and shows a linewidth slightly narrower than freely dissolved GdCl₃ (dashed green line), where the Gd³⁺ is coordinated by the solvent. 4MMDPA, plotted as a solid red line, shows a linewidth nearly twice as broad as the others.

3.3 cw EPR on a bis-Gd³⁺ complex

Two Gd595 moieties can be tethered with a flexible chemical linker to form a bis-Gd³⁺ (C2-Gd595) complex with a flexible bridge, which was used as a model for a flexible, doubly-labeled biomolecular structure.²⁸ Recent Ka-band (32 GHz) DEER measurements⁴¹ examined the distance distribution of C2-Gd595, and found it to be peaked at ~1.6 nm. The study utilized a specialized dielectric resonator and short, well-separated microwave pulses to reliably measure even short interspin distances. The study claims reliable distribution information down to ~0.8–0.9 nm, but we used the full distance distribution published in their manuscript, which extends down to 0.5 nm.

Both the mono-Gd³⁺ and bis-Gd³⁺ structures are shown in Fig. 7A. As discussed above, the central transition of a frozen solution of 1 mM Gd595 has a peak-to-peak linewidth of only 0.45 mT at 240 GHz and 10 K (Fig. 7B). In contrast, the spectrum of a frozen solution of 1 mM C2-Gd595 taken under identical conditions (overlaid in Fig. 7B) shows a central linewidth of ~1.5 mT, which is more than three times broader than that of the mono-Gd³⁺ species. This demonstrates that strong broadening is visible for a close interspin distance even with flexibly tethered spin-pairs. Further analysis (discussed in 4.2) shows that the observed broadening is consistent with the dipolar broadening observed in random solutions of GdCl₃ with comparable average interspin distances.

Fig. 7.

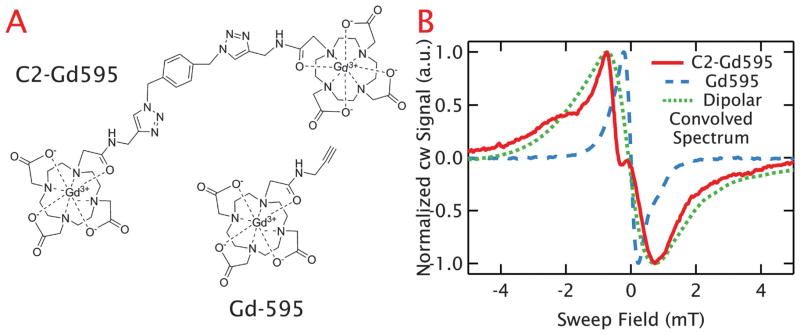
Dipolar broadening in spin-pair system. (A) Shows the chemical structure of Gd595, a single Gd³⁺ chelating structure, and C2-Gd595²⁸ where two of these molecules are tethered with an average separation of ~1.6 nm. (B) The central cw-EPR lineshape at a 1 mM concentration for C2-Gd595 is plotted as a solid red line and the mono-Gd595 line is plotted as a dashed blue line. The dramatic lineshape broadening can be attributed to strong dipolar coupling between the Gd³⁺ pair. This is confirmed from the agreement between the linewidth of C2-Gd595 and the dipolar-convolved lineshape shown as a dotted green line, where the Gd595 line was numerically broadened based on the interspin distance distribution from literature.

4 Analysis

4.1 Dipolar broadening calculations

To better quantify the role of dipolar broadening in our measured spectra, we carried out numeric calculations of the dipolar-broadened lineshape following the approach used for cw distance measurement with nitroxide probes at X-band.⁷ For a pair of spins of given magnetic moments, the dipolar interaction depends on the interspin distance and the relative orientation of the spins. Thus, in a random solution, where the orientations can be considered isotropic, the dipolar interaction can be fully characterized by the interspin distance distribution. The distance distribution can be used to generate the dipolar-broadening function, which describes the response of an infinitely narrow resonance to dipolar broadening. In the case of a single, rigid distance the dipolar-broadening function is given by a Pake pattern.⁴² As we are measuring just the |−1/2〉→|1/2〉 transition, but the neighbors will sample from all the Zeeman spin states of an S = 7/2 species, this is done by generalizing the spin-1/2 Pake pattern⁴² to model the interaction of an S = 1/2 species coupled to an S = 7/2 species. For the case of high-spin ions at high fields, the shape of the Pake pattern depends strongly on temperature as this varies the populations of the Zeeman spin states. Therefore, a temperature dependent weighting for the population of the Zeeman spin states is included. For this work, the Pake pattern is calculated in the “weak-coupling” approximation where the pseudo-secular parts of the dipolar interaction are neglected.⁹ This is justified by the broad extent of the Gd³⁺ spectrum (>0.2 T) compared to the strength of the dipolar interaction. However, for the |−1/2〉 → |1/2〉 transition the width becomes comparable to the dipolar interaction for shorter distances, and this may introduce errors as considered discussion section. Additionally, exchange interactions were neglected as the 4f electrons are found to be well shielded by the 5s and 5p outer electrons, and at both 260 K and 10 K the samples are highly viscous (or completely frozen).⁴³ A series of these Pake patterns for various interspin distances are subjected to a weighted sum according to the distance distribution to find the final dipolar-broadening function.

In order to generate the dipolar-convolved lineshape, which should represent the expected experimental lineshape in the presence of dipolar interactions, we measure an experimental lineshape in the absence of dipolar interactions, then convolve it with the numerically-calculated, dipolar-broadening function. For this approach to be valid, the unbroadened spectrum should be measured so that the spin experiences the same environment as in the broadened spectrum, except with no or negligible dipolar interaction. With this approach, only the unbroadened spectra and a distance distribution are necessary to calculate the dipolar-convolved spectrum. Therefore, there is no need for complete spectral simulation, which would necessitate careful determination of many spin-parameters, most notably for Gd³⁺ the ZFS parameters.

The average nearest-neighbor distance distribution for a given spin concentration can be easily calculated from literature.³⁶ The experimental lineshape of aqueous Gd³⁺ was found not to change with increasing average interspin distance above r̄ = 5 nm (2.5 mM), ensuring that the r̄ = 14.1 nm (100 μM) samples are a good approximation of the intrinsic spectrum. Dipolar-convolved spectra generated with this intrinsic lineshape and the distributions are compared to experimental results in Fig. 3B and C for the cases of r̄ = 3.0 nm (10 mM) and r̄ = 3.8 nm (5 mM), respectively. As refractive broadening will further broaden the line, we have minimized its impact by comparing with the narrowest line observed. By generating a series of dipolar-convolved spectra for various spin concentration we obtain the expected lineshape, and from this the expected linewidth, as a function of the corresponding average interspin distance in a random solution. The expected linewidths are overlaid in Fig. 3A and agree well with the narrowest lineshapes observed for the samples with average interspin distances longer than r̄ = 2.4 nm (20 mM). For shorter distances we consistently measure substantially broader lineshapes. For example, at r̄ = 1.8 nm (50 mM), the difference between the experimental data and the dipolar-convolved linewidth is dramatic. However, as will be discussed below, the experimental and dipolar-convolved linewidths agree for the shortest distance sample when calculations are used to remove the refractive broadening from the experimental lineshapes, leaving only the dipolar effects. The overall agreement observed utilizing the dipolar-convolved spectra clearly demonstrates the potential to use fitting of broadened spectra to determine the broadening function and extract interspin distances from Gd³⁺ lineshapes.

For GdCl₃ at 260 K, the dipolar-broadening function is different than at 10 K due to the temperature dependence of the Zeeman spin state populations for a high-spin system at high magnetic fields. Using the lowest concentration lineshape (r̄ = 6.6 nm (1 mM)) measured at 260 K as the new unbroadened spectrum, we compute the expected dipolar-convolved linewidths as a function of average nearest-neighbor distance at 260 K. The resulting linewidths (overlaid in Fig. 5) agree with the experimental linewidths for the longest interspin distances, but begin to underestimate the lineshape substantially for distance below r̄ = 3.0 nm (10 mM).

We also generate dipolar-convolved linewidths with an identical intrinsic linewidth and distance distributions, but this time assuming that both spins are S = 1/2 (i.e. using the Pake patterns from a pair of S = 1/2 spins), to compare the resulting broadening to the dipolar line broadening caused by high spin Gd³⁺. As seen in Fig. 8, the calculations show that, as observed in experiments, broadening for Gd³⁺ is somewhat weakened at higher temperatures, but is still substantially stronger than would be expected with conventional S = 1/2 probes (at high or low temperatures). The reduction in broadening at high temperatures is a result of the relatively symmetric Pake pattern at high temperatures that is narrower than the Pake patterns at lower temperatures (Fig. S7 in ESI^†).

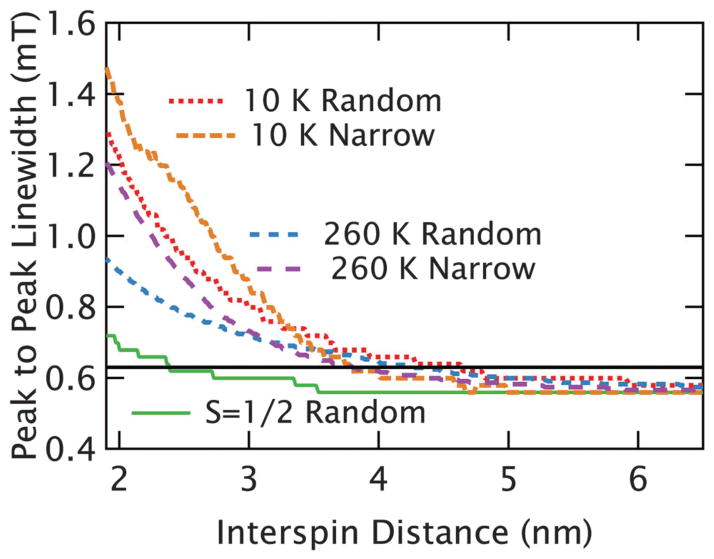
Fig. 8.

Calculated broadening from dipolar interactions. The peak-to-peak linewidths of the calculated dipolar-convolved spectra are shown as a function of average interspin distance for several different scenarios. When the large distribution of nearest neighbors found in a random solution is used, the broadening at both 10 K (dotted red line) and 260 K (dashed blue line) from the S = 7/2 species is substantially stronger than the S = 1/2 species (which is largely independent of temperature between 10 K and 260 K) plotted with a solid green line. When the random solutions are compared to a model of pairwise interactions, where the distribution width is fixed to be narrow, at both 10 K (dashed orange) and 260 K (dotted purple) we find that the distance limit is reduced, but still substantially longer than for an S = 1/2 spin. For illustration, the black, horizontal line indicates a width of ~0.62 mT, corresponding to a roughly 10% broadening of the intrinsic line.

The calculations above address the experimental conditions where the distances distribution is random. The case that is more commonly relevant for biological studies is that of a narrower distribution about a mean—for example, in a protein that has been spin-labeled at two sites. With a broad distribution, the 1/r³ dependence of the dipolar interactions makes the shorter distances in the wings of the distribution the dominant contributor to broadening. To address this and establish the relevant distance limits for narrow distance distributions, calculations were carried out using narrow Gaussian distance distributions, where the full width at half max (FWHM) of the distribution was fixed at 0.4 nm. The results of these calculations are plotted in Fig. 8 for both 10 K and 260 K. As expected, the region between 4 nm and 5 nm becomes difficult to resolve in the case of narrow distance distributions. Nonetheless, in both the 260 K and 10 K cases we can observe clearly meaningful broadening (here defined as a linewidth more than 0.62 mT: 110% of the original width) up to ~3.8 nm distances. For comparison, in the case of a random distribution the limit is ~4.2 nm at 260 K and ~4.5 nm at 10 K.

For the bis-Gd³⁺ complexes studied here, the distance distribution is known from recently reported PDS results.⁴¹ Here the Gd595 spectrum is used as a reasonable estimate for the unbroadened spectrum of bis-Gd³⁺, as the moieties around the Gd³⁺ ion are largely identical. The resulting, computed, dipolar-convolved spectrum from the known distance distribution is overlaid on to the experimental bis-Gd spectrum in Fig. 7B. This again demonstrates good agreement with the experimentally measured peak-to-peak linewidth, though the more complex features are absent from the dipolar-convolved spectrum.

4.2 Refractive broadening

In addition to the effects of dipolar broadening, large susceptibilities were found to contribute to line broadening in high-concentration samples. This effect is clearly observed at high Gd³⁺ concentrations where the linewidths and lineshapes proved to be strongly dependent on sample size and geometry. The origin of this lineshape effect, which we call refractive broadening, is not generally observed in EPR, and only emerges in our work because of the high-spin nature of the Gd³⁺ probes, the high magnetic field, the narrowness of the central transition, and the high concentrations used to access short average interspin distances in this study (i.e. r̄ ≤ 3.0 nm or above ~10 mM). This effect has been discussed previously as a “propagation effect”, and was treated similarly to the discussion here.⁴⁴

Generally in EPR, the magnitude of the complex susceptibility (χ = χ′ + iχ″) is small compared to one, and so the change in reflection from a sample is linear in χ. As our spectrometer measures the reflection from the sample, the cw EPR signal for most systems is given by the real and imaginary parts of the susceptibility, independent of the sample geometry. However, in the case that χ′ or χ″ approach one, due to a strong and narrow resonance, the refractive properties of the material change appreciably around resonance. In these cases the reflection is a more complex function of χ, and must be computed from a model. The method of calculating the reflection is discussed below and in the ESI,^† where the explicit equations are presented. We estimate that for Gd³⁺, χ′ and χ″ approach ~0.1 (and therefore no longer ≪1) at r̄ = 3.0 nm (10 mM). This agrees well with the Gd³⁺ concentration above which our experiments become difficult to reproduce and confirms that refractive broadening is expected to be irrelevant in biological samples as even short interspin distances are pursued in strategically doubly-labeled biomolecules at overall concentrations of order 100’s of μM or less. For comparison, at 10 GHz and 10 K, a nitroxide concentration in excess of 5 M is necessary to reach a strong enough susceptibility response to expect refractive broadening.

The effects of refractive broadening were investigated by using the Fresnel equations to explicitly calculate the reflection from the sample and mirror to obtain theoretical lineshapes that could be compared to the experimental spectra. In order to model the reflections from the sample, a flat sample directly backed by a mirror was used as an approximation of the sample geometry. Further, we approximated the complex susceptibility response (i.e. the real and imaginary parts of the susceptibility as a function of magnetic field around resonance) as a simple Lorentzian. Thus, the model of the sample reflections depends only on the thickness of the sample, and the width and amplitude of the Lorentzian response. The amplitude of the response is set by known parameters, such as temperature, static field and concentration, so that only the width of the susceptibility response remains a variable. The width of the susceptibility response is the critical parameter as it corresponds to the true EPR linewidth, which will include dipolar broadening effects, but is obscured at high concentrations by refractive broadening in the reflection from the sample.

As expected, when the susceptibility response amplitude is taken to be small, corresponding to low (≪10 mM) Gd³⁺ concentrations, the calculated sample reflection is identical to the susceptibility response. However, at larger susceptibility response amplitudes, corresponding to higher Gd³⁺ spin concentrations, the calculated reflection is substantially different than the assumed susceptibility response. At concentrations near 10 mM (such as 10 mM and 20 mM), this difference can be subtle, corresponding to some broadening of the lineshape. At still higher concentrations (for instance, 50 mM) the line can take on a substantial altered shape. We demonstrate this in Fig. 9 for the case of an r̄ = 1.78 nm (50 mM) sample, where we are able to reasonably reproduce the experimental spectrum with the theoretical model, but only using a susceptibility response (that is the true EPR linewidth) much narrower than the measured lineshape. We can identify the true EPR linewidth for each of the r̄ = 1.78 nm (50 mM) samples (whose lineshapes show substantial variations from batch to batch) by repeating this process and determining the width of the susceptibility response that best reproduces the experimental lineshapes. The determination of the best fit widths is described in full detail with accompanying error landscapes in the ESI.^†

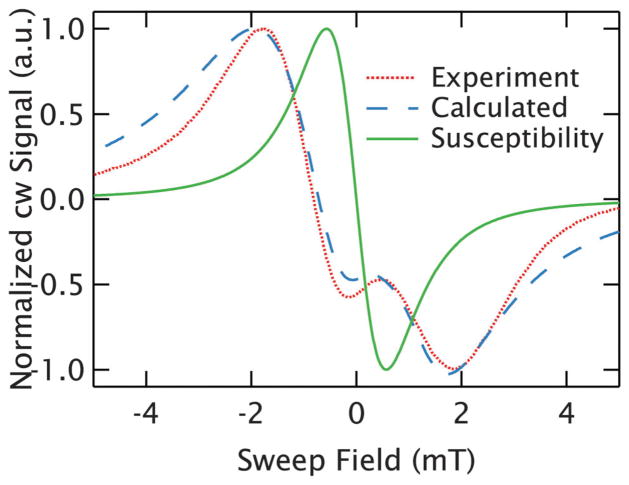
Fig. 9.

Eliminating the effects of refractive broadening. The complex lineshape of an r⃗ = 1.8 nm (50 mM) GdCl₃ sample (spectrum 3 of Fig. 4) is plotted as a dotted, red line and can be well described by accounting for the effects of refractive broadening in a simple calculation of the resonance (dashed, blue line). This allows the determination of the true width of the resonance from the susceptibility response, which is shown with the solid, green line and demonstrates how dramatically the refractive broadening artificially broadens the measured lineshape at high concentration.

In Fig. 3A, we, present the best estimate of the corrected linewidth for the r̄ = 1.8 nm (50 mM) samples. For each r̄ = 1.8 nm (50 mM) sample the extracted linewidth and an uncertainty determined from the error landscapes is found and used to determine the average and error bar. The error bar for the average, extracted linewidth was determined from the unbiased, weighted variance of the individual extracted widths. The average of these corrected linewidths agrees well with the computed, dipolar-convolved linewidth for r̄ = 1.8 nm (50 mM) (1.35 mT vs. 1.40 mT). Further, the extension of this technique to spin-pair systems is supported by the agreement between these corrected GdCl₃ linewidths for the r̄ = 1.8 nm (50 mM) samples and the measured linewidth of C2-Gd595 (1.35 mT vs. 1.46 mT), which represent similar average interspin distances (though the bis-Gd³⁺ is slightly shorter and therefore its lineshape is slightly broader). From these calculations and the error bars in experimental measurements we expect that refractive broadening also affects the r̄ = 2.4 nm (20 mM) and the r̄ = 3.0 nm (10 mM) samples. However, the distortion of the lineshape was too subtle to unambiguously determine corrected susceptibility widths with our fitting model at these concentrations.

5 Discussion

When using cw-lineshapes for distance measurements, a narrow intrinsic linewidth is important to resolve long interspin distances. Therefore, details of the Gd³⁺ chelating structure, which affects the zero-field parameters and in turn the intrinsic EPR linewidths, is critical in evaluating the suitability of Gd³⁺ labels for distance measurements by cw EPR. The highly symmetric environment of Gd³⁺ in water—surrounded by 9 water molecules—gives the narrow line observed. Three equivalent Cl⁻ ions serve as counter ions to Gd³⁺ in GdCl₃ solution, but are not directly coordinating the central ion. Meanwhile in Gd595, Gd³⁺ is coordinated by 4 oxygen and 4 nitrogen atoms that are symmetrically distributed, and one water molecule, yielding a similar, though measurably narrower lineshape. In contrast, 4MMDPA, which is easily employed as a commercially-available, cysteine-compatible spin label, is coordinated by two oxygen atoms, one nitrogen atom, and six waters molecules, and has a substantially broader line resulting from the less symmetric environment. This makes 4MMDPA non-ideal for lineshape-based distance measurements. Fortunately, the availability of alternative Gd³⁺ chelates and significant ongoing research efforts in this area makes the task of developing Gd³⁺-based spin labels with narrower linewidths that are optimal for cw-distance measurements a surmountable problem. Recent work by Yagi et al.²⁷ provide a glimpse at a very promising outlook: they employed symmetric DOTA ligands²⁶ with exceptionally narrow EPR linewidth (expected to be ~0.45 mT at 240 GHz) as cysteine-binding spin labels, upon custom chemical modifications to ensure high rigidity for the Gd³⁺ compound.

Although we have identified Gd³⁺ species with linewidths sufficiently narrow to dramatically extend the distance ceiling, we have not undertaken a systematic study to determine the chemical makeup that provides the narrowest possible central linewidth. Thus, the current long distance limit may be further extended by alternative Gd³⁺-based spin labels that are optimized for a narrower central transition. Alternatively, moving to higher magnetic fields can further narrow the central line for samples where the ZFS is the dominant source of the central transition’s intrinsic linewidth. For Gd595, the contribution of the ZFS (D~20 mT)²⁸ to the linewidth is estimated²⁸ to be only ~0.3 mT, while the measured width is ~0.45 mT. Thus, we expect the intrinsic line to be ~0.25 mT by approximating the line as a Voigt combination of the ZFS width (Gaussian) and an intrinsic width (Lorentzian). Therefore even for Gd595, the narrowest chelate investigated, moving to even higher fields may help further reduce the linewidth. However, even doubling the field to reduce that ZFS width by a factor of 2, would only reduce the line to ~0.34 mT, offering a modest increase of ~10% in the distance range. Due to the rough approximation of the ZFS width, experimental measurements at higher fields would be necessary to confirm this. Alternatively, for chelates with larger zero-field splitting parameters, such as 4MMDPA spin-labels, the line is likely to narrow substantially at higher fields, making them more attractive probes for cw distance measurement.

The extended distance range that is shown to be accessible with Gd³⁺-based probes is partially due to the simple, narrow central feature of Gd³⁺ at high fields acting as a sensitive probe of broadening. At the same time, the increased strength of dipolar interactions between high-spin ions causes increased line broadening for a given distance, which is critical for extending the distance range. The lineshape broadening from dipolar interactions arises from the differences in local field experienced by a spin from the spin state of neighbouring spins. Although ZFS is present in the Gd³⁺ spectrum, at 240 GHz it is much smaller than the static field (B₀ = 8.6 Tesla while D < 50 mT) and so can be neglected for investigation of the dipolar interactions.^21,28 As Gd³⁺ is S = 7/2, there are 8 possible spin states for a neighbour, as opposed tomerely |1/2〉 and |−1/2〉 for an S = 1/2 system. The zero-order dipolar interaction can be written as $W_{\text{dipolar}}^0\propto 1/{\overline{r}}^3({\overline{S}}^1{\overline{S}}^2-3S_Z^1{S}_Z^2)$ so that higher-spin Zeeman states (i.e. the quantum states |m_z〉 with m_z≠±1/2) cause larger shifts in the local field than the |−1/2〉 states.³² Therefore, the presence of these states contributes to the wider broadening profile of Gd³⁺ compared to S = 1/2 species. Simply, a high-spin ion is a stronger local magnet and therefore a more effective broadening agent. This is demonstrated through our experiments with GdCl₃ and confirmed through the dipolar-convolution calculations as presented in Fig. 8, where the broadening for S = 7/2 spins is predicted to be substantially stronger than for S = 1/2. The limit of ~3.8 nm (in the case of a narrow distribution) is reasonable based on limits observed using nitroxides, which we take to be ~2.0 nm. The central line of nitroxides at X-band is ~1.1 mT, whereas the GdCl₃ width is ~0.55 mT. Assuming the broadening function of the Gd³⁺ is ~3.5 times broader than that of a nitroxide (approximated from the ratio of the extent of broadening in Fig. 8), the distance limit should be raised by (1.1/0.55 × 3.5)^(1/3) = 1.91 corresponding to a limit of ~3.8 nm.

As discussed in the analysis section, in order to calculate the dipolar broadening patterns, the Pake-pattern of two interacting spins was calculated. Experimentally, the Gd³⁺ spectrum extends over ~0.2 T due primarily to the strength and distribution of ZFS parameters. Thus, the majority of spin packets are separated in frequency by far more than the strength of the dipolar interaction. This permitted calculating the broadening as entirely in the “weak” coupling regime. However, the |−1/2〉 → |1/2〉 transition of Gd³⁺ is narrow, which could result in strong coupling as a pair of interacting |±1/2〉 spins are more likely to be separated (in frequency) by less than the dipolar frequency. For nitroxide moieties at X-band, strong coupling is dominant for interspin distances below ~0.7 nm, while entirely weak coupling emerges above ~1.5 nm, with a region of intermediate coupling in between.¹⁰ The full-width at half-max of the absorption spectrum for the |−1/2〉 → |1/2〉 transition of Gd³⁺ at 240 GHz is ~25 MHz (roughly twice the peak-to-peak width), which is ~7 times narrower than the typical width of a nitroxide spectrum at 10 GHz.⁹ Thus, by a scaling argument for the interaction of neighboring |±1/2〉 states, the applicable ranges of strong and weak coupling should be increased by a factor of $\sqrt[3]{7}=1.9$, yielding intermediate coupling between 1.3 nm and 2.9 nm. Thus, while for the majority of spin states, the coupling (between spin S = 1/2 and S = 7/2 states) is likely well described in the weak interaction regime, there is a large region of relevance where the broadening from neighboring |+1/2〉 and |−1/2〉 are in the intermediate broadening regime. For nitroxides, measuring within the intermediate broadening range introduces an uncertainty due to the 3/2 larger broadening for strong dipolar coupling that is of order ~15%.⁹ However, given that we only expect this to occur for a fraction of the broadening pattern (resulting from the |±1/2〉 spin states), this is an upper limit for the Gd³⁺ spectrum. In fact, at 10 K the |−7/2〉 and |−5/2〉 states contain~90% of the spins, and only ~3% are in the |±1/2〉 states. This suggests that at low temperatures the effect will be truly negligible and at higher temperatures will introduce a small error.

In applying the dipolar broadening for random solutions at 10 K, we see good agreement to the measured lineshapes for sufficiently dilute systems where refractive broadening is negligible. However, in the case of the C2-Gd595 flexible bridge, the dipolar convolution fails to capture the details of the experimental spectrum, though it did predict the spectral width. The precise source of these discrepancies could not be identified unequivocally. However, given the broad distance distribution centered around a short distance (~1.6 nm), a sizable population of very short (<1 nm) distances is expected to contribute. These distances present potential problems for the distance analysis here. For instance, exchange interactions are neglected in our analysis, and while through-solvent exchange interactions are predicted to be weak in Gd³⁺, they may become important at these short distances and could cause some of the spectral features. Alternatively, through-bond exchange could reasonably exist in the bis-Gd³⁺ complex. As discussed above, at 10 K the effect of strong dipolar coupling of the |−1/2〉 and |1/2〉 spin states is negligible due to small number of spins in the |±1/2〉. However, it is possible that at very short distances some sizeable populations of other spin states with frequency differences comparable to the dipolar broadening enter the intermediate/strong coupling regime. Finally, the distance distribution for C2-Gd595 below ~0.9 or 0.8 nm may have been incompletely captured as this falls outside the range accessible with the DEER measurements carried out by Raitsimring et al.⁴¹ More work remains with the particulars of these short distances to accurately produce the experimental shapes. However, this does not detract from the opportunity brought about by the strong dipolar broadening observed with Gd³⁺ probes that can act as a rough ruler of interspin distance at short distances, and does not impinge on the region of greatest relevance, which are longer distances.

The observed temperature dependence of the broadening effects in Gd³⁺ is interesting, as cw-distance measurements in nitroxides at X-band are not strongly affected by temperature. This is because an S = 1/2 system at 0.35 Tesla is not substantially polarized, even at low temperatures, meaning the population of the |±1/2〉 states are roughly equal. Further, once frozen, the intrinsic lineshape of a nitroxide does not change substantially with temperature. Conversely, for a S = 7/2 ion at 8.6 T, the populations of the various Zeeman spin states are strongly temperature dependent between 260 and 10 K, which drastically affects the shape of the broadening functions. At a temperature ~10 K, roughly 90% of the spins are in either the |−7/2〉 and |−5/2〉 Zeeman states. This yields a strongly asymmetric broadening function. When this function is averaged over a distance distribution, it is measurably broader than at 260 K, where the populations of all levels are nearly equal. Thus, in both experiments and in the calculated dipolar-convolved spectra, overall narrower lines and shallower distance-dependence are observed at higher temperatures. Further, as the polarization of the |−1/2〉 →|1/2〉 transition is reduced by a factor of ~1/3 from 10 K to 260 K, refractive broadening becomes less effective at 260 K, which may further narrow the high concentration linewidths. Still, although the dipolar broadening is somewhat reduced at higher temperatures, Fig. 8 demonstrates that for narrow distance distributions, broadening effects become visible at ~3.8 nm at both 10 K and 260 K.

At 260 K, the dipolar-convolved lineshapes are substantially narrower than the experimental spectrum. Some effect from refractive broadening can be expected at the highest concentrations, but does not account for the ~0.1 mT discrepancy at ~3.0 nm inter-Gd³⁺ distances (10 mM), where refractive broadening should be absent at this temperature. This discrepancy leads us to investigate broadening mechanisms besides that of the static, dipolar interactions valid in frozen situations. At higher temperatures we may see effects from modulation of the dipolar interaction by motion⁴⁵ or by the longitudinal relaxation (T_1e).^46,47 However, neither of these interactions should play an extensive role due to the extremely high viscosity of the solvent under these conditions. Based on models for T_1e of DOTA contrast agents in liquid⁴⁸ (which cannot be directly measured at these fields), we estimate that the T_1e exceeds 100 ns due to the increased viscosity of the sample. This corresponds to a ~0.1 mT FWHM linewidth, which is <1/10 of the intrinsic linewidth. Alternatively, the effect of dipolar-enhanced relaxation can only emerge from translational motion (as rotational motion does not significantly modulate the dipole interaction between neighbouring monomers). However, we can estimate the translational correlation times as τ ~ 42–100 ns based on approximate viscosity (140× more viscous than water at 298 K). Based on previous work, we estimate that for these slow motions distances shorter than at least 4.1 nm are not substantially averaged.^45,49 As this falls at the edge of the limit of our resolution of dipolar interactions, the effect of dipolar relaxation enhancement is assumed to be negligible or at least weak for these systems (though would naturally emerge for less viscous liquids, i.e. in water at room temperature). Further details of these approximations are found in the ESI.^† Thus, we find the broadening should be well described by a static dipolar interaction, even at 260 K, and the disagreement observed between calculations and experiment can only be attributed to a subtle refractive broadening.

With an extended distance range, cw EPR becomes a powerful alternative to PDS in situations where measurements above 200 K are desirable. Because PDS relies on phase memory times long enough to observe the dipolar oscillation, it is not easily applied at non-cryogenic temperatures. In addition, such measurments are highly succeptible to short T₁ values that cause random flips that will destroy the DEER effect. Alternatively, cw EPR can be performed even when the phase memory time is too short to measure an echo and so is viable at higher temperatures. We report on an alternative approch where dipolar line broadening was measured up to average spin distances up to ~3.8 nm at 260 K in a viscous solution. Further, cw EPR measurements can be run in an hour, allowing multiple samples to be measured in a single day. Even without a resonator, a good SNR is demonstrated at 100 μM with ~10 μL of sample, which is comparable to or somewhat better than typical sensitivities of X-band DEER experiments carried out on commercial spectrometers. These sensitivity levels suggest that Gd³⁺ can find broad use in systems currently suitable for many kinds of application, with the at times critical advantage of operating at higher temperatures. The state-of-the-art in PDS has pushed the sensitivity limits beyond the levels commonly encountered at standard commercial X-band spectrometers, often by leveraging higher magnetic fields with sufficient microwave power.^50–53 While current cw-measurements of Gd³⁺ at 240 GHz do not achieve this level of concentration or absolute sensitivity, further optimization of the spectrometer will offer improved sensitivity, particularly in achieving a uniform, flat sample as the current “bucket-style” holder can give rise to variable sample shapes.

It is worth noting, however, that PDS is capable of determining the complete distance distribution, and even when the precise shape of the distribution cannot be resolved it offers a quantitative measurement of the width of distributions.⁵⁴ In contrast, the cw EPR technique does not permit the direct extraction of the distance distribution, but cw EPR can distinguish broad and narrow distributions, and, with fitting, can quantify the widths using a model for the distance distribution (e.g. assuming a Gaussian distribution). Thus, cw EPR measurements do not offer the full and model-free distribution information, which is a powerful advantage of PDS. Another disadvantage of the cw EPR method is that it requires the comparison of two samples, singly-and doubly-labeled, as opposed to a single doubly-labeled sample for PDS.

Although sensitivity is reduced at higher temperatures, for Gd³⁺ the polarization of the |−1/2〉 to |1/2〉 transition is only ~3× smaller at 260 K compared to 10 K, suggesting that lowered sensitivity will not restrict these measurements at higher temperatures. This capability to measure at these temperatures promises exciting prospects, as proteins studied at temperatures above the protein glass transition will better represent the sampling of conformational states found under biological conditions, ^18–20 and there is no fundamental limitation to extend this methodology to physiological temperatures (if tumbling can be kept slow).⁴⁹ In addition, any conformational changes that modulate the dipolar coupling on the time scale of sub-μs to μs at these temperatures should be visible as changes to the broadening of the linewidth, offering the potential of using EPR to track aspects of conformational changes out to ~3.8 nm.

6 Conclusions

We demonstrate that simple cw EPR lineshape analysis can exploit the potential of Gd³⁺-based spin labels at high fields and frequencies for the determination of long interspin distances. This strong broadening is demonstrated in systems with broad distance distributions and calculations indicate that for narrower distribution, interspin distances out to 3.8 nm can be probed at 10 K as well as 260 K, which is above the typical protein glass transition temperature. This work shows that these distances will be accessible when utilizing a suitable chelating agent that offers a small zero-field splitting, yielding a narrow central line. Potential candidates include DOTA-derived spin labels that have EPR central lines even narrower than the aqueous Gd³⁺ ions. Explicit calculations of the dipolar broadening function reproduce the effects of experimentally measured dipolar broadening, so that distance extraction from the lineshape is a feasible next step. More work is necessary to account for discrepancies between the dipolar-convolved spectra and experimental lineshapes of the bis-Gd³⁺ model sample, and to develop suitable fitting methods. However, it should already be possible to use Gd³⁺ to gauge long-range distances and distance changes in biological samples, even without the full capability of distance extraction. Finally, as the central linewidth determines the distance limitation, even greater sensitivity for probing longer distances and finer distance resolution can be expected if specially designed Gd³⁺ chelating structures with narrower lines can be employed.

7 Materials and methods

7.1 Sample preparation

The compound 4MMDPA was purchased from Cedarlanes. Gd595 and C2-Gd595 were synthesized following established procedures.^55–57 GdCl₃·6H₂O (Gadolinium chloride hexahydrate), D₂O was purchased from Sigma Aldrich. Deuterated glycerol was purchased from Cambridge Isotope labs. All chemicals were used as purchased without further purification. GdCl₃ samples were made by dissolving GdCl₃·6H₂O in a solution of D₂O–D-glycerol (0.4 : 0.6, v : v). Both Gd-595 and C2-Gd-595 samples were prepared in solutions of D₂O–D-glycerol (0.4 : 0.6, v : v). 4MMDPA solutions were also prepared in D₂O–D-glycerol (0.4 : 0.6, v : v), to which a 1 : 1 molar ratio of GdCl₃·6H₂O was added.

7.2 cw EPR measurements

The spectrometer is a dual, pulsed and cw EPR spectrometer operational at 240 GHz, using a low power solid state source developed to operate as the staging instrument for a Free Electron Laser-powered EPR spectrometer.⁵⁸ It is similar in operation to spectrometers described elsewhere.⁵⁹ It utilizes a frequency multiplier source (Virginia Diodes Inc.) which multiplies a 15 GHz source 16× to achieve a frequency of 240 GHz with cw power of order 30 mW. The system utilizes a quasi-optical bridge and induction mode detection.⁶⁰ Super-heterodyne detection is employed using a Schottky subharmonic mixer (Virginia Diodes Inc.) and a homebuilt IF stage at 10 GHz, which is then mixed down to baseband for detection. The detector system has a noise temperature of ~1300 K, and the overall spin sensitivity at room temperature is measured to be ~10¹² spins per mT in cw operation.⁵⁸ The samples were between 3 and 15 μL (with smaller volumes used for higher concentrations) and placed in one of two Teflon sample cups. The larger cup is roughly ~4 mm inner diameter and ~6 mm in height, the smaller was ~2 mm inner diameter and ~5 mm in height. The samples were frozen in liquid nitrogen before being mounted within a modulation coil at the end of a ~1.25 meter long overmoded waveguide (Thomas Keating Ltd.). The waveguide is placed with the sample at the center of a sweepable, actively shielded, 12.5 T magnet (Oxford Instruments plc). The magnet is outfitted with a continuous flow cryostat (Janis Research Company LLC) mounted in the room temperature bore of the magnet, allowing continuous operation between ~2.3–300 K and down to ~1.5 K in batch mode.

cw measurements were carried out using field modulation at 20 kHz with modulation amplitude between 0.05 and 0.2mT—to keep modulation <1/5 of the linewidth that typically was between 0.45 and 2.0 mT—and measured in quadrature using lock-in amplifiers (Stanford Research Instruments Inc. SR830). The incident power was highly attenuated with a wiregrid polarizer, and was on the order of μW at the sample. A super conducting sweep coil, separate from the main coil of the super conducting magnet, capable of sweeping the field up to ±60 mT was used to carry out cw measurements.

The cw spectra were rephased in post-processing to determine the derivative lineshape by equalizing the positive and negative peaks of the derivative shape. The locations of the peaks of the spectrum were determined by fitting near the peak with a 3rd order polynomial and determining the location of the maximum. This was done to minimize the effect of noise on the peak estimate, but did not yield substantially different peak locations than simply selecting the maximum and minimum points of the spectrum. For measuring the full width of the Gd³⁺ spectra, as presented in Fig. 1, the field was swept using the main coil of the magnet.

The echo-detected spectrum was measured using a 175 ns–τ–275 ns–τ (with τ = 1 μs) spin-echo pulse sequence using the maximum available power of the solid state source (~30 mW) and the area under the echo signal measured in magnitude mode was recorded using an oscilloscope (Lecroy Corporation DDA-120).

7.3 Convolution broadening of lineshapes

Pake patterns for a given interspin distance by modeling two coupled spins (S = 1/2 and S = 7/2) with no broadening parameters, no exchange interactions, and neglecting the ZFS splitting.⁴² This model of the broadening is valid as a result of measuring only the |1/2〉 → |−1/2〉 (effectively an S = 1/2 system), which is then coupled to the neighboring S = 7/2 ions. This is done by extension of the Pake pattern for a pair of S = 1/2 spins emerging from the S = 1/2 interacting with the |±1/2〉, |±3/2〉, |±5/2〉, and |±7/2〉 spin states

$$F(B,T,r)=\sum _n{f}_n(B,T,r)/{\alpha }_n$$ (2)

$$f_n(B,T,r)=\{\begin{array}{c}{P}_n(T){\left(\frac{B}{{\alpha }_n(r)}+1\right)}^{-\frac{1}{2}},-{\alpha }_n(r)<B<2{\alpha }_n(r)\\ P_{-n}(T){\left(-\frac{B}{{\alpha }_n(r)}+1\right)}^{-\frac{1}{2}},-2{\alpha }_n(r)<B<\alpha (r)\end{array}\text{for}n=\pm 1/2,\pm 3/2,\pm 5/2,\text{and}\pm 7/2$$ (3)

Where P_n(T) = 1/Z exp[−nħω/(k_bT)] is the temperature-dependent population of the |n〉 Zeeman state ( $Z={\displaystyle \sum _n}exp[-n\hslash \omega /(k_{\mathrm{b}}T)]$ is the partition function), and α_n(r) = 2n0.931/r³ mT nm³ is the splitting caused by the |±n〉 Zeeman states. The factor of 1/α_n in (2) is to normalize each of the f_n(B,T,r) by their total widths. No major deviations are observed when the results of these calculations were compared to a simulated Pake pattern using Easy-spin⁶¹ utilizing a coupled S₁ = 1/2, S₂ = 7/2 system where the g-values are spaced from one another to achieve a “weak-coupling” spectrum. This method for calculating the high-spin Pake patterns was substantially faster and more flexible than utilizing Easyspin, though the use of the spectral simulation software would allow more advanced parameters (such as exchange interactions, or full spectral simulations) to be included. Temperature and field were explicitly included in the calculation of Pake patterns to account for the effect of the populations of the Zeeman levels on the shape of the Pake patterns. The spacing of the field axis was selected to coincide with the experimental field sweep. A broadening function was then generated by summing the Pake patterns weighted by the known distance distribution for the system. In the case of the C2-595 complex, the distance distribution was taken from literature, ⁴¹ whereas we used the average nearest-neighbor distance distribution, at the known concentration, for GdCl₃ samples. Interspin distances below 0.5 nm were ignored as being unphysical. The broadening function was then convolved with the in-phase component of the intrinsic EPR lineshape (taken as a low concentration spectrum, where no broadening is observed). Because the experimental lineshapes were all phased to be symmetric, the phase of the broadened function was made to be symmetric by shifting the phase of intrinsic cw spectra before convolution. All calculations were carried out in Matlab (Mathworks 2011a).

7.4 Refractive broadening calculations

Calculations of the refractive broadening were carried out in Matlab (Mathworks 2011a). For a given concentration, the intrinsic susceptibility was calculated using an approximation of a Lorentzian lineshape, parameterized by the width of the resonance. From this response, the reflected signal from a disk shaped sample is calculated for a particular sample thickness. This lineshape is then phase- and offset-matched to the experimental lineshape, and the error between the calculated and experimental line is determined. This process is then iterated through various Lorentzian widths and sample thicknesses to generate an error map, which can be used to identify the true EPR linewidth when the refractive broadening obscures the dipolar broadening of the lineshape. Further details of the calculations, as well as how the error maps were used to identify reasonable values of the true linewidth, can be found in the ESI.^†