Characterization of Protein Flexibility Using Small-Angle X-Ray Scattering and Amplified Collective Motion Simulations

Abstract

Large-scale flexibility within a multidomain protein often plays an important role in its biological function. Despite its inherent low resolution, small-angle x-ray scattering (SAXS) is well suited to investigate protein flexibility and determine, with the help of computational modeling, what kinds of protein conformations would coexist in solution. In this article, we develop a tool that combines SAXS data with a previously developed sampling technique called amplified collective motions (ACM) to elucidate structures of highly dynamic multidomain proteins in solution. We demonstrate the use of this tool in two proteins, bacteriophage T4 lysozyme and tandem WW domains of the formin-binding protein 21. The ACM simulations can sample the conformational space of proteins much more extensively than standard molecular dynamics (MD) simulations. Therefore, conformations generated by ACM are significantly better at reproducing the SAXS data than are those from MD simulations.

Introduction

Flexibility within a protein is often critical for its function. For example, a multidomain protein consists of two or more domains connected by flexible linkers (1,2) that determine the extent of interdomain motions and, further, lead to large-scale functionally relevant conformational transitions. Structure determination of the multidomain protein containing flexible linkers is experimentally difficult. It could be rather challenging to use x-ray crystallography to solve a structure with multiple conformations, since this methodology is more applicable to a well-folded protein with a single dominant state. Although solution nuclear magnetic resonance (NMR) is limited to proteins of moderate molecular weight, electron microscopy (EM) usually works best for large-size biomolecular complexes. Small-angle x-ray scattering (SAXS) has been identified in recent years as a promising technique for structure elucidation of proteins (3–6). Although SAXS resolution is inherently low, since a complex 3D structure is reduced to a 1D scattering profile that is orientationally averaged, it can still provide valuable information regarding, for example, the size and shape of the protein. In principle, SAXS has no size limits, which has been successfully demonstrated in various systems from individual proteins to complexes.

SAXS is particularly useful in characterizing the flexibility of a protein in solution. However, traditional analysis methods, such as DAMMIN (7) or GASBOR (8), which use SAXS data to build a single molecular envelope, cannot provide a picture of the highly dynamic protein. Therefore, in recent years, several studies have explored the possibility of combining experimental SAXS data with computational simulations to interpret protein dynamics in solution (9–16). Many of these methods share a similar strategy, namely, using computer simulations to generate a large pool of protein conformations and then selecting the ensemble of structures that best reproduce the SAXS data.

Among the computational techniques, molecular dynamics (MD) simulation, which has been very successfully used in the study of protein dynamics (17–19), is gaining in popularity. However, the computational cost of MD is generally expensive. For a multidomain protein, because an MD simulation at a timescale of microseconds is time-consuming, a timescale of nanoseconds is usually used. On the other hand, under physiological conditions, the protein could be trapped in its locally stable states in the MD simulation while conformational transitions between the different states are rarely sampled due to the frustrating nature of the protein energy landscape (20). Thus, the inefficient sampling of protein conformations in the MD simulation due to the aforementioned issues may fail to interpret the experimental SAXS data properly. To overcome this problem, various methods have been utilized, such as rigid-body modeling (9–11,14), coarse-grained (CG) simulations (13–15), and enhanced sampling techniques (11,14,21).

We previously developed a sampling method called amplified collective motions (ACM) that utilizes a few collective modes obtained from an elastic network model (ENM) to guide the atomic MD simulation (22). The ENM (23,24) is a residue-based CG model that can efficiently calculate collective modes that describe functionally relevant domain motions in proteins (25–28). In ACM, the collective motions obtained from the ENM are accelerated by coupling them to a high-temperature bath. With this strategy, the protein would be able to escape from the traps and explore different conformational states on the energy landscape in a relatively short simulation time. Applications to different proteins support the ability of ACM simulations to sample the conformational space much more extensively than can standard MD simulations (22,29–31). In this article, we combine the simulation results of ACM and SAXS data to reveal various conformational states of multidomain proteins in solution. The results show that the ACM sampling does a much better job than MD at reproducing the SAXS data.

In the next section, we introduce computational details of ACM and control MD simulations, SAXS data acquisitions, and the SAXS-based ensemble optimization method (EOM). In the Results and Discussion section, the protocol is applied to two multidomain proteins, bacteriophage T4 lysozyme (T4L) and tandem WW domains of the formin-binding protein 21 (FBP21-WWs). The ACM method is then compared with some other simulation techniques in combination with SAXS data. The final section is devoted to concluding remarks.

Theory and Methods

Conformational sampling using MD and ACM simulations

T4L

T4L is a two-domain protein with 164 amino acid residues. The N-terminal (residues 13–65) and C-terminal (residues 75–162) domains are connected by an α-helix. The active site between the two domains is responsible for oligosaccharide binding. The many available experimental structures of T4L and its variants indicate the presence of a hinge-bending domain motion that opens or closes the active site (32).

MD simulation

An open conformation of T4L with a resolution of 2.7 Å was chosen from Protein Data Bank (PDB) entry 178L (32). The structure, containing four mutations (C54T, C97A, D127C, and R154C), was changed back to the wild-type form, and the simulation was then set up using the GROMACS-4.5.5 package (33) and the CHARMM27 force field (34). The protein was placed in a cubic box, with a minimum distance of 1.3 nm between the solute and the box boundary. The box was then filled with TIP3P water molecules (35). The energy of the system (protein and waters) was minimized by the steepest-descent method, until the maximum force was <1000 kJ mol⁻¹ nm⁻¹. Eight Cl⁻ ions were added by replacing the same number of waters with the most favorable electrostatic potential to compensate the net positive charges on the protein. The final system (protein, waters, and ions) was minimized again using the steepest descent followed by the conjugate-gradient method, until the maximum force was <100 kJ mol⁻¹ nm⁻¹. The simulation was conducted by using the leap-frog algorithm (36) with a time step of 2 fs. The initial atomic velocities were generated according to a Maxwell distribution at 300 K. An equilibration simulation with positional restraints (using a force constant of 1000 kJ mol⁻¹ nm⁻²) was carried out for 100 ps and followed by a production run of 20 ns. The simulation was performed under the constant NPT condition. Each of the three groups (protein, solvent, and ions) was coupled to a thermostat at 300 K using the velocity-rescaling algorithm (37) with a relaxation time of 0.1 ps. The pressure was coupled to 1 bar with a relaxation time of 0.5 ps and a compressibility of 4.5 × 10⁻⁵ bar⁻¹. All the bonds in the protein were constrained using the P-LINCS algorithm (38). Twin range cutoff distances for the van der Waals interactions were set to be 0.9 and 1.4 nm, respectively, and the neighbor list was updated every 20 fs. The long-range electrostatic interactions were calculated by the PME algorithm (39), with an interpolation order of 4 and a tolerance of 10⁻⁵.

ACM simulation

The ACM method was implemented in the GROMACS 4.5.5 package. Accelerated sampling of the structure was started after the equilibration simulation. Many parameters were the same as for the standard MD simulation, except that collective motions described by the ENM (23) were amplified by coupling them to a high-temperature bath. From an all-atom structure of the protein in the simulation, an ENM was built with CG sites located at the center of mass (COM) of residues. The potential energy function of the ENM takes the harmonic form

$$V=\sum _{i,j>i}\frac{1}{2}{k}_{ij}\Delta r_{ij}^2,$$ (1)

where Δr_ij is the fluctuation of the bond connecting residues i and j, and k_ij is the spring constant. For any two residues i and j, with their COM distance r_ij, the spring constant between them was

$$k_{ij}=\{\begin{array}{ll}1.0c& r_{ij}\le 0.7\text{nm}\\ {10}^{-2}c& 0.7<r_{ij}\le 1.1\text{nm}\\ 5\times {10}^{-4}c& 1.1<r_{ij}\le 1.4\text{nm}\\ 0& r_{ij}>1.4\text{nm}\end{array},$$ (2)

where c could be any nonzero value, and the four-range spring constants described the interactions in the protein from strong to weak. The short cutoff distance, 0.7 nm, defined the first coordination shell, and the long cutoff distance, 1.4 nm, was chosen to avoid unrealistic large-amplitude fluctuations in some residues along particular directions (23). A middle cutoff value of 1.1 nm was set between the short and long cutoff distances. A Hessian matrix of the second derivatives of the overall potential (Eq. 1) was constructed and then diagonalized to yield a matrix of eigenvectors and corresponding eigenvalues. Each eigenvector with a nonzero eigenvalue is called a normal mode, and the corresponding eigenvalue is proportional to the squared frequency of the motion along the mode. Note that the value of c is not important here, because it only affects the eigenvalues, not the eigenvectors (collective modes). Usually only a few ENM modes with the lowest frequencies are dominant in collective motions of the protein. For T4L, we took the three slowest modes to define an essential subspace. At each time step, the velocity of each atom was divided into two parts, the part projected onto the essential subspace and the remainder. By modifying the weak coupling method (40), the component of velocity in the essential subspace was coupled to a high temperature of 800 K, whereas the remaining velocity was coupled normally to 300 K, and thus the updated velocity was the combination of these two components. During the ACM simulation, collective modes were updated on the fly by doing ENM calculations every 100 time steps according to the new generated protein conformation. The simulation time was 20 ns in total.

FBP21-WWs

As a structural component of the mammalian spliceosomal A/B complex, FBP21 plays an important role in pre-mRNA splicing (41). The protein consists of a matrin-type zinc finger and two group-III WW domains. Huang et al. have solved the NMR structure of the tandem WW domains (42), which contains 75 amino acid residues. The two domains, denoted as WW1 (residues 6–32) and WW2 (residues 47–73), respectively, are connected by a highly flexible linker. The above structure information and ¹⁵N relaxation data both suggest a very mobile interdomain movement, which may enable cooperative binding of these domains with different ligands.

MD simulation

Model 1 of the NMR ensemble (PDB entry 2JXW) was selected as the initial structure. Besides the 75 residues, the protein sample for SAXS measurement has a Met at the N-terminus and an eight-residue His tag (LEHHHHHH) at the C terminus. We added these additional residues to the NMR structure by MODELER (43), and the system with 84 residues in total was used to start an MD simulation. The set-up procedures and parameters were the same as those in the MD simulation of T4L except as follows. A rhombic dodecahedron water box was used, and the minimum distance between the protein and the box boundary was 1.4 nm. Ninety-nine Na⁺ and 91 Cl⁻ ions were added, not only to compensate for the net negative charges on the protein but also to mimic the salt concentration (300 mM) of the SAXS sample. The energy of the final system was minimized using the steepest descent and then the conjugate-gradient method, until the maximum force was <180 kJ mol⁻¹ nm⁻¹. Initial atomic velocities for the equilibration simulation were generated according to a Maxwell distribution at 310 K, and the subsequent production run was 20 ns under the constant NPT condition. The four groups (protein, solvent, Na⁺ ions, and Cl⁻ ions) were coupled separately to a reference temperature of 310 K.

ACM simulation

Parameters for the ACM simulation of FBP21-WWs were largely the same as those for T4L, except as follows. The velocities along the three slowest ENM modes were coupled to 500 K, whereas the rest of the velocities were coupled to 310 K. Note that to accelerate the collective motions of FBP21-WWs, we used a lower temperature than that used for T4L, because FBP21-WWs is more mobile than T4L, with easier transit between different conformational states. Those collective modes were updated on the fly every 50 time steps. The ACM simulation was 20 ns long.

SAXS data

Simulated SAXS profile of T4L

From various experimental structures of wild-type T4L and its mutants, we selected 38 structures that may represent possible conformations of the protein in solution (44). Each mutant was changed back to the wild-type form, and its theoretical SAXS curve was computed by the CRYSOL program (45). Thus, a multiconformational SAXS profile of T4L was obtained by taking the average,

$$I\left(q\right)=\frac{1}{N}\sum _{n=1}^N{I}_n\left(q\right).$$ (3)

Here, N = 38 is the number of experimental structures, I_n(q) is the theoretical SAXS profile of a single structure, n, and $q=4\pi \sin \theta /\lambda$ is the momentum transfer, where 2θ is the scattering angle and λ is the wavelength.

Experimental SAXS data of FBP21-WWs

The SAXS experiment of FBP21-WWs was performed at the beamline 12ID-B of the Advanced Photon Sources at Argonne National Laboratory, with a wavelength of 1.033 Å. Data were acquired from three concentrations (1.0, 3.0, and 5.0 mg/mL) and analyzed by the ATSAS package (46,47). After subtracting buffer scattering, the data curves from different concentrations were scaled and merged using PRIMUS (48). GNOM (49) was employed for calculating the pair distance distribution function (PDDF). The radius of gyration (R_g) of the protein was estimated by Guinier plot.

SAXS fitting

The EOM (9) was selected to identify a small ensemble of representative conformations from a large pool of protein structures, such as an MD or ACM trajectory, to best fit the experimental SAXS data. The search procedure is achieved by minimizing the residual between the experimental and calculated SAXS curves:

$$\chi ={\left\{\frac{1}{K-1}{\sum _{m=1}^K\left[\frac{\mu I\left(q_m\right)-I_{exp}\left(q_m\right)}{\sigma \left(q_m\right)}\right]}^2\right\}}^{1/2},$$ (4)

where K is the number of data points in I_exp(q), and σ(q) are standard deviations of the experimental data. I(q) is the average of the SAXS profiles (Eq. 3) of these conformations in the small ensemble, and μ is a scaling factor. In EOM, χ (Eq. 4) is minimized by using the genetic algorithm (50) to pick the optimal ensemble of structures.

Results and Discussion

T4L

The simulated SAXS profile of T4L is shown in Fig. 1 (black line) to be somewhat different from the SAXS curve of either an open (Fig. 1, red dashed line) or a closed (Fig. 1, green dashed line) structure. To reproduce the simulated SAXS profile, one has to sample not only the open but also the closed conformations of T4L in simulations.

Figure 1.

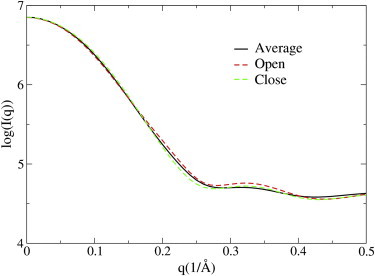
The simulated SAXS profile of T4L (black line) that is the average from the 38 experimental structures (Eq. 3). The theoretical SAXS curves of an open conformation (red dashed line) and a closed conformation (green dashed line) of the protein are shown for comparison. To see this figure in color, go online.

Starting from the open structure, T4L remains in its open state during the 20 ns MD simulation. Root mean-square deviations (RMSDs) of the C_α atoms of residues 1–162 are mostly <2.0 Å (Fig. 2 a, black trace). The relatively large RMSD values for the closed structure (Fig. 2 a, red trace) also indicate that T4L does not access the closed state in the MD simulation. Conversely, the protein transits between the open and closed states frequently during the 20 ns ACM simulation (Fig. 2 b). RMSDs of the respective N-terminal (residues 13–65) and C-terminal (residues 75–162) domains were also calculated. In the MD simulation, the RMSD of the N-terminal domain is ∼0.6 ± 0.1 Å, and the values of the C-terminal domain are ∼0.7 ± 0.1 Å. In the ACM simulation, the RMSD values of both domains are ∼0.7 Å. That is to say, each domain in the ACM simulation is as stable as that in the MD simulation, which indicates that ACM does not break the internal structures of the domains. These RMSD results strongly affirm that the ACM method not only allows for extensive sampling of collective domain motions, but also preserves the local structures of the protein. In the ACM simulation, only a very few degrees of freedom (the first three slowest ENM modes) are coupled to the high temperature, whereas most of the degrees of freedom are coupled to room temperature, which distinguishes ACM from a high-temperature MD simulation. In the latter, the internal structure of each domain would be destroyed.

Figure 2.

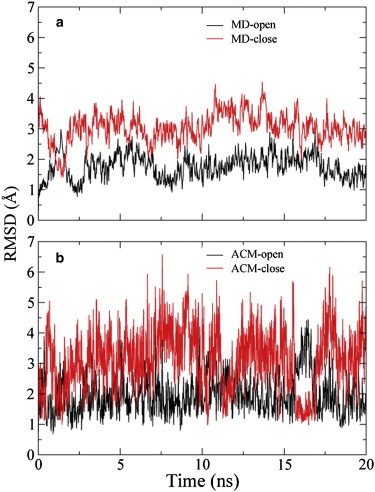
RMSD in the MD simulation (a) and the ACM simulation (b) of T4L. The values are calculated from C_α atoms of residues 1–162. In each panel, the RMSD curve for the open structure is colored black, and that for the closed structure red. To see this figure in color, go online.

From experimental structures of T4L and its mutants in the PDB, 38 structures were selected to constitute a protein ensemble (32,44,51). Principal component analysis (PCA) was performed on the ensemble (52) using the C_α atoms of residues 1–162 to yield PCA modes describing collective motions of T4L. The results indicate that there are two PCA modes that contribute ∼90% of the total fluctuation in the protein. One mode describes an open-closed domain motion, and the other represents a twist motion between the domains. The 38 experimental structures were projected onto the plane spanned by the above two PCA modes, which clearly form two distinct clusters along the open-closed mode (Fig. 3, blue). The cluster on the right contains closed structures and that on the left consists of open structures. The trajectories of the MD and ACM simulations were also projected onto the plane to compare their efficiency of sampling of the domain motions. The MD simulation starting from the open structure of T4L only samples a limited region on the left side of the plane (Fig. 3, black), which partially covers the cluster of open structures but not the cluster of closed structures. That is to say, the protein is trapped in the open state and conformational transitions do not occur during the 20 ns MD simulation. The ACM simulation (Fig. 3, red), which can already cover the two clusters of T4L structures, explores significantly larger areas on the plane than does MD. We estimated potential energies of the conformations in the respective MD and ACM trajectories by replacing explicit water molecules with an implicit generalized Born surface area solvent model (53). The energy differences between the MD and ACM simulations are marginal (Fig. S1 in the Supporting Material), which suggests that the protein conformations sampled by ACM have fairly low energies compared to those from MD under room temperature conditions. Thus, the ACM simulation is unlike a standard MD simulation under high temperature in that the latter would mainly sample the conformational space with high energies.

Figure 3.

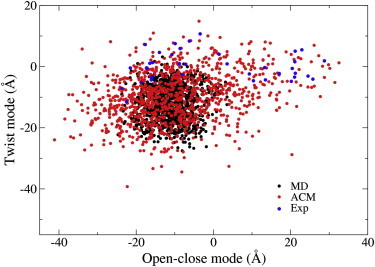
Projections of the T4L structures onto the 2D essential subspace defined by the open-closed and twist modes. PCA was performed on the ensemble of 38 experimental structures of the T4L, and the first two eigenvectors with the largest eigenvalues defined the essential subspace. Each point on the plane represents a conformation. The 38 experimental structures of T4L are colored blue. The projections of MD (black) and ACM (red) indicate their sampling efficiency. To see this figure in color, go online.

A pool of 2000 protein conformations was constructed from the respective MD and ACM trajectories of T4L. The theoretical SAXS profiles of all the structures were precomputed by CRYSOL (45) and were used to select a small number (up to 20) of conformations to fit the simulated SAXS curve of T4L (Eq. 3) by EOM (9). Fifty independent EOM calculations were run on the respective MD and ACM pools. The χ values (Eq. 4) plotted in Fig. 4 a clearly indicate that the small ensembles selected from ACM always have smaller χ than those from MD. The minimal χ determined by EOM for the MD pool is 0.179, and the corresponding ensemble contains all open conformations of T4L (Fig. 4 b). The EOM applied to the ACM pool obtains a minimal χ of 0.007, and the corresponding ensemble includes both open and closed conformations (Fig. 4 c). Since the simulated SAXS profile of T4L is the average from 38 experimental structures (Eq. 3) that consist of both open and closed conformations (Fig. 3, blue), the ACM simulation, which samples diverse conformations, is superior to the MD simulation at reproducing the SAXS profile.

Figure 4.

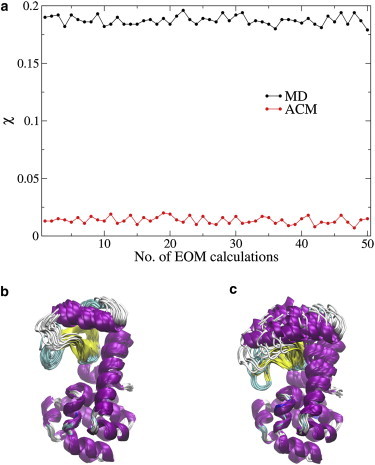
EOM analysis of T4L. (a) χ values of 50 independent EOM calculations for the respective MD (black) and ACM (red) trajectories. (b and c) Structure ensemble with the minimal χ = 0.179 from MD (b) and structure ensemble with the minimal χ = 0.007 from ACM (c). The structures are superimposed by the C-terminal domain (residues 75–162). All the structures, including those in the Supporting Material, were created by VMD (59). To see this figure in color, go online.

FBP21-WWs

Fig. 5 shows the experimental SAXS curve of FBP21-WWs (Fig. 5 a), and the corresponding PDDF computed by GNOM (49). The shape of the PDDF (Fig. 5 b) suggests that the protein may be able to take an extended structure in solution, which is possible, since the linker between the two WW domains is very mobile (42). The R_g of the protein, estimated from a Guinier plot, is ∼19.0 Å.

Figure 5.

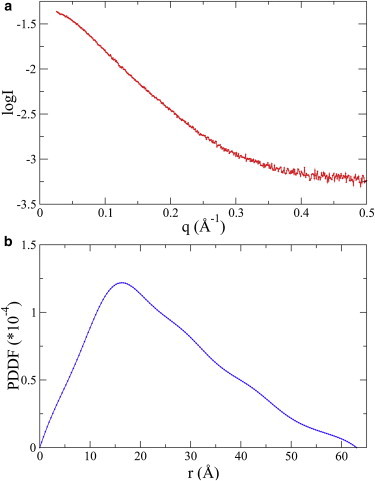
SAXS data of FBP21-WWs. (a) Plots of experimental SAXS curve, with data points up to q = 0.5 Å⁻¹. (b) PDDF calculated by GNOM (49). To see this figure in color, go online.

From the respective MD and ACM trajectories of FBP21-WWs, pools containing 2000 conformations were built. After precomputing the theoretical SAXS profiles of all the structures, 50 cycles of EOM were run to select from the MD and ACM pools small ensembles that best reproduce the experimental SAXS data. As in the case of T4L, the ensembles selected from the ACM pool of FBP21-WWs give a much better fit to the SAXS data than those from the MD pool, based on their χ values (Eq. 4) (Fig. 6 a). The starting model of FBP21-WWs is compact, and the two WW domains essentially stay close to each other during the 20 ns MD simulation, although their relative orientations change. Therefore, all the ensembles selected from the MD pool consist of compact structures (Fig. 6 b), and the minimal χ is 0.592. In the 20 ns ACM simulation, although the internal structure of each WW domain is well preserved, the distance between the two changes widely, as do the domain orientations. The ensembles selected from the ACM pool contain not only compact but also extended structures (Fig. 6 c), and the minimal χ is 0.186, significantly smaller than that from the MD pool (Fig. 6 b). The results indicate that FBP21-WWs may transit between the compact and extended conformations in solution. The average R_g of those conformations in the ensemble from the ACM pool (Fig. 6 c) is around 19 Å, which is consistent with the Guinier analysis.

Figure 6.

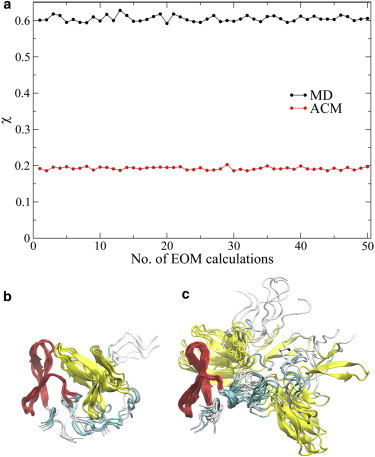
EOM analysis of FBP21-WWs. (a) χ values of 50 independent EOM calculations of the MD (black) and ACM (red) trajectory. (b and c) Structure ensemble with the minimal χ = 0.592 from MD (b) and structure ensemble with the minimal χ = 0.186 from ACM (c). The structures are superimposed by the WW1 domain (residues 6-32 (red)), to show the relative orientation of the WW2 domain (residues 47-73 (yellow)). To see this figure in color, go online.

Convergence of ACM in fitting the SAXS data

It is clear that the ACM method can significantly enhance conformational sampling and does a better job of reproducing the SAXS data compared to normal MD. One may ask whether or not different ACM simulations of the same protein can offer similar results of SAXS fitting. We have performed multiple ACM simulations of T4L and FBP21-WWs that 1), start from different conformations; 2), accelerate different numbers of collective modes; 3), choose different high temperatures for ACM coupling, and 4), end with different simulation times. The results indicate a reasonable convergence of the SAXS-fitting calculations, that is, different ACM simulations can yield similar structure ensembles via the EOM. More details can be found in the Supporting Material.

Comparison with other sampling methods in combination with SAXS

To our knowledge, there are several methods that integrate SAXS data with computational modeling to characterize dynamic multidomain proteins in solution (9,11,13,14). In the EOM (9), if there is no outside trajectory of a multidomain protein, the program Pre_bunch will produce a large pool of conformations by rigid-body modeling. Individual domains are treated as rigid bodies, which are connected by self-avoiding linkers. We used Pre_bunch (54) to generate 10,000 conformations of FBP21-WWs and the EOM to pick from these a small ensemble to fit the SAXS data. Compared to the ensembles from the ACM trajectories (Figs. 6 c and S7), the ensemble from the structure pool generated by Pre_bunch consists of significantly more diverse conformations (Fig. S8). In Pre_bunch, only a simple interaction is considered, to avoid steric clashes in the generated models, so the two WW domains may take various orientations. However, the ACM simulations of FBP21-WWs are all-atom simulations with a refined molecular force field, so the conformations should be physically more reasonable than those from Pre_bunch, and clearly some clusters of structures exist in the ensembles (Figs. 6 c and S7). Therefore, although the ensembles from ACM and those from Pre_bunch have nearly the same χ values in fitting the SAXS data, the former are likely more realistic than the latter. Since the SAXS data are inherently low-resolution, the SAXS fitting from a large structure pool is susceptible to over-fitting. The ACM simulations may avoid this issue to some extent, because they can produce realistic conformations of proteins.

In the minimal ensemble search (11), rigid-body MD simulations (called BILBOMD) are used to generate a wide range of protein conformations for SAXS analysis. Additional strategies, such as reduced nonbonded interactions, large time-step size, and high-temperature coupling to domain linkers, are implemented to enhance sampling efficiency. The basis-set-supported SAXS (BSS-SAXS) reconstruction (13) developed by Yang et al. samples a large number of conformations using MD simulations based on a one-site-per-residue CG model. Hummer and co-workers have developed a method called ensemble refinement of SAXS (EROS) (14), in which the residue-level CG model is also used and the domains are represented as rigid bodies in replica-exchange Monte Carlo simulations. In the ACM simulation, the internal structure of each domain would be naturally preserved, since only the collective motions between domains are accelerated by high-temperature coupling; this obviates the need for rigid-body approximation. This may be one of the advantages of ACM, because it is not always intuitive to predetermine which parts should be treated as rigid bodies in some proteins. The applications of ACM in this article are actually all-atom simulations including explicit solvent, which may make it possible to sample physically more reasonable conformations but with more computational cost than the aforementioned methods.

In addition to ACM, there are other MD-based enhanced sampling methods, such as replica-exchange MD (55) and accelerated MD (aMD) (56), which also can be used for SAXS fitting. However, REMD of a protein like FBP21-WWs (with explicit solvent) would be computationally quite expensive, since many replicas must be run under a series of temperatures. aMD improves the sampling by using a boost potential to reduce energy barriers between different states of the protein. A standard MD simulation must be run first to determine a proper value of the boost potential. Our ACM method has only a minor additional computational cost compared to MD. Instead of altering the potential energy surface, ACM accelerates the collective motions and lets the protein cross the energy barriers more easily than does conventional MD. For conformational sampling of a multidomain protein, ACM is expected to be more efficient than aMD, since these collective modes, directly related to the domain motions, are excited in ACM, whereas the sampling in aMD would not focus along particular reaction coordinates. In this sense, aMD may work better than ACM for intrinsically disordered proteins, because there may be no collective motions in such proteins.

Conclusion

SAXS is an efficient and important complement to other techniques for structure elucidation, especially in the case of highly dynamic multidomain proteins. High-resolution techniques (x-ray crystallography and solution NMR) are able to solve the structures of individual domains. However, it would be difficult to crystallize a flexible multidomain protein, such as FBP21-WWs. Also, it is generally not easy to obtain NMR restraints between the domains connected by flexible linkers. A protein like FBP21-WWs is too small to be investigated by electron microscopy. Data can be collected faster by SAXS than by other techniques, and they provide useful information, such as the size and domain orientations of the multidomain protein.

Due to the low-resolution nature of SAXS, it should be combined with computational simulations to extract structure information about the multidomain protein. From a starting structure, a large number of protein conformations are generated by simulations, and an ensemble of structures is then selected from the pool to best reproduce the experimental SAXS data. In the case of simulations, a key issue is to sample the conformational space of the protein adequately, but this is a nontrivial problem. The study described in this article contributes a useful tool that combines the ACM sampling method and the SAXS data. Results of the two multidomain proteins, T4L and FBP21-WWs, support the idea that ACM simulations are significantly better than control MD simulations at reproducing the SAXS data and interpreting protein flexibility in solution. In the study of FBP21-WWs, it was found that the compact and extended conformations can coexist in solution, although this was not detected by NMR studies (42).

It should be noted that the ACM sampling is a nonequilibrium simulation and does not generate a proper Boltzmann ensemble. Therefore, the protein conformations produced by ACM need to be reweighted to recover the canonical distribution. This issue has been addressed elsewhere in the literature (57,58), where the idea of accelerating collective motions is combined with other sampling methods that can retain the correct ensemble. This strategy may help us to tackle the reweighting problem in our ongoing improvement of the ACM method. Alternatively, we can simply use the current version of ACM to efficiently generate possible conformations of the protein and then rely on appropriate SAXS fitting to recover the correct relative population between different states. The key issue of how to prevent overfitting can be tackled by determining a small number of clusters from the large structure pool. The weights of these clusters, which usually represent possible conformational states of the protein, are then optimized by best fitting the SAXS data using some advanced approaches, such as the Bayesian-based Monte Carlo algorithm (13) and the maximum-entropy method (14).

Generally, there is a trade-off between the sampling efficiency and the accuracy of the generated conformations. For a very large multidomain protein or complex, the all-atom ACM simulation with explicit solvent would be rather time-consuming. The protein may not be able to achieve an adequate sampling within a simulation time of nanoseconds. In this case, ACM can be combined with some simplified models, such as implicit solvent (53) and CG protein models (13–15), to achieve further acceleration of the conformational sampling. This would be one focus for future research.