Abstract
Semiparametric methods have been developed to increase efficiency of inferences in randomized trials by incorporating baseline covariates. Locally efficient estimators of marginal treatment effects, which achieve minimum variance under an assumed model, are available for settings in which outcomes are independent. The value of the pursuit of locally efficient estimators in other settings, such as when outcomes are multivariate, is often debated. We derive and evaluate semiparametric locally efficient estimators of marginal mean treatment effects when outcomes are correlated; such outcomes occur in randomized studies with clustered or repeated-measures responses. The resulting estimating equations modify existing generalized estimating equations (GEE) by identifying the efficient score under a mean model for marginal effects when data contain baseline covariates. Locally efficient estimators are implemented for longitudinal data with continuous outcomes and clustered data with binary outcomes. Methods are illustrated through application to AIDS Clinical Trial Group Study 398, a longitudinal randomized clinical trial that compared the effects of various protease inhibitors in HIV-positive subjects who had experienced antiretroviral therapy failure. In addition, extensive simulation studies characterize settings in which locally efficient estimators result in efficiency gains over suboptimal estimators and assess their feasibility in practice. Clinical trials; Correlated outcomes; Covariate adjustment; Semiparametric efficiency
1 Introduction
Semiparametric estimators are appealing because of their robustness to distributional assumptions and model misspecification. In the analysis of randomized trials, semiparametric theory has been used to develop estimators of treatment effects that improve efficiency of inferences by incorporating baseline covariates, where ‘baseline’ describes data measured prior to randomization. In this paper, we present a semiparametric locally efficient estimator to improve efficiency of inferences in randomized experiments with correlated outcomes when baseline covariates are available. We begin with a review of current estimators for multivariate outcomes and then introduce our semiparametric locally efficient estimator.
Correlated outcomes are often observed in medical research studies, such as those that randomize clusters of subjects or that randomize individual subjects but collect repeated measures of the response. We denote the outcome for the ith independent randomized unit, i = 1, …, m, in such studies by the ni-dimensional response vector , which may represent longitudinal measurements from a single subject or a set of responses from subjects within a cluster defined by a family, hospital, or class. Considering the substantial costs incurred by such studies, it is of interest to maximize efficiency in the estimation of treatment effects by using all available data.
In general, studies collect data on i.i.d. observations Oi = (Yi,Ai,Xi), where Ai denotes a scalar treatment assignment to 1 of K possible treatments, and Xi is a matrix of baseline covariates. Throughout we allow ni to be fixed or random and assume ignorability when ni is random. Longitudinal data also include a time variable denoting time points at which outcomes are measured. As in the case of unit size ni, we allow ti to be either fixed or random but ignorable. When repeated measures are taken on the same subject, baseline covariates are measured at tij = 0; thus Xij = Xi for all j = 1, 2, …, ni, resulting in a single level of baseline covariate information. Clustered data, however, may include pre-treatment covariates at the level of the group or the individual, creating two layers of auxiliary data. In the longitudinal context, we refer to the vector Yi as the subject, or independent unit and Yij as observation- or measurement-level data. For clustered data, we refer to Yi as cluster-level and Yij as individual-level observations.
Semiparametric estimation often involves specifying a restricted mean model. When estimating marginal treatment effects, a model for the expected outcomes given treatment assignment is usually assumed. Consequently, only data on the treatment and outcome are used in estimation. For example, in longitudinal studies, the marginal effect of treatment over time may be measured by assuming the restricted mean model
| (1) |
where f1(tij) is a function of ti. The main effect βA, which measures imbalance in E(Yij|Ai,tij) at baseline, is expected to be zero when randomization successfully balances covariate profiles across treatment arms. The post-baseline effect of treatment is measured by βA,t. Parameters βt and βA,t may be vector-valued, as the function describing the effect of time on expected outcomes may be of some polynomial form. Similarly, for clustered data, the semiparametric model
| (2) |
may be assumed, with treatment effects determined by inference on β1.
Estimating equations are determined by geometric arguments that distinguish parameters of interest, such as the treatment-outcome association (β) in the context of randomized studies, from other components needed to fully specify the data-generating distribution, which are represented by η. For parameters of interest, we aim to derive regular asymptotically linear (RAL) estimators, where an asymptotically linear estimator is one for which there exists a function ψ(Oi) such that
| (3) |
Regularity conditions ensure that variance bounds are well-defined and exclude superefficient estimators that have undesirable properties under local alternatives (Newey (1990)). The function ψ(Oi) is called the influence function of and determines its limiting distribution. As (3) suggests, any RAL estimator may be obtained by solving an influence function equation. To derive the class of estimating functions under an assumed model ℳ, one first defines the nuisance scores ∂log(ℒη)/∂η for the data-generating distribution ℒη; one then determines the subspace defined by the closed linear span of all scores of smooth parametric submodels ℒη in model ℳ. This nuisance tangent space is denoted by Λnuis (Bickel, Klassen, Ritov, and Wellner (1993)). The orthogonal complement of Λnuis, defines the set {ψ(h) : h}, indexed by h, which contains the set of influence functions of all regular asymptotically linear estimators (Bickel et al. (1993); van der Vaart (1998)). For correlated outcomes, the geometric arguments of semiparametric theory may be viewed as a generalization of the quasilikelihood approach of Liang and Zeger (1986) in deriving generalized estimating equations (GEE). We denote as ℳ1 the set of distributions of Wi = (Yi,Ai) with known treatment process satisfying (1). Under model ℳ1, defines the estimating equations
| (4) |
for estimating the p–dimensional vector β. The index or weight h(Ai,ti) is a p × ni function of a random treatment variable Ai and time ti, and . We use bold g(Ai, ti; β) to denote the vector-valued mean function and g(Ai, tij; β) to represent its scalar components.
A locally efficient estimator of a semiparametric model is defined as an estimator that achieves the semiparametric efficiency bound (minimum asymptotic variance among all RAL estimators) at a given submodel for the data-generating law, but remains consistent outside the data-generating submodel (Bickel et al. (1993)), provided that the marginal model is correct. More explicity, semiparametric models parametrize specific components of a data-generating process and leave others unspecified. Estimation may require working models of unspecified components; a locally efficient estimator achieves the semiparametric efficiency bound when such working models are correctly specified, but also remains consistent when only the parametric component is correctly specified. A semiparametric locally efficient estimator is determined by finding the optimal estimating function, referred to as the efficient score, which for GEE requires finding the optimal h(·). When no baseline covariates are observed, Chamberlain (1986) showed that the efficient score of β, is obtained by setting , where Vi is the ni × ni variance-covariance matrix of Yi, and . The estimator remains consistent, however, when a working covariance other than the true covariance is substituted into the estimating equations, thereby demonstrating that consistency is achievable outside of the data-generating law.
For model ℳ2, defined by observations Oi, marginal model (1), and known treatment process, the set of influence functions was derived by Robins, Rotnitzky, and Zhao (1994) and arises by augmenting the influence functions of β under model ℳ1. Augmented estimators are constructed by subtracting the orthogonal projection of the standard estimating function onto the span of the scores of the treatment mechanism from the standard estimating function (Robins et al. (1994), Robins (1999)). For correlated outcomes, , and augmented GEE are
| (5) |
where for K-level treatment Ai, P(Ai = a) = πa. Fixing h(Ai, ti), the most efficient estimating function sets (Robins et al. (1994), Robins (2000); van der Laan and Robins (2003); Zhang, Tsiatis, and Davidian (2008)). The augmentation therefore involves estimation of the conditional mean outcome regression model E(Yi|Xi,Ai), which may be related the marginal parameter of interest in the binary treatment setting by β = E{E(Yi|Xi,Ai = 1) − E(Yi|Xi,Ai = 0)} under an identity link and β = logit[E {E(Yi|Xi,Ai = 1)}]−logit[E {E(Yi|Xi,Ai = 0)}] under the logit link. When baseline covariates are predictive of the outcome augmentation reduces variability in estimated treatment effects, irrespective of the outcome distribution. For the longitudinal marginal model (1), if outcomes Yij are restricted to post-baseline measurements, the baseline measurement Yi0 may be utilized as a baseline covariate and included in Xi. The βA,t term is then no longer required to assess a post-baseline effect of treatment and may be removed from the model, leaving βA to capture the marginal treatment effect. The interaction term βA,t may still be required for correct model specification even when the baseline outcome is included as a covariate if the treatment effect varies in time.
Semiparametric locally efficient estimators of parameters in restricted mean models of marginal treatment effects have been implemented for univariate data in the presence of baseline covariates by Robins (2000), Bang and Robins (2005), van der Laan and Rubin (2006), Tsiatis, Davidian, Zhang, and Lu (2008), Zhang et al. (2008), Moore and van der Laan (2009b) and Moore and van der Laan (2009a). In these developments, the choice of h(·) has no impact on the resulting asymptotic variance and is therefore not considered for deriving efficient estimators. For a univariate outcome, the model gs(Ai;β) = E[Yi|Ai] defined by a unique parameter for each treatment level is saturated, and the choice of h(·) is inconsequential. When Yi is multivariate, gs(Ai;β) = E[Yij|Ai] is not saturated because a single parameter β is shared across components of the vector E[Yi|Ai]. As a result, provides a larger set of estimating functions than the orthogonal complement of the nuisance tangent space of the corresponding restricted mean model for a univariate outcome. Each element in is indexed by h(·); the choice of h(·) impacts efficiency, and the optimal h(·) must be found to achieve minimum variance. A similar discussion of h(·), model saturation, and estimating functions was included in Neugebauer and van der Laan (2007).
The efficient score in model ℳ2 does not generally have the same optimal index h(Ai, ti) as the efficient score in model ℳ1. When incorporating auxiliary covariates in the estimation of marginal treatment effects via augmented GEE, the choice , while resulting in a consistent estimator, is no longer optimal in model ℳ2. The efficient score is determined by optimizing over all p × ni index functions h(Ai, ti) (Robins et al. (1994); Robins (1999); van der Laan and Robins (2003)). Robins (1999) established general theory for deriving the efficient score of treatment effects in marginal structural models (MSMs) of time-dependent exposures, including the case of multivariate outcomes. Application of the Robins (1999) theory to establish locally efficient estimators in specific settings, such as for randomized trials with correlated outcomes, requires further derivation. Additionally, the locally efficient estimators of Robins (1999) were not implemented nor evaluated for practical use. Models (1) and (2) may be viewed as examples of MSMs for a point exposure; the Robins (1999) theory therefore equally applies. Although the efficient score may be obtained theoretically, it is often computationally intensive to calculate. Consequently, inefficient estimators are typically used. The suboptimal estimator based on augmenting GEE with was shown to improve efficiency by Zhang et al. (2008) within the context of the linear mixed model and Stephens, Tchetgen Tchetgen, and De Gruttola (2011) for general continuous and binary outcomes. In subsequent text, we refer to unaugmented GEE (4) under model ℳ1 with the index function as standard GEE, and the suboptimal estimator obtained by augmenting standard GEE is referred to as simple augmented GEE. Here we show how to further improve on simple augmented GEE by deriving the corresponding semiparametric locally efficient estimator for model ℳ2. We then evaluate the feasibility of achieving such improvement in practice.
The following section presents the efficient score and derives a locally efficient estimator of marginal treatment effects in randomized trials with correlated outcomes when auxiliary data are available as in model ℳ2. We also discuss an implementation procedure detailing how to appropriately estimate each component of the efficient score. In Sections 3 and 4 we compare the derived semiparametric locally efficient estimator to standard and simple augmented GEE through a simulation study and application to the AIDS Clinical Trial Group study 398, a randomized longitudinal HIV intervention trial.
2 Methods
2.1 The Efficient Score
We consider the setting of longitudinal data and note that results follow analogously for clustered data by omitting ti. Before presenting the main result, some additional notation is required. Conditioning on ti, the matrix h(Ai, ti) takes K possible values, which may be denoted by K p×ni constant matrices h0(ti), h1(ti),…, hK−1(ti). For binary treatment, we have h1 = h1(ti) and h0 = h0(ti), which denote the index functions under treatment (A = 1) and control (A = 0), respectively. Let , the ni-dimensional vector of the difference in the conditional and marginal mean outcomes given time. Using this construction, let h = [h0,h1,…,hK−1], the complete index matrix of dimension p × Kni. Using a result from Newey and McFadden (1994), we show in the supplementary material that the optimal index hopt(A, t) and resulting efficient score may be determined by solving a generalized information equality. Here we present our main result:
Proposition 1
The efficient score for model ℳ2 is
| (6) |
C = C1 − C2, where
and
As shown above, C is of dimension Kni × Kni and may be decomposed into the difference C = C1 − C2, where C1 is a block diagonal matrix with diagonal components πaV (Y|A = a, t). The block diagonal of C2 contains the matrices , and off-diagonal block components are determined by .
When treatment is binary, C simplifies to
where π0 = 1−π1. Inverting C analytically and letting ,
| (7) |
Expressing the optimal index as in (7) demonstrates that hopt incorporates information on the treatment assignment and auxiliary covariates X through ζa,a′, while the standard index hstd = DT(A)V(A)−1, does not. The matrix ζa,a′ is by definition the covariance of E(Yi|Xi,a,ti) and E(Yi|Xi,a′,ti), the expected outcomes given baseline covariates and treatment assignment to a and a′, respectively. The optimal index hopt therefore boosts efficiency by incorporating information on the covariance in expected outcomes when weighting the residuals Yi−g(Ai;β) in the marginal model estimating equations. To implement locally efficient GEE for model ℳ2, estimates of V(Yi|Ai,ti), E[Yi|Xi,Ai,ti], and ζaa′ for all unique pairs of treatment levels {a,a′}, including a = a′, are needed. The next section details an estimation procedure for each component of hopt when Yi is continuous and g(·) is the identity link, or Yi is binary and g(·) is the inverse logit link.
2.2 Estimation of hopt
The semiparametric locally efficient estimator requires estimates of 3 additional parameters:
E[Yi|Xi,Ai,ti]
ζa,a′ = Cov{E(Yi|Xi,Ai = a,ti),E(Yi|Xi,Ai = a′,ti)|Ai,ti}
V(Yi|Ai,ti).
These quantities may be linked by the law of total variance, V(Yi|Ai,ti) = E[V(Yi|Xi,Ai,ti)|Ai,ti]+V(E[Yi|Xi,Ai,ti]|Ai,ti). For the ith independent unit, the ni-dimensional vector E[Yi|Xi,Ai,ti] determines the ni × ni matrix V(E[Yi|Xi,Ai,ti]|Ai,ti) and ultimately impacts the form of the marginal variance matrix V(Yi|Ai,ti). Observing the relationship among each of these parameters provides guidance for estimation. For example, the working marginal covariance selected must be compatible with the working model chosen for E[Yi|Xi,Ai,ti]. More generally, the models for each component of hopt must be specified so that the model selected for one component does not preclude the choice of model chosen for another. One approach that ensures compatibility is to start by estimating E(Yij|Xij,Ai,tij) through an appropriate regression technique to provide an estimate . The conditional mean outcome may be modeled by
| (8) |
where Xij represents the collection of covariates for the jth measurement in the ith unit. The next step is to estimate the conditional expectation by noting how the model of E(Yij|Xij,Ai = a,ti) impacts the form of the matrix ζa,a′. The final step is estimation of V(Yi|Ai,ti) by summing the estimates of E[V(Yi|Xi,Ai,ti)|Ai,ti] and V(E[Yi|Xi,Ai,ti]|Ai,ti).
2.2.1 General estimation of ζa,a′ and V(Y|A)
Since ζa,a′ is a covariance matrix, it may generally be estimated in a similar fashion to estimating the correlation parameters in standard GEE. Let ζa,a′ = R1/2SR1/2, where R is a ni × ni diagonal matrix with the jth diagonal component Rj,j = Cov(E[Yij|Xij,Ai = a,tij], , the covariance of the predicted outcomes of element j under treatments a and a′, and S is a ni × ni correlation matrix with Sj,j = 1 and Sj, j′ = f (τa,a′) for a function f (·) of correlation parameter τa,a′ that denotes the correlation in the predicted outcomes of element j under treatment a and element j′ under treatment a′. The parameters τa,a′, which may be a vector, and characterize the covariance in conditional mean outcomes under treatments a and a′. Letting where is an initial estimate of β obtained, for example, by maximum likelihood inference for Generalized Linear Models, may be estimated by
where pξ is the dimension of the outcome regression parameter ξ. The correlation parameter τa,a′ is then estimated by the moment equations
For a = a′, we obtain an estimate of ζa,a = V(E[Yi|Xi,|Ai = a,ti]|Ai,ti).
As an alternative approach, one may also derive an expression of , the j, j′ element of ζa,a′, that depends on and the covariance in baseline covariates. An empirical estimate of Cov(Xi) may then be substituted into this expression.
After estimating ζa,a, the conditional variance of Yi, V(Yi|Xi,Ai,ti), may be estimated using the correlation parameters from GEE based on the conditional mean model (8). Under homoscedasticity V(Yi|Xi,Ai,ti) = λ for all i. To ensure compatibility of all parameters, the marginal variance V(Yi|Ai,ti) is then estimated by , where and are estimates of ζa,a and λ, respectively.
2.2.2 Estimation of ζa,a′ for clustered data or longitudinal data with ξX,t = 0
For clustered data and longitudinal data with ξX,t = 0 in (8), calculating ζa,a′ is straightforward. When data are clustered, ξt = ξA,t = ξX,t = 0, leaving . In this setting, is calculated as . If auxiliary covariates Xij,Xij′ are equally correlated among subjects within a cluster for all j, j′. This holds for all link functions g(·). For longitudinal data when ξX,t = 0 (i.e. the effects of baseline covariates on the conditional mean outcome do not vary over time) If g(·) is the identity link, this reduces to for all j, j′. For clustered data ρa,a′ is a constant that depends on Cov(Xij, Xij′), and ξA,X, whereas for longitudinal data, Cov(Xij, Xij′) is replaced by Var(Xi) since Xij = Xi for all j.
2.2.3 Estimation of V(Yi|Ai = a) under a compatible standard form
In some special cases where summing E[V(Yi|Xi,Ai,ti)|Ai,ti] and V(E[Yi|Xi,Ai,ti]|Ai,ti) results in a marginal covariance matrix V(Yi|Ai,ti) with a standard form, e.g., exchangeable, V(Yi|Ai,ti) may be estimated directly while maintaining compatibility with E[Yi|Xi,Ai,ti|Ai,ti] and ζa,a. As stated above, if individual-level covariates Xij are equally correlated among subjects within the ith cluster, the model E[Yij|Xij,Ai = a] imposes compound symmetry on ζa,a′, where diagonal components depend on Var(Xij) and off-diagonal components are determined by Cov(Xij,Xij′). If the conditional variance V(Yi|Xi,Ai) is also exchangeable, V(Yi|A,ti) is the sum of two exchangeable matrices and therefore also has an exchangeable structure. The optimal index hopt may then be calculated by estimating V(Yi|Ai,ti) directly as in standard or simple augmented GEE and using the above procedure to estimate ζa,a′.
A consistent estimator of the asymptotic variance of , the solution to the augmented estimating equations (5) evaluated under (6), may be calculated using the sandwich variance formula of Huber (1964).
3 Simulation Study
Semiparametric locally efficient GEE for model ℳ2 were compared to standard and simple augmented GEE through a simulation study. Simulations were completed for clustered data with continuous and binary outcomes and longitudinal data with continuous outcomes. Results are based on 1,000 Monte Carlo datasets.
3.1 Continuous outcomes
3.1.1 Clustered Data
Data for m = 500 clusters were generated, with ni=2,4,6,8,10,12 with equal probability for the first set of simulations and ni=10,20,30,40,50 in the second set. Auxiliary covariates Xij1, Xij2, and Xij3 were each generated from a multivariate normal distribution with Var(Xij1)=2, Var(Xij2)=6, and Var(Xij3)=5. Correlation was induced among individual-level covariates within the same cluster by setting , and Cov(Xij3,Xij′3)=1. Covariance terms and were varied from 0.5 to 2 and 1.5 to 6, respectively, to evaluate the effect of auxiliary covariate correlation on the performance of locally efficient augmented GEE. At and covariates were weakly correlated among individuals in the same cluster, while at and , covariates were perfectly correlated, thereby becoming cluster-level. The exact values considered for and were (0.5, 1, 1.5, 2) and (1.5, 3, 4.5, 6), for simulation sets 1–4 at each set of cluster sizes. Within the jth individual in the ith cluster, auxiliary covariates were independent. The treatment variable Ai was drawn from the Bernoulli distribution with p=1/2. Clustered responses were generated from the following model, with individual-level error terms εij ~ N(0,40) and cluster-level effects . The proportion of variability in Yij explained by auxiliary covariates Xij was held fixed at roughly 25%. Simulations were completed with and , representing the case in which covariates account for all between-cluster heterogeneity (V(Y|X,A) independent) and the alternative of some intracluster correlation caused by an unmeasured variable (V(Y|X,A) exchangeable), respectively.
For each dataset, the marginal effect of treatment was estimated by fitting model (2) through standard, simple augmented, and locally efficient GEE for ℳ2. The impact of misspecification on the locally efficient estimator and its efficiency relative to simple augmented and standard GEE was evaluated by fitting various models to estimate E(Y|X,A). The correct model for E(Y|X,A), denoted by ‘C’ in tables and figures, was , and two additional models Model 1, ‘M1’=E(Yij|Xij,Ai) = ξ0 + ξ1Xij1 + ξ2Xij2 + ξ3Ai and Model 2, . ‘Model 1’ evaluated the impact of misspecifying the functional form of Xij1, while ‘Model 2’ examined the effect of adding noise to the outcome regression model. All working covariance matrices were fit under exchangeable structure.
Efficiency comparisons relative to standard GEE are summarized in Figures 1a–1b, while the Monte Carlo Relative Efficiency (MCRE) of the locally efficient estimator for ℳ2 to simple augmented GEE may be found in Table 1. Small cluster figures are included in the supplementary material. Across all levels of correlation, augmented estimators resulted in increased efficiency compared to the unaugmented estimator (MCRE 1.25–11.6). For low correlation among Xij simple augmented and locally efficient augmented estimators performed similarly. Simple augmented GEE and locally efficient GEE for ℳ2 also resulted in similar efficiency when the conditional mean model did not include the data-generating quadratic term or the true conditional variance was exchangeable (MCRE locally efficient to simple augmented GEE 0.99–1.01). When correlation was increased among Xij within a cluster, the assumed conditional mean model included all important covariates in the correct functional form, and baseline covariates accounted for all within-subject correlation, locally efficient GEE for ℳ2 gained in efficiency over the simple augmented GEE (MCRE locally efficient to simple augmented GEE 1.04–1.22). Increased covariance among auxiliary covariates also resulted in greater efficiency gains for any augmented GEE relative to the standard estimator. Trends were more pronounced for large average cluster size (average ni=30 vs. average ni=7).
Figure 1.
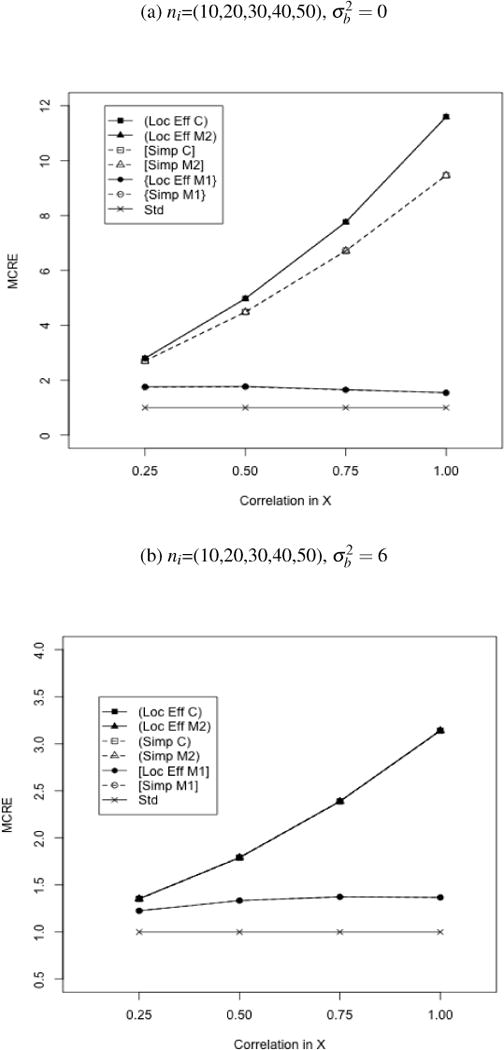
MCRE of Locally Efficient and Simple Augmented GEE Relative to Standard (Unaugmented) GEE. Continuous clustered outcomes. Estimators corresponding to each curve are denoted by ‘Estimator-Outcome Regression’ using the abbreviations: Loc Eff-Locally Efficient, Simp-Simple Augmented, Std-Standard; C-Correct, M1-Model 1, M2-Model 2. All estimators use exchangable working covariance for V(Y|A) and V{E(Y|X,A)}. The order of curves in the legend follows the order curves on the figure, with sets of superimposed curves denoted by ‘()’, ‘[]’, or ‘{}’.
Table 1. Monte Carlo Relative Efficiency of Locally Efficient Augmented GEE to Suboptimal Augmented GEE.
Continuous clustered outcomes. Working Marginal Covariance (WMCov): Exchangeable (Exch). Outcome Regression (OR): Correct (C), Model 1(M1), Model 2 (M2). First entry , second entry . All estimators use exchangable working covariance for V(Y|A) and V{(Y|X,A)}.
| Cluster Size = 2,4,6,8,10,12
| ||||
|---|---|---|---|---|
| Correlation among Xij | ||||
|
| ||||
| WMCov/OR | 0.25 | 0.50 | 0.75 | 1.00 |
| Exch/C | 1.0115 | 1.0450 | 1.0907 | 1.1464 |
| 1.0036 | 0.9991 | 1.0010 | 1.0085 | |
| Exch/M1 | 1.0062 | 1.0089 | 1.0064 | 1.0038 |
| 1.0006 | 1.0008 | 1.0018 | 1.0019 | |
| Exch/M2 | 1.0114 | 1.0448 | 1.0905 | 1.1462 |
| 1.0036 | 0.9990 | 1.0009 | 1.0083 | |
| Cluster Size =10,20,30,40,50
| ||||
|---|---|---|---|---|
| Correlation among Xij | ||||
|
| ||||
| Cov/OR | 0.25 | 0.50 | 0.75 | 1.00 |
| Exch C | 1.0356 | 1.1096 | 1.1563 | 1.2259 |
| 1.0005 | 0.9999 | 1.0002 | 1.0011 | |
| Exch M1 | 1.0126 | 1.0081 | 1.0050 | 1.0032 |
| 1.0000 | 1.0000 | 1.0001 | 1.0003 | |
| Exch M2 | 1.0352 | 1.1090 | 1.1556 | 1.2247 |
| 1.0006 | 0.9998 | 1.0001 | 1.0009 | |
3.1.2 Longitudinal Responses
For each Monte Carlo dataset, m=500 longitudinal response vectors Yi were generated from the model , where , and Cov(εij, εij′) had an AR-1 structure with correlation parameter α = 0.1,0.3, or 0.5 for different sets of simulations. Covariates Xi1 and Xi2 were normally distributed with mean 0 and variance and , respectively. Variance parameters , , and were varied so that baseline covariates accounted for 10–60% of the variability in Y|A in increments of 10%. Subjects were randomly assigned to treatment (Ai=1) with probability 1/2. For each subject , where ni varied from 1 to 8, as might be the case in a longitudinal study with staggered entry.
Standard GEE, simple augmented GEE, and locally efficient GEE for ℳ2 were applied to each Monte Carlo dataset to estimate marginal treatment effects. All GEE were fit based on the marginal mean model E(Yij|Ai) = β0 + β1Ai + β2tij with inferences on the treatment effect completed through β1. Standard and simple augmented GEE were applied to each Monte Carlo dataset with AR-1, exchangeable, and true working covariance structures, with the true structure under the marginal model being a summation of AR-1 and exchangeable matrices as described in section 2. Locally efficient GEE for ℳ2 were fit under the true covariance structure and a misspecified marginal AR-1 working covariance. Baseline covariates were incorporated fitting several outcome regression models. We use ‘C’ to denote the correct model , which corresponds to the true data generating mechanism; ‘M1’ indicates the model E(Yij|Xi,Ai,tij) = ξ0 + ξ1Ai + ξ2tij + ξ3Xi1 + ξ4Xi2, omitting the exponent on Xi1; and ‘M2’ is the model that includes a noisy covariate Xi3, such that .
Efficiency comparisons are summarized in Figure 2 and Table 2. Additional figures may be found in the supplementary material. For well-specified variance components and conditional mean models, the locally efficient GEE for ℳ2 was more efficient than the simple augmented GEE, with the difference in efficiency increasing with the percent variability explained by Xi (MCRE of locally efficient to simple augmented GEE 1.0–1.27). Similarly, all augmented estimators were more efficient than standard GEE, with efficiency gains from augmenting increasing with correlation in Y and X (MCRE of Augmented GEE to Standard GEE 1.36–5.28). For poorly specified conditional mean models, locally efficient GEE for ℳ2 and simple augmented GEE were nearly equally efficient (MCRE of locally efficient to simple augmented GEE 0.97–1.0), but when the marginal variance was also misspecified locally efficient GEE were less efficient than simple augmented GEE (MCRE 0.88–0.99). This demonstrates that the locally efficient GEE for ℳ2 is a bit more sensitive to working marginal covariance misspecification than simple augmented GEE. Among the simple augmented estimators, the estimator with the incorrect marginal AR-1 working covariance resulted in the β1 estimate with the lowest variability. This illustrates an important distinction between locally efficient and suboptimal estimating functions. Considering estimators using a suboptimal index, misspecified models for parameters in the index may result in more efficient inferences than correctly specified models. For the locally efficient estimator, semiparametric asymptotic efficiency is achieved only in the absence of model misspecification of all parameters in hopt(·).
Figure 2.
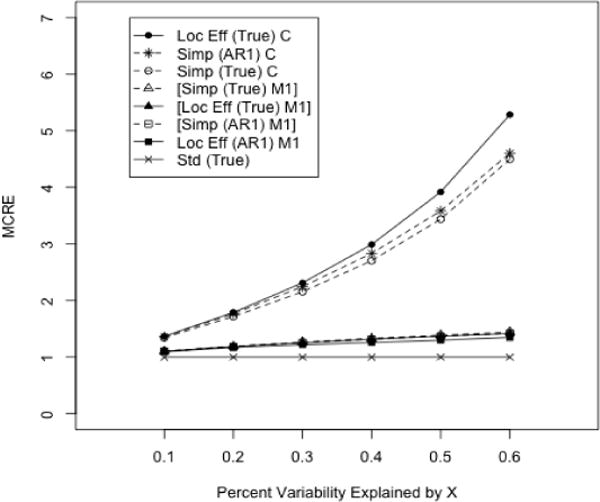
MCRE of Locally Efficient and Simple Augmented GEE Relative to Standard (Unaugmented) GEE. Continuous longitudinal outcomes. Estimators corresponding to each curve are denoted by ‘Estimator (Marginal Working Covariance) Outcome Regression’ using the abbreviations: Loc Eff-Locally Efficient, Simp-Simple Augmented, Std-Standard; AR1-Autoregressive(1) V(Y|A), True-Exchangeable/AR1 for V{E(Y|X,A)} and V(Y|X,A), respectively; C-Correct, M1-Model 1;α=0.3. The order of curves in the legend follows the order of curves on the figure, with the set of superimposed curves denoted by ‘[]’.
Table 2. Monte Carlo Relative Efficiency of Locally Efficient Augmented GEE to Suboptimal Augmented GEE.
Continuous longitudinal outcomes. Working Marginal Covariance (WMCov): 1) True, exchangeable for V(E(Y|X,A)|A) and AR1 for V(Y|X,A) 2) AR1 for V(Y—A). Outcome Regression (OR): Correct (C), Model 1(M1), Model 2 (M2). First entry α = 0.1, second entry α = 0.3, third entry α = 0.5.
| Correlation between Y and X | ||||||
|---|---|---|---|---|---|---|
|
| ||||||
| WMCov/OR | 10 | 20 | 30 | 40 | 50 | 60 |
| True/C | 1.0281 | 1.0700 | 1.1168 | 1.1662 | 1.2175 | 1.2702 |
| 1.0166 | 1.0425 | 1.0728 | 1.1055 | 1.1398 | 1.1752 | |
| 1.0090 | 1.0234 | 1.0409 | 1.0603 | 1.0811 | 1.1028 | |
| True/M1 | 0.9995 | 0.9929 | 0.9851 | 0.9783 | 0.9735 | 0.9717 |
| 1.0006 | 0.9974 | 0.9930 | 0.9887 | 0.9854 | 0.9837 | |
| 1.0009 | 0.9999 | 0.9982 | 0.9961 | 0.9943 | 0.9931 | |
| True/M2 | 1.0284 | 1.0703 | 1.1171 | 1.1664 | 1.2176 | 1.2701 |
| 1.0168 | 1.0428 | 1.0731 | 1.1058 | 1.1401 | 1.1754 | |
| 1.0092 | 1.0237 | 1.0412 | 1.0606 | 1.0814 | 1.1031 | |
| AR1/M1 | 0.9916 | 0.9645 | 0.9300 | 0.8902 | 0.8832 | 0.8887 |
| 0.9972 | 0.9858 | 0.9707 | 0.9567 | 0.9481 | 0.9481 | |
| 0.9996 | 0.9958 | 0.9903 | 0.9849 | 0.9811 | 0.9802 | |
3.2 Clustered Binary Data
As for continuous outcomes, data for m=500 clusters of variable size were generated with ni=2,4,6,8,10,12 for small cluster settings and ni=10,20,30,40,50 for the large cluster scenario. The binary treatment variable Ai was simulated from the Bernoulli(1/2) distribution. Individual-level covariates Xij1, Xij2, and Xij3 were each generated from a multivariate normal distribution with , inducing marginal correlation among individuals within the same cluster. Covariance parameters were varied to evaluate the impact of covariance in auxiliary covariates on the performance of augmented estimators, with and , for different sets of simulations. For low levels of , covariates were weakly correlated, while for , covariates were cluster-level. Binary outcomes were simulated from the model logit[E(Yij|Xij,Ai,bi)] = 0.7Xij12+0.4Xij2−0.5Ai+bi, where bi was drawn from the bridge distribution for the logit link (Wang and Louis (2003)) with scale parameter θ. Simulations were completed with two values of the bridge distribution scale parameter, θ = 1 and θ = 0.8, representing settings in which all sources of between-cluster heterogeneity are measured through auxiliary covariates, or when unmeasured sources of between-cluster heterogeneity are present. A total of 16 sets of simulations were done, varying cluster size, correlation in X, and θ.
Standard, simple augmented, and locally efficient GEE for ℳ2 were applied to each dataset and compared for efficiency. For each estimator, the restricted mean model of interest was model (2) with g(·) the inverse logit link and β1 measuring the marginal effect of treatment. Among augmented estimators, four outcome regression models were considered: 1) ‘C’-Correct, ; 2) ‘M1’-Model 1, E(Yij|Xij,Ai) = g(ξ0+ξ1Xij1+ξ2Xij2+ξ3Ai); 3) ‘M2’-Model 2, ; and 4) ‘M1 OLS’-Model 1 OLS, E(Yij|Xij,Ai) = ξ0+ξ1Xij1+ξ2Xij2+ξ3Xij3+ξ4Ai. With the exception of model 4, which was fit through ordinary least squares (OLS), all outcome regression models were fit by logistic regression. All estimators were fit with exchangeable working covariances.
Large cluster results are shown in figures 3a–3b and Table 3, while small cluster results are included in the supplementary material. Conclusions are similar to those obtained for continuous outcomes. Efficiency improvement with augmented estimators relative to standard GEE increased with correlation in auxiliary covariates (MCRE 1.10–10.54), as did the additional efficiency gains for the locally efficient GEE for ℳ2 over simple augmented GEE (MCRE 1.0–1.23). Simple and locally efficient augmented estimators were equally efficient for θ = 0.8 or when conditional mean models left out important transformations, but differences in efficiency favoring the optimal estimator were observed for θ = 1 and well-specified covariate-adjusted models.
Figure 3.
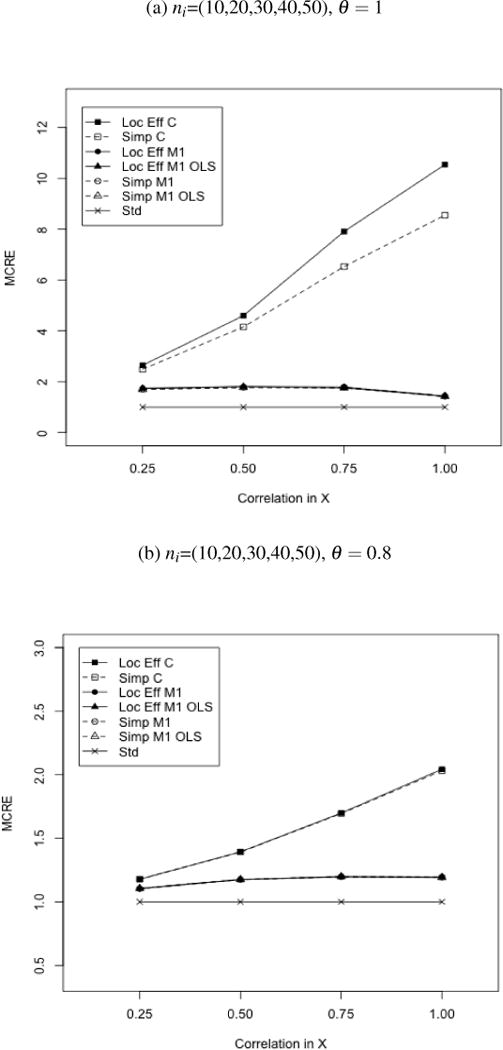
MCRE of Locally Efficient and Simple Augmented GEE Relative to Standard (Unaugmented) GEE. Binary clustered outcomes. Estimators corresponding to each curve are denoted by ‘Estimator-Outcome Regression’ using the abbreviations: Loc Eff-Locally Efficient, Simp-Simple Augmented, Std-Standard; C-Correct, M1-Model 1, M1 OLS-Model 1 OLS. All estimators use exchangable working covariance for V(Y|A) and V{E(Y|X,A)}. The order of curves in the legend follows the order of curves on the figure, with sets of superimposed curves denoted by ‘()’and ‘[]’.
Table 3. Monte Carlo Relative Efficiency of Locally Efficient Augmented GEE to Suboptimal Augmented GEE.
Binary clustered outcomes. Working Marginal Covariance (WMCov): Exch-Exchangeable. Outcome Regression (OR): Correct (C), Model 1 (M1), Model 2 (M2), Model 1 OLS (M1 OLS). First entry θ = 1, second entry θ = 0.8. All estimators use exchangable working covariance for V(Y|A) and V{E(Y|X,A)}.
| Correlation between Y and X | ||||
|---|---|---|---|---|
|
| ||||
| WMCov/OR | 0.25 | 0.50 | 0.75 | 1.00 |
| Exch/C | 1.0624 | 1.1068 | 1.2113 | 1.2329 |
| 0.9996 | 1.0009 | 1.0025 | 1.0057 | |
| Exch/M1 | 1.0247 | 1.0179 | 1.0025 | 1.0015 |
| 1.0001 | 1.0003 | 1.0002 | 1.0001 | |
| Exch/M2 | 1.0630 | 1.1072 | 1.2080 | 1.2353 |
| 0.9995 | 1.0009 | 1.0024 | 1.0056 | |
| Exch/M1 OLS | 1.0238 | 1.0171 | 1.0016 | 1.0008 |
| 1.0001 | 1.0003 | 1.0001 | 1.0000 | |
3.3 Simulation Study Summary
Results from the various simulation settings provide insight into the performance of the locally efficient GEE for model ℳ2 and its practical value. The locally efficient estimator theoretically achieves minimum asymptotic variance when all components of hopt(·) and the augmentation are correctly specified. The results show that achieving the efficiency bound is not robust to model misspecification of working covariances and conditional means; the locally efficient GEE for ℳ2 was only more efficient than simple augmented GEE when all mean models included important covariates in the correct polynomial form, and the correct structure was specified for working covariances. Even under well-specified models, the locally efficient GEE only improved over the simple augmented GEE when the data-generating mechanism was such that the underlying conditional variance, V(Y|X,A) had a sparse structure, such as AR1 or independence. The difficulty of correctly specifying models for nuisance parameters, particularly covariances, as well as measuring all sources of correlation so that V(Y|X,A) is sparse present challenges for successfully implementing locally efficient estimators in real-world analysis. This challenge is further illustrated in the following section with application to AIDS Clinical Trial Group Study 398.
4 Application
The semiparametric locally efficient estimator of marginal treatment effects for correlated outcomes was applied to data from AIDS Clinical Trial Group Study 398 (ACTG 398) (Hammer, Vaida, Bennett, Holohan, Sheiner, Eron, Wheat, Mitsuyasu, Gulick, Valentine, Aberg, Rogers, Karol, Saah, Lewis, Bessen, Brosgart, De Gruttola, and Mellors (2002)). ACTG 398 was a multicenter, double-blind trial, in which 481 HIV-infected patients were randomized to one of four arms, A) saquinavir, B) indinavir, C) nelfinavir, or D) placebo based on their past protease inhibitor (PI) treatment. Patients were only randomized to drugs to which they had no prior exposure. Randomized treatments were added to a common antiviral regimen for all subjects. Subjects’ CD4 counts were measured at weeks 0 (baseline), 4, 8, and every 8 weeks thereafter until 48 weeks or dropout. Here, we apply the GEE estimators to compare the nelfinavir and placebo arms among patients who were eligible for both according to the stratified randomization scheme. Additional baseline covariates were age, sex, past PI use, past non-nucleoside reverse transcriptase inhibitor (NNRTI) exposure, weight, Karnofsky score, intravenous drug use, and race/ethnicity. Weeks 4–32 of followup were included for analysis, with CD4 measurements at week 4 and beyond included as outcomes and week 0 CD4 included as a baseline covariate. Data were approximately 90% complete through week 32. In evaluating the effect of treatment on CD4, the marginal model was E(Yij|Ai) = β0+β1Ai+β2tij, where tij indicates the week of the jth measurement on the ith individual, and Ai was an indicator for the placebo arm. This model was chosen by minimizing the prediction error from 10-fold cross validation of several candidate parametric models that included categorical time, quadratic time, or an interaction of time and treatment. Since only follow-up measurements were modeled as outcomes and no interaction was detected between treatment and time, the effect of treatment was captured by β1.
Standard, simple augmented, and locally efficient GEE for ℳ2 were applied to estimate β1. Several candidate outcome regression models for augmented GEE were identified through model selection procedures. Cross validation was used to select the final model, , where CD40 is baseline CD4. The QIC goodness-of-fit statistic (Pan (2001)) was compared among GEE fit to unaugmented marginal and conditional models to guide the choice of working covariance structures. To enforce compatibility of the marginal variance, conditional variance, and outcome regression in fitting locally efficient augmented GEE, the additive estimate of the marginal covariance was used. The working conditional variance was chosen by selecting the covariance structure resulting in the lowest QIC when fitting GEE on the conditional mean model. Simple augmented GEE were computed under all possible working marginal covariance structures, including the additive estimator motivated by the locally efficient GEE.
Results are shown in Table 4. Regarding covariance selection, unstructured working covariance resulted in the lowest QIC for the conditional model (supplementary material), suggesting the semiparametric locally efficient estimator should be fit assuming an unstructured form of V(Yi|Xi,Ai). Several other covariance structures were also implemented for the locally efficient estimator to explore variance misspecification. Among simple augmented estimators, the additive marginal covariance obtained by summing the unstructured V(Y|X,A,t) and V(E[Y|X,A,t]|A,t) induced by the chosen conditional mean model resulted in lower variability than estimators using standard marginal covariance structures. Estimated treatment effects exhibited variability across estimators but fell within a range of one standard deviation within the class of estimator considered (standard, simple augmented, or semiparametric locally efficient). Comparing standard GEE with different working covariance models, the estimated difference in average CD4 for the placebo arm versus nelfinavir ranged from 9.9 to 20.17. The direction of the effect was reversed for estimators that incorporated baseline co-variates, with average CD4 on the placebo arm 0.07 to 8.11 units lower than the nelfinavir arm. Treatment did not have a significant impact on CD4 at the 0.05 level for any of the estimators considered.
Table 4. Application of Standard, Simple Augmented, and Locally Efficient Augmented GEE to AIDS Clinical Trial Group Study 398.
Estimator (Working Marginal Covariance). Estimator: Unaugmented GEE (Standard), Simple Augmented GEE (Simple Aug. GEE), Locally Efficient Augmented GEE (Loc. Eff.). Working Marginal Covariance: Independence (Ind), Exchangeable (Exch), Autoregressive(1) (AR1), Unstructured (Un), Exchangeable for V(E(Y|X,A)|A) and Unstructured for V(Y|X,A)(Exch/Un), Exchangeable for V(E(Y|X,A)|A) and AR1 for V(Y|X,A)(Exch/AR1). Sandwich Standard Error (SE). Relative Efficiency (RE)
| Estimator |
|
SE | RE | |
|---|---|---|---|---|
| Standard (Ind) | 9.971 | 20.772 | 0.942 | |
| Standard (Exch) | 14.182 | 20.593 | 0.958 | |
| Standard (AR1) | 16.977 | 20.222 | 0.993 | |
| Standard (Un) | 20.173 | 20.156 | 1.000 | |
| Standard (Exch/Un) | 14.615 | 20.347 | 0.981 | |
|
| ||||
| Simple Aug. (Ind) | −8.110 | 9.203 | 4.797 | |
| Simple Aug. (Exch) | −6.385 | 8.904 | 5.124 | |
| Simple Aug. (AR1) | −3.059 | 9.244 | 4.754 | |
| Simple Aug. (Un) | −0.079 | 9.411 | 4.587 | |
| Simple Aug. (Exch/Un) | −5.972 | 8.571 | 5.530 | |
| Simple Aug. (Exch/AR1) | −5.048 | 8.920 | 5.106 | |
|
| ||||
| Loc. Eff. (Ind) | −8.110 | 9.203 | 4.797 | |
| Loc. Eff. (Exch) | −6.821 | 8.953 | 5.068 | |
| Loc. Eff. (Exch/AR1) | −5.715 | 9.073 | 4.936 | |
| Loc. Eff. (Exch/Un) | −6.277 | 8.601 | 5.492 | |
|
| ||||
| Adjusted (Un) | −6.649 | 8.621 | 5.467 | |
Estimators that incorporated baseline covariates greatly increased efficiency, with for standard GEE and among augmented estimators (Relative efficiency augmented to standard GEE ≈ 5.0). Simple augmented and locally efficient GEE for ℳ2 resulted in similar efficiency-a result that may be explained by several factors: 1) Subjects had the same number of follow-up visits. For GEE, the index impacts efficiency most when the number of observations per unit is variable, 2) The unstructured conditional variance is not sparse, and 3) The components of hopt may be misspecified. As a benchmark for efficiency, we also fit unaugmented GEE assuming the conditional mean model with an unstructured working covariance. This estimator represents the most efficient estimator of β1 that may be obtained using Xi, which requires assuming that the more restrictive conditional mean model is correct. From this estimator, we can determine that for this particular case, there is little additional efficiency to be gained by locally efficient GEE if simple augmented GEE are fit under the best working covariance (Table 4).
5 Discussion
We derived and implemented a closed-form expression of the efficient score and a semiparametric locally efficient estimator in model ℳ2 for correlated outcomes. This estimator requires correct specification of the marginal mean model, but is consistent and asymptotically normal under misspecification of the variance or conditional mean working models. To avoid misspecification of the marginal mean model, we recommend several modeling approaches. In cluster randomized studies misspecification of the marginal mean model may be avoided by including a unique parameter for each treatment level. Under exchangeable correlation structures, which are typically assumed, the marginal mean model is then correct. In longitudinal studies with a small number of visits, fixed effects for each visit time and an interaction of time and treatment may be used to avoid misspecification. When continuous time measurement prevents such a strategy, nonparametric methods may be used to suggest appropriate functional forms. Through simulation, we demonstrated that the semiparametric locally efficient estimator is more efficient than corresponding suboptimal estimators in certain settings, particularly when randomized units vary in size, baseline covariates account for a large portion of the within-unit correlation, and baseline covariates are at least moderately predictive of the outcome. In longitudinal studies, variable size may occur when studies have staggered entry or as subjects are lost to follow-up. The estimator derived is only semiparametric locally efficient in the first case, as the locally efficient estimator for incomplete data incorporates information on the missingness process.
There are several challenges to achieving semiparametric local efficiency, some of which stem from the parametric nature of the model of the marginal treatment effect parameter. Assuming the mean model is correct, accounting for correlation through measured covariates and correctly specifying the form of correlation can be difficult in practice. This challenge may be addressed through the use of scientific knowledge and covariance structure diagnostic tools, but is still likely to make local efficiency unachievable in most practical settings, rendering the simple augmented GEE the more useful option. When the marginal mean model is not correct, the semiparametric locally efficient estimator does not yield a consistent treatment parameter, regardless of the index used. The need for correct specification is yet another challenge to the presented estimator, but this challenge is common across all GEE estimators. Although theoretically possible, the prize of implementing semiparametric local efficiency for restricted mean models of marginal treatment effects with baseline covariates in the context of correlated outcomes is typically not worth the chase. The correlated outcome setting gives rise to the possibility of multiple estimators; the semiparametric locally efficient estimator does not offer much practical gain compared to the augmented estimator using the index function from standard GEE after taking into account the possibility of model misspecification of nuisance parameters.
There are several alternatives to the semiparametric locally efficient and suboptimal augmented estimators we consider. A nonparametric approach to modeling marginal treatment effects in longitudinal designs was shown in Neugebauer and van der Laan (2007). Compared to our semiparametric locally efficient estimator the non-parametric strategy has the advantage of providing an interpretable causal parameter when the marginal mean model is possibly misspecified, but it does not utilize information on the correlation in outcomes and therefore would not be locally efficient in the setting of a time-fixed treatment with a correctly specified marginal model for the mean. Another semiparametric approach considers estimation of the conditional mean model followed by marginalization (the G-formula), but this relies on correct specification of the conditional mean model, whereas augmented estimators do not. Despite the shortcomings of the optimal augmented estimator, large efficiency gains were shown for longitudinal analysis when the baseline level of the outcome was incorporated in estimation as an auxiliary covariate. Baseline levels of outcomes can be highly predictive of followup levels, suggesting that in the analysis of data from longitudinal studies, failing to incorporate baseline covariates can be highly inefficient. These results suggest the value of incorporating baseline covariates in both interim and final analyses of data from randomized clinical trials.
Supplementary Material
Acknowledgments
This research was supported by NIH grants R37 51164, T32AI007358, R01AI104459-01A1, and 1R21ES019712-01.
Footnotes
Supplementary Material
The reader is referred to the on-line Supplementary Materials for the derivation of the efficient score and additional simulation and data analysis results.
References
- Bang H, Robins JM. Doubly robust estimation in missing data and causal inference models. Biometrics. 2005;61:962–972. doi: 10.1111/j.1541-0420.2005.00377.x. [DOI] [PubMed] [Google Scholar]
- Bickel PJ, Klassen CAJ, Ritov Y, Wellner JA. Efficient and Adaptive Estimation for Semiparametric Models. The Johns Hopkins University Press; Baltimore: 1993. [Google Scholar]
- Chamberlain G. Asymptotic efficiency in semi-parametric models with censoring. Journal of Econometrics. 1986;32:189–218. [Google Scholar]
- Hammer SM, Vaida F, Bennett K, Holohan MK, Sheiner L, Eron J, Wheat LJ, Mitsuyasu RT, Gulick RM, Valentine FT, Aberg JA, Rogers MD, Karol CN, Saah AJ, Lewis RH, Bessen LJ, Brosgart C, De Gruttola V, Mellors JW. Dual vs. single protease inhibitor therapy following antiretroviral treatment failure. Journal of the American Medical Association. 2002;288:169–180. doi: 10.1001/jama.288.2.169. [DOI] [PubMed] [Google Scholar]
- Huber PJ. Robust estimation of a location parameter. The Annals of Mathematical Statistics. 1964;35:73–101. [Google Scholar]
- Liang KY, Zeger SL. Longitudinal data analysis for discrete and continuous outcomes. Biometrics. 1986;42:121–130. [PubMed] [Google Scholar]
- Moore KL, van der Laan MJ. Application of time-to-event methods in the assessment of safety in clinical trials. In: Peace KE, editor. Design, Summarization, Analysis & Interpretation of Clinical Trials with Time-to-Event Endpoints. Chapman & Hall; 2009a. [Google Scholar]
- Moore KL, van der Laan MJ. Covariate adjustment in randomized trials with binary outcomes: Targeted maximum likelihood estimation. Statistics in Medicine. 2009b;28:39–64. doi: 10.1002/sim.3445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neugebauer R, van der Laan MJ. Nonparametric causal effects based on marginal structural models. Journal of Statistical Planning and Inference. 2007;137 [Google Scholar]
- Newey WK. Semiparametric efficiency bounds. Journal of Applied Econometrics. 1990;5:99–135. [Google Scholar]
- Newey WK, McFadden D. Chapter 36 large sample estimation and hypothesis testing. Elsevier; 1994. pp. 2111–2245. URL http://www.sciencedirect.com/science/article/pii/S1573441205800054. [Google Scholar]
- Pan W. Akaike’s information criterion in generalized estimating equations. Biometrics. 2001;57:120–125. doi: 10.1111/j.0006-341x.2001.00120.x. [DOI] [PubMed] [Google Scholar]
- Robins J. Robust estimation in sequentially ignorable missing data and causal inference models. Proceedings of the American Statistical Association Section on Bayesian Statistical Science 1999. 2000:6–10. [Google Scholar]
- Robins JM. Marginal structural models versus structural nested models as tools for causal inference. In: Berry D, Halloran ME, editors. Statistical Models in Epidemiology: The Environment and Clinical Trials. Vol. 116. NY: Springer-Verlag; 1999. pp. 95–134. [Google Scholar]
- Robins JM, Rotnitzky A, Zhao LP. Estimation of regression coefficients when some regressors are not always observed. Journal of the American Statistical Association. 1994;89:846–866. [Google Scholar]
- Stephens AJ, Tchetgen Tchetgen EJ, De Gruttola V. Augmented gee for improving efficiency of inferences in cluster randomized trials by leveraging cluster and individual-level covariates. Statistics in Medicine. 2011 doi: 10.1002/sim.4471. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsiatis AA, Davidian M, Zhang M, Lu X. Covariate adjustment for two-sample treatment comparisons for randomized clinical trials: A principled yet flexible approach. Statistics in Medicine. 2008;27:4658–4677. doi: 10.1002/sim.3113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Laan MJ, Robins JM. Unified Methods for Censored Longitudinal Data and Causality. NY: Springer-Verlag; 2003. [Google Scholar]
- van der Laan MJ, Rubin D. Targeted maximum likelihood learning. The International Journal of Biostatistics. 2006;2:1–40. doi: 10.2202/1557-4679.1211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Vaart AW. Asymptotic Statistics. Cambridge University Press; 1998. [Google Scholar]
- Wang A, Louis TA. Matching conditional and marginal shapes in binary random intercept models using a bridge distribution function. Biometrika. 2003;90:765–775. [Google Scholar]
- Zhang M, Tsiatis AA, Davidian M. Improving efficiency of inferences in randomized clinical trials using auxiliary covariates. Biometrics. 2008;64:707–715. doi: 10.1111/j.1541-0420.2007.00976.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


