Polarizable Empirical Force Field for Hexopyranose Monosaccharides Based on the Classical Drude Oscillator

Abstract

A polarizable empirical force field based on the classical Drude oscillator is presented for the hexopyranose form of selected monosaccharides. Parameter optimization targeted quantum mechanical (QM) dipole moments, solute–water interaction energies, vibrational frequencies, and conformational energies. Validation of the model was based on experimental data on crystals, densities of aqueous-sugar solutions, diffusion constants of glucose, and rotational preferences of the exocylic hydroxymethyl of d-glucose and d-galactose in aqueous solution as well as additional QM data. Notably, the final model involves a single electrostatic model for all sixteen diastereomers of the monosaccharides, indicating the transferability of the polarizable model. The presented parameters are anticipated to lay the foundation for a comprehensive polarizable force field for saccharides that will be compatible with the polarizable Drude parameters for lipids and proteins, allowing for simulations of glycolipids and glycoproteins.

Introduction

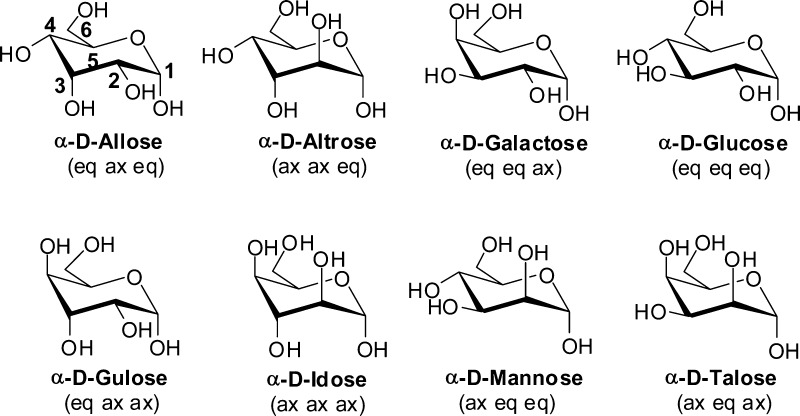
Carbohydrates are ubiquitous in biology, playing diverse roles on their own as well as in conjunction with other biomolecules such as proteins and lipids.^1,2 Carbohydrates themselves function as metabolic intermediates, fuels and in energy storage while their role in glycoproteins and glycolipids include molecular recognition, cell signaling, protein stabilization, and cryoprotection, among others.³ Biotechnology has created new roles for carbohydrates such as biocompatible and biodegradable materials⁴⁻⁶ and as ‘biofuels’.⁷⁻⁹ Members of aldohexopyranose class of monosaccharides have the same chemical composition (e.g., C₆H₁₂O₆), but differ with respect to the stereoisomers defining the configuration of the hydroxyl groups (Figure 1). This variation in the configurations of the hydroxyls gives rise to significant differences in chemical and physical properties of the sugars, contributing to the diverse functional activity of these biologically important molecules.¹⁰

Figure 1.

Chemical structures of the α anomer of each of the eight hexapyranose diasteromers is shown with the numbering of the carbons shown on α-d-allose. Shown in parentheses are the configuration (eq – equatorial; ax – axial) of the hydroxyls of each diastereomer at the C2, C3 and C4 positions.

To understand the diverse biological roles of hexopyranose monosaccharides at a molecular level, knowledge of their three-dimensional structure and their conformational preferences in different environments is essential.¹¹⁻¹³ A wide range of experimental and theoretical studies have addressed the conformational preferences of pyranose monosaccharides.^11,12 In simple terms, they resemble the well-known cyclohexane system.¹⁴⁻¹⁶ For example, puckering of the pyranose ring can be realized in terms of approximate chair, boat, or twist-boat conformations.¹⁵ However, the hydroxyl groups, with their varied configurations in the different diastereomers (Figure 1), and exocyclic hydroxymethyl group add significant complexity for the conformational preferences at the monosaccharide level.¹⁷ For instance, in aqueous solution the torsion involving the exocyclic hydroxymethyl group, O5–C5–C6–O6 (ω), shows a preference for gauche (gt and gg) orientations over the anti-orientation (tg) in glucopyranosides, whereas ω in galactopyranosides displays a high proportion of gt and tg over the gg rotamer in solution.¹⁸⁻²⁵ In addition, experimental information on the conformational preferences of oligosaccharides and polysaccharides is limited as opposed to other classes of biomolecules (e.g., proteins, nucleic acids).²⁶⁻²⁹ This is due to the high intrinsic flexibility of oligo- and polysaccharides and additional forces associated with intra- and intermolecular interactions among monosaccharides in the polymers.^12,30,31

Both quantum mechanical (QM) and molecular mechanical (MM) computational chemistry approaches have been employed to study a range of properties of carbohydrates.^23,32−41 Additive force fields (FF) such as CHARMM,⁴²⁻⁵⁰ AMBER,⁵¹ GROMOS⁵² and OPLS^53,54 are being used to study the various properties of carbohydrates and other biomolecules. However, their lack of treatment of the explicit effect of electronic polarizability⁵⁵ can lead to significant limitations in describing simultaneously the differential electronic response in polar versus nonpolar environments, a key property for the biologically important carbohydrates. To overcome this limitation, polarizable force fields^56,57 are being developed based on different formalisms such as inducible point dipoles,⁵⁸⁻⁶¹ fluctuating charges, or charge equilibration (CHEQ),⁶²⁻⁶⁸ including a CHEQ model of N-acetyl-β-glucosamine,^69,70 a combination of induced dipole and fluctuating charge,⁷¹ and classical Drude oscillators.^72,73

Ongoing efforts in our laboratory, in collaboration with Roux and co-workers, involve the development of a comprehensive biomolecular force field that introduces electronic polarizability via classical Drude oscillators on each non-hydrogen atom. In the Drude model,⁷⁴ charge-carrying auxiliary ‘Drude’ particles are linked to each non-hydrogen atomic core via a harmonic bond thereby creating distinct local electronic polarizability.⁷³ This approach has been successfully applied to model compounds including water,⁷⁵⁻⁷⁷ alkanes,⁷⁸ alcohols,⁷⁹ amides,⁸⁰ ethers,^81,82 aromatics,⁸³ nitrogen-containing heterocycles,^84,85 and sulfur-containing compounds.⁸⁶ The concept and the implementation of the Drude model for proteins,⁸⁷ lipids⁸⁸ and ions^89,90 are discussed in recent articles. In addition, we recently reported a polarizable Drude model for acyclic polyalcohols that was able to reproduce the experimental heat of vaporization of glycerol, which was in error by over 14% with the additive CHARMM36 FF.⁹¹ This improvement was shown to be due to the polarizable model being able to accurately model the cooperative hydrogen bonding of the three vicinal hydroxyls in glycerol, a phenomenon that is of inherent importance in carbohydrates in general. In the present work, these efforts are extended to optimization of a polarizable force field for a series of hexopyranoses monosaccharides (Figure 1).

Computational Details

Empirical force field calculations were performed with the program CHARMM⁴³ and the SWM4-NDP water model.⁷⁶ Gas phase energy minimizations on the model compounds were performed with all nonbonded interactions treated explicitly. Minimizations initially involved relaxation of the Drude particles with the remaining atoms constrained using the steepest-descent (SD) algorithm followed by minimization of all degrees of freedom with the 500 steps of SD followed by the 1000 steps of adopted-basis Newton–Raphson (ABNR) algorithm to an RMS gradient of 10^–4 kcal/mol/Å. Potential energy scans (PES) were performed with a harmonic restraint of 10,000 kcal/mol/radian applied to the targeted dihedrals; all other degrees of freedom were allowed to relax. MM vibrational analysis was performed using the MOLVIB utility⁹² in CHARMM and internal coordinate assignment was done according to Pulay et al.⁹³

QM calculations were performed with the Gaussian03 program.⁹⁴ QM interaction energies for glucose and water were obtained at MP2/cc-pVQZ//MP2/6-31G(d) model chemistry; with correction made for the basis set superimposition error (BSSE).⁹⁵ Dipole moments and dihedral PES were obtained at the MP2/cc-pVTZ//MP2/6-31G(d) model chemistry. QM geometries and vibrational spectra of the model compounds were obtained at the MP2/6-31G(d) model chemistry. A scale factor of 0.9434 was applied to vibrational modes to account for limitations in the level of theory.⁹⁶

Monte Carlo Simulated Annealing

Optimization of the atomic polarizabilities, alpha, and the Thole scale factors was performed using Monte Carlo Simulated annealing (MCSA) with an in-house code as previously used in our research group^75,87 and by others.⁹⁷ The initial temperature was set to 500 K and was scaled by a factor of −0.75 every 1600 steps during the annealing until the temperature approached 0 K. A detailed description of the MCSA protocol is given below in the Results and Discussion section.

Molecular Dynamics

Molecular dynamics (MD) simulations were performed using the isothermal, isobaric ensemble (NPT), unless noted, at 1 atm, with periodic boundary conditions (PBC) and the velocity Verlet integrator that includes treatment of Drude particles via an extended Lagrangian double thermostat formalism.⁷² A mass of 0.4 amu was transferred from the real atoms to the corresponding Drude particles. The temperature of the Drude particles was controlled with a separate low-temperature thermostat (at T = 1.0 K) to ensure that their time course approximates the self-consistent field (SCF) regimen. The integration time step was 1 fs with a relaxation time of 0.1 ps applied to all real atoms. The SHAKE algorithm⁹⁸ was used to constrain covalent bonds involving hydrogen. Lennard-Jones (LJ) interactions⁹⁹ were treated explicitly out to 12 Å with switch smoothing applied over the range of 10–12 Å, and nonbond pair lists were maintained out to 16 Å. Particle mesh Ewald summation¹⁰⁰ with a coupling parameter 0.34 and sixth order spline for mesh interpolation was used during the simulations. Additionally, in all simulations, an additional anharmonic restoring force was included on the parent atom to Drude distance to prevent excessively large excursions of the Drude particle away from the parent atom.⁹⁰

All the crystal simulations were started with coordinates obtained from the Cambridge Structural Database¹⁰¹ (CSD, version 5.34, November 2012). Unit cells were built using the appropriate transformations to the reduced unit cell. All simulations were performed at 298.15 K except for three crystal structures, ADGALA03, GLUCSA03, and GLUCSE02, which were simulated at low temperatures of 95, 140, and 95 K, respectively, to match the experimental conditions. Each crystal simulation was started with 100 ps of equilibration followed by 10 ns of production, which was used for analysis.

To calculate the densities of the sugar solutions, nine different simulations in a cubic box of 1167 water molecules were performed with concentrations ranging from 1 to 5 M and temperatures ranging from 278.15 to 318.15 K for d-glucose, d-galactose and d-mannose. In each of the simulations a ratio of 1:2 of the α- and β-anomers was used so as to reflect the equilibrium distribution in aqueous solutions. For instance, in the cases of 1 M solutions of d-glucose and d-galactose, 7 molecules of glucose were of the α type and 14 molecules were of the β type, while in the case of 1 M d-mannose, 14 molecules of mannose were of the α type and 7 molecules were of the β type. Each simulation was equilibrated for 500 ps followed by 10 ns of production.

The continuous (unfolded) center-of-mass time series from the 1, 2, and 5 M d-glucose simulations were used to compute the mean-squared displacement ⟨r²⟩ of the glucose molecules. Diffusion coefficients, D_PBC, were then obtained from a linear fit of ⟨r²⟩ versus t based on the Einstein relation for diffusion.¹⁰² Diffusion coefficients evaluated from PBC simulations, D_PBC, were corrected,¹⁰³ which yielded D_Sim.

1

where η is the viscosity of the solution calculated from separate NVT simulations, and L is the cubic box length.

Conformational sampling of the exocyclic group of α-, β-d-glucose and α-, β-d-galactose was performed using Hamiltonian Replica Exchange (HREX) simulations with the REPDSTR module in a modified version of CHARMM c37b2.^104,105 Pre-equilibration of 200 ps for each system using standard MD was performed prior to 10 ns of production HREX simulation. Additionally, the center of mass of the monosaccharide was restrained near the origin by using the MMFP module¹⁰⁶ in CHARMM with a harmonic restraint of 1.0 kcal·mol^–1·Å^–2. An exchange between neighboring replicas was attempted every 1000 MD steps, and the coordinates were saved every 1 ps. For all analyses, the trajectories obtained from the 10 ns of the unperturbed replica (ground state replica) were used. The present study used a Saxon–Wood potential as the biasing potential across the different replicas for the ω dihedral angle as given in eq 2.

2

where h = −0.5n kcal mol^–1, with n going from 0 to 7 for replicas 1–8; P₁ = 0.1; P₂ = 0.4; and θ_ref = 60° in each system.

Three different homonuclear ³J(H5,H6R), ³J(H5,H6S), ²J(C4,C6) and three heteronuclear ³J(C4,H6R), ³J(C4,H6S), ²J(H5,C6) coupling constants, as given in eqs 3–8, were utilized for calculating the J-coupling constants for comparison with the experimental data.^107,108

3

4

5

6

7

8

The respective torsion angles associated with the J-couplings were calculated every 1 ps from the unperturbed replicas, amounting to 10 000 points (10 ns) from the HREX MD simulations. The sampling from the simulations was used to directly calculate the populations of the three conformational states of ω, i.e., gt (60°), gg (−60°) and tg (180°).

Results and Discussion

The successful development of the polarizable water⁷⁵⁻⁷⁷ and parametrization of a collection of small model compounds representative of the functional groups in proteins, nucleic acids, lipids, and carbohydrates provided guidance for optimization of the current Drude polarizable model for the hexopyranose monosaccharides.^{72,74,78,79,81−88,90,91,109−112} The procedure involves a hierarchical process such that the majority of parameters were transferred from the previously developed parameters of model compounds. In this study, this involved transfer of parameters from tetrahydropyran (THP),^81,82 ethanol⁷⁹ and glycerol⁹¹ to the 16 hexapyranoses (Table 1). Electrostatic parameters for the ring hydroxyl moieties (CHOH) were from the central group in glycerol, the exocyclic hydroxyl was from ethanol, and the ring O5 oxygen was from THP, with the charges on the C1 atom adjusted to achieve electrostatic neutrality. Bonded parameters were assigned in a similar fashion. Subsequent analysis indicating that only a few parameters, in addition to the new dihedral parameters associated with construction of the full monosaccharides, required additional optimization, as described below.

Table 1. RMS Differences between Empirical and QM Molecular Dipole Moments for Different Electrostatic Models^b.

		direct transfer	Isomerfit	Anomerfit	Globalfit	additive FF
compd.a	no. of conf.	RMSD	RMSD	RMSD	RMSD	RMSD
d-glucose	13	0.400	0.096	0.129	0.188	0.843
	17	0.300	0.101	0.121	0.154	0.749
d-altrose	13	0.380	0.045	0.105	0.133	0.658
	17	0.320	0.063	0.077	0.210	0.716
d-allose	15	0.280	0.014	0.044	0.138	0.719
	17	0.280	0.031	0.077	0.112	0.835
d-gulose	16	0.210	0.057	0.062	0.153	0.577
	16	0.230	0.046	0.070	0.171	0.738
d-idose	16	0.380	0.075	0.100	0.163	0.636
	10	0.530	0.090	0.160	0.205	0.996
d-mannose	14	0.600	0.056	0.112	0.147	0.817
	17	0.390	0.050	0.119	0.161	0.741
d-talose	16	0.660	0.117	0.209	0.206	0.713
	13	0.560	0.046	0.138	0.177	1.151
d-galactose	14	0.350	0.087	0.087	0.165	0.707
	13	0.400	0.157	0.140	0.241	0.834
avg. RMSDb		0.392	0.071	0.107	0.170	0.777

^aThe first row of data for each conformer is for the α anomer and the second row for the β anomer.

^bRMS differences over 237 conformations of the 16 diastereomers.

Initial tests involved the validation of the directly transferred electrostatic model. Comparison of the ability of that model to reproduce the QM dipole moments of multiple conformations of the monosaccharides showed the level of agreement, though an improvement over the additive C36 FF, to be less than satisfactory (Table 1). Therefore, further optimization of the electrostatic model was undertaken involving only the atomic polarizability (alpha) and Thole terms. This was performed to maintain the balance between the charges and LJ parameters that yielded good agreement with a range of experimental data for the small model compounds and to attain the goal of achieving a transferrable set of parameters.

MCSA optimization of the alpha and Thole scale factor for each carbon and oxygen atom in the hexapyranoses (24 variables) targeted the molecular dipole moments of multiple conformations of all 16 diastereomers (237 conformations, Table 1) obtained at the MP2/cc-pVTZ//MP2-6-31G(d) model chemistry. Optimization was performed using an MCSA protocol with predefined upper and lower boundaries assigned to the targeted terms. Three different optimization strategies were adopted. The first strategy, termed Isomerfit, included individual MCSA runs for each sugar isomer, yielding 16 sets of alpha and Thole terms. The second strategy, termed Anomerfit, was to constrain the terms for the two anomers for each diastereomer to be identical, yielding 8 sets of alpha and Thole terms. The third strategy consisted of one single MCSA run, termed Globalfit, thereby yielding a single set of alpha and Thole terms, as well as the previously determined partial atomic charges, for all 16 diastereomers. The error function defined during the MCSA run was the average root-mean-square difference (RMSD) between MM and QM total dipole moments of the 237 unique conformations. The parameter step sizes were adjusted during the MCSA run to achieve a 50% acceptance ratio. Each MCSA run was considered converged if the RMSD between two MCSA steps was less than 0.001. Figure S1 (Supporting Information) shows the convergence behavior of the error function in terms of RMSD between MM and QM values for the Globalfit MCSA run. It can be seen that the RMSD between MM and QM values decreased rapidly during initial part of the run and started to converge after the 50th MCSA step. This shows that the MCSA method efficiently facilitated the optimization of the selected electrostatic parameters to reproduce the total QM dipole moments of the studied monosaccharides.

The initial electrostatic parameters obtained directly from the model compounds showed an average RMSD of 0.392 between the QM and MM dipole moments (Table 1). Subsequent MCSA fitting using all three methods gave significant improvements over the directly transferred parameters, with the Isomerfit modeling yielding an RMSD of 0.071. The quality of this fit justified the optimization of only the alpha and Thole terms, while maintaining the partial atomic charges at values based on the model compounds. While excellent agreement is obtained with the Isomerfit model, the resultant electrostatic model is obviously not transferrable. Accordingly, the Anomerfit and Globalfit models were developed yielding RMSD values of 0.107 and 0.170, respectively. Given the relatively small decrease in the quality of the fit in the Globalfit model, its ability to reproduce a range of target data as described below, and to keep a single set of electrostatic parameters for all 16 diastereomers, the Globalfit model was selected as the basis for further model development.

The reproduction of the QM interaction energies and distances of the model compounds with water is an important criterion in deriving the optimal electrostatic parameters during the force field parametrization process.¹¹³ However, as we have retained the partial atomic charges and carried out reoptimization of the alpha and Thole terms based on molecular dipole moments, the reproduction of the QM interactions with water represents a validation of the model rather than target data for the optimization typical in our FF optimization studies. Specifically, this data allows for further justification of the selection of the Globalfit model.

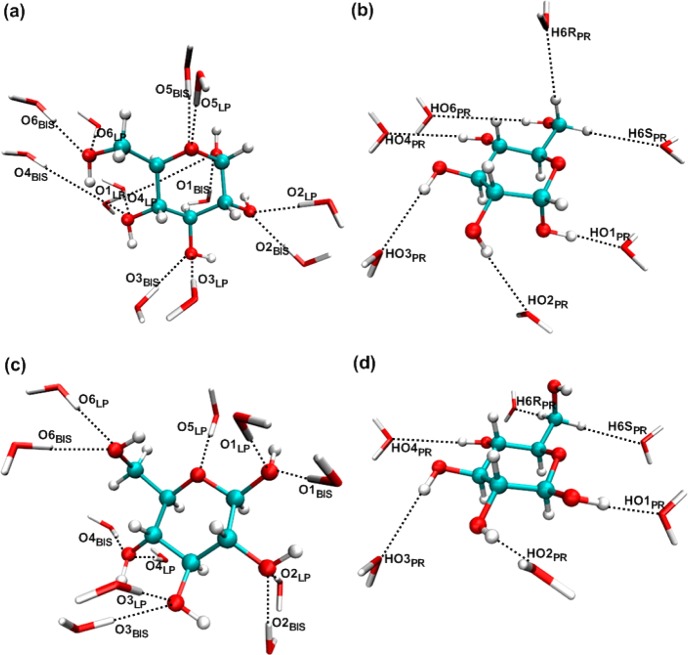
Gas phase minimum interaction energies and distances between individual water molecules and glucose were obtained at the MP2/cc-pVQZ//MP2/6-31G(d) model chemistry. Interactions were obtained for one representative conformation from α-d-glucose (AGLC) and from β-d-glucose (BGLC) for the monohydrates as shown in Figure 2. Individual water molecules were placed at locations where the waters probe hydrogen bond donor sites and lone pairs at the hydrogen bond acceptor sites including both in and out-of-plane interaction orientations of the individual waters.

Figure 2.

α- and β-d-glucose–water interaction geometries. (a) Acceptor type interactions from α-d-glucose with water hydrogen, where LP represents lone pair direction and BIS represents bisector angle based interactions. (b) Donor type interactions (PR) from α-d-glucose with water oxygen. (c) Acceptor type interactions from β-d-glucose with water hydrogen, where LP represents lone pair direction and BIS represents bisector angle based interactions. (d) Donor type interactions (PR) from β-d-glucose with water oxygen.

Overall comparison of the interactions with water and the different electrostatic models is shown in Table 2. The polarizable set based on direct transfer from the model compounds, yielded relatively poor agreement with the QM data, being significantly worse than the additive C36 model. As anticipated, additional optimization of the alpha and Thole terms targeting the molecular dipoles lead to improved agreement with the QM data. Interestingly, the level of agreement is seen to improve upon going from the Isomerfit to the Anomerfit to the Globalfit models. The Globalfit model performs slightly better than additive force field based on the RMSD and average error in the interaction energies. The observed improvement in water interactions for the Globalfit parameters over the directly transferred parameters as well as the Isomerfit and Anomerfit model, support the reoptimization of the alpha and Thole polarizability parameters and, importantly, the selection of the Globalfit model over the Isomerfit and Anomerfit models despite the decreased agreement with the QM molecular dipole moments. The improved agreement of the Globalfit model is suggested to be due to overfitting of the molecular dipoles at the expense of the interactions with water, which were included as target data in the optimization of the small model compounds used to create the initial electrostatic model, where a balance of the electrostatic and LJ parameters was emphasized. The present results indicate that if that balance is significantly perturbed, there is a significant degradation in the ability of the model to reproduce the QM interactions with water. Detailed comparison of the water interaction energies and distances for QM and direct transfer, Isomerfit, Anomerfit and Globalfit electrostatic parameters and additive C36 force field for AGLC and BGLC are given in Supporting Information Tables S1–S10.

Table 2. Statistical Summary of the Drude FF (Direct Transfer, Isomerfit, Anomerfit and Globalfit Parameters) and the Additive CHARMM36 FF-Based Interactions of the AGLC and BGLC with Water Molecules.

		Drude FF				additive FF
compd.	energy	direct transfer	Isomerfit	Anomerfit	Globalfit	CHARMM36
AGLC	ave. diff.	–0.187	–0.352	–0.070	0.005	–0.063
	RMS diff	0.911	0.755	0.756	0.548	0.683
	ave. abs. error	0.718	0.647	0.571	0.454	0.586
BGLC	ave. diff.	–0.660	–0.605	–0.573	–0.337	–0.211
	RMS diff	0.720	0.833	0.764	0.510	0.733
	ave. abs. error	0.813	0.775	0.770	0.506	0.698

Bonded Parameter Optimization

With the transfer and validation (see below) of most of the bonds, angles and some of the dihedral parameters from the model compounds, all that was needed to create a complete force field for the pyranose monosaccharide diastereomers was optimizing the missing dihedral parameters. Dihedral parameters to be determined mainly represent the rotation of hydroxyl groups at C1, C2, C3, and C4 positions, i.e., H1–O1–C1–C2, H1–O1–C1–O5, H2–O2–C2–C1, H2–O2–C2–C3, H3–O3–C3–C2, H3–O3–C3–C4, H4–O4–C4–C3, H4–O4–C4–C5, rotation around the C5–C6 and C6–O6 exocyclic bonds represented by dihedrals O5–C5–C6–O6 and C5–C6–O6–H6, respectively, and some of the torsions involved in the ring deformations, i.e., O5–C1–C2–O2, O1–C1–O5–C5, O5–C5–C4–O4. During the development of additive force field for the hexopyranose monosaccharide, it was observed, consistent with other studies,⁴⁵ that the MP2/cc-pVTZ//MP2/6-31(d) level of theory was adequate for generating the QM target data for the optimization. QM data used in our previous study included PES of all of the hydroxyl moieties, the exocyclic group and the ring degrees of freedom. The same set of energy scans, which includes over 1800 target data points, were used in this work and are summarized in Table 3. Considering the complexity and variation in possible axial–axial, axial–equatorial, and equatorial-equatorial hydroxyl orientations at the C1, C2, C3 and C4 positions, the α- and β-pyranose forms of glucose (Figure 1) and of altrose (Figure 1) were selected to comprehensively cover the range of orientations. For example, the C2–C3 and C3–C4 pairs in glucose are equatorial-equatorial while in altrose the C2–C3 pair is axial–axial and the C2–C3 pair is axial–equatorial. In addition to exocyclic rotation and ring deformation scans from α- and β-d-glucose (Figure 1) and of the altrose pyranosides, ring deformation potential energy scans for the α- and β-galactose ring were included as target data.

Table 3. Pyranose Monosaccharide Conformational Energies at the MP2/cc-pVTZ//MP2/6-31G(d) Level Used as the Training Set for Dihedral Parameter Fitting.

monosaccharide	type of conformational scan	no. of conformations
α-glucose	exocyclic + ring + C1, C2, C3, C4 and C6 hydroxyl torsions	352
β-glucose	exocyclic + ring + C1, C2, C3, C4 and C6 hydroxyl torsions	330
α-altrose	exocyclic + ring + C1, C2, C3, C4 and C6 hydroxyl torsions	446
β-altrose	exocyclic + ring + C1, C2, C3, C4 and C6 hydroxyl torsions	448
α-galactose	exocyclic + ring	86
β-galactose	exocyclic + ring	88
β-mannose	C2-hydroxyl	24
α-talose	C3-hydroxyl	24
β-gulose	C4-hydroxyl	24
β-idose	C3-hydroxyl	24
Total		1846

exocyclic = O5–C5–C6–O6 torsion, ring = O1–C1–O5–C5, O2–C2–C1–O5 and O4–C4–C5–O5 torsions.

Dihedral parameter optimization targeted the RMSD between the QM and MM energies using an in-house least-squares dihedral fitting program. Reference MM energies were obtained by using the respective QM-optimized conformations as the starting MM conformations. During fitting, all the HOCC dihedrals except C5–C6–O6–H6 were treated as equivalent so as to prevent overfitting and maintain parameter transferability. Dihedral phases were fixed at 0° or 180° with multiplicities of 1, 2, and 3 allowed for 7 unique sets of dihedrals. All the parameters to be fit were allowed to vary simultaneously during the fitting, resulting in a 21-dimensional fitting problem (7 sets of dihedrals with n = 1, 2, 3 multiplicities each). The RMSD with the force constants on the parameters to be fit set to 0 was 3.42 kcal/mol over all 1846 data points. Least squares fitting reduced the RMSD to 1.18 kcal/mol (Figure 3). The quality of fit represents an improvement over the C36 additive force field value of 1.69 kcal/mol as well as a model fit based on the directly transferred electrostatic parameters, which yielded an RMSD of 1.38 kcal/mol. This later results indicates that the improvements in the electrostatic model associated with the explicit treatment of electronic polarizability lead to an improvement in the ability of the model to treat the conformational energies of this class of molecules. Finally, to improve the reproduction of the experimental solution properties of the exocyclic torsion, dihedral parameters obtained from the automated fitting for the exocyclic group (O5–C5–C6–O6, C4–C5–C6–O6 and C5–C6–O6–H6) were empirically adjusted which yielded finalized parameters.

Figure 3.

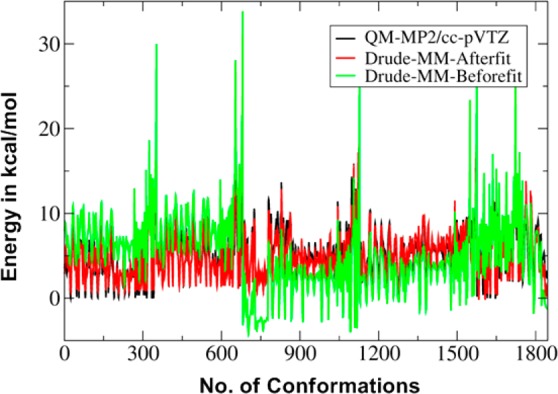
Hexopyranose monosaccharide relative energies from the MP2/cc-pVTZ//MP2/6-31G(d) model chemistry (black), from the Drude force field before torsion fitting (green), and from the Drude force field after torsion fitting (red). Both sets of MM data have been RMS aligned to the QM data.

Beyond the dihedral parameters that were optimized, only a few bonded parameters were adjusted. These include the equilibrium bond length for C1–O1 being reduced by 0.03 Å compared to that from the polyol series. The C–C–O(H) equilibrium angle was decreased by 2° as compared to the same angle in glycerol. Similarly, C5–C6–O6 equilibrium angle was decreased by 1.5° as compared to angle in ethanol. To improve agreement with MP2/6-31G(d) vibrational frequencies of α- and β-d-glucopyranose (Supporting Information, Tables S11a and S11b, respectively), force constants for the C–O bond to the C1 hydroxyl group and ring C5–O5 bond were reduced. Given that the C1 atom is the anomeric carbon while there are two substituents on the C5 atom in the hexapyranoses versus the single substitution in THP, the need for additional optimization was not unexpected.

Parameter Validation

Once the final set of parameters was selected, additional calculations were performed to validate and to test the transferability of the model. Validation included the ability of the model to treat conformational energies and dipole moments of selected diastereomer conformations not included in the training set, crystal MD simulations of multiple monosaccharides, densities of selected monosaccharides in aqueous solution, and the conformational sampling of the exocyclic group.

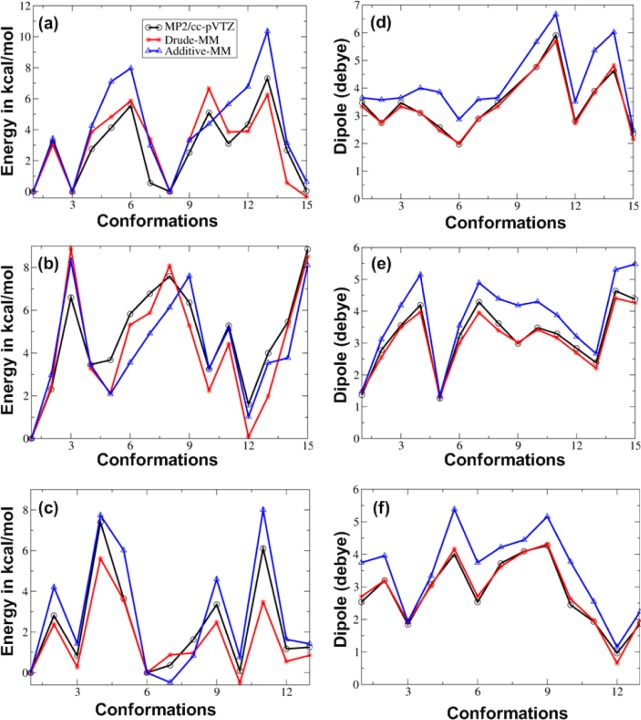
Conformational energies and dipole moments were validated based on 43 random conformations from three diastereomers; β-allose (15 conformers), β-gulose (15 conformers) and α-mannose (13 conformers). These 43 conformers represent different conformations of the hydroxyls, the exocyclic group, including gt, gg and tg rotamers, and twist-boat conformations associated with ring deformation. Energetic evaluation for the Drude as well as additive force fields (Figure 4a–c) showed an improvement for the Drude force field although differences in the MM and QM relative energies are evident in both force fields. RMSDs for the Drude and C36 additive models were 1.08 and 1.34, respectively. However, the Drude force field showed significant improvement with respect to the QM data over the additive force field for total dipole moments of all 43 conformers (Figure 4d–f). These results illustrate the transferability of the dihedral parameters and the electrostatic model to anomers outside the training set.

Figure 4.

Conformational energies of β-allose (a), β-gulose (b) and α-mannose (c) at the MP2/cc-pVTZ//MP2/6-31G(d) model chemistry (black), from the Drude force field (red) and from the additive C36 force field (blue). Dipole moment comparisons are given for β-allose (d), β-gulose (e), and α-mannose (f).

Further validation of the developed force-field parameters was performed using crystal simulations. These simulations allow for testing the ability of the FF to reproduce experimental bond lengths, valence angles, and torsion angles as well as nonbonded interactions based on the reproduction of the crystal lattices. A set of 12 hexopyranose monosaccharide crystals were selected from the CSD.¹⁰¹ Of the 12 structures 3 were crystals of α-d-glucose (CSD ID: GLUSA10, GLUCMH11 GLUCSA03), two crystals of β-d-glucose (GLUCSE01, GLUCSE02), two from α-d-galactose (CSD ID codes ADGALA01, ADGALA03), one crystal of β-d-galactose (BDGLOS01), one crystal of α-d-mannose (ADMANN), one crystal of α-d-talose (ADTALO01), one crystal of β-d-allose (COKBIN), and one crystal of β-d-altrose (EFUWEI). The selection was based on (i) availability of full coordinates, (ii) representation of different isomers, (iii) temperature (i.e., ideally room temperature) of the crystal and (iv) R factor. Crystal structures with ions or other cocrystallized molecules were excluded except GLUCMH11, which represents the monohydrated α-d-glucose. Most of the selected systems had four molecules in the unit cell, except β-d-altrose (EFUWEI), which had three, and α-d-mannose (ADMANN), which had eight molecules. Three crystal structures were at low temperatures (ADGALA03, GLUCSA03, and GLUCSE02 at 95, 140, and 95 K, respectively).

Calculated and experimental intramolecular geometries of the crystal structures are presented in Table 4. Results are presented as the average over the room temperature crystal structures, averaged over the 237 conformations of the diastereomers subjected to QM calculations and over the averages from the MD simulations for the corresponding crystal structures. In addition, for comparative purpose average geometries over all the α and β anomers are presented individually in Supporting Information Tables S12 and S13, respectively. Overall, the agreement with the experimental crystal data is excellent. A couple valence angles and dihedral angles are systematically under- or overestimated, but this is always less than 2° and 3°, respectively. Thus, the direct transfer of the majority of the bonded parameters from the model compounds yields excellent intramolecular geometries.

Table 4. Average Internal Geometries of Hexopyranose Monosaccharides.

	crystala	Drude	difference	QMb	Drude	difference
Bonds
C1–C2	1.52	1.54	0.02	1.53	1.54	0.01
C2–C3	1.53	1.54	0.01	1.52	1.54	0.02
C3–C4	1.52	1.54	0.02	1.53	1.54	0.01
C4–C5	1.53	1.54	0.01	1.53	1.54	0.01
C5–O5	1.45	1.43	–0.01	1.44	1.43	–0.01
C1–O5	1.43	1.44	0.01	1.42	1.44	0.02
C1–O1	1.40	1.40	0.00	1.41	1.40	–0.01
C2–O2	1.43	1.45	0.02	1.43	1.45	0.02
C3–O3	1.43	1.45	0.02	1.43	1.45	0.02
C4–O4	1.43	1.45	0.01	1.43	1.45	0.02
C5–C6	1.51	1.53	0.02	1.52	1.53	0.01
C6–O6	1.42	1.43	0.01	1.42	1.43	0.01
avg. error			0.01			0.01
Angles
C2–C1–O5	109.65	111.17	1.52	110.50	110.58	0.07
C1–C2–C3	109.71	110.21	0.50	110.38	110.76	0.38
C2–C3–C4	109.99	110.10	0.11	110.61	110.44	–0.17
C3–C4–C5	109.83	109.90	0.07	110.26	110.37	0.11
C4–C5–O5	109.07	110.94	1.87	109.89	111.23	1.34
C5–O5–C1	113.41	112.24	–1.18	113.17	112.55	–0.62
C5–C6–O6	110.86	112.13	1.28	111.26	111.81	0.55
O5–C5–C6	106.87	106.16	–0.71	106.18	106.63	0.45
C4–C5–C6	113.15	112.76	–0.39	113.15	112.79	–0.36
O5–C1–O1	109.46	109.83	0.37	110.05	109.68	–0.37
C2–C1–O1	109.85	109.65	–0.20	108.70	109.01	0.31
C1–C2–O2	109.42	110.80	1.38	109.50	110.10	0.59
C2–C3–O3	108.49	109.85	1.36	109.68	109.57	–0.11
C3–C4–O4	109.95	109.87	–0.07	109.05	109.06	0.01
O2–C2–C3	111.03	109.74	–1.29	109.39	109.01	–0.39
O3–C3–C4	110.75	110.43	–0.32	109.29	109.54	0.25
O4–C4–C5	110.09	110.43	0.35	110.51	110.16	–0.34
avg. error			0.27			0.10
Dihedrals
C1–C2–C3–C4	–54.12	–52.47	1.65	–51.54	–50.83	0.71
C2–C3–C4–C5	55.18	52.46	–2.72	52.09	50.56	–1.53
C3–C4–C5–O5	–57.01	–56.34	0.67	–54.16	–53.76	0.40
C4–C5–O5–C1	61.63	60.56	–1.07	58.24	58.13	–0.11
C5–O5–C1–C2	–61.69	–60.27	1.42	–57.99	–57.96	0.03
O5–C1–C2–-C3	56.73	55.24	–1.50	53.65	53.83	0.19
avg. error			–0.26			–0.05

^aData are from simulations of α-d-glucose (GLUCSA10), β-d-glucose (GLUCSE01), α-d-galactose (ADGALA01), β-d-galactose (BDGLOS01), α-d-talose (ADTALO01), β-d-allose (COKBIN), α-d-mannose (ADMANN) and β-d-altrose (EFUWEI) for which experimental data were at 298 K and 1 atm.

^bQM data were obtained from 237 conformations representing all 16 diastereomers optimized at MP2/6-31G(d) level of theory.

Analysis of the crystal lattice parameters is presented in Table 5. From the crystal simulation analysis, it is evident that the average volumes of the crystal unit cells are slightly larger than experimental values, and systematically overestimated in all three x, y, and z dimensions of the lattices. However, the overestimations in the Drude force field are systematically lower than those obtained with the C36 additive force field. For instance, over all the 12 crystal simulations, average percentage error of the total volume for the Drude force field was around 3.5% while the additive FF showed approximately 6% overestimation as compared to experimental values. Interestingly, low temperature crystal simulations of the α-d-glucose, β-d-glucose and α-d-galactose using Drude force field showed further improvement for the volume estimation, whereas the agreement was still relatively poor for the additive force field at low temperature.

Table 5. Crystal Lattice Parameters and Volumes from Experiment and Calculated from the Monosaccharide Crystal Simulations.

crystala	method	a (Å)	% error	b (Å)	% error	c (Å)	% error	volume (Å3)	% error
GLUCSA10	expt.	10.37		14.85		4.98		765.90
	Drude	10.51	1.35	15.05	1.35	5.04	1.20	798.21	4.22
	additive	10.27	–0.96	14.58	–1.82	5.44	9.24	814.60	6.36
GLUCSE01	expt.	9.21		12.64		6.65		774.20
	Drude	9.27	0.65	12.72	0.63	6.69	0.60	789.60	1.99
	additive	9.13	–0.87	12.93	2.29	6.81	2.41	802.80	3.69
ADGALA01	expt.	5.94		7.87		15.80		738.60
	Drude	6.01	1.18	7.97	1.27	16.01	1.33	767.89	3.97
	additive	6.20	4.38	8.08	2.67	15.85	0.32	792.70	7.32
BDGLOS01	expt.	12.66		7.77		7.70		757.30
	Drude	12.82	1.26	7.87	1.29	7.80	1.30	787.96	4.05
	additive	11.93	–5.77	8.21	5.66	8.04	4.42	786.50	3.86
ADTALO01	expt.	8.10		12.13		7.66		752.00
	Drude	8.18	0.99	12.25	0.99	7.73	0.91	774.99	3.06
	additive	8.36	3.21	12.65	4.29	7.49	–2.22	790.50	5.12
COKBIN	expt.	4.92		11.93		12.81		751.00
	Drude	4.99	1.42	12.11	1.51	13.01	1.56	787.34	4.84
	additive	5.19	5.49	12.19	2.18	12.66	–1.17	800.50	6.59
ADMANN	expt.	23.45		9.46		6.89		1528.50
	Drude	23.75	1.28	9.58	1.27	6.98	1.31	1588.45	3.92
	additive	24.82	5.84	9.65	2.01	6.82	–1.02	1632.50	6.80
EFUWEI	expt.	7.18		7.18		12.74		568.05
	Drude	7.31	1.81	7.31	1.81	12.98	1.88	600.68	5.74
	additive	7.38	2.79	7.38	2.79	13.10	2.83	617.70	8.74
GLUCMH11	expt.	8.80		5.09		9.71		430.70
	Drude	8.95	1.70	5.18	1.77	9.87	1.65	453.60	5.32
	additive	8.78	–0.23	5.41	6.29	9.88	1.75	460.50	6.92
GLUCSE02b	expt.	6.60		9.02		12.72		756.16
	Drude	6.62	0.30	9.04	0.22	12.76	0.31	764.44	1.10
	additive	6.68	1.21	9.13	1.22	12.89	1.34	786.67	4.03
GLUCSA03b	expt.	4.95		10.34		14.85		759.67
	Drude	4.99	0.81	10.43	0.87	14.98	0.88	780.34	2.72
	additive	5.03	1.62	10.51	1.64	15.09	1.62	797.86	5.03
ADGALA03b	expt.	5.90		7.84		15.69		725.82
	Drude	5.93	0.51	7.88	0.51	15.77	0.51	737.44	1.60
	additive	6.03	2.19	8.01	2.17	16.03	2.17	774.77	6.74
average	Drude		1.11		1.12		1.12		3.54
std. dev.			0.47		0.49		0.48		1.48
average	additive		1.64		2.47		1.70		5.68
std. dev.			4.29		2.32		4.09		1.47

^aCSD (Cambridge Structural Database) ID.

^bADGALA03, GLUCSA03, and GLUCSE02 obtained at experimental temperatures 95, 140, and 95 K, respectively.

Additional validation of the parameters using the crystal simulations involved analysis of ring puckering. Two distinct formalisms, (i) reported by Cremer and Pople,¹¹⁴ and (ii) described as the virtual α torsions by Rao,¹⁵ were used to define the puckering (Table 6 and Table 7 respectively). Cremer and Pople define puckering in the six membered ring with three parameters: total puckering amplitude (Q), magnitude of distortion (θ), and ϕ. For the ideal ⁴C₁ chair conformation, the magnitude of distortion is zero (θ = 0), the puckering amplitude is around 0.63 and ϕ varies from 0 to 360°. Near the poles (i.e., θ = 0 or 180°) in the MD simulations as well as in the crystal structures, ϕ has large fluctuations, such that this particular pucker parameter has not been considered for the analysis, as previously discussed.⁴⁵ With θ it was previously observed that calculation of the ensemble averages for θ (⟨θ⟩) gave rise to noticeably larger RMS differences, which were inconsistent with those observed for the virtual α torsions (detailed explanation can be found in the Appendix of ref (45)). This was due to non-Gaussian distributions of θ being obtained from the MD simulations leading to the errors based on the ensemble distributions, such that the pucker properties were calculated from the averaged structures as well as from ensemble averages from the crystal simulations.

Table 6. Monosaccharide Crystal Cremer and Pople Ring Pucker Parameters Calculated from the Average Structures and from the Simulation Average.

	average structure			simulation average
crystala	Q	θ	ϕ	Q	θ	ϕ
GLUCSA10 (expt.)	0.566	3.54	324.47
simulation	0.571	4.32	258.87	0.581	8.65	230.38
difference	–0.006	–2.56		–0.013	–5.27
GLUCSE01	0.584	6.90	319.11
simulation	0.563	4.02	221.22	0.571	8.58	207.31
difference	0.021	2.88		0.013	–1.68
ADGALA01	0.582	2.10	127.80
simulation	0.558	5.47	44.92	0.565	8.65	119.25
difference	0.024	–3.37		0.017	–6.55
BDGLOS01	0.591	5.20	305.66
simulation	0.575	5.07	338.83	0.582	7.92	203.88
difference	0.016	0.13		0.009	–2.72
ADTALO01	0.588	2.98	233.60
simulation	0.575	2.63	297.77	0.581	6.59	211.82
difference	0.013	0.35		0.007	–3.59
COKBIN	0.611	2.90	70.13
simulation	0.574	4.54	10.33	0.572	8.90	185.29
difference	0.037	–1.64		0.039	–6.00
ADMANN	0.566	2.30	112.08
simulation	0.556	1.66	98.51	0.565	7.74	158.22
difference	0.010	0.64		0.001	–5.44
EFUWEI	0.584	2.25	35.80
simulation	0.527	2.69	0.62	0.563	8.95	172.77
difference	0.057	–0.44		0.021	–6.70
GLUCMH11	0.561	4.86	302.54
simulation	0.556	4.60	270.93	0.564	8.64	234.17
difference	0.005	0.26		–0.003	–3.78
GLUCSA03	0.570	3.90	323.47
simulation	0.573	6.97	287.30	0.576	8.22	279.11
difference	–0.003	–3.07		–0.006	–4.32
GLUCSE02	0.575	7.89	318.17
simulation	0.568	4.28	221.09	0.571	5.77	219.18
difference	0.007	3.61		0.004	2.12
ADGALA03	0.600	2.48	107.07
simulation	0.586	3.78	45.96	0.588	4.72	91.31
difference	0.014	–1.30		0.012	–2.24
RMSD	0.020	1.83		0.018	4.75

^aCSD (Cambridge Structural Database) ID.

Table 7. Monosaccharide Crystal Ring Pucker Parameters Based on Virtual α Torsions Calculated from the Average Structures and from the Simulation Average.

	average structure			simulation average
crystala	alpha1	alpha2	alpha3	alpha1	alpha2	alpha3
GLUCSA10 (expt.)	–32.79	–29.27	–35.41
simulation	–33.05	–31.45	–32.63	–33.24	–31.39	–32.69
difference	0.26	2.18	–2.78	0.45	2.12	–2.72
GLUCSE01	–33.12	–29.91	–35.33
simulation	–30.11	–33.62	–34.17	–30.13	–33.58	–34.19
difference	–3.01	3.71	–1.16	–2.99	3.67	–1.14
ADGALA01	–34.38	–33.75	–32.37
simulation	–36.31	–27.60	–32.97	–36.29	–27.55	–32.93
difference	1.93	–6.15	0.60	1.91	–6.20	0.56
BDGLOS01	–33.61	–30.85	–38.68
simulation	–34.90	–28.20	–37.72	–34.88	–28.17	–37.73
difference	1.29	–2.65	–0.96	1.27	–2.68	–0.95
ADTALO01	–31.63	–35.02	–35.24
simulation	–32.79	–31.23	–36.65	–32.75	–31.22	–36.65
difference	1.16	–3.79	1.41	1.12	–3.80	1.41
COKBIN	–38.04	–33.22	–32.94
simulation	–36.54	–28.26	–35.39	–36.54	–27.61	–35.39
difference	–1.50	–4.96	2.45	–1.50	–5.61	2.45
ADMANN	–34.09	–32.91	–29.01
simulation	–33.83	–31.40	–32.07	–33.74	–31.36	–31.99
difference	–0.26	–1.51	3.06	–0.35	–1.55	2.98
EFUWEI	–36.36	–31.33	–33.28
simulation	–35.77	–28.57	–32.55	–35.11	–28.62	–33.77
difference	–0.58	–2.76	–0.72	–1.25	–2.71	0.50
GLUCMH11	–31.29	–28.76	–36.32
Simulation	–29.69	–31.43	–36.23	–29.65	–31.36	–36.20
Difference	–1.59	2.67	–0.10	–1.64	2.60	–0.12
GLUCSA03	–32.76	–29.21	–35.78
simulation	–29.44	–30.21	–38.92	–29.43	–30.18	–38.95
difference	–3.31	1.01	3.14	–3.33	0.97	3.17
GLUCSE02	–32.18	–27.10	–39.98
simulation	–30.02	–34.02	–34.35	–30.03	–34.00	–34.36
difference	–2.16	6.92	–5.63	–2.15	6.90	–5.62
ADGALA03	–36.26	–34.48	–33.31
simulation	–36.92	–30.51	–34.13	–36.92	–30.50	–34.12
difference	0.66	–3.97	0.82	0.66	–3.98	0.81
RMSD	1.94	3.96	2.30	1.92	4.07	1.69
avg. RMSD	2.73			2.56

^aCSD (Cambridge Structural Database) ID.

From analysis of the Q values, it is evident that the total puckering amplitude deviates slightly from the ideal value of the ⁴C₁ chair conformation in both the experiments and the calculations. Such deviations are common for many pyranoid rings as previously noted.¹¹⁴ RMSD between the experimental and calculated values are only 0.02 and 0.018 for the averaged structures and ensemble averages, respectively. In the experimental structures θ ranges from 2.25° in EFUWEI to 7.89° in GLUCSE02, while for the simulations, the average structures range from 1.66° in ADMANN to 6.97° for GLUCSA03 and for the ensemble averages from 4.72° in ADGALA03 to 8.95° for EFUWEI. The θ values calculated from the averaged structures for all the crystals are <5°, matching very well with the experimental values with an RMSD of 1.83°. However, θ values calculated from the ensemble averages are generally >5° (except for ADGALA03) with RMSD of 4.75°, due to the issues with the non-Gaussian distributions discussed above.

In the definition of puckering by Rao et al. the virtual α torsions, α1, α2, and α3 represent the respective positions of the C1, C3, and C5 ring atoms relative to the plane defined by C2, C4, and O5. The ideal ⁴C₁ chair conformation has α1 = α2 = α3 = −35°. The corresponding pucker values calculated from the crystal structures and from the simulations are given in Table 7. Calculated average values of all three virtual torsions remain close to −35° with larger fluctuations observed for α2. Figure 5 shows probability distributions the α1, α2 and α3 from the crystal simulations along with average values from crystals and the simulated average and ensemble-based values. The calculated average values for all three virtual dihedrals over all crystal structures either from averaged structure (α1 = −33.02°, α2 = −30.61°, α3 = −35.13°) or ensemble averages (α1 = −32.95°, α2 = −30.53°, α3 = −35.20°) are in excellent agreement with the experimental average values (α1 = −33.88°, α2 = −30.32°, α3 = −34.80°). The average RMSD for all three torsions for averaged structure and ensemble averages are 2.73° and 2.56°, respectively. Overall, the agreement between the computed and experimental ring pucker parameters is very good across all 12 monosaccharide crystals, demonstrating the quality as well as the transferability of the dihedral parameters.

Figure 5.

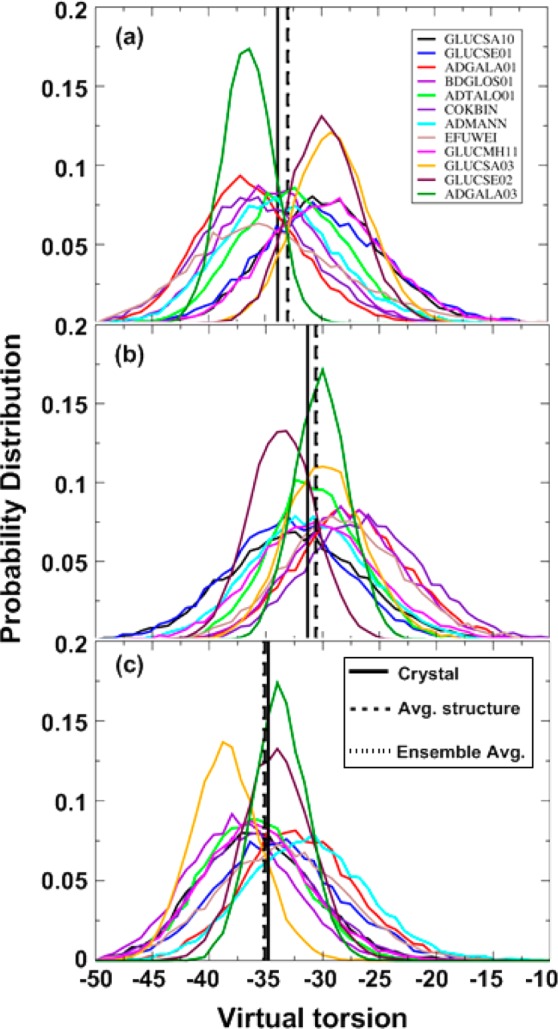
Probability distribution of α1 (a), α2 (b) and α3 (c). All figures also include average values from experimental structures, from average structures of the simulations and from ensemble averages of the simulation. Note that the ensemble average dotted lines cannot be seen as they coincide with the average structure dashed lines in all cases.

Density, Structure, and Diffusion Constants of Monosaccharide Solutions

Aqueous phase calculations allow for further validation of (i) nonbonded parameter transferability from the model compounds and (ii) the internal consistency of the parameters to ensure the proper balance of solute–solute, solute–water, and water–water interactions in the condensed phase. Accordingly, aqueous solutions of d-glucose at various concentrations and temperatures, d-mannose at 1 and 1 M d-galactose at different temperatures were simulated under the experimental conditions. The calculated densities showed very good agreement with the experimental values across all three sugar solutions. For all solutes and all densities, the calculated solution densities showed an error within 1% (Table 8). For the 9 aqueous solutions that were simulated, the average total error in the densities is only −0.11%. Moreover, the Drude model is able to reproduce experimental results for different concentration as well as for different temperatures. In conjunction with the crystal calculations, these results validate the quality of the presented force field for condensed phase simulations.

Table 8. Experimental and Calculated Solution Densities of d-Glucose, d-Mannose and d-Galactose and Translational Diffusion Coefficients, D_Exp and D_Sim, of Glucose.

			density (g/cm3)
sugar	concentration (M)	temp (K)	experiment	simulation	% error	DExp(116) (10–-6 cm2/s)	DSim (10–6 cm2/s)
d-glucose	1	298	1.065117	1.060	0.20	5.31	5.31
			1.058118,119
	2	298	1.108120	1.106	–0.20	4.25	3.16
	5	298	1.209121	1.203	–0.60	2.29	1.37
	1	313	1.052120	1.048	–0.40
	2	313	1.101120	1.094	–0.70
d-mannose	1	298	1.058122	1.060	0.20
	1	278	1.065123	1.075	1.00
d-galactose	1	298	1.060118,119	1.061	0.10
	1	318	1.051123	1.045	–0.60
average error					–0.11

The translational diffusion coefficient, D_Sim, of glucose for three different concentrations at 298 K were also calculated (Table 8). At 1 M the agreement with experiment is excellent. However, at the higher concentrations, the diffusion coefficients are lower than the experimental values, a problem that was previously encountered with the additive C36 carbohydrate FF.^115,116 Such a result indicates that the interactions between monosaccharides may be slightly too favorable or the solvation of the monosaccharides is slightly underestimated. Studies are ongoing to address this issue.

Conformational Dynamics of Exocylic Group Rotation

NMR experiments of monosaccharides in aqueous solutions have provided insight into the dynamical conformational preferences of the exocyclic torsion ω in the hexopyranose mannosaccharides. We studied six different types of J couplings that are dependent on ω; ³J(H5,H6R), ³J(H5,H6S), ²J (H5,C6), ²J(C4,C6), ³J(C4,H6R), and ³J(C4,H6S). The experimental and calculated J-couplings are presented in Table 9. The ³J(H5,H6R) and ³J(H5,H6S) Drude values are generally in agreement with experiment with deviation of ∼1 Hz for ³J(H5,H6R). The ³J(H5,H6R) values calculated with the additive force field show good agreement for d-glucose, but deviations of ∼2 Hz for both anomers of galactopyranosides are present. In addition, the calculated coupling constants ²J(C4,C6) with ∼0.5 Hz values and negative values for the ²J(H5,C6) for all compounds are in qualitative agreement with the experimental values (Table 9). The ³J(C4,H6R) and ³J(C4,H6S) coupling constants calculated using the Drude force field for all four compounds are in good agreement with the experimental data (with <1 Hz deviation). With the additive force field ³J(C4,H6R) and ³J(C4,H6S) coupling constants are overestimated by ∼1 Hz for glucopyranosides and ∼2 Hz for galactopyranosides. Minor discrepancies are noted between the calculated and experimental J-coupling values in all compounds, which may be attributed in part to the relative differences in the population distribution. For instance, the slight under-population of gg rotamer populations found in both anomers of glucose from that of experiment (see below) is clearly reflected in the deviation of calculated ³J(H5,H6R) from the corresponding experimental values. In addition, slight overestimation of the gg population for galactopyranosides correlates with the slight underestimation of the corresponding ³J(H5,H6S) coupling constants. However, limitations in the NMR studies and in the Karplus equations used for calculation of the rotamer populations could contribute to the differences as a wide range of estimates have been reported: 30–55/45–70/–25–25 for gt/gg/tg rotamer populations in glucopyranosides and 55–78/10–25/2–30 for gt/gg/tg rotamer population percentage in galactopyranosides.^23,108

Table 9. ²J and ³J Coupling Constants (in Hz) for Both Anomers of d-Glucose and d-Galactose Associated with ω (O5–C5–C6–O6) Obtained from Experiments and Calculated from Dihedral Distributions from Drude-Based HREX MD Simulations (10 ns) and C36 Additive Force Field Standard MD Simulations (20 ns).

	α-d-glucose			β-d-glucose			α-d-galactose			β-d-galactose
J couplings	E	D	A	E	D	A	E	D	A	E	D	A
3J(H5,H6R)	5.6	6.78	5.21	6.2	7.61	6.26	8.2	7.32	6.17	7.9	7.72	6.22
3J(H5,H6S)	2.3	2.82	2.27	2.3	2.67	2.39	4.2	3.47	5.95	4.4	3.47	5.54
3J(C4,C6)	∼0.5	0.43	0.25	∼0.5	0.75	0.57	∼0.5	0.55	0.72	∼0.5	0.67	0.74
2J(H5,C6)	–1.4	–1.74	–0.76	–2.2	–2.5	–1.64	–5.2	–2.14	–3.29	–5.5	–2.46	–3.22
3J(C4,H6R)	1.1	1.94	1.95	1.2	1.89	1.98	1.9	2.37	4.07	1.9	2.36	3.82
3J(C4,H6S)	2.8	2.55	3.81	2.4	2.14	3.16	1.7	2.19	2.79	1.8	1.96	2.81

E = experimental, D = Drude, A = additive.

Relative populations of the exocyclic torsion are presented for d-glucose and d-galactose along with the experimental and C36 additive force field values (Table 10). Consistent with the J-coupling analysis, the developed force field shows qualitative agreement with the experiments, indicating significant sampling of the gt and gg rotamers in glucopyranosides and the gt and tg rotamers in galactopyranosides. The ability of the HREX simulation method to efficiently sample the exocyclic torsion is shown in Figure S2, Supporting Information, where multiple transitions are observed between the different rotamers. The quality of the Drude model to reproduce the experimental NMR data further validates the force field in reproducing proper aqueous behavior for exocyclic rotation for d-glucose and d-galactose.

Table 10. ω Rotamer Distributions of the Both Anomers of d-Glucose and d-Galactose Using HREX MD (10 ns)^a.

	% gt (60°)			% gg (−60°)			% tg (180°)
compd.	exp.	Drude	additive	Exp.	Drude	additive	exp.	Drude	additive
d-glucoseb	53.0	52.3	44.6	40.0	30.5	47.2	7.0	17.2	6.2
	61.0	66.3	59.0	31.0	19.7	33.7	8.0	14.0	7.3
d-galactoseb	74.0	56.0	46.0	3.0	20.0	4.4	23.0	24.0	49.6
	72.0	61.2	48.6	3.0	15.5	6.3	25.0	23.3	45.1

^aDistributions binned from 0° to 120° for gt, from −120° to 0° for gg, and from 120° to 180° and −120° to −180° for tg rotamers in the interval −180° to 180°. For comparison, experimental data as well as data from C36 additive force field standard MD simulations (20 ns) are also given.

^bThe first row of data for each conformer is for the α anomer and the second row for the β anomer.

Conclusions

The development of a polarizable empirical force field based on the classical Drude oscillator for the hexopyranose form of monosaccharides is presented. The majority of bonded and nonbonded parameters were transferred from smaller model compounds with selected electrostatic parameters (alpha and Thole terms), selected bonds and valence angles and a number of dihedral parameters optimized as part of the present study. Notably, an electrostatic model that applies the same partial atomic charges, atomic polarizabilities, and Thole scale factors (Globalfit) is shown to satisfactorily reproduce QM dipole moments and solute–water interaction energies as compared to models in which the electrostatic parameters were allowed to vary to greater degrees between the different diastereomers (Isomerfit and Anomerfit). Dihedrals parameters not present in the model compounds were optimized targeting the energies for over 1800 monosaccharide conformations.

Validation of the developed parameters included additional QM conformational energies, crystal data such as crystal geometries, crystal unit cell parameters and molecular volumes and aqueous solution properties including densities and sampling of the exocyclic torsion rotatmers. Both the Drude and additive force fields slightly overestimated experimental crystal volumes; however, the Drude force field showed RMSD of only 3.5% versus the 6% increase with the additive force field. Performance of both Drude and additive C36 force fields in terms of puckering parameters are equivalent. Although, there was slight overestimation of crystal volume, aqueous phase density calculations of concentrated solutions of d-glucose, d-mannose and d-galactose are in very good agreement with the experimental densities with an average error of −0.11%. Also, both the crystal and aqueous phase density simulations showed the correct sensitivity of the calculated volumes with varying temperature. The diffusion constants for glucose at 2 and 5 M are underestimated from experiment but comparable to the additive force field. Rotational preferences of the exocyclic hydroxymethyl of d-glucose and d-galactose in solution showed that the developed force field is in qualitative agreement with the experiment, where an equilibrium between the gt and gg rotamers is present in the glucopyranosides and between the gt and tg rotamers in galactopyranoside. Based on the agreement of the Drude model with this range of experimental and QM data, it is anticipated that the model will be of utility for studies of this important class of biomolecules. The hexapyranose monosaccharide will also set the foundation for a more comprehensive polarizable force field for carbohydrates based on the classical Drude oscillator.

The presented parameters may be accessed via the MacKerell laboratory web page at http://mackerell.umaryland.edu/CHARMM_drude_ff_params.html. In addition, a new utility, the “Drude Prepper,” has been added to the CHARMM-GUI¹²⁴ that allows for pre-equilibrated additive CHARMM coordinates and the corresponding PSF file to be upload and converted to Drude formatted files along with the creation of input files for polarizable MD simulations using the CHARMM⁴³ and NAMD^125,126 programs.

Supporting Information Available

Included are α- and β-d-glucose–water interaction tables (Table S1–S10), comparative QM and MM vibrational analyses for α- and β-d-glucose (Table S11), average geometries of α and β anomers (Table S12 and S13) and figures for the RMSD from the MCSA optimization (Figure S1) and rotamer population distributions (Figure S2). The topology (Table S14) and parameter (Table S15) information for the presented Drude force field are also included. This material is available free of charge via the Internet at http://pubs.acs.org

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States