Lubrication by Polyelectrolyte Brushes

Abstract

We develop a scaling model relating the friction forces between two polyelectrolyte brushes sliding over each other to the separation between grafted surfaces, number of monomers and charges per chain, grafting density of chains, and solvent quality. We demonstrate that the lateral force between brushes increases upon compression, but to a lesser extent than the normal force. The shear stress at larger separations is due to solvent slip layer friction. The thickness of this slip layer sharply decreases at distances on the order of undeformed brush thickness. The corresponding effective viscosity of the layer sharply increases from the solvent viscosity to a much higher value, but this increase is smaller than the jump of the normal force resulting in the drop of the friction coefficient. At stronger compression we predict the second sharp increase of the shear stress corresponding to interpenetration of the chains from the opposite brushes. In this regime the velocity-dependent friction coefficient between two partially interpenetrating polyelectrolyte brushes does not depend on the distance between substrates because both normal and shear forces are reciprocally proportional to the plate separation. Although lateral forces between polyelectrolyte brushes are larger than between bare surfaces, the enhancement of normal forces between opposing polyelectrolyte brushes with respect to normal forces between bare charged surfaces is much stronger resulting in lower friction coefficient. The model quantitatively demonstrates how polyelectrolyte brushes provide more effective lubrication than bare charged surfaces or neutral brushes.

1. Introduction

Many processes in nature and technology involve polymer-decorated surfaces in liquid media, and therefore understanding of interactions between such surfaces is important from both academic and technological points of view. Dense grafting of polymer chains to a surface leads to the extension of these polymers due to interchain repulsions resulting in structures called polymer brushes.

Interactions between polymer brushes determine their effectiveness in steric stabilization, controlled by the normal forces between polymer-decorated surfaces. These interactions also determine friction between brushes, which is conventionally characterized by the friction coefficient, defined as the ratio of shear and normal forces between the two substrates sliding over each other. It was demonstrated experimentally that solid substrates decorated with charged polymer brushes have low friction coefficient when sheared against each other in polar solvents.¹ In contrast to sliding solid surfaces with typically velocity-independent friction coefficient, shear force between two surfaces with a liquid or brush layer between them increases with shear velocity. Since the friction coefficient of these sliding surfaces is velocity-dependent, the shear stress in this case is better described by the effective viscosity² defined as the ratio of shear stress and the effective shear rate.

The normal and shear forces between polymer-decorated surfaces were extensively studied over several decades.^1,3−15 The theoretical predictions for normal forces arising upon compression of neutral brushes were found to be in reasonable agreement with experiments and computer simulations.,^8,9,6 The Alexander–de Gennes scaling model of neutral brushes,^16,17 was generalized to incorporate the shear-induced deformation of tethered polymers in nonlinear response regime.⁸

The understanding of interactions between polyelectrolyte (PE) brushes is not as complete as between neutral ones. The Poisson–Boltzmann model of a pair of apposing PE brushes,^18,19 described the density profiles of polymer segments strongly coupled to the distribution of mobile counterions. The increase in normal force upon compression of apposing polyelectrolyte-decorated substrates is due to the increase of counterion concentration in the midplane between them (as there is no electric field at the midplane).²⁰ Since most counterions are confined within the brushes, the sharpest increase of the normal force upon compression occurs at the distance between grafted surfaces on the order of brush thickness. At this distance the concentration of counterions at the midplane changes from a very low value outside the brushes to a very high value inside the brushes.¹⁹ One of the predictions of these works,^18,19 is the existence of a polymer-free gap filled with solvent and counterions between brushes compressed against each other due to partial contraction of PE chains. The computer simulations²¹ confirmed the shrinking of apposing PE brushes upon compression. The early theoretical studies^11,12 extended the scaling models^22,23 of PE brushes to analyze the change in conformations of tethered polyelectrolytes in strong flows under a constant normal load. They demonstrated the coupling between normal and shear forces due to tilting and stretching of polyions in apposing PE brushes in the direction of flow and predicted equilibrium distance between brush-decorated substrates as a function of shear and normal stresses.

In this paper we consider two planar substrates decorated with charged polymer brushes sliding over each other, and examine how the resulting shear force depends on length and degree of ionization of tethered polyelectrolytes, chain grafting density, and solvent quality. We demonstrate that charged polymer brushes enhance both normal and lateral forces between substrates in comparison to bare surfaces with equivalent charge densities. The normal force between strongly charged bare surfaces involves only distal Gouy–Chapman tails of counterions,²⁰ and is therefore much smaller than the normal force between compressed polyelectrolyte brushes separated by the same distance. The friction between bare charged surfaces is governed by the solvent viscosity and is also smaller than the friction between brushes at similar distances. We demonstrate that the enhancement of normal force by polyelectrolyte brushes with respect to bare charged surfaces is much larger than the corresponding increase of friction force resulting in lower friction coefficient between polyelectrolyte brushes. The behavior of polyelectrolyte brushes in salt-free solutions considered in this paper is also retained in solutions with added salt as long as counterion concentration is higher than that of salt ions. The mechanism of relatively low friction at high normal pressure maintained in polyelectrolyte brushes and gels sheds some light on lubrication phenomenon in biological systems, e.g., low friction at high load in synovial joints.

The rest of the paper is organized as follows. In section 2, we review the behavior of planar polyelectrolyte brushes immersed in a salt-free solvent (section 2.1), the normal force between a pair of polyelectrolyte brushes (section 2.2) and their interpenetration (section 2.3). Our results on the friction between polyelectrolyte brushes are presented in section 3 and compared with the friction between bare charged surfaces in section 4. In section 5, we formulate the conclusions. In the Appendix, we estimate the solvent penetration length for neutral brushes and for PE brushes in the osmotic regime.

2. Polyelectrolyte Brushes

2.1. Single Brush

Properties of a single planar polyelectrolyte (PE) brush in contact with a salt-free solution depend on the following parameters: (i) contour length Nb where N is the number of Kuhn segments of length b, (ii) degree of chain ionization f (fraction of charged Kuhn segments), (iii) Bjerrum length l_B defined as the distance at which two elementary charges e interact with thermal energy k_BT = e²/(εl_B) in a solvent with dielectric constant ε, (iv) grafting density ρ (number of chains tethered per unit surface area). Each polyion has fN elementary charges e uniformly distributed along its backbone, and the same number fN of mobile monovalent counterions distributed in solution above the grafted surface (both inside the brush and outside it). We assume relatively low charge density along the chain (less than one charge per Bjerrum length, or l_B < bf^–ν). Brushes with higher charge density and the resulting Manning condensation of counterions are considered in section 5. Nonelectrostatic interactions between monomers determine local chain statistics: size r ≃ bg^ν for a small chain section with g Kuhn monomers with exponents ν ≈ 3/5 and ν = 1/2 for good and Θ solvent conditions, respectively.

Free Chain in a Dilute Solution

Balancing Coulomb electrostatic energy

1

of a polyion with end-to-end distance L and backbone elastic free energy²⁴

2

leads to the average end-to-end distance of a polyion in a dilute salt-free solution,²⁵

3

where we define the dimensionless ratio u of Bjerrum length l_B and Kuhn length b

4

The exponent of the effective interaction parameter uf² in eq 3 is 1/3 in a Θ solvent with ν = 1/2, and 2/7 in a good solvent with ν = 3/5. A single polyion can be envisioned as a stretched string of N/g_e electrostatic blobs with size

5

containing

6

monomers each. On length scales smaller than ξ_e, the electrostatic energy is less than thermal energy k_BT, and the local chain statistics is almost unperturbed (ξ_e ≃ bg_e^ν). On length scales larger than ξ_e, polyion is stretched by electrostatic repulsion between charges, and its end-to-end distance in a salt-free solution is L ≃ ξ_eN/g_e (see eq 3).

Charged Mushroom (CM) Regime

If polyions are sparsely tethered to the substrate, with grafting density ρ ≪ L^–2, the grafted layer is considered to be in charged mushroom (CM) regime with characteristic end-to-end distance of chains given by eq 3. In contrast to neutral grafted chains in mushroom regime, polyelectrolytes in charged mushroom (CM) regime interact with each other. This long-range interaction can result in their orientation perpendicular to the grafted surface. The electric field due to grafted chains with charge efN on each creates surface charge density efNρ and electric field in solvent with dielectric constant ε

7

This field imposes a force on each grafted chain

8

The energy gain due to orienting chain perpendicular to the grafted surface (along the field) is on the order of the product of this force and chain size L (see eq 3)

9

which is the energy cost of rotating one chain in the electric field of other grafted chains by an angle on the order of unity. The onset of the orientation occurs at grafting densities ρ_orient at which this electrostatic orientation energy per chain U_elec is on the order of thermal energy k_BT. This onset of grafted polyelectrolytes, orienting each other in the CM regime, occurs at

10

At lower grafting densities ρ < ρ_orient, tethered polyelectrolytes are almost noninteracting and freely rotating. At higher grafting densities ρ > ρ_orient, intermolecular interaction (eq 9) is strong enough to orient polyelectrolytes primarily perpendicular to the grafted surface, but not strong enough to deform them significantly. At these grafting densities, the intramolecular electrostatic repulsion (eq 1) is much stronger than the intermolecular one and controls chain extension (see the first plateau in Figure 1). This crossover grafting density at which the intermolecular electrostatic interaction energy (eq 9) becomes on the order of the intramolecular one (eq 1) corresponds to the separation between chains on the order of their size L (eq 3),

11

Figure 1.

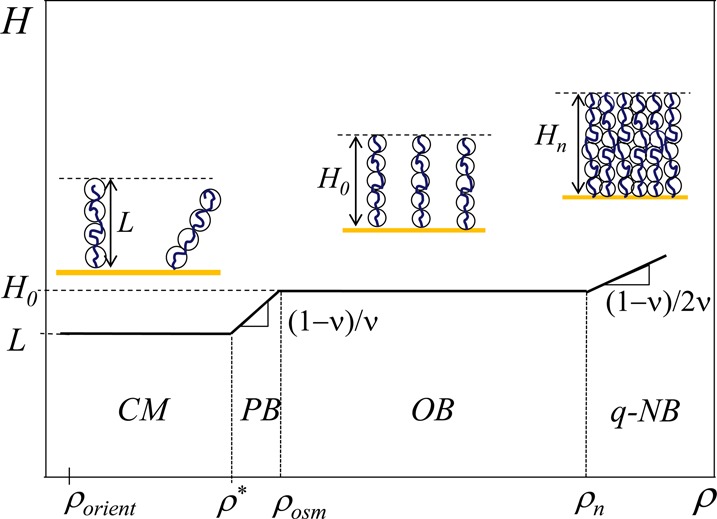
Schematic dependence of PE brush thickness H on chain grafting density ρ in logarithmic coordinates.

In contrast to tethered neutral chains, the crossover between charged mushroom and charged brush regimes occurs prior to the overlap of chain projections onto grafted surface. Note that for polyions elongated by the intramolecular Coulomb repulsions between charged monomers ρ_orient ≪ ρ*.

Pincus Brush (PB) Regime

At higher grafting densities ρ > ρ* tethered polyions create an electric field E (eq 7) which stretches each chain beyond the size of a free polyion L (eq 3). The size of the chain in this regime is determined by the balance of the electrostatic energy per chain (eq 9 with L replaced by H)

12

and elastic free energy per chain (eq 2 with L replaced by H)

13

resulting in the brush height

14

increasing with grafting density ρ linearly in a Θ solvent and with exponent 2/3 in a good solvent (see Figure 1). This regime of unscreened electrostatics (referred to as Pincus regime) continues as long as counterions are able to escape from the brush. The counterion confinement length Λ (called Gouy–Chapman length) is defined as the distance at which the energy of counterion attraction to the charged surface is higher than that at the surface by the thermal energy k_BT. Half of all counterions are located within the Gouy–Chapman length²⁰

15

from the charged surface. The upper boundary of the Pincus regime corresponds to Λ = H or to the grafting density

16

where H₀ is the thickness of the brush with grafting density at or above the crossover value ρ_osm (see eq 17 below). Note that Pincus regime (ρ* < ρ < ρ_osm) exists only for weakly charged grafted polyions with bf^–ν > l_B, while for strongly charged polyelectrolytes (bf^–ν < l_B) with condensed counterions there is no Pincus regime and ρ* ≃ ρ_osm (see section 5).

Osmotic Brush (OB) Regime

At higher grafting densities ρ > ρ_osm, counterions become localized within the brush, and their entropy (osmotic pressure) dominates the brush properties. This main regime of polyelectrolyte brushes is called osmotic brush (OB) regime. Here, the size of the brush is determined by the balance of the osmotic pressure of counterions, trying to maximize their entropy by increasing the brush volume, and the elasticity of tethered chains opposing this tendency. The balance of the two forces corresponds to both, osmotic and elastic parts of the free energy per chain ∼ fNk_BT, independent of the grafting density. Therefore, the scaling model^22,23 predicts the brush thickness in this osmotic regime

17

to be independent of the grafting density ρ (see the second plateau in Figure 1). The chain size H₀ in the osmotic brush regime of weakly charged polyions (with bf^–ν > l_B) is strongly stretched compared to its free polyelectrolyte size L with effective tension blobs²⁴ containing one elementary charge and consisting of g_P ≈ 1/f monomers of size

18

Thus, the size of the stretched chain (and the thickness of the osmotic brush) is H₀ ≈ ξ_PN/g_P (see eq 17).

Quasi-Neutral Brush (q-NB) Regime

At very high grafting densities

19

the distance between chains ρ^–1/2 becomes smaller than the Pincus blob size ξ_P (eq 18) and the energy of short-range excluded volume interactions between monomers becomes higher than the counterion osmotic contribution to the brush free energy. For these very high grafting densities ρ > ρ_n tethered polyions enter the quasi-neutral brush (q-NB) regime. PE brushes in q-NB regime have the same properties as neutral brushes. The thickness of a neutral brush is determined by the balance of short-range excluded volume repulsion and chain elasticity. It can be estimated by the Alexander–de Gennes scaling model¹⁶ as the length of a stretched array of correlation blobs with the size of each blob on the order of the distance between grafting points, ξ_n = ρ^–1/2. The number of correlation blobs per chain is N/g_n = N(ρb²)^1/(2ν), and the brush thickness increases with grafting density as

20

Figure 1 shows the increase in brush thickness H with grafting density ρ in this quasi-neutral regime with the scaling exponent (1−ν)/(2ν) which is half of the exponent in the Pincus brush regime. In Θ solvent with ν = 1/2, the exponent (1−ν)/(2ν) = 1/2 while in good solvent with ν = 3/5 the exponent (1−ν)/(2ν) = 1/3.

Parabolic Molecular Field

In the Alexander–de Gennes model of neutral brushes,^16,17 all chain ends are assumed to be located in the outmost blob, and the density is assumed to be uniform throughout the brush. In more sophisticated models of neutral brushes,²⁶⁻²⁸ chain ends are distributed throughout the brush in such a way that the effective molecular field acting on chain segments is parabolic. This results in the almost parabolic density profile of solvated neutral brushes in good solvents.

As in neutral brushes, the molecular field in polyelectrolyte brushes with fractional charge ef per Kuhn monomer is also almost parabolic.¹⁹ However, this field in the charged brushes is essentially electrostatic acting on the charged monomers. Therefore, the electrostatic potential inside a polyelectrolyte brush is parabolic, resulting in the Gaussian distribution of counterions, as dictated by the Boltzmann law.¹⁹ This parabolic electrostatic potential is produced by the combined electric charges of both tethered polyions and counterions. The parabolic shape of the electrostatic potential indicates that electric field (derivative of the electrostatic potential) in the brush increases linearly with the distance from the grafted surface. Linear increase of the electric field implies by the Gauss law that the net charge density in the brush is uniform. This net charge density is the difference between charges on the chains and counterions. Therefore, the polymer density profile follows that of counterions and is also Gaussian to ensure that the difference between counterion and polymer charge profiles is distance-independent. Since the net charge of the brush is not exactly zero, the compensating counterions (Δn per chain) escape from the brush and form Gouy–Chapman layer of thickness λ. These escaped counterions create a capacitor with characteristic thickness H₀ + λ and the escaped charge eΔn is related to Gouy–Chapman length λ (cf. eq 15) outside the brush

21

The electrostatic energy per unit area of this capacitor

22

is balanced by the entropic part of free energy per unit area gained by escaped counterions

23

with concentration c₀ = fNρ/H₀ of ions inside the brush and concentration of ions c_out = Δnρ/λ in the Gouy–Chapman layer. This balance leads to the width of Gouy–Chapman layer λ comparable to the polyelectrolyte brush thickness H₀ in the osmotic regime (eq 17)

24

up to logarithmic correction on the order of ln(c₀/c_out).

The net number of charges escaped from the brush per unit area is therefore reciprocally proportional to the product of the brush thickness H₀ and Bjerrum length l_B,

25

Note that the concentration of counterions in the Gouy–Chapman layer outside the brush, c_out = ρΔn/λ ≃ ρ²l_BΔn² ≃ (l_BH₀²)⁻¹, is much smaller than concentration of counterions inside the brush, c₀ = fNρ/H₀, in the osmotic regime, ρ ≫ ρ_osm, with the ratio of the two concentrations (see eq 16)

26

determined by how deep the brush is inside the osmotic regime ρ/ρ_osm. We emphasize the difference between Gouy–Chapman length Λ due to all charges (eq 15) and Gouy–Chapman length λ due only to charges Δn escaped from the brush (eq 21).

We estimate the boundaries between different PE brush regimes using the values of parameters close to those in¹⁴ For grafted polyelectrolyte chains with N = 200 Kuhn monomers of length b ≈ l_B = 0.7 nm, and degree of ionization f = 0.5 one finds crossover surface densities: ρ_orient ≃ 2 × 10^–8 nm^–2, ρ* ≃ 1.3 × 10^–4 nm^–2, ρ_osm ≃ 1.4 × 10^–4 nm^–2, and ρ_n ≃ 1 nm^–2. Note that the experimentally relevant and the widest range of surface densities of grafted chains corresponds to the osmotic regime. For example, the experimentally studied surface density of grafted chains¹⁴ ρ ≈ 0.2 nm^–2 is in the osmotic regime of PE brush with predicted brush thickness H₀ ≃ 100 nm much larger that the “bare” Gouy–Chapman length Λ ≃ 0.01 nm and therefore with very large ratio c_inside/c_outside ≃ H₀/Λ ≃ 10⁴. Below we consider polyelectrolyte brushes prepared in this main (OB) regime. Note that upon strong compression they could enter the quasi-neutral regime.

2.2. Normal Force between a Pair of Polyelectrolyte Brushes

The main focus of this paper is on the interactions between two polyelectrolyte brushes. In contrast to neutral brushes, polyelectrolyte brushes repel each other at distances D between grafted surfaces much larger than twice the thickness H₀ of each brush. The source of this long-range interaction is the confinement of counterions in the space between two surfaces. The free energy of dissociated counterions is dominated by their translational entropy, which is much larger than interaction part of their free energy. The self-energy of counterions does not change upon brush deformation and therefore does not contribute to the variation of free energy.

The resulting pressure P felt by the surfaces is given by Van’t Hoff (ideal gas-like) law for counterion density c_i(D/2) in the middle of the gap, P = k_BTc_i(D/2). At distances between grafted surfaces D ≫ λ ≃ H₀, the pressure

27

is determined by the “tail” of the Gouy–Chapman counterion distribution, c_i(z) ≈ (l_Bz²)⁻¹ at distance z = D/2. Note that this pressure is independent of brush parameters and depends only on the separation D between grafted surfaces and Bjerrum length l_B (for monovalent counterions).

At stronger compressions, D < H₀, counterions are distributed almost uniformly between the two grafted surfaces with concentration c_i = 2fNρ/D, and produce osmotic pressure

28

Note that there is sharp crossover between these two expressions, eqs 27 and 28, with rapidly increasing pressure from a low value of kT/(l_BH₀²) to a high value of kTc₀ ≃ kTfNρ/H₀ by a large factor fNρH₀l_B ≃ λ/H₀ upon the decrease of separation D by the factor on the order of unity (for example, from D = 2H₀ to D = H₀) as depicted in Figure 2. The crossover between two asymptotic dependences of osmotic pressure (lines with slopes −2 and −1 given by respective eqs 27 and 28) is indicted by the vertical dashed line.

Figure 2.

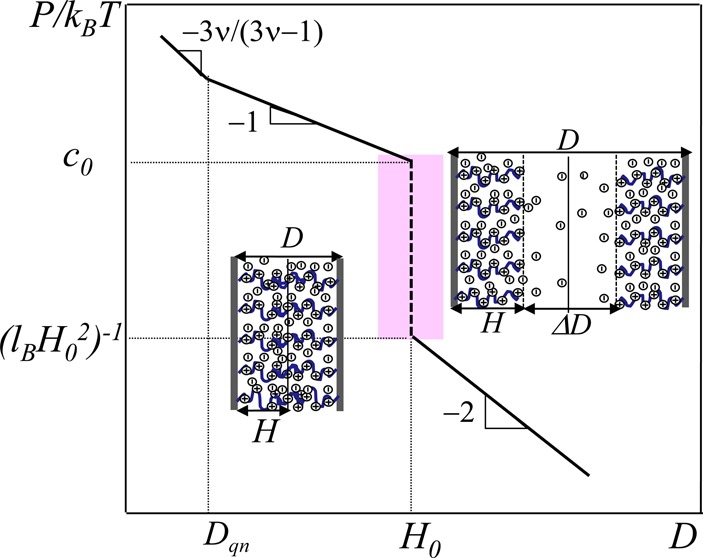
Normal force per unit area in compressed osmotic PE brushes as a function of distance D between surfaces in logarithmic coordinates. c₀ = fNρ/H₀. The interval of D with a sharp increase in force is shadowed pink.

The normal force between compressed polyelectrolyte brushes is dominated by counterions (eq 28) as long as there is more than one free counterion per correlation volume. The normal pressure at higher compression is controlled by direct interactions between polymer chains and is similar to the pressure in neutral brushes (see eqs 38 and 39 below)

29

where c is the monomer number density c = 2Nρ/D.

2.3. Interpenetration of Polyelectrolyte Brushes

In contrast to neutral brushes, polyelectrolyte brushes contract upon compression leaving the gap of width ΔD = D – 2H filled with solvent and counterions.¹⁹ Therefore, there is a regime of intermediate compression without physical contact and interpenetration of monomers from apposing brushes. This gap acts as a lubrication layer upon shear of apposing brushes at distances between plates D > L larger than the size of a free polyion (eq 3).

At smaller separations between surfaces D < L, polyions penetrate into apposing brushes up to characteristic distance, called penetration length δ.

The polymer penetration length δ_n in neutral brushes with parabolic molecular field was estimated in refs (29 and 30)

30

It increases upon brush compression (a decrease in brush thickness H = D/2). Equation 30 is applicable for chains with Gaussian elasticity in both dry (solvent-free) and solvated neutral brushes. It can also be applied to compressed polyelectrolyte brushes on scales larger than correlation length ξ, as we demonstrate below (see eq 34).

At strong compressions D ≪ L, polyelectrolyte chains uniformly fill the space between grafted surfaces similar to semidilute salt-free polyelectrolyte solution with concentration c = 2Nρ/D and correlation length^31,32

31

This solution could be envisioned as densely packed melt of correlation blobs with size ξ. At distances r smaller than correlation length ξ, polyelectrolytes retain the extended conformations of dilute solution polyions, and blob size ξ is related to the number of monomers g in the blob according to eq 3

32

At larger distances r ≫ ξ polyions are envisioned as Gaussian chains of N/g correlation blobs each. The end-to-end distance of unconstrained polyions in a semidilute polyelectrolyte solution is³²

33

which is on the order of the fluctuation size of a polyelectrolyte chain at this concentration.

We distinguish two cases for a pair of apposing polyion brushes in strongly compressed regime (D < L) depending on the separation between grafted surfaces D in comparison to this fluctuation size R (eq 33). If R < D < L the grafted chains are stretched in comparison to their “happy” fluctuation size (H > R) and the interpenetration between apposing brushes is only partial (δ < H). If the separation between plates is smaller than the fluctuation size D = 2H < R the grafted chains are compressed and the two brushes fully interpenetrate (δ ≈ H).

2.3.1. Partial Interpenetration

In a compressed polyelectrolyte brush with thickness H in the interval R < H < L, the chains of blobs of size ξ each are stretched in the normal direction. To optimize their free energy, tethered polyions distribute free ends throughout the slit between surfaces with partial penetration into apposing brush. Similarly to dry (solvent-free) brush of neutral polymers, tethered chains of correlation blobs experience parabolic potential, and interpenetration length δ for polyions can be found by substituting b → ξ and N → N/g and H = D/2 in eq 30 to give

34

Note that fluctuation size R of polyelectrolyte chain in solution (eq 33) decreases with concentration c as R ∼ c^–1/4 ∼ D^1/4. Therefore, interpenetration width δ in eq 34 is independent of spacing D between plates in the regime of partial interpenetration. In the case of weak interpenetration δ ≪ D, only a small fraction δ/D of all monomers is in the interpenetration zone. The total number of blobs per unit area in the interpenetration zone is n_B = δ/ξ³ with n_B/2 from each brush. Each chain section in the interpenetration zone is almost unstretched with (δ/ξ)² blobs per section. The number of chain sections per unit area in the interpenetration zone 1/(δξ) is smaller than the total grafting density ρ = D/(ξ³N/g) by the factor

35

where we used eqs 33 and 34, ξ²N/g ≃ R² ≃ δ^3/2D^1/2. Therefore, the fraction of polyions with free ends in the interpenetration zone is (δ/D)^1/2, while the fraction of monomers in this zone δ/D, leading to the average number of monomers per chain section in the interpenetration zone N(δ/D)^1/2.

2.3.2. Full Interpenetration

A decrease in spacing between plates D eventually results in the full interpenetration of apposing brushes, δ ≃ D, at plate separation D ≃ R. At smaller distances D < R, there is full interpenetration of apposing brushes, δ = D, with total number of “interpenetrating” blobs per unit area n_B = D/ξ³ where blob size ξ is given by eq 31.

At distances D between plates smaller than

36

the correlation length ξ in compressed polyelectrolyte brushes is governed by the nonelectrostatic interactions,

37

As long as there are many counterions (with translational entropy ≃ k_BT each) per correlation blob with size ξ (eq 37), the normal force P is dominated by the osmotic pressure of counterions. This mixed regime with correlation length controlled by nonelectrostatic interactions (eq 37), but osmotic pressure dominated by counterions is expected in the interval of distances between surfaces D_qn < D < D_n. At the lower boundary of this interval

38

there is one counterion per correlation volume. At even stronger compressions with D < D_qn, the number of counterions per correlation blob becomes smaller than unity. Here, both correlation length ξ and osmotic pressure

39

are determined by the nonelectrostatic interactions between monomers. In this interval of plate separations (D < D_qn), compressed polyelectrolyte brushes behave as quasi-neutral ones.

3. Friction between Polyelectrolyte Brushes

3.1. Bare Surfaces

Before describing the effect of PE brushes on the friction between substrates, consider the friction between bare planar surfaces with charge number density Nfρ immersed in a Newtonian liquid with viscosity η_s. We assume that shear does not perturb the Gouy–Chapman counterion distribution. The normal force P is determined by the counterion pressure in the middle of the gap between surfaces²⁰

40

The shear stress σ_bare (friction force per unit area) experienced by planar surfaces in laminar flow with effective velocity gradient V/D equal to the actual strain rate

41

is

42

Therefore, in the case of bare surfaces the effective viscosity defined as the ratio of measured shear stress σ and externally imposed effective shear rate V/D

43

is equal to the solvent viscosity η_s.

3.2. Polyelectrolyte Brushes

The shear of polymer-covered substrates with a low sliding velocity V results in linear velocity dependence of shear stress (friction force per unit area) σ ∼ V. Velocity V in this linear regime is low enough to allow complete relaxation of polyion conformations with almost unperturbed distribution of monomers in PE brush in both normal and lateral directions.

3.2.1. Regime of Weak Compression (D ≫ H₀)

In the case of weak compression there is a gap between brushes acting as a lubrication layer. The flow of solvent within the brush is suppressed on hydrodynamic screening length scale ξ_h much smaller than PE brush thickness H₀. The shear-induced laminar flow of the solvent is therefore limited to the gap of thickness D – 2H + 2ξ_h = ΔD + 2ξ_h, where ξ_h is the flow penetration length into each of the brushes. The thickness of this gap is estimated in the Appendix for the polyions with the Gaussian elasticity. The shear stress σ_brush is obtained in this regime of weak PE brush compression by substituting D by ΔD + 2ξ_h in eq 42,

44

with effective viscosity

45

enhanced with respect to the solvent viscosity η_s by the geometric factor D/(ΔD + 2ξ_h). If the thickness H₀ of the PE brush is much smaller than spacing between grafted surfaces H₀ ≪ D, the shear stress

46

is similar to the shear stress between two bare charged surfaces (eq 42). The effective viscosity η_eff (eq 45) in this regime of weak PE brush compression is approximately equal to the solvent viscosity η_s. The reduced viscosity

is close to unity, as depicted in Figure 3 by the plateau located at distances between surfaces D > H₀.

Figure 3.

Reduced effective viscosity η_eff/η_s (equal to enhancement of shear stress σ_brush/σ_bare) as a function of distance D between surfaces in logarithmic coordinates. Charges on polyions and mobile ions are not shown, brush interpenetration regions are shadowed gray, the gap of laminar solvent flow with width ΔD + 2ξ_h is shadowed blue. Regions with sharp increase in reduced effective viscosity η_eff/η_s are shadowed pink.

3.2.2. Regime of Intermediate Compression (L < D < H₀)

As the distance between grafted surfaces approaches the thickness of uncompressed brushes D ≈ H₀, the size of the gap D – 2H + 2ξ_h rapidly decreases. The corresponding shear stress (eq 44) and the effective viscosity (eq 45) increase and become much larger than in the case of the bare charged surfaces at the same spacing D (eqs 42 and 43). The reduced viscosity becomes much larger than unity η_eff/η_s ≫ 1 (see Figure 3).

As the spacing between the surfaces becomes smaller than the uncompressed brush thickness D ≲ H₀, the width ΔD of the polymer-free gap between apposing brushes decreases below the hydrodynamic penetration length ξ_h, and the thickness of the effective gap saturates at 2ξ_h with

47

estimated assuming Gaussian elasticity of polyions (see Appendix for details). In this case the shear stress due to penetration of flow inside polyelectrolyte brushes weakly increases with decreasing separation D between plates

48

and the reduced effective viscosity

49

is much larger than unity and decreases with decreasing D (see Figure 3). The sharp increase of the effective viscosity at plates separation D ≈ H₀ is by the large factor (ρH₀²)^2/5. Note that although the effective viscosity is much higher than the solvent viscosity, the actual viscosity in the lubrication layer is still solvent-like η_s because the concentration of polymer segments in this layer is small.

3.2.3. Regime of Strong Compression (D < L)

The solvent-like friction is replaced with the polymer solution-type friction at the boundary between intermediate and strong compression regimes D ≃ L. This corresponds to another sharp increase of shear stress and effective viscosity upon compression (see the vertical dashed line at H = L in Figure 3). The concentration of polymer segments c = 2Nρ/D in the regime of strong compression D ≪ L, becomes almost uniform in the gap between the grafted surfaces.

Subregime of Partially Penetrating PE Chains (D_* < D < L)

In this subregime, the lateral force σ_brush is governed by the polymer solution - type friction in the interpenetration zone with thickness δ. Polymer segments from one brush in this zone are dragged with velocity ∼V with respect to segments from the apposing brush. Assuming that hydrodynamic interactions are screened on length scales on the order of correlation length ξ and that the chains are unentangled, the friction force per correlation blob of size ξ can be estimated by the Stocks law as Vη_sξ. Therefore, the total shear stress is given by

50

where n_B ≈ δ/ξ³ is the number of correlation blobs per unit area in the interpenetration zone. The interpenetration length δ for partially interpenetrating PE brushes can be estimated using eq 34

51

and is compression-independent and does not depend on distance D between plates in the interval of D* < D < L. The resulting friction stress

52

increases linearly with concentration c = 2Nρ/D or reciprocally with spacing D between grafted surfaces upon PE brush compression (σ ∼ c ∼ D^–1). Therefore, the reduced effective viscosity

53

is independent of the distance between grafted surfaces D in this strong compression regime with partially interpenetrating PE brushes. This behavior of reduced effective viscosity η_eff/η_s is depicted by the high plateau located to the left of the dashed vertical lines in Figure 3. The jump of the effective viscosity at D ≈ L is by the factor (ρL²)^4/15.

This regime of constant reduced effective viscosity η_eff/η_s ends at the separation between grafted surfaces D on the order of the compression-independent interpenetration length δ (eq 51)

54

Note that at this boundary of the subregime the plate separation D_* (eq 54) is on the order of the fluctuations of the polyelectrolyte chains R (eq 33)—the size of unstretched chains, as expected for the interpenetration zone.

Subregime of Fully Penetrating PE Chains (D < D_*)

At smaller separations between grafted surfaces, D < R, there is full interpenetration between chains from apposing brushes and all D/ξ³ correlation blobs per unit area contribute to the friction force. The resulting friction stress in this regime

55

is D-independent. The corresponding effective viscosity η_eff = σD/V is proportional to the separation D between grafted surfaces. This behavior of the reduced viscosity

56

is depicted by the solid line with slope 1 in Figure 3.

Subregime of Quasi-Neutral Chains

At very strong compressions with D < D_n (eq 36) the correlation length ξ of the space between plates is governed by the nonelectrostatic interactions (eq 37), and the friction stress σ approaches the value for neutral brushes⁸

57

with the effective viscosity

58

This effective viscosity is independent of distance D between grafted surfaces for a brush in Θ-solvent with ν = 1/2. In good solvent with ν = 3/5 the effective viscosity in quasi-neutral regime decreases as square root of plate separation D. The reduced viscosity η_eff/η_s in this quasi-neutral regime is indicated by the line with slope (4ν–2)/(3ν–1) in the left part of Figure 3.

4. Discussion

4.1. Bare Charged Surfaces vs PE Brushes

Comparison of forces between bare charged and polyelectrolyte-decorated surfaces with the same surface charge density (eqs 42, 44, 52, and 55) indicates that polyelectrolyte brushes considerably enhance both normal and lateral forces at distances smaller than original brush thickness D ≲ H₀. This enhancement for planar substrates decorated with PE brushes with respect to bare plates with equivalent surface charge density efNρ is demonstrated in Figure 3 displaying the ratio of lateral (friction) stresses σ_brush/σ_bare = η_eff/η_s and in Figure 4 presenting the ratio of normal pressures P_brush/P_bare as functions of the separation between plates D.³⁷

Figure 4.

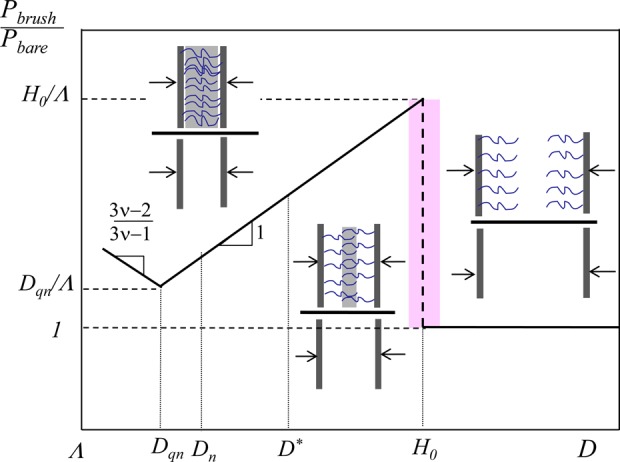
Ratio of normal forces per unit area P_brush/P_bare for PE brush-decorated and bare surfaces with the same surface charge density as a function of distance D in logarithmic coordinates. Region of sharp increase in P_brush/P_bare is shadowed pink.

Comparison of Normal Stresses

The enhancement of normal force per unit area P is very large: the ratio is

59

with the largest value on the order of H₀/Λ at plate separation D ≈ H₀. The ratio of normal stresses P_brush/P_bare remains much larger than unity in the whole interval of compressions D < H₀ passing through a minimum at distance between plates D ≃ D_qn, as shown in Figure 4. The physical reason for this large enhancement of pressure (eq 59) is the difference between the counterion distributions in the two cases. Counterions are localized within the volume of the polyelectrolyte brush and the pressure P_brush quickly increases upon compression of the PE brush down to D ≃ H₀. In the case of bare charged surfaces, counterions are localized very close to the surfaces with half of them within the Gouy–Chapman layer of thickness Λ much smaller than the brush thickness Λ ≪ H₀. Therefore, the normal stress P_bare between bare surfaces is due to the confinement of loose tails of ion distributions (eq 40) at distances Λ < D < H₀, and is very small because counterion concentration is very low outside the Gouy–Chapman layer. At separations between plates smaller than D_qn at which polyelectrolyte brushes exhibit quasi-neutral behavior (eq 39), the ratio of normal forces is

60

with exponent −(2 – 3ν)/(3ν – 1) (see Figure 4) equal to −1 in Θ solvents and −1/4 in good solvents.

Comparison of Friction Stresses

Friction forces between polymer-decorated surfaces are also considerably enhanced compared to these for bare surfaces (see Figure 3). The distribution of counterions is not as important because counterions do not directly participate in friction. The first sharp increase of shear stress upon compression of brushes

61

is due to the reduction of the thickness of lubrication layer from H₀ to ξ_h at plate separations D ≈ H₀. The enhancement of shear stress in the intermediate compression regime is (see eq 49)

62

The second sharp increase of shear stress by the factor (ρL²)^4/15at plate separations D ≃ L, occurs because solvent-like friction is substituted by polymer solution-type friction in the interpenetration zone between apposing brushes. The high ratio of friction stresses (eq 53)

63

is independent of plate separation D in the first regime of strong compression because interpenetration length δ is D-independent in this regime (see plateau in Figure 3).

In the second regime of strong compression with full interpenetration of apposing brushes the ratio of friction stresses (eq 56)

64

decreases linearly with distance between plates D (see eq 56). Note that enhancement of friction stresses between grafted surfaces σ_brush/σ_bare in all regimes with D < H₀ is smaller than the ratio of normal forces P_brush/P_bare. This explains why polymer brushes are better lubricants than simple liquids as discussed in detail below.

4.2. Friction Coefficient

Friction coefficient is conventionally defined¹ as the ratio of friction to normal forces

65

The normal force–pressure P between apposing brushes is velocity-independent in the linear regime, while the shear stress σ is linearly proportional to sliding velocity V. Therefore, friction coefficient μ for brushes is a velocity-dependent quantity, and thus does not directly characterize the properties of participating surfaces unlike the friction coefficient between solid surfaces. In particular, one can always select small enough velocity to obtain as low friction coefficient μ as one would like. Note that the friction coefficient μ_bare between bare charged surfaces is also velocity-dependent

66

where we used eqs 40, 42, and 65, while the case D < Λ is not of practical interest for strongly charged surfaces with Λ ≲ b.

Nevertheless the velocity-dependent friction coefficients μ can be compared between different pairs of surfaces at similar shear conditions. By using the results of previous subsections, we compare friction coefficients for two systems: planar surfaces decorated by osmotic polyelectrolyte brushes and bare charged surfaces with equivalent charge density

67

For polyelectrolyte-decorated surfaces at large distances D ≫ H₀ between plates, the friction coefficient (calculated with eqs 27 and 46)

68

is almost unaffected by the presence of polymer brushes. This behavior of μ is indicated in Figure 5a by solid line with slope 1 at large separations D ≫ H₀ between plates and is the same as between bare surfaces (eq 66).

(see the corresponding horizontal line in Figure 5b).

Figure 5.

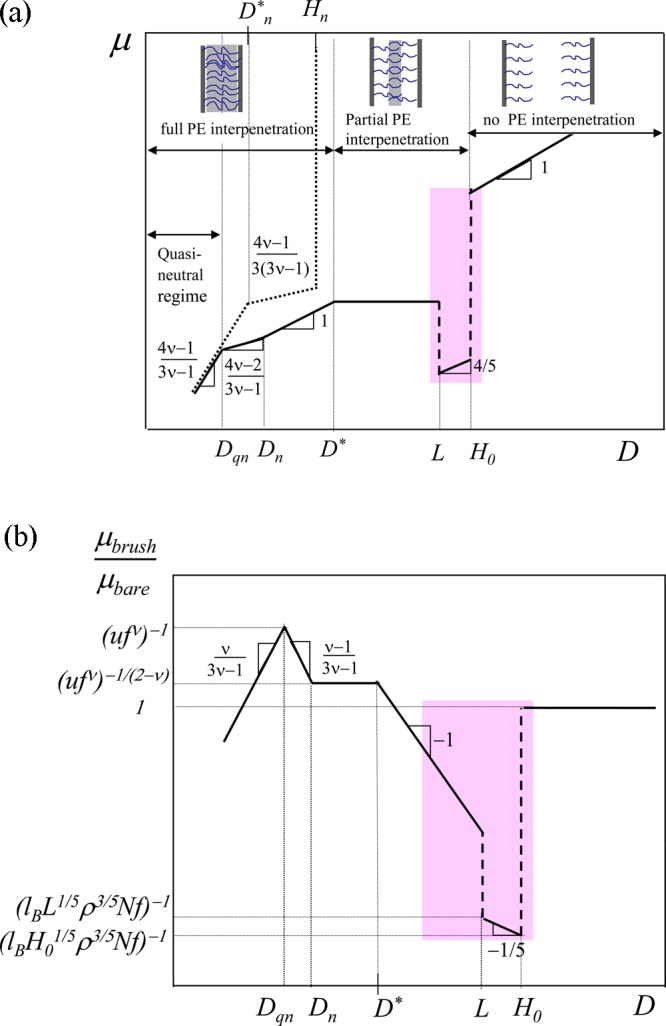
(a) Friction coefficient μ between planar surfaces decorated by PE brushes (solid lines) and neutral brushes with the same degree of chain polymerization N and grafting density ρ (dotted lines) as a function of distance D between surfaces in logarithmic coordinates. (b) Ratio of friction coefficients μ_brush/μ_bare for PE brush-decorated and bare surfaces with the same surface charge density in logarithmic coordinates. The region of enhanced lubrication by PE brushes is shadowed pink.

At the boundary between weak and intermediate compressions (D ≈ H₀) both the normal and shear stresses sharply increase, but the friction coefficient μ_brush drops because enhancement of normal force by factor H₀/Λ is stronger than enhancement of friction stress between the brush-decorated surfaces by factor (ρH₀²)^2/5at relatively high grafting densities of polyions in the osmotic regime with ρ/ρ_osm>(uf ^ν)^−2/3 > 1. This case is depicted in Figure 5b.

In the regime of intermediate compression, L < D < H₀, the friction stress σ_brush is still solvent-like, but is enhanced in comparison to shear stress between bare charged surfaces due to very thin lubrication layer between brushes. In this regime of intermediate compression the thickness ΔD of the gap between brushes is already much smaller than the hydrodynamic penetration length ξ_h. The latter determines the effective gap thickness where the friction remains solvent-like. The normal pressure P_brush between brushes is enhanced more than shear stress σ_brush due to the contribution to the pressure from almost all counterions. In this interval of distances D, the friction coefficient μ_brush is estimated assuming Gaussian elasticity of polyions (using eqs 28 and 48) as

69

decreasing as μ_brush ∼ D^4/5 upon the decrease in plate separation D (see line with slope 4/5 in Figure 5a). The ratio of friction coefficients

70

drops sharply at D ≃ H₀ and weakly increases as μ_brush/μ_bare ∼ D^–1/5 with decreasing D (see Figure 5b).

The sharp increase of the friction coefficient μ_brush at D ≃ L indicated by the left vertical dashed line in Figure 5a is associated with the interpenetration of PE chains and the appearance of polymer solution-type friction. PE brushes start to overlap in the regime of strong compressions at distances between plates D < L and the friction coefficient (calculated using eqs 28 and 52)

71

is independent of the distance D between plates. This behavior of μ_brush is shown by the horizontal line in Figure 5a. The ratio of friction coefficients in this regime

72

varies reciprocally with spacing between plates D (μ_brush/μ_bare ∼ D^–1, see the line with slope −1 in Figure 5b).

As polyelectrolyte brushes fully interpenetrate each other at distances D_n < D < D_*, eqs 28 and 55 give friction coefficient

73

linearly proportional to plate separation (as indicated by the solid line with slope 1 at D < D_* in Figure 5a). The ratio of friction coefficients

74

is independent of plate spacing D (left horizontal line in Figure 5b). Note that uf ^ν < 1 for charge density f below Manning condensation threshold³³ and uf _eff^ν = 1 for highly charged chains with f above this threshold. Therefore, the ratio of friction coefficients in this regime is greater than or on the order of unity, indicating that polyelectrolyte brushes can produce solvent-like friction at very high normal loads.

At larger compressions D_qn < D < D_n, correlation length ξ is governed by nonelectrostatic interactions (eq 37) while the normal pressure is still determined by mobile counterions. By using eqs 28 and 57 one finds friction coefficient in this mixed subregime,

75

with no D-dependence in Θ-solvent (ν = 1/2) and decreasing as μ ∼ D^1/2 upon further compression under good solvent conditions (ν = 3/5). Scaling dependence for μ in this subregime is shown in Figure 5a by the solid line with exponent (4ν – 2)/(3ν – 1). The corresponding ratio of friction coefficients in this mixed regime

76

increases with decreasing D as indicated by the line with slope (ν – 1)/(3ν – 1) in Figure 5b.

Finally the compressed polyelectrolyte brushes behave as quasi-neutral at distances between plates D < D_qn. The friction coefficient in this subregime is determined by eqs 39 and 57 as

77

and decreases upon compression as sketched in Figure 5a by the solid line with exponent (4ν – 1)/(3ν – 1). In Θ solvent with ν = 1/2, this exponent is equal to 2 while in good solvent with ν = 3/5 it decreases to 7/4. The ratio of friction coefficients between a pair of quasi-neutral brushes μ_brush and a pair of bare charged surfaces μ_bare

78

decreases with decreasing D, as indicated by the line with slope ν/(3ν – 1) in Figure 5b and can become less than unity at high enough compression as long as polymer volume fraction between plates is still low.

As shown in Figure 5b, the brush-decorated surfaces can produce noticeably smaller friction coefficient compared to friction between bare charged surfaces. A significant drop in μ_brush/μ_bare is achieved for polyelectrolyte brushes in the interval of distances between plates D_* < D < H₀. This range of conditions is marked by shadowed (pink) region in Figure 5b. Here, charged polymer brushes behave as better lubricants than low molecular weight liquids, while supporting much higher loads. Different regimes of friction between polyelectrolyte brushes are summarized in Table 1.

Table 1. ^a Normal Pressure P_brush/(k_BT), Reduced Effective Viscosity η_eff/η_s, and Ratio of Friction Coefficients μ_brush/μ_bare between a Pair of Apposing Polyelectrolyte Brushes with Weakly Charged Chains bf^–ν < l_B.

regimes	Pbrush/(kBT)	ηeff/ηs = σbrush/σbare	μbrush/μbare
D ≫ H0	(lBD2)−1	1	1
L < D < H0	fNρ/D	(ρD2)2/5	(lBD1/5ρ3/5)−1
D* < D < L	fNρ/D	(ρL2)2/3	(ρL2)2/3/(f N lBρD)
Dn < D < D*	fNρ/D	ρDL	(uf ν)−1/(2−ν)
Dqn < D < Dn	fNρ/D	(Nρb3/D)2ν/(3ν–1) (D/b)2	(1/uf)(Nρb3/D)(1−ν)/(3ν–1)
D < Dqn	b–3(Nρb3/D)3ν/(3ν–1)	(Nρb3/D)2ν/(3ν–1) (D/b)2	(1/u)[D/(Nρb3)]ν/(3ν–1)

^aHere σ_bare ≈ η_sV/D and μ_bare ≈ η_sVl_BD/k_BT are shear stress and friction coefficient between bare surfaces with the same charge density e f N ρ as polyelectrolyte brushes.

Note that the volume fraction of monomers cb³ ≈ Nρb³/D in the compressed brushes is assumed to be much less than unity in all regimes to avoid the effect of high monomeric friction coefficient and glass transition of bulk polymers.

The schematic behavior of the friction coefficient μ for neutral polymer brushes (with fraction of charged monomers f = 0) and the same grafting density ρ is depicted by the dotted lines in Figure 5a. In contrast to polyelectrolyte brushes, neutral polymer brushes start to interact with each other at distances D ≃ H_n with unperturbed brush thickness H_n specified by eq 20 (indicated by the dotted vertical line in Figure 5a). At stronger compressions, D_n^* < D < H_n (with distance D_n on the order of unperturbed chain length in semidilute polymer solution with concentration Nρ/D_n^*), neutral brushes are partially interpenetrating, and the decrease in friction coefficient μ in this subregime is indicated by the dotted line with slope (4ν – 1)/[3(3ν – 1)] (that is, 7/12 for ν = 3/5, and 2/3 for ν = 1/2). In the regime of full interpenetration of neutral brushes at distances D < D_n, friction coefficient μ is described by eq 77 and is depicted by the dotted line with slope (4ν – 1)/(3ν – 1) (that is, 7/4 for ν = 3/5, and 2 for v = 1/2) in Figure 5a. As shown in Figure 5a, polyelectrolyte brushes provide lower friction coefficient than neutral brushes at the same conditions (same sliding velocity, mass per unit area, and plate separation) except for very strong compressions with distance between plates D < D_qn at which polyelectrolyte brushes exhibit quasi-neutral behavior and friction coefficients of polyelectrolyte and neutral brushes are similar.

Our theoretical predictions were obtained for salt-free solutions, but they are also applicable for solutions with added salt as long as salt concentration c_s is lower than the concentration of counterions, c_i = 2fNρ/D. The concentration of counterions c_i in the gap between apposing brushes increases upon compression (with the decrease of the spacing D between plates), and the applicability of our results expands at stronger compressions.

4.3. Effect of Counterion Condensation on Friction between Polyelectrolyte Brushes

The equations discussed above and summarized in Table 1 were derived for flexible weakly charged polyelectrolytes with degree of ionization below the Manning condensation threshold (bf^–ν < l_B, where f is the number of elementary charges per Kuhn length b). If the charge density f, increases up to the value of f ≈ u^–1/ν both the size of electrostatic blob (ξ_e), and the distance between charges along the chain (L/fN) approach the value of the Bjerrum length (l_B). At higher bare charge densities f > u^–1/ν the Manning condensation of counterions maintains the distance l_B between the uncondensed charges along the polyion with the effective charge density f_eff ≈ u^–1/ν. There is no Pincus regime with intermolecularly induced stretching for such strongly charged brushes with condensed counterions because ρ_osm ≈ ρ* ≈ L^–2 (see eqs 11 and 16). In this counterion condensation regime with f_eff ≈ u^–1/ν, brush height H ≈ H₀ ≈ L ≃ bNu^(ν–1)/ν is independent of chain grafting density ρ (eq 17 and 3).

For these brushes with condensed counterions the regime of intermediate compression with interval of distances L < D < H₀ between surfaces shrinks into the crossover region between the regime of weak compression (with D ≫ H₀ ≃ L) and the regime of strong compression (with D < L). There is also no mixed subregime with interval of distances between surfaces D_qn < D < D_n. The two remaining crossover distances separating various subregimes in the regime of strong brush compression (eqs 54, 36, and 38) are D_* ≃ (bNu^{[(2ν–1)(1−ν)]/[ν(2−ν)]}/ρ)^1/3 and D_n ≃ D_qn ≃ b³Nρu^(3ν–1)/ν. By substituting the effective charge density f_eff ≈ u^–1/ν and L ≃ Nbu^(ν–1)/ν into the corresponding equations for shear stress σ_brush and the friction coefficient μ, one finds the reduced effective viscosity η_eff/η_s and the ratio of friction coefficients μ_brush/μ_bare for strongly charged (f > u^–1/ν) flexible polyions with electrostatic interaction parameter u = l_B/b > 1 (see Table 2).

Table 2. Normal Pressure P_brush/(k_BT), Reduced Effective Viscosity η_eff/η_s, and Ratio of Friction Coefficients μ_brush/μ_bare between a Pair of Apposing Polyelectrolyte Brushes with Strongly Charged (bf^–ν > l_B) Flexible (b < l_B) Chains^a.

regimes	Pbrush/(kBT)	ηeff/ηs = σbrush/σbare	μbrush/μbare
D ≫ H0 ≃ L	(lBD2)−1	1	1
D* < D < L	u–1/νNρ/D	ρ2/3(bNu(ν–1)/ν)4/3	b1/3N1/3u(ν–1)/3ν/(ρ1/3D)
Dn < D < D*	u–1/νNρ/D	ρDbNu(ν–1)/ν	1
D < Dqn ≃ Dn	b–3(Nρb3/D)3ν/(3ν–1)	(Nρb3/D)2ν/(3ν–1) (D/b)2	(1/u)[D/(Nρb3)]ν/(3ν–1)

^aHere σ_bare ≈ η_sV/D, μ_bare ≈ η_sVl_BD/k_BT are shear stress and friction coefficient between bare surfaces with the same charge density efNρ as polyelectrolyte brushes.

In the case of stiff chains with b > l_B there is another regime with increasing charge density f preceding counterion condensation regime. If charge density f is higher than u^–1/2 the electrostatic blob size ξ_e becomes smaller than Kuhn length b. These stiff polyelectrolyte chains are almost fully stretched with end-to-end distance approaching contour length bN but for u^–1/2 < f < u^–1 there is no counterion condensation. At higher charge densities f > u^–1 counterions condense on these almost fully stretched polyions saturating the effective charge density at the Manning value of one charge per Bjerrum length corresponding to effective charge density f ≈ 1/u charges per Kuhn length.

For flexible polyelectrolytes with a typical Kuhn segment length b ≃ 1.5–2.0 nm, the value of electrostatic parameter u = l_B/b is estimated in water to be u ≃ 0.3–0.5. That is, in scaling terms u = l_B/b is close to unity, and many experimental systems (e.g., ref (13)) are at the crossover between the scaling regimes with u ≫ 1 and u ≪ 1. For strongly charged polyelectrolytes with condensed counterions, one can approximate this crossover region by substituting u = 1 in the equations presented in this subsection to find brush thickness H₀ ≃ L ≃ bN, and two threshold spacings between surfaces D_* ≃ (bN/ρ)^1/3 and D_n ≃ D_qn ≃ b³Nρ. The subregime of quasi-neutral brush behavior is shifted to very high polymer concentrations b³Nρ/D_n ≃ 1 in the gap between surfaces, and is thereby eliminated. By substituting u = 1 in Table 2 above we find the reduced effective viscosity η_eff/η_s and relative friction coefficient μ_brush/μ_bare for the case of crossover electrostatic parameter u = l_B/b ≃ 1 (Table 3).

Table 3. ^a Normal Pressure P_brush/(k_BT), Reduced Effective Viscosity η_eff/η_s, and Ratio of Friction Coefficients μ_brush/μ_bare between a Pair of Apposing Strongly Charged (bf^–ν > l_B) Polyelectrolyte Brushes with l_B = b.

regimes	Pbrush/(kBT)	ηeff/ηs = σbrush/σbare	μbrush/μbare
D ≫ bN	(lBD2)−1	1	1
D* < D < bN	Nρ/D	ρ2/3(bN)4/3	D*/D < 1
D < D*	Nρ/D	ρDbN	1

^aHere the crossover plate separation D_* ≃ (bN/ρ)^1/3.

At separations D between surfaces much larger than brush thickness bN, effective viscosities, shear stresses, and friction coefficients between pairs of apposing brushes and between pairs of bare surfaces are almost the same (all ratios are ≈1). Upon intermediate compression with partial interpenetration between brushes (D_* < D < bN) the enhancement of shear stress σ_brush/σ_bare is smaller than the enhancement of normal stress P_brush/P_bare and the relative friction coefficient between brushes μ_brush is smaller than friction coefficient between bare surfaces μ_bare by the factor μ_brush/μ_bare ≈ D_*/D. Upon further compression (D < D_*) friction coefficients between polyelectrolyte brushes and bare surfaces are the same, but brushes support much higher load.

5. Conclusions

The scaling theory developed in this paper is applicable for brushes with relatively short polyelectrolyte chains with no entanglements at salt-free conditions and for low sliding velocities V (linear response regime with friction stress σ proportional to shear rate). In addition to the electrostatic interactions between charged species, the model accounts for the short-range two-body and three-body monomer–monomer interactions (with scaling exponents ν = 3/5 and ν = 1/2 for good or Θ solvent conditions, respectively). The simple scaling model neglects the higher order nonelectrostatic interactions between monomers and the changes in the dielectric constant and monomeric friction coefficient that become significant at higher polymer concentrations (i.e., at strong compressions of the brushes).

The decrease in distance D between brush-decorated surfaces gives rise to a sequence of regimes that are characterized by different scaling dependences for friction coefficient μ. The full set of regimes is predicted for grafting densities of polyions ρ < b^–2N^–1/2 that are not too high. For this interval of grafting densities, at the maximum compression of brushes to the polymer volume fraction between surfaces close to unity, the distance between surfaces D is smaller than the Gaussian size of the polyions. For higher grafting densities ρ > b^–2N^–1/2some subregimes predicted for strong compressions of brushes disappear.

We demonstrate that enhanced lubricating properties of polyelectrolyte brushes compared to bare surfaces with equivalent surface charge density are linked to confinement of mobile counterions in the volume of PE brush in the osmotic regime. Compression of apposing PE brushes with interplate distances Λ < D < H₀ leads to the increase in osmotic pressure of confined counterions, P_brush ∼ D^–1, while bare charged surfaces experience much smaller normal force, P_bare ∼ D^–2, due to significantly lower counterion concentration outside the Gouy–Chapman layer of thickness Λ ≃ (l_BρfN)⁻¹. Although shear stress σ_brush arising upon interpenetration of sliding PE brushes is larger than the stress σ_bare between bare charged surfaces, the friction coefficient μ = σ/P remains smaller for PE brushes due to considerably higher values of pressure P_brush ≫ P_bare at interplate distances Λ < D < H₀. This enhancement in lubrication is provided by polyelectrolyte brushes with grafting densities of polyions ρ > (uf ^ν)^−2/3ρ_osm. In the opposite case of very low grafting densities of polyions, ρ_osm < ρ < (uf ^ν)^−2/3ρ_osm, the friction coefficient μ between bare charged surfaces is smaller than between polyelectrolyte brushes under similar conditions (same sliding velocity V and distance Λ < D < H₀ between surfaces).

Comparison of friction coefficient μ = σ/P for charged and neutral polymer brushes with the same mass per unit area revealed enhanced lubrication (i.e., smaller values of μ) between PE brushes. Only at strong compressions of the tethered polyions in the interval of distances D < D_qn (in the quasi-neutral regime, see Table 1 and Figure 5a) do the friction coefficients for the two systems become similar. Recent computer simulations,^34,35,15 confirmed smaller values of friction coefficient μ for charged brushes compared to neutral systems under similar conditions. However, the simulations mostly focused on the nonlinear regime with V-dependent width of the interpenetration zone¹⁵ and shear stress σ described by the sublinear dependence³⁴ on the sliding velocity V. Therefore, a comprehensive comparison between the results of computer simulations as well as experiments and the predictions of our model is still missing. The corresponding simulations are currently under way and the results and comparison between simulations and theory will be presented in a future publication.

Appendix

1. Neutral Brushes

Θ Solvent Conditions

Consider a tethered layer of neutral flexible chains with N ≫ 1 Kuhn monomers (each with size b) immersed in a Θ solvent. At grafting densities ρ ≫ (b²N)⁻¹, the chains stretch due to the ternary repulsive interactions between monomers, and form a brush with thickness (see eq 20 with ν = 1/2)

79

Under Θ-solvent conditions, the chains are almost ideal and exhibit Gaussian statistics on all length scales, and the molecular field in the brush is parabolic.²⁶ This results³⁶ in the “classic” polymer density profile within the brush with thickness H_θ

80

and the distribution function of the free ends

81

where z is the distance from the grafted surface. Because of the thermal fluctuations, the density profile has fluctuation-induced “tail” with the characteristic width ≃ b⁴N^2/3/H_θ^1/3.

A laminar flow will penetrate into such a brush down to the distance ξ_h from the brush edge z = H_θ. We estimate ξ_h as the distance at which chain sections at free ends in the layer of thickness H_θ – ξ_h start to overlap with each other, i.e., give rise to mesh with size ≃ ξ_h. This requirement is formulated as

82

to give

83

where R₀² ≈ Nb² are the mean square fluctuations of the chain in a Θ solvent. Therefore, the hydrodynamic penetration length ξ_h in unperturbed neutral polymer brush in a Θ solvent is on the order of the tail (fluctuation) length δ_n (eq 30) with H = H_θ (eq 79).

2. Charged Brushes

Consider polyions with charge fN on each, tethered with grafting density ρ > ρ_osm at salt-free conditions. If polyions exhibit Gaussian elasticity on all length scales, the molecular field in the brush is parabolic. This molecular field in the charged (PB) and the osmotic brush regimes is of the electrostatic origin, and therefore electrostatic potential in the brush in these regimes is parabolic. The Poisson–Boltzmann model of polyelectrolyte brushes¹⁹ predicts the truncated Gaussian decay of the polymer density profile,

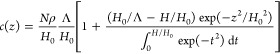84

and the distribution of the free ends

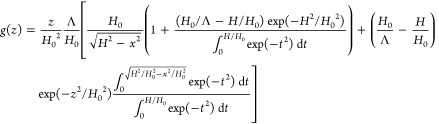85

where z is the distance from the grafted surface, and H is the brush thickness. Equations 84 and 85 are applicable to apposing brushes with distances D between grafted surfaces providing the dominance of ionic contributions over the non-electrostatic interactions between monomers. Under these conditions, the brush thickness H is specified by the solution of equation

86

with parameter β related to the width 2ΔD = D – 2H of the gap between brush edges as

87

In the osmotic brush regime, the ratio of the characteristic brush thickness (eq 17 with ν = 1/2)

and Gouy-Chapman length Λ (eq 15), is very large H₀/Λ ≫ 1. To determine the flow penetration length ξ_h in this regime we use the same arguments as for the neutral brushes. That is, we assume that hydrodynamic interactions become screened at distance ξ_h ≪H if chain sections of grafted polymers above height H – ξ_h overlap and create mesh with size ≃ ξ_h. One then can use eq 82 (with H_θ replaced by H) to find ξ_h. At distances x ≲ H distribution function of the free ends g(z) in eq 85 is dominated by the first term in square brackets and is estimated in the osmotic brush regime with H₀/Λ ≫ 1 as

88

By substituting eq 88 into eq 82, one finds that the hydrodynamic penetration length in the apposing polyelectrolyte brushes,

89

decreases as a function of distance D < H₀ between surfaces as ξ_h ∼ D^1/5, and saturates at larger distances D ≳H₀.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States