ASTRAL: genome-scale coalescent-based species tree estimation

Abstract

Motivation: Species trees provide insight into basic biology, including the mechanisms of evolution and how it modifies biomolecular function and structure, biodiversity and co-evolution between genes and species. Yet, gene trees often differ from species trees, creating challenges to species tree estimation. One of the most frequent causes for conflicting topologies between gene trees and species trees is incomplete lineage sorting (ILS), which is modelled by the multi-species coalescent. While many methods have been developed to estimate species trees from multiple genes, some which have statistical guarantees under the multi-species coalescent model, existing methods are too computationally intensive for use with genome-scale analyses or have been shown to have poor accuracy under some realistic conditions.

Results: We present ASTRAL, a fast method for estimating species trees from multiple genes. ASTRAL is statistically consistent, can run on datasets with thousands of genes and has outstanding accuracy—improving on MP-EST and the population tree from BUCKy, two statistically consistent leading coalescent-based methods. ASTRAL is often more accurate than concatenation using maximum likelihood, except when ILS levels are low or there are too few gene trees.

Availability and implementation: ASTRAL is available in open source form at https://github.com/smirarab/ASTRAL/. Datasets studied in this article are available at http://www.cs.utexas.edu/users/phylo/datasets/astral.

Contact: warnow@illinois.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Species tree estimation is difficult in the presence of gene tree conflict, which can result from incomplete lineage sorting [ILS, modelled by the multi-species coalescent (Kingman, 1982)] as well as other causes. ILS is equivalent to ‘deep coalescence’, which occurs with high probability whenever the time between speciation events is short relative to the population size (Maddison, 1997). When ILS is present, gene trees can differ from each other and from the species tree, presenting substantial challenges to phylogeny estimation methods (Degnan and Rosenberg, 2009; Edwards, 2009). For example, the standard approach, concatenation (which concatenates the multiple sequence alignments for different genes together into one super-alignment, and then estimates a tree on the super-alignment) can return incorrect trees with high confidence (Kubatko and Degnan, 2007). Furthermore, under some conditions, even the most probable gene tree topology may not be identical to the species tree topology (Degnan, 2013; Degnan and Rosenberg, 2006, 2009), a condition called ‘the anomaly zone’.

However, there are no anomalous rooted three-taxon species trees (Degnan and Rosenberg, 2009) and no anomalous unrooted four-taxon species trees (Allman et al., 2011; Degnan, 2013), a key fact that underlies the design of some summary methods and their proofs of statistical consistency. While several methods are established to be statistically consistent under the multi-species coalescent model, MP-EST (Liu et al., 2010) and the population tree returned by BUCKy (Larget et al., 2010) are among the leading methods. BUCKy-pop is more computationally intensive but can work with unrooted gene trees, while MP-EST requires rooted gene trees but easily scales to hundreds of gene trees and so has been used in many phylogenomic studies (Song et al., 2012; Zhao et al., 2013; Zhong et al., 2013). Other statistically consistent species-tree estimation methods include BEST (Liu, 2008) and *BEAST (Heled and Drummond, 2010), which co-estimate gene trees and species trees from input sequence alignments; however, these methods are extremely computationally intensive on datasets with ≥100 genes (Bayzid and Warnow, 2013; Smith et al., 2014), so that only summary methods are feasible for use on genome-scale datasets.

However, even the best coalescent-based summary methods have not been reliably more accurate than concatenation (Bayzid and Warnow, 2013; DeGiorgio and Degnan, 2010), and performance on biological datasets has in some cases resulted in species trees that were less well resolved and biologically feasible than concatenation (Kimball et al., 2013; McCormack et al., 2013). Hence, the choice between coalescent-based estimation and concatenation is highly controversial (Springer and Gatesy, 2014).

We present ASTRAL (Accurate Species TRee ALgorithm), a new coalescent-based species tree method. ASTRAL provides a statistically consistent estimation of the true species tree from unrooted gene trees, under the multi-species coalescent model. Furthermore, ASTRAL runs in polynomial time and can analyse genome-scale datasets in minutes.

We evaluate ASTRAL in comparison with two statistically consistent methods (MP-EST and BUCKy-pop), two simple summary methods [MRP (Ronquist, 1996) and the greedy consensus] and concatenation under maximum likelihood (CA-ML) using RAxML (Stamatakis, 2006), on a collection of biological and simulated datasets. We explore genome-scale analyses, analysing datasets with hundreds to thousands of genes, which are too large for BUCKy-pop and *BEAST to analyse. ASTRAL is more accurate than the other summary methods under all the simulated model conditions we explore. As expected, the relative accuracy of ASTRAL and concatenation depends on the amount of ILS, with ASTRAL having an advantage when ILS levels are at least moderate, and concatenation having an advantage when ILS levels are low. Thus, ASTRAL enables highly accurate large-scale phylogenomic estimation, even in the presence of high levels of gene tree conflict because of ILS.

2 APPROACH

The input to ASTRAL is a set of unrooted gene trees; ASTRAL finds the species tree that agrees with the largest number of quartet trees induced by the set of gene trees.

This optimization problem is NP-hard (Jiang et al., 2001), and so ASTRAL has two versions: an exact version that is guaranteed to return the globally optimal tree, and a heuristic version that can be used on large datasets. For the heuristic version, ASTRAL constrains the search space to reduce the running time, by including a set $\mathcal{X}$ of bipartitions (splits of the leaf set into two disjoint sets) as part of the input, and requiring that the output species tree T draw its bipartitions from $\mathcal{X}$. Thus, for every edge e in T, the deletion of e splits the leaf set into two parts, and that bipartition must be in $\mathcal{X}$. Finding a tree that has the optimum score but draws its bipartitions from the set $\mathcal{X}$ can be solved in polynomial time (Theorem 1). Thus, ASTRAL can be used to find optimal trees for small enough numbers of species, or heuristically for larger numbers of species. We formalize this approach as the Maximum Quartet Support Species Tree (MQSST) problem:

• Input: set $\mathcal{T}$ of unrooted gene trees, each leaf-labelled by species set S, and set $\mathcal{X}$ of bipartitions on S.

• Output: tree T on species set S that draws its bipartitions from $\mathcal{X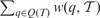}$ such that is maximized, where Q(T) is the set of quartet trees induced by T and $w(q,\mathcal{T})$ is the number of the trees in $\mathcal{T}$ that induce quartet topology q.

The default mode sets $\mathcal{X}$ to be all bipartitions from the input set of unrooted gene trees; however, $\mathcal{X}$ can be any set of bipartitions.

We note that MQSST takes into account the relative frequency of all three alternative quartet topologies and weights them accordingly. Thus, if the dominant (i.e. most frequent) quartet topology is much more frequent than the alternatives, trees that do not induce the dominant topology are penalized, but if the three alternative quartet topologies all have frequencies close to 1/3, that quartet will contribute little to the optimization problem. This approach is in contrast to some other quartet-based methods such as BUCKy-pop that first try to find the dominant quartet topologies and then summarize them. Estimation of the dominant quartet tree is susceptible to error (because of insufficient gene sampling and estimation error), and the MQSST accounts for this.

ASTRAL uses a dynamic programming (DP) approach to solve the MQSST optimization problem, so that it does not need to explicitly enumerate the set of all possible quartet trees. For a given unrooted binary tree T and four leaves $i,j,k,l$ in the tree, the induced subtree of T connecting the four leaves will have exactly two nodes u and v that have degree >2. Thus, a quartet tree on $i,j,k,l$ induced by an unrooted binary tree is associated to the pair of nodes {u, v} defined in this way. Furthermore, given any node x of the tree, it is easy to count the number of quartets that are associated to pairs {x, y} (for some other node y), as we now show. Deleting x from the tree T separates it into three parts, A, B and C; this is called a ‘tripartition’ and is denoted $(A|B|C)$. We pick one of these sets (say A), and pick two leaves from it, and then pick one leaf from each of the remaining sets. Therefore, if a, b and c give the sizes of A, B and C, respectively, then the number of quartets mapped to u is $\left(\begin{array}{c}a\\ 2\end{array}\right)bc+a\left(\begin{array}{c}b\\ 2\end{array}\right)c+ab\left(\begin{array}{c}c\\ 2\end{array}\right)=\frac{abc(a+b+c-3)}{2}$. Therefore, we can associate the quartet tree on $i,j,k,l$ induced by T with two tripartitions—one associated with the internal node u and the other associated with the internal node v, where the quartet tree is associated with the pair {u, v}.

Our algorithm uses a DP approach that is similar to the DP algorithm first introduced in Hallett and Lagergren (2000) for constructing species trees from sets of gene trees, minimizing the total number of duplications and losses, and subsequently used to construct species trees minimizing deep coalescence (Yu et al., 2011). Instead of explicitly calculating quartet trees, we use the set $\mathcal{X}$ to generate a set of tripartitions, and then for each tripartition, we calculate the number of quartet trees induced by the input set of gene trees that would be associated to that tripartition and therefore would be satisfied by any species tree that includes that tripartition. Thus, the species tree can be constructed by calculating a score for individual tripartitions based on a recursive formula that defines the DP.

Recall that $\mathcal{X}$ is a set of bipartitions that can be used in the output tree T; we define ${\mathcal{X}}^{*}$ to be the set of subsets of S that appear as parts of these bipartitions (i.e. $A\in {\mathcal{X}}^{*}$ if and only if the bipartition $(A|S-A)\in \mathcal{X}$). Then, the recursion in the DP finds a way of dividing each set $A\in {\mathcal{X}}^{*}$ into $A\prime$ and $A-A\prime$ (each of which must be in ${\mathcal{X}}^{*}$) such that the number of quartets satisfied by an optimal rooted tree on $A\prime$ and $A-A\prime$, in addition to those satisfied by the tripartition $(A\prime |A-A\prime |S-A)$, is maximized. Thus, the recursion is given by

$$C(A)=\underset{A\prime \subset A;A\prime \in {\mathcal{X}}^{*}}{\max }(C(A\prime )+C(A-A\prime )+W(A\prime |A-A\prime |S-A))$$

where $W(A|B|C)$ counts the number of gene tree quartets associated to tripartition $(A|B|C)$ (which we call the weight of the tripartition). The function C(X) denotes the total contribution to the support of the best rooted tree T_X on taxon set X, where each quartet tree in the set of input gene trees contributes 0 if it conflicts with T_X or only intersects it with one leaf, and otherwise contributes 1 or 2, depending on the number of nodes in T_X it maps to. We set the boundary condition to be $C(\{x\})=0$. At the end of the algorithm, C(S) gives the final score, and backtracking gives the final tree. Because each quartet is associated to exactly two nodes, our described DP counts each quartet tree induced by gene trees exactly twice, and hence, the final score needs to be divided by two to get the quartet score.

The weight of a tripartition is calculated by counting the number of quartet trees mapped to each node of each gene tree that is also mapped to that tripartition. For calculating this, we just need to find the intersection of clusters of the tripartition and all the tripartitions from all gene trees (see Supplementary Materials). For the special case of A = S, we set $W(A\prime |A-A\prime |S-A)=0$.

Theorem 1 —

ASTRAL finds an optimal solution to MQSST, and runs in $O(n^2{x}^{2}k)$ time, where n is the number of species, x is the number of bipartitions in $\mathcal{X}$ and k is the number of gene trees. If $\mathcal{X}$ is the set of bipartitions from the input gene trees, then $x=O(nk)$, and so ASTRAL runs in $O(n^4{k}^3)$ time.

Because of space constraints, we provide the proof in the Supplementary Materials.

Theorem 2 —

ASTRAL is a statistically consistent estimator of the species tree topology under the multi-species coalescent model, even when run in default mode–so that $\mathcal{X}$ is the set of bipartitions from the input gene trees.

Proof Sketch —

Let T* be the species tree. Given a candidate species tree T, let $w_{\mathcal{T}}(q,T)$ be the number of trees in $\mathcal{T}$ that induce a topology identical to T for a quartet q of taxa. Unrooted quartet trees do not have anomaly zones (Degnan, 2013); therefore, given a large enough number of gene trees, each quartet topology induced by the species tree will have higher probability than either of the two alternative topologies, and hence appear with greater frequency in $\mathcal{T}$ with high probability. Therefore, for every quartet q and every possible tree T, with high probability. By extension, if $\mathcal{Q}$ is the set of all quartets of taxa, the score attains its (unique) maximum value when $T=T^{*}$ with high probability. $C_{\mathcal{T}}(T)$ is the score optimized in MQSST; hence, when ASTRAL is run exactly it solves MQSST and so is statistically consistent. The constrained default version of ASTRAL is also statistically consistent because when a large enough number of gene trees is given, then with high probability at least one of the gene trees will be topologically identical to the species tree, $T^{*}$, and so the set $\mathcal{X}$ will contain all the bipartitions from $T^{*}$. When this occurs, ASTRAL run in its default mode will return $T^{*}$. (Note also that $\mathcal{X}$ may contain all the bipartitions from $T^{*}$ even without having $T^{*}$ among its gene trees.)

Note that the MQSST optimization problem could be expressed as finding a median tree, where instead of finding a species tree that maximizes the total number of quartet trees that it satisfies, we would seek a species tree that has a minimum total distance to the input gene trees, where the distance is the number of quartet trees that it violates. Then, Theorem 2 asserts that the median tree (under this definition) is a statistically consistent estimator of the species tree, under the multi-species coalescent model.

3 EXPERIMENTS

Overview

We explore performance on a collection of biological and simulated datasets. We compare the estimated species trees to the model species tree (for the simulated datasets) or to the scientific literature (for the biological datasets), to evaluate accuracy. Tree error is measured using the Robinson–Foulds (RF) (Robinson and Foulds, 1981) rate; because all trees estimated here are completely bifurcating, this is the same as the missing branch rate (proportion of internal edges in the model tree missing in the estimated tree).

100-taxon simulated datasets

We briefly describe the process used to generate these data, and direct the reader to the original publication (Yang and Warnow, 2011) for details. The 100-taxon model species tree was created by a birth–death process, and 25 genes evolved within the species tree under the multi-species coalescent, producing ultrametric gene trees. Nucleotide sequences with 1000 sites were evolved down each gene tree under a process with GTRGAMMA substitutions as well as insertions and deletions, using ROSE (Stoye et al., 1998). True alignments were used to generate estimated gene trees using RAxML.

37-taxon ‘mammalian’ simulated datasets

We simulated this collection of datasets based on a 37-taxon mammalian dataset with 447 genes studied in Song et al. (2012). First, we used MP-EST to estimate a species tree on the biological dataset from Song et al. (2012), and then used it as a model species tree, with branch lengths in coalescent units. We evolved gene trees down the model tree under the multi-species coalescent model using Dendropy (Sukumaran and Holder, 2010), and then rescaled the gene trees to deviate from the molecular clock and produce branch length patterns observed in the biological dataset. We then evolved sequences with 500 and 1000 sites down each gene tree under the GTR model of site evolution, using GTR parameters estimated on the biological dataset. This produces the ‘default’ model condition that has the amount of ILS estimated for this dataset by MP-EST. We varied this protocol by scaling the model species tree branch lengths up (2× and 5×) or down (0.2× and 0.5×) to modify the amount of ILS (so that longer branch lengths reduces ILS, and shorter branch lengths increases ILS). The default model tree conditions (including the number of genes, sequence length distribution and amount of ILS) were set to produce a dataset called the ‘mixed condition’ that most resembled the biological dataset.

The average bootstrap support (BS) in the biological data was 71%, and so we generated sequence lengths that produced estimated gene trees with BS values bracketing that value—500 bp alignments produced estimated gene trees with 63% average BS and 1000 bp alignments produced estimated gene trees with 79% BS. The ‘mixed dataset’ of 400 genes was produced using 200 genes with 63% BS and 200 genes with 79% BS, and had average BS of 71%—like the biological data.

For each model condition (specified by the ILS level, the number of genes and the sequence length), we created 20 replicates, except for the 1600- and 3200-gene model conditions where we created 10 and 5 replicates, respectively. We then used RAxML to produce estimated gene trees on the simulated sequence alignments, and we generated 200 ML bootstrap replicates for the mixed dataset.

Biological datasets

We analysed three biological datasets: the mammalian dataset from Song et al. (2012), containing 37 species and 447 genes, the plant dataset from Zhong et al. (2013), containing 32 species and 184 genes, and also the amniota dataset from Chiari et al. (2012), containing 16 species and 248 genes.

Methods

We compare ASTRAL with MP-EST, BUCKy-pop (the population tree from BUCKy), MRP (a supertree method), the Greedy Consensus and concatenated analysis using maximum likelihood (CA-ML), as computed by RAxML. For 100-taxon datasets and the mixed mammalian datasets, we ran summary methods using three different procedures: using maximum likelihood gene trees as input (bestML), using all bootstrap replicates of all genes as input (All BS) and using the site-only multi-locus bootstrapping (MLBS) procedure (Seo, 2008). For MLBS, we used the greedy consensus of 200 replicate species trees, each computed on an input consisting of one bootstrap replicate tree per gene. BUCKy-pop uses a distribution of gene trees as input, which we approximate using bootstrap gene trees; thus, BUCKy-pop can only be run with a procedure analogous to All BS. In subsequent analyses, where we study the impact of various model parameters, we only study the bestML approach. For the biological datasets, we used the multi-locus bootstrapping procedure (Seo, 2008) to obtain BS values.

For the simulated datasets, we set X to be the set of bipartitions from the input set of trees. On the amniota dataset, as the number of taxa is small, we ran the exact version of ASTRAL. The mammalian biological dataset has a large number of genes that contain all the species, so we used the default setting for ASTRAL. However, the plant dataset has fewer genes and substantial missing data, and so we extended $\mathcal{X}$ to include bipartitions from species trees estimated using MP-EST, CA-ML and MRP, as well as trees published by Chiari et al. (2012) (see Supplementary Materials) This ad hoc approach can improve ASTRAL’s ability to find near-optimal solutions, when the exact version is not feasible.

4 RESULTS

Results on mammalian simulated datasets

The first experiment (Fig. 1) shows results on the mixed mammalian dataset, which most closely resembles the biological dataset studied in Song et al. (2012). We compare ASTRAL, MP-EST, Greedy, MRP, BUCKy-pop and CA-ML and three types of inputs to summary methods. For MRP, MP-EST and ASTRAL, using bestML input trees produced more accurate species trees than using bootstrap replicates, either as one input (All BS) or using MLBS. The purpose of using bootstrap replicates is to take gene tree uncertainty (resulting from insufficient sequence length, for example) into account, but these results indicate that for this model condition, these two simple approaches do not improve species tree estimation. However, it is possible that other model conditions [perhaps smaller numbers of genes, as studied in Knowles et al. (2012)] or other ways of addressing gene tree uncertainty might show some advantage over the BestML approach. Therefore, we use bestML input trees in the remaining experiments.

Fig. 1.

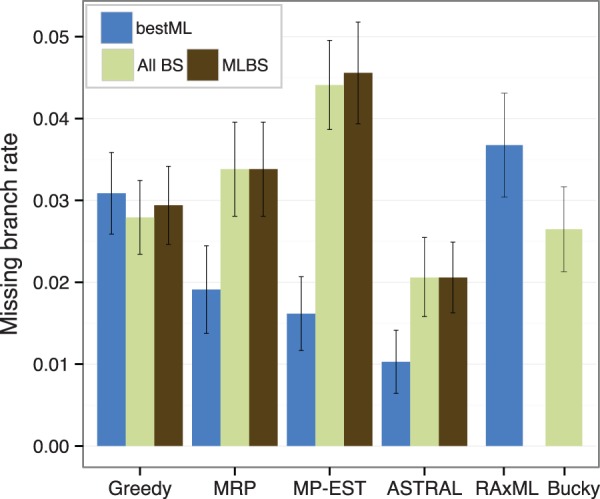
Species tree estimation error on the default mammalian datasets with 37 genes and 400 genes (half with 500 bp and half with 1000 bp and with 71% mean BS). We show the missing branch rates for estimated species trees computed using summary methods (MRP, MP-EST, greedy, BUCKy-pop and ASTRAL) as well as concatenation using RAxML. Results are shown for running summary methods on maximum likelihood gene trees (bestML) and on the set of all bootstrap replicates from all genes (All BS), as well as the greedy consensus of running summary methods on individual bootstrap replicates from all genes (MLBS). CA-ML is run on the true alignment. Average and standard error shown based on 20 replicates

For the mixed model condition and using bestML trees, ASTRAL is the most accurate of these methods, MP-EST the next most accurate, followed by the other summary methods, and finally by CA-ML. ASTRAL with any of the three sets of inputs is also more accurate than BUCKy-pop; however, differences between ASTRAL on All BS and BUCKy-pop are relatively small.

The next experiment explored variants of the basic mammalian simulation, exploring the impact of changes to the ILS level (by scaling the species tree branch lengths), number of genes and gene sequence length, on the absolute and relative performance of various methods using bestML input. ASTRAL was generally more accurate than all the other summary methods (Fig. 2). However, for a few cases, ASTRAL and one or more summary methods had similar accuracy; for example, on 800 true gene trees from default ILS levels, all summary methods (except for Greedy) produced the true species tree. Furthermore, ASTRAL was more accurate than CA-ML, except when the amount of ILS is low. The relative performance between ASTRAL and CA-ML depended on the amount of ILS, so that CA-ML was more accurate than ASTRAL under low levels of ILS, and otherwise ASTRAL was more accurate than CA-ML.

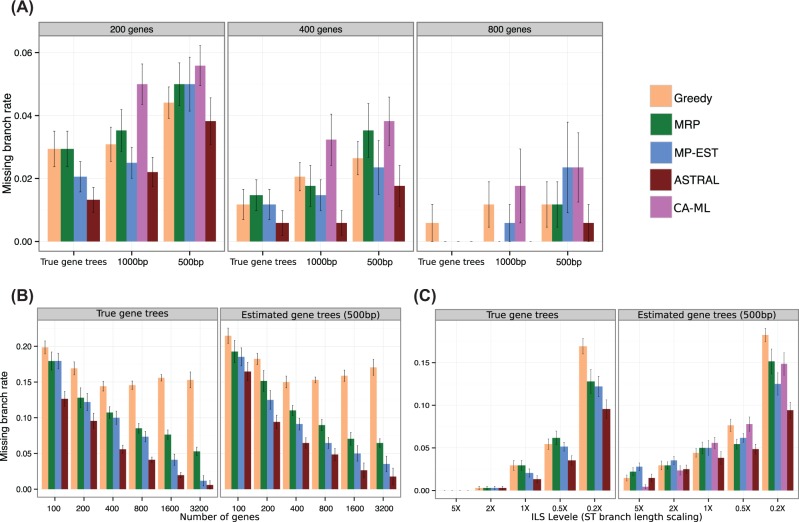
Fig. 2.

Species tree estimation error on the simulated mammalian datasets. We show the missing branch rates for estimated species trees computed using summary methods (MRP, MP-EST, greedy and ASTRAL) as well as CA-ML. Summary methods are run on RAxML bestML gene trees. We also show performance of summary methods on the true gene trees. Subfigure (A) shows results under default levels of ILS, varying the number of genes and gene tree resolution; (B) shows results under increased ILS levels, varying the number of genes, and on both true gene trees and estimated gene trees and (C) shows results on 200 genes, varying the amount of ILS from very low (5× species tree branch lengths) to very high (0.2× species tree branch lengths)

Some observed trends were expected: all summary methods gave improved accuracy as the sequence length in each gene increased from 500 to 1000 bp; using true gene trees gave the best results (Fig. 2a); species tree error rates generally reduced as the number of genes increased (Fig. 2b); and species tree error rates increased as ILS levels increased (Fig. 2c).

However, some other observed trends were surprising. For example, unlike the other methods, Greedy did not continue to improve with increased numbers of gene trees, but could be more accurate than many other summary methods (including MP-EST but not ASTRAL) when the number of gene trees and gene sequence lengths were both small (Fig. 2a). In addition, we observed that MRP, a simple supertree method that is not known to be statistically consistent, was in some cases more accurate than MP-EST. For example, while MP-EST was always at least as accurate as MRP on true gene trees or on estimated gene trees with high ILS, there were cases (Fig. 2a and c) where MRP was more accurate than MP-EST (although the differences are small).

Analyses with large numbers of species

We evaluated the feasibility of using ASTRAL on datasets with large numbers of taxa using the 100-taxon simulated datasets, with 25 genes and 10 replicates. Because there is no single outgroup, the estimated trees are not rooted, and so we could not use MP-EST. ASTRAL had no difficulty analysing these data (completing in <1 s). ASTRAL had average missing branch rate of 6.1%, better than MRP and Greedy (6.4%), but not as good as CA-ML (5.7%); differences are not statistically significant (P > 0.1; paired Wilcoxon test).

Results on biological datasets

Song et al. (2012) analysed a dataset with 447 genes across 37 mammalian species using MP-EST. Two of the questions of greatest interest were the placement of bats (Chiroptera) and tree shrew (Scandentia), where their MP-EST analysis differed from the concatenated analyses they performed.

In our analysis of this dataset, we noted the distance of estimated gene trees to other gene trees; this produced a distribution with two clear outliers (see Supplementary Materials). We also identified 21 genes with mislabelled sequences [easily confused taxon names, subsequently confirmed by the authors of Song et al. (2012)]. We removed all 23 outliers from the dataset, and reanalysed the reduced dataset.

We used a multi-locus bootstrapping procedure with 100 replicates, with both site and gene resampling, to be consistent with Song et al. (2012). We re-estimated the gene trees using RAxML on the gene sequence alignments produced by Song et al. (2012). We recomputed the MP-EST tree, obtaining a tree topologically identical to the MP-EST tree reported in Song et al. (2012), but with lower bootstrap for the placement of Scandentia (62% in our analysis). CA-ML analyses of the full and reduced datasets were topologically identical and had similar branch support. Thus, the CA-ML and MP-EST trees on the reduced dataset still differed in the placement of both Scandentia and Chiroptera.

We compare ASTRAL to MP-EST in Figure 3. Both ASTRAL and MP-EST trees placed Chiroptera as the sister to all other Laurasiatheria except Eulipotyphyla, whereas CA-ML placed Chiroptera as the sister to Cetartiodactyla. The ASTRAL tree placed Scandentia as sister to Glires with 74% support and thus agrees with the CA-ML tree but differs from the MP-EST tree.

Fig. 3.

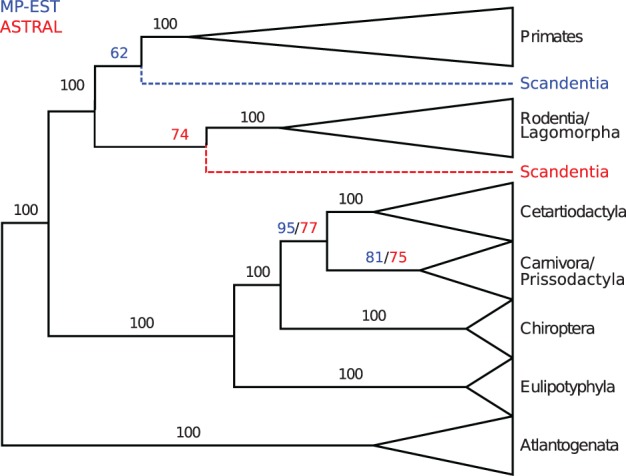
Analysis of the Song et al. mammals dataset using ASTRAL and MP-EST. We show the result of applying ASTRAL and MP-EST to 424 gene trees on 37-taxon mammalian species. MP-EST is based on rooted gene trees; ASTRAL is based on unrooted gene trees, and then rooted at the branch leading to the outgroup. Branch support values in black are for both methods, those in red are for ASTRAL and values in blue are for MP-EST. See Supplementary Materials for trees with full resolution

Plant dataset

We analysed a plant dataset from Zhong et al. (2013) of 32 species and 184 genes using ASTRAL, adding bipartitions to $\mathcal{X}$ (see Supplementary Materials). The question of greatest interest is the sister group to land plants. Previous analyses have inferred many different possible sister clades, including the following four major hypotheses: Zygnematales, Coleochaetales, Zygnematales + Coleochaetales and Charales. Zhong et al. (2013) used MP-EST to analyse their data and inferred Zygnematales as the sister with 64% BS. A reanalysis of the same data using STAR was performed by Springer and Gatesy (2014), who obtained Zygnematales + Coleochaetales with 44% BS.

We analysed this dataset using ASTRAL and obtained a tree that generally has high BS on the branches (i.e. with the exception of four branches, all branches have support at least 86%, and most have 100% support). However, one edge had low support (only 18%). After collapsing the single branch with low support, we obtained a tree (see Supplementary Materials) in which the Charales + land plants hypothesis is rejected with moderately high support (86%); however, it is not determined whether Zygnematales, Coleochaetales or Zygnematales + Coleochaetales are the sister group to land plants (the branch that distinguishes between these three hypotheses is the one with 18% support). Thus, ASTRAL’s analysis of this dataset can be seen as suggesting that this dataset is insufficient to completely resolve the sister relationship to land plants. However, the most interesting question is whether Charales are sister to land plants, and the ASTRAL tree rejects that hypothesis with 86% support.

Amniota dataset

Chiari et al. (2012) assembled a dataset of Amniota to resolve the position of turtles relative to birds and crocodiles. Most recent studies favour an Archosaurus hypotheses that unites birds and crocodiles as sister groups (Hugall et al., 2007). The MP-EST analyses by Chiari et al. (2012) resolved this relationship differently when AA and DNA gene trees were used; thus, AA had 99% support for the Archosaurus clade, but DNA rejected Archosaurus with 90% support. We analysed the same dataset using the exact version of ASTRAL and found that both AA and DNA recover Archosaurus; however, while ASTRAL on AA gene trees recovered Archosaurus with 100% support, ASTRAL on DNA gene trees had only 55% support for Archosaurus.

Running time

Comparisons between coalescent-based methods reveal substantial differences in running time. For example, on the mammalian dataset from Song et al. (2012) with 37 taxa and 421 genes, MP-EST (run with 10 random starting points) used 83 min per bootstrap replicate, while ASTRAL used 7 s. Analyses of the simulated mammalian datasets allow us to explore the limits of BUCKy-pop, as well as obtain other comparisons. We examine running times under moderate ILS, gene sequences of length 500 bp, and with 400 and 800 genes and with bestML input trees (except for BUCKy-pop).

BUCKy-pop strictly runs in serial, using a Bayesian Markov Chain Monte Carlo (MCMC) technique, which can take a long time and substantial memory to reach convergence. On the 37-taxon mammalian simulated datasets, BUCKy-pop ran to completion for datasets with up to 400 genes (where it took ∼5 h), but failed to complete (due to memory issues) on the 800-gene dataset.

MP-EST completed relatively quickly—∼100 min—for both the 400-gene and 800-gene datasets. We ran MP-EST with 10 random starting points, so this time could be reduced by using just one starting point, but with a potential decrease in accuracy.

ASTRAL completed in 3.3 s on the 400-gene dataset and in 5.3 s on the 800-gene dataset. Thus, ASTRAL is dramatically faster than the other methods and able to run on these phylogenomic datasets in reasonable time frames. However, BUCKy is used with 200 bootstrapped gene trees for each gene and outputs support values. Running ASTRAL and MP-EST using MLBS to obtain support values would increase their running times if run in serial, but ASTRAL would still be much faster than BUCKy (e.g. 11 min on the 400-gene dataset rather than 5 h). In addition, parallelizing MLBS is trivial because each bootstrap replicate is independent. See Supplementary Materials for more information about running times under different model conditions.

5 DISCUSSION AND CONCLUSIONS

This study introduced ASTRAL, a method for estimating species trees from unrooted gene trees. We proved that ASTRAL is statistically consistent under the multi-species coalescent model. In our study, ASTRAL was more accurate than MP-EST and BUCKy-pop, two leading coalescent-based methods, and improved or matched the accuracy of CA-ML under many conditions, except when the amount of ILS was low, where concatenation was more accurate. Results on the biological datasets show that statistically consistent coalescent-based methods can differ in terms of support for established clades, and produce different resolutions of biologically interesting relationships.

The differences in performance are the result of different algorithmic techniques, which can result in greater or lesser robustness to missing data (Springer and Gatesy, 2014) and gene tree estimation error (Bayzid and Warnow, 2013). Hence, the choice of coalescent-based method matters. This study also showed that concatenation can be more accurate than coalescent-based estimation, provided that the amount of ILS is low enough. However, the best coalescent-based methods can be more accurate than concatenation under biologically realistic conditions.

This study suggests the possibility that some of the observed discrepancies between previous coalescent-based analyses and concatenation in previous studies (Springer and Gatesy, 2014) might be the result of the choice of coalescent-based method, and that improved coalescent-based analyses might not only help to identify alternate relationships but might also confirm prior hypotheses produced using concatenation.

The algorithmic design of ASTRAL can be improved. When run in default mode, ASTRAL’s accuracy is limited by the bipartitions in the input gene trees. Including estimated species trees in $\mathcal{X}$ enlarges the search space and allows ASTRAL to produce highly accurate species trees, but other less ad hoc approaches for expanding $\mathcal{X}$ should also be developed. The running time we have given is polynomial and fast enough to run on genome-scale datasets, but improved algorithmic designs with better asymptotic performance could also be developed.

Using bootstrap replicate gene trees instead of best ML gene trees did not improve species tree estimation accuracy on the simulated mixed mammalian dataset—and in fact made species tree estimations less accurate for MRP, MP-EST and ASTRAL. This suggests the possibility that the topological error in bootstrap gene trees is large enough to offset any improvement in species tree estimation obtained by taking gene tree uncertainty into account. However, it is possible that an improvement might be obtained under other conditions, or that using a sample of gene trees estimated by a Bayesian MCMC analysis might be better-suited to coalescent-based species tree estimation methods than maximum likelihood bootstrap trees, as suggested by DeGiorgio and Degnan (2014) [although see Yang and Warnow (2011)]. Knowles et al. (2012) found varying impact in species tree topology estimation through taking gene tree estimation error into account, but only examined small numbers of species and genes; thus, to some extent, the results we obtained might be because of the large number of genes and perhaps species in our studies.

In summary, advances in algorithmic strategies for coalescent-based estimation can enable highly accurate species tree estimation in the presence of massive ILS. ASTRAL provides one such advance, but new and more accurate coalescent-based methods are needed to enable these analyses, especially for genome-scale datasets where missing data and extremely low phylogenetic signal in individual genes may be a substantial problem.