Fast randomization of large genomic datasets while preserving alteration counts

Abstract

Motivation: Studying combinatorial patterns in cancer genomic datasets has recently emerged as a tool for identifying novel cancer driver networks. Approaches have been devised to quantify, for example, the tendency of a set of genes to be mutated in a ‘mutually exclusive’ manner. The significance of the proposed metrics is usually evaluated by computing P-values under appropriate null models. To this end, a Monte Carlo method (the switching-algorithm) is used to sample simulated datasets under a null model that preserves patient- and gene-wise mutation rates. In this method, a genomic dataset is represented as a bipartite network, to which Markov chain updates (switching-steps) are applied. These steps modify the network topology, and a minimal number of them must be executed to draw simulated datasets independently under the null model. This number has previously been deducted empirically to be a linear function of the total number of variants, making this process computationally expensive.

Results: We present a novel approximate lower bound for the number of switching-steps, derived analytically. Additionally, we have developed the R package BiRewire, including new efficient implementations of the switching-algorithm. We illustrate the performances of BiRewire by applying it to large real cancer genomics datasets. We report vast reductions in time requirement, with respect to existing implementations/bounds and equivalent P-value computations. Thus, we propose BiRewire to study statistical properties in genomic datasets, and other data that can be modeled as bipartite networks.

Availability and implementation: BiRewire is available on BioConductor at http://www.bioconductor.org/packages/2.13/bioc/html/BiRewire.html

Contact: iorio@ebi.ac.uk

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

In the past few years, next-generation sequencing (NGS) technologies have progressed swiftly, and currently hundreds of genomes can be simultaneously sequenced in a matter of weeks, at more affordable costs. This opens a wide range of new avenues in biological and biomedical research. In particular, because of the established impact of the genomic background on disease progression and response to drug treatment, cancer research has significantly benefited from these advances. Comprehensive catalogues of mutations in multiple cancer types have been assembled and fruitfully used to identify new diagnostic, prognostic and therapeutic targets (Barretina et al., 2012; Garnett et al., 2012; ICGC et al., 2010; TCGA et al., 2008). Existing large-scale projects, such as the Cancer Genome Atlas (TCGA; TCGA et al., 2008), the International Cancer Genome Consortium data portal (ICGC et al., 2010) and, recently, the Genomics of Drug Sensitivity in Cancer (Garnett et al., 2012) and the Cancer Cell Line Encyclopedia (Barretina et al., 2012), provide invaluable opportunities to explore molecular alterations that could potentially play a crucial role in a plethora of different cancer types and their response to therapy (Stratton et al., 2009).

A key task in these projects is to distinguish between driver mutations (i.e. those conferring selective clonal growth advantage) and functionally neutral passenger mutations (which do not contribute to tumour development) (Bignell et al., 2010; Greenman et al., 2007). Once key driver mutated genes are identified, a fruitful analysis is to consider them in the context of the pathways where they operate. This allows the identification of cancer driver biological networks, whose altered functionality results in the acquisition of a cancer hallmark (Hanahan and Weinberg, 2011; Vogelstein et al., 2013). One of the ideas exploited to identify these networks is based on the assumption that sets of mutations exhibiting statistically significant levels of mutual exclusivity (ME) are likely to alter genes involved in a common biological process that drives cancer development. It has been noted that driver mutations in cancer occur in a limited number of pathways and driver lesions in the same pathway do not tend to occur in the same patient (Yeang et al., 2008). A possible biological explanation is that if a crucial node is altered in an oncogenic pathway, a secondary mutation on the same pathway is unlikely to provide further selective advantage to the cancer cell, thus it does not tend to be selected during somatic evolution. Hence, sets of mutations exhibiting statistically significant levels of ME are likely to alter genes involved in a common biological process that drives cancer development. On the other hand, mutations of genes participating in different biological pathways may exert a synergistic effect in conferring growth advantages to tumour cells. Therefore, investigations have been devoted to searching for groups of genes that are simultaneously mutated more often than expected by random chance (Thomas et al., 2007; Uren et al., 2008).

Based on these premises, the emergence of combinatorial properties among patterns of genomic events has been investigated in a number of recent studies, through the application of novel statistical measures quantifying, for example, the ‘mutual exclusivity’ or the ‘co-occurrence’ of different genomic lesions (Ciriello et al., 2012; Cui, 2010; Gu et al., 2010; Miller et al., 2011; Vandin et al., 2012; Yeang et al., 2008). Among these studies, those aimed at identifying groups of genes whose mutation patterns tend to ME are based on the same principle and are conceptually similar (Ciriello et al., 2012; Miller et al., 2011; Vandin et al., 2012), although they differ in two crucial methodological aspects:

1. The way sets of genes to be tested for ME are selected.

2. The way ME of a gene set is assessed and its statistical significance is quantified.

In (Ciriello et al., 2012), for example, the authors designed MEMo, a computational framework in which gene sets to be tested for ME are derived from cliques (i.e. groups of genes with complete pair-wise connectivity) identified in functional networks, assembled from publicly available signalling and pathway maps. For the statistical assessment of ME, a variety of strategies have been followed. Vandin et al. (2012) perform a significance test simulating a null model by independently permuting the mutations of each gene across patients, thus preserving the mutation frequency gene-wise (but not sample-wise). In (Miller et al., 2011), authors make use of tools from coding theory, and the ME significance for a set of genes is computed algorithmically. In contrast to these two methods, MEMo quantifies the sample coverage (SC) of a set of genes in terms of the number of samples in which at least one of them is mutated. Then the ME of the gene set under consideration is computed as the divergence of its SC from expectation. To evaluate the statistical significance of this ME measure, P-values are computed under an appropriate null model. This can be achieved by randomly permuting the analysed dataset, while preserving the overall distribution of observed alterations across both genes and samples. This is crucial to preserve tumour specific alterations, heterogeneity in mutation/copy-number alteration rates across patients and to let the SC significance be proportional to the gene set ME. To generate this null model, the authors make use of a permutation strategy based on a random network generation model referred to as the switching-algorithm (Milo et al., 2003). First the relevant information in the data is represented as a binary event matrix (BEM) (Fig. 1A): a ‘0–1 table’ in which the generic entry $w_{(i,j)}$ is equal to 1 if in the i-th sample, the j-th gene is altered (by a non-synonymous somatic mutation, a homozygous deletion or an amplification), and is equal to 0 otherwise.

Fig. 1.

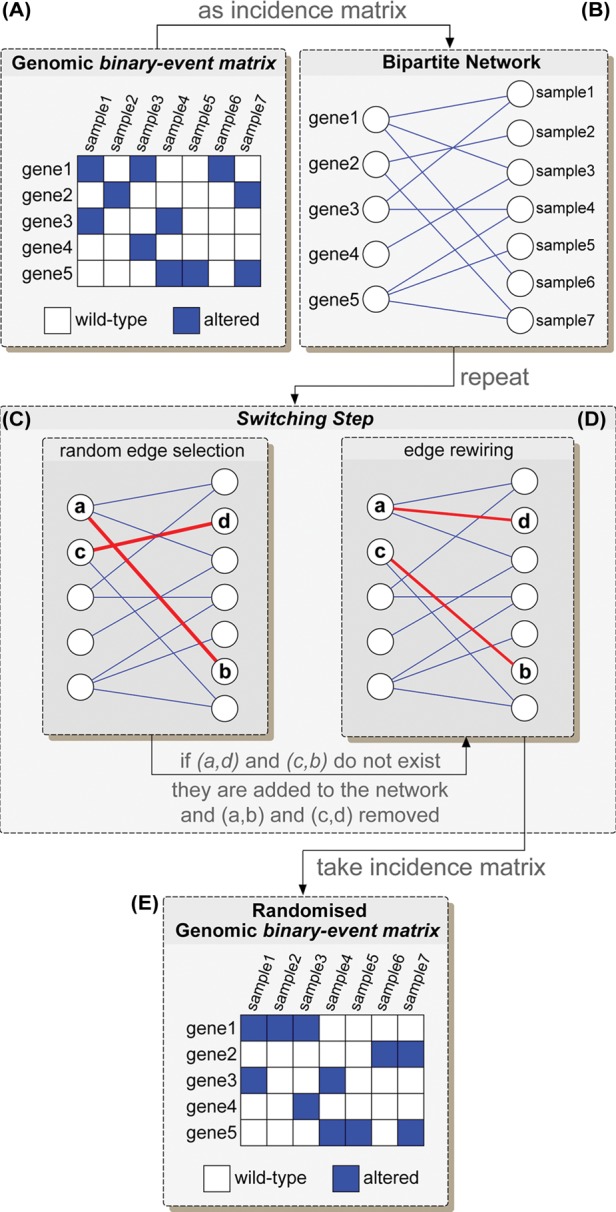
BEM randomization through the switching-algorithm. A bipartite graph (B) is derived from the initial BEM by considering it as a graph incidence matrix (A). A sequence of switching-steps (C and D) is performed. In each of these steps, two edges (a,b) and (c,d) are randomly chosen (C) and, if the edges (a,d) and (c,b) do not exist yet, they are added to the network, while (a,b) and (c,d) removed (D). A rewired version of the BEM is derived by considering the incidence matrix of the resulting network after a sufficiently long sequence of switching-steps (E)

The uniform distribution on the set of 0–1 tables with fixed marginal totals (i.e. with prescribed row-wise and column-wise sums) is used as a null model in various contexts (Besag and Clifford, 1989; Ponocny, 2001; Rasch, 1993). In ecological research 0–1 tables, called ‘presence–absence’ matrices (PAMs) (Miklós and Podani, 2004) are randomized to evaluate the deviation of observed phenomena, such as the co-occurrence of different species in the same habitat, from random expectations (Connor and Simberloff, 1979; Gotelli, 2000; Wilson, 1987). Several algorithms exist to generate constrained and non-constrained null models depending on which basic features of the PAM are retained in the computations (Gotelli, 2000; Gotelli and Entsminger, 2001). Nevertheless, the randomization of moderately large matrices in a short space of time is still challenging.

Ciriello et al. took advantage of tools from graph theory by considering a BEM as the incidence matrix of a bipartite graph (Gross and Yellen, 2006) (Fig. 1B). Then, they adapted the switching-algorithm for network randomization with node degree preservation to the problem of randomizing a BEM while preserving its row- and column-wise sums (Milo et al., 2003). If a BEM derived from a genomic dataset is considered as the incidence matrix of a bipartite network G, then nodes in the first set of G correspond to genes, and those in the second set correspond to samples. Additionally, a node i in the first set is connected to a node j in the second set if the gene mapped by node i is altered in the sample mapped by node j (Fig. 1A and B). Defining the degree of a node as the number of its incident links, row-wise sums of the BEM will correspond to degrees of the nodes in the first set, whereas column-wise sums of the BEM will correspond to degrees of the nodes in the second set. The problem of randomizing a BEM while preserving its row- and column-wise sums can then be reduced to the problem of shuffling the links in the corresponding network G while preserving its node degrees, or ‘network rewiring’, with the additional constraint that the shuffling should preserve bipartiteness (i.e. nodes in the same subset should never be connected). Based on these premises, in MEMo (Ciriello et al., 2012), randomized versions of a BEM are generated by adapting the switching-algorithm to bipartite networks. This method proceeds through a series of Monte Carlo switching-steps to produce rewired networks, starting from the original one, and preserving its degree distribution, as summarized in Figure 1. For the Markov chain underlying this algorithm to ‘forget’ the initial network (thus to minimize the initial bias), a sufficiently large number of switching-steps should be performed.

The presence of trends in the time series of network metrics along the sample path of a Markov chain simulation is evidence that the chain has not yet reached its stationary distribution (Ray et al., 2012) (the required uniform distribution). If the Markov chain has a slow mixing time (Stanton and Pinar, 2012), then the number of iterations required to reach (approximate) stationarity (the so-called burn-in time) may be very long. In (Milo et al., 2003), the authors propose on empirical grounds that 100 times the number of existing links ($\left|E\right|$) is an adequate burn-in time, and this lower bound is generally used. In what follows, we will refer to this bound as the ‘empirical bound’ (N′). The desired number of random networks needed to compute empirical P-values should then be multiplied by this number to obtain an estimation of the total time requirements. When dealing with a large number of tests (as are often required in the identification of cancer network drivers, where the number of gene sets to test is potentially very large), to achieve significance after multiple hypothesis test correction, the number of random networks to be generated (hence of switching-algorithm runs) could be in the order of hundreds of thousands. Consequently, the amount of time required to accomplish this task could be very high. This would make routine analyses practical only on server clusters. Here we propose a novel, analytically derived, approximate lower bound to the number of switching-steps required by the switching-algorithm to generate randomized versions of a BEM, preserving genomic event distributions both across samples and genes. Finally, we have implemented BiRewire, an R package (Ihaka and Gentleman, 1996) allowing users

1. to study and visualize trends in metrics over different numbers of switching-steps for a given BEM;

2. to determine the minimum number of switching-steps required to reach the approximate stationary distribution (here the uniform distribution on the set of allowed BEMs);

3. to generate randomized BEMs using the switching-algorithm with the number of switching-steps set to either this lower bound or a user-defined one.

We illustrate the application of BiRewire with examples where the BEMs are derived from real datasets from the TCGA (TCGA et al., 2008) and other studies, after the applications of state-of-the-art filters for the identification of somatic mutations affecting protein function and cancer-specific driver genes. Finally, we compare the obtained execution times and P-value computations with those obtained with different implementations of the switching-algorithm and different bounds.

2 METHODS

We analytically derived an approximate lower bound for the number of switching-steps to be performed by the switching-algorithm, when applied to a bipartite network $G=(V,E)$ (where V is the set of vertices and E the set of links, with $V=\{V_r,V_c\}$). This bound is equal to

$$N=\frac{\left|E\right|}{2(1-d)}\ln (1-d)\left|E\right|$$ (1)

where d is the edge density of the original network, defined as the ratio between $\left|E\right|$ and the number of edges of a fully connected bipartite graph with the same number of nodes in the two classes: $d=\left|E\right|/(\left|V_r\right|\times \left|V_c\right|)$. With respect to the empirical bound proposed in (Milo et al., 2003) (i.e. $N\prime =100\left|E\right|$), our bound can be expressed as

$$N=\frac{N\prime }{200(1-d)}\ln \frac{(1-d)N\prime }{100}$$ (2)

at least for bipartite graphs.

In what follows, we will denote with $G^{(k)}$ a rewired version of the bipartite network G obtained with the switching-algorithm through k switching-steps. We assume intuitively that $G^{(k)}$ is a rewired version of G if

1. The average similarity between G and its rewired version $G^{(k)}$ tends to remain constant when k is further increased (i.e. performing additional switching-steps does not make $G^{(k)}$ more different from G, on average);

2. The average similarity between G and $G^{(k)}$ is sufficiently close to the expected similarity between any pair of random bipartite networks with the same size, edge density and node degrees of G (i.e. between any pair of rewired versions of G).

The first condition above is often used when monitoring convergence of the sampler, where trends within chains are studied to quantify the ‘forgetting’ of the initial state (Brooks and Gelman, 1998). Taken together, the two conditions are necessary and sufficient to claim that after k switching-steps the initialization bias of the underlying Markov chain reaches a minimum. When they are verified, performing additional switching-steps does not make $G^{(k)}$ any more different from G, on average. The second property guarantees that G and $G^{(k)}$ are indistinguishable from any pair of networks sampled independently from the null distribution. As a consequence, $G^{(k)}$ can be considered as an approximate observation drawn from the uniform distribution of all the possible bipartite networks with the same number of nodes, links and degrees as G. By running the switching-algorithm on bipartite networks of different sizes and edge densities, we first verified that after a specified number k of switching-steps, which is much lower than N′, Conditions 1 and 2 are met. Then, we went on to empirically verify that the fulfilment of our convergence criteria provides a good estimation of the autocorrelation time (Stanton and Pinar, 2012): a standard tool for estimating the convergence of a Markov chain to its stationary distribution (Sokal, 1989). Finally, we present a novel approximate lower bound N (which was derived analytically) for the number of switching-steps k at which our two conditions hold. We show that after N switching steps the distribution of the Jaccard index (JI; a measure of similarity) between $G^{(k)}$ and G reaches the same steady state as is reached at N′, at least on the tested networks. These networks were chosen to have topological features make their incidence matrix comparable with a BEM derived from a typical large-scale NGS dataset. These results were obtained using an efficient implementation of the switching-algorithm, detailed in the Supplementary Materials, and the R package igraph (Csardi and Nepusz, 2006).

3 RESULTS

3.1 Randomness convergence across switching step

Based on the same premises of the output-based method proposed in (Johnson, 1996), to show that after a specified number of k switching-steps the average similarity between G and $G^{(k)}$ converges (i.e. it tends to remain constant even if applying additional switching-steps), we generated several random bipartite networks containing a total number of $n_c\times n_r=20,000$ nodes (with $n_c=\left|V_c\right|$ and $n_r=\left|V_r\right|$), a fixed edge density equal to 15% (3000 edges) and different levels of squareness (i.e. $n_c/n_r$ ratio). By adopting an experimental setting similar to that described in (Stanton and Pinar, 2012), for a given level of squareness, each of the corresponding networks G was then given as input to 50 different instances of the switching-algorithm, each performing $N\prime =100\times 3000=3\times {10}^5$ switching-steps. The output of each of these instances was then sampled every 100 switching-steps and collected, at the j-th sample time, into a set of rewired networks $R_j=\left\{G^{(100j),i}\right\}$ with $i=1,\dots ,50$ and $j=1,\dots ,100$. Finally, at each sample time j, the average similarity between each rewired network in R_j and the original network was computed (to verify Condition 1), as well as the average pair-wise similarity between each pair of networks in R_j (to verify Condition 2). To quantify the extent of similarity between two networks, the Jaccard Index (JI) (Jaccard, 1901) between their incidence matrices was computed. If we denote with B the incidence matrix of the network G and with B^k the incidence matrix of its rewired version $G^{(k)}$, then it can be easily verified that the JI between G and $G^{(k)}$ is equal to

$$JI(G,G^{(k)})=\frac{x^{(k)}}{2\left|E\right|-x^{(k)}}$$ (3)

where $\left|E\right|$ is the number of links contained in G (equal to that of $G^{(k)}$) and $x^{(k)}={\sum }_{i,j}{B}_{i,j}{B}_{i,j}^k$, is the bitwise sum of the Hadamard product between the two matrices (i.e. the number of ones in common between them, hence the number of common links across the two networks). Results of this simulation are depicted in Supplementary Figure S1A. After an adequate number of switching-steps (which is much lower than N′), both the average similarity between the rewired networks and the initial networks (indicated by the blue curves) and the average pair-wise similarity computed between each pair of rewired networks (red curves) plateau at the same level (consistently with Conditions 1 and 2). These results suggest that the true lower bound for the number of switching-steps required by the switching-algorithm to rewire bipartite networks, providing them with the maximal level of randomness, is much lower than N′. For reference, we include in Supplementary Figure S1A the expected similarity between any pair of random bipartite networks with the same number of nodes and edges of G (green line in Supplementary Fig. S1A) but with possibly different node degrees, derived as detailed in the Supplementary Materials. This gives an indication of how much the distribution of networks under the null model differs from the distribution under the alternative model in which node degrees are not preserved. Results from a similar simulation but starting from bipartite networks containing $\left|V_r\right|=100$ and $\left|V_c\right|=200$ nodes and different levels of edge densities are shown in Supplementary Fig. S1B. Also in this case, after an adequate number of switching-steps (which is again much lower than N′), the average similarity between the rewired networks and the initial ones (indicated by the blue curves) reaches a plateau level that is equal to the one reached by the average pair-wise similarity computed between pairs of rewired networks (consistently with Conditions 1 and 2). A final empirical study showing that the fulfilment of our convergence criteria provides a good estimation of the autocorrelation time (Stanton and Pinar, 2012), hence of the mixing of the underlying Markov chain, is detailed in the Supplementary Materials and Supplementary Figure S2.

3.2 A novel lower bound to the number of switching-steps required to rewire bipartite networks

In this section, we summarize the derivation of a lower bound N to the number of switching-steps that the switching-algorithm should perform to rewire a bipartite network, as a function of its number of nodes and edges. The starting point of our proof is the definition of similarity between a bipartite network G and its rewired version $G^{(k)}$ (defined in the previous section) based on the JI:

$$s^{(k)}=\frac{x^{(k)}}{2\left|E\right|-x^{(k)}}$$ (4)

In the first part of our proof (provided as Supplementary Material), we formulate the mean-field equation (Barabási et al., 1999) for $x^{(k+1)}$ (see Lemma 1 of the proof) and consequently for Equation (4). Then from this mean-field equation, we derive a fixed point $\overline{x}$ and a convergence time N, in terms of the number of switching-steps k (Lemma 2). Finally, we show that the switching-algorithm can be used to approximate null models for G through a minimum number of N switching-steps (Lemma 3). The mean-field equation for $x^{(k+1)}$ is equal to

$$x^{(k+1)}={\displaystyle \sum _{i=1}^5{p}_i^{(k)}}{f}_i(x^{(k)})$$ (5)

where the functions $f(x^{(k)})$ represent five possible values of $x^{(k+1)}$ given $x^{(k)}$, depending on the switching step performing successfully or not, and $p_i^{(k)}$ are the probabilities associated with these values (see Propositions 1, 2, 3 in the proof). Specifying these probabilities allow the mean-field Equation (5) to be written as a second-order linear recursive sequence $x^{(k+1)}=(\left|E\right|+1)x^{(k)}-\left|E\right|x^{(k-1)}$ for which a closed form is provided in (Brousseau, 1971). This yields

$$x^{(k)}=m^k\left(\left|E\right|-\frac{q}{1-m}\right)+\frac{q}{1-m}$$ (6)

where m and q can be expressed as $m=\frac{(t\left|E\right|-2t+2\left|E\right|)}{\left|E\right|t}$, and $q=\frac{(2t\left|E\right|-2{\left|E\right|}^2)}{t^2}$, with $t=\left|V_r\right|\times \left|V_c\right|$ the number of possible edges preserving bipartiteness.

For a fixed ε, where $0<\epsilon \le 1$, we estimate N as the minimum value such that

$$\left|x^{(N)}-\overline{x}\right|<\epsilon \leftrightarrow N>{\log }_{m}g(z,\epsilon )$$ (7)

with $g(z,\epsilon )=\frac{\epsilon t}{t\left|E\right|-{\left|E\right|}^2}$, and $\overline{x}$ is the fixed point of the recursion in Equation (6).

As shown in our proof (Proposition 4), for the purpose of finding a lower bound N (rather than the exact value of required switching-steps), we can take $\overline{x}={\left|E\right|}^2/t$ as the unique fixed point of 6, (Proposition 5 in the proof).

Fixing $\epsilon =1$, from the asymptotical equivalence ln (1 + x) ∼ ln x and Lemma 2 of the proof it follows that

$$N=\frac{\left|E\right|}{2(1-d)}\ln (1-d)\left|E\right|$$

where $\left|E\right|$ and d are defined as in the previous sections.

With a similar procedure, a mean-field equation can also be estimated for the similarity between any pair of networks $B^{(k)}$ and $C^{(k)}$ derived from the original network G through two different instances of the switching-algorithm, performing k switching-steps (Lemma 3 of the proof). Briefly, we derived a recursive sequence for $r^{(k)}=s(B^{(k)},C^{(k)})$. As shown in the proof (Proposition 6, 7) and similarly to Equation (6), this sequence can be expressed as a second-order linear sequence:

$$r^{(k)}=m^k\left(\left|E\right|-\frac{q}{1-m}\right)+\frac{q}{1-m}$$ (8)

but with parameters $m=\frac{(\left|E\right|-4)t^2-({\left|E\right|}^2-8\left|E\right|)t-4{\left|E\right|}^2}{\left|E\right|t^2-{\left|E\right|}^{2}t}$ and $q=-4\frac{(\left|E\right|t^2-2t{\left|E\right|}^2+{\left|E\right|}^3)}{\left|E\right|t^2-t^3}$. Comparing the two mean-field Equations (6) and (8), it follows that $r^{(k)}\le x^{(k)}$. This implies that the average similarity between any two rewired versions of a network G cannot be greater than the similarity between G and each of the two individual rewired versions. As a conclusion, our proof shows that our novel bound guarantees a maximal level of edge mixing, and that the similarity between any pair of rewired versions of a given network can not be greater than those between them and the original one.

Finally, we conducted an empirical study to show that after N switching steps, the initial bias of the Markov chain underlying the switching-algorithm, quantified by the residual similarity to the original network (i.e. $x^{(k)}$), is minimized at least as much as it is minimized after $N\prime =100\left|E\right|$ switching steps [i.e. the empirical bound proposed in (Milo et al., 2003)]—details are provided in the Supplementary Materials and Supplementary Figures S3 and S4. Taken together with our formal proof, and empirical study of equivalence between our convergence criteria and the auto-correlation time estimation criteria (detailed in the Supplementary Materials and Supplementary Fig. S2), these results suggest that N can be considered as a good ‘burn-in time’ (in terms of switching-steps) for the Markov chain underlying the switching-algorithm. As a consequence, N switching-steps are enough to simulate samples from the uniform distributions of all the possible bipartite networks with prescribed node degree, through individual consecutive executions of the switching-algorithm, with an approximation power equal to the one attainable when performing N′ switching-steps.

3.3 Time requirements and statistics comparison for different bounds and implementations on real datasets

We compared the performances of the switching-algorithm when applied to a real large cancer genomics dataset, in terms of execution time on a typical desktop computer, by using different software implementations and two user-defined numbers of required switching-steps: our novel lower bound N and the empirical one suggested in (Milo et al., 2003), N′. For the purpose of this comparison, we used breast cancer samples and their respective mutations downloaded from the TCGA (TCGA et al., 2008) data portal. A BEM (provided as Supplementary Dataset) was constructed from the deleterious somatic mutations derived from this dataset (as detailed in the Supplementary Materials), yielding 757 rows (i.e. samples), 9757 columns (i.e. genes), 19 758 non-null entries (i.e. variants), corresponding to an edge density equal to 0.27% in the corresponding bipartite network. For this dataset, the lower bound to the number of switching step computed with our method corresponds to N = 97 951, whereas the empirical one is $N\prime =1975800$ (Supplementary Fig. S5). Results, in terms of execution times required to generate 10 000 rewired versions of the resulting BEM through our implementation of the switching-algorithm, the rewire function of the igraph package (Csardi and Nepusz, 2006), the commsimulator function of vegan package (one of the most famous packages for ecology research) (Dixon, 2003) and two different numbers of required switching-steps (respectively, N and N′), are summarized in Table 1.

Table 1.

Performance comparisons in terms of execution time and residual bias across different algorithms and bounds

	BiRewire	igraph v0.6.1	igraph v0.6.5	vegan swap	vegan Patefield
(A) Execution time
N	53 min 20 s	5 h 58 s	43 days	154 days	5 h 21 min 29 s
			6 h 21 min	21 h 36 mina
			28 s
N′	9 h	47 days	2 years 145 days	8 years 114 days
	37 min 30 s	7 h 37 min 55 s	41 min 12 sa	22 h 53 min 20 sa
(B) Residual average Jaccard similarity
N	0.006716	0.907788	0.006744	0.006762a	0.006921
N′	0.006744	0.299971	0.006723a	0.006879a

Note: ^aEstimations.

In Table 1, we report also the residual average Jaccard similarity scores of the rewired networks with respect to the original one. First columns of the table refer to our optimized implementation of the switching-algorithm, while data in the second and the third ones refer to the rewire function, provided in two different versions of the igraph package (respectively, v0.6.1 and the latest v0.6.5) (Csardi and Nepusz, 2006). In the fourth column, we report time requirements of the commsimulator function contained in the vegan package (Dixon, 2003) when used with the ‘swap’ method parameter (i.e. the switching-algorithm). The rewire function contained in igraph v0.6.1 does not implement the switching-algorithm but proceeds through a series of rewiring steps (detailed in the Supplementary Materials) through a strategy that systematically biases the edge selection and requires, at each step, a local exploration of the network that is generally slower than storing and retrieving individual edges from an edge list (time complexity analysis provided in the Supplementary Materials). In the rewire function contained in the latest version of the igraph package (v0.6.5), authors implemented the switching-algorithm. As a consequence, for this version of the package, executing N switching-steps guarantees that the residual similarity reaches its plateau (as shown in the third column of Table 1). However, computational time requirements for this implementation (third column in Table 1) are vastly higher than the previous one, making this function practically unusable on large genomics datasets. A detailed analysis of its asymptotical time complexity (far from being trivial) has not been included yet in the documentation of the package. In Table 1, the performance scores marked with (a) have been estimated starting from the execution time requirements and the average residual similarities observed on limited number of samples of rewired versions of the original network. For reference, we also include in Table 1 the performances (in terms of time requirements and residual similarity to the original network) of the r2dtable function, included in the vegan package, to generate 10 000 random 0–1 tables with same marginal totals of our BEM. This function makes use of Patefields algorithm (Patefield, 1981). Also in this case, the time requirements were significantly higher ($\sim 1.92\times {10}^4$ s versus $\sim 3.2\times {10}^3$ s), and the residual similarity is comparable with the one obtained with our implementation of the switching-algorithm and our bound.

Finally, to investigate the consistency of ME significance when using null models generated with different number of switching steps, we analysed ME patterns for the protein affecting mutations of a colorectal cancer dataset assembled from the TCGA (TCGA et al., 2008) and other studies, as described in the Supplementary Material. This yielded a small BEM (provided as Supplementary Dataset) composed by 206 rows (i.e. samples), 78 columns (i.e. genes), 793 non-null entries (i.e. variants), corresponding to an edge density equal to 5% in the corresponding bipartite network. For this dataset, the lower bound to the number of switching step computed with our method corresponds to N = 2497, whereas the empirical one is $N\prime =79300$. We tested the ME significance (as described in the MEMo approach and in the previous sections) for all the possible 3003 gene pairs by using two different null models, simulated by generating 10 000 randomized version of the BEM through N and N′ switching steps, respectively. We observed an overall concordance of resulting coverage P-values across the two null models and a perfect match between the corresponding two sets of gene pairs with a significant ME (P < 0.05 and $fdr<20\%$ after Benjamini–Hochberg correction of the P-values for multiple hypothesis testing). Results for gene pair with coverage $>50\%$ are provided as Supplementary Data and Figure 2.

Fig. 2.

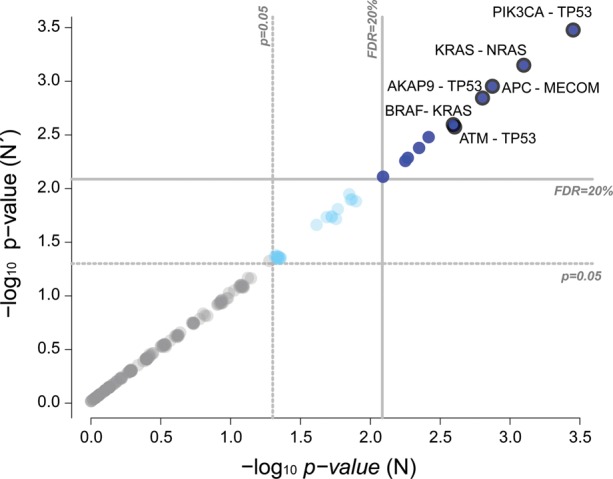
ME P-value comparisons. ME P-values for 237 gene pairs, whose coverage is $>50\%$ in the BEM derived from the colorectal cancer dataset. Positions on the two axes indicate $-{\log }_{10}$ P-values computed by using two different null models simulated by generating 10 000 randomized version of the original BEM, through the switching algorithm and different numbers of switching steps: our novel lower bound and the empirical one. An overall consistency of P-values can be observed and a set of 11 gene pairs has a significant level of ME (at a false discovery rate $<20\%$) on both the null models

3.4 The BiRewire package

We have developed R package BiRewire (available on Bioconductor; Gentleman et al., 2004), which provides high-performing routines for generating random bipartite graphs with prescribed node degrees (using the switching-algorithm), for the analysis of convergence diagnostics across switching-steps, and the estimation of the minimal number of steps according to the formula described in Equation (1). BiRewire is vastly faster than other existing implementations, not only because it uses our new lower bound but also because it implements an optimal version of the switching-algorithm, as detailed in the Supplementary Materials. Specifically, with BiRewire, users can (i) create bipartite graphs starting from genomic binary event matrices (or, generally, from any kind of PAMs), (ii) perform an analysis, which consists of studying the sample path (time series) of the JI across switching-steps (with user-defined sampling times), and estimating the lower bound to achieve convergence to the uniform distribution on the set of allowed bipartite networks, (iii) generate rewired versions of a bipartite graph with the analytically derived bound of switching-steps or a user-defined one and (iv) derive projections of the starting network and its rewired version and perform different graph-theory analysis on them. All the functions of the package are written in C and R-wrapped.

4 CONCLUSIONS

We presented a novel approximate lower bound for the minimal number of steps required by the switching-algorithm to simulate genomic datasets from relevant null models. This new lower bound was derived analytically, and it considerably reduces the computational time for estimating the significance of combinatorial metrics such as mutation mutual exclusivity and co-occurrence under these null models. We showed that this novel bound strongly reduces computational time requirements, when tested on a real dataset and a typical desktop computer architecture paired with the R package BiRewire (which we have developed). Our methods can be readily adapted to the computation of P-values under similar null models, which are appropriate for other kinds of data that can be modelled as a presence-absence matrix (hence, a bipartite network) preserving the ‘presence-distributions’ both across rows and columns. We believe that its applicability range covers different fields of computational biology and will grow in the future, as increasingly more data for which bipartite graphs provide a natural representation become available.