A logrank test-based method for sizing clinical trials with two co-primary time-to-event endpoints

Abstract

We discuss sample size determination for clinical trials evaluating the joint effects of an intervention on two potentially correlated co-primary time-to-event endpoints. For illustration, we consider the most common case, a comparison of two randomized groups, and use typical copula families to model the bivariate endpoints. A correlation structure of the bivariate logrank statistic is specified to account for the correlation among the endpoints, although the between-group comparison is performed using the univariate logrank statistic. We propose methods to calculate the required sample size to compare the two groups and evaluate the performance of the methods and the behavior of required sample sizes via simulation.

1. Introduction

In many clinical trials, two or more time-to-event endpoints may be investigated as co-primary, with the aim of providing a comprehensive picture of the intervention’s (treatment’s or preventative treatment’s) benefits and harms. For example, a major ongoing HIV treatment trial within the AIDS Clinical Trials Group, “A Phase III Comparative Study of Three Non-Nucleoside Reverse Transcriptase Inhibitor (NNRTI)-Sparing Antiretroviral Regimens for Treatment-Naïve HIV-1-Infected Volunteers (The ARDENT Study: Atazanavir, Raltegravir, or Darunavir with Emtricitabine/Tenofovir for Naïve Treatment)” is designed with two co-primary endpoints: time-to-virologic failure (efficacy endpoint) and time to discontinuation of randomized treatment due to toxicity (safety endpoint). Co-infection/comorbidity studies may utilize co-primary endpoints to evaluate multiple comorbities, e.g. a trial evaluating therapies to treat Kaposi’s sarcoma (KS) in HIV-infected individuals may have the time to KS progression and the time to HIV virologic failure, as co-primary endpoints. Other infectious disease trials may use time-to-clinical cure and time-to-microbiological cure as co-primary endpoints.

Trials that have more than one primary endpoint are generally designed under one of two alternatives, appropriately sizing the trial to: (1) demonstrate effects for all of the endpoints or (2) demonstrate effects for at least one endpoint. Recently, there have been several cases in which regulators have requested that sponsors design clinical trials with the objective of establishing favorable results on all endpoints in drug development (Offen and others, 2007). This problem of multiple co-primary endpoints is related to the intersection–union problem (Hung and Wang, 2009). We focus on the situation of (1) and discuss sample size calculation for a trial with time-to-event outcomes.

An important challenge is designing a trial with such multiple co-primary endpoints, as well as analyzing the data and interpreting the results. Hypothesis testing for all co-primary endpoints can be performed as usual, and adjustments to protect type I error is not necessary. However, the type II error increases as the number of co-primary endpoints increases. Trial design must account for this to control error rates.

Appropriate adjustments must also account for the potential correlation between the endpoints. Sample size calculations that take into account the correlations among continuous or binary co-primary endpoints have been studied, e.g. by Xiong and others (2005), Sozu and others (2006), Kordzakhia and others (2010), and Sozu and others (2010). We discuss the case of time-to-event outcomes, focusing on the discussion of the case where the number of co-primary endpoints is two, and the correlation between the endpoints is positive, as this is a common case in practice. We consider a two-arm parallel-group superiority trial designed to evaluate if an experimental intervention is superior to a standard.

To derive the sample size formula, we model the bivariate time-to-event endpoints with a given correlation structure using typical copula models. The logrank statistic is used to compare the two groups. We specify the correlation structure of the bivariate logrank statistic, consider the calculation of the variance–covariance (Section 2), and propose a method for calculating the sample size required to compare two groups with respect to two co-primary time-to-event endpoints (Section 3). We evaluate the performance of the method and the behavior of the required sample size via simulation, and provide a real example (Section 4). The method discussed here becomes simpler if one can assume that the time-to-event outcomes are exponentially distributed (see Hamasaki and others, 2012).

2. Bivariate survival data and test statistic

2.1. Setting and statistical hypothesis

Suppose that n participants are assigned randomly to two interventions composed of control (k=1) and test (k=2) groups and then they are followed up to evaluate bivariate survival times of two co-primary endpoints. Let 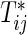and C_ij be the underlying continuous survival time and potential censoring time of the jth co-primary endpoint for the ith participant (j=1,2; i=1,…,n). Denote the marginal hazard function and its cumulative function for 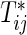in the group k by

where g_i is the group index k (2 if the ith participant belongs to the test, and 1 otherwise). A superiority trial of interest is designed to test the hypothesis

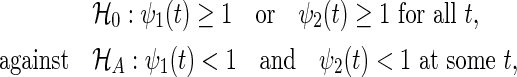(2.1)

where ψ_j(t) is the hazard ratio 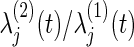between the two groups. In the trial, the bivariate survival data of 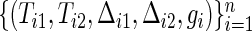are observed under the independent censoring condition, where 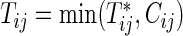and 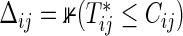( 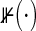is the index function). Generally, C_i1 and C_i2 may be correlated and have different marginal distributions. For example, in HIV clinical trials, if T_i1 is time to infant HIV infection and T_i2 is time to infant Hepatitis B infection, the subjects who do not experience the both events yet are censored at the same time (with C_i1=C_i2) in the end of follow-up period.

2.2. Dependence measures

Let 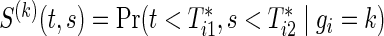and 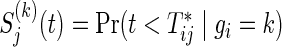, j=1,2, be the joint and marginal survival functions for 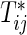in the group k, respectively. Although there are several measures for the dependence among bivariate time-to-event variables, throughout this paper we select the correlation between cumulative hazard variates (Hsu and Prentice, 1996),

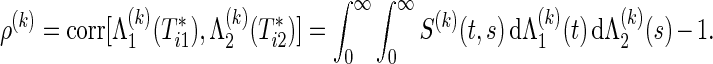(2.2)

If the marginals of the bivariate survival data are exponential, ρ^(k) is the same as the correlation coefficient of raw data 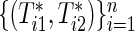because of 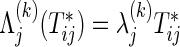. In the absence of censoring, ρ^(k) can be estimated by replacing the functions 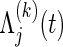, j=1,2, with the Nelson–Aalen estimators. Hsu and Prentice (1996) and Shih and Louis (1995) evaluate the estimation methods of ρ^(k) in the presence of arbitrary right censorship.

Let 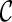be a function which generates the joint survival function S^(k)(t,s) from the two marginal 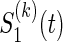and 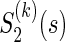, i.e.

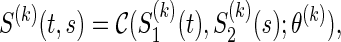where the association parameter θ^(k) included in 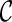is a one-to-one function of ρ^(k) (for the reason, θ^(k) is a scalar value) and characterize a level of dependence between 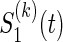and 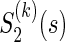. Then, we can calculate the correlation (2.2) by . In order to derive the required sample size to test the hypothesis (2.1), it may be prudent to model 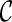which yields S^(k)(t,s). In this paper, we consider the three typical copulas: Clayton, Gumbel, and Frank models, which have different characteristics of bivariate dependence. For these details, see Section A of supplementary material available at Biostatistics online.

2.3. Bivariate logrank statistic and testing procedure

For testing (2.1), we consider the bivariate weighted logrank statistic processes

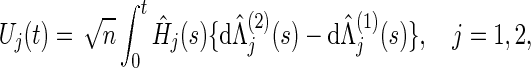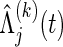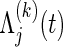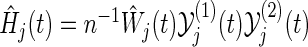
where, for the jth co-primary endpoint (j=1,2), is the Nelson–Aalen estimator of , , 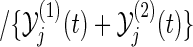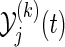is the at-risk process in the group k, i.e. and 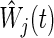is a weight factor (the logrank test uses 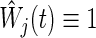). The analysis is performed using the fact that the standardized test statistics

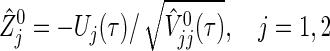are approximately distributed as standard normal N(0,1) under 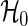, where τ is the maximum observed follow-up time and 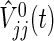is the well-known conditional variance of U_j(t) based on the hypergeometric distribution theory under 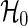. All notational details of 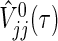and 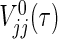, V ₁₂(τ) and μ_j(τ) that appear below are moved in Section B of supplementary material available at Biostatistics online. The testing procedure for (2.1) is

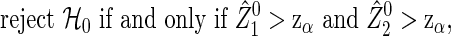(2.3)

for the type I error α, where z_α is the 100(1−α) percentile of N(0,1). Consider the statistical power of 1−β for the procedure (2.3). Because 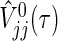includes some randomness based on data, it may be difficult to derive the sample size using 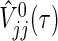. However, if the test statistic 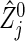can be replaced by 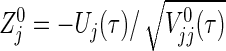, then we can obtain a simple power formula, where 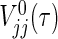is the limit form of 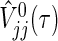. For sufficiently large n, 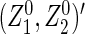is approximately bivariate normally distributed with mean vector 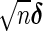and variance–covariance matrix `Σ (see Theorem 1 in Section B of supplementary material available at Biostatistics online), where

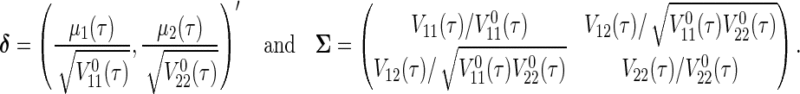Hence, the power is approximately obtained as

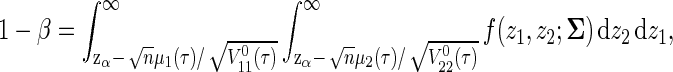(2.4)

where f(z₁,z₂;`Σ) is the bivariate normal density function with zero mean vector and covariance matrix `Σ. Therefore, the required sample size to achieve the desired power is obtained by the minimum n such that the right-hand side of (2.4) is not less than 1−β. In the remaining sections, we discuss how one can derive the required sample size from (2.4).

3. Sample size calculation

3.1. Calculations of mean vector and variance–covariance matrix of the statistic

The moment calculation of the bivariate logrank statistic is an important task in the derivation of the sample size required in the procedure (2.3). Limiting to 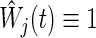(the logrank statistic is used for testing (2.1)), assume the same censoring stated in Section 2.1, i.e. C_i1=C_i2. For simplicity, we write , j=1,2, since the marginals of C_ij, j=1,2, are common. So, the joint survival function for the censoring variables is .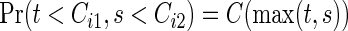

Generally, it is difficult to find analytic solutions for the integrals included in μ_j(τ), V _jj(τ), V ₁₂(τ), and 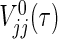, even if the marginals of 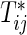are simple (e.g. exponential distribution). Hence, the numerical integration is needed for practical implementation of the calculations except when there is no censoring. Hereafter, τ is treated as a terminal time of the follow-up planned in advance.

Let t₀<t₁<t₂<⋯<t_M be a partition of the interval [0,τ], where t₀=0 and t_M=τ. For discretized functions applied to 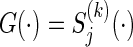, , 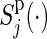, 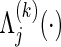C(⋅), and S^(k)(⋅,⋅) which appear hereafter, define the notation rules by

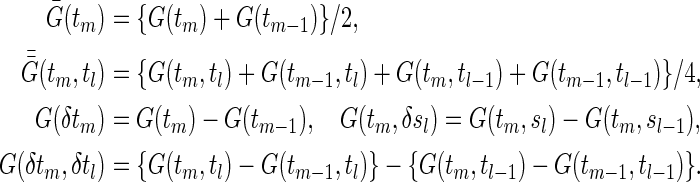(3.1)

Using a trapezoidal rule for numerical integration, under true parameters on 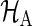, μ_j(τ), V _jj(τ) and V ₁₂(τ) accompanied by the logrank statistic can be approximated as

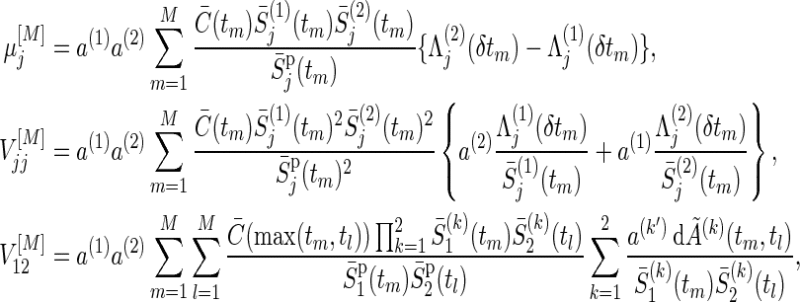respectively, where k′=3−k (k=1,2), 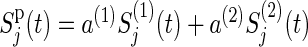, a^(k) is the ratio of participants assigned to the group k to the total number n of participants and

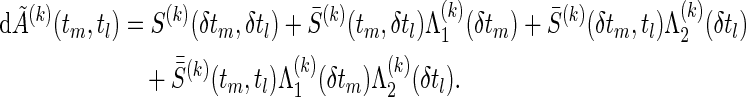Similarly, 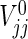, j=1,2, can be approximated by

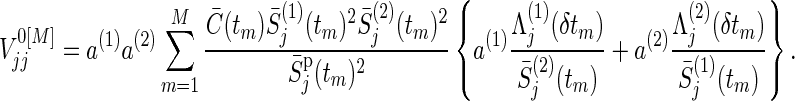Details for these derivations (including an extension to Simpson’s rule and numerical comparison) are provided in Sections C.1 and C.2 of supplementary material available at Biostatistics online.

3.2. Sample size formula for the total number of participants

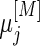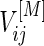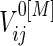Under a general censoring distribution, we provide a method to calculate the required total number of participants directly using the approximated mean and covariances, , and discussed in Section 3.1. For simplicity, we write

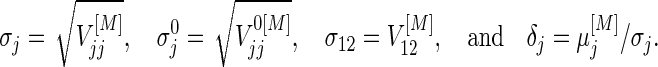The required sample size is the smallest n such that the left-hand side of (2.4) is not less than the targeted power. This procedure may be easily implemented, but the relationships between the required sample size with important factors, such as type I and II errors, effect sizes, and correlation, are not readily apparent. Alternatively, we can obtain the sample size formula for correlated co-primary endpoints via a manner similar to Sugimoto and others (2012). That is, the total number of participants to achieve the power (2.4) is

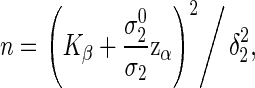(3.2)

where K_β is the solution of the integral equation

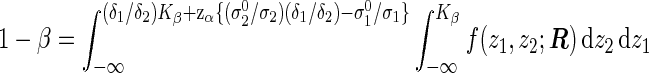(3.3)

and

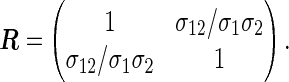Formula (3.2) can be commonly used because the numerical integration is still necessary for computing the correlation between the log-rank test statistics even in simple cases. The detailed derivation of (3.2), the algorithm to solve the integral equation (3.3), and the corresponding R implementation are provided in Sections C.3 and E of supplementary material available at Biostatistics online.

3.3. Additional considerations: on the number of events

We may consider the total sample size based on the number of events, as Freedman (1982)’s formula succeeded in univariate data. The required number of events is immediately obtained by applying the developed theory to the uncensored data. Here, unlike Section 3.2, suppose that ψ_j, j=1,2, are sufficiently close to 1, and let us rewrite

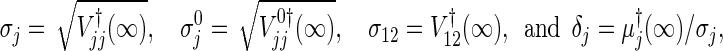where these elements (for the derivations and notations, see Section C.4 of supplementary material available at Biostatistics online) are simply given in

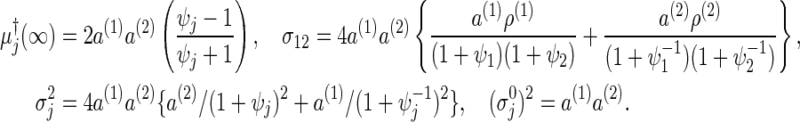Hence, similarly to (3.2), the required number of events to achieve the power 1−β is

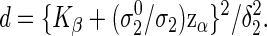(3.4)

Using simulation, we will be able to know that formula (3.4) for the number of events performs well, similarly to results in univariate data. However, we encounter difficulty when we recalculate the total sample size from (3.4). For example, consider the case of Table 1, of which the model is designed using ψ₁=ψ₂=1.5⁻¹, a⁽¹⁾=a⁽²⁾=0.5 and the same censoring distribution under ρ⁽¹⁾=ρ⁽²⁾=0.8. Being generated from the same marginals, the three models have the same marginal probabilities 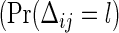, l=0,1) on observing the two co-primary endpoints. The required total sample sizes are calculated as n=672, 626, and 616 in the Clayton, Gumbel, and Frank copulas via (3.2), respectively (see Table 2, the third line from the bottom). The required number of events obtained from (3.4) are common d=230 in the three copulas. A main challenge in calculating the total size n from the number of events d is deciding how to weight the individuals for which one co-primary endpoint is uncensored and another is censored (such as Δ_i1=1 and Δ_i2=0). Supposing half of a unit to such an observation, we have, in the Clayton, Gumbel, and Frank copulas, 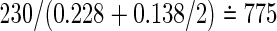, 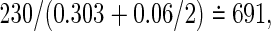and 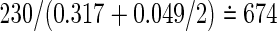, respectively. However, because these total sizes are quite larger than those from (3.2), sensitivity analyses to varying weights should be examined. We will consider this problem in future work.

Table 1.

Observed probability of two co-primary endpoints 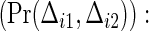an example when ρ⁽¹⁾=ρ⁽²⁾=0.8

		CPE1 (co-primary endpoint 1): Δi1
		Clayton copula			Gumbel copula			Frank copula
Probability of (Δi1,Δi2) (%)		1	0	Sum	1	0	Sum	1	0	Sum
CPE2: Δi2	1	22.8	13.8	36.6	30.3	6.26	36.6	31.7	4.94	36.6
	0	13.8	49.7	63.4	6.26	57.2	63.4	4.94	58.5	63.4
	Sum	36.6	63.4	100	36.6	63.4	100	36.6	63.4	100

Table 2.

Total numbers of required participants (n) calculated from (3.2) and the corresponding empirical powers 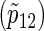under a⁽¹⁾=a⁽²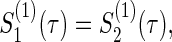⁾, and ρ⁽¹⁾=ρ⁽²⁾. n_ind is corresponding to n when ρ⁽¹⁾=ρ⁽²⁾=0.

				Clayton			Gumbel			Frank			Marginal
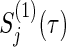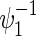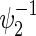			ρ(k)	nsim	n		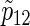nsim	n		nsim	n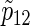
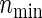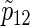0.1	1.2	1.2	0.0	1540	1544	80.1	1540	1544	80.1	1540	1544	80.1	1174	64.3
0.1	1.2	1.3	0.0	1215	1220	80.2	1215	1220	80.2	1215	1220	80.2	1174	78.6
0.1	1.2	1.5	0.0	1173	1174	80.1	1173	1174	80.1	1173	1174	80.1	1174	80.2
0.1	1.2	1.2	0.3	1511	1516	80.2	1498	1502	80.1	1494	1498	80.4	1174	66.9
0.1	1.2	1.3	0.3	1207	1210	80.3	1205	1206	80.1	1203	1206	80.2	1174	79.1
0.1	1.2	1.5	0.3	1173	1174	80.3	1174	1174	80.1	1173	1174	80.3	1174	80.2
0.1	1.2	1.2	0.5	1486	1488	80.2	1458	1462	80.2	1451	1452	80.2	1174	68.9
0.1	1.2	1.3	0.5	1199	1202	80.3	1195	1194	80.0	1190	1192	80.3	1174	79.5
0.1	1.2	1.5	0.5	1173	1174	80.3	1174	1174	80.1	1173	1174	80.3	1174	80.2
0.1	1.2	1.2	0.8	1409	1410	80.0	1371	1374	80.3	1336	1340	80.4	1174	73.0
0.1	1.2	1.3	0.8	1182	1184	80.4	1176	1178	80.2	1174	1176	80.2	1174	79.9
0.1	1.2	1.5	0.8	1173	1174	80.3	1174	1174	80.1	1173	1174	80.3	1174	80.2
0.1	1.5	1.5	0.0	328	334	81.1	328	334	81.1	328	334	81.1	253	65.2
0.1	1.5	1.6	0.0	290	296	81.1	290	296	81.1	290	296	81.1	253	72.8
0.1	1.5	1.8	0.0	259	264	80.8	259	264	80.8	259	264	80.8	253	79.1
0.1	1.5	1.5	0.3	322	328	81.0	319	324	80.9	318	324	81.0	253	67.6
0.1	1.5	1.6	0.3	286	292	81.0	283	288	81.1	283	288	81.0	253	74.5
0.1	1.5	1.8	0.3	257	262	80.9	257	262	81.0	256	262	81.1	253	79.6
0.1	1.5	1.5	0.5	317	322	80.9	311	316	80.8	310	314	80.9	253	69.5
0.1	1.5	1.6	0.5	281	286	80.8	276	282	81.0	275	280	80.8	253	75.8
0.1	1.5	1.8	0.5	255	260	80.8	253	258	80.7	253	258	80.8	253	80.0
0.1	1.5	1.5	0.8	302	306	80.7	293	298	81.0	284	290	81.0	253	73.5
0.1	1.5	1.6	0.8	270	274	80.7	264	268	80.9	257	262	80.7	253	78.4
0.1	1.5	1.8	0.8	252	256	80.7	251	254	80.7	250	254	80.8	253	80.5
0.5	1.2	1.2	0.0	3141	3144	80.2	3141	3144	80.2	3141	3144	80.2	2392	78.3
0.5	1.2	1.3	0.0	2487	2490	80.1	2487	2490	80.1	2487	2490	80.1	2392	80.1
0.5	1.2	1.5	0.0	2389	2394	80.2	2389	2394	80.2	2389	2394	80.2	2392	66.3
0.5	1.2	1.2	0.3	3113	3116	80.1	3049	3052	80.0	3060	3062	80.1	2392	74.7
0.5	1.2	1.3	0.3	2478	2480	80.1	2459	2458	79.9	2462	2462	80.1	2392	79.7
0.5	1.2	1.5	0.3	2393	2394	80.2	2395	2394	79.9	2393	2394	80.1	2392	71.8
0.5	1.2	1.2	0.5	3090	3092	80.1	2969	2972	80.0	2979	2978	79.9	2392	75.7
0.5	1.2	1.3	0.5	2472	2472	80.0	2432	2434	80.1	2436	2436	80.1	2392	79.9
0.5	1.2	1.5	0.5	2393	2394	80.1	2390	2392	80.0	2391	2392	80.2	2392	73.6
0.5	1.2	1.2	0.8	3009	3014	80.1	2811	2812	80.0	2755	2760	80.0	2392	77.5
0.5	1.2	1.3	0.8	2445	2446	80.0	2402	2402	80.0	2390	2398	80.2	2392	80.1
0.5	1.2	1.5	0.8	2391	2392	80.2	2392	2392	80.0	2391	2392	80.2	2392	69.5
0.5	1.5	1.5	0.0	692	700	80.7	692	700	80.7	692	700	80.7	532	64.6
0.5	1.5	1.6	0.0	614	622	80.5	614	622	80.5	614	622	80.5	532	72.0
0.5	1.5	1.8	0.0	550	558	80.7	550	558	80.7	550	558	80.7	532	78.4
0.5	1.5	1.5	0.3	687	694	80.7	672	680	80.7	675	682	80.7	532	66.7
0.5	1.5	1.6	0.3	612	618	80.6	602	606	80.6	601	608	80.5	532	73.4
0.5	1.5	1.8	0.3	549	556	80.5	543	550	80.7	544	550	80.7	532	78.9
0.5	1.5	1.5	0.5	681	688	80.5	653	662	80.6	660	664	80.8	532	68.3
0.5	1.5	1.6	0.5	608	614	80.6	585	592	80.5	587	594	80.6	532	74.5
0.5	1.5	1.8	0.5	547	554	80.5	537	544	80.5	539	544	80.4	532	79.2
0.5	1.5	1.5	0.8	665	672	80.5	619	626	80.4	613	616	80.4	532	71.7
0.5	1.5	1.6	0.8	594	600	80.4	560	566	80.5	556	558	80.3	532	76.9
0.5	1.5	1.8	0.8	541	548	80.5	531	536	80.7	529	534	80.2	532	79.9

4. Numerical studies

4.1. Performance comparison of the proposed formula with some practical solutions

For practicality, it is important to evaluate how formula (3.2) compares with alternative practical solutions (PSs) of simple approximations and simulation. A simple approach is to assume that the bivariate target power 1−β is approximated by p₁p₂ (PS_ind) of the independence or 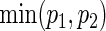(PS_min) of the marginal minimum, where each p_j is the univariate power corresponding to the endpoint j (=1,2). It is worth remarking that formula (3.2) under zero correlations (ρ⁽¹⁾=ρ⁽²⁾=0) yields the PS_ind, which is not so easily obtained if two effect sizes are different. Calculation of the sample size using simulation (PS_sim) is another alternative.

Monte-Carlo (MC) trials with 100 000 replications are performed to obtain empirical powers under the total sample size derived from (3.2), where M=500 for numerical integration. We generate bivariate survival data supposing that marginals of T_i1 and T_i2 are exponential, i.e. the marginal survival functions 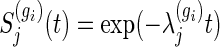, j=1,2. Details regarding the method of data generation are moved to Section A.3 of supplementary material available at Biostatistics online. We consider a clinical trial, where the censoring times are generated by C_ij=τ_aU(0,1)+τ_f, where τ_a and τ_f are the lengths of the entry period to the trial and follow-up period, respectively, and U(0,1) denotes a uniform random number on (0,1). That is, assuming that all participants do not drop out until total observable time τ=τ_a+τ_f, the censoring distribution is 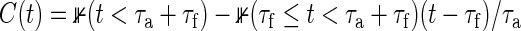. The target power of 1−β=0.8, the significance level of α=0.025, and the censoring distribution of τ_a=2 and τ_f=3 are used throughout this simulation.

Consider typical cases that group size ratios a^(k) and correlations ρ^(k) in two groups (k=1,2) and τ-time survival rates 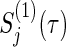of the control group are equal, respectively (i.e. a⁽¹⁾=0.5, ρ⁽¹⁾=ρ⁽²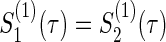⁾, ). Under the three copulas, Table 2 displays the required total sample sizes n, n_sim, n_ind, and 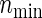calculated by (3.2), PS_sim, PS_ind, and PS 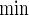with the empirical powers 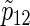(%), respectively, where 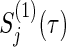, ψ_j, and ρ^(k) are varied following combinations from 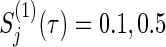, ρ^(k)=0,0.3,0.5,0.8, 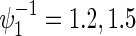and some of 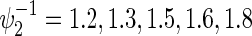satisfying 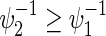. Note that 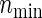is calculated via the univariate version of formula (3.2) (which gives the total numbers of participants required to detect the difference of the single endpoint) and the corresponding 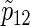to n_sim is the average empirical power (%) on the three copulas. The empirical powers corresponding to n_sim are omitted in Table 2 because they are almost equivalent to the targeted power. These experiments are performed on a computer with an Intel Core2 Quad processor with 3 GHz and with 8 GB of main memory.

From the results of Table 2 and the other simulations (the additional results can be found in Section D of supplementary material available at Biostatistics online), the sample sizes n from (3.2) usually provides slightly conservative results compared with n_sim of PS_sim, and the corresponding empirical powers 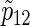are preferable considering the 95% estimation error of 0.5%, although their 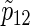tend to be slightly larger than the targeted power as two hazard ratios are larger than 1. Times to compute n_sim increase linearly with sample sizes, where it takes about 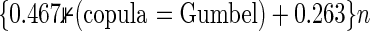seconds (R²=0.99) per an MC trial with 100 000 replications in the data of Table 2. For example, when n_sim=1000, the time is 730 s if the copula is Gumbel’s, and 263 s otherwise. Because MC trials are repeated many times until we determine n_sim, the computational cost is much higher if the effect size is smaller. Formula (3.2) greatly reduces the cost, regardless of the effect size, and is also useful as an initial value to search n_sim.

In comparison with PS_ind and PS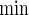, 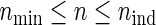holds as a matter of course. Because 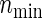and n_ind are farther away as the ratio ψ₂/ψ₁ (more directly, effect size ratio δ₂/δ₁) of two hazards is closer to 1, it is reasonable to use formula (3.2) considering the correlations ρ^(k) between the co-primary endpoints if δ₂/δ₁ is near 1. Note the n’s from (3.2) are usually closer to n_ind’s than 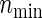’s in the situation of δ₂/δ₁≈1, even if ρ^(k)’s are in high levels such as ρ^(k)=0.8. However, 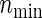, n, and n_ind are mutually approaching regardless of the copula type and its correlations, according as the proportion δ₂/δ₁ is farther from 1. This is good news for practicians because of the savings of not having to investigate the copula types and levels of dependence. When ρ⁽¹⁾=ρ⁽²⁾=0, the sample sizes from all copulas are the same, but note that PS_ind is not necessarily obtained easily without our formula (3.2) if two effect sizes are different.

Hence, we can say that formula (3.2) is valid for practical use in many situations (including Table 2 and the other simulations in Section D of supplementary material available at Biostatistics online), in particular, as long as the group sizes are not extremely unbalanced and/or n calculated from (3.2) is not too small. One reason that (3.2) gives such a conservative n will arise from the difference between the actual statistic 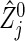and its approximation 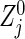as described in Section 3.3. Also, from the simulation results, the larger the right-censored rates are, the greater the required sample sizes under the Clayton copula with a late dependence will be, relative to the Gumbel and Frank copulas. The relationship between the Gumbel and Frank copulas in sample size is slightly complicated. The higher correlation ρ^(k) under the Frank copula is, the more the bivariate logrank statistics are correlated relative to the Gumbel copula. A heavy censored rate weakens the correlation between the test statistics under the Frank copula compared with the Gumbel with an early dependence. Thus, it is important to examine the correlation structure between the two co-primary time-to-event variables and then select an appropriate copula model.

4.2. Practical illustration

We discuss the ARDENT study mentioned in Section 1, which is a phase III, randomized, open-label study designed to investigate three different NNRI-sparing antiretroviral regimens. The study duration is 96 weeks after enrollment of the last subject. The original total sample size of 1800 was calculated for the pairs comparison of the three regimens with respect to the two primary endpoints, not taking into account the potential correlation, with 3% inflation to the adjustment for interim monitoring. The study had (a) a power of 0.90 to establish non-inferiority in the risk reduction of virologic failure with the non-inferiority margin of 10% and the virologic failure rate of 25% at 96 weeks and a one-sided type I error rate of 0.0125 and (b) a power of 0.85 to detect a 10% difference in regimen failure due to tolerability with a two-sided type I error of 0.025 and a regimen failure rate of 45% at 96 weeks. For the illustration, we will suppose that the objective was to establish joint statistical significance with respect to both virologic and regimen failure in a two-intervention superiority comparison.

Figure 1 displays the contour plots of the required total sample size with the hazard ratios of time-to-events of virologic and regimen failures, and correlation for the three copulas. The sample size was calculated to detect the joint reduction for both time-to-event outcomes with the overall power of 0.90 at the one-sided significance level of 0.0125, where ρ=ρ⁽¹⁾=ρ⁽²⁾=0,0.3,0.5, and 0.8; 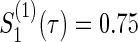and 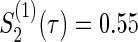; τ_a=0 and τ_f=96; a⁽¹⁾=0.5. The figure shows how the sample size behaves with the two time-to-event outcomes and its correlations: commonly observed in all of the three copulas, when the two hazard ratios are approximately equal, the sample size changes with the correlation. When one hazard ratio is relatively smaller (or larger) than the others, the sample size is nearly determined by the hazard ratio closer to 1, and it does not change with the correlation. In addition, the sample size calculated by the Clayton copula is always larger than those by the Gumbel and Frank copulas. Based on the original assumption of 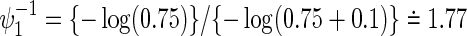and , the total sample size is 928 commonly for the three copulas when ρ=0. When ρ=0.3, 0.5, and 0.8, they are 928, 926, and 924 for the Clayton copula; 926, 922, and 920 for the Gumbel copula; and 926, 924, and 920 for the Frank copula. As the values of hazard ratios used for the sample size calculation are different between the two endpoints, the sample size does not change with the correlation and then among copulas. Therefore, conservatively, we may choose the largest sample size of 928 for the joint statistical reduction in both virologic and regimen failures.

Fig. 1.

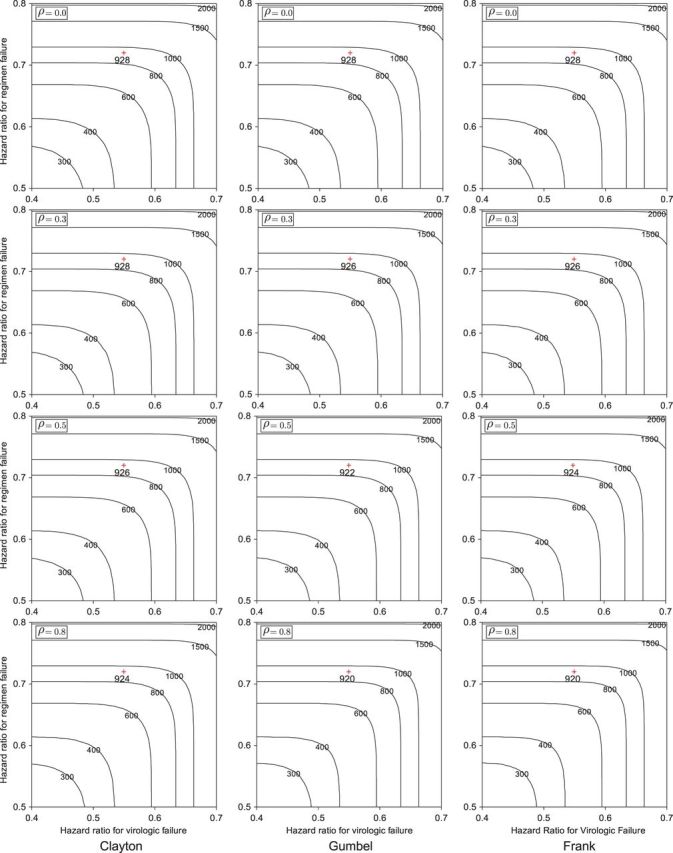
Contour plots of the required total sample size with the hazard ratios of time-to-events of virologic and regimen failures, and correlation for the three copulas. The sample size was calculated to detect the joint reduction for both time-to-event outcomes with the overall power of 0.90 at the one-sided significance level of 0.0125, where ρ=ρ⁽¹⁾=ρ⁽²⁾=0.0, 0.3, 0.5, and 0.8; 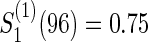, and 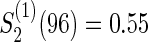; τ_a=0, and τ_f=96; a⁽¹⁾=0.5.

In the process of determining the sample size for the two time-to-event correlated outcomes, we must carefully consider the two aspects: one is the choice of copula to model the shape of the association between the time-to-event outcomes and the other is whether the correlation is incorporated into the calculation. The shape of association and correlation may be estimated from external or internal pilot data, but they are usually unknown. As we could see in the previous section and the figure, when it is observed that one hazard ratio is much larger than the other from the external data, there may be no difficulty in determining the sample size. This is because the three copulas may provide the same sample size, which does not change much with the correlation. On the other hand, when the two hazard ratios are approximately estimated to be the same from the external data, the misidentification of the shape of association and value of correlation may lead to too small a sample size and thus important effects may not be detected. One alternative solution is that, conservatively, one could assume zero correlations among the endpoints as the overall power to detect the effects is smallest when the correlations are zeros.

5. Discussion

We propose a method for evaluating the sample size for clinical trials with a primary objective of evaluating the joint effects of an intervention on all of a set of co-primary endpoints, and discuss the case of two time-to-event outcomes. We outline the calculation of the variance–covariance matrix of the bivariate logrank statistic and describe the sample size formula under a correlation structure of three copula models. We evaluate the performance of the methods and investigate the behavior of the required sample sizes via simulation. The sample size formula is valid in practice as long as the sample sizes per group are not extremely unbalanced. Properties of the logrank statistic under small samples have been investigated by several authors (e.g. Kellerer and Chmelevsky, 1983; Hsieh, 1992; Strawderman, 1997). Some correction for an unbalanced design under a small sample size is possible by a bivariate extension of Strawderman (1997). Also, there is room for further improvement. Considering the difference between the statistic 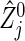used actually and its approximation 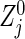used to construct (2.4), a delta method provides

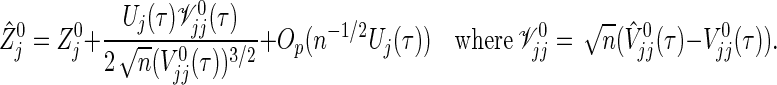A correction of (3.2) based on this method may be accomplished by complicated martingale calculus. However, several modifications under small sample sizes are not discussed further. The purpose of this paper is to propose the simple formula (3.2) without complicated correction and to investigate how it works. Although we mainly discuss the sample size calculation for the logrank statistic, the extension to the weighted logrank statistic is entirely straightforward.

When a temporal relationship can be assumed between the two time-to-event endpoints, e.g. time-to-death vs. time-to-progression in an oncology trial, then alternative bivariate modeling, distinct from the standard copula models considered in this paper, may be desirable. Also, the proposed method should not be applied directly to the overall survival and the other survival endpoints associated with dependent censoring. For an illustration, consider the following classification of censored observations which occur in bivariate survival data: (i) two co-primary endpoints are censored with different times; (ii) two co-primary endpoints are censored at the same time (e.g. by the end of the study or patient drop-out); (iii) one co-primary endpoint is censored by the other co-primary endpoint being completely observed, e.g. death censors a clinical event. The case of (iii) describes a competing risk (dependent censoring). If there is a non-zero correlation between the endpoints, then the assumption of independent censoring is violated, which is beyond the scope of this paper because an extensive study to modify the standard logrank test would be needed for handling dependent censoring. However, in this case, researchers may attempt to address the problem of (iii) by considering the development of composite endpoints (e.g. death and composite of death and the other intermediate events). Although we do not consider a temporal ordering of the two event-time variables, such an application can be achieved only by replacing the joint survival models considered in this paper with other bivariate modeling satisfying a time-ordered relationship. Hence, the proposed methods provide an important foundation for appropriately sizing clinical trials with co-primary endpoints.

Supplementary material

Supplementary material is available at http://biostatistics.oxfordjournals.org.

Funding

This research is financially supported by JSPS KAKENHI grant numbers 23700336, 23500348; the Pfizer Health Research Foundation, Japan; and the Statistical and Data Management Center of the Adult AIDS Clinical Trials Group grant 1 U01 068634.