Invasion from a cell aggregate – the roles of active cell motion and mechanical equilibrium

Abstract

Cell invasion from an aggregate into a surrounding extracellular matrix is an important process during development and disease, e.g., vascular network assembly or tumor progression. To describe the behavior emerging from autonomous cell motility, cell-cell adhesion and contact guidance by extracellular matrix filaments, we propose a suitably modified cellular Potts model. We consider an active cell motility process in which internal polarity is governed by a positive feedback from cell displacements, a mechanism that can result in highly persistent motion when constrained by an oriented extracellular matrix structure. The model allows to explore the interplay between haptotaxis, matrix degradation and active cell movement. We show that for certain conditions the cells are able to both invade the ECM and follow ECM tracks. Furthermore, we argue that enforcing mechanical equilibrium within a bulk cell mass is of key importance in multicellular simulations.

1. Introduction

Several developmental, physiologic and pathologic processes involve cell invasion into an extracellular matrix (ECM) rich environment. Well studied examples include the movement of mesodermal cells during gastrulation [1, 2], the formation of the vascular network [3, 4] or the heart valves [5]. Tumors developing in loose connective tissue, a frequently used in vivo tumor progression assay [6], also infiltrate an ECM environment [7]. Accordingly, the roles and regulation of molecular cell-ECM contacts in the cell motility process is a rapidly expanding area of research.

Recent studies investigating cell movement within three dimensional in vivo and in vitro environments revealed a complex diversity of invasion modes, each with characteristic cell-cell and cell-ECM interactions [8, 9, 10]. Cell movements may or may not involve substantial degradation of the ECM [11, 12, 13]. If cells do degrade the ECM, the resulting cell tracks may form a “tunnel” which can guide other cells to follow [14, 7, 13]. Cells can move through the ECM both individually and in groups [7]. When moving in groups, tip cells, which degrade the ECM, are functionally different from the bulk/stalk cells which follow along and do not initiate the formation of new sidebranches [15, 16].

To understand the tissue- or organ-level consequences of invasive behavior, one must explain how multicellular structures and multicellular dynamics emerge from local cell-cell interactions. Therefore, cell invasion is a subject of several recent theoretical studies [17, 18, 19, 20, 21, 22, 23, 24]. Multicellular movement patterns and structures are often explained utilizing theoretical models that represent individual adherent cells as “fluid” droplets, like the cellular Potts model (CPM) [25], or the off lattice subcellular element model [26]. Such model choices are motivated by the demonstrated non-Newtonian fluid-like behavior of simple cell aggregates [27]. An obvious possibility is to include objects that explicitly represent the ECM into these models [28, 18, 24], yet we are unaware of a systematic investigation of the consequences of such modeling assumptions in simple, well-controlled and thus fully explorable theoretical models. A reliable model of cell emigration from a cell mass, however, is an essential component of more complex models that aim to explain developmental and pathological processes.

In this study we consider a simple, but frequently utilized in vitro experimental setting which consists of a cell aggregate placed within a three dimensional ECM (usually collagen I) gel [12, 17, 29]. As we review in the next section, several cell types of interest, like tumor or endothelial cells leave the aggregate and invade the ECM. We set up a minimalistic model that represents individual cells and ECM filaments in section 3. This model is explored using numerical simulations in section 4, where we show that in order to model cell invasion from a spheroid, one need to consider both active cell migration and a reasonable mechanism to ensure proper mechanical equilibrium within the bulk of the cell aggregate.

2. Overview of empirical data

2.1. Invasion from tumor spheroids

While invasion from tumor spheroids into a collagen I gel is a widely used experimental model, here we focus on the experiments of [12], in which a variety of tumor cell lines were compared by characterizing their invasive phenotypes during a course of four days. The cells’ ability to adhere together and degrade the ECM was characterized for each line by determining the expression profile of cadherins and matrix metalloproteases, respectively. The study found a close to linear increase in the invasion depth over the time course of four days. The radius of invaded ECM volume increased with a typical speed of 200 μm/day ≈ 10 μm/h. Cells within the ECM were often arranged in multicellular, linear, radially oriented structures. Less adhesive cell lines also displayed a halo consisting of scattered individual cells. Cells that were able to degrade the collagen at a greater rate were observed to form a cavity (devoid of both cells and ECM) within, or in place of, the initial aggregate. Cells with minimal ability to degrade the collagen, however, were also able to invade the surrounding ECM.

2.2. Invasion without cell proliferation

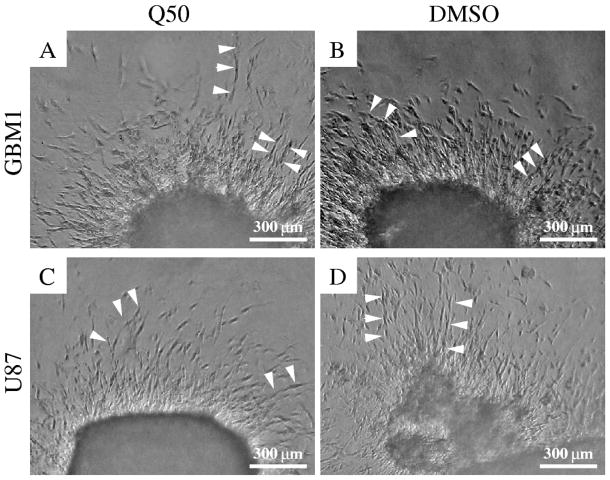
As we focus on the role of cell motility during the invasion process, we repeated some of the invasion experiments of [12] in the presence of a cell division inhibitor Q50. As shown in Fig. 1, after one day in culture the proliferation-inhibited cells form very similar structures to those observable in 3D cultures of normally dividing cells, and both morphologies are similar to those reported previously [12]. Of particular interest are the radially oriented, elongated cells that invade the gel. Some of these cells form multicellular chains. The finding that the early invasion process does not require cell proliferation is consistent with the estimate that the duplication time of glioblastoma cells is in the order of 40 hours under optimal culture conditions [30].

Figure 1.

GBM1 (A,B) and U87 (C,D) cells substantially invade collagen gels after one day in culture. The initial invasion patterns are independent of cell division: cells treated with Q50 (A,C) invade the surrounding matrix with similar speeds as the control cultures do (B,D). In each experiment cells invade the matrix radially outwards from the aggregate and often form radially oriented chains (arrowheads).

2.3. Invasion of vascular cells

Endocardial explants are a widely utilized culture technique to study a normal cell population which seeds the extended cardiac basement membrane (the cardiac jelly) and contributes to the formation of cardiac valves [5]. Time lapse recordings of the invasion of endocardium-derived cells revealed highly persistent, radially outward directed cell movements with speeds ≈ 10 μm/h and persistence times exceeding 10 hours [31]. The persistent cell movement was conditional on the presence of the explant (A. C. unpublished observation): when the explant is removed after the initialization of the invasion, the remaining cells embedded in the ECM displayed a random walk-like motion with little persistence, similar to the movement reported for fibroblasts in collagen gels [32].

While endocardium-derived cells migrate individually and create a “halo” of cells scattered around the explant, vascular endothelial cells sprout into the collagen gels mimicking angiogenesis [33]. If emigrating from an explant, the invading cells are organized into radially oriented straight structures. Depending on the growth factors present, the reported maximal speed of invasion could reach 200 μm/day ≈ 10 μm/h. Both endocardial [31] and endothelial [14] cells leave degraded ECM fragments or a “channel” behind.

2.4. ECM structure

The ability to reorganize the ECM is well documented for tissue explants or cell aggregates embedded within an ECM gel. As revealed by the early experiments of Harris and Stoplak [34] and studied in more detail recently [35], cell traction creates ECM tracks radiating away from the aggregate. Even individual cells can reorganize and align collagen fibers [36]. The developing oriented ECM structure in turn, can guide cell migration [37, 38], in a similar manner to magnetically oriented collagen gels [36, 39, 40, 41] or laser-burnt ECM microtracks [42]. These observations resulted in continuum theories of cell-ECM assemblies [43, 44, 45] which are instrumental to explain a vasculogenesis model system within a loose, deformable ECM environment [46] as well as other morphological and pathological processes in which the interplay of cell traction and ECM deformation plays a key role [47]. ECM channels created by protease activity (instead of by traction forces) are another important class of ECM patterns that guide cell motility in a 3D ECM environment [14, 48].

3. Computational model with active cell motility and ECM

3.1. Cellular Potts model

To model the process of cell invasion into an ECM environment we adopted the two dimensional cellular Potts model (CPM) approach. In theoretical studies the CPM is a frequently used method to represent movement of closely packed cells [25, 49, 50, 51, 52, 53, 54, 55]. The main advantage of the CPM is that cell shape is explicitly represented; thus, the simulation has the potential to describe dynamics in which controlled cell shape plays an important role [49, 51, 54].

To obtain a biologically plausible, yet simple model we make the following assumptions:

• A1The model is two dimensional: the simulation may represent a plane section through a three dimensional structure.
• A2Each cell is a simply connected area with an approximately constant, pre-set size.
• A3We consider ECM structures comparable to the cell size, so ECM is resolved explicitly on the simulation grid. We assume that the ECM is rigid (fixed in space) and occupies a subset of cell free sites.
• A4Cells can adhere to their neighbors or to the ECM.

In some simulations we also assume that

• A5When in contact with the ECM, cells are capable of autonomous (active) motility, regulated by a positive feedback between cell displacements and an internal polarity vector [56]. This active persistent motion is absent within the bulk of the aggregate [27].
• A6A cell aggregate is close to mechanical equilibrium, its shape is determined by the constrains of ECM contact points.

Following [25], a discrete symbol (here an integer) σ is assigned to each lattice site x within a two-dimensional square grid (A1). Lattice sites adjacent to site a are denoted by B₁(a) and B₂(a): these sites share either a side (primary neighbors) or connect via a corner (secondary neighbors), respectively. Cells are represented as simply connected domains, i.e., a set of adjacent lattice sites sharing the same label σ (A2). It is convenient to set the label as the cell index i (1 ≤ i ≤ N, where N is the number of cells in the simulation). Sites that belong to the arbitrarily shaped (unconstrained) area devoid of cells will be marked by the symbols σ = σ₀ = 0 and σ = σ_ECM = −1 depending on the absence or presence of ECM at that site, respectively.

Cell movement is the result of a series of elementary steps, and each step attempts to alter the state of a single, randomly chosen lattice site a from σ(a) to σ′. Differing from the usual choice of CPM elementary stapes, this change can be either an insertion of a cell free site (see Supplement Figure S1) as

$${\sigma }^{\prime }={\sigma }_0\text{if}\sigma (\mathit{a})\notin \{{\sigma }_0,{\sigma }_{\mathit{ECM}}\}$$ (1)

or the expansion of an adjacent domain from site b ∈ B₁(a) + B₂(a) as

$${\sigma }^{\prime }=\sigma (\mathit{b})\text{if}\sigma (\mathit{b})\notin \{\sigma (\mathit{a}),{\sigma }_{\mathit{ECM}}\}.$$ (2)

In each elementary step either (1) or (2) is chosen randomly, with a probability 1/9 and 8/9, respectively. In case of choosing (2), site b is selected by assigning equal probabilities to the 8 sites in B₁(a) + B₂(a). If the conditions specified in (1) or (2) are not satisfied, the considered elementary step is abandoned. These rules thus ensure that the model ECM does not expand, decay or move (A3).

If the conditions listed in (1) or (2) are satisfied, the elementary step is executed with a probability p(σ(a) → σ′). If the domains remain simply connected (A2), and thus cells do not break apart or form holes, the probability assignment rule ensures the maintenance of a target cell size (A2), adhesion of cells (A4) and active cell movements (A5). For convenience and historical reasons p is given as

$$lnp(\sigma (\mathit{a})\to {\sigma }^{\prime })=min[0,-\mathrm{\Delta }u(\sigma (\mathit{a})\to {\sigma }^{\prime })+w(\sigma (\mathit{a})\to {\sigma }^{\prime })],$$ (3)

where, as specified below in detail, w represents a bias responsible for the cell-specific active behavior considered, u is a goal function to be minimized, and Δu is its change during the elementary step considered.

Since updating each lattice position takes more steps in a larger system, the elementary step cannot be chosen as the measure of time. In a system of linear size L the usual choice for time unit is the Monte Carlo step (MCS), defined as L² elementary steps (irrespective whether executed or not) [51].

3.2. Evaluating configurations

In the CPM approach, a goal function (‘energy’) is assigned to each configuration [25]. The goal function guides cell behavior by distinguishing between favorable (low u) and unfavorable (high u) configurations as

$$u=\frac{1}{2}\sum _{\mathit{x}}\sum _{\begin{array}{c}{\mathit{x}}^{\prime }\\ {\mathit{x}}^{\prime }\in B_1(\mathit{x})+B_2(\mathit{x})\end{array}}{J}_{\sigma (\mathit{x}),\sigma ({\mathit{x}}^{\prime })}+\lambda \sum _{i=1}^N\delta A_i^2.$$ (4)

The first term in (4) enumerates cell boundary lengths with various weights J depending on the local configuration. The second term in expression (4) is responsible for maintaining a preferred cell area (A1). For each cell i, the deviation of its area from a pre-set value is denoted by δA_i. Parameter λ adjusts the tolerance for deviation, therefore, λ is related to the compressibility of cells in the 2D plane, and also determines the magnitude of cell area fluctuations.

The J_i,j weights are zero when i = j. For i ≠ j and a homogeneous cell population

$$J_{i,j}=\{\begin{array}{llll}\alpha ,\hfill & \text{for}\hfill & ij>0\hfill & (\text{intercellular}\text{boundary})\hfill \\ \beta ,\hfill & \text{for}\hfill & ij=0\hfill & \text{and}i,j\ge 0(\text{free}\text{cell}\text{boundary})\hfill \\ \gamma ,\hfill & \text{for}\hfill & ij<0\hfill & (\text{cell}-\text{ECM}\text{boundary})\hfill \\ 0,\hfill & \text{for}\hfill & ij=0\hfill & \text{and}i,j\le 0(\text{free}\text{ECM}\text{boundaries}\text{are}\text{ignored}).\hfill \end{array}$$ (5)

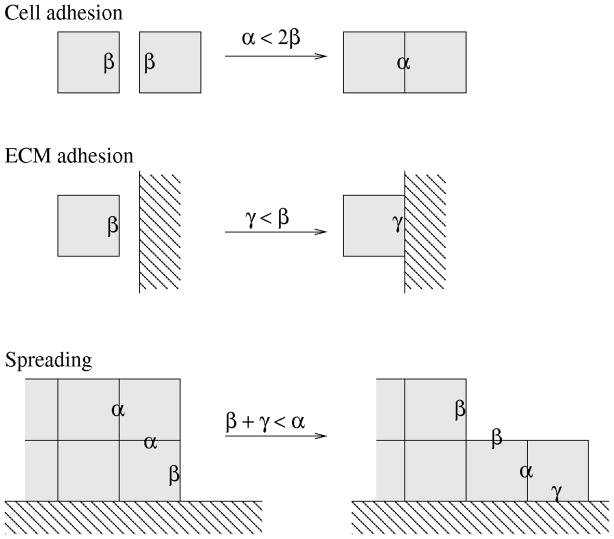
The surface energy-like parameters α, β and γ characterize both cellular adhesiveness and cell surface fluctuations in the model. The magnitude of these values determines the roughness of cell boundaries: small magnitudes allow dynamic, long and hence curvy boundaries, while large magnitudes restrict boundaries to straight lines and thus freeze the dynamics. Note, that the weights may be negative: in fact, cell spreading (an acute contact angle) along the ECM requires negative γ.

In addition to cell boundary roughness, the relation of these parameters also specifies the preference of intercellular connections over free cell surfaces, or cell-ECM boundaries (A4) (Fig. 2). Cell-cell adhesiveness is controlled by the sign of 2β − α [25]: if two adherent cells are separated by inserting a layer of empty sites between them, then the change in u is proportional to β − α/2 at each site along the boundary line affected. Therefore, for 2β > α free cell boundaries are penalized and cells are adhesive. The matrix is adhesive or repulsive depending on the sign of the difference β − γ. Cell spreading along the ECM boundary is controlled by all three parameters α, β and γ. If we consider first-neighbor interactions only, cells spread along the ECM if γ + β < α. This relationship expresses the change in (4) when a cell boundary site is moved to be in contact with the ECM as shown in Fig. 2. In the model, however, we consider first-, and second-neighbor interactions as well, and the analogous condition for spreading is

Figure 2.

Boundary weights α, β and γ modify the simulated cell behavior. Boundaries that change contribution to (4) are marked with the corresponding weights. Cells are adhesive for α < 2β, and adhere to the ECM if γ < β. Cells spread along the ECM if β + γ < α. These rules are demonstrated for first-neighbor (B₁) interactions in (4), but the cell-adhesion and matrix-adhesion relations remain the same for the implemented, second-neighbor (B₁ + B₂) interactions as well. The condition for spreading in this latter case, however, changes to (β + 3γ)/2 < α.

$$\frac{3\gamma +\beta }{2}<\alpha .$$ (6)

3.3. Cell polarity and active motility

While u evaluates configurations, w is assigned directly to the elementary steps and therefore allows the specification of a broader spectrum of cellular behavior. In this study we consider two non-equilibrium effects, active cell motility and irreversible ECM degradation:

$$w=w_p+w_{\mathit{ECM}}.$$ (7)

We model active cell motility according to [56]. We assign a polarity vector p_k to each cell k and increase the probability of those elementary conversion steps that advance the cell center in the direction parallel to p_k as

$$w_p(\sigma (\mathit{a})\to {\sigma }^{\prime })=P\sum _k\frac{\mathrm{\Delta }{\mathit{X}}_k(\sigma (\mathit{a})\to {\sigma }^{\prime }){\mathit{p}}_k}{\mid {\mathit{p}}_k\mid }.$$ (8)

Parameter P sets the magnitude of the bias and ΔX_k represents the displacement of the center of cell k during the elementary step considered.

Cell polarity vectors are updated by assuming a spontaneous decay and a positive feedback from cell displacements (A5). In each MCS the change in p_k is

$$\mathrm{\Delta }{\mathit{p}}_k=-\frac{{\mathit{p}}_k}{T}+\mathrm{\Delta }{\mathit{X}}_k,$$ (9)

where parameter T, the polarity decay time, is the characteristic time needed to change cell polarity and ΔX_k is the displacement of the center of cell k during the MCS considered.

3.4. Extracellular matrix: adhesion, degradation and structure

In addition to serve as adhesive sites for β > γ, the presence of ECM can also restrict cell movements. This is modelled by decreasing the alteration probability of ECM sites:

$$w_{\mathit{ECM}}(\sigma (\mathit{a})\to {\sigma }^{\prime })=\{\begin{array}{l}-Q,\text{for}\sigma (\mathit{a})={\sigma }_{\mathit{ECM}}\hfill \\ 0\text{otherwise}.\hfill \end{array}$$ (10)

Thus, for Q ≫ 1 the ECM-containing sites are effectively immutable. When the elementary step (2) does convert an ECM-containing site to a cell-occupied site, we interpret this event as degradation: the site will be restored to an empty site after cells leave.

The random, but possibly oriented, filamentous structure of the ECM is modeled by a Markov chain, resulting in patterns that are used as initial conditions for simulations. The probability that a given site x = (x, y) contains ECM depends only on the state of its left neighbor:

$$p(\sigma (x,y)={\sigma }_{\mathit{ECM}})=\{\begin{array}{lll}{p}_{11}\hfill & \text{if}\hfill & \sigma (x-1,y)={\sigma }_{\mathit{ECM}}\hfill \\ p_{01}\hfill & \text{if}\hfill & \sigma (x-1,y)={\sigma }_0\hfill \end{array}$$ (11)

and

$$p(\sigma (x,y)={\sigma }_0)=\{\begin{array}{lll}{p}_{10}\hfill & \text{if}\hfill & \sigma (x-1,y)={\sigma }_{\mathit{ECM}}\hfill \\ p_{00}\hfill & \text{if}\hfill & \sigma (x-1,y)={\sigma }_0,\hfill \end{array}$$ (12)

with p₀₀ + p₀₁ = p₁₀ + p₁₁ = 1. The surface fraction of ECM covered sites, p_ECM, is given by the condition for translation invariance of the probabilities

$$p_{\mathit{ECM}}=p_{11}{p}_{\mathit{ECM}}+p_{01}(1-p_{\mathit{ECM}}).$$ (13)

Thus, in this simple model the ECM structure is controlled by two independent parameters only: its surface fraction p_ECM and its tendency to cluster into lines p₁₁ (Fig. 3).

Figure 3.

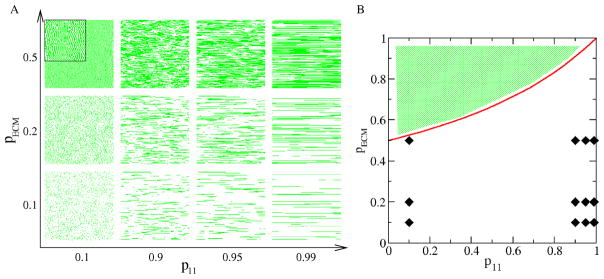
Simulation of an anisotropic, horizontally structured ECM. A: Parameters p_ECM and p₁₁ define the ECM density and filament length, respectively, as demonstrated for selected parameter values. Areas shown are 300 × 300 pixels in size, filament width is 1 pixel. B: The probability values used to generate the configurations of panel A are indicated in a parameter map. The two parameters, according to Eq. (13), satisfy the inequality p_ECM < (2 − p₁₁)⁻¹ (red line) Thus, the various combinations of probabilities p₀₁ and p₁₁ cannot generate a surface fraction value p_ECM that falls into the shaded area.

3.5. Relaxation to mechanical equilibrium

In most simulations we apply a procedure which ensures the relaxation of the cell mass to mechanical equilibrium (A6). If external constrains or forces are only applied at the boundary of the cell aggregate (as in the case of an aggregate within a cavity), the bulk of the aggregate reaches mechanical equilibrium in a much shorter time (seconds) compared to the time required for active cell movements (minutes) [27]. We implement the relaxation process by a sufficiently large number of elementary steps after each usual MCS cycle, calculated with w = 0. The (biochemically passive) mechanical relaxation process is assumed to preserve cell-ECM adhesion sites as alteration of cell-ECM attachment usually requires active, biochemically controlled processes. Thus, cell sites that are adjacent to ECM are immutable during the relaxation process. The length of the relaxation process depends on the system size – reaching equilibrium can be detected as a steady value of the goal function u. The typical duration of the relaxation process was chosen as 1000 L² elementary steps.

3.6. Initial conditions

Simulations were performed with two different initial conditions. For the description of the equilibrium model, 49 cells were initialized within a cavity, a square area devoid of ECM. The linear size of the cavity was L = 60 lattice sites and was surrounded by a continuous, immutable ECM.

ECM invasion was simulated in systems of 500 × 500 lattice sites. Cells were placed in a rectangular area, 210 lattice units wide, on the left. The remaining cell-free area was filled with horizontally directed ECM structures according to rules (11) and (12).

Preferred cell size was set to 50 lattice sites. A comparison of the average simulated cell size with the typical cell size in [12] calibrates a lattice unit as 1 μm. We calibrate 1 MCS as 1 minute in real time as this choice yields realistic cell speeds in the range of 10–30 μm/h (see Section 2). These calibration values are compatible with the values used in other CPM studies [51, 54, 57].

4. Simulation Results

4.1. Morphologies in the equilibrium model

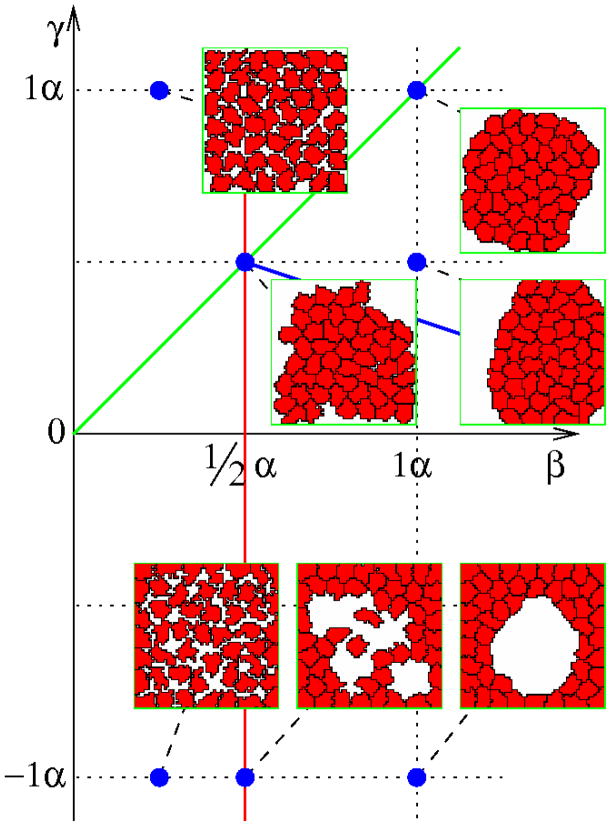
The effects of α, β, and γ surface weights (‘energies’) can be demonstrated in a simple equilibrium system (w = 0) where cells are within a cavity lined by immutable ECM-containing sites. In CPM simulations u reaches a steady state value after an initial transient. Fig. 4 shows characteristic morphologies obtained in this steady state regime for α = λ = 1 and various values of β and γ. Scaling these values by the same factor changes the smoothness of cell boundaries, but results in similar morphologies.

Figure 4.

Morphology diagram of the equilibrium model (w = 0) as a function of the free (β) and ECM-bound (γ) cell surface weights (‘energies’). These values are compared to α, the weight for intercellular boundaries. Configurations shown were obtained in the steady-state regime at t=10,000 MCS, with parameters α = 1 and λ = 1.

Cell-cell adhesiveness is controlled by the sign of 2β − α [25]. Thus, the red line in Fig. 4 divides the parameter space into two domains where cells are either adhesive (right) or non-adhesive (left). The green line in Fig. 4 indicates neutral ECM. Above and below this line the matrix is repulsive and attractive, respectively. Finally, the blue line corresponds to condition (6), and demarcates an area where cells spread along the ECM, i.e., where an increase in cell perimeter is offset by the low expense associated with cell-ECM adhesion sites.

4.2. Mechanical equilibrium of the aggregate

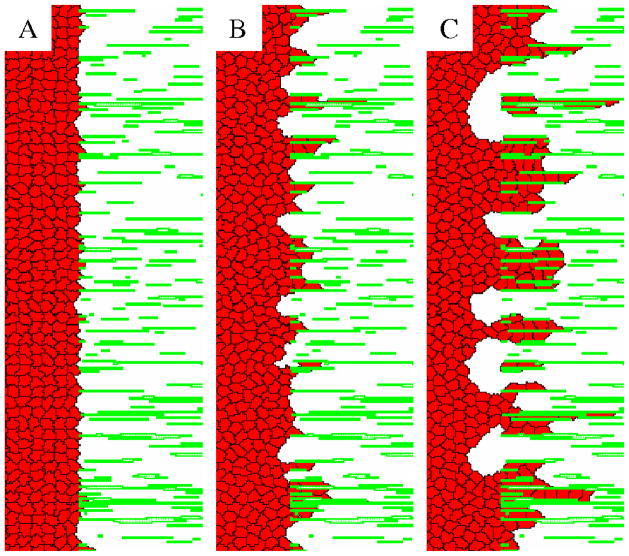
Applying the simple equilibrium model (w = 0) in simulations where adhesive cells can spread and invade an area filled with ECM filaments (Fig. 5 and Movie 1) yields unrealistic dynamics. Cells which enter the ECM leave the area adjacent to the matrix depopulated. So, despite the preference of cells to adhere to ECM filaments, in CPM simulations the cell density decreases close to the ECM. Such depopulation in experiments, however, is usually not observed. Rather, in accordance with the steady-state analysis in the previous section, a hole (cell free area) appears inside the aggregate [12].

Figure 5.

Bulk cell movement at the ECM-cavity interface is unrealistic in the equilibrium (w = 0) Potts model. Cells that adhere to the ECM are able to invade the space between the ECM filaments. Cells in the bulk, however are unable to adjust and shift to the right fast enough. Thus, cells separate and decrease the average cell density at the cavity-matrix interface. Panels A, B and C demonstrate the process, showing an area of 110 × 360 μm² from a 500 × 500 μm² system at 50, 1000 and 10,000 MCS (1, 16 and 166 h) after the start from an initial smooth aggregate interface, respectively. The full time sequence is shown in Movie 1.

We argue that this discrepancy reflects a shortcoming of the usual CPM where active (like protrusive activity) and passive (like elastic deformation response to external forces) cell movements are not distinguished. Passive movements are indeed negligible in conventional monolayer cultures where cells adhere to a rigid, two dimensional plastic or glass surface. In contrast, a passive (viscoelastic or elasto-plastic) response to mechanical stress may move cells in soft or embryonic tissues, as well as in culture systems consisting of cell aggregates or three dimensional ECM gels. In the particular invasion experiments considered here the bulk of cells hangs freely, attached to the cavity wall, and is in mechanical equilibrium with respect to forces acting at the surface of the aggregate. Thus, cell adhesion at the cavity-ECM interface can move (and slightly deform) the whole cell mass towards the ECM.

To better demonstrate the problem of inadequate mechanical equilibrium and to test our suggested solution, we defined the ‘piston test’, a simple system in which a cell aggregate adheres to a moving adhesive surface while the remaining aggregate surface is free (Fig. 6, Movie 2). In these simulations the surface, located at X, is shifted one lattice site to the right after each T_shift MCS. At the time of these shifts lattice sites immediately in front of the surface (x = X − 1) are “extended” into the sites previously occupied by the moving boundary as

Figure 6.

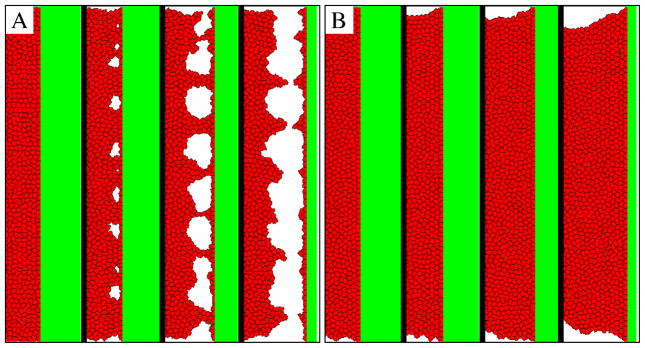
The ‘piston test’ demonstrates the shortcoming of the strictly local dynamics of the cellular Potts formalism (panel A) and our suggested solution that enforces mechanical relaxation (panel B). Cells adhere to the ECM surface (shown in green), which is shifted one pixel every T_shift=100 MCS, thus the speed of the piston is rather slow, 0.6 μm/h. Cells in the bulk cannot adjust to the changing boundary and holes appear near the attachment surface. The holes expand and finally the cells separate from the adhesive surface. The images show the moving ECM boundary, the aggregate extends to the left where it has free boundaries. The four configurations in panels A and B depict the 110 μm wide interface area of a 500 × 500 μm² system at t=0,1000,3000 and 5000 MCS, i.e., t=0, 16, 50 and 83 hours. The full time sequence is shown in Movie 2.

$${\sigma }^{\prime }(X,y)=\sigma (X-1,y).$$ (14)

For sufficiently slow movements the entire cell mass follows the surface. For faster movements cells become stretched in the vicinity of the surface and eventually holes develop. This process can lead to detachment of the cell mass as demonstrated in Fig. 6A. A real cell aggregate, where cells are attached to the culture surface of a dish, is Galilei-invariant: acceleration-free movements of the dish are completely irrelevant.

In the Supplement (Fig. S2) we present the analysis of a simplified, essentially one dimensional piston scenario. When the system dynamics utilizes a series of small elementary steps, the analysis shows – in qualitative agreement with simulation results – that a spatially localized mechanical perturbation propagates through the system as a diffusive front. This behavior is analogous to that of an overdamped elastic system, where the friction force is proportional to the local absolute velocity. Thus, the time needed to accommodate changes, enforced at the boundary, throughout a domain of length L is proportional to L². Furthermore, even an arbitrarily slow, continuous driving of the forced boundary results steady state cell configurations in which cell stretch increases linearly with the distance from the free boundary (instead of a stretch-free steady state). For a given piston speed, the magnitude of the steady state stretch at the forced boundary is proportional to the system size, hence, for even arbitrarily slow driving artifacts are expected within large enough systems.

To ensure proper mechanical equilibrium, we let the configuration relax through several elementary steps which are not counted in the progression of a MCS. The (biochemically passive) mechanical relaxation process is assumed to preserve cell-ECM adhesion sites as alteration of cell-ECM attachment usually requires active, biochemically controlled processes. Thus, cell sites that are adjacent to ECM are immutable during the relaxation process. The elasticity of the CPM is encoded in the goal function u. Accordingly, we set w = 0 and thereby eliminate all cell-autonomous effects in addition to keeping the ECM adhesion sites fixed. The length of the relaxation process depends on the system size – reaching equilibrium can be detected as a steady value of the goal function u (see Supplement Fig. S3). Thus, the procedure results in a configuration, still subject to the constraints of fixed cell-ECM attachments, where the goal function u is minimal. The simulation thus alternates normal CPM steps according to (3) – that may involve changes in ECM adhesion, polarized movement or ECM degradation – with “biochemically passive” mechanical relaxation steps that ensure mechanical (elastic) equilibrium of the freely floating cell mass. As Fig. 6B demonstrates, such an approach to enforce mechanical equilibrium results in realistic behavior, even for fast movement of the boundary.

4.3. Invasion without degradation or self-propulsion

As cells with minimal ECM proteolytic activity can also invade dilute collagen gels, first we consider simulations without ECM degradation (i.e., high value of parameter Q). Under such circumstances the volume (surface) fraction of the matrix, p_ECM, is crucial to allow cell movements in model simulations. If p_ECM is too high ECM-free areas become too narrow for the cells to pass and a percolating (continuous) barrier can form which completely restricts cell invasion just as in epidemic propagation models [58].

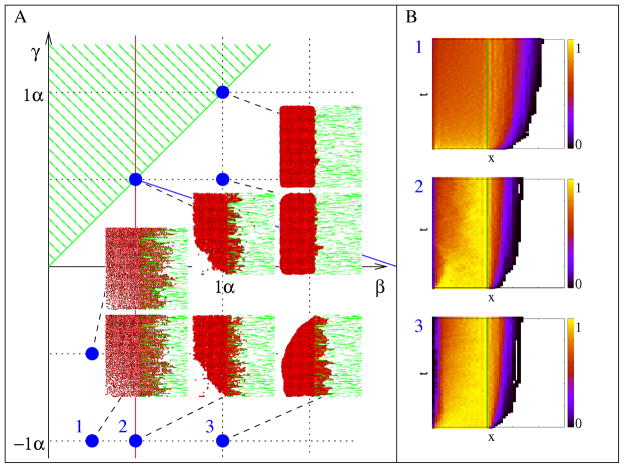
As previously, we set α = λ = 1 and investigate the effect of parameters β and γ which determine cell-cell and cell-ECM adhesiveness in simulations ensuring proper mechanical relaxation of the bulk aggregate. If the matrix is adhesive, a haptotactic effect moves cells from the cavity-ECM boundary into the bulk ECM (Fig. 7A, Movie 3). A sufficiently adhesive ECM can organize otherwise non-adhesive cells along the filaments. Increasing cell-cell adhesion slows down the expansion process and creates smoother interfaces by maintaining a compact cell mass. The invasion dynamics is controlled by a cell density gradient inside the ECM (Fig. 7B), which together with steric constraints translate random cell shape changes into a net (diffusive) cell transport. As the invasion depth ℓ increases, the density gradient decreases as 1/ℓ. Thus, the speed of invasion (as measured by e.g., the speed of the invasion front, dℓ/dt) also decreases as 1/ℓ. This simple analysis predicts $\ell ~\sqrt{t}$, which indeed approximates the data shown in Fig. 7B.

Figure 7.

Cells without spontaneous motility and ECM degradation invade an anisotropic, oriented ECM. A: Morphology diagram of the invasion process for various values of the surface penalty (‘energy’) parameters β and γ, characterizing free and ECM-bound cell surfaces, respectively. As in Fig. 4, the other parameters are kept constant (α = 1, λ = 1). Configurations shown were obtained at t=10,000 MCS (7 days). B: Cell density changes along the direction of invasion reveals a decreasing invasion speed. Color-code indicates cell density compared to conuency. The temporal and spatial ranges represented on the vertical and horizontal axes are 10,000 MCS and 500 lattice units, respectively. Plots annotated as 1, 2 and 3 correspond to parameter values marked accordingly in panel A. The full time sequence is shown in Movie 3.

The $\ell ~\sqrt{t}$ behavior, however, is not consistent with the experimental observations that report close to linear expansion of the invasion envelope [12]. Furthermore, the simulated expansion is too slow: it requires 7 days (10,000 MCS) for the invasion front to expand 100–200 μm. In contrast, the experimentally observed expansion rate is 100–250 μm/day. Thus, we turn our attention to the active motility of invading cells.

4.4. ECM alignment can increase motion persistence

A remarkable property of cells invading the ECM from explants or multicellular aggregates is their highly persistent motion [31]. While this radially directed cell migration may be also guided by factors diffusing from the central aggregate, it is well established that traction forces exerted by the aggregates rearrange the surrounding ECM and radially orient the ECM filaments [37], and the resulting aligned ECM can guide cell movement [32]. Thus, below we explore our model for active cell motility (A5) within a structured ECM environment.

We simulated actively moving individual cells in both single cell wide ECM channels, as well as within the unconstrained plane using the same microscopic parameters. The persistence of motion was established by comparing the cells’ mean squared displacements to the elapsed time (Fig. 8A). Highly oriented excluded volume constraints can indeed increase the persistence of cellular motion substantially, by a factor of 4–5 (Fig. 8B) without effecting the cell speed (data not shown). In particular, when the polarization decay time parameter is T = 20 min, the persistence time, T_p, is ≈ 2h for unconstrained motion and ≈ 10h in a constrained ECM environment. Both persistence time values are in reasonable agreement with previous empirical estimates [56, 31].

Figure 8.

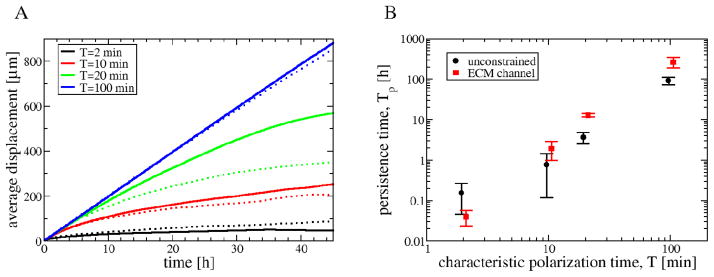
Aligned, anisotropic ECM enhances the persistence of cell motion. A: Persistence of motion was evaluated by fitting the displacement vs elapsed time data with the Ornstein-Fürth formula (16). Individual, actively migrating cells were simulated in an unconstrained plane (dotted lines) as well as in an ECM channel (solid lines). B: The fitted persistence time, T_p, is a monotonic function of the polarization decay time of the model, T.

4.5. Invasion of self-propelled cells, without ECM degradation

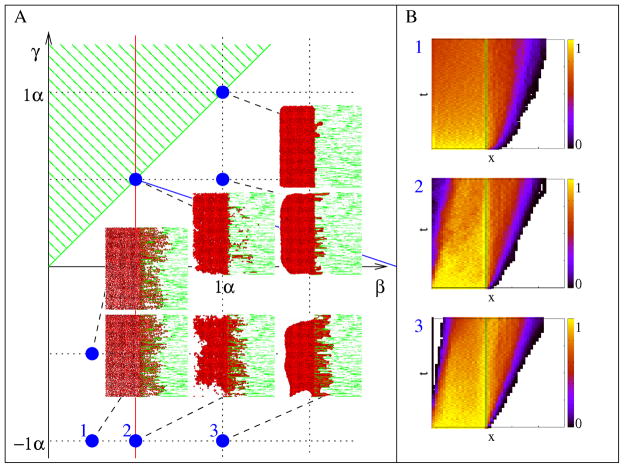
Simulations shown in Fig. 7 were also performed with cells that actively migrate when in contact with the ECM, and the obtained behavior is presented in Fig. 9 and Movie 4. While morphologies are similar both in the presence and absence of active migration, the temporal dynamics is rather different. If cells move actively, their persistent motion results in a linear expansion of the invasion front during the investigated time scales. Moreover, the invasion is substantially faster: it takes only 1.5 days for the front to advance 200 μm, compatible with experimental observations. Actively moving non-adhesive cells spread over a larger area and create a loose halo of individual cells. Strongly adhesive cells are more likely to invade in cords. While strong ECM anisotropy enhances the roughness of the aggregate-ECM interface, multicellular sprouts also develop in simulations with weakly anisotropic ECM (Supplemental Fig. S4).

Figure 9.

Cells with spontaneous motility and without ECM degradation invade an ansitropic, aligned ECM environment. A: Morphology diagram of the invasion process for various values of parameters β and γ. Other parameters are kept constant (α = 1, λ = 1). Configurations shown were obtained at t=1,000 MCS (17 hours). B: Cell density changes along the direction of invasion reveals a steady invasion speed. Color-code indicates cell density compared to confluency. The temporal and spatial ranges represented on the vertical and horizontal axes are 2,000 MCS and 500 lattice units, respectively. Plots annotated as 1, 2 and 3 correspond to parameter values marked accordingly in panel A. Full time sequence is shown in Movie 4.

4.6. Matrix degradation

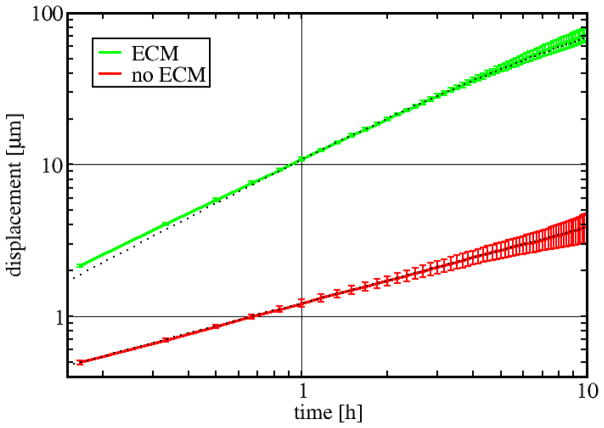
Matrix degradation (Q ~ 1) results in a strong motion bias towards the ECM, perpendicular to the cell-ECM interface. This bias is resulted from the asymmetry between the processes of forward protrusion (which creates additional cell-ECM boundaries) and protrusion retraction (which creates free cell boundary segments). Thus, simulated cells adjacent to the ECM tend to invade. In case of a single cell this mechanism creates highly persistent trajectories as Fig. 10 demonstrate.

Figure 10.

ECM degradation results in persistent invasive motion. Average displacements during various time intervals are plotted for a single cell in an adhesive and degradable ECM environment (β = 1, γ = 0, Q = 1, green) as well as in a ECM-free environment (red line) (α = λ = 1). Dotted lines indicate the fitted Ornstein-Fürth formula (16) for the ECM dataset (persistence time T_p = 2.3 h, speed S = 11.5μm/h), and a square-root function $D\sqrt{t}$ for the ECM-free data (D = 1.216 μmh^−1/2). Errorbars represent standard deviation, obtained from 10 independent runs.

The matrix degradation mechanism, however, will not result in cells following the ‘tunnels’ created by earlier invasion. Rather, each cell creates a new side-branch tunnel perpendicular to the first one (Movie 5). In contrast, actively migrating cells can follow tunnels, and if they can also degrade the ECM then the balance of self propulsion and the ability to ECM degradation determines the frequency of initiating new ECM tunnels (Movie 6).

5. Discussion

5.1. The problem of cell invasion

We narrowed the focus of this study to a relatively simple problem, cell invasion from an aggregate into an extracellular matrix (ECM) environment. A large body of empirical data is available for the invasive behavior of various cell types including tumor and vascular cells (see, e.g., [12, 17, 31, 29] and references therein). This problem is the subject of several theoretical studies as well. Several modeling efforts in the context of tumor progression focused mainly on cell proliferation [17, 59, 60]. Cell motility, however, is often a key factor of tumor invasiveness [20, 9, 10]. In this paper we provide additional experimental evidence that cell proliferation does not play an important role in the early stages of the particular invasion process we have chosen as our experimental benchmark (Fig. 1).

One modeling approach characterizes the system with density fields and corresponding partial differential equations. In such an approach cell movement is usually represented as a flux, which includes a diffusion term to account for random cell movement, a chemotaxis/haptotaxis term to gide cell migration [61], and a local integral to describe cell-cell adhesion [20, 45, 23]. In the other modeling approach individual cells and ECM filaments are explicity represented – such models thus correspond more obviously to the biological system, but often limit analytical understanding. Representing individual cells may be aslo required when the forming structures contain only a handful of cells and the finite cell size affects the system’s dynamics [51, 53].

Individual-cell based models, however, often aim to explain complex multicellular behavior [28, 52, 19, 18, 24, 60]. In contrast, in this study we investigate a cell-based model, but keep the complexities at a minimum. In accord, we aim to clarify how various modeling assumptions specifying cellular features effect the collective (large-scale) behavior of the invasion process.

5.2. Parameters

Our proposed minimalistic model still has five relevant parameters effecting the dynamics and two additional parameters specifying the ECM structure as an initial condition. We refrain from using a temperature-like parameter, as rule (3) of [25], analogous to our rule (3), simply scales each CPM parameter by the temperature, a constant. Thus, when comparing our studies with those that include a temperature in the simulations, our parameter values are to be compared with the corresponding values divided by the temperature. Furthermore, we set the CPM parameters α = λ = 1 as we do not expect constraints on cellular shape and area play a fundamental role in the process. The remaining two CPM parameters specifying cell adhesiveness, β and γ, are well understood under equilibrium conditions.

The two parameters characterizing active cell motility, P and T, has been extensively studied for single cells and monolayer cultures [56]. Here we demonstrate the role of spatial constraints in guiding active cell motility, and provide simulation results in which both oriented adhesion sites and a cell density gradient are present.

The fifth parameter, Q, sets how easily cells can degrade the ECM. We show that for small enough Q and γ < β the CPM inherently yields a highly persistent invasive behavior. This behavior is analogous to surface tension inhomogeneity-driven moving droplets [62]. Yet, this motile behavior makes all cell-ECM contacts unstable which, for a homogeneous cell population, contradicts empirical observations such as invading cell chains or cells following older cell tracks. Thus we argue, that an additional, spontaneous cell motility apparatus must be considered as well.

5.3. Modeling assumptions

While our model could be easily defined in three dimensions, to explore its behavior we studied it with two dimensional simulations. In our view the computational simplicity of a 2D system is in fact advantageous to the complexities involved in 3D simulations. We expect that our main findings – i.e., oriented adhesion substrates can increase directional persistence of polarized cells, and mechanical equilibrium must be ensured for a cell mass adhering only at its surface – would hold in a three dimensional simulation as well. We expect, however, that an improved method is needed in 3D to bring the system into mechanical equilibrium as the relaxation by several independent local steps is inefficient to find the configuration corresponding to the minimum of the goal function (4).

Cells in invasion assays often emigrate in a highly persistent fashion (see, e.g. [31]). This directional motion can involve at least two potential guidance mechanisms: a response to a concentration gradient (chemotaxis or haptotaxis) and, as we argue in this study, motion along oriented ECM filaments (contact guidance). We are not yet aware of conclusive empirical findings to assess the relative importance of these mechanisms either in vitro or in vivo. While our assumptions of a highly oriented and rigid ECM is clearly unrealistic, yet this model provides a possibility to evaluate the potency of contact guidance under highly favorable conditions.

We assumed that active cell motility is stimulated by contact with the ECM. While signaling through integrins is a plausible underlying molecular mechanism [63], and a motile and less motile cell population are often distinguished in models [22] – this assumption is needed to avoid the development of complex streaming movements inside the aggregate (data not shown). While such movements are indeed observed in 2D monolayers [56], we do not think that this model gives a correct description of active cell movements within a cell aggregate where cells can get traction from each other rather than from an external substrate. Thus, the restriction of active cell movement to cells that are in contact with the ECM is essential to obtain a plausible model.

Our proposed model suggests that the increased persistence during the cell invasion process may be a consequence of two effects: (i) a space-constrained polarized motion and (ii) adhesion to and degradation of the ECM. The former is more relevant when cells move in established microchannels, while the latter is relevant for “tip” cells at the front of invading sprouts. If cells are able to degrade the ECM, then the tendency to invade is determined by the two time scales characterizing intracellular polarity and ECM degradation. Even if ECM degradation is slow, the model allows invasion of cells that maintain intracellular polarity for a sufficiently long time. According to our simulations, haptotaxis and ECM degradation (without active cell motility coupled to an autonomous, internal polarity) destabilizes multicellular sprouts as each cell tries to invade the ECM. In contrast, when both haptotaxis and polarized motion is present in the model, even a homogenous cell population organizes into multicellular sprouts within an inhomogenous ECM environment. We expect that further refinement of the model to include differences between ECM degradation (like distinguishing “tip” and “stalk” cells) would increase the stability and length of the invading sprouts.

5.4. Mechanical equilibrium

The viscoelastic or viscoplastic behavior of cell aggregates [27] are in the forefront of current theoretical interest [64, 65, 66]. As the CPM has been proposed to describe various developmental processes [67], some of which involves large free floating cell masses like the embryonic epiblast [68] – the CPM dynamics should be compared to a biologically plausible elasto-plastic behavior, and if needed, the model rules should be modified accordingly. In this study we demonstrated (Fig. 6) that an unintended friction force can emerge between the cells and the simulation grid in those CPM simulations, where elementary steps are single spin flips. We also expect a similar friction effect when cells are represented by the off lattice subcellular element model [26]. The overdamped Langevin equations – like the equation used in the subcellular element model – can be derived from an equation of motion that contains a strong friction force proportional to the particle’s velocity. This velocity is measured relative to a lab frame of reference where the bulk of the fluid that constitutes the particle’s environment is in rest. Thus, overdamped equations implicitly assume friction forces with a (potentially non existing) local, external reference body. We propose that in models that are not Galilei invariant (e.g., contain an explicit absolute velocity in the governing equations) a variant of our piston test can estimate the magnitude of the friction artefact.

6. Methods

6.1. Cell aggregate invasion assays

Three dimensional cell aggregates were prepared from confluent cell cultures (GBM1 or U87) grown on TC dishes using a modified version of the protocol used in [12]. The adherent human brain tumor cells were grown in DMEM (Sigma) culture medium supplemented with 10% FBS (Lonza, Switzerland), 10 mg/ml of penicillin-streptomycin (Sigma-Aldrich, St Louis, MO). Cell suspensions were obtained through trypsinization (0.1% trypsin, Sigma) and were centrifuged at 2000g for 3 min. The resulting pellet was drawn into 200 μl pipette tips, which were incubated for 30 mins in the cell culture incubator. After the incubation the cylindrical aggregates were immediately embedded into the collagen gel.

Collagen gel was prepared from rat-tail collagen type I (Sigma-Aldrich). Briefly, the powder was dissolved in 1M acetic acid and the pH adjusted with 7.5% NaHCO₃ solution to neutral. The final dilution to the concentration of 1 mg/ml was done with regular culture medium or with medium complemented with a cytostatic inhibitor compound. The ice-cold collagen solution was aliquoted at 200 μl/well in 96-well plates. To initiate gelation, the plate was kept at room temperature for 10 min and then cell aggregates were embedded into the collagen. The plate was transferred to the 37°C incubator for 30 min to allow complete gelation. Finally, the gel was covered with 100 μl of complete growth medium. Samples were subsequently kept at 37°C with 5% CO₂. The medium was changed every other day. The invasion was recorded by daily image acquisition using a phase-contrast Nikon microscope and a Nikon Coolpix 5000 digital camera. The experiments were repeated independently three times.

6.2. Arresting cell proliferation

To block cell divisions, we utilized the research compound Q50 (Avidin Ltd, Hungary). Videomicroscopic recordings of two dimensional adherent GBM1 cell cultures showed an 82% decrease in the number of cell divisions during 48 hours following treatment of the cells with 2.5 μM Q50 while there was no significant decrease in cell migration (data not shown). In invasion assays 2.5 μM Q50 was added at the time of collagen gelation.

6.3. Cell displacement as a function of time

The motility of cells is described by calculating the average displacement, d, during time intervals of various length, t, defined as

$$d(t)=\sqrt{{\langle {(X_i(t+t_0)-X_i(t_0))}^2\rangle }_{t_{0,i}}},$$ (15)

where X_i(t₀) is the position of the center of mass of cell i at time t₀. The 〈…〉_t0,i denotes average over times t₀ and the cell population. To avoid finite size effects, simulated cell trajectories were not sampled after the invading cells reached the system boundary.

6.4. Persistent cell speed and persistence time

To describe the motion of cells, we apply the persistent diffusion description [69]. The displacement over time function (15) of the cells was fitted by

$$d(t)=\sqrt{4D[t-T_p(1-e^{-t/T_p})]},$$ (16)

where T_p is the persistence time of cell motion, and D is the diffusion coefficient of the long-term motion. Thus, for short times, cells move persistently with a speed $S=\sqrt{2D/T_p}$.

6.5. CPM simulations

We have chosen the open source Tissue Simulation Toolkit ([51]) as our CPM framework, in which we implemented our extensions as C++ codes. Active cell motility was implemented according to [56], as summarized in Section 3.3. We implemented ECM degradation and mechanical relaxation routines as described in Sections 3.4 and 3.5, respectively. The simulation code is freely available upon request.

6.6. Cell density along the direction of invasion

In the simulation of ECM invasion, the invasion speed and depth is measured by the relative cell density. Initially, the cell-ECM interface is parallel to one of the system boundaries (y-axis) and is defined to be at the x = 0 position. The invasion is directed towards the positive x-axis. The relative cell density is then defined as:

$$\rho (x_i,t)=\frac{n(x_i,t)}{n_0},$$ (17)

where n(x_i, t) denotes the number of cells, whose centers fall between x_i and x_i+1 = x_i+b at time t, where the bin width is chosen to be b = 10μm. The density is normalized with the initial, confluent cell density,

$$n_0={\langle n(x,t=0)\rangle }_{x<0}.$$ (18)