Statistical Classification of Multivariate Flow Cytometry Data Analyzed by Manual Gating: Stem, Progenitor, and Epithelial Marker Expression in Nonsmall Cell Lung Cancer and Normal Lung

Abstract

The use of supervised classification to extract markers from primary flow cytometry data is an emerging field that has made significant progress, spurred by the growing complexity of multidimensional flow cytometry. Whether the markers are extracted without supervision or by conventional gate and region methods, the number of candidate variables identified is typically larger than the number of specimens (p < n) and many variables are highly intercorrelated. Thus, comparison across groups or treatments to determine which markers are significant is challenging. Here, we utilized a data set in which 86 variables were created by conventional manual analysis of individual listmode data files, and compared the application of five multivariate classification methods to discern subtle differences between the stem/progenitor content of 35 non-small cell lung cancer and adjacent normal lung specimens. The methods compared include elastic-net, lasso, random forest, diagonal linear discriminant analysis, and best single variable (best-1). We described a broadly applicable methodology consisting of: (1) variable transformation and standardization; (2) visualization and assessment of correlation between variables; (3) selection of significant variables and modeling; and (4) characterization of the quality and stability of the model. The analysis yielded both validating results (tumors are aneuploid and have higher light scatter properties than normal lung), as well as leads that require followup: Cytokeratin+ CD133+ progenitors are present in normal lung but reduced in lung cancer; diploid (or pseudo-diploid) CD117+CD44+ cells are more prevalent in tumor. We anticipate that the methods described here will be broadly applicable to a variety of multidimensional cytometry problems.

Analysis of flow cytometry data is usually performed in two steps. In primary analysis, variables such as the proportion of events having given properties (e.g., percent CD3+ of CD45+) are extracted from individual Flow Cytometry Standard (FCS) files. Secondary analysis involves statistical comparison of the tabulated variables between groups or treatments. Although the use of statistical classification methods to automate the extraction of markers from raw or minimally processed FCS is an emerging field (1–4), the application of the similar methodologies to secondary data analysis has not been exploited. Regardless of the method of primary analysis, the number of candidate variables detected in multidimensional cytometry data may exceed the number of specimens to be compared. Thus, simple bivariate comparison, one variable at a time, lacks statistical power to detect between group differences and is blind to correlations that may exist between variables. Clearly, a multivariate approach is needed for the secondary analysis of the large number of variables that are routinely extracted from multidimensional FCS files. When the number of specimens is limited, the conventional approach of nonoverlapping training and validation data sets is not feasible. In such cases, a naïve multivariate analysis may overfit the data, and then optimistically estimate the magnitude of the association between the variables and the group or treatment, resulting in findings that cannot be replicated. Further, small changes in the data or classification method may change those variables are identified as significant when intercorrelation is significant. There are a number of suitable contemporary computational methods for variable selection and modeling, but they have fundamentally different theoretical motivations, require tuning and can choose different variables as "significant." Analysts who have success with one method on one data set tend to apply that method to subsequent data sets. Thus, the results of a particular analysis may become reified without a sense of their sensitivity to different variable selection methods or random variation.

In this report, we propose an analysis workflow to address these issues. Given a previously published set of variables assessed on a limited number of specimens (5), our goal is to identify an appropriate analytical method to select variables related to a dichotomous condition (nonsmall cell lung cancer versus normal lung), to build a model of the condition as a mathematical function of the variables that can be used to classify subsequent specimens and to characterize the robustness of the analysis. By focusing on a flow cytometry data set previously analyzed using simple bivariate comparisons between tumor and adjacent lung specimens, the present analysis will address hazards particular to flow cytometry data: (1) highly correlated variables result in competing models that are difficult to compare; (2) statistical tests summarized by p-values do not necessarily produce sets of variables that reproducibly discriminate between conditions; (3) estimates of sensitivity and specificity must be adjusted when the number of specimens is insufficient to form independent training and testing sets. The proposed workflow, summarized here, and presented in detail as online Supporting Information, provides a practical approach to the secondary analysis of multidimensional flow cytometry data.

METHODS

Terminology

Because the statistical and cytometry literature often attribute different meanings to the same terms (e.g., parameter, sample), we have used the following terminology. A flow cytometry assay assesses a limited number of features (e.g., forward light scatter, 525/40 fluorescence intensity) on hundreds of thousands or millions of events (d, e.g., cells) that are typically acquired from a limited number (n) of specimens (e.g., lung tumor specimens). Feature expression can either be treated as continuous (e.g., fluorescence intensity of an event), or dichotomous (present or absent on a given event). These features are then combined through a gating process to define a number of markers (e.g., CD90+/CD44+). Variables (p) are derived from markers as either: (1) ratios of the numbers of events having or not having these markers as determined by a gating process (e.g., proportion of CD90+/CD44+ cells among cytokeratin+ cells); (2) absolute number (events per volume) of events having a given marker; or (3) the numerical value of a feature in a population of events defined by a marker (e.g., the mean fluorescence intensity of CD90-PE among CD90+/CD44+/cytokeratin+ events).

Acquisition of Data by Flow Cytometry

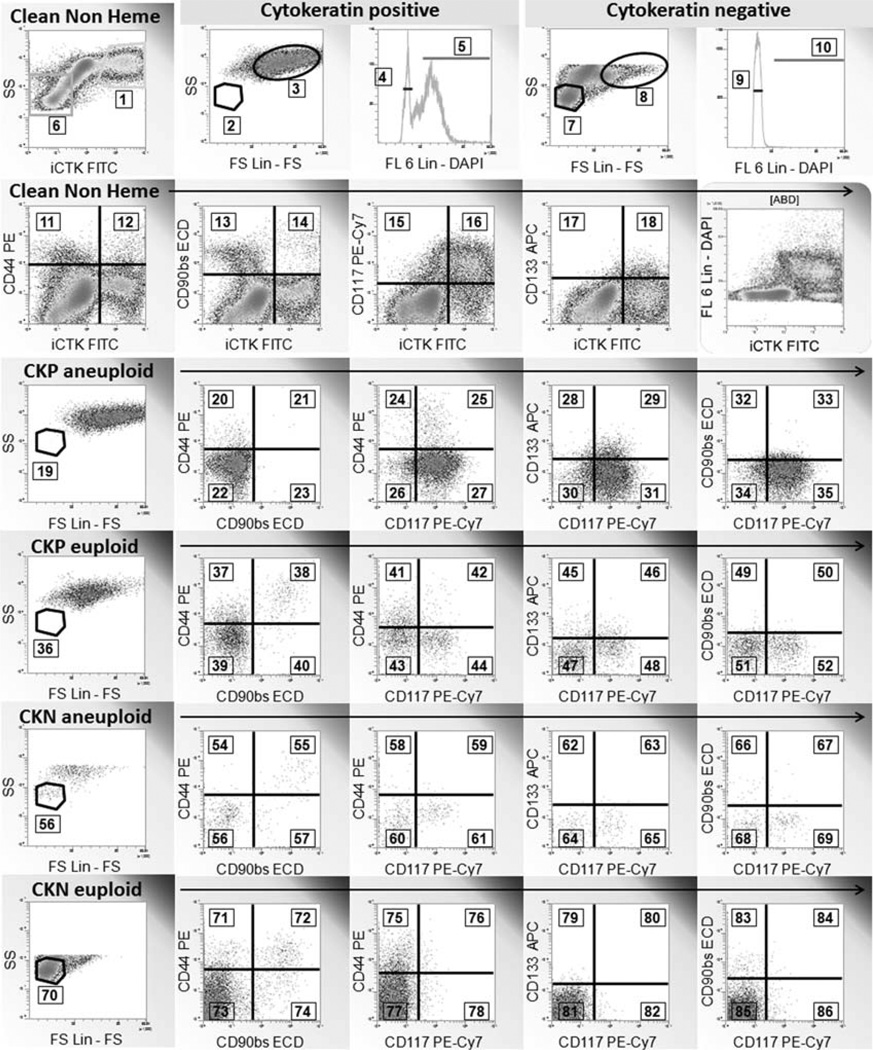
Eight-color, 11-feature data were collected for 16 paired nonsmall cell lung tumors/normal lung specimens, plus three additional tumor specimens. All specimens were collected under IRB approval (UPCI 99-053). Specimens, specimen processing, data acquisition, and variable extraction using conventional (gate and region) analysis have been reported in detail, including a MIFlowCyt checklist (5). Following artifact removal (6,7), the analysis was focused on the comparison of stem/progenitor marker expression (CD44, CD90, CD117, CD133) on tumor cells and cells from adjacent normal lung. After limiting the analysis to CD45−/CD14−/CD33−/glycophorin A-cells, we subseted based on cytokeratin expression (epithelial versus nonepithelial or pre-epithelial) and ploidy (2N vs.>2N), yielding four classes of cells on which to assess variables (proportion of cells positive for stem/progenitor markers, proportion with low versus high light scatter, Fig. 1). The reason for using DNA content as a grouping variable is that, in tumor specimens, we could be certain that the majority of aneuploid cells were of bona fide tumor origin (as opposed to normal stromal or epithelial cells). The analytical regions in Figure 1, numbered 1–86, are linked to variable names and descriptions in Table 1. The data for all listmode files were analyzed using VenturiOne software (Applied Cytometry Systems, Dinnington, UK) in one session to standardize the placement of analytical regions. Region data (event counts) were exported to a comma-separated variable (.csv) file for statistical analysis. The data are available to interested investigators by request to the corresponding author.

Figure 1.

Regions and gates used in mutivariate analysis. This example shows a lung adenocarcinoma. Logical gates applied to each histogram are shown above the histogram frame. The “Clean Non Heme” gate was created on CD45-/CD14-/CD33-/glycophorin A-singlet events with DNA content ≥ 2N (not shown). The region numbers indicate the markers used for multivariate analysis and are keyed to Table 1. CKP + cytokeratin+, CKN = cytokeratin negative Euploid = gated on region 4 or 9. Aneuploid = gated on region 5 or 10. The euploid and low light scatter regions were matched to tissue infiltrating lymphocytes (not shown).

Table 1.

Variable names and descriptions keyed to the analytical regions in Figure 1

REGION	VARIABLE NAME	DESCRIPTION (MARKER)	DENOMINATOR (MARKER)
1	CKP	Cytokeratin+	Singlet ≥ 2N DNA events
2	CKP_SM	Cytokeratin+ lymphoid scatter	Cytokeratin+
3	CKP_LG	Cytokeratin +, > lymphoid scatter	Cytokeratin+
4	CKP_2N	Cytokeratin+ euploid	Cytokeratin+
5	CKP_GT2N	Cytokeratin+ aneuploid	Cytokeratin+
6	CKN	Cytokeratin negative	Singlet ≥ 2N DNA events
7	CKN_SM	Cytokeratin negative lymphoid scatter	Cytokeratin negative
8	CKN_LG	Cytokeratin negative > lymphoid scatter	Cytokeratin negative
9	CKN_2N	Cytokeratin negative euploid	Cytokeratin negative
10	CKN_GT2N	Cytokeratin negative aneuploid	Cytokeratin negative
11	CKN_44P	Cytokeratin negative CD44+	Cytokeratin negative
12	CKP_44P	Cytokeratin+ CD44+	Cytokeratin+
13	CKN_90P	Cytokeratin negative CD90+	Cytokeratin negative
14	CKP_90P	Cytokeratin+ CD90+	Cytokeratin+
15	CKN_117P	Cytokeratin negative CD117+	Cytokeratin negative
16	CKP_117P	Cytokeratin+ CD117+	Cytokeratin+
17	CKN_133P	Cytokeratin negative CD133+	Cytokeratin negative
18	CKP_133P	Cytokeratin+ CD133+	Cytokeratin+
19	CPG2_SMALL	Cytokeratin+ aneuploid lymphoid scatter	Cytokeratin+ aneuploid
20	CPG290N44P	Cytokeratin+ aneuploid CD90 negative CD44+	Cytokeratin+ aneuploid
21	CPG290P44P	Cytokeratin+ aneuploid CD90+ CD44+	Cytokeratin+ aneuploid
22	CPG290N44N	Cytokeratin+ aneuploid CD90 negative CD44 negative	Cytokeratin+ aneuploid
23	CPG290P44N	Cytokeratin+ aneuploid CD90+ CD44 negative	Cytokeratin+ aneuploid
24	CPG2117N44P	Cytokeratin+ aneuploid CD117 negative CD44+	Cytokeratin+ aneuploid
25	CPG2117P44P	Cytokeratin+ aneuploid CD117+ CD44+	Cytokeratin+ aneuploid
26	CPG2117N44N	Cytokeratin+ aneuploid CD117 negative CD44 negative	Cytokeratin+ aneuploid
27	CPG2117P44N	Cytokeratin+ aneuploid CD117+ CD44 negative	Cytokeratin+ aneuploid
28	CPG2117N133P	Cytokeratin+ aneuploid CD117 negative CD133+	Cytokeratin+ aneuploid
29	CPG2117P133P	Cytokeratin+ aneuploid CD117+ CD133+	Cytokeratin+ aneuploid
30	CPG2117N133N	Cytokeratin+ aneuploid CD117 negative CD133 negative	Cytokeratin+ aneuploid
31	CPG2117P133N	Cytokeratin+ aneuploid CD117+ CD133 negative	Cytokeratin+ aneuploid
32	CPG2117N90P	Cytokeratin+ aneuploid CD117 negative CD90+	Cytokeratin+ aneuploid
33	CPG2117P90P	Cytokeratin+ aneuploid CD117+ CD90+	Cytokeratin+ aneuploid
34	CPG2117N90N	Cytokeratin+ aneuploid CD117 negative CD90 negative	Cytokeratin+ aneuploid
35	CPG2117P90N	Cytokeratin+ aneuploid CD117+ CD90 negative	Cytokeratin+ aneuploid
36	CP2_SMALL	Cytokeratin+ euploid lymphoid scatter	Cytokeratin+ euploid
37	CP90N44P	Cytokeratin+ euploid CD90 negative CD44+	Cytokeratin+ euploid
38	CP90P44P	Cytokeratin+ euploid CD90+ CD44+	Cytokeratin+ euploid
39	CP90N44N	Cytokeratin+ euploid CD90 negative CD44 negative	Cytokeratin+ euploid
40	CP90P44N	Cytokeratin+ euploid CD90+ CD44 negative	Cytokeratin+ euploid
41	CP2117N44P	Cytokeratin+ euploid CD117 negative CD44+	Cytokeratin+ euploid
42	CP2117P44P	Cytokeratin+ euploid CD117+ CD44+	Cytokeratin+ euploid
43	CP2117N44N	Cytokeratin+ euploid CD117 negative CD44 negative	Cytokeratin+ euploid
44	CP2117P44N	Cytokeratin+ euploid CD117+ CD44 negative	Cytokeratin+ euploid
45	CP2117N133P	Cytokeratin+ euploid CD117 negative CD133+	Cytokeratin+ euploid
46	CP2117P133P	Cytokeratin+ euploid CD117+ CD133+	Cytokeratin+ euploid
47	CP2117N133N	Cytokeratin+ euploid CD117 negative CD133 negative	Cytokeratin+ euploid
48	CP2117P133N	Cytokeratin+ euploid CD117+ CD133 negative	Cytokeratin+ euploid
49	CP2117N90P	Cytokeratin+ euploid CD117 negative CD90+	Cytokeratin+ euploid
50	CP2117P90P	Cytokeratin+ euploid CD117+ CD90+	Cytokeratin+ euploid
51	CP2117N90N	Cytokeratin+ euploid CD117 negative CD90 negative	Cytokeratin+ euploid
52	CP2117P90N	Cytokeratin+ euploid CD117+ CD90 negative	Cytokeratin+ euploid
53	CNG2_SMALL	Cytokeratin negative aneuploid lymphoid scatter	Cytokeratin negative aneuploid
54	CNG290N44P	Cytokeratin negative aneuploid CD90 negative CD44+	Cytokeratin negative aneuploid
55	CNG290P44P	Cytokeratin negative aneuploid CD90+ CD44+	Cytokeratin negative aneuploid
56	CNG290N44N	Cytokeratin negative aneuploid CD90 negative CD44 negative	Cytokeratin negative aneuploid
57	CNG290P44N	Cytokeratin negative aneuploid CD90+ CD44 negative	Cytokeratin negative aneuploid
58	CNG2117N44P	Cytokeratin negative aneuploid CD117 negative CD44+	Cytokeratin negative aneuploid
59	CNG2117P44P	Cytokeratin negative aneuploid CD117+ CD44+	Cytokeratin negative aneuploid
60	CNG2117N44N	Cytokeratin negative aneuploid CD117 negative CD44 negative	Cytokeratin negative aneuploid
61	CNG2117P44N	Cytokeratin negative aneuploid CD117+ CD44 negative	Cytokeratin negative aneuploid
62	CNG2117N133P	Cytokeratin negative aneuploid CD117 negative CD133+	Cytokeratin negative aneuploid
63	CNG2117P133P	Cytokeratin negative aneuploid CD117+ CD133+	Cytokeratin negative aneuploid
64	CNG2117N133N	Cytokeratin negative aneuploid CD117 negative CD133 negative	Cytokeratin negative aneuploid
65	CNG2117P133N	Cytokeratin negative aneuploid CD117+ CD133 negative	Cytokeratin negative aneuploid
66	CNG2117N90P	Cytokeratin negative aneuploid CD117 negative CD90+	Cytokeratin negative aneuploid
67	CNG2117P90P	Cytokeratin negative aneuploid CD117+ CD90+	Cytokeratin negative aneuploid
68	CNG2117N90N	Cytokeratin negative aneuploid CD117 negative CD90 negative	Cytokeratin negative aneuploid
69	CNG2117P90N	Cytokeratin negative aneuploid CD117+ CD90 negative	Cytokeratin negative aneuploid
70	CN2_SMALL	Cytokeratin negative euploid lymphoid scatter	Cytokeratin negative euploid
71	CN90N44P	Cytokeratin negative euploid CD90 negative CD44+	Cytokeratin negative euploid
72	CN90P44P	Cytokeratin negative euploid CD90+ CD44+	Cytokeratin negative euploid
73	CN90N44N	Cytokeratin negative euploid CD90 negative CD44 negative	Cytokeratin negative euploid
74	CN90P44N	Cytokeratin negative euploid CD90+ CD44 negative	Cytokeratin negative euploid
75	CN2117N44P	Cytokeratin negative euploid CD117 negative CD44+	Cytokeratin negative euploid
76	CN2117P44P	Cytokeratin negative euploid CD117+ CD44+	Cytokeratin negative euploid
77	CN2117N44N	Cytokeratin negative euploid CD117 negative CD44 negative	Cytokeratin negative euploid
78	CN2117P44N	Cytokeratin negative euploid CD117+ CD44 negative	Cytokeratin negative euploid
79	CN2117N133P	Cytokeratin negative euploid CD117 negative CD133+	Cytokeratin negative euploid
80	CN2117P133P	Cytokeratin negative euploid CD117+ CD133+	Cytokeratin negative euploid
81	CN2117N133N	Cytokeratin negative euploid CD117 negative CD133 negative	Cytokeratin negative euploid
82	CN2117P133N	Cytokeratin negative euploid CD117+ CD133 negative	Cytokeratin negative euploid
83	CN2117N90P	Cytokeratin negative euploid CD117 negative CD90+	Cytokeratin negative euploid
84	CN2117P90P	Cytokeratin negative euploid CD117+ CD90+	Cytokeratin negative euploid
85	CN2117N90N	Cytokeratin negative euploid CD117 negative CD90 negative	Cytokeratin negative euploid
86	CN2117P90N	Cytokeratin negative euploid CD117+ CD90 negative	Cytokeratin negative euploid

Data Analysis Workflow

We analyzed the data according to the following steps: (1) transformation and standardization; (2) visualization and assessment of correlation between variables; (3) selection of significant markers and modeling; (4) characterization of the quality and stability of the model. All of the analytic steps applied to the data in the .csv file were performed using the open-source statistical package R (8). A diagram of the workflow (Fig. S1) and the associated R code is included in the online Supporting Information.

Transformation and Standardization

Because the variables analyzed in this data set were proportions (e.g., proportion of cytokeratin+ viable cells), it was necessary to address their statistical properties. First, when a population of cells is divided into a set and its complement, the two proportions are perfectly correlated (r = −1). Similarly, large fractions are often highly correlated. For example, cytokeratin+ and cytokeratin negative, expressed as a proportion of nucleated cells, are highly inversely correlated. Second, mid-range proportions (e.g., aneuploid tumor cells as a proportion of cytokeratin positive cells) tend to be normally distributed, but proportions that are close to 0 or 1 have asymmetric distributions over the specimens. Third, proportion estimates on small denominators (<50 cells) are unreliable. Finally, zero proportions do not necessarily indicate an impossible event, but, possibly, a rare, yet informative event, especially when denominators are small. We addressed these issues by unzeroing, stabilization, and standardization.

Unzeroing

Some numerical transformations (e.g., logarithmic) cannot operate on zeros or ones, and some statistical classifiers perform worse on highly skewed data. We replaced zeros by a random value between zero and one-tenth the smallest nonzero value and ones by a random value between 1 and 1 − (1 − m)/10, where m is the largest value less than 1. Additional details are presented in the Supporting Information.

Stabilization

Some statistical classification methods assume that the variables have Gaussian distributions (e.g., Fisher’s linear discriminant analysis) or do not accommodate highly skewed data well. We used the logit transform in our analysis because it is symmetric and its range is all positive and all negative numbers. The logit and inverse logit transformations are shown in Supporting Information Figure S2, where merits of various transformations are discussed.

Standardization

For each variable, we subtracted the mean and divided by the standard deviation, so that, over specimens from all conditions, mean equals 0 and the observed standard deviation equals 1. This was required because some computational algorithms are unstable when operating simultaneously on values with multilog differences in scale.

Visualization of Data and Assessment of Correlation Between Variables

The transformed, standardized data were scanned for artifacts, influence points, and obvious classifiers before analysis. Outliers, in the usual sense of very large (positive or negative) values, are not present in transformed, standardized proportions. However, influence points (single values that induce correlations), such as clusters of 0 and 1 counts, were evident in the data and required unzeroing as described above.

Initial Assessment of Variables for Classification

We performed comparisons of the individual variables versus the condition by t-tests and/or rank sum tests to determine whether modeling was feasible (Table 2). Because a number of significant differences were observed, we proceeded with the analysis. Although a small p-value does not necessarily indicate a good classifier, if none of the p-values were significant, we would have terminated the analysis.

Table 2.

P-values of unpaired t- and rank-sum tests on tumor versus normal lung specimens. The 32 variables with the smallest P-values (t-test) are shown

	P-VALUES
VARIABLE	T-TEST	RANK SUM TEST
CKP_GT2N	0.00044	0.00099
CPG2117N133P	0.00055	0.00175
CKP_2N	0.00056	0.0014
CNG2117P44N	0.00576	0.02728
CKP_SM	0.00637	0.00934
CP2117P44P	0.01037	0.00417
CP2117N90N	0.01227	0.0113
CP2117P90N	0.01378	0.0254
CP90P44N	0.01406	0.04156
CNG2117P90N	0.02459	0.13389
CNG2117P133N	0.0254	0.32797
CN2117P90P	0.02604	0.07043
CP2117P90P	0.02838	0.02851
CN2117P90N	0.03012	0.08804
CN2117P44N	0.03157	0.02228
CP2117P44N	0.04039	0.10825
CP90P44P	0.04301	0.08205
CP2117P133N	0.04342	0.04512
CKP_117P	0.04358	0.10827
CP2117N90P	0.04361	0.07645
CKN_LG	0.04424	0.02766
CKP_LG	0.0519	0.01636
CP2_SMALL	0.05602	0.0417
CKN_GT2N	0.05917	0.08813
CN2117P133N	0.06373	0.14972
CPG2117P133N	0.06616	0.16938
CNG2117P90P	0.08081	0.35498
CP2117P133P	0.0812	0.08487
CKN_117P	0.08168	0.26727
CN2117N133P	0.09289	0.07113
CPG2117N90N	0.09721	0.16938
CKN_2N	0.14364	0.3625

Selection of Significant Variables and Modeling of Condition

We tested a number of methods in a resampling framework to determine if: (1) some methods classify the specimens better than others; (2) there is agreement between the methods on which variables are important; (3) there are any specimens that have particular influence over the variables selected as important and/or coefficient estimates; and (4) the estimated coefficients are sensitive to small perturbations in the data. We used two resampling methods to address these issues: cross-validation and bootstrapping.

Cross-Validation

The data were partitioned into 10 disjoint subsets. At each of 10 iterations, a different subset was set aside and modeling parameters were estimated from the other 9 subsets, pooled together. We estimated the sensitivity and specificity, and set tuning parameters using the set-aside test set.

Bootstrapping

In the nonparametric bootstrap (9), a sample of specimens, the same size as the original sample specimen data set, was constructed by random draws from the original sample with replacement. That is, once an observation was selected for the bootstrap sample, it was replaced in the pool of eligible observations where it could be sampled again. All of the methods were trained on the bootstrap sample, and the specimens that were excluded from the sample (equal, on average, to (1 − 1/n)ⁿ ≈ 0.37 of the sample size, n) were treated as the test set. These excluded samples are referred to as out-of-bag (OOB). The bootstrapping process was repeated 500 times, each bootstrap iteration testing the full set of methods on different training and test sets, both of which were drawn from the full sample. Once the bootstrap iterations were completed, the average and the variability of the cross-validated sensitivity, specificity, accuracy, selected variables, influential specimens, and estimated coefficients of the different methods were estimated by the empirical distribution of bootstrap estimates. Further discussion and software code appears in the online Supporting Information.

Variable Importance

Within each bootstrap iteration, variables were chosen as either significant contributors to the discriminator, or nonsignificant. The proportion of iterations in which a given variable was considered significant is a measure of the robustness of its power as a discriminator. The correlation of selection between variables (where each variable is coded 1 if it is selected, and 0 otherwise) was interpreted as a descriptor of structure; variables whose selection indices are negatively correlated are possibly associated with a pathway.

Influential Observations

We also calculated the proportion of bootstrap iterations in which each test specimen was correctly classified as tumor or normal lung. Specimens that are consistently misclassified by one method, but not another, may indicate that a nonlinear partition may be required, or that the specimen is dissimilar from other specimens with the same condition. A specimen that is misclassified in close to ½ of the bootstrap iterations probably lies close to the partition boundary.

Candidate Classifiers

We focused on three methods that reflect different philosophies of model building: diagonal linear discrimination (DLDA), random forests, and elastic net. DLDA is frequently used in very high-dimensional analyses; it is structurally very simple, and reduces computationally complexity by ignoring interactions between the variables. Random forest is a nonparametric machine learning method that itself uses a resampling method to form a partition of the variable space that may be highly nonlinear. Elastic net is a “regularized” version of logistic regression that is designed for stability in the presence of highly correlated variables and has a built-in variable selection scheme. We also used the lasso (which is a special case of elastic net), and a naïve classifier, best-single marker. All of these methods were embedded in the bootstrap loop; all methods were applied to each bootstrap sample, and then the results were compared. Details and code for all these methods are in the online Supporting Information.

RESULTS

Visualization and Assessment of Correlation Within Subjects and Between Variables

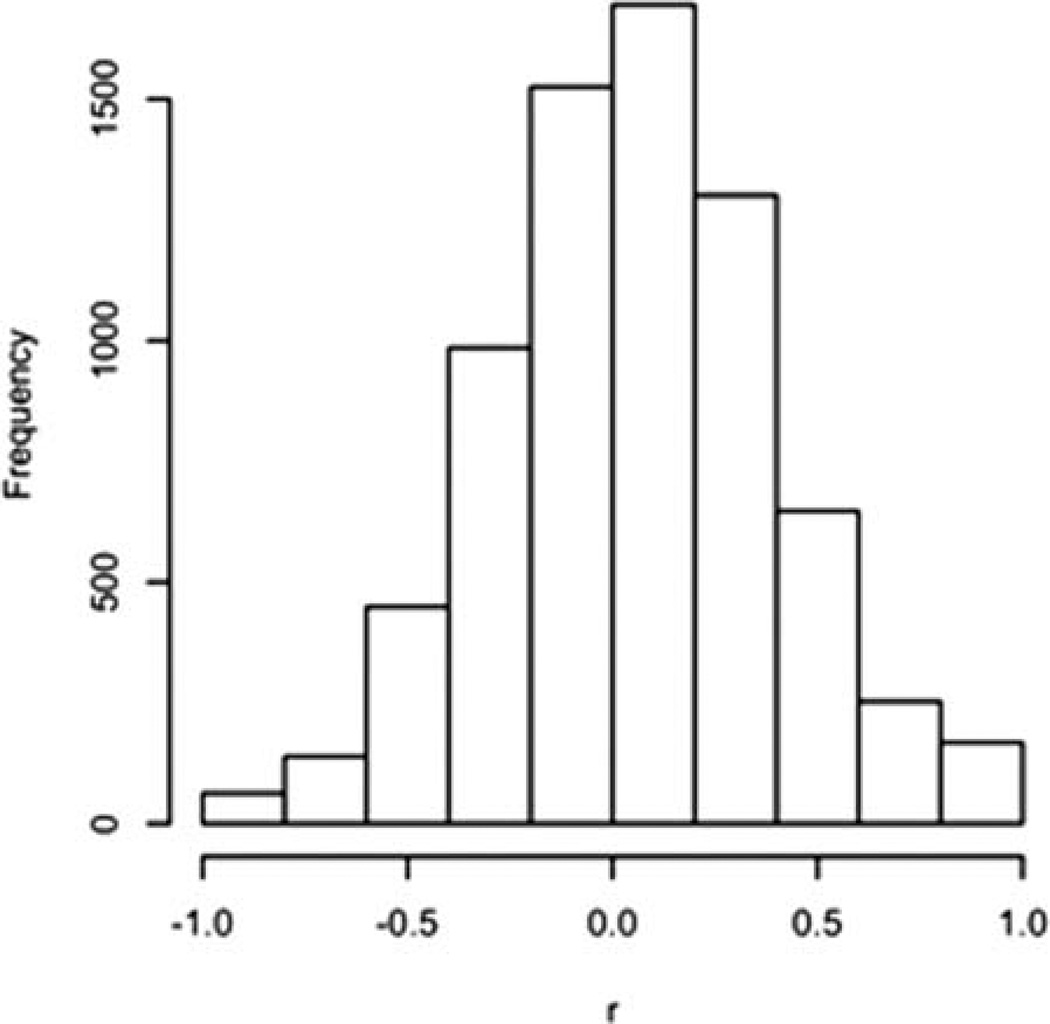
Before logit transformation, centering, and scaling, we jittered 0 values to between 1/10 of the smallest non-zero value and 0. Values of 1 were treated analogously. The intrasubject correlation (between tumor and normal lung) on the 86 variables was measured on the 16 pairs of specimens (three tumor specimens did not have paired normal tissue). The median of the 86 correlation coefficients was 0.22, and ranged from −0.63 to 0.87. The low mean of the correlations indicated that an analysis based on differences within subject was unlikely to be useful. We decided not to analyze the data as paired (tumor and normal specimens), but to treat the specimens as independent. Scatterplots of variables (tumor versus normal) with large coefficients indicated that many of the largest correlations (either positive or negative) were artifactual. The distribution of the 86 × (86 − 1)/2 = 3655 pairwise correlation coefficients (tumor vs. normal lung) is illustrated in Figure 2. A heat map and dendrogram of the normal lung and tumor specimens in the lung data set did not immediately indicate a dominant cluster of discriminating variables (Fig. S3). The closest two single variables are CKN_44P (cytokeratin negative/CD44+) and CN2117N44P (cytokeratin negative, euploid, CD117 negative/CD44+), which are highly correlated (r = 0.96) because the latter is a subset of the former.

Figure 2.

Distribution of between-variable correlations in the example data set.

Initial Assessment of Variables for Classification

Table 2 displays the p-values of Student’s t and Wilcoxon rank sum tests comparing the distributions between normal lung and tumor specimens for all of the variables, from most significant (Student’s t) to least significant. It is seen that there are some significant differences, so that further classification analysis is warranted, but that the distributions of most variables in normal lung and tumor specimens are similar, so the final discriminators are not expected to include many variables.

Sensitivity and Specificity

The sensitivity, specificity, and accuracy of the discriminators, estimated over the 500 bootstrap samples, are presented in Table 3. The bootstrapped estimates are calculated by classifying the OOB samples (averaged over all bootstrap iterations), whereas the resubstitution estimates are obtained by classifying the training samples (also averaged over all bootstrap iterations). DLDA, random forests, elastic net, and the lasso produce essentially equivalent accuracy; random forest is different from the other three in that its estimated specificity is larger than its sensitivity. The differences between sensitivity and specificity in these methods are more likely due to peculiarities of the example set than the methods themselves. Best-1 accuracy is lower than the other four methods, which is not surprising, given that it is restricted to a single variable. The bootstrapped estimates of sensitivity, specificity, and accuracy are much less optimistic than the resubstitution estimates. Resubstitution estimates of the operating characteristics of Best-1 were not as optimistic, but the bootstrapped estimates were not as good as the other methods.

Table 3.

Sensitivity, specificity, and accuracy of the five methods

		E-NET	RANDOM FOREST	DLDA	LASSO	BEST-1
Bootstrapped Estimates	Sensitivity	0.696	0.623	0.691	0.694	0.659
	Specificity	0.659	0.692	0.617	0.658	0.548
	Accuracy	0.679	0.654	0.658	0.678	0.609
Resubstitution Estimates	Sensitivity	0.895	1	0.895	0.895	0.684
	Specificity	0.938	1	0.875	0.938	0.750
	Accuracy	0.914	1	0.886	0.914	0.714

Sensitivity is defined as true positives (TP)/(TP + false negatives (FN)), Specificity = true NEGATIVES (TN)/(TN + False positives (FP)), Accuracy = (TP+TN)/(TP+TN+FP+FN).

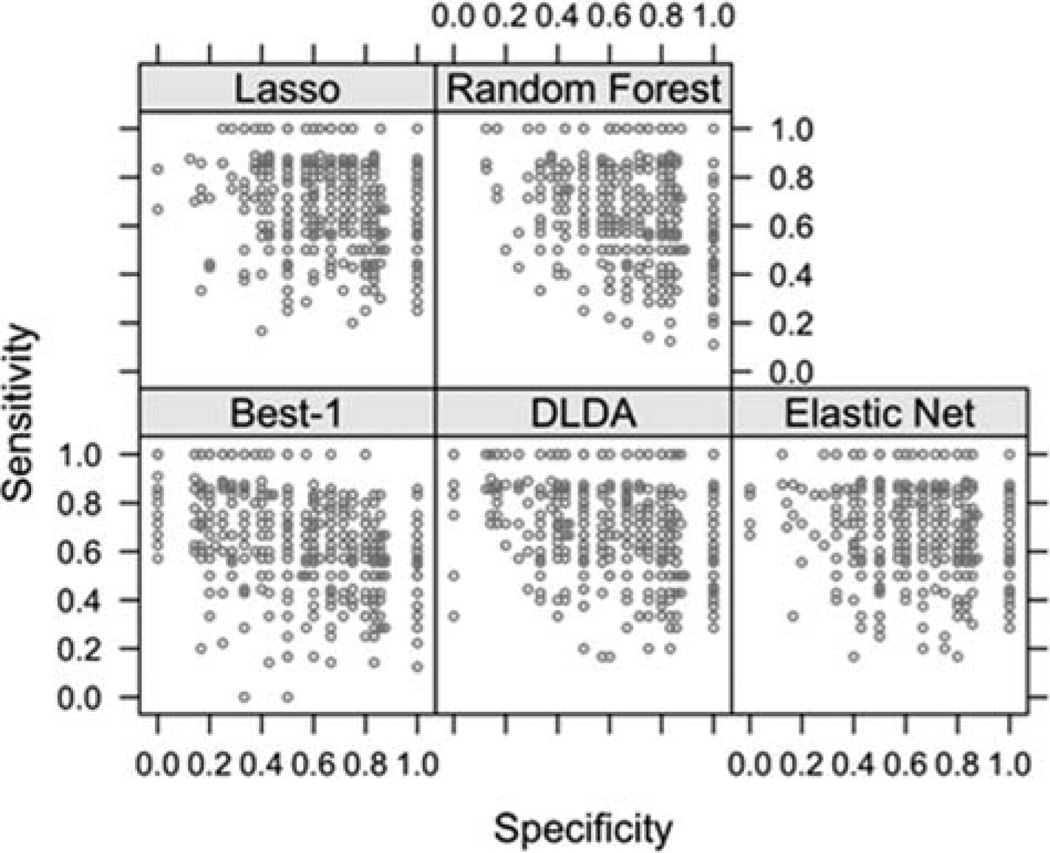
Figure 3 is a scatterplot of the estimates of sensitivity and specificity over all 500 bootstrap samples for the five methods. This plot demonstrates the variability in sensitivity and specificity that could occur when sampling from the population from which the study sample was drawn. If there was no evaluation of the variability of estimation, then the observed sensitivity and specificity could be any one of the graphed values, and it would not be possible to determine how typical or atypical those estimates might be. It is seen that the observed sensitivities and specificities (Table 3) are roughly at the modes in Figure 3.

Figure 3.

Specificity and sensitivity of 500 bootstrap samples.

Variables Selected

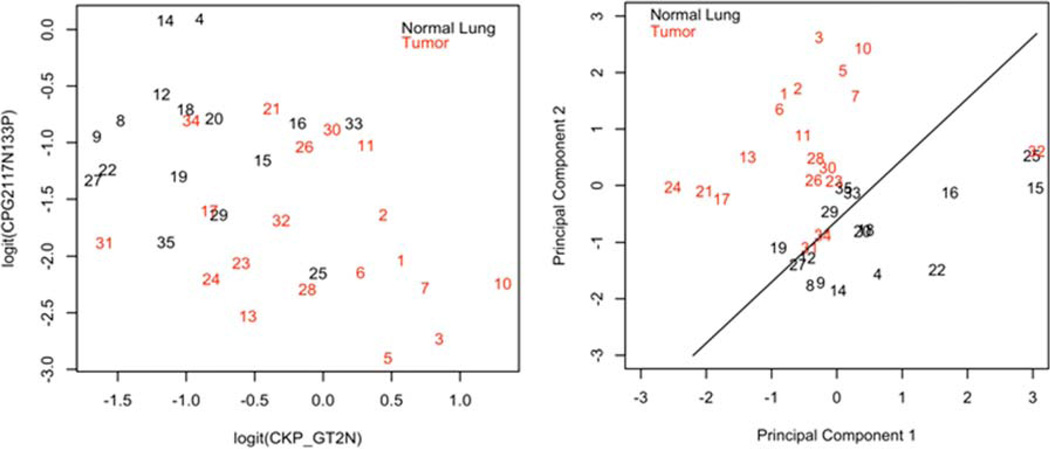
Table 4 presents the importance index of each variable on a scale of 0–500 (the number of bootstrap iterations). The values for elastic net, random forest, DLDA, and lasso are much larger than those for Best-1 discrimination because the total number of variables chosen over 500 bootstrap iterations of Best-1 is fixed at a total of 500. The table is ordered by the average importance index over the five methods, where the top variables are, on average, most important. There is a fairly large drop in importance after the fifth most important variable, CKN_SM (cytokeratin negative, lymphoid scatter). Except for CKN_SM and CPG2117N133P (cytokeratin+ aneuploid CD117 negative CD133+), the five most important variables do not cluster together (Fig. S3), suggesting that they represent different processes. Figure 4 shows the first two principal components of the top five variables. The variables commonly chosen are mostly coherent on the average, but different methods can be fairly discordant on the same bootstrap sample. Table 5 displays the concordance of the five methods in choosing CKP_GT2N (cytokeratin+ aneuploid), the variable with the highest mean importance index, across the bootstrap samples. Even though elastic net and lasso are similar in concept, they are discordant in 86/500 = 17.2% of the bootstrap samples. Best-1, which is not smoothed or regularized in any way, is usually discordant with the other methods.

Table 4.

Importance of variables on a scale of 0–500

	E-NET	RANDOM FOREST	DLDA	LASSO	BEST-1
CKP_GT2N	408	321	391	342	84
CPG2117N133P	386	293	378	350	130
CP2117P44P	357	246	229	318	33
CKP_2N	265	289	366	180	67
CKP_SM	335	254	270	246	42
CNG2117P44N	116	158	328	76	35
CP2117P90P	264	60	125	231	20
CP2_SMALL	193	201	139	114	1
CP90P44N	192	94	188	156	15
CN2117P44N	197	162	121	142	1
CKN_GT2N	213	127	93	164	1
CP2117N90N	120	167	203	93	9
CN2117P90P	129	131	149	106	9
CP2117P90N	105	118	195	84	9
CKN_133P	238	33	30	207	0
CN2117P90N	103	121	121	71	2
CNG2117P90N	89	57	174	76	9
CKN_LG	83	135	105	59	3
CKP_LG	49	144	145	35	5
CP2117N90P	86	117	75	53	1
CP90P44P	83	75	84	66	1
CPG2117P90P	146	13	26	119	0
CPG2_SMALL	57	167	46	30	0
CNG2117N133P	107	83	10	78	1
CNG2117P90P	24	107	90	21	7
CN2117N133P	46	89	67	33	1
CNG2_SMALL	83	63	25	62	0
CNG2117P133N	32	23	151	20	1
CPG2117P133P	99	24	13	80	0
CKN_SM	88	32	31	63	0
CN2117P133N	44	84	45	36	0
CNG2117P133P	106	6	14	80	0
CP2117N44N	76	32	40	55	2
CN90P44N	95	22	12	69	0
CN2117P44P	70	36	30	43	1
CP90N44N	88	8	17	55	0
CN2_SMALL	45	50	36	33	1
CP2117P44N	18	50	86	7	0
CPG290P44N	63	11	37	47	0
CN2117P133P	54	21	34	45	3
CKN_117P	52	21	33	47	0
CN2117N133N	54	50	6	38	0
CKP_117P	44	17	56	25	1
CP2117P133P	25	38	64	10	2
CKN	49	27	26	36	0
CKN_2N	47	27	40	22	0

The variables are sorted in order of their average importance across all five methods. Variables chosen as significant (modal number) by the different methods are shaded. Red shading indicates that the value of the variable is greater in tumor than in normal, green shading indicates the converse. The most important 32 variables are shown.

Figure 4.

Two most important variables versus principal component analysis discriminating between tumor and normal lung. The plot on the left shows ability of the two most predictive variables (cytokeratin+ aneuploid and cytokeratin+ aneuploid CD117 negative CD133+) to distinguish between tumor and normal lung. The plot on the right shows the two principal components of five most important variables (Table 4). Numbers refer to the specimen ID column in Table 6. The case number indicates the frequency with which the case was correctly classified (lower number more frequently classified correctly). [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Table 5.

Concordance between methods in choosing CKP_GT2N (cytokeratin+ aneuploid cells) as a significant classifying variable over 500 bootstrap iterations

		RF		DLDA		LASSO		BEST-1
		N	Y	N	Y	N	Y	N	Y
EN	N	46	35	35	46	75	6	80	1
	Y	107	312	63	356	80	339	309	110
RF	N			68	85	65	88	142	11
	Y			30	317	90	257	247	100
DLDA	N					51	47	98	0
	Y					104	298	291	111
Lasso	N							148	7
	Y							241	104

Two by two tables are shown for each pair of methods. “Y” indicates the given model included CKP_GT2N, “N” indicates that it was excluded.

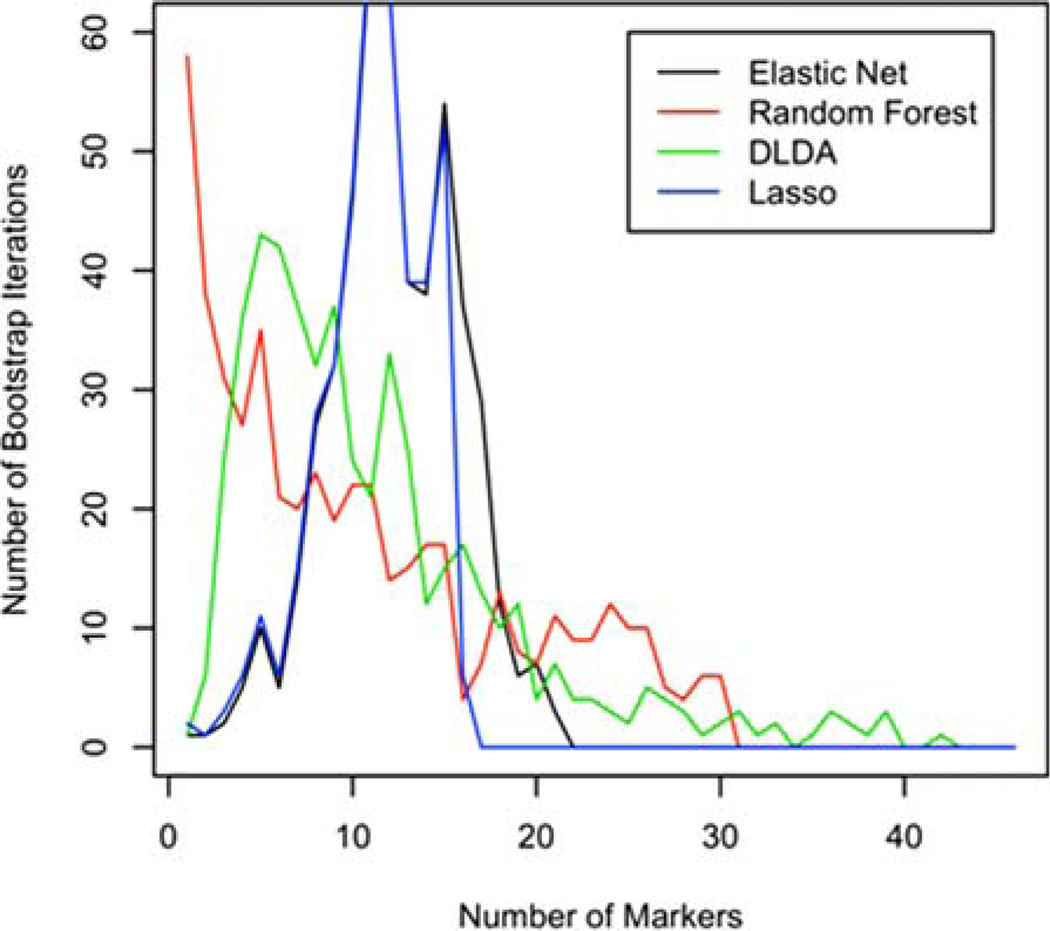
Figure 5 displays the distributions of the numbers of variables selected by the different methods across the bootstrap samples (Best-1 is not included because it always chooses exactly one variable). As expected, the numbers of variables in the elastic net models with the most variables were larger than similar numbers associated with the lasso (Fig. 5). Reducing the mixing parameter α shifts the elastic net curve to the right, capturing more variables, but not increasing the accuracy of classification (data not shown). Although DLDA’s number of variables is smaller than the first two, it has a longer tail, describing a few runs where over 20 variables were selected. Random forest tends to build more parsimonious models, but also sometimes will indicate that 20 or even 30 variables are useful in classifying specimens.

Figure 5.

Numbers of variables chosen by individual method (Best-1 always chooses one variable). [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Classification of Individual Specimens

Table 6 shows the frequency with which each specimen was correctly classified (tumor or normal lung) by each method over 500 bootstrap iterations. The column labeled c.v. is a measure of concordance of the methods, with low coefficients of variation indicating better concordance. All of the methods have difficulty with specimens 27 through 35.

Table 6.

Proportion of correct classifications by method for each specimen

	ID	E-NET	RANDOM FOREST	DLDA	LASSO	BEST-1	C.V.
LungCATSC076/TUMOR	1	0.9941	0.9822	0.9941	1.0000	0.9704	0.0120
LungCATSC094/TUMOR	2	0.9830	0.9830	0.9943	0.9886	0.9830	0.0052
CircLungCATSC028/TUMOR	3	1.0000	0.9593	0.9884	1.0000	0.9651	0.0196
LungCATSC098/NL	4	0.9830	0.9886	0.9886	0.9830	0.9148	0.0328
LungCATSC072/TUMOR	5	0.9887	0.9605	0.9774	0.9774	0.9379	0.0205
LungCATSC101/TUMOR	6	0.9672	0.9672	0.9836	0.9672	0.8962	0.0359
LungCATSC074/TUMOR	7	0.9763	0.8817	0.9941	0.9704	0.7988	0.0893
CircLungCATSC029/NL	8	1.0000	0.9846	0.9026	1.0000	0.7026	0.1384
CircLungCATSC028/NL	9	0.9748	1.0000	0.8994	0.9686	0.7233	0.1232
CircLungCATSC025/TUMOR	10	0.9697	0.7727	0.9596	0.9747	0.8081	0.1095
CircLungCATSC023/TUMOR	11	0.9711	0.9653	0.9538	0.9595	0.6012	0.1816
LungCATSC092/NL	12	0.8497	0.9016	0.9378	0.8549	0.7772	0.0701
LungCATSC087/TUMOR	13	0.9055	0.8358	0.9204	0.9005	0.6915	0.1113
LungCATSC081/NL	14	0.9322	0.7627	0.6836	0.9322	0.6328	0.1762
LungCATSC087/NL	15	0.7988	0.9290	0.8462	0.7929	0.4970	0.2115
CircLungCATSC023/NL	16	0.7354	0.7725	0.7778	0.7460	0.4497	0.1996
LungCATSC121/TUMOR	17	0.7472	0.5506	0.7921	0.7247	0.6517	0.1364
LungCATSC089/NL	18	0.5529	0.8235	0.6706	0.5412	0.6765	0.1754
LungCATSC101/NL	19	0.6705	0.7443	0.5568	0.6818	0.5966	0.1137
LungCATSC072/NL	20	0.6374	0.8304	0.4678	0.6374	0.5965	0.2051
LungCATSC098/TUMOR	21	0.6213	0.8107	0.6272	0.5799	0.4793	0.1926
CircLungCATSC027/NL	22	0.5774	0.6845	0.4881	0.5952	0.6488	0.1255
LungCATSC089/TUMOR	23	0.6850	0.5750	0.5350	0.6650	0.5050	0.1335
CircLungCATSC029/TUMOR	24	0.6973	0.4162	0.4919	0.6919	0.4703	0.2380
CircLungCATSC024/NL	25	0.6923	0.5621	0.6864	0.6450	0.1479	0.4187
LungCATSC081/TUMOR	26	0.6382	0.2613	0.4422	0.6884	0.4925	0.3359
LungCATSC121/NL	27	0.5000	0.4202	0.4681	0.5000	0.4787	0.0693
LungCATSC115/TUMOR	28	0.4780	0.3297	0.4560	0.4835	0.6099	0.2113
LungCATSC115/NL	29	0.4036	0.3193	0.3373	0.3855	0.4036	0.1059
CircLungCATSC024/TUMOR	30	0.2047	0.2632	0.4971	0.2281	0.4854	0.4277
PE89/TUMOR	31	0.2934	0.1976	0.2695	0.2814	0.3653	0.2128
CircLungCATSC027/TUMOR	32	0.0851	0.1064	0.1436	0.0798	0.6170	1.1189
CircLungCATSC025/NL	33	0.1910	0.2079	0.1180	0.1966	0.2416	0.2371
LungCATSC092/TUMOR	34	0.0663	0.1327	0.1990	0.0663	0.2500	0.5692
LungCATSC094/NL	35	0.0684	0.1632	0.0421	0.0737	0.2789	0.7767

A value close to 1 indicates the specimen was almost always classified correctly. The c.v. column indicates the coefficient of variation of the five methods; higher values indicate more variability in the classification of the given observation between methods. Specimen IDs correspond to Figure 4.

DISCUSSION

The secondary analysis of multidimensional flow cytometry data can be daunting, in part because there are arbitrary many ways that data can be parsed when conventional gate/region-based analysis is used. During exploratory data analysis, such as the example presented here, there is usually a fundamental objective that drives the analysis. In this case, it was to discern any differences in the expression of stem/ progenitor markers between non-small cell lung tumors and adjacent normal lung. As tumors are heterogeneous and also contain much non-neoplastic tissue (stromal, vascular, and immune cells) our objectives were to: (1) First, examine cytokeratin (a definitive epithelial marker) versus the stem/ progenitor markers, one at a time; and then (2) break the data into four classes (cytokeratin + euploid, cytokeratin + aneuploid, cytokeratin negative euploid and cytokeratin negative aneuploid) to study the light scatter properties and the coexpression of the stem/progenitor markers in a pairwise fashion. As the latter categories are subsets of the former, it is expected that many of the variables derived from them will be correlated. Another problem inherent to multivariate cytometry data sets is that the number of variables (derived from proportions of analytical regions) is great, often larger than the number of specimens. In this example, we had 86 variables (p) and only 35 specimens (n). Conventional bivariate analysis would require adjustment for the number of comparisons, greatly diluting the statistical power to detect differences.

In this report, we offer an objective method to deal with multidimensional data sets where there is the potential for highly correlated variables and where p >> n. We used five different methods and found two, elastic net and the lasso, particularly useful for this data set, because they consistently chose a manageable number of variables (Fig. 5) that resulted in excellent discrimination between tumor and normal (Fig. 4). Random forest and DLDA were also useful and might prove superior for other data sets. Only best-1 was inadequate to the purpose of this analysis, because it inherently chooses the single best discriminating variable (Fig. 3). An area which was not addressed in this study is the effect of the variance of individual measurements. As raw event counts vary between variables and between samples, not all measured results are equally certain. Future analytical models can take this into account.

Classifying multivariate data against known categories (tumor and normal) can accomplish two important objectives: picking out differences of potentially biological importance for further exploration, and model building for prospective classification of unknowns. Requirements for accuracy are more relaxed for the first application, and considerably more stringent if the model is going to be used prospectively to classify unknown individual cases. In the present data set the model performed excellently for the first application, but consistently misclassified specific individual cases (Table 6). Given that we evaluated 86 variables covering the expression and coexpression of four stem/progenitor associated markers, the similarity in expression patterns between tumor and normal was striking (Fig. S3), suggesting that even among the most deranged tumor cells, these proteins serve important functions that are conserved. Among the most important markers that did distinguish tumor and normal were those in routine use by pathologists, such as cytokeratin + aneuploid cells in tumors, and cytokeratin + small (low scatter), and euploid cells in normal lung. In addition to these known discriminators, selection of which validates the methodology proposed here, there are also several interesting leads (Table 4) such as the expression of the stem/progenitor marker CD133 (CPG2117N133P) and the coexpression of CD117 and CD44 (CP2117P44P). Indeed, CD133, coexpressed with the proliferation marker Ki67 has recently been proposed as a marker of poor prognosis in non-small cell lung cancer (19), but our comparison with normal tissue reveals a greater prevalence of cytokeratin+ cycling CD117 negative/CD133+ cells in normal lung (chosen by all 5 methods, Table 4). Similarly coexpression of CD117, a lung stem cell-associated growth factor receptor (20), in euploid (or pseudo-diploid) cells and CD44 a principal marker associated with tumorigenicity in breast cancer (7,21) also distinguished tumor from normal. Although small data sets such as ours cannot by their nature offer conclusive proof that such markers are of mechanistic, diagnostic or prognostic significance, they provide a sound rational for prospective studies and a model for confirmatory data analysis.