Single-shot stand-off chemical identification of powders using random Raman lasing

Significance

The long-range stand-off chemical identification of materials has been a high profile goal of science in recent years. In this article, we demonstrate the stand-off identification of chemical compounds from kilometer-scale distances in a single laser pulse by detecting the emission from random Raman lasing processes in the target. This technique opens up the door to rapid identification of potentially hazardous chemicals from a safe distance.

Abstract

The task of identifying explosives, hazardous chemicals, and biological materials from a safe distance is the subject we consider. Much of the prior work on stand-off spectroscopy using light has been devoted to generating a backward-propagating beam of light that can be used drive further spectroscopic processes. The discovery of random lasing and, more recently, random Raman lasing provide a mechanism for remotely generating copious amounts of chemically specific Raman scattered light. The bright nature of random Raman lasing renders directionality unnecessary, allowing for the detection and identification of chemicals from large distances in real time. In this article, the single-shot remote identification of chemicals at kilometer-scale distances is experimentally demonstrated using random Raman lasing.

The ability to remotely identify materials in real time has long been a scientific holy grail. The search for extraterrestrial life, the necessity to assess the source of climate change, and the growing need of agriculture further drive the interest in developing chemically specific stand-off identification of materials (1–6). The remote identification of organic compounds would aid in the search for extraterrestrial life and assist in the detection and monitoring of biological weapons (7, 8). The detection of nitrates at long distances would enable the detection of explosives from safe distances (9, 10). Traditionally, optical remote detection schemes have relied on nondirectional incoherent processes (2–5). These methods lack efficiency, limiting the maximum effective distance of the technique or requiring excessive integration times for chemically specific identification. More recent advances have used white-light generation in filaments (6) or lasing processes in atmospheric gases (11–14) to generate backward-propagating radiation that can be used to drive coherent spectroscopic techniques, such as coherent anti-Stokes Raman scattering (CARS) (7, 15). However, these approaches are only applicable to atmospheric sensing.

With only the human eye, it is very difficult to distinguish between a harmless white powder and one that can be used in the production of high-powered explosives (Fig. 1). However, each of these chemicals possess a distinct vibrational spectrum, allowing for chemical identification via vibrational spectroscopy. Raman scattering, the inelastic scattering of light from a vibrational level of a molecule, has been used for decades as a tool for nondestructive, label-free, chemical analysis of samples (16). It is a powerful analytical technique with one significant drawback; the signal generated is extremely weak. Only about 1 in 10¹⁰ photons that enter a sample undergo spontaneous Raman scattering. However, once the incident intensity reaches a certain threshold, the process of stimulated Raman scattering (SRS) takes place, leading to the exponential growth of the Raman signal (17, 18). The discovery of random lasing (19–21) leads naturally to the question of whether it is possible to achieve SRS in a random medium and ultimately random Raman lasing.

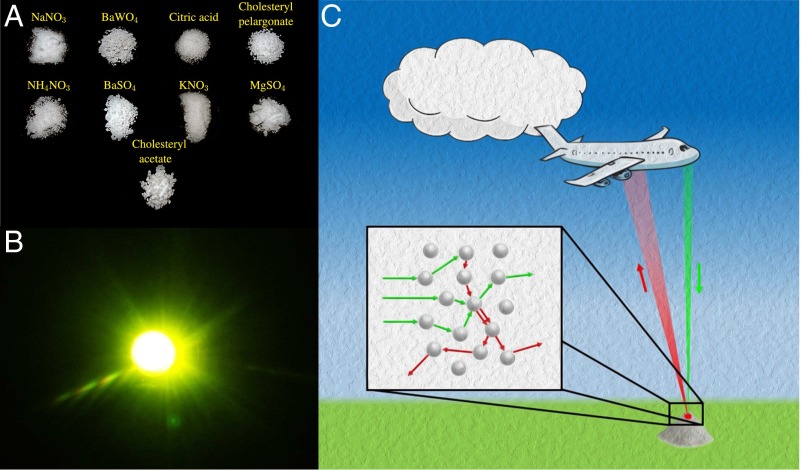
Fig. 1.

The concept of remote chemical sensing through random Raman lasing. (A) A photograph of the various white powders where random Raman lasing has been observed. The “whiteness” of these powders depends on the illumination and the viewing angle, whereas SRS spectra provide excellent discrimination of these compounds in a single laser pulse. (B) A photograph of random Raman laser emission in BaSO₄ powder illustrating the brightness. (C) Conceptual drawing illustrating remote detection of white powders via random Raman lasing.

It is commonly thought that strong light scattering acts like diffusion to spread out light as it travels through a turbid medium, making nonlinear optical effects extremely inefficient. However, if the incident beam has spatial dimensions exceeding the characteristic diffusion length of light, the photons cannot quickly leave the excitation volume, and multiple scattering effects result in a substantial intensity buildup. This high-intensity region promotes stimulated Raman gain, which above a certain threshold, leads to random Raman lasing. Random Raman lasing is much more efficient than spontaneous Raman scattering, and conversion efficiencies of several percent have been experimentally observed (22). Recent advancements in optical wavefront optimization brings hope that it might be possible to remotely control the intensity distribution inside a scattering medium (23, 24), opening up room for further improvements in the efficiencies of random Raman lasing.

Here, we report on the single-shot stand-off identification of closely related chemical species via SRS from a distance of 400 m. When corrected for losses incurred by clipping losses and imperfect reflections, this corresponds to an effective distance of more than 1 km. The light generated via the random Raman lasing process is emitted isotropically due to multiple elastic scattering. It is demonstrated that this leads to a signal that is dependent on the inverse square of the distance from the sample. However, the random Raman lasing process produces a very bright emission (Fig. 1). This ultra-bright signal makes long-distance, single-shot identification of materials possible. Additionally, we show that the random Raman lasing process is robust against the kind of wavefront degradation that can be introduced from atmospheric effects.

Results

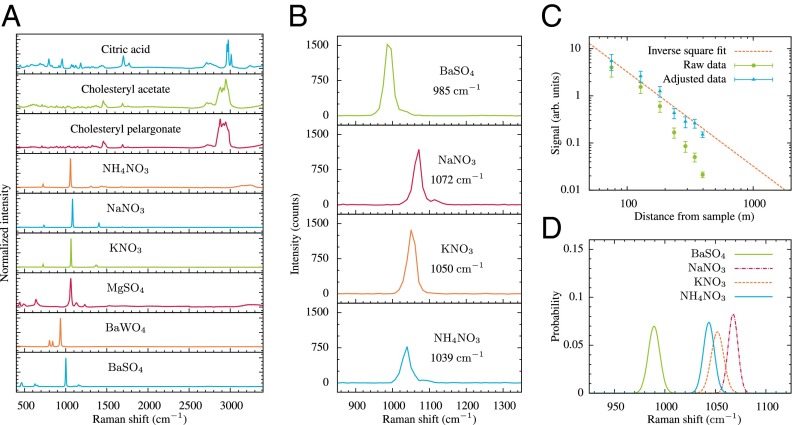
Typical single-shot SRS spectra, taken at the maximum 400-m distance allowed by our setup, are shown for four chemically similar compounds in Fig. 2. The spectral resolution of the spectrometer available for those measurements (USB2000; Ocean Optics) was limited by the 200-μm slit to be 40 cm⁻¹. These spectra illustrate two very important aspects of the proposed approach: first, there is sufficient signal to allow the detection to be made at much longer distances, and second, similar chemical compounds can be identified using only the single Raman line that appears in SRS spectra. The latter point is somewhat masked by the poor spectral resolution of the spectrometer. However, a major motivation for this demonstration was to achieve robust remote chemical sensing using a very moderate budget. If a higher-resolution spectrometer with a more sensitive and less noisy array detector were used, 100% specificity of chemical identification would be possible at much greater distances. To demonstrate that it is possible to uniquely identify the chemicals based on only a single pixel difference, Fig. 2 shows the distribution of the wavenumbers corresponding to the maximum value of the SRS peak over many shots fit using Gaussian statistics. The spectral position of a Raman peak changes very little from shot to shot, i.e., less than the spectral resolution provided by a single pixel on the spectrometer (about 11 cm⁻¹ at these wavelengths). Thus, any variation in this peak value from shot to shot must be due to noise in the CCD, which is Gaussian in nature. By fitting the distribution of the SRS peaks to a Gaussian distribution, chemical identification can be obtained with a degree of confidence determined by the Welch t test (25). Due to their similar SRS spectra, the most difficult chemicals to distinguish were ammonium nitrate (NH₄NO₃) and sodium nitrate (NaNO₃); however, the spectra for these powders were statistically different with a two-tailed probability of 0.9999998. Thus, it is possible to distinguish very similar chemicals with a high degree of certainty even when the peaks differ by less than the resolution of the spectrometer by simply comparing the two distributions of the peak heights.

Fig. 2.

Remote identification of chemically similar samples. (A) Spontaneous Raman spectra of all of the chemicals where random Raman lasing has been observed. (B) Stimulated Raman spectra of similar chemicals taken at a distance of 400 m using a single laser pulse, illustrating that minute changes in the molecular makeup can be distinguished via SRS even with a relatively low resolution Ocean Optics USB2000 spectrometer with a spectral resolution of only 40 cm⁻¹. (C) The detected intensity from BaSO₄ as a function of distance from the sample the adjusted data are corrected for both mirror reflections and clipping losses. The error bars represent the SD of the 50 shot data set taken at each distance. (D) Distribution of the peak value of the stimulated Raman spectra fit using Gaussian statistics, illustrating that nearly identical chemicals are still distinguishable.

Due to the multiple elastic scattering dynamics present in the powder, the generated Raman light is largely emitted isotropically. This isotropic emission leads to an inverse square dependence of the signal on the distance from the sample. Using this and correcting for the losses incurred by mirror clipping and imperfect reflections in our setup, the signal level that we were able to detect at 400 m corresponds to a straight light distance of more than 1 km.

Nonlinear processes are highly dependent on the local intensity of the light. In a nonscattering environment, this leads to a strong dependence of the output intensity on the beam quality of the pump pulse. This dependence on the local intensity presents a substantial problem when considering remote detection schemes where the pump beam must propagate over long distances. Not only do these long propagation distances make it difficult to form a tight focus due to the diffraction limit, but processes such as scintillation greatly degrade the beam quality over these distances. Scintillation is an effect caused by small variations in the refractive index due to small temperature fluctuations in the air; these fluctuations lead to a time-dependent spatial modulation of the pump pulse (Movie S1). Thus, it is very important that a viable remote-sensing technique is relatively insensitive to beam quality fluctuations. To generate a “distorted beam” experimentally, the beam was passed through a metal mesh before it was focused onto the sample. In barium sulfate (BaSO₄) powder, the distorted beam exhibited a 28% increase in the energy required to achieve random Raman lasing. This increase is quite small compared with the 51% increase in the Raman lasing threshold observed in a 4-cm quartz cell filled with DMSO. This observation was confirmed theoretically using a previously developed Monte Carlo model (26, 27), in which we simulated the nonlinear propagation of a Gaussian [transverse electromagnetic (TEM)_0,0] beam and compared it with a TEM_3,1 as an oversimplified representation of the distorted beam. This oversimplified representation will not quantitatively line up directly with the experiment; however, it will provide a good qualitative analog. In this simulation, the SRS threshold was seen to increase by 85% in BaSO₄ and 131% in DMSO. Fig. 3 illustrates that random Raman lasing is much more robust against poor beam quality than ordinary SRS in a nonscattering medium.

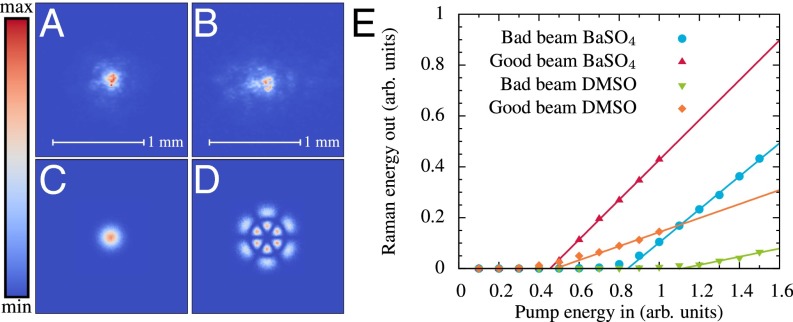
Fig. 3.

The effect of the incident beam quality. (A) Experimental beam profile of our laser at the surface of the sample, referred to as good beam. (B) Experimental beam profile of our laser at the surface of the sample once a mask was placed in its path, referred to as distorted beam. (C) Simulated Gaussian good beam used in the Monte Carlo simulations. (D) Simulated Laguerre-Gauss TEM_1,3 distorted beam used in the Monte Carlo simulations. (E) Efficiency plot generated by Monte Carlo simulations showing how beam quality affects the threshold dynamics of random Raman lasing compared with SRS in nonscattering environments.

Materials and Methods

Two laser systems were used for these experiments. The majority of the work was done using the 532-nm radiation generated by means of the second harmonic conversion of the 1,064 nm produced by a Quanta-Ray GCR-3RA (Spectra Physics). The GCR-3RA was injection seeded with a 10-ps pulse generated by a Vangaurd HM532 laser (Spectra Physics). At the output, as much as 20 mJ of energy was available at 532 nm in a 50-ps pulse. The second system was a GCR-130 (Spectra Physics) that was capable of producing 250-mJ, 8-ns pulses at 532 nm. A half-wave plate followed by a polarizing beam splitter was used to control the pump power, allowing for intensity adjustment without affecting beam quality. The pump was focused over a distance of 8.5 m onto the sample using a slightly offset 1.5× telescope constructed from a −10.0-cm focal length plano-concave lens followed by a 15.0-cm focal length plano-convex lens. The pump source was directed to the powder sample, which was packed into a plastic dish with a diameter of 1.0 cm. The Fresnel reflections from a 0.16-cm-thick BK7 window, placed at 45°, were coupled into an energy meter (J4-09; Coherent) and used as a reference signal to measure the pump power.

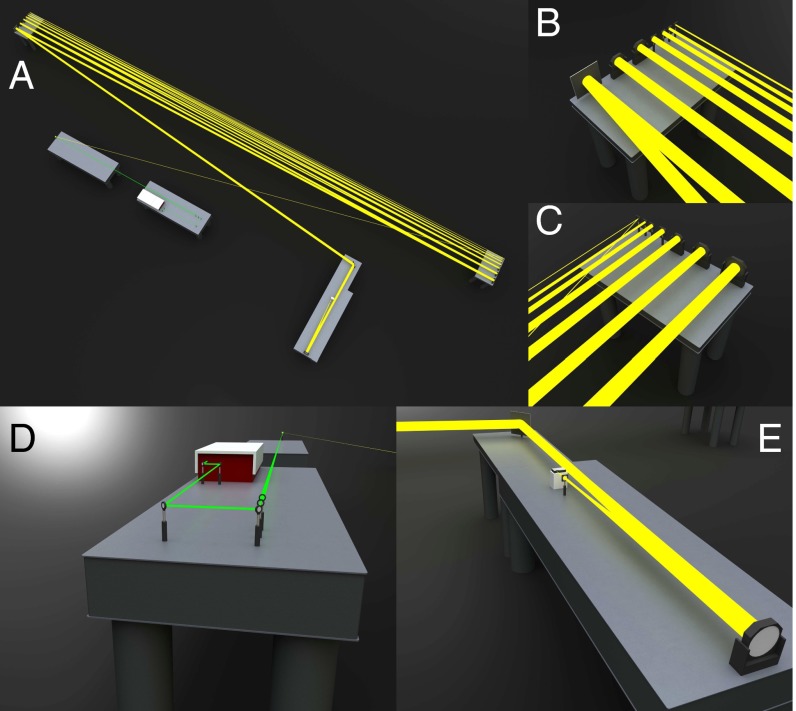
To obtain a substantial optical path length in the laboratory, optical tables were set up at each end of the laboratory separated by a distance of 26.9 m. Seven broadband dielectric mirrors and metallic mirrors ranging in size from 5.08 cm diameter to 30.5 × 30.5 cm were placed on each table. The first of these mirrors was placed 22.2 m from the sample. The system of relay mirrors was aligned as to allow for 13 bounces of the Raman signal, each 26.9 m in distance. A 30.5 × 30.5-cm pick-off mirror was placed on a third optical table located a distance of 21.3 m from the final relay mirror. Finally, a 20.3-cm off-axis parabolic mirror with a focal length of 0.25 m was placed at a distance of 4.18 m from the pick-off mirror, resulting in a total optical path length from sample to primary collection optic of 397.4 m. The collected light from the 20.3-cm off-axis parabolic mirror was focused into the 200-μm entrance slit of a spectrometer (USB2000; Ocean Optics). A 5.08-cm-diameter 19.3-cm focal length achromatic doublet was placed near the focus of the parabolic mirror to help further couple the beam onto to slit. A 532-nm notch filter (Thorlabs) was used to reject the remaining pump light before the spectrometer. Alignment was achieved with the use of a He-Ne laser that was directed down the same optical path as the pump source. To avoid stray light collection due to extraneous reflections off any of the relay mirrors in the system, each mirror was individually blocked before each measurement to verify that the alignment system did not support any other optical paths. This setup is shown in Fig. 4.

Fig. 4.

Schematic of the experimental setup. (A) To-scale drawing of the experimental setup. For reference the large optical tables are 12 ft in length, and the total path length of the sample beam from sample to the primary collection optic is 397.4 m. (B) Close-up view of the mirrors on the left end table. (C) Close-up view of the mirrors on the right end table. (D) Zoomed-in view of the preparation of the pump beam. The beam is focused onto the sample a distance of 8.5 m away from the slightly offset 1.5× telescope. (E) Close-up view of the detection scheme. The light is focused with a 2.54-m off-axis parabolic mirror onto the slits of an OceanOptics USB2000 spectrometer. A 19.3-cm achromatic doublet was used to further focus the signal onto the spectrometer.

The inverse-square dependence of the intensity was measured using the same optical system described above with the spectrometer replaced by an energy meter (J3S-05; Coherent). Barium sulfate powder (Sigma-Aldrich) was used as the sample for these measurements. To alter the optical path length between the sample and the final collection optic, a mirror was removed from each of the optical tables. For each pair of mirrors that were removed, the detection distance was reduced by 53.8 m. Mirror reflectivity was taken into account by assuming the metallic mirrors each had a reflectivity of 0.9 and the broadband dielectric mirrors had a reflectivity of 0.99. Clipping was calculated by finding the limiting aperture and calculating the percentage of the light cone that was reflected. For this calculation it was assumed that only 90% of the diameter of the mirror was useful for reflecting the signal. It is important to note that the output light from the random Raman laser persists only for hundreds of picoseconds to a few nanoseconds; thus, it was possible to time gate the detector to minimize the effects of the sun and other ambient light.

The spontaneous Raman spectra were collected using a custom-built Raman microscope. A 140-mW, 473-nm continuous-wave diode-pumped solid-state laser (DHOM-M-473-100; UltraLasers) was used as the excitation source. The reflection off a dichroic mirror (LM01-480-25; Semrock) was directed into a microscope objective (MPlan 20×/0.4 NA; Olympus). The Raman scattered light was collected by the same objective and passed through the dichroic and a long-pass filter (Semrock BLP01-473R-25) before being imaged onto the 10-μm entrance slit of a 1/3-m spectrometer (Acton). For each sample, 30 averages were collected at two separate locations in the sample. Integration times varied from powder to powder, but all other acquisition parameters remained the same. The fluorescence background was removed from the spectra using a modified polyfit method with 250 integrations and a fifth-order polynomial (28).

The dependence of SRS on beam quality is often overlooked in laboratory experiments, as most lasers output high-quality nearly Gaussian beams. However, as these beams propagate through air, their beam quality degrades due to small variations in the refractive index, a process known as scintillation. To demonstrate that random Raman lasing is robust against poor beam quality, we compared it to the generation of an SRS signal in a 1.0 × 4.0-cm cuvette filled with DMSO. We denote the “good” beam as the beam that we used for all of the experiments. To generate a distorted beam, several metal wires were placed in the beam path before it was focused down toward the target. The energy threshold was measured as the point when signal first becomes visible to the naked eye. In DMSO, the good beam had a threshold pulse energy of 0.680 ± 0.048 mJ, whereas the distorted beam passed through threshold at 1.03 ± 0.072 mJ, an increase in the threshold by 51%. In BaSO₄, the good beam began to lase at 2.98 ± 0.21 mJ, whereas the distorted beam required 3.80 ± 0.27 mJ, which is only a 28% increase compared with the good beam. Thus, although some effect on beam quality can be seen, the effect is relatively minor compared with traditional SRS generation.

To further understand the dependence of random Raman lasing on beam quality, we made use of a Monte Carlo model very similar to previously developed models (26, 27). For the good beam, we chose a pure Gaussian beam, whereas the distorted beam was modeled using a Laguerre-Gauss TEM_1,3 mode. To simulate DMSO, we used a 0.0125-cm-thick piece of glass followed by 4.0 cm of DMSO with an additional 0.0125-cm-thick piece of glass. The glass was used to simulate the effects of the cuvette. The medium was taken to be infinite in the transverse directions. The glass was given an index of refraction n_glass = 1.5 and an absorption coefficient μ_a = 0.3 cm⁻¹. The DMSO was given an index of refraction n_DMSO = 1.479 and an absorption coefficient μ_a = 0.3 cm⁻¹. The BaSO₄ was assumed to be 1.0 cm thick and was given an index of refraction $n_{{\text{BaSO}}_4}=1.6$, a scattering anisotropy factor g = 〈cos(θ)〉 = 0.6, and a scattering coefficient of μ_s = 10.0 cm⁻¹. Both materials were given the exact same Raman characteristics, which are described by two parameters in the simulation: first, a Raman coefficient of μ_R = σ_RN = 0.001 cm⁻¹, and second, a Raman gain coefficient μ_SRS = 10⁻⁵ cm². The physical meaning of the Raman coefficient is quite analogous to that of μ_s and μ_a in that 1/μ_R is the mean distance a pump photon travels before it undergoes Raman scattering. It is analogous to say that spontaneous Raman scattering is linear; thus, it too will follow Beer’s law. This coefficient must be taken artificially large due to computational constraints and is explained and justified more fully in refs. 27 and 29. The Raman gain coefficient is a measure of how strong the stimulated effect is and enters into the simulation by assigning a probability of a pump photon converting to a Raman photon of P = 1 − exp(−μ_SRS ρ_SRS δr), where δr is a small radius around the pump photon, and ρ_SRS is the local Raman photon density.

To simulate the TEM_3,1 beam we must first solve and then invert the following equation for χ:

$${\displaystyle \underset{a}{\overset{\chi }{\int }}\rho \left(x\right)\text{d}x}=\xi ,$$ [1]

where a represents the minimum value of the distribution, ξ is a uniformly distributed random number between 0 and 1, and ρ(x) is the probability distribution function. To create a method that can simulate not only TEM_3,1 distributions but other distributions as well, we chose to handle this numerically. To accomplish this, we make use of the well-known Simpson’s method for the integration and Brent’s method for the subsequent inversion.

In summary, we demonstrated a method for chemically specific remote identification of powders that takes advantage of the bright emission from random Raman lasing. Chemical identification of several similar chemical species was shown at an effective distance of over 1 km using an inexpensive setup (we estimate the overall cost to be of the order of $25,000). The random Raman lasing process that facilitates these signals has been proven, through both experiment and Monte Carlo simulation, to be robust against the poor beam quality that is likely to occur when propagating a laser beam over long distances. The ability to remotely detect chemicals in real time at large distances opens the door to a variety of applications ranging from explosives monitoring and detection to monitoring nitrate levels for smart agriculture.