Fast single-molecule FRET spectroscopy: theory and experiment

Abstract

Single-molecule spectroscopy is widely used to study macromolecular dynamics. Although this technique provides unique information that cannot be obtained at the ensemble level, the possibility of studying fast molecular dynamics is limited by the number of photons detected per unit time (photon count rate), which is proportional to the illumination intensity. However, simply increasing the illumination intensity often does not help because of various photophysical and photochemical problems. In this Perspective, we show how to improve the dynamic range of single-molecule fluorescence spectroscopy at a given photon count rate by considering each and every photon and using a maximum likelihood method. For a photon trajectory with recorded photon colors and inter-photon times, the parameters of a model describing molecular dynamics are obtained by maximizing the appropriate likelihood function. We discuss various likelihood functions, their applicability, and the accuracy of the extracted parameters. The maximum likelihood method has been applied to analyze the experiments on fast two-state protein folding and to measure transition path times. Utilizing other information such as fluorescence lifetimes is discussed in the framework of two-dimensional FRET efficiency-lifetime histograms.

1. Introduction

Since the first optical detection of single molecules,¹ the application of single-molecule spectroscopy has been greatly expanded and now it is widely used in various research areas in physics, chemistry, and biology.^2-5 One of the great advantages of single-molecule measurements over ensemble measurements is the capability to monitor heterogeneous molecular processes and rare events in real time. This allows investigations of the distribution of molecular structures and dynamics instead of averaged properties of an ensemble. In particular, single-molecule spectroscopy has been very useful for studying conformational dynamics and molecular interactions of macromolecules such as proteins and nucleic acids.^6-15 However, in many cases, molecular dynamics are too fast to be captured by typical single-molecule methods. In fluorescence measurements, the time resolution is determined by a flux of photons, which are emitted by the fluorophores attached to a molecule. In principle, it is possible to illuminate a fluorophore at very high intensity to excite the fluorophore as soon as it returns to the ground state to maximize fluorescence emission. However, this is often not possible in practice due to a variety of photophysical and photochemical problems, such as “blinking,” in which the fluorophore is transiently converted to a non-fluorescent state, or “bleaching,” where fluorescence stops permanently. With the aid of various chemicals that reduce these interfering processes,^16-19 the typical time resolution is 1 – 10 ms.

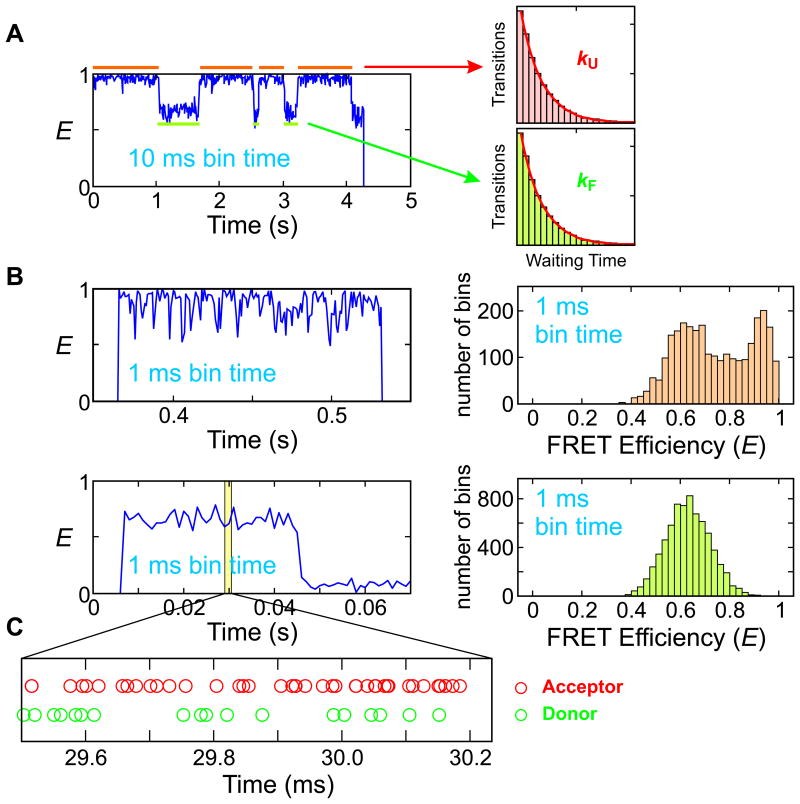
The examples in Fig. 1 illustrate the time resolution problem. At equilibrium, a protein with donor and acceptor labels is constantly inter-converting between the folded and unfolded states. (The transitions are random in time, so at the ensemble level there is no change in any average property.) The photons emitted by the donor and acceptor are collected in time bins and the FRET efficiency of each bin is calculated as a fraction of the acceptor photons. When the kinetics are slower than the bin time, the folded and unfolded states can be clearly resolved in the FRET efficiency trajectory (see Fig. 1A). The rate of inter-conversion can be determined from the distribution of waiting times (the times that a molecule spends in each state, also called residence times or dwell times). When the kinetics become comparable to or faster than the bin time, however, it is not possible to distinguish the two states clearly, as shown in Fig. 1B. Then, how can we obtain the kinetics information from this data? One way to extract this information is to analyze the shape of the FRET efficiency distribution.^14,20-32 The shape depends on whether the transitions between the states are on a time scale comparable to or faster than the bin time ^33,34 (see Fig. 1B). If we record the arrival times of individual photons, it is possible to more reliably measure the dynamics faster than the bin time by analyzing photon trajectories (the strings of colors and arrival times of individual photons) directly without binning.

Figure 1.

Kinetic measurement in single-molecule spectroscopy. (A) Slow two-state transitions. Two states with high (folded) and low (unfolded) FRET efficiencies are clearly seen in the FRET efficiency trajectory (left). Folding and unfolding rate coefficients can be obtained from the decay of the waiting time distributions (right). (B) When the timescale of the kinetics is similar to or faster than the bin time, the waiting time distribution cannot be constructed because states are not distinguishable. The FRET efficiency trajectories (left) and histograms (right) were obtained from two-state proteins α₃D (top) and the WW domain (bottom) near the mid-point of guanidine hydrochloride (GdmCl) denaturation. (C) A photon trajectory from the WW domain can be used to determine the waiting times in the folded and unfolded states deduced from the color patterns, but a rigorous statistical analysis (maximum likelihood method) is required to obtain accurate model parameters. Data and figures from Refs. 27,35,36.

Fig. 1C shows a photon trajectory in a ∼ 700 μs window of a fast folding protein, the FBP28 WW domain. It appears that there is only one state, as the FRET efficiency trajectory in Fig. 1B shows no transition and there is only one peak in the FRET efficiency distribution. However, there are color pattern changes in the photon trajectory. It begins with similar numbers of donor and acceptor photons followed by a series of acceptor photons. Then, both donor and acceptor photons appear again. Since this alternating color pattern change indicates folding and unfolding transitions, it may be possible to visually separate the trajectory into folded and unfolded states and construct waiting time distributions to measure the kinetics. However, in this way, there would be a large uncertainty in the determination of transition points and many transitions with short waiting times would be missed. Therefore, a more rigorous and objective statistical analysis method is required to probe the kinetics of fast processes.

In this Perspective, we discuss the analysis of photon trajectories from single-molecule FRET data. Our main focus is on the maximum likelihood method, which allows one to get information about fast transitions between the states. The likelihood-based methods and hidden Markov modeling have been used in the analysis of ion channel experiments,^37-39 and is now widely used to obtain kinetics and dynamics information from single-molecule data after binning^40-44 or at the single photon level.^45-55 We will review and discuss the theory and our recent applications of this method to experimental measurement of fast kinetics and transition path times in protein folding.^{27,35,36,52,56,57} Since this method requires a kinetics model, it is important to cross-validate the result by comparing with simulated data and/or using independent methods such as correlation analyses. We will also discuss the accuracy of the determined parameters through various simulations. In the end we briefly consider histograms obtained from binned photon trajectories and discuss how additional information from donor fluorescence lifetimes can be utilized in two-dimensional FRET efficiency-lifetime histograms.

2. Maximum likelihood method: Theory

Consider a molecule labeled with a donor and an acceptor. The molecule is illuminated by a laser and emits donor and acceptor photons. A sequence of photons with recorded colors and arrival times is the observed photon trajectory. We assume that the molecule has several states. Each state i is characterized by the acceptor and donor photon count rates, n_Ai and n_Di, or, alternatively, by the apparent FRET efficiency, E_i = n_Ai/(n_Ai + n_Di), and the total count rate, n_i = n_Ai + n_Di. The apparent FRET efficiencies are related to the inter-dye distances. A “conformational state” can be any state of a molecule that has a different FRET efficiency. This can be not only the states with different inter-dye distances, but also photophysical states of fluorophores. Transitions between the states are described by a rate matrix K (its element K_ij is the rate coefficient of a transition j → i and the diagonal elements are $K_{ii}=-\sum _j{K}_{ji}$). The maximum likelihood method⁵² described below finds the model parameters (i.e., the FRET efficiencies or the photon count rates of the states and the transition rates) that are most consistent with the observed photon trajectories by maximizing the appropriate likelihood function.

We use two different likelihood functions. The first one depends only on the apparent FRET efficiencies and transition rates and does not involve photon count rates. It can be applied to analyze diffusing molecules, where the count rates fluctuate as the molecule diffuses through a confocal volume.²⁷ The likelihood function of the j^th photon trajectory (or the j^th burst of photons in the case of diffusing molecules) is obtained from the probability to observe this trajectory:⁵²

$$L_j={\mathbf{1}}^{\mathrm{T}}\prod _{k=2}^{N_j}[\mathbf{F}(c_k)exp(\mathbf{K}{\tau }_k)]\mathbf{F}(c_1){\mathbf{p}}_{\mathit{\text{eq}}}.$$ (1)

Here K is the rate matrix specified by the model, F(c_k) is a diagonal matrix, which depends on the color of the k^th photon c_k, F(acceptor) = E and F(donor) = I - E, E is the diagonal matrix with the apparent FRET efficiencies on the diagonal, I is the unity matrix, 1^T is the unit row vector (T means transpose), and p_eq is the vector of equilibrium populations of the conformational states. The above expression reads from the right to the left. Before observing any photon, the molecule is in the equilibrium, which is described by p_eq. When the first photon is detected, the vector is multiplied by a matrix F(c₁) that modifies the vector of equilibrium populations depending on the color of the first photon c₁. The propagation of the states during the time interval between the first and second photons, τ₂, is described by the rate equation, dp/dt = Kp, and therefore is accounted for by the transition matrix exp(Kτ₂). This procedure is repeated for N_j photons and N_j -1 inter-photon times and finished by summation over all states, which is equivalent to multiplying 1^T.

For the two-state model describing folding,

$$\mathrm{F}\underset{k_F}{\overset{k_{\mathrm{U}}}{\rightleftarrows }}U,$$ (2)

there are 4 model parameters: the rate coefficients, k_F and k_U, and the apparent FRET efficiencies of the folded and unfolded states, E_F and E_U. The matrix of FRET efficiencies, the rate matrix, and the vector of the equilibrium populations are given by

$$\mathit{E}=\left(\begin{array}{cc}{E}_F& 0\\ 0& E_U\end{array}\right),\mathbf{K}=\left(\begin{array}{cc}-k_U& k_F\\ k_U& -k_F\end{array}\right),\text{and}{\mathbf{p}}_{\mathit{\text{eq}}}=\left(\begin{array}{c}{p}_F\\ 1-p_F\end{array}\right),$$ (3)

where p_F = k_F / (k_F + k_U) is the equilibrium population of the folded state.

The likelihood function in Eq. (1) is rigorously applicable when the total count rate does not depend on states.⁵² In the case of two-state folding, this means that the total count rates in the folded and unfolded states are the same. When this is not the case, we use another likelihood function without this restriction, which, however, involves the count rates of the states:

$$L_j={\mathbf{1}}^{\mathrm{T}}\prod _{k=2}^{N_j}[\mathcal{N}(c_k)e^{(\mathbf{K}-{\mathcal{N}}_{\mathit{\text{tot}}}){\tau }_k}]\mathcal{N}(c_1){\mathbf{p}}_{\mathit{\text{eq}}}/\langle n\rangle .$$ (4)

Here, 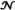(c_k) is a diagonal matrix, which depends on the color of the k^th photon, 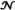_tot = 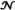(acceptor) + 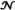(donor), and 〈n〉 = 1^T 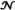_totp_eq. The diagonal elements of 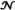(c_k) (= 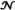_totF(c_k)) are the acceptor or donor photon count rates of the individual states. For the two-state system in Eq. (2), the diagonal elements of the 2 × 2 matrix 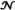(acceptor) are n_AF and n_AU, which are the photon count rates of the acceptor in the folded and unfolded state, respectively, and the diagonal elements of 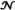(donor) are n_DF and n_DU, which are the photon count rates of the donor in the folded and unfolded state, respectively.

The likelihood function with the photon count rates in Eq. (4) is applicable when the total count rates of the states are not the same. However, there are several advantages to using the reduced likelihood function in Eq. (1) with FRET efficiencies, besides the fact that there are fewer parameters. First, it can be used to analyze freely diffusing molecules, in which case the photon count rate continuously varies depending on the location of the molecule in the focal volume. Second, it is unaffected by donor blinking, as discussed in Sec. 5. Even when the photon count rates vary over the states, the likelihood function with FRET efficiencies may still be applied and result in reasonable model parameters (see discussion in Sec. 3 and 4).

The likelihood functions in Eqs. (1) and (4) differ from the likelihoods used in Hidden Markov Models (HMM) for binned photon trajectories, in which the numbers of photons in a bin are recorded. In standard HMM, time (bin number) is discrete and the observables are photon counts^44,58 or FRET efficiencies^41,59 in a bin. The likelihood function is presented as a product of the transition and “emission” (Poissonian or Gaussian) probabilities. This representation, which implies that all photons in a bin are emitted from a single conformational state, can be used when conformational dynamics are slow compared to the time scale of the bin time.⁶⁰

The maximum likelihood method can be readily extended to models where the conformational coordinate q is continuous by discretizing space and constructing the rate matrix from the finite difference approximation. As an example, consider conformational dynamics described by diffusion in the presence of the potential of mean force G(q). The distribution of q, p(q), satisfies the diffusion equation

$$\frac{\partial }{\partial t}p(q)=\frac{\partial }{\partial q}D(q)e^{-\beta G(q)}\frac{\partial }{\partial q}{e}^{\beta G(q)}p(q),$$ (5)

where D(q) is the position-dependent diffusion coefficient. By discretizing the coordinate q_i = (i-1/2)Δ, where i = 1, 2, …, M, one can approximate the diffusion operator as an M × M tridiagonal matrix K with elements⁶¹

$$K_{i\pm 1i}=\frac{D(q_{i\pm 1/2})exp[-\beta U(q_{i\pm 1/2})]}{exp[-\beta U(q_i)]{\Delta }^2}.$$ (6)

This rate matrix is then used in the likelihood functions Eq. (1) or (4). The potential of mean force G(q) and the diffusion coefficient D(q) can be specified by a few parameters, which are found by maximizing the likelihood function. The calculation of the likelihood functions in Eqs. (1) and (4) is performed by repeated matrix-vector multiplications. The calculation is more efficient when the matrix exponentials are diagonalized as described in Ref. 52. The total likelihood of all photon trajectories (or bursts of photons in the case of diffusing molecules) is obtained by multiplying the likelihoods of individual trajectories (L_j) and optimized with respect to model parameters. Practically, the sum of the log-likelihoods, $lnL=\sum _{j}ln{L}_j$, is calculated and maximized numerically. The parameter errors are estimated from the curvature of the likelihood function at the maximum. Namely, the standard errors are the square roots of the diagonal terms in the covariance matrix, which is the reciprocal of the negative Hessian matrix (i.e., the matrix of the second derivatives with respect to the model parameters).

The computation of the likelihood in Eqs. (1) and (4) can be problematic because of numerical underflow. This problem can be solved by a scaling procedure.⁶² The basic idea is the following. After each matrix-vector multiplication, the resulting vector v_k is multiplied by a scaling coefficient α_k that does not depend on states (e.g., α_k = 1/1^Tv_k). In the end, the log-likelihood is adjusted by subtracting the logs of those coefficients, $\sum _{k}ln{\alpha }_k$.

Generally, as described in Ref. 52, there is no need to modify the methods to account for the leakage of donor photons into the acceptor channel and background photons. These effects, as well as dye rotation on sub-μs time scale, influence only the values of the extracted apparent FRET efficiencies and count rates, and can be corrected for later.⁶¹

3. Application of the maximum likelihood method: two-state protein folding

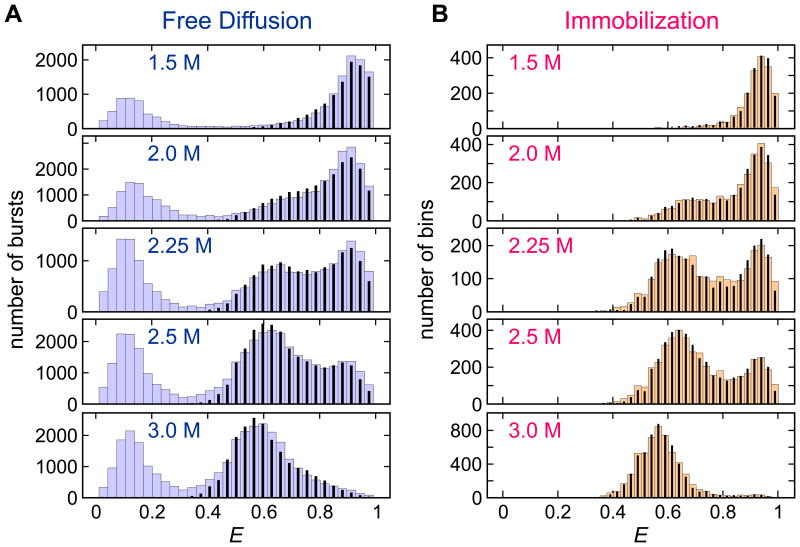
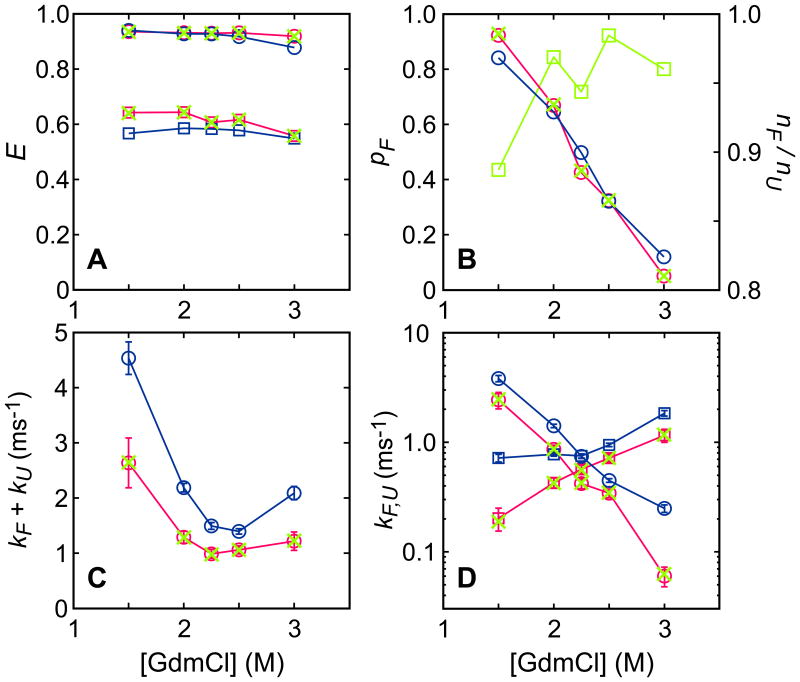
In this section, we will discuss the application of the maximum likelihood method to proteins that exhibit fast two-state transitions between folded and unfolded states. Fig. 2 and 4A show the FRET efficiency histograms obtained from the binned FRET efficiency trajectories of α₃D²⁷ and the WW domain³⁶ at various experimental conditions. The timescale of the kinetics is comparable to or faster than the bin time of 1 ms (immobilization data) or 2 ms (free diffusion data). The bin time cannot be reduced to clearly separate the folded and unfolded states because the number of photons in a bin would be too small. The FRET efficiency histograms of α₃D in Fig. 2 show that the equilibrium is shifted from the folded state (high FRET efficiency, E ∼ 0.9) to the unfolded state (low FRET efficiency, E ∼ 0.6) as the GdmCl concentration is raised. At the lowest (1.5 M) and highest (3 M) GdmCl concentrations, the fraction of the minor population is very small. Nevertheless, as shown in Fig. 3, the model parameters can be extracted over this wide range of the relative population of 0.1 – 0.9 very accurately, as deduced from the small errors of the extracted parameters. The rate coefficients obtained from the free diffusion and immobilization experiments agree with each other to within a factor of 2.

Figure 2.

Experimental (wide bars) and recolored (narrow bars) FRET efficiency histograms of Alexa 488/Alexa 594-labeled α₃D in the free diffusion experiment (A) and immobilization experiment (B) at various GdmCl concentrations. In the free diffusion experiment, histograms were constructed from bins (2 ms bin time) containing more than 30 photons. Histograms for the immobilization experiment (1 ms bin time) were constructed from the trajectories with the mean photon count rate > 15 ms^-1. In the free diffusion data, the peak at E ∼ 0.1 corresponds to the molecules missing an acceptor or with an inactive acceptor. Such molecules were filtered out in the immobilization data. For the recolored histograms, the photons in the trajectories were recolored using the two-state model parameters obtained by maximizing the likelihood function in Eq. (1). Figures from Ref. 27.

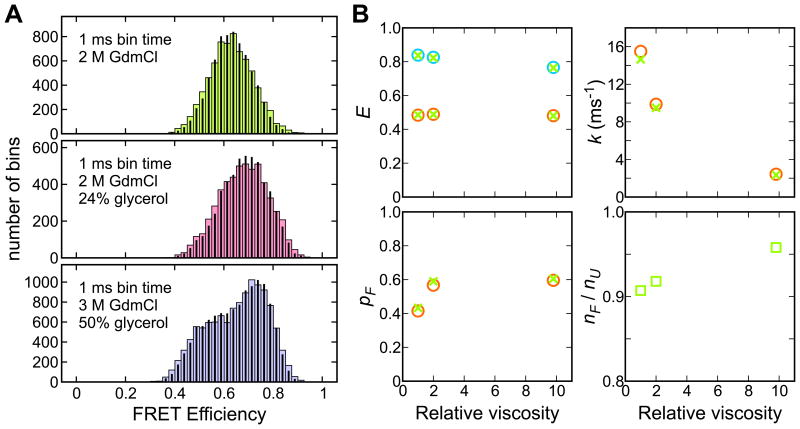
Figure 4.

(A) Experimental (wide bars) and recolored (narrow bars) FRET efficiency histograms of the Alexa 488/Alexa 647-labeled WW domain immobilized on the glass surface at various solvent viscosities. The FRET efficiency histograms (1 ms bin time) were constructed from the trajectories with the mean photon count rate > 50 ms^-1. Figures from Ref. 36. (B) Parameters obtained by maximizing the likelihood functions in Eq. (1) (circles) and Eq. (4) (green crosses and squares).

Figure 3.

Parameters obtained by maximizing the likelihood function with FRET efficiencies, Eq. (1), for free diffusion (blue) and immobilization (red) experiments and the likelihood function with count rates, Eq. (4), for the immobilization experiment (green crosses). (A) FRET efficiencies of folded and unfolded states. (B) Fraction of folded molecules p_F (circle). Green squares show the ratio of the photon count rate in the folded state to that in the unfolded state n_F/n_U. (C) Relaxation rates k_F + k_U. (D) Individual folding (k_F, circle) and unfolding (k_U, square) rate coefficients. Figures from Ref. 27.

The accuracy of the analysis can be further tested by comparing the experimental histograms with those from the simulated photon trajectory data using the extracted parameters. Instead of simulating completely new photon trajectories, we use the “recoloring” procedure, that is closely related to the likelihood function in Eq. (1).⁵² In this procedure, we erase all colors from the experimental photon trajectories, but preserve other information such as the inter-photon times, number of photons, variations in the photon count rate, and length of trajectories. The trajectories are “recolored” according to the extracted model parameters. This produces a simulation data set that is most similar to the experimental data. The most valuable feature of the recoloring test is that it can be applied to the data from diffusing molecules, in which one does not need to simulate the fluctuation of the photon count rate caused by the diffusion in a focal spot. Fig. 2 clearly shows that the histograms from the recolored photon trajectories are very close to the experimental histograms, suggesting that the two-state model is appropriate and the extracted parameters are accurate.

The above analysis was performed using the likelihood function with FRET efficiencies, Eq. (1), which assumes that the total count rate in the folded and unfolded states should be similar. To test this assumption, we also analyzed the data using the likelihood function in Eq. (4). This can be done only for the data from the immobilization experiment. The extracted parameters are shown in Fig. 3 (green crosses) and they are very close to the values obtained using Eq. (1). This is not surprising because the extracted ratio of the total count rates in the folded and unfolded states is close to 1 (the deviation is less than 10%) in the most experimental conditions, as shown in Fig. 3B.

The WW domain folds and unfolds much faster than α₃D. Since multiple folding and unfolding events occur during the 1 ms bin time, the FRET efficiency is averaged³³ and the FRET efficiency distribution (2 M GdmCl) is a single peak, as shown in Fig. 4A. This phenomenon is similar to fast chemical exchange in NMR.^27,34 When the kinetics are slowed by the increased solvent viscosity, the folded and unfolded peaks become visible, indicating that there are two states. The maximum likelihood method (using Eqs. (1) or (4)) allows one to accurately extract the parameters of the two-state model, even though the relaxation time is more than ten times shorter than the bin time (Fig. 4B). The extracted parameters are tested by comparing the experimental and recolored FRET efficiency histograms, which are in good agreement.

4. Accuracy of the parameters in the maximum likelihood method

The maximum likelihood method allows one to successfully extract transition rates and state populations in real experimental systems, as shown in the previous section. In this section, we study the range of parameters where the method performs reliably. To estimate this range, we simulated photon trajectories with typical experimental parameters and compared the extracted parameters with the modeled ones.

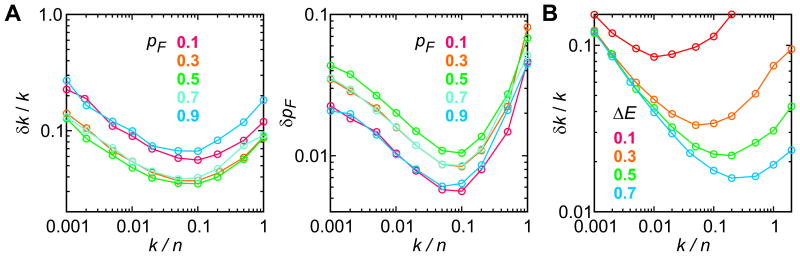
In the first example, we simulated photon trajectories for two-state folding (Eq. (2)) and analyzed them using the likelihood function in Eq. (1). The total count rates (n) in the folded and unfolded states are the same in this example, hence the likelihood function in Eq. (1) is exact. The extracted parameters coincide with the modeled ones in the limit of a large number of photons, so that we study the errors of the parameters, which are obtained using the curvature of the likelihood function at the maximum. Fig. 5 shows the standard errors of the extracted relaxation rates (k = k_F + k_U) and of the folded state populations (p_F) at various values of the modeled rates, populations, and FRET efficiencies. For the parameters used in the simulations (150,000 photons), the relative error of the relaxation rate (Fig. 5A) is less than 10% over the range of 0.001 < k/n < 1 when the folded and unfolded fractions are comparable (p_F = 0.3, 0.5, 0.7). The error dramatically depends on the difference of the FRET efficiencies in the folded and unfolded states, as shown in Fig. 5B.

Figure 5.

(A) The accuracy of the determination of the relaxation rate (k = k_F + k_U) and the fraction in the folded state (p_F) using the maximum likelihood method. Photon trajectories were simulated for 50 combinations of k/n (0.001 – 1) and p_F = (0.1, 0.3, 0.5, 0.7, and 0.9). For each combination, 100 of 30 ms-long trajectories were simulated with a photon count rate of n = 50 ms^-1 (same for the folded and unfolded states) and E_F = 0.9 and E_U = 0.6. 150,000 is the typical number of photons analyzed in the experiment. The errors, δk and δp_F, are the average standard deviations (5 simulation data set) obtained from the curvature of the likelihood function at the maximum (the diagonal elements of the covariance matrix). (B) The accuracy of the determination of the relaxation rate (k) at various FRET efficiency differences between two states (ΔE = E_F − E_U). E_F = 0.9.

It is interesting that the relative error of the relaxation rate is a non-monotonic function of the relaxation rate k. When the relaxation rate increases, the error decreases, reaches the minimum, and increases again. When the relaxation rate is small, the uncertainty is large because the number of transitions between folded and unfolded states is small. The number of transitions between the states during time T is proportional to kT, so the error decreases as $1/\sqrt{kT}$. In the opposite limit of large relaxation rate, the error in the extracted transition rates becomes large because photons become less correlated (completely uncorrelated photons do not contain information about the transition rates). The combination of these two effects is minimized at k/n ∼ 0.1 for the FRET efficiencies of 0.6 and 0.9. The highest accuracy of the relative relaxation rate is achieved when the folded and unfolded states are equally populated and the FRET efficiencies of the states are well separated.

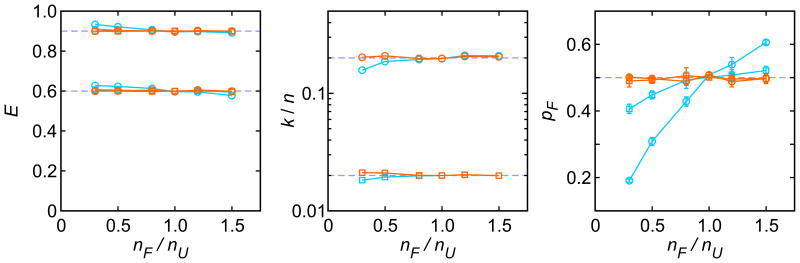
In the second example, we examined the accuracy of the parameters determined using the likelihood function in Eq. (1) when the total count rates in the folded and unfolded states are not the same and the likelihood function is not exact anymore. We simulated photon trajectories for the two-state system in Eq. (2) with different count rates in the folded (n_F) and unfolded (n_U) states. Fig. 6 shows the parameters extracted using the likelihood function in Eq. (1) (blue). The two FRET efficiencies and the relaxation rate can be determined with remarkable accuracy over the wide range of the ratio of the photon count rates (n_F/n_U). The fraction of the folded state is the most sensitive parameter, especially when the relaxation rate is large. When the data are analyzed with the likelihood function in Eq. (4), which is exact for this model, the parameters can be determined very accurately, as expected (Fig 6, orange). This option (the analysis using Eq. (4)) is available only for immobilization data, in which the total count rate can be independently determined for the photon trajectory of each molecule and the ratio n_F/n_U is an additional model parameter. However, for diffusing molecules only Eq. (1) can be used. As shown in Fig. 6, the requirement of equal count rates for Eq. (1) can be relaxed, especially when the relaxation rate is small compared to the photon count rate.

Figure 6.

The dependence of the maximum likelihood parameters on the ratio of the photon count rates in the folded and unfolded states (n_F / n_U). The amount of the simulated data is the same as that in Fig. 5 and k/n = 0.02 (square) and 0.2 (circle) and p_F = 0.5. n_F and n_U were varied so that the average count rate (n_F + n_U)/2 is equal to 50 ms^-1. The data were analyzed using the likelihood functions with FRET efficiencies (Eq. (1), blue) and with photon count rates (Eq. (4), orange). The error bars indicate the standard deviation obtained from 5 simulation data set. In the plots of E and k/n, all errors are smaller than the size of markers.

5. Modification of the kinetics model: Photoblinking effect

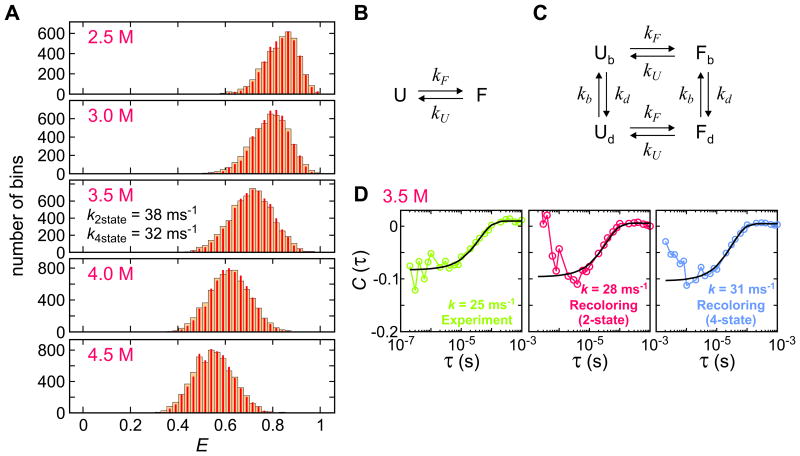
Even though the above simulation results show that it is possible to extract the kinetic rates that are comparable to the photon count rate, in practice there are problems as the timescale of the kinetics of interest becomes closer to those of other processes. One example is demonstrated in Fig. 7 for the case of a fast folding protein, villin. The FRET efficiency histograms show a single peak at all GdmCl concentrations, similar to that of the WW domain in Fig. 4A. Assuming a two-state model (Eq. (2)), one can obtain the parameters of the two-state folding by maximizing the log-likelihood function. The extracted relaxation rate coefficient is very large (38 ms^-1 at the denaturation mid-point), which agrees with the histograms that show a single peak.

Figure 7.

(A) Experimental (wide bars) and recolored (narrow bars) FRET efficiency histograms of the Alexa 488/Alexa 647-labeled villin immobilized on a glass surface at various GdmCl concentrations. Quoted relaxation rates were obtained from the maximum likelihood method with (B) two-state kinetics model and (C) four-state kinetics model including acceptor blinking. Subscripts b and d stand for the bright and dark states, respectively. (D) Donor–acceptor cross-correlation functions calculated from the experimental data at 3.5 M GdmCl (green), recolored experimental photon trajectories using the two-state kinetic model maximum likelihood parameters (red), and recolored experimental photon trajectories using the four-state kinetic model that includes acceptor blinking (blue). Quoted relaxation rates were obtained from exponential fitting (black solid line). Data and figures from Ref. 56.

To test the accuracy of parameters, one can compare the FRET efficiency histograms from the recolored photon trajectories (two-state model) with the experimental ones. Since the folding/unfolding kinetics is much faster than the bin time, this test is not very sensitive to the value of the relaxation rate. As an alternative test, we compare the results with the donor-acceptor cross-correlation function obtained from the same experimental data. Fig. 7D shows that the decay rate (k) of the cross-correlation function (C_DA(τ) = -A exp(-kτ)) is smaller (25 ms^-1 for the experimental data and 28 ms^-1 for the data recolored with the two-state maximum likelihood parameters) than the extracted relaxation rate of 38 ms^-1. Moreover, the correlation function from the recolored data at short times (< 10 μs) is different from the experimental correlation function. These discrepancies indicate that some processes other than folding and unfolding affect the analysis.

The most likely additional process that would affect the rates is blinking of donor and acceptor dyes. Although various chemicals are used to prevent photoblinking,^16,18,19 they cannot completely suppress blinking. Slow blinking compared to the bin time can be easily detected and excluded from the analysis, but blinking on the sub-10 μs time scale cannot be so easily determined. When donor blinking occurs, no donor or acceptor photon is emitted. This leads to the fluctuation of the total (acceptor and donor) number of photons. As in the case with diffusing molecules, the intensity fluctuations due to donor blinking do not affect the maximum likelihood analysis when the likelihood function in Eq. (1) is used.⁵¹⁵⁵ The cross-correlation function obtained from the recolored photon trajectories includes the donor blinking effect automatically. The intensity fluctuations are manifested as the decay with the positive amplitude (τ < 10 μs, middle panel in Fig. 7D). The flat experimental correlation function on this time scale (left panel in Fig. 7D) indicates that the donor blinking effect is compensated by other anti-correlation components such as acceptor blinking.

Acceptor blinking can be incorporated by using a four-state kinetic model (Fig. 7C). In this model, each of the folded and unfolded states exists in both “bright” (fluorescing) and “dark” (non-fluorescing) states. The folding and unfolding rate coefficients in the bright state are assumed to be the same as those in the dark state and the residence times in both bright and dark states are exponentially distributed.⁶³ In this four-state model (Fig. 7C), k_b is the rate coefficient for the transition from the dark state to the bright state of the acceptor, which is independent of the illumination intensity. On the other hand, as the probability of the transition from the bright state to the dark state increases linearly with the time spent in the excited state, the rate coefficient of the transition to the acceptor dark state is proportional to the photon count rate as k_d = k₀(n/n₀), where n is the average photon count rate of a photon trajectory and k₀ is the rate coefficient at the reference photon count rate (n = n₀). The relaxation rate obtained using the maximum likelihood method with this kinetics scheme is k = 32 ms^-1. This is smaller than that of the two-state model and more consistent with the decay rate obtained from the correlation analysis, suggesting that this model and parameters are more consistent with the experimental data. In addition, the four-state model is further supported by the smaller value of the Bayesian Information Criterion,⁶⁴ which is one of the criteria for model selection (ΔBIC = -338, BIC = -2lnL + n_plnN_p, where L is the likelihood of the model, n_p is the number of model parameters (4 for two-state model and 6 for four-state model), and N_p is the number of photons analyzed).

The above example shows that the maximum likelihood analysis can be readily extended by employing realistic kinetics models and cross-validation. The extended four-state model improves the accuracy of the folding parameters, but it does not guarantee the accuracy of the blinking model and the blinking parameters because blinking kinetics are faster than the photon count rate. In Fig. 7D, the two opposite effects of donor and acceptor blinking compensate each other to produce a flat correlation function on the time scale < 10 μs in the experimental correlation function (left), while the compensation is incomplete in the correlation function of the re-colored data using four-state model (right). This disagreement indicates that the blinking parameters or the model can be inaccurate. For example, it is possible that there are more than one dark state that will produce a multi-exponential waiting time distribution or other unknown processes.

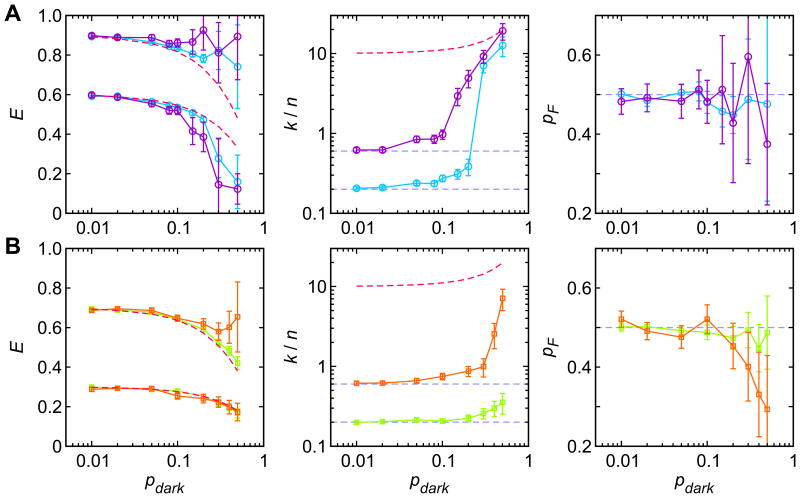
This example raises a question about the influence of fast acceptor blinking on the folding and unfolding rates obtained using the two-state model. When blinking is fast compared to the average inter-photon time, one would expect that transitions between the dark and bright states are averaged out between two consecutive photons, so that only the values of the FRET efficiencies would be affected by blinking, but not the folding rates. Although this is true in the limit of very fast blinking, the folding rates can be influenced by blinking, especially when the FRET efficiencies of the states are not well separated.

To illustrate this effect, we simulated photon trajectories according to the four-state model in Fig. 7C (two-state folding together with acceptor blinking) and analyzed them using the two-state model, Eq. (2) and Fig. 7B, with the likelihood function in Eq. (1). The extracted two-state parameters (FRET efficiencies, the relaxation rate k = k_F + k_U, and the fraction of the folded state p_F) are plotted as a function of the population in the dark state, p_d = k_d/(k_d + k_b). Since the blinking rates are high, one would expect that the four-state model can be reduced to the two-state model with the effective FRET efficiencies E_Fp_b + E_Dp_d and E_Up_b + E_Dp_d, where p_b = 1 - p_d is the population of the bright state and E_D (= 0.06) is the FRET efficiency in the dark state of the acceptor (E_D is not 0 because of the leak of the donor photons into the acceptor channel, often called “cross-talk”). Indeed, when the population of the dark state is small, the extracted FRET efficiencies are close to these expected values (red dashed lines on the left panels of Fig. 8). When the population of the dark state increases, this two-state system is not appropriate anymore. The reason is that the difference between the FRET efficiencies in the folded and unfolded states is smaller than that in the bright and dark states. In the limiting case when the values E_U and E_F are the same, the appropriate two-state model is the model with the bright and dark states. Therefore, the parameters of the extracted two-state model change as the population of the dark state increases, showing a transition from the folded-unfolded to the bright-dark two-state model. When E_F = 0.9 and E_U = 0.6 (close to the experimental data in Fig. 7A), ∼ 10% of the population in the dark state is large enough to affect the extracted rates (see Fig. 8A). This effect is smaller when the folding relaxation rate is small (compare k/n = 0.2 (light blue circle) and k/n = 0.6 (purple circle)). Fig. 8B also shows the same analysis for the FRET efficiencies 0.7 and 0.3, in which the separation of the folded and unfolded states is increased and the separation of the bright and dark states is decreased. The critical value of the dark state population in this case is larger (∼ 20%).

Figure 8.

The effect of the dark state population (p_dark) on the two-state maximum likelihood parameters. 5 sets of 100 30 ms-long photon trajectories with a photon count rate n = 50 ms^-1 were simulated using 4 model parameter sets. (A) E_F = 0.9, E_U = 0.6, k/n = 0.2 (light blue circle) and E_F = 0.9, E_U = 0.6, k/n = 0.6 (purple circle). (B) E_F = 0.7, E_U = 0.3, k/n = 0.2 (light green square) and E_F = 0.7, E_U = 0.3, k/n = 0.6 (orange square). p_F = 0.5, k_b = 500 ms^-1, and k_d = k_b(1- p_b)/p_b. Horizontal dashed lines indicate these model parameters. The red dashed curves in the left panels guide the effective FRET efficiencies in the fast blinking limit E_Fp_b + E_Dp_d and E_Up_b + E_Dp_d. The red dashed curve in the middle panels guides the relaxation rate between the bright and dark states (k_b + k_d). The errors are the average standard deviations obtained from the curvature of the likelihood function at the maximum.

6. Measurement of the transition path time

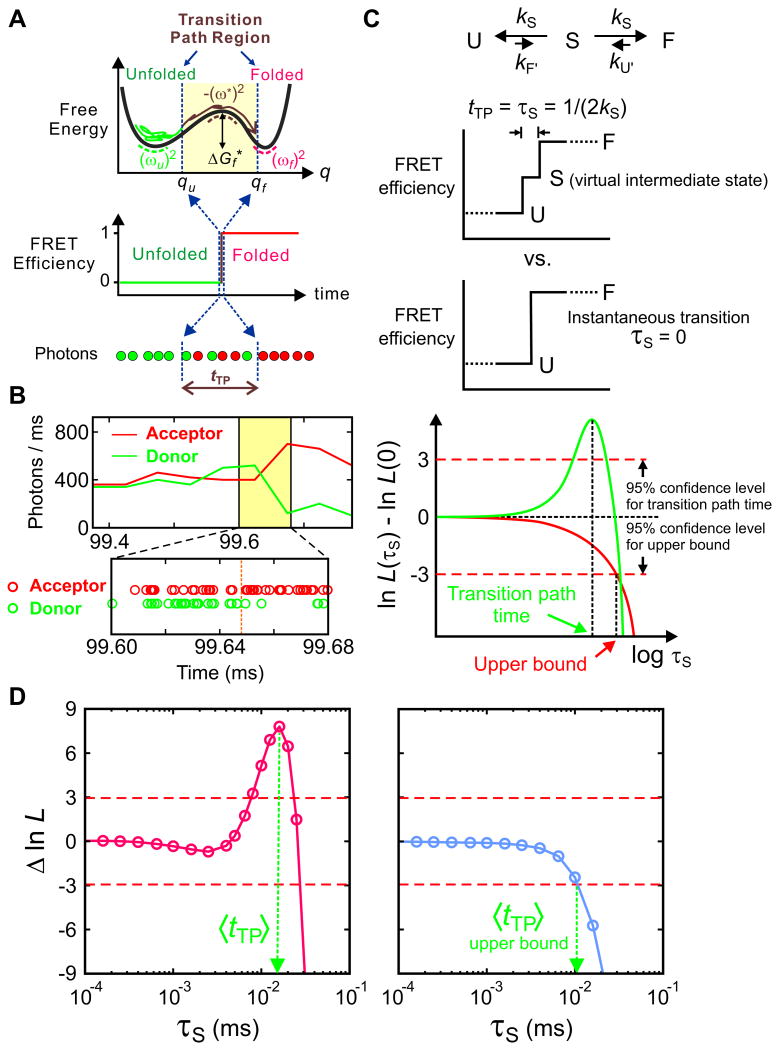
The analyses presented so far assume that transitions between states are instantaneous. However, an instantaneous transition is impossible. The time taken for a transition is just much, much shorter than the average waiting time in each state. Because it is so fast, the transition appears as a jump in a binned single-molecule trajectory. This jump corresponds to the molecular trajectory of free-energy barrier crossing, which is called the transition path (Fig. 9A). In fact, this brief moment of a transition contains the most important information of a process. Especially in the case of two-state proteins presented above, in which there is no well-defined intermediate state, all the mechanistic details of folding are contained in the transition path. Since the molecular events occurring during waiting either in the folded or unfolded states are predominately random conformational fluctuations, the conformational changes that are the most relevant to the folding/unfolding process occur in the transition path. Despite its importance, since transitions occur stochastically, the transition path is impossible to detect using ensemble measurements. It can be visualized only by observing one molecule at a time as in molecular dynamics simulations.^65-67 A big hurdle toward visualizing the transition path by employing single-molecule spectroscopy is the low time resolution of the measurement. Therefore, the transition path has not been explored experimentally. The first step toward this direction is measuring the average transition path time by improving the time resolution of the measurement. Compared to the previous two-state analysis, measuring this time is much more challenging because the transition path is a very tiny fraction of a trajectory that connects folded and unfolded states.

Figure 9.

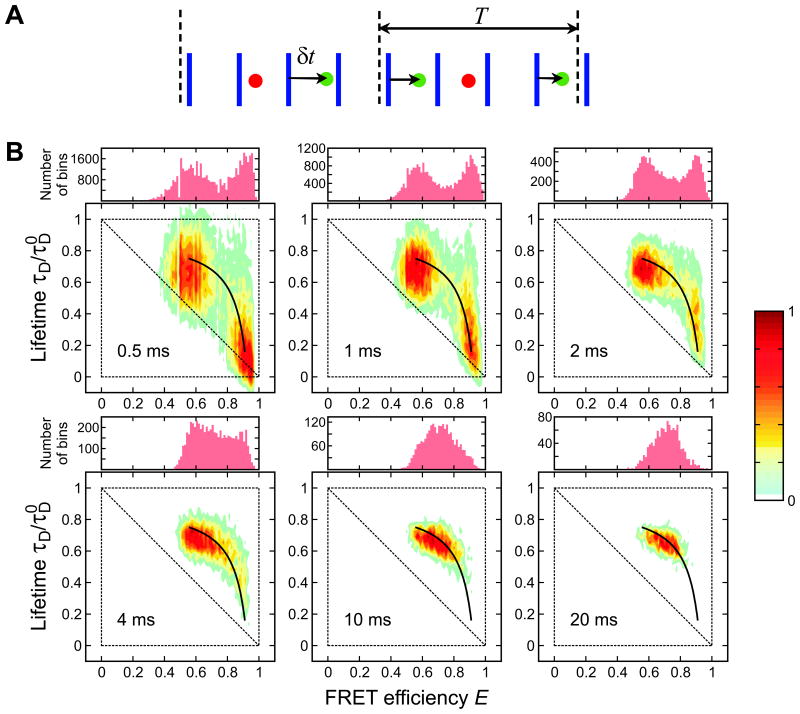
(A) Schematics of a folding transition path for a two-state protein in a one-dimensional free energy profile as a function of a reaction coordinate (q). In the folding reaction, a protein spends most of the time in the unfolded well exploring the unfolded conformations to cross the free energy barrier to the folded state. The transition path is one that leaves the unfolded well, crosses q_u on the reaction coordinate, and reaches q_f on the other side of the barrier without re-crossing q_u (brown trajectory). The transition path corresponds to the ‘jump’ in the FRET efficiency trajectory. (B) Representative binned fluorescence trajectory and photon trajectory of the WW domain. (C) Maximum likelihood method to determine the average transition-path times. The average transition path time, t_TP, is equal to the lifetime of a virtual intermediate state S [τ_S = (2k_S)⁻¹] in the three-state model describing the transition path from the unfolded (U) to the folded (F) states. The plot of the difference of the log-likelihood, Δln L = ln L(τ_S) − ln L(0), compares the two models: three-state model with a finite transition path time and a two-state model with an instantaneous transition. The horizontal dashed line at Δln L = +3 represents the 95% confidence limit for the significance of the peak for the measurement of the transition path time and the intersection of the likelihood function with the horizontal dashed line at Δln L = −3 yields the 95% confidence limit for the upper bound of the transition path time. (D) The transition path time of the WW domain is 16 μs at 10 cP (50% glycerol, 3 M GdmCl), which is extrapolated to ∼ 2 μs at aqueous viscosity and the upper bound of the transition path time of protein G B1 domain is 10 μs (4 M urea). Data and figures from Ref. 36 and 57.

Recently, the maximum likelihood method has been used to measure the average transition path times of several two-state proteins.^36,57 In these experiments, photon trajectories were collected at high illumination intensity to produce a high photon count rate of 500 – 1000 ms^-1 (Fig. 9B), and photons detected near transitions were analyzed using a three-state kinetics model (Fig. 9C). Although the transition path is not a real state (no free energy minimum exists at the top of the barrier in Fig. 9A), the average transition path time, t_TP, can be measured effectively by treating the transition path as an intermediate state and use a three-state model (Fig. 9C) to calculate the likelihood function. The rate matrix of this model is given as

$$\mathbf{K}=\left(\begin{array}{ccc}-k_{U^{\prime }}& k_{\mathrm{S}}& 0\\ k_{U^{\prime }}& -2k_{\mathrm{S}}& k_{F^{\prime }}\\ 0& k_{\mathrm{S}}& -k_{F^{\prime }}\end{array}\right)$$ (7)

Here, notations F′ and U′ are used for the folded and unfolded states to distinguish these from those in the two-state model with an instantaneous transition. The lifetime of the intermediate state S, τ_S = 1/(2k_S) is the same as the average transition path time t_TP. In the analysis, all the parameters (rate coefficients and FRET efficiencies) except k_S can be pre-determined so that the transition path time can be determined from the maximum of the likelihood plot as a function of τ_S (Fig. 9C).

Since the transition path time is expected to be very short compared to the waiting times in the folded and unfolded states, the analysis can be easily interfered by other processes such as acceptor blinking. (Donor blinking does not affect the likelihood function in Eq. (1), as discussed in Section 5.) For example, in the three-state model the FRET efficiency of the transition path is the midway between the folded and unfolded states (E_S = (E_F + E_U)/2), but if acceptor blinking occurs at or near a folding/unfolding transition, the value in the actual data becomes the FRET efficiency of the acceptor dark state, which is close to zero. In this case, the model is very inconsistent with the data and the likelihood becomes very small. If this interference happens frequently, it would not be possible to detect a peak in the likelihood plot in Fig. 9C. To avoid this complication, the data containing clear acceptor blinking near folding/unfolding transitions (e.g. the presence of more than 7 consecutive donor photons within a 60 μs window of a transition)³⁵ were excluded from the analysis. More sophisticated filters can be devised and used, but it is important not to remove too many transitions that may bias the analysis and produce a false peak in the likelihood plot. Alternatively, the acceptor blinking kinetics can be incorporated in the model as shown in Section 5.

The transition path time of the WW domain measured using the three-state model (Fig. 9C) was 16 μs at ∼ 10 cP (50% glycerol solution), which can be extrapolated to the aqueous viscosity value, ∼ 2 μs, using the fact that the folding time is linearly proportional to the solvent viscosity. In addition, even if there is no peak higher than the 95% confidence level, it is possible to determine the upper bound of the transition path time in this analysis,³⁶ which resulted in the upper bound of 10 μs for a slow folding protein, protein G B1 domain (Fig. 9D).

These results are particularly interesting because the transition path times are very similar for the two proteins with very different folding rates. The folding time, t_f, (the inverse of the folding rate coefficient) of protein G B1 domain is 1 s, which is 10,000 times longer than t_f of the WW domain, 100 μs. The insensitivity of the transition path time to the folding kinetics can be explained by the theory of diffusive barrier crossing. Folding of small two-state proteins can be effectively described by diffusion on a 1-dimentional free energy profile with two wells separated by a barrier.^68-70 In this case, t_f and t_TP, are given by

$$t_f=\frac{2\pi }{\beta D\ast \omega \ast {\omega }_u}exp\left(\beta \Delta G_f^{\ast }\right)$$ (8)

$$t_{\mathit{\text{TP}}}\approx \frac{1}{\beta D\ast {(\omega \ast )}^2}ln\left(2e^{\gamma }\beta \Delta G_f^{\ast }\right),$$ (9)

where D* is the diffusion coefficient at the free energy barrier top, (ω*)² and (ω_u)² are the curvatures of the free energy at the barrier top and the unfolded well, respectively, and ΔG_f* is the free energy barrier height for the folding transition (Fig. 9A). β = 1/k_BT, where k_B is the Boltzmann constant, T is the absolute temperature, and γ is Euler's constant (= 0.577…). Equation (8) is the inverse of the Kramers' rate constant⁷¹ and equation (9) is Szabo's formula^35,72 for the transition path time in the high barrier limit (see Electronic Supplementary Information for a self-contained derivation of Eq. (9)). t_f is the average waiting time spent in the unfolded well before making a transition to the folded side (Fig. 9A). t_TP is the average time that a molecule spends on a transition path (brown trajectory in Fig. 9A). As the above equations show, the folding time t_f is very sensitive to the barrier height while the transition path time t_TP is insensitive. Therefore, if the diffusion coefficient and the curvature for the WW domain and protein G B1 domain are similar, the transition path times are also similar despite the large difference in the folding times. On the other hand, we measured a much longer transition path time of an all-α helical protein, α₃D, 12 μs in an aqueous solution,⁵⁷ suggesting that the diffusion coefficient D* of α₃D is much smaller than that of the WW domain due to its rougher energy landscape.⁷³

7. Utilizing fluorescence lifetime information

So far, we discussed how to analyze photon colors and arrival times. In pulsed laser experiments, times between laser pulses and photon arrivals (delay times) can also be recorded, in addition to photon colors and inter-photon times (see Fig. 10A). The advantages of the simultaneous detection and analysis of both lifetimes and fluorescence intensities have been emphasized by several groups.^14,30,74,75 In this section we present a theory and an experimental demonstration that utilize the additional information from the donor lifetime. Here we focus on two-dimensional (2D) FRET efficiency - donor lifetime histograms.

Figure 10.

(A) A schematic representation (not to scale) of a sequence of donor (green) and acceptor (red) photons detected after pulsed laser excitations (blue). For each donor photon, the time δt between the laser pulse and the photon (delay time) is recorded. The photon sequence is divided into bins of duration T. Figure from Ref. 77. (B) Bin time (0.5 – 20 ms) dependence of the FRET efficiency histograms and two-dimensional (2D) density plots of donor fluorescence lifetime vs. FRET efficiency of α₃D ([GdmCl] = 2.3 M). The two peaks in the FRET efficiency histograms merge into one peak as the bin time increases due to averaging by folding/unfolding transitions. In the 2D plots, the two peaks corresponding to the folded and unfolded states merge into one peak along the two-state dynamic line calculated using Eq. (12). The parameters in Eq. (12) are the apparent FRET efficiencies and the mean lifetime of the unfolded and folded states obtained from the 2D plot at the bin time of 0.5 ms. Each 2D histogram is normalized to its maximum value.

For binned photon trajectories, the donor fluorescence lifetime in a bin is defined as the mean of all donor delay times in that bin. The lifetime changes from bin to bin as does the apparent FRET efficiency (defined as the fraction of acceptor photons in a bin). These can be histogrammed together resulting in a 2D FRET efficiency-donor lifetime histogram. Since both the FRET efficiency and the lifetime depend on the energy transfer rate, they are related. The relationship depends on the time scale of inter-dye distance fluctuations, so 2D histograms can give a better insight into the molecular dynamics and photophysics.

As an illustration we consider 2D histograms for a two-state protein, α₃D, with transitions between the folded and unfolded states on the ms time scale. Similar to 1D FRET efficiency histograms, the 2D histograms are sensitive to the bin time when the bin time is comparable to the folding and unfolding times (see Fig. 10B). When the bin time is so short that transitions do not occur in most of the bins, the histograms show two peaks centered on the FRET efficiencies and lifetimes of the folded and unfolded states. The peak corresponding to the folded state (with high FRET efficiency) is located on the diagonal of the 2D plot (a small shift from the diagonal is due to the background noise, the effect of which is relatively large for the peak with high FRET efficiency). This is because the inter-dye distance in the folded state does not change significantly. In this case, the mean donor lifetime τ_DF and FRET efficiency E_F in the folded state are related by a simple well-known relationship⁷⁶

$${\tau }_{\mathit{\text{DF}}}/{\tau }_D^0=1-E_F,$$ (10)

where ${\tau }_D^0$ is the donor lifetime in the absence of the acceptor.

The peak corresponding to the unfolded state is noticeably shifted above the diagonal, which indicates the presence of dynamics on the sub-microsecond time scale.^14,30 Similar shift in the 2D histograms⁷⁴ has been attributed to the fluctuations of the inter-dye distances in the unfolded state. To understand why fast dynamics in the unfolded state lead to the increase of the donor fluorescence lifetimes, consider the fluctuations of the energy transfer rate as the inter-dye distance changes. When the energy transfer rate, say, increases, not only the donor excited state lifetime decreases, but also the number of donor photons decreases. In other words, less donor photons are detected with shorter delay times and vice versa. Therefore, the mean donor delay time (the fluorescence lifetime) increases when the energy transfer rate fluctuates. The shift above the diagonal can be estimated when the dynamics in the unfolded state are faster than the inter-photon times, but slower than the donor fluorescence lifetime⁷⁷

$${\tau }_{\mathit{\text{DU}}}/{\tau }_D^0=1-E_U+\frac{{\sigma }_c^2}{1-E_U},$$ (11)

where τ_DU and E_U are the lifetime and FRET efficiency of the unfolded state, σ_c² is the FRET efficiency variance, ${\sigma }_c^2={\int }_0^{\infty }\varepsilon {(r)}^{2}p(r)dr-{({\int }_0^{\infty }\varepsilon (r)p(r)dr)}^2$, ε(r) = (1 + (r/R₀)⁶)⁻¹ is the FRET efficiency when the donor-acceptor distance is r, R₀ is the Förster radius, and p(r) is the normalized distribution of the inter-dye distances. For the Gaussian chain model, p(r) = 4πr²(3/(2π〈r²〉))^3/2exp(−3r²/2〈r²〉), and the only free parameter of this distribution, 〈r²〉, can be obtained by fitting E_U to $E_U={\int }_0^{\infty }\varepsilon (r)p(r)dr$.⁷⁵ To estimate the rate of the inter-dye fluctuations, one needs to invoke complementary techniques.^78-80

The relations in Eqs. (10) and (11) are valid for the “true” lifetimes and FRET efficiencies, and therefore, the extracted parameters for the folded and unfolded states should be corrected for the background noise, crosstalk and γ-factor (the ratio of the quantum yields and detection efficiencies of acceptor and donor photons) before using these equations. For example, the apparent FRET efficiency obtained from the maximum likelihood method are E_F = 0.91 and E_U = 0.55. After the corrections for the background (1.5 ms^-1 for the acceptor and 1.3 ms^-1 for the donor with the average total photon count rate of 65.4 ms^-1), donor leak (7%), and γ = 1.20, the true FRET efficiencies are E_F = 0.89 and E_U = 0.50. Using the corrected E_U and ${\tau }_{DU}/{\tau }_D^0=0.714$, obtained from fitting the lifetime data, we can calculate the FRET efficiency variance σ_c² = 0.11.

As the bin time increases, transitions between the folded and unfolded states occur during the bin time. The transitions result in the increased density between the two states (see Fig. 10B). In the limit when the photon count rates are so large that shot noise is negligible, the FRET efficiency-lifetime distribution is confined to a curved line (two-state dynamic line) where τ_D and E are related by

$$\frac{{\tau }_D-{\tau }_{\mathit{\text{DF}}}}{{\tau }_{\mathit{\text{DU}}}-{\tau }_{\mathit{\text{DF}}}}=\frac{1-E_U}{E_F-E_U}(1-\frac{1-E_F}{1-E}).$$ (12)

This equation is equivalent to Eq.(8) in Ref. 77 and reduces to Eq. (9d) in Ref. 30 in the special case when there are no sub-microsecond dynamics in the states. The two-state dynamic line connects the folded and unfolded peaks on the 2D histogram. It involves only the parameters of the two states (i.e., the mean lifetimes and FRET efficiencies τ_DF, τ_DU, E_F, and E_U). The parameters in this equation do not need to be corrected for the background noise, crosstalk, and γ-factor.

At longer bin times, the distribution collapses to a single peak centered on the average FRET efficiency and lifetime and located on the two-state line, as seen in Fig. 10B. The distribution along the two-state dynamic line as well as the collapse to a single peak with the increase of the bin time indicate the transitions between the folded and unfolded states on the time scale of the bin time.

8. Concluding remarks

Conformational dynamics of macromolecules such as protein folding are intrinsically heterogeneous. Single-molecule measurements have become a common tool to study such processes on the time scale from milliseconds to seconds. To study the details of a process, it is important to improve the time resolution of single-molecule techniques. This allows one to directly compare the experimental results with the molecular dynamics simulations, among other advantages.^81,82

In this Perspective, we have presented how to enhance the time resolution of single-molecule FRET spectroscopy up to microsecond time scale by analyzing individual photons. We described the maximum likelihood approaches that can be used to measure kinetics among states or diffusion coefficients in a 1D energy profile. This method has been applied to the experimental measurement of fast folding kinetics and average transition path times in protein folding. We also discussed the accuracy of the extracted parameters and the range of parameters that can be reliably determined for a given photon count rate through the analyses of simulated photon trajectories. When additional interfering processes are present, such as photoblinking of dyes, we showed that correct parameters still can be extracted by employing a reasonable kinetics model that includes the photoblinking process. In respect of utilizing available information as much as possible,^14,35,83-86 it is expected to incorporate the lifetime information in the likelihood function⁷⁷ and use other properties of photons such as polarization when the fluorescence anisotropy depends on protein conformational states. Here we showed how donor fluorescence lifetimes can be used to demonstrate the presence of conformational dynamics in two-dimensional FRET efficiency-lifetime histograms.

Although the application of the method so far has been primarily to two-state systems, it can be easily extended to a system with multiple states and complex kinetics. In this case, there will be advantages to using three or more fluorophores.^87-90 The development of multi-color FRET experiments is particularly important, because they provide information about time dependence of several possibly correlated distances, which is required to describe molecular dynamics in more detail. Likelihood-based methods will prove to be a powerful tool for the analysis of multi-color FRET.