Protonation of Nickel–Iron Hydrogenase Models Proceeds after Isomerization at Nickel

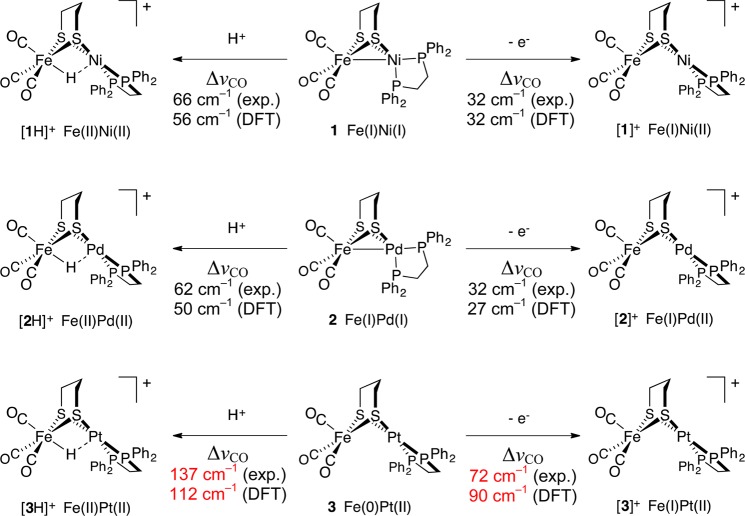
Abstract

Theory and experiment indicate that the protonation of reduced NiFe dithiolates proceeds via a previously undetected isomer with enhanced basicity. In particular, it is proposed that protonation of (OC)₃Fe(pdt)Ni(dppe) (1; pdt^2– = ^–S(CH₂)₃S^–; dppe = Ph₂P(CH₂)₂PPh₂) occurs at the Fe site of the two-electron mixed-valence Fe(0)Ni(II) species, not the Fe(I)-Ni(I) bond for the homovalence isomer of 1. The new pathway, which may have implications for protonation of other complexes and clusters, was uncovered through studies on the homologous series L(OC)₂Fe(pdt)M(dppe), where M = Ni, Pd (2), and Pt (3) and L = CO, PCy₃. Similar to 1, complexes 2 and 3 undergo both protonation and 1e^– oxidation to afford well-characterized hydrides ([2H]⁺ and [3H]⁺) and mixed-valence derivatives ([2]⁺ and [3]⁺), respectively. Whereas the Pd site is tetrahedral in 2, the Pt site is square-planar in 3, indicating that this complex is best described as Fe(0)Pt(II). In view of the results on 2 and 3, the potential energy surface of 1 was reinvestigated with density functional theory. These calculations revealed the existence of an energetically accessible and more basic Fe(0)Ni(II) isomer with a square-planar Ni site.

Introduction

The protonation of metal complexes and clusters continues to attract much attention because of its relevance to catalysis involving proton and hydride transfer reactions. In organometallic and heterogeneous catalysis, protonation is a step in substrate hydrogenation and hydrogen evolution.^1,2 In biology, metal protonation is implicated in the reduction of CO₂ and N₂, not to mention hydrogen evolution.^2,3 For all of these reactions, a central question is the regiochemistry of the protonation. For compounds with metal–metal bonds, protonation can in principle occur at a single metal or at the metal–metal bond.

The regiochemistry of protonation is relevant to a mechanistic understanding of the [NiFe]- and [FeFe]-hydrogenases, which also feature Ni–Fe and Fe–Fe bonding interactions.^4,5 By proton transfer, these complexes equilibrate protons and dihydrogen, i.e., 2H⁺ + 2e^– ⇌ H₂ in accordance with the local redox environment and activities of H⁺ and H₂. Functional models for the active sites of these enzymes present opportunities for translating biological insights into practical catalytic systems.⁶ In addition to being fast and operating at low overpotentials, the hydrogenases are attractive targets for functional modeling because they utilize earth abundant metals.⁷ For the above reasons, much effort has been directed, both computationally⁸ and experimentally,⁹ at understanding the details of proton transfer to and from synthetic NiFe and FeFe complexes.

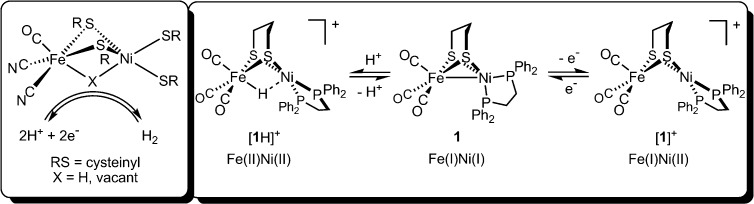
While many complexes engage separately in acid–base and redox reactions, few exhibit both kinds of reactivity, providing a possible explanation for the paucity of functional hydrogenase (H₂ase) models. With respect to the [NiFe]-H₂ases (Figure 1, left), the premier example of such a model is (OC)₃Fe(pdt)Ni(dppe) (1).¹⁰ Tricarbonyl 1 and analogous phosphine-substituted derivatives undergo: (i) protonation to afford rare examples of nickel–iron hydrides and (ii) 1e^– oxidation to give Fe(I)Ni(II) derivatives (Figure 1, right). Several examples of charge-neutral Fe(I)Ni(I) species, as well as their related Fe(II)Ni(II) hydrides¹¹⁻¹³ and Fe(I)Ni(II) cations,^14,15 have been characterized.

Figure 1.

Active site of [NiFe]-H₂ase, a bidirectional catalyst, participates in redox and acid–base chemistry (left). Similar behavior is observed for the prototypical model complex 1 (right).

The [NiFe]-H₂ase active site features Ni bound to four Cys ligands in a distorted tetrahedral (SF₄-like) arrangement. Two of the thiolates link to an Fe center whose coordination sphere includes the unusual CO and CN^– cofactors, the latter H-bonding to neighboring Ser and Arg residues.⁴ In the active states of the enzyme, the FeNi core appears to be relatively conformationally rigid, with the Fe···Ni distance and coordination geometry being rather insensitive both to redox state and the presence/absence of H^– substrate.¹⁶ The rigidity of the active site is undoubtedly a factor in the high rates and low overpotentials at which the interconversion of H⁺ and H₂ is mediated.

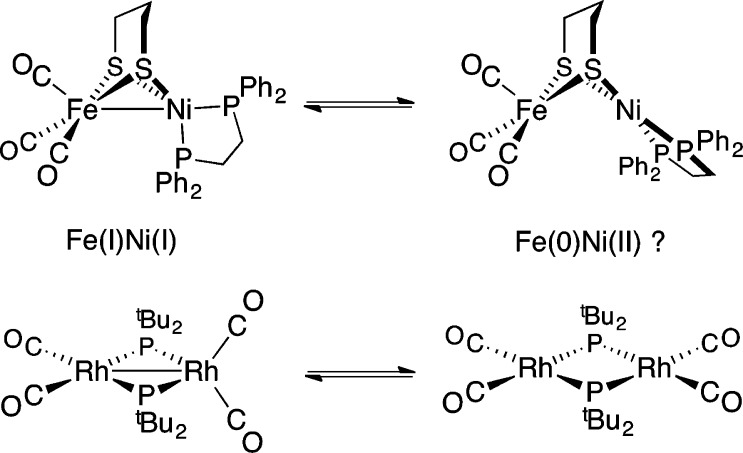
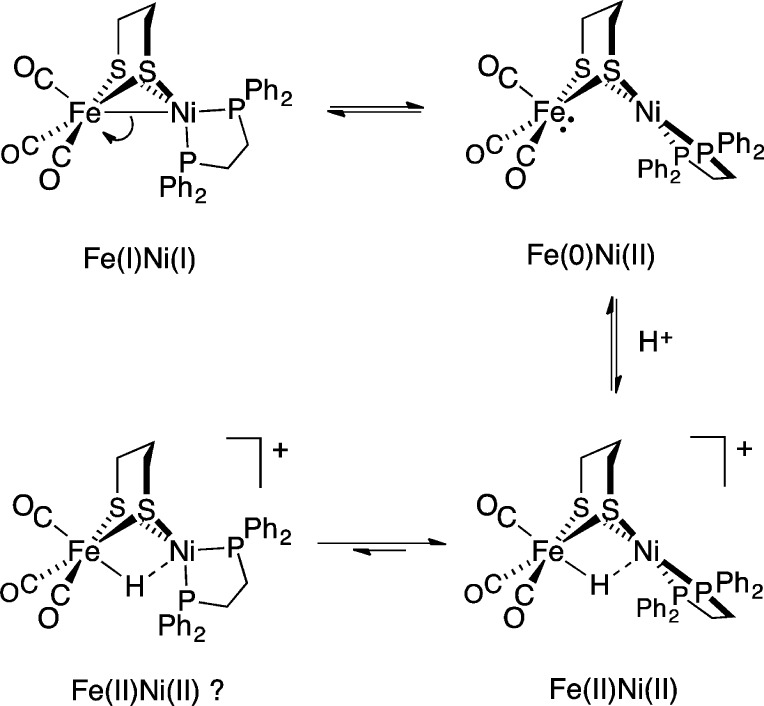
In contrast to the rigid active site, small molecule mimics are conformationally dynamic. For example, 1 undergoes a tetrahedral → square-planar twist at Ni upon oxidation or protonation (Figure 1). While the structures of 1, [1]⁺, and [1H]⁺ are established,¹⁰⁻¹⁵ those of any intermediates are not. Such transformations may, for example, involve “pre-twisting” of the Ni coordination in 1 (Scheme 1, top).

Scheme 1.

Distortion of the ground-state structure of 1 could well affect oxidation states by inducing 2e^– mixed-valency.¹⁷ Furthermore, the degree of Fe–Ni bonding and, most importantly, reactivity would also be perturbed. While ligand-centered isomerism is a common theme in the chemistry of multimetallic compounds, drastic differences in coordination geometry and metal–metal bonding between two (or more) interconverting species are extremely rare. They are, however, not without precedent; for example, Jones and co-workers reported X-ray structures for two complexes of formula (OC)₂Rh(μ-PR₂)₂Rh(CO)₂ (Scheme 1, bottom).¹⁸ One species takes the form of a red compound featuring Rh–Rh bonding (2.761 Å), in which one Rh center is square-planar and the other tetrahedral. A second (orange) isomer was also observed, in which non-interacting Rh centers (3.717 Å) adopt square-planar geometries.

The present study involves parallel experimental and density functional theory (DFT) investigations to obtain a complete structural, energetic, and mechanistic picture of complexes derived from FeNi complex 1. This work was extended to FePd and FePt species such that a homologous series can be interrogated for information regarding conformational motions and metal–metal bonding.

Results and Discussion

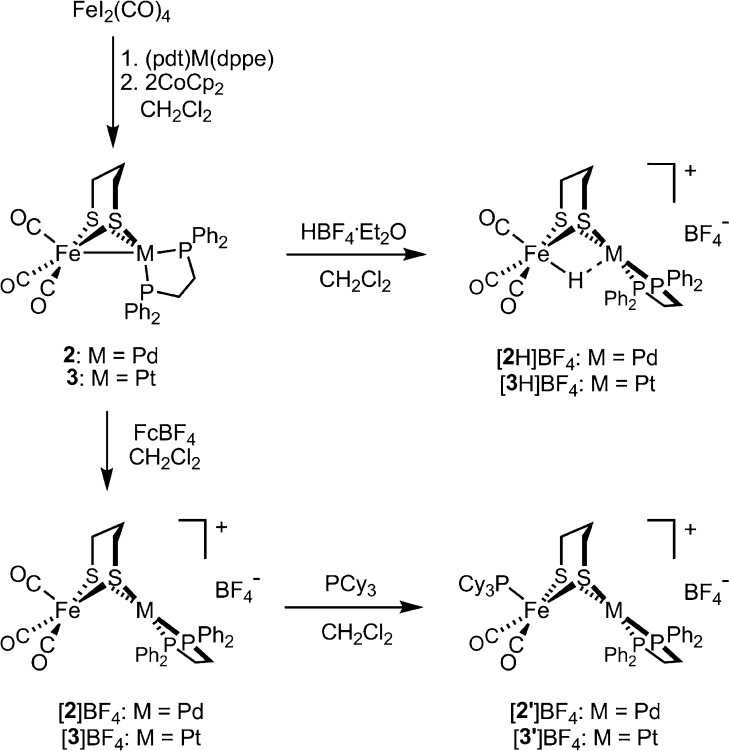
The major routes to low-valent FeNi complexes of type (OC)₃Fe(pdt)Ni(diphosphine) involve treatment of (pdt)Ni(diphosphine) with either (i) Fe₂(CO)₉ or (ii) FeI₂(CO)₄/CoCp₂. As applied to the Pd and Pt derivatives, the second route proved more attractive, giving the diamagnetic heterobimetallics (OC)₃Fe(pdt)Pd(dppe) (2) and (OC)₃Fe(pdt)Pt(dppe) (3) (Scheme 2).¹⁹

Scheme 2.

Isolated as dark-green needles, 2 is sensitive to O₂ (decomposing to CO-free paramagnetic species) but is thermally stable in the solid state under N₂. The energies of the two ν_CO bands (A + E modes) compare well with those observed for 1 (Table 1).

Table 1. IR Data (ν_CO/cm^–1) for FeM (M = Ni, Pd, Pt) Compounds in CH₂Cl₂ Solution.

compound	FeNi	FePd	FePt
(OC)3Fe(pdt)M(dppe)	2028, 195220	2024, 1955	1962, 1883, 1870
[(OC)3FeH(pdt)M(dppe)]BF4	2082, 202420	2081, 2020	2081, 2022
[(OC)3Fe(pdt)M(dppe)]BF4	2057, 198613	2058, 1986	2058, 1987
[Cy3P(OC)2Fe(pdt)M(dppe)]BF4	1966, 189912	1964, 1900	1966, 1900

The FePd species 2 is similar to 1 in that its room temperature ³¹P{¹H} NMR spectrum features a broad singlet resonance (δ 51.3) for the dppe ligand. At lower temperature, the resonance for 1 decoalesces into two peaks (well-resolved at −68 °C), consistent with a dynamic process that interconverts the ³¹P sites. The previously reported coalescence temperature (−30 °C)¹² corresponds to a free energy barrier of 9.5 kcal/mol for the FeNi species 1. This process presumably occurs via an intermediate or transition state with square-planar Ni. No decoalescence was observed for 2 even at −85 °C, behavior suggestive of either: (i) a tetrahedral Pd ground state with a particularly low rotational barrier or (ii) a square-planar Pd ground state. The second possibility is ruled out based on the similarity of the IR data for 1 and 2. The structure of 2 in the solid state was confirmed crystallographically (Figure 2).

Figure 2.

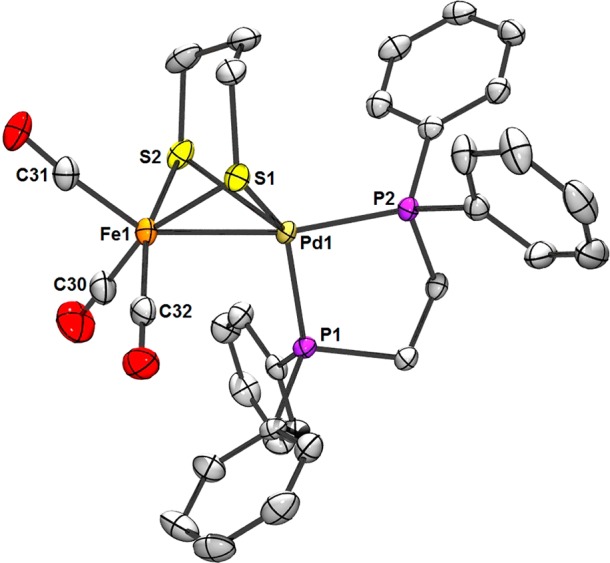
ORTEP of 2 with ellipsoids drawn at the 50% probability level and H atoms omitted for clarity. Selected distances (Å) (mean DFT values in parentheses): Pd1–Fe1, 2.561 (2.56); Pd1–P1, 2.249; Pd1–P2, 2.271 (2.26); Pd1–S1, 2.573; Pd1–S2, 2.402 (2.49); Fe1–S1, 2.299; Fe1–S2, 2.275 (2.30); Fe1–C30, 1.795; Fe1–C31, 1.793; Fe1–C32, 1.798 (1.77). Selected angles (deg) (mean DFT values in parentheses): P1–Pd1–S1, 135.2; P1–Pd1–S2, 118.83; P2–Pd1–S1, 115.7; P2–Pd1–S2, 122.5 (135.1); S1–Fe1–C30, 162.2; S2–Fe1–C32, 163.1 (161.1).

Given the covalent radii of Pd (1.39 Å) and low-spin Fe (1.32 Å),²¹ the Fe–Pd distance of 2.561 Å suggests the presence of bonding between the metal centers in 2. The intermetallic separation is somewhat shorter in 1 (2.467 Å). Metal–metal interactions aside, the Pd and Fe centers in 2 exist in roughly tetrahedral and square-pyramidal (τ = 0.01 indicates a low degree of trigonality)²² coordination geometries, respectively. The complex is isostructural to its Fe(I)Ni(I) congener, and it is expected that an Fe(I)Pd(I) description is appropriate, particularly considering the tetrahedral Pd coordination, as such a geometry is unlikely for Pd(II).

The structures of several complexes reported here were calculated using DFT, and the optimized structures were in excellent agreement with available crystal structures (selected metrics are presented in Tables S3 and S4). In the case of 2, calculations accurately predicted the geometry of Pd, as well as its proximity to Fe. Additional isomers characterized as minima with DFT will be discussed below. NBO (natural bond orbital)²³ analysis revealed the Fe–Pd bond to arise from overlap of an Fe-centered d(z²) orbital with a Pd-centered orbital with d character (Figure S56b). NBO analysis of FeNi congener 1 also revealed metal–metal bonding (Figure S56a) consistent with previous DFT analyses of this system.¹⁰ NBO analysis of other Fe–M complexes discussed herein did not indicate mixing of metal d orbitals; hence, no Fe–M bonding is expected for these species.

Mixed-Valence Derivatives

The cyclic voltammogram of 2 features reversible and quasi-reversible oxidations at E_1/2 = −0.87 and +0.26 V, respectively (vs ferrocene/ferrocenium, Fc^0/+; Figure 3). The reversible wave, assigned to the [2]^0/+ couple, is 300 mV more negative than the wave for [1]^0/+,¹⁵ a result reflective of the more reducing nature of the heavier group 10 metal.

Figure 3.

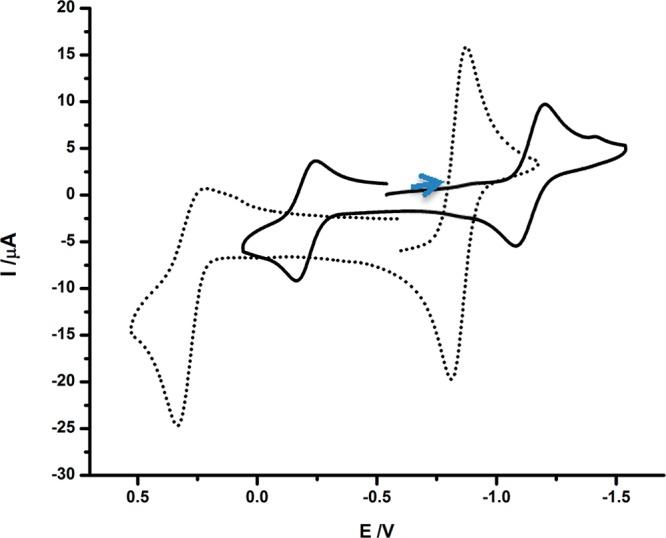
Cyclic voltammograms of 2 (dotted trace) and [2′]BF₄ (solid trace) acquired in CH₂Cl₂ with 100 mM NBu₄PF₆. Potentials (V vs Fc^0/+) were swept at 100 mV s^–1.

DFT was used to calculate the potentials associated with the two couples for each [L(CO)₂Fe(pdt)M(dppe)]^0/+/2+ (L = CO, PCy₃; M = Ni, Pd, Pt) system. The calculated potentials are in excellent agreement with the experimental values for the neutral/monocation couples, while the values for the monocation/dication couples are in qualitative but not quantitative agreement. The latter discrepancies are mainly a result of these more anodic couples being only partially reversible, the associated potentials being less thermodynamically reliable.

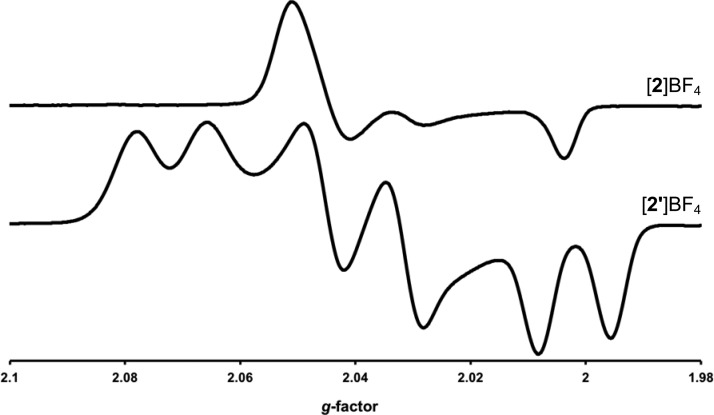
Chemical oxidation of 2 with FcBF₄ afforded [(OC)₃Fe(pdt)Pd(dppe)]BF₄ ([2]BF₄), isolated as an olive-brown powder. Positive ion ESI-MS analysis (m/z 749.8) was consistent with the formula, and the lability of [(OC)₃Fe(pdt)Pd(dppe)]⁺ was evidenced by observation of CO dissociation products (m/z 721.8, 693.8). The ν_CO bands for [2]⁺ (2058, 1986 cm^–1) are only modestly shifted from those of 2, implicating oxidation at the Pd center. EPR measurements also indicated an Fe(I)Pd(II) description for [2]⁺, the assignment being based on the magnitude of the g shifts and the absence of ³¹P hyperfine coupling (Figure 4, top; for simulated EPR spectra and parameters see Figure S23 and Table S1, respectively). The data are similar to those for Fe(I)Ni(II) complexes, for which theory indicated an Fe-centered d(z²) doublet ground-state singly occupied molecular orbital (SOMO).¹⁵ These computational results, as well the implied absence of spin–orbit coupling expected for a d(z²) ground state, are consistent with a resonance in the vicinity of g_e. Owing to the inversion of the pdt^2– ring, the [(OC)₃Fe(pdt)M(dppe)]⁺ radicals exist as two conformers, one giving rise to an axial pattern and the other to a rhombic pattern.

Figure 4.

X-band EPR spectra (CH₂Cl₂/PhMe, 110 K) of [2]BF₄ and [2′]BF₄.

DFT analysis of spin densities was used to determine the localization of the unpaired electron in [2]⁺ as well as all other mixed-valence bimetallics (Table 3). In each case, the spin is entirely Fe-centered, consistent with the Fe(I)M(II) assignments from EPR analyses. The spin density distribution is unaffected by inversion of the pdt^2– ring, as observed for related FeNi complexes.^14,15

Table 3. Calculated Spin Densities on Metal Centers in Mixed-Valence Fe(I)M(II) Species.

complex	ρ(M)	ρ(Fe)
[(OC)3Fe(pdt)Ni(dppe)]+ ([1]+)	0.04	1.03
[Cy3P(OC)2Fe(pdt)Ni(dppe)]+ ([1′]+)	0.01	1.14
[(OC)3Fe(pdt)Pd(dppe)]+ ([2]+)	0.03	1.04
[Cy3P(OC)3Fe(pdt)Pd(dppe)]+ ([2′]+)	0.03	1.06
[(OC)3Fe(pdt)Pt(dppe)]+ ([3]+)	0.03	1.03
[Cy3P(OC)3Fe(pdt)Pt(dppe)]+ ([3′]+)	0.04	1.05

Cation [2]⁺ undergoes substitution with PCy₃ to afford [Cy₃P(OC)₂Fe(pdt)Pd(dppe)]BF₄ ([2′]BF₄) as a yellow-brown solid. Similar to its tricarbonyl precursor, [2′]⁺ is also described as an Fe(I)Pd(II) compound, the rhombic signals split by interaction of the SOMO with ³¹PCy₃ (A(³¹P) = 54, 61, 57 MHz). The data are distinct from those of the green Fe(I)Ni(II) analog [1′]⁺, which show ³¹P hyperfine to be absent due to structural distortions at Fe.

As with 2, the cyclic voltammogram of [2′]BF₄ features two waves, the events at E_1/2 = −1.14 and −0.20 V being assigned to [2′]^0/+ and [2′]^+/2+ couples, respectively. The waves are cathodically shifted relative to the tricarbonyl parent, with a smaller shift in the first wave (ΔE_1/2 = −0.27 V) than in the second (ΔE_1/2 = −0.46 V). These trends were also reproduced by DFT calculations (Table 2). The fact that ligand substitution at Fe perturbs the anodic wave to a greater degree points to this redox event being Fe-centered. These data are consistent with the sequence: Fe(I)Pd(I) ⇌ Fe(I)Pd(II) ⇌ Fe(II)Pd(II). The reversibility of the Fe(I)Pd(II)/Fe(II)Pd(II) ([2′]^+/2+) couple is greater than that of [2]^+/2+, the ligands in the former case being better suited to stabilize the ferrous state.

Table 2. Redox Potentials (V vs Fc^0/+, Experimental and DFT-Calculated) and Associated Eletrochemical Data (Recorded at 0.1 Vs^–1) for FeNi, FePd, and FePt Complexes (1 mM) in NBu₄PF₆ Electrolyte (100 mM CH₂Cl₂ Solution).

	E1/2 (FeIMII/FeIIMII) (|ipc/ipa|, |ΔEp|)	E° (FeIMII/FeIIMII) DFT	E1/2 (FeIMI/FeIMII) (|ipa/ipc|, |ΔEp|)a	E° (FeIMI/FeIMII) DFT
1	+0.34b	+0.52	–0.59 (0.90, 0.059)	–0.62
[1′]BF4	–0.14 (0.68, 0.076)b	–0.14d	–0.92 (1.00, 0.072)c	–0.92d
2	+0.26 (0.29, 0.115)	+0.39	–0.87 (0.98, 0.061)	–0.92
[2′]BF4	–0.20 (0.67, 0.080)	–0.20e	–1.14 (0.83, 0.122)	–1.14e
3	+0.33 (0.49, 0.168)	NDf	–0.93 (0.97, 0.105)g	–0.91g
[3′]BF4	–0.19 (0.50, 0.076)	–0.24	–1.37 (0.66, 0.067)g	–1.38

^aΔE_p(Fc^0/+) = 0.064 V under these conditions.

^bAnodic potential for irreversible oxidation.

^cData from ref (15).

^dCalculated and experimental values for [1′]BF₄ agree by construction and were used as references for the corresponding [1] waves.

^eCalculated and experimental values for [2′]BF₄ agree by construction and were used as references for the corresponding [2], [3], and [3′] waves.

^fThis value was not determined as difficulties arising from local minima led to inconclusive results.

^gThis wave is assigned to a Fe⁰Pt^II/Fe^IPt^II couple (vide infra).

Palladium–Iron Hydride

The protonation of 2 with HBF₄ affords the hydride salt [2H]BF₄, the formation of which is signaled by the appearance of high energy ν_CO bands (2081, 2020 cm^–1) suggestive of an Fe(II)HPd(II) product. A high-field ¹H NMR signal (δ −4.3) and a single downfield ³¹P NMR resonance (δ 62.8) are consistent with [2H]⁺ adopting a C_s-symmetric structure in solution. When the acidification of 2 was performed in the presence of CD₃OD, ESI-MS and ²H NMR spectroscopy confirmed formation of the deuteride isotopologue [2D]⁺. The evidence for the solution structure of [2H]⁺ is complemented by crystallographic analysis (Figure 5).

Figure 5.

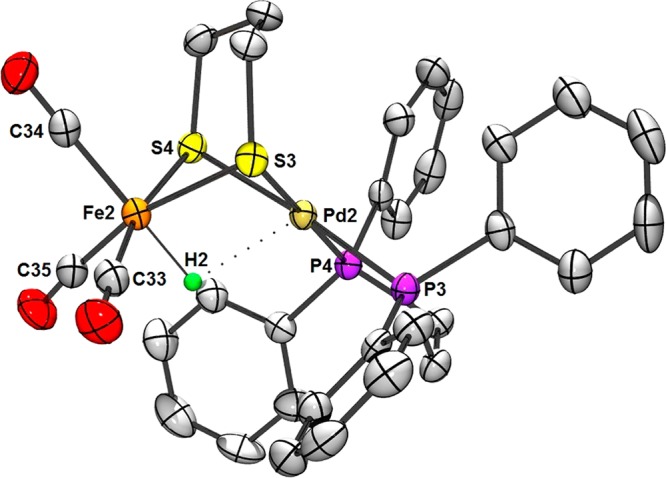
ORTEP of one of two independent complexes in [2H]BF₄·THF·0.5Et₂O with ellipsoids drawn at the 50% probability level. The solvate molecules, BF₄^– anion and H atoms (except the H^– ligand) are omitted for clarity. Mean distances in the complexes (Å) (mean DFT values in parentheses): Pd2–Fe2, 2.882 (2.92); Pd2–H2, 2.173 (2.19); Pd2–P3, 2.253; Pd2–P4, 2.270 (2.30); Pd2–S3, 2.367; Pd2–S4, 2.363 (2.39); Fe2–S3, 2.330; Fe2–S4, 2.338 (2.34); Fe2–H2, 1.483 (1.54). Mean angles in the complexes (deg) (mean DFT values in parentheses): Pd2–H2–Fe2, 102.4 (101.2); P3–Pd2–S4, 171.5; P4–Pd2–S3, 177.7 (177.6); S3–Fe2–C35, 165.4; S4–Fe2–C33, 167.1 (165.8).

By single crystal X-ray diffraction, two structurally similar FePd hydrides were found in the asymmetric unit of [2H]BF₄, in each case with the Fe–Pd distance (2.845, 2.918 Å) being greater than the sum of the covalent radii (2.71 Å).²¹ Protonation at Fe is accompanied by rotation of the Pd(dppe) center, affording square-planar Pd linked by the pdt^2– group to octahedral Fe. Indeed, the arrangement of metal centers in [2H]⁺ is analogous to that in [(OC)₃FeH(pdt)Ni(dppe)]⁺ ([1H]⁺). The H^– ligand in [2H]⁺ was located in the difference map and allowed to refine; its final location was significantly closer to the Fe center. Considering the covalent radius of H (0.31 Å),²¹ the H^– ligand in [2H]⁺ is formally bonded to Fe (1.469 Å), whereas its interaction with Pd is weak (2.168 Å). DFT calculations also predict unsymmetrical binding of the hydride ligand, which, despite being poised between the metals, can be viewed as a terminal ligand.

Platinum–Iron Complexes

The first indication of the unusual structure of (CO)₃Fe(pdt)Pt(dppe) (3), which is red-brown, is that its UV–vis spectrum features two absorptions (480, 360 nm), whereas single bands were observed for the green complexes 1 (398 nm) and 2 (376 nm). The IR spectrum of 3 is also distinctive, with the ν_CO bands (1962, 1883, 1870 cm^–1) observed at energies ∼70 cm^–1 lower than those for Fe(I)Ni(I) and Fe(I)Pd(I) analogs. The ³¹P{¹H} NMR spectrum for 3 consists of a singlet (and ¹⁹⁵Pt-coupled doublet) and is temperature-invariant down to −85 °C. The chemical shift (δ 44.1) and ¹J_PPt (3277 Hz) are close to those of the (pdt)Pt^II(dppe) precursor (δ 44.5, ¹J_PPt = 2717 Hz). While NMR data are in line with Pt coordination being either (i) highly fluxional tetrahedral or (ii) square-planar, the latter is most consistent with low-energy ν_CO bands. Square planarity at Pt is corroborated by DFT geometry optimization (Figure 6).

Figure 6.

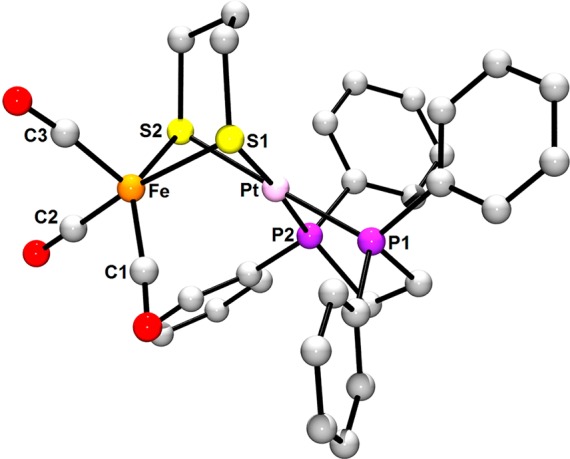
Energy-minimized structure of 3 obtained with DFT. Selected distances (Å): Fe–Pt, 2.87; Fe–C1, 1.75; Fe–C2, 1.75; Fe–C3, 1.76; Fe–S1, 2.34; Fe–S2, 2.37; Pt–S1, 2.37; Pt–S2, 2.38; Pt–P1, 2.28; Pt–P2, 2.28. Selected angles (deg): C1–Fe–S2, 136.8; C2–Fe–S1, 169.4; S1–Pt–P2, 176.1; S2–Pt–P1, 177.7.

Indeed, rather than being isostructurual to 1 and 2, 3 is predicted to feature a square-planar Pt site, with the angle between the PtP₂ and PtS₂ planes being 4°. The calculated Fe–Pt distance (2.87 Å) exceeds the sum of the covalent radii (2.68 Å),²¹ suggesting an absence of Fe–Pt bonding and a purely pentacoordinate Fe. This site, in contrast to the square-pyramidal Fe(I) in 2, is distorted trigonal bipyramidal (τ = 0.54). As mentioned previously, NBO analysis did not reveal d orbital mixing, which was observed in 1 and 2. Overall, the coordination geometries are consistent with an Fe(0)Pt(II) description for 3.

Quasi-reversible oxidations for (CO)₃Fe(pdt)Pt(dppe) were observed at −0.93 and +0.33 V (Figure S29), potentials similar to those for the FePd analog 2. The proposed sequence of 1e^– events: Fe(0)Pt(II) ⇌ Fe(I)Pt(II) ⇌ Fe(II)Pt(II). This sequence is supported by the IR spectrum for [(OC)₃Fe(pdt)Pt(dppe)]BF₄ ([3]BF₄, prepared from 3 and FcBF₄), in which the ν_CO bands (2058, 1987 cm^–1) are at virtually identical energies to the bona fide Fe(I)M(II) species [1]⁺ and [2]⁺. While the EPR spectrum of [3]⁺ indicates some unpaired spin resides on Pt (A(¹⁹⁵Pt) ≈ 97 MHz, A(³¹P) ≈ 11 MHz), the g-shifts suggest an Fe(I)Pt(II) description to be appropriate, as mirrored in the spin density calculations (Table 3). The paramagnetic salt [3]BF₄ undergoes ligand substitution with PCy₃ to afford dicarbonyl [Cy₃P(OC)₂Fe(pdt)Pt(dppe)]BF₄ ([3′]BF₄), the characterization for which mirrors that for [2′]BF₄.

As expected, reaction of low-valent 3 with HBF₄ furnished the hydride salt [(OC)₃FeH(pdt)Pt(dppe)]BF₄ ([3H]BF₄), for which a ¹H NMR resonance at δ −3.57 is particularly diagnostic. The small coupling observed for the satellites (¹J_HPt = 173 Hz) indicates that the H···Pt interactions are rather weak. For comparison, square-planar platinum hydrides exhibit ¹J_HPt from ∼650 to 1700 Hz,²⁴ with ¹J_HPt being at the low end of this range for five-coordinate complexes of the type [Pt(PR₃)₄H]⁺.²⁵ Thus, [3H]⁺ is similar to its FePd analog in that the H^– ligand can be considered terminally Fe-bound, as also supported by the ³¹P NMR resonances for 3 being insensitive to protonation at Fe (for [3H]⁺ δ 46.4, ¹J_PPt = 3220 Hz). In contrast, the energies of the ν_CO bands for the FePt conjugate acid and base species are very different–those for [3H]⁺ (2081, 2022 cm^–1) are greatly shifted relative to those for 3 (the average shift, taking into account the A + E patterns was Δν_CO = 137 cm^–1). A similar shift (139 cm^–1) was observed by Angelici and co-workers upon protonation of the Fe(0) species Fe(dppe)(CO)₃ to give the ferrous hydride [FeH(dppe)(CO)₃]⁺.²⁶ Taken together, these data are consistent with Fe(0)Pt(II), Fe(I)Pt(II), and Fe(II)HPt(II) assignments for 3, [3]BF₄, and [3H]BF₄, respectively.

While only a handful of FePt complexes bearing H^– and CO ligands exist, the compounds (CO)₃FeH(μ-PR₂)Pt(PR′₃)₂ are particularly pertinent.²⁷ These complexes interconvert between isomers with terminal ((H)Fe^IIPt₀) and bridging (Fe₀(μ-H)Pt^II) hydride ligands. When these FePt species feature the substituents R = Ph, R′ = OPh, a non-fluxional terminal hydride results (¹J_HPt = 28 Hz), whereas when R = Cy, R′ = Et the hydride is evenly shared (¹J_HPt = 520 Hz). One would expect values double the latter (∼1000 Hz) for purely terminal Pt–H moieties. (28)

Comparison of CO Frequencies

Good agreement was found between experimental and calculated shifts in weighted average CO vibrational frequency (Δν_CO) induced by protonation and oxidation of bimetallics 1–3 (Scheme 3). Protonation of the FeNi and FePd complexes is predicted to shift ν_CO by ∼50 cm^–1. In contrast, the shift induced by protonation of the FePt analog is much greater, with Δν_CO ∼110 cm^–1. These Δν_CO values correlate with the formal changes in Fe oxidation state: from +I to +II upon protonation of 1 and 2 as well as from 0 to +II upon protonation of 3. Trends in Δν_CO for the couples [1]^0/+, [2]^0/+, and [3]^0/+ are similar to those seen for protonation, the effects again being greater for the Pt case. The Δν_CO values for these oxidations are consistent with their occurring remote from the Fe(CO)₃ center in [1] and [2] but directly at this center in [3].

Scheme 3.

Stereochemical Non-Rigidity

As discussed above, the fluxionality of 1 and 2, evidenced by the broad singlet in their ³¹P{¹H} NMR spectra, implicate the presence of a transient or intermediate species featuring square-planar Ni/Pd centers (Scheme 1, top). This conformational motion is likely to perturb both the oxidation states and intermetallic bonding of the Fe and M centers. Two optimized DFT structures characterized as minima were calculated for each bimetallic 1–3: one in which the (pdt)M(dppe) fragment is tetrahedral, and one in which it is square-planar. Selected bond lengths and angles are provided in Table S5. In each case, the Fe center is within bonding distance of M when the latter adopts a tetrahedral geometry, while the Fe–M distance is elongated when M is planar. The Fe–M elongation is subtle in the FeNi case (0.13 Å) but more pronounced for FePd and FePt (∼0.30 Å). The relative stability of the two isomers was computed, and the reaction free energies (ΔG°) and free energy barriers (ΔG^†) associated with tetrahedral to square-planar isomerization are presented in Table 4.

Table 4. Calculated Reaction Free Energies and Free Energy Barriers (kcal/mol) for Rotation from Tetrahedral to Square-Planar Geometry at the M(dppe) Site in Compounds 1–3.

complex	ΔG° DFT	ΔG† DFTa	ΔG† exptc
(OC)3Fe(pdt)Ni(dppe) (1)	–0.67	6.66	9.5
(OC)3Fe(pdt)Pd(dppe) (2)	+0.99	3.29	<7.2
(OC)3Fe(pdt)Pt(dppe) (3)	–30.42	NDb	ND

^aThe potential energy surface was found to be extremely flat along the isomerization pathway. As a result, the single imaginary frequency for the transition state (TS) was <20 cm^–1 for the two barriers given in this table. Each TS was verified to lead to the relevant tetrahedral and square-planar geometries by following the intrinsic reaction coordinate (IRC) for 4 or 5 steps in both directions and subsequently optimizing the geometries. As the imaginary frequencies may be below the numerical accuracy of the methodology, and the complete IRC was not obtained, the free energy barriers should be viewed with caution. Moreover, multiple TSs were found for 1, suggesting a ruffled potential energy surface connecting the two isomers, and only the highest free energy barrier is reported.

^bThe TS was not determined for 3 as the isomerization was found to be significantly exergonic.

^cEstimated according to the Gutowsky–Holm relation using the coalescence temperature of 243 K (detailed in SI), but the DFT free energies were calculated at 298 K for consistency with other experiments. Note that the calculated and experimental free energy barriers are not exactly equivalent.

For the FeNi and FePd congeners, the isomerization is close to thermoneutral (ΔG° = −0.67 and +0.99 kcal/mol, respectively). Given the error associated with the calculations, it is not possible to determine a thermodynamic preference for the coordination geometry at Ni/Pd. The reaction free energies calculated using various other density functionals and basis sets with geometry optimization in CH₂Cl₂ solvent are qualitatively consistent with the results presented here, although certain levels of theory do not predict a stable square-planar intermediate for geometry optimizations in the gas phase (see Tables S6–S8). The calculated free energy barriers are relatively low, consistent with the fluxionality of 1 and 2 observed in their room temperature NMR spectra. Because the potential energy surfaces for 1 and 2 were found to be extremely flat along the isomerization pathway, the calculated free energy barriers may not be quantitatively accurate and can be analyzed only qualitatively. The calculated free energy barrier of 6.66 kcal/mol for 1 is qualitatively consistent with, although somewhat lower than, the free energy barrier of 9.5 kcal/mol estimated from the coalescence temperature in the NMR measurement. Moreover, the lower calculated free energy barrier of 3.29 kcal/mol for 2 is consistent with the lack of decoalescence observed in the NMR experiments for 2. The observation of a particularly flat potential energy surface along the isomerization pathway has implications for the enzymatic system, where the geometry at the Ni site is between tetrahedral and square-planar.

The similarity in free energies and the relatively low free energy barriers suggest that the two isomers of 1 and 2 may interconvert. In addition, the free energy change associated with oxidation of 1 and 2 is similar for the two different isomers, with the calculated reduction potentials of the square-planar and tetrahedral isomers differing by only ∼0.03 V, which is within the estimated error of the methodology. It is thus a distinct possibility that the Ni/Pd centers in 1 and 2 “preorganize” into square-planar geometries prior to 1e^– loss. In the case of FePt complex 3, the square-planar isomer is overwhelmingly favored, consistent with the high stability characteristic of square-planar Pt(II) centers. Calculations indicate that ν_CO energies for the tetrahedral isomer of 3, which was found to be a local minimum, are within 10 cm^–1 of those for 1 and 2. Square-planar isomers of 1 and 2, while not observed experimentally, have calculated ν_CO bands 55–65 cm^–1 lower in energy than the respective tetrahedral conformers. This ν_CO shift is consistent with the change in conformation inducing a change in oxidation state.

Given the dynamics in the neutral species 1 (as well as 2), we set about investigating hydride [1H]⁺ to yield further insight into the mechanism of protonation. At room temperature, [(CO)₃FeH(pdt)Ni(dppe)]⁺ displays a single ³¹P NMR peak owing to its C_s-symmetry. In view of the difficulty with determining whether or not Ni(dppe) twisting is occurring here, we interrogated an analogous hydride of lower symmetry, which entailed preparation of the new bimetallic (CO)₃Fe(pdt)Ni(S,S-chiraphos) (S,S-chiraphos = 2S,3S-bis(diphenylphosphino)butane, Scheme 4). Analogous to 1, this species gave rise to a single ³¹P NMR resonance at room temperature, with decoalescence observed on cooling to −90 °C, at which temperature Ni(S,S-chiraphos) twisting is slowed (Figure S49).

Scheme 4.

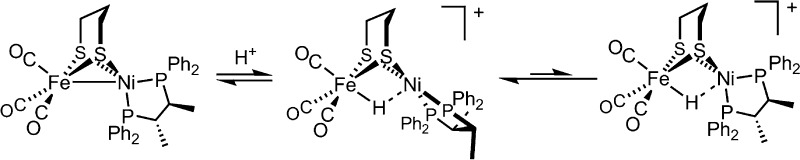
While (CO)₃Fe(pdt)Ni(S,S-chiraphos) twists rapidly at room temperature, its conjugate acid does not; the nonequivalent³¹P nuclei in the chiral hydride [(CO)₃FeH(pdt)Ni(S,S-chiraphos)]⁺ (Scheme 4, center) give rise to two broad signals (resolved into two ³¹P-coupled doublets at −70 °C). If twisting and equivalencing of the ³¹P sites were to be facile, it would be necessary for a tetrahedral hydride (Scheme 4, right) to be energetically accessible, which appears not to be the case. In general, it is proposed that twisting of neutral species is associated with “on/off” switching of Fe–M bonding in the FeNi and FePd (but not FePt) complexes. It is now evident that the twisting of hydride species is slower, perhaps reflecting the rigidifying influence of the H···M interactions (despite their weakness).

These observations are supported by computational work: the twisting of hydride [1H]⁺ was investigated, and two optimized DFT structures characterized as minima were calculated for the isomers of [1H]⁺. The relative free energies of the structures, which feature either square-planar or tetrahedral (pdt)Ni(dppe) fragments (Figure 7), were also calculated.

Figure 7.

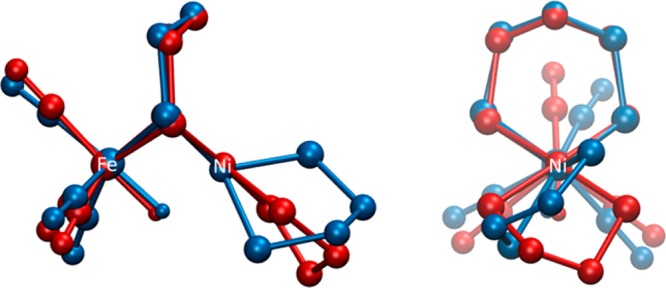
Energy-minimized structures obtained with DFT for [1H]⁺ with the (pdt)Ni(dppe) moiety either square-planar (red) or distorted tetrahedral (blue). The optimized geometries are superimposed and presented in two views. Other (higher energy) isomers/tautomers proposed can be found in Figure S57.

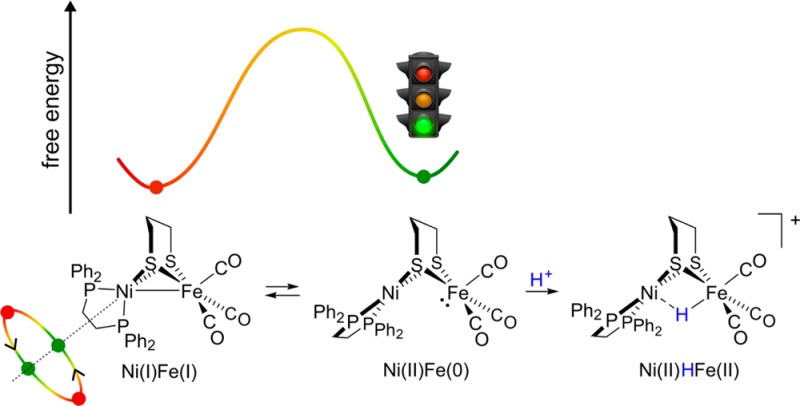
Twisting of the square-planar (pdt)Ni(dppe) site in [1H]⁺ to adopt a tetrahedral geometry was calculated to be significantly endergonic (ΔG° = +11.47 kcal/mol). The tetrahedral conformer is predicted by DFT to be far (∼10⁸ ×) more acidic than the square-planar state (the experimental pK_a(MeCN) for [1H]⁺ is 10.7).¹¹ Considering the conjugate bases for the two isomers of [1H]⁺, these results suggest that 1 has greatly enhanced basicity when in the square-planar form, consistent with its description as Fe(0)Ni(II) (Scheme 1). Thus, it is reasonable that this isomer is responsible for the rich acid–base and redox chemistry exhibited by 1 and related complexes.

Conclusions

Numerous studies have examined the protonation and 1e^– oxidation of complexes of the type (CO)₃Fe(pdt)Ni(diphosphine) and substituted derivatives thereof. This paper presents evidence that the protonations, and possibly the oxidations, proceed via a latent 2e^– mixed-valence intermediate (Scheme 5).

Scheme 5.

Despite previous computational analyses,^10,13,15 this key square-planar species had not been identified as an energetically accessible isomer of 1. The first clue for this unsuspected structure was provided by the ³¹P NMR properties of 1, which implicate a transient or intermediate square-planar species that interconverts the ³¹P sites. The new and compelling evidence for the intermediate comes from (i) DFT calculations that suggested thermodynamically accessible rotation at the non-Fe center and (ii) spectroscopic and electrochemical properties of the FePt complex, the protonation and redox behavior of which mirrors that of Fe(0) diphosphines.^26,29 The 2e^– mixed valency of 1 contrast with that for (cymene)Ru(pdt)Ni(dppe), which features a rigidly tetrahedral Ni(0) center.³⁰

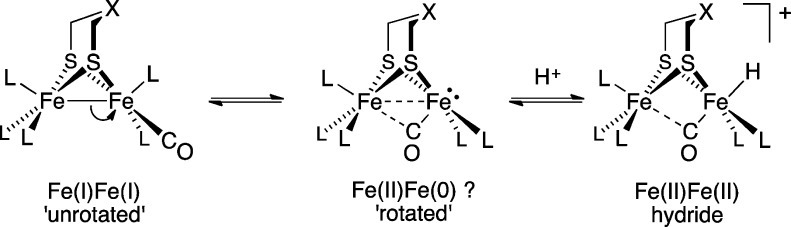
The rotation-induced 2e^– mixed-valence behavior also has implications for understanding active site mimics of the [FeFe]-H₂ases. Prior to protonation, model complexes almost invariably feature Fe₂(SR)₂L₆ cores wherein terminal coordination sites are unavailable for H⁺ binding. Protonation of these Fe(I)Fe(I) complexes has been proposed to proceed via a “rotated intermediate” (Scheme 6).³¹ Models for this rotated state have been crystallized, revealing that Fe–Fe bonding is weakened and a terminal site on one Fe center is vacant.³² By analogy to the results in this paper, such rotated diiron complexes should perhaps be described as Fe(II)Fe(0), thus underlining the role of latent, but highly reactive intermediates.

Scheme 6.

Overall, the work reported here shows that the geometry at Ni decisively influences the reactivity of a neighboring Fe site. For small molecule [NiFe]-H₂ase mimics, it has been demonstrated that perturbation of the Ni site greatly alters the acid–base properties of these complexes. With respect to the hydrogenases themselves, the results suggest that the distorted nature of the Ni(Cys)₄ site is likely an important factor in tuning basicity and redox potentials, thereby enabling their remarkable activity.

Experimental Section

Unless otherwise stated, chemicals were purchased from commercial sources and used as received. Chromatography was performed using SiO₂ (40–63 μm, 230–400 mesh) as the stationary phase. CD₂Cl₂ was distilled from CaH₂. The complexes 1,²⁰ FeI₂(CO)₄, Cl₂Ni(S,S-chiraphos),³³ (pdt)Pd(dppe), and (pdt)Pt(dppe)³⁴ were prepared according to the literature methods. All reactions and purifications were conducted in an MBraun glovebox equipped with a solvent purification system; the concentrations of O₂ and H₂O in the N₂ atmosphere were typically no higher than 2 and 0.2 ppm, respectively. Glassware used in the preparation of deuteride [2D]BF₄ was washed with D₂O and dried prior to use. Solution IR spectra were recorded on a PerkinElmer Spectrum 100 FTIR spectrometer. A Waters Micromass Quattro II spectrometer was used to acquire ESI-MS data for analytes in dilute CH₂Cl₂ or CD₂Cl₂ solution. Analytical data were acquired using an Exeter Analytical CE-440 elemental analyzer. Unless otherwise stated, NMR data were acquired at room temperature, with samples under an atmosphere of N₂. ¹H and ³¹P{¹H} NMR spectra were recorded on a Varian VXR500 or U500 spectrometer at 500 and 202 MHz, respectively. ²H NMR spectra were recorded on a Varian UI 500NB spectrometer at 77 MHz. Chemical shifts (δ/ppm) are referenced to CHDCl₂/CH₂Cl₂ (5.32 ppm for ¹H) and external 85% H₃PO₄ (0 ppm for ³¹P). Cyclic voltammetry was carried out in a single compartment glass cell using a CH Instruments CHI630D electrochemical analyzer. The working, counter, and pseudoreference electrodes were glassy C, Pt, and Ag, respectively. The analyte (1 mM) and NBu₄PF₆ (100 mM) were dissolved in CH₂Cl₂, and potentials (reported here relative to internal Fc/Fc⁺) were swept at 0.1 V s^–1. Crystallographic data were collected using a Siemens SMART diffractometer equipped with a Mo K_α source (λ = 0.71073 Å) and an Apex II detector. EPR spectra of complexes (∼1 mM in CH₂Cl₂/PhMe, 1:1) were recorded on a Varian E-line 12″ Century Series X-band CW spectrometer.

(OC)₃Fe(pdt)Pd(dppe) (2)

At −28 °C, a mixture of FeI₂(CO)₄ (29.5 mg, 70 μmol) and (pdt)Pd(dppe) (42.8 mg, 70 μmol) were dissolved in CH₂Cl₂ (1 mL) with stirring. After 1 min, the solution was treated with CoCp₂ (26.5 mg, 140 μmol) in CH₂Cl₂ (1 mL) and allowed to warm to room temperature, before it was concentrated to ∼0.5 mL and chromatographed (∼10 cm SiO₂, CH₂Cl₂ eluent). The fourth band, deep green in color, was concentrated to ∼2 mL, layered with pentane (∼20 mL), and allowed to stand overnight at −28 °C. The solids that formed were isolated by filtration, washed with pentane (2 × 1 mL), and dried briefly to afford the title compound as dark-green plates (9.0 mg, 12 μmol, 17%). ¹H NMR (CD₂Cl₂): δ 7.74 (m, 8H, o-Ph), 7.43 (m, 8H, m-Ph), 7.42 (m, 4H, p-Ph), 2.59 (ddd, ²J_HH = 13.5 Hz, ³J_HH = 5.8 Hz, ³J_HH = 3.3 Hz, 2H, equatorial CH₂CH₂CH₂), 2.35 (m, 2H, PCH₂CH₂P), 2.22 (m, 2H, PCH₂CH₂P), 1.94 (m, 2H, axial CH₂CH₂CH₂), 1.29 (m, 2H, CH₂CH₂CH₂). ³¹P{¹H} NMR (CD₂Cl₂): δ 51.3. ESI-MS: m/z 749.8 [M]⁺, 721.8 [M – CO]⁺, 693.8 [M – 2CO]⁺ (ionization induced by addition of Fc[B(C₆H₃-3,5-(CF₃)₂)₄]). Anal. calcd for C₃₂H₃₀O₃S₂P₂NiPd·0.2CH₂Cl₂: C, 50.36; H, 3.99; N, 0.00. Found: C, 50.35; H, 3.57; N, 0.00. Green plates of 2 formed upon slow diffusion of pentane layered onto a concentrated CH₂Cl₂ solution of the title compound at −28 °C. One crystal (0.377 × 0.232 × 0.058 mm³) was subjected to X-ray diffraction at 168 K. Its space group was determined to be triclinic P-1 with cell parameters: a 8.900 Å, b 12.883 Å, c 14.778 Å, α 104.64°, β 106.73°, γ 90.98°. Integration of 6798 reflections and solution by direct methods using SHELXTL V6.12 afforded a model with R1 = 0.0285 and wR2 = 0.0684.

[(OC)₃Fe(pdt)Pd(dppe)]BF₄ ([2]BF₄)

A stirred solution of 2 (11.3 mg, 15 μmol) in CH₂Cl₂ (1 mL) was treated with FcBF₄ (4.1 mg, 15 μmol) in CH₂Cl₂ (1 mL). After 1 min, pentane (20 mL) was added, and the mixture allowed to stand overnight at −28 °C. The solids were isolated by filtration, washed with pentane (2 × 1 mL), and dried briefly to afford the title compound as an olive-brown powder (3.5 mg, 4.2 μmol, 28%). ESI-MS: m/z 749.8 [M – BF₄^–]⁺, 721.8 [M – CO – BF₄^–]⁺, 693.8 [M – 2CO – BF₄^–]⁺. Anal. calcd for C₃₂H₃₀FeO₃P₂PdS₂BF₄·0.5CH₂Cl₂: C, 44.35; H, 3.55; N, 0.00. Found: C, 44.26; H, 3.19; N, 0.54.

[(OC)₃FeH(pdt)Pd(dppe)]BF₄ ([2H]BF₄)

A solution of 2 (22.5 mg, 30 μmol) in CH₂Cl₂ (1 mL) was treated with HBF₄ (54% Et₂O solution, 14.6 mg, 90 μmol) in CH₂Cl₂ (1 mL). The solution was evaporated to dryness, and the oily residue triturated with Et₂O (3 mL). The resulting solid was isolated by filtration, washed with Et₂O (2 × 1 mL), and dried briefly to afford the title compound as an orange powder (21.1 mg, 25 μmol, 84%). ¹H NMR (CD₂Cl₂): δ 7.70 (m, 8H, o-Ph), 7.64 (t, ²J_HH = 6.7 Hz, 4H, p-Ph), 7.57 (m, 8H, m-Ph), 2.87 (m, 4H, PCH₂CH₂P), 2.63 (m, 1H, equatorial CH₂CH₂CH₂), 2.30 (m, 4H, CH₂CH₂CH₂), 1.29 (m, 1H, axial CH₂CH₂CH₂), −4.3 (s, 1H, FeH). ³¹P{¹H} NMR (CD₂Cl₂): δ 62.8. ESI-MS: m/z 750.8 [M – BF₄^–]⁺. Orange blocks of [2H]BF₄·THF·0.5Et₂O formed upon slow diffusion of Et₂O vapor into a THF solution of the title compound at −28 °C. One crystal (0.377 × 0.232 × 0.058 mm³) was subjected to X-ray diffraction at 178 K. Its space group was determined to be monoclinic P2₁/n with cell parameters: a 11.466 Å, b 20.692 Å, c 34.720 Å, α 90.00°, β 97.41°, γ 90.00°. Integration of 9965 reflections and solution by direct methods using SHELXTL V6.12 afforded a model with R1 = 0.0369 and wR2 = 0.0754.

[(OC)₃FeD(pdt)Pd(dppe)]BF₄ ([2D]BF₄)

A solution of 2 (22.5 mg, 30 μmol) in CH₂Cl₂ (1 mL) and CD₃OD (0.1 mL) was treated with HBF₄ (54% Et₂O solution, 14.6 mg, 90 μmol) in CD₃OD (0.3 mL). The solution was evaporated to dryness, and the oily residue triturated with Et₂O (3 mL). The resulting solid was isolated by filtration, washed with Et₂O (2 × 1 mL), and dried briefly to afford the title compound as an orange powder (19.6 mg, 23 μmol, 78%). ²H NMR (CH₂Cl₂): δ −4.3 (m). ³¹P{¹H} NMR (CH₂Cl₂): δ 64.3. ESI-MS: m/z 751.9 [M – BF₄^–]⁺. Anal. calcd for C₃₂H₃₀DFeO₃P₂PdS₂BF₄·0.25CH₂Cl₂: C, 44.99; H, 3.69; N, 0.00. Found: C, 45.03; H, 3.82; N, 0.00.

[Cy₃P(OC)₂Fe(pdt)Pd(dppe)]BF₄ ([2′]BF₄)

Compound 2 (15.0 mg, 20 μmol) and FcBF₄ (5.4 mg, 20 μmol) were dissolved in CH₂Cl₂ (1 mL) with rapid stirring. After 1 min the solution was added dropwise to PCy₃ (28.0 mg, 100 μmol) in CH₂Cl₂ (0.5 mL). The solution was stirred for a further 0.5 min, and pentane (−28 °C, 15 mL) was added and the mixture allowed to stand overnight at −28 °C. The solids were isolated by filtration, washed with pentane (−28 °C, 2 × 2 mL), and dried briefly to afford the title compound as a yellow-brown powder (5.9 mg, 5.4 μmol, 27%). ESI-MS: m/z 1002.4 [M – BF₄^–]⁺, 974.3 [M – CO – BF₄^–]⁺. Anal. calcd for C₄₉H₆₃FeO₂P₃PdS₂BF₄·0.25CH₂Cl₂: C, 53.23; H, 5.76; N, 0.00. Found: C, 53.16; H, 5.82; N, 0.20.

(OC)₃Fe(pdt)Pt(dppe) (3)

A mixture of solid FeI₂(CO)₄ (25.3 mg, 60 μmol) and (pdt)Pt(dppe) (42.0 mg, 60 μmol) was cooled to −28 °C and dissolved in CH₂Cl₂ (2 mL) with stirring. After 1 min, the solution was treated with CoCp₂ (22.7 mg, 120 μmol) in CH₂Cl₂ (1 mL) and allowed to warm to room temperature before it was concentrated to ∼0.5 mL and chromatographed (∼10 cm SiO₂, CH₂Cl₂ eluent). The olive-brown band (following the rapidly eluting orange band containing Fe₂(pdt)(CO)₆) was concentrated to ∼2 mL, layered with pentane (∼20 mL), and allowed to stand overnight at −28 °C. The supernatant was removed, the dark residue triturated with pentane (2 × 5 mL), and dried briefly to afford the title compound as a brown powder (17.0 mg, 20.2 μmol, 34%). ¹H NMR (CD₂Cl₂): δ 7.86 (m, 8H, o-Ph), 7.48 (m, 8H, m-Ph), 7.46 (m, 4H, p-Ph), 2.57 (m, 2H, CH₂CH₂CH₂), 2.22 (m, 4H, PCH₂CH₂P), 1.58 (m, 2H, CH₂CH₂CH₂), 1.29 (m, 2H, CH₂CH₂CH₂). ³¹P{¹H} NMR (CD₂Cl₂): δ 44.1 (s, d, ¹J_PPt = 3280 Hz). ESI-MS: m/z 838.9 [M]⁺ (ionization induced by addition of Fc[B(C₆H₃-3,5-(CF₃)₂)₄]). Anal. calcd for C₃₂H₃₀FeO₃P₂PtS₂: C, 45.78; H, 3.60; N, 0.00. Found: C, 46.36; H, 3.22; N, 0.05.

[(OC)₃Fe(pdt)Pt(dppe)]BF₄ ([3]BF₄)

This compound was prepared analogously to [2]BF₄, instead using 3 as the precursor. Yield: 81%, yellow-green powder. ESI-MS: m/z 838.9 [M – BF₄^–]⁺.

[(OC)₃FeH(pdt)Pt(dppe)]BF₄ ([3H]BF₄)

This compound was prepared analogously to [2H]BF₄, instead using 3 as the precursor. Yield: 69%, orange powder. ¹H NMR (CD₂Cl₂): δ 7.70 (m, 8H, o-Ph), 7.64–7.54 (m, 12H, m,p-Ph), 2.88 (m, 2H, PCH₂CH₂P), 2.7 (m, 2H, PCH₂CH₂P), 2.59 (m, 1H, equatorial CH₂CH₂CH₂), 2.43 (m, 4H, CH₂CH₂CH₂), 1.29 (m, 1H, axial CH₂CH₂CH₂), −3.57 (s, d, ¹J_HPt = 173 Hz, 1H, FeH). ³¹P{¹H} NMR (CD₂Cl₂): δ 46.4 (s, d, ¹J_PPt = 3220 Hz). ESI-MS: m/z 839.9 [M – BF₄^–]⁺. Anal. calcd for C₃₂H₃₁FeO₃P₂PtS₂BF₄·0.5CH₂Cl₂: C, 40.25; H, 3.33; N, 0.00. Found: C, 40.10; H, 2.93; N, 0.04.

[Cy₃P(OC)₂Fe(pdt)Pt(dppe)]BF₄ ([3′]BF₄)

This compound was prepared analogously to [2′]BF₄, instead using 3 as the precursor. Yield: 72%, yellow powder. ESI-MS: m/z 1091.7 [M – BF₄^–]⁺. Anal. calcd for C₄₉H₆₃FeO₂P₃PtS₂BF₄·0.75CH₂Cl₂: C, 48.09; H, 5.23; N, 0.00. Found: C, 48.06; H, 5.42; N, 0.52.

(pdt)Ni(S,S-chiraphos)

This compound was prepared analogously to (pdt)Ni(dppe), instead using Cl₂Ni(S,S-chiraphos) as the precursor.³³ Yield: 95%, orange powder. ¹H NMR (CD₂Cl₂): δ 8.15 (m, 4H, p-Ph), 7.63–7.47 (m, 16H, o,m-Ph), 2.19 (m, 4H, CH₂CH₂CH₂), 2.03 (m, 2H, CH), 1.81 (qu, ³J_HH = 6.3 Hz, 4H, CH₂CH₂CH₂), 0.96 (dd, ³J_PH = 10.6 Hz, ³J_HH = 6.2 Hz, 6H, CH₃). ³¹P{¹H} NMR (CD₂Cl₂): δ 56.1. ESI-MS: m/z 590.4 [M]⁺. Anal. calcd for C₃₁H₃₄S₂P₂Ni: C, 62.96; H, 5.79; N, 0.00. Found: C, 62.22; H, 5.69; N, 0.41.

(CO)₃Fe(pdt)Ni(S,S-chiraphos)

The complexes (pdt)Ni(S,S-chiraphos) (118.3 mg, 200 μmol) and Fe₂(CO)₉ (72.8 mg, 200 μmol) were dissolved in CH₂Cl₂ (3 mL) with stirring. After 18 h, the deep green solution was concentrated to ∼0.5 mL and chromatographed (∼10 cm SiO₂, CH₂Cl₂ eluent). An olive-green band was collected, treated with MeCN (∼5 mL), concentrated to ∼1 mL and cooled to −28 °C. The solids were isolated by filtration, washed with MeCN (−28 °C, 2 mL) and pentane (−28 °C, 2 × 2 mL), and dissolved in CH₂Cl₂ (1 mL) and MeCN (5 mL). The solution was concentrated to ∼1 mL and cooled to −28 °C. The crystals that formed were isolated by filtration, washed with MeCN (−28 °C, 2 mL) and pentane (−28 °C, 2 × 2 mL), and dried to afford the title complex as dark green crystals (46.9 mg, 64.1 μmol, 32%). ¹H NMR (CD₂Cl₂): δ 8.11 (m, 4H, Ph), 7.62 (m, 4H, Ph), 7.52–7.39 (m, 12H, Ph), 2.57 (ddd, ²J_HH = 13.4 Hz, ³J_HH = 7.1 Hz, ³J_HH = 7.1 Hz, 1H, equatorial CH₂CH₂CH₂), 2.17 (ddd, ²J_HH = 13.2 Hz, ³J_HH = 7.3 Hz, ³J_HH = 7.1 Hz, 1H, equatorial CH₂CH₂CH₂), 1.98 (m, 2H, CH), 1.91 (m, 1H, equatorial CH₂CH₂CH₂), 1.82 (m, 2H, axial CH₂CH₂CH₂), 1.31 (m, 1H, axial CH₂CH₂CH₂), 0.87 (m, 6H, CH₃). ³¹P{¹H} NMR (CD₂Cl₂): δ 63.8. ³¹P{¹H} NMR (CD₂Cl₂, −90 °C): δ 75.0, 52.6. FTIR (CH₂Cl₂): ν_CO = 2026, 1953 cm^–1. ESI-MS: m/z 729.3 [M]⁺ (ionization induced by addition of Fc[B(C₆H₃-3,5-(CF₃)₂)₄]). Anal. calcd for C₃₄H₃₄O₃S₂P₂NiFe: C, 55.84; H, 4.69; N, 0.00. Found: C, 55.15; H, 4.53; N, 0.57.

[(CO)₃FeH(pdt)Ni(S,S-chiraphos)]BF₄

This compound was prepared analogously to [2H]BF₄, instead using (CO)₃Fe(pdt)Ni(S,S-chiraphos) as the precursor. Yield: 82%, orange-brown powder. ¹H NMR (CD₂Cl₂): δ 7.89 (dd, ³J_HH = 10.8 Hz, ³J_HH = 8.0 Hz, 4H, p-Ph), 7.80–7.57 (m, 16H, o,m-Ph), 2.60 (m, 2H, CH), 2.37 (ddd, ²J_HH = 14.4 Hz, ³J_HH = 2.9 Hz, ³J_HH = 2.9 Hz, 1H, equatorial CH₂CH₂CH₂), 2.29 (dm, ²J_HH = 13.8 Hz, 1H, equatorial CH₂CH₂CH₂), 2.15 (dm, ²J_HH = 13.7 Hz, 1H, equatorial CH₂CH₂CH₂), 1.91 (m, 1H, axial CH₂CH₂CH₂), 1.82 (ddd, ²J_HH = 13.7 Hz, ³J_HH = 13.7 Hz, ³J_HH = 2.0 Hz, 1H, axial CH₂CH₂CH₂), 1.30 (m, 1H, axial CH₂CH₂CH₂), 0.87 (m, 6H, CH₃)–3.57 (t, ²J_HP = 4.8 Hz, 1H, FeH). ³¹P{¹H} NMR (CD₂Cl₂): δ 71.7, 67.9. ³¹P{¹H} NMR (CD₂Cl₂, −70 °C): δ 72.6 (d, ²J_PP = 67 Hz), 67.2 (d, ²J_PP = 67 Hz). FTIR (CH₂Cl₂): ν_CO = 2082, 2022 cm^–1. ESI-MS: m/z 730.4 [M – BF₄^–]⁺. Anal. calcd for C₃₄H₃₅O₃S₂P₂FeNiBF₄·0.5CH₂Cl₂: C, 48.10; H, 4.21; N, 0.00. Found: C, 48.12; H, 4.11; N, 0.40.

Calculations

DFT calculations were performed using the B3P86 density functional with the SDD pseudopotential and basis set³⁵ for the Fe, Ni, Pd, and Pt atoms, the 6-31G** basis set³⁶ for μ-H ligands, and the 6-31G* basis set^37,38 for all other atoms. The starting geometries for 1,¹⁰ [1H]⁺,²⁰2, and [2H]⁺ were obtained from crystal structures. The starting coordinates for atoms in 3 and [3H]⁺ were obtained from the crystal structure of [2H]⁺, where the metal center and hydride were manually altered prior to optimization. Solvation effects were included using the conductor-like polarizable continuum model^39,40 with Bondi atomic radii⁴¹ and included the non-electrostatic contributions of dispersion,^42,43 repulsion,^42,43 and cavitation energies.⁴⁴

For the results presented in the main paper, the geometry optimizations were performed in the gas phase. Geometry optimizations were also performed in solution and were found to be consistent with the gas phase optimizations; these results are provided in the Supporting Information. In all cases, the minimum-energy structures were confirmed to have no imaginary frequencies. The ν_CO values were calculated with DFT and were scaled by the standard factor of 0.9850.⁴⁵ The transition states (TSs) for the tetrahedral to square-planar isomerization were identified using the synchronous transit-guided quasi-Newton method,^46,47 and the resulting structures were confirmed to have only a single imaginary frequency. Each TS was verified to lead to the relevant tetrahedral and square-planar geometries by following the IRC using the local quadratic approximation⁴⁸ for 4 or 5 steps in both directions and subsequently optimizing the geometries. Because the potential energy surface was found to be very flat, the single imaginary frequencies were small, and the complete IRC connecting the two isomers through the TS could not be obtained.

Thermochemical data were calculated at T = 298.15 K. The reaction free energies (ΔG°) and free energy barriers (ΔG^†) associated with the tetrahedral to square-planar isomerization in solution included zero-point energy, entropic contributions, and solvation effects. The relative reduction potentials and pK_a’s were calculated from the corresponding reaction free energies using methodology described elsewhere.⁴⁹ Chemical bonding analysis was performed using NBO.²³ All calculations were performed using the Gaussian 09 electronic structure program.⁵⁰ Structures and energies of the systems studied herein are provided in the Supporting Information.

Supporting Information Available

Supporting Information: experimental and computational data. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Contributions

^† These authors contributed equally.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States