Effect of Calcium on the Oxidative Phosphorylation Cascade in Skeletal Muscle Mitochondria

Abstract

Calcium is believed to regulate mitochondrial oxidative phosphorylation, thereby contributing to the maintenance of cellular energy homeostasis. Skeletal muscle, with an energy conversion dynamic range of up to 100-fold, is an extreme case for evaluating the cellular balance of ATP production and consumption. This study examined the role of Ca²⁺ on the entire oxidative phosphorylation reaction network in isolated skeletal muscle mitochondria and attempted to extrapolate these results back to the muscle, in vivo. Kinetic analysis was conducted to evaluate the dose response effect of Ca²⁺ on the maximum velocity of oxidative phosphorylation (V_maxO) and the ADP affinity. Force-flow analysis evaluated the interplay between energetic driving forces and flux to determine the conductance, or effective activity, of individual steps within oxidative phosphorylation. Measured driving forces (extramitochondrial phosphorylation potential (ΔG_ATP), membrane potential, and redox states of NADH and cytochromes b_H, b_L, c₁, c, and a,a₃) were compared with flux (oxygen consumption) at 37°C. 840 nM Ca²⁺ generated a ∼2 fold increase in V_maxO with no change in ADP affinity (∼43 μM). Force-flow analysis revealed that Ca²⁺ activation of V_maxO was distributed throughout the oxidative phosphorylation reaction sequence. Specifically, Ca²⁺ increased the conductance of Complex IV (2.3-fold), Complexes I+III (2.2-fold), ATP production/transport (2.4-fold), and fuel transport/dehydrogenases (1.7-fold). These data support the notion that Ca²⁺ activates the entire muscle oxidative phosphorylation cascade, while extrapolation of these data to the exercising muscle predicts a significant role of Ca²⁺ in maintaining cellular energy homeostasis.

Exercise presents a severe challenge to energetic homeostasis in skeletal muscle as tissue-specific oxygen consumption rates can increase over 100-fold from rest to maximal aerobic exercise (1). Increases in skeletal muscle work rate are associated with modest decreases in the cytosolic ATP free energy (ΔG_ATP) primarily through increases in [ADP] and [Pi] (2-4). Since both muscle contraction and ion transport processes are dependent on ΔG_ATP, minimizing the reduction in ΔG_ATP during increases in energy demand is critical to the maintenance of normal cellular functions, such as ion gradients for signaling, as well as allowing peak muscle performance. Calcium (Ca²⁺) release from the sarcoplasmic reticulum (SR) and subsequent binding to troponin C allows muscle contraction and the associated energy utilization to occur, while Ca²⁺ influx into mitochondria has been shown to result in increased energy conversion potential (5-9). This balanced activation of both energy conversion and utilization pathways has been proposed to play a key role in the maintenance of energetic homeostasis in contracting muscle (10-13).

Ca²⁺ has long been known to stimulate flux through the citric acid cycle by activation of pyruvate, isocitrate, and 2-oxoglutarate dehydrogenases (14). More recently, Ca²⁺ has also been shown to directly stimulate ATP production through activation of the F₁F_o-ATP synthase (9), and flux through Complex III of the electron transport chain (ETC) may also be stimulated by Ca²⁺ (15). Despite the importance of Ca²⁺ for both skeletal muscle contraction and activation of oxidative phosphorylation, few studies have examined the effects of Ca²⁺ on skeletal muscle mitochondrial energy conversion. Martin et al. (16) found that increasing Ca²⁺ lowered the respiratory control (RCR) and ADP/O ratios in isolated skeletal muscle mitochondria, though the free Ca²⁺ concentrations used in that study (0.4 – 19.1 μM) were tailored to answer questions about aging and apoptosis and not resting and exercising muscle (<0.05 – 1.5 μM) (17-19). Kavanagh et al. (6) reported that skeletal muscle mitochondria in the presence of Ca²⁺ have an increase in flux through the substrate oxidation pathway for NAD-linked fuels as well as the phosphorylation pathway regardless of fuel. However, the inhibitor titrations used by Kavanagh et al. (6) make it difficult to discern Ca²⁺ effects on the ETC from those on the substrate dehydrogenases and/or the ATP producing/transporting enzymes.

The purpose of this study was to determine the role of Ca²⁺ in modulating oxidative phosphorylation in isolated porcine skeletal muscle mitochondria. We hypothesized that Ca²⁺ would increase the maximum velocity of oxidative phosphorylation, as seen in other systems (8, 9, 15, 20), and that this effect would be the result of a distributed activation of reactions within the oxidative phosphorylation network. This was evaluated by establishing the dose response effect of Ca²⁺ on oxidative phosphorylation and performing force-flow analyses of the oxidative phosphorylation network using concurrent measures of the redox states of NADH and the cytochromes, the extramitochondrial free energy of ATP (ΔG_ATP), and mitochondrial membrane potential (ΔΨ) to estimate the effective conductance of several of the reaction steps of oxidative phosphorylation in the presence and absence of Ca²⁺.

Experimental Procedures

Mitochondrial Isolation and Normalization

All procedures were approved by the National Heart, Lung, and Blood Institute Animal Care and Use Committee and performed in accordance with the guidelines described in the Animal Care and Welfare Act (7 USC 2142 § 13). Skeletal muscle mitochondria from the oxidative, porcine vastus intermedius were isolated using a Percoll gradient as described previously (21). Mitochondria were normalized to the optically-determined cytochrome a,a₃ (cyt a) content since this assay was very fast, did not require a standard curve, and provided the actual amount of mitochondrial oxidative phosphorylation complex in the sample independent of cytosolic contaminates. Cyt a content was measured as described previously (22), typically yielding a final mitochondrial suspension of 20 – 35 nmol cyt a/ml. Purified porcine skeletal muscle mitochondria contain ∼1.0 nmol cyt a/mg protein (21).

Mitochondrial Respiration, NADH, and Membrane Potential

Mitochondrial oxygen consumption (J_o), NADH fluorescence, and membrane potential (ΔΨ) were measured simultaneously and continuously in a water-jacketed chamber maintained at 37°C as described previously (9, 23). Experiments were carried out with mitochondria (375 pmol cyt a) in a 1.5-ml final volume of respiration medium (RM) containing (in mM) 100 KCl, 50 MOPS, 20 glucose, 15 NaCl, 10 MgCl₂, 1 EGTA, and 0.2% w/v BSA, pH 7.0. J_o was measured using a Clark electrode and an oxygen solubility of 199 nmol/ml at 37°C (24).

NADH reduction level was calculated relative to the fully oxidized (Ca²⁺-depleted mitochondria, no added substrates, with ADP and Pi) and fully reduced (mitochondria with added substrates and Ca²⁺ at anoxia) states. ΔΨ was determined based on the distribution of the lipophillic cation TPP⁺ across the inner mitochondrial membrane using a TPP⁺ sensitive microelectrode (KWIKTPP, World Precision Instruments). TPP⁺ binding to mitochondria was accounted for as described previously (9). With 10 mM Pi in the RM for all experiments along with sodium in the medium, the contribution of the pH gradient (ΔpH) to the protonmotive force (ΔpH + ΔΨ) was assumed to be insignificant (25).

Experimental Conditions

For all respiration experiments, mitochondria were incubated in RM at 37°C in the presence of sodium and in the absence of exogenous substrates or energy phosphates in order to deplete endogenous Ca²⁺ from the mitochondrial matrix (5, 6, 9). After the depletion step, 10 mM Pi and 0.13 mM ADP were added, followed by glutamate (G, 10 mM) and malate (M, 1 mM) ± Ca²⁺. Addition of fuel (G+M) initiated a submaximal increase in J_o followed by a subsequent transition to State 4 J_o. For experiments designed to measure maximal J_o, State 3 was then elicited with a bolus of 1.3 mM ADP which resulted in consumption of all the oxygen in the chamber providing the fully reduced state (anoxia). Free Ca²⁺ concentrations were made using the calculator programs of Fabiato and Fabiato (26) translated to Labview VIs (National Instruments Corp, Austin, TX) by Reitz and Pollack (27).

Steady-state, intermediate J_o was attained using a progressive creatine kinase (CK) energetic clamp (28), we have recently modified (29). Briefly, by utilizing a large total creatine pool, excess CK, a known [ATP], and the CK equilibrium constant (K_CK, 150 (30)), the extramitochondrial ATP/ADP ratio, and thus, free energy of ATP hydrolysis (ΔG_ATPe) can be calculated from the added phosphocreatine (PCr)/creatine (Cr) ratio:

$$\mathrm{\Delta }{\mathrm{G}}_{\text{ATPe}}=\mathrm{\Delta }{\mathrm{G}}_{\text{ATP}}\circ -2.3*\text{RT}*log([\text{PCr}]*{\mathrm{K}}_{\text{CK}}/([\text{Cr}]*[\text{Pi}]))$$ (1)

where ΔG_ATP° is the standard ΔG_ATP (-7.592 kcal/mol), R is the gas constant (1.987 cal·K^-1·mol^-1), and T is temperature (310°K). Mitochondria oxidizing G+M at State 4 were given 2.5 mM PCr, 5 mM Cr, 5 mM ATP, and 75 U/ml CK, resulting in a J_o of ∼2/3 of State 3. Subsequent additions of PCr (to 3.75, 5, 7.5, and 10 mM) were made to slow J_o to ∼1/3 of State 3.

Additional experiments with pyruvate were conducted similar to those from Messer et al. (28). Briefly, mitochondria in the presence of saturating M were exposed to the CK clamp as described above with a PCr/Cr ratio of 0.25. Pyruvate was then titrated in stepwise at 10, 25, 50, 100, and 500 μM to increase respiration. The novel aspect of this experiment was that upon reaching a steady state with 500 μM pyruvate, stepwise additions of PCr were then made to slow J_o. Thus, in a single experiment, J_o was changed by both “Push” (pyruvate titration) and “Pull” (CK clamp) mechanisms.

Mitochondrial Optical Absorption

A system was developed from our earlier work with an integrating sphere to minimize the effects of light scattering on the visible spectrum of mitochondrial suspensions (23). Our current implementation permits studies on well-mixed samples at physiological temperatures with a complete linear regression analysis of the chromophores of oxidative phosphorylation (31). Briefly, a 6-inch integrating sphere (model RTC-060-SF, LabSphere, Inc., North Sutton, NH, USA) was used with a custom-designed, 1.2-cm diameter, cylindrical, water-jacketed, center-mounted chamber to hold the mitochondrial suspension. The volume used in this chamber was 2 ml. The sample was uncapped and oxygen consumption measurements in the chamber were not attempted due to the optical interference of electrodes. All oxygen consumption data was collected in parallel in a dedicated polarography chamber at the same temperature. All experiments were conducted at 37°C. White light (model CS-16-500, Jobin-Yvon, Inc., Spex^® Forensics Division, Edison, NJ, USA) was impinged on the sample and the absorbed light was collected via a fiber optic using the sampling port on the sphere. Rapid-scanning optical spectra (1 spectrum/100 msec) were collected using a photodiode array (model QE-65000, Ocean Optics, Inc.) from ∼300 to 800nm. Analysis was conducted on the β and α bands of the cytochromes from the 466 to 630nm region since this provided the best discrimination of the absorbance bands (31).

Data analysis was performed by completely fitting the absorbance difference spectra to 7 reference difference spectra for FAD, cytochrome b_H, cytochrome b_L, cytochrome c₁, cytochrome c, cytochrome a₃ peroxy form (a₆₀₇), cytochrome a₃ ferryl form (a₅₈₀), and a simple linear term for baseline corrections as previously described using linear regression fitting (31). The fully oxidized state was taken as mitochondria in the absence of carbon substrates and the addition of ADP and Pi. The fully reduced state for FAD and cytochromes b_H, c₁, c, and a₆₀₇ was obtained by adding a small amount of sodium hydrosulfite at the end of the experiment. Cytochromes b_L and a₅₈₀ were most reduced under State 4 conditions, thus, State 4 was considered as full reduction for these two species. Cytochrome a₅₈₀ reduction level was then normalized to total cyt a content assuming a 1:2 extinction coefficient ratio for a₅₈₀ and a₆₀₇, respectively (32, 33).

Driving Forces and Pathway Conductances

In this study, the force-flow behavior for different regions of the oxidative phosphorylation network was used to estimate the effective conductance (or resistance) of each region during active oxidative phosphorylation. This is in contrast to studies on isolated protein complexes in native gels or which alter the pathway using inhibitor titrations where oxidative phosphorylation is not proceeding under normal conditions. To accomplish this task, the oxidation/reduction (redox) potentials (E_h) of the products and reactants of a reaction segment, as well as ΔΨ when appropriate, must be determined for the driving force, while J_o provides the flux for all of the elements. Mitochondrial Complex E_h for redox pairs was calculated as:

$${\mathrm{E}}_{\mathrm{h}}={\mathrm{E}}_{\mathrm{m}}+2.3*(\text{RT}/\text{nF})*log([\text{oxidized}]/[\text{reduced}])$$ (2)

where E_m is the midpoint potential (-320 mV for NAD/NADH, +230 for cyt c₁, +270 mV for cyt c, +280 mV for cyt a₆₀₇, and +820 mV for O₂/H₂O (34-37)), n is the number of electrons to be transferred, and F is the Faraday constant (23.062 cal·mV^-1·mol^-1). Free energies (ΔG) were calculated assuming that a single NADH donates 2 electrons (n) to the ETC resulting in 10 protons pumped (m) which, in turn, yields 2.7 ATP (p):

$$\mathrm{\Delta }{\mathrm{G}}_{\text{redox}}=-\text{nF}(\mathrm{\Delta }{\mathrm{E}}_{\mathrm{h}}+\mathrm{z}\mathrm{\Delta }\mathrm{\Psi })$$ (3)

$$\mathrm{\Delta }{\mathrm{G}}_{\mathrm{\Delta }\mathrm{\Psi }}=-\text{mF}\mathrm{\Delta }\mathrm{\Psi }$$ (4)

$$\mathrm{\Delta }{\mathrm{G}}_{\text{ATP}}=\mathrm{p}\mathrm{\Delta }{\mathrm{G}}_{\text{ATPe}}$$ (5)

where Eq. 3 is used for the free energy driving electron transfer with ΔE_h as the redox potential difference and z as the relative distance across the mitochondrial inner membrane relative to the matrix side between two redox pairs, Eq. 4 is used for the free energy associated with pumping protons across the mitochondrial inner membrane, and Eq. 5 is used for the stoichiometric free energy of ATP hydrolysis. For electron transfer steps within the ETC, m was varied according to the number of protons moved across the mitochondrial inner membrane between the respective electron donors and acceptors, and z was assumed to be 1, 0, 0, and -1 for electron transfer between NADH and cyt c₁, cyt c₁ and cyt c, cyt c and cyt a₆₀₇, and cyt a₆₀₇ and O₂, respectively, yielding a value of 0 for electron flow down the entire ETC.

Flux down an oxidative phosphorylation pathway was assumed to vary according to the thermodynamic driving forces acting on it using classical irreversible thermodynamic approaches (38, 39):

$$\mathrm{J}=\mathrm{L}(\mathrm{\Delta }{\mathrm{G}}_1-\mathrm{\Delta }{\mathrm{G}}_2)$$ (6)

where J is the flux down the pathway, L is the phenomenological transport coefficient of the reaction, and ΔG₁ and ΔG₂ are the driving forces acting on the front and back ends of the pathway, respectively. For the purposes of this discussion we will refer to the transport coefficient, L, as a “conductance” since many of the reactions we are evaluating involve the displacement of charged species. Simultaneous measurement of oxygen flux (J_o) and the thermodynamic driving forces for oxidative phosphorylation (ΔG_redox, ΔG_ΔΨ, and ΔG_ATP) thus allows for the calculation of the conductances of the ETC (ΔG_redox - ΔG_ΔΨ), ATP synthesis/transport (ΔG_ΔΨ - ΔG_ATP), and complete oxidative phosphorylation pathways (ΔG_redox - ΔG_ATP). Under conditions of saturating oxidative substrates, we considered the free energy associated with the added fuel to be constant. As such, we were also able to calculate the conductance of the fuel transport/dehydrogenase pathway (ΔG_Fuel – ΔG_NADH) and of the complete mitochondrial energy conversion process (ΔG_Fuel – ΔG_ATP) using the ΔG_NADH and ΔG_ATP relationships with J_o, respectively.

Stoichiometries

The ratios of protons pumped across the inner membrane per electron passed (H⁺/e^-) were measured using the force ratio (40-42). Briefly, the ratio of the respective thermodynamic forces was plotted against J_o, and from the resultant linear relationship, the force ratio at zero flux (x-intercept) could be extrapolated. Under equilibrium conditions, plugging Equations 3 and 4 into Equation 5 and rearranging arrives at the following:

$$\mathrm{m}/\mathrm{n}=\mathrm{\Delta }{\mathrm{E}}_{\mathrm{h}}/\mathrm{\Delta }\mathrm{\Psi }+\mathrm{z}$$ (7)

where m/n is the H⁺/e^- ratio. The experimentally-determined stoichiometries were then compared to those used in the ΔG calculations to provide a measure of validity.

Statistical Analysis

For the Ca²⁺ titration experiments, significant differences were assessed using a repeated measures ANOVA with a Tukey-Kramer multiple comparisons post-hoc test. Differences in slopes between Ca²⁺ and no Ca²⁺ conditions were assessed using a two-tailed, paired Student's t-test. A P-value of 0.05 was used to determine statistical significance.

Results

Maximal Respiration

State 3 J_o as well as State 3 and 4 NADH levels rose with increasing [Ca²⁺] up to 840 nM, beyond which a plateau occurred (Figure 1). The initial increase in State 3 with Ca²⁺ was linear with a slope of 0.33 nmol O₂/min/nmol cyt a/nM Ca²⁺. The optimal Ca²⁺ dose (840 nM) for respiration resulted in a 1.8-fold increase in State 3 J_o (405.9 ± 12.6 nmol O₂/min/nmol cyt a) compared to that with no Ca²⁺ (226.8 ± 17.5 nmol O₂/min/nmol cyt a). Surprisingly, the optimal Ca²⁺ dose had no effect on ΔΨ at State 3 and State 4 despite the large increase in NADH and J_o. This result implies that the effects of Ca²⁺ cannot be through alterations in ΔΨ alone as other processes must be affected.

Figure 1.

Calcium titration. A: State 3 and 4 J_o at added free calcium concentrations from 0 to 1500 nM. B: State 3 and 4 NADH at added free calcium concentrations from 0 to 1500 nM. C: State 3 and 4 ΔΨ at added free calcium concentrations from 0 to 1500 nM. Filled squares – State 4, open diamonds – State 3. Error bars signify standard error. * denotes significance difference from no calcium condition. n = 4.

The mitochondrial isolation process typically results in mitochondria with high endogenous levels of Ca²⁺ (43, 44). Depletion of endogenous calcium for these experiments was achieved through a 6 minute mitochondrial incubation period at 37°C without added substrates and in the presence of 15 mM sodium (to stimulate Na⁺/Ca²⁺ exchange) which we have previously shown to remove nearly all Ca²⁺ from the mitochondrial matrix (45). This incubation step resulted in a State 3 J_o that was 49% of the rate without incubation or NaCl (Table 1). Addition of Ca²⁺ after the incubation period resulted in a State 3 J_o that was 88% of the rate without incubation which is consistent with the notion that the effects of the incubation period are primarily due to a depletion of Ca²⁺.

Table 1. Oxygen Consumption, NADH % Reduction, and Membrane Potential at Maximal and Resting Respiration.

Incubation Conditions	Jo		NADH		ΔΨ
	State 4	State 3	State 4	State 3	State 4	State 3
No Calcium (n=9)	31.0 ± 3.2	226.8 ± 17.5+	59.9 ± 5.1	17.8 ± 1.3	-202.1 ± 2.6	-171.5 ± 4.1
Calcium (n=9)	39.8 ± 3.1*	405.9 ± 12.6*+	72.4 ± 2.9*	30.0 ± 1.3*	-203.1 ± 1.5	-174.9 ± 2.2
No NaCl,
No Depletion,	29.3 ± 3.7	463.2 ± 19.0
No Calcium (n=12)

Skeletal muscle mitochondria oxidizing 10 mM glutamate and 1 mM malate. Values are means ± SE.

^*denotes significant difference between Calcium and No Calcium.

⁺denotes significant difference from No Depletion condition. J_o values are in nmol O₂/min/nmol cyt a. NADH values are % reduced. ΔΨ values are in mV.

Steady-State, Intermediate Respiration

A representative trace of a CK clamp experiment is shown in Figure 2, and the resultant linear relationship between ΔG_ATPe and J_o is presented in Figure 3A (3, 46, 47). A roughly two-fold increase in respiration was observed with calcium at each clamped ΔG_ATPe value (Figure 3 A). Therefore, the ability to produce ATP with fixed substrate and product concentrations was increased by Ca²⁺. This result implied that the V_max of the mitochondria for producing ATP was increased by Ca²⁺. To confirm this notion, these data were reformulated to extract the affinity of oxidative phosphorylation for ADP. In Figure 3B, the dose response curve of [ADP] versus J_o reveals typical saturating kinetics. The Eadie- Hofstee plot in Figure 3C demonstrates that the increase in J_o with Ca²⁺ was not due to a change in ADP affinity, ∼43 μM, but rather, due to a doubling of the V_max from ∼200 to ∼425 nmol/min/nmol cyt a, consistent with the data presented in Figure 1. It is important to note that combining the increase in V_max due to Ca²⁺ with the change in ADP from resting muscle (∼5 μM) to that during modest concentric exercise (∼25 μM) in humans (48) can explain an ∼7-fold increase in respiration rate. These physiological points are highlighted in Figure 3B and the combined effects of Ca²⁺ and ADP are further developed in the Discussion.

Figure 2.

Representative CK energetic clamp experiment. A: ΔΨ and NADH during stepwise PCr additions and at anoxia. B: J_o and [O₂] during stepwise PCr additions and at anoxia.

Figure 3.

Kinetic effect of calcium on oxidative phosphorylation intermediate respiration. A: Relationship between ΔG_ATPe and J_o with and without calcium. B: Michaelis-Menten relationship between J_o and ADP with and without calcium. The open square and open circle signify the ADP values reported for human skeletal muscle at rest and during moderate exercise, respectively. C: Eadie-Hofstee plot for the relationship between J_o and ADP where y= -(K_mADP)x + V_max. Filled squares – calcium, open diamonds – no calcium. Error bars signify standard error. n = 12. Slopes, regression analyses, and the resultant p-values for A and C are reported in Table 2 under ΔG_ATPe and K_mADP, respectively.

The remaining studies focused on isolating the elements within oxidative phosphorylation responsible for the increase in V_max by Ca²⁺. To evaluate the contribution of different steps in the oxidative phosphorylation network, the phenomenological conductance was determined for each step where the net driving forces could be measured. The primary potential energy for oxidative phosphorylation, especially with the substrates we utilized, is the free energy in NADH which is then converted into ΔΨ. The force:flow relationships for these parameters are presented in Figure 4 where the convention of the force, net NADH or ΔΨ, is plotted on the X-axis, and flow, J_o, is plotted on the Y-axis. The force:flow relationships for NADH and ΔΨ were linear for both the control and Ca²⁺ conditions. Ca²⁺ increased the force:flow slopes by ∼0.7- and 2.1-fold for NADH and ΔΨ, respectively (Table 2). These data are consistent with previous observations in porcine heart mitochondria (9). The relationships in Figure 4 provide only a measure of the balance between production and utilization of the respective free energies, NADH or the resulting ΔΨ, thus, many different parameters could contribute to the Ca²⁺-induced changes in total velocity and slope, including dehydrogenase activity, ADP kinetics on F₁F_oATPase velocity, or any alterations within the ETC. Thus, to determine the specific locations of Ca²⁺ sensitivity, we used the free energy differences measured across various spans of the mitochondrial energy conversion pathway along with J_o to determine the conductance, or reciprocally, the resistance to energy flow of each span. Figure 5 depicts the thermodynamic driving forces measured and the energy conversion steps for which conductances were calculated.

Figure 4.

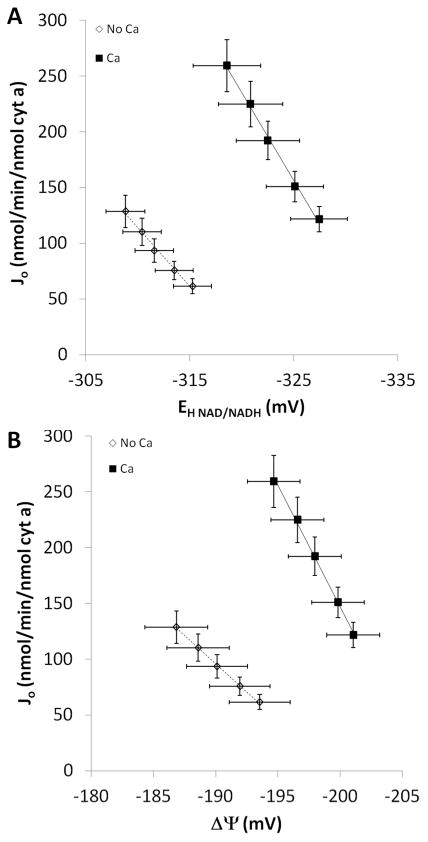
Effect of calcium on oxidative phosphorylation energetic driving forces and J_o during intermediate respiration. A: Relationship between NADH and J_o with and without calcium. B: Relationship between ΔΨ and J_o with and without calcium. Filled squares – calcium, open diamonds – no calcium. Error bars signify standard error. n = 12. Slopes, regression analyses, and the resultant p-values are reported in Table 2.

Table 2. Mean Values for Force:Flow Relationships in Figures 3, 4, 6, 8, and 9.

	Slope		r2
	No Calcium	Calcium	No Calcium	Calcium	p-value
NADH (mV)	12.2 ±2.6	20.5 ±4.0*	0.981 ±0.004	0.960 ±0.013	0.010
Cyt bH (% reduced)	16.0 ±2.9	-75.6 ±40.5	0.518 ±0.192	0.558 ±0.200	0.108
Cyt bL (% reduced)	-3.0 ±0.2	-8.2 ±1.1*	0.961 ± 0.006	0.937 ±0.018	0.021
Cyt c1 (% reduced)	-15.9 ±27.7	-31.8±21.2	0.527 ±0.168	0.268 ±0.139	0.587
Cyt c (% reduced)	-53.6 ±10.5	-16.1 ±53.0	0.568 ±0.119	0.498 ±0.109	0.518
Cyt a607 (% total cyt a)	67.9 ± 17.9	87.8 ±32.5	0.937 ±0.022	0.893 ±0.053	0.678
Cyt a580 (% total cyt a)	4.6± 13.1	95.2 ±24.4	0.528 ±0.235	0.799 ±0.055	0.073
ΔΨ (mV)	10.3± 1.4	22.1 ±2.5*	0.989 ±0.004	0.989 ±0.002	0.000
ΔGATPe (kcal/mol)	80.0 ± 11.3	163.2 ±17.9*	0.991 ±0.002	0.990 ±0.002	0.000
KmADp(μM)	42.3 ±6.6	44.4 ±6.3	0.963 ±0.010	0.942 ± 0.023	0.687
LFuel/DH	-263.5 ± 57.3	-445.3 ±87.1*	0.981 ±0.004	0.960 ±0.013	0.010
Lcl+iii	-101.9 ±20.9	-224.7 ± 17.0*	0.992 ±0.001	0.927 ±0.043	0.012
Lc1c	-91.0 ±116.2	269.3 ±191.7	0.228 ± 0.078	0.122 ±0.081	0.266
LCIVa	226.4 ± 56.0	543.7 ±46.3*	0.935 ±0.016	0.856 ± 0.064	0.043
LCIVb	-55.8 ±13.5	-123.8 ±25.9*	0.989 ±0.004	0.970 ±0.021	0.036
LETC	-39.3 ±5.6	-96.0 ±11.1*	0.988 ±0.005	0.980 ±0.008	0.000
LATPase	-79.5 ±37.1	-192.5 ±33.7*	0.889 ±0.035	0.969 ±0.010	0.005
LOxphos	-29.8 ±4.8	-60.9 ±7.9*	0.989 ±0.003	0.990 ±0.003	0.000
LMito	-29.6 ±4.2	-60.4 ± 6.6*	0.991 ± 0.002	0.990 ±0.002	0.000

Values are means ± SE.

^*denotes significantly different from No Calcium condition.

P-value compares No Calcium and Calcium slopes.

Figure 5.

Simple model of the mitochondrial energy conversion cascade. The path of energy flow is depicted in the top half of the figure while the measured energetic driving forces and how they relate to the calculation of conductances or resistances is depicted in the lower portion of the figure.

The conductance of the entire oxidative phosphorylation cascade, L_Oxphos, was determined by plotting J_o versus ((ΔG_NADH - ΔG_O2) - ΔG_ATP), the potential energy across the oxidative phosphorylation process. It is important to note that since the ΔG_NADH is included in this calculation, the effects of dehydrogenase activation are eliminated from this force:flow relationship which is presented in Figure 6A. The overall L_Oxphos increased 2.0-fold in the presence of Ca²⁺. These data are consistent with the notion that the ability of oxidative phosphorylation to generate ATP at a given free energy is improved in the presence of Ca²⁺.

Figure 6.

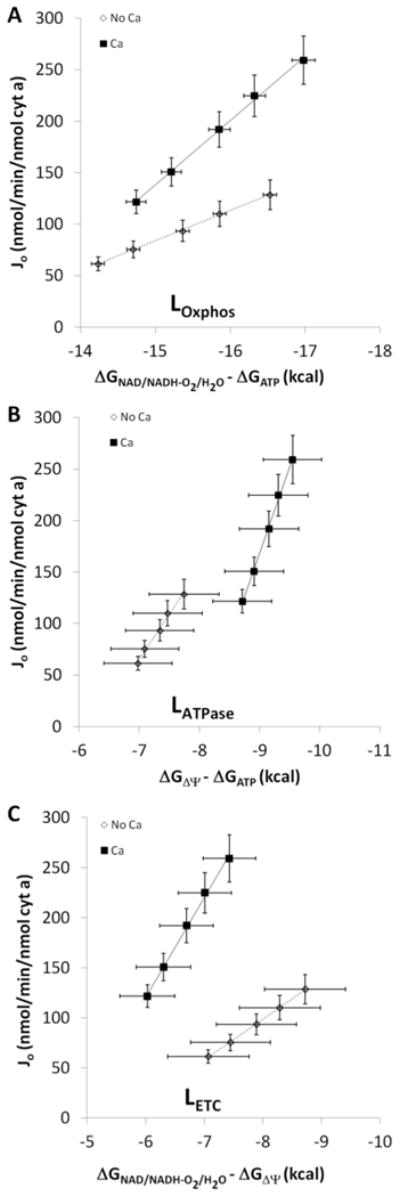
Effect of calcium on mitochondrial conductances. A: Relationship between J_o and the free energy difference between NADH and ΔG_ATP with and without calcium. B: Relationship between J_o and the free energy difference between ΔΨ and ΔG_ATP with and without calcium. C: Relationship between J_o and the free energy difference between NADH and ΔΨ with and without calcium. Filled squares – calcium, open diamonds – no calcium. Error bars signify standard error. n = 12. Slopes, regression analyses, and the resultant p-values for A, B, and C are reported in Table 2 under L_Oxphos, L_ATPase, and L_ETC, respectively.

It has been previously established that Complex V maximal activity is increased by Ca²⁺ (9). We confirmed that the ATP synthesis mechanism, L_ATPase, which includes both Complex V and the adenylate nucleotide translocase (ANT), was activated by Ca²⁺ by plotting J_o versus ΔΨ-ΔG_ATP in Figure 6B. The calculated L_ATPase increased by a factor of 2.4 in the presence of Ca²⁺ (Table 2) consistent with previous results in the porcine heart (9) and recent biochemical analysis (49).

To eliminate L_ATPase from the conductance calculation, we determined the conductance of the electron transport chain, L_ETC, using ((ΔG_NADH - ΔG_O2) - ΔG_ΔΨ) to take into account only the free energy driving the ejection of charge and not ATP synthesis. As seen in Figure 6C, L_ETC was increased 2.4-fold in the presence of Ca²⁺. These data suggest that Ca²⁺ is activating the ETC independent of effects on Complex V or dehydrogenases.

Using the cytochrome spectra as shown in Figure 7, we could isolate different regions of the ETC to examine whether Ca²⁺ was altering the reaction kinetics. Force:flow relationships for cytochromes b_H, b_L, c₁, c, and a peroxy (a₆₀₇) and ferryl (a₅₈₀) with and without Ca²⁺ are shown in Figure 8A-F. Ca²⁺ caused a greater reduction of all cytochromes with the exception of b_L. However, the slope of the relationship between b_L and J_o was increased 2.7-fold by Ca²⁺. The thermodynamic relationships and the chromophores detected provided the differential driving forces for the flux between NADH and cyt c₁ (for calculating L_CI+III), cyt c1 to cyt c (for calculating L_c1c), cyt c and cyt a₆₀₇ (for calculating L_CIVa) as well as cyt a₆₀₇ with oxygen (for calculating L_CIVb). The use of cyt b redox forms for calculating a driving force was complicated by the Q cycle, thus, Complex III was lumped with Complex I in L_CI+III.

Figure 7.

Representative spectra and fits for mitochondrial cytochromes. A: Representative raw, fit, and error residual spectra of a transition from State 4 to intermediate respiration. B: Individual cytochrome components of the fit spectrum from A. C: Representative fit spectra from a CK clamp experiment without calcium. D: Representative fit spectra from a CK clamp experiment with calcium.

Figure 8.

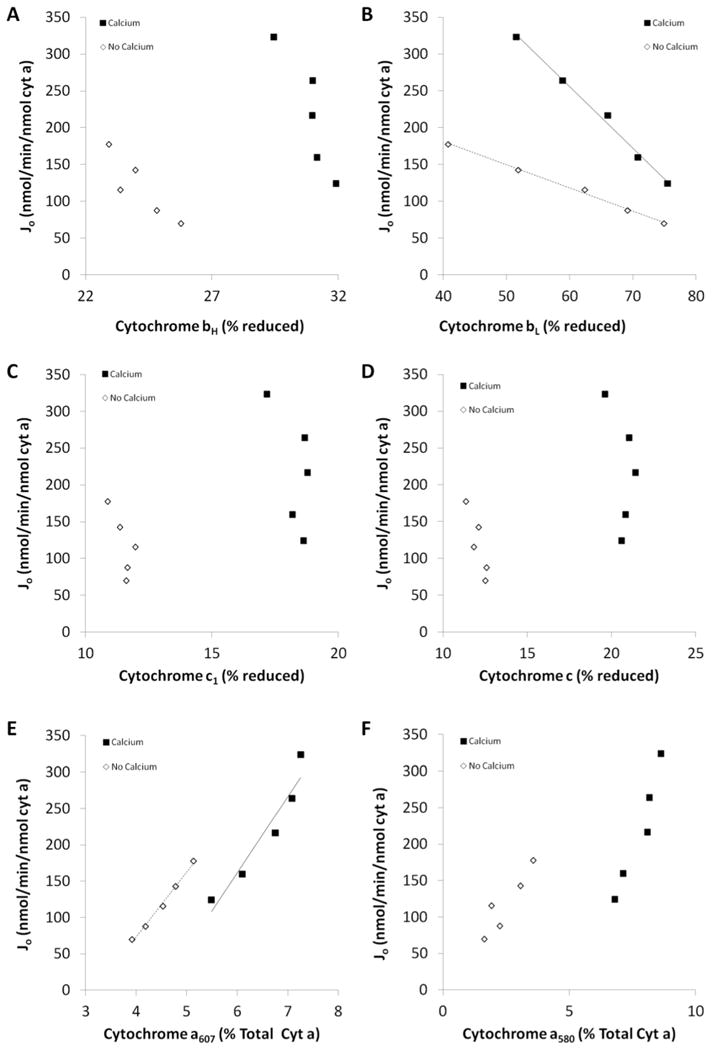
Effect of calcium on the kinetic relationship between cytochrome redox state and flux. A: Relationship between cytochrome b_H and J_o with and without calcium. B: Relationship between cytochrome b_L and J_o with and without calcium. C: Relationship between cytochrome c₁ and J_o with and without calcium. D: Relationship between cytochrome c and J_o with and without calcium. E: Relationship between cytochrome a₆₀₇ and J_o with and without calcium. F: Relationship between cytochrome a₅₈₀ and J_o with and without calcium. Filled squares – calcium, open diamonds – no calcium. Trendlines are included for relationships with R² values above 0.8. n = 4. Slopes, regression analyses, and the resultant p-values are reported in Table 2.

The calculations of the conductance of the different portions of the ETC are presented in Figure 9A-D. All of the Complexes of the ETC were activated by Ca²⁺ with L_CI+III increasing 2.2-fold (Figure 9A), L_CIVa increasing 2.4-fold (Figure 9C) and the terminal reaction with oxygen, L_CIVb, increasing 2.2-fold (Figure 9D). These calculations suggest that Ca²⁺ had a ubiquitous effect on the activity of the electron transport system consistent with activation within Complex I/Complex III and the interactions within Complex IV.

Figure 9.

Conductances within the electron transport chain. A: Conductance of electron flux between NADH and cytochrome c₁ with and without calcium. B: Conductance of electron flux between cytochromes c₁ and c with and without calcium. C: Conductance of electron flux between cytochromes c and a₆₀₇ with and without calcium. D: Conductance of electron flux between cytochrome a₆₀₇ and O₂ with and without calcium. Filled squares – calcium, open diamonds – no calcium. Trendlines are included for relationships with R² values above 0.8. n = 4. Slopes, regression analyses, and the resultant p-values are reported in Table 2 for A-D as L_CI+III, L_c1c, L_CIVa, and L_CIVb, respectively.

Resistance to Mitochondrial Energy Conversion

By considering mitochondrial energy conversion as flux across a series of resistors (see Figure 5), we were able to calculate the contribution of each span of the energy conversion process to the total resistance to energetic flux. These results are shown in Table 3 where, in the absence of Ca²⁺, Complex IV was determined to provide the most resistance to flux followed by Complex I+III, ATP production/transport, and fuel transport/dehydrogenases. Note that the resistance from cyt c to cyt a₆₀₇ was considered negligible as ΔG_{cyt c - cyt a607} became more positive as J_o increased (Figure 9C) suggesting this reaction provides no flux control. Resistance between cyt c₁ and cyt c was also omitted from this analysis as there was little change in this free energy difference with neither a positive or negative relationship to flux (Table 2). Despite increasing conductances throughout the entire mitochondrial energy conversion pathway, Ca²⁺ addition caused a shift in the relative contribution to resistance away from the ETC (both Complex I+III and Complex IV).

Table 3. Contribution of Each Pathway to the Total Mitochondrial Resistance to Energy Transfer.

	Fuel Transport/Dehydrogenases	Complex I+III	Complex IV	ATP Production/Transport	Total Resistance (Ohms/nmol cyt a)
No Calcium	10.4 ± 0.8% (467)	27.1 ± 2.4% (1211)	37.7 ± 3.3% (1685)	24.7 ± 4.0% (1106)	4471 ± 558
Calcium	14.8 ± 3.2% (345)	21.2 ± 2.5%* (495)	30.5 ± 3.6%* (711)	29.1 ± 4.1%* (678)	2332 ± 441*

The mitochondrial energy conversion process was considered as a series of resistors where the total resistance is the sum of the individual parts. Resistance was calculated as the reciprocal of conductance and assuming 1 nmol O₂ = 4 × 6.02e¹⁴ electrons, 6.24e¹⁸ electrons = 1 coulomb and 23.062 V = 1 kcal/mol. N = 8.

^*denotes significantly different from No Calcium. Values are means ± SE with mean resistance in Ohms/nmol cyt a in parentheses.

Stoichiometries

Measuring the force ratios for the spans of the ETC provided validation for the stoichiometries chosen for making the free energy, and thus, conductance calculations described above. The ∼10% difference between measured and used values in Table 4 suggest that the numbers of electrons (n) and protons (m) were correctly assigned when using Equations 3 and 4 for the relationships depicted in Figures 6 and 9 and Tables 2 and 3.

Table 4. Thermodynamic Stoichiometries for Individual Spans of the Electron Transport Chain.

Stoichiometry	Ox Phos Span	Measured		Used	% Difference
		No Ca	Ca		No Ca	Ca
H+/e-	NADH to cyt c1	3.9 ± 0.0	3.8 ± 0.0	4.0	-2.5	-5.0
	Cyt c1 to cyt c	0.1 ±0.0	0.1 ±0.1	0.0	-	-
	Cyt c to cyt a607	0.3 ±0.0	0.3 ±0.0	0.0	-	-
	Cyt a607 to O2	1.1 ±0.1	1.1 ±0.0	1.0	10.0	10.0
	NADH to O2#	5.4 ±0.1	5.2 ±0.1	5.0	8.0	4.0
	NADH to O2*	5.4 ±0.1	5.3 ±0.0	5.0	8.0	6.0

^#Measured values are the sum of NADH to cyt c₁, cyt c₁ to cyt c, cyt c to cyt a₆₀₇, and cyt a₆₀₇ to O₂.

^*Measured values are from NADH to O₂ directly. N = 4.

Discussion

Steady-state Kinetic Analysis

Skeletal muscle free Ca²⁺ levels are typically less than 50 nM at rest and, at the onset of exercise, can transiently rise to 0.5 – 1.5 μM, depending on both intensity and modality (17, 18, 50). Using the reported skeletal muscle values as a guide, Ca²⁺- depleted skeletal muscle mitochondria were incubated with concentrations up to 1.5 μM to determine the steady-state kinetic relationship between Ca²⁺ and State 3 and State 4 J_o, NADH, and ΔΨ, as well as the optimal Ca²⁺ dose to stimulate oxidative phosphorylation (Figure 1). The kinetic relationship to Ca²⁺ was similar between J_o and NADH, with both being maximally stimulated at 840 nM Ca²⁺. Thus, the optimal Ca²⁺ dose for oxidative phosphorylation in isolated mitochondria is similar to that in exercising muscle, and, as a result, the Ca²⁺ levels used in this study may offer some insight into the Ca²⁺ activation of mitochondria in the transition from rest to exercise. It should be noted that temporal kinetics of Ca²⁺ exposure to the mitochondria in these studies with constant step changes is much different than the transient nature of cytosolic Ca²⁺, in vivo. Thus, these steady state, in vitro kinetics can only be estimates of the in vivo conditions. Further kinetic analysis revealed that the increase in State 3 J_o with Ca²⁺ was the result of an increase in the apparent V_max of oxidative phosphorylation and not due to changes in ADP affinity (Figure 3C) as previously shown by Scaduto's group in heart mitochondria (8). However, since we used saturating concentrations of carbon substrates and a limited number of substrates, we cannot reach conclusions regarding carbon substrate affinity changes to Ca²⁺. The remainder of the study focused on unraveling the mechanism of the Ca²⁺-induced V_max increase in skeletal muscle mitochondria under these conditions.

Force:Flow Analysis

Simultaneous measurement of J_o, ΔΨ, and the NADH and cytochrome redox states at several different respiration rates allows for a novel evaluation of the impact of Ca²⁺ on metabolic flux and thermodynamic driving forces. The CK clamp provides mitochondria with extramitochondrial ΔG_ATP and [ADP_f] values similar to those observed in human skeletal muscle in vivo (48, 51, 52). Thus, we were able to examine the effects of Ca²⁺ in an environment which may more closely approximate in vivo conditions compared to experiments using inhibitors and/or excess ADP.

Initial force:flow analyses examined the effect of Ca²⁺ on the conductance of the overall mitochondrial energy conversion cascade (L_Mito) by measuring the slope of the relationship between flux (J_o) and the difference between the forward (ΔG_Fuel) and reverse (ΔG_ATP) driving forces (Eq. 6 and Figure 5). Since ΔG_Fuel is assumed to be constant at the high substrate concentrations used, (ΔG_Fuel - ΔG_ATP) reduces to ΔG_ATP for this analysis. Using this simplification, the 2.0-fold increase in the J_o/ΔG_ATP slope shown in Figure 3A represents a 2.0-fold increase in L_Mito, nearly identical to the Ca²⁺-induced increase in State 3 J_o discussed above. However, L_Mito, much like State 3 J_o, gives only a global view of the effect of Ca²⁺ on oxidative phosphorylation with no information on the specific sites that are affected. To remove the influence of fuel transportation and substrate dehydrogenases on L_Mito, we used the NADH redox status along with ΔG_ATP to calculate L_Oxphos, or the conductance of the oxidative phosphorylation reactions. Just as with L_Mito, Ca²⁺ caused a 2.0-fold increase in L_Oxphos (Figure 6A). Thus, oxidative phosphorylation was activated by Ca²⁺ independent of the well known effects of Ca²⁺ on dehydrogenases and substrate transport (53). We then split L_Oxphos into two separate elements, the combination of Complex V and ANT (ATP production/transport, L_ATPase) and the ETC (L_ETC), by using the measured intermediate, ΔΨ. L_ATPase was increased 2.4-fold by Ca²⁺ (Figure 6B) similar to previous reports demonstrating that Ca²⁺ activates cardiac Complex V (9, 49) and in skeletal muscle where Ca²⁺ activated the phosphorylation subsystem (6).

The conductance of the ETC, L_ETC, was also increased 2.4-fold by Ca²⁺ (Figure 6C). Since a pathway with greater conductance necessitates lower driving forces to achieve a given flux, and reactive oxygen species (ROS) production has been correlated with ETC driving forces (54), the increased conductance of the ETC with Ca²⁺ levels typical of exercising muscle may suggest a role for Ca²⁺ in minimizing ROS production upon the onset of exercise. Indeed, though Ca²⁺ given to inhibited mitochondria or in supraphysiologic doses causes an increase in ROS production (55), control mitochondria produce less ROS from Complexes I and III when given physiological levels of Ca²⁺ (56, 57).

Recent advancements in optical absorbance spectroscopy (31) have allowed for measurement of the status of individual complexes of the ETC without the use of artificial electron donors/acceptors or inhibitors and under conditions similar to those typically used in mitochondrial respiration studies. We employed these methods together with the force:flow analyses described above to determine the conductances of individual elements within the ETC. Surprisingly, we found that Ca²⁺ activated nearly every step within the ETC (Figure 9) with a 2.2-fold effect on L_CI+III, a 2.4-fold effect on L_CIVa, and a 2.2-fold effect on L_CIVb. Unfortunately, we were unable to measure the redox status of ubiquinone which precluded the separation of Complexes I and III. However, based on our measurements of the redox status of cytochrome b_H and the proposed equilibrium between b_H and ubiquinone (58-60), we can predict that the Ca²⁺ effect on L_CI+III would be shared by both Complex I and Complex III. There have been few other reports on a Ca²⁺ stimulation of the ETC. Bender and Kadenbach (61) showed that Ca²⁺ recovered the inhibition of Complex IV activity by cAMP in bovine liver mitochondria, however, Ca²⁺ had no effect when cAMP was not present nor did it directly activate the isolated enzyme. Murphy et al. (15) suggested that the Ca²⁺ sensitivity of rat liver mitochondria was largely due to activation of flow through Complex III, but not Complex IV. However, Murphy et al. (15) reported a Ca²⁺-stimulated maximal flux through Complexes III and IV (from ubiquinone to O₂) that was more than twice as high as the flux through Complex IV alone (from TMPD + ascorbate to O₂), suggesting that maximal Complex IV flux was not attained with TMPD + ascorbate as substrate in that study.

To our knowledge, the current broadband, spectroscopic approach is the first report of Ca²⁺ activation of multiple steps within the ETC. This activation of the ETC by Ca²⁺ may significantly contribute to the Ca²⁺ stimulation of ATP production during exercise. Hogan's lab recently found that a ‘priming’ bout of contractions removed an apparent limitation to flux caused by the ETC at the onset of contractions in an isolated single muscle fiber (62). These authors speculated that an increase in mitochondrial Ca²⁺ may have been responsible, at least in part, for the removal of the limitation to flux by the ETC, though Ca²⁺ levels were not specifically measured (62).

Network Thermodynamic Analysis

By calculating the conductances for sequential steps within the mitochondrial energy conversion cascade, we are also able to treat the system as a series of resistors where the resistance of each part is the reciprocal of its conductance. The total resistance of the series of reactions is then equal to the sum of the individual resistances within the system. This approach is similar to network thermodynamic approaches used for modeling multiple reaction steps in a metabolic cascade (63, 64). Further, we can calculate the resistance of each individual element as a percentage of the total resistance and examine whether Ca²⁺ alters the distribution of resistances within the energy conversion elements. Ca²⁺ addition resulted in a 1.9-fold decrease in the total resistance to mitochondrial energy conversion as well as a decrease in the resistance of each element (Table 3). However, the distribution of the resistances within the reaction series was altered by Ca²⁺. The ETC contributed 64.8% of the total resistance to flux in the absence of Ca²⁺, while the presence of Ca²⁺ reduced the contribution of the ETC to 51.7% of the total resistance to energy conversion. Despite the well-known effects of Ca²⁺ on increasing the activity of substrate dehydrogenases (7, 65), Ca²⁺ trended towards an increase (p=0.09), not decrease, in resistance of the fuel transport/substrate dehydrogenase pathway relative to the other components of mitochondrial energy transfer (Table 3). Thus, while Ca²⁺ did activate fuel transport/substrate dehydrogenases (L_Fuel/DH, Table 2), the effects were relatively greater on downstream pathways. This was not surprising, however, as it was recently pointed out that Ca²⁺ stimulation of respiration cannot be explained by activation of dehydrogenases alone (53).

The data in Table 3 also suggest that Complex IV and Complex V and/or ANT are critical sites of flux control within mitochondria respiring at intermediate rates, as these sites make the greatest contribution to the total mitochondrial resistance to energy conversion. Complex IV, Complex V, and ANT have each previously been reported as important loci of flux control in heart mitochondria (66-68), though the simulations of Korzeniewski and Mazat (69) suggested that, in skeletal muscle mitochondria, these three sites have little or no flux control during intermediate respiration. However, the hexokinase-ATPase system utilized by Korzeniewski and Mazat assumed 85% of the flux control during intermediate respiration with an additional 8% coming from the proton leak, leaving little room for flux control by any mitochondrial enzyme. The CK energy clamp system used here exerts no flux control itself (68), thus allowing for greater sensitivity in detecting the relative control of mitochondrial sites over energy conversion (70).

The observation that multiple steps of oxidative phosphorylation are regulated by Ca²⁺ is consistent with previous control strength analyses, using the approach of Kascer and Burns (71), finding that the control of oxidative phosphorylation is highly distributed under phosphorylating conditions (72-74). These studies used inhibitor titrations of different steps in the reaction series to establish if “excessive” activity was present and estimate the control strength of a given step based on the overall flux sensitivity to inhibitor action. These titrations, which did not compensate for changes in reaction driving forces as done here and which relied on the specificity of complex inhibitors, also revealed that Complex IV, ANT, and other steps within the ETC all contribute to the overall rate limitation of State 3 oxidative phosphorylation. In the absence of large changes in metabolite or intermediate concentrations, shared flux control among many sites within the energy conversion process necessitates a coordinated modulation of each site in order to achieve the large increases in flux observed in vivo (75). This theoretical prediction was bolstered by the in silico results of Korzeniewski (11, 76, 77) which, using a simplified model of oxidative phosphorylation, suggested that the V_max's of the entire mitochondrial energy conversion process should be modulated by an external signal consistent with notions previously presented by Balaban (10) and Hochachka and Matheson (78) based on experimental data. Although previous cellular and whole tissue studies have found both pyruvate dehydrogenase (PDH) and Complex V to be activated by the onset of contractile work (49, 66, 79), experimental evidence for simultaneous, multi-site modulation by an external effector has been limited (6, 9, 80). The near ubiquitous activation across the mitochondrial energy conversion cascade observed here suggests that Ca²⁺ may play a role in the stimulation of oxidative phosphorylation in vivo contributing to the near metabolic homeostasis observed. However, the molecular mechanism for this effect is yet to be fully elucidated with the exception of a few dehydrogenases.

Contribution of Conductance and Driving Force to Flux

The force:flow and network thermodynamic analyses discussed above were done under the assumption that energetic flux can be explained by Ohm's Law. In other words, the current (J_o) must be equal to the voltage (ΔG) multiplied by the conductance (L) (Eq. 6). The linearity displayed in Figures 3, 4, 6, and 9 suggests that this was a valid assumption for nearly all steps within the oxidative phosphorylation cascade. With the establishment of flux as the product of driving force and conductance, we can then determine how much of the increase in flux due to Ca²⁺ can be attributed to a change in driving force versus a change in conductance. Ca²⁺ caused an average 2.01-fold increase in J_o (Figure 3A) when comparing mitochondria provided the same extramitochondrial conditions (fuel and ΔG_ATP). The driving force for oxidative phosphorylation (ΔG_NADH – ΔG_ATP) increased on average by only 1.03-fold with Ca²⁺ (Figure 6A); consequently, 97% of the increase in J_o must be explained by an increase in the conductance of this pathway (L_Oxphos). The overall driving force for the ETC (ΔG_NADH – ΔG_ΔΨ) actually decreased by 15% with Ca²⁺ (Figure 6C), and, as a result, the increase in L_ETC is able to explain the entire Ca²⁺- induced increase in flux down this pathway. Within the ETC, 100% and 98% of the greater flux observed with Ca²⁺ is explained by an increase in the conductances of Complex I+III (Figure 9A) and Complex IV (Figures 9C-D), respectively. Similarly, the driving force for the combined fuel transport and substrate dehydrogenase pathways (ΔG_Fuel – ΔG_NADH) decreased slightly with Ca²⁺, suggesting that a change in conductance, and not driving force, is entirely responsible for the increase in flux observed with Ca²⁺. Although the level of NADH and ΔΨ merely reflect the balance of their respective production and utilization and do not offer direct insight into the specific location of any conductance changes, similar comparisons of the contribution of driving force versus conductance to the observed increase in flux can also be made for these two energetic intermediates. Ca²⁺ caused a 4% increase in both NADH and ΔΨ (Figure 4); thus, the contribution of these two driving forces to the 2.01-fold increase in J_o was minimal compared to the associated increases in conductance due to Ca²⁺.

Conversely, addition of Ca²⁺ led to an average 1.25-fold increase in ΔG_ΔΨ – ΔG_ATP (Figure 6B), thus, only 76% of the increase in flux through the ATP production and transport reactions can be explained by L_ATPase. That (ΔG_ΔΨ – ΔG_ATP) was also able to explain a significant fraction of the Ca²⁺-stimulated flux suggests that this thermodynamic parameter itself may play an important role in flux control. Similarly, the reduction level of cyt a₆₀₇ (Figure 8e) is reported to be a primary controller of flux through Complex IV (67). Just as with (ΔG_ΔΨ – ΔG_ATP), the increase in reduction level of cyt a₆₀₇ is able to explain 54% of the increase in flux through Complex IV due to Ca²⁺, leaving 46% to be explained by activation of the enzyme. Moreover, in preliminary experiments where J_o was manipulated first by titrating increasing amounts of fuel (Push) and subsequently by increasing the PCr/Cr ratio (Pull), of the energetic parameters measured here, only (ΔG_ΔΨ – ΔG_ATP) and the reduction level of a₆₀₇ maintained a positive, linear relationship with J_o during both the Push and Pull phases (Figures S1 and S2). Thus, these data suggest that (ΔG_ΔΨ – ΔG_ATP), the reduction level of cyt a₆₀₇, and the conductances through each step all play an important role in determining the rate of mitochondrial energy conversion.

Extrapolation to In Vivo Skeletal Muscle

The extrapolation of these data to in vivo conditions is complicated by the mitochondrial isolation process, the incubation conditions, and the removal from the local, cellular environment. However, these comparisons are useful in understanding these limitations. The addition of Ca²⁺ to levels similar to those observed during exercise in vivo provided a two-fold increase in the maximum velocity of mitochondrial energy conversion in vitro (Figure 3). Ca²⁺ has been proposed to play a significant role in the matching of energy supply with demand in the heart (12, 81) where AT P turnover can increase five-fold with no change in the cellular energy level (82). Evidence for a balanced activation of the energy supply and demand pathways in skeletal muscle had been limited to in silico models (11, 76, 77) until recently when Wüst et al. (13) reported that the rapid rise in J_o observed at the onset of muscle contractions in vivo was best described by a model of ‘parallel activation.’ These authors showed that the increase in [ADP] at the onset of exercise was insufficient to account for the fast rise in J_o observed; instead, an increase in the apparent V_max of oxidative phosphorylation was required to explain their results. The [ADP] and K_m values reported for the canine gastrocnemius in the study by Wüst et al. (13) covered the range evaluated here (range: 17 – 66 μM, K_m: 43 μM), however, they reported ∼17-fold increase in J_o over this range of [ADP] in vivo, whereas we find a 4.2-fold increase in J_o with the combined effects of ADP and Ca²⁺ in vitro (Figure 3B). The lower dynamic range in vitro is also demonstrated by the respiratory control ratio of ∼15 (Table 1) when the in vivo values have been reported to approach 100 (1). The lower dynamic range of our measures could be due to a lower maximum rate of oxidative phosphorylation or due to a higher ‘resting’ rate. Combining the measured cytochrome a,a₃ content of 11.8 ± 1.6 nmol cyt a/g wet weight for the porcine vastus intermedius with the measured in vitro J_o at ∼66 μM ADP (259.2 nmol O₂/min/nmol cyt a) approaches the in vivo value reported by Wüst et al. (∼65 ml O₂/kg muscle/min) while at ∼17 μM ADP – Ca²⁺, the rates were 15.2 ml O₂/kg muscle/min (in vitro) and 3.8 ml O₂/kg muscle/min (in vivo) suggesting that the maximum rate is similar under both conditions and that the discrepancy primarily resided in the resting rates (note that ‘resting’ here is defined as the 17 μM ADP, no Ca²⁺ condition). The reasons for this may be several-fold. First, in order to make simultaneous, quantitative measurements of J_o, NADH, and ΔΨ, we used isolated mitochondria removed from their native, reticular environment. Though these mitochondria were of high purity (21) and functional integrity, it is likely that the isolation process alters mitochondrial function to some degree (83). Indeed, PDH is reported to be activated after mitochondrial isolation (28, 84), and, together with other dehydrogenases, may contribute to a higher resting J_o in vitro. Similar results have been obtained for Complex IV and Complex V where heart biopsies had 2 – 4 fold lower activity compared to mitochondria isolated from the same tissue (49). Second, these studies were performed with an excess of glutamate and malate to ensure there would be no fuel limitations and to help maintain the steady state. This could result in a higher than normal delivery of reducing equivalents and also increase the ‘resting’ J_o. Finally, the leak rate may also be enhanced during the highly disruptive mitochondrial isolation process (83). Taking these points together, the combination of excess substrates, alterations in membrane leaks, and the activation of metabolic enzyme activity by the mitochondrial isolation process is likely to explain much of the increased ‘resting’ J_o in vitro compared to in vivo. However, the resultant lower J_o dynamic range in vitro would be expected to render the mitochondria less sensitive to Ca²⁺; thus, the results presented here may actually underestimate the effect of Ca²⁺ in vivo. Indeed, simultaneous measures of mitochondrial ΔΨ, NADH, cytochrome redox state and phosphorylation potential in the intact functioning muscle should provide a better understanding of how the mechanisms outlined in isolated mitochondria may be in play in vivo.

Assumptions and Calculations

The nature of these experiments cannot distinguish between mitochondrial surface and matrix calcium effects. It was assumed that most of these effects are primarily due to changes in matrix calcium based on several factors. First, it has been shown that matrix Ca²⁺ rises in vivo with muscle contraction. Rogers et al. (85) demonstrated using Ca²⁺- sensitive bioluminescence probes that the mitochondrial Ca²⁺ activity does increase with skeletal muscle contraction in an in vivo transgenic mouse. These data support the results of earlier, more invasive studies (86) and confirm the notion that an influx of Ca²⁺ into the mitochondrial matrix is occurring in the exercising muscle. Second, as reviewed by Glancy and Balaban (53), most of the effects on mitochondrial metabolism by Ca²⁺ are eliminated by blocking Ca²⁺ entry into the mitochondrial matrix. Extra-mitochondrial Ca²⁺ can impact some mitochondrial transporters, such as aralar (87) which, as part of the malate-aspartate shuttle (MAS), has been shown to play an important role in flux control in brain mitochondria (88). However, we believe there is little flux control by aralar in skeletal muscle mitochondria as aralar activity is five-fold higher in mitochondria from skeletal muscle compared to brain for any given [Ca²⁺] (89). Thus, while Ca²⁺-stimulation of aralar may remove a limitation to flux in brain mitochondria, the basal activity of aralar in skeletal muscle mitochondria is likely sufficient as to not impede flux. Moreover, in preliminary experiments, we gave mitochondria G+M and used arsenite to inhibit 2-oxoglutarate dehydrogenase, ensuring that only the mitochondrial components of the MAS were capable of providing NADH to the ETC and that aralar was the primary site of glutamate entry into the matrix. In these conditions, State 3 J_o was no different with and without Ca²⁺ and was similar to the No Ca²⁺ condition without arsenite present (data not shown). These results suggest that the two-fold activation of J_o with Ca²⁺ as shown in Figure 1 was largely through effects beyond those on aralar.

The calculation of the various ΔG values reported here requires a number of additional assumptions to be made. The first is the attainment of the fully oxidized and reduced states for each redox pair. For cytochromes c₁ and c, we used sodium hydrosulfite to reach full chemical reduction at the end of each experiment. However, we are unable to use this method with NADH because, in addition to the NADH fluorescent enhancement by binding to Complex I (90), the fluorescent signal is dependent on mitochondrial integrity and is severely disturbed by sodium hydrosulfite. As a result, fully reduced NADH was determined at anoxia and in the presence of Ca²⁺ for every experiment. The fully oxidized state for NADH and the cytochromes was determined after the 6-minute Ca²⁺ depletion and subsequent additions of 10 mM Pi and 0.13 mM ADP. Under this condition, the fluorescent NADH signal is ∼10% above that of the dark current even without correcting for non-NADH fluorescent background in the mitochondria, suggesting that NADH can only be further oxidized a maximum of ∼10%. This implied that the primary reducing equivalent source for the cytochromes was highly oxidized under these conditions, supporting our assumption that this was a reasonable estimate of the fully oxidized state of the “downstream” cytochromes. We were unable to measure full chemical (ferricyanide) oxidation in intact mitochondria due to the disruption of the mitochondrial structure with this agent.

The next step in the ΔG calculations involves calculating redox potentials (E_h) from % reduced values (Eq. 1) and requires a midpoint potential (E_m) for each redox pair. E_m values, especially for the various forms of cyt a as well as cyt c, are highly variable throughout the literature, and while the choice of E_m to use for each redox pair does alter the absolute ΔG values, the slopes in Figures 4, 6, 8, and 9 do not change regardless of the E_m chosen. Thus, the E_m values chosen have no effect on the relative conclusions made herein with regard to Ca²⁺. The final assumptions made in the ΔG calculations are the values to use for the number of electrons transferred (n), the relative distance electrons travel across the width of the inner membrane between redox pairs (z), the number of protons pumped (m), and the P/O ratio (p) (Eqs. 3-5). All ΔG calculations were made assuming 1 NADH donated 2 electrons (n) yielding 10 protons (m) resulting in 2.7 ATP (p) from the consumption of ½O₂. The pumping of 4, 4, and 2 protons per 2 electrons passed by Complexes I, III, and IV, respectively, has been widely accepted. Further validation of the values chosen for n, m, and z and the E_m values is provided by the measurement of force ratios (40-42) which provides the value for the number of protons pumped per electron transferred under equilibrium, or static head, conditions. Table 4 shows the close matching between the theoretical and measured stoichiometry values used in the free energy calculations, and perhaps more importantly, that there was no difference with the addition of Ca²⁺.

The number of protons required to elicit a 360° rotation of the γ subunit of Complex V and synthesize 3 ATP is thought to be determined by the size of the c ring within Complex V (91). Mammalian Complex V has 8 c subunits (92), thus H/ATP is 8/3 or 2.67. However, transport of ATP out of the mitochondria also comes at the expense of one proton, thus, the overall H/ATP is 3.67 yielding a P/O ratio of 10/3.67 or 2.7. This value represents the theoretical maximal P/O ratio, as the actual value may be lower due to contribution of the proton leak. Unfortunately, we did not measure proton leak kinetics here; however, based on the respiratory control ratios reported in Table 1, the contribution of the proton leak in these mitochondria under phosphorylating conditions is likely very low. By assuming that proton leak is 100% of State 4 respiration and zero at State 3 and utilizing a standard relationship between membrane potential and proton leak, we can estimate that accounting for the proton leak would alter the slopes in Figure 6B by ∼10% and have a less than 5% effect on the No Ca²⁺/Ca²⁺ ratio between slopes. Further, we do not expect a difference in proton leak between Ca²⁺ and No Ca²⁺ conditions as Ca²⁺ doesn't alter proton leak kinetics in either heart (80) or skeletal muscle mitochondria (6) oxidizing NAD-linked substrates and we find no difference in ADP/O with Ca²⁺ in heart mitochondria (9).

Additionally, we did not attempt to measure the contribution of the pH gradient to the protonmotive force in this study. Lambert and Brand (25) found that increasing [Pi] lowered the pH gradient in skeletal muscle mitochondria, and extrapolation of their data to 10 mM Pi as used here would make the pH gradient nearly zero. Moreover, the use of 15 mM sodium in our medium, and the resultant sodium/proton exchange, would be expected to drive the pH gradient even lower than that observed by Lambert and Brand (25). In addition, we previously reported that there was no pH gradient in phosphorylating mitochondria under similar conditions to those used in this study (23). Finally, Kavanagh et al. (6) reported that the pH gradient did not change across a wide range of respiration rates in skeletal muscle mitochondria given NAD-linked substrates with and without Ca²⁺. Thus, any contribution of the pH gradient could be expected to be the same for all points in the force:flow plots, thereby yielding no effect on the slopes and, therefore, the results reported here.

Initial free energy analyses involving cyt a were done similarly to those mentioned above where sodium hydrosulfite was used to determine the fully reduced state using the spectral peak observed at 605 nm, redox potential was determined using a published E_m value, ΔG was calculated using the appropriate proton and electron stoichiometries, and these assumptions were validated by the measurement of the force ratios (Table 4). However, as discussed in previous work (31), closer examination revealed that the spectral peak for cyt a in the presence of oxygen was consistently observed at 607 nm and not 605 nm, suggesting that the detected species was the peroxy form of cyt a₃ (31, 32). The peroxy form of cyt a₃ is just one of several intermediates within the catalytic cycle of Complex IV and is not present in both oxidized and reduced forms as with the b and c cytochromes. Further complicating matters, maximum occupancy of a₆₀₇ has been reported to represent only ∼30% of the total enzyme (93, 94), suggesting that most of the enzyme complex is in different redox states. These findings bring into question the validity of the assumptions made in the quantification of ΔG_{cyt a607} discussed above. It should be noted that the determination of cyt a content in detergent extracts with chemical reducing agents does not suffer from this complication since the entire Complex is moved to the fully reduced state. Fortunately, we can use the measurements of L_ETC and L_CI+CIII to subtract the conductance of Complex I+III from the conductance of the entire ETC to yield another measurement of the conductance of Complex IV. Using this calculation, Ca²⁺ still provides a more than two-fold increase in the conductance of Complex IV, and the subsequent calculation of resistances as in Table 3 suggests that Complex IV is still the primary site of resistance in the absence of Ca²⁺ and that the relative resistance is reduced upon the addition of Ca²⁺ (data not shown). Additionally, calculation of the conductance of Complex IV can be done by combining L_CIVa and L_CIVb and plotting (ΔG_{cyt c – O2/H2O} - ΔG_ΔΨ) versus J_o. Again, this calculation provides similar results with regard to the effect of Ca²⁺ on the conductance of Complex IV and its resistance relative to the entire energy conversion cascade. These two calculations, combined with the validity provided by the force ratio measurements, suggest that the interpretations resultant from the initial analyses on the effect of Ca²⁺ on Complex IV were justified. Moreover, we performed additional analyses on the conductance of electron transfer within Complex IV using a method similar to Wikström and Morgan (32) where the peroxy and ferryl forms of cyt a were considered one redox couple and the ferryl and oxidized forms were considered another. These results are displayed in Figure 10 and further suggest that Ca²⁺ activates Complex IV by altering the conductance of electron transfer within the catalytic cycle of the enzyme in addition to reducing the contribution of Complex IV to the overall resistance to energy conversion.

Figure 10.

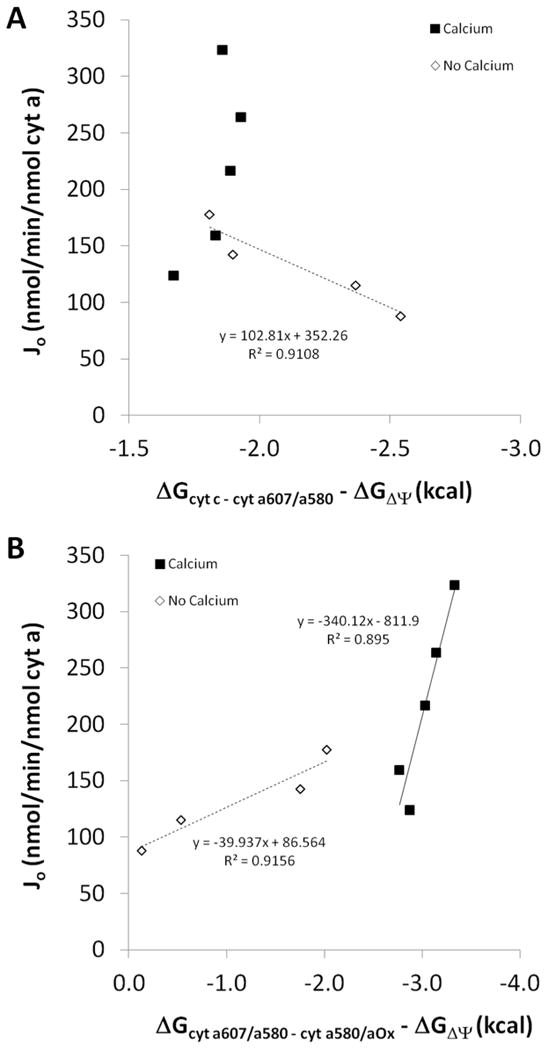
Conductance of electron transfer within Complex IV. A: Conductance of electron flux between the cytochrome c and cytochrome a₆₀₇/a₅₈₀ redox couples. B: Conductance of electron flux between the cytochrome a₆₀₇/a₅₈₀ and cytochrome a₅₈₀/oxidized redox couples. Filled squares – calcium, open diamonds – no calcium. Trendlines are included for relationships with R² values above 0.8. n = 4.

Ca²⁺ has also been shown to induce a spectral shift in heme a of Complex IV (95, 96), and it is possible that this confounded our results with respect to the Ca²⁺ activation of Complex IV depicted in Figures 9 and 10. To investigate this possibility, we repeated the experiments of Kirichenko et al. (95) using solubilized porcine mitochondria where cyt a was reduced by KCN, ascorbate, and TMPD. Indeed, addition of Ca²⁺ induced a red shift of cyt a (data not shown). However, the addition of Ca²⁺ to intact, respiring mitochondria where Complex IV is more than 90% oxidized induced no such shift in the peak for cyt a suggesting that the observed Ca²⁺ activation of Complex IV is not simply due to a Ca²⁺-induced spectral shift.

Summary

These data present the first experimental evidence of a systemic modulation of the oxidative phosphorylation cascade by Ca²⁺. This stimulation involves the near balanced activation of the entire mitochondrial energy conversion process from the generation of NADH and reduction of oxygen to the formation of ATP from ADP and Pi. While the mechanism explaining this systemic modulation with Ca²⁺ has yet to be elucidated, current evidence suggests that it is not direct Ca²⁺ binding as studies on isolated membrane enzymes and submitochondrial particles find no effect of Ca²⁺ (61, 97). Thus, it seems likely that Ca²⁺ is acting through an as yet unknown coordination of post-translational modifications (PTMs). Whether this involves alterations in supercomplex structure (98), changes in phosphorylation, multiple PTMs, or other possibilities will be the subject of future work. Additionally, extrapolation of these data to the conditions observed during exercise in skeletal muscle in vivo reveals that a significant fraction of the metabolic activation associated with exercise could be attributed to Ca²⁺ effects on oxidative phosphorylation coupled with an increase in [ADP], thereby contributing to the metabolic homeostasis of this dynamic tissue.