Structure guided simulations illuminate the mechanism of ATP transport through VDAC1

Abstract

The voltage-dependent anion channel (VDAC) mediates metabolite and ion flow across the outer mitochondrial membrane of all eukaryotic cells. The open channel passes millions of ATP molecules per second, while the closed state exhibits no detectable ATP flux. High-resolution structures of VDAC1 revealed a 19-stranded β-barrel with an α-helix partially occupying the central pore. To understand ATP permeation through VDAC, we solved the crystal structure of mouse VDAC1 (mVDAC1) in the presence of ATP, revealing a low-affinity binding site. Guided by these coordinates, we initiated hundreds of molecular dynamics (MD) simulations to construct a Markov State Model (MSM) of ATP permeation. These simulations indicate that ATP flows through VDAC using multiple pathways, consistent with our structural data and experimentally determined physiological rates.

Each day, humans turnover an amount of ATP equivalent to their body weight¹. The mitochondria are the principal source of ATP generation where a high number of ATP molecules must exit the organelle—primarily through VDACs. In mammals, there are three VDAC isoforms (VDAC1, VDAC2 and VDAC3), which form the main conduits for this large flux of metabolites across the outer membrane from the mitochondrial intermembrane space (IMS) to the cytosol. In addition to its role in bioenergetics, VDAC acts as a scaffold, influencing mitochondrial and cellular physiology through interactions with a variety of proteins and small molecules^2–6. In accordance with these crucial functions, VDAC is expressed in all eukaryotes⁷ and knockouts in mice give rise to respiratory defects, embryonic lethality and sterility⁸.

Three independent structures of VDAC1 have been reported^9–11, providing new insight into the architecture and function of the channel. All structures revealed a 19-stranded β-barrel fold with an N-terminal α-helix in the central pore adjacent to the wall (Fig. 1). The channel has a 27 Å wide opening facing both the cytosol and IMS, but tapers to 14 Å wide in the center of the channel owing to the presence of the helical segment (Fig. 1). In the absence of a membrane potential, VDAC1 adopts a high conductance (450–580 pS in 100 mM KCl), anion selective (1.7–1.9 anion over cation) state, capable of passing millions of ATP molecules per second in vitro¹⁰ and up to 100,000 ATP per second under physiological conditions^12,13. Meanwhile, membrane voltages above or below ±30 mV, as well as several other environmental cues, induce a conformation(s) with reduced conductance (220 pS in 100 mM KCl) that is slightly cation selective and lacks detectable ATP flux^12–14. Continuum calculations¹⁵ and atomistic MD simulations¹⁶ both demonstrated that the solved structures are likely in the open state since these computations revealed anion selectivity and a high single-channel conductance.

Fig. 1. Cartoon representations of the refined mVDAC1 in complex with ATP.

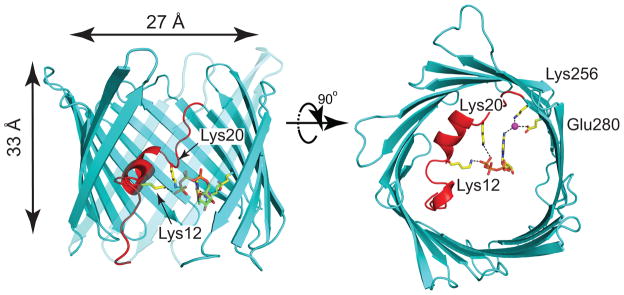
mVDAC1 in complex with ATP viewed from within the plane of the membrane (left) and from the cytosol (right). ATP is bound to mVDAC1 at the center of the pore, forming hydrogen bonds between the side chain nitrogens of residues Lys12 and Lys20 with the O2γ and O1γ of the phosphate tail (2.3 and 3.3 Å, respectively). A structural water (magenta) interacts the N6 nitrogen on the adenosine ring (N6-water oxygen distance is 3.2 Å), and the water also hydrogen bonds to Lys256 Nζ and Glu280 Oε2 (distances to water oxygen are 2.7 and 2.9 Å, respectively). The polypeptide chain is in cartoon representation with the β-barrel and the N-terminal α-helix segment colored cyan and red, respectively. All highlighted interactions are indicated by black dashed lines. The side chains and ATP are shown in ball-and-stick representation. To facilitate visualization of ATP, strands 7–10 are partially transparent. The inner pore dimensions are indicated in the left panel.

Many biochemical and computational studies have validated these crystal structures; however, some researchers still debate whether they represent a physiologically relevant state. In particular, it has been argued that the transmembrane (TM) topology in the crystal structures is inconsistent with several biochemical and functional studies (see reference 17 for a review of these data) and that this inconsistency stems from misfolding of the channel during the refolding step of protein purification. Based on these later experiments, a model in which VDAC has 13 transmembrane spanning β-strands and a single TM α-helix as part of the protein’s pore was proposed^8,18. Yet, other researchers contend that the channel radius derived from the high-resolution structures is consistent with that measured from electron micrographs of native VDAC in mitochondrial outer membranes (reviewed in reference 19). Moreover, early bioinformatics analysis of the primary sequence suggested that the protein has 19 strands²⁰, consistent with the three dimensional structures. Regardless, there are strong arguments from both sides in this debate and only additional research will resolve the current contradictions in the literature.

Here, we set out to determine if, and how, the mVDAC1 structure conducts ATP through a combination of X-ray crystallography and MD simulations. A crystal structure of the channel in the presence of ATP uncovers a weak binding site in the pore domain, the location of which is in excellent agreement with earlier mass spectrometry studies²¹ and predictions from our MD simulations. While 1–5 μs long MD simulations failed to reveal a full ATP passage event, the application of a Markov State Model of permeation predicts that ATP traverses the channel on the 10–50 μs timescale, consistent with the channel being in the open state. We used transition path theory analysis to visualize how ATP moves through mVDAC1, and the results indicate that the molecule exploits a number of distinct, interconnected pathways composed of basic, pore-lining residues to cross the channel.

RESULTS

An ATP binding site identified via X-ray crystallography

Earlier experiments using current fluctuations²², structure specific noise generation²³ and mass spectrometry²¹, demonstrated that ATP weakly interacts with the N-terminal α-helix of VDAC1 as well as a patch of basic residues on the β-barrel wall. To identify specific binding site(s), we undertook the structural characterization of the VDAC–ATP complex by soaking mVDAC1 crystals for one hour in 50 mM ATP (see Online Methods for details on the soaking procedure). Structure determination revealed a lone ATP binding site, adjacent to the N-terminal α-helix, in which the molecule directly contacts Lys12 and Lys20 (Fig. 1). In the refined structure, the side chain nitrogen of Lys12 is 2.3 and 3.2 Å from the O2γ and O3β phosphate oxygen atoms, respectively, while the side chain nitrogen of Lys20 is 3.3 Å from O1γ. The importance of Lys20 to ATP binding was also recently demonstrated for human VDAC1 using NMR²⁴. Additionally, we observe that nitrogen N6 from the adenosine ring interacts with a structural water molecule (distance to water oxygen is 3.2 Å), which itself hydrogen bonds to Lys256 Nζ and Glu280 Oε2 (distances to water oxygen are 2.7 and 2.9 Å, respectively) (Fig. 1). While the presence of extra-density at the ATP site was unequivocal based on Fourier difference maps between the ATP-soaked and native datasets, the ATP displayed weak electron density and high B-factors with a reasonable real-space map-correlation of 0.8. This observation is consistent with a low-affinity binding site and suggests that ATP is highly mobile in the pore (see Online Methods, Supplementary Fig. 1, and Table 1 for more details on the structural refinement). Additionally, despite having 50 mM Mg²⁺ in the crystallization conditions, we did not observe clear density for the ion due to either the high ATP mobility or a lack of Mg²⁺ coordination to the bound complex. Other than the addition of the lone ATP binding site, the channel remained virtually unaltered with respect to the apo structure¹⁰, having a 0.36 Å root-mean-squared deviation (RMSD).

Table 1.

Data collection and refinement statistics

	VDAC ATP
Data collection
Space group	C 1 2 1
Cell dimensions
a, b, c (Å)	100.15, 58.37, 66.55
α, β, γ (°)	90.00, 99.25, 90.00
Resolution (Å)	50.00–2.28 (2.42–2.28) *
Rmerge	0.03415 (0.6297)
I/σI	23.13(2.21)
Completeness (%)	99.3(99.2)
Redundancy	3.64(3.3)
Refinement
Resolution (Å)	19.497–2.28
No. reflections	61557
Rwork/Rfree	0.204/0.261
No. atoms
Protein	2212
Ligand/ion	143
Water	54
B factors
Protein	70.40
Ligand/ion	125.70
Water	53.10
r.m.s. deviations
Bond lengths (Å)	0.007
Bond angles (°)	1.109

^*The data set was measured from a single crystal.

^*Values in parentheses are for highest-resolution shell.

Long, unbiased simulations do not reveal ATP permeation

In an effort to monitor ATP flux through the pore, we carried out long, multi-microsecond MD simulations using the Anton special-purpose supercomputer²⁵. The apo mVDAC1 structure²⁶ was embedded in a homogenous dimyristoylphosphatidylcholine (DMPC) bilayer with both termini facing the lower bath, corresponding to the IMS^27,28, while a single Mg²⁺-coordinated ATP molecule was placed in either the upper or the lower baths (5 mM effective concentration). Several independent simulations lasting 0.6–4.8 μs were initiated from both configurations (Supplementary Table 1). In all cases, including simulations performed with an applied transmembrane potential, ATP entered the pore but failed to permeate the entire channel (Supplementary Fig. 2a, c). For the majority of each simulation, the phosphate tail of the ATP remained in contact with basic residues Lys12, Arg15 and Lys20 on the N-terminal α-helix demonstrating the importance of the helix in forming favorable interactions with ATP, in agreement with previous studies^21–23 as well as with our crystallographic structure. Meanwhile, the adenine ring processively explored different portions of the channel including residues on the β-barrel wall opposite the helix (Supplementary Fig. 2b, d, Supplementary Movie 1).

mVDAC1 ion conduction properties revealed from simulation

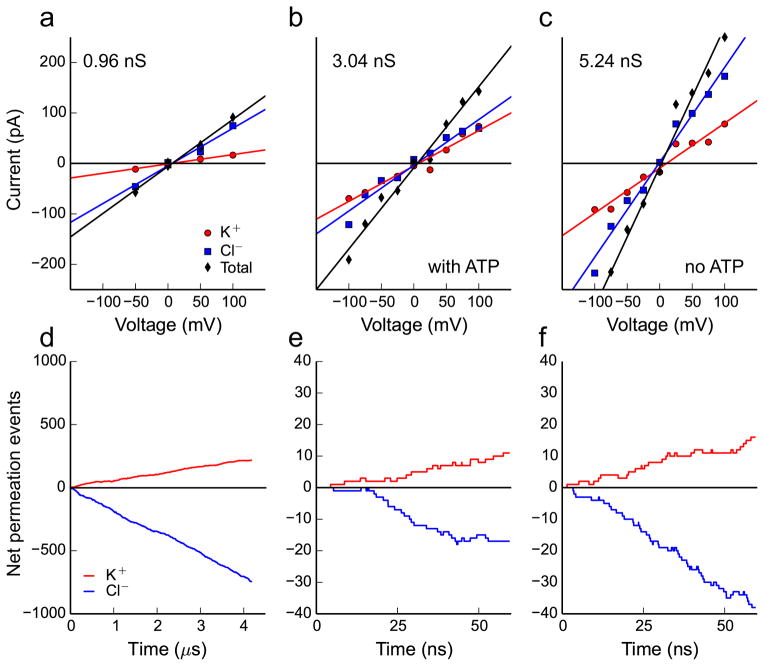
While ATP does not cross the entire channel on the low microsecond timescale, we observed hundreds of independent Cl⁻ and K⁺ permeation events from the Anton simulations. The current-voltage curve (Fig. 2a) was constructed by counting the total number of ion-translocation events per unit time in simulations carried out under various membrane potentials (Fig. 2d). After correcting for the simulated ion diffusion coefficients (see Online Methods), the single channel conductance was 0.96 nS in 142 mM KCl. Experimental estimates range from 0.45 to 0.58 nS in 100 mM KCl¹², which extrapolates to 0.64 to 0.83 nS in 142 mM KCl. Thus, our theoretical value is within 16% of the upper end of the experimental range, which is a dramatic improvement over our earlier estimate based on continuum electro-diffusion theory¹⁵.

Fig. 2. Simulated current-voltage curves and ion permeation rates for mVDAC1.

a–c, Current-voltage curves under different ionic and ATP conditions. The current carried by K⁺ is represented by red circles, the Cl⁻ current is represented by blue squares and the total current is their sum represented by black diamonds. The lines are linear regressions of the respective data points, and they represent the current-voltage curves for the total current (black line), Cl⁻ current (blue line) and K⁺ current (red line). Panel a is compiled from 16.9 μs of aggregate simulation time carried out on a system in 142 mM KCl with ATP in the channel pore. Panels b and c are compiled from shorter 60 ns simulations under high salt (900 mM KCl) with or without ATP in the pore, respectively. d–f, The cumulative net number of channel crossing events by Cl⁻ (blue traces) and K⁺ (red traces) tracked over the time course of each simulation at +50 mV for physiological salt (142 mM) in d, high salt (900 mM) with ATP in the pore in e, and high salt (1 M) with no ATP in the pore in e.

Next, we calculated the current voltage curves with and without ATP in the channel to determine if ATP occupancy influenced the channel’s conduction properties (Fig. 2b and c, respectively). At each membrane potential, a relatively short 60 ns simulation was run, and the KCl concentration was increased to ~0.9 M to increase the number of ion translocation events. Below each curve, in panels d–f, are the corresponding cumulative Cl⁻ and K⁺ translocation events recorded at +50 mV (data for other voltages is not shown). The single channel conductance values with and without ATP, determined from the slopes of the lines in b and c, are 3.04 and 5.24 nS, respectively. Thus, ATP reduced the conductance by 42%, in excellent agreement with the experimental drop of 43% observed in single channel currents under saturating ATP²². Moreover, the simulated conductance values are within 13% and 27% of the experimental range of 3.51 to 4.10 nS, which was extrapolated from 1 M^29,30 down to 0.9 M KCl. Interestingly, our simulations revealed that mVDAC1 has a moderate anion-to-cation selectivity of 4.0 in low KCl concentrations (based on the ratio of the Cl⁻ to K⁺ currents in Fig. 2a), and a much lower selectivity of 2.1 in high salt (Fig. 2c). Our calculations recapitulate the experimental finding that VDAC1 selectivity is ~5 (Cl⁻-to-K⁺) in physiological salt concentrations³¹ and 1.7–1.9 under a 1 M to 0.1 M KCl gradient¹². Lastly, we found that ATP further reduced the anion selectivity of the channel by 40% from 2.1 to 1.3 in high salt (Fig. 2b, c).

A Markov State Model of ATP permeation

As an alternative approach to determine the ATP permeation pathway, we employed a computational method known as Markov State Modeling (MSM)^32,33. A MSM of ATP movement through the channel was constructed by combining the results of 453 short simulations, each lasting 40–130 ns. These multiple simulations were initiated from an ensemble of ATP configurations located throughout the pore and bathing solutions, including a pre-refined version of the crystal structure. In total, we generated 40 μs of aggregate simulation time, resulting in 10 million snapshots saved at 4 ps intervals. All snapshots were aligned to a common reference structure by superposing the non-hydrogen atoms of the β-barrel. Next, we used the hybrid k-centers k-medoids algorithm within the software MSMBuilder³⁴ to cluster the positions of all ATP molecules within the pore domain of the channel with a 6.5 Å cluster radius, resulting in 210 conformational states. The representative conformation for each state is known as the generator. The transition probability matrix, P_i,j(τ), for ATP starting in state i and moving to state j in lag time τ was constructed from the simulation data using a maximum likelihood reversible estimator³⁴. Based on our analysis in Supplementary Fig. 3, we chose a lag time of 5 ns. To focus the computational effort on the slow transitions, we developed a framework for coupling an atomistic MSM with a continuum treatment of ATP diffusion in bulk solution similar to previous work on proton transport by rotary ATPases³⁵. Additional details concerning MSM construction can be found in the Online Methods and Supplementary Note.

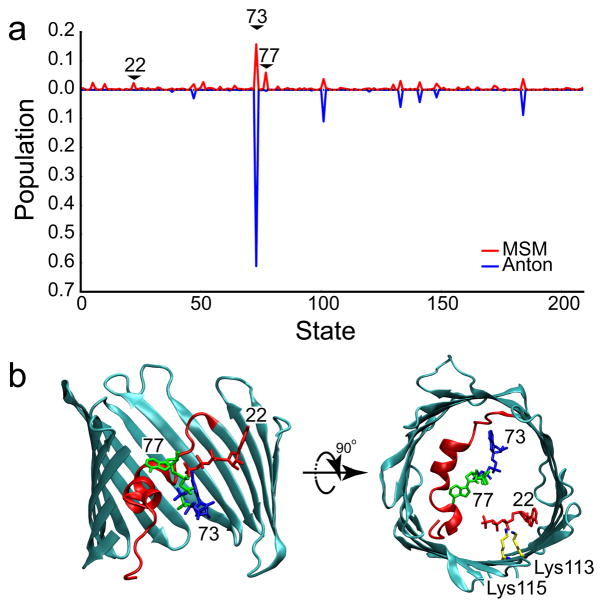
The individual simulations showed that ATP is highly mobile in the pore. In 20% of the simulations, the ATP moved greater than 15 Å along the z-axis (Supplementary Fig. 4), resulting in either entry into the pore from the bulk, or exit to the upper or lower baths (see Supplementary Movies 2–5). The equilibrium distribution of ATP in the channel was determined from the transition probability matrix, and the probability of each of the 210 conformational states in the MSM is shown in Fig. 3a. The dominant state has a modest occupancy of 16%, while occupancies of the next 9 most populated states range from 2–6%. We observed considerable overlap between the most populated states in the MSM and the states most frequently visited by the longest Anton simulation (4.8 μs) (Fig. 3a), lending strong validation to the MSM approach. Additionally, the Anton simulation showed that these stable ATP configurations interconvert on the microsecond timescale. However, the long simulation did not visit all MSM states, indicating superior coverage by the MSM simulations. The two most stable configurations show ATP interacting with N-terminal α-helix residues Lys12, Arg15 and Lys20 (Fig. 3b). The next 8 most populated states are structurally distinct, which likely explains the weakness of ATP binding in the crystal structure. We note, in particular, that the 9^th most populated state corresponds to a configuration where the phosphate tail interacts with β-barrel residues Lys113 and Lys115 (Fig. 3b) – residues in the middle of a 10 residue stretch previously shown to interact with ATP via mass spectrometry²¹.

Fig. 3. ATP adopts many conformations in the mVDAC1 pore.

a, Steady state distribution of ATP in the pore domain, defined as −18 Å ≤ z ≤ 20 Å, calculated from the Markov State Model (red). The most stable state (#73) has 16% occupancy. The data from the longest Anton simulation (4.8 μs) was projected onto the MSM states (blue), and the time spent in each state was used to determine the relative probability of occupancy (plotted in the negative direction for clarity). b, The most stable ATP configurations are structurally diverse. The generators for the 1^st (#73, blue), 2^nd (#77, green), and 9^th (#22, red) most populated states are depicted. The phosphate tails of states 73 and 77 interact with basic residues (Lys12, Arg15 and Lys20) on the N-terminal helix, while the phosphate tail of state 22 interacts with Lys113 and Lys115 on the wall of the β-barrel.

Predicted ATP configurations agree with X-ray structure

Based on RMSD values between the X-ray structure and the generator molecule for each state in the MSM, the crystal structure most closely resembles the 1^st (state #73, 5.80 Å), 10^th (state #148, 5.31 Å) and 19^th (state #58, 5.29 Å) most populated states. Thus, some of the most stable configurations from our model, including the most stable state, are the best matches to the experimental structure. One could argue that our MSM identified the X-ray structure as a stable site because simulations were initiated from this configuration; however, we believe that this is not the case, because the Anton simulations, which started with ATP in the bulk, also predicted state #73 to be extremely stable (Fig. 3a). To visualize the structural similarity between the simulations and experiment, we overlaid the closest ATP configuration from each state with the pose observed in the X-ray structure (Fig. 4a–c). While the generator for state #58 has the smallest RMSD to the X-ray structure, individual configurations belonging to state #148 (10^th most populated) and state #73 (1^st most populated) most closely match the X-ray structure with RMSDs of 2.7 Å and 2.8 Å, respectively. Lastly, given the close structural similarity between all of these states, it is not surprising that the transition probability matrix indicates that ATP quickly interchanges between states #73 and #148, and slower exchange occurs between states #58 and #73 as well as states #58 and #148.

Fig. 4. Comparison between experimental ATP structure and MSM configurations.

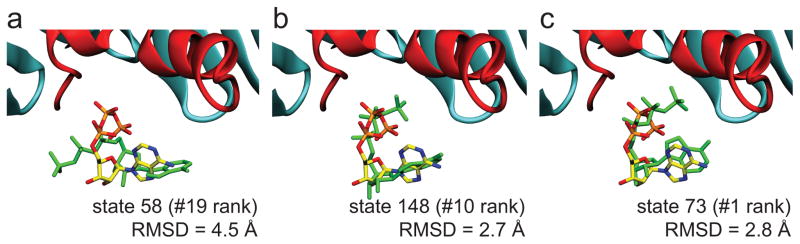
Overlay of the X-ray structure with ATP configurations taken from the top three most structurally similar MSM states: a, state 58 (19^th most populated), b, state 148 (10^th most populated) and c, state 73 (1^st most populated). In each panel, the ATP coloring scheme for the X-ray structure is as in Fig. 1, and each structure from the MSM is solid green. The RMSD value between the experimentally determined ATP molecule and the representative MSM configuration is shown in the corresponding panel.

Mean First Passage Times indicate an open channel

The ATP flux through the channel can be computed from the MSM, which allows us to compare our simulated translocation rate with the experimental value. To do this, we calculated the mean first passage time (MFPT) between states, the reciprocal of which is the associated reaction rate³⁶. The MFPT is determined from the transition probability matrix by solving the following set of linear equations (see reference 32 and Supplementary Note):

$$m_{i,j}=P_{i,j}\tau +\sum P_{i,k}(m_{k,j}+\tau ),$$

where m_i,j is the MFPT from state i to j. Our simulations predicted that the MFPT to move from the IMS to the cytoplasm is 32 μs (95% confidence interval 20–51 μs) under a 5 mM to 0 mM ATP gradient applied using the continuum coupling model, while the reverse MFPT, with bathing concentrations switched, is 15 μs (95% confidence interval 10–22 μs). The 95% confidence intervals were generated using a statistical bootstrapping procedure³⁷, as described in the Supplementary Note. While these rates should be identical based on symmetry considerations, the MSM boundaries do not extend fully into the bulk, giving rise to slight asymmetries. The average rate based on these MFPTs is ~49,000 ATP/sec, which is in excellent agreement with the experimental value of 50,000 ATP/sec recorded from Neurospora crassa VDAC channels recorded in high ATP concentrations and extrapolated down to 5 mM ATP^13,38. Thus, the ATP flux computed from the MSM again suggests that the crystallographic mVDAC1 structure represents the native, open conformation.

Additional uncertainties in the computed rates arise from how the MSM is constructed. MSMs can be sensitive to the choice of cluster size and lag time. When the clusters are too large, states are composed of heterogeneous configurations, which may interchange more slowly than the lag time leading to non-Markovian dynamics. On the other hand, if the cluster radius is too small, a large number of states are created, and it is difficult to adequately sample all of the interstate transition probabilities. To explore dependence on cluster size, we varied the cluster radius from 5 to 8 Å, and computed the corresponding MFPTs (Supplementary Fig. 6e). The IMS to cytoplasmic MFPTs ranged from 70 to 14 μs, while the reverse times ranged from 32 to 10 μs. For the reasons stated above, we believe that the values at 5 Å dramatically increase due to insufficient sampling, while we believe that the values at 8 Å are artificially low due to clustering of kinetically distinct configurations. Meanwhile, state splitting analysis indicated that over 90% of the states in our model at radius 6.5 Å exchange faster than the lag time (Supplementary Fig. 5), and removing these poorly connected states from our analysis did not affect the MFPTs. We also varied the lag time to determine its influence on the kinetics. If τ is too short, the system will display non-Markovian dynamics, whereas increasing τ requires simulation data to be discarded leading to poorer sampling. Our analysis revealed that the cytoplasm to IMS MFPT is remarkably constant over lag times from 5 to 30 ns, potentially due to good sampling of the bottleneck transition. However, the reverse time increases monotonically to 160 μs at τ equal 30 ns (Supplementary Fig. 6f), most likely due to reduced sampling, which diminishes the quality of the MSM.

ATP permeates VDAC via several distinct pathways

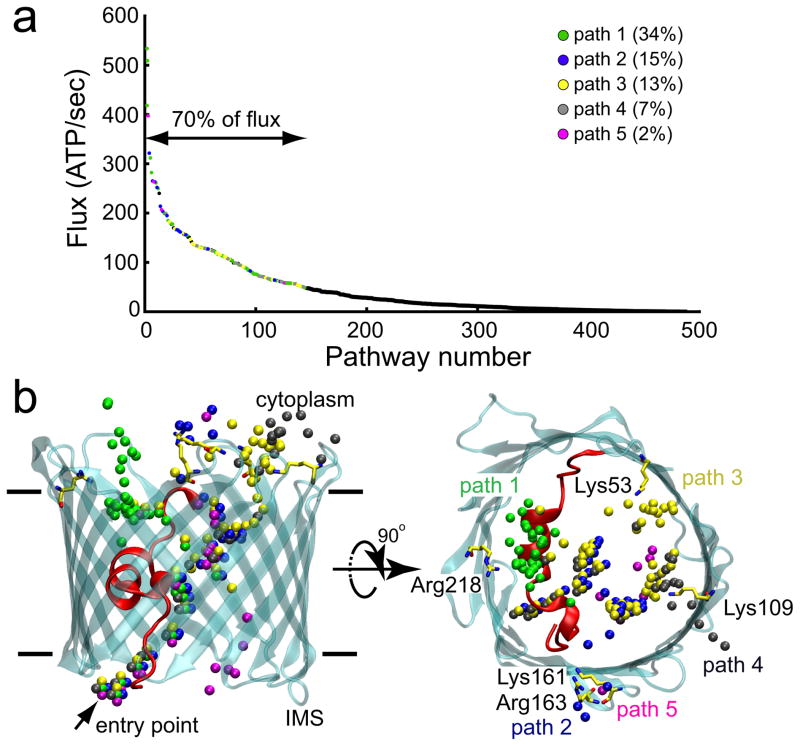
The mechanism that ATP uses to pass from the IMS to the cytoplasm was determined by applying transition path theory (TPT)^39–41 to the MSM (Fig. 5a). Our analysis shows that permeation occurs via a number of distinct – and often intersecting – routes (Fig. 5b) involving 18 of the 28 pore-facing, basic residues (Fig. 6a–c). The top 5 paths, which account for ~70% of the total flux, were visualized by plotting the coordinates of the γ-phosphate for each state comprising a single path (Fig. 5b). In all pathways, ATP enters the channel at a single entry point through simultaneous interactions with the protein N-terminus and Lys174 on the barrel wall. Along paths 1–4, Lys174 maintains an interaction with the γ-phosphate of ATP as the nucleotide is passed to Lys12 on the helix (Fig. 6a, b). ATP then interconverts among a series of stable states that involve interactions with helix-residues Lys12, Arg15 and Lys20 (Fig. 6a, b). Along path 1, which carries 32% of the flux, ATP is released from the helix and transferred to Arg218 before exiting into the cytosol. Along paths 2–4, the phosphate tail breaks free from the N-terminal helix and moves across the channel to associate with Lys113 and Lys115 on the barrel wall. From there, paths 2, 3 and 4 diverge as ATP jumps to different basic residues lining the outer mouth of the channel (Fig. 6b). Path 3 is similar to the trajectory reported by Noskov and coworkers based on their simulations of ATP in mVDAC1⁴². For paths 1–4, the rate-limiting step is dissociation of ATP from the α-helix. Along path 5, which is unique in that no interactions are seen between the ATP and the α-helix basic residues, translocation involves a sequential move along a series of lysine residues (Lys174, Lys119 and Lys96) on the β-barrel wall, opposite to the α-helix (Fig. 6c). The ATP then reaches Lys61, and the transition to Arg139, closer to the cytosol, is the rate-limiting step. From there, path 5 joins path 2 and exits via interactions with Lys161 and Arg163. Interestingly, while accounting for only 2% of the calculated flux, path 5 displays one of the highest ATP flux rates (Fig. 5a).

Fig. 5. A high ATP flux is achieved through multiple, distinct pathways.

a, Rank ordering of all distinct ATP flux pathways through the channel from the IMS to the cytoplasm as identified via transition path analysis. The highest flux pathways giving rise to 70% of the total flux were identified and grouped into 5 primary paths based on spatial analysis in panel b. Paths were numbered according to their probability and color coded. b, The γ-phosphate of ATP was plotted for all of the highest flux pathways identified in panel A. The arrow indicates the common entry point for all paths.

Fig. 6. ATP permeates via a network of basic residues.

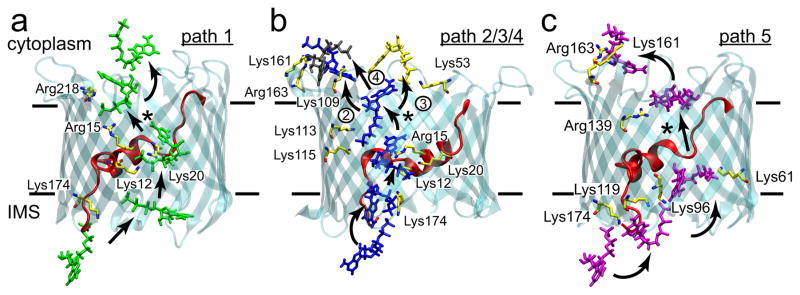
a, The highest probability pathway (34%) from the IMS to the cytoplasm moves up and over the N-terminal helix. In all panels, arrows indicate the direction of flow from the IMS to the cytosol, and * indicate the rate limiting steps. For paths 1–4, the rate-limiting step is release from the patch of basic residues on the helix (Lys12, Arg15 and Lys20). Solid lines delineate the membrane boundaries. b, Paths 2–4 (15%, 13% and 7% probability, respectively) share many states in common, except for the final state prior to escape to the cytoplasm. Numbers next to the final transition differentiate the paths. c, Path 5 (2% probability) is the least probable path, and it avoids the basic residues on the helix.

DISCUSSION

Our combined structural and computational studies indicate that ATP is loosely bound in the pore of mVDAC1, where it associates with basic residues on the N-terminal helix. The simulations reveal that the molecule is highly mobile in the pore, which corroborates the weak binding suggested by the crystal structure. Despite this high degree of mobility, the long simulations on Anton failed to reveal a full permeation event on the timescale of the simulations and instead the ATP remained affixed to the N-terminal helix. There was, nevertheless, very good agreement between the X-ray structure, Anton simulations and the MSM analysis concerning the most stable configuration in the pore (Fig. 4). This agreement highlights the usefulness of atomistic simulations, and of MSM models in particular, in identifying and ranking poses of small molecules in proteins, especially when interactions are too weak or too dynamic to easily be resolved via high-resolution structural techniques.

As mentioned already, a controversy still exists as to whether the published VDAC structures represent the native, open state of the protein. Our simulations may help to resolve this issue, as they faithfully predicted several biophysical properties of the open VDAC1 channel. First, the single channel ion conductance values computed from simulations in low salt and high salt were within the experimental range or 16–27% above them. Additionally, the drop in ion conductance resulting from the presence of ATP in the pore is in excellent agreement with experimental measurement²². Finally, our Anton simulations reproduced the increase in anion selectivity observed in experiments conducted in physiological salt concentrations³¹. Altogether, these observations support the hypothesis that the reported high-resolution structures of VDAC1^9–11 represent its native, open state. An important question is how the channel rearranges to close, and it has been hypothesized that this occurs via structural changes in the N-terminal helix^43–45. Interestingly, our nearly 60 μs of simulations indicate that the helix is quite stable in the crystallized conformation (data not shown), and this might be expected since channel closure occurs on the timescale of seconds³¹.

Our simulated ATP flux of 49,000 ATP/s closely matches the experimental estimates^13,38, but our parameter analysis based on results in Supplementary Fig. 6 places relatively conservative bounds on the rate between 100,000 and 6,000 ATP/s. Therefore, we caution against over interpreting the close correspondence of our prediction to experiment especially given that there are additional sources of error stemming from both computational and experimental considerations. As with all simulations of rare events, finite sampling may introduce error into the calculated quantities. There are also errors associated with molecular force fields, and it has long been appreciated that charge-charge interactions are overly stabilized in several force fields^46–48, including the one used here⁴⁹. We believe that a reduction in electrostatic interactions between the protein and ATP would reduce the dwell time in the channel potentially resulting in faster permeation rates. With regard to experimental uncertainties, no flux studies have been carried out specifically in 5 mM ATP. The seminal work by Rostovtseva and Colombini calculated rates at 50 mM ATP and higher^13,37, and then interpolate back to 5 mM. Additionally, these experiments were carried out on mixtures of VDAC subtypes. Future studies performed on purified channels of a single subtype carried out in 5 mM ATP are needed to provide a more quantitative comparison between theory and experiment.

More work must be done to determine the role of divalent cations, specifically Mg²⁺, in the permeation process. It has been suggested that ATP permeates VDAC in the −4 charge state^13,22 based on the observation that ATP flux is smaller than citrate³⁻ flux, which in turn is smaller than the flux of succinate^{2− 13}. Current noise analysis has also shown that small molecule binding to VDAC increases with the charge on the molecule⁵⁰, and a recent NMR study concluded that ATP⁴⁻ binds more strongly in the absence of Mg^{2+ 24}. This later observation may explain why we fail to observe Mg²⁺ bound to ATP in the structure. However, in our simulations we never observe Mg²⁺ dissociate or change its coordination state with ATP, which implies that ATP permeates with a net −2 charge. Under physiological conditions, the majority of ATP is in complex with Mg^{2+ 51}, and since Mg²⁺ also reduces ATP’s binding affinity to the channel, it has been suggested that transport through VDAC occurs primarily in the Mg-ATP state²⁴. Additional simulations in the absence of Mg²⁺ are needed to test this hypothesis.

From a more general point of view, our work demonstrates that the MSM approach to small molecule transport bears the potential to overcome the current limitations of MD simulations in terms of providing a statistically valid description of slow processes. Here, we illuminated how ATP passes through VDAC by ‘hopping’ along a series of weak binding sites (composite movies of full crossing events via paths 1 and 2 are provided as Supplementary Movies 6 and 7, respectively). The MSM revealed the myriad of pathways available for ATP permeation, and it provided their relative probabilities along with the occupancy of distinct ATP conformations in the channel. Such a rich statistical description is generally difficult to attain with individual, long MD simulations, but our work demonstrates that it is tractable using MSMs. The use of MSM generated steady state distributions, along with transition pathway analysis, thus provides a novel framework for studying ligand binding to membrane proteins, as well as ion or small molecule permeation through channels and transporters.

Online Methods

VDAC production and purification

Protein production and purification were performed largely as described previously¹⁰. In short, a histidine-tagged mVDAC1 was expressed in Escherichia coli M15 cells. Inclusion bodies were isolated, solubilized and purified on a Talon affinity column. mVDAC1 was subsequently refolded and further purified to homogeneity using a Superdex 75 size-exclusion column. The purified mVDAC1 sample was concentrated to 15 mg/ml in a solution containing 20 mM Tris HCl (pH 8.0), 50 mM NaCl and 0.1% LDAO (Protein Solution).

Crystallization and diffraction data collection

mVDAC1 crystals were formed in bicelles using the hanging-drop vapor diffusion technique by mixing the Protein Solution with a 35% Bicelle Solution in 4:1 ratio, respectively. The final concentration of the sample used for crystallization was 12 mg/ml in 7% bicelles. The Protein/Bicelle Solution was mixed at a 1:1 ratio with mother liquor (18–20% MPD, 0.1 M Tris HCl (pH 8.5) and 10% PEG400) and set up over the mother liquor to allow for equilibration at 20° C. Crystals appeared after 3–5 days.

The resulting crystals were soaked in a solution containing all constituents of the Protein and mother liquor solutions with the addition of 50 mM ATP and 50 mM MgCl₂. The crystals were soaked for 1 hour and subsequently transferred to a fresh solution containing the same components supplemented with 18% glycerol for 10 seconds and rapidly flash-froze in liquid nitrogen.

mVDAC1 crystal diffract X-rays up to 2.3 Å. One hundred eighty frames of data were collected at the Advanced Light Source (Berkeley, Ca) at beamline 5.0.2 using an oscillation angle of 1°, T = 100 K and λ = 1.00 Å.

Structure refinement

ATP-soaked-mVDAC1 diffraction data were integrated and scaled between 19.51 and 2.3 Å using XDS and XSCALE⁵². PHENIX⁵³ was used for a rigid body refinement against the previously solved mVDAC1 structure (Protein Data Bank ID: 3EMN)¹⁰, devoid of water and lipid. No prominent positive density peaks that could be interpreted as ATP were observed in the pore of ATP-soaked-mVDAC1 in the initial Fo-Fc map; however, the 2Fo-Fc map clearly indicated the presence of extra density in the vicinity of the internal α-helix. Structural refinement of the model was carried out using PHENIX followed by iterative cycles of model building with Coot⁵⁴. After thoroughly refining the polypeptide structure, CNS was used to calculate a Fourier difference map (Fo^ATP-Fo^Native) between the structure factor amplitudes of the ATP-soaked-mVDAC1 data set and those of a native mVDAC1 data set. The structure-factor amplitude-differences were q-weighted to improve the signal-to-noise ratios of the Fourier difference maps^55,56 (Supplementary Fig. 1a). The two most prominent peaks of the (Fo^ATP-Fo^Native) map (5.1 and 5.7 σ) were found in the mVDAC1 pore, overlaying with the previously mentioned 2Fo-Fc peaks. Neither map provided a clear assignment for positioning ATP; therefore, a tentative ATP molecule was placed into the Fo-Fc map (displayed at 2.5 σ) with its atom occupancies set to zero. Subsequently, a solvent-annealed (annealing to 550 K, cooling steps of 25 K; 100 final steps of conjugate gradient minimization) omit map was calculated using CNS⁵⁷ (Supplementary Fig. 1b). The resulting map was interpretable and allowed for the fitting of an ATP molecule in the center of the pore. Based on this map, two ATP orientations were possible, and we refined each one of the orientations independently. The ATP orientation that was subsequently deposited and reported herein was chosen because it had a lower R_free, a higher real space map correlation of the ATP molecule, and an increased number of contacts between the ATP and the protein. In the refined model, two atoms from the ATP molecule (O2γ and O1γ) direct contact protein atoms Lys12 Nζ and Lys20 Nζ at 2.3 and 3.3 Å, respectively (Fig. 1). The final ATP real space map correlation is 0.8, and the average B-factor is 214.1 Ų (Supplementary Fig. 1c). These values are consistent with weak binding between the ATP molecule and VDAC, and suggest that ATP only binds transiently while passing through the channel.

Overall data collection and refinement statistics are listed in Table 1 with 95.8% of the final backbone dihedral angles in the Ramachandran favored region and only 0.7% in the Ramachandran outlier region. Poor density was observed for residue Asn269 on the loop between β-strands 18 and 19.

Simulation setup

Models of VDAC were generated using the crystal structure of mVDAC1 (Protein Data Bank ID: 3EMN)¹⁰. The channel was centered at the origin, and the pore axis was aligned along the z axis placing both N- and C-termini in the lower half of the simulation cell (z < 0). All ionizable groups were left in the dominant protonation state at pH 7.0, except residue Glu73, which was protonated since it faces lipid. A pre-refined structure of the ATP molecule from the co-crystal was coordinated with a Mg²⁺ ion and used to initiate molecular dynamics simulations. The ion was coordinate to the β- and γ-phosphate oxygen atoms of the ATP in accordance with experiments on ATP in solution⁵⁸ and previous simulations⁵⁹. As described in Supplementary Notes, the pre-refined ATP structure was placed in different regions of the channel to initiate additional MD simulations for Markov State Model construction. To do this, the ATP-Mg²⁺ configuration was rigidly translated and/or rotated in the simulation box. Each model was then embedded in a DMPC lipid bilayer and solvated with a neutralizing quantity of KCl (140–150 mM depending on the exact setup) using the CHARMM-GUI Membrane Builder⁶⁰. A hexagonal unit cell was employed which consisted of 36,000 atoms. Simulations employed the CHARMM additive force field C22 parameter set⁶¹ with CMAP corrections⁶² for the protein and the C36 parameter set for the lipids⁶³. Parameters for the ATP were taken from the nucleic acids section of the C27 parameter set^64,65, and water molecules were represented by the TIP3P model⁶⁶.

Molecular dynamics simulation details

Molecular dynamics simulations were performed on two different computational platforms. Four hundred and fifty three simulations ranging in length from 40–130 ns were used to construct a Markov State Model of ATP permeation through VDAC using resources at the Texas Advanced Computing Center. Additionally, a number of long trajectories ranging from 600–5000 ns were generated using the Anton supercomputer⁶⁷ at the Pittsburgh Supercomputing Center (Supplementary Table 1).

All of the simulations reported here share a common equilibration protocol, which was carried out using NAMD 2.7⁶⁸. First, a 2000 step energy minimization was performed using the conjugate gradient algorithm during which all non-hydrogen atoms of the protein and ATP-Mg²⁺ were harmonically restrained to the pre-equilibration model coordinates (k = 5 kcal/mol/Ų). The system was then gradually heated to 303 K over 0.3 ns with the same set of external restraints used during the minimization. After thermalizing the system, the harmonic restraints were gradually removed over 2 ns. During each of these steps, an external force was applied to all water molecules outside of the hydrated channel to prevent them from entering the protein-membrane interface or penetrating the hydrophobic core of the membrane.

For equilibration and production runs, the temperature was controlled through Langevin dynamics with a damping coefficient of 5 ps⁻¹. A constant pressure of 1 atm was maintained with a Nosé-Hoover Langevin piston barostat with a piston period and decay timescale of 200 fs and 100 fs, respectively. The three orthogonal dimensions of the periodic cell were allowed to fluctuate independently during the simulation. The dynamics were propagated with a multiple time-stepping algorithm in which bonded and short-range non-bonded interactions were evaluated every 2 fs, and long-range electrostatics interactions every 4 fs. Short-range non-bonded interactions were truncated smoothly with a spherical cutoff radius of 10 Å and a switching distance of 8 Å. Long-range electrostatic interactions were calculated using the particle mesh Ewald (PME) method, with a grid density of approximately 1 ų. All hydrogen atom-heavy atom bond lengths were constrained using the SHAKE algorithm⁶⁹. Subsequent production simulations used to construct the MSM employed the same parameters, but without biasing forces.

Simulations performed on Anton were prepared as above except using a larger rectangular box containing 57,000 atoms. The equilibration protocol above was then extended 20 ns in NAMD followed by an additional 40 ns using the simulation package Desmond version 2.2.9.1⁷⁰. In Desmond, the dynamics were propagated with constant temperature (312 K) and pressure (1 atm) using the Martyna-Tobias-Klein (MTK) method⁷¹, with a coupling constant of 2.0 ps⁻¹ for the thermostat and barostat and a 2 fs time step. The barostat was isotropic in x and y, but independent in z. Hydrogen positions were constrained using the M-SHAKE algorithm with a tolerance of 1.0 × 10⁻⁸. Long-range electrostatics were computed using the PME method with 90 Fourier mesh points along each cell axis. Non-bonded and electrostatic interactions were cutoff at a radius of 10 Å.

Production simulations on Anton were initiated from the final snapshot of the corresponding equilibration runs on Desmond. A multi-timestep integration scheme was used to propagate the dynamics based on a Nosé-Hoover themostat and the MTK method to maintain constant pressure. Long-range electrostatic interactions were calculated using the k-space Gaussian Split Ewald method⁷². All simulations involving a membrane potential were carried out as in reference 73. Briefly, a membrane potential, V, across the lipid bilayer was imposed by applying a force, F_i = q_iE, perpendicular to the plane of the membrane to every atom i, proportional to its partial charge q_i. The constant electric field, E, was chosen to give the desired membrane potential according to: V = EL, where L is the equilibrium, membrane width.

Details on Markov state modeling can be found in the Supplementary Note.

Current-voltage and selectivity analysis

The selectivity and conductance of mVDAC1 were determined by calculating the current-voltage relationship for the channel under varying applied electric fields. We determined the cumulative number of K⁺ and Cl⁻ permeation events from the trajectories generated on Anton, as well as an additional data set generated on Stampede, but distinct from the trajectories used to build the MSM of ATP permeation. The Anton simulations were carried out in 142 mM KCl, and the Stampede simulations were carried out in ~0.9 M KCl. A particular ion was required to move from one bulk region of the simulation box to the other, through the channel to count as a complete permeation event. At each voltage, the current contributed by each species of mobile ion was determined via a linear regression of the net ion crossing events as a function of the simulation time. The total current was simply the sum of the net K⁺ current minus the net Cl⁻ current. The raw conductance was taken as the slope of the total least-square linear regression to the individual current values plotted at each voltage⁷⁴, and these fits are shown in Fig. 2a–c. The same fitting procedure was used to determine the slopes of the K⁺ and Cl⁻ currents, and the selectivity was determined from the ratio of the fitted slopes.

The final reported channel conductance for each system was then determined by multiplying the raw conductance values (0.94, 1.61, and 2.77 nS for Fig. 2 panels a, b and c, respectively) by a correction factor that accounted for simulated errors in the ion diffusion coefficient values. While the diffusion coefficients of Cl⁻ and K⁺ calculated from our long simulations on the Anton supercomputer (1.97 × 10⁻⁵ cm²/s and 1.63 × 10⁻⁵ cm²/s, respectively) are in good agreement with experimental values (2.02 × 10⁻⁵ cm²/s and 1.96 × 10⁻⁵ cm²/s, respectively⁷⁵), values obtained for our simulations run on Stampede using NAMD are notably lower. In the simulations lacking ATP, the diffusion constants were 1.07 × 10⁻⁵ cm²/s and 0.70 × 10⁻⁵ cm²/s for Cl⁻ and K⁺, respectively. The discrepancy most likely arises from our use of different temperature coupling schemes and their parameterization employed by NAMD and Anton. Temperature coupling protocols can perturb the kinetics of a molecular dynamics simulation in a systematic way, and Langevin thermostats, like the one used in the NAMD simulations, can non-trivially slow the diffusion of mobile species⁷⁶. Since the majority of the current is carried by the Cl⁻ ions, we correct for this effect by scaling all of our calculated conductance values by the ratio of the experimental to simulated Cl⁻ diffusion coefficients. Specifically, conductance values from Anton simulations are scaled by 2.02/1.97, and all conductance values from Stampede simulations are scaled by 2.02/1.07, the value determined in ATP free conditions.