Pooling Designs for Outcomes under a Gaussian Random Effects Model

Summary

Due to the rising cost of laboratory assays, it has become increasingly common in epidemiological studies to pool biospecimens. This is particularly true in longitudinal studies, where the cost of performing multiple assays over time can be prohibitive. In this article, we consider the problem of estimating the parameters of a Gaussian random effects model when the repeated outcome is subject to pooling. We consider different pooling designs for the efficient maximum likelihood estimation of variance components, with particular attention to estimating the intraclass correlation coefficient. We evaluate the efficiencies of different pooling design strategies using analytic and simulation study results. We examine the robustness of the designs to skewed distributions and consider unbalanced designs. The design methodology is illustrated with a longitudinal study of premenopausal women focusing on assessing the reproducibility of F2-isoprostane, a biomarker of oxidative stress, over the menstrual cycle.

1. Introduction

Estimating the sources of variation in new biomarkers is an important initial step in early biomarker development. For example, estimating the between- and within-subject variations as well as the intraclass correlation coefficient (ICC) is especially important for designing future studies. This is important for a number of reasons. First, biomarkers with similar biological function with the highest ICC can be considered the most reproducible and therefore can then be selected as important markers for future studies. Second, estimates of the ICC can be used for designing studies where the biomarker is an outcome measure. Specifically, the ICC will dictate the trade-off in efficiency between taking an increased number of individuals or an increased number of repeated measurements. Third, for risk modeling when the biomarker is a measure of exposure, estimates of the ICC will aid investigators in correcting for measurement error (Fleiss, 1986).

The usual designs for estimating the ICC require repeated measurements taken on multiple subjects. However, resources to conduct reproducibility studies are limited given that such studies are often considered ancillary to the major research objectives. To reduce the cost of these reproducibility studies, pooling multiple samples either across individuals or across time may be advantageous. This article investigates various pooling strategies for estimating the variance components as well as the ICC under a Gaussian random effects model. These designs involve combining multiple samples across either time or individuals and performing the assays on the resulting pooled samples.

Others have investigated the utility of pooling designs in various situations. The statistical implications of pooling measurements across subjects have been considered for the problem of efficient identification of rare positive cases (blood testing problem) (Dorfman, 1943; Sterrett, 1957), for evaluation of diagnostic testing (Faraggi, Reiser, and Schisterman, 2003; Mumford et al., 2006; Vexler, Schisterman, and Liu, 2008), for a longitudinal model (Albert and Shih, 2011), for detecting random effects model misspecification via coarsened data (Huang, 2011), and for logistic regression (Weinberg and Umbach, 1999; Vansteelandt, Goetghebeur, and Verstraeten, 2000; Chen, Tebbs, and Bilder, 2009; Zhang and Albert, 2011). Pooling in microarray experiments has been discussed by Kendziorski et al. (2003) and Shih et al. (2004). Schisterman et al. (2010b) proposed a hybrid pooled–unpooled design to maximize efficiency while minimizing cost in a univariate biomarker setting. In this article, we investigate various pooling strategies for estimating the variance components under a Gaussian random effects model.

This article proposes design strategies for pooling in repeated measures analysis. In Section 2, we describe a motivating example where investigators were interested in assessing the reproducibility of F2-isoprostane, a measure of oxidative stress, to design future studies where this biomarker can be used as an outcome or as a measure of exposure. In Section 3, we present the model and review methods of parameter estimation for the Gaussian random effects model. In Section 4, we describe and compare different pooling strategies for balanced designs where we pool over individuals, pool over repeated time points, and pool over individuals and time points. In Section 5, we investigate the effect of imbalance on the design results developed for balanced designs. In Section 6, with extensive simulations we investigate the sensitivity of our results to the normal assumptions in both the between- and within-subject variations. In Section 7, we illustrate the design methodology by analyzing the F2-isoprostane data and show the efficiencies of different pooling design strategies for estimating the ICC in this application. In Section 8, we provide a summary and discussion. All proofs and additional relevant materials are presented in the online Supplementary Web Appendix.

2. A Motivating Example: BioCycle Study

F2-isoprostane is a biomarker that measures oxidative stress, an important measure of both exposure and disease outcome. F2-isoprostane levels may be a surrogate for outcome of cardiovascular disease, while F2-isoprostane may also be a marker for exposure in determining the risk of cardiovascular disease (Roest et al., 2008). For a number of reasons, understanding the reproducibility of measures of oxidative stress estimated by the ICC is important for designing future studies where this measure can be used either as an outcome or as a measure of exposure. The BioCycle Study was a longitudinal study designed to assess the effects of endogenous hormones (i.e., estrogen and progesterone) on biomarkers of oxidative stress and antioxidant status during the menstrual cycle. Women aged 18–44 years from western New York State were followed prospectively during 2005–2007. One objective of the BioCycle Study was to assess the reproducibility of F2-isoprostane over the menstrual cycle. However, the cost of the F2-isoprostane assay is about $130, making this reproducibility assessment an expensive proposition that cannot easily be repeated in the future. The BioCycle Study design involved measuring a series of oxidative stress biomarkers (including F2-isoprostane) at eight times over two menstrual cycles among 259 women (Wactawski-Wende et al., 2009; Schisterman et al., 2010a). If our goal were simply to estimate reproducibility of oxidative stress biomarkers, the cost of this design would have been prohibitive. Designs where we pool samples either across time points or over individuals may be cost-effective alternatives to analyzing all repeated assays or to analyzing a random sample of measurements on individuals.

The F2-isoprostane measurements in the BioCycle data are used to illustrate the different designs in this article. In the next section, we describe the model for reproducibility that we will be considering.

3. Random Effects Model

In this section we present results for a Gaussian random effects model, where we do not pool samples. Let Y_ij denote a continuous random variable with common mean μ, where i = 1, …, l indexes individuals, and j = 1, …, n indexes repeated measurements on a given individual. When we do not pool, each measurement Y_ij is obtained from a separate assay.

We assume the following random effects model

$$Y_{\mathit{\text{ij}}}=\mu +A_i+e_{\mathit{\text{ij}}},$$ (1)

where individual random effects are denoted by A_i, the random error is denoted by e_ij, and A_i and e_ij are assumed to be Gaussian, each with mean zero and variances ${\sigma }_A^2$ and ${\sigma }_e^2$, respectively. The random variables A_i and e_ij reflect the between- and within-subject variations, respectively, and are assumed to be independent from each other. These assumptions lead to Cov(Y_ij, Y_i′j′) = 0 if i ≠ i′ and $\text{Cov}(Y_{\mathit{\text{ij}}},Y_{\mathit{\text{ij}}\text{'}})={\sigma }_A^2$ if j ≠ j′ and $Var(Y_{\mathit{\text{ij}}})={\sigma }_A^2+{\sigma }_e^2$. Model (1) is a standard random effects model which can be used to analyze the reproducibility of F2-isoprostane in the BioCycle Study.

The popular measure of reproducibility of the within-subject measurements is the ICC, defined as $\mathrm{\gamma }=\frac{{\sigma }_A^2}{{\sigma }_A^2+{\sigma }_e^2}$. This is the correlation coefficient between two measurements from the same individual. Values of γ near one indicate higher reproducibility among measurements from the same individual, and values near zero indicate low reproducibility.

Mean and variance component estimation as well as random effects prediction for model (1) can be found in Searle, Casella, and McCulloch (1992) and in the Supplementary Web Appendix to this article. The asymptotic (l → ∞) variance matrix for the maximum likelihood estimation (MLE) of the variance components can be expressed as

$$\begin{array}{l}{Var}_F\left[{\left({\stackrel{\sim }{\sigma }}_e^2,{\stackrel{\sim }{\sigma }}_A^2\right)}^{\prime }\right]\\ \simeq 2{\sigma }_e^4\left(\begin{array}{cc}\frac{1}{l(n-1)}& \frac{-1}{ln(n-1)}\\ \frac{-1}{ln(n-1)}& \frac{1}{n^2}\left(\frac{{\tau }^4/{\sigma }_e^4}{l}+\frac{1}{l(n-1)}\right)\end{array}\right),\end{array}$$ (2)

where ${\tau }^2={\sigma }_e^2+n{\sigma }_A^2$. The subscript F in the equation above denotes a design where a separate assay is performed on every repeated measurement. Designs of this type will be called Design F and will be used as a benchmark for comparisons of pooling designs that we will develop in the next section.

Define $\stackrel{\sim }{\mathrm{\gamma }}=\frac{{\stackrel{\sim }{\sigma }}_A^2}{{\stackrel{\sim }{\sigma }}_A^2+{\stackrel{\sim }{\sigma }}_e^2}$ as the estimated ICC. Because ${\stackrel{\sim }{\sigma }}_A^2$ and ${\stackrel{\sim }{\sigma }}_e^2$ are MLE of ${\sigma }_A^2$ and ${\sigma }_e^2$, it follows from the in variance property of maximum likelihood that γ̃ is the maximum likelihood estimator of γ. The asymptotic variance of γ̃ can be obtained from equation (2) using the Delta method (see Fisher, 1925; Donner, 1986) for the details):

$${Var}_F(\stackrel{\sim }{\mathrm{\gamma }})\simeq \frac{2{(1-\mathrm{\gamma })}^2{[1+(n-1)\mathrm{\gamma }]}^2}{n(n-1)l}.$$ (3)

The results in this section correspond to the situation where sample taken from the same individual at different times are analyzed with separate assays. In the next section, we consider strategies where we pool samples across individuals or repeated samples to reduce the total number of assays needed in the study.

4. Pooling Strategies

In many situations, funding is limited to covering only the cost of M assays, M < ln. Recall that l is the number of individuals and n is the number of repeated measurements. We will compare different designs to obtain the efficient MLE for ICC γ. These designs involve combining multiple samples across either time or individuals and performing the assays on the resulting pooled samples. To reduce ln assays to M assays, we will use pooling. In any of the pooling strategies that we are considering, we will not allow the pooling of samples more than once. For example, we do not allow for designs where a biological sample for a given individual at a given time point is in multiple pools.

We begin with a discussion about the optimal pooling design. From model (1), it follows that Y ∼ MVN(μ1_N, V), where Y = (Y₁₁,…, Y_ln)′, 1_N = (1, 1,…,1)′, N = ln, and V is a block-diagonal matrix with l identical matrices of the form $V_0={\sigma }_e^2{I}_n+{\sigma }_A^2{J}_n$ (I_n = diag(1_n), $J_n=1_n{1}_n^{\text{'}}$) in the diagonal. Pooling designs can be specified with a transformation matrix Q that operates on the original data Y and results in data from a pooled sample Y*. The transformation for a general Q can be written as

$$Y\ast =\mathit{\text{QY}}\sim \mathit{\text{MVN}}\left(Q\mu 1_N=\mu 1_M,\mathit{\text{QV}}{Q}^{\prime }={\sum }_Q\left({\sigma }_A^2,{\sigma }_e^2\right)\equiv V\ast \right).$$ (4)

The objective in obtaining an optimal design is to find a transformation Q such that the asymptotic (l → ∞) variance of the MLE of γ̃ is minimized. It is important to note that under our pooling mechanism V* is guaranteed to be full rank.

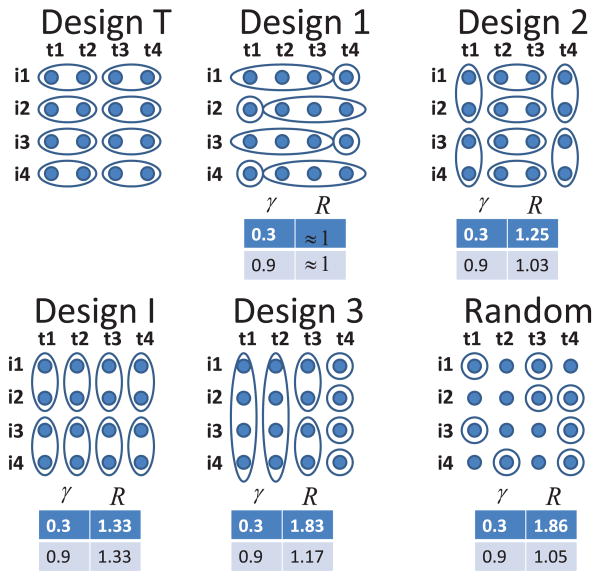
Generally it is difficult to obtain the optimal design for variance estimation. However, for some important design classes it is possible to express the asymptotic variances of γ, ${\sigma }_A^2$ and ${\sigma }_e^2$ in closed form. To do this, we will distinguish between two types of designs, as follows. Symmetric designs are designs in which we pool all data in equivalently sized groups only across time (Design T) or only across individuals (Design I). Figure 1 provides an example of both a T design and an I design. In this example, for Design T we pool every two measurements over time, while for Design I we pool every two measurements over individuals. Nonsymmetric pooling designs are ones for which pool sizes are not equal or where pooling may be done across both individuals and time points. Designs 1, 2, and 3 in Figure 1 are examples of such designs.

Figure 1.

Nonsymmetric pooling designs (Designs 1, 2, 3) versus symmetric designs (Designs T,I), and random sample, where i1, i2, i3, i4 denotes the individuals and t1, t2, t3, t4 denotes the repeated measurements. R = Var_d(γ̃)/Var_T (γ̃), d= Design d. We evaluate designs with eight assays. In the random design we randomly choose eight (marked) points. (This figure appears in color in the electronic version of this article.)

In the following example we demonstrate a nonsymmetric pooling strategy using the transformation Y* = QY with M = 4 (total assays), l = 2 (individuals), and n = 3 (repeated measurements). A design where we pool the last two measurements of each individual over time can be expressed as

$$\begin{array}{cc}Y\ast & =\mathit{\text{QY}}=\left(\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 1/2& 1/2& 0& 0& 0\\ 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 1/2& 1/2\end{array}\right)\left(\begin{array}{c}{Y}_{11}\\ Y_{12}\\ Y_{13}\\ Y_{21}\\ Y_{22}\\ Y_{23}\end{array}\right)\\ & =\left(\begin{array}{c}{Y}_{11}\\ (Y_{12}+Y_{13})/2\\ Y_{21}\\ (Y_{22}+Y_{23})/2\end{array}\right).\end{array}$$

We discuss both symmetric and nonsymmetric designs in turn.

4.1 Symmetric Pooling Design

Pooling across individuals, Design I

Suppose that l = P_Ik and we combine samples into P_I pools, with each pool containing k samples (e.g., Design I in Figure 1 with l = 4, P_I = 2, and k = 2). In the terms of equation (4), we have $Y\ast ={(Y_1^{\ast },\dots ,Y_{\mathit{\text{PI}}}^{\ast })}^{\prime }$, where $Y_p^{\ast }={(Y_{p1}^{\ast },\dots ,Y_{\mathit{\text{pn}}}^{\ast })}^{\prime }$ and $Y_{\mathit{\text{pj}}}^{\ast }=\frac{1}{k}{\sum }_{i=(p-1)k+1}^{\mathit{\text{pk}}}{Y}_{\mathit{\text{ij}}}$ for p = 1, …, P_I, j = 1, …, n. In this case, model (1) becomes: $Y_{\mathit{\text{pj}}}^{\ast }=\mu +A_p+e_{\mathit{\text{pj}}}$, with $A_p\sim N(0,{\sigma }_A^2/k),e_{\mathit{\text{pj}}}\sim N(0,{\sigma }^2/k)$, e_pj ∼ N(0, σ²/k), where p = 1, …, P_I and j = 1, …, n.

In Result 1, we derive the asymptotic (l → ∞) covariance matrix for the MLE of the variance components under Design I.

Result 1.

$$\begin{array}{l}{Var}_I\left[{\left({\stackrel{\sim }{\sigma }}_e^2,{\stackrel{\sim }{\sigma }}_A^2\right)}^{\prime }\right]\\ \simeq 2{\sigma }_e^4\left(\begin{array}{cc}\frac{1}{P_I(n-1)}& \frac{-1}{P_{I}n(n-1)}\\ \frac{-1}{P_{I}n(n-1)}& \frac{1}{n^2}\left(\frac{{\tau }^4/{\sigma }_e^4}{P_I}+\frac{1}{P_I(n-1)}\right)\end{array}\right)\end{array}$$ (5)

and

$${Var}_I(\stackrel{\sim }{\mathrm{\gamma }})\simeq \frac{2{(1-\mathrm{\gamma })}^2{[1+(n-1)\mathrm{\gamma }]}^2}{n(n-1)P_I}.$$ (6)

The proof is given in the Supplementary Web Appendix.

Using equations (3) and (6), the efficiency of Design F relative to Design I is $\frac{{Var}_I(\stackrel{\sim }{\mathrm{\gamma }})}{{Var}_F(\stackrel{\sim }{\mathrm{\gamma }})}=\frac{l}{P_I}=k$. Therefore, the efficiency of Design I (i.e., we pool l individuals to P_I groups of size k) is the same as the efficiency of an unpooled design (Design F) with P_I individuals. This result also applies to estimating ${\sigma }_e^2$ and ${\sigma }_A^2$.

Pooling across time, Design T

Suppose that n = P_Tk and we pool across time into P_T pools, each one of size k (e.g., Design T in Figure 1 with l = 4, P_T = 2, and k = 2). In terms of equation (4) we have $Y\ast ={\left(Y_1^{\ast },\dots ,Y_l^{\ast }\right)}^{\prime }$, where $Y_i^{\ast }={\left(Y_{i1}^{\ast },\dots ,Y_{{\mathit{\text{iP}}}_T}^{\ast }\right)}^{\prime }$ and $Y_{\mathit{\text{ip}}}^{\ast }=\frac{1}{k}{\sum }_{j=(p-1)k+1}^{\mathit{\text{pk}}}{Y}_{\mathit{\text{ij}}}$ for p = 1, …, P_T, i = 1,…,l. In this case, model (1) becomes: $Y_{\mathit{\text{ip}}}^{\ast }=\mu +A_i+e_{\mathit{\text{ip}}}$, with $A_i\sim N(0,{\sigma }_A^2),e_{ip}\sim N(0,{\sigma }_e^2/k)$, where p = 1,…, P_T and i = 1,…, l.

In Result 2, we derive the asymptotic (l → ∞) covariance matrix for the MLE of the variance components under pooling across time (Design T).

Result 2.

$$\begin{array}{l}{Var}_T\left[{\left({\stackrel{\sim }{\sigma }}_e^2,{\stackrel{\sim }{\sigma }}_A^2\right)}^{\prime }\right]\\ \simeq 2{\sigma }_e^4\left(\begin{array}{cc}\frac{1}{l(P_T-1)}& \frac{-1}{ln(P_T-1)}\\ \frac{-1}{ln(P_T-1)}& \frac{1}{n^2}\left(\frac{{\tau }^4/{\sigma }^4}{l}+\frac{1}{l(P_T-1)}\right)\end{array}\right)\end{array}$$ (7)

and

$${Var}_T(\stackrel{\sim }{\mathrm{\gamma }})\simeq \frac{2{(1-\mathrm{\gamma })}^2{[1+(n-1)\mathrm{\gamma }]}^2}{n(n-1)l}\frac{P_T/(P_T-1)}{n/(n-1)}.$$ (8)

The proof is given in the Supplementary Web Appendix.

Using equations (3) and (8), the efficiency of Design F relative to Design T is

$$1<\frac{{Var}_T\stackrel{\sim }{(\mathrm{\gamma })}}{{Var}_F\stackrel{\sim }{(\mathrm{\gamma })}}=\frac{P_T/(P_T-1)}{n/(n-1)}<2.$$ (9)

We can see from equation (9) that the ratio of asymptotic variance of γ̃ for Design T versus Design F does not depend on γ and that the ratio is bounded above by two. We can also see from equation (9) that the efficiency of the T design is minimized when the number of repeated measurements is large and for each individual the measurements are separated into two pools. Overall, compared with Design I, Design T is an efficient alternative to Design F for ICC estimation, because the variance ratio is bounded regardless of pool size for Design T but is proportional to pool size for Design I.

Result 2 has important design implications for estimating the individual variance components. Combining equations (2) and (7), we derive the following results. First, $\frac{{Var}_T({\stackrel{\sim }{\sigma }}_e^2)}{{Var}_F({\stackrel{\sim }{\sigma }}_e^2)}=\frac{n-1}{P_T-1}>\frac{n}{P_T}=k$. Hence, we can conclude that for estimating ${\sigma }_e^2$, the loss of precision is at least proportional to the size the pooled group. Second, $\frac{{Var}_T({\stackrel{\sim }{\sigma }}_A^2)}{{Var}_F({\stackrel{\sim }{\sigma }}_A^2)}=\frac{{(1+\mathrm{\gamma }(n-1))}^2+\frac{{(1-\mathrm{\gamma })}^2}{P-1}}{{(1+\mathrm{\gamma }(n-1))}^2+\frac{{(1-\mathrm{\gamma })}^2}{n-1}}\equiv f(\mathrm{\gamma })$, and it is easy to see that the function f(γ) is a convex decreasing function of γ ∈ [0,1], with $f(0)=\frac{P_T/(P_T-1)}{n/(n-1)}<2$ and f(1) = 1. Hence, we can conclude that we lose less information as γ becomes larger, and in the worst case the variability of ${\stackrel{\sim }{\sigma }}_A^2$ with Design T is less than twice that with Design F.

Alternatively, we can find the number of repeated measurements in a nonpooled design, which would result in an asymptotic variance equivalent to that of a particular Design T. Specifically, we have to find x (number of nonpooled repeated measurements), which solves the following equation

$$\begin{array}{l}{Var}_F(\stackrel{\sim }{\mathrm{\gamma }})\simeq \frac{2{(1-\mathrm{\gamma })}^2{[1+(x-1)\mathrm{\gamma }]}^2}{x(x-1)l}\\ ={Var}_T(\stackrel{\sim }{\mathrm{\gamma }})\simeq \frac{2{(1-\mathrm{\gamma })}^2{[1+(n-1)\mathrm{\gamma }]}^2}{n(n-1)l}\frac{P_T/(P_T-1)}{n(n-1)}.\end{array}$$ (10)

Result 3. Equation (10) has a single positive solution, which is

$$\begin{array}{lll}x\hfill & =\hfill & \frac{(2\mathrm{\gamma }(1-\mathrm{\gamma })+E)+{(4(1-\mathrm{\gamma })E+E^2)}^{1/2}}{2(E-{\mathrm{\gamma }}^2)},\text{where}\hfill \\ E\hfill & =\hfill & \frac{{[1+(n-1)\mathrm{\gamma }]}^2}{n^2}\frac{P_T}{P_T-1}.\hfill \end{array}$$

The proof is given in the Supplementary Web Appendix.

4.2 Nonsymmetric Pooling Design

It is not possible to get analytical expressions for the MLE of ${\sigma }_A^2$ and ${\sigma }_e^2$, and therefore for the MLE of ICC, for most nonsymmetric pooling designs. Recall that it was shown in equation (4) that the pooled data Y* are distributed according to $\mathit{\text{MVN}}\left(\mu 1_M,\mathit{\text{QV}}{Q}^{\prime }={\sum }_Q\left({\sigma }_A^2,{\sigma }_e^2\right)\right)$. It follows that in most cases, using a nonsymmetric pooling strategy introduces dependence among individuals, and it is therefore very difficult to calculate the information matrix in closed form. (In Design I, we also induce dependence within the pooling groups, but in this case the pooling groups have the same size and using appropriate reparametrization allows us to derive the estimators in the same way as for the full data.) Therefore, we evaluate the asymptotic (l → ∞) variance of γ̃ for nonsymmetric designs using Monte Carlo numeric approximations.

In Figure 1, we present different design schemes with l = 4, n = 4 and evaluate designs with M = 8 assays. We compare each Design d to the most efficient Design T through the ratio R = Var_d(γ̃)/Var_T (γ̃) for two values of ICC, γ = 0.3, 0.9, and present the results under each scheme. We evaluated Var_dγ̃ in the following way. Using 2500 Monte Carlo simulations, we approximate the information matrix of vector Y* in equation (4), which is $-E\left(\frac{{\partial }^{2}logL(Y\ast ;\theta )}{\partial \theta \partial {\theta }^{\prime }}\right)$, where $\theta ={\left({\sigma }_A^2,{\sigma }_e^2\right)}^{\prime }$ and L(Y*;θ) is the likelihood function. In this case we calculated in closed form the matrix $\frac{{\partial }^{2}logL(Y\ast ;\theta )}{\partial \theta \partial {\theta }^{\prime }}$ and evaluated the expectation using Monte Carlo approximation. The inverse of the information matrix provides a Monte Carlo approximation of $Var({\stackrel{\sim }{\sigma }}_A^2)$, $Var({\stackrel{\sim }{\sigma }}_e^2)$, and $\text{Cov}\left({\stackrel{\sim }{\sigma }}_A^2,{\stackrel{\sim }{\sigma }}_e^2\right)$. Further, an additional Delta method calculation is used to evaluate Var_d (γ̃). Figure 1 shows that we have increasing efficiency as we pool less across individuals and more across repeated measures. A comparison of many nonsymmetric and symmetric designs suggests that Design T is the most efficient design. In Figure 1, the Designs T and 1 have the same efficiency. In Design T, we pool four repeated measurements into two groups of size 2, and in Design 1 we pool four repeated measurements in two groups of sizes 3 and 1. In the following result (Result 4) we provide theoretical justification of this result and show that every pooling design across repeated measurements with a given number of groups has the same efficiency.

Until now, we have considered pooling designs under the assumptions of a balanced design and normal error distributions. These assumptions may not hold in practical biomarker studies like the F2-isoprostane example. In Sections 5 and 6, we examine the appropriateness of our design results when these assumptions are not met.

5. Unbalanced Case

The previous results are limited to balanced designs. However, in many situations, these repeated measures designs may have a different number of repeated measurements on each subject. Of practical importance is extending our previous results to the case of unbalanced designs. This section presents two results which apply to unbalanced designs. First, we show in Result 4 that for Design T (where we pool over repeated measurements), all possible pooling strategies with a fixed number of pooled groups have the same asymptotic efficiency. The practical importance of this result is that, for both balanced and unbalanced designs, it does not matter how we allocate samples into pools. In this case, what matters for efficiency is only the number of pooled groups. Second, we show in Result 5 that if the number of repeated measurements follow a distribution, the difference in expected information between Designs T and I across n_i is equal to the difference in the information matrices for the average n_i. This suggests that the efficiency of Design T relative to Design F under imbalance will be close to the relative efficiency of a balanced design with n repeated measurements, where n is the expected value on n_i. Practically, this has important implications in that we can design studies based on what we expect will be the ‘average’ balanced design, and the relative efficiencies will be valid under imbalance.

With regard to Result 4, we focused on the comparison between the T and F designs for the unbalanced case, because Design I is difficult to characterize in this situation. We extend our model (1) to allow for the unbalanced case, where i = 1,…,l (individuals), j = 1,…, n_i (repeated measurements). For each individual i, we pool all repeated measurements in P groups with size $k_{\mathit{\text{ip}}}⩾1,{\sum }_{p=1}^P{k}_{\mathit{\text{ip}}}=n_i,i=1,\dots ,l$. We call this Design T*. We also denote the unbalanced design without pooling as Design F*. The following result follows from the fact that the information matrix of the T* design does not depend on the values of pooled group sizes, k_ip, i = 1,…,l; p = 1,…,P, and depends only on the number of pooled groups P for each individual i = 1,…, l.

Result 4. Suppose that we pool n_i measurements of each individual i, i = 1,…,l into P groups (P ⩽ min_i(n_i)) of sizes $k_{i1},k_{i2},\dots ,k_{\mathit{\text{ip}}}\left({\sum }_{j=1}^P{k}_{\mathit{\text{ij}}}=n_i,k_{\mathit{\text{ij}}}⩾1\right)$. Then all ${\mathbf{\Pi }}_{i=1}^l\left(\begin{array}{c}{n}_i-1\\ P-1\end{array}\right)$ different pooling designs have the same efficiency for estimating parameters ${\sigma }_A^2$, ${\sigma }_e^2$, and γ. The proof is given in the Supplementary Web Appendix.

Liu and Schisterman (2003) have observed a similar result for independent univariate data, where they show that all designs with P groups have the same efficiency for variance estimation.

We now present a result (Result 5) which shows that the design results for the balanced case are useful for unbalanced designs. With the information matrices $I_{F\ast }\left(\stackrel{\sim }{\mu },{\stackrel{\sim }{\sigma }}_e^2,{\stackrel{\sim }{\sigma }}_A^2\right)$ and $I_{T\ast }\left(\stackrel{\sim }{\mu },{\stackrel{\sim }{\sigma }}_e^2,{\stackrel{\sim }{\sigma }}_A^2\right)$ (see Supplement), we can calculate using the Delta method the asymptotic variance of the ICC for unbalanced Designs F* and T*, but unlike for the balanced case, the results are complex and provide no insight into the comparison of the two designs. However, with a new result, we now show that the analytic result presented for the balanced case can be applied for unbalanced designs. Suppose that n_i, i = 1,…,l are independent random variables from distribution G with expectation n. In this general case, we can show that the difference between the information matrices of Designs F* and T* is equivalent to the difference between the information matrices of the average balanced Designs F and T (Result 5).

Result 5. Suppose that n_i is a random variable from distribution G with finite first two moments and expectation n. In this case, the information matrix is defined as the expectation with respect to G, say, $E_G\left(I\left(\stackrel{\sim }{\mu },{\stackrel{\sim }{\sigma }}_e^2,{\stackrel{\sim }{\sigma }}_A^2\right)\right)$. Then, we have

$$\begin{array}{l}{E}_G\left(I_{F\ast }\left(\stackrel{\sim }{\mu },{\stackrel{\sim }{\sigma }}_e^2,{\stackrel{\sim }{\sigma }}_A^2\right)-I_{T\ast }\left(\stackrel{\sim }{\mu },{\stackrel{\sim }{\sigma }}_e^2,{\stackrel{\sim }{\sigma }}_A^2\right)\right)\\ =I_{F,n}\left(\stackrel{\sim }{\mu },{\stackrel{\sim }{\sigma }}_e^2,{\stackrel{\sim }{\sigma }}_A^2\right)-I_{T,n}\left(\stackrel{\sim }{\mu },{\stackrel{\sim }{\sigma }}_e^2,{\stackrel{\sim }{\sigma }}_A^2\right),\end{array}$$

where I_F,n and I_T,n are the above information matrices with fixed n_i = n, i = 1,…,l for the F and T designs, respectively.

The proof is given in the Supplementary Web Appendix.

This result has important practical implications in that it implies that we can design studies for an average balanced design, and the result would apply to the actual unbalanced design. We demonstrate that the designs work well in expectation with the following example. We assume that $n_i\sim G=\text{Uniform}\left[\frac{n}{2},\frac{3n}{2}\right]$ and fix ${\sigma }_e^2=1$. We calculated the ratio of the two ratios Rs, $\mathit{\text{RR}}=\frac{{Var}_{T,n}\stackrel{\sim }{(\mathrm{\gamma })}/{Var}_{F,n}\stackrel{\sim }{(\mathrm{\gamma })}}{{Var}_{T\ast }\stackrel{\sim }{(\mathrm{\gamma })}/{Var}_{F\ast }\stackrel{\sim }{(\mathrm{\gamma })}}$. The ratio R for the unbalanced design was evaluated with Monte Carlo simulations of size 10, 000. We observed that the maximum change in the relative ratio (|RR − 1|*100%) of Designs T and F versus T* and F* is only 2.4% when n is 4 and P is 2. When n is 16 and P is 2, the relative difference is less than 0.5%. Thus, ratios comparing the efficiencies of the T and F designs under imbalance are very close (small relative ratio) to the corresponding ratios for the average balanced design.

6. Robustness to the Additive Gaussian Assumption

The analytic results derived in Section 4 assume additive Gaussian random effects and error distributions. Practically, this may not be realistic assumption for many biomarker studies. With extensive simulations, we investigated the sensitivity of our results to the more realistic scenario where random effect and residual variation are not additive and the variance depends on the mean. The data were simulated from the following model,

$$\begin{array}{l}{Y}_{\mathit{\text{ij}}}|\left|A_i\right|\sim \text{Gamma}(\alpha ,\beta ),\alpha =\mu +\left|A_i\right|,\beta =1,\\ A_i\sim N(0,{\sigma }_A^2),\mu \ge 0,\end{array}$$ (11)

where i = 1,…,l and j = 1,…, n, and we compare Designs F, T, and I for estimating γ. We fixed γ to be 0.25, 0.75, 0.9, and ${\sigma }_A^2$ is calculated under model (11) with Expression (S0) in the Supplementary Web Appendix. We set l = 1000 and n = 8. For Designs T and I, we consider strategies where we pool every two repeated measurements and where we pool every two individuals, respectively. In the estimation step we assume the additive random effects model (1) and estimate the variance components ${\sigma }_e^2$ and ${\sigma }_A^2$ using the method of moments (analysis of variance [ANOVA]) for each Design F, T, and I. Table 1 presents the results from 10, 000 simulated realizations. The fourth, sixth and ninth columns of Table 1 present the estimators for γ under Designs F, T, and I, respectively. The eighth and eleventh columns are estimators of R_TF = Var_T(γ̃)/Var_F(γ̃) and R_IF = Var_I (γ̃)/Var_F (γ̃), respectively. It follows from Result 1 and Result 2 that under normal assumptions, R_TF = 117, R_IF = 2. The simulation results show (Table 1) that we get nearly unbiased estimators of ICC under the nonadditive gamma-normal model for Designs F, T, and I. Monte Carlo estimators of R_TF, R_IF also are very close to values computed under additive normal model (1). These results have practical importance in that they show that the efficiency comparisons derived under an additive Gaussian assumptions are robust to this assumption.

Table 1.

Robustness to the additive Gaussian assumption under gamma distribution (model (11)): l = 1000, n = 8, k = 2 with 10, 000 Monte Carlo simulations. γ̃ are ANOVA estimators of ICC under Designs F, T, and I. R_TF = Var_T(γ̃)/Var_F(γ̃), R_IF = Var_I (γ̃)/Var_F (γ̃) and R_IT = Var_I (γ̃)/Var_T (γ̃) (Monte Carlo estimators). It follows from Result 1 and Result 2 that under normal assumptions, R_TF=1.17,R_IF=2.

μ	${\sigma }_A^2$	γ	Design F		Design T			Design I
			γ̃	105Var	γ̃	105Var	RTF	γ̃	105Var	RIF
0	0.536	0.25	0.2498	18.81	0.250	23.27	1.24	0.2499	33.78	1.80
	43.39	0.75	0.7497	9.46	0.7496	11.75	1.24	0.7493	18.45	1.95
	390.52	0.90	0.8998	2.02	0.8998	2.53	1.25	0.8997	3.91	1.94
10	11.67	0.25	0.2496	17.56	0.2499	20.40	1.16	0.2499	33.26	1.89
	167.92	0.75	0.7498	10.04	0.7497	11.56	1.15	0.7493	18.58	1.85
	810.15	0.90	0.8998	2.04	0.8998	2.47	1.21	0.8997	3.98	1.95

7. The F2-Isoprostane Example Continued

We analyzed the F2-isoprostane data from the BioCycle Study described in Section 2. The BioCycle Study enrolled 259 women with five to eight study visits. To examine the pooling strategies under both balanced and unbalanced designs, we focused on the subset with six complete measurements (n = 174) and on the complete dataset. Using the balanced subset, we compared Design T, where we pool every three repeated measurements for each individual, with Design I, where at each time point we pool the measurements for three individuals. The pooling strategies applied to the balanced subset would have allowed us to perform only one third the numbers of assays needed for the unpooled design, thereby reducing the cost of the study substantially. Specifically, assuming that the cost of an assay is $130, the full design would cost $135,720, while the pooled designs would cost only $45,240. For the complete dataset, we compared Design T, where we pooled every individual's repeated measurements into two pools (of equal size for an even number of repeated measurements or approximately equal for an odd number of measurements), with Design F. Here the full design would cost $254,800, while the pooled design would cost only $67,340.

For both analyses, ANOVA estimators of γ were used because the error distributions were highly skewed for F2-isoprostane. Because the error distributions were highly skewed, we used the bootstrap to construct confidence intervals for ICC and to demonstrate the validity of the theoretical results. For the F and T designs, the bootstrap was applied by resampling individuals with replacement and by resampling pools (preserved over time for the I design). The results are presented in Table 2 for the balanced and unbalanced designs. The point estimates of the ICC are similar across both designs and datasets, with the estimated ICC ranging between 0.68 and 0.74. Further, the relative efficiencies across designs are close to what would be expected based on our analytical design comparisons.

Table 2.

F2-isoprostane example: Estimates of γ for 174 women with six complete measurements (upper table), all 259 women with five to eight measurements (in total 1960) (lower table), number of bootstrap is 10,000.

Design	ANOVA est.	Boot est	104 $\widehat{Var}$ (Boot)	Boot 95% CI
F	0.743	0.739	8.262	[0.677, 0.789]
T	0.687	0.687	20.635	[0.589, 0.767]
I	0.681	0.670	26.320	[0.557, 0.757]
F	0.732	0.728	7.817	[0.667, 0.777]
T	0.696	0.693	9.165	[0.630, 0.748]

8. Discussion

In this article, we proposed various pooling design strategies for estimating the variance components and the ICC under a Gaussian random effects model. In this setting, pooling is particularly attractive, because conducting longitudinal reproducibility studies is prohibitively expensive when the assay costs are high. We were able to develop closed-form expressions for the efficiencies of Design T (across time) and Design I (across individuals) relative to full data designs (no pooling) under the assumption of normal error distributions, balanced designs, and no technical variation. Using these expressions, we showed that designs where we pool samples over time on individuals (T) are more efficient than designs where we pool over individuals at the same time point (I).

Our analytic design results were developed under assumptions that may not be realistic in at least some biomarker studies. For example, the BioCycle Study is unbalanced and F2-isoprostane markers are highly skewed, with the variances increasing with the mean. We showed that the analytic results apply to unbalanced designs. Specifically, we can design studies based on the average balanced design. Further, through extensive simulations, we showed that the analytical results still apply under realistic departures from an additive Gaussian model; namely, the T design is a highly efficient alternative to both the full and I designs. Although the ICC does not have a direct relationship with the sources of variation under the nonadditive model, it still has an interpretation as the correlation coefficient between repeated measurements. Thus, even under the nonadditive non-Gaussian model, the ICC can be used for assessing the reproducibility of biomarkers and for designing studies where the biomarker is an outcome measure. However, it is not directly useable as a correction for measurement error when the biomarker is treated as a covariate in regression analysis.

The analytic results were developed under the assumption of no technical variation. This is reasonable for the F2-isoprostane biomarkers, where technical variation is expected to be very small. We show in the Supplementary Web Appendix how to incorporate technical variation into the estimation. We also show that when the technical variation is more sizable, Design T is still optimal.

Model (1) can be extended to allow for a more flexible mean structure. All our analytic results for estimating the ICC extend to this model, because MLEs of the mean structure and variance components are independent from each other. The correct estimation of the ICC relies on the correct specification of the mean structure. However, particularly for Design T, the specification of the correct mean structure may be difficult to justify empirically in practical situations. Therefore, a limitation of pooling across time (Design T) is that we need either to assume a constant mean or to specify the mean structure based on biological information.

The analytic results in this article were developed for a simple one-way ANOVA. In practice, more complex hierarchical random effect structures may be appropriate. We conducted simulations that examined the performance of our design results when an additional source of variation was added. Specifically, we examined a model that incorporates a center effect, where individuals are nested within centers. These simulations along with a discussion of the results are included in the Supplementary Web Appendix. Overall, Design T is still more efficient than Design I even when the center effect is large.

Practical issues related to biomarker development need to be considered in the designs of longitudinal studies with pooling. Although limit of detection was not a concern in our applications, it may be an issue for other biomarkers. Hughes (1999) developed a Gaussian random effects model for longitudinal data with detection limits. Future work will focus on extending this approach to allow for pooling. Fortunately, in our example F2-isoprostane is not subject to a limit of detection.

A dilution effect may be an issue for some biomarkers (particularly if the pool size is large). A dilution effect is a type of technical variation discussed in the Supplementary Web Appendix, where the effect can be viewed as e^M having a nonzero mean which depends on pool size. We could account for this effect by estimating the mean of e^M as a function of pool size as long as we have pools of different sizes. This is an area of future research.

The BioCycle study example has intermittent missingness. Result 5 deals with unbalanced designs, which can be described as a type of intermittent missingness where data are missing at random. Future work will focus on developing inference and designs for longitudinal data with pooling under a more general missing data mechanism.

In summary, designs where we pool over time will provide a practical, efficient alternative to performing assays at each time point. Of course, it is important not to pool all measurements on a given person, because in this case, between- and within-subject variations are not identifiable.