Semiparametric modeling of grouped current duration data with preferential reporting

Abstract

Current duration data arise in cross-sectional studies from questions on the length of time from an initiating event to the time of interview. For example in the National Survey on Family Growth, women who were considered at risk for pregnancy were asked (a) “Are you currently attempting pregnancy?” and (b) “If yes, how many months have you been attempting to get pregnant?” The responses to (b), referred to as the current durations, are length-biased because women with longer durations are more likely to answer yes to question (a) and therefore be included in the sample. Previous methods to analyze such data include continuous time nonparametric and parametric approaches. In this article, we propose a semiparametric Cox model and a piecewise constant baseline model (used to account for digit preference) to analyze grouped current duration data. We discuss and investigate through simulation studies, the robustness properties of the proposed methods when digit preference is present. Lastly, we present an analysis of the current duration data resulting from the 2002 National Survey on Family Growth.

1. Introduction

Infertility is defined as the absence of pregnancy despite 12+ months of regular unprotected intercourse [1], and is estimated to affect 6% of married women in the United States [2] when using the National Survey on Family Growth (NSFG). However, recent evidence suggests that this construct-derived figure underestimates infertility prevalence by more than half. Specifically, the prevalence of infertility in the United States using the NSFG data was estimated to be 16% when querying women and 12% when querying men [3, 4]. These figures were estimated using the current duration based method proposed by Keiding et al. [5], and are more consistent with estimates based on incident data obtained from the few prospective cohort studies followed through 12 months of trying [6, 7, 8]. Underestimation of the prevalence of infertility lessons the perceived impacts of the condition, which includes social stigma in some societies [9], relationship stressors [10], and financial costs associated with treatments or adoption that are often not covered by health insurance [11].

The data we consider in this paper arise from two questions in the NSFG (a) “Are you currently attempting pregnancy?” and (b) “If yes, how many months have you been attempting to get pregnant?” The current duration approach [5, 12, 13] uses responses to (b), denoted by Y, to make inference on the unobserved total duration of pregnancy attempt, denoted by T. The Y values are an entirely right-censored sample from T, commonly referred to as backwards recurrence times [14]. Further, Y is only observed for those who are currently attempting pregnancy, which creates a length-bias because those with long pregnancy attempts are more likely to be in an attempt when surveyed. Statistical methods for analyzing current duration data have focused on continuous time parametric and nonparametric approaches. For example, Keiding et al. [5] developed nonparametric and parametric methods to estimate the survivor function of T from continuous Y values (see also [15]), and Keiding et al. [16] proposed the use of continuous time accelerated failure time (AFT) models to estimate exposures’ effect on the distribution of T.

Methodological research on statistical methods to analyze TTP data have mostly focused on prospective [17, 18, 19], or retrospective [12, 20, 21] study designs. Unlike the retrospective and prospective study designs, a benefit of the current duration method is the ability to use a cross-sectional sample of reproductive aged women that are representative of the population. This sample can include ‘non-planners’ that can be missed in prospective studies, and couples that will never get pregnant who are missed in retrospectively reported TTP (see [13, 22] for a thorough review of the statistical issues in various TTP study designs).

In this article, we propose a semiparametric proportional hazards model for the total duration of pregnancy attempt. Specifically, we propose a semiparametric grouped backward recurrence Cox model to analyze current duration data. The model results in estimates of exposures effect on the distribution of T, and an estimate of the survivor function of T conditional on covariate values. Some AFT models have no straightforward method of assuring that survivor function of T can be estimated (discussed further in Section 2). This is troublesome since estimating the survivor function of T is a key goal in current duration analyses. Furthermore, parametric inference based on the AFT models may be restrictive, especially when little is known about the true distribution of T. By using a semiparametric framework, the proposed methods are flexible to the distribution of T and result in a proper estimate of the survivor function of T.

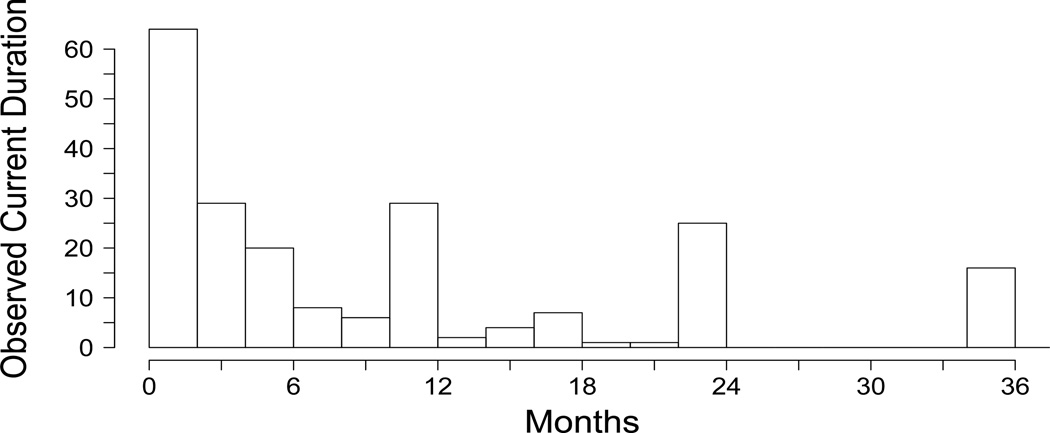
An additional challenge with survey-based responses is the presence of digit preference, as reflected in Figure 1 for the 2002 NSFG data. Digit preference is especially detrimental when interest lies in estimating the survivor function at a point of digit preference (i.e., at 6, 12, or 24 months). For example, in the NSFG we are interested in estimating the survivor function at 12 months (i.e., estimating the proportion of infertile couples). When digit preference is present, estimates of the survivor function at 12 months exhibit considerable bias (> 40% in our simulation studies). As a result, we propose a piecewise constant specification for the grouped baseline hazard to control for digit preference. We discuss knot selection of the piecewise model, and apply it to data with and without covariates.

Figure 1.

Histogram of observed current durations from the National Survey on Family Growth. Apparent digit preference is displayed at 12, 24, and 36 months

Our methods are based on observed current durations that are integer valued, and allow for Y = 0 observations which are problematic with continuous time methods. For example, some parametric models are not defined at zero (e.g., the generalized gamma distribution), a constant must be added to Y to implement AFT models, and methods to estimate continuous nonparametric approaches cannot incorporate zeros or ties. In the NSFG data, Y represents the number of completed months of a pregnancy attempt. Thus, Y = 0 represents a woman who was surveyed before the completion of the first month of her pregnancy attempt. Approximately 30% of women are reported to conceive in the first menstrual cycle of trying [7], and the only way of including women who would get pregnant in their first menstrual cycle (which is approximately one month) is by allowing for Y = 0 observations. As a result, including such observations is critical to insure the sample is representative of the population.

The paper is organized as follows. In Section 2, we present preliminary theoretical results on backwards recurrence times, and discuss their implications on the current modeling approaches. In Sections 2.1 and 2.2, we propose a semiparametric backward recurrence proportional hazards model when the distribution of T is discrete and continuous, respectively. In Section 2.3, we discuss how to account for digit preference by assuming the baseline hazard is piecewise constant. The estimation of model parameters is discussed in Section 3, and we investigate the properties of our model through simulation studies in Section 4. In Section 5, we illustrate our methods using data from the 2002 NSFG. In the supporting information, we present a discrete nonparametric method for estimating the survivor function of the total duration of pregnancy attempt, additional simulation studies, and the R code to implement the proposed methods.

2. Methods

Current duration data consist of observations, Y, that indicate the length of the current pregnancy attempt. Our interest lies in estimating the distribution of the total duration of pregnancy attempt T. Here, T = min(X, U) where X denotes the couples’ time-to-pregnancy (TTP) and U denotes the end of a pregnancy attempt without becoming pregnant (note that E(T) < ∞ since U < ∞). The unobserved T could arise from a continuous or discrete distribution. The issue of whether T is best regarded as continuous or discrete was discussed in depth by Keiding et al. [13]. As will be demonstrated in Section 2.2, our estimation methods are robust for discrete or continuous distributions on T.

As described previously [5, 13], the observed current duration of pregnancy attempt represents a length-biased sample of backward recurrence times [14]. To discuss the relationship between T and Y, we initially assume that both arise from either continuous or discrete distributions. Let g denote the density (or mass) function of Y. Under regularity conditions discussed below,

$$g(y)=\frac{\mathrm{F̄}(y)}{{\mu }_T}$$ (1)

[23] where F̄(t) = Pr(T > t), μ_T = E(T) and g is non-increasing. One can use an estimate of g, denoted by ĝ, to estimate F̄ via $\widehat{\overline{F}}(t)=ĝ(t)/ĝ(0)$ where μ̂_T = 1/ĝ(0). Let 𝒫 be the space of all probability measures, and ℱ the space of all survival functions (i.e., the space of non-increasing positive functions with F̄(0) = 1). Viewing the current duration operation as a mapping from ℱ → 𝒫, non-surjectivity will arise since there exists g ∈ 𝒫 with no corresponding F̄ ∈ ℱ. Letting 𝒫₀ denote the space of all non-increasing probability measures with g(0) < ∞, all g ∈ 𝒫₀ have a corresponding F̄ ∈ ℱ. For g ∉ 𝒫₀ we can have either (a) g(t)/g(0) is increasing for some t, or (b) F̄(0) is not defined (when g(0) is not finite). Estimation procedures that restrict ĝ ∈ 𝒫₀ (i.e., that map ℱ → 𝒫₀) are surjective, and will result in an $\widehat{\overline{F}}$ which is non-increasing with $\widehat{\overline{F}}(0)=1$. Conversely, an unrestricted estimation procedure is non-surjective and can result in ĝ ∉ 𝒫₀. A benefit of the proposed estimation procedure is that it is surjective and results in a valid estimate of F̄. The AFT model does not use the ĝ ∈ 𝒫₀ restriction, thus it is non-surjective and can result in ĝ with no corresponding F̄.

The relationship between the distributions of T and Y given in (1) assumes that the renewal process is in equilibrium with the renewal distribution, or that the process is in a ‘steady state’ (cf. [24]). Specifically, the steady state assumption assumes (i) the calendar times at which women are beginning their pregnancy attempts occur at a constant rate, and (ii) the distribution of T is independent of calendar time. Assumption (i) is a stationarity assumption and is satisfied if women are entering pregnancy attempts according to a homogeneous Poisson process. We also assume that (iii) the observations are independent. We discuss the validity of the assumptions in Section 6.

In Section 2.1, we propose a modeling procedure when Y and T are each discrete random variables. In Section 2.2, we consider the situation where Y is a grouped outcome and T is continuous.

2.1. Discrete backwards recurrence Cox model

In this section, we assume a discrete proportional hazards model for T, and we propose a model to estimate regression coefficients and the survivor function F̄. Let T have discrete hazard probability P(T = y|T ≥ y, Z) = 1 − exp{−α_y exp(β^⊤ Z)}, where α_y ≥ 0. The survivor function of T takes the form

$$\mathrm{F̄}(t|\mathit{Z})=\text{exp}\{-\text{exp}({\mathit{\beta }}^{\top }\mathit{Z})\sum _{j=0}^t{\alpha }_j\},$$

where α₀ ≡ 0. This model has been used for the analysis of TTP data by Scheike and Jensen [20] and Sundaram et al. [19], and corresponds to the grouped version of the continuous time proportional hazards model [25]. The discrete current durations Y have probability mass function

$$g(y|\mathit{Z})=g(0|\mathit{Z})\text{exp}\{-\text{exp}({\mathit{\beta }}^{\top }\mathit{Z})\sum _{j=0}^y{\alpha }_j\}$$ (2)

where α_j ≥ 0 for all j with α₀ ≡ 0 and

$$g(0|\mathit{Z})={\left[\sum _{y=0}^{\infty }\text{exp}\right\{-\text{exp}({\mathit{\beta }}^{\top }\mathit{Z})\sum _{j=0}^y{\alpha }_j\left\}\right]}^{-1}.$$ (3)

Notice g(y|Z) is non-increasing in y with maximum value equal to g(0|Z), where $g^{-1}(0|\mathit{Z})={\sum }_{y=0}^{\infty }\mathrm{F̄}(t|\mathit{Z})={\mu }_T$.

2.2. Grouped backwards recurrence Cox model

When T is continuous, the actual current durations, denoted by Y*, have a continuous density equal to F̄(y)/μ_T. However, we observe the grouped continuous outcomes. We assume the continuous outcomes are grouped by rounding down, rounding upwards or to the closest value can be handled similarly. As a result, Y = ⎿Y*⏌ = {y; Y* ∈ [y, y + 1)} has probability mass function

$$g(y)=\frac{1}{{\mu }_T}{\int }_y^{y+1}\mathrm{F̄}(u)du,\text{for}y=1,2,\dots$$ (4)

We can apply the mean value theorem to (4) to get g(y) = F̄(y′)/μ_T for some y′ ∈ [y, y + 1]. Similarly, there exists a y″ ∈ [0, 1] such that g(0) = F̄(y″)/μ_T. As a result,

$$g(y)=\frac{g(0)\mathrm{F̄}(y\prime )}{\mathrm{F̄}(y″)}=g(0)\text{exp}[-\{\mathrm{\Lambda }(y\prime )-\mathrm{\Lambda }(y″)\}]$$ (5)

for some y′ ∈ [y, y + 1] and y″ ∈ [0, 1], where Λ denotes the cumulative hazard function of T.

To incorporate exposures into the model, we assume that T is distributed with proportional hazards form [26] with Λ(t|Z) = exp(β^⊤Z)Λ₀(t) and F̄(t|Z) = exp{−Λ(t|Z)}, where Z a q-dimensional vector of exposures and β a q-dimensional vector of parameters. Under this model, (5) motivates modeling Y with

$$g(y|\mathit{Z})=g(0|\mathit{Z})\text{exp}\{-H(y)\text{exp}({\mathit{\beta }}^{\top }\mathit{Z})\},$$ (6)

where H(y) = Λ₀(y′) − Λ₀(y″) for some y′ ∈ [y, y + 1] and y″ ∈ [0, 1] with H(0) ≡ 0. Notice that if we set $H(y)={\sum }_{j=0}^y{\alpha }_j$, (2) and (6) are equivalent. As a result, we can use the method in Section 2.1 regardless of whether F̄ is discrete or continuous to estimate of β. The form for g in (6) is an approximation of the true mass function of Y which is $g^{*}(y|\mathit{Z})={\mu }_T^{-1}(\mathit{Z}){\int }_y^{y+1}\mathrm{F̄}(u|\mathit{Z})du$ where ${\mu }_T^{-1}(\mathit{Z})=g^{*}(0|\mathit{Z})/{\int }_0^1\mathrm{F̄}(u|\mathit{Z})du$. Directly modeling g* would require knowledge of F̄(u|Z) over [y, y + 1] for all y. When T follows an exponential distribution with Λ₀(t) = θt, we have g*(y|Z) = g*(0|Z) exp {−H(y) exp(β^⊤Z)} where H(y) = θt. As a result, (6) is equal to g* and the survivor function of T is F̄(y|Z) = exp{−H(y) exp(β^⊤Z)}. In the non-exponential setting, F̄(y|Z) ≈ exp{−H(y) exp(β^⊤Z)}. In our simulation studies, the estimates of F̄(y|Z) and β when Λ₀(t) = θt^γ were relatively unbiased, suggesting that (6) was a close approximation to g*.

2.3. Piecewise constant baseline model

Previous methods of analyzing data with digit preference include Ridout and Morgan [27], Pickering [28], Price and Seaman [29], and Bar and Lillard [30]. In many circumstances, the parameters governing the digit preference, such as the probability that someone reports Y = 12 when actually Y = 10, are nuisance parameters. In this case, digit preference can be controlled for by imposing smoothness restrictions on the probability mass function [28], i.e., imposing smoothness restrictions on g(y|Z). This type of correction assumes that the rounding in the data is at random, and that people are equally likely to round up as they are to round down. Heitjan and Rubin [31] referred to this assumption as coarsening at random (CAR), for more on CAR see [32, 33].

The models in Sections 2.1 and 2.2 are smoothed by having the α_j’s be constant over disjoint intervals. The piecewise constant model is implemented by creating a disjoint partition (t₀, t₁], (t₁, t₂], …, (t_L−1, t_L] with t₀ ≡ 0 and t_L ≥ max{Y}. We then assume α_j = γ_l for all j ∈ (t_l−1, t_l]. Following the results in Section 2.1 and 2.2, the probability mass function of Y is

$$g_P(y|\mathit{Z})=g_P(0|\mathit{Z})\text{exp}[-\text{exp}({\mathit{\beta }}^{\top }\mathit{Z})\sum _{\{j:t_{j-1}<y\}}{\gamma }_j\{(y\mathrm{\wedge }{t}_j)-t_{j-i}\}],$$ (7)

where x ⋀ y = min(x, y) and g_P (0|Z) takes a form similar to (3). The piecewise estimate of survivor function of T is F̄_P (y|Z) = g_P (y|Z)/g_P(0|Z).

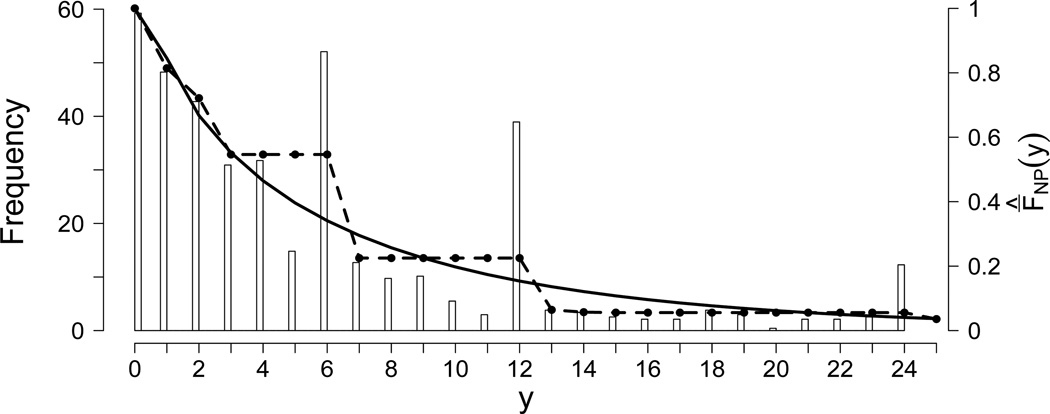
Popular methods of knot selection, such as using the percentiles of the observed Y or information criterion, will not suffice because they will not impose the desired smoothness on g. To specify the t_l’s, we consider the shape of a nonparametric estimate of the survivor function of T, given by ${\widehat{\overline{F}}}_{NP}(y)={ĝ}_{NP}(y)/{ĝ}_{NP}(0)$. In Appendix A of the supporting information, we discuss the estimation of ĝ_NP and $\widehat{\overline{F}}NP$. In Figure 2, we present a histogram of data with digit preference, the corresponding estimate of ${\widehat{\overline{F}}}_{NP}$ and the true F̄.

Figure 2.

A histogram of data simulated to have digit preference at y = 6, 12, and 24, overlayed with an unconstrained nonparametric current duration survivor function estimate (dashed line, axis on right) and the true survivor function (solid line).

When digit preference is present, Figure 2 demonstrates that ${\widehat{\overline{F}}}_{NP}(y)$ has large jumps at 7 and 13 months and is flat over the interval [7, 12] months. Heuristically, this results in positive bias over [5, 6] and negative bias over [7, 8] (similarly for [11, 12] and [13, 14], respectively). Let D₀ = {d₁, d₂, …} denote the set of points of digit preference, which we assume are known, and let D_k = {d₁ + k, d₂ + k, …} be the set of points k units after the points of digit preference. In general, ${\widehat{\overline{F}}}_{NP}(y)$ will have large jumps for y ∈ D₁, and be flat over [d_j−1 + 1, d_j] for j > 1, which results in ${\widehat{\overline{F}}}_{NP}(y)$ having positive bias for y ∈ {D₋₁, D₀}, and negative bias for y ∈ {D₁, D₂}.

To smooth the estimate of ${\widehat{\overline{F}}}_{NP}$ we propose choosing the t_l’s such that t_l ∉ {D₋₁, D₀, D₁, D₂} for l = 1, 2, …, L. Under these guidelines note that all (t_l−1, t_l] such that d_j ∈ (t_l−1, t_l] contain the set of points {d_j − 1, d_j, d_j + 1, d_j + 2}. As a result, the knots are chosen such that all intervals that contain a point of digit preference, include points with positive and negative bias, mainly {d_j − 1, d_j} and {d_j + 1, d_j + 2}, respectively. This method acknowledges the difficulty in estimating the grouped baseline hazard around the d_j’s, and balances the effect of digit preference. When the maximum observed Y is in D₀ we leave the last interval open ended by setting t_L = ∞. Our simulation study found that if t_l ∈ {D₋₁, D₀, D₁, D₂} for all l, the choice of knots had relatively little effect of the results.

3. Estimation

In this section, we discuss maximum likelihood estimation of the models proposed in Section 2. Let Y = {Y₁, Y₂, …, Y_n}, and Y₍₁₎, Y₍₂₎, …, Y_(m) denote the observed current durations, and the ordered and distinctly observed current durations, respectively. When there is no censoring (2) and (6) can be estimated by setting α_y = ∞ for y > Y_(m), thus ${\sum }_{y=0}^{Y_{(m)}}g(y|\mathit{Z})=1$, and α_y = 0 for all y ∉ {Y₍₂₎, Y₍₃₎, …, Y_(m)}. Notice that by setting α_y = 0 for y < Y₍₂₎ we have g(y|Z) = g(0|Z) for all 0 ≤ y < Y₍₂₎, which ensures that (3) is identifiable. We then estimate β and α = {α_Y(2), α_Y(3), …, α_Y(m)} using maximum likelihood.

It is common to censor all current durations greater than a fixed value, denoted by τ, after which they are not considered to be reliable. Let Ỹ = {Ỹ₁, Ỹ₂, …, Ỹ_n} denote the possibly censored current durations, where Ỹ_i = min(Y_i, τ) and δ_i = I(Y_i ≤ τ). Let Ỹ ₍₁₎, Ỹ₍₂₎, …, Ỹ_(m) ≤ τ denote the ordered and distinctly observed uncensored current durations, and $Ḡ(y|\mathit{Z})=1-{\sum }_{j=0}^{y}g(j|\mathit{Z})$. When censoring is present we cannot set α_y = ∞ for y > Ỹ_(m) because the likelihood for those censored at τ would be Ḡ(τ|Z) = 0. To allow for Ḡ(τ|Z) > 0 we introduce an additional parameter α_τ, and set α_y = α_τ for all y > Ỹ _(m).

To estimate β and α_τ = {α_Y(2), …, α_Y(m), α_τ}, we use maximum likelihood estimation. The likelihood corresponding to the observed Ỹ, δ = {δ₁, δ₂, …, δ_n}, and 𝒵 = {Z₁, Z₂, …, Z_n} takes the form $L(\mathit{\beta },{\mathit{\alpha }}_{\tau }|\mathit{Y},\mathit{\delta },𝒵)={\prod }_{i=1}^{n}g{({Ỹ}_i|{\mathit{Z}}_i)}^{{\delta }_i}Ḡ{({Ỹ}_i|{\mathit{Z}}_i)}^{1-{\delta }_i}$ with maxima denoted by β̂ and α̂_τ. The survivor function of the unobserved T’s at given value of Z is estimated by ${\widehat{\overline{F}}}_{SP}(y|\mathit{Z})=\text{exp}\{-\text{exp}({\mathit{\beta ̂}}^{\top }\mathit{Z}){\sum }_{j=0}^y{\mathrm{\alpha ̂}}_j\}$ where α̂₀ ≡ 0.

For the piecewise constant model the details of the estimation proceed similarly. That is, for a given {t₀, t₁, …, t_L} we use g_P given in (7) and ${Ḡ}_p(y|\mathit{Z})=1-{\sum }_{j=0}^y{g}_P(j|\mathit{Z})$ to form the likelihood. If there are censored values at τ ≥ Ỹ_(m), an additional parameter γ_τ is used, or set t_L = ∞, so that Ḡ_p(τ |Z) > 0. After β and γ = {γ₁, …, γ_L, γ_τ} have been estimated, the piecewise constant estimate of F̄ at given value of Z is given by ${\widehat{\overline{F}}}_{PC}(y|\mathit{Z})=\text{exp}[-\text{exp(}{\mathit{\beta ̂}}^{\top }\mathit{Z}){\sum }_{\{j:t_{j-1}<y\}}{\mathrm{\gamma ̂}}_j\{(y\wedge t_j)-t_{j-1}\}]$.

The R programs [34] to implement the semiparametric and piecewise constant models to simulated data are contained in Appendix B of the supporting information. In our data analysis and simulation study, we estimated the standard error of β̂ with a numerical approximation to the hessian matrix. If T is continuous, exp(β̂_j) corresponds to the estimated hazard ratio, associated with a one unit increase in Z_j. For discrete T, β̂_j can be interpreted as the approximate logarithms of subject-specific risk or odds ratios associated with a one unit increase in Z_j (cf. [35]).

4. Simulation Studies

To test the properties of our models with moderate sample sizes, numerous simulation studies were performed. The current duration for the ith subject was simulated by generating the unobserved total durations as T_ij~F for j = 1, 2, …, K, where $K=\text{min}(K;{\sum }_{j=1}^k{T}_{ij}>M)$ and M is a fixed large integer, replicating a renewal process in equilibrium with renewal distribution (see [36] for details). For the continuous scenario discussed in Section 2.2, the backward recurrence times were grouped with Y_i = ⎿M − T_iK−1⏌. For the discrete scenario discussed in Section 2.1, the continuous T_ij were grouped with $T_{ij}^{*}=\lceil T_{ij}\rceil$ and $Y_i=M-T_{i{K}^{*}-1}^{*}$ where $K^{*}=\text{min}(k;{\sum }_{j=1}^k{T}_{ij}^{*}>M)$. Here, F had hazard function λ(t|Z_i) = λ₀(t) exp(β^⊤Z_i), and Z_i = (Z_i1, Z_i2) were independently generated as Bernoulli(0.5) and N(0, 0.5²), respectively. The baseline hazard was set to λ₀(t) = θγt^γ−1 with θ = 0.3 and α = 0.75. Note that α_j ≠ α_j+1 for all j, so the piecewise constant model is not correctly specified. In Section 4.1 we test the effect digit preference would have on the results, and in Section 4.2 we test continuous and discrete distributions on T. For brevity, the results for the piecewise model with a continuous F are not presented since they were similar to what was found with discrete F. In Section B of the supporting information, we present expanded simulation studies with piecewise model with a continuous F, an asymmetric rounding mechanism (where CAR is violated), and a comparison to the Weibull AFT model. We found that asymmetric rounding can result in bias in the survival function estimates. Further, the β estimates from the proposed model performed similarly to the Weibull AFT model.

4.1. Digit preference and knot selection

In this section, we explore the effect digit preference has on the proposed methods, and the knot selection for the piecewise model. The discrete scenario was used, and the data were randomly grouped as follows, if 4 ≤ Y_i ≤ 9 then Y_i was rounded to 6 with probability 0.4, if 10 ≤ Y_i ≤ 18 then Y_i was rounded to 12 with probability 0.6, if Y_i > 18 then Y_i was rounded to the nearest multiple of 12 with probability 0.8. The piecewise constant model was fit with four separate knot scenarios, each used 7 knots, the locations for knot scenarios A–C were {1, 2, 4, 9, 18, 30,∞}, {1, 2, 4, 9, 15, 27,∞}, and {1, 2, 4, 10, 17, 29,∞}, respectively, while scenario E used the percentiles of the observed Y_i. For scenarios A–C note that the knots did not coincide with {D₋₁, D₀, D₁, D₂} as recommended in Section 2.3, and the majority of knots were close to 0. The last interval is open ended (i.e., t_L = ∞) since it is likely that Y_(m) ∈ D₀.

In Table 1, we present the results of the digit preference simulation for β₁, β₂, F̄(6|0), F̄(12|0), F̄(24|0) and the l₂-norm defined as $\parallel \mathrm{F̄}-\tilde{\overline{F}}{\parallel }_2={\sum }_{y=1}^{200}{\{\mathrm{F̄}(y|\mathbf{0})-\tilde{\overline{F}}(y|\mathbf{0})\}}^2$ where $\tilde{\overline{F}}(t|\mathbf{0})=N^{-1}{\sum }_{j=1}^N{\widehat{\overline{F}}}_j(t|\mathbf{0})$, and ${\widehat{\overline{F}}}_j(t|\mathbf{0})$ is the estimated survivor function for iteration j evaluated at Z = 0. The estimates of β showed little bias. In general, the piecewise estimates of β had more bias than the semiparametric estimates. The average estimate of F̄ for knot scenarios A–C were closer to the truth than the semiparametric model, or knot scenario E. This was especially true for the points of digit preference 6, 12, and 24. For these points the semiparametric model showed significant over estimation. Overall, the results from scenarios A–C with the piecewise model were the most robust to digit preference. Further, knot selection did not have a large effect on the estimates under the guidelines discussed in Section 2.3.

Table 1.

Summary of 1, 000 simulated samples with n = 250 for the piecewise constant and semiparametric (SP) models when digit preference is present. The piecwise model was fit with knot scenario A {1, 2, 4, 9, 18, 30, Y_(m)}, scenario B {1, 2, 4, 9, 15, 27, Y_(m)}, scenario C {1, 2, 5, 8, 11, 18, Y_(m)}, and scenario E that uses empirical percentiles. Displayed is the empirical bias (bias), empirical standard deviation (sd), and ${\parallel \mathrm{F̄}-\tilde{\overline{F}}\parallel }_2(l_2)$.

		Piecewise knot scenario
		A	B	C	E	SP
	true	bias (sd)	bias (sd)	bias (sd)	bias (sd)	bias (sd)
β1	−0.5	−0.002 (0.12)	−0.009 (0.12)	−0.016 (0.13)	−0.019 (0.13)	0.004 (0.13)
β2	−0.5	−0.012 (0.30)	−0.021 (0.30)	−0.027 (0.30)	−0.029 (0.31)	−0.007 (0.30)
F̄(6)	0.317	0.026 (0.06)	0.025 (0.06)	0.026 (0.06)	0.109 (0.10)	0.127 (0.08)
F̄(12)	0.145	−0.004 (0.03)	−0.007 (0.03)	−0.005 (0.03)	0.024 (0.05)	0.063 (0.05)
F̄(24)	0.039	−0.003 (0.01)	−0.001 (0.01)	−0.001 (0.01)	−0.004 (0.01)	0.005 (0.02)
l2	-	0.077	0.074	0.068	0.155	0.217

4.2. Continuous versus discrete F

In this section, we present the results of simulations designed to test differences when the underlying distribution for T is continuous versus discrete. In Table 2, we present the results from the piecewise constant (discrete F only) and semiparametric models for discrete and continuous F. The piecewise model used 7 knots with locations {1, 2, 5, 8, 11, 18, Y_(m)}.

Table 2.

Summary of 1,000 simulated samples with n = 250, and 500 for the piecewise constant and semiparametric models under the discrete (true F is discrete) and continuous (true F is continuous) scenarios. Displayed is the average coefficient (mean), empirical standard deviation (sd), empirical coverage probabilities (ecp), and l₂ norm (l₂)

		Discrete F				Continuous F
		Piecewise		Semiparametric		Semiparametric
	true	mean(sd)	ecp	mean(sd)	ecp	mean(sd)	ecp
				n=250
β1	−0.5	−0.505 (0.148)	0.964	−0.510 (0.162)	0.950	−0.511 (0.167)	0.949
β2	−0.5	−0.507 (0.354)	0.951	−0.509 (0.368)	0.945	−0.510 (0.389)	0.952
l2		0.068		0.053		0.056
β1	0.0	−0.005 (0.143)	0.948	−0.002 (0.145)	0.950	−0.003 (0.143)	0.953
β2	0.0	0.005 (0.349)	0.955	−0.003 (0.356)	0.947	0.008 (0.375)	0.944
l2		0.074		0.053		0.049
				n=500
β1	−0.5	−0.506 (0.105)	0.952	−0.507 (0.104)	0.956	−0.509 (0.115)	0.944
β2	−0.5	−0.506 (0.252)	0.949	−0.505 (0.245)	0.965	−0.507 (0.259)	0.954
l2		0.050		0.029		0.026
β1	0.0	0.002 (0.095)	0.948	0.002 (0.097)	0.950	−0.002 (0.100)	0.947
β2	0.0	0.007 (0.230)	0.965	−0.002 (0.241)	0.950	−0.017 (0.251)	0.957
l2		0.050		0.034		0.031

The results from the piecewise constant and semiparametric models showed little bias for β with either discrete or continuous F̄. The bias tended to decrease as the sample size increased. The empirical coverage probabilities for β = 0 suggest that hypothesis tests of β_j = 0 will have proper type I error. Further, the empirical coverage probabilities for nonzero β were close to the nominal 0.95 level. For the semiparametric model, properties of the β estimates were similar for the discrete and continuous scenario. The values of l₂ norm showed that the estimates of the survivor function accurately estimated the distribution for both scenarios. Notice that the l₂ norm for the continuous setting is similar to the l₂ norm for the discrete setting. This is noteworthy since g is modeled in the continuous setting using (6), which is an approximation to the true mass function of Y, while in the discrete setting g is modeled using the true mass function of Y. These results indicate that (6) is an accurate form for this distribution.

5. Data Analysis

We use a nationally representative cross-sectional sample of 7,643 US women aged 15–44 years from the 2002 NSFG to demonstrate the proposed methods. Details of the study design and survey have been described previously [37]. For this analysis, we included 270 eligible women aged 15–44 years (mean age 31 years) who reported the current duration of their pregnancy attempt (see [3] for further details). Initially we present unadjusted analyses of the data, and then we incorporate covariates and present a comparison to a Weibull AFT model. The validity of the current duration values decrease for longer durations [38], but can be considered reliable over shorter periods of time [39]. As a result, we censor current duration responses at a value after which they are not considered to be reliable. In this analysis, we censored all durations longer than 36 months (21.4% of the data).

To estimate the unadjusted distribution of T, we analyzed the NSFG data with the piecewise constant model without covariates ${\widehat{\overline{F}}}_{PC}$. We compare ${\widehat{\overline{F}}}_{PC}$ to a discrete nonparametric estimate, denoted by ${\widehat{\overline{F}}}_{NP}$, which can handle zeros and ties. The computation and asymptotic properties of ${\widehat{\overline{F}}}_{NP}$ are discussed in Appendix A of the supporting information. After censoring, the points of digit preference for this data are 6, 12, 24, and 36 months. For the piecewise constant model we tested various locations and sizes for the vector of knots and did not see any marked difference in the results. The analyses presented here used seven knots with locations {1, 2, 4, 9, 18, 30, ∞}. Confidence intervals were calculated using the percentiles of 270 bootstrap survivor function estimates.

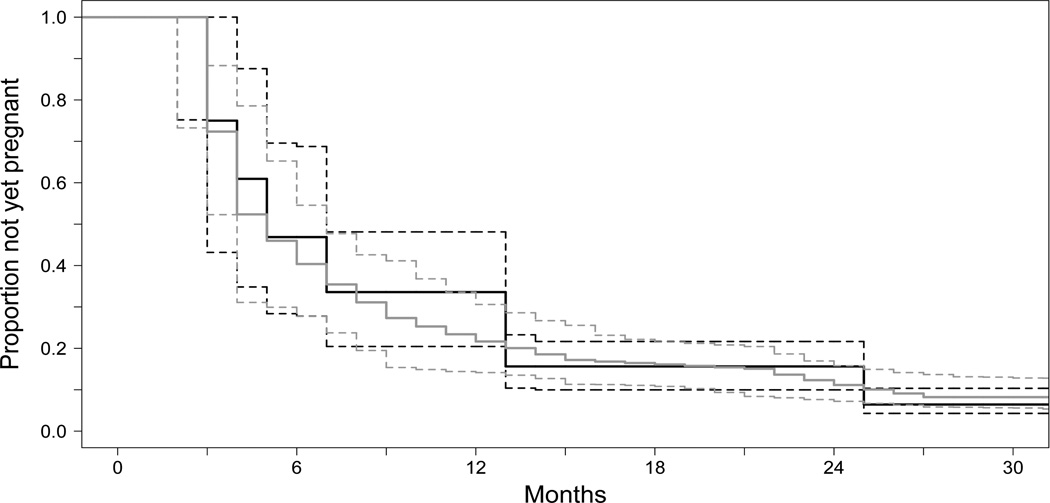
The estimated piecewise constant and nonparametric survivor functions are given in Figure 3, along with 95% pointwise confidence intervals (CI). In Table 3, we present point estimates and confidence intervals for the probability that a pregnancy attempt is longer than 12 or 24 months. The nonparametric method found ${\widehat{\overline{F}}}_{NP}(12)=0.336$ with 95% CI (0.212, 0.481), while the piecewise constant method found ${\widehat{\overline{F}}}_{PC}(12)=0.223$ with 95% CI (0.148, 0.310). Here, ${\widehat{\overline{F}}}_{PC}(12)$ is closer to historical values than ${\widehat{\overline{F}}}_{NP}(12)$. The over estimation of ${\widehat{\overline{F}}}_{NP}$ at the points of digit preference corroborates the results in Section 4.1.

Figure 3.

Current duration estimate of the survivor function of TTP for the NSFG data (solid line), with 95% pointwise bootstrap confidence intervals (dashed line) for the nonparametric method (black) and the unadjusted piecewise constant model (gray).

Table 3.

(Top) Unadjusted estimates and 95% confidence intervals (95% CI) for the prevalence of total durations longer than 12 and 24 months for the nonparametric and piecewise constant approaches. (Bottom) Regression coefficients and estimates intertility prevalence for 31-year old women that are parous (F̄(12|1, 0)) or nulliparious (F̄(12|0, 0)) from the semiparametric, and piecewise constant models.

Unadjusted
	Nonparametric		Piecewise
	est	95% ci	est	95% ci
F̄(12)	0.336	(0.212, 0.481)	0.223	(0.148, 0.310)
F̄(24)	0.223	(0.162, 0.290)	0.123	(0.082, 0.167)
Covariate Adjusted
	Semiparametric		Piecewise
	est	95% ci	est	95% ci
Parity	0.492	(0.257, 0.728)	0.747	(0.206, 1.289)
Age	−0.035	(−0.054,−0.015)	−0.036	(−0.074,0.003)
F̄(12|1, 0)	0.303	(0.138, 0.463)	0.191	(0.110, 0.295)
F̄(12|0, 0)	0.475	(0.291, 0.610)	0.358	(0.244, 0.473)

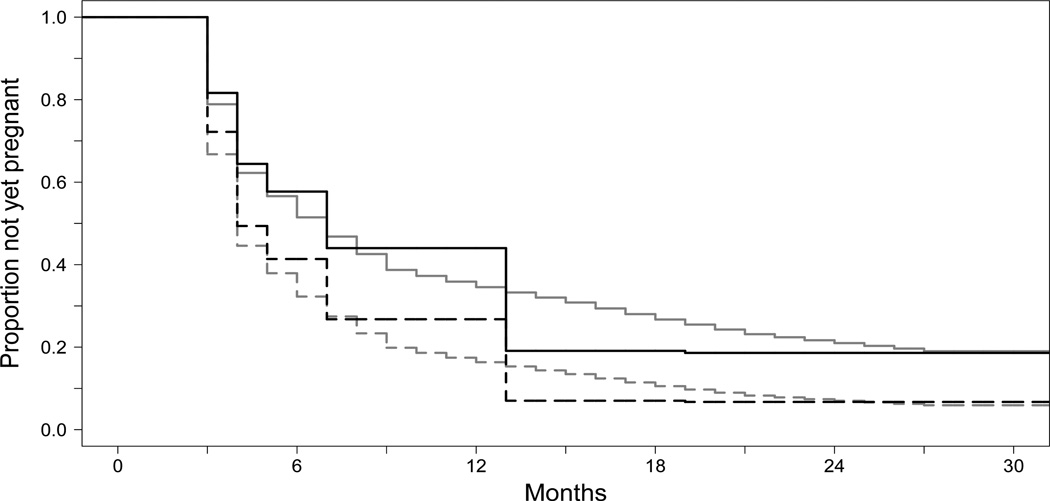
To assess the association between exposures and the distribution of T, we used the proposed backwards recurrence Cox model (piecewise and semiparametric). The covariates used in the model were parity (z₁), the indicator of at least one live birth, and the woman’s age minus 31 years (z₂). A woman is said to be parous if she has had a previous live birth (z₁ = 1), and nulliparous otherwise (z₁ = 0). In Table 3, we present the estimated β coefficients, and the estimated probability that T > 12 months for a 31-year old parous woman, denoted by F̄(12|1, 0), and a 31-year old nulliparous woman, denoted by F̄(12|0, 0). In Figure 4, we display the estimated survivor functions $\widehat{\overline{F}}(·|1,0)$ and $\widehat{\overline{F}}(·|0,0)$.

Figure 4.

Semiparametric (black) and piecewise constant (gray) current duration estimates of the survivor function of TTP for parous women (dashed line), nulliparous women (solid line).

The point estimates for the effect of parity on T were consistent for both models. These estimates suggest that parous women become pregnant faster than nulliparous women. The effect of age was negative in both models, and achieved significance at the 0.05 level for the semiparametric model. The estimates for the prevalence of infertility corroborate the nonparametric results, showing that at the points of digit preference there appears to be over estimation of the survivor function for the semiparametric model. Further, the width of the 95% confidence intervals indicates greater precision for the piecewise model in the survivor function estimate. These results indicate that with 0.358 probability, a 31-year-old nulliparous women will have 12+ month pregnancy attempt.

We compared the above results to those obtained from the parametric AFT model proposed in [16]. To fit the AFT model we altered the data to T* = T + C where C = 0.5, and fit log(T*) = −(μ+ γZ) + ∈/γ where ∈has an extreme value distribution. The estimates of the coefficients from the fitted model were in the same direction as those presented in Table 3, where γ̂₁ = 0.76 and γ̂₂ = −0.06 for parity and age, respectively, and both were significant at the 0.05 level. Further, the estimated shape was γ̂ = 0.84. Note that γ̂ < 1 and ĝ(0|Z) is unbounded. Thus, using the notation in Section 2, ĝ ∉ 𝒫₀ and F̄ cannot be estimated from this model (see [13] for further discussion on this issue). The results were similar for C = 0.1 and 1.

6. Discussion

The current duration approach is an evolving method that is gaining attention in light of global concerns about declining human fecundity accompanied by purported increases in the prevalence of infertility. In this paper, we have proposed semiparametric and piecewise constant backward recurrence Cox models to estimate the distribution of the total length of pregnancy attempt from the observed current length of pregnancy attempt. The use of the semiparametric framework is advantageous over the parametric AFT model, since little is known about the underlying distribution. As discussed in Section 2, applying the AFT model to current duration data is a non-surjective operation since estimates of ĝ can have no corresponding F̄. The proposed methods result in valid estimates of F̄, and can incorporate issues that will be encountered in practice, such as current durations equal to zero and digit preference. This gives the proposed methods practical relevance to those analyzing current duration data.

Our findings suggest that inattention to digit preference overestimates the percentage of women not achieving pregnancy at 12 and 24 months. Specifically, when controlling for digit preference we estimated that 21.7% of parous women aged 31 years will require a 12+ month attempt for pregnancy, when ignoring such reporting preferences this value was more than 50% larger at 33.6%. Our analyses also examined the effect that exposures have on the distribution of the total length of pregnancy attempt. Assuming that F is continuous, the semiparametric model found that the rate of the total length of pregnancy attempts was 1.64 times higher for parous women than it was for nulliparous women, and that an additional year of maternal age lowers this rate by 0.97. When the Weibull AFT model was used, the estimated coefficients resulted in a model where F̄ could not be estimated. As a result, a different modeling approach would need to be implemented to estimate F̄. The proposed modeling approach has assumed a proportional hazards form for T, which can not be verified by the observed data. One could, however, check if (2) shows signs of lack of fit based on the observed Y values. This would not guarantee that the proportional hazards assumptions holds, but it would verify if the data are consistent with the assumed structure. Validity and recall bias of current duration data has not been studied and if present could bias parameter estimates.

Current duration analyses provides inference on the total length of pregnancy attempt (T), which is the minimum of TTP (X) and the length of an unsuccessful pregnancy attempt (U). The fact that the outcome is total length of pregnancy attempt and not TTP needs to be taken into consideration when interpreting model estimates. For example, if we had found that older age was associated with shorter T it could be due to older age being related to shorter U, and thus not related to the outcome of interest X (we found older age being associated with longer T so this was not an issue). Development of statistical methods that can delineate between the competing factors that end pregnancy attempts is an area of future development.

The steady state assumptions given in Section 2 would be violated if there is a change in fecundity over time, or if there was a pattern to the initiations of the women’s pregnancy attempts. With regard to the former the research has been mixed [40, 41], and this assumption should be reasonable over the time period of interest (1999–2002). In a short time frame such as this (censored at 3 years), the variation in attempt times would mainly be due to seasonal differences in pregnancy attempts over a given year. Sensitivity analyses discussed in Slama et al. [42] showed some seasonal fluctuation in the distribution of starting dates for planned pregnancies; however, they found little difference in findings when accounting for this variation in their model. An area of future research is the development of methods to address the validity of the steady state assumptions.

The field of fecundity has greater relevancy in light of sociodemographic changes in childbearing for most developed countries, resulting in women or couples’ expectation for more immediate pregnancy results. This underscores the relevancy of monitoring couple fecundity as measured by TTP [8] for estimating fecundity related impairments such as conception delay or infertility. The benefit of the current duration approach is that it can incorporate women who are not planning to become pregnant (missed in prospective cohorts), and women that have never been pregnant (missed in most retrospective studies). The difficulty with current duration data is the lack of methods available to estimate the distribution of the total length of pregnancy attempt (previously, only nonparametric and parametric methods are available), and to estimate the association exposures have with the total length of pregnancy attempt (previously, only parametric methods are available). The proposed proportional hazards methods are semiparametric. Further, digit preference, which is common in studies where recall is involved, has been addressed with the piecewise model.