Abstract
Understanding the charging mechanism of electrospray ionization is central to overcoming shortcomings such as ion suppression or limited dynamic range and explaining phenomena such as supercharging. Towards that end, we explore what accumulated observations reveal about the mechanism of electrospray. We introduce the idea of an intermediate region for electrospray ionization (and other ionization methods) to account for the facts that solution charge state distributions (CSDs) do not correlate to those observed by ESI– MS (the latter bear more charge) and that gas phase reactions can reduce, but not increase the extent of charging. This region incorporates properties, e.g., basicities, intermediate between solution and gas phase. Assuming that droplet species polarize within the high electric field leads to equations describing ion emission resembling those from the equilibrium partitioning model. The equations predict many trends successfully, including CSD shifts to higher m/z for concentrated analytes and shifts to lower m/z for sprays employing smaller emitter opening diameters. From this view, a single mechanism can be formulated to explain how reagents that promote analyte charging (“supercharging”) such as m–NBA, sulfolane, and 3–nitrobenzonitrile increase analyte charge from “denaturing” and “native” solvent systems. It is suggested that additives’ Brønsted basicities are inversely correlated to their ability to shift CSDs to lower m/z in positive ESI, as are Brønsted acidities for negative ESI. Because supercharging agents reduce an analyte's solution ionization, excess spray charge is bestowed on evaporating ions carryingfewer opposing charges. Brønsted basicity (or acidity) determines how much ESI charge is lost to the agent (unavailable to evaporating analyte).
Keywords: electrospray ionization, protein conformation, charge state distributions, supercharging
Introduction
Understanding the charging mechanism of electrospray ionization (ESI) is central to overcoming shortcomings such as ion suppression or limited dynamic range and explaining phenomena such as supercharging. The genesis of this article occurred when, in considering means by which supercharging agents increase analyte charge, we realized that the implications and ramifications of various hypotheses always returned to the unresolved mechanism of ESI. Fortunately, decades of accumulated experimental observations arm us with the data needed to query and refine different models, in search of one that might unify all experimental results. Here we explore what some of those accumulated observations reveal about the mechanism of electrospray.
Since the introduction of electrospray ionization (ESI) as an ion source for mass spectrometry (MS), its mechanism for ion emission has been debated. Theories have been developed [1-13], and curious observations have accumulated (e.g., wrong-way round ionization, the increased charge and narrower charge state distributions produced by smaller spray orifices, and the non-denaturing surfactants that reduce surface tension while increasing analyte charge). It is clear that many parameters (e.g., analyte composition, solvent gas-phase basicity, solution-phase conformation) affect charge state distributions, but a unifying view remains elusive. In the interest of spurring debate and discussion, we revisit the mechanism of ESI, focusing on solution phase, gas phase, and the region in-between, and attempt to discern what these and other curious observations tell us about the mechanism of ESI.
A Three–Regime View of Electrospray Ionization
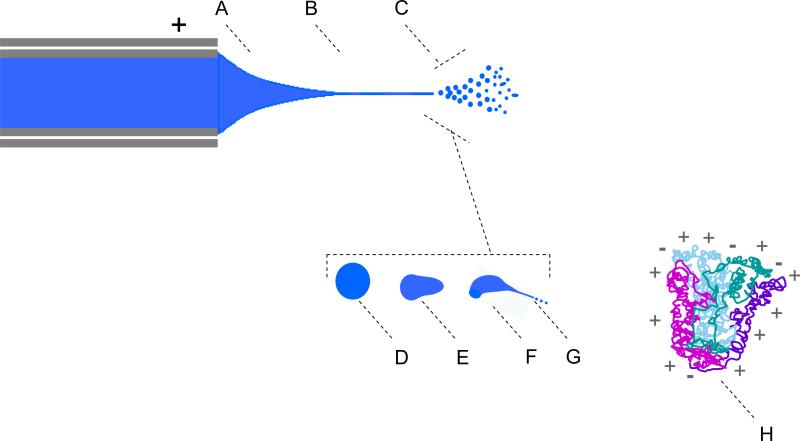
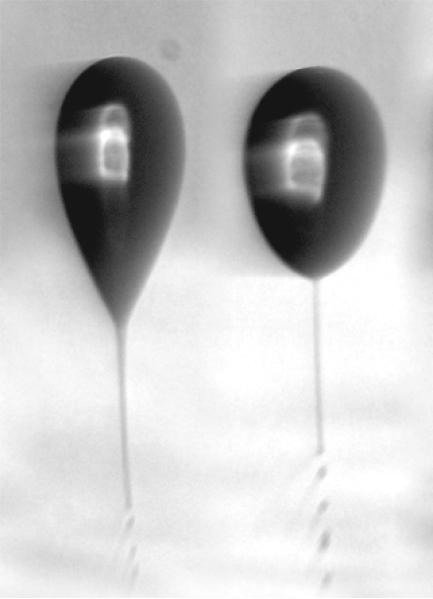
We introduce a three–regime view of ESI, with solution, intermediate, and gas phase regimes (Fig. 1). It is assumed that solution species are described by classic chemical equilibria. Ions from solution may enter the intermediate regime, and ions released from the intermediate regime enter the gas phase to persist unchanged, or be transformed according to gas phase kinetics and thermodynamics. Intermediate regime species are assumed to have properties lying between those of solution and gas phase; hence, apparent solution and gas phase basicities remain relevant. Intermediate regime ions contact solvent transiently in a high electric field e.g., a liquid filament jet emerging from an unstable droplet, such as one produced by electrospray or by a vibrating orifice generator (Fig. 2)), facilitating charge losses or gains inconsistent with solution equilibria or gas phase chemistry. Intermediate–regime ions can undergo intermolecular charge transfer or they can redistribute charge intramolecularly, e.g., charge can migrate from a protonated amine to a carboxylate anion. Once highly charged analytes emerge from the intermediate regime and enter the gas phase, they may continue to redistribute charge intramolecularly, or, if kinetically favored, may transfer charge to other molecules they encounter. Gas phase basicity limits or reduces charging only when appropriately reactive species are available, depending, in part, on the population (density) of gas–phase reactants. Like–charge repulsion dictates that gas phase ions cannot increase charge, regardless of whether they unfold in this region; they can only maintain, reduce, or redistribute it.
Figure 1.
Three–Regime View of Electrospray Ionization for a spray operating in cone–jet mode. Region A corresponds to liquid from the edge of the emitter tip through the Taylor cone up to the jet, B corresponds to the jet and C to the point where the jet disrupts to initiate an electrospray plume. An expanded view of the plume shows stages of ESI droplet evolution, regions D, E, F, and G. As droplet D evaporates, the increasing electrostatic repulsion causing it to distort (E), and ultimately eject its own secondary droplets by asymmetric fission (F). Excess charge is disbursed to primary droplets in region C, and to secondary droplets in G. Steps D–G may repeat to produce higher order droplet progeny, until the volatile droplet evaporates. Our model assumes that ions, as well as droplets are ejected from regions C and/or G to yield H, a gas phase analyte ion (likely solvated). Our model considers that a small number of opposing charges may also be present in the gas phase ion.
Figure 2.
Droplets released by a vibrating orifice aerosol generator are subjected to electric fields to induce distortion and jetting, as part of field induced droplet ionization (FIDI). (Reprinted with permission from R. L. Grimm and J. L. Beauchamp, J. Phys. Chem. B. 109, 8244–8250 (2005), copyright 2005 American Chemical Society.)
Why is it useful to consider an intermediate regime?
The intermediate regime is the only region where macroion charge can increase beyond that defined by solution equilibria. For “wrong–way round” ionized solutions to yield mass spectra; i.e., solutions sprayed with electrical biases opposite the analyte polarity in solution [14-18,10], assorted neutralizations and charge inversions must be performed here to “flip” macroion charge, prior to relocating to the gas phase. By introducing charge transfer and other accommodations that analytes undergo when exiting the bulk solution, this concept rationalizes observations that ion intensities vary little over pH 3–11, despite massive changes in solution opulations [17-19]. Within this intermediate environment, unique equations are needed to describe ion energetics, reactant densities, etc. For example, at pH 7, solution phase equilibria predict amine and guanidino protonation and carboxylate deprotonation. In the gas phase, however, carboxylate anions have higher gas phase basicities than uncharged amine and guanidino groups [20-22]. Thus, if a pH 7 protein was instantly transported to the gas phase, protons sited at positions conferring the most stability to the solution–phase protein would almost certainly differ from those maximally stabilizing gas phase ions. Perhaps protons would subsequently migrate intramolecularly. If the relocation is not instantaneous, however, and occurs in a region of high electric field with density between solution and gas phase; e.g., a nano–jet breaking into progeny droplets or a filament protruding from a decomposing droplet, intermolecular charge transfers inconsistent with bulk solution equilibria will be facilitated, increasing charge.
As in the bulk solution or gas phase [23], an individual site's acidity or basicity will be modulated by its environment and by aliquots of charge positioned near or far away. This modulation impacts the width of charge distributions based on the steepness of (Δbasicity)/charge or (Δacidity)/charge within this region. Although protein conformation has frequently been cited as affecting widths of charge distributions [24,25], it does not provide a reason for that width a priori. Instead, consider that for compact, folded proteins the basicity of individual sites decreases sharply with addition of each proton, yielding sharp titration curves, while for large, unfolded proteins, an additional bound proton exerts little impact on the basicity of distant sites, making the change in basicity per unit charge a shallower function, leading to a broader population of charges. These ideas are akin to arguments that widths of charge distributions reflect solution ΔpKa values [26], but when applied to the intermediate regime, explain wrong–way round ionization and other observations.
Where is this intermediate regime? In principle, a 3–regime construct could be envisioned for the charge residue model (CRM), ion evaporation model (IEM), or other proposed models [1-10], particularly as distinctions between them blur in attempts to explain non–conforming observations [27-29]. It could be argued that Fenn's non–spherical, elongated droplets, analyte–stabilized to allow deformation and charge accumulation beyond that permitted by solvent surface tension, fit such a framework [4,5]. The elongated droplets are not gas phase, nor are they described by bulk liquid properties. Also fitting an intermediate regime is Kaltashov's model [29] where protein–sized droplets extend from liquid jets. In the case of the CRM, an intermediate regime could reflect the period between existence of a droplet with the minimum number of solvent molecules displaying bulk solution behavior and complete evaporation to the residue. “Hidden” processes occurring in the CRM intermediate regime would transfer droplet charge to the analyte in a way reconciled with the macroion's chemical properties.
Following, we will discuss why CRM may not be the dominant process releasing highly charged protein ions to the gas phase, although suggestions [30] that lesser–charged, non–specific multimer aggregates may be the residues of larger droplets appear reasonable. Here, we define the intermediate regime to include the liquid jet extending from a precursor droplet, similar to Kaltashov [29], and perhaps, as well, the Taylor cone jet, originally proposed by Siu and colleagues as the source of ESI–generated ions [31,32]. We will consider jets extending from fissioning primary, secondary, and even smaller droplets as potential sources of protein ions.
Challenges to Existing Models: Diameter of the Emitter Opening and Spray Current Affect ESI Charging
Several laboratories reported that protein (native and denatured) charge state distributions (CSDs) undergo a small, but reproducible shift to higher charge when delivered by nanospray versus standard electrospray [33,34]. Smaller and smaller emitter openings yield higher and higher average charge states for peptides, too [35], arguing that the behavior is unrelated to macromolecular conformation. Because most CRM formulations link maximum charging to final droplet (analyte) size, and because analytes experience multiple droplet fission cycles in CRM, governed by solvent properties, no memory of nascent droplets should persist.
One could reasonably consider a charge residue model in which analyte charge had little relationship to droplet charge, perhaps defined only by the droplet residue's chemical properties and environment. Such a model might predict that the protein CSDs obtained by analyzing a particular solution composition with fixed instrument settings would be well-defined and constant (displaying no day-to-day variation). Unless they altered the sprayed solution properties significantly, changes in the diameter of the ESI emitter opening would not be expected to affect these CSDs, either. Thus, both charge-dependent and –independent CRM ormulations fail to explain these curious observations.
Ubiquitin spectra from water were reported to vary between two charge state distributions [36], a dominant CSD centered on 8+, and a 6+–centered distribution arising from spontaneous spray fluctuations reducing ESI current. CRM predictions, unrelated to the nascent droplet and lacking a link to spray current, again fail to explain the observation. These curious behaviors encourage us to consider mechanisms releasing ions earlier than CRM. Perhaps they reflect ion emission from droplet protrusions, as smaller droplets yield finer filaments sustaining higher electric fields.
Droplet size has also been linked to the bound:free ratios observed for non–covalently associated species. Gabelica, et al. [37] noted that ions appeared to be sampled differently from individual nanospray capillaries, as ratios of a (DNA)2(protein)2 complex to double–stranded DNA varied with individual capillaries. Gas phase dissociation, yielding only single–stranded DNA, could not be responsible for the observation. Similarly, spraying from larger capillaries was observed to reduce the observed ratio of RNase–CTP complex to free ribonuclease (RNase) [38]. Relative detection sensitivity was linked to surface activity in arguments favoring ionization of surface-active species, based on assumptions that excess charge is tied to the droplet surface [39]. Folded proteins have been argued to yield less ion signal than denatured ones in ESI [40], because residues with smaller accessible surface areas are less likely to capture protons. Accounting for how variations in droplet size affect CSDs and analyte ratios is a challenge for all models.
Supercharging—Another Challenge to Existing Models?
The term “supercharging” was applied by Williams and colleagues [41] to describe the increased charging observed in spectra obtained from solvents supplemented with m-nitrobenzyl alcohol (m-NBA, 0–20%), glycerol (0–50%), dimethyl sulfoxide (DMSO, 0–50%), m– chlorophenol (0–40%), formamide (0–10%), and 2–methoxyethanol (0–25%) [41-43]. Its usage has expanded to encompass different phenomena, including the increased charging associated with adduction of trivalent lanthanum cations [44], and “electrothermally–induced” denaturation from native solutions [45], subsequently linked to CO2-outgassing from bicarbonate buffer [46]. Here, we restrain application of the term “supercharging” to analytes’ increased positive or negative charge associated with limited addition of certain agents to native or denaturing solutions, but, for native ESI, only when that increase is not accompanied by classic denaturation signatures. Additive-associated charge increases for analytes sprayed from denaturing solutions have been attributed to increased surface tension (γ) [41], as predicted by extending the Rayleigh stability limit (equation 1) to the charged residue model [5].
| (1) |
In contrast, increases observed when native solutions are supplemented have been blamed on protein denaturation [47,48]. The mechanism of supercharging is debated, as are molecules classified as superchargers.
One element of the debate is that protein data presented to support dependence on surface tension were acquired from denaturing solvents [41], yet many researchers believe that the CRM (and thus the surface tension dependence), do not apply to denatured proteins, as only native charge distributions conform to Rayleigh predictions [5,4,49].
Other examples and arguments countering surface tension's role have been offered. (1) Šamalikova and Grandori established that protein CSDs in the presence of low surface tension, low vapor pressure additives are either the same absent those additives or present much smaller changes than calculated from the Rayleigh equation [49]. (2) CSDs for short oligonucleotide anions lacking defined conformations and sprayed from methanol/H2O were found to increase charging upon addition of m–NBA, opposing surface tension–based predictions [50]. (3) Comparing ESI spectra obtained from water–HCl to those from water–acetic acid revealed little difference in CSDs, despite the argued large difference in surface tensions for late–stage ESI droplets [36,51]. (4) Data from m-NBA addition to dendrimeric poly(propyl)eneimine polymer DAB–16 are often cited to support surface tension effects [43], yet the data for polymer DAB-64 counter this view. (5) Assumptions underpinning analyses supporting surface tension effect have also been questioned, i.e., that late–stage ESI droplets contain the component lowest in vapor pressure almost exclusively, rather than enriching species with the lowest evaporation rates [51,3]. These questions arise because, unlike distillations, liquid and vapor are not in equilibrium in electrospray aerosols, arguing that evaporation rates should be predicted from butyl acetate–referenced scales, instead [52].
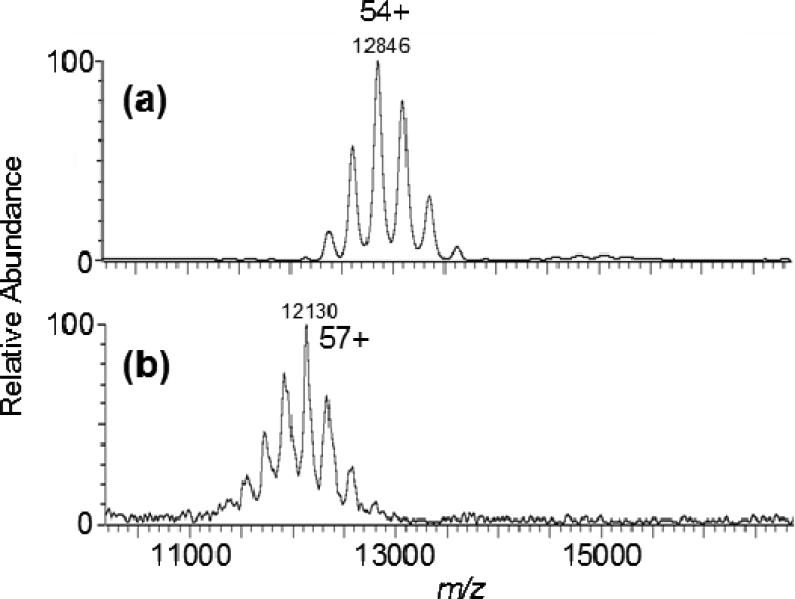
Later reports by Lomeli et al. [53,54] emphasized the utility of adding m–NBA to aqueous solutions to increase charging for a range of protein complexes. Figure 3 illustrates that subunit interactions can be maintained, despite the increased charging that results when m–NBA is added to aqueous solutions of the 690 kDa 20S proteasome. With a surface tension below H2O, m–NBA should not increase charge, at least according to Rayleigh limit theory. Subunit losses were not observed from any of the four multimeric complexes to which m–NBA (to at least 0.5% v/v) was added [53,54]. Nor was any evidence found for loss of heme from holo–myoglobin, zinc from carbonic anhydrase II or ATP from adenylate kinase [55], and the binding locations obtained by MS/MS of those “supercharged” species were consistent with literature reports. Circular dichroism (CD) and H/D exchange measurements revealed no effect from 0.5% m–NBA on aqueous myoglobin structure [53].
Figure 3.
Subunit interactions are maintained, despite the increased charge borne by a 28-mer complex. ESI-MS of Methanosarcina thermophila 20S proteasome (690-kDa) (a) without, and (b) with 0.25% m-NBA. (Reprinted Fig. S1, with permission, from Lomeli, et al [53].
Additional data also illustrate that non–covalent complexes can assume significantly more charge at reagent concentrations below those detaching subunits [56,57]. Adding 0.5% m–NBA to a solution of GroEL increased the average charge of the tetradecamer from 66+ to 71+, while revealing very limited disruption of the complex [56].
Initially, it was argued [47] that the increased charge observed in non–covalent complex and native protein MS with m–NBA present resulted from droplet heating, as the high boiling point of m–NBA reduced evaporative cooling. The authors considered charge state distributions obtained from solutions heated to 92oC to be similar to those containing 0.4% amounts of m–NBA, although there is disagreement on that interpretation. Comparisons of Fig. 2 in that manuscript [47] to Figure S2b in Lomeli et al. [53] or to Figs. 1 and S2 in a latter manuscript [54] suggest that myoglobin ions in the Berkeley study received more activation in the atmospheric pressure-vacuum interface, impacting the results.
Arrival time distributions (ATDs) from a traveling wave ion mobility spectrometer (TWIMS) suggested that higher charge state myoglobin ions formed by m–NBA or sulfolane addition to aqueous solutions were significantly expanded versus lower charge state ions [58], although the extent of ion activation applied by the TWIMS is hard to assess from the uncalibrated data [59]. Questions arise because ATDs acquired from identical charge states without and with m–NBA and sulfolane were not measurably different and because ATDs for the higher charge states, accessed with additives, showed no dependence on reagent concentration. Circular dichroism showed that myoglobin helicity was not reduced in aqueous solutions for sulfolane concentrations from 0–0.8 M, and adding ~250 mM sulfolane appeared to make aqueous myoglobin more resistant to thermally–induced reductions in helicity. For 0.8 M sulfolane solutions, significant losses of helicity were observed above 50°C [58]. NBA and sulfolane addition to aqueous protein solutions had relatively little effect on structure at concentrations < 0.5% and < 1 M, respectively [53,58]. That structure could be lost by combining sulfolane addition with temperature elevation or guanidinum hydrochloride addition led to a proposal that sulfolane-associated charge increases reflect denaturation from superimposed thermal and reduced stability effects [58,60,48], making it relevant to consider what temperatures would be attainable by stable (non–evaporating) droplets moving through a bath of room temperature, atmospheric pressure laboratory air.
Hogen et al. [61] applied an atmospheric pressure differential mobility analyzer–mass spectrometer (DMA–MS) to compare the mass and mobility of monomeric and multimeric phosphorylase B ions electrosprayed from charge reducing triethylammonium formate in water (pH 6.8) with and without sulfolane. Inclusion of the triethylammonium buffer enabled comparison of identical charge states. Unlike TWIMS, DMAs measure cross–sections directly, rather than inferring them from multipoint calibrations performed against known structures under identical conditions. Secondly, the DMA measures mobilities upstream of the MS interface, immediately following solvent evaporation, (thus still enduring the temperature elevations hypothesized by the Williams lab) [58,60,48], but prior to any collisional heating or declustering applied in the atmosphere–to–vacuum interface. Clearly, a trade–off for this latter benefit is that analyte ions may be solvated when mobility–analyzed, but subsequently desolvated by collisions in the atmospheric pressure–vacuum interface. In contrast to the ~60% mobility decreases found between folded and unfolded proteins [62], mobilities were decreased by only ~6–10% with 138 mM sulfolane.
Subsequently, TWIMS cross–sections were reported for concanavalin A (con A) tetramers that revealed few differences in cross sections for modest additions of supercharging agents [48]. Cross sections for the 19+ to 25+ charge states of the con A tetramer were essentially the same, independent of supercharging agent concentration (states 19+–22+ were present with 0% m–NBA). Also, cross–sections for states 26+–28+ were within 5% of those for the less highly charged ions. Because little difference was observed in cross sections for m–NBA–exposed tetramers, as well as for m–NBA–exposed anthrax toxin multimers, it was argued that chemical and/or thermal “destabilization” could cause charge shifts without extensive unfolding [48].
We continue to be swayed by the counter arguments presented above along with some additional points:
Adding supercharging agents in modest, but increasing amounts to aqueous and “denaturing” solutions monotonically shifts protein CSDs to higher charge. That behavior is illustrated here for additions to 5% v/v of propylene carbonate, another reagent we identified [63,64] (Fig. 4), as well as previously for additions of sulfolane to 276 mM (Fig. S2 of Lomeli et al.) [54]. In contrast, CSDs for proteins undergoing a cooperative folding transition change in a different fashion, typically moving from a single charge envelope to two discrete envelopes or to a bimodal distribution [24,25,65,66]. As the unfolding coordinate is traversed, one envelope increases in abundance as the other decreases. In contrast, only at high concentrations do some supercharging reagents display denaturation signatures with characteristic bimodal distributions, or binding altered from “native” conditions. Hence, it is important that charging behavior be evaluated for a range of additive concentrations.
The aqueous solubility of many reagents is low [54], potentially limiting the extent of enrichment attainable in late stage ESI droplets, before reagent aggregation or precipitation occur; e.g., solid supercharging reagents such as m–nitroacetophenone and m–nitrobenzonitrile are both water–soluble to less than 2 mM.
Grimm and Beauchamp [67] found that high concentrations of m–NBA inhibited droplet evaporation in their standard spray conditions; e.g., methanol droplets with 2% v/v typically stopped evaporating at 5–10 m in size and attained only 20–50% of their Rayleigh limit charge. That charge shifting of peptides and proteins scales with additive concentration to 3.4% and even 6.7% [41], suggests that the CRM does not account for most of the ions observed in supercharging experiments.
Requiring two different mechanisms to explain how the supercharging reagents m–NBA, sulfolane, 3–(trifluoromethyl) benzenemethanol, etc. increase charge, one applied to “denaturing” solvents and one applied to “native” solvents is cumbersome. That so many reagents increase charge from both solutions does not seem coincidental. Can a single mechanism explain all observations?
Figure 4.
Supercharging agents increase charge monotonically as more and more reagent is added, whereas the onset of denaturation is marked by the sharp onset of a second distribution. ESI-MS of equine holo-myoglobin with (a) 0%, (b) 0.5% (c) 2%, and (d) 5% propylene carbonate (v/v) show smoothly increasing CSDs.
A Mechanism for Supercharging based on the Three Regime View of Electrospray Ionization and Brønsted Acid–Base Properties
Additive basicity's role in charge elevation was dismissed previously [60], because the gas phase basicities of NBA and sulfolane lie above H2O. However, if we consider that gas phase reactions would only be able to reduce an analyte's charge, not increase it, then we conclude that the important properties driving the extent of charging must operate before or during ion emission, when charge is allocated between droplet and analyte, not in the gas phase. Here, low volatility reagents less basic than solvent (in the intermediate regime, and likely, in solution) can feasibly increase charge in positive mode, while reagents less acidic than the solvent can increase charge in negative ion mode. Once in the gas phase, the extent to which an analyte will lose charge by transferring protons to species with higher gas phase basicity depends on the latter's gas phase population and, hence, volatility.
Supercharging capacity is displayed not only by m–NBA, but by ortho– and para– isomers, too, despite the fact that chemical isomers typically possess different surface tensions. That so many structurally related compounds (e.g., aromatic nitro molecules or sulfones (3–chlorothiete–1,1–dioxide, sulfolene, and sulfolane) [68] supercharge efficiently, implies that chemical, rather than bulk physical properties are key. NBA [54], propylene carbonate (Fig. 4d), [63,64] and sulfolane [68] adhere preferentially to high charge states (Fig. 5), despite the greater activation (proportional to charge) received during air–vacuum transport. This behavior demonstrates that additives interact with proteins [54].
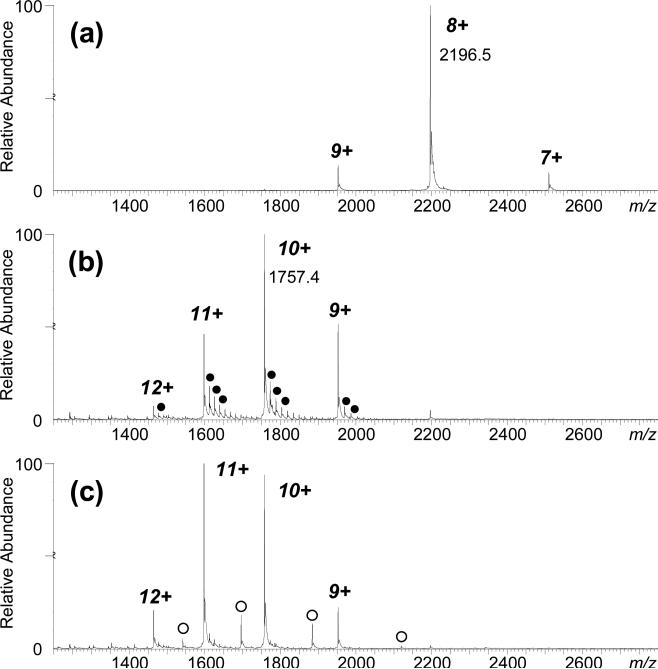
Figure 5.
(a) Positive ion ESI-MS with +15 V trap-cell collision energy of equine holo myoglobin in 20 mM ammonium acetate, and (b) adding 0.5% m-NBA, and (c) with 0.5% m-NBA and +40 V trap-cell. Increasing collision energy reduces m-NBA adducts (●), increases the abundance of higher charge states, and induces heme-loss to yield apo-protein (○). Preferential clustering to high charge states of holo–myoglobin by supercharging reagents, and their detachment as neutrals, reveals that additives have low gas phase basicities (as compared to analyte) and that they interact with the protein. (Reprinted Fig. S2, with permission, from Lomeli, et al [53].
At low m/z, spectra obtained from aqueous 20 mM NH4OAc showed NBA ions or clusters charged by NH +4 and Na+ addition, but not H+, reflecting NBA's relatively low Brønsted basicity versus other species present (see supplementary Fig. S-1, online resource). Many agents with little or no efficacy to increase ESI charge, such as pyridine N–oxide (PNO), displayed abundant (M+H)+ ions and, often, protonated cluster ions. These observations led us to consider Brønsted acid–base contributions to ESI charging and supercharging, partitioning of charge between analyte and solution, and their integration with ion emission from the intermediate regime.
Class 1 Reagents (Shift Native & Denaturing Solutions)
Reagents found capable of increasing the positive charge carried by proteins sprayed from aqueous NH4OAc solutions included sulfolane, propylene carbonate, o–NBA, m–NBA, p–NBA, 3–nitrophenylethanol, 3–nitroacetophenone, 3–nitrobenzonitrile, benzyl alcohol, and 3– (trifluoromethyl)benzene methanol [54,63,64]. Although high concentrations of some reagents do unfold proteins in NH4OAc/H2O, as evidenced by holo–myoglobin heme loss and/or bimodal charge state distributions, these reagents can be employed over a range of concentrations that increase charge without displaying hallmarks of denaturation. Moreover, sulfolane, 3– nitrobenzonitrile, and 3–(trifluoromethyl)benzene methanol were also investigated with acidic denaturing solutions (0.1% formic acid/H2O or 1:1 H2O:CH3CN) and found to increase charge under those conditions, too. Even large polypeptides such as immunoglobin G can be supercharged, as illustrated in Fig. S-2 (see supplementary material in online resource).
Fifteen years ago, non–ionic saccharide detergents were shown to increase charge from native and denaturing solvents [69]. The gentle, non–denaturing surfactants n–octyl sucrose, n–dodecyl sucrose, n–dodecyl–β–D–maltoside, n–hexyl–β–D–glucoside, n–octyl–β–D–glucoside, n–decyl–β–D–glucoside, n–dodecyl–β–D–glucoside, and n–octyl–β–D–thioglucoside increased charge in proteins and in the peptide KRTLRR. Interestingly, non–ionic polyoxyethylene surfactants Triton X–100, TWEEN–20, Nonidet P40 (NP40) and Thesit displayed no ability to increase charge, nor did the zwitterionic or anionic surfactants 3–(3–cholamidopropyl) dimethyl–ammonio–1–propane sulfonate (CHAPS), sodium cholate, sodium taurocholate, and sodium dodecyl sulfate (SDS). Cationic surfactant cetyl trimethyl ammonium bromide (CTAB) decreased charge.
The evidence is clearly inconsistent with attribution of increased charging to higher surface tensions or protein denaturation, because (1) surfactants reduce surface tension, (2) short peptides such as KRTLRR are not expected to have well–defined higher order structures, and (3) high concentrations of non–ionic saccharide detergents have been shown to retain membrane complex associations during ESI–MS [70].
The Brønsted basicity of a neutral compound in solvent H2O is described in terms of the equilibrium constant (KBH+) of its conjugate acid BH+, or by pKBH+. See equations 2–4.
| (2) |
| (3) |
| (4) |
Values of pKBH+ have been obtained in various solvents, and, in an attempt to relate different solvent scales, have been extrapolated to values for water, pKBH+w. Values of pK+BHw have been specified for sulfolane, H2O, and methanol as −12.5, −1.74, and -2.05, respectively [71]. Values for NBA, 3–nitrophenylethanol, 3–nitroacetophenone, 3–nitrobenzonitrile 3– trifluoromethylbenzene methanol and benzyl alcohol are not available, but values for related compounds provide guidance. Strong electron–withdrawing groups (e.g., nitro– and trifluoromethyl–) reduce basicity, suggesting that the pKBH+w of 3–nitroacetophenone and 3– nitrobenzonitrile should lie significantly below those of acetophenone and benzonitrile, −6.2 and −10.5, respectively [71]. Aromatic compounds tend to be weaker bases than aliphatic compounds because of the destabilizing electron withdrawing character of the former; i.e., in sulfuric acid solvent, ethyl benzoate has a pKBH+ that is 10 times lower than that of ethyl acetate. Nitrobenzene, pKBH+w = −11.38, has been employed as a solvent for acid–base titrations because its low basicity enables pKa values for very strong acids to be measured. Hence, (trifluoromethyl)benzene methanol, nitrophenylethanol, and nitrobenzyl alcohol should have feeble basicities in solution. Propylene carbonate and other non–aqueous solvents are ranked in basicity as dimethyl sulfoxide (DMSO) > methanol > acetone > propylene carbonate > acetonitrile. We predict that benzyl alcohol would have solution basicity somewhat lower than methanol and ethanol. Glycoside basicities may be approximated from their closest structural analogues, ethers, possessing pKBH+w values ranging from −3 to −4. The inductive effect of oxygen should decrease basicity such that glycosides should have pKBH+w <−4. Thus, all of the class 1 reagents have very low solution basicities.
Class 2 Reagents (Shift under denaturing conditions)
In NH4OAc/H2O, some reagents’ charge elevating abilities were limited by low aqueous solubility. In other cases, reagents and conditions that strongly destabilized proteins were not pursued from aqueous solutions, because the associated CSD shifts could not differentiate unique supercharging mechanisms from shifts accompanying unfolding. As above, destabilization was judged by the onset of bimodal charge state distributions or of holo–myoglobin heme loss.) Nevertheless, these reagents did increase the charge carried by proteins solubilized in 0.1% formic acid/49.9% H2O/50% CH3CN, a typical denaturing solvent. For example, 1.5 mM nitrobenzene, close to its solubility limit, did not reproducibly increase the average charge of holo–myoglobin sprayed from aqueous solutions. However, when present in acidified H2O/CH3CN at 1.0% v/v, it increased insulin's average charge from 4.2 to 4.8. (See supplementary Fig. S-3, online resource.) Nitrobenzene's aqueous efficacy was limited by low solubility and spray instability. Similarly, 2 mM 4–nitrophenylacetonitrile increased insulin charging from acidified H2O/CH3CN, but its low solubility limited increases in aqueous solutions. Finally, 2–phenylethanol (1% v/v in acidified H2O/CH3CN) shifted insulin's most abundant charge state from 4+ to 5+, showing efficacy with denatured solutions, but when added to 20 mM NH4OAc/H2O at 0.0–0.3% v/v, it elevated myoglobin's average charge by only ~0.26 units. It appeared to initiate holo–myoglobin denaturation from NH4OAc/H2O at > 0.3% v/v. Aslam et al. [72] ranked values for Lewis basicity, B (nucleophilicity), as benzyl alcohol<methanol<2–phenylethanol, but these values were relatively close, and Lewis basicities do not always correlate with pKBH+. Lewis basicity scales, which reflect the ability to form hydrogen–bonded complexes, should relate to supercharging in some manner, because they gauge the ability of reagent and analyte to interact. But Brønsted basicity ultimately governs which species retains the proton within the intermediate regime.
Class 3 Reagents (Acids Active Only in Low Polarity Solvents)
Charge shifts were observed with 10 mM 3–nitrophenol (3–NP) supplementation under some conditions. Higher charge states were observed for 3–NP addition to disulfide–intact lysozyme from 50% CH3CN/49.9% H2O/0.1% formic acid and 50% CH3CN/50% H2O, but not from 50% MeOH/49.9% H2O/0.1% formic acid, 50% MeOH/50% H2O, or 99.9% H2O/0.1% formic acid; only a small shift is observed from 100% H2O. (See Figs. S-4 through S-6, online resource.) This behavior contrasts with sulfolane and m–NBA, reagents which increased lysozyme charging not only from CH3CN–containing solvents, but also from H2O/formic acid. Adding 3–NP to CH3CN–containing solvents similarly increased charge for insulin and β– lactoglobulin A sprayed from 50% CH3CN/49.9% H2O/0.1% formic acid: insulin charges ranged from 3+–6+ (4.3 average) in the unadulterated ESI solvent, but increased to 4+–7+ (5.3 average) when 20 mM 3–NP was included (cf. Fig. S-3). IgG in CH3CN/H2O/formic acid also revealed increased charging from 3–NP supplementation.
We selected 3–nitrophenol for investigation, expecting that its low basicity, similar to that of nitrobenzyl alcohol isomers, could supercharge under some conditions. A key difference between m–NBA and 3–NP is that the former reagent is both a very weak base and very weak acid (pKa=14.9), whereas the latter reagent is a very weak base, but also acidic (pKa=8.4). We see that 3–NP supercharging can be attenuated in aqueous solutions via ion–pairing; i.e., nitrophenolate anion–binding to protonated sites on the protein. Such complexes decrease overall charge when present and when collisionally dislodged as neutrals.
Ion pairing effects on charging have been discussed previously [73,74], and can be rationalized (in positive mode) as reflecting the gas phase disparity between analyte basicity for adding an nth proton and the anion's basicity [74]. Ion pairs are typically transferred to the gas phase from solution, where they were governed by solvent properties. Solvent dielectric constant is a key factor modulating solution associations and has been demonstrated to impact ESI charging [7]. However, values for methanol (32.7) and acetonitrile (37.5) are fairly similar and clearly lower than H2O (78.5). Hence, dielectric constant does not explain the increased charging that 3–NP displays in CH3CN vs. methanol. However, solvent basicity or acidity also shift ionic equilibria, metering the concentration of conjugate acid or base available to associate with analyte, as do solvents’ abilities to donate and/or accept hydrogen bonds. These latter properties do explain why 3–NP is more efficacious at increasing charge from CH3CN–containing solutions. Although low reagent solution basicity promotes positive ion supercharging, that behavior is modulated by reagent acidity and solvent hydrogen bonding and dielectric constant.
Class 4 Reagents (Decrease charge) and Class 5 Reagents (No effect)
Pyridine N–oxide (PNO, pKBH+w=0.79) showed no effect on myoglobin charge distributions under denaturing conditions, despite additions to 500 mM. Nor did charge increase under native conditions; increased charging was only associated with denaturation (Fig. S-7). Additives that decreased protein charging in 20 mM NH4OAC included α–(4–Pyridyl N–oxide)–N–tert–butylnitrone (POBN) and dimethylformamide (DMF). Addition of 0, 5, and 20 mM POBN yielded abundance-weighted average charge values for holo–myoglobin of 8, 7.2, and 6.6, respectively. POBN is expected to be more basic in solution than PNO.
We found that modest amounts of dimethylformamide, (DMF), generally reduce charge. Average charge on actin monomers decreased from ~11.5+ to 9.5+ with 0.3% (v/v) DMF, while CSDs moved from spanning 13+–10+ to 11+–8+. This amount of DMF did not affect non– covalent binding of inhibitors to actin, however. Similar results have been reported previously for 0.5% DMF [75]. In contrast, Valeja, et al. [76] reported that a DMF concentration of 20% was optimal for increasing charge in apo–myoglobin and cytochrome c. In our hands, when disulfide–intact transferrin, denatured in 50% CH3CN/49.9% H2O/0.1% formic acid, was heavily supplemented with DMF to 20% (v/v), the average charge decreased from ~36.5 to ~32+. We find that low DMF concentrations, insufficient to disrupt non–covalent interactions, tend to decrease charge. Charge reduction by DMF has been exploited to reduce the collisional activation applied to sensitive non-covalent complexes entering the MS [77].
Iavarone and Williams [43] listed DMSO as supercharging in 2003, based on charge increases experienced by cytochrome c with up to 50% added DMSO. Marshall's laboratory [76] noted charge increases for proteins eluted from a reversed phase column with DMSO– containing mobile phase. In contrast, Tjernberg et al. [75] reported that DMSO concentrations below 2% v/v reduce charge for aqueous analytes, but that higher concentrations denature proteins, as reflected by the onset of multimodal CSDs and reduced inhibitor binding. Reduced charging from dilute DMSO was also described earlier in work monitoring a receptor ligand– interaction [78]. Recently, Sterling, et al. and others reported reduced charging from low DMSO concentrations [77,79,60].
That proteins can be denatured by medium to high DMSO concentrations is clear. However, the ESI behavior observed with modest DMSO addition is illuminating. We observed that as DMSO was dispensed to 0, 35 and 70 mM concentrations (0, 0.25, and 0.5 % v/v), the average charge of holo–myoglobin decreased from 8.4 to 7.7 and 7.2, respectively, with no heme loss. Increasing DMSO to 140 mM (1%) and higher, however, broadened charge distributions and switched the direction for variation in average charge state, i.e., a discontinuous change in CSD consistent with a conformational transition. Moreover, adding DMSO (0, 35, 70, and 140 mM) to insulin in the denaturing solvent CH3CN/H2O/formic acid similarly lowered peptide average charge (to 4.3, 4.2, 4.1, and 4.0), respectively. Recently, decreased charging observed from low concentrations of DMSO was attributed to “global compaction” of higher order structure [60], but existing biophysical data [75] from differential scanning calorimetry, analytical ultracentrifugation, circular dichroism, and dynamic light scattering contradict that suggestion, establishing reduced stability in the 0.5% DMSO, conditions that reduced ESI positive charge in the tested proteins. The compaction rationalization is also inconsistent with the charge reductions observed from +ESI of insulin and tryptic peptides in denaturing solutions.
Because they do not appear to increase charge independent of conformational effects, we do not consider DMF, DMSO, and POBN to be supercharging agents in positive ion mode. Indeed, they appear to be “sub–charging” agents [79]. DMSO's solution basicity is considered close to that of water, although the comparison depends heavily on the solvent employed for the measurement. The DMSO cation's dissociation constant has been estimated as pKBH+w=−1.54, versus −1.74 for water [71]. It can be challenging to extrapolate and compare basicities for different classes of molecules, but for a range of conditions, basicity order among relevant reagents is DMSO > DMF > H2O > acetone > propylene carbonate > acetonitrile. Charge reduction from gas phase proton transfer can superimpose further complexity. Additives that decrease charge independent of conformational effects have higher solution basicities than those found to increase charge.
Intermediate Regime Model Explains Several Perplexing Observations: why CSDs Vary with Analyte Concentration, Emitter Opening Diameter, and Flow Rate
Fig. 1 is a sketch of an electrospray operating in cone–jet mode. Region A corresponds to liquid from the edge of the emitter tip through the Taylor cone, B to the jet filament, and C to the point where the jet disrupts to initiate an electrospray plume. An expanded view of the plume shows regions D, E, F, and G, stages of ESI droplet evolution. As droplet D evaporates, the increasing electrostatic repulsion causing it to distort (E), and ultimately eject its own secondary droplets by asymmetric fission (F). Excess charge is disbursed to primary droplets in region C, and to secondary droplets in G. Steps D–G may repeat to produce higher order droplet progeny, until the volatile droplet evaporates. Our model assumes that ions, as well as droplets are ejected from regions C and G to yield H, a gas phase analyte ion (likely solvated).
Species in region A are described by solution equilibria, while the ensemble of H analyte ions is described by their ESI mass spectrum, albeit potentially altered a bit by desolvation and gas phase charge reduction. From each decomposing droplet, we assume that the distribution of emitted gas phase ions is governed by constants defining the likelihood of their being emitted at the point where excess charge is disbursed and by the population distribution at the emission point. Appendix I derives these relationships.
The treatment in Appendix I. resembles the model of Kebarle and Tang which divided droplet charge between analyte and background electrolyte [3], but we also allocate charge to solvent. We differentiate intrinsically charged ions from protonated species, and express the charge carrier concentration in terms of contributions from excess droplet charge and from solution acid-base dissociation. Some aspects of the equations resemble the equilibrium partitioning model [80], because both formulations describe a competition for charge. However, our arguments and assumptions are quite different; equilibrium partitioning assumes all analytes are ionized and ion-paired, unless surface-localized and only to the extent of available excess charge (as defined by ESI current and flow rate). The model proposes that surface-active, hydrophobic compounds always enjoy an advantage over hydrophilic species, although surface activity has also been demonstrated to be unrelated to protein responses [81], and to be more important in larger droplets [82]. Because larger initial droplets require more fission events prior to ion release, suppression of hydrophilic analytes becomes substantial under conditions generating large droplets, yet minor under nanospray conditions [28].
From the treatment for singly charged ions in Appendix I, it can be concluded that:
Analyte response will be linear with concentration as long as most of the charge emitted in the form of gas phase protonated ions is not bound to analyte; that is, as long as many, many fewer analyte ions are emitted from droplets than solvent or buffer ions. This dependence arises, because the amount of charge released is finite, and altering the concentrations of analyte, buffer, or other solution components that associate with protons also alters (H+)N, the hydrogen ion concentration at the point where the elongated droplet decomposes. When most of the charge released as protons is not carried by analyte, a doubling of analyte concentration will have a negligible impact on (H+)N. However, when protonated analyte emission accounts for most of the protons lost by the droplet, the impact is significant and leads to the non-linear response.
The concentration at which analyte response deviates from linearity is independent of the amount of Na+, K+, N(CH3) +4, or other fixed charge ions in the solution. Emission of fixed charge ions reduces the overall charge available to be conferred to solvent, buffer, and analyte molecules, but the overall ratios at which they are emitted would be unaffected.
In cone–jet mode, the ESI current, is roughly independent of flow–rate. Consequently, the analyte, solvent, and buffer ion signals should also be roughly independent of flow–rate.
Evidence for the veracity of the Appendix I approach is that it successfully recapitulates dynamic range limitations at high analyte concentrations, including the observation that saturation occurs at approximately the same analyte concentration, regardless of electrolyte concentration [83,80]. It elucidates the suppression of analyte signal by sample matrix and its amelioration by dilution [84].
For μL/min flow rates and concentrations to ~10−5 M, overall ESI signal response is linearly proportional to analyte concentration, but has little dependence on flow rate [7,81]. However, in analyses of multiply charged analytes, it is seen that employing increasing analyte concentrations [85,86] or higher flow rates [34,38,85] shifts charge state distributions to lower average charge. Still odder are the observations that the larger emitter openings of standard ESI sources yield CSDs shifted to lower charge than distributions obtained from nano–ESI sources [33-35,87]. Because the CRM relates analyte charge to the final, protein–sized droplet, it predicts CSDs that would be independent of initial spray conditions, in conflict with these observations.
In Appendix II, we extend the kinetic treatment from Appendix I to multiply charged ions, based on partitioning excess charge from the decomposing droplet. It offers explanations to many of the perplexing observations above. From Appendix II we derive that, for an analyte capable of carrying up to 4 charges that is emitted from droplet N, the relative intensities of the 4+ and 3+ charge states would be:
| (5) |
or, simplified,
| (6) |
where kgAH4, and kgAH3, correspond to probabilities of ejecting AH44+ and AH33+, respectively, from the intermediate regime to the gas phase, while kAH4, corresponds to the probability within the intermediate regime of adding a proton to AH33+, also dependent on the intermediate regime's concentration of H+, or (H+)N. (H+)N, described below and in Appendix I, is comprised of several terms. In principle, parameters related to surface activity could be incorporated into kgAH4, and kgAH3, although its importance appears to be a function of primary droplet size [28,82]. Key features and results from the Appendix II treatment are that:
The intensity ratio of adjacent charge states is related to the proton concentration at the point of charge dispersal.
The value of kAH4, in equations 7–8 above, need not match either the bulk solution constant, (pKa of the conjugate base), nor the gas phase basicity, although it should lie between them.
Few assumptions are made about kgAH4 and kgAH3; e.g., spherical droplets are not assumed, but we do treat these terms as constants, which may be justified for decompositions at the Rayleigh limit.
Concentrations are expressed in parentheses, rather than the traditional square brackets, because they describe concentrations only in the region where charge is released. Homogeneous, equilibrium solution concentrations are not assumed, to allow for charge polarization within the droplet.
The hydrogen ion concentration at the point where charge is released from the decomposing droplet, (H+)N, is expressed in terms of the proton concentration that would have been present at that point (and external electric field) in a neutral droplet of identical solvent, buffer, analyte, and fixed charge composition, incremented by an amount related to the excess charge from the ESI source (cf. Appendix I).
For the same ESI current and flow rate, spraying from a smaller orifice diameter can yield higher charge states. Although the initial charge/volume ratio is identical, a smaller emitter opening yields a larger number of droplets smaller in volume. Smaller primary droplets evaporate a larger percentage of their solvent before reaching the Rayleigh limit; hence, they attain higher excess charge concentrations prior to decomposing. This prediction of higher charging from smaller droplets contrasts with a recent prediction [12].
The lower charging (higher m/z CSDs) sometimes observed with desorption electrospray ionization (DESI) [88-90], solvent–assisted inlet ionization (SAII) [91,92], matrix–assisted inlet ionization (MAII) [93], and surface acoustic wave nebulization (SAWN) [94] versus ESI may reflect production of larger analyte ion-evaporating droplets. As compared to nanospray, methods such as DESI bring additional considerations such as the potential for ion emission not only from droplets, but also from the charged surfaces of solvent streams [95]. Lower charging in DESI has also been ascribed to charge loss at the sample surface [96].
Higher flow rates produce larger droplets [97,98,28,99]. At constant ESI current, these higher flow rates can reduce the average charge state observed in electrospray ionization.
If a multiply charged analyte's concentration increases with little change in ESI current, and a significant portion of the charge emitted by the ESI source is in the form of gas phase, protonated analyte ions, analyte CSDs will shift to lower charge. Proportionally more protons will associate with analyte, but that association will be weighted towards lower charge states, with their lower order dependences on the amount of excess charge.
Defining the charge dependence of kgAHz values is beyond the scope of this paper. However, the charge dependence of kAHz parameters reflects the steepness of (Δbasicity)/charge or (Δacidity)/charge within the intermediate and gas phase regimes. In both regimes, the acidity or basicity of individual sites is modulated by the environment and aliquots of charge positioned nearby. These kAHz parameters impact CSD widths for analyte ions emitted from a decomposing droplet. Because (i) ions can be emitted from an ensemble of droplet sizes; i.e., primary, secondary, and nth generation droplets, and (ii) smaller droplets can emit more highly charged ions due to higher concentrations of excess charge, the mass spectrum's CSD is the sum of CSDs over all emitting droplets.
For a particular analyte, the width of its CSD may decrease for solvent/spray conditions depositing so much charge onto molecules that, e.g., in positive ion mode, accommodating the zth proton would spur an enormous decrease in kAH(z+1) and accommodating the (z+1)th proton would lead to a still larger drop in kAH(z+2). That is, an increasingly steep ( basicity)/charge may yield narrower CSDs for conditions that generate ions with extremely high charge densities. These considerations also rationalize observations that protein CSDs are narrower when solutions are sprayed from tips with inner diameters < 70 nm instead of 1 μ [87].
Should the extent of charging be limited by gas phase proton transfer reactions, e.g., when amines are delivered to react with gas phase analytes at a defined pressure, the product CSD would be described by calculating how an initial, spray-produced CSD would evolve over time, modulated by the ensemble of analyte- and reagent-specific proton transfer rates and the reagent population. When the rate of reaction depends strongly on charge; i.e., (Δrate)/charge is steep, the breadth of CSDs will also be reduced. In summary, our model suggests that the bell-shaped charge state distributions typically observed in ESI-MS are shaped by the size range of droplets emitting ions in concert with the distribution of values for kAHz, kAH(z+1), kAH(z+2), etc. When the values for relevant kAHz, kAH(z+1), and kAH(z+2) differ by many orders of magnitude, distributions can be narrow, explaining how different proteins sprayed from identical solution and spray conditions can differ in the widths of CSDs they display. CSDs may also be modified by gas phase proton transfer reactions, reflecting the reaction rate's dependence on charge. This rationalization does not conflict with some others attributing width variations to differences in higher order structure, because structure directly affects values for kAHz, kAH(z+1), and kAH(z+2), by impacting the local environment of ionizable residues. Differences in the size distributions of droplets that release analyte ions explain another phenomenon, the small day-to-day variations in CSDs observed for identical protein solutions analyzed under identical instrumental conditions.
Supercharging and the Intermediate Regime
Derivations in the appendices establish the impact of solvent's and solution additives’ acceptance of droplet charge. Ion distributions, initially defined by solution equilibria, are modified as they traverse the intermediate regime to the gas phase. Recall that we define supercharging as increased analyte charging (CSD shifts to lower m/z) that cannot be attributed to global conformational change (denaturation). It is proposed that effective positive ion supercharging reagents must (1) be soluble, (2) interact with analytes, (3) be very weak Brønsted bases (pKBHw < −1.7) and, usually, (4) be similarly or less volatile than the bulk solvent to concentrate in the droplet, although this latter requirement may possibly be offset by large analyte interactions. For non–denaturing solutions, the reagent must shift protein CSDs when present at concentrations below those inducing conformational changes (distinguishing supercharging from denaturation).
The Brønsted definition, describing proton transfer, may be too narrow to fully describe protonation in ESI, although Lewis basicity constants that describe ability to form complexes, but not transfer protons, are also inadequate.
Adding a weak base to water alters the aqueous H–bonding network. An important consequence is that neutral acids become less likely to ionize (pKa's increase), as the solvent becomes less adept at accepting protons. The pKa's of cationic acids (e.g., protonated amines) increase for the same reason. Thus, adding a very weak base to an aqueous protein solution decreases the population of carboxylate anions while increasing the population of protonated lysines and arginines, increasing analyte positive charge overall. Similarly, adding a very weak acid to water suppresses the protonation of neutral bases (reduces pKa's of cationic acids) while enhancing ionization of neutral acids (decrease pKa's). Hence, adding a very weak acid should increase analyte negative charging. Class 1 and 2 supercharging reagents above have both weak bases and weak acid character. The main effect of such additives in the bulk solution is to reduce analyte ionization overall, hardly a prescription for supercharging.
But moving from the bulk liquid of the droplet to the intermediate regime requires considerations differing from simple solution ionization. Rather than attempting to predict the extent of ionization at equilibrium, the interest is in predicting how excess droplet charge will be distributed between i) progeny droplets and ii) evaporating ions, including protonated solvent clusters, solvated supercharging agents, and solvated analyte. Differentially affecting analyte and solvent acidities, basicities, and the hydrogen bonding network, supercharging agents alter the formula for allocating charge in favor of the analyte. From the point of view of Appendix II, equation 6, supercharging agents alter the constants CS, CB, CAH, CAH2, CAH3, and CAH4. Supercharging reagents can potentially alter kAHz values and, importantly, (H+)N, the amount of H+ at the point where the elongated droplet decomposes. Positive ion supercharging agents reduce solvent basicity throughout the droplet, driving an increase in (H+)N. (Alternatively, recall that in any solvent S, the strongest acid is SH+. If S is an exceptionally weak base, then SH+ is an exceptionally strong acid.) Interactions between supercharging agents and analyte (facilitated by favorable dipole interactions [68], perturb the local environment and may assist in stabilizing analyte charge prior to accessing the gas phase. Thus, (1) the weak base character of positive ion mode supercharging agents can increase charge by increasing protonation of analyte basic sites in the intermediate regime, and sometimes equally important to increasing absolute charge, is (2) their ability to suppress ionization of analyte acidic sites throughout the droplet. This latter point revisits Grandori's arguments favoring opposing charges and the zwitterionic nature of gas phase protein ions [22]. The average charge increase (from 2.4 to 2.8) when sulfolane is added in-spray to substance P [100], a peptide without anionic sites, is consistent with mechanism 1.
While we are comfortable with the idea of considerable zwitterionic character existing at neutral pH, (because average amino acid pKa values suggest that most glutamic acid and aspartic acid residues would be ionized, as would arginine and lysine residues), the idea that some zwitterionic character might persist in denatured proteins is less clear. Intrinsically unfolded proteins within an aqueous solution provide one example where we can readily imagine unfolded zwitterionic proteins. Unusual local structures, even in an acid-denatured protein, can perturb pKa's to yield an opposing charge. It is conceivable that some denatured analytes retain a bit of zwitterionic character in certain environments.
Negative Ion Supercharging
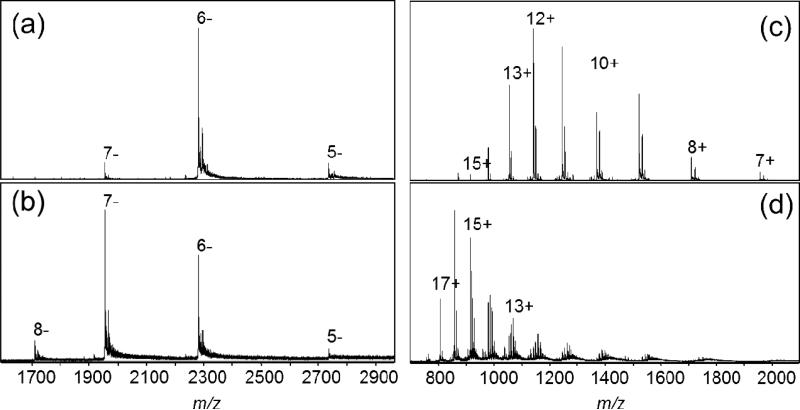
The ability to increase charge in both + and -ESI does not differentiate between the Rayleigh limit/surface tension model and our solvent acidity/basicity model; both predict it, although not necessarily for the same reagents. We predict that very weak Brønsted acids (pKa > 15.7) should be effective negative ion supercharging reagents. The Berkeley lab's surface tension arguments are independent of polarity, predicting that all reagents shown to supercharge an analyte in one polarity should be similarly effective at supercharging in the opposite polarity. Experimentally, some investigators have found increasing protein charge in negative ion mode to be harder to achieve for some analytes than in positive mode [68] and, for the same reagent, negative ion efficacy seemed reduced from that observed in positive ion mode [42,58]. Our hypothesis predicts reagents able to supercharge in only one polarity. Figure 6 shows negative and positive ion spectra of RNase A sprayed from 10 mM NH4OAc with and without sulfolane.
Figure 6.
(a) Negative ion ESI spectra of RNase A from 50% CH3CN/H2O and 10 mM NH4OAc without, and (b) with 200 mM sulfolane. (c) Positive ion ESI spectra without, and (d) with 200 mM sulfolane.
We note that aprotic solvents such as sulfolane, both a weak Brønsted base and weak Brønsted acid ((sulfolane)H+ has pKBH+w = −12.9; sulfolane has pKa >31), are renowned for their inability to solvate small anions, (e.g., acetate) making them ideal solvents for nucleophilic reactions, but limiting their ability to interact with anionic analytes [101]. Hence, m–NBA has an advantage over sulfolane for interacting with carboxylates; it donates a hydrogen bond. Consistent with that notion, m–NBA is often found to supercharge proteins in negative ion mode better than sulfolane.
Inferior anion solvation has an additional effect. High sulfolane concentrations were observed [68] to yield cytochrome c spectra with abundant counterion adducts, presumably HSO –4. Increased adduction is also observed in ribonuclease (Fig. 6). Because adducts were less prominent with sulfolane absent, it was suggested that sulfolane oxidation at the anodic tip produced additional sulfate [68]. Solvation considerations suggest an alternative explanation: sulfolane's poor solvation of sulfate anions increased ion pairing to cytochrome c.
Striking examples of negative ion mode supercharging have been reported for non– proteins. Huang et al. [102] found that adding 105 mM sulfolane increased both charge and ion signal for heparin sulfate oligosaccharides, benefitting tandem mass spectrometry by minimizing SO3 loss and maximizing ion abundances from backbone dissociations. Similarly, 1% m–NBA (84 mM) invariably increased charging and ion signal for oligonucleotide anions [50]; e.g., with GTTTTT, the highest observed charge state was seen to shift from 2- to 5- following m–NBA addition, while that of GGAATTAACCAA shifted from 4- to 8-. Although m–NBA readily supercharged oligonucleotide anions, it showed no ability to increase oligonucleotide charge in positive ion mode, a further illustration of polarity differences in reagent efficacy. Of particular interest was the observation that adding m–NBA increased oligonucleotide signals for both negative and positive ion mode. This increase is consistent with reduced buffer ionization from bulk solutions supplemented with weak acid/weak base supercharging agents. Reducing NH4OAc ionization in the droplet reduces the excess charge emitted as NH4+ or OAc-. For glycosaminoglycan anions [102], ammonium adduction was minimized and overall signal strengths increased 3–9 fold with sulfolane, suggesting that less negative charge was emitted as formate anions.
Aspects of the manipulation of oligonucleotide charging in negative ion mode by basic solution additives [103]; e.g., pyrazole, imidazole, piperidine and triethylamine, can also be understood by considering Brønsted acidities. If we recall the previous, positive ion mode discussion of “class 3” supercharging reagent 3–nitrophenol and its ability to increase protein positive charge only from low basicity solvents, we see that the oligonucleotide example is the inverted case. Positive charge was increased when effects from weakly basic, neutral 3– nitrophenol exceeded effects from analyte ion paired to higher gas phase basicity nitrophenolate. Similarly, negative charge can be increased when effects from weakly acidic, neutral piperidine and triethylamine exceed effects from analyte ion pairing to the population of piperidinium and triethylammonium cations. In the absence of conformational changes, class 3 reagents should only increase charge in one polarity.
Alteration of Gas Phase Protein Structure at High Concentrations of Supercharging Agent
Non–covalent complexes may be disrupted at high levels of added supercharging agent. Structural disruption may occur in solution, during droplet evaporation, within the intermediate regime, or in the gas phase. (Gas phase unfolding will not increase charge.)
Even small structural changes, unimportant to a solution–phase protein, may have important ramifications downstream (after the electrospray dispersed protein enters the gas phase), where dominant electrostatic interactions could drive a minor structural variant into a major gas phase conformational change. Transformations are also driven by excess thermal or collisional energy (e.g., as applied for desolvation). Of course, unfolded gas phase proteins may be detected by ion mobility, but differentiating gas phase unfolding from droplet unfolding may require examination of temperature and voltage dependences, or elucidation by high pressure mobility analyzers that are less likely than their low pressure siblings to drive gas phase unfolding by collisional excitation [61].
Additional Data to Test the Intermediate Regime Hypothesis
As this manuscript was being finalized, a relevant study by Teo and Donald [104] was released, reporting over 10% increases in the average positive charge deposited onto cytochrome c for 5% additions of m-nitrobenzyl alcohol, o-nitroanisole, p-nitroanisole, sulfolane, dimethyl sulfone, ethylene glycol, propylene carbonate, and ethylene carbonate to the denaturing solvent 44% methanol/1% acetic acid/55% H2O. These increases are consistent with our hypothesis and observations for m-NBA, sulfolane, and propylene carbonate [63,64] because the 8 reagents are all weaker bases than H2O; e.g., ethylene glycol is a useful solvent for titrating weak bases because it increases BH+ stability in solution [105-107]. The study also reported that cytochrome c average charge was unchanged or increased by < 5% for dimethyl carbonate, diethyl carbonate, nitrobenzene, 1-chloro-2-nitrobenzene, crotononitrile, and 2-pyridinecarbonitrile additions. On the basis of basicity, we would only expect 2-pyridinecarbonitrile to supercharge poorly [108]. Indeed, we have observed 1% v/v nitrobenzene to increase the average charge on insulin (50% CH3CN/49.9% H2O/0.1% formic acid) from +4.3 to +4.8. It may be that low aqueous solubilities of nitrobenzene and, perhaps, 1-chloro-2-nitrobenzene are problematic under some conditions; we found the former's solubility to be limiting in aqueous solvent. Although Brønsted basicities of dimethyl and diethyl carbonate should be similar to those of ethylene and propylene carbonate [106], their evaporation rates are much higher. Dimethyl and diethyl carbonate actually evaporate about 10 and 3 times faster than H2O, respectively, leaving their enrichment within evaporating droplets doubtful [109]. Although butyl-acetate-referenced evaporation rates are not available for cis- and trans-crotononitrile, their boiling points are ~107 and 120°C, respectively, and both have vaporization enthalpies (25°C) that are 10% lower than that of H2O [110], suggesting that they, too, are not enriched. In general, these newly introduced reagents behave in accordance with our hypothesis.
Conclusions
After excavating a rich trove of observations on electrospray ionization, we have settled on an ESI mechanism in which ions evaporate from the filamentous protrusions of decomposing droplets. The mechanism correctly predicts trends in signal intensity and notably, CSD shifts to higher m/z for high analyte concentrations and/or large diameter emitter openings. It details factors impacting widths of charge state distributions. Supercharging additives alter charge partitioning between analyte and solvent, shifting CSDs and/or increasing analyte ionization overall. Effective positive ion supercharging reagents must be soluble, interact with analytes, be very weak Brønsted bases (pKa < −1.7) and, usually, be similarly or less volatile than the bulk solvent. Effective negative ion supercharging reagents must have similar properties, except that they must be very weak Brønsted acids, (pKa > 15.7); i.e., less acidic than water. Reagents capable of supercharging in both positive and negative ion mode should be very weak bases and very weak acids in their non-ionized form. Weak acid/weak base supercharging agents, concentrating in progeny droplets, reduce an analyte's solution ionization in aqueous solutions, thus evaporating ions accorded the excess charge of the spray, but bearing fewer opposing charges.
Supplementary Material
Acknowledgments
We thank Ivory Peng, Sabrina Benchaar, Carly Ferguson, and Shirley Lomeli for many useful measurements that they performed, enabling us to develop the ideas presented here. Support from the US National Institutes of Health (R01GM103479) and the US Department of Energy (UCLA Institute of Genomics and Proteomics; DE-FC03-02ER63421) are acknowledged.
APPENDIX I
How is Charge Disbursed from a Decomposing Droplet in the Intermediate Regime? A Treatment for Singly Charged Analytes
An ESI source dispenses total charge, QT, at a rate defined by the ESI current. Consider decomposing droplet N, composed of solvent S. We assume that the total charge present on decomposing droplet N, QTN, will partition between liquid and gas phase ions. That is, some charge QDN, will be held by the sum of the smaller progeny droplets and the remnant of the precursor droplet, while other charge will be allocated to gas phase ion species, divided among those from solvent, QSN, (emitted as solvent ions or cluster ions), from buffer B, QBN, from analyte A, QAHN, and to any ions of fixed charge Z+; e.g., Na+ or K+, whose charge aliquot shall be referred to here as QZN. We consider only singly charged ions in Appendix I.
The gas phase charge, ΔQTN, emitted from droplet N can be expressed as the difference between the initial droplet charge and that retained by progeny and precursor after decomposition:
| (1) |
Allocation of gas phase charge, QTN, is complicated. In the bulk solution, charge allocation would be defined by acid/base equilibria, but in the gas phase it would be defined by gas phase basicities. Because electrospray species rapidly transition from solution to gas phase, knowledge of “constants” is limited and a kinetic treatment may be preferable to an equilibrium one. General expressions can provide some insight, however.
We shall reserve terms in square brackets for bulk droplet concentrations (Fig. 1, region F) and terms in parentheses to represent concentrations at the point where charge is disbursed from a decomposing droplet (Fig. 1, region G). Hence, at the instant of decomposition, region G need not be identical in ionic composition to F, although the solvent, SN, is assumed to be equal in concentration and composition at F and G.
In a liquid, the concentration of protonated analyte, AH+, would be related to the amount of A, to a factor related to how likely A is to bind a proton, kAH, and to the amount of H+. Of course, defining the amount of H+ at the point of decomposition for the elongated droplet, (H+)N is complicated. It can be described as the sum of two contributions:
| (2) |
where (H+)DN corresponds to the proton concentration that would have been present at that point (and external electric field) in a neutral droplet of identical solvent, buffer, analyte, and fixed charge ion composition, while (H+)EXN increments the proton concentration by an amount related to the excess charge from the ESI source. (Because some of the excess charge associates with other species; e.g., analyte, (H+)EXN is not equal to the excess droplet charge.) When considering the amount of charge released to the gas phase as analyte ions, QAHN, let us assume that from the amount of AH+ present at the intermediate regime, (AH+)N, an amount proportional to kgAH could be ejected to the gas phase.
| (3) |
We are treating as constants the kg terms, (probabilities for ejection to the gas phase), a simplification that may be justified when all decompositions occur at the Rayleigh limit. Similarly,
| (4) |
| (5) |
| (6) |
Let us consolidate:
| (7) |
| (8) |
| (9) |
Substituting into equation 1 and rearranging, we obtain the expression for the gas phase charge emitted by decomposing droplet N.
| (10) |
k(Z+)N describes emission of fixed charge ions, while the three terms within square brackets on the right hand side of the equation describe emission of gas phase ions from protonated solvent, buffer, and analyte, respectively. Assuming that the total amount of charge released to the gas phase by droplet N, ΔQTN, is independent of analyte concentration, as is fixed charge ion emission, it can be seen that for analyte response to appear to depend linearly on concentration, the condition:
| (11) |
must be fulfilled. That is, as long as many, many fewer ions are emitted from analyte than from solvent and buffer, the analyte ion intensity will appear to scale linearly with concentration. The amount of charge is finite and must be partitioned in accordance with equation 10. Increasing (A)N, holding (S)N and (B)N constant, leads to a decrease in (H+)N, as more protons associate with the added A. When the condition in eq. 11 is met, that change in (H+)N is negligible, enabling AH+ ion signal to appear linearly related to the amount of A in solution. When the eq. 11 condition is not met, the changing (H+)N leads to a non-linear relationship between the AH+ ion signal and the amount of A in solution.
According to equation 1 and assuming complete solvent evaporation before sampling by the mass spectrometer, the total charge conferred by the ESI plume, QT, corresponds to
| (11) |
Although many parameters in equation 10 are undefined, we expect for relatively modest rates of ion emission that the concentrations of A, B, and Z+ will increase as solvent evaporates. Thus, if the condition specified by equation 11 continues to hold when integrated over all droplets in the plume, we would predict an analyte (without fixed charge) to deliver an ESI response that would be linearly dependent on concentration.
More complexity could be incorporated within the expressions above; e.g., mixed solvent systems may be expressed as mole fractions, and anions (ionization of acidic molecules) could also be expressed. By dropping (H+)EXN from equation 2, one could predict saturation characteristics of ions potentially emitted directly from primary, neutral droplets; e.g., vibration orifice aerosol generators [111] or solvent assisted inlet ionization [92]. In contrast, ions emitted from the secondary or higher order droplets produced by these methods would carry excess charge and thus be described by the same equations here presented for electrospray.
To summarize:
Analyte response will depend linearly on analyte concentration as long as most of the charge emitted in the form of gas phase protonated ions is not bound to analyte; that is, as long as many, many fewer analyte ions are emitted from droplet N than from solvent and buffer.
The concentration at which analyte response deviates from linearity is independent of the amount of Na+ or other fixed charge ions in the solution. Emission of fixed charge ions reduces the overall charge available to be conferred to solvent, buffer, and analyte molecules, but the overall ratios at which they are emitted would be unaffected.
In cone–jet mode, the ESI current, is roughly independent of flow–rate. Consequently, the analyte, solvent, and buffer ion signals should also be roughly independent of flow– rate.
APPENDIX II
Charge state distributions of multiply charged analytes can depend on ESI solution and source conditions
If one now considers an analyte A, capable of carrying multiple protons; e.g., AH+, AH22+, AH33+, and AH44+, equation 3 of Appendix I, describing the charge deposited on analyte at the point where charge is disbursed from a decomposing droplet, and the amount of analyte that is ejected to the gas phase, must be extended for all charge states of analyte ions. We begin by deriving expressions for the amounts of charge ejected as different charge states of A. Terms are defined analogously to those in Appendix I. In particular, QAH2N refers to the charge released as gas phase AH22+ ions, kAH2 reflects the probability that AH+ will accept a second proton, and kgAH2 reflects the probability that any AH22+ present would be ejected to the gas phase. For simplicity, we shall continue to assume that the fixed charge species Z+ is only singly charged, as in Appendix I.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
The expressions above may be substituted into an expanded version of equation 9 from Appendix I, to yield ΔQTN, the total charge ejected from decomposing droplet N. Constants CAH2, CAH3, etc., are defined analogously to CAH in Appendix I.
| (6) |
Equation 6 illustrates that for more highly charged ions there is a higher order dependence on (H+)N, which was defined in equation 2 of Appendix I, and is presented again below,
| (7) |
For spherical droplets at the Rayleigh limit, the amount and concentration of charge are governed by droplet diameter (amount is proportional to surface area; concentration is amount divided by volume). Hence, (H+)EXN will depend on the size of the droplet, leading equation 6 to predict that smaller droplets can yield more highly charged ions. We assume that an ensemble of droplet sizes emits ions, but it can be seen that with smaller initial droplets, potentially more highly charged ions can be created. It is this feature that explains observations [33-35] of smaller diameter emitter openings yielding spectra with small CSD shifts to lower m/z (higher charge). Higher flow rates in electrospray ionization tend to release larger primary droplets, explaining why, at relatively high analyte concentrations, CSDs were observed [34,38,85] to shift towards higher m/z (lower charge) with increasing solution flow.
To ensure a linear relationship between ESI response and analyte concentration, it was stated in Appendix I that most of the charge emitted in the form of gas phase, protonated ions must not be bound to analyte. That condition applies to multiply charged analytes, as well. Non–linear responses arise when high analyte concentrations reduce (H+)N significantly, as more protons associate with the added analyte. Across the analyte's charge state envelope, the highest charge state intensities are most dependent on (H+)N. That dependence explains the observation [81] that charge–weighted analyte ion intensities appeared to scale linearly with concentration despite an apparent shift in CSD to higher m/z (lower charge) with increasing analyte concentration.
These equations lead us to conclude that:
For the same ESI current and flow rate, spraying from a smaller orifice diameter can yield higher charge states. Although the charge/volume ratio is identical, a smaller diameter emitter opening yields a larger number of droplets smaller in volume. Smaller primary droplets evaporate a larger percentage of their solvent before reaching the Rayleigh limit; hence, they attain higher excess charge concentrations prior to decomposing.
Higher flow rates produce larger droplets. At constant ESI current, these higher flow rates can reduce the average charge state observed in electrospray ionization.
As described in appendix I, these equations can be applied to solvent–assisted inlet ionization and other ambient ionization methods, even if electric fields are not employed. If these methods produce larger initial droplets (or chunks of sublimed material) than nano–spray, their spectra of multiply charged ions will be shifted towards lower CSDs.
If a multiply charged analyte's concentration increases with little change in ESI current, and a significant portion of the charge emitted by the ESI source is in the form of gas phase, protonated analyte ions, analyte CSDs will shift to lower charge. Proportionally more protons will associate with analyte, but that association will be weighted towards lower charge states, with their lower order dependences on the amount of excess charge.
It will be interesting to compare electrospray charge distributions to those created from the same solution by desorption electrospray ionization (DESI) [88-90], solvent–assisted inlet ionization (SAII) [91,92], matrix–assisted inlet ionization (MAII) [93], surface acoustic wave (SAW) [94] ionization and by other ionization methods. We suggest that the lower charging (CSDs shifted to higher m/z) observed with these methods may reflect larger initial droplets.
The elevated inlet temperatures employed with MAII and the melting points of suitable MAII matrices suggest that for MAII to produce multiply charged ions, the solid matrix must liquefy [93]. Hence, ion production by SAII, and MAII can conceivably be described by our intermediate regime model. In contrast, ion production by matrix–assisted ionization vacuum (MAIV) occurs with sublimation. It has been proposed that effective matrices for MAIV must sublime and be triboluminescent [112]. Triboluminescence primarily occurs in piezoelectric crystals, which have the ability to separate charge across a developing crystal fracture [113]. Light is emitted when the charge separation induces an electric discharge. Mechanically– stressed piezoelectric materials separate charge even without crystal fracture or luminescence. It is reasonable to speculate that stresses exerted by sublimation can generate an electric field by separating positive and negative charges across piezoelectric crystal faces, and that charge polarization, rather than photochemistry, is the key property. Charge acquisition during sublimation and vapor deposition is established [114]. This piezoelectric polarization, reminiscent of charge–polarized electrospray or thermospray droplets, hints at a related mechanism to release multiply charged analyte ions from subliming crystal shards.
References
- 1.Dole M, Mack LL, Hines RL, Mobley RC, Ferguson LD, Alice MB. Molecular Beams of Macroions. Journal of Chemical Physics. 1968;49(5):2240–2249. [Google Scholar]
- 2.Iribarne JV, Thomson BA. On the Evaporation of Small Ions from Charged Droplets. Journal of Chemical Physics. 1976;64:2287–2294. [Google Scholar]
- 3.Kebarle P, Tang L. From Ions in Solution to Ions in the Gas Phase - The Mechanism of Electrospray Mass Spectrometry. Anal. Chem. 1993;65(22):A972–A986. [Google Scholar]
- 4.Fenn JB, Rosell J, Nohmi T, Shen S, Banks FJJ. Electrospray Ion Formation: Desorption Versus Desertion. ACS Sym. Ser. 1996;619:60–80. [Google Scholar]
- 5.Fernández de la Mora J. Electrospray Ionization of Large Multiply Charged Species Proceeds via Dole's Charged Residue Mechanism. Anal. Chim. Acta. 2000;406:93–104. [Google Scholar]
- 6.Kebarle P, Peschke M. On the Mechanisms by which the Charged Droplets Produced by Electrospray Lead to Gas Phase Ions. Analytica Chimica Acta. 2000;406:11–35. [Google Scholar]
- 7.Cole RB. Some Tenets Pertaining to Electrospray Ionization Mass Spectrometry. J. Mass Spectrom. 2000;35:763–772. doi: 10.1002/1096-9888(200007)35:7<763::AID-JMS16>3.0.CO;2-#. [DOI] [PubMed] [Google Scholar]
- 8.Marginean I, Znamenskiy V, Vertes A. Charge Reduction in Electrosprays: Slender Nanojets as Intermediates. J. Phys. Chem. B. 2006;110:6397–6404. doi: 10.1021/jp055708k. [DOI] [PubMed] [Google Scholar]
- 9.Kaltashov IA, Abzalimov RR. Do Ionic Charges in ESI MS Provide Useful Information on Macromolecular Structure? J. Am. Soc. Mass Spectrom. 2008;19:1239–1246. doi: 10.1016/j.jasms.2008.05.018. [DOI] [PubMed] [Google Scholar]
- 10.Kebarle P, Verkerk UH. On the Mechanism of Electrospray Ionization Mass Spectrometry (ESIMS). In: Cole RB, editor. Electrospray and MALDI Mass Spectrometry. Wiley; Hoboken: 2010. pp. 3–48. [Google Scholar]
- 11.Labowsky M. A Model for Solvated Ion Emission from Electrospray Droplets. Rapid Commun. Mass Spectrom. 2010;24:3079–3091. doi: 10.1002/rcm.4738. [DOI] [PubMed] [Google Scholar]
- 12.Konermann L, Rodriguez A, Liu J. On the Formation of Highly Charged Gaseous Ions from Unfolded Proteins by Electrospray Ionization. Anal. Chem. 2012;84:6798–6804. doi: 10.1021/ac301298g. [DOI] [PubMed] [Google Scholar]
- 13.Consta S, Malevanets A. Classification of the Ejection Mechanisms of Charged Macromolecules from Liquid Droplets. Journal of Chemical Physics. 2013;138:044314. doi: 10.1063/1.4789018. in press. [DOI] [PubMed] [Google Scholar]
- 14.Kelly MA, Vestling MM, Fenselau CC, Smith PB. Electrospray Analysis of Proteins: A Comparison of Positive-Ion and Negative-Ion Mass Spectra at High and Low pH. Organic Mass Spectrometry. 1992;27:1143–1147. [Google Scholar]
- 15.Loo JA, Udseth HR, Smith RD. Collision Effects on the Charge Distribution of Ions from Large Molecules, Formed by Electrospray Ionization-Mass Spectrometry. Rapid Commun. Mass Spectrom. 1988;2:207–210. [Google Scholar]
- 16.LeBlanc JCY, Wang J, Guevremont R, Siu KWM. Electrospray Mass Spectra of Protein Cations Formed in Basic Solutions. Organic Mass Spectrometry. 1994;29:587–593. [Google Scholar]
- 17.Hiraoka K, Murata K, Kudaka I. Do the Electrospray Mass Spectra Reflect the Ion Concentrations in Sample Solution? J. Mass Spectrom. Soc. Japan. 1995;43:127–138. [Google Scholar]
- 18.Mansoori BA, Volmer DA, Boyd RK. ‘Wrong-Way-Round’ Electrospray Ionization of Amino Acids. Rapid Commun. Mass Spectrom. 1997;11:1120–1130. [Google Scholar]
- 19.Wang G, Cole RB. Disparity between solution-phase equilibria and charge state distributions in positive-ion electrospray mass spectrometry. Organic Mass Spectrometry. 1994;29:419–427. [Google Scholar]
- 20.Grandori R. Origin of the Conformation Dependence of Protein Charge-State Distributions in Electrospray Ionization Mass Spectrometry. J. Mass Spectrom. 2003;38:11–15. doi: 10.1002/jms.390. [DOI] [PubMed] [Google Scholar]
- 21.Prakash H, Mazumdar S. Direct Correlation of the Crystal Structure of Proteins with the Maximum Positive and Negative Charge States of Gaseous Protein Ions Produced by Electrospray Ionization. J. Am. Soc. Mass Spectrom. 2005;16:1409–1421. doi: 10.1016/j.jasms.2005.04.002. [DOI] [PubMed] [Google Scholar]
- 22.Marchese R, Grandori R, Carloni P, Raugei S. On the Zwitterionic Nature of Gas-Phase Peptides and Protein Ions. PLOS Comput. Biol. 2010;6:e1000775. doi: 10.1371/journal.pcbi.1000775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ogorzalek Loo RR, Smith RD. Proton Transfer Reactions of Multiply Charged Peptide and Protein Cations and Anions. J. Mass Spectrom. 1995;30:339–347. [Google Scholar]
- 24.Chowdhury SK, Katta V, Chait BT. Probing Conformational Changes in Proteins by Mass Spectrometry. J. Am. Chem. Soc. 1990;112:9012–9013. [Google Scholar]
- 25.Loo JA, Ogorzalek Loo RR, Udseth HR, Edmonds CG, Smith RD. Solvent-induced Conformational Changes of Polypeptides Probed by Electrospray Ionization-Mass Spectrometry. Rapid Commun. Mass Spectrom. 1991;5(3):101–105. doi: 10.1002/rcm.1290050303. [DOI] [PubMed] [Google Scholar]
- 26.Le Blanc JCY, Guevremont R, Siu KWM. Electrospray Mass Spectrometry of Some Proteins and the Aqueous Solution Acid/Base Equilibrium Model in the Negative Ion Detection Mode. Int. J. Mass Spectrom. Ion Proc. 1993;125:145–153. [Google Scholar]
- 27.Verkerk UH, Kebarle P. Ion-Ion and Ion-Molecule Reactions at the Surface of Proteins Produced by Nanospray. Information on the Number of Acidic Residues and Control of the Number of Ionized Acidic and Basic Residues. 2005;16:1325–1341. doi: 10.1016/j.jasms.2005.03.018. [DOI] [PubMed] [Google Scholar]
- 28.Juraschek R, Dülcks T, Karas M. Nanoelectrospray—More Than Just a Minimized-Flow Electrospray Ionization Source. J. Am. Soc. Mass Spectrom. 1999;10:300–308. doi: 10.1016/S1044-0305(98)00157-3. [DOI] [PubMed] [Google Scholar]
- 29.Kaltashov IA, Mohimen A. Estimates of Protein Surface Areas in Solution by Electrospray Ionization Mass Spectrometry. Anal. Chem. 2005;77:5370–5379. doi: 10.1021/ac050511+. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Winger BE, Light-Wahl KJ, Ogorzalek Loo RR, Udseth HR, Smith RD. Observation and Implications of High Mass-to-Charge Ratio Ions from Electrospray Ionization Mass Spectrometry. J. Am. Soc. Mass Spectrom. 1993;4:536–545. doi: 10.1016/1044-0305(93)85015-P. [DOI] [PubMed] [Google Scholar]
- 31.Siu KWM, Guevremont R, Le Blanc JCY, O'Brien RT, Berman SS. Is Droplet Evaporation Crucial in the Mechanism of Electrospray Mass Spectrometry? Organic Mass Spectrometry. 1993;28:579–584. [Google Scholar]
- 32.Ke F, Le Blanc JCY, Guevremont R, Siu KWM. The Effects of Stearyl and Cetyl Alcohol on the Electrospray Mass Spectrometry of Proteins and their Implications on the Electrospray Mechanism. Eur. Mass Spectrom. 1995;1:253–260. [Google Scholar]
- 33.Fenselau C, Szilágyi Z, Williams TJ. Intercharge Distances in Zn7-Metallothionein Analyzed by Nanospray on a Quadrupole Ion Trap and Molecular Modeling. Mass Spectrom. Soc. Jpn. 2000;48:23–25. [Google Scholar]
- 34.Nesatyy VJ. Mass Spectrometry Evaluation of the Solution and Gas-Phase Binding Properties of Noncovalent Protein Complexes. Int. J. Mass Spectrom. 2002;221:147–161. [Google Scholar]
- 35.Li Y, Cole RB. Shifts in Peptide and Protein Charge State Distributions with Varying Spray Tip Orifice Diameter in Nanoelectrospray Fourier Transform Ion Cyclotron Resonance Mass Spectrometry. Anal. Chem. 2003;75:5739–5746. doi: 10.1021/ac0301402. [DOI] [PubMed] [Google Scholar]
- 36.Šamalikova M, Matecko I, Müller N, Grandori R. Interpreting Conformational Effects in Protein Nano-ESI-MS Spectra. Anal. Bioanal. Chem. 2004;378:1112–1123. doi: 10.1007/s00216-003-2339-6. (Samalikova, M. Matecko, I. Muller, N. Grandori, R.) [DOI] [PubMed] [Google Scholar]
- 37.Gabelica V, Vreuls C, Filee P, Duval V, Joris B, DePauw E. Advantages and Drawbacks of Nanospray for Studying Noncovalent Protein-DNA Complexes by Mass Spectrometry. Rapid Commun. Mass Spectrom. 2002;16:1723–1728. doi: 10.1002/rcm.776. [DOI] [PubMed] [Google Scholar]
- 38.Benkestock K, Sundqvist G, Edlund PO, Roeraade J. Influence of Droplet Size, Capillary–Cone Distance and Selected Instrumental Parameters for the Analysis of Noncovalent Protein–Ligand Complexes by Nano-Electrospray Ionization Mass Spectrometry. J. Mass Spectrom. 2004;39:1059–1067. doi: 10.1002/jms.685. [DOI] [PubMed] [Google Scholar]
- 39.Cech NB, Enke CG. Effect of Affinity for Droplet Surfaces on the Fraction of Analyte Molecules Charged during Electrospray Droplet Fission. Anal. Chem. 2001;73:4632–4639. doi: 10.1021/ac001267j. [DOI] [PubMed] [Google Scholar]
- 40.Konermann L. A Minimalist Model for Exploring Conformational Effects on the Electrospray Charge State Distribution of Proteins. J. Phys. Chem. 2007;111(23):6534–6543. doi: 10.1021/jp070720t. [DOI] [PubMed] [Google Scholar]
- 41.Iavarone AT, Jurchen JC, Williams ER. Supercharged Protein and Peptide Ions Formed by Electrospray Ionization. Anal. Chem. 2001;73:1455–1460. doi: 10.1021/ac001251t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Iavarone AT, Williams ER. Supercharging in Electrospray Ionization: Effects on Signal and Charge. Int. J. Mass Spectrom. 2002;219:63–72. [Google Scholar]
- 43.Iavarone AT, Williams ER. Mechanism of Charging and Supercharging Molecules in Electrospray Ionization. J. Am. Chem. Soc. 2003;125:2319–2327. doi: 10.1021/ja021202t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Flick TG, Williams ER. Supercharging with Trivalent Metal Ions in Native Mass Spectrometry. J Am Soc Mass Spectrom. 2012;23:1885–1895. doi: 10.1007/s13361-012-0463-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Sterling HJ, Cassou CA, Susa AC, Williams ER. Electrothermal Supercharging of Proteins in Native Electrospray Ionization. Anal. Chem. 2012;84:3795–3801. doi: 10.1021/ac300468a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Hedges JB, Vahidi S, Yue X, Konermann L. Effects of Ammonium Bicarbonate on the Electrospray Mass Spectra of Proteins: Evidence for Bubble-Induced Unfolding. Anal. Chem. 2013;85:6469–6476. doi: 10.1021/ac401020s. [DOI] [PubMed] [Google Scholar]
- 47.Sterling HJ, Williams ER. Origin of Supercharging in Electrospray Ionization of Non-Covalent Complexes from Aqueous Solution. J. Am. Soc. Mass Spectrom. 2009;20:1933–1943. doi: 10.1016/j.jasms.2009.06.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Sterling HJ, Kintzer AF, Feld GK, Cassou CA, Krantz BK, Williams ER. Supercharging Protein Complexes from Aqueous Solution Disrupts their Native Conformations. J. Am. Soc. Mass Spectrom. 2011;23:191–200. doi: 10.1007/s13361-011-0301-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Šamalikova M, Grandori R. Protein Charge-State Distributions in Electrospray-Ionization Mass Spectrometry Do Not Appear to be Limited by the Surface Tension of the Solvent. J. Am. Chem. Soc. 2003;125:13352–13353. doi: 10.1021/ja037000u. [DOI] [PubMed] [Google Scholar]
- 50.Brahim B, Alves S, Cole RB, Tabet J-C. Charge Enhancement of Single-Stranded DNA in Negative Electrospray Ionization Using the Supercharging Reagent meta- Nitrobenzyl Alcohol. J. Am. Soc. Mass Spectrom. 2012 doi: 10.1007/s13361-013-0732-8. in press, reviewed. [DOI] [PubMed] [Google Scholar]
- 51.Šamalikova M, Grandori R. Testing the Role of Solvent Surface Tension in Protein Ionization by Electrospray. J. Mass Spectrom. 2005;40(4):503–510. doi: 10.1002/jms.821. [DOI] [PubMed] [Google Scholar]
- 52.Gardner HA, Sward GG. Paint Testing Manual. ASTM International; Lutherville-Timonium, MD: 1972. p. 173. [Google Scholar]
- 53.Lomeli SH, Yin S, Ogorzalek Loo RR, Loo JA. Increasing Charge While Preserving Noncovalent Protein Complexes for ESI-MS. J. Am. Soc. Mass Spectrom. 2009;20:593–596. doi: 10.1016/j.jasms.2008.11.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Lomeli SH, Peng IX, Yin S, Ogorzalek Loo RR, Loo JA. New Reagents for Increasing ESI Multiple Charging of Proteins and Protein Complexes. J. Am. Soc. Mass Spectrom. 2010;21:127–131. doi: 10.1016/j.jasms.2009.09.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Yin S, Loo JA. Elucidating the Site of Protein-ATP Binding by Top-Down Mass Spectrometry. J. Am. Soc. Mass Spectrom. 2010;21(6):899–907. doi: 10.1016/j.jasms.2010.01.002. [DOI] [PubMed] [Google Scholar]
- 56.van Duijn E. Current Limitations in Native Mass Spectrometry Based Structural Biology. J. Am. Soc. Mass Spectrom. 2010;21:971–978. doi: 10.1016/j.jasms.2009.12.010. [DOI] [PubMed] [Google Scholar]
- 57.Enyenihi AA, Yang H, Ytterberg AJ, Lyutvinskiy Y, Zubarev RA. Heme Binding in Gas-Phase Holo-Myoglobin Cations: Distal Becomes Proximal? J. Am. Soc. Mass Spectrom. 2011;22:1763–1770. doi: 10.1007/s13361-011-0182-0. [DOI] [PubMed] [Google Scholar]
- 58.Sterling HJ, Daly MP, Feld GK, Thoren KL, Kintzer AF, Krantz BA, Williams ER. Effects of Supercharging Reagents on Noncovalent Complex Structure in Electrospray Ionization from Aqueous Solutions. J. Am. Soc. Mass Spectrom. 2010;21:1762, 1774. doi: 10.1016/j.jasms.2010.06.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Merenbloom SI, Flick TG, Williams ER. How Hot are Your Ions in TWAVE Ion Mobility Spectrometry? J. Am. Soc. Mass Spectrom. 2012;23:553–562. doi: 10.1007/s13361-011-0313-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Sterling HJ, Prell JS, Cassou CA, Williams ER. Protein Conformation and Supercharging with DMSO from Aqueous Solution. J. Am. Soc. Mass Spectrom. 2011;22:1178–1186. doi: 10.1007/s13361-011-0116-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Hogan CJ, Jr., Ogorzalek Loo RR, Loo JA, Fernández de la Mora J. Ion Mobility–Mass Spectrometry of Phosphorylase B Ions Generated with Supercharging Reagents but in Charge-Reducing Buffer. Phys. Chemistry Chem. Phys. 2010;12:13476–13483. doi: 10.1039/c0cp01208d. [DOI] [PubMed] [Google Scholar]
- 62.Valentine SJ, Counterman AE, Clemmer DE. Conformer-Dependent Proton-Transfer Reactions of Ubiquitin Ions. J. Am. Soc. Mass Spectrom. 1997;8:954–961. [Google Scholar]
- 63.Loo JA, Lomeli SH, Ogorzalek-Loo RR. Factors that Promote ESI Multiple Charging for Proteins.. Paper presented at the 58th ASMS Conference on Mass Spectrometry and Allied Topics; Salt Lake City, Utah. May 23–27, 2010. [Google Scholar]
- 64.Ogorzalek-Loo RR, Lakshmanan R, Zhang J, Loo JA. Supercharging and Subcharging Proteins and Protein Complexes to Explore Electrospray Ionization.. Paper presented at the 60th ASMS Conference on Mass Spectrometry and Allied Topics; Vancouver, British Columbia, Canada. May 21–24, 2012. [Google Scholar]
- 65.Ogorzalek Loo RR, Smith RD. Investigation of the Gas-Phase Structure of Electrosprayed Proteins using Ion-Molecule Reactions. J. Am. Soc. Mass Spectrom. 1994;5:207–220. doi: 10.1016/1044-0305(94)85011-9. [DOI] [PubMed] [Google Scholar]
- 66.Konermann L, Douglas DJ. Acid-Induced Unfolding of Cytochrome c at Different Methanol Concentrations: Electrospray Ionization Mass Spectrometry Specifically Monitors Changes in the Tertiary Structure. Biochemistry. 1997;36:12296–13302. doi: 10.1021/bi971266u. [DOI] [PubMed] [Google Scholar]
- 67.Grimm RL, Beauchamp JL. Evaporation and Discharge Dynamics of Highly Charged Multicomponent Droplets Generated by Electrospray Ionization. 2010 doi: 10.1021/jp907162w. [DOI] [PubMed] [Google Scholar]
- 68.Douglass KA, Venter AR. Investigating the Role of Adducts in Protein Supercharging with Sulfolane. J. Am. Soc. Mass Spectrom. 2012;23:489–497. doi: 10.1007/s13361-011-0319-1. [DOI] [PubMed] [Google Scholar]
- 69.Ogorzalek Loo RR, Dales N, Andrews PC. The Effect of Detergents on Proteins Analyzed by Electrospray Ionization. In: Chapman JR, editor. Methods in Molecular Biology: Protein and Peptide Analysis by Mass Spectrometry. Vol. 61. Humana Press; Totowa, NJ: 1996. pp. 141–160. [DOI] [PubMed] [Google Scholar]
- 70.Barrera NP, Di Bartolo N, Booth PJ, Robinson CV. Micelles Protect Membrane Complexes from Solution to Vacuum. Science. 2008;321(5886):243–250. doi: 10.1126/science.1159292. [DOI] [PubMed] [Google Scholar]
- 71.Laurence C, Gal J-F. Lewis Basicity and Affinity Scales. Wiley; Chichester, United Kingdom: 2010. [Google Scholar]
- 72.Aslam MH, Collier G, Shorter J. The Influence of the Solvent on Organic Reactivity. Part 4. Spectroscopic Parameters of Lewis Basicity and Acidity of Hydroxylic Solvents. A Comprehensive Correlation Analysis of the log k Values for the Reactions of Diazodiphenylmethane with Benzoic Acid in Aprotic and Hydroxylic Solvents at 37°C 1572-1576. J. Chem. Soc. Perkin Trans. 1981;2:1572–1576. [Google Scholar]
- 73.Mirza UA, Chait BT. Effects of Anions on the Positive Ion Electrospray Ionization Mass Spectra of Peptides and Proteins. Anal. Chem. 1994;66(18):2898–2904. doi: 10.1021/ac00090a017. [DOI] [PubMed] [Google Scholar]
- 74.Liu X, Cole RB. A New Model for Multiply Charged Adduct Formation Between Peptides and Anions in Electrospray Mass Spectrometry. J. Am. Soc. Mass Spectrom. 2011;22:2125–2136. doi: 10.1007/s13361-011-0255-0. [DOI] [PubMed] [Google Scholar]
- 75.Tjernberg A, Markova N, Griffiths WJ, Hallen D. DMSO-Related Effects in Protein Characterization. J. Biomol. Screening. 2006;11(2):131–137. doi: 10.1177/1087057105284218. [DOI] [PubMed] [Google Scholar]
- 76.Valeja SG, Tipton JD, Emmett MR, Marshall AG. New Reagents for Enhanced Liquid Chromatographic Separation and Charging of Intact Protein Ions for Electrospray Ionization Mass Spectrometry. Anal. Chem. 2010;82:7515–7519. doi: 10.1021/ac1016858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Landreh M, Alvelius G, Johansson J, Jornvall H. Protective Effects of Dimethyl Sulfoxide on Labile Protein Interactions during Electrospray Ionization. Anal. Chem. 2014;85:4135–4139. doi: 10.1021/ac500879c. doi:dx.doi.org/10.1021/ac500879c. [DOI] [PubMed] [Google Scholar]
- 78.Lengqvist J, Griffiths WJ, Perlmann T, Sjovall J. Detection of a Receptor-Ligand non-Covalent Complex using a Triple Quadrupole Mass Spectrometer. Rapid Commun. Mass Spectrom. 2002;16:2003–2206. doi: 10.1002/rcm.811. [DOI] [PubMed] [Google Scholar]
- 79.Meyer JG, Komives EA. Charge State Consolidation During Electrospray Ionization Improves Peptide Identification by Tandem Mass Spectrometry. J. Am. Soc. Mass Spectrom. 2012;23:1390–1399. doi: 10.1007/s13361-012-0404-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Cech NB, Enke CG. Practical Implications of Some Recent Studies in Electrospray Ionization Fundamentals. Mass Spectrom. Rev. 2001;20:362–387. doi: 10.1002/mas.10008. [DOI] [PubMed] [Google Scholar]
- 81.Pan P, McLuckey SA. Electrospray Ionization of Protein Mixtures at Low pH. Anal. Chem. 2003;75:1491–1499. doi: 10.1021/ac020637w. [DOI] [PubMed] [Google Scholar]
- 82.Loo JA, Ogorzalek Loo RR. Desolvation of Noncovalently-Bound Complex Ions for ESI-MS Analysis.. 43rd ASMS Conference on Mass Spectrometry and Allied Topics; Atlanta, Georgia. May 21-May 26 1995.p. 235. [Google Scholar]
- 83.Kostiainen R, Bruins AP. Effect of Multiple Sprayers on Dynamic Range and Flow Rate Limitations in Electrospray and Ionspray Mass Spectrometry. Rapid Commun. Mass Spectrom. 1994;8:549–558. [Google Scholar]
- 84.Stahnke H, Kittlaus S, Kempe G, Alder L. Reduction of Matrix Effects in Liquid Chromatography-Electrospray Ionization-Mass Spectrometry by Dilution of the Sample Extracts: How Much Dilution is Needed? Anal. Chem. 2012;84:1474–1482. doi: 10.1021/ac202661j. [DOI] [PubMed] [Google Scholar]
- 85.Kuprowski MC, Konermann L. Signal Response of Coexisting Protein Conformers in Electrospray Mass Spectrometry. Anal. Chem. 2007;79:2499–2506. doi: 10.1021/ac0620056. [DOI] [PubMed] [Google Scholar]
- 86.Wang G, Cole RB. Mechanistic Interpretation of the Dependence of Charge State Distributions on Analyte Concentrations in Electrospray Ionization Mass Spectrometry. Anal. Chem. 1995;67:2892–2900. [Google Scholar]
- 87.Yuill EM, Sa N, Ray SJ, Hieftje GM, Baker LA. Electrospray Ionization from Nanopipette Emitters with Tip Diameters of Less than 100 nm. Anal. Chem. 2013;85:8498–8502. doi: 10.1021/ac402214g. [DOI] [PubMed] [Google Scholar]
- 88.Takáts Z, Wiseman JM, Gologan B, Cooks RG. Mass Spectrometry Sampling Under Ambient Conditions with Desorption Electrospray Ionization. Science. 2004;306(5695):471–473. doi: 10.1126/science.1104404. [DOI] [PubMed] [Google Scholar]
- 89.Liu Y, Miao Z, Lakshmanan R, Ogorzalek Loo RR, Loo JA, Chen H. Signal and Charge Enhancement for Protein Analysis by Liquid Chromatography-Mass Spectrometry with Desorption Electrospray Ionization. Int. J. Mass Spectrom. 2012;325-327:161–166. doi: 10.1016/j.ijms.2012.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Ferguson CN, Benchaar SA, Miao Z, Loo JA, Chen H. Direct Ionization of Large Proteins and Protein Complexes by Desorption Electrospray Ionization-Mass Spectrometry. Analytical Chemistry. 2011;83:6468–6473. doi: 10.1021/ac201390w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Pagnotti VS, Inutan ED, Marshall DD, McEwen CN, Trimpin S. Inlet Ionization: A New Highly Sensitive Approach for Liquid Chromatography/Mass Spectrometry of Small and Large Molecules. Anal. Chem. 2011;83:7591–7594. doi: 10.1021/ac201982r. [DOI] [PubMed] [Google Scholar]
- 92.Pagnotti VS, Chubatyi ND, McEwen CN. Solvent Assisted Inlet Ionization: An Ultrasensitive New Liquid Introduction Ionization Method for Mass Spectrometry. Anal. Chem. 2011;83:3981–3985. doi: 10.1021/ac200556z. [DOI] [PubMed] [Google Scholar]
- 93.Li J, Inutan ED, Wang B, B. LC, Green DR, Manly CD, Richards AL, Marshall DD, Lingenfelter S, Ren Y, Trimpin S. Matrix Assisted Ionization: New Aromatic and Nonaromatic Matrix Compounds Producing Multiply Charged Lipid, Peptide, and Protein Ions in the Positive and Negative Mode Observed Directly from Surfaces. J. Am. Soc. Mass Spectrom. 2012;23(10):1625–1643. doi: 10.1007/s13361-012-0413-z. [DOI] [PubMed] [Google Scholar]
- 94.Heron SR, Wilson R, Shaffer SA, Goodlett DR, Cooper MM. Surface Acoustic Wave Nebulization of Peptides as a Microfluidic Interface for Mass Spectrometry. Anal. Chem. 2010;82:3985–3989. doi: 10.1021/ac100372c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Venter A, Sojka PE, Cooks RG. Droplet Dynamics and Ionization Mechanisms in Desorption Electrospray Ionization Mass Spectrometry. Anal. Chem. 2006;78:8549–8555. doi: 10.1021/ac0615807. [DOI] [PubMed] [Google Scholar]
- 96.Douglass KA, Venter AR. Protein Analysis by Desorption Electrospray Ionization Mass Spectrometry and Related Methods. J. Mass Spectrom. 2013;48:553–560. doi: 10.1002/jms.3206. doi:DOI: 10.1002/jms.3206. [DOI] [PubMed] [Google Scholar]
- 97.Fernández de la Mora F, Loscertales IG. The Current Emitted by Highly Conducting Taylor Cones. J. Fluid Mech. 1994;260:155–184. [Google Scholar]
- 98.Gomez A, Tang K. Charge and Fission of Droplets in Electrostatic Sprays. Phys. Fluids. 1994;6:404–414. [Google Scholar]
- 99.Schmidt A, Karas M, Dülcks T. Effect of Different Solution Flow Rates on Analyte Ion Signals in Nano-ESI MS, or: When does ESI Turn into Nano-ESI? J. Am. Soc. Mass Spectrom. 2003;14:492. doi: 10.1016/S1044-0305(03)00128-4. [DOI] [PubMed] [Google Scholar]
- 100.Miladinovic SM, Fornelli L, Lu Y, Piech KM, Girault HH, Tsybin YO. In-Spray Supercharging of Peptides and Proteins in Electrospray Ionization Mass Spectrometry. Anal. Chem. 2012;84:4647–4651. doi: 10.1021/ac300845n. [DOI] [PubMed] [Google Scholar]
- 101.Alexander R, Ko ECF, Parker AJ, Broxton TJ. Solvation of Ions. XIV. Protic-Dipolar Aprotic Solvent Effects on Rates of Bimolecular Reactions. Solvent Activity Coefficients of Reactants and Transition States at 25°. J. Am. Chem. Soc. 1968;90:5049–5069. [Google Scholar]
- 102.Huang Y, Shi X, Yu X, Leymarie N, Staples GO, Yin H, Killeen K, Zaia J. Improved Liquid Chromatography-MS/MS of Heparan Sulfate Oligosaccharides via Chip-Based Pulsed Makeup Flow. Anal. Chem. 2011;83:8222–8229. doi: 10.1021/ac201964n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Ganisi B, Taucher M, Riml C, Breuker K. Charge as you Like! Efficient Manipulation of negative Ion net Charge in Electrospray Ionization of Proteins and Nucleic Acids. Eur. J. Mass Spectrom. 2011;17:333–343. doi: 10.1255/ejms.1140. [DOI] [PubMed] [Google Scholar]
- 104.Teo AC, Donald WA. Solution Additives for Supercharging Proteins beyond the Theoretical Maximum Proton-Transfer Limit in Electrospray Ionization Mass Spectrometry. Anal. Chem. 2014;85:4455–4462. doi: 10.1021/ac500304r. [DOI] [PubMed] [Google Scholar]
- 105.Wawrzynów A, Chmurzyński L. A Comparison of Acid–Base Properties of Substituted Pyridines and their N-Oxides in Propylene Carbonate. J. Chem. Thermodynamics. 1998;30:713–722. [Google Scholar]
- 106.Schäffner B, Schäffner F, Verevkin SP, Börner A. Organic Carbonates as Solvents in Synthesis and Catalysis. Chem. Rev. 2010;110:4554–4581. doi: 10.1021/cr900393d. [DOI] [PubMed] [Google Scholar]
- 107.Zikolov P, Zikolova T, Budevsky O. Acid-Base Equilibria in Ethylene Glycol-III. Selection of Titration Conditions in Ethylene Glycol Medium, Protolysis Constants of Alkaloids in Ethylene Glycol and its Mixtures. Talanta. 1976;23:587–590. doi: 10.1016/0039-9140(76)80240-8. [DOI] [PubMed] [Google Scholar]
- 108.Hazardous Substance Databank (HSDB) U. S. National Library of Medicine. [2014].
- 109.JEFFSOL Alkylene Carbonates . Comparative Solvents Data. 1089-0206. Huntsman Corporation; The Woodlands, Texas: 1999. [Google Scholar]
- 110.Konicek J. Design and Testing of a Vaporisation Calorimeter. Enthalpies of Vaporisation of Some Alkyl Cyanides. Acta Chemica Scandinavica. 1973;27:1496–1502. [Google Scholar]
- 111.Grimm RL, Beauchamp JL. Field-Induced Droplet Ionization Mass Spectrometry. J. Phys. Chem. B. 2003;107:14161–14163. [Google Scholar]
- 112.Trimpin S, Inutan ED. Matrix Assisted Ionization in Vacuum, A Sensitive and Widely Applicable Ionization Method for Mass Spectrometry. J. Am. Soc. Mass Spectrom. 2013;24:722–732. doi: 10.1007/s13361-012-0571-z. [DOI] [PubMed] [Google Scholar]
- 113.Sweeting LM. Triboluminescence with and without Air. Chem. Mater. 2001;13:854–870. [Google Scholar]
- 114.Williams ER, Zhang R, Rydock J. Mixed Phase Microphysics and Cloud Electrification. J. Atmos. Sci. 1991;48:2195–2203. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.