Direct Evidence of Catalytic Heterogeneity in Lactate Dehydrogenase by Temperature Jump Infrared Spectroscopy

Abstract

Protein conformational heterogeneity and dynamics are known to play an important role in enzyme catalysis, but their influence has been difficult to observe directly. We have studied the effects of heterogeneity in the catalytic reaction of pig heart lactate dehydrogenase using isotope edited infrared spectroscopy, laser-induced temperature jump relaxation, and kinetic modeling. The isotope edited infrared spectrum reveals the presence of multiple reactive conformations of pyruvate bound to the enzyme, with three major reactive populations having substrate C2 carbonyl stretches at 1686, 1679, and 1674 cm^–1, respectively. The temperature jump relaxation measurements and kinetic modeling indicate that these substates form a heterogeneous branched reaction pathway, and each substate catalyzes the conversion of pyruvate to lactate with a different rate. Furthermore, the rate of hydride transfer is inversely correlated with the frequency of the C2 carbonyl stretch (the rate increases as the frequency decreases), consistent with the relationship between the frequency of this mode and the polarization of the bond, which determines its reactivity toward hydride transfer. The enzyme does not appear to be optimized to use the fastest pathway preferentially but rather accesses multiple pathways in a search process that often selects slower ones. These results provide further support for a dynamic view of enzyme catalysis where the role of the enzyme is not just to bring reactants together but also to guide the conformational search for chemically competent interactions.

Introduction

While the importance of protein conformational heterogeneity and dynamics in enzymatic catalysis is well established, it has been difficult to observe their influence directly.^1,2 The fluctuation of protein structures is implicit to modern descriptions of catalytic function ranging from preorganization of the active site to induced fit. Conformational equilibria that occur on the nanosecond to millisecond time scale are of particular interest because they perturb average values of reactive structures, such as the donor–acceptor distance for hydride transfer, and thereby modulate the catalytic rate.³⁻⁵ Despite the importance of these concepts, the most widely used approach to analyze enzyme kinetics in the literature and textbooks still relies on the Michaelis–Menten model and transition state theory. This approach has served its purpose as an organizing framework for interpreting enzyme kinetics, but it tends to oversimplify enzyme reaction pathways. The Michaelis–Menten model describes product formation stemming from a single enzyme–substrate complex known as the Michaelis state.^6,7 Transition state theory further develops this concept by postulating a single barrier to proceeding from the Michaelis state to the product state and thus a single transition state that dictates enzyme selectivity and function.^8,9 Together they describe a single pathway for catalytic competency with only a few populated structures. However, it has long been recognized that proteins, and enzymes specifically, do not exist in unique three-dimensional conformations. Instead, proteins are best described in a hierarchy of interconnected conformations or substates.^10,11 The existence of such substates suggests that the progress of an enzymatic reaction from reactive conformations is substantially more complicated than transition state theory would have it.¹² Accurate models of enzyme catalysis must address this landscape of viable conformations.

We have studied the role of conformational heterogeneity and dynamics in the catalysis of hydride transfer by the enzyme lactate dehydrogenase from pig heart (phLDH). This enzyme catalyzes the reduction of pyruvate to lactate mediated by the transfer of a hydride from NADH to C-2 of pyruvate, as shown in Figure 1. phLDH is a good model system for our studies for many reasons. The phLDH reaction is rigorously ordered: NADH binds first, followed by pyruvate and then the on-enzyme chemistry.¹³ The catalytic mechanism has been well-studied previously with various methods.¹⁴⁻²³ Finally, the system may be prepared such that, at equilibrium, half occupies the pyruvate side of the reaction and half the lactate side.²⁴ Hence, the actual Michaelis complex may be studied without resorting to the use of substrate mimics.

Figure 1.

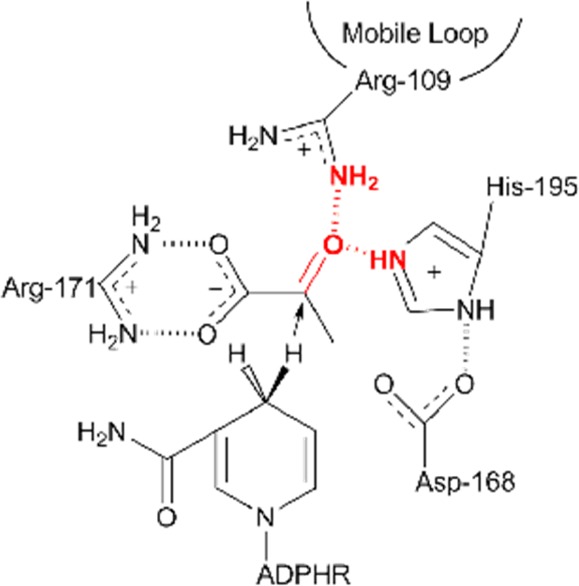
Schematic of the LDH active site showing the residues stabilizing the substrate pyruvate and the proximity of the cofactor, NADH. The catalytically key surface loop (residues 98–110) closes over the active site, bringing residue Arg109 in hydrogen bond contact with the ligand, forcing water to leave the pocket, and, accompanied by the motions of mobile areas in the protein, rearranges the pocket geometry to allow for favorable interactions between the cofactor and the ligand that facilitate on-enzyme catalysis. Of particular interest to this work are the hydrogen bonds formed between Arg-109 and His-195 to the C2 carbonyl of pyruvate (emphasized in red). These bonds dictate the polarity of the carbonyl when pyruvate is bound.

We have previously reported on the existence of a heterogeneous population of phLDH-bound pyruvate substates while at equilibrium.²⁵ Our previous work observed this heterogeneity using isotope-edited difference FTIR methods to detect multiple C-2 pyruvate carbonyl stretches characteristic of enzyme-bound substrate that are present simultaneously at equilibrium. Heterogeneity at the C-2 carbonyl of pyruvate is particularly relevant to questions about catalysis in LDH because it has been previously shown that the electrostatic interactions between this carbonyl and the protein residues His195 and Arg109 are responsible for as much as a 10⁶ catalytic rate enhancement of the overall 10¹⁴ enhancement from the enzyme.²⁶ The equilibrium difference infrared spectrum was resolved into four unique bands characteristic of enzyme-bound pyruvate at 1674, 1679, 1686, and 1703 cm^–1 as compared to free pyruvate at 1710 cm^–1. These four bands are direct evidence of the multiple available conformations in the Michaelis complex but do not report on the reactivity or catalytic relevance of any of the observed substates. Here we present a study of the catalytic relevance of these substates by observing the relaxation kinetics of each substate using temperature-jump infrared (T-jump IR) spectroscopy. We then present a scheme for the catalytic landscape that incorporates each of these substates based on kinetic modeling of the relaxation data.

Materials and Methods

Materials

NAD⁺, NADH, and pig heart LDH (phLDH) were purchased from Roche Diagnostics (Indianapolis, IN). [¹⁵N]ammonium chloride, [U-¹³C]glucose, and [2-¹³C]pyruvate were purchased from Cambridge Isotope Laboratories (Tewksbury, MA). [2-¹³C]Lactate was enzymatically produced by phLDH from [2-¹³C]pyruvate as described previously.²⁵

phLDH obtained from Roche was prepared prior to use as described previously.^24,27 The production of [U-¹⁵N, -¹³C]phLDH has been described previously.²⁵ Briefly, the phLDH gene was obtained from Zyagen’s (San Diego, CA) pig heart cDNA library. The gene and a six-residue His tag were subcloned into pET14b plasmids from Novagen (Merck KGaA, Darmstadt, Germany) and transformed into C43(DE3) competent E. coli cells from OverExpress (Imaxio, Saint-Beauzire, France). The cells were grown in minimal media supplemented with the labeled glucose and ammonium chloride indicated above. Expression of phLDH was induced by IPTG. The resulting uniformly labeled protein was purified in the same manner described for unlabeled phLDH.²⁸ All experiments described here, except where noted, utilized [U-¹⁵N, -¹³C]phLDH and the resulting uniformly labeled enzyme will be referred to simply as LDH.

FTIR Spectroscopy

Static FTIR spectroscopy was carried out on a Magna 760 Fourier transform spectrometer (Nicolet, Instrument Corporation, Madison, WI) using an MCT detector as described previously.^25,29 Infrared cells consisted of CaF₂ windows with 15 μm Teflon spacers. Spectra were collected in the range 1100–4000 cm^–1 with 2 cm^–1 resolution. A Blackman–Harris three-term apodization and a Happ–Genzel apodization were applied, respectively. Omnic 4.1a (Nicolet Instruments, Corp.) software was used for data collection and analysis. All samples were prepared in D₂O buffer with 100 mM phosphate at pH 7.2 (pH meter reading). The LDH reaction mixture was prepared at the initial concentrations of 4:4:20 mM (LDH•NAD⁺•lactate, where LDH concentration refers to active sites). Under such conditions, about half of the NAD⁺ was converted to NADH, yielding an on-enzyme pyruvate concentration of about 2 mM as determined by UV–vis measurements.²⁷ This high protein concentration is required to observe the weak absorbance of a single substrate carbonyl bond in the large enzyme complex, as each protein active site only binds one substrate. We did not observe protein aggregation at this concentration on the basis of the complete absence of the intense IR marker bands for aggregation. Additionally, we performed temperature-dependent FTIR measurements on this same reaction mixture. The sample cell was in thermal contact with the stage. The temperature of the stage was controlled by a water bath. Collection of spectra and temperature control were automated by Labview (National Instruments, Austin, TX) routines written in our lab.

Temperature-Jump IR Spectroscopy

T-jump IR spectroscopy was performed with a previously described setup.^30,31 Briefly, a 1.91 μm pump beam is produced by the first Stokes shift of the fundamental line from a Nd:YAG laser (30 mJ/pulse, 10 Hz repetition rate, 10 ns pulse width, Spectra Physics (Mountain View, CA)) pumping a H₂-filled Raman shifter. The 1.91 μm pump beam is absorbed weakly by the combination bands of the D₂O solution, allowing for near uniform heating of the solution. The heated region is probed by a quantum cascade laser (Daylight Solutions Inc., Poway, CA) tunable from 1565 to 1723 cm^–1. Changes in probe beam transmission are detected by a fast (200 MHz) photovoltaic MCT detector (Kolmar Technologies, Newburyport, MA), and the signal is filtered and amplified in a low noise preamplifier (SR560, Stanford Research Systems). Typically, 10000 pump–probe events are averaged for each probe frequency of interest. The sample cell path length was 200 μm. Temperature jumps of 8 and 15 °C were employed in this study. A consistent final temperature of 30 °C was used so that all results were reporting on the same thermal equilibrium. The useful time range of the instrument used in this study is from 10 μs to 1 ms. The lower limit of this range is set by the bandwidth of the preamplifier. The geometry of our cell arrangement is such that heat diffuses out of the irradiated volume with a lifetime of a few ms; this determines the duration of the T-jump and thus sets an upper limit to the useful time range.

The relaxation spectra of the enzyme complexes with infrared probes at pyruvate frequencies contain signals not only from pyruvate but also from the protein, because it has a broad background absorbance in this region. Two types of difference methods were used to remove the contributions from the protein kinetics in these data. The first was to use the isotope edited methods similar to that for the static infrared studies, as described in detail in refs (25, 29, and 32). In this approach, the pyruvate-specific infrared probes were used on both enzyme complexes with cofactor/pyruvate and with cofactor/[2-¹³C]pyruvate. The contribution from protein in the relaxation transient can be eliminated by subtraction of the IR transient of the enzyme complex with [2-¹³C]pyruvate from the unlabeled complex. The second method is to use an infrared probe that is off resonance from the pyruvate frequencies so that only the background protein relaxation transient is obtained. In our case, 1695 cm^–1 is used as a reference probe frequency, since the static data indicate that the pyruvate C2=O stretch mode is absent at this frequency. Subtraction of the protein kinetics from the data with infrared probes specific for pyruvate substates yields the relaxation kinetics of only those substates. We have found the kinetic results obtained by these two methods are very similar, especially in the frequency region of the heterogeneous broadened 1680 cm^–1 band.

Kinetic Modeling

Modeling a proposed reaction scheme to fit the measured temperature-jump kinetics was performed with MATLAB 2013b (MathWorks, Natlick, MA) using routines written in our lab. A standard curve fitting approach is not applicable to this problem because there is not enough information known about the rate constants at each step and such an approach would be underdetermined. Instead, our overall approach was to test how well the predicted relaxation kinetics from an input reaction scheme match the experimental relaxation (temperature-jump) results. A detailed explanation is presented in the Supporting Information. This approach necessitates a large number of variables to fully describe the system. The routine involves four main steps and requires an input reaction scheme, a set of rate constants, and activation energies that define the scheme at a given temperature, initial and final jump temperatures, and initial concentrations of each component in the reaction scheme. Step one generates rate constants for the scheme at the experimentally relevant temperatures. Step two determines equilibrium concentrations of all states at each temperature using a master equation approach. Step three calculates relaxation times and amplitudes by an eigenvalue decomposition approach. Step four calculates a time-dependent profile of each state based on the parameters calculated in the previous steps. To quantitatively compare similarity between a predicted set of results and the experimental data, we devised a scoring method that considers all of the transient data at five different probe frequencies. First, we calculated an accuracy score for each transient, as shown in eq 1

1

where j is each probe frequency, n is the total number of points in the transient, and i is a given point in time. This method gives a direct measure of how accurately the predicted transient matches the experiment and ignores whether the predicted data over- or underestimates the experimental data. A perfect score is zero. Finally, a composite score for an entire fitting run is compiled as the summation of all the transient scores, as shown in eq 2.

2

The total score is used for comparison as the whole process is cycled in a Monte Carlo fashion where a rate constant is randomly modified, the steps are repeated, and the score is computed to determine if the fit is improved. To test multiple trajectories with many Monte Carlo steps in a reasonable amount of time, the calculations were performed on a multiprocessor cluster in the Emerson Center for Scientific Computation.

Results and Discussion

Equilibrium FTIR Studies

Figure 2 displays the infrared isotope edited difference spectra of LDH-bound pyruvate at 5, 15, 25, and 35 °C. The difference spectra were generated by subtracting the protein-bound [2-¹³C]pyruvate spectra from the protein-bound [2-¹²C]pyruvate spectra at each temperature. The resulting difference spectra report only on the infrared bands that are affected by the label; therefore, these IR difference features report directly on the reactive carbonyl bond involved in the catalytic turnover. The [2-¹²C]pyruvate carbonyl stretches are the positive bands in the spectrum, whereas the [2-¹³C]pyruvate carbonyl stretches would appear as negative bands at lower energy; the negative bands are visible in Figure S1 (Supporting Information). The carbonyl infrared stretch overlaps with strong H₂O absorption bands and the amide I bands of the protein backbone. To minimize this spectral overlap, we worked with D₂O solutions of uniformly isotope-labeled [U-¹⁵N, -¹³C]LDH. The larger molecular mass shifts the protein amide-I infrared absorbance to lower energy, away from the pyruvate ¹²C2=O stretch frequency.

Figure 2.

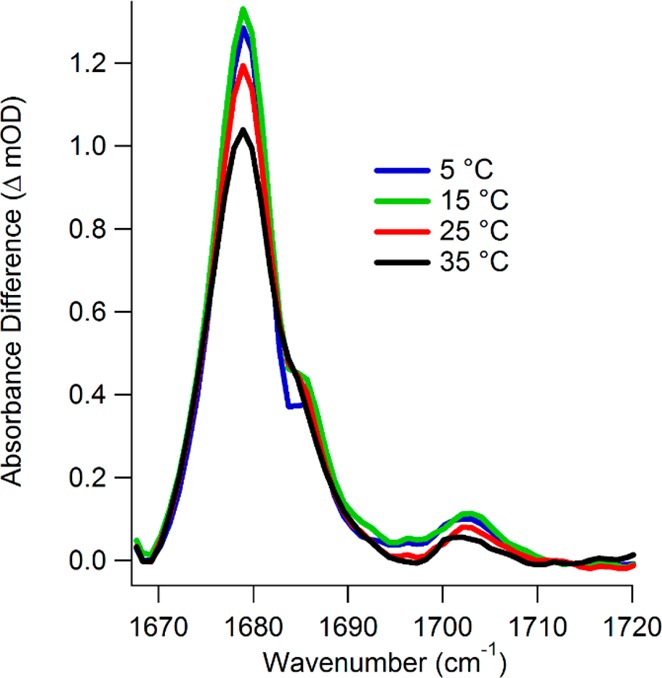
Isotope-labeled difference FTIR spectra of [U-¹⁵N, -¹³C]LDH•NADH•[2-¹²C]pyruvate minus [U-¹⁵N, -¹³C]LDH•NADH•[2-¹³C]pyruvate at the indicated temperatures.

The ¹²C2=O stretch IR spectrum of bound pyruvate is heterogeneously broadened. Gaussian fits to the spectrum reveal several sub-bands that we assign to different enzyme-bound pyruvate conformational substates.²⁵ A reasonable fit of the data was produced by the sum of four Gaussian sub-bands with center frequencies at 1674, 1679, 1686, and 1703 cm^–1, although we cannot rule out the possibility that each of these bands could be composed of more than one overlapping substate. These Gaussian sub-bands are shown in Figure S1 (Supporting Information). There is also the likelihood of sparsely populated substates that are not apparent in the IR difference spectra due to limited sensitivity.³³ Two observations illustrate that the substate distribution is temperature-dependent. First, all band intensities tend to decrease as the temperature is raised. This indicates the population shifts away from bound pyruvate either to free pyruvate or to the product side (bound or free lactate) at higher temperature. The IR difference spectra do not allow us to track the lactate population directly, because upon conversion to lactate the C2 carbonyl infrared stretch is lost and the corresponding lactate vibration is not observed in this spectral region (it is at lower frequency and obscured by protein absorbance). The second observation is that a new equilibrium is established among the substates when comparing the lowest temperature spectrum to higher ones. This trend is visible by comparing the more dramatic decrease in absorption at 1679 cm^–1 to the minimal decrease in absorption at 1674 and 1686 cm^–1. Therefore, changing temperature is a viable method for disturbing the LDH equilibrium and can be used to study the dynamics of this redistribution.

Temperature-Jump Kinetics

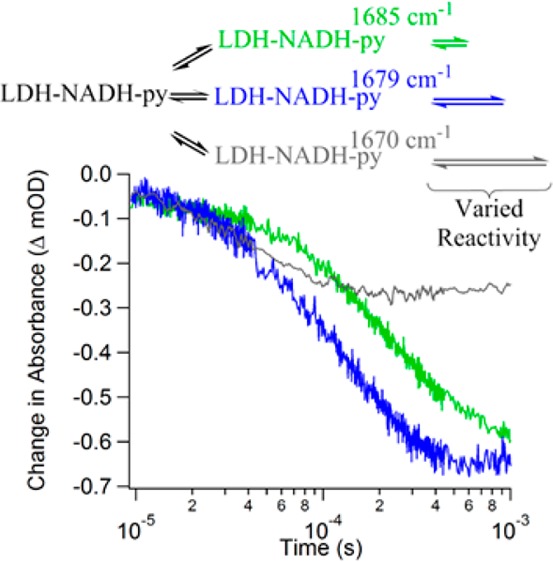
The relaxation times for establishing new equilibria among the IR detected substates and the product states are determined by laser-induced temperature jump relaxation spectroscopy employing IR probes at infrared frequencies representative of each of the substates noted above. We used 1710 cm^–1 to study the free pyruvate population as well as 1704, 1685, 1679, and 1670 cm^–1 to study the 1703, 1686, 1679, and 1674 cm^–1 protein-bound pyruvate bands, respectively, under an assumption of one substate for each probe frequency. Although it is possible, and probably likely, that there are more than these five pyruvate substates present and contributing overlapping signals, this is the minimum number of states that can fit our equilibrium data. At the probe frequencies used to study the bound pyruvate substates, we can safely assume that the dominant contributor to each spectroscopic signal is the assigned substate from equilibrium. Using the fitting parameters presented in ref (25), we can estimate the relative contribution of each of the substates to a given probe frequency. This analysis suggests that the probe frequencies are dominated by the assigned substate in a range of 75–100% contribution. The full analysis is presented in Table S1 (Supporting Information).

Figure 3 shows the relaxation transient at each probe wavelength from 10 μs to 1 ms. The lower limit of this range is set by the response time of the instrument, and the upper limit is determined by the cooling time of the sample after the temperature jump occurs (typically several ms for this sample configuration). The data presented in the figure represent jumps of the sample to the same final temperature, 30 °C, but different initial temperatures. T-jumps to a final temperature of 30 °C optimize the change in the ¹²C2=O stretch infrared absorbance from any of the lower temperatures (Figure 2) while avoiding cavitation artifacts observed at higher temperature. The 1710 and 1704 cm^–1 IR transients were obtained with a jump from an initial temperature of 15 °C. The other three probe frequencies had an initial temperature of 22 °C. The initial temperature determines the populations of the various states, whereas the final temperature has a direct effect on the relaxation kinetics, depending on the activation energies. The difference in the initial temperatures affects the amplitude of the transients, scaling to a good approximation as the size of the temperature jump. Therefore, the transient relaxation lifetimes for jumps to the same final temperature are comparable directly, but comparison of the magnitude requires adjustment to the size of the T-jump. Beyond 1 ms, the solution begins to cool and it is not possible to separate further changes in the IR signal due to the enzyme dynamics from the cooling induced changes. The relaxation transients are all well fit to a single function, as shown in Figure 3, except for the 1704 cm^–1 data. A double exponential function is required to achieve a reasonable fit of the 1704 cm^–1 transient. The fit lifetimes are provided in Table 1.

Figure 3.

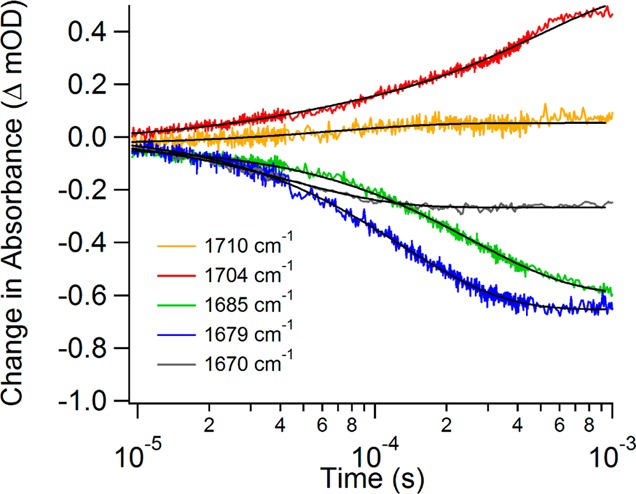
Isotope-labeled IR difference temperature-jump relaxation transients of [U-¹⁵N, -¹³C]LDH•NADH•[2-¹²C]pyruvate minus [U-¹⁵N, -¹³C]LDH•NADH•[2-¹³C]pyruvate at various probe frequencies. Each probe frequency is plotted as a different color as specified in the legend, and the exponential fits are plotted as black lines.

Table 1. Exponential Fit Lifetimes for Temperature-Jump Data.

probe frequency	experimental relaxation lifetime	simulation relaxation lifetime
1710 cm–1	69 ± 6 μs	63.6 ± 0.6 μs
1704 cm–1	33 ± 3 μs (14%)a	332.0 ± 0.6 μs
	480 ± 20 μs (86%)a
1685 cm–1	254 ± 3 μs	245.6 ± 0.6 μs
1679 cm–1	128 ± 1 μs	134.0 ± 0.4 μs
1670 cm–1	44.2 ± 0.6 μs	93.81 ± 0.04 μs

^aPercent contribution of the phase to the overall fit.

The 1685, 1679, and 1670 cm^–1 transients each show a negative amplitude signal with a sub-millisecond relaxation lifetime that depends on the probe frequency; the fit lifetime decreases as the probe frequency decreases. The negative amplitudes indicate a net flux out of the Michaelis states at the final temperature of the T-jump. The observed relaxation rate at each probe frequency depends on both the flux into (the loop closure step) and out of (the hydride transfer step) the Michaelis states. The kinetics model we developed to describe the overall reaction (described below) indicates that the relaxation is dominated by the chemistry step, leading to an overall decrease in population of the Michaelis states. Consequently, the rate of the hydride transfer is inversely correlated with the frequency of the C2 carbonyl stretch (the rate increases as the frequency decreases). Because the C2 carbonyl stretch frequency is directly related to the bond strength, or the polarization of the bond, it correlates with the reactivity toward hydride transfer. Such a correlation is consistent with previous studies relating the frequency of the C2 carbonyl vibration to the rate of enzymatic turnover.^26,34,35 Previous studies generated a series of mutations of LDH from B. stearothermophilus to alter the hydrogen bonding network at the active site. Isotope edited FTIR spectroscopy was used to determine the effect of these mutations on the frequency of the C2 carbonyl stretch and thus how the altered hydrogen bonding affects the polarity of the C2 carbonyl. These studies concluded that an increase in the polarity of the bond is directly correlated to an increase in the hydride transfer rate.

The present work is a more direct observation of the relationship between carbonyl bond polarity and the rate of hydride transfer, because it compares different conformations of the same enzyme. The transients observed for the substates probed by 1685, 1679, and 1670 cm^–1 depend on the rate of chemical transition from pyruvate to lactate. This conclusion is also consistent with the observation that in the equilibrium measurements this cluster of infrared bands has the lowest stretch frequency and highest polarity, and therefore it represents substates closest to forming lactate. Importantly, the amplitudes of these transients are all negative, indicating a decrease in population of the substates, due at least in part to shifting the equilibrium toward lactate. Furthermore, the substate transients are independent in time, and there is no evidence of correlated changes expected for direct interconversion of one substate to another. Specifically, if substate A is directly converted to substate B, then we should observe a decrease in the infrared absorbance of A and a corresponding increase in the infrared absorbance of B; these signals would be correlated in time with amplitudes of comparable but opposite sign. We have previously observed direct interconversion in studies of phLDH with the Michaelis complex substrate analogue, oxamate.²⁹ Such behavior is not observed in the present case. Therefore, we assign this cluster of bands to a set of activated conformations within a parallel reaction pathway. In this context, activated indicates the complexes are ready to perform chemistry, analogous to the Michaelis complex in a simplified reaction scheme. We have also previously reported evidence of a parallel reaction pathway in the phLDH•NADH•oxamate system.²⁹ The observation that the substates follow parallel pathways and have different reactivities is important because it is in direct contrast to conventional enzyme models in which the chemistry occurs by crossing a single dominant activation barrier.

In contrast, the 1704 cm^–1 transient shows a positive absorbance change and the 1710 cm^–1 absorbance of free pyruvate is changed very little. The 1704 cm^–1 transient is fit to a faster phase with an approximately 35 μs time constant that contributes 14% of the total signal intensity and a slower, 500 μs, phase that contributes the rest. This transient forms an important counterpart to the 1685, 1679, and 1670 cm^–1 transients. Since the 1704 cm^–1 transient has an intensity of the opposite sign and also effectively spans the time scale of the lower frequency bleaches, we conclude that a fraction of the population of the three Michaelis complex substates is transforming directly into the 1704 cm^–1 substate. The 1704 cm^–1 transient absorbance only accounts for about half of the sum of the bleach features, however, meaning the rest of the population of the Michaelis states is converting to product. We assign the 1704 cm^–1 band as an encounter complex formed between LDH•NADH and pyruvate at an early stage of binding along the reaction pathway, characterized by weak hydrogen bonding between the protein and C2=O moiety of pyruvate. Evidence for such a state has been observed before in other studies with phLDH.^29,30,36 The 1710 cm^–1 transient signal of free pyruvate shows a small increase on a fast time scale that is not well correlated with the other signals. The small magnitude of this transient and its uncorrelated time dependence imply that only a small amount of free pyruvate is formed in response to the T-jump, most likely from the encounter complex directly and not from the Michaelis states.

To summarize, the transient IR data indicate three features of the enzyme reaction mechanism: first, the existence of several Michaelis complex conformations well advanced along the reaction pathway that do not directly interconvert and are characterized by varied reactivity for the chemical conversion of pyruvate to lactate; second, the existence of an encounter complex that interconverts to the activated conformations; third, the lack of a direct pathway between free pyruvate and the Michaelis states, meaning the encounter complex is an obligatory intermediate. The simplest model that incorporates all of the above conclusions from the temperature-jump data is presented in Scheme 1 below.

Scheme 1.

Additional support for this scheme comes from a significant body of previous work. The salient points are initial binding via the formation of a weakly interacting encounter complex,^29,30,36 protein conformational changes associated with forming the Michaelis complex,³⁷ multiple well populated conformations within the Michaelis complex which do not directly interconvert, and one of these populations being incompetent toward conversion to lactate.^16,38,39 A key finding from previous work is that a slow conformational motion within the enzyme is likely rate limiting, not the chemistry step itself. The protein motion that limits enzyme turnover involves the closure of the surface loop (residues 98–110) to bring the key residue, Arg109, into the active site (see Figure 1), accompanied by changes far from the active site.³⁷ This conformational change is represented in Scheme 1 as the transition between the encounter complex (1704 cm^–1) and the reactive Michaelis states. Steady state kinetics measurements of the LDH enzyme yielded a k_cat of 245 s^–1 with a KIE of 1.4 comparing enzyme loaded with NADD versus NADH.²⁵ This value for the H/D primary KIE is lower than expected; a characteristic value of six or more would be observed if the chemical step were rate limiting. We conclude that the various protein atomic rearrangements occurring within the phLDH•NADH•pyruvate complex are on a similar time scale as the chemical step (steps 2 and 3, respectively, in Scheme 1), such that they are strongly coupled kinetically.

Kinetic Modeling

To test the validity of Scheme 1, we developed a computational routine to fit the reaction scheme to previous results (fluorescence T-jumps) as well as the new results from the IR temperature-jump data. The details of this routine are discussed in the Materials and Methods section and in the Supporting Information. In essence, the routine searches for rate constants to define a given reaction scheme that will match input relaxation data. This method incorporates all coupled reaction steps and does not require making simplifying assumptions about dominant pathways. The fit data in Table 1 show that the transients are changing on similar time scales; therefore, making assumptions about dominant pathways is unwarranted.

We first attempted to fit the relaxation data with the mechanism presented in Scheme 1. We used the rate constants and activation energies adapted from previous optical absorption and emission T-jump studies of phLDH as initial guesses.²⁴ However, the calculations did not fit well to all of the experimental transients with the calculations consistently reporting scores of 50–100 (lower is better, see the Materials and Methods) for the trajectories. Starting trajectories with random rate constants did not produce better scores. Upon analysis of the results, two types of fits were produced. Either all of the transients except the 1704 cm^–1 transient were fit well or the 1704 cm^–1 was fit well and the rest were not. Figure 4A shows a representative fit using the kinetics model defined by Scheme 1. Step-wise adjustments to the reaction mechanism were made to test how well new models fit to the experimental data. We include a representative sample of some of these other schemes in the Supporting Information. Still, none of the various models attempted were significantly better. We conclude that the mechanism presented in Scheme 1 is not sufficient to describe the relaxation data.

Figure 4.

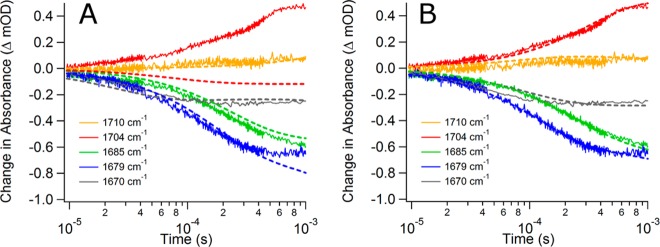
Comparison of the simulated relaxation kinetics (dashed lines) with the experimental data (solid lines). Graph A uses Scheme 1 as the reaction model for simulated results. Graph B uses Scheme 2 as the reaction model for simulated results. The most significant change is the better fit for the 1704 cm^–1 transient when Scheme 2 is used.

Various other possible kinetic schemes were tried; these mostly involved tweaking the treatment of the 1704 cm^–1 substate (see the Supporting Information), which produced dramatic improvement of the model. We focused on this substate because the results, like those of Figure 4A, indicate that 1704 cm^–1 was somehow different than the other substates. The best model was the inclusion of a second encounter complex with the constraint that it could be populated only from free pyruvate (and hence is not along the reaction pathway to lactate formation). Scheme 2 summarizes this new kinetic mechanism. In this scheme, the encounter complex state labeled LDH•NADH•py has no discernible IR signature. The lack of an IR signal is probably due to the heterogeneous nature of this state. Most likely what we are labeling as one state is in reality a multitude of similar weakly bound pyruvate states along a productive pathway. This heterogeneity would lead to a very broad infrared band that would be hard to detect except at high concentrations. Our simulations indicate that this substate has a concentration of 2.9 μM at equilibrium. In contrast, the 1704 cm^–1 substate has a distinct, tightly bound pyruvate conformation leading to a narrower IR band that allows detection of this state even at low (3.8 μM) concentration. There is previous computational evidence for an array of bound pyruvate structures in lactate dehydrogenase that support this concept.³³ The addition of an additional substate resulted in two more microscopic rate constants. Previously experimentally derived rate constants were assumed for the competent encounter complex.²⁴ The values are presented in Table S2 (Supporting Information). The result of the change was to increase the overall population of this state at elevated temperature in the simulation and therefore increase the absorbance at 1704 cm^–1.

Scheme 2.

The model summarized in Scheme 2 fits the experimental data well in a number of ways. It is qualitatively obvious by looking at Figure 4B that the new model better matches each of the experimental transients than the fits shown in Figure 4A. Quantitatively, the routine-specific score values of 3–5 were drastically better for the new model as compared to the original model’s scores of 50–100. Finally, we can see by comparison in Table 1 that the observed relaxation lifetimes calculated by fitting the theoretical transients are similar to the observed relaxation lifetimes from the experimental data. The inclusion of a dead-end or noncompetent state along the reaction pathway is not a new concept. We have previously seen evidence for a dead-end complex when studying the phLDH system with the substrate mimic oxamate using infrared as the probing method.²⁹ However, the oxamate work suggested the observed dead-end complex was a well-populated Michaelis conformation instead of an encounter complex. Scheme 2 is not intended to assert that there are no additional Michaelis conformations, or that all activated conformations are productive. Instead, Scheme 2 is the simplest model that fits the experimental data, and it supports multiple enzyme conformations at both the encounter and Michaelis complex stages of the reaction pathway. There is no evidence for dead-end complexes when the pyruvate system is studied using only NADH fluorescence as a probe.²⁴ In work on a nitrated mutant enzyme, Clarke and co-workers did see evidence of multiple enzyme-bound pyruvate states where one such state was significantly slower reacting at cryo-temperatures using stopped flow.⁴⁰ They suggested these states could slowly interconvert directly. It is possible that our second encounter complex may in fact be the second pathway they suggest but that it is interconverting or reacting too slowly to observe in our experiments and is essentially nonproductive.

There are differences between the experimental and simulated transients, even for the best fit to Scheme 2, including the best fit of the 1704 cm^–1 transient to a single exponential and a longer lifetime for the 1670 cm^–1 transient in the simulation. The simulated lifetime for the 1704 cm^–1 transient is in between the two lifetimes of the double exponential fit of the experimental data. This difference is likely due to the noise and small subtraction artifacts present in the experimental data that make it difficult to fit the data. The simulation also predicts a longer lifetime for the 1670 cm^–1 transient than what is observed experimentally. The transient IR signal for this state is very small due to its low population, making it difficult to fit. It is also possible that the rate constants for this state are not fully optimized in the simulation, since it only contributes a small fraction of the total reaction flux. It is important to point out that, despite these small discrepancies, the model still predicts a decreasing lifetime with decreasing probe frequency.

The defining feature of the kinetic model in Scheme 2 is parallel pathways with Michaelis states of varied reactivity. Furthermore, the model indicates that the reactivity scales with the frequency of the pyruvate C2 carbonyl stretching frequency: the lower the frequency, the higher the reactivity (shorter lifetime for the chemistry step). This relationship can be understood in terms of the relationship of the vibrational frequency to the force constant and hence the bond distance or the degree of polarization of the bond. In the diatomic approximation, a shift of the carbonyl mode from 1710 to 1679 cm^–1 represents a lengthening of the C=O bond by 0.01 Å,⁴¹ making it more susceptible to nucleophilic attack by the hydride. It is interesting to note that the enzyme does not primarily bind pyruvate in the most reactive substate. At equilibrium, the 1679 cm^–1 substate is clearly the most populated one, as shown in Figure 2. Since these substates do not interconvert directly, the net flux through each depends on the branching from the initial encounter complex. Apparently the enzyme is not optimized to primarily use the fastest pathway, and the overall turnover rate is a population weighted average of the multiple parallel pathways. The model outlined in Scheme 2 predicts an ensemble averaged turnover rate of k_cat = 179 s^–1 (see the Supporting Information), which is similar to the average turnover rate determined from NADH absorbance measurements, k_cat = 245 s^–1.²⁵ Thus, the IR measurements provide a high-resolution view of all of the relevant substates in the enzyme reaction pathway in contrast to simply observing the ensemble turnover rate.

Conclusions

In this work, we examined the reaction pathway of pig heart LDH using infrared absorbance. Through analysis of equilibrium spectra, relaxation transients, and subsequent kinetic modeling, we developed a novel scheme for LDH catalysis that involves several branching pathways and supports the presence of a dead-end complex. Our results not only provide direct evidence for the population of various enzyme conformations, but they also indicate that the enzyme samples multiple conformations while performing catalysis. This observation provides further support for a dynamic view of enzyme catalysis where the role of the enzyme is not just to bring reactants together but also to guide the conformational search for chemically competent interactions.

The inclusion of substates that are off an optimal kinetic pathway is particularly interesting when considering the induced fit framework for understanding enzyme reactions. In this framework, the binding of substrate induces conformational changes in the enzyme that are necessary for catalytic action.⁴² The presence of a noncompetent encounter complex complicates this framework because it suggests the induced conformational change can be wrong. Because this noncompetent encounter complex does not convert to the competent one directly, the enzyme must release the substrate and try again. This result also implies that the enzyme is not perfectly preorganized for any interactions with substrate but is instead in a dynamic search for the correct interaction with substrate that will lead to catalysis. The presence of similar heterogeneity in the activated conformations indicates this search is not complete once substrate binds to the enzyme. The search continues throughout the reaction pathway. Furthermore, our results indicate that the various Michaelis states are catalytically competent at different rates. This finding implies that the enzyme’s conformational search is not necessarily for one optimal pathway or conformation but simply for one that will work. The enzyme, therefore, has not eliminated the search for the correct reactant interaction, as compared to solution-phase chemistry, but instead provides a platform for greatly reducing the search. The nonoptimized nature of many enzymes has already been noted by other researchers, so it is interesting to consider whether the imperfection in the search process is part of the evolutionary fine-tuning of an enzyme to keep turnover rates from becoming so fast as to throw off biological equilibrium.⁴³ For this reason, we expect populations of catalytically relevant heterogeneous structures to be an important conserved feature of many enzymes.

Supporting Information Available

A more detailed explanation of the kinetic modeling, examples of additional reaction mechanisms tested, details of simulation results presented in Figure 4, and a description of how we estimated k_cat for out model. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States