Abstract
Cardiac and skeletal myosin assembled in the muscle lattice power contraction by transducing ATP free energy into the mechanical work of moving actin. Myosin catalytic/lever-arm domains comprise the transduction/mechanical coupling machinery that move actin by lever-arm rotation. In vivo, myosin is crowded and constrained by the fiber lattice as side chains are mutated and otherwise modified under normal, diseased, or aging conditions that collectively define the native myosin environment. Single-myosin detection uniquely defines bottom-up characterization of myosin functionality. The marriage of in vivo and single-myosin detection to study zebrafish embryo models of human muscle disease is a multiscaled technology that allows one-to-one registration of a selected myosin molecular alteration with muscle filament-sarcomere-cell-fiber-tissue-organ- and organism level phenotypes. In vivo single-myosin lever-arm orientation was observed at superresolution using a photoactivatable-green-fluorescent-protein (PAGFP)-tagged myosin light chain expressed in zebrafish skeletal muscle. By simultaneous observation of multiphoton excitation fluorescence emission and second harmonic generation from myosin, we demonstrated tag specificity for the lever arm. Single-molecule detection used highly inclined parallel beam illumination and was verified by quantized photoactivation and photobleaching. Single-molecule emission patterns from relaxed muscle in vivo provided extensive superresolved dipole orientation constraints that were modeled using docking scenarios generated for the myosin (S1) and GFP crystal structures. The dipole orientation data provided sufficient constraints to estimate S1/GFP coordination. The S1/GFP coordination in vivo is rigid and the lever-arm orientation distribution is well-ordered in relaxed muscle. For comparison, single myosins in relaxed permeabilized porcine papillary muscle fibers indicated slightly differently oriented lever arms and rigid S1/GFP coordination. Lever arms in both muscles indicated one preferred spherical polar orientation and widely distributed azimuthal orientations relative to the fiber symmetry axis. Cardiac myosin is more radially displaced from the fiber axis. Probe rigidity implies the PAGFP tag reliably indicates cross-bridge orientation in situ and in vivo.
Introduction
Skeletal and cardiac muscle myosins are cellular movers tasked with transducing ATP free energy into the mechanical work produced by muscle contraction. Myosin is comprised of a motor domain containing ATP and actin-binding sites; a lever arm that undergoes rotation, impelling bound actin; and a tail forming the thick filament with other myosins. The lever arm converts torque generated in the motor into linear displacement known as step size and undergoes shear strain due to the resisting load. Bound myosin essential and regulatory light chains (ELCs and RLCs, respectively) stabilize the lever arm (1–3) and adapt its mechanical coupling of motor torque to resisting load, referred to henceforth as mechanical coupling. Hereditary skeletal myopathies linked to myosin lead to muscle weakness (4) or affect myosin isoforms expressed during development, leading to arthrogryposis syndromes (5). Inheritable cardiomyopathies (ICs) are more frequently linked to myosin mutations than to any other sarcomeric protein. IC mutations are located throughout the myosin molecule, affecting many protein functional characteristics. Some disease-linked mutations and other normal posttranslational modifications affect the myosin mover specifically in its ability to adapt mechanical coupling (6). Our long-term goal is to discover how the myosin mover adapts mechanical coupling in response to changing demands on muscle power output, the effects of disease, or effects of aging.
We tagged the C terminus of human ventricular RLC (gene MYL2) with green fluorescent protein (GFP), then exchanged the RLC-GFP chimer into permeabilized skeletal (7) or cardiac papillary muscle fibers (8). In both cases, full recovery of isometric contraction from extensively and specifically exchanged myosin cross bridges in the fibers implied that the GFP did not deter muscle contraction. The photoactivatable GFP variant (PAGFP)-tagged RLC (RLC-PAGFP) could be individually activated in the exchanged papillary muscle fibers isolating single myosin cross bridges in situ. Single cross-bridge lever-arm orientation was measured at superresolution from fibers in rigor, relaxation, and active isometric conditions. Single-molecule orientation was also measured for the exchanged RLC-PAGFP modified by single IC-linked mutations to the RLC (6). The exchanged mutant RLC lowered lever-arm stiffness and impaired lever-arm mechanical coupling. The in situ single-molecule experimentation quantitated the effect of myosin light chain mutation position on mechanical coupling indicating light-chain control points that are natural therapy targets. Our interim goal is to adapt the relevant single-molecule technology to in vivo experimentation in zebrafish embryos. We have accomplished this goal with the research described here.
The zebrafish is a newer model organism for human cardiovascular disease research with a sequenced genome indicating zebrafish homologs for most protein-coding human genes (9). Forward genetic screening identified fish mutants that cause cardiac defects, which provided fresh insight into causes of inheritable human cardiac disease including dilated cardiomyopathy (DCM) (10) and cardiac valve defects (11). The zebrafish has been used increasingly to model human cardiac disease in reverse genetic approaches due to zebrafish/human disease phenotype similarities (12) and their applicability to high-throughput screening methods (13). Zebrafish embryos are suited to muscle research because they develop externally, skeletal and cardiac muscle comprises a large fraction of their body volume, and they begin to move very soon after gastrulation (14). A muscle-specific promoter directs gene expression in the musculature for the temporal and spatial pattern desired. The unc45b promoter is a small and muscle-specific promoter that drives robust gene expression throughout the zebrafish musculature (15). Transient injection of the target gene was carried out using established techniques for Tol2 transposon-based transgenesis (16).
The zebrafish embryo is transparent to visible and infrared light, allowing unprecedented access for three-dimensional imaging using wide-field fluorescence microscopy with sheet (17) or highly inclined thin (HILO) illumination (18). These methods utilize a narrow illumination depth to lower fluorescence background excited by scattering in the inhomogeneous specimen. HILO was implemented using the total internal reflection fluorescence (TIRF) illuminator, but with the laser beam incident on the coverslip/specimen interface near, but below, the critical angle, causing highly inclined transmission of the parallel light beam into the specimen.
Plasmids containing the human RLC-GFP construct and muscle promoter injected into zebrafish embryos at the single-cell stage expressed in a mosaic pattern in skeletal trunk muscle. Microscopic observation at 3–5 days postfertilization (dpf) showed expression in skeletal muscle localized to myosin in the A-band in a striated pattern, indicating specific incorporation with the myosin heavy chain (MHC). Single-cell embryos were identically injected with plasmid containing human RLC-PAGFP. Sparse photoactivation of the PAGFP-tagged myosin cross bridges produced images of the skeletal muscle with bright points of emitted light over a low-fluorescence-level background in the striated pattern of the A-band. Image sequences reflecting the time dependence of the PAGFP intensity identified single-molecule events with quantized activation over background intensity or quantized photobleaching back to background from the points of light appearing in the image over time.
Single-molecule intensity patterns from the PAGFP-tagged zebrafish embryo skeletal muscle myosins in relaxation convert to emission dipole-moment coordinates (β′,α′), as described (19). β′ and α′ are spherical polar and azimuthal angles in muscle fiber coordinates where the z axis is the fiber symmetry axis. The in vivo fish data indicate a more orientationally confined myosin lever arm than the in situ cardiac myosin lever arm, revealing the significance of its in vivo context, differences in thick-filament structure for skeletal versus cardiac myosin, or both. Multiple (β′,α′) coordinates, each corresponding to a different single molecule, constrain the S1/PAGFP docking coordination. We develop the methodology and describe results of to our knowledge the first experimental structural determination of this docked complex. We now express our findings as myosin lever-arm conformations in the muscle lattice.
Throughout this manuscript, myosin atomic structure is that of human β-cardiac myosin subfragment 1 (βS1) from the homology modeling (20) of its sequence using the chicken skeletal myosin S1 crystal structure PDB 2mys (21). The myosin lever-arm orientation is defined by the symmetry axis of its α-helix at the RLC binding site.
Methods
Methods are summarized in three main sections, Biological samples, Microscopy, and S1/GFP docking. All sections rely on a large inventory of work referenced in the literature. The section on docking describes to our knowledge a new approach developed for this application. The section on microscopy develops the orientation superresolution method. It is an adaptation of spatial superresolution to the specifics of our application. The first section, on the preparation of biological samples, summarizes previously published work.
Biological samples
Live PAGFP tagged zebrafish embryo and permeabilized porcine papillary muscle fiber preparations are described in the Supporting Material. All experiments were conducted on relaxed muscle at room temperature (20–22°C).
Microscopy
Microfluidic chamber for TIRF, HILO, and second harmonic generation microscope measurements
All microfluidic chambers were constructed from polydimethylsiloxane (PDMS) for use in either inverted or upright microscope configurations using the toner-transfer method for pattern transfer to brass substrate (22), and as described previously (6).
Porcine permeabilized fiber bundles with exchanged RLC-PAGFP were placed on a specially designed channel and observed with TIRF microscopy on an inverted microscope, as described previously (6).
Embryos were confined in an aqueous buffer droplet then placed into a 200 μm deep, 3 mm wide, and 10 mm long microfluidic channel with the channel side up. The device with the embryo was inverted, then placed on top of a No. 0 glass coverslip, forming a water tight seal with the glass, as shown in Fig. 1, A and B. The top view (Fig. 1 B) is through the actual device. Inlet/outlet holes through the PDMS allowed solution to be exchanged as needed using a 20 μL pipette. The embryo was constrained by the size of the channel to lie flat, although tail-flipping movement was observed. Embryos lived for hours under continuous observation. Fluorescence or reflected second harmonic generation (SHG) was observed via an inverted wide-field microscope under HILO illumination through the glass coverslip or an upright scanning microscope through the PDMS, respectively. Individual zebrafish embryos were imaged with HILO rather than TIRF, because the fish trunk muscle is beyond the ∼100 nm penetration depth of the evanescent field. The HILO beam from an oil immersion, 100×, 1.3 NA objective is visualized in Fig. 1 C. The PDMS cube doped with rhodamine B creates a cavity on top of the coverslip. The beam leaves the glass coverslip at the bottom and propagates through an aqueous solution containing fluorescein that imitates the fish medium in a fish-confinement microfluidic channel. The emergent beam angle of 74° results from an incident angle of ∼57.7°.
Figure 1.

The PDMS microfluidic on a glass coverslip forming the zebrafish embryo confinement chamber. (A) Schematic side view of the chamber showing its aqueous, PDMS, and glass components and depth. (B) The actual device and confined embryo in top view as it would be imaged by the 2-P upright microscope objective. Inlet and outlet ports are for solution exchange. (C) A PDMS cube creates a cavity filled with an aqueous solution containing fluorescein, imitating the fish medium in a microfluidic channel. The HILO beam is created by an oil immersion objective (100×, 1.3 NA, and 200 μm working distance) and emerges into the aqueous side of the interface at ∼74°.
Microscopes
The single-molecule TIRF microscope setup using photoactivatable probes with permeabilized porcine papillary fibers is identical to that described previously (6,8,19).
Observation of SHG uses a multiphoton excitation (MPE) scanning upright microscope (Olympus FV1000 and BX61, Center Valley, PA) and a 25×, 1.05 NA water immersion objective. The objective has 2 mm of working distance to image the zebrafish embryo through 1 mm of PDMS just as described (6). SHG from striated muscle originates from thick-filament myosin rod domains, but not from S1 (23). Incident light at 800 nm produces ∼400 nm SHG that we detect as back-scattered light.
Observation of single molecules under HILO illumination in a wide-field microscope (IX71, Olympus) uses a 100×, 1.3 NA oil immersion objective. The objective has a working distance of 200 μm, permitting in-focus observation of the embryo anywhere in the microfluidic channel. Fig. 2 shows the HILO excitation pathway. The figure shows incident (i), reflected (r), and transmitted (t) beams in the Lx′Ly′ plane and the s- or p-polarization for the transmitted beam relative to the apparent symmetry axis of the muscle fiber. Incident light has σ ∼ 58° and a refracted beam transmitted at ∼74° from Ly′. Not shown is an aperture in the exciting-beam pathway conjugate to the objective image plane. The conjugate aperture restricts illuminated region size on the sample.
Figure 2.
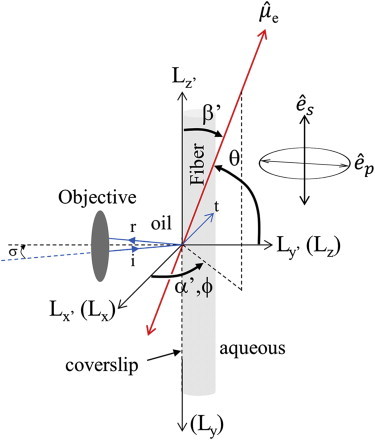
The excitation pathway schematic for HILO illumination. Incident (i), reflected (r), and transmitted (t) beams in blue have s- or p-polarization for the transmitted beam. They are parallel or perpendicular to the apparent symmetry axis of the in vivo skeletal muscle fiber. Lab fixed coordinates are of two types, TIRF coordinates (θ,ϕ) relative to (Lx,Ly,Lz) and fiber coordinates (β′,α′) relative to (Lx′,Ly′,Lz′), depicting the orientation of the (photoactivated) emission dipole, . Symbol σ is the incidence angle of the exciting beam. To see this figure in color, go online.
The objective collects fluorescence from the muscle that is focused by the tube lens into a real image on the EMCCD camera (C9100-13, Hamamatsu, Hamamatsu City, Japan). Images are acquired over time at a frame rate of 0.5–1 Hz, depending on the sample. GFP tag rotational mobility is static compared to the 3 ns chromophore lifetime, since the rotational relaxation time of the 50 kDa GFP moiety is ∼30 ns and longer for the S1/GFP complex (24). Static averaging blurs the intensity spatial pattern, contributing to its degradation together with that of extraneous background light and other noise, all of which are quantitated in the error estimate for (β′,α′) coordinates discussed below.
Photoactivation and photoselection
The total probe molecules, N, convert from unphotoactivated (NB) to photoactivated (NA) species by irreversible isomerization, NB→NA, where N = NB + NA. For a single molecule, the probability of its photoactivation, qp,s, is
| (1) |
where κ is a constant proportional to the activating light pulse duration and dependent on other factors excluding probe dipole orientation, is the absorption dipole moment for the unphotoactivated species (B species with wavelength band centered near 405 nm), and is the photoactivating (pump) light electric-field polarization vector for p- or s-polarized light. In all experiments, p- or s-polarization is perpendicular or parallel, respectively, to the fiber axis, and κ is small to ensure that a sparse population of probes is photoactivated and to achieve the most selective orientation distribution of photoactivated probes. Orientation of , the absorption dipole moment of an activated single molecule, sets the absolute intensity of the emission pattern but does not influence measurement of the orientation of , the emission dipole moment of the activated single molecule. The orientation measurement is done by pattern recognition.
Pattern recognition of single-molecule emission
The single-molecule image is a three-dimensional pattern that devolves into six basis patterns dependent on spatial coordinates and with coefficients that depend algebraically on dipole orientation. Spherical polar coordinates (θ,ϕ) describe dipole orientation relative to lab coordinates {Lx,Ly,Lz} and are convenient for microscope optics with the z axis normal to the coverslip and pointing into the aqueous medium containing the muscle (Fig. 2). Fluorescence intensity on the camera is given by
| (2) |
where Fb is the background, F0 the single-molecule intensity amplitude, h the Hellen factor correcting for the effect of the glass/aqueous interface on the emission pattern (25), and Ii,j the normalized intensity patterns containing all the spatial dependence (19). Given the basis patterns, we can invert an observed image to deduce their coefficients using maximum likelihood fitting for Poisson or Gaussian distributed data. The coefficients define a 1:2 correspondence between pattern and dipole-moment orientations, because a particular dipole and its spatial inversion give the same emission pattern (8,19). In practice, we found that combining the six basis patterns in Eq. 2 into three, such that
| (3) |
where bi contains the ϕ and spatial dependencies, provides more reliable inversion for ϕ values on a grid with 0 ≤ ϕ ≤ π. The π < ϕ < 2π domain is redundant due to the inversion symmetry. The maximum-likelihood method estimated θ at each ϕ value with the best overall (θ,ϕ) choice giving the best overall fit. The intensity data were better described by Gaussian than by Poisson statistics.
We represent probe dipole-moment orientation with (θ,ϕ) and (β′,α′) coordinates. β′ and α′ are the spherical polar and azimuthal angles in lab-frame coordinates {Lx′,Ly′,Lz′}, where the z′ axis is parallel to the fiber symmetry axis, the x′ axis is in the plane of the coverslip, and the y′ axis is normal to the coverslip plane and points into the aqueous medium (Fig. 2). The relationship between microscope and muscle fiber (lab-frame) coordinates is a rotation about Lx′. Dipole inversion symmetry implies that (β′,α′) and (π − β′,α′ + π) are equivalent and that, hence, the entire solution set of dipole orientations can be shown on the domain defined by 0 ≤ β′ ≤ π and 0 ≤ α′ ≤ π.
Orientation superresolution
Gaussian distributed data in the maximum likelihood estimation for error imply that χ2-minimization gives the best-fit parameter. Hence, we estimate error in the average fitted θ using the method of Bobroff (26). Variation in χ2 near its minimum is given by
| (4) |
where pixel address (i,j) is the fluorescence spatial dependence at focus, the minimum χ2, and the photon count variance. Variance includes camera noise and counting noise from background plus dipole emission photons and is estimated from the data. The Hellen factor in F (Eq. 3) is negligible for the HILO configuration, because the interface is in the far field of the dipole. Then,
| (5) |
The quantity is also estimated from data, using Eq. 5 for intensity above background. The one standard deviation (1σ) level has Δ = 2.3 (27) for a two-parameter (θ and ϕ) fit, giving
| (6) |
A similar expression was constructed for ϕ. We obtained error of 1–8° (excluding one outlier) for estimates and 12–36° for estimates. The signal/noise ratio, S/N, for the in vivo and in situ data collected from muscle in relaxation is 3–12.
S1/GFP docking
Estimating S1/GFP coordination
The objective is to dock GFP with myosin in a manner consistent with constraints imposed by crystal structures of GFP and myosin and with GFP dipole orientation constraints imposed by single-molecule data from GFP-tagged skeletal myosin in zebrafish embryos and cardiac myosin in porcine papillary fibers. The first step is to relate the relevant coordinate frames in which the GFP dipole, the GFP crystal structure, and the myosin crystal structure are described. Fig. S1 in the Supporting Material is a diagram of the relevant coordinate frames, where Greek symbols are used to represent angles and Roman characters to represent direction cosines, vectors, or coordinate axes, except for absorption and emission dipoles, and , which keep their traditional Greek symbol nomenclature.
The βS1 structure, designated 2bys, is a homology model (6) derived from the skeletal myosin crystal structure 2mys (21). It has a crystal frame with axes {am,bm,cm} used for the myosin coordinates. An analogous crystal frame, {ag,bg,cg}, is used for the GFP coordinates from 1emb (28). Coordinates {am,bm,cm} are related to the lever-arm helix dipole molecular frame, {rm,sm,tm}, using rotation matrix MY, where MY · {am,bm,cm} = {rm,sm,tm}, giving
| (7) |
for unit vector = {za,zb,zc}, the helix dipole moment with direction cosines za, zb, and zc. Unit vector = {xa,xb,xc} is perpendicular to and in the plane containing and the RLC C terminus, and = {ya,yb,yc} is related to and by . The helix dipole moment points along the myosin lever-arm α-helix symmetry axis computed by averaging CA atom positions for residues 808–827, where RLC binds. This is the relevant myosin fixed frame for the docked GFP, because the tag is linked to the RLC C terminus by an 11-residue tether (GGGGGGVPVEK).
Coordinates {ag,bg,cg} are related to the GFP chromophore molecular frame, {rg,sg,tg}, using rotation matrix MG, where MG · {ag,bg,cg} = {rg,sg,tg} is given by
| (8) |
where and unit vector is normal to the chromophore plane and computed from the chromophore atomic coordinates with direction cosines za, zb, and zc. Unit vector is at the intersection of the chromophore and ab planes, and the absorption dipole, , lies in the rs plane at an angle ζ from , as shown in Fig. S1. Geometrical constructions and data describing the GFP dipole are from Boxer et al. (29,30). We detect the emission dipole, , defined relative to another chromophore fixed frame where the emission dipole lies along the u axis and is in the uw plane at an angle η from the w axis. The rs and uw planes are coincident. Rotation matrix ME, relating the two chromophore fixed coordinates {u,v,w} = ME · {rg,sg,tg}, is given by
| (9) |
for the angles defined in Fig. S1. Angles (ζ,η) were measured previously. Angle η was estimated to be 40° using polarized absorption spectra from single WT GFP crystals reported in Rosell and Boxer (30). Angle ζ was estimated to be ∼13° using fluorescence polarization anisotropy from immobilized and randomly oriented RLC-PAFGP in solution (31). Using our constructions, we obtained the chromophore absorption dipole moment, , and the line normal to the chromophore, , in the crystal frame of 1emb, which differ only slightly from the values of Rosell and Boxer (30), probably due to our unique selection of the atoms in the chromophore to define the molecular frame.
Quantities discussed so far are known from the referenced experimental work. Unknown Euler angles (γ,ρ,ω) relate chromophore fixed coordinates, {u,v,w}, to the helix dipole molecular frame, {rm,sm,tm}, by {u,v,w} = Eu(γ,ρ,ω) · {rm,sm,tm} for
| (10) |
Summarizing the above relationships, we rotate the crystal coordinates of the GFP to the crystal coordinates of the myosin using
| (11) |
We determine (γ,ρ,ω) by combining constraints from the single-molecule experimental data with docking simulations using ZDOCK (32), as described in the next two sections.
Interpreting single-molecule measurements
Photoactivation of single absorption dipoles uses a linearly polarized electric field with polarization direction along unit vector for p- or s-polarized light. Vectors expressed in the laboratory frame {Lx′,Ly′,Lz′} are defined in Fig. 2. Field polarization and absorption/emission dipoles in the laboratory frame are
| (12a) |
| (12b) |
| (12c) |
| (12d) |
| (12e) |
| (12f) |
where n1 and n2 are the refractive indices of water and glass, σ the incidence angle of the HILO beam, EuT the transpose of the Euler matrix defined in Eq. 10, (α,β)the spherical polar coordinates of the helix dipole in the lab frame, (α′,β′) the spherical polar coordinates for in the lab frame measured with single-molecule orientation superresolution, {aL,bL,cL} the lab coordinates of the myosin crystal structure, and the absorption dipole related to the lab frame by coordinates (α′,β′,γ′) in a Euler rotation. Euler angles (α′,β′,γ′) characterize the orientation of the PAGFP moiety as it resides on the cross-bridge lever arm. Coordinates (α′,β′), defining the emission dipole moment, differ for each cross bridge at a different spatial position in the muscle. The third angle, γ′, defines PAGFP protein orientation relative to the dipole-moment vector and has special significance because it is constant when the PAGFP moiety is rigidly fixed to the cross bridge.
Myosin dimers in the skeletal muscle fiber form crowns with threefold symmetry about the fiber axis in the α-degree of freedom. Crowns repeat in approximate helical symmetry every 429 Å along the fibers axis. Opposed half-sarcomeres have complementary β-degrees of freedom. The α-degree of freedom for single heads will vary over the Lz′-dimension of the fiber, because myosin crowns maintain quasihelical symmetry, whereas the β-degree of freedom will not vary over spatial dimensions except for the complementarity of opposed half-sarcomeres. The p-polarization will selectively choose heads with the absorption dipole of PAGFP-tagged myosin aligned with the Ly′-axis. The s-polarization is selective for dipole alignment with the Lz′-axis. We expect the data to reflect a narrow range of β or π − β values indicating the orientation of the lever arms in opposed half-sarcomeres relative to the Lz′-axis and a wide variation of α values because of their variability in the spatial z-dimension.
Equations 12c–12f correspond to six nonlinear equations that relate the unknown Euler angles (γ,ρ,ω) linking protein and dipole coordinates, protein helix dipole coordinates (α,β), and absorption dipole coordinate γ′ to the known emission dipole coordinates (α′,β′). The six equations reduce to four constraints, because the absorption and emission dipole moments are normalized. Only three equations are independent. We solved the equations for (α,β) and γ′ as a function of emission dipole coordinates (α′,β′) and Euler angles (γ,ρ,ω). In practice, it is easier to solve the polynomial equations for six parameters (cosα, sinα, cosβ, sinβ, cosγ′, and sinγ′) subject to the additional requirements cos2α + sin2α = 1, cos2β + sin2β = 1, and cos2γ′ + sin2γ′ = 1. Solutions for (α,β) computed over a multidimensional grid of values for (γ,ρ,ω) with −π ≤ γ < π, 0 ≤ ρ ≤ π, and −π ≤ ω < π at 10° resolution were ranked for agreement with experimental data (i.e., comparing observed and simulated emission dipole moments, , and the expectation that β values fall into narrow ranges near βk or π − βk, for {β0, β1, β2, …, β9} = {0, 10, 20, …, 90}°. The latter fulfills the known preference for lever-arm distributions in β to vary over a restricted but unknown range of values. No requirement on α reflects the expectation that their values vary widely. Ranked agreement is weighted by the photoactivation probability appropriate for p- or s-polarization (Eq. 1) and by the reciprocal of data-point variance estimated from Eq. 6. Data-point variance is discussed below (see Results).
We find that the fish skeletal and porcine cardiac lever arms have an unmistakable preference for selected intervals in βk but that this preference is satisfied equally well by many combinations of the (γ,ρ,ω) parameters. The grid points that best satisfy constraints identified (γ,ρ,ω) triplets specifying receptor/ligand complexes from the 2bys.pdb/1emb.pdb structures using Eq. 11. These complexes are not docked but have the appropriate myosin-to-GFP or -PAGFP orientation. The S1/PAGFP orientations are compared to those from the docked complexes generated by ZDOCK (see below) to identify a set of candidate complexes.
ZDOCK-derived complexes
ZDOCK 3.0.2 software (32) was downloaded from http://zlab.umassmed.edu/zdockconv3d/ and installed on the Mayo Research Computing Facility (RCF) cluster according to the installation instructions. We used 2bys.pdb as the receptor for the GFP ligand 1emb.pdb. Docking was conducted under two conditions according to which only RLC or only RLC and ELC but no heavy chain in 2bys.pdb (conditions 1 or 2) were allowed to dock with GFP. ZDOCK produced 2000 candidate complexes for each condition. The best 1000 complexes from each condition were screened in a Mathematica program, prman.nb. On the first pass over the 2000 total structures, complexes with an RLC C terminus >30 Å from the GFP N terminus were rejected, eliminating all but 13 or 1 structure(s) for conditions 1 or 2. These 14 structures were compared to the S1/GFP coordination in complexes derived from the single emission dipole data. Only three S1/GFP coordinations align between the two data sets.
Final refinement
For final refinement of the three docked structures, the S1/GFP coordination was interpolated within the grid used for angles (γ,ρ,ω) with simultaneous maximization of agreement with emission dipole data, expectations for β, and agreement with ZDOCK-derived complexes. Final refinement does not involve alteration of the ZDOCK-derived complexes. Zebrafish skeletal and porcine papillary data were refined separately.
Results
Single-molecule emission from tagged skeletal and cardiac myosin in relaxed muscle
Fig. 3 overlays simultaneously collected two-photon (2-P) images from 810 nm infrared light exciting fluorescence at ∼500 nm (green) and SHG at 405 nm (blue) in an RLC-GFP-tagged live embryo confined to the microfluidic shown in Fig. 1. Shown are a wide view of the trunk skeletal muscles in the tail (left) and a close-up of two single fibers (right). SHG originates exclusively from the myosin in the A-band (23) and the fluorescence from the RLC-GFP. The M-line separates the opposing myosin dimers in the thick filament. The I-band contains the actin thin filament. M-lines are separated by ∼2.1 μm. The single fiber image demonstrates that the fluorescence and SHG colocalize, implying that the tag labels the myosin lever arm, as demonstrated previously in rabbit skeletal and porcine cardiac permeabilized muscle fibers (7,8).
Figure 3.

Simultaneous RLC-GFP fluorescence and myosin SHG in vivo by 2-P excitation. Infrared light at 810 nm excites fluorescence at ∼500 nm (green) and SHG at 405 nm (blue) in the wide view of the trunk skeletal muscles in the tail (left) and in the close-up of two individual fibers (right). The I-band, with actin but no myosin, and the M-line, without myosin cross bridges, are dark in comparison to the A-band, which contains both myosin cross bridges and actin. The A-band shows both GFP fluorescence and SHG signals indicating colocalization of RLC-GFP with the cross bridge. Sarcomere length is ∼2.1 μm.
Fig. 4 compares RLC-PAGFP- (upper) to RLC-GFP-tagged (lower) embryos under HILO illumination with 488 nm excitation. The M-line, A-band, and I-band are identified. The HILO beam propagating through the sample at 74° to the microscope optical axis has an ∼4 μm illumination depth. Narrower depths, down to ∼1 μm, are achievable using the 100× 1.49 NA objective or reducing the beam diameter using the conjugate aperture (see Microscopes in the Methods section), though the latter technique gives a smaller illuminated field. The RLC-PAGFP-tagged sample is sparsely photoactivated, with several instances of photoactivated probes emitting brightly over a background of weakly fluorescing, unphotoactivated RLC-PAGFP in the striated pattern of the A-band. Images are 1 s exposures. We identified single-molecule events by their quantized intensity change due to photoactivation or photobleaching from the points of light appearing in the image over time. Fig. S2 shows two examples of single-molecule events by the quantized activation over background intensity followed by quantized photobleaching back to background.
Figure 4.

In vivo images of RLC-PAGFP- (upper) to RLC-GFP-tagged myosin (lower) from zebrafish embryos in relaxation under HILO illumination.
Single-molecule intensity patterns from zebrafish embryo skeletal muscle myosins in relaxation were fitted using the pattern recognition algorithm and subjected to orientation superresolution analysis (19,26). The fitted image pattern measures the emission dipole moment in TIRF coordinates (θ,ϕ) for the spherical polar, θ, and azimuthal, ϕ, angles in the lab coordinates defined in Fig. 2 with the z axis perpendicular to the coverslip and pointing into the aqueous medium containing the fish or cardiac fiber. Fig. S3 shows the scatter plots with error bars for p- and s-polarization photoactivation. Orientation superresolution has a mean error of 3° for θ and 25° for ϕ. Fig. S3 also shows the scatter plots and error bars in fiber coordinates (β′,α′) for the spherical polar, β′, and azimuthal, α′, angles defined in Fig. 2 with the z axis parallel to the fiber symmetry axis. It is derived from the TIRF coordinate plots by rotation.
Fig. 5 compares relaxed zebrafish skeletal and porcine cardiac muscle data. The shape of the scatter plot depends chiefly on the unknown parent distribution of all PAGFPs in the zebrafish muscle. p- or s-polarized light photoactivated PAGFP in the zebrafish muscle and created subpopulations of photoactivated probes from the parent distribution. s-polarization along the fiber symmetry axis creates a dipole subpopulation better confined to the center of the (β′,α′) scatter plot than is the p-polarized photoactivated subpopulation. p-polarization perpendicular to the fiber axis creates the more heterogeneous PAGFP subpopulation. The scatter plots show (β′,α′) codependency information, which indicates that extremes in the domain, 0 and 180° for either α′ or β′, and in the central region where (β′,α′) ≈ (90,90), are unpopulated. These extremes are excluded by steric/crowding forces originating from the thick filament, but not from strong interaction with actin, because the muscle is relaxed. Steric/crowding forces are highly significant and not replicated in vitro (8). The scatter plots also show that in vivo fish myosin lever arms are more orientationally confined than the in situ porcine myosin lever arms, indicating the significance of the in vivo context, differences between skeletal and cardiac myosin cross bridges, species-specific myosin differences, or a combination of these factors (Fig. 5 B). The single fish myosins occupy a tight distribution of angles in narrow bands off the central depleted zone.
Figure 5.
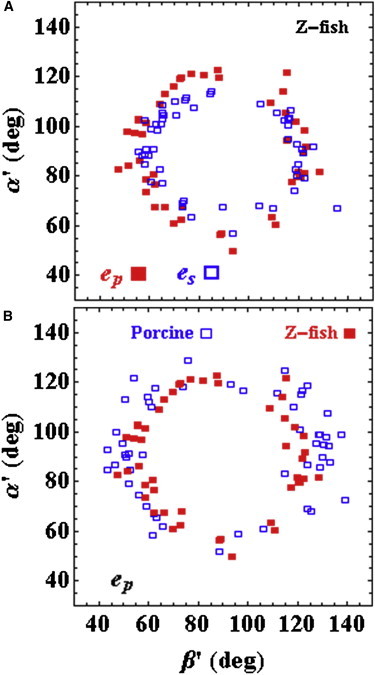
Zebrafish skeletal and porcine cardiac muscle data from relaxed fibers. (A) Comparison of zebrafish skeletal myosin data for p- and s-polarized photoactivation. (B) Comparison of data for p-polarized photoactivation porcine cardiac myosin and zebrafish skeletal myosin.
S1/GFP coordination in skeletal and cardiac myosin
The three Euler angles (γ,ρ,ω) linking GFP and S1 crystal frames were examined for agreement with the single-molecule data in Fig. 5 by satisfying Eqs. 12c–12f and the constraint that lever-arm helix β values fall into a narrow domain or complementary (π − β) domain for each single myosin detected. Data points in Fig. 5 are weighted by the reciprocal of their variance. Variance for each (β′,α′) point was computed using the square of the length of the error bar in Fig. S3. Independently, the spatial relationship of GFP and S1 was estimated with ZDOCK (32) using the additional constraint that the myosin-bound RLC C terminus and GFP N-terminus locate to within 30 Å of each other to accommodate the 11-residue span linking them. With the former procedure, we obtained a list of 2000 triplets (γ,ρ,ω) ordered by decreasing satisfaction of constraints, and with the latter procedure, we obtained 14 S1/GFP complexes from the better half of 4000 structures generated in ZDOCK. Intersection of these independently obtained S1/GFP coordinations produced three S1/GFP complexes that were subjected to additional refinement.
The three candidate S1/GFP docked complexes orient the symmetry axis of the GFP β-barrel roughly perpendicular to the lever-arm α-helix where RLC binds (MHC residues 808–827) and with the side of the GFP β-barrel contacting the RLC. Final refinement identified structures 725 and 506 from the condition 1 subset as the best for skeletal and cardiac myosin. They are represented in stereo in Fig. 6. These structures reproduce the (β′,α′) dependence of the single-molecule emission dipole data for the skeletal or cardiac myosins, as shown in Fig. 7. In the Fig. 6 structures, the MHCs are blue, with a black section in the lever-arm α-helix where the RLC binds. The helix axis of the black section is related to the lab frame by coordinates (β,α), also referred to as lever-arm coordinates. In Fig. 6, the RLC is red, GFP is green, and their linker is white. The ELC is shown in silver. Structures 725 and 506 have practically identical 3-D structures and perspectives in the figure, except for their GFP moiety. The GFP moiety is differently docked in the two structures, principally by an ∼10° rotation about the lever-arm α-helix symmetry axis.
Figure 6.
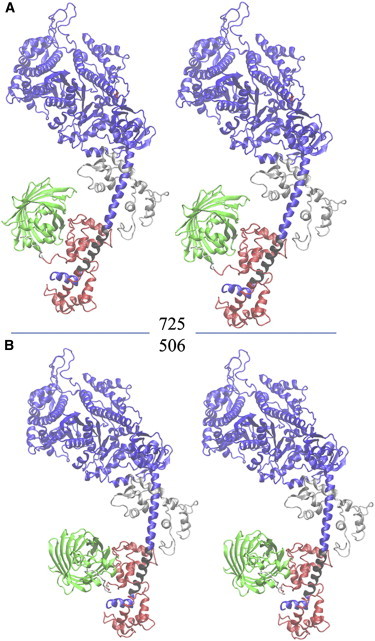
Stereo representations of S1/GFP. The myosin sequence shows the MHC (blue or black), the RLC (red), the GFP (green), and the ELC (silver). The 11-residue sequence linking the RLC C terminus to the GFP N terminus is white. The black section of the MHC where RLC binds to the lever arm defines an α-helix symmetry axis with spherical polar coordinates (β,α) defined relative to the lab coordinates (Lx′,Ly′,Lz′) in Fig. 2. (A) Structure 725 is the best S1/GFP representation of fish skeletal myosin. (B) Structure 506 is the best S1/GFP representation of porcine cardiac myosin.
Figure 7.
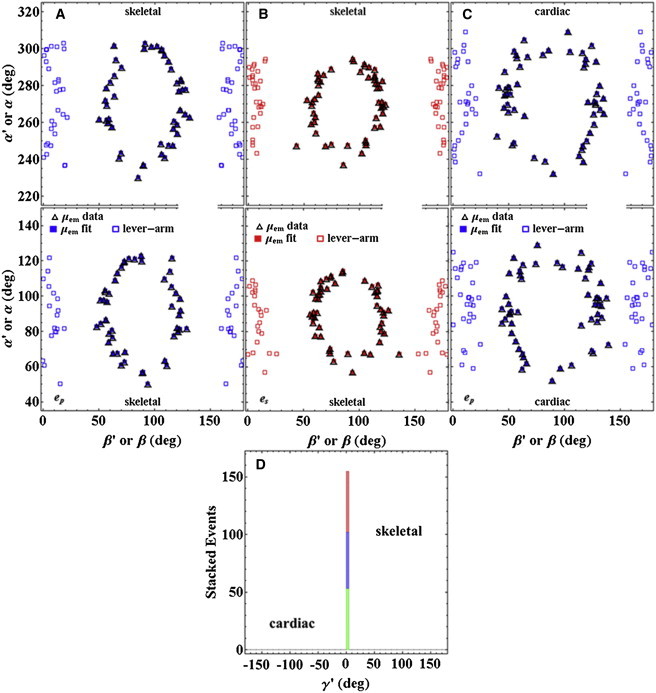
Scatter plots for single emission-dipole and lever-arm orientation coordinates, (β′,α′) or (β,α), respectively, from skeletal (A and B) and cardiac muscle (C) in relaxation. Blue and red symbols represent p-polarized (ep) and s-polarized (es) photoactivating light polarization. Open squares (lever-arm) are calculated from the emission dipole moments of photoactivated probes with orientation coordinates (β′,α′) (open triangles). The fitted points (solid blue and red squares (μemfit)) were derived from structures 725 (skeletal) and 506 (cardiac) in Fig. 6. (D) Stacked histogram for the absorption dipole coordinate, γ′, defined in Eq. 12d. The histogram specifies one of the Euler angles relating the emission molecular frame ({u,v,w} in Fig. S1) to the lab frame ({Lx′,Ly′,Lz′} in Fig. 2). The narrow-profile histogram indicates that PAGFP is rigidly immobilized on the cross bridge in both skeletal and cardiac muscle. The skeletal histogram has events from both p- and s-polarization (blue and red, respectively) photoactivated dipoles. The cardiac histogram has just the p-polarization photoactivated dipoles (green).
Lever-arm orientation in skeletal and cardiac muscle
Fig. 7, A–C, shows single lever-arm orientation coordinates (β,α) (blue and red open squares) determined from the emission dipole moments of photoactivated probes with orientation coordinates (β′,α′) (open triangles and solid blue and red squares) using the 725 (skeletal) or 506 (cardiac) structures in Fig. 6. Lever-arm orientation refers to the lever-arm α-helix at the RLC binding site shown in black. Inversion symmetry data scatter plots are shown for each instance (points (β′,α′) and (π − β′,π + α′) are equivalent), because the accompanying lever-arm distribution is not symmetrical for inversion of the probe dipole moments. The two protein distributions in the 0 ≤ α < π and π ≤ α < 2π domains are dependent information, since the points from one domain can be calculated from the points in the other, albeit they are different representations of the information. Fish skeletal muscle data for p- and s-polarization ( and ) (Fig. 7, A and B, respectively) reflect the same parent distribution of lever arms but with individual selections weighted by photoselection. Lever arms in opposed half-sarcomeres fall mostly in the β ≈ 0∼10° or 180 − (0∼10)° domains (Fig. 7, open symbols). The distribution in α is spread out over 80° and centered on α ≈ 90°. Error analysis (Fig. S3) indicates larger uncertainty for α′ compared to β′, particularly for the s-polarized photoactivated probes. We expect α′ and α to be widely distributed in our single-molecule measurements based on our understanding of fish fiber structure (33). Porcine cardiac lever arms under p-polarization photoactivation (Fig. 7 C) are more widely distributed in β and are predominantly in the β ≈ 10∼20° or 180 − (10∼20)° domains.
Fig. 7 D indicates the probe absorption dipole coordinate, γ′, for skeletal and cardiac muscle. Angle γ′ is not directly observed or superresolved but is computed for each (β′,α′) pair. Its error is estimated from the standard deviation of values computed from the data points in Fig. 7, A–C, for skeletal muscle with p- or s-polarization photoactivation (blue or red, respectively) or for cardiac muscle with p-polarization photoactivation (green). A computed value has the best overlap of the observed (β′,α′) distribution in space with the most likely distribution estimated from the probability for photoactivation (computed from the square of the projection of onto or for p- or s-polarized photoactivation).Values are stacked in the histogram, since all points fall into one 5° wide bin near γ′ ≈ 0. The narrow distribution in γ′ values strongly indicates S1/PAGFP rigidity in both skeletal and cardiac muscle.
Discussion
In vivo, the skeletal or cardiac myosin cross bridge is crowded into the muscle fiber lattice and its side chains subjected to the dynamic environment inside the muscle cell. Single myosin detection in vivo provides a unique opportunity to characterize elementary myosin function with the motor in its native state.
Earlier single-molecule work on skeletal and cardiac muscle used permeabilized muscle fibers and the RLC-PAGFP exchanged onto the cross bridge. The construct efficiently exchanged in situ and did not measurably deter muscle functionality (6,8,19,31). Single myosins sample individual orientation states of the system and distinguish features of myosin lever-arm rotation that are lost in an ensemble average due to fiber lattice symmetry and asynchronous myosin head movement (34,35). Notably, the approach distinguished substates of the active isometric myosin lever arm (8) and detected their redistribution in the active fiber after introduction of the disease-implicated mutants at positions M20, E134, and G162 to the exchanged RLC-PAGFP (6). Disease-implicated mutants spanned the RLC structure and indicated position-dependent change to lever-arm stiffness culminating in loss of motor work production efficiency. These results aligned the mutant side-chain position with lever-arm stiffness change, defining a correspondence that can be exploited to exercise control over transduction/mechanical coupling and ultimately over myosin power output.
We have successfully adapted the imaging technology to the in vivo zebrafish embryo model system where RLC-PAGFP is expressed in zebrafish skeletal muscle. Imaging was aided by a microfluidic designed to spatially confine the embryo and permit its illumination with either infrared light for 2-P excitation of fluorescence or SHG, or, thin HILO illumination for 1-P excitation. RLC-PAGFP specificity in vivo was verified by its exact colocalization with myosin (Fig. 3). Single-molecule detection was verified by quantized photoactivation or photobleaching of the PAGFP tag in the skeletal muscle in vivo (Fig. S2).
Single emission dipole moment spatial pattern quantitation at superresolution measured the dipole TIRF spherical polar coordinates (θ,ϕ). Fig. S3 indicates the spread for θ- and ϕ-values from the zebrafish skeletal muscle. These values transform to the fiber coordinates indicated with a mapping where the left or right side of the TIRF scatter plot maps to the right or left side, respectively, of the fiber scatter plot. The data summary in Fig. 5, including in situ data from porcine papillary fibers, indicate that in vivo fish myosin is more orientationally confined than in situ porcine myosin, due either to differences between the in situ and in vivo contexts, differences between skeletal and cardiac myosin cross bridges, species-specific myosin differences, or a combination of these factors.
We estimated (PA)GFP moiety coordination with the myosin lever-arm in RLC-(PA)GFP-tagged myosin. The method chooses the best agreement between simulated S1/GFP complexes generated using ZDOCK (32) and experimental data measuring (β′,α′) in Fig. 7 converted to S1/GFP coordination trials using the crystal structures of S1 (21) and GFP (28), chromophore dipole orientation in the GFP crystal structure (30), and the expected relationship between myosin in opposite half-sarcomeres in the muscle fibers. This process selected several S1/GFP coordinations simultaneously satisfying dipole-moment orientation data and docking constraints. Final refinement favored the S1/GFP docking indicated in Fig. 6. Given the S1/GFP coordination, single-molecule detection of the GFP tag orientation is expressible in terms of the myosin lever-arm conformation.
Fig. 7, A and B, indicates the (β,α) codependency for the zebrafish lever-arm distribution in relaxation and for photoactivation by p- or s-polarization. Fig. 7 C indicates analogous quantities for the cardiac lever arms. Lever-arm conformation refers to its helical axis at the RLC (Fig. 6, black segment). Comparing Fig. 7, A and B, with Fig. 7 C, it can be seen that cardiac cross bridges are somewhat more disordered and have a mean β angle 3.1 ± 1.6° larger than that for the fish skeletal cross bridges. This implies that the cardiac cross bridges extend farther away from the thick-filament axis. The rigidity of the S1/PAGFP interaction is indicated in Fig. 7 D. It confirms that the RLC-PAGFP is a reliable indicator of cross-bridge orientation in skeletal and cardiac muscle.
We did not explicitly model lever-arm β-dependence to include two or more unique orientations, but our approach does not exclude this possibility. If the relaxed myosin had a competing contribution from a second orientation at β > 20°, it would appear in Fig. 7 in one or all of of the scatter plots (Fig. 7, A–C). The same concept is true for a unique α-dependence, which would appear as a subset of lever arms separated from other lever arms in the scatter plot. Multiple preferred orientations are not apparent in the scatter plots. Lever arms in both muscles indicated one preferred spherical polar orientation and widely distributed azimuthal orientations relative to the fiber symmetry axis. Aside from the larger radial displacement of the cardiac cross bridges from the thick filament, skeletal and cardiac myosin cross bridges are similarly disposed in the intact fiber. Other, more complex scenarios are not ruled out by the data. For instance, two conformations for cross bridges in a myosin dimer are indicated by blocked and free S1s in electron microscopy (EM) reconstructions of smooth-muscle heavy meromyosin (36) and cardiac thick filaments (37,38). This appears to be a general myosin regulation mechanism (39) probably related to the superrelaxed state identified in skeletal and cardiac muscle (40,41). It is possible that the PAGFP at its binding site on the lever arm sterically prevents the intramolecular interaction, since the EM reconstructions indicate that this is a crowded region on the thick filament, but this hypothetical steric inhibition does not affect maximum isometric contraction in permeabilized skeletal or cardiac muscle fibers (7,8). Our observations are in vivo, a condition very different from that used for the EM reconstruction, and they are limited to ∼50 single myosin heads in the live skeletal muscle and in situ cardiac muscle. More experience with this system is needed to understand the full implications of in vivo conditions.
Conclusions
In vivo imaging of zebrafish embryos allows unprecedented access to skeletal myosin structure and dynamics by using fluorescence from lever-arm-bound GFP-tagged RLC expressed in the muscle and label-free SHG from myosin. In vivo single RLC-PAGFP orientation superresolution defines a bottom-up quantitative characterization of myosin in its native environment. We devised a method to ascertain the S1/GFP coordination from the single myosin measurements, then converted our observations to direct implications for myosin lever-arm orientation. Experiments performed in vivo on skeletal and in situ on cardiac muscle fibers in relaxation show that the cardiac cross bridges are slightly more disordered and apparently distributed at larger radial distance from the thick filament compared to skeletal cross bridges. The data also shows that the S1/GFP coordination is rigid for both species. The rigidity of the interaction confirms that RLC-PAGFP reliably indicates cross-bridge orientation in skeletal and cardiac muscle.
Acknowledgments
We thank Katalin Ajtai for critiquing the manuscript and Kevin Buchs from the Mayo Research Computing Facility for installing ZDOCK and for assistance with running the software.
This work was supported by National Institutes of Health grants R01AR049277 and R01HL095572 (T.P.B.), National Science Foundation award IOS-0818993 (E.A.S.), and the Mayo Foundation.
Supporting Material
Supporting Citations
References (42–45) appear in the Supporting Material.
References
- 1.Lowey S., Waller G.S., Trybus K.M. Function of skeletal muscle myosin heavy and light chain isoforms by an in vitro motility assay. J. Biol. Chem. 1993;268:20414–20418. [PubMed] [Google Scholar]
- 2.Sherwood J.J., Waller G.S., Lowey S. A point mutation in the regulatory light chain reduces the step size of skeletal muscle myosin. Proc. Natl. Acad. Sci. USA. 2004;101:10973–10978. doi: 10.1073/pnas.0401699101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Pant K., Watt J., Moore J.R. Removal of the cardiac myosin regulatory light chain increases isometric force production. FASEB J. 2009;23:3571–3580. doi: 10.1096/fj.08-126672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Oldfors A. Hereditary myosin myopathies. Neuromuscul. Disord. 2007;17:355–367. doi: 10.1016/j.nmd.2007.02.008. [DOI] [PubMed] [Google Scholar]
- 5.Toydemir R.M., Rutherford A., Bamshad M.J. Mutations in embryonic myosin heavy chain (MYH3) cause Freeman-Sheldon syndrome and Sheldon-Hall syndrome. Nat. Genet. 2006;38:561–565. doi: 10.1038/ng1775. [DOI] [PubMed] [Google Scholar]
- 6.Burghardt T.P., Sikkink L.A. Regulatory light chain mutants linked to heart disease modify the cardiac myosin lever arm. Biochemistry. 2013;52:1249–1259. doi: 10.1021/bi301500d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Burghardt T.P., Ajtai K., Zheng Y. GFP-tagged regulatory light chain monitors single myosin lever-arm orientation in a muscle fiber. Biophys. J. 2007;93:2226–2239. doi: 10.1529/biophysj.107.107433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Burghardt T.P., Josephson M.P., Ajtai K. Single myosin cross-bridge orientation in cardiac papillary muscle detects lever-arm shear strain in transduction. Biochemistry. 2011;50:7809–7821. doi: 10.1021/bi2008992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Howe K., Clark M.D., Stemple D.L. The zebrafish reference genome sequence and its relationship to the human genome. Nature. 2013;496:498–503. doi: 10.1038/nature12111. (Errata in Nature. 505:248) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Xu X., Meiler S.E., Fishman M.C. Cardiomyopathy in zebrafish due to mutation in an alternatively spliced exon of titin. Nat. Genet. 2002;30:205–209. doi: 10.1038/ng816. [DOI] [PubMed] [Google Scholar]
- 11.Hurlstone A.F.L., Haramis A.-P.G., Clevers H. The Wnt/β-catenin pathway regulates cardiac valve formation. Nature. 2003;425:633–637. doi: 10.1038/nature02028. [DOI] [PubMed] [Google Scholar]
- 12.Bakkers J. Zebrafish as a model to study cardiac development and human cardiac disease. Cardiovasc. Res. 2011;91:279–288. doi: 10.1093/cvr/cvr098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Burns C.G., Milan D.J., Fishman M.C. High-throughput assay for small molecules that modulate zebrafish embryonic heart rate. Nat. Chem. Biol. 2005;1:263–264. doi: 10.1038/nchembio732. [DOI] [PubMed] [Google Scholar]
- 14.Bassett D.I., Currie P.D. The zebrafish as a model for muscular dystrophy and congenital myopathy. Hum. Mol. Genet. 2003;12:R265–R270. doi: 10.1093/hmg/ddg279. [DOI] [PubMed] [Google Scholar]
- 15.Berger J., Currie P.D. 503unc, a small and muscle-specific zebrafish promoter. Genesis. 2013;51:443–447. doi: 10.1002/dvg.22385. [DOI] [PubMed] [Google Scholar]
- 16.Fisher S., Grice E.A., McCallion A.S. Evaluating the biological relevance of putative enhancers using Tol2 transposon-mediated transgenesis in zebrafish. Nat. Protoc. 2006;1:1297–1305. doi: 10.1038/nprot.2006.230. [DOI] [PubMed] [Google Scholar]
- 17.Planchon T.A., Gao L., Betzig E. Rapid three-dimensional isotropic imaging of living cells using Bessel beam plane illumination. Nat. Methods. 2011;8:417–423. doi: 10.1038/nmeth.1586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tokunaga M., Imamoto N., Sakata-Sogawa K. Highly inclined thin illumination enables clear single-molecule imaging in cells. Nat. Methods. 2008;5:159–161. doi: 10.1038/nmeth1171. [DOI] [PubMed] [Google Scholar]
- 19.Burghardt T.P. Single molecule fluorescence image patterns linked to dipole orientation and axial position: application to myosin cross-bridges in muscle fibers. PLoS ONE. 2011;6:e16772. doi: 10.1371/journal.pone.0016772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Martí-Renom M.A., Stuart A.C., Sali A. Comparative protein structure modeling of genes and genomes. Annu. Rev. Biophys. Biomol. Struct. 2000;29:291–325. doi: 10.1146/annurev.biophys.29.1.291. [DOI] [PubMed] [Google Scholar]
- 21.Rayment I., Rypniewski W.R., Holden H.M. Three-dimensional structure of myosin subfragment-1: a molecular motor. Science. 1993;261:50–58. doi: 10.1126/science.8316857. [DOI] [PubMed] [Google Scholar]
- 22.Easley C.J., Benninger R.K., Piston D.W. Rapid and inexpensive fabrication of polymeric microfluidic devices via toner transfer masking. Lab Chip. 2009;9:1119–1127. doi: 10.1039/b816575k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Plotnikov S.V., Millard A.C., Mohler W.A. Characterization of the myosin-based source for second-harmonic generation from muscle sarcomeres. Biophys. J. 2006;90:693–703. doi: 10.1529/biophysj.105.071555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Swaminathan R., Hoang C.P., Verkman A.S. Photobleaching recovery and anisotropy decay of green fluorescent protein GFP-S65T in solution and cells: cytoplasmic viscosity probed by green fluorescent protein translational and rotational diffusion. Biophys. J. 1997;72:1900–1907. doi: 10.1016/S0006-3495(97)78835-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hellen E.H., Axelrod D. Fluorescence emission at dielectric and metal-film interfaces. J. Opt. Soc. Am. B. 1987;4:337–350. [Google Scholar]
- 26.Bobroff N. Position measurement with a resolution and noise-limited instrument. Rev. Sci. Instrum. 1986;57:1152–1157. [Google Scholar]
- 27.Lampton M., Margon B., Bowyer S. Parameter estimation in x-ray astronomy. Astrophys. J. 1976;208:177–190. [Google Scholar]
- 28.Brejc K., Sixma T.K., Remington S.J. Structural basis for dual excitation and photoisomerization of the Aequorea victoria green fluorescent protein. Proc. Natl. Acad. Sci. USA. 1997;94:2306–2311. doi: 10.1073/pnas.94.6.2306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Boxer S.G., Kuki A., Xuong N.H. Oriented properties of the chlorophylls: electronic absorption spectroscopy of orthorhombic pyrochlorophyllide a-apomyoglobin single crystals. Proc. Natl. Acad. Sci. USA. 1982;79:1121–1125. doi: 10.1073/pnas.79.4.1121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Rosell F.I., Boxer S.G. Polarized absorption spectra of green fluorescent protein single crystals: transition dipole moment directions. Biochemistry. 2003;42:177–183. doi: 10.1021/bi0266535. [DOI] [PubMed] [Google Scholar]
- 31.Burghardt T.P., Li J., Ajtai K. Single myosin lever arm orientation in a muscle fiber detected with photoactivatable GFP. Biochemistry. 2009;48:754–765. doi: 10.1021/bi8017703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Pierce B.G., Hourai Y., Weng Z. Accelerating protein docking in ZDOCK using an advanced 3D convolution library. PLoS ONE. 2011;6:e24657. doi: 10.1371/journal.pone.0024657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Al-Khayat H.A., Squire J.M. Refined structure of bony fish muscle myosin filaments from low-angle x-ray diffraction data. J. Struct. Biol. 2006;155:218–229. doi: 10.1016/j.jsb.2006.03.029. [DOI] [PubMed] [Google Scholar]
- 34.Burghardt T.P., Ajtai K. Single-molecule fluorescence characterization in native environment. Biophys. Rev. 2010;2:159–167. doi: 10.1007/s12551-010-0038-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Borejdo J., Szczesna-Cordary D., Gryczynski I. Single molecule detection approach to muscle study kinetics of a single cross-bridge during contraction of muscle. In: Bujalowski W.M., editor. Spectroscopic Methods of Analysis. Humana Press; Totowa, NJ: 2012. pp. 311–334. [DOI] [PubMed] [Google Scholar]
- 36.Wendt T., Taylor D., Taylor K. Three-dimensional image reconstruction of dephosphorylated smooth muscle heavy meromyosin reveals asymmetry in the interaction between myosin heads and placement of subfragment 2. Proc. Natl. Acad. Sci. USA. 2001;98:4361–4366. doi: 10.1073/pnas.071051098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.González-Solá M., Al-Khayat H.A., Kensler R.W. Zebrafish cardiac muscle thick filaments: isolation technique and three-dimensional structure. Biophys. J. 2014;106:1671–1680. doi: 10.1016/j.bpj.2014.01.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Al-Khayat H.A., Kensler R.W., Morris E.P. Atomic model of the human cardiac muscle myosin filament. Proc. Natl. Acad. Sci. USA. 2013;110:318–323. doi: 10.1073/pnas.1212708110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Jung H.S., Komatsu S., Craig R. Head-head and head-tail interaction: a general mechanism for switching off myosin II activity in cells. Mol. Biol. Cell. 2008;19:3234–3242. doi: 10.1091/mbc.E08-02-0206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Hooijman P., Stewart M.A., Cooke R. A new state of cardiac myosin with very slow ATP turnover: a potential cardioprotective mechanism in the heart. Biophys. J. 2011;100:1969–1976. doi: 10.1016/j.bpj.2011.02.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Stewart M.A., Franks-Skiba K., Cooke R. Myosin ATP turnover rate is a mechanism involved in thermogenesis in resting skeletal muscle fibers. Proc. Natl. Acad. Sci. USA. 2010;107:430–435. doi: 10.1073/pnas.0909468107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kwan K.M., Fujimoto E., Chien C.-B. The Tol2kit: a multisite gateway-based construction kit for Tol2 transposon transgenesis constructs. Dev. Dyn. 2007;236:3088–3099. doi: 10.1002/dvdy.21343. [DOI] [PubMed] [Google Scholar]
- 43.Higashijima S., Okamoto H., Eguchi G. High-frequency generation of transgenic zebrafish which reliably express GFP in whole muscles or the whole body by using promoters of zebrafish origin. Dev. Biol. 1997;192:289–299. doi: 10.1006/dbio.1997.8779. [DOI] [PubMed] [Google Scholar]
- 44.Hirata H., Saint-Amant L., Kuwada J.Y. accordion, a zebrafish behavioral mutant, has a muscle relaxation defect due to a mutation in the ATPase Ca2+ pump SERCA1. Development. 2004;131:5457–5468. doi: 10.1242/dev.01410. [DOI] [PubMed] [Google Scholar]
- 45.Brenner B., Schoenberg M., Eisenberg E. Evidence for cross-bridge attachment in relaxed muscle at low ionic strength. Proc. Natl. Acad. Sci. USA. 1982;79:7288–7291. doi: 10.1073/pnas.79.23.7288. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


