An Engineered Membrane to Measure Electroporation: Effect of Tethers and Bioelectronic Interface

Abstract

This article reports on the construction and predictive models for a platform comprised of an engineered tethered membrane. The platform provides a controllable and physiologically relevant environment for the study of the electroporation process. The mixed self-assembled membrane is formed via a rapid solvent exchange technique. The membrane is tethered to the gold electrode and includes an ionic reservoir separating the membrane and gold surface. Above the membrane, there is an electrolyte solution, and a gold counterelectrode. A voltage is applied between the gold electrodes and the current measured. The current is dependent on the energy required to form aqueous pores and the conductance of each pore. A two-level predictive model, consisting of a macroscopic and a continuum model, is developed to relate the pore dynamics to the measured current. The macroscopic model consists of an equivalent circuit model of the tethered membrane, and asymptotic approximations to the Smoluchowski-Einstein equation of electroporation that is dependent on the pore conductance and the energy required to form aqueous pores. The continuum model is a generalized Poisson-Nernst-Planck (GPNP) system where an activity coefficient to account for steric effects of ions is added to the standard PNP system. The GPNP is used to evaluate the conductance of aqueous pores, and the electrical energy required to form the pores. As an outcome of the setup of the device and the two-level model, biologically important variables can be estimated from experimental measurements. To validate the accuracy of the two-level model, the predicted current is compared with experimentally measured current for different tethering densities.

Introduction

Electroporation is a phenomenon that causes the permeability of a biological membrane to increase in response to an applied electric field. Electroporation has applications in electrochemotherapy for anti-tumor treatment, protein insertion, cell fusion, debacterialization, and gene and drug delivery (1,2). Designing a stable platform for obtaining reliable experimental measurements of electroporation is an important challenge. This article presents a believed-novel engineered tethered membrane platform for measuring electroporation (see Fig. 1). A key feature of the platform is that the experimentalist can select the desired density of tethers, the physiological environment, and membrane composition (3–6). The tethers are included to mimic the physiological response of the cytoskeletal supports of real cell membranes. The platform is constructed using modified archaebacterial lipids, allowing the tethered membrane to have a lifetime of several months (5,7,8).

Figure 1.

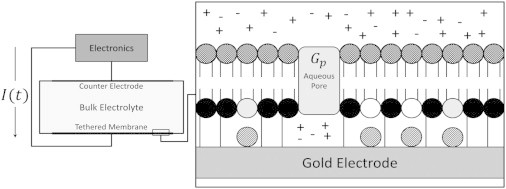
Overview of the engineered tethered membrane, model, and measured and predicted current I(t). The Electronics block represents the electronic system, which produces the drive potential between the electrode and counter electrode, and records the current response I(t). The test chamber contains the synthetic tethered membrane. The tethered membrane layer is composed of the lipid components: zwitterionic DphPC (C20 diphytanyl-ether-glycerophosphatidylcholine) (shaded), C20 diphytanyl-diglyceride ether (open), and benzyl disulfide diphytanyl bis-tetra-ethyleneglycol (solid). Spacer molecules (i.e., benzyl disulfide tetra-ethyleneglycol) are used to control the spacing between the tethered lipids (cross-hatch fill). The mobile lipid layer (square fill) is composed of the DphPC lipids. For the 100% tether density, the membrane is composed of a membrane-spanning lipid (structure provided in Krishna et al. (19)) with no spacer molecules. The tethered membrane does not contain any ion channels; therefore, all current passing through the tethered membrane takes place via conducting aqueous pores with an electrical conductance denoted by G_p.

Another important challenge is to model the dynamics of electroporation. This article constructs a two-level predictive model for the dynamics of electroporation, as observed by the platform that we now briefly outline in the following.

Macroscopic dynamics

At the highest level of abstraction, the macroscopic dynamics of the platform are modeled using the equivalent circuit model shown in Fig. 2. The conductance of the tethered membrane is dependent on the population and dynamics of pore radii. Using asymptotic approximations to the Smoluchowski-Einstein equation (9–13), we construct a model that relates the aqueous pore conductance and electrical energy required to form a pore to the membrane conductance. The energy required to deform the tethers is accounted for by using an energy model identical to that used for the cytoskeletal network in real cells (14).

Figure 2.

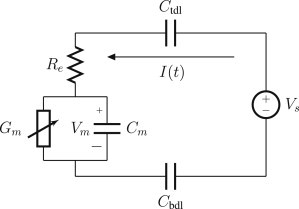
Schematic of the macroscopic lumped circuit model of the electroporation platform. R_e is the electrolyte resistivity, C_m is the membrane capacitance, G_m is the membrane conductance, C_bdl is the electrode capacitance, C_tdl is the counterelectrode capacitance, and V_m is the transmembrane potential. Equation 1 in the main text displays the dynamics of this model.

Continuum dynamics

At a lower level of abstraction, we use a generalized Poisson-Nernst-Planck (GPNP) system with a Langmuir-type activity coefficient. If the activity coefficient is neglected, then the standard Poisson-Nernst-Planck (PNP) system results. The GPNP continuum model is effective in modeling the electrodiffusive dynamics of asymmetric electrolytes, multiple ionic species, and the Stern and diffuse electrical double layers (15) that are present in the platform (16–18). GPNP is used to compute the ionic flux and potential field for evaluating important electroporation parameters. The pore conductance is computed from the transmembrane potential and the total ionic flux (i.e., current) through the aqueous pore, and the electrical energy required to form a pore is computed using the potential field on the pore boundary, and the Maxwell stress tensor.

In the above two-level model, we will link the macroscopic dynamics to the continuum dynamics via the pore conductance and energy required to form a pore contained in the Smoluchowski-Einstein equation. Therefore, the two-level model accounts for the electrodiffusive effects present in the engineered tethered membrane. As an outcome of the setup of the device and the two-level model, important biological parameters for the design of electroporation therapies (i.e., the characteristic voltage of electroporation, ratio of hydrophilic and hydrophobic pore radii, and the spring constant of tethers) can be estimated from the model-given experimental measurements.

The accuracy of the two-level model proposed in this article is verified by comparing the predicted performance with experimental results. Different tethering densities and lipid compositions are used to validate the accuracy of the models and exemplify the contribution the tethers and bioelectronic interface have on the electroporation process. Specifically, the electroporation parameters of the engineered tethered membrane (19) in Fig. 1 are estimated for the membrane tether densities of 1 and 10% for the tethered DphPC lipid bilayer, and the 100% tethered DphPC monolayer membrane.

Literature review

Experimental platforms to study electroporation include synthetic bilayer lipid membranes and in vitro cells (20,21). However, synthetic bilayer lipid membranes do not provide a good representation of physiological systems because the effects caused by the cytoskeletal network are not present (11,22). Using real cells provides a physiological system for validation (23,24); however, it is impossible to fully define the physiological environment that effects properties associated with electroporation. This motivates the need for an engineered tethered membrane platform that gives the experimentalist control over tethering density, membrane composition, and physiological environment, unlike the synthetic lipid membrane- and cell-based platforms.

Next, we give a brief review of models for electroporation: Models of the electroporation process employ the Smoluchowski-Einstein equation derived from statistical mechanics (11–13) with the pore energy models given in the literature (9,14,25–30). The pore energy models are constructed by assuming the membrane is a dielectric and elastic continuum (25,31–36). The Smoluchowski-Einstein equation is numerically prohibitive to solve, and the pore energy provided in the literature does not include effects caused by asymmetric electrolytes, multiple ionic species, and the Stern and diffuse electrical double layers present. To overcome these limitations, the electroporation model presented in this article is constructed using asymptotic approximations to the Smoluchowski-Einstein equation and the GPNP for modeling the electrodiffusive dynamics. To couple the results of the Smoluchowski-Einstein equation with the experimentally measured current requires an estimate of the aqueous pore conductance. In Li and Lin (2), assuming symmetric electrolytes and electroneutrality, the aqueous pore conductance was estimated via the PNP system (37).

In the tethered membrane platform, there are electrical double layers at the surface of the membrane and electrode contacts (15) that can be modeled using the GPNP (16). Note that, near a pore entrance, significant nonlinear potential gradients are present that restrict the current flowing through the pore; this effect is denoted as the spreading conductance and is dominant for pore radii significantly larger than the membrane thickness, causing the pore conductance to scale proportionally to the pore radius (2,12,22,38–40). In this article, GPNP is used to predict the pore conductance. It is found that the pore conductance scales proportionally to the pore radius for all pore radii, suggesting that the spreading conductance is dominant as a result of the electrode in proximity to the membrane surface and the nonlinear potential gradients present.

Materials and Methods

The construction and predictive models of the engineered tethered membrane are provided in this section. The accuracy of the models are verified using experimental measurements of the engineered tethered membrane with different tethering densities.

Formation of the engineered tethered membrane

The engineered tethered membrane (Fig. 1) is composed of a self-assembled monolayer of mobile lipids, and a self-assembled monolayer of tethered and mobile lipids. The tethered lipids are anchored to the inert gold electrode via polyethylene glycol chains. Spacer molecules are used to ensure the tethers are evenly spread over the gold electrode. The intrinsic spacing between tethers and spacers is maintained by the benzyl disulfide moieties, which bond the spacers and tethers to the electrode surface. The ratio of the total number of tethers to spacers, and tether molecules, in the engineered tethered membrane are given by the tethering density (i.e., a 10% tether density defines that, for every nine spacer molecules, there is one tether molecule). In the special case of 100% tethering, the engineered tethered membrane is composed of a tethered archaebacterial based monolayer with no spacer molecules. As experimentally illustrated in Heinrich et al. (7), it is not possible to construct a 0% tethered membrane, because any formed membrane binds to the gold surface. Inasmuch as the electrolyte reservoir separating the membrane and electrode surface is required for the normal physiological function of the membrane, and noting that all prokaryotic and eukaryotic cell membranes contain cytoskeletal supports with a 1–10% tether density, the inability to construct a 0% tethered membrane does not inhibit the study of the electroporation process in a physiologically relevant environment.

As shown in Fig. 1, the engineered membrane is supported by a 25 × 75 × 1 mm polycarbonate slide onto which is patterned a 100-nm, sputtered-gold electrode array, possessing six 0.7 × 3 mm active areas of membrane, each of which is enclosed in a flow cell with a common gold return electrode. The formation of the tethered membrane is performed in two stages, as follows:

The first stage anchors the inner layer of the membrane to the gold surface via benzyl disulphide groups. The inner layer components are introduced to the freshly deposited gold surface as ethanolic solutions of 370-μM benzyl disulphide concentrations in engineered ratios of tethers and spacers. For example, the inner layer solution for the 10% tethering density is prepared by codissolving benzyl disulphide C20 diphytanyl bis-tetra-ethylene glycol and benzyl disulphide tetra-ethylene glycol in the ratio 1:10. The solution is exposed to the coating solution for 30 min and the electrode is then rinsed in ethanol and air-dried for ∼2 min. The coated slide is immediately assembled into a flow cell cartridge, comprising six individual membranes with a common large-area gold return electrode facing the membranes and separated by a 100-μm laminate defining the flow-cell chamber height.

The second stage of the membrane formation now occurs with the addition of 8 μL of 3 mM C20 diphytanylether lipids comprising a 70:30 mol of C20 diphytanylether glycerophosphatidylcholine/C20 diphytanylether diglyceride being added to each of the flow chambers covering the membrane areas. The solution is incubated for 2 min at 20°C, after which 300 μL of phosphate-buffered saline was flushed through each flow cell, forming the tethered bilayer. Using this rapid solvent exchange technique to construct the membrane reduces the defect density as compared with membranes constructed with the frequently used vesicle-fusion technique; it allows the engineered membrane to have a lifetime of several months (5,7,8).

The quality of the bilayer is measured continuously using an SDx tethered-membranes tethaPod Swept Frequency Impedance Reader operating at frequencies of 1000, 500, 200, 100, 40, 20, 10, 5, 2, 1, 0.5, and 0.1 Hz and an excitation potential of 20 mV (SDx Tethered Membranes, Roseville, Sydney). The membrane was equilibrated for 30 min before the electroporation measurements. The electroporation measurements were performed using an eDAQ ER466 Potentiostat (eDAQ, Denistone East, NSW, Australia) and an SDx tethered-membrane tethaPlate Adaptor (SDx Tethered Membranes) to connect to the assembled electrode and cartridge. Individual triangular voltage ramps were applied from 0 to 500 mV with a period of 2–10 ms. Waveforms of current versus time were recorded.

Macroscopic electroporation model of the engineered tethered membrane

At the highest level of abstraction, the tethered membrane platform is modeled using a lumped circuit model (4,7,19,41,42). To link the lumped circuit model to the electroporation dynamics, the conductance of the membrane is modeled using asymptotic approximations to the Smoluchowski-Einstein equations for electroporation. In subsequent sections, the GPNP, which constitutes the lower level of abstraction in our two-level model, is used to refine the pore conductance and electrical energy required to form a pore (both included in the asymptotic Smoluchowski-Einstein equation of the macroscopic model).

The tethered membrane platform is composed of three distinct regions: the electrical double layers at the gold electrodes, the bulk electrolyte reservoir, and the tethered membrane. The bulk electrolyte solution is modeled as completely Ohmic with resistance R_e. The electrical double layers contain a tightly bound region of ions on the order of an atomic radii, and a diffuse region of length on the order of the Debye-Hückel thickness. The Stern layer and diffuse charge layers are modeled using an overall capacitance of C_tdl and C_bdl for the counterelectrode and electrode, respectively. The tethered membrane is modeled as a uniformly polarized structure such that the charging dynamics of the membrane are represented by a capacitance C_m. The tethered membrane conductance G_m(t,V_m) is both time-dependent and membrane-voltage-dependent, with V_m denoting the transmembrane potential. The dependency of G_m is a result of the process of electroporation that takes place to generate/destroy aqueous pores in the membrane. The excitation potential V_s(t) applied across the two electrodes closes the circuit. The equivalent circuit model of the tethered membrane platform is given in Fig. 2.

The governing dynamics for the lumped circuit model of the tethered membrane (Fig. 2) are given by

$$\begin{array}{l}\frac{d{V}_m}{dt}=-\left(\frac{1}{C_m{R}_e}+\frac{G_m}{C_m}\right)V_m-\frac{1}{C_m{R}_e}{V}_{dl}+\frac{1}{C_m{R}_e}{V}_s,\\ \frac{d{V}_{dl}}{dt}=-\frac{1}{C_{dl}{R}_e}{V}_m-\frac{1}{C_{dl}{R}_e}{V}_{dl}+\frac{1}{C_{dl}{R}_e}{V}_s,\\ I=\frac{1}{R_e}\left(V_s-V_m-V_{dl}\right).\end{array}$$ (1)

Here C_dl is the total capacitance of C_tdl and C_bdl in series. Given V_s(t), the circuit parameters C_tdl, C_bdl, R_e, C_m, and the membrane conductance G_m can be estimated from the measured current I(t). However, for drive potentials <∼50 mV, the membrane conductance is approximately constant and is assumed at its equilibrium value G_o such that G_m(t,V_m) ≈ G_o. The circuit parameters G_o, R_e, C_tdl, C_bdl, and C_m remain constant and are independent of the electroporation phenomenon; they are only necessary to model the dynamics of the double-layer charging and electrolyte resistance (refer to Results and Discussion for further information).

For transmembrane potentials >50 mV, the membrane conductance G_m can be modeled by

$$\begin{array}{l}{G}_m=\sum _{i=1}^{\lfloor N\left(t\right)\rfloor }{G}_p\left(r_i\right),\\ \frac{d{r}_i}{dt}=-\frac{D}{k_{\text{B}}T}\frac{\partial W\left(r\right)}{\partial r_i}\text{for}{r}_i\in \left\{\mathrm{1,2}\dots \lfloor N\left(t\right)\rfloor \right\},\\ \frac{dN}{dt}=\alpha e^{{\left(\frac{V_m}{V_{ep}}\right)}^2}\left(1-\frac{N}{N_o}{e}^{-q{\left(\frac{V_m}{V_{ep}}\right)}^2}\right).\end{array}$$ (2)

In Eq. 2, α is the pore creation rate coefficient, V_ep is the characteristic voltage of electroporation, N_o is the equilibrium pore density at V_m = 0, and q = (r_m/r^_∗)² is the squared ratio of the minimum energy radius r_m, at V_m = 0 with r^_∗ the minimum energy radius of hydrophilic pores (43–46). The parameters α, V_ep, N_o, and γ are estimated by fitting the measured current response I to the predicted current response from Eqs. 1 and 2, given the drive voltage V_s. The classical free energy model for a hydrophobic aqueous pore W, in Eq. 2, in the membrane consists of four energy terms: the pore edge energy γ, the membrane surface tension σ, the electrostatic interaction between lipid heads, and the transmembrane potential energy contribution W_es(r,V_m). The pore energy W in Eq. 2 is given by Neu and Krassowska (9),

$$W\left(r,V_m\right)=2\pi \gamma r-\pi \sigma r^2+{\left(\frac{C}{r}\right)}^4+W_{es}\left(r,V_m\right)+W_m,$$ (3)

with the energy contribution from the mechanobiological properties of the tethers included as W_m. The linkages of the tethers to the membrane are analogous to springs and act to restrain the enlargement of aqueous pores. This is similar to the experimentally measured results in Chang and Reese (47), which suggests that irreversible electroporation cannot create pores that are larger than the cytoskeletal network anchors. Modeling the mechanical properties of the membrane as an elastic continuum and assuming a permanent tethered network anchorage, the effect of the tethers is accounted for via the energy required to deform the Hookean springs—formally, the energy contribution can be modeled using W_m = 0.5 K_tr², with K_t denoting the spring constant of the tethers (14). Note that the energy model for tethers is identical to that of the cytoskeletal network presented in Kanthou et al. (48), Teissié and Rols (49), Rols and Teissié (50), and Rosazza et al. (51).

The derivation of Eq. 2 is based on making physiologically relevant approximations to the Smoluchowski-Einstein equation for electroporation. The Smoluchowski-Einstein equation governs the distribution of pores as a function of their radius r and time t (11–13). If we denote n(r,t) as the pore density distribution function, then the Smoluchowski-Einstein equation is given by

$$\frac{\partial n}{\partial t}=D\frac{\partial r}{\partial }\left[\frac{n}{k_{\text{B}}T}\frac{\partial W}{\partial r}+\frac{\partial n}{\partial r}\right]+S\left(r\right),$$ (4)

where D is the diffusion coefficient of pores, k_B is the Boltzmann constant, T is the temperature, W is the pore energy, and S(r) models the creation and destruction rate of pores. Making the physiologically relevant assumption that diffusion term (i.e., ∂n/∂r) in Eq. 4 is negligible, and the characteristic timescale of W is longer than 0.1 μs, the process of electroporation can then be modeled by Eq. 2. Note that Eq. 2 has been used by several authors for modeling DNA translocation into cells (23,24,43–46).

How can we experimentally verify that the formed membrane does not contain significant defects? Possible membrane defects include patches with the gold electrode directly exposed to the bulk electrolyte, or with portions of bilayer sandwiched together. Using the measured current response resulting from an excitation potential <50 mV, we can compute the mean-squared error (MSE) between the predicted current from Eq. 1 and the experimentally measured current. If a significant MSE is obtained, then the model of a homogeneous membrane Eq. 1 is not suitable and the membrane is concluded to contain inhomogeneities (i.e., defects). A major concern when performing electroporation experiments is the detection of the catastrophic voltage breakdown of the membrane, causing separated areas of membrane to degrade. This effect can be detected by a high MSE and a significant increase in the estimated membrane conductance C_m resulting from the electrode surface capacitance coming into contact with the bulk electrolyte. Typical values for membrane capacitance and conductance are 0.5–1.3 μF/cm² and 0.5–2.0 μS for an intact 1–100% tethered membrane with surface area 2.1 mm².

GPNP continuum model for the electrodiffusive dynamics in the engineered tethered membrane

The GPNP model presented in this section constitutes the lower level of abstraction in the two-level model proposed in this article. The GPNP is used to compute the potential and ionic flux necessary for evaluating the pore conductance G_p, and the electrical energy of an aqueous pore W_es in the membrane, both contained in the macroscopic model Eq. 2.

To compute the potential and ionic flux, the GPNP continuum model must account for the electrodiffusion dynamics of ions in the engineered tethered membrane system. In the engineered tethered membrane platform there exists asymmetric electrolytes, multiple ionic species, and the Stern and diffuse electrical double layers at the surface of the electrodes and membrane. The electrodiffusion dynamics that takes these into account in the platform can be modeled by the GPNP given by (16)

$$\begin{array}{c}\frac{\partial c^i}{\partial t}=-\nabla \cdot \left(J^i\right),\\ J^i=-D^i\nabla c^i-F{z}^{i}q{u}_m^i{c}^i\nabla \varphi -D^i{c}^i\nabla \text{In}\left(1-\sum _{i=1}^N{N}_{\text{A}}{a}_i^3{c}^i\right),\end{array}$$ (5a)

$$\nabla \cdot \left(\epsilon \nabla \varphi \right)=-\sum _{i}F{z}^i{c}^i.$$ (5b)

In Eq. 5a, Jⁱ is the concentration flux; cⁱ is the concentration; ϕ is the electrical potential; Dⁱ is the diffusivity; N_A is Avogadro’s number; a_i is the effective ion size; and u_mⁱ is the ionic mobility, with i denoting the ionic species. In Eq. 5b, F is Faraday’s constant where the superscript defines the chemical species i, q is the elementary charge, z_i is the charge valence, and ε is the electrical permittivity. Note that for

$${\sum }_{i=1}^N{N}_{\mathrm{A}}{a}_i^3{c}^i\ll 1,$$

the steric effects are negligible in Eq. 5 and the standard PNP formulation can be used to model the electrolyte dynamics.

Initially, stable pores that form in the membrane are approximately cylindrical (43). As expansion occurs, the pores become toroidal in shape. This toroidal structure is in agreement with the estimated hydrophobic pore shape obtained from molecular dynamics simulations (52–54). Here, we consider the toroidal pore structure illustrated in Fig. 3 to compute the conductance of a pore. To solve Eq. 5 in the pore structure in Fig. 3 requires that the material parameters and boundary conditions in Ω_w, Ω_m, Ω_r, ∂Ω_m, ∂Ω_w, ∂Ω_e, and ∂Ω_ec be defined. The diffusion coefficient Dⁱ in Eq. 5a is spatially dependent, inasmuch as the tethering reservoir has a lower diffusion than the bulk electrolyte solution with no tethers present. The spatially dependent diffusion coefficient is given by

$$D^i\left(x\right)=\{\begin{array}{cc}{D}_r^i& \text{if}x\in {\text{Ω}}_r\\ D_w^i& \text{if}x\in {\text{Ω}}_w.\end{array}$$ (6)

The dielectric permittivity in Eq. 5b is spatially dependent, as

$$\epsilon \left(x\right)=\{\begin{array}{ll}{\epsilon }_w\hfill & \text{if}x\in {\text{Ω}}_r\cup {\text{Ω}}_w\hfill \\ {\epsilon }_m\hfill & \text{if}x\in {\text{Ω}}_m.\hfill \end{array}$$ (7)

The membrane surface is assumed to be perfectly polarizable (i.e., blocking) such that the normal ionic flux vanishes at the surface of the membrane. There are no surface reactions present at the gold electrode-electrolyte interface; therefore, we have a no-flux boundary condition present at the gold surface. Formally, these no-flux interface and boundary conditions are given by

$$n\cdot J^i=0\text{in}\partial {\text{Ω}}_m\cup \partial {\text{Ω}}_e\cup \partial {\text{Ω}}_{ec},$$ (8)

with n the normal vector pointing into the electrolyte solution and J_i defined below Eq. 5. To ensure the well-posedness of the Poisson equation Eq. 5b, the internal boundary conditions on the membrane-electrolyte interface are satisfied by the following (55):

$$\begin{array}{c}{\varphi }_m-{\varphi }_w=0\text{in}\partial {\text{Ω}}_m,\\ {\epsilon }_m\nabla {\varphi }_m\cdot n-{\epsilon }_w\nabla {\varphi }_w\cdot n=0\text{in}\partial {\text{Ω}}_m.\end{array}$$ (9)

Figure 3.

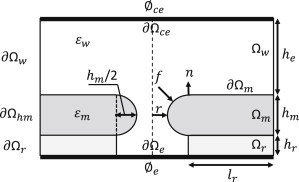
The aqueous pore is modeled as rotationally symmetric about the axis of rotation (dotted line) with dimensions given by r, l_r, h_r, h_m, and h_e for the cylindrical and toroidal geometries. The tethered membrane platform is modeled with three distinct regions: the electrolyte solution Ω_w, the electrolyte reservoir Ω_r, and the membrane Ω_m. The electrode-electrolyte interface (thick black line) is denoted by ∂Ω_e and ∂Ω_ec for the electrode and counterelectrode, respectively. ∂Ω_m denotes the interface between the membrane and electrolyte solution. The boundary conditions ∂Ω_w and ∂Ω_r define the ambient conditions of the electrolyte and membrane. The potentials at each electrode are defined by ϕ_e and ϕ_ec, respectively. The electrolyte has an electrical permittivity ε_w and the membrane an electrical permittivity ε_m. The electrical force acting on the membrane is denoted by f and is defined in Oldham (15). The value n is the normal vector pointing from the membrane domain to the electrolyte domain.

Next, it is necessary to model the Stern layer at the electrode surface given by C_s. This is modeled using the boundary conditions

$$\begin{array}{c}{C}_s\left({\varphi }_e-\varphi \right)+{\epsilon }_{w}n\cdot \nabla \varphi =0\text{in}\partial {\text{Ω}}_e,\\ C_s\left({\varphi }_{ec}-\varphi \right)+{\epsilon }_{w}n\cdot \nabla \varphi =0\text{in}\partial {\text{Ω}}_{ec},\end{array}$$ (10)

with ϕ_e and ϕ_ec as the prescribed potentials at the respective electrodes. The ambient boundary conditions of the axisymmetric pore are given by

$$\begin{array}{c}{c}^i=c_o^i\text{in}\partial {\text{Ω}}_w\cup \partial {\text{Ω}}_r,\\ n\cdot \nabla \varphi =0\text{in}\partial {\text{Ω}}_{hm},\end{array}$$ (11)

with c_oⁱ as the initial concentration (refer to Fig. 3).

The expressions in Equation 5, with material parameters Eqs. 6 and 7, boundary conditions Eqs. 8–11, and pore geometry given in Fig. 3, are used to estimate the ionic flux Jⁱ and the electric potential ϕ. The values Jⁱ and ϕ are both used to evaluate the pore conductance G_p and the electrical energy required to form a pore W_es contained in the macroscopic model Eq. 2.

Refining the macroscopic model using the continuum GPNP model

Having detailed the two-level model above, we are now ready to link the macroscopic and continuum models. The macroscopic and continuum models are linked via the pore conductance G_p and electrical energy required to form a pore W_es. In this section we evaluate G_p and W_es using the computed ionic flux Jⁱ and voltage potential ϕ from the GPNP defined in Eq. 5. To compare with previous models of G_p proposed in the literature, Appendix A provides a relation between the G_p model in this section and the electroneutral model (EM) presented in Li and Lin (2). Appendix B provides a comparison between the W_es estimated using the GPNP model, and previous estimates of W_es using the EM, and Laplace model (LM) in Neu et al. (29).

The current through the pore is obtained by integrating the total ionic flux from Eq. 5 over the minimum radius of the pore, which is defined later in Fig. 5. The current and associated pore conductances are given by

$$\begin{array}{c}{I}_p=F\sum _i\underset{0}{\overset{r}{\int }}{J}^{i}2\pi rdr,\\ G_p=\frac{I_p}{V_m},\end{array}$$ (12)

where Jⁱ and V_m are computed using Eq. 5 with the material properties defined by Eqs. 6 and 7, the boundary conditions Eqs. 8–11, and geometry given in Fig. 3.

Figure 5.

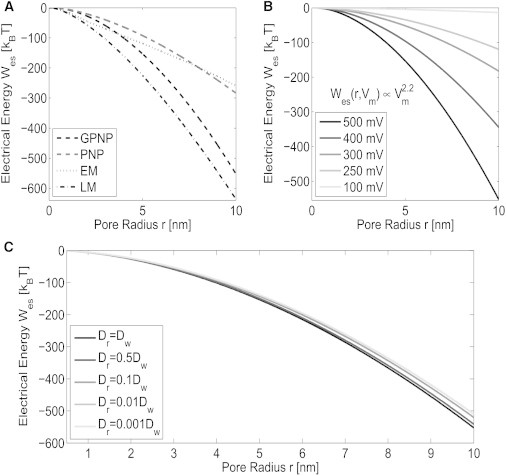
Numerically predicted electrical energy W_es, Eq. 13, required to form an aqueous pore. (A) Comparison of the predicted W_es computed using the GPNP, PNP, EM, and LM models defined in the Materials and Methods for the transmembrane potential of V_m = 500 mV. (B) Estimates of W_es computed using the GPNP for the transmembrane potentials listed. (C) Estimates of W_es computed using the GPNP for V_m = 500 mV for different tether reservoir diffusivities. The parameters of the governing equations and boundary conditions can be found in Table S1.

To evaluate W_es, the force causing a displacement of the pore structure must be computed. Consider the pore structure presented in Fig. 3. The pore boundary is assumed to only expand in the radial direction r. If we denote F(r) as the total force acting on the pore boundary of radius r, then the electromechanical energy can be computed using (29,56,57)

$$W_{es}\left(r\right)=-\underset{0}{\overset{r}{\int }}F\left(r\right)dr.$$ (13)

F(r) is computed using the Maxwell stress tensor for the pore geometry in Fig. 3. The electric field induces a stress on the membrane surface given by the Maxwell stress tensor T (29,57–64)

$$T=\epsilon \left(\frac{1}{2}|\nabla \varphi {|}^{2}I-\nabla \varphi \otimes \nabla \varphi \right).$$ (14)

In Eq. 14, I denotes the identity matrix, ⊗ is the dyadic product (i.e., ∇ϕ ⊗ ∇ϕ = ∇ϕ∇ϕ^T), and ε and ϕ are defined below Eq. 5. The stress on the membrane from the electrolyte p_w, and the stress on the electrolyte from the membrane p_m are

$$\begin{array}{c}{p}_w=-T_{w}n=-{\epsilon }_w\left(\frac{1}{2}|\nabla {\varphi }_w{|}^{2}I-\nabla {\varphi }_w\otimes \nabla {\varphi }_w\right)n,\\ p_m=T_{m}n+f=-{\epsilon }_m\left(\frac{1}{2}|\nabla {\varphi }_m{|}^{2}I-\nabla {\varphi }_m\otimes \nabla {\varphi }_m\right)n+f,\end{array}$$ (15)

where f is the stress induced from all other elastic properties of the membrane (65–67). Note that f denotes the electrical force density acting on the membrane surface.

The membrane is assumed to be at local mechanical equilibrium at the pore surface such that f = (T_w – T_m)n. Therefore, to maintain local equilibrium the total force acting on the pore boundary, F(r) is given by

$$F\left(r\right)=\underset{S}{\int }n\cdot \left(p_w-p_m\right)dS,$$ (16)

with p_w and p_m defined in Eq. 15, and the surface S and normal vector n given in Fig. 3. Given ϕ computed using Eq. 5, we can compute F(r) using Eq. 16. Substituting F(r) into Eq. 13 gives the electrical energy contribution to pore formation in the membrane, which includes electrical double layer and electrodiffusive effects caused by asymmetric electrolytes.

Note that for narrow cylindrical pores, ∂ϕ/∂r ≈ 0 and ∂ϕ/∂z ≈ V_m/h_m on S. Substituting into Eqs. 15 and 16, we see that F(r,V_m) ∝ V_m², with V_m as the transmembrane potential. The proportionality of F(r,V_m) ∝ V_m², which also implies W_es(r,V_m) ∝ V_m², is critical for the derivation of the electrical energy required to form a pore in Pastushenko and Chizmadzhev (22), Neu et al. (29), and Abidor et al. (68). This allows the computation of F(r,V_m) using a single instance of F(r) for a given transmembrane potential V_m to estimate the proportionality constant.

Results and Discussion

In this section, the predictive accuracy of the two-level model is verified using experimental measurements of tethered DphPC membranes with a tethering density of 1, 10, and 100%. The numerical methods and model parameters are provided in the Supporting Material.

Numerically predicted aqueous pore conductance and electrical energy required to form a pore

Numerical estimates of the aqueous pore conductance G_p and electrical energy required to form a pore W_es are performed using the GPNP, PNP, EM, and LM models defined in the Materials and Methods.

In Fig. 4 the estimated pore conductance computed using the GPNP, PNP, and EM models is presented. As seen, the pore conductance predicted using the GPNP follows a G_p ∝ r relationship. For membranes with sufficiently large electrolyte baths and pore radii (i.e., electrolyte bath is hundreds of nanometers thick and r > t_m), the pore conductance follows G_p ∝ r (2,12,22,40), in agreement with the spreading conductance derived from Laplace’s equation in Newman (39) and Dickens (69). Note that the effect G_p ∝ r for r < t_m and h_r = 4 nm is only predicted when the effects caused by asymmetric electrolytes, finite ion size, and Stern and diffuse layers are accounted for. In Fig. 4 A, the GPNP and PNP models produce differing conductance estimates as a result of the steric effects present. Recall that for

$${\sum }_{i=1}^N{N}_{\text{A}}{a}_i^3{c}^i\ll 1$$

the steric effects are negligible, and the estimated conductance using the GPNP and PNP models would be identical. As seen by comparing the estimated conductance G_p in Fig. 4 A, the assumption of electroneutrality causes a noticeable decrease in the computed conductance G_p. As mentioned in the Introduction, the pore conductance G_p may be dominated by the spreading conductance, which follows a G_p ∝ r proportionality, when the electrolyte solution is sufficiently geometrically constrained. From Fig. 3, the tethering reservoir is h_r = 4 nm, and from Fig. 4 A we see that G_p ∝ r; therefore, we conclude that the conductance of an aqueous pore in the engineered tethered membrane is dominated by the spreading conductance. As the diffusivity in the tethering reservoir, D_r, decreases, the pore conductance decreases, as seen in Fig. 4 B. This is expected, inasmuch as fewer ions can flow through the pore as a result of reduced ion mobility.

Figure 4.

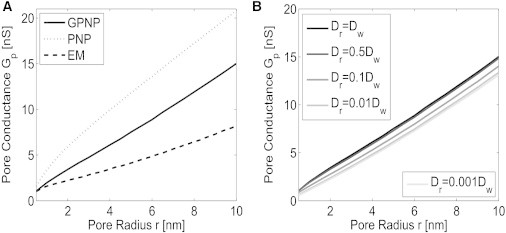
Numerically predicted pore conductance G_p, defined in Eq. 12. (A) Predicted pore conductance G_p, computed using the GPNP, PNP, and EM models. (B) Predicted G_p for different tethering reservoir diffusivities. The geometry of the pore is given in Fig. 3, and the parameters of the governing equations and boundary conditions are provided in Table S1 in the Supporting Material.

Fig. 5 compares the computed electrical energy required to form a pore using the GPNP, PNP, EM, and LM defined in the Materials and Methods. For small pores below 1 nm all the models provide similar estimated for W_es, as seen in Fig. 5 A. The PNP and EM models provide a significantly lower estimate of W_es compared to the GPNP and LM models for large pore radii above 4 nm. The discrepancy between the estimated W_es is a result of the assumption of negligible steric effects in the PNP model, and the assumption of negligible steric effects and electroneutrality in the EM model. Note that although the GPNP and LM models provide similar predictions of W_es, the LM assumes negligible steric effects, electroneutrality, and steady-state current (i.e., ∇cⁱ = 0), which results in the estimated voltage distribution on the surface of the membrane to differ with the voltage distribution predicted from the GPNP. Qualitatively, at the surface of the membrane, the GPNP model has the interface condition from Eq. 9 such that ε_m∇ϕ_m ⋅ n = ε_w∇ϕ_w ⋅ n; however, the interface condition for the LM model in Eq. 18 causes ε_m∇ϕ_m ⋅ n ≠ ε_w∇ϕ_w ⋅ n on the surface.

This results in the LM overestimating the voltage potential when compared with the GPNP. From Eq. 15, the overestimated potential causes the computed W_es to be larger when using the LM model as compared with the GPNP model. As discussed, the assumption of W_es(r,V_m) ∝ V_m² is typically invoked to simplify the computation of W_es(r,V_m) (22,29,68). From Fig. 5 B, we compute W_es(r,V_m) explicitly for several transmembrane potentials, and find that the proportionality follows a fractional power law. This illustrates the importance of including effects caused by electrodiffusion. As illustrated in Fig. 5 C, reducing the diffusion coefficient in the tethering reservoir D_r causes a slight reduction in the estimated W_es. In comparing Fig. 5 B with Fig. 5 C, the main contribution to the change in W_es results from a change in transmembrane potential.

Experimental verification of predictive models

Below the predicted pore conductance G_p (Eq. 12), the electrical energy W_es value (Eq. 13) and the electroporation model (given by Eqs. 1 and 2) are used to predict the current response of the engineered tethered membrane. The predicted current response is compared to experimentally measured data to validate the accuracy of the model. Note that all electroporation processes were reversible, and did not cause permanent damage to the membrane.

From Eqs. 1 and 2, if the drive potential V_s is applied and the resulting current is I_s, then if the drive potential −V_s is applied the resulting current must be −I_s if only the process of electroporation is present. For all the tethering densities and membrane compositions tested, this relation was observed in all experimental current measurements. We therefore concluded that the only process present is that of electroporation. The drive potential V_s(t) used to produce the results in Figs. 6 and 7 is defined by a linearly increasing potential of 100 V/s for 5 ms proceeded by a linearly decreasing potential of −100 V/s for 5ms.

Figure 6.

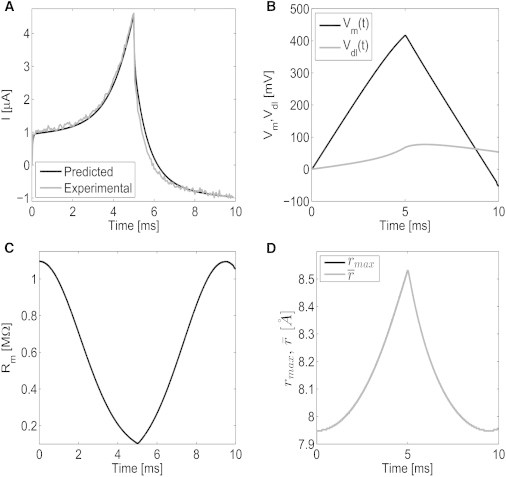
The measured and predicted current, voltage potentials, membrane resistance, and pore radii for the drive potential V_s(t), defined at the beginning of this section, for the 10% tether density DphPC bilayer membrane. (A) Measured and predicted current; (B) predicted transmembrane V_m and double-layer potential V_dl defined in Eq. 1; (C) estimated membrane resistance; and (D) estimated maximum r_max radius, and mean pore radius $\overline{r}$. All predictions are computed using Eqs. 1 and 2 with the parameters defined in Table S2.

Figure 7.

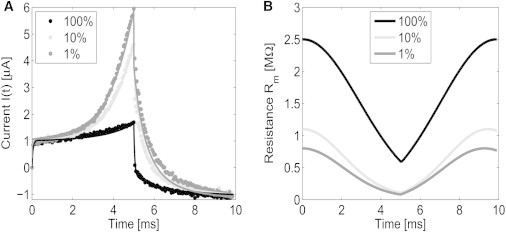
Experimentally measured and numerically predicted current I(t) (A), and membrane resistance R_m = 1/G_m (B) for the drive potential V_s(t) defined at the beginning of this section. The tethering densities 1 and 10% correspond to the DphPC bilayer, and the 100% corresponds to the DphPC monolayer. All predictions are computed using Eqs. 1 and 2 with the parameters defined in Table S2.

The experimental measurement and predicted voltages, pore radii, membrane resistance, and current are presented in Fig. 6 for the 10% tethered DphPC bilayer membrane. From Fig. 6 A, the experimentally measured and numerically predicted currents are in excellent agreement. As seen in Fig. 6 B, the application of the voltage excitation immediately causes an increase in the double-layer voltage V_dl as a result of the charge increase in the charge distribution at the electrode surface. The transmembrane potential V_m simultaneously increases as a result of the excitation potential. The increase in V_m results in the formation of pores. As seen in Fig. 6 C, a dramatic change in the resistance results after the application of the drive potential. In Fig. 6 D, the maximum radius r_max and mean radius $\overline{r}$ are provided to illustrate the spread in pore radii. As V_m increases, pores are generated and expand according to Eq. 2. From Eq. 2, all pores diffuse to the minimum-energy pore radius given by ∂W/∂r_i = 0 with an advection velocity proportional to D/k_BT. As seen in Fig. 6 D, generated pores rapidly expand to the minimum-energy pore radius inasmuch as the spread between r_max and $\overline{r}$ is negligible. This allows the number of pores N, from Eq. 2, to be computed using the relation

$$N=1/\left(R_m{G}_p\left(r_{\text{max}}\right)\right)$$

with G_p given in Fig. 4 A.

The results of the predictive model are in excellent agreement with the measured current (see Fig. 6). How are the model parameters in Eqs. 1 and 2 selected, and how sensitive is the predicted current response to errors in the model parameters? The parameters G_o, C_m, C_dl, and R_e are intrinsic to the measurement platform and remain constant independent of the electroporation phenomenon; however, they are necessary for predicting the current response of the tethered membrane. Therefore, a single impedance measurement is made to compute G_o, C_m, C_dl, and R_e for each tethered membrane (refer to the Supporting Material for the impedance data). This single measurement can be viewed as a form of calibration because these parameters will not change in subsequent electroporation experiments. The electroporation parameters γ, σ, C, and D are obtained from the literature (9,13,43,44,70,71). To estimate the important parameters V_ep, α, q, and K_t, current response measurements are used.

Because α and q are not dependent on the tether density, only a single measurement was used to estimate these parameters, and found to be consistent with what has been determined in DeBruin and Krassowska (23,72) and Glaser et al. (70). To gain insight into the sensitivity of the predicted current response to variations in model parameters, Table S2 in the Supporting Material provides the uncertainty associated with each parameter. The uncertainty is computed by finding the range in which the parameter can vary and still have the predicted current response from Eqs. 1 and 2 and be in good agreement with the experimentally measured current. Specifically, the electrolyte resistance R_e has a negligible effect on the current response because the membrane conductance and capacitive charging dominate the current flow. The initial jump in current at the start of the triangular drive potential is dominated by C_m. The slope of the current preceding the initial jump at 0.5 ms in Fig. 6 B is proportional to G_o.

At 2 ms, there is a deviation from the linear current response as a result of the electroporation process. The double-layer capacitance C_dl dominates the current response as the triangular drive potential decreases. As expected, C_m, R_m, and C_dl can be determined accurately. The electroporation parameters α and N_o have a large uncertainty because dN/dt, given by Eq. 2, is exponentially dependent on V_m, V_ep, and q, and linearly dependent on N_o and α. Given that G_m is dependent on N, it is expected that the uncertainty of α and N_o is larger than V_ep and q. The tether spring constant K_t has a large uncertainty because effects caused by K_t are only pronounced in the current response if large pores (i.e., r >> r_m) are present. As seen in Fig. 6, because the pore radii are only slightly larger than r_m, the current is dominated by the nucleation and destruction of pores.

Fig. 7 provides the experimental current measurement and the predicted current and membrane resistance R_m = 1/G_m for the 1 and 10% DphPC bilayer, and the 100% DphPC monolayer membrane. In comparing the resulting current among the 1, 10, and 100% tethered cases (Fig. 7 A), we see that as the tethering density increases, the effects of electroporation decreases. This is an expected result, inasmuch as the tethers provide structural support hindering the nucleation of pores reducing the equilibrium pore density N_o and increasing the characteristic voltage of electroporation V_ep. As seen in Fig. 7 B, the resistance begins to change at ∼1 ms when the transmembrane potential reaches a sufficiently high value to cause the nucleation of pores. The estimated spring constant K_t for the 1, 10, and 100% tethering densities are 0, 2 ± 0.5, and 20 ± 4 mN/m, respectively. For the 1% tether density, the spring constant is negligible, as expected. For the 100% tethering case, pores cannot expand as a result of the spring constant K_t, therefore the decrease in resistance is primarily a result of pore nucleation and destruction governed by Eq. 2. For the 100% tether density membrane, it may be the case that all pores in the membrane are hydrophilic, inasmuch as the tethers may prevent the transition from the hydrophilic to the hydrophobic structure. If only hydrophilic pores are present, the membrane resistance would be dominated by the nucleation of pores and not the dynamics of the pores.

Note that the molecular structure of the aqueous pores cannot be reliably inferred using continuum theory models and would require the use of molecular dynamics or similar noncontinuum models. Interestingly, for the 1% membrane structures, the resistance begins to decrease at 9.2 ms, and for the 10% membrane, at 9.4 ms after the initial application of the drive potential V_s(t) (defined at the beginning of this section). This is a result of the charge accumulation in the electrical double layers at the gold electrode surface, V_dl, discharging causing an increase in the magnitude of the transmembrane potential V_m. This illustrates the importance of including electrical double-layer effects when modeling gold electrodes.

Note also that when using Eqs. 1 and 2 for estimating the effects of electroporation for rapidly changing drive potentials, the double-layer capacitance in Eq. 1 can become time-dependent (16). In such cases, the dynamics of the time-dependent capacitance can be estimated using the GPNP model defined in Eq. 5, using the method outlined in Wang et al. (16) with the electroporation model developed in this article. The thickness of the membrane can be estimated using h_m = ε_mA_m/C_m, with A_m = 1.2 mm², the area of the membrane surface; and ε_m and C_m as given in Table S1 and Table S2. For the 1, 10, and 100% membranes, we obtain a thickness of 3.54, 3.54, and 3.40 nm, respectively. These values are in excellent agreement with the results of neutron reflectometry measurements of similar DphPC-based tethered membranes (7). As seen, the thickness of the tethered DphPC membrane is approximately constant between the 1 and 10% tether densities. The 100% DphPC monolayer is slightly thinner than the 1 and 10% DphPC-bilayer membrane. The reduction in thickness between the 100%, and the 1 and 10%, is a result of the combined effect of an increased tether density and the dibenzyl group that binds the phytanyl tails in the tethered DphPC monolayer.

In Fig. 8, the experimentally measured current as well as the current obtained from our two-level predictive model I(t) is displayed for several different linearly increasing and decreasing drive potentials. As seen from Fig. 8, A–D, there is excellent agreement between the experimentally measured and numerically predicted current. For small-magnitude drive potentials, one would expect the membrane resistance to remain constant, inasmuch as the effects of electroporation, governed by Eqs. 1 and 2, are negligible. Indeed from Fig. 8, A and D, we see that the electroporation effects are negligible for drive potentials from 50 to 80 V/s for the 1-ms rise, and 10–40 V/s for the 5-ms rise. The reason the 5-ms rise (Fig. 8, A and C) has larger relative electroporation effects, as compared with the 1-ms rise (Fig. 8, B and D), is that the nucleation and dynamics of pore radii evolve for a longer period of time at a sufficiently high transmembrane potential.

Figure 8.

Experimentally measured and numerically predicted current response I(t) for the 10% tethering density DphPC membrane (A and B) and 1% tether density DphPC membrane (C and D). (A and C) Drive potential V_s(t) is defined by 1 ms linearly increasing with a rise time of 50–500 V/s in steps of 50 V/s proceeded by a linearly decreasing potential of −50 to −500 V/s in steps of −50 V/s for 1 ms. (B and D) Drive potential V_s(t) is defined by a 5-ms linearly increasing potential for 10–100 V/s in steps of 10 V/s proceeded by a linearly decreasing potential of −10 to −100 V/s in steps of −10 V/s for 5 ms. The numerical predictions are computed using Eqs. 1 and 2 with the parameters defined in Table S2.

As expected, the magnitude of the current response for the 10% tethered membrane, Fig. 8, A and B, is less than the current response for the 10% tethered membrane, Fig. 8, C and D, because of the tethers hindering the nucleation and expansion of pores. The estimated electrical double-layer capacitance used to compute the current for the 10% membrane is C_dl = 65 nF, and that for the 1% tether density is C_dl = 39 nF. In reference to Table S2, the expected value is C_dl ∈[118,137] nF. Despite this minor discrepancy, the estimated current, using the model given in Eqs. 1 and 2, is in excellent agreement with the experimentally measured current.

Conclusion

The construction and two-level predictive model for an engineered tethered membrane is presented in this article. The self-assembled membrane provides a stable platform for reproducible experiments in electroporation. The two-layer model presented reveals several interesting features regarding how the Stern and diffuse double layers, and tethers, effect the electroporation process. The model proposed in this article predicts that the electrical energy required to form a pore is proportional to the transmembrane potential to a fractional power, and the pore conductance is proportional to the radius of the pore. As shown, the experimental results compare favorably with the results computed from the predictive models.

Appendix A: Electroneutral Model of Pore Conductance

Assuming electroneutrality, i.e.,

$$\sum _i{z}^i{c}^i=0$$

and no steric effects a_i = 0 (2), the governing equations of ϕ_w, the electrical potential in the electrolyte solution, Ω_w, can be derived by substituting the time derivative of Eq. 5b into Eq. 5a for charge neutrality. The resulting elliptic equation is given by

$$\begin{array}{c}\nabla \cdot \left(\varsigma \nabla \varphi +\nabla \kappa \right)=0,\\ \varsigma =\sum _{i=1}^N\frac{{\left(q{z}^i\right)}^2{D}^i}{k_{\text{B}}T}{c}^i,\\ \kappa =\sum _{i=1}^{N}q{z}^i{D}^i{c}^i,\end{array}$$ (17)

with the parameters defined below from Eq. 5. The boundary conditions of Eq. 17 at the electrode surfaces ∂Ω_e and ∂Ω_ce, and at the ambient boundary ∂Ω_w, ∂Ω_hm, and ∂Ω_r, are given by Eqs. 10 and 11, respectively (see also Fig. 3). In the membrane domain Ω_m, the electrostatic potential ϕ_m is governed by Laplace’s equation for electrostatics ∇ ⋅ (ε_m∇ϕ) = 0. The interface conditions between the domains Ω_w and Ω_m are given by

$$\begin{array}{c}n\cdot \nabla {\varphi }_w=0\text{in}\partial {\text{Ω}}_m,\\ {\varphi }_m={\varphi }_w\text{in}\partial {\text{Ω}}_m.\end{array}$$ (18)

From the continuity of potential on ∂Ω_m from Eq. 18, there exists a surface charge on the membrane given by ρ_s = ε_mn ⋅ ∇ϕ_m − ε_wn ⋅ ∇ϕ_w; therefore, the system of equations from Eq. 17 with boundary conditions from Eq. 18 implicitly includes the membrane surface charge ρ_s (2,29,73).

We denote the governing equations from Eq. 5a with a_i = 0 coupled with Eq. 17, the material parameters defined by Eqs. 6 and 7, and the boundary conditions Eqs. 8, 10, 11, and 18 given as the electroneutral model (EM). Given the solution of the EM system of equations, the conductance G_p, Eq. 12, can be estimated.

Appendix B: Electroneutral and Laplace Model of Electrical Energy Required to form a Pore

Assuming electroneutrality, i.e.,

$$\sum _i{z}^i{c}^i=0$$

and no steric effects a_i = 0, the electric potential ϕ can be computed using the EM, defined in Appendix A. Given ϕ from the EM, F(r) is computed using Eq. 16. Substituting F(r) into Eq. 13 gives W_es, the electrical energy required to form a pore. If steady-state current (i.e., ∇cⁱ = 0) is also assumed (29), the electrical potential ϕ is governed by Laplace’s equation ∇ ⋅ (ε∇ϕ) = 0 with ε defined by Eq. 7, and the interface and boundary conditions defined by Eqs. 10, 11, and 18. We denote this as the Laplace model (LM). Given ϕ from the LM, an estimate of W_es can be computed using the same method as for the EM above.

Supporting Citations

References (74–78) appear in the Supporting Material.