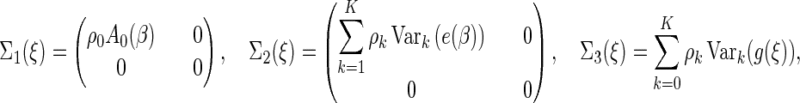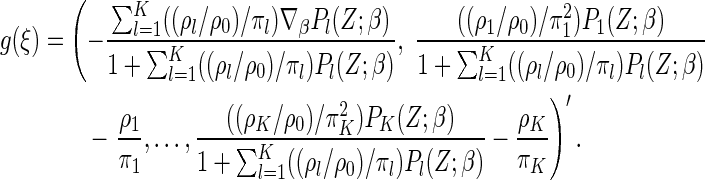Abstract
Motivated by the need from our on-going environmental study in the Norwegian Mother and Child Cohort (MoBa) study, we consider an outcome-dependent sampling (ODS) scheme for failure-time data with censoring. Like the case-cohort design, the ODS design enriches the observed sample by selectively including certain failure subjects. We present an estimated maximum semiparametric empirical likelihood estimation (EMSELE) under the proportional hazards model framework. The asymptotic properties of the proposed estimator were derived. Simulation studies were conducted to evaluate the small-sample performance of our proposed method. Our analyses show that the proposed estimator and design is more efficient than the current default approach and other competing approaches. Applying the proposed approach with the data set from the MoBa study, we found a significant effect of an environmental contaminant on fecundability.
Keywords: Biased-sampling, Empirical likelihood, Proportional hazards model, Survival analysis
1. Introduction
In many epidemiologic studies and disease prevention trials, much of the cost is spent on acquiring measurements of the main exposure variable. Large cohort studies with simple random sampling are too expensive to conduct for investigators with a limited budget. Alternative cost-efficient designs and procedures are therefore desirable and may play a critical role in reaching the prespecified power level for many studies with a limited budget. Outcome-dependent sampling (ODS) (e.g. the case–control study) is a retrospective sampling scheme that enhances the efficiency and reduces the cost of a study by allowing investigators observe the exposure with a probability that depends on the value of the outcome (e.g. Cornfield, 1951; Weinberg and Wacholder, 1993; Whittemore, 1997). Recent work has focused on a more general ODS design for continuous outcomes (Zhou and others, 2002; Chatterjee and others, 2003; Weaver and Zhou, 2005). The principle idea of such a design is to concentrate resources on a segment of the population that conveys the most information about the exposure–response relationship (Song and others, 2009; Zhou, Song and others, 2011; Zhou, Wu and others, 2011).
For the time-to-event data, the case-cohort design (Prentice, 1986) is a well-known biased-sampling scheme for censored failure-time data. The case-cohort design measures the covariates on a simple random sample (SRS) (subcohort) as well as on all the failures at the end of study (e.g. Sun and others, 2004; Lu and Tsiatis, 2006; Breslow and Wellner, 2007; Tsai, 2009). When the number of failures is large, a generalized case-cohort design has been proposed where, in addition to a random sample, the information on covariates is assembled only for a subset of the failures instead of all the failures to reduce the cost (e.g. Chen, 2001; Cai and Zeng, 2007; Kang and Cai, 2009). Case-cohort and generalized case-cohort designs are especially advocated when censoring of cases is frequent.
Our research is motivated by a recent substudy of the Norwegian Mother and Child Cohort (MoBa) about the potential health effects of perfluoroalkyl substances (PFASs) (Whitworth and others, 2012). PFASs are man-made chemicals that are widely used as industrial surfactants and emulsifiers and in a variety of consumer products. Two of the most widely detected and studied PFASs are perfluorooctane sulfonate (PFOS) and perfluorooctanoic acid (PFOA). Both PFOS and PFOA have shown the potential for toxicity in animal studies (e.g. Johansson and others, 2008). In human studies, several studies have linked PFOS and PFOA levels to lower birth weight, increased cholesterol, increased rates of cancer (e.g. Alexander and others, 2003), and reduced human fertility (e.g. Fei and others, 2009).
Our interests are focused on assessing the relationship between exposure to PFASs and women's subfecundity. Measurements to estimate fecundity were ascertained as time to pregnancy (TTP), reported by women around gestational week 17. Because of the expense measuring the PFAS levels, Whitworth and others (2012) chose two groups of women for measurement of PFAS levels: an overall SRS of 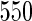 women from the cohort and a supplemental sample of
women from the cohort and a supplemental sample of 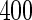 women sampled from those who delivered a child and had a TTP
women sampled from those who delivered a child and had a TTP 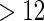 months. The MoBa substudy was designed to take advantage of the ODS scheme to yield more powerful and efficient inferences. In this paper, we consider a general failure-time ODS sampling scheme for the MoBa data.
months. The MoBa substudy was designed to take advantage of the ODS scheme to yield more powerful and efficient inferences. In this paper, we consider a general failure-time ODS sampling scheme for the MoBa data.
One frequent approach in epidemiology for the above MoBa data is to dichotomize the TTP and apply logistic regression for a binary response. The odds ratios based on this logistic regression are then computed (e.g. per ng/ml of PFOA). Loss of information and bias may result. There is also the risk for misclassification and the estimations may not be comparable if different cutpoints are chosen to dichotomize the outcome. We assess the relationship between the exposure of interest and time-to-event response by analyzing the right-censored data obtained by the above ODS scheme under the framework of the proportional hazards model (Cox, 1972). We develop an estimated maximum semiparametric empirical likelihood approach where we replace the baseline cumulative hazard function and survival function of censoring time in the joint likelihood with some consistent estimators and then maximize it by an empirical approach without specifying the marginal distribution of covariates. We illustrate the proposed method through simulations and compare it with the results from different competing methods. Software and practical recommendations are provided to researchers who will deal with biased-sampling failure-time data in practice.
The layout of the remainder of this article is as follows. In Section 2, we describe the proposed failure-time ODS design, present an estimated semiparametric empirical likelihood estimator, and develop the asymptotic properties of the proposed estimator. In Section 3, we conduct simulation studies to compare its efficiency with some alterative methods. In Section 4, we apply our proposed method to analyze a data set from the MoBa study. In Section 5, we give some final remarks.
2. Design and estimation
2.1. ODS design and notations
Suppose that there exists a large, but finite, study population of 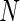 independent individuals. Let
independent individuals. Let 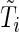 denote the failure time and
denote the failure time and 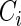 denote the censoring time for subject
denote the censoring time for subject 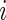 (
(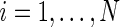 ). The observed time is
). The observed time is 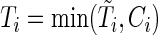 . Let
. Let 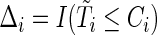 denote the right-censoring indicator for subject
denote the right-censoring indicator for subject 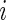 ,
, 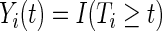 denote the at-risk process, and
denote the at-risk process, and 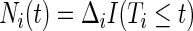 denote the counting process, where
denote the counting process, where 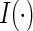 is an indicator function. We confine our attention to non-time-dependent covariates. Let
is an indicator function. We confine our attention to non-time-dependent covariates. Let 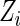 be a
be a 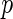 -dimensional covariate for subject
-dimensional covariate for subject 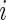 . Assume that
. Assume that 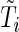 and
and 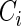 are conditionally independent given
are conditionally independent given 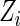 . Let
. Let 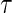 denote the end time for the study.
denote the end time for the study.
Suppose that the failure-time 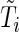 follows the following proportional hazards model (Cox, 1972):
follows the following proportional hazards model (Cox, 1972):
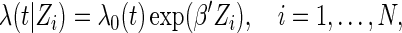 |
(2.1) |
where 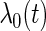 is the unspecified baseline hazard function, and
is the unspecified baseline hazard function, and 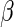 is a
is a 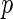 -dimensional regression coefficient of primary interest. We assume that the range of observed failure time of all the cases is partitioned into
-dimensional regression coefficient of primary interest. We assume that the range of observed failure time of all the cases is partitioned into 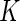 mutually exclusive and exhaustive strata:
mutually exclusive and exhaustive strata: 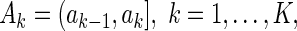 by some known constants
by some known constants 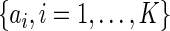 which satisfy
which satisfy 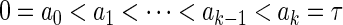 . We consider the following ODS design where
. We consider the following ODS design where 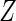 is observed: First, a random sample of size
is observed: First, a random sample of size 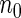 from the full cohort, denoted by the SRS sample, is selected. In addition, we select a supplemental sample of size
from the full cohort, denoted by the SRS sample, is selected. In addition, we select a supplemental sample of size 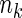 from each of the above
from each of the above 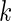 th stratum of cases. The samples from these two components constitute the ODS sample. We suppose that
th stratum of cases. The samples from these two components constitute the ODS sample. We suppose that 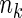 is fixed by design for
is fixed by design for 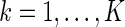 . We denote
. We denote 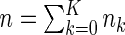 to be the total size of the ODS sample. Let
to be the total size of the ODS sample. Let 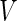 ,
, 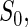 and
and 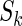 be the index set of the total ODS sample, the SRS sample, and the supplemental sample from the
be the index set of the total ODS sample, the SRS sample, and the supplemental sample from the 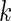 th stratum, respectively. Hence, the observed data for our ODS design can be summarized as
th stratum, respectively. Hence, the observed data for our ODS design can be summarized as
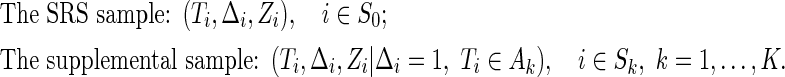 |
(2.2) |
The likelihood function corresponding to the observed data described in (2.2) is
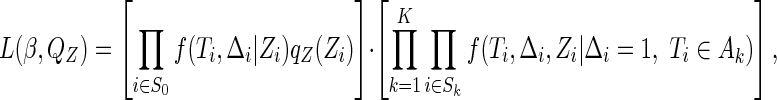 |
(2.3) |
where 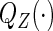 and
and 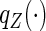 denote the cumulative distribution and density function of
denote the cumulative distribution and density function of 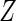 , respectively,
, respectively, 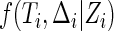 denotes the conditional distribution function of
denotes the conditional distribution function of 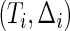 given
given 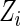 , and
, and 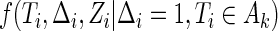 denotes the joint density function of
denotes the joint density function of 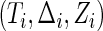 , conditional on the censoring indicator
, conditional on the censoring indicator 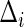 being 1, and the failure-time
being 1, and the failure-time 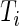 being in interval
being in interval 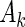 . By applying Bayes’ Law to the supplemental samples in the second bracket of (2.3), we can rewrite (2.3) as
. By applying Bayes’ Law to the supplemental samples in the second bracket of (2.3), we can rewrite (2.3) as
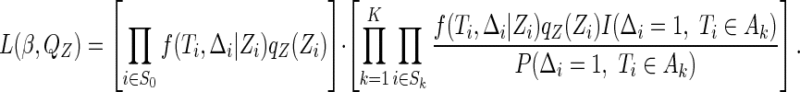 |
(2.4) |
Under random censorship, 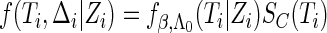 when
when 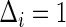 and
and 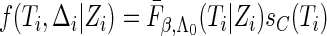 when
when 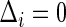 , where
, where 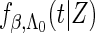 and
and 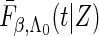 are the conditional density function and survival function of
are the conditional density function and survival function of 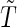 given
given 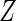 with the baseline cumulative hazard function
with the baseline cumulative hazard function 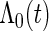 , respectively, and
, respectively, and 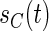 and
and 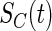 are the density function and survival function of the censoring time
are the density function and survival function of the censoring time 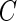 , respectively. We assume that
, respectively. We assume that 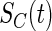 is independent on the covariate
is independent on the covariate 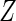 . Thus, we have
. Thus, we have 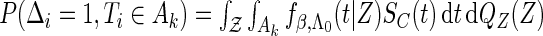 . The likelihood function in (2.4) is proportional to
. The likelihood function in (2.4) is proportional to
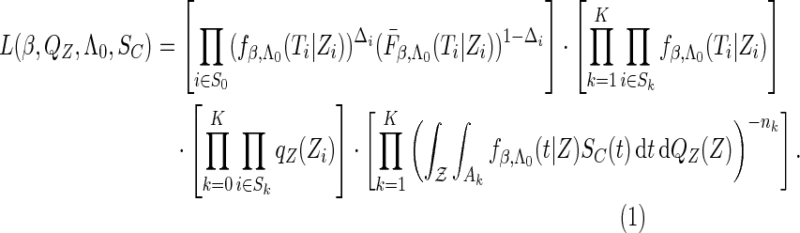 |
(2.5) |
Note that the non-parametric portion  cannot be separated from the above likelihood function that combines both the conditional parametric likelihood and the marginal semiparametric likelihood. Clearly, the inference for the underlying parameters requires methods to deal with
cannot be separated from the above likelihood function that combines both the conditional parametric likelihood and the marginal semiparametric likelihood. Clearly, the inference for the underlying parameters requires methods to deal with  , which are effectively infinite-dimensional nuisance functions. For all these challenges, we develop next an estimated maximum semiparametric empirical likelihood approach, in which we replace
, which are effectively infinite-dimensional nuisance functions. For all these challenges, we develop next an estimated maximum semiparametric empirical likelihood approach, in which we replace  in the joint likelihood
in the joint likelihood 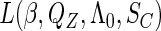 with their estimators to get an estimated likelihood function
with their estimators to get an estimated likelihood function 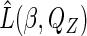 , and then maximize
, and then maximize 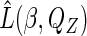 with respect to
with respect to 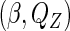 by a semiparametric empirical approach without specifying
by a semiparametric empirical approach without specifying 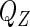 .
.
2.2. An estimated maximum semiparametric empirical likelihood approach
First, we estimate the baseline cumulative hazard function 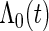 by the Breslow–Aalen estimator
by the Breslow–Aalen estimator
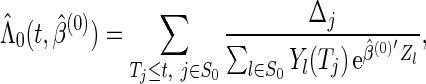 |
and the survival function 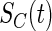 of censoring time
of censoring time 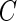 by the Nelson–Aalen estimator
by the Nelson–Aalen estimator
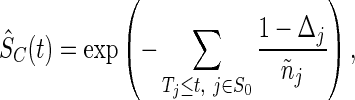 |
where 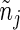 denotes the number of subjects at risk at a time prior to
denotes the number of subjects at risk at a time prior to 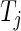 (for
(for 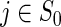 ) and
) and 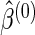 is the estimate of
is the estimate of 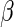 based only on the SRS portion. Replacing
based only on the SRS portion. Replacing 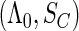 in the likelihood function (2.5) with
in the likelihood function (2.5) with 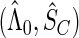 , we obtain the estimated log-likelihood function:
, we obtain the estimated log-likelihood function:
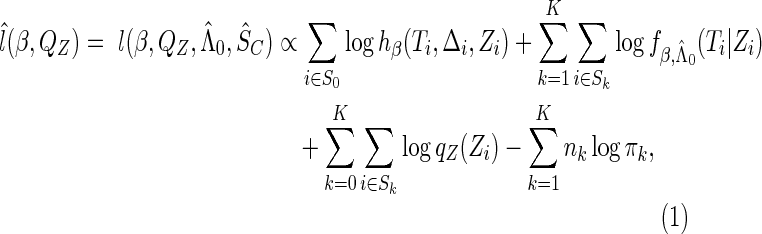 |
(2.6) |
where
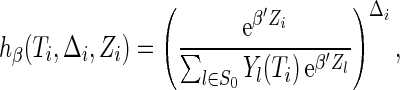 |
which is obtained by an extension of the result of Johansen (1983) for the Cox model, and
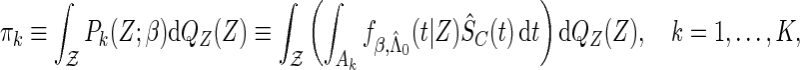 |
which are the stratum-specific estimated probabilities of the failure time across all cases.
Maximizing 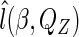 with respect to
with respect to 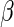 without specifying
without specifying 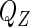 is not straightforward. We first profile the likelihood function in (2.6) by fixing
is not straightforward. We first profile the likelihood function in (2.6) by fixing 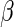 and replacing
and replacing 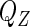 with the empirical likelihood function (Vardi, 1982, 1985). To maximize
with the empirical likelihood function (Vardi, 1982, 1985). To maximize 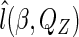 over all distributions whose support contains the observed
over all distributions whose support contains the observed 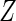 values, we only need to consider the discrete conditional distribution of
values, we only need to consider the discrete conditional distribution of 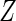 with jumps at each of the observed points (Owen, 1990). Denote
with jumps at each of the observed points (Owen, 1990). Denote
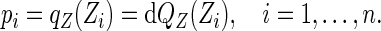 |
For a fixed 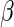 , we have
, we have
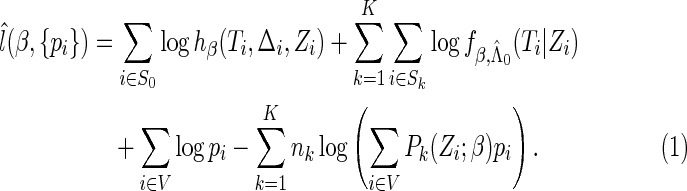 |
(2.7) |
We use the Lagrange multiplier argument to search for 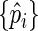 that maximize (2.7) under the constraints
that maximize (2.7) under the constraints 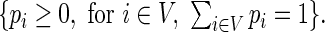 The Lagrange function can be written as
The Lagrange function can be written as
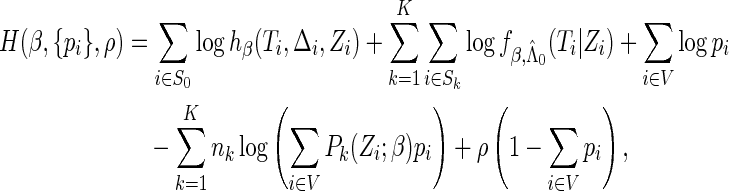 |
where 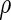 denotes the Lagrange multipliers. It can be shown that the solutions to the score equation of
denotes the Lagrange multipliers. It can be shown that the solutions to the score equation of 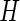 with respect to
with respect to 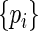 have the form:
have the form:
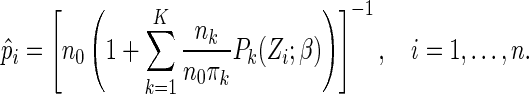 |
By plugging 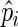 back into
back into 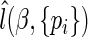 in (2.7), we have the resulting profile likelihood function
in (2.7), we have the resulting profile likelihood function
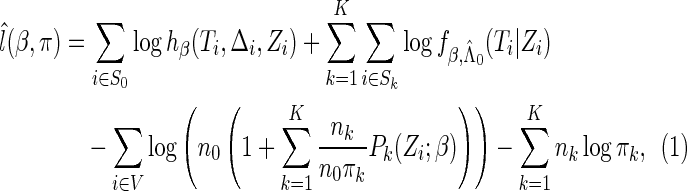 |
(2.8) |
where 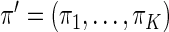 . The proposed estimated maximum semiparametric empirical likelihood estimator (EMSELE) is the
. The proposed estimated maximum semiparametric empirical likelihood estimator (EMSELE) is the 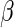 that maximizes (2.8). Define
that maximizes (2.8). Define 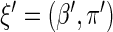 , and denote the EMSELE for
, and denote the EMSELE for 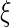 to be
to be 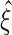 and the EMSELE for parameter
and the EMSELE for parameter 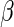 to be
to be 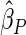 , the corresponding portion of
, the corresponding portion of 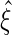 . A Newton–Raphson algorithm can be used to obtain
. A Newton–Raphson algorithm can be used to obtain 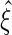 .
.
2.3. Asymptotic properties of EMSELE
To present the large-sample result, we introduce the following notations:
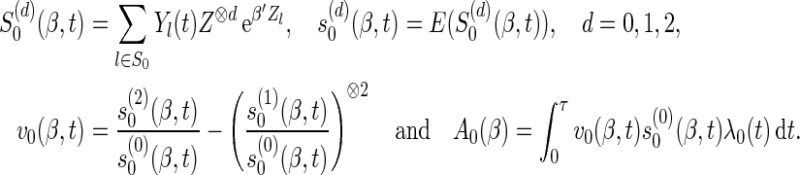 |
Here, for a vector 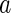 ,
, 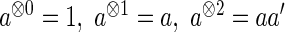 . We indicate the true values of a parameter by superscript “0”. Let
. We indicate the true values of a parameter by superscript “0”. Let 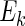 denote expectation conditional on
denote expectation conditional on 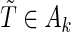 , so that, for any function
, so that, for any function 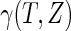 ,
,
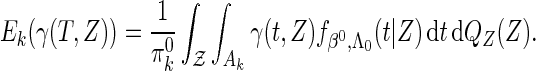 |
(2.9) |
Under some general regularity conditions (see Appendix of supplementary material available at Biostatistics online) and assuming that 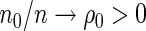 and
and 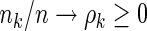 for
for 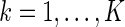 , the following theorem establishes the asymptotic properties of the EMSELE
, the following theorem establishes the asymptotic properties of the EMSELE 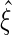 as well as a consistent estimator for the asymptotic variance matrix.
as well as a consistent estimator for the asymptotic variance matrix.
Theorem 2.1 —
Under general regularity conditions,
converges in probability to
, while
has an asymptotic normal distribution with mean zero and with a variance matrix in the form
where
is the limiting Hessian matrix of the profile likelihood
, and
where
, and
A consistent estimator for the asymptotic covariance matrix
is
, where
,
,
, and
are obtained by replacing the large-sample quantities in
,
,
, and
with their corresponding small-sample quantities.
The proof for Theorem 2.1 is given in Appendix (see supplementary material available at Biostatistics online).
3. Simulation studies
We conducted simulation studies to assess the finite sample properties of our proposed method. We consider the following Cox's proportional hazards model:
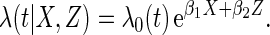 |
(3.1) |
We took the marginal distribution of failure-time 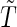 to be exponential with failure rate
to be exponential with failure rate 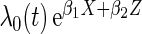 . The baseline hazard function
. The baseline hazard function 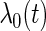 was set to be
was set to be 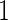 . The covariate
. The covariate 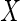 was generated from a standard normal distribution and
was generated from a standard normal distribution and 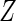 was generated from a Bernoulli distribution with
was generated from a Bernoulli distribution with 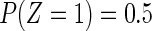 . We set
. We set 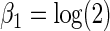 and
and 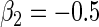 . The censoring time
. The censoring time 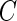 was generated from a uniform distribution
was generated from a uniform distribution 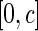 with
with 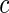 chosen to depend on the desired percentage of censoring. We considered censoring rates of approximately
chosen to depend on the desired percentage of censoring. We considered censoring rates of approximately 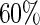 and
and 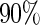 with the corresponding
with the corresponding 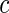 values
values 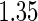 and
and 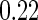 .
.
For our ODS design, we first generated the SRS sample of 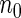 . We then partitioned all the cases into three strata, separated by quantiles
. We then partitioned all the cases into three strata, separated by quantiles 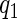 and
and 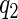 of failure times in the cases. We sampled the supplemental sample of
of failure times in the cases. We sampled the supplemental sample of 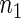 and
and 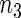 subjects from the low stratum and the high stratum, respectively. In addition to various configurations for the parameter values, we also chose two pairs of the cutpoints (
subjects from the low stratum and the high stratum, respectively. In addition to various configurations for the parameter values, we also chose two pairs of the cutpoints (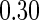 and
and 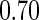 quantiles, and
quantiles, and 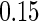 and
and 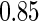 quantiles, respectively), to investigate the impact of different cutpoints for our ODS design for creating the supplemental samples.
quantiles, respectively), to investigate the impact of different cutpoints for our ODS design for creating the supplemental samples.
Under each configuration, we compared the proposed estimator, 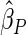 , with three competing estimators: the maximum likelihood estimator based on a SRS of the same size as the ODS sample (
, with three competing estimators: the maximum likelihood estimator based on a SRS of the same size as the ODS sample (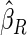 ); the weighted estimator under generalized case-cohort design developed by Kang and Cai (2009) (
); the weighted estimator under generalized case-cohort design developed by Kang and Cai (2009) (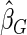 ); the estimator under the case-cohort design developed by Prentice (1986) (
); the estimator under the case-cohort design developed by Prentice (1986) (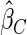 ). For calculating
). For calculating 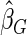 , we first selected a subcohort of
, we first selected a subcohort of 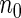 by simple random sampling. We then selected a SRS of cases of
by simple random sampling. We then selected a SRS of cases of 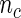 in the remaining cases, which we set to be the same size as the supplemental samples in ODS design, i.e.
in the remaining cases, which we set to be the same size as the supplemental samples in ODS design, i.e. 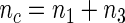 . We used the weighed estimating equation provided in Kang and Cai (2009) with the time-invariant weight function to obtain
. We used the weighed estimating equation provided in Kang and Cai (2009) with the time-invariant weight function to obtain 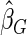 . For calculating
. For calculating 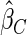 , we randomly sampled a subcohort of
, we randomly sampled a subcohort of 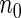 and took all the remaining cases. In order to obtain an approximate sample size with the ODS samples, we adjusted the size of the full cohort according to different subcohort sizes and different censoring rates. For example, we set the full cohort size to be
and took all the remaining cases. In order to obtain an approximate sample size with the ODS samples, we adjusted the size of the full cohort according to different subcohort sizes and different censoring rates. For example, we set the full cohort size to be 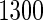 when the subcohort size
when the subcohort size 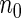 was
was  and the censoring rate was
and the censoring rate was 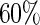 , and the mean of sample sizes for case-cohort design under
, and the mean of sample sizes for case-cohort design under 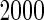 simulations was
simulations was 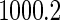 .
.
The estimated means (Means), standard deviations (SDs), mean of the variance estimates (SEs), and 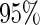 nominal confidence intervals coverages (CPs) for each estimator were obtained from
nominal confidence intervals coverages (CPs) for each estimator were obtained from 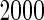 independently generated data sets. The results are summarized in Table 1. Under all of the cases considered here, the four estimators for
independently generated data sets. The results are summarized in Table 1. Under all of the cases considered here, the four estimators for 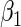 and
and 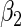 are all unbiased. Our proposed variance estimator provides a good estimation for the sample standard errors and the confidence intervals attain coverage close to the nominal
are all unbiased. Our proposed variance estimator provides a good estimation for the sample standard errors and the confidence intervals attain coverage close to the nominal 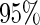 level. We note that the estimation of the sample SDs become less stable at the very high censoring rate (e.g.
level. We note that the estimation of the sample SDs become less stable at the very high censoring rate (e.g. 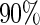 ), which indicates a higher sample size may be needed. Further, the efficiency gains are higher when the cutpoint is further out (
), which indicates a higher sample size may be needed. Further, the efficiency gains are higher when the cutpoint is further out (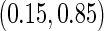 vs.
vs. 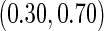 ). We also note that the proposed estimator
). We also note that the proposed estimator 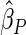 is the most efficient among all the estimators compared under all the different censoring rates.
is the most efficient among all the estimators compared under all the different censoring rates. 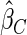 is more efficient than
is more efficient than 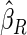 when the censoring rate is
when the censoring rate is 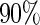 .
. 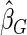 is more efficient than
is more efficient than 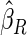 when the censoring rate is
when the censoring rate is 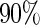 .
. 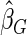 and
and 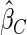 are comparable under censoring rate of
are comparable under censoring rate of 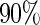 . The fact that
. The fact that 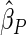 is more efficient than
is more efficient than 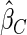 and
and 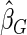 indicates that our ODS design for the survival analysis can be a more efficient alternative to the case-cohort design and the generalized case-cohort design. Further, comparing the results in Table 1, we note that, for a given total ODS sample size (
indicates that our ODS design for the survival analysis can be a more efficient alternative to the case-cohort design and the generalized case-cohort design. Further, comparing the results in Table 1, we note that, for a given total ODS sample size (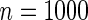 ), the efficiency improves as we allocate more individuals in the supplemental samples (e.g.
), the efficiency improves as we allocate more individuals in the supplemental samples (e.g. 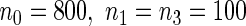 vs.
vs. 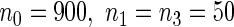 ).
).
Table 1.
Results are based on the model 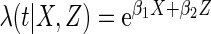 , where
, where 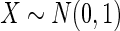 and
and 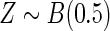
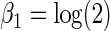 |
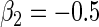 |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
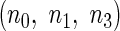 |
Cutpoints | 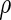 |
Mean | SD | SE | CP | Mean | SD | SE | CP | |
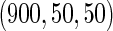 |
(0.30, 0.70) | 0.60 | 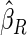 |
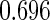 |
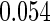 |
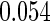 |
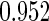 |
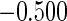 |
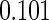 |
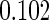 |
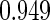 |
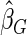 |
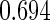 |
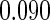 |
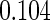 |
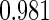 |
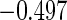 |
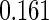 |
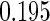 |
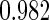 |
|||
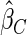 |
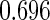 |
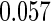 |
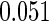 |
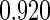 |
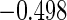 |
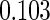 |
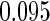 |
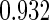 |
|||
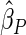 |
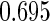 |
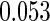 |
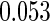 |
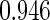 |
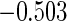 |
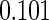 |
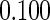 |
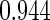 |
|||
| 0.90 | 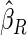 |
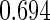 |
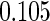 |
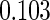 |
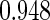 |
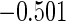 |
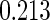 |
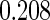 |
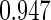 |
||
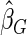 |
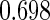 |
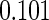 |
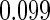 |
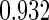 |
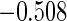 |
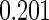 |
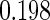 |
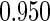 |
|||
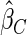 |
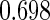 |
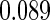 |
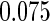 |
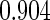 |
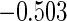 |
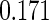 |
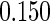 |
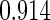 |
|||
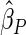 |
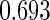 |
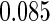 |
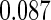 |
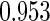 |
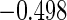 |
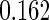 |
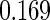 |
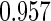 |
|||
| (0.15, 0.85) | 0.60 | 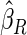 |
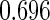 |
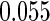 |
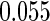 |
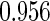 |
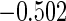 |
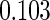 |
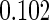 |
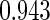 |
|
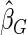 |
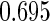 |
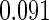 |
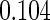 |
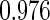 |
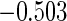 |
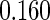 |
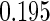 |
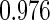 |
|||
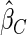 |
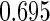 |
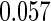 |
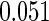 |
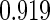 |
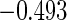 |
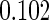 |
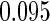 |
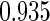 |
|||
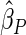 |
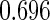 |
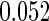 |
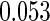 |
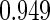 |
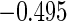 |
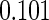 |
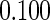 |
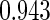 |
|||
| 0.90 | 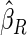 |
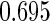 |
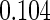 |
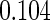 |
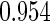 |
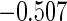 |
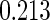 |
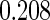 |
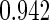 |
||
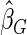 |
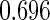 |
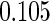 |
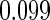 |
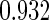 |
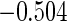 |
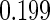 |
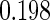 |
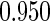 |
|||
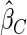 |
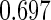 |
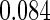 |
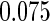 |
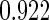 |
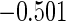 |
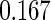 |
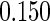 |
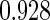 |
|||
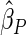 |
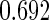 |
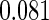 |
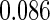 |
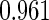 |
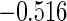 |
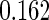 |
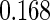 |
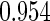 |
|||
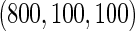 |
(0.30, 0.70) | 0.60 | 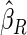 |
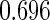 |
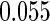 |
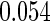 |
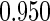 |
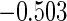 |
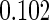 |
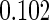 |
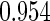 |
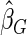 |
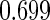 |
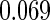 |
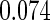 |
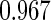 |
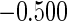 |
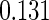 |
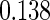 |
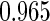 |
|||
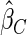 |
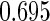 |
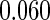 |
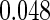 |
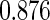 |
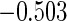 |
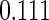 |
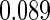 |
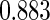 |
|||
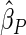 |
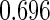 |
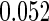 |
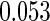 |
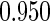 |
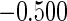 |
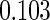 |
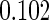 |
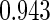 |
|||
| 0.90 | 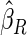 |
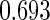 |
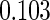 |
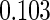 |
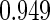 |
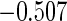 |
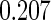 |
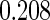 |
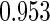 |
||
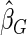 |
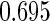 |
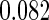 |
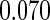 |
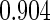 |
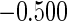 |
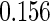 |
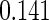 |
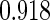 |
|||
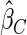 |
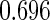 |
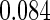 |
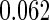 |
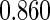 |
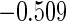 |
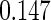 |
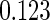 |
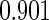 |
|||
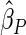 |
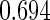 |
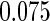 |
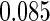 |
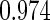 |
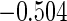 |
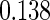 |
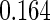 |
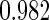 |
|||
| (0.15, 0.85) | 0.60 | 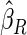 |
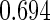 |
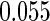 |
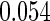 |
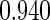 |
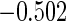 |
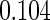 |
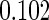 |
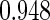 |
|
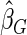 |
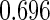 |
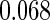 |
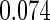 |
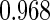 |
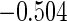 |
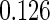 |
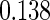 |
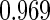 |
|||
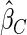 |
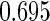 |
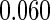 |
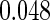 |
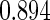 |
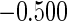 |
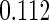 |
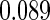 |
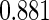 |
|||
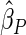 |
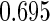 |
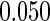 |
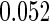 |
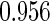 |
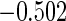 |
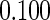 |
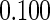 |
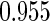 |
|||
| 0.90 | 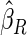 |
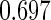 |
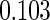 |
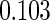 |
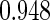 |
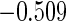 |
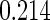 |
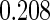 |
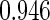 |
||
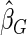 |
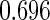 |
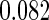 |
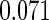 |
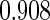 |
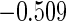 |
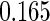 |
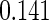 |
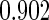 |
|||
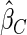 |
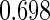 |
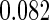 |
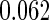 |
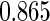 |
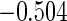 |
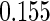 |
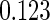 |
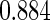 |
|||
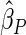 |
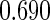 |
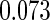 |
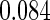 |
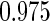 |
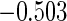 |
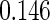 |
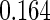 |
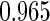 |
|||
The cutpoints for the ODS design were 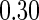 and
and 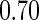 sample quantiles and
sample quantiles and 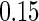 and
and 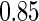 sample quantiles, respectively;
sample quantiles, respectively; 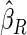 denotes the estimator from a simple random sample of the same size as the ODS sample;
denotes the estimator from a simple random sample of the same size as the ODS sample; 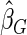 denotes the generalized case-cohort estimator developed by Kang and Cai (2009);
denotes the generalized case-cohort estimator developed by Kang and Cai (2009); 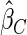 denotes the case-cohort estimator developed by Prentice (1986), and the average sample size is 1000 by adjusting the full cohort sample size to different censoring rate
denotes the case-cohort estimator developed by Prentice (1986), and the average sample size is 1000 by adjusting the full cohort sample size to different censoring rate 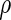 ;
; 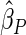 denotes the proposed EMSELE estimator. Simulation results are based on 2000 simulations with the total ODS sample size
denotes the proposed EMSELE estimator. Simulation results are based on 2000 simulations with the total ODS sample size 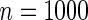 .
.
Table 2 provides additional simulation results on the sensitivity analysis and the unbalanced pattern of ODS supplemental samples allocations. We investigated the performance of the proposed estimator under unbalanced values of 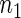 and
and 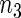 by choosing
by choosing 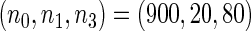 ,
, 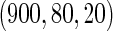 ,
, 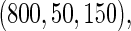 and
and 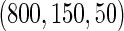 , respectively. The results reported in Table 2 indicate that, overall, the observed properties of
, respectively. The results reported in Table 2 indicate that, overall, the observed properties of 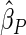 under Table 1 is consistent for the balanced and unbalanced values of
under Table 1 is consistent for the balanced and unbalanced values of 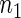 and
and 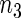 .
.
Table 2.
Results are based on the model 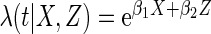 , where
, where 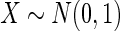 and
and 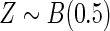
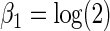 |
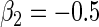 |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
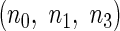 |
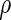 |
Mean | SD | SE | CP | Mean | SD | SE | CP | |
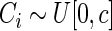 |
||||||||||
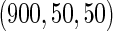 |
0.60 | 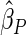 |
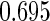 |
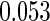 |
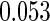 |
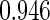 |
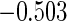 |
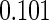 |
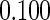 |
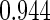 |
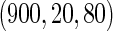 |
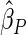 |
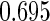 |
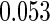 |
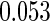 |
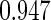 |
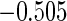 |
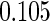 |
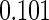 |
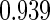 |
|
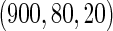 |
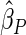 |
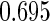 |
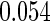 |
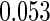 |
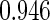 |
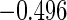 |
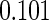 |
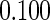 |
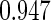 |
|
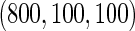 |
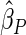 |
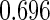 |
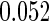 |
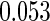 |
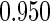 |
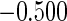 |
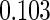 |
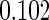 |
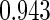 |
|
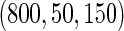 |
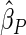 |
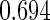 |
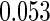 |
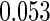 |
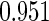 |
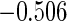 |
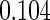 |
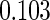 |
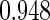 |
|
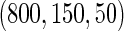 |
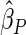 |
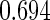 |
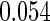 |
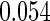 |
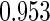 |
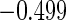 |
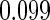 |
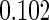 |
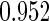 |
|
Censoring Scenario I: 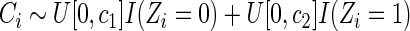
|
||||||||||
 |
0.60 |  |
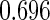 |
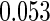 |
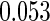 |
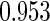 |
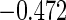 |
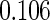 |
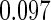 |
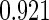 |
| 0.90 | 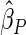 |
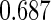 |
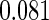 |
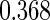 |
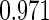 |
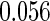 |
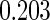 |
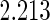 |
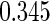 |
|
Censoring Scenario II: 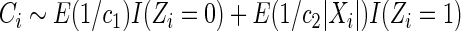
|
||||||||||
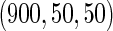 |
0.60 | 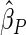 |
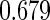 |
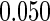 |
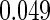 |
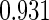 |
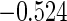 |
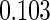 |
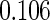 |
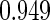 |
| 0.90 | 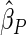 |
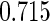 |
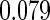 |
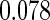 |
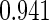 |
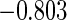 |
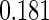 |
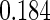 |
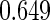 |
|
The cutpoints for the ODS design were 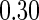 and
and 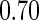 sample quantiles. Censoring Scenario I:
sample quantiles. Censoring Scenario I: 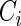 was generated from the distribution
was generated from the distribution  ; Censoring Scenario II:
; Censoring Scenario II: 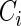 was generated from the distribution
was generated from the distribution 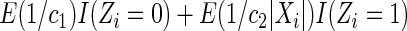 . The results are based on
. The results are based on 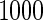 replicates for each setting. Simulation results are based on the total ODS sample size
replicates for each setting. Simulation results are based on the total ODS sample size 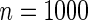 .
.
The second component in Table 2 was conducted to evaluate the performance of 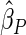 when the censoring time depends on the covariates. We considered the following two scenarios: Scenario I:
when the censoring time depends on the covariates. We considered the following two scenarios: Scenario I: 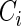 was generated from the distribution
was generated from the distribution  , and
, and 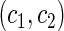 was chosen to be
was chosen to be 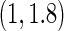 and
and 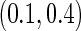 ; Scenario II:
; Scenario II: 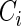 was generated from the distribution
was generated from the distribution 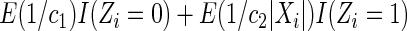 , and
, and 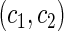 was chosen to be
was chosen to be 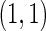 and
and 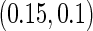 . The results in Table 2 indicate that the dependence of censoring time on the covariates will lead to biased estimates of
. The results in Table 2 indicate that the dependence of censoring time on the covariates will lead to biased estimates of 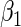 and
and 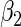 . This suggests there is a need to check for censoring dependence on covariates before using the estimator in real analysis.
. This suggests there is a need to check for censoring dependence on covariates before using the estimator in real analysis.
4. Analysis of the MoBa study data
The MoBa study is an ongoing pregnancy cohort study conducted by the Norwegian Institute of Public Health. Pregnant women in Norway were enrolled from 1999 to 2008 and completed questionnaires regarding demographic and lifestyle factors, and medical and reproductive history. Women were asked if their pregnancy was planned and reported TTP. Subfecundity was defined as having a TTP 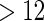 months. Our data set was based on women enrolled from 2003 to 2004 who delivered a live born child. Five hundred and fifty subjects were randomly sampled from the cohort who reported a TTP with
months. Our data set was based on women enrolled from 2003 to 2004 who delivered a live born child. Five hundred and fifty subjects were randomly sampled from the cohort who reported a TTP with 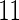 subjects excluded. Four hundred subjects were supplementally sampled from women whose TTP was
subjects excluded. Four hundred subjects were supplementally sampled from women whose TTP was 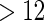 months (Whitworth and others, 2012). In this data set, there was no censoring. Hence, there is no need to check the independence of censoring on covariates here.
months (Whitworth and others, 2012). In this data set, there was no censoring. Hence, there is no need to check the independence of censoring on covariates here.
Among these 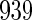 eligible women, blood samples were collected around gestational week
eligible women, blood samples were collected around gestational week 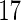 . Concentrations of PFOS and PFOA were measured from the maternal blood samples by high performance liquid chromatography/tandem mass spectrometry based on
. Concentrations of PFOS and PFOA were measured from the maternal blood samples by high performance liquid chromatography/tandem mass spectrometry based on 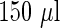 of plasma. In the analysis, we included the following variables as potential confounders: pre-pregnancy body mass index (BMI), maternal plasma albumin concentration (Alb), maternal consumption of lean fish and oily fish (Leanfish, Oilyfish), maternal age (MotherAge), paternal age (FatherAge), maternal education (MotherEdu), paternal education (FatherEdu), maternal smoking (Smoke3 for smoking
of plasma. In the analysis, we included the following variables as potential confounders: pre-pregnancy body mass index (BMI), maternal plasma albumin concentration (Alb), maternal consumption of lean fish and oily fish (Leanfish, Oilyfish), maternal age (MotherAge), paternal age (FatherAge), maternal education (MotherEdu), paternal education (FatherEdu), maternal smoking (Smoke3 for smoking 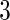 months before pregnancy, Smoke17 for smoking at gestational week
months before pregnancy, Smoke17 for smoking at gestational week 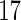 ), maternal self-reported alcohol intake
), maternal self-reported alcohol intake 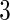 months before pregnancy (MotherDrink), frequency of sexual intercourse
months before pregnancy (MotherDrink), frequency of sexual intercourse  month before pregnancy (SexFreq), maternal diseases (endometriosis (Endo), ovary/fallopian tube infection (Ovary), sexually transmitted disease (Std), diabetes), and calendar year of blood draw (Yeardraw). Table 3 provides the demographic characteristics for all
month before pregnancy (SexFreq), maternal diseases (endometriosis (Endo), ovary/fallopian tube infection (Ovary), sexually transmitted disease (Std), diabetes), and calendar year of blood draw (Yeardraw). Table 3 provides the demographic characteristics for all 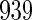 women.
women.
Table 3.
Demographics and characteristics of the MoBa study
| All individuals | TTP 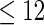 months months |
TTP  12 months 12 months |
|
|---|---|---|---|
PFOS, 
|
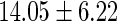 |
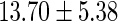 |
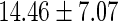 |
PFOA, 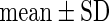
|
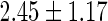 |
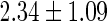 |
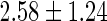 |
BMI, 
|
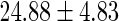 |
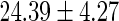 |
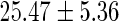 |
FatherAge 
|
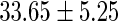 |
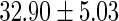 |
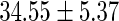 |
Alb, 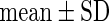
|
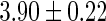 |
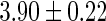 |
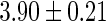 |
Oilyfish, 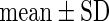
|
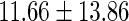 |
 |
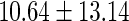 |
Leanfish, 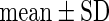
|
 |
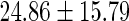 |
 |
| MotherAge (%) | |||
 25 25 |
17.36 (163/939) | 13.95 (71/509) | 21.40 (92/430) |
| 25–29 | 41.21 (387/939) | 41.45 (211/509) | 40.93 (176/430) |
| 30–34 | 31.63 (297/939) | 34.18 (174/509) | 28.60 (123/430) |
 35 35 |
9.80 (92/939) | 10.41 (53/509) | 9.07 (39/430) |
| MotherEdu (%) | |||
 High school High school |
8.86 (83/937) | 6.69 (34/508) | 11.42 (49/429) |
| High school and other | 31.70 (297/937) | 30.51 (155/508) | 33.10 (142/429) |
| Some college | 41.73 (391/937) | 43.90 (223/508) | 39.16 (168/429) |
 College College |
17.72 (166/937) | 18.90 (96/508) | 16.32 (70/429) |
| FatherEdu (%) | |||
 High school High school |
12.29 (112/911) | 10.44 (52/498) | 14.53 (60/413) |
| High school and other | 44.13 (402/911) | 44.18 (220/498) | 44.07 (182/413) |
| Some college | 26.89 (245/911) | 27.71 (138/498) | 25.91 (107/413) |
 College College |
16.68 (152/911) | 17.67 (88/498) | 15.50 (64/413) |
| Smoke3 (%) | |||
| None | 69.86 (656/939) | 73.48 (374/509) | 65.58 (282/430) |
| Sometimes | 10.12 (95/939) | 9.63 (49/509) | 10.70 (46/430) |
| Daily | 20.02 (188/939) | 16.90 (86/509) | 23.72 (102/430) |
| Smoke17 (%) | |||
| None | 76.25 (716/939) | 79.57 (405/509) | 72.33 (311/430) |
| Stopped | 15.76 (148/939) | 14.73 (75/509) | 16.98 (73/430) |
| Sometimes | 1.28 (12/939) | 1.38 (7/509) | 1.16 (5/430) |
| Daily | 6.71 (63/939) | 4.32 (22/509) | 9.53 (41/430) |
| MotherDrink (%) | |||
 1 per week 1 per week |
7.22 (67/928) | 7.17 (36/502) | 7.28 (31/426) |
| 1 per week | 15.41 (143/928) | 18.73 (94/502) | 11.50 (49/426) |
| 1–3 per month | 32.87 (305/928) | 34.86 (175/502) | 30.52 (130/426) |
 1 per month or never 1 per month or never |
44.50 (413/928) | 39.24 (197/502) | 50.70 (216/426) |
| SexFreq (%) | |||
 1 per week 1 per week |
18.45 (171/927) | 17.33 (87/502) | 19.76 (84/425) |
| 1–2 per week | 37.97 (352/927) | 33.67 (169/502) | 43.06 (183/425) |
 2 per week 2 per week |
43.58 (404/927) | 49.00 (246/502) | 37.18 (158/425) |
| Endo (%) | |||
| Yes | 3.09 (29/939) | 0.59 (3/509) | 6.05 (26/430) |
| No | 96.91 (910/939) | 99.41 (506/509) | 93.95 (404/430) |
| Ovary (%) | |||
| Yes | 2.66 (25/939) | 2.36 (12/509) | 3.02 (13/430) |
| No | 97.34 (914/939) | 97.64 (497/509) | 96.98 (417/430) |
| Std (%) | |||
| Yes | 12.57 (118/939) | 12.38 (63/509) | 12.79 (55/430) |
| No | 87.43 (821/939) | 87.62 (446/509) | 87.21 (375/430) |
| Diabete (%) | |||
| Yes | 1.60 (15/939) | 0.39 (2/509) | 3.02 (13/430) |
| No | 98.40 (924/939) | 99.61 (507/509) | 96.98 (417/430) |
| YearDraw (%) | |||
| 2003 | 49.52 (465/939) | 50.10 (255/509) | 48.84 (210/430) |
| 2004 | 50.48 (474/939) | 49.90 (254/509) | 51.16 (220/430) |
Odds ratio approach. We first implemented a standard epidemiologic approach by dichotomizing the subfecundity measurement as binary response, i.e.  for TTP
for TTP 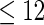 months and
months and  for TTP
for TTP 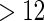 months, and used logistic regression to model the association between PFOA and subfecundity odds ratio adjusted for the confounders listed above. The result for this approach is summarized in the first column in Table 4. Due to missing values for covariates, the final sample size for the analysis included
months, and used logistic regression to model the association between PFOA and subfecundity odds ratio adjusted for the confounders listed above. The result for this approach is summarized in the first column in Table 4. Due to missing values for covariates, the final sample size for the analysis included 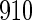 women,
women, 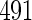 with TTP
with TTP 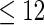 months, and
months, and 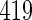 with TTP
with TTP 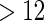 months. We note that the odds of subfecundity increases by
months. We note that the odds of subfecundity increases by 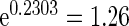 times when PFOA level increases one unit. The second and third columns of Table 4 show results for the cutpoints
times when PFOA level increases one unit. The second and third columns of Table 4 show results for the cutpoints 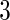 and
and 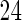 months. Comparing across the columns, we note that different choices of the cutpoints result in different inferences. The odds ratios for TTP
months. Comparing across the columns, we note that different choices of the cutpoints result in different inferences. The odds ratios for TTP 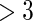 , TTP
, TTP 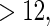 and TTP
and TTP 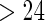 are
are 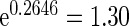 ,
, 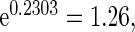 and
and 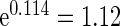 , respectively. Further, the effect of PFOA becomes not significant when the cutpoint changes from
, respectively. Further, the effect of PFOA becomes not significant when the cutpoint changes from 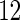 to
to 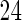 months (
months (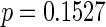 ).
).
Table 4.
Logistic regression analyses for covariate effects on subfecundity in the MoBa study with different cutpoints
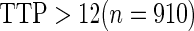 |
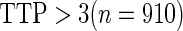 |
 |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Est. | SE |
 -value -value |
Est. | SE |
 -value -value |
Est. | SE |
 -value -value |
|
| Intercept |
 7.2631 7.2631 |
1.0236 |
 0.0001 0.0001
|
 5.1018 5.1018 |
1.0265 |
 0.0001 0.0001
|
 9.0628 9.0628 |
1.2646 |
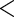 0.0001 0.0001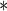
|
| PFOA | 0.2303 | 0.0652 | 0.0004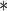
|
0.2646 | 0.0694 | 0.0001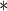
|
0.1114 | 0.0779 | 0.1527 |
| BMI | 0.0563 | 0.0153 | 0.0002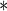
|
0.0418 | 0.0158 | 0.0081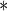
|
0.0402 | 0.0182 | 0.0271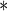
|
| MotherAge | 0.7001 | 0.1078 |
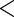 0.0001 0.0001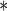
|
0.5182 | 0.1068 |
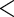 0.0001 0.0001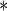
|
0.9220 | 0.1404 |
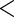 0.0001 0.0001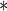
|
| MotherEdu |
 0.1428 0.1428 |
0.0853 | 0.0939 |
 0.2258 0.2258 |
0.0864 | 0.0090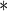
|
 0.3258 0.3258 |
0.1124 | 0.0037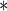
|
| FatherAge | 0.1293 | 0.0183 |
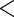 0.0001 0.0001
|
0.1123 | 0.0188 |
 0.0001 0.0001
|
0.1421 | 0.0209 |
 0.0001 0.0001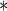
|
| SexFreq |
 0.3372 0.3372 |
0.0983 | 0.0006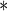
|
 0.3080 0.3080 |
0.0996 | 0.0020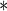
|
 0.1915 0.1915 |
0.1274 | 0.1328 |
| Endo | 2.4183 | 0.6341 | 0.0001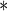
|
2.8997 | 1.0290 | 0.0048
|
2.2673 | 0.4307 |
 0.0001 0.0001
|
 Parameter estimate is significant at 5% level.
Parameter estimate is significant at 5% level.
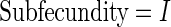 (
(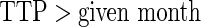 ).
).
Proposed ODS design and analysis. Using the 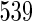 women sampled randomly as the SRS portion and
women sampled randomly as the SRS portion and 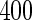 women sampled additionally from those with TTP
women sampled additionally from those with TTP 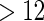 months as a supplemental sample, we implemented our EMSELE method adjusted for all potential confounders. Due to missing values of covariates, the sample sizes of SRS and supplemental samples for the final fitted model were
months as a supplemental sample, we implemented our EMSELE method adjusted for all potential confounders. Due to missing values of covariates, the sample sizes of SRS and supplemental samples for the final fitted model were 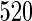 and
and 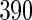 , respectively. The result of the final fitted model is listed in the first column in Table 5.
, respectively. The result of the final fitted model is listed in the first column in Table 5.
Table 5.
Cox regression analyses for covariate effects on TTP in the MoBa study
| ODS design (n_0=520, n_3=390) |
Naive design (n_v=n_0+n_3=910) |
SRS design (n_0=520) |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Est. | SE |
 -value -value |
Est. | SE |
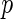 -value -value |
Est. | SE |
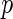 -value -value |
|
| PFOA |
 0.0567 0.0567 |
0.0253 | 0.0251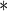
|
 0.0479 0.0479 |
0.0331 | 0.1473 |
 0.0633 0.0633 |
0.0419 | 0.1304 |
| BMI |
 0.0148 0.0148 |
0.0056 | 0.0090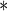
|
 0.0222 0.0222 |
0.0063 | 0.0004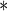
|
 0.0110 0.0110 |
0.0091 | 0.2282 |
| MotherAge |
 0.2155 0.2155 |
0.0342 |
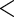 0.0001 0.0001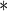
|
 0.4066 0.4066 |
0.0467 |
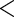 0.0001 0.0001
|
 0.1662 0.1662 |
0.0674 | 0.0137
|
| MotherEdu | 0.0968 | 0.0333 | 0.0037
|
0.1179 | 0.0396 | 0.0029
|
0.0730 | 0.0523 | 0.1630 |
| FatherAge |
 0.0470 0.0470 |
0.0059 |
 0.0001 0.0001
|
 0.0801 0.0801 |
0.0087 |
 0.0001 0.0001
|
 0.0415 0.0415 |
0.0117 | 0.0004
|
| SexFreq | 0.1089 | 0.0396 | 0.0060
|
0.1133 | 0.0488 | 0.0203
|
0.0968 | 0.0649 | 0.1359 |
| Endo |
 1.2153 1.2153 |
0.2906 |
 0.0001 0.0001
|
 0.7830 0.7830 |
0.1879 |
 0.0001 0.0001
|
 0.8424 0.8424 |
0.5027 | 0.0938 |
 Parameter estimate is significant at
Parameter estimate is significant at 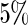 level.
level.
We note that the estimate for PFOA is negative suggesting that PFOA level increases the risk of subfecundity (i.e. TTP 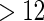 ). Women with a higher PFOA level tend to have a longer TTP, and per unit increment in PFOA, the risk of subfecundity increases with hazard ratio
). Women with a higher PFOA level tend to have a longer TTP, and per unit increment in PFOA, the risk of subfecundity increases with hazard ratio 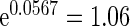 . Unsurprisingly, older mothers and fathers are more likely to have a longer TTP. Women who had endometriosis before pregnancy have a higher risk, hazard ratio
. Unsurprisingly, older mothers and fathers are more likely to have a longer TTP. Women who had endometriosis before pregnancy have a higher risk, hazard ratio 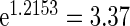 . One advantage of our proposed method is that, given covariates, we can predict the risk probability of TTP
. One advantage of our proposed method is that, given covariates, we can predict the risk probability of TTP 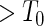 for any TTP time
for any TTP time 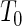 . In contrast, only one risk probability (i.e. only for TTP
. In contrast, only one risk probability (i.e. only for TTP 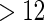 ) in the logistic method.
) in the logistic method.
The analysis results using only the SRS portion of the ODS sample and treating the ODS sample as a SRS (Naive) are given in columns 3 and 2 of Table 5, respectively. Among the three estimation methods compared, the estimators are consistent and our proposed method is the most efficient one. However, the significant impact of PFOA level shows in neither Naive Design nor SRS Design. The proposed estimator is unbiased and more efficient.
Following another standard epidemiologic approach, we used the discrete-time analog of the Cox model to estimate the fecundability odds ratio (FOR). The analyses were adjusted by the same confounders used in Tables 4 and 5. The resulted FOR is 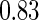 with SE
with SE 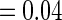 ,
, 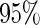 CI
CI 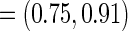 and
and 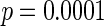 . Note the FOR reflects the fecundability odds ratio for 1 month, which is different from the hazard ratio from the Cox model.
. Note the FOR reflects the fecundability odds ratio for 1 month, which is different from the hazard ratio from the Cox model.
In summary, the proposed method provides an efficient and consistent estimate, utilizes fully the available survival data and takes advantage of the nature of the ODS design. It does not have the inconsistent issue of the existing odds ratio approach used by epidemiologists.
5. Discussion
In this paper, motivated by the need to assess the relationship between the PFASs on women's subfecundability on our study of the MoBa study, we designed a general ODS sampling scheme for survival studies with a failure-time outcome. To reap in the benefit of such a survival ODS design, we developed a new inferential method and provide an EMSELE for the parameters of primary interest. Our proposed ODS method is an improvement over the current odds ratio approach used in epidemiology as well as improvement over the case-cohort and the generalized case-cohort designs. Because we allow the sample selection of cases to depend on the timing of disease endpoints, i.e. by oversampling subjects from the most informative regions, the proposed ODS design for survival data can enhance study efficiency and reduce study cost.
Simulation studies suggest that the small-sample performance of the proposed method approximates the asymptotic properties well. Our proposed estimator is the most efficient one among the four competing estimators: the maximum likelihood estimator based on the Cox's likelihood from a sample random sample of same size as the ODS sample, the estimator under case-cohort design developed by Prentice (1986), and the weighted estimator under generalized case-cohort design developed by Kang and Cai (2009). The efficiency gain shows that our proposed method is a cost-efficient alternative to case-cohort and generalized case-cohort designs.
A few comments on the behavior of the proposed design/estimator and some cautionary points on practical applications of the proposed method are presented. First, we note that the proposed ODS design and our estimator is more efficient than the SRS design when censoring rate is high. This is due to the fact that at high censoring cases, the SRS design will have substantial fewer failures than the ODS design. This suggests that ODS design is particularly useful when censoring is high. Secondly, we caution users that when censoring is extremely high (e.g. at 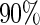 and
and 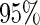 ), our variance estimator based on the asymptotic properties could overestimate the true variance. One would need to either increase the sample size or employ some alternative variance estimator, such as the bootstrap estimator, in the small-sample situations. Thirdly, our estimator from (2.6) is based on assuming censoring is independent of covariates. Biases in effect estimation could result if this is violated (Table 2). A good practice is to check this assumption in real data analysis using the SRS sample. Finally, we estimated
), our variance estimator based on the asymptotic properties could overestimate the true variance. One would need to either increase the sample size or employ some alternative variance estimator, such as the bootstrap estimator, in the small-sample situations. Thirdly, our estimator from (2.6) is based on assuming censoring is independent of covariates. Biases in effect estimation could result if this is violated (Table 2). A good practice is to check this assumption in real data analysis using the SRS sample. Finally, we estimated 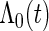 with a simple consistent estimator from the SRS sample. Alternative estimators that use more available data could be used.
with a simple consistent estimator from the SRS sample. Alternative estimators that use more available data could be used.
Application of the proposed ODS method to analyze the MoBa data suggested that women with higher PFOA levels tend to have a longer TTP. On the other hand, the default epidemiologic approach for the odds ratio under different TTP cutpoints yields inconsistent results. Comparing with competing designs, our proposed ODS method provides a feasible design and efficient estimates. Future study includes developing models and estimation procedures appropriate for studies with multiple disease outcomes. In some studies, researchers may need to consider several diseases or several subtypes of disease (Lu and Shih, 2006; Kang and Cai, 2009). For example, in the Busselton Health Study (Cullen, 1972), it was of interest to study the relationship between serum ferritin and coronary heart disease and stroke events.
Supplementary material
Supplementary material is available at http://biostatistics.oxfordjournals.org.
Funding
This research was supported in part by U.S. National Institute of Health grants (R01 ES021900, UL1 RR025747, P01 CA142538), and the Intramural Research Program of the National Institutes of Health, National Institute of Environmental Health Sciences. The Norwegian Mother and Child Cohort Study is supported by the Norwegian Ministry of Health and the Ministry of Education and Research, NIH/NIEHS (N01-ES-75558), NIH/NINDS (UO1 NS 047537-01, UO1 NS 047537-06A1), and the Norwegian Research Council/ FUGE (151918/S10). This research is also funded in part by National Science Foundation of China (11101314 to J.D. and 11171263, 11371299 to Y.L.).
Supplementary Material
Acknowledgements
We are grateful to all the participating families in Norway who take part in this ongoing cohort study. Conflict of Interest: None declared.
References
- Alexander B. H., Olsen G. W., Burris J. M., Mandel J. H., Mandel J. S. Mortality of employees of a perfluorooctanesulphonyl fluoride manufacturing facility. Occupational and Environmental Medicine. 2003;60:722–729. doi: 10.1136/oem.60.10.722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breslow N. E., Wellner J. A. Weighted likelihood for semiparametric models and two-phase stratified samples, with application to cox regression. The Scandinavian Journal of Statistics. 2007;34:86–102. doi: 10.1111/j.1467-9469.2007.00574.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai J., Zeng D. Power calculation for case-cohort studies with nonrare events. Biometrics. 2007;63:1288–1295. doi: 10.1111/j.1541-0420.2007.00838.x. [DOI] [PubMed] [Google Scholar]
- Chatterjee N., Chen Y. H., Breslow N. E. A pseudoscore estimator for regression problems with two-phase sampling. Journal of the American Statistical Association. 2003;98:158–168. [Google Scholar]
- Chen K. Generalized case-cohort sampling. Journal of the Royal Statistical Society, Series B. 2001;63:791–809. [Google Scholar]
- Cornfield J. A method of estimating comparative rates from clinical data. Applications to cancer of lung, breast, and cervix. Journal of National Cancer Institute. 1951;11:1269–1275. [PubMed] [Google Scholar]
- Cox D. R. Regression models and life-tables. Journal of the Royal Statistical Society, Series B. 1972;34:187–220. [Google Scholar]
- Cullen K. J. Mass health examinations in the busselton population, 1966 to 1970. The Medical Journal of Australia. 1972;2:714–718. doi: 10.5694/j.1326-5377.1972.tb103506.x. [DOI] [PubMed] [Google Scholar]
- Fei C. Y., McLaughlin J. K., Lipworth L., Olsen J. Maternal levels of perfluorinated chemicals and subfecundity. Human Reproduction. 2009;24:1200–1205. doi: 10.1093/humrep/den490. [DOI] [PubMed] [Google Scholar]
- Johansen S. An extension of Cox's regression Model. International Statistical Review. 1983;51:165–174. [Google Scholar]
- Johansson N., Fredriksson A., Eriksson P. Neonatal exposure to perfluorooctane sulfonate (PFOS) and perfluorooctanoic acid (PFOA) causes neurobehavioural defects in adult mice. Neurotoxicology. 2008;29:160–169. doi: 10.1016/j.neuro.2007.10.008. [DOI] [PubMed] [Google Scholar]
- Kang S., Cai J. Marginal hazards model for case-cohort studies with multiple disease outcomes. Biometrika. 2009;96:887–901. doi: 10.1093/biomet/asp059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu S., Shih J. H. Case-cohort designs and analysis for clustered failure time data. Biometrics. 2006;62:1138–1148. doi: 10.1111/j.1541-0420.2006.00584.x. [DOI] [PubMed] [Google Scholar]
- Lu W., Tsiatis A. A. Semiparametric transformation models for the case-cohort study. Biometrika. 2006;93:207–214. [Google Scholar]
- Owen A. B. Empirical likelihood for confidence regions. The Annals of Statistics. 1990;18:90–120. [Google Scholar]
- Prentice R. A case-cohort design for epidemiologic cohort studies and disease prevention trials. Biometrika. 1986;73:1–11. [Google Scholar]
- Song R., Zhou H., Kosorok M. R. On semiparametric efficient inference for two-stage outcome dependent sampling with a continuous outcome. Biometrika. 2009;96:221–228. doi: 10.1093/biomet/asn073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun J., Sun L., Flournoya N. Additive hazards model for competing risks analysis of the case-cohort design. Communications in Statistics—Theory and Methods. 2004;33:351–366. [Google Scholar]
- Tsai W. Y. Pseudo-partial likelihood for proportional hazards models with biased-sampling data. Biometrika. 2009;96(3):601–615. doi: 10.1093/biomet/asp026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vardi Y. Nonparametric estimation in the presence of length bias. The Annals of Statistics. 1982;10:616–620. [Google Scholar]
- Vardi Y. Empirical distributions in selection bias models. The Annals of Statistics. 1985;13:178–203. [Google Scholar]
- Weaver M. A., Zhou H. An estimated likelihood method for continuous outcome regression models with outcome-dependent sampling. Journal of The American Statistical Association. 2005;100:459–469. [Google Scholar]
- Weinberg C. R., Wacholder S. Prospective analysis of case-control data under general multiplicative-intercept risk models. Biometrika. 1993;80:461–465. [Google Scholar]
- Whittemore A. S. Multistage sampling designs and estimating equations. Journal of the Royal Statistical Society, Series B. 1997;59:589–602. [Google Scholar]
- Whitworth K. W., Haug L. S., Baird D. D., Becher G., Hoppin J. A., Skjaerven R., Thomsen C., Eggesbo M., Travlos G., Wilson R., Longnecker M. P. Perfluorinated compounds and subfecundity in pregnant women. Epidemiology. 2012;23:257–263. doi: 10.1097/EDE.0b013e31823b5031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou H., Song R., Qin J. Statistical inference for a two-stage outcome dependent sampling design with a continuous outcome. Biometrics. 2011;67:194–202. doi: 10.1111/j.1541-0420.2010.01446.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou H., Weaver M., Qin J., Longnecker M., Wang M. C. A semiparametric empirical likelihood method for data from an outcome dependent sampling scheme with a continuous outcome. Biometrics. 2002;58:413–421. doi: 10.1111/j.0006-341x.2002.00413.x. [DOI] [PubMed] [Google Scholar]
- Zhou H., Wu Y., Liu Y., Cai J. Semiparametric inference for a 2-stage outcome-auxiliary-dependent sampling design with continuous outcome. Biostatistics. 2011;12:521–534. doi: 10.1093/biostatistics/kxq080. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.