Visualizing time-related data in biology, a review

Abstract

Time is of the essence in biology as in so much else. For example, monitoring disease progression or the timing of developmental defects is important for the processes of drug discovery and therapy trials. Furthermore, an understanding of the basic dynamics of biological phenomena that are often strictly time regulated (e.g. circadian rhythms) is needed to make accurate inferences about the evolution of biological processes. Recent advances in technologies have enabled us to measure timing effects more accurately and in more detail. This has driven related advances in visualization and analysis tools that try to effectively exploit this data. Beyond timeline plots, notable attempts at more involved temporal interpretation have been made in recent years, but awareness of the available resources is still limited within the scientific community. Here, we review some advances in biological visualization of time-driven processes and consider how they aid data analysis and interpretation.

INTRODUCTION

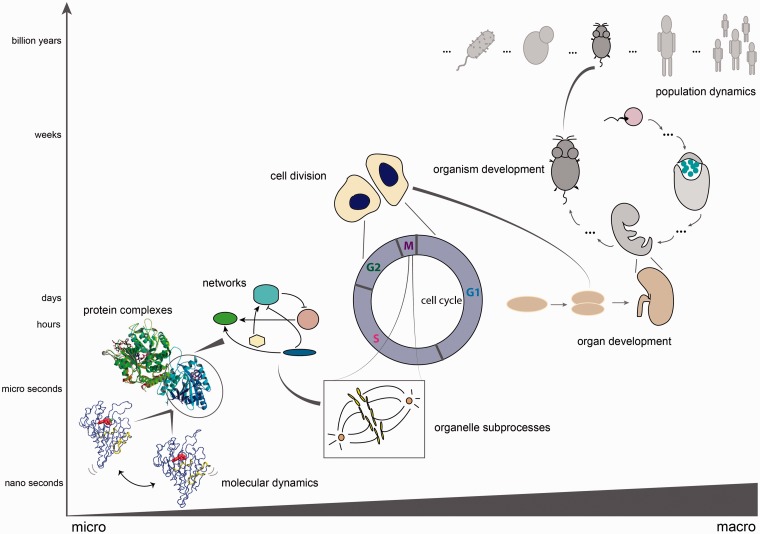
Time, like many other aspects of biology, is fractal in nature [1], when considered at a range of scales spanning, for example, species-level interactions to the cellular and molecular level (Figure 1). All cellular functions and fate decisions are governed by spatiotemporal design principles: circadian rhythms, cell division, development, metabolism, etc. These processes are orchestrated by an intricate network of dynamic interactions, within which individual partners also change considerably in time depending on the environment. Temporal complexity also scales with structural complexity: more complex organisms need increased regulation of various biological processes, hence the emergence of different levels of time-coupled responses.

Figure 1:

Different biological time scales. Timing of processes scales with size: from the long-term evolutionary processes at the population level, to dynamics within a single population, timing during organism and organ development, down to cellular and subcellular processes: cell division as the final point of the cell cycle, which is orchestrated by a large network of proteins interacting to achieve several states (shown: mitotic spindle checkpoint). Within the network of proteins, timing does not only play a role at the level of transient interactions or complex formation (shown: a kinesin complexed to microtubule, PDB code 2P4N), but also at the level of single molecules (shown: dynamics simulations of kinesin motor protein, as obtained from the DSMM database [2]).

Inevitably, the complexity and variation produced by temporal changes introduces a challenge on the system in maintaining robustness [3]. This is reconciled through modularity [4] and synchronization [5]. Modularity is clearly seen in periodic processes like circadian rhythms or the cell cycle. These and other processes are temporally regulated through a precise orchestration of transcriptional events and post-translational modifications. Thus, tracing gene expression changes, mRNA and protein half-lives [6–8] allows the development of useful models for the understanding of biorhythms. This brings us to the latter point: synchronization. We should emphasize here the common tendency to regard protein interactions as static, when in fact time is a limiting factor for them, as they occur at higher or lower degrees of stochasticity. Some interactions, even though theoretically viable, may never occur in vivo because the proteins are not in proximity to each other or because they are asynchronized with respect to some process. This is seen for many transient interactions [9]. The interactions themselves are subject to temporal variation, with weaker interactions having shorter lifetimes [10]. This variation enables fast response to intrinsic or extrinsic perturbation [11]. Different feedback rewiring or variations in kinetic parameters of signalling pathways lead to different modes of spatiotemporal organization, from sustained response, to oscillations, or switch-like responses with two stable steady states [12].

Higher levels of organization, like populations and species, also exhibit temporal variation. Robustness emerges as an evolvable property [13], as systems adapt to stress in changing environmental conditions through mutations and genetic drift [14, 15]. These changes span much longer time scales. The adaptation to perturbation imposes a selection pressure and does not come as a fast response but rather as an evolved phenotypic outcome in a sloppy space [16–18].

Studying the dynamic patterns of biological processes helps identify control points, modules and sources of robustness [5]. Since patterns are visual outcomes, they are best captured through visualization techniques. Hence, building software tools to depict temporal information is critical for improving our knowledge of intrinsic dynamics of cellular components.

Visualization in the biological sciences has played an important role since early times, starting in the 17th century with Robert Hooke’s ‘Micrographia’, which contained detailed drawings of microscopic organisms. This book was one of the first to draw attention to the fascinating world of microbiology, and it was mainly the visualization of previously unseen life forms that managed to attract public interest. Since then, visualization in biology has taken more complex forms and moved from a fully manual (hand-drawn) to a more automated process of representing different biological aspects, with the help of emerging computer technology. Physics principles brought forward the visualization of protein structures [19], biological cycles, fluxes and attractors [20]. With the sequencing of the first complete genomes, awareness rose at the necessity to synthesize huge amounts of data into comprehensible forms, thus leading to a new revolution in data representation [21]. Visualization is nowadays essential to explore the vast informational space uncovered by high-throughput technologies.

Concerning time-related visualization, methods have long been established in other fields, such as geography or geopolitics, where geospatial data are integrated with temporal analysis [22]. In the biological sciences, one of the first and most persistent visual concepts of time, with roots in ancient mythology, was proposed by Charles Darwin in his seminal book ‘On the origin of species’: the tree of life described the relationships between different categories of living forms from an evolutionary perspective. This visual representation is now widely used in phylogenetic studies [23]. Besides this, many representations of time have stemmed from the field of mathematics, like in the case of modelling biochemical reactions, where linear plots are used to study dynamic properties of a system [24]. More powerful graphic tools have expanded the visualization repertoire for temporal changes in biological processes, as we will detail in the next sections.

Although all these efforts have contributed significantly to our understanding of biological phenomena, there are still many challenges to face. Some of the biggest bottlenecks are the heterogeneity of the data and the diversity of systems that can be represented and analysed [25]. Moreover, in the past few years, there has been an increased shift in biology from 2D to 4D-5D (spatiotemporal) network analysis [26]. Adding to the complexity is the issue of the limits on temporal resolution: what time range is sufficient to capture a useful understanding of processes? Efforts have been put into tackling all these aspects and expounding the temporal outlook in biology. Here, we review the traditional ways of representing time visually, as well as some of the more recent techniques used to elucidate the intricacies of the temporal dimension.

VISUAL DEPICTIONS OF TIME IN BIOLOGY

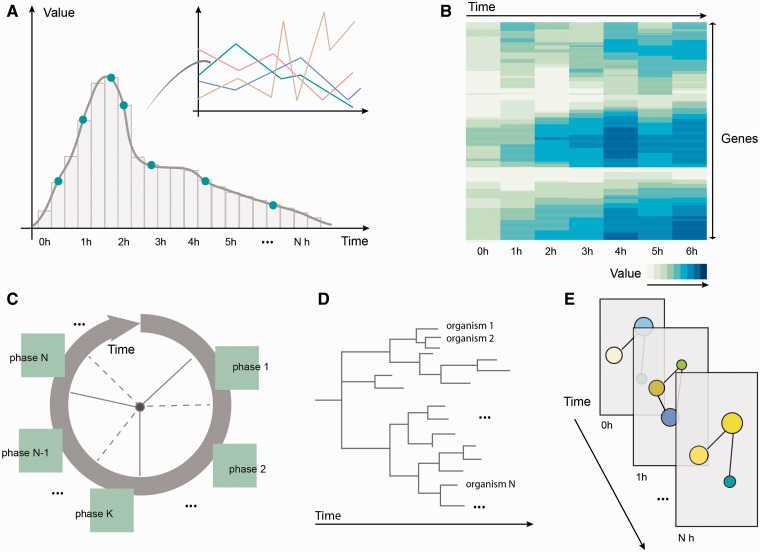
Representations of time vary greatly with the purpose of these representations and the targeted users. However, in the field of biology, one can identify five main approaches to represent time: (i) linear representations, (ii) heat maps, (iii) circular design, (iv) tree-like diagrams and (v) layers, as depicted in Figure 2. While linear representations, like line, bar or parallel coordinate plots, confer a sense of continuity and enable point-by-point tracking of the evolution of a variable (e.g. enzyme concentration changes over time), heat maps serve well at comparing and grouping similar factors, like genes with similar expression profiles [27]. Circular design is suitable for describing recurring processes, like phases of the cell cycle or circadian rhythms, and extends to concepts like limit cycles [28] or spiral waves [29]. Tree diagrams (dendograms) are mostly used in biology in phylogenetic analysis, for evolutionary relationship inference [30]. Layers help distinguish processes or levels of information, in a comparative and integrative manner, e.g. by distributing network components according to their cellular localization [31]. More complex representations, like splines, contour plots, phase space trajectories or bifurcation diagrams [32, 33], build on top of these, many of them inspired from approaches in other fields [34].

Figure 2:

Different representations of time in biology: (A) Linear representations of temporal processes: expression profiles for genes can be displayed one by one or in parallel (using a parallel coordinates representation); (B) Heat maps cluster genes or other entities according to the similarity of their time course profiles; (C) Circular depictions divide recurring processes like the cell cycle into phases that can be subsequently described; (D) Tree diagrams represent phylogenetic relationships, indicating the evolutionary distance between different organisms; (E) Layers enable simultaneous comparison of network states at different time points.

The choice between continuous and discrete representations of time provides both advantages and disadvantages. While for visualization techniques, the discrete representation is usually preferred, animations provide a way to depict continuous changes in the data. There is a trade-off between a temporally flat representation that can often confuse the user and a chronological representation with successive states visualized, where the temporal context might be lost. Flat representations of time often exhibit a high level of data compression into one image and possibly unrealistic co-localization of entities that exist at different time points. In animations, on the other hand, transitions are sometimes hard to observe given the short time span, and sequential time points cannot be compared [35]. The current approaches to visualizing time in biology often aim for a partial reconciliation between the two modes, as described in the following section.

TOOLS FOR REPRESENTING TIME IN BIOLOGY

An excellent review [8] that draws the attention on the necessity of switching from a static to a dynamic view of biological systems details the different algorithms and methods of analysing time in biology. Visualization is always accompanied by statistical analysis, and this spans a broad spectrum of methods by itself. Singular value decomposition (SVD), principal component analysis (PCA) [36], self-organizing maps (SOMs) [37], recurrence quantification analysis (RQA) [38], fast Fourier transform (FFT) [39], wavelet decomposition [40] or time warping algorithms [41] are some of the most widely used tools to study different dynamic aspects. These range from species variation studies like community developments in the gut microbiome [42] to systems processes like cell cycle-imposed oscillations in a single cell or a cell colony [43, 44], organ dynamics like age-dependent heartbeat rhythms [45], genetic network organization derived from expression measurements [46], genome-wide effects of cellular regulators [47] and even macromolecule properties resulting from sequences viewed as time series [48]. While the previously mentioned methods are mostly used to identify periodicities or help synchronize time series data, other approaches exist to explore more general properties of a system, like stability and attractor dynamics, feedback loops, deterministic and stochastic behavior [49]. We will not discuss these in detail, because the scope of this article is the visual rather than the statistical aspect of interpreting time series data.

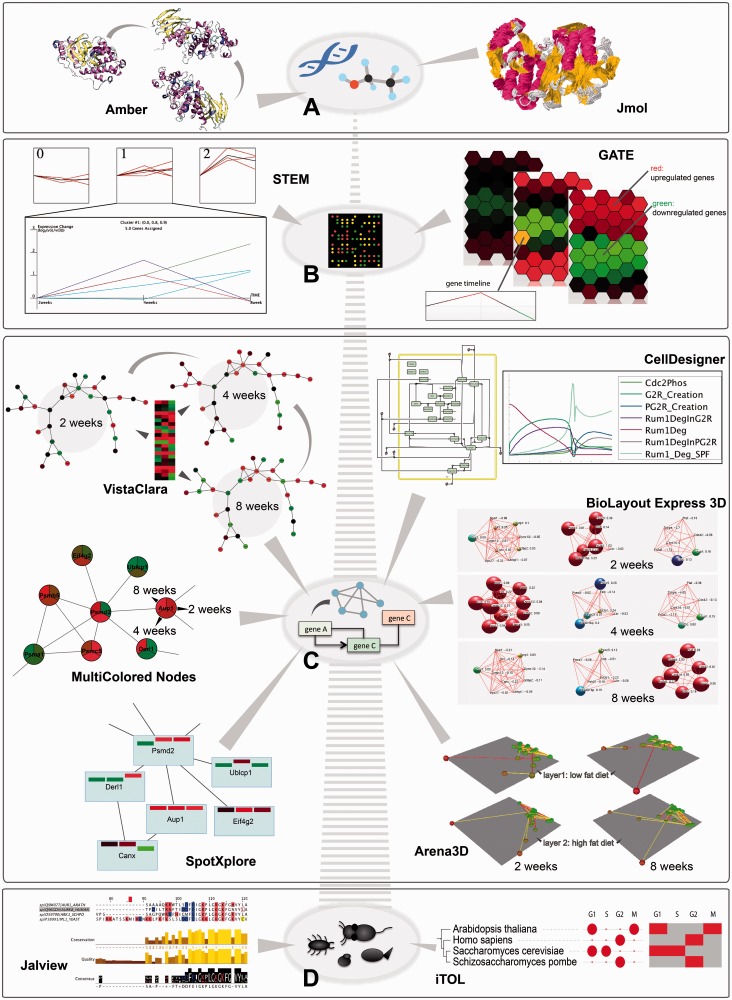
Here, we will focus on some of the most widely used tools that have been specifically designed with the purpose of visually integrating the temporal component. Table 1 in the Supplementary Material summarizes some of the most popular ones, and Figure 3 gives an overview of methods for representing time at different levels of (sub)cellular-, organism- or population-wide organization. The list is by no means exhaustive, but it tries to focus on examples of different approaches to visualization and particularly on those that have as primary purpose the representation of the time component.

Figure 3:

Temporal depictions of biological processes at different scales are shown, along with a selection of tools that perform the task. (A) At the molecular level, simulations of molecular movement can be followed in an animation using Amber or as trajectory traces using Jmol (example shows MAP kinase P38, as taken from MoDEL library [50]); (B) At the gene level, time course expression data reflecting high fat diet effects on small intestine in mouse (dataset GDS3357 from Gene Expression Ominbus [51]) is visualized in clustered timeline plots using STEM or in an adjacent hexagon display using GATE; (C) At the network level, time course changes can be tracked using different Cytoscape plugins, e.g. by animating colour changes in the network with VistaClara [52], drawing pie chart slices with MultiColored Nodes [53], or using bar charts embedded in the network nodes with SpotXplore [54]. Fluxes through pathways can be simulated deterministically or stochastically and illustrated in line plots using CellDesigner. BioLayout Express 3D simulates changes in gene expression in 3D through colour and node size increase or decrease in an animation (connections represent correlations). Arena3D depicts changes at every time point through colour and clustering on separate 3D layers, corresponding to different phenotypes (low and high fat effects) that can be compared (connections represent correlations). The data used for these examples are the same as in (B). (D) At the organismal level, multiple sequence alignment visualizers, like Jalview, and phylogenetic tree builders, like iTOL, depict evolutionary distances between entities of different organisms. The example shows such depictions for aurora kinase B orthologs in four species. In the case of iTOL, additional time course data can be visualized in the form of discs, heat maps or animations (here we show the phases in the cell cycle where this gene has a periodic peak of transcription, as obtained from Cyclebase [55]).

Time at the molecular level

For single proteins, understanding the molecular dynamics and conformation transitions is supported by molecular dynamics simulation software like Amber [56] (Figure 3A, left), Gromacs [57], CHARMM [58], NAMD [59] or Desmond [60]. The trajectories of the molecules can then be visualized using tools like VMD [61], UCSF Chimera [62], Discovery Studio Modeling Environment (developed by Accelrys Software Inc. [63]), Sirius [64], MacroModel [65], Yasara [66] and others. PyMOL [67, 68] and Jmol [69] (see Figure 3A, right) can also be used, even though it is less common. Many of these have been extensively reviewed in [70]. Molecular dynamics simulations involve many calculations of protein state evolution based on molecular entropy and are computationally costly. Hence, only very short time scales (in the range of microseconds) can be simulated and visualized [71]. The bottleneck here is thus not the visualization itself, but the calculations required to determine the amino acid positions at every time point. From the visualization point of view, it is the area that is most developed in biology: the tools offer impressive 3D visual depictions of static and dynamic conditions of proteins, based on advanced graphic libraries, ray tracing and image rendering packages.

Time at the gene level

With the introduction of the microarray technology [72], biology has taken an important step into understanding gene regulation under a variety of conditions and a huge amount of data containing gene expression profiles has been produced [73, 74]. RNA-Seq methods have taken this a step further, and now genome-wide expression levels are readily measurable [75]. Analysing time course gene expression information is rather standardized nowadays, heat maps being the most widely used tool to get a comparative insight into changes in gene expression for a certain dataset. There are, however, notable attempts at more comprehensive visual depictions of gene expression dynamics, as described below.

Tools like STEM [76] (see Figure 3B, left) or XMAS [77] provide linear methods to visualize changes and correlations in gene expression patterns, through profile reordering, functional enrichment analysis or multiple trajectory tracking. Others, like GATE [78] (Figure 3B, right), mimic the microarray set-up in a grid of hexagonal cells positioned to denote similarities in gene expression time course profiles. Clustering, animations and network reconstruction enhance the informational content.

Beyond gene expression measurements, recent technology like ChIP-chip or ChIP-seq also enables us to measure temporal variation in chromatin state, histone marks or transcription factor and polymerase occupancy, like in [79] or [80]. Furthermore, some genome-wide association studies allow estimation of time-dependent genetic effects on dynamic traits like body weight, tumour size or drug response [81]. Quantitative trait loci affecting developmental trajectories can be visualized using software like fGWAS [82, 83], which captures genotypic differences underlying phenotypic curves.

The main limitation in this area is creating a good balance between the level of visualization and the scale of the system, while at the same time integrating more information (functional, network etc.). It is harder to understand temporal changes for larger and more complex gene networks, so better tools are needed especially for upcoming time-resolved genome-wide measurements of expression. Furthermore, better visualization approaches are needed for studying phenotypic consequences of combinatorial genotypic effects in a temporal context.

Time at the network level

When it comes to representing network dynamics, there are two approaches depending on whether one wants to understand the changes in the system biochemically or on a binary level of on–off interactions. The former looks at the biochemical reactions between system components and uses different mathematical algorithms to study the properties of the system. These are afterwards summarized mostly in linear plots illustrating concentration trends and other characteristics. Examples are CellDesigner [84] (as shown in Figure 3C), COPASI [85, 86], Dizzy [87], etc.

The latter approach looks at time-wise changes in the links of the network or in the concentration levels of the different proteins. Tools like Cytoscape [88], VANTED [89], VisANT [90, 91], etc. visualize expression changes directly on the graph representation of the network, using movement, colour changes or embedding of bar charts within the metanode. See Figure 3C for examples that use the VistaClara [52], MultiColored Nodes [53] and SpotXplore [54] plug-ins within Cytoscape. Regarding dynamics of interactions between proteins, the only example of software that deals with this so far (to our knowledge) is TVNViewer [92], which rewires the network connections at every time point.

Other tools, like BioTapestry [93], MODAM [94] or BioLayout Express 3D [95] Figure 3C), go a step further and partially combine the two approaches for tracking fluxes through pathways and integrating multi-omics data. They highlight the different active reactions at every time point within the network.

The main limitation at this level remains the size: the larger the network, the harder it is to capture temporal patterns. Another factor is the temporal resolution, i.e. the availability of information about timings of different processes and their duration. We anticipate that these aspects will be better integrated in the future by using a temporal framework that combines different modelling techniques, from Boolean logic to stochastic methods and beyond, to optimally simulate different parts of the system and then incorporate them into a common platform.

Time at the cellular level

At the cellular level, time-resolved data comes from a wide variety of experiments, ranging from live imaging of cellular processes or developmental stages to fMRI scans of brain activities. Although there is specialized software to deal with this kind of data, it mostly focuses on image-processing techniques for extracting the data rather than computational representations targeted at simulation and analysis [96]. One exception would be STSE, a set of tools that perform spatiotemporal simulations based on microscopy images [97].

Until recently the only attempts at visualization of processes in the context of the whole cell had been done in a qualitative manner only and mostly through animation with educational purposes, like the BioVisions project from Harvard University in collaboration with XVIVO [98] or the Virtual Cell Animation Collection from NSDU [99]. We expect a complete revolution in this area with the arrival of the first whole-cell computational model that is able to simulate a different range of cellular processes and predict phenotypes upon mutations [100]. Although this is not so much a visually driven approach, we envision that it will trigger subsequent developments and collaborations in the visualization area, similar to those started with E-Cell [101], VCell [102] or VisibleCell/Illoura [103] projects, to aid understanding of whole-cell systems.

Time at the organismal level

At the organismal level, visualization of processes in different types of cells and tissues would be desired, but is not achievable with the current technology. Nevertheless, physiological models of tissue anatomy and function are often used to simulate different processes in development, e.g. pancreatic organogenesis [104], or disease, e.g. tumour growth and spreading [105]. Furthermore, gene expression data at different time points for different tissues has been measured and can be visualized using techniques described in the previous sections. One tool that goes further in the direction of simultaneously comparing different cellular states or different tissues is Arena3D [106, 107] (Figure 3C). Tissues and their respective phenotypes can be visualized on different layers in 3D, highlighting the corresponding gene networks for each tissue and enabling comparison and linking between layers at every time point.

However, a better integration of the data in the context of networks, cellular conditions, stress and other factors is desired for a better comparison of tissue-level regulation. We thus expect developments in the area of integrative visualization that would comprise these aspects.

Time at the population level

Mathematical models for population outgrowth and interactions have been developed early on [108], but usually the fluctuations in populations are represented using simple line graphs that indicate the population spread over time. A more visual approach is encountered at the level of tracking the spread of diseases in a population, like in the suggestively titled SPREAD software [109]. It uses a Bayesian framework for inferring and visualizing phylogeographic history and traces the spatial and temporal trajectory of diseases throughout the globe based on given population data. The trajectories are mapped as arcs connecting different locations on a map and the dynamics of connections forming can be visualized in an animation.

Time at evolutionary scales

At the species level, time is implicit when talking about evolution, even if it does not always directly appear on one of the axis of the representation. Naturally all multiple sequence alignment or phylogeny tools (like ClustalX [110], Jalview [111], TreeView [112], MEGA [113], etc.) and other similar software reflect changes or differences between organisms that are the result of the time component [114]. Colouring of conserved amino acids in the former case, and dendograms, in the latter, are the classical depictions for this kind of data. Tools like Circos [115], Vista [116] or MizBee [117] extend this analysis to whole-genome level, enabling tracking of genome evolution by highlighting sequence and structural variation features or comparative genomics by aligning genomes of different organisms and finding conservation relationships. Besides these, there are also tools where changes imposed by time at a smaller scale are incorporated along with the phylogenetic analysis. The Interactive Tree of Life (iTOL) [118] is one example. It is a phylogeny tree display and annotation tool that allows the user to add different types of information about the different organisms or strains visualized, in the form of gradients, heatmaps, domains, pie charts and others (example shown in Figure 3D).

To facilitate whole-genome comparison, a potential solution has been recently proposed in the form of evolutionary barcodes [119]. Inspired from the DNA barcodes [120], these are graphical representations of evolutionary histories at genomic scale, pre-calculated and assigned to each human protein. The visual representation takes the form of a heat map where colours describe multiple statistical parameters assessed for the respective protein in different species.

Statistical tools are often incorporated to estimate population diversity, mutation rates, ancestral sequences, etc. and to test different hypotheses about the forces that shape the evolution of genes, networks, communities and species [121, 122]. However, despite the large repertoire of tools, the ability to perform whole-genome alignments and comparisons for different species in a phylogenetic context is still limited and we expect future endeavours in this direction.

OPEN CHALLENGES IN VISUAL EXPLORATION OF BIOLOGICAL SYSTEMS

When it comes to biological systems in the context of visualization and information integration, most of the tools focus on visualizing microarray data and gene expression information, while the network context is often neglected. More in-depth analysis is largely missing especially in the case of metabolic pathways, even though some software is already available [123]. The fact that temporal variations are present in ranges of several orders of magnitude adds another layer of complexity [8].

The heterogeneity of biological data imposes the challenge of tackling large datasets. Visual representations become more complex with increasing size, noise and number of relationships to be taken into account. Differences in the states of the system, the scale of the system and other properties stand as proof that handling biological data is not as straight forward as it seems and can become quite a daunting task if a global approach is aimed at [124]. Improving methods for data dimensionality reduction or borrowing and extending new ones from computer science or related fields are, in our view, the best approaches for this. As data becomes bigger, it becomes progressively harder to handle not only because of size but also because of the increasing amount of noise. Noise elimination and scaling down to extract essential features of the data is therefore required in visualization: even if we could visualize everything, there would be too much information for efficient processing.

Connecting back to the different levels of biological information discussed previously, we foresee some needed changes in particular areas. At the genomic level, there is a serious absence of visualization methods for changes of the data with time. Humans accumulate more and more mutations throughout their life, so resequencing of genetic information should be coupled with tools able to visualize these changes in time and make insightful inferences and correlations. This would be very useful for tracking or predicting disease evolution.

At the cell level, the ideal would be to develop a simulation tool that is able to visualize changes both at the molecular level and in the cell morphology upon perturbation. This would go along the lines of recent work on whole-cell simulation resources [100], but with greater emphasis on the visual representation as an aid to analysis. Such a system would enable in silico studies of mutation effects in a combinatorial manner, such that complex phenotypes would be predicted at a low cost and in less time, without the need to spend many resources in experimental laboratories. Like all predictive models, this would act as a pre-screening method before in vivo validation of interesting targets.

We foresee a significant impact of time-related visualization in future research, especially in overcoming the information deluge and clarifying developmental processes and disease progression. The strategy will likely move more towards combining the extraction of patterns from ‘big data’ [125] with multidimensionality and concept linking. Using intelligent visualization techniques can alleviate the bottleneck of data deluge from genome-wide studies or ‘omics’ experiments. In the context of systems biology, visualization will serve as an integrative platform for heterogeneous data, to discover individual and system-wide changes. Most importantly, visualization is and will continue to be a critical component in filtering true biological results, leading to better experiment design: outcomes of visualization techniques feed back into the research framework and help guide future analysis methods.

The ultimate goal would be to develop an integrated visualization environment spanning several biological dimensions, from micro to macro. This system should also integrate data from different databases or at least link to them, an aspect that is largely missing in visualization of time series data but would be very useful. This tool should be able to deal with any type of network and provide thorough insight into the spatiotemporal states and evolution of the biological system under analysis, while at the same time allowing for flexibility from the user’s side and easy comprehension and manipulation of the structures. While rather too optimistic for the present, we are confident that this vision is accomplishable in the future, with the aid of sustained developments in computer power and graphic devices.

Shaping all this into a viable user-friendly application would not only save a lot of time and effort by synthesizing hours of searching through different articles and databases in a visually comprehensive analysis at a click of a button, but would also potentially enable the discovery of new relationships between proteins, hypotheses about biological functions, links between processes and patterns in evolution.

SUPPLEMENTARY DATA

Supplementary data are available online at http://bib.oxfordjournals.org/.

Key points.

• Temporal representations in biology differ depending on the scale and are suited to answer specific questions at that scale.

• Linear, heat map, circular, tree-like, layered depictions and combinations of these are used to represent time in biology.

• An extended repertoire of visualization tools has been developed to analyse biological data at every temporal scale, from molecular to organismal and evolutionary level, but a proper integration into one common platform for comprehensive insight is still missing.

• Challenges like heterogeneity, size and noise in the data should be overcome in the future with the help of improved algorithms, simplified graphical depictions and increased computer power.

Biographies

Maria Secrier is a PhD student in Computational Biology at EMBL Heidelberg. Her research focuses on developing visualization tools for the analysis of dynamic patterns and phenotypic outcomes in biological processes.

Reinhard Schneider is the Head of the Bioinformatics Core Facility at LCSB in Luxembourg. His group coordinates the efficient data flow between the experimental- and medical-oriented groups and develops new algorithms for data analysis.

FUNDING

This work was supported by TAMAHUD (LSHC-CT-2007-037472) and FORSYS-ViroQuant; and the EMBL PhD Program to M.S.