Usefulness of Multiparental Populations of Maize (Zea mays L.) for Genome-Based Prediction

Abstract

The efficiency of marker-assisted prediction of phenotypes has been studied intensively for different types of plant breeding populations. However, one remaining question is how to incorporate and counterbalance information from biparental and multiparental populations into model training for genome-wide prediction. To address this question, we evaluated testcross performance of 1652 doubled-haploid maize (Zea mays L.) lines that were genotyped with 56,110 single nucleotide polymorphism markers and phenotyped for five agronomic traits in four to six European environments. The lines are arranged in two diverse half-sib panels representing two major European heterotic germplasm pools. The data set contains 10 related biparental dent families and 11 related biparental flint families generated from crosses of maize lines important for European maize breeding. With this new data set we analyzed genome-based best linear unbiased prediction in different validation schemes and compositions of estimation and test sets. Further, we theoretically and empirically investigated marker linkage phases across multiparental populations. In general, predictive abilities similar to or higher than those within biparental families could be achieved by combining several half-sib families in the estimation set. For the majority of families, 375 half-sib lines in the estimation set were sufficient to reach the same predictive performance of biomass yield as an estimation set of 50 full-sib lines. In contrast, prediction across heterotic pools was not possible for most cases. Our findings are important for experimental design in genome-based prediction as they provide guidelines for the genetic structure and required sample size of data sets used for model training.

IN the context of quantitative trait locus (QTL) mapping, multiparental populations have been suggested to be advantageous over biparental families due to their greater allelic diversity and the possibility of evaluating allelic effects in multiple genetic backgrounds (Muranty 1996; Xu 1998; Verhoeven et al. 2006). Especially if the multiparental population consists of several families connected by common parents, they can provide greater power of QTL detection and better resolution of QTL localization compared to individual families (Rebai and Goffinet 1993; Jannink and Jansen 2001; Blanc et al. 2006; Yu et al. 2008; Bardol et al. 2013; Mackay et al. 2014). In the context of genome-based prediction (Meuwissen et al. 2001), accuracies achieved within large biparental families are assumed to be the maximum that can be obtained with a given sample size (Crossa et al. 2014), because of medium allele frequencies, absence of genetic substructure, and equal linkage phases between markers and functional polymorphisms. However, prediction accuracies of newly generated progenies from different crosses will be poor. This is especially true if the respective germplasm exhibits broad allelic diversity and is unrelated to the biparental family from which single nucleotide polymorphism (SNP) effects were derived. Thus, as for QTL mapping, similar arguments in favor of multiparental populations hold in the context of genome-based prediction.

The accuracy of genome-based prediction based on multiparental populations has been reported for a number of species, traits, and statistical methods (Legarra et al. 2008; Asoro et al. 2011; Zhao et al. 2011; Ornella et al. 2012; Resende et al. 2012; Schulz-Streeck et al. 2012; Peiffer et al. 2013; Albrecht et al. 2014; Scutari et al. 2014). While these results are promising for the implementation of genome-based prediction in breeding, the optimum design of the population to be employed in model training is still an open question and more research needs to be put into this direction (Crossa et al. 2014). Recently, Riedelsheimer et al. (2013) addressed the effect of the composition of the estimation set on prediction of disease and kernel traits with five interconnected biparental maize families. They found a strong decrease in predictive abilities when full-sib lines were replaced by half-sib lines in model training despite the fact that their parental lines originated from the same breeding program and were highly related. Thus, an emerging question from their study was how prediction performance across full- and half-sib lines is affected when parental lines represent a wide spectrum of genetic diversity. It is expected that quantitative genetic parameters relevant for prediction accuracy such as genetic variances and heritabilities vary greatly between families, as has been shown for the U.S. maize nested association mapping (NAM) population (Hung et al. 2012). Thus, the predictive power of individual families in a half-sib design might strongly depend on the magnitude and variation of these parameters.

From theory and empirical studies it is known that the sample size of the population employed in model training (estimation set) has a strong impact on prediction accuracy (Daetwyler et al. 2008; Lorenzana and Bernardo 2009; Zhong et al. 2009; Albrecht et al. 2011; Guo et al. 2012; Combs and Bernardo 2013; Wimmer et al. 2013). Restricting genome-based prediction to within biparental families puts upper limits on sample sizes employed in model training. While sample sizes of biparental families generated in the breeding process rarely exceed 100, the use of multiparental populations permits increasing the size of the estimation set by adding progenies from connected crosses. To our knowledge, the question of how many half-sib lines are required to obtain the same predictive ability as a given sample of full-sib lines has empirically not been addressed in a formal manner. In addition it is not clear if all available progenies from a few crosses or rather a small sample of progenies from many crosses should form the augmented training set.

Since the emergence of genome-based prediction, many studies have focused on developing and testing different statistical methods to obtain maximum prediction accuracy. Genome-based best linear unbiased prediction (GBLUP) (Habier et al. 2007) or the equivalent ridge regression (Hoerl and Kennard 1970) are widely adapted in the context of genome-based prediction. In many experimental studies they yielded higher or equal prediction accuracies compared to variable selection or Bayesian methods (for review, see de los Campos et al. 2013a and Gianola 2013). This was especially the case in plant populations with high linkage disequilibrium (LD) (Heslot et al. 2012; Lehermeier et al. 2013; Wimmer et al. 2013). However, it was postulated that variable selection methods such as LASSO or BayesCπ might be advantageous when predictions are performed across diverse genetic material and/or if large-effect QTL are segregating (Hayes et al. 2009; Zhong et al. 2009; Lorenz et al. 2011). Multiparental populations derived from a set of diverse parental lines should be highly suitable for testing differences between these approaches as they provide sufficient allelic diversity and can be assumed to show segregation for large-effect QTL.

Here, we address the above-mentioned questions by investigating the efficiency of genome-based prediction with two diverse half-sib maize (Zea mays L.) panels representing a broad spectrum of allelic diversity of the European dent and flint heterotic group, respectively. The employed design is similar to the U.S. NAM panel (McMullen et al. 2009) except that all lines are fully adapted to the test environments and heterotic pools were kept separate to allow evaluation of testcrosses. The specific objectives of our study were to (1) compare prediction within biparental families with prediction in multiparental populations for different traits, (2) determine the number of half-sib lines required to obtain predictive abilities achieved within biparental families, (3) show the impact of relatedness on prediction in multiparental populations, (4) assess the ability to predict complex traits across heterotic maize pools, and (5) investigate LD and linkage phases and discuss their impact on prediction in multiparental populations.

Materials and Methods

Plant material

Two large half-sib panels comprising a diverse set of genotypes from each of the two important European heterotic pools dent and flint were generated within the European PLANT-KBBE (Transnational PLant Alliance for Novel Technologies – towards implementing the Knowledge-Based Bio-Economy in Europe) CornFed project (Table 1). The generation and genetic structure of the two panels is described in detail in Bauer et al. (2013). Briefly, in the dent panel, 10 diverse dent founder lines were crossed to a common central dent line, F353. In the flint panel, 11 flint founder lines were crossed to a common central flint line, UH007. Here, we refer to each biparental family by its specific founder line. From each cross, doubled haploid (DH) lines were generated from F1 plants. The resulting biparental families contained on average 79 DH lines, ranging from 17 (EP44) to 133 (F283) DH lines, which were phenotyped and genotyped. Overall, 841 lines from the dent and 811 lines from the flint panel were used for further analyses.

Table 1. Total number of lines (n) and simple matching coefficient (SM) between parental lines for 10 dent (F353 × founder) and 11 flint (UH007 × founder) families. Mean, variance components, and heritabilities (± standard errors) of each family for the traits dry matter yield and dry matter content.

			Dry matter yield (dt/ha)				Dry matter content (%)
Founder	n	SM	$\overline{x}$	${\sigma }_g^2$	${\sigma }_{ge}^2$	$h^2$	$\overline{x}$	${\sigma }_g^2$	${\sigma }_{ge}^2$	$h^2$
B73	64	0.608	193.35	93.82 ± 27.49	112.18 ± 29.01	0.65 ± 0.08	33.08	1.38 ± 0.36	0.96 ± 0.30	0.74 ± 0.06
D06	99	0.642	189.89	78.21 ± 17.17	42.27 ± 19.61	0.68 ± 0.06	35.32	1.68 ± 0.32	0.82 ± 0.24	0.79 ± 0.04
D09	100	0.668	187.44	31.21 ± 11.05	61.90 ± 19.74	0.46 ± 0.10	36.36	1.07 ± 0.25	1.09 ± 0.30	0.65 ± 0.07
EC169	66	0.617	184.18	46.49 ± 18.89	82.22 ± 31.01	0.49 ± 0.12	36.92	2.28 ± 0.53	0.84 ± 0.42	0.79 ± 0.05
F252	96	0.671	178.08	120.75 ± 21.88	40.27 ± 14.49	0.83 ± 0.03	37.99	1.81 ± 0.40	1.95 ± 0.37	0.69 ± 0.06
F618	104	0.645	194.70	20.18 ± 9.96	66.15 ± 20.96	0.33 ± 0.12	33.10	2.25 ± 0.40	1.09 ± 0.26	0.82 ± 0.03
Mo17	53	0.627	184.51	89.04 ± 34.79	194.84 ± 42.90	0.54 ± 0.11	32.30	2.15 ± 0.56	1.38 ± 0.35	0.79 ± 0.05
UH250	94	0.634	187.53	67.37 ± 18.63	73.86 ± 29.00	0.57 ± 0.08	35.82	2.21 ± 0.40	0.45 ± 0.29	0.83 ± 0.04
UH304	81	0.765	192.51	47.71 ± 14.08	39.26 ± 22.62	0.58 ± 0.09	35.30	2.29 ± 0.46	0.72 ± 0.31	0.81 ± 0.04
W117	84	0.625	176.16	76.46 ± 21.51	99.73 ± 27.86	0.62 ± 0.08	35.66	3.10 ± 0.60	0	0.84 ± 0.03

D152	72	0.749	172.39	121.09 ± 25.65	38.94 ± 19.94	0.82 ± 0.04	32.78	1.56 ± 0.36	0.47 ± 0.38	0.75 ± 0.05
EC49A	29	0.656	186.06	57.84 ± 29.06	79.69 ± 48.64	0.58 ± 0.14	30.64	0.99 ± 0.42	1.45 ± 0.54	0.68 ± 0.11
EP44	17	0.615	178.99	121.83 ± 57.48	35.26 ± 52.58	0.78 ± 0.10	29.39	0.99 ± 0.53	0.68 ± 0.66	0.70 ± 0.13
EZ5	26	0.613	187.08	115.06 ± 51.92	128.49 ± 69.36	0.65 ± 0.12	29.32	0.74 ± 0.36	0	0.61 ± 0.12
F03802	129	0.753	186.30	85.19 ± 15.68	59.28 ± 19.82	0.71 ± 0.04	34.47	1.51 ± 0.26	0.88 ± 0.28	0.75 ± 0.04
F2	54	0.723	176.94	123.27 ± 30.78	42.88 ± 26.50	0.81 ± 0.05	32.66	1.36 ± 0.36	0.16 ± 0.39	0.76 ± 0.06
F283	133	0.716	185.16	273.47 ± 38.19	59.09 ± 17.81	0.89 ± 0.02	32.22	3.17 ± 0.45	0.36 ± 0.26	0.88 ± 0.02
F64	64	0.621	187.62	109.11 ± 27.91	97.81 ± 28.29	0.72 ± 0.06	29.23	1.16 ± 0.30	0.73 ± 0.35	0.72 ± 0.06
UH006	94	0.791	179.61	152.21 ± 27.49	55.04 ± 19.60	0.83 ± 0.03	33.49	2.82 ± 0.50	0.24 ± 0.35	0.85 ± 0.03
UH009	98	0.815	185.55	51.53 ± 12.37	30.25 ± 19.19	0.64 ± 0.06	33.09	0.82 ± 0.19	0.31 ± 0.27	0.67 ± 0.06
DK105	95	0.738	188.32	230.48 ± 38.86	53.33 ± 20.53	0.88 ± 0.02	33.45	3.19 ± 0.57	0.92 ± 0.38	0.84 ± 0.03

Mean ($\overline{x}$), genetic variance component (${\sigma }_{\text{g}}^2$), genotype by environment variance component (${\sigma }_{\text{ge}}^2$), and heritability (h²; ±SE).

Field trial design and analysis

The DH lines were evaluated as testcrosses in the year 2011, with the central line from the opposite pool used as tester; i.e., UH007 was the tester for all dent lines and F353 for all flint lines. The dent panel field trials were conducted in four European locations [Mons (France), Einbeck, Wadersloh, Roggenstein (Germany)]. Trials were laid out as augmented p-rep designs according to Williams et al. (2011). At each location, 960 entries consisting of 841 testcrosses of DH lines and parental testcrosses were planted with one-fourth of the entries replicated. Trials were laid out in 120 incomplete blocks consisting of 10 plots each, and hybrid NK Falcone was used as check. Field trials for the flint panel were conducted at six European locations [Ploudaniel (France), Eckartsweier, Einbeck, Roggenstein, Wadersloh (Germany), and La Coruña (Spain)]. The field design also comprised 960 entries, consisting of 811 testcrosses of DH lines and parental testcrosses, at each location. In the flint panel one-third of the entries were replicated in each location. Trials were laid out in 160 incomplete blocks consisting of eight plots each and hybrid A287 was used as check variety. Five phenotypic traits were recorded in both panels, namely biomass dry matter yield (DMY, dt/ha), biomass dry matter content (DMC, %), plant height (PH, cm), days to tasseling (DtTAS, days), and days to silking (DtSILK, days). Phenotypic data are provided in Supporting Information, File S1. Phenotypic data analyses were conducted separately for the dent and flint panels. For DMY and DMC, plots containing <70% of the median number of plants per location were classified as missing data. Outlying observations were consecutively detected and removed on the basis of maximum deviate residuals (test according to Grubbs 1950; $\alpha =0.05$) from a mixed model including genotype, location, genotype × location interaction, replication, and block effects. For each trait <0.9% of plots were discarded in the dent trials and <1.2% in the flint trials. Individual variance components for each family were estimated using the model

$$y_{ijklm}=\mu +{\text{fam}}_l+g{\left({\text{fam}}_l\right)}_i+{\text{loc}}_j+g\cdot \text{loc}{\left({\text{fam}}_l\right)}_{ij}+{\text{rep}}_{k(j)}+{\text{block}}_{m(jk)}+e_{ijklm},$$ (1)

where $y_{ijklm}$ is the plot observation for genotype i of family l at location j in replication k in block m. The model contains an overall mean μ, the random effects ${\text{fam}}_l$, $g{\left({\text{fam}}_l\right)}_i$, ${\text{loc}}_j$, $g\cdot \text{loc}{\left({\text{fam}}_l\right)}_{ij}$, ${\text{rep}}_{k(j)}$, and ${\text{block}}_{m(jk)}$, for the lth family, for genotype i conditional on family l, for the jth location, the genotype × location interaction conditional on family l, for the kth replication nested within locations, and the mth block nested within replications within locations, respectively. Plot specific residuals $e_{ijklm}$ were assumed to be normally distributed with mean zero and family-specific variance: $e_{ijklm}\sim \text{N}(0,{\sigma }_{\left(l\right)}^2).$ For each family l unique genetic $({\sigma }_{\text{g}(l)}^2)$ and genotype × location interaction variance components $({\sigma }_{\text{ge}(l)}^2)$ were modeled. Variance components and their standard errors were obtained by restricted maximum-likelihood estimation using the ASReml-R package (Butler et al. 2009). Trait heritabilities on a line mean basis were estimated within each family l according to standard procedures in plant breeding using Hung et al. (2012)

$$h^2=\frac{{\sigma }_{\text{g}(l)}^2}{{\sigma }_{\text{g}(l)}^2+{\sigma }_{\text{ge}(l)}^2/L+{\sigma }_{(l)}^2/L\cdot R},$$

where ${\sigma }_{\text{g}(l)}^2$ is the genotypic variance, ${\sigma }_{\text{ge}(l)}^2$ is the genotype by environment (G × E) variation, ${\sigma }_{(l)}^2$ is the residual variance within family l, L is the number of locations (L = 4 for dent and 6 for flint), and R is the number of replications (R = 5/4 for dent and 4/3 for flint). Standard errors of heritability estimates were derived from standard errors of corresponding variance components using the delta method (Holland et al. 2003). For calculation of adjusted means for each trait and genotype, model (1) was modified by treating the genotype effect as fixed and excluding family effects.

Analysis of genotypic data, relatedness, and linkage phases

All 1652 DH lines and parental lines of the dent and flint panel were genotyped with the Illumina MaizeSNP50 BeadChip containing 56,110 SNPs (Ganal et al. 2011). Genotypic data were deposited in a previous project (Bauer et al. 2013) at National Center for Biotechnology Information (NCBI) Gene Expression Omnibus as data set GSE50558 (http://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE50558). As we have fully homozygous DH lines, heterozygous calls were treated as missing values. Markers with a call frequency <0.9, a GenTrainScore <0.7, a minor allele frequency (MAF) <0.01, or >10% missing values were discarded. Missing values were imputed as in Lehermeier et al. (2013) based on family information and on flanking markers using the software BEAGLE (Browning and Browning 2009) implemented within the R function codeGeno() from the R package synbreed (Wimmer et al. 2012). In the dent (flint) panel, marker genotypes were coded based on the number of alleles that differed from the central line F353 (UH007) with values 0 or 2. For the joint analyses of the dent and flint data set the same SNP selection scheme was performed, which resulted in 34,116 high-quality polymorphic SNPs. Here, marker genotypes were coded according to the number of copies of the minor allele.

As similarity measure between pairs of lines, the simple matching coefficient, which counts the fraction of shared alleles among lines, was calculated (Sneath and Sokal 1973). To investigate the genotypic relatedness between lines, we performed agglomerative hierarchical clustering on parental lines using pair-group averages from the R package cluster (Maechler et al. 2013). Principal component analysis (PCA) was performed separately on dent and flint DH lines. For the analyses of genotypic relatedness a subset of SNP markers known to generate ascertainment bias (Frascaroli et al. 2013) was excluded.

The similarity of linkage phases across two populations was calculated according to Technow et al. (2012) for SNP pairs polymorphic in both populations under consideration. We calculated the fraction of SNP pairs with equal sign of the linkage disequilibrium $D_{AB}=p_{AB}-p_A{p}_B$ in both populations, where $p_{AB}$ denotes the haplotype frequency of AB, $p_A$ the frequency of allele A at one marker locus, and $p_B$ the frequency of allele B at the other locus. $D_{AB}=0$ was considered as different linkage phase when compared to positive or negative values. As LD was calculated only for pairs of polymorphic SNPs, the number of cases with $D_{AB}=0$ was negligible.

Genome-based prediction model

We performed GBLUP by using the model

$$y=X\beta +Zu+e,$$

where y is an n-dimensional vector of adjusted means obtained from the phenotypic analysis for a given trait. The vector β is c-dimensional and includes fixed population effects (c = 10 for the dent, c = 11 for the flint, and c = 21 for the combined dent and flint data set) and u is an n-dimensional vector of random testcross effects that is assumed to be normally distributed with $u\sim \text{N}(0,U{\sigma }_u^2)$, where U is an $n\times n$ realized kinship matrix calculated on the basis of marker data following Habier et al. (2007) and ${\sigma }_u^2$ is the testcross variance pertaining to the GBLUP model. The n-dimensional vector of residuals e is assumed to be normally distributed with equal variance: $e\sim \text{N}(0,I{\sigma }_e^2)$, where I denotes the $n\times n$ identity matrix and ${\sigma }_e^2$ is the residual variance pertaining to the GBLUP model. The design matrices X $\left(n\times c\right)$ and Z $\left(n\times n\right)$ assign the adjusted means to the fixed and random effects, respectively. In addition to GBLUP, we used the Bayesian model BayesCπ for prediction of genotypic values (Habier et al. 2011). Here, posterior means of marker effects were estimated within R function BGLR (Pérez and de los Campos 2014) using a chain length of 50,000 where the first 10,000 samples were discarded as burn-in.

Validation

We performed different validation schemes to compare prediction within biparental families with prediction across multiparental families and to perform prediction across heterotic pools. To assess predictive abilities within biparental families 10 times replicated fivefold cross-validation with random sampling (10 × 5-fold R-CV) was performed. To assess predictive abilities within biparental families with constant estimation set size, we performed prediction by randomly sampling 50 lines without replacement in the estimation set and the rest of the lines of the same family were used as test set (R-CV). The sampling procedure was randomly repeated 50 times. The predictive ability was calculated as Pearson correlation between observed and estimated testcross values from the test set, averaged over all replications. In all settings where estimation set size was restricted to a minimum of 50 lines, we excluded the three smallest flint families with Spanish origin (EC49A, EP44, EZ5).

Further, we performed leave-one-cross-out cross-validation (LOCO-CV). Here, we predicted testcross values of all individuals of one biparental family based on genotype (GBLUP) or SNP (BayesCπ) effects derived from genotypic and phenotypic information of DH lines of all other families of the same heterotic pool (dent or flint, respectively). Thus, all lines of one family formed the test set and all other lines from the same heterotic pool formed the estimation set. Predictive ability is stated as correlation of predicted and observed testcross values from the test set together with standard errors derived from 1000 Bootstrap samples with replacement (Efron and Tibshirani 1993). Additionally, the sample size of the estimation set in LOCO-CV was varied from 25 to 675 DH lines in increments of 25. Sampling in the estimation set was performed randomly across lines from all families and was repeated 100 times. Here, predictive ability of LOCO-CV is reported as the average over 100 replications. To investigate the influence on prediction within families if half-sib lines are added to the estimation set we performed CV within each biparental family using 50 full-sib lines in the estimation set as described above but additionally included all available half-sib lines in each estimation set. For the prediction across heterotic pools, we predicted testcross values of the dent lines using effects estimated on the basis of flint lines and vice versa. As in LOCO-CV, standard errors of predictive abilities were derived from 1000 Bootstrap samples.

To investigate the impact of relatedness on predictive ability, we performed cross-with-cross prediction (CwC). Here, genotypic values of lines from one family were predicted using each of the other families as estimation sets. To avoid confounding effects due to differences in sample size of the different families, each family was restricted to equal size by randomly sampling 50 lines. Sampling was repeated 100 times and predictive ability is stated as mean predictive ability from those 100 replications. Predictive abilities from CwC prediction within each pool were compared with the simple matching coefficient of the founder lines forming the estimation and the test set using the Mantel test (Mantel 1967). The simple matching coefficient was calculated on the basis of all SNPs and based on SNPs that were polymorphic in the two families under consideration. The Mantel statistic is the correlation of the $c\left(c-1\right)/2$ entries below the diagonal of two symmetric $c\times c$-dimensional matrices. The significance of the correlation is evaluated by permuting columns and rows of the first matrix while keeping the second matrix fix. For this purpose, predictive abilities from all reciprocal estimation and test set pairs were averaged to obtain a symmetric matrix of predictive abilities.

Results

Genetic diversity of multiparental populations

We investigated the marker-based similarity of the parental lines and their progeny within and across the two half-sib panels. Molecular analyses largely confirmed a priori expectations on the diversity of the investigated material. Cluster analysis clearly separated parental lines originating from the dent and the flint pool (shown in Bauer et al. 2013). Within the two heterotic pools, parental lines clustered according to their respective origins and breeding history. Principal component analyses on the DH lines clearly depicted the multiparental family structure in both panels (Figure S1). Within the dent panel the first principal component (7.9% variance explained) separated families descending from the breeding program of the University of Hohenheim (founder lines D06, D09, and UH250) from the remaining dent families. Within the flint panel, the first principal component (7.4% variance explained) separated the families derived from the more recent German founder lines (UH006, UH009) from the families derived from French founder lines (F03802, F283) and from DK105. The second principal component (6.0% variance explained) separated families of Spanish (EC49A, EP44, EZ5) and Argentinian (F64) origin from the other families.

For all pairs of the 1652 DH lines, simple matching and realized kinship coefficients were calculated (Figure S2). On average, the similarity among flint lines was higher than that among dent lines as parental lines were more related with the central line UH007. As expected, realized kinship among full-sib lines (sharing both parents) was higher than among half-sib lines (sharing the central line as parent). High average similarities among half-sib lines were observed in both panels for the material originating from the University of Hohenheim (dent: D06, D09, UH250; flint: D152, UH006, and UH009). DH lines derived from the dent parent UH304 showed a higher similarity with all other dent lines as the founder line UH304 is related with the common dent parent F353, both sharing an Iodent background (Bauer et al. 2013). The genetic similarity of DH lines originating from opposite pools (flint or dent) was low.

Predictive power of multiparental compared to biparental families

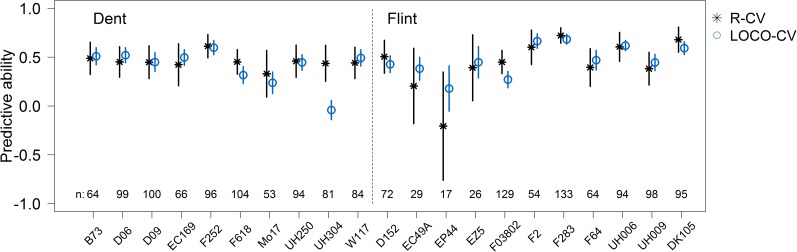
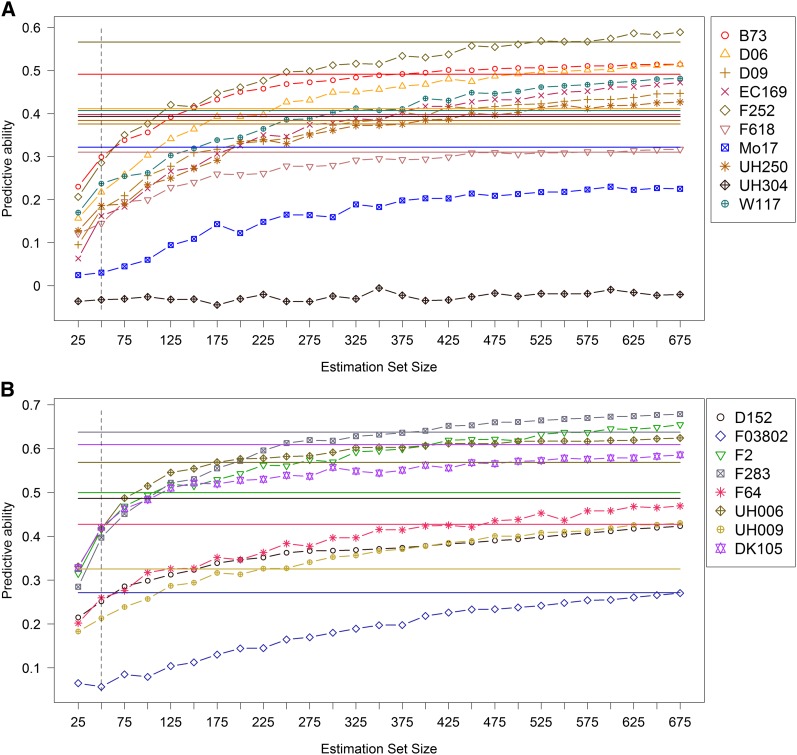
First, we compared prediction of genetic values within biparental families and in multiparental families. Predictive abilities for DMY within the 21 biparental families using 10 × 5-fold R-CV and LOCO-CV are presented in Figure 1. Predictive abilities from GBLUP and BayesCπ differed only marginally for both validation schemes and the different traits (results not shown). Thus, we report only results obtained with GBLUP in the remainder of the article. For DMY, Figure 1 shows that prediction of the genetic values of DH lines from a specific family was similarly efficient when the model was trained on all their half-sib relatives (LOCO-CV) as compared to model training on their full-sib relatives (10 × 5-fold R-CV). To eliminate bias due to different sample sizes in estimation sets of 10 × 5-fold R-CV and LOCO-CV, we refined this analysis. We compared prediction of testcross performance within biparental families to prediction across multiparental families by varying the sample size of the estimation set. Predictive abilities for DMY obtained within dent families using 50 full-sib lines as estimation set ranged from 0.31 to 0.57, with an average value of 0.41 (Figure 2). With equal estimation set size of 50 lines, predictive abilities from multiparental family prediction reached an average value of 0.17. In the flint pool, predictive abilities obtained from prediction within biparental families showed more variation among families compared to the dent panel (${\text{range}}_{\text{flint}}=[0.27,0.64]$), with an average value of 0.48. By using 50 half-sib lines instead of 50 full-sib lines in the estimation set, predictive abilities were on average 0.30 in the flint pool. With increasing estimation set size, predictive abilities from LOCO-CV increased monotonically and reached the predictive ability achieved within biparental families for almost all families. An exception was family UH304 in the dent pool. Genetic values of lines derived from UH304 could not be predicted with the other dent lines, and predictive abilities stayed slightly below zero for all estimation set sizes, whereas its within-family predictive ability was about 0.39. For the majority of families, 375 half-sib lines in the estimation set were sufficient to reach the prediction performance of 50 full-sib lines for DMY. For two dent (Mo17, UH304) and two flint families (D152, DK105) the predictive power of full-sib lines could not be reached by half-sib lines with the available number of 675 lines. However, except for UH304, predictive abilities still increased with increasing estimation set size. Less than 200 half-sib lines were enough to reach the prediction performance of 50 full-sib lines for the flint families F2 and UH006.

Figure 1.

Mean predictive ability obtained with GBLUP for dry matter yield from 10 × 5-fold random cross-validation (R-CV) within biparental families and from leave-one-cross-out cross-validation (LOCO-CV) for dent and for flint families. Vertical lines indicate the standard deviations of the 50 CV folds (R-CV) and Bootstrap standard errors (LOCO-CV), respectively, and n is the number of lines per family.

Figure 2.

Mean predictive ability of dry matter yield (DMY) from leave-one-cross-out cross-validation (LOCO-CV) for increasing estimation set size. Mean predictive ability from prediction within biparental families (R-CV) is shown by different colored horizontal lines. (A) Dent. (B) Flint. The dashed vertical lines label predictive abilities at an estimation set size of 50.

For DMC, the results of prediction within biparental families and LOCO-CV are illustrated in Figure S3. Here, predictive abilities from prediction within biparental families were on average higher than those for DMY with a mean predictive ability of 0.58 for dent families and 0.52 for flint families. When 50 half-sib lines were used as estimation set instead of 50 full-sib lines, predictive ability decreased to an average value of 0.22 for dent families and 0.25 for flint families. For DMC, predictive abilities from LOCO-CV increased for all families with increasing estimation set size, but the high predictive power of full-sib lines could not be reached with 675 half-sib lines for most families. On average, LOCO-CV with estimation set size of 675 yielded predictive abilities of 0.45 for dent families and 0.47 for flint families.

For PH and flowering time (DtTAS, DtSILK), the comparison of predictive abilities within biparental families and from LOCO-CV is shown in Figure S4, Figure S5, and Figure S6. On average, these three traits showed predictive abilities higher than those of DMY and DMC, and the predictive ability from LOCO-CV increased monotonically with sample size. Further, we observed a pattern similar to that of DMY. For the majority of families, an estimation set consisting of 675 half-sib lines reached the same predictive performance as 50 full-sib lines.

For all five traits, we calculated predictive abilities on the basis of estimation sets comprising a combination of 50 full-sib and all available half-sib relatives of the lines in the test set. Compared to prediction within biparental families, predictive abilities increased for most families and traits (Figure S7). On average over all traits and the 18 families with n > 50 there was a substantial increase in mean predictive ability from 0.54 to 0.63 if in addition to full-sib relatives half-sib families were included in the estimation set.

One advantage of prediction within biparental families is that linkage phases between marker and QTL are identical for all DH lines. To investigate the situation in LOCO-CV, we compared linkage phases between DH lines from a given family (test set in LOCO-CV) with DH lines from all other families of the same heterotic group (estimation set in LOCO-CV). For all dent (flint) families the fraction of equal linkage phases with all other dent (flint) families was >0.95 (0.94) for neighboring SNP pairs (distance Δ<0.05 Mb) and did not drop <0.80 (0.78) with increasing distance (Figure S8). The fraction of equal linkage phases among estimation and test set, measured as area under the respective curve of Figure S8, was positively correlated with predictive ability from LOCO-CV (full sample size) averaged over all five traits ($r_{\text{dent}}=0.48$, $r_{\text{flint}}=0.53$); however, correlations were not significant, most likely due to a lack of statistical power.

Relationship between quantitative genetic parameters and predictive ability

The diversity of the parental lines was also reflected in significant mean differences and differences in genetic variance and trait heritability between families within the two half-sib panels. Results for DMY and DMC are shown in Table 1, for the other traits in Table S1, Table S2, and Table S3. The genetic variance of a specific family or trait could not be predicted from the simple matching coefficient of the respective parental line with the central line (Table 1 and Figure S9).

The genetic and genotype × environment interaction variance as well as family-specific trait heritabilities varied substantially among families for all five traits. We investigated the influence of the family-specific trait heritability on predictive abilities within biparental families for DMY. High and significant $(P<0.01)$ correlations were observed for both half-sib panels ($r_{\text{dent}}=0.86,$$r_{\text{flint}}=0.93$). For all other traits, correlations were >0.47 for dent families and >0.70 for flint families. However, correlations were not significant for DMC and the flowering traits, except for DtTAS within flint families. Additionally we calculated prediction accuracy as approximation of the correlation of predicted values with true genetic values by dividing predictive abilities with the square root of the heritability within the family of the respective test set (Dekkers 2007). As expected, the correlation between family-specific heritability and accuracy generally decreased compared to the correlation with predictive ability due to a high negative autocorrelation between the two parameters. For dent families, correlations were no longer significant. For flint families significant $(P<0.01)$ correlations persisted for DMY, PH, and DtTAS ($r_{\text{DMY}}=0.89$, $r_{\text{PH}}=0.92$, $r_{\text{DtTAS}}=0.90$).

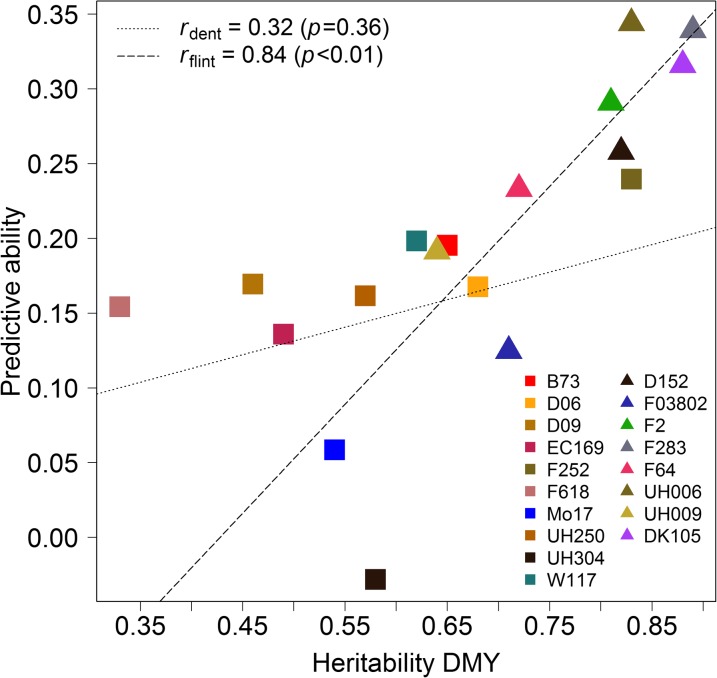
We also investigated if the magnitude of the family-specific trait heritability had an impact on the ability of this family to predict genetic values of DH lines of a different family (CwC). We averaged predictive abilities from CwC prediction obtained with a given family and correlated it with its respective trait heritability. Figure 3 shows the results for DMY for both half-sib panels. For flint families the correlation was high with 0.84 $(P<0.01)$. A nonsignificant correlation of 0.32 was observed for dent families. For all other traits correlations were positive, for dent families between 0.13 and 0.74 and for flint families between 0.17 and 0.82 (Figure S10). However, correlations were significant $(P<0.05)$ only for DtSILK in both panels and for DMC in the flint panel. Here, correlations changed only marginally when prediction accuracies instead of predictive abilities were considered.

Figure 3.

Predictive ability from cross-with-cross prediction (CwC) for dry matter yield (DMY) averaged over all combinations involving the same full-sib family in the estimation set compared to the heritability of this family. Colors indicate the founder line of the family in the estimation set.

Impact of relatedness between parental lines on predictive ability

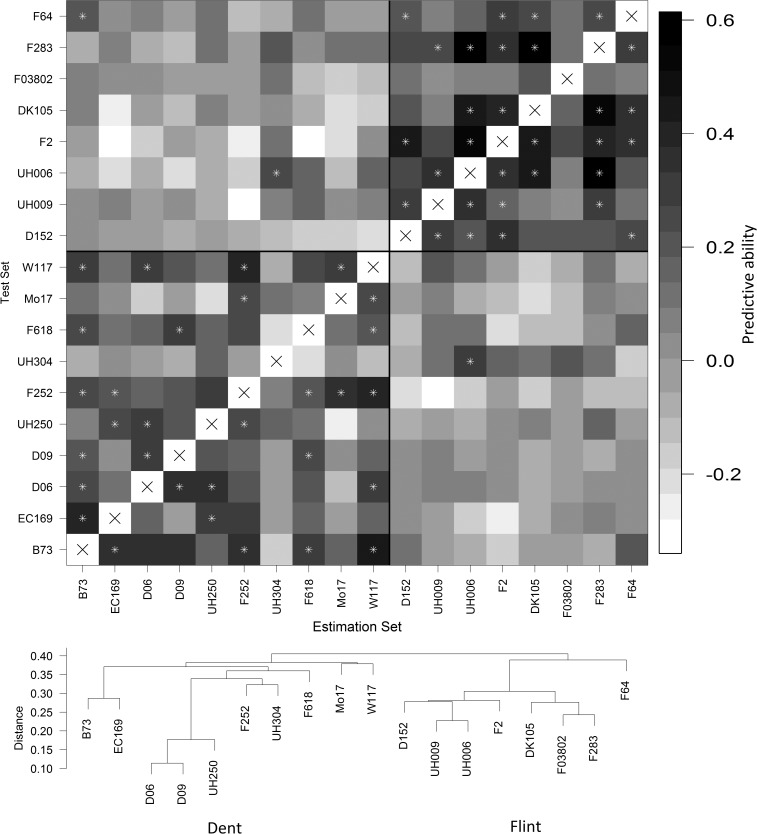
The impact of the genetic similarity between parental lines of half-sib families on their mutual predictive ability was inferred from their respective CwC predictions. Figure 4 shows the heatmap of predictive abilities for DMY from CwC prediction, with families ordered on the basis of the dendrogram of parental lines. Predictive abilities varied strongly (−0.34–0.61) and were generally higher for highly related families (parental lines close to each other in the dendrogram). We compared predictive abilities from CwC prediction within each pool with the simple matching coefficient between pairs of founder lines. Correlations of predictive abilities of DMY with marker-based genetic similarity of founder lines were weak and nonsignificant (P > 0.05) in both panels when all SNPs were included in the analysis. When the similarity between founder lines was calculated on the basis of SNP markers segregating in either or both of the two families of the CwC prediction, the correlation between predictive ability and founder line similarity increased substantially in both panels $\left(r_{\text{dent}}=0.39,r_{\text{flint}}=0.47\right)$ but correlations in the dent panel were mainly driven by the high simple matching coefficient of the related parental lines D06, D09, and UH250 (Figure S11). A similar relationship between genetic similarity and predictive ability was observed for all other traits (data not shown).

Figure 4.

Heatmap of predictive ability of dry matter yield from cross-with-cross prediction (CwC). Families are ordered by the dendrogram of founder lines. Asterisks indicate predictive abilities >2 standard deviations derived from 100 replicated samplings.

Prediction across maize heterotic pools

As differences in linkage phases between markers and QTL are known to affect predictive ability, we compared linkage phases of SNP pairs for dent and flint DH lines (Figure S12). Among neighboring SNP pairs a fraction up to 81% showed equal linkage phases across both pools. However, for SNPs further apart the fraction of equal linkage phases dropped rapidly <0.6 for a distance >0.25 Mb and was close to 0.5 for a distance of 1 Mb. When comparing linkage phases of each dent with all flint families individually for 5 – 10 Mb distant marker pairs, the fraction of equal linkage phases varied from 0.49 to 0.63 (Figure S13).

Predictive abilities across pools, defined as correlations between observed and predicted testcross values of dent lines (flint lines) when flint lines (dent lines) were in the estimation set, are reported in Table 2 with Bootstrap standard errors obtained from 1000 random samples. Generally, prediction across pools was not possible. Only for the flowering traits predictive abilities were slightly higher than zero for both comparisons. We evaluated correlations between observed and predicted genotypic values from across pool prediction for each family individually (Table S4). We observed that for DMY, lines from family UH304 could be better predicted with families from the opposite pool than with dent families and showed quite high across pool predictive abilities over all traits (0.18–0.39). For most other families, predictive abilities across pools were close to zero or even negative.

Table 2. Predictive abilities (± Bootstrap standard error from 1000 Bootstrap samples) for the five traits dry matter yield (DMY), dry matter content (DMC), plant height (PH), days to tasseling (DtTAS), and days to silking (DtSILK) when dent lines are in the estimation set (ES) and flint lines are in the test set (TS), and vice versa.

ES/TS	DMY	DMC	PH	DtTAS	DtSILK
Dent/flint	−0.072 ± 0.030	0.136 ± 0.034	0.197 ± 0.036	0.098 ± 0.034	0.186 ± 0.037
Flint/dent	0.010 ± 0.033	−0.119 ± 0.036	−0.134 ± 0.036	0.194 ± 0.034	0.075 ± 0.043

Discussion

We analyzed the prediction of testcross performance in a large maize data set consisting of 21 biparental families from two distinct maize pools, dent and flint, arranged in two half-sib panels. This comprehensive new data set allowed us to address important questions relevant for genome-based prediction of testcross performance for highly relevant agronomic traits in multiparental populations. We investigated the impact of linkage phases, quantitative genetic parameters, and relatedness on the optimal design of estimation sets for multiparental families and across heterotic pools.

Overall, observed levels of predictive abilities within heterotic pools were in a medium range for all five traits. For complex traits such as biomass yield, predictive abilities within pools ranging from 0.4 to 0.6 were satisfactory, indicating that for most families the sample size was sufficiently large to obtain meaningful results. Similar predictive abilities within biparental maize families were observed for kernel and resistance traits in Riedelsheimer et al. (2013). Crossa et al. (2014) also reported for grain yield predictive abilities of 0.4, when prediction was performed within biparental maize populations.

LD structure and relatedness within biparental and multiparental families

We investigated LD and linkage phases for our set of multiple biparental families, because the consistency of marker-QTL linkage phases between estimation set and selection candidates is a crucial assumption for efficient genome-based prediction (Goddard and Hayes 2007; De Roos et al. 2009; Hayes et al. 2009). In biparental and multiparental populations, different factors contribute to the creation of LD. Within a single biparental DH family, population structure is absent and LD is purely generated by linkage. For DH lines derived from the same cross of two homozygous parents the LD $D_{AB}$ between two polymorphic loci can be calculated on the basis of the recombination frequency r as $\pm 0.25(1-2r)$ with the sign depending on the linkage phase of the parents (same linkage phase of both parental gametes returns a positive value). Thus, $D_{AB}$ can take values 0.25 or −0.25 if no recombination takes place $(r=0)$. If at least one locus is monomorphic or if recombination frequency is at its maximum value of 0.5, $D_{AB}=0$. Thus, two biparental families with one common parent (half-sib lines) are expected to have equal linkage phases because only gametes with the same linkage phase will show polymorphism with the common parent at both loci. In our data this was seen in the comparison of linkage phases between two families from the same heterotic pool, where as expected all SNP pairs had equal linkage phases (results not shown).

If two biparental families are combined, the arising LD is calculated as the weighted mean of the LD within each family plus the LD that arises due to admixture because of differences in allele frequencies (Nei and Li 1973),

$$D_{AB}={\pi }_1{D}_{A{B}_1}+{\pi }_2{D}_{A{B}_2}+{\pi }_1{\pi }_2(p_{A_1}-p_{A_2})(p_{B_1}-p_{B_2}),$$

where ${\pi }_1$ (${\pi }_2$) is the frequency of family 1 (2) in the admixed population, $D_{A{B}_1}$ ($D_{A{B}_2}$) is the value of LD in family 1 (2), and $p_{A_1}$ ($p_{A_2}$) and $p_{B_1}$ ($p_{B_2}$) are the frequencies of alleles A and B in family 1 (2), respectively.

According to this, if two half-sib families are combined, the sign of $D_{AB}$ can change only compared to a third half-sib family if allele frequencies differ between the two families because $D_{A{B}_1}$ and $D_{A{B}_2}$ have equal sign. Allele frequencies within biparental families are expected to be 0.5 for segregating loci, but main differences emerge if one family segregates whereas the other family does not segregate for specific loci. If multiple families (say K families) are combined, as in the estimation set of LOCO-CV in our study, with frequencies ${\pi }_k$ $(k=1,\dots ,K;$ ${\displaystyle {\sum }_{k=1}^K{\pi }_k}=1)$, the above formula for the LD in the combined population can be extended according to Charcosset and Essioux (1994) to

$$D_{AB}={\displaystyle \sum _{k=1}^K{\pi }_k}{D}_{A{B}_k}+{\displaystyle \sum _{k=1}^K{\pi }_k}\left(p_{A_k}-{\displaystyle \sum _{k=1}^K{\pi }_k}{p}_{A_k}\right)\left(p_{B_k}-{\displaystyle \sum _{k=1}^K{\pi }_k}{p}_{B_k}\right).$$

Here, ${\displaystyle \sum {\pi }_k{p}_{A_k}}$ and ${\displaystyle \sum {\pi }_k{p}_{B_k}}$ are the allele frequencies $p_A$ and $p_B$ in the combined population. If A and B denote the alleles at locus 1 and locus 2 of the common parent of K half-sib families, all families have LD value of $D_{A{B}_k}\ge 0$ (k = 1, …, K) and the allele frequencies $p_A$ and $p_B$ are expected to be >0.5. Thus, for loci in linkage equilibrium within every family $(D_{A{B}_k}=0,$ for all k) or with low LD, $D_{AB}$ can become negative if at least one family does not segregate for one locus $(p_{A_k}=1$ and $p_{B_k}=0.5,$ or vice versa). This leads to differences in allele frequencies for the different families and consequently to creation of negative LD in a combination of multiple half-sib families due to admixture. However, if there is strong LD within families, the probability that linkage phases change from one full-sib family compared to a combination of connected full-sib families is low. By investigating the linkage phases of each dent (flint) family compared to the combination of all other dent (flint) families, we observed that the concordance of linkage phases varied for individual families but was in general very high for SNP pairs <5 Mb apart (>0.8; Figure S8). This variation of linkage phases is related to the genetic similarity of a founder line with all other founder lines. The average simple matching coefficient of one dent (flint) founder line with the other dent (flint) founder lines was highly correlated with the respective area under the curve of Figure S8 $\left(r_{\text{dent}}=0.96,r_{\text{flint}}=0.96\right)$ reflecting the relationship between the variation in linkage phases and SNP allele frequencies in the admixed estimation sets. As expected from the high correlation of the mean simple matching coefficient between founder lines and the fraction of equal linkage phases, both factors were similarly associated with predictive abilities from LOCO-CV.

The impact of relatedness of the founder lines contributing to estimation and test set was further investigated using results from CwC prediction within both half-sib panels. Here, as shown by theory, linkage phases are identical between estimation and test set. As a general trend we found that high relatedness tended to result in high prediction performance and low relatedness to yield low prediction performance. However, association between relatedness and predictive ability was generally quite weak. This confirms results from Daetwyler et al. (2013) who found associations between relatedness and accuracy at the “macro level” but not at the “micro level.” Interestingly, we observed in the CwC procedure that prediction was higher than expected across families derived from lines originating from the same breeding program, although lines belonged to distant genetic pools and despite only little relatedness could be observed with marker data. This could be due to similar selection strategies and adaptation to similar environmental conditions within one breeding program. Therefore, there might be other factors that affect prediction performance, which cannot be explained or captured by SNP markers alone.

Prediction across multiparental families compared to within biparental families

Due to the advantages of high LD and absence of population structure, Crossa et al. (2014) considered accuracies from prediction within biparental families as the maximum obtainable. On the other hand, maximum allelic diversity is sampled on diversity panels as described for maize by Rincent et al. (2012) and Riedelsheimer et al. (2012). Multiparental populations combine the advantages of both approaches as (i) the superiority of marker-based over pedigree-based prediction capitalizes on capturing the Mendelian sampling term within families, and (ii) by combining several biparental families in the estimation set, the chance that there is segregation for QTL that are relevant for the family in the test set is higher.

Our results showed that for a given family, similar predictive abilities could be obtained by combining several half-sib families in the estimation set as compared to predicting within this family, but only with an increase in estimation set size. When testcross performance of a family was predicted with all available half-sib lines (LOCO-CV), predictive abilities over all traits and families were on average 0.50, whereas with full-sib lines in the estimation set (R-CV) predictive abilities were 0.54. This prediction performance could be further increased to an average value of 0.63 by adding all additional available half-sib families to the estimation set consisting of 50 full-sib lines. One possible reason why the prediction with multiple half-sib families worked equally well with a sufficient estimation set size is that the probability of changing linkage phases between estimation and test set is low if several half-sib families are combined into one estimation set. For practical applications it is appealing that our results show that new crosses can be predicted with high accuracy if multiple half-sib families are used in the estimation set as long as they share one common parent, and thus linkage phases between markers and QTL are largely consistent. Predictive abilities did not significantly change if four, six, or nine half-sib families constituted the estimation set of size n = 200 (data not shown). Including additional lines from the opposite pool (i.e., unrelated families with different linkage phases) to the estimation set of LOCO-CV had no impact on predictive abilities in our study (results not shown). This might be surprising as one might expect that including unrelated families to the estimation set should lead to a decrease of prediction performance as different linkage phases between markers and QTL might exist that in turn lead to wrongly estimated marker effects (Riedelsheimer et al. 2013). However, as the relationship between dent and flint lines observed by markers is close to zero, as seen on the heatmap of the realized kinship, the GBLUP model does not borrow information from lines of the other pool for prediction of lines from the same pool. Accordingly, it was also stated by de los Campos et al. (2013b) that data from unrelated individuals contribute little to prediction performance.

In the dent panel, the prediction performance of LOCO-CV relative to R-CV differed for the investigated traits. For DMY, predictive abilities obtained with R-CV were ∼0.4 and the same prediction performance could be reached with half-sib lines in LOCO-CV. For DMC however, predictive abilities within families were much higher (0.48–0.77) and could generally not be reached with the full set of half-sib lines in LOCO-CV. The substantially decreased prediction performance of LOCO-CV compared to prediction within families for DMC might indicate that there are specific genetic factors contributing to variation in DMC within each biparental family.

In our data, an outlier was found with dent family UH304 for the trait DMY, but not for the other traits. Lines of this family could not be predicted on the basis of other dent families for DMY in the LOCO-CV scenario. As all dent families are equally connected through one common parent, no relevant differences in linkage phases were observed between UH304 and the other dent families. Thus, differences in linkage phases as it has been suggested in other outlying cases of low prediction performance (Riedelsheimer et al. 2013; Würschum et al. 2013) cannot be a reason for the poor prediction performance here. UH304 was the only Iodent founder line within the dent pool and thus less related to the other founder lines. Additionally, UH304 is a more recently developed line compared to the other founder lines and may have experienced different selection pressure, especially for DMY. DH lines of this family had a higher genetic similarity among each other compared to the other dent families, as the two parental lines UH304 and F353 have both an Iodent background and showed high relatedness. However, despite the low genotypic variation observed from marker data, family UH304 showed an intermediate variation of phenotypic values, which may have contributed to the low predictive ability for this family.

Prediction across maize heterotic pools

One of the most extreme settings in maize is the prediction across heterotic pools that are used for hybrid production; in Central Europe these are mainly dent and flint. Generally, the prediction across the two maize pools failed in our study with predictive abilities close to zero. This can be readily explained by the missing relatedness and inconsistent linkage phases between the pools (Figure S12 and Figure S13). Recently, Technow et al. (2013) investigated predictive abilities across dent and flint lines for line per se performance of the trait Northern corn leaf blight resistance. They obtained slightly higher predictive abilities than those observed in our study, with a predictive ability up to 0.25 for the prediction of line per se performance across flint and dent heterotic pools. Their findings are in line with our observation of slightly increased prediction performance across pools for flowering traits. In breeding, selection of lines is mainly based on their testcross performance for yield and heterosis is maximized if opposite alleles are fixed in each pool. Thus, dent and flint lines are assumed to differ mainly at QTL affecting yield related traits. A companion study on QTL mapping using the same data detected <15% common QTL for both pools across the five traits and no overlapping QTL in dent and flint for DMY, indicating that selection favored different alleles in the two pools (H. Giraud, C. Lehermeier, E. Bauer, M. Falque, V. Segura, C. Bauland, C. Camisan, L. Campo, N. Meyer, N. Ranc, W. Schipprack, P. Flament, A. E. Melchinger, M. Menz, J. Moreno-González, M. Ouzunova, A. Charcosset, C.-C. Schön, L. Moreau, unpublished results).

To date, predicting completely distinct genetic material is not possible. Further research would be necessary to develop new models adapted to such prediction scenarios. It has been assumed that Bayesian and variable selection models rely more on information from LD whereas GBLUP mainly uses information from relatedness (Habier et al. 2007). Thus, it was assumed in the literature that sparse models can be used in a broader sense and are superior to GBLUP for across family prediction or prediction across generations (Meuwissen 2009; Daetwyler et al. 2013). Generally, variable selection methods did not improve prediction performance across pools in our data and results from BayesCπ were highly similar compared to results from GBLUP (results not shown).

Impact of quantitative genetic parameters on prediction performance

We observed a strong association between family-specific heritability and predictive abilities obtained with R-CV within biparental families. Here, heritability is equal for estimation and test set and higher prediction performance comes from a higher signal-to-noise ratio within both the estimation and the test set. To account for the signal-to-noise ratio within the phenotypic values in the test set, a common approach is to calculate prediction accuracies by dividing the predictive ability by the square root of the heritability within the test set (Dekkers 2007; Daetwyler et al. 2013). However, this introduces a high negative autocorrelation between family-specific heritability and accuracy, which needs to be taken into account when interpreting results. In within-family prediction of the flint pool, the significant association between family-specific trait heritabilities and prediction performance persisted when based on prediction accuracies, thus indicating a significant effect of the trait heritability of the estimation set on prediction performance. This was not the case in the dent families, which were evaluated in fewer locations and had a much larger range of family-specific heritabilities. However, for both half-sib panels we also observed a positive correlation of predictive ability (and accuracy) with family-specific trait heritabilities in the estimation set of CwC, which confirms the desirability to use estimation sets with high heritability and high genetic variance (Guo et al. 2014). However, it was not possible to predict the genetic variance of the progenies of a specific cross from the molecular similarity of the respective founder and the central line. This is in accordance with observations of Hung et al. (2012) based on the U.S. NAM population and numerous other studies investigating the relationship between genetic similarity and variance in various crops (Helms et al. 1997; Burkhamer et al. 1998; Melchinger et al. 1998; Gumber et al. 1999). Thus, the appropriate choice of parental lines for new crosses yielding large genetic variance and an efficient estimation set for prediction remains a challenge.

Conclusions

We showed that if several half-sib families are combined, linkage phases between markers and QTL can change only slightly and thus, half-sib lines are beside full-sib lines an appropriate basis for the construction of an estimation set. Our findings have an important impact on the experimental design of estimation sets used for genome-based prediction in breeding programs for crops. Instead of relying on prediction within families, we can construct larger estimation sets by including half-sib lines. With only a few hundred half-sib lines, reasonable predictive abilities could be obtained for prediction of testcross performance in maize—an order of magnitude that is available in commercial breeding programs. Additionally, adding half-sib lines to an estimation set consisting of full-sib lines could further increase prediction performance. It was shown that without relatedness the prediction of complex traits across distinct heterotic groups is not possible. In cross-with-cross prediction, no strong linear association between relatedness of founder lines and predictive ability could be observed. Our results indicated that prediction performance is higher among lines that originate from the same breeding program, even if no relatedness could be observed on the basis of marker data.