Skip to main content
PMC home page
Genetics logoLink to Genetics
. 2014 Jul 17;198(1):409–421. doi: 10.1534/genetics.114.167155

Insights into the Effects of Long-Term Artificial Selection on Seed Size in Maize

Candice N Hirsch *, Sherry A Flint-Garcia †,‡, Timothy M Beissinger §,**, Steven R Eichten ††, Shweta Deshpande ‡‡, Kerrie Barry ‡‡, Michael D McMullen †,‡, James B Holland †,§§, Edward S Buckler †,***,†††, Nathan Springer ††, C Robin Buell ‡‡‡,§§§, Natalia de Leon §,****, Shawn M Kaeppler §,****,1
PMCID: PMC4174951  PMID: 25037958

Abstract

Grain produced from cereal crops is a primary source of human food and animal feed worldwide. To understand the genetic basis of seed-size variation, a grain yield component, we conducted a genome-wide scan to detect evidence of selection in the maize Krug Yellow Dent long-term divergent seed-size selection experiment. Previous studies have documented significant phenotypic divergence between the populations. Allele frequency estimates for ∼3 million single nucleotide polymorphisms (SNPs) in the base population and selected populations were estimated from pooled whole-genome resequencing of 48 individuals per population. Using FST values across sliding windows, 94 divergent regions with a median of six genes per region were identified. Additionally, 2729 SNPs that reached fixation in both selected populations with opposing fixed alleles were identified, many of which clustered in two regions of the genome. Copy-number variation was highly prevalent between the selected populations, with 532 total regions identified on the basis of read-depth variation and comparative genome hybridization. Regions important for seed weight in natural variation were identified in the maize nested association mapping population. However, the number of regions that overlapped with the long-term selection experiment did not exceed that expected by chance, possibly indicating unique sources of variation between the two populations. The results of this study provide insights into the genetic elements underlying seed-size variation in maize and could also have applications for other cereal crops.

Keywords: copy-number variation, maize, natural variation, seed size, selection signatures

GRAIN produced by cereal crops is a staple food source in many regions of the world in terms of direct human consumption and as an animal feed source. Understanding the molecular mechanisms underlying cereal grain yield and exploiting that knowledge through improved cultivars is essential to providing a stable food source to an ever-growing human population. Yield-component traits are of particular interest, as they generally have a higher heritability than grain yield per se (Austin and Lee 1998). For example, increasing seed size has been hypothesized as one method for increasing grain yield in cereal crops (Odhiambo and Compton 1987; Kesavan et al. 2013), and positive correlations between seed size and grain yield have been shown in maize (Peng et al. 2011) as well as other cereals such as Sorghum bicolor (L.) Moench (Yang et al. 2010). Maize is a prime species with which to explore natural and artificial variation related to grain-yield and yield-component traits in the cereals, as it is the most widely grown cereal crop worldwide and has vast genetic resources for probing the genetic basis of seed traits.

The maize seed is composed of the embryo and endosperm that develop from double fertilization, the aleurone, which is an epidermal layer that covers the endosperm, and the maternal pericarp tissue. The endosperm, the primary storage component of the seed in maize, consists primarily of starch, while the embryo is high in oil content (Kiesselbach 1999). Storage proteins also accumulate in the developing endosperm of maize, with the main class of storage proteins being zeins (Paulis and Wall 1977). Large effect mutants such as Miniature1 (Mn1) (Cheng et al. 1996), opaque-2 (o2) (Schmidt et al. 1990), shrunken-2 (sh2) (Bhave et al. 1990), stunter1 (stt1) (Phillips and Evans 2011), Zea mays Outer Cell Layer1 (ZmOCL1) (Khaled et al. 2005), and others (Neuffer et al. 1997) have been identified and affect overall seed and/or endosperm development in maize. Additionally, recent work has begun to elucidate the regulatory networks involved in maize seed development (Fu et al. 2013). Despite these studies on overall seed development, the genetic basis of seed-size variation in maize and other cereal crops is still largely unknown.

Selection increases the frequency of favorable alleles in a population. Therefore, the assessment of allele frequency change is a useful technique for identifying genomic regions that were targeted by selection (Lewontin 1962). Specific methods vary depending on the populations under study and the genotyping methods employed (Wright 1951; Akey et al. 2002; Sabeti et al. 2002; Oleksyk et al. 2008; Wisser et al. 2008; Turner et al. 2011). For example, in natural populations, statistics that measure population divergence such as FST (Wright 1951) can be calculated and loci displaying extreme values above an empirically determined genome-wide threshold are implicated as potentially associated with selection (Akey et al. 2002; Oleksyk et al. 2008). Identification of selection signatures has successfully been used to reveal the genetic basis of several traits across numerous species, including heat tolerance in yeast (Parts et al. 2011), body-size variation in Drosophila melanogaster (Turner et al. 2011) and chickens (Johansson et al. 2010), milk production in Holstein cattle (Pan et al. 2013), and prolificacy (Beissinger et al. 2014) and northern leaf blight resistance (Wisser et al. 2008) in maize.

The goal of this study is to dissect the genetic architecture of seed-size variation in cereal crops using maize as a model. Long-term artificial-selection experiments contain a wealth of information about trait architecture and, with the advent of next-generation sequencing, we can now harness that information. To unravel the genetic architecture of seed-size variation in maize, we compared pooled whole-genome resequencing data from populations from a divergent selection experiment for small and large seed size (Odhiambo and Compton 1987; Russell 2006) (Figure 1). Previous work has demonstrated significant phenotypic variation among the three Krug populations for seed weight and other morphological and compositional traits (Sekhon et al. 2014). In this study, we explored genetic variation between the extreme populations for both single nucleotide polymorphisms (SNPs) and copy-number variation (CNV), identified regions under selection during the long-term selection experiment, and compared these results to naturally occurring genetic variation in maize for seed weight to elucidate the genetic architecture of seed size in an important cereal crop.

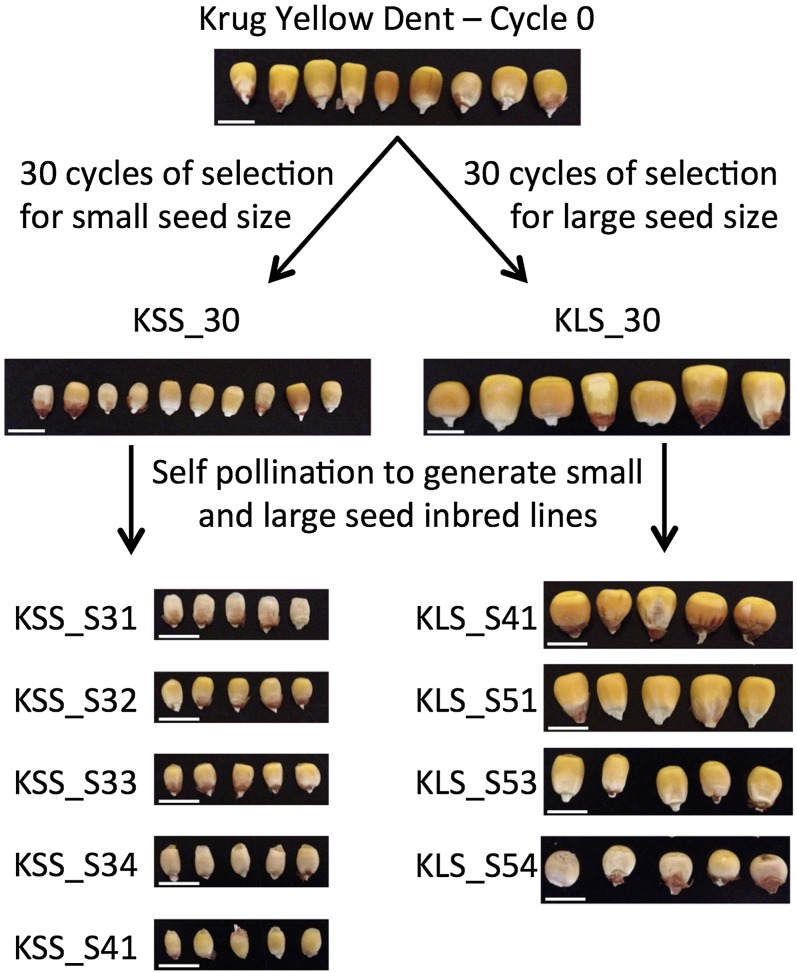
Figure 1.

Figure 1

Open in a new tab

Phenotypic response to selection for large and small seed size. Thirty cycles of divergent selection for seed size was conducted from the base population Krug Yellow Dent to generate KLS_30 (selected for larger seeds) and KSS_30 (selected for smaller seeds). Inbred lines were generated from both KLS_30 and KSS_30 by self-pollinating random plants from each population for at least five generations.

Materials and Methods

Plant material, nucleic acid isolation, and SNP genotyping

The open pollinated maize population Krug Yellow Dent (PI 233006) and its derivatives were evaluated in this study. Thirty cycles of divergent mass selection for seed size were conducted to generate KLS_30 (selected for large seed size; PI 636488) and KSS_30 (selected for small seed size; PI 636489) (Odhiambo and Compton 1987; Russell 2006). Briefly, in each cycle of selection, 1200 to 1500 plants from each divergently selected population were grown in separate isolation blocks, ears with the consistently largest or smallest seeds were selected (minimum of 100 ears per population), and an equal number of seeds from each ear was bulked to constitute the population for the next cycle of selection. Additionally, inbred lines were generated from both KLS_30 and KSS_30 by self-pollinating random plants from each population for at least five generations without selection for seed characteristics (Figure 1; KLS_S41, KLS_S51, KLS_S53, KLS_S54, KSS_S31, KSS_S32, KSS_S33, KSS_S34, and KSS_S41).

Plants from the three populations and the nine inbred lines were grown under greenhouse conditions (27°/24° day/night and 16 /8 hr light/dark). Leaf tissue was harvested from 48 individuals from each population and the nine inbred lines. DNA was extracted using the cetyl(trimethyl)ammonium bromide (CTAB) method (Saghai-Maroof et al. 1984). Genotyping was performed by Pioneer Hi-Bred International (Johnston, IA) on individual DNA samples using an Illumina BeadArray 768 SNP assay (Jones et al. 2009).

Library construction and sequencing

Three equimolar pools of total DNA were created from the 48 individuals within each population (Krug Yellow Dent, KLS_30, and KSS_30). Libraries were prepared using the Illumina protocol (San Diego, CA) with a target insert size of 270 bp. Sequencing was performed at the Joint Genome Institute (Walnut Creek, CA) using an Illumina HiSeq (San Diego, CA) to generate 2 × 100 nucleotide paired-end sequence reads. Sequence reads are available in the National Center for Biotechnology Information Sequence Read Archive study accession no. SRP013705. The FastQC program (http://www.bioinformatics.babraham.ac.uk/projects/fastqc/) was used to examine sequence quality. Reads with insufficient quality were removed from downstream analyses.

Genomic sequence analysis

Genomic reads were cleaned using the FASTX toolkit (http://hannonlab.cshl.edu/fastx_toolkit/index.html) and mapped using Bowtie v. 0.12.7 (Langmead et al. 2009) according to previously described methods (Beissinger et al. 2014) with the exception that reads were mapped only as single-end reads using the “SE pipeline.” For each population, valid alignments were processed using SAMtools v. 0.1.12a (Li et al. 2009) as previously described (Beissinger et al. 2014) to identify polymorphic positions and determine frequencies of each nucleotide at each position.

It is possible that some of the polymorphic loci were actually the result of multiple copies of a genomic region in one or more of the individuals mapping to a single locus in the B73 reference sequence. As such, a high confidence set of SNPs was identified by placing a constraint on coverage at each position, requiring coverage ±2 standard deviations of the mean across the populations and a minimum coverage of 20× to ensure accurate estimation of allele frequencies in the populations (20× and 79× coverage). After this filtering, 3,090,214 high-confidence SNPs were retained.

A permutation test was used to determine the probability of the difference in observed mean minor allele frequency (MAF) between the SNPs that were fixed in both populations in the same direction and the SNPs that were fixed in both populations in opposite directions. The set of 447,328 SNPs that were polymorphic in Krug Yellow Dent and reached fixation in both populations (in the same and opposite direction) were randomly shuffled 10,000 times and the number of instances when the difference in mean MAF exceeded the empirical observation was recorded.

The distribution of read-depth variation across the genome was used as a proxy to evaluate CNV between the three populations. Read depth was determined for 5-kb windows. Copy-number variation windows were defined as having an absolute value greater than two for the number of standard deviations away from the mean in KLS_30 minus the number of standard deviations away from the mean in KSS_30. Graphical images were generated using R v. 2.13.2 (R Development Core Team 2014) and Circos v. 0.56 (Krzywinski et al. 2009).

Comparative genomic hybridization

Comparative genome hybridization (CGH) was performed on the nine inbred lines generated from the KLS_30 and KSS_30 populations and the B73 maize reference inbred line using a previously described microarray design (Eichten et al. 2013; GEO Platform GPL15621) and hybridization methodology (Swanson-Wagner et al. 2010). Pair files exported from NimbleScan (Nimblegen Inc.) were normalized to correct for signal variations within and between arrays using variance stabilization and calibration (vsn; Huber et al. 2002). Normalized samples were exported as log2(sample/B73 reference) values. The nine individual samples, as well as contrasts between the average KLS and KSS inbred values, were processed into segments via DNAcopy (Venkatraman and Olshen 2007) to identify regions exhibiting CNV. Segments were filtered to require a 0.7-fold change between the two samples to be classified as a CNV.

Estimating effective population size

Three methods were used to measure the effective population size throughout selection in the two directional selection experiments. The first method was based on population demographics as previously described (Crow and Kimura 1970), based on the relationship Ne= (4NmNf)/(Nm+Nf), where Nm and Nf are the number of mating males and females, respectively. Next, an estimate was made on the basis of a temporal assessment of molecular markers. Effective population size based on the Illumina BeadArray SNPs was estimated using the equation Ne= 1/2(1−Ht/H0t) , where Ht and H0 are the mean levels of heterozygosity in the tth and 0th generation, respectively (Crow and Kimura 1970). A third analysis was conducted on the basis of linkage disequilibrium (LD) among the same set of SNPs. Unlike the previous two approaches, this technique allows the estimation of Ne for each of the three populations independently and also provides a confidence interval around the estimates. The program LDNe (Waples and Do 2008) was used for this analysis. All SNPs with allele frequencies ≥0.05 were included, and confidence intervals were estimated using the JackKnife approach.

Simulations of drift

Two sets of drift simulations that assumed linkage equilibrium were conducted using R v. 2.15.3 (R Development Core Team 2014). The first set was based on population demography, mimicking the selection protocol exactly. The second set assumed equal males and females and assumed the Ne values estimated from LDNe (Waples and Do 2008), which suggested an effective population size of ∼14 males and 14 females for both KLS_30 and KSS_30. In both cases, 1000 simulations were conducted. For each simulation, 1,000,000 polymorphic SNPs were sampled, with replacement, from observed polymorphic cycle zero SNPs to create a simulated base population with 1,000,000 allele frequencies. Then, binomial sampling was conducted to mimic 30 generations of drift with the prescribed population size, to generate simulated KLS_30 and KSS_30 populations. Binomial sampling of 96 alleles from each of the three simulated populations (Krug Yellow Dent, KLS_30, and KSS_30) was conducted to mimic sampling individuals to be sequenced. Sequencing was simulated by binomial sampling, for each SNP, the number of reads that were actually sequenced for that SNP in the experiment. SNPs that were simulated to be fixed in the same direction in all three populations were removed, since our SNP calling protocol would not have identified these as polymorphic. The mean percentage of SNPs fixed in opposing directions between KLS_30 and KSS_30 was calculated for each set of simulations, as well as 95% intervals.

Scan for selection

A genome-wide scan for selection was conducted. The use of pooled sequencing prevented estimation of LD in the populations, making accurate simulations to establish precise significance levels impossible. Instead, a window-based scan was used to classify genomic regions as empirically divergent or not divergent. The most divergent sites represent candidates for selection. This approach has been implemented in other studies that have documented strong selection and dramatic phenotypic changes (Beissinger et al. 2014) as is the case in this study.

The high confidence set of SNPs described above was further filtered to include only biallelic SNPs (2,944,220 SNPs included). Minor allele frequency as defined in Krug Yellow Dent was calculated in all three populations using a maximum-likelihood estimate. A sliding window approach was used to evaluate divergence between the populations, as there is a substantial sampling error inherent to pooled sequencing.

For each SNP, three FST values were calculated, corresponding to comparisons between Krug Yellow Dent and KLS_30, Krug Yellow Dent and KSS_30, and KLS_30 and KSS_30. FST was calculated using a method assuming a large sample size, given by

FST^= s2p¯(1−p¯)+s2/r,  

where p¯ is the mean allele frequency across populations, s2 is the variance of allele frequency between populations, and r is the number of populations (Weir and Cockerham 1984). FST values were averaged over 25-SNP sliding windows, centered on each SNP in turn, to reduce sampling error. This approach assumes that SNP density is high enough that regions under selection will contain multiple SNPs and thus exhibit large FST values after averaging.

Outlying SNPs, for which the window-averaged FST value exceeded a 99.9% or 99.99% empirically determined threshold, were identified. These outlier threshold levels were not chosen to represent a specific level of significance; rather they provide candidates for strong (99.9%) or extremely strong (99.99%) selection. To define regions that were putatively under selection, single or adjacent SNPs that displayed an outlying window-averaged FST value were first identified. Then, if any other SNPs within 5 Mb displayed an outlying window-averaged FST value, the selected region was extended to include these SNPs. This process was repeated until no significant SNPs were found within 5 Mb of the up- or downstream region boundaries. To ensure that region boundary declarations were conservative, we extended the boundaries to include all of the SNPs in the windows for those SNPs within the extended selection regions (Supporting Information, Table S1 and Table S2).

A map of centimorgans per megabase in the intermated B73 × Mo17 (IBM) population (Lee et al. 2002) was previously estimated (Liu et al. 2009). This map was used to approximate the relative levels of recombination across the genome of the Krug long-term selection populations. This analysis assumes that recombination hot and cold spots are likely similar across populations. Each of the FST -based regions that exceeded the 99.9% outlier level was assigned a value for centimorgans per megabase according to the IBM map. The Pearson correlation between region size and region centimorgans per megabase was tested. This was conducted for every region identified, as well as for each comparison separately (KLS_30 vs. KSS_30, Krug Yellow Dent vs. KLS_30, Krug Yellow Dent vs. KSS_30).

Evaluation of natural variation

The maize nested association mapping (NAM) population (Yu et al. 2008; Mcmullen et al. 2009) was used to evaluate natural variation for seed weight, excluding the two sweet corn families (IL14H and P39). In total, 4196 recombinant inbred lines (RILs) from the non-sweet corn families were used in this study.

The NAM RILs were grown at four locations in 2006 (Clayton, NC; Aurora, NY; Homestead, FL; and Ponce, PR) and at one location in 2007 (Clayton, NC). At each location, a single replicate with checks was planted in an augmented design as previously described (Buckler et al. 2009). Seed weight was measured as the weight of 20 representative seeds from two self-pollinated plants per plot. The best linear unbiased predictions (BLUPs) of RILs across environments were calculated with ASREML v. 2.0 software (Gilmour et al. 2006) as previously described (Hung et al. 2012). The BLUPs were used for subsequent analysis.

Joint linkage mapping was performed according to previously described methods (Buckler et al. 2009) using 1106 SNP markers (McMullen et al. 2009). Based on 1000 permutations, the appropriate P-value for inclusion of a marker in the joint linkage mapping was determined to be 2.03 × 10−6. Genome-wide association studies (GWAS) were performed using 1.6 million SNPs from the maize HapMap v. 1 project (Gore et al. 2009) projected onto the NAM RILs as previously described (Tian et al. 2011). Briefly, SNP associations were tested for each chromosome separately. RIL residual values from a model containing QTL identified by the joint linkage model outside of the test chromosome were used as the input phenotype values to GWAS for a particular chromosome. Forward regression was performed on one chromosome at a time, and significance thresholds for each chromosome were determined by 1000 permutations (range from 6.6 × 10−9 to 7.3 × 10−8). Additionally, the resampling model inclusion probability (RMIP) method for GWAS was performed as previously described (Tian et al. 2011). For this method, 80% of the RILs from each family were randomly selected without replacement and forward regression was performed. This method was repeated 100 times, and SNPs that were selected in the regression model in five or more subsamples were considered significant (RMIP ≥ 0.05).

Results

Effective population size in the Krug Yellow Dent long-term artificial selection experiment

In the original selection experiment, ∼1200 plants per cycle were evaluated, from which ∼100 females were selected (Odhiambo and Compton 1987; Russell 2006). Assuming random mating throughout the experiment, the effective population size based on population demographics was estimated to be ∼369 for both KLS_30 and KSS_30. Using the 768 SNP markers on individual plants, the effective population size based on observed reductions in heterozygosity was estimated to be 76 and 312 for KSS_30 and KLS_30, respectively. Estimates based on LD for each population using the 768 SNP markers were 33.5 (95% confidence interval, 32.8–34.3) for Krug Yellow Dent, 29.0 (28.3–29.7) for KSS_30, and 27.6 (27.0–28.2) for KLS_30. The differences in Ne resulting from the heterozygosity-based method compared to the LD method may result because the heterozygosity method does not incorporate information about Ne in the base population (Krug Yellow Dent), while the LD method depicts it as relatively low. Still, only a slight reduction in Ne was observed between the base and selected populations based on the LD method, which is in general agreement with the fact that larger Ne was estimated according to reductions in heterozygosity.

Single nucleotide polymorphism detection and estimates of allele frequencies

We generated a total of 462 Gb of sequence across the three population pools, with theoretical coverage of 71.1×, 48.3×, and 81.6× for Krug Yellow Dent, KLS_30, and KSS_30, respectively. The maize genome is highly repetitive (Schnable et al. 2009) and as such it is not possible to map to the majority of the genome when a sequence read is required to have a unique alignment. Despite this characteristic, coverage of 58–63% of the base pairs in the reference sequence across the three populations was observed, and 7–18% of the genome had >20× coverage (Table S3).

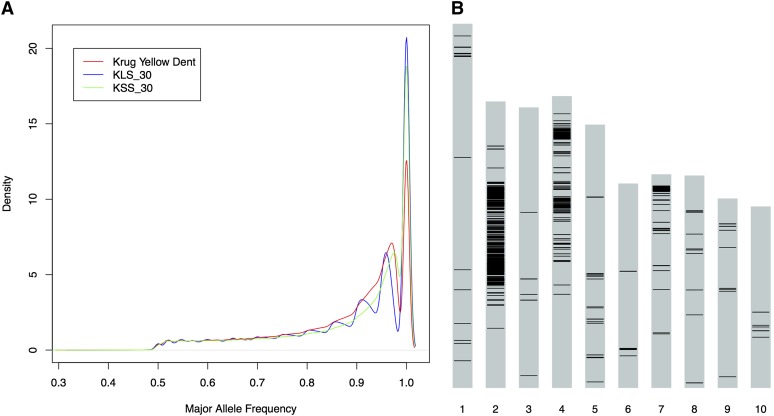
The result of 30 generations of divergent selection is reflected in probability density curves of the major allele frequency, where the density at a major allele frequency of one is greater in KLS_30 and KSS_30 relative to Krug Yellow Dent (Figure 2A). Interestingly, for 25% of the polymorphic loci, alleles were observed in KLS_30 or KSS_30 that were not present in Krug Yellow Dent (Figure S1). Most likely this is the result of alleles that were present at too low a frequency in Krug Yellow Dent to be detected through sampling of 96 gametes and subsequent sequencing of only a subset of these. Alternatively, this could be the result of accidental introgression or mutations that arose during the experiment and were selected upon.

Figure 2.

Figure 2

Open in a new tab

SNP diversity in Krug Yellow Dent, KLS_30, and KSS_30. (A) Probability density function of major allele frequencies for each population based on 3,090,214 high-confidence SNPs with at least 20× coverage and no more than 79× coverage. The area under each curve equals one. (B) Distribution of SNPs that reached fixation in both KLS_30 and KSS_30 with opposing alleles in the extreme populations, reflecting the divergent selection.

Identification of regions that exhibit substantial divergence

The genome was scanned to identify candidate regions under selection using an outlier-based approach. Regions exceeding either the 99.9 or 99.99% levels of the empirical distribution were identified. Comparisons were made between Krug Yellow Dent and KLS_30, Krug Yellow Dent and KSS_30, and KLS_30 and KSS_30 (Figure 3, Figure S2, Table S1, and Table S2). A window-based approach was implemented to minimize the effect of sampling error incurred through pooled sequencing while retaining signal from selected regions due to the relatively dense SNP markers that were identified. However, in regions with small selection signatures or relatively low SNP density, this approach can result in undetected selection signatures.

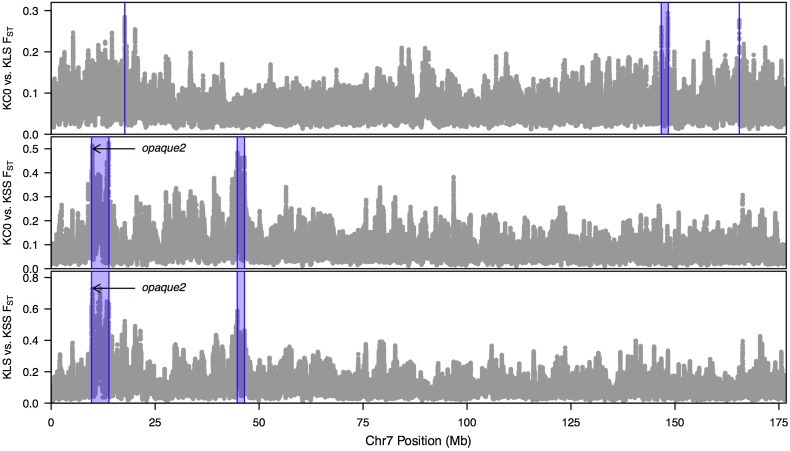
Figure 3.

Figure 3

Open in a new tab

Window-averaged FST values for the SNPs on chromosome 7. FST values were calculated using a 25-SNP sliding window approach for the biallelic SNPs. Comparisons were made between Krug Yellow Dent and KLS_30, Krug Yellow Dent and KSS_30, and KLS_30 and KSS_30. Purple areas indicate candidate regions under selection at the 99.9% level. Plots for all chromosomes with 99.9 and 99.99% threshold values are available in Figure S1. KC0, Krug Yellow Dent; KLS, KLS_30; KSS, KSS_30.

In total, 94 regions that encompass 147.2 Mb (6.4%) of the maize v. 2 reference genome sequence (including N’s) were identified as divergent at the 99.9% outlier level and these included 23 regions (25.1 Mb) at the 99.99% level (Table S1 and Table S2). The selected regions contained 2423 and 305 annotated genes at the 99.9% and 99.99% levels, respectively. Among the regions identified at the 99.9% level, 63 were identified in KLS_30 and 27 in KSS_30, based on comparison with Krug Yellow Dent, while direct comparison of KLS_30 and KSS_30 identified 23 regions. Considerable overlap of regions identified in the three comparisons was observed (Figure 4).

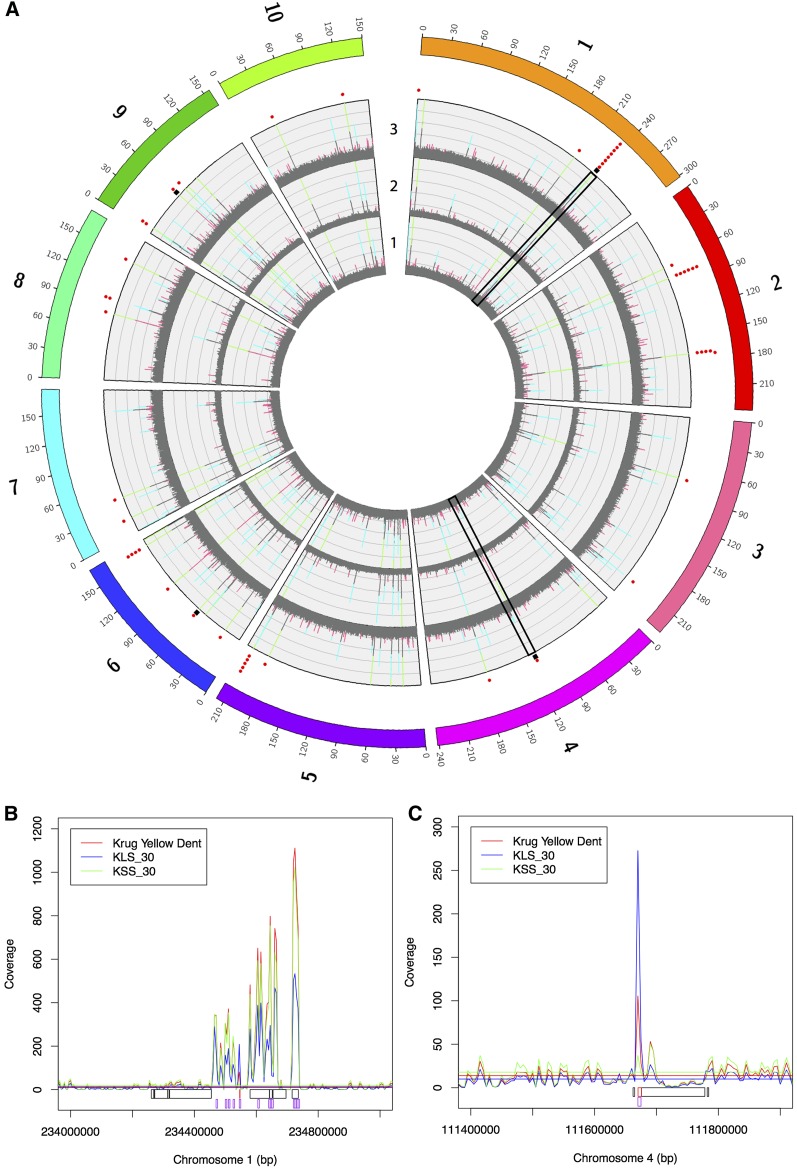
Figure 4.

Figure 4

Open in a new tab

Distribution of genetic variation in the Krug Yellow Dent divergent long-term selection experiment for seed size and quantitative trait loci for seed weight in the maize nested association (NAM) population along the 10 maize chromosomes. Opposite fixed SNPs are those that have reached fixation in both KLS_30 and KSS_30 with opposing alleles. Krug Yellow Dent vs. KLS_30, Krug Yellow Dent vs. KSS_30, and KLS_30 vs. KSS_30 show candidate genomic regions under selection observed in the various comparisons at the 99.99% level (opaque colors) and 99.9% level (transparent colors). Opaque green bars indicate copy-number variation (CNV) regions that were identified from pooled resequencing data from the populations and transparent green bars indicate regions that were identified from comparative genome hybridization (CGH) with inbred lines derived from KLS_30 and KSS_30. Significant NAM SNPs include SNPs identified using both joint linkage analysis and genome wide association studies.

Based on a previously described recombination map (Liu et al. 2009), no significant correlation between the size of selected regions and the expected relative level of recombination in the corresponding area of the genome was observed (Figure S3). This was the case for regions identified from Krug Yellow Dent vs. KLS_30 (P-value = 0.2152), Krug Yellow Dent vs. KSS_30 (P-value = 0.4081), KLS_30 vs. KSS_30 (P-value = 0.9142), and all identified regions at once (P-value = 0.2276). However, even though no significant correlation was observed, the largest region located on chromosome 2, which displayed evidence of selection based on all three comparisons, did fall in an area of very limited recombination.

Across the three comparisons, the number of genes within 5 kb of selected regions ranged from 0 to 233 with a mean of ∼27 (Table S1 and Table S2). However, a small number of large candidate regions skewed this value upward. Interestingly, candidate regions for selection were observed on chromosome 2 and 4 in the KSS_30 population (Figure S2), and the heterozygosity-based estimate of effective population size was lower in KSS_30 compared with KLS_30. It is unknown, however, if an undocumented bottleneck resulted in these large candidate regions of selection, or if large sweeps caused a bottleneck to occur in the population.

In contrast to the mean number of genes per region, the median number of genes within the identified regions was six, and 28 regions contained only one or zero genes within the region. Candidate genes were identified within some of the regions. For example, region 20 on chromosome 7 (Figure 3 and Table S2) contained o2, which is known to regulate expression of genes encoding 22-kDa zein proteins (Schmidt et al. 1990, 1992) and is expressed almost exclusively in developing seed tissue with the highest expression levels observed in endosperm tissue (Sekhon et al. 2011). While SNPs from this study within o2 did not show evidence of changes in allele frequency, significant differences in expression were observed throughout development between KLS_30 derived inbred lines and KSS_30 derived inbred lines (Figure S4) (Sekhon et al. 2014).

In a previous study, gene coexpression network modules that distinguish KLS_30 and KSS_30 derived inbred lines were identified, one of which was enriched with cell-cycle genes (Sekhon et al. 2014). Nineteen genes within 14 different genomic regions identified at the 99.9% level were within this cell-cycle-enriched module (Table S4). One of these genes (GRMZM2G069078) has previously been shown to have an effect on seed development in the maize UniformMu mutant population (McCarty et al. 2005; Hunter et al. 2014). Interestingly, expression patterns in the KLS_30 and KSS_30-derived inbred lines indicate differences in developmental timing, with the gene expressed longer in the KLS_30 inbred lines (Figure S5)(Sekhon et al. 2014).

Four genes within our identified regions were within another gene coexpression network module that was enriched in zein proteins from the same network analysis (Sekhon et al. 2014). One of these genes was annotated as a starch binding domain containing protein (GRMZM2G161534; genomic region 70, chromosome 6; Table S1) and one as a 22-kDa alpha zein protein 21 (GRMZM2G397687; selective sweep 36, chromosome 4; Table S1).

A large number of single nucleotide polymorphisms reached fixation in the selected populations

In total, 1,111,384 loci that were polymorphic in Krug Yellow Dent reached fixation in KLS_30 and/or KSS_30 (Figure S1). Many of these observed positions could be due to sampling of alleles that were in low frequency in the base population and were sampled in only one of the selected populations. There was, however, a subset of these SNPs (2729; 0.088% of analyzed SNPs) that reached fixation in both KLS_30 and KSS_30 with opposing fixed alleles between the two extreme populations that were distributed across the 10 chromosomes (Figure 2B). A large number of the oppositely fixed SNPs were clustered near the centromere on chromosome 2 and on the short arm of chromosome 4 (Figure 2B). As was expected, significant overlap was observed with the candidate regions identified by the outlier-based scan of the genome described above (Figure 4). Interestingly, however, small regions of fixation, in some cases a single oppositely fixed SNP, that did not overlap with the regions identified using the window-based outlier-based approach were observed. However, in many cases the oppositely fixed SNPs were consistent with allele frequency changes at surrounding loci that simply had not yet reached fixation.

The MAF of SNPs that were fixed in opposite directions was substantially higher (mean MAF 0.233) than that observed for SNPs that reached fixation in only one population (mean MAF 0.175) and for all SNPs in the base population (mean MAF 0.175; Figure S6). Permutation analysis showed a significant difference in the mean MAF between the two classes of fixed SNPs (fixed in both populations in the same or opposite directions; P-value = 0.0001). The probability of differential fixation can be calculated as P(1 − P), where P is the probability of fixation. Based on this equation, differential fixation becomes more likely as MAF approaches 0.5. Thus, the observed SNPs that were fixed in opposite directions likely resulted, at least in part, from drift during the 30 cycles of selection.

Simulations were also conducted to determine the expected number of SNPs to be fixed in opposite directions due to drift alone. The mean percentage of opposite-fixed SNPs based on simulations with effective population size determined according to demography was 2.8 × 10−6% (95% interval: 0.0%–1.05 × 10−4%), which is substantially fewer than the observed percentage. It should be noted, however, that the mean percentage of opposite-fixed SNPs based on simulations with effective population size determined by LDNe (Waples and Do 2008), which provided the lowest estimate of Ne among the methods utilized, was 0.7% (95% interval 0.77–0.81%).

Copy-number variation was highly prevalent between KLS_30 and KSS_30

Using read-depth variation as a proxy for CNV, 57 variable 5-kb windows were identified between the selected populations (Figure 5A and Table S5). Some of the CNV regions contained multiple significant windows in close proximity (Figure 5B), while others had only a single window above the background noise (Figure 5C). Interestingly, CNV regions that did not contain any annotated gene models and may be involved in regulation of gene expression were identified.

Figure 5.

Figure 5

Open in a new tab

CNV in Krug Yellow Dent, KLS_30, and KSS_30 based on read-depth variation and comparative genome hybridization (CGH). (A) Distribution of average read depth in 5-kb windows for Krug Yellow Dent (track 1), KLS_30 (track 2), and KSS_30 (track 3). Pink indicates a window that is >1 SD above the mean for the given population, aqua indicates a window that is >2 SD above the mean for a given population, and green indicates a window that has >250× read depth and extends beyond the chart. Red dots outside of track 3 show windows with evidence of CNV based on read depth (defined as the number of SD away from the mean in KLS_30 minus the number of SD away from the mean in KSS_30 being greater than two). Black squares outside of track 3 show CGH probes with significant CNV between KLS_30 and KSS_30-derived inbred lines that are concordant with sequence-based CNV regions at the population level. (B) Close-up of a significant CNV region on chromosome 1. (C) Close-up of a significant CNV region on chromosome 4. In both B and C, black boxes indicate CGH regions that do not show CNV, red boxes indicate CGH regions that show CNV, and purple boxes indicate 5-kb read-depth variation windows.

The putative CNV regions from read-depth variation were identified from a pool of 48 individuals. Thus, these may represent regions that had modest changes in copy number in many individuals or extreme changes in copy-number variation in a small number of individuals. To provide perspective on the basis of the CNV regions identified from the pooled resequencing experiment, CGH was performed on individual inbred lines derived from the populations. From the CGH, 479 regions were identified with variation between the average of the large and small seeded inbred lines derived from the extreme populations (Figure 1 and Table S6). Notably, four of the read-depth variants were also identified using the CGH method (Figure 5A), which significantly exceeds the overlap expected by chance (Figure S7). Using the two methods, a total of 532 CNV regions were identified between the extreme populations (53 unique to the read depth variants, 475 unique to the CGH CNVs, and 4 overlapping regions).

Of the 532 CNV regions identified, 148 contained or overlapped at least one gene annotated in the maize v. 2 reference sequence. Of the CNV regions containing annotated genes, 15 contained genes important for photosynthetic activity including photosystem I and photosystem II proteins and a RuBisCO large-chain protein. Interestingly, previous phenotypic evaluation of these populations revealed variation for mature plant dry weight in addition to seed size (Sekhon et al. 2014). Eight cell-cycle genes, such as cyclin protein-coding genes, were also present in the CNV regions. As discussed above, previous comparison of whole transcriptomes between the KLS_30 and KSS_30-derived inbred lines identified a gene coexpression module that differentiated the inbred lines and contained a large number of cell-cycle-related genes (Sekhon et al. 2014). Notably, three of the genes identified in regions with CNV were contained in this module including one annotated as an auxin-independent growth promoter on chromosome 5.

Overlap was also observed between the CNV regions and the regions that were identified as the most likely to be affected by selection based on SNP allele frequencies. However, the overlap exceeded only that expected by chance for the CNV regions identified by CGH (Figure S8). Across the 94 regions that were identified at the 99.9% level, 29 were within 5 kb of a CNV region identified by CGH (28) or sequence depth (2). Of particular interest, region 71 on chromosome 6 overlapped with both CGH and sequence-depth-identified CNV regions, and this region also contained three genes that were in the cell-cycle-enriched gene coexpression module described above (Table S4) (Sekhon et al. 2014). Additionally, two of the three CNV regions on chromosome 2 were within the SNP divergently fixed regions (Figure 2B).

Natural genetic variation for seed weight validates regions identified in the Krug Yellow Dent selection experiment

To compare artificial selection in the Krug long-term selection experiment with natural variation for seed size, 20-kernel seed weight, a trait highly correlated with seed size (Peng et al. 2011), was evaluated in the maize NAM population (Yu et al. 2008; McMullen et al. 2009). Briefly, the NAM population includes 25 RIL families, each with B73 as a common reference parent. The 25 NAM founders were selected to maximize diversity from a worldwide collection of maize inbred lines based on microsatellite markers (Liu et al. 2003; Flint-Garcia et al. 2005; Yu et al. 2008) and are thus a good representation of natural variation in maize inbreds. The two sweet corn families in the NAM population were excluded from the analysis due to their extreme seed weight phenotypes. The parents of the included families were both genotypically and phenotypically diverse, with 20-kernel seed weights ranging between 2.18 and 5.32 g. In comparison, the average 20-kernel seed weight for the KSS_30 and KLS_30 populations was previously reported to be 1.96 and 9.35 g, respectively (Sekhon et al. 2014).

Using joint linkage analysis, 18 QTL peaks were identified for seed weight (Table S7), which accounted for 60% of the total phenotypic variation, with the range in additive allelic effect size between −0.012 and 0.013 g per 20 kernels. Overlap was observed between seed weight and seed composition QTL identified in a previous study (starch, 9 QTL; protein, 7 QTL; oil, 7 QTL) that used the same germplasm (Cook et al. 2012b), providing additional evidence that seed composition likely contributes to seed size and weight. Single forward regression GWAS using the 1.6 million SNPs from the HapMap v. 1 data set identified 21 SNPs associated with seed weight (Table S8). The RMIP GWAS method using the same HapMap v. 1 data set identified 76 SNPs associated with weight (Table S9), which validated 20 of the 21 SNPs from the single forward regression GWAS model. In total, 74 regions of the genome were associated with seed weight based on joint linkage analysis and GWAS in the NAM population when allowing overlapping regions to be within 500 kb of an adjacent significant SNP (Figure 6, Table S7, Table S8, and Table S9).

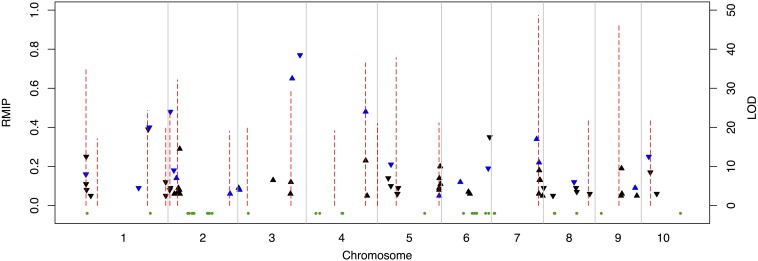
Figure 6.

Figure 6

Open in a new tab

Position and magnitude of genetic variation underlying natural variation for seed weight in the maize NAM population. Red dotted lines depict significant QTL peaks based on joint linkage analysis (scale log of odds, LOD). Triangles depict associations identified from GWAS using the subsampling method (resampling model inclusion probability, RMIP ≥ 0.05). Triangles pointing upward indicate a positive effect and triangles pointing downward indicate a negative effect relative to B73. Blue triangles indicate associations detected using the subsampling and forward regression methods (scale RMIP). Green dots indicate selective sweeps observed in the Krug long-term selection experiment at the 99.99% outlier level.

Overlap was observed between the variable regions identified in the Krug Yellow Dent divergent selection experiment and the regions identified in NAM, in terms of the read-depth-based CNV regions (6 NAM SNPs), CGH-based CNV regions (25 NAM SNPs), and selective sweeps (12 NAM SNPs) when requiring SNPs to be within 500 kb of a variable region (Figure S8). For both CNV detection methods, this level of overlap exceeded the number expected by chance (Figure S7). Of particular interest was overlap with the large CNV region on chromosome 1 that was detected by both read-depth analysis of the extreme populations and CGH analysis of the population-derived inbred lines (Figure 5B). However, no obvious candidate genes were identified in either the CNV region or in the gene containing the significant NAM SNP. The level of overlap with the regions that exceeded the outlier threshold did not exceed the number of overlapping regions expected by chance with the selective sweeps. This could indicate the presence of many unique regions of the genome underlying the phenotypic variation observed within each population or it could reflect random false positives observed in each population.

Discussion

Cereal crops, including maize, are an important food source worldwide. Understanding the genetic architecture of grain yield and yield component traits is important to producing sufficient food to feed the human population. The populations derived out of the Krug long-term selection experiment (Odhiambo and Compton 1987; Russell 2006) provided a powerful tool for identifying regions of the genome-controlling seed weight and grain yield. The relatively large effective population size that was maintained throughout the experiment, as well as the divergent populations, allowed for separation of selection and drift effects. By resequencing pooled individuals from the base and selected populations, we were able to identify regions of the genome that were altered in response to selection for seed size.

Our observation of no significant relationship between recombination rate and the size of FST -based regions has interesting implications from an evolutionary standpoint. Generally speaking, selection sweeps can be classified as “hard sweeps,” for which a mutation arises and is immediately beneficial in the population (Maynard Smith and Haigh 1974), and “soft sweeps,” for which standing variation becomes beneficial due to a change in selection pressure (Hermisson and Pennings 2005). It is unlikely that any type of selection pressure occurred before the artificial selection program began, and because of the limited number of generations of selection, novel mutations affecting the trait are improbable. In an independent maize population subjected to a comparable selection protocol, soft sweeps were predominantly observed (Beissinger et al. 2014), and our a priori expectation was that mostly soft sweeps had occurred in this study. Unlike the findings by Beissinger et al. (2014), where most sweeps were classified as soft according to size, a large and relatively continuous distribution of region size was observed in the Krug long-term selection experiment (Figure S3). Additionally, region size in the Krug population did not appear to be controlled primarily by recombination rate. While inconclusive, these results indicate that the populations may have undergone classical hard sweeps, soft sweeps, and a combination thereof.

Some of the regions identified in our current study were small and allowed for candidate genes under selection to be identified. For example, o2 was contained in one of the selective sweeps and has been extensively studied for its role in endosperm development, namely in regulating expression of genes encoding 22-kDs zein proteins (Schmidt et al. 1990, 1992). Additionally, the significant GWAS signal at the end of the long arm of chromosome 2 is <100 kb from the window to which stt1 was mapped (Phillips and Evans 2011).

Large candidate regions for selection that likely resulted from genetic hitchhiking (Maynard Smith and Haigh 1974) were also observed in this study. For these regions that contained up to 233 genes, extensive genetic dissection and incorporation of multiple sources of evidence will be required to determine the variant and/or variants underlying them. The gene GRMZM2G069078 on chromosome 8 is a prime example where utilizing multiple sources of evidence including selective sweep analysis, gene coexpression network analysis (Sekhon et al. 2014), and mutation analysis (Hunter et al. 2014) allowed for the identification of a gene that was likely selected in the Krug long-term selection experiment.

Interestingly, there were also regions that contained no annotated genes. It is well documented that variants in noncoding regions can have a large effect on phenotypic variation. For example, variants in the maize Vgt1 region, which is 70 kb upstream of the ZmRap2.7 gene, were shown to be associated with a flowering time quantitative trait locus (Salvi et al. 2007; Ducrocq et al. 2008). It is also possible that genes are present in the reference sequence that were not annotated, are present in the reference inbred line B73 yet absent in the assembly, which has been documented to be incomplete (Schnable et al. 2009; Lai et al. 2010; Hansey et al. 2012; Hirsch et al. 2014), or are dispensable genes that are absent from the reference inbred line, but are present at some frequency within the Krug populations.

Previously extensive CNV has been shown across diverse maize inbred lines (Springer et al. 2009; Lai et al. 2010; Swanson-Wagner et al. 2010; Chia et al. 2012). It has long been hypothesized that this variation is in part underlying the large phenotypic variation in maize. A recent example of aluminum tolerance was associated with three tandem copies of the MATE1 gene in tolerant lines relative to the sensitive lines that carry only one copy of the gene (Maron et al. 2013). Likewise, resistance to the soybean cyst nematode was associated with increased copy numbers of three distinct genes (Cook et al. 2012a). In the current study, a large number of regions were identified that have altered copy number between the selected populations, KLS_30 and KSS_30 as estimated by read-depth variation and CGH.

A large number of the genes in the CNV regions were related to photosynthetic activity. Phenotypic evaluation of the KLS_30 and KSS_30 populations revealed variation for mature plant dry weight (Sekhon et al. 2014), consistent with the presence of photosynthesis-related genes in the CNV regions. Additionally, a number of cell-cycle-related genes were within the CNV regions. Cell-cycle programs are involved in multiple stages of endosperm development including acytokinetic mitosis, cellularization, cell proliferation, and in the cereals, endoreduplication (Kowles et al. 1990; Sabelli and Larkins 2009). The presence of cell-cycle genes within CNV regions in this study provides additional support for a growing body of evidence demonstrating the role of master cell-cycle regulators in endosperm formation, development, and seed and plant size (Sabelli and Larkins 2009; Sekhon et al. 2014).

Interestingly, obvious candidate genes were not identified in the CNV region on chromosome 1 that was identified by both read depth and CGH or in the gene containing the significant NAM SNP in close proximity to the region. However, there is a B-type response regulator (GRMZM2G379656) that lies between these two regions. In Arabidopsis thaliana, B response regulators have been shown to play a role in plant development including mean rosette diameter and mean seed length through regulation of the cytokinin signaling pathway (Argyros et al. 2008). A microarray-based gene expression atlas of 60 tissues from the maize reference inbred line B73 showed expression of this gene in leaf tissue at the V5, V9, V10, and R2 developmental stages across three biological replicates (Abendroth et al. 2011; Sekhon et al. 2011). Additionally, two of the three endosperm replicates at 20 days after pollination showed expression above background, indicating that this gene may also be important in both vegetative and seed development in maize.

This study provides valuable candidate genes that will be useful in characterizing control of seed weight and grain yield in cereals. The results are consistent with the importance of both cell-cycle regulation and seed composition in observed phenotypic variation for seed size/weight and ultimately grain yield. This study also provides insight into long-term artificial selection in crop plants, supporting the hypotheses of many genes with small effects underlying seed size and a role for noncoding sequences and copy-number variation in contributing to phenotypic response to selection.

Supplementary Material

Supporting Information
supp_198_1_409__index.html (5.4KB, html)

Acknowledgments

We are grateful to Dupont–Pioneer Hi-Bred International, Inc., for providing SNP data. This research was performed using the computer resources and assistance of the UW—Madison Center For High Throughput Computing (CHTC) in the Department of Computer Sciences. The CHTC is supported by UW—Madison and the Wisconsin Alumni Research Foundation and is an active member of the Open Science Grid, which is supported by the National Science Foundation and the U.S. Department of Energy’s Office of Science. This work was funded by the Department of Energy (DOE) Great Lakes Bioenergy Research Center (DOE BER Office of Science DE-FC02-07ER64494). The work conducted by the U.S. DOE Joint Genome Institute was supported by the Office of Science of the U.S. DOE under contract no. DE-AC02-05CH11231. T.B. was supported by the University of Wisconsin Graduate School and by a gift to the University of Wisconsin—Madison Plant Breeding and Plant Genetics program from Monsanto.

Footnotes

Sequence data from this article have been deposited with the Sequence Read Archive at the National Center for Biotechnology Information study under accession no. SRP013705.

Communicating editor: A. H. Paterson

Literature Cited

  1. Abendroth L. J., Elmore R. W., Boyer M. J., Marlay S. K., 2011.  Corn growth and development. PMR 1009 Iowa State University Extension, Ames, Iowa [Google Scholar]
  2. Akey J. M., Zhang G., Zhang K., Jin L., Shriver M. D., 2002.  Interrogating a high-density SNP map for signatures of natural selection. Genome Res. 12: 1805–1814 [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Argyros R. D., Mathews D. E., Chiang Y. H., Palmer C. M., Thibault D. M., et al. , 2008.  Type B response regulators of Arabidopsis play key roles in cytokinin signaling and plant development. Plant Cell 20: 2102–2116 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Austin D. F., Lee M., 1998.  Detection of quantitative trait loci for grain yield and yield components in maize across generations in stress and nonstress environments. Crop Sci. 38: 1296–1308 [Google Scholar]
  5. Beissinger T. M., Hirsch C. N., Vaillancourt B., Deshpande S., Barry K., et al. , 2014.  A genome-wide scan for evidence of selection in a maize population under long-term artificial selection for ear number. Genetics 196: 829–840 [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bhave M. R., Lawrence S., Barton C., Hannah L. C., 1990.  Identification and molecular characterization of shrunken-2 cDNA clones of maize. Plant Cell 2: 581–588 [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Buckler E. S., Holland J. B., Bradbury P. J., Acharya C. B., Brown P. J., et al. , 2009.  The genetic architecture of maize flowering time. Science 325: 714–718 [DOI] [PubMed] [Google Scholar]
  8. Cheng W. H., Taliercio E. W., Chourey P. S., 1996.  The Miniature1 seed locus of maize encodes a cell wall invertase required for normal development of endosperm and maternal cells in the pedicel. Plant Cell 8: 971–983 [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Chia J. M., Song C., Bradbury P. J., Costich D., de Leon N., et al. , 2012.  Maize HapMap2 identifies extant variation from a genome in flux. Nat. Genet. 44: 803–807 [DOI] [PubMed] [Google Scholar]
  10. Cook D. E., Lee T. G., Guo X., Melito S., Wang K., et al. , 2012a Copy number variation of multiple genes at Rhg1 mediates nematode resistance in soybean. Science 338: 1206–1209 [DOI] [PubMed] [Google Scholar]
  11. Cook J. P., McMullen M. D., Holland J. B., Tian F., Bradbury P., et al. , 2012b Genetic architecture of maize kernel composition in the nested association mapping and inbred association panels. Plant Physiol. 158: 824–834 [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Crow J. F., Kimura M., 1970.  An Introduction to Population Genetic Theory. Harper & Row, New York [Google Scholar]
  13. Ducrocq S., Madur D., Veyrieras J. B., Camus-Kulandaivelu L., Kloiber-Maitz M., et al. , 2008.  Key impact of Vgt1 on flowering time adaptation in maize: evidence from association mapping and ecogeographical information. Genetics 178: 2433–2437 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Eichten S. R., Vaughn M. W., Hermanson P. J., Springer N. M., 2013.  Variation in DNA methylation patterns is more common among maize inbreds than among tissues. Plant Gen. 6: 1–10 [Google Scholar]
  15. Flint-Garcia S. A., Thuillet A. C., Yu J., Pressoir G., Romero S. M., et al. , 2005.  Maize association population: a high-resolution platform for quantitative trait locus dissection. Plant J. 44: 1054–1064 [DOI] [PubMed] [Google Scholar]
  16. Fu J., Cheng Y., Linghu J., Yang X., Kang L., et al. , 2013.  RNA sequencing reveals the complex regulatory network in the maize kernel. Nat. Commun. 4: 2832. [DOI] [PubMed] [Google Scholar]
  17. Gilmour, A., B. Gogel, B. Cullis, and R. Thompson, 2006 ASReml User Guide Release 2.0 VSN Intl., Hemel, Hempstead, UK. [Google Scholar]
  18. Gore M. A., Chia J. M., Elshire R. J., Sun Q., Ersoz E. S., et al. , 2009.  A first-generation haplotype map of maize. Science 326: 1115–1117 [DOI] [PubMed] [Google Scholar]
  19. Hansey C. N., Vaillancourt B., Sekhon R. S., de Leon N., Kaeppler S. M., et al. , 2012.  Maize (Zea mays L.) genome diversity as revealed by RNA-sequencing. PLoS ONE 7: e33071. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Hermisson J., Pennings P. S., 2005.  Soft sweeps: molecular population genetics of adaptation from standing genetic variation. Genetics 169: 2335–2352 [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Hirsch C. N., Foerster J. M., Johnson J. M., Sekhon R. S., Muttoni G., et al. , 2014.  Insights into the maize pan-genome and pan-transcriptome. Plant Cell 26: 121–135 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Huber W., von Heydebreck A., Sultmann H., Poustka A., Vingron M., 2002.  Variance stabilization applied to microarray data calibration and to the quantification of differential expression. Bioinformatics 18(Suppl. 1): S96–S104 [DOI] [PubMed] [Google Scholar]
  23. Hung H. Y., Browne C., Guill K., Coles N., Eller M., et al. , 2012.  The relationship between parental genetic or phenotypic divergence and progeny variation in the maize nested association mapping population. Heredity 108: 490–499 [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Hunter C. T., Suzuki M., Saunders J., Wu S., Tasi A., et al. , 2014.  Phenotype to genotype using forward-genetic Mu-seq for identification and functional classification of maize mutants. Front. Plant Sci. 4: 545. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Johansson A. M., Pettersson M. E., Siegel P. B., Carlborg O., 2010.  Genome-wide effects of long-term divergent selection. PLoS Genet. 6: e1001188. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Jones E., Chu W.-C., Ayele M., Ho J., Bruggeman E., et al. , 2009.  Development of single nucleotide polymorphism (SNP) markers for use in commercial maize (Zea mays L.) germplasm. Mol. Breed. 24: 165–176 [Google Scholar]
  27. Kesavan M., Song J. T., Seo H. S., 2013.  Seed size: a priority trait in cereal crops. Physiol. Plant. 147: 113–120 [DOI] [PubMed] [Google Scholar]
  28. Khaled A. S., Vernoud V., Ingram G. C., Perez P., Sarda X., et al. , 2005.  Engrailed-ZmOCL1 fusions cause a transient reduction of kernel size in maize. Plant Mol. Biol. 58: 123–139 [DOI] [PubMed] [Google Scholar]
  29. Kiesselbach T. A., 1999.  The Structure and Reproduction of Corn. Cold Spring Harbor Laboratory Press, Cold Spring Harbor, NY [Google Scholar]
  30. Kowles R. V., Srienc F., Phillips R. L., 1990.  Endoreduplication of nuclear DNA in the developing maize endosperm. Dev. Genet. 11: 125–132 [Google Scholar]
  31. Krzywinski M., Schein J., Birol I., Connors J., Gascoyne R., et al. , 2009.  Circos: an information aesthetic for comparative genomics. Genome Res. 19: 1639–1645 [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Lai J., Li R., Xu X., Jin W., Xu M., et al. , 2010.  Genome-wide patterns of genetic variation among elite maize inbred lines. Nat. Genet. 42: 1027–1030 [DOI] [PubMed] [Google Scholar]
  33. Langmead B., Trapnell C., Pop M., Salzberg S. L., 2009.  Ultrafast and memory-efficient alignment of short DNA sequences to the human genome. Genome Biol. 10: R25. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Lee M., Sharopova N., Beavis W. D., Grant D., Katt M., et al. , 2002.  Expanding the genetic map of maize with the intermated B73 × Mo17 (IBM) population. Plant Mol. Biol. 48: 453–461 [DOI] [PubMed] [Google Scholar]
  35. Lewontin R. C., 1962.  Interdeme selection controlling a polymorphism in the house mouse. Am. Nat. 96: 65–78 [Google Scholar]
  36. Li H., Handsaker B., Wysoker A., Fennell T., Ruan J., et al. , 2009.  The sequence alignment/map format and SAMtools. Bioinformatics 25: 2078–2079 [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Liu K., Goodman M., Muse S., Smith J. S., Buckler E., et al. , 2003.  Genetic structure and diversity among maize inbred lines as inferred from DNA microsatellites. Genetics 165: 2117–2128 [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Liu S., Yeh C. T., Ji T., Ying K., Wu H., et al. , 2009.  Mu transposon insertion sites and meiotic recombination events co-localize with epigenetic marks for open chromatin across the maize genome. PLoS Genet. 5: e1000733. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Maron L. G., Guimaraes C. T., Kirst M., Albert P. S., Birchler J. A., et al. , 2013.  Aluminum tolerance in maize is associated with higher MATE1 gene copy number. Proc. Natl. Acad. Sci. USA 110: 5241–5246 [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Maynard Smith J., Haigh J., 1974.  The hitch-hiking effect of a favourable gene. Genet. Res. 23: 23–35 [PubMed] [Google Scholar]
  41. McCarty D. R., Settles A. M., Suzuki M., Tan B. C., Latshaw S., et al. , 2005.  Steady-state transposon mutagenesis in inbred maize. Plant J. 44: 52–61 [DOI] [PubMed] [Google Scholar]
  42. McMullen M. D., Kresovich S., Villeda H. S., Bradbury P., Li H., et al. , 2009.  Genetic properties of the maize nested association mapping population. Science 325: 737–740 [DOI] [PubMed] [Google Scholar]
  43. Neuffer M. G., Coe E. H., Wessler S. R., 1997.  Mutants of Maize. Cold Spring Harbor Laboratory Press, Plainview, NY [Google Scholar]
  44. Odhiambo M. O., Compton W. A., 1987.  Twenty cycles of divergent mass selection for seed size in Corn1. Crop Sci. 27: 1113–1116 [Google Scholar]
  45. Oleksyk T. K., Zhao K., De La Vega F. M., Gilbert D. A., O’Brien S. J., et al. , 2008.  Identifying selected regions from heterozygosity and divergence using a light-coverage genomic dataset from two human populations. PLoS One 3: e1712. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Pan D., Zhang S., Jiang J., Jiang L., Zhang Q., et al. , 2013.  Genome-wide detection of selective signature in Chinese Holstein. PLoS ONE 8: e60440. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Parts L., Cubillos F. A., Warringer J., Jain K., Salinas F., et al. , 2011.  Revealing the genetic structure of a trait by sequencing a population under selection. Genome Res. 21: 1131–1138 [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Paulis J. W., Wall J. S., 1977.  Comparison of the protein compositions of selected corns and their wild relatives, teosinte and Tripsacum. J. Agric. Food Chem. 25: 265–270 [Google Scholar]
  49. Peng B., Li Y., Wang Y., Liu C., Liu Z., et al. , 2011.  QTL analysis for yield components and kernel-related traits in maize across multi-environments. Theor. Appl. Genet. 122: 1305–1320 [DOI] [PubMed] [Google Scholar]
  50. Phillips A. R., Evans M. M., 2011.  Analysis of stunter1, a maize mutant with reduced gametophyte size and maternal effects on seed development. Genetics 187: 1085–1097 [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. R Development Core Team , 2014.  R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna [Google Scholar]
  52. Russell W. K., 2006.  Registration of KLS_30 and KSS_30 populations of maize. Crop Sci. 46: 1405–1406 [Google Scholar]
  53. Sabelli P., Larkins B., 2009.  The contribution of cell cycle regulation to endosperm development. Sex. Plant Reprod. 22: 207–219 [DOI] [PubMed] [Google Scholar]
  54. Sabeti P. C., Reich D. E., Higgins J. M., Levine H. Z., Richter D. J., et al. , 2002.  Detecting recent positive selection in the human genome from haplotype structure. Nature 419: 832–837 [DOI] [PubMed] [Google Scholar]
  55. Saghai-Maroof M. A., Soliman K. M., Jorgensen R. A., Allard R. W., 1984.  Ribosomal DNA spacer-length polymorphisms in barley: mendelian inheritance, chromosomal location, and population dynamics. Proc. Natl. Acad. Sci. USA 81: 8014–8018 [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Salvi S., Sponza G., Morgante M., Tomes D., Niu X., et al. , 2007.  Conserved noncoding genomic sequences associated with a flowering-time quantitative trait locus in maize. Proc. Natl. Acad. Sci. USA 104: 11376–11381 [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Schmidt R. J., Burr F. A., Aukerman M. J., Burr B., 1990.  Maize regulatory gene opaque-2 encodes a protein with a “leucine-zipper” motif that binds to zein DNA. Proc. Natl. Acad. Sci. USA 87: 46–50 [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Schmidt R. J., Ketudat M., Aukerman M. J., Hoschek G., 1992.  Opaque-2 is a transcriptional activator that recognizes a specific target site in 22-kD zein genes. Plant Cell 4: 689–700 [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Schnable P. S., Ware D., Fulton R. S., Stein J. C., Wei F., et al. , 2009.  The B73 maize genome: complexity, diversity, and dynamics. Science 326: 1112–1115 [DOI] [PubMed] [Google Scholar]
  60. Sekhon R. S., Lin H., Childs K. L., Hansey C. N., Buell C. R., et al. , 2011.  Genome-wide atlas of transcription during maize development. Plant J. 66: 553–563 [DOI] [PubMed] [Google Scholar]
  61. Sekhon R. S., Hirsch C. N., Childs K. L., Breitzman M. W., Kell P., et al. , 2014.  Phenotypic and transcriptional analysis of divergently selected maize populations reveals the role of developmental timing in seed size determination. Plant Physiol. 165: 658–669 [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Springer N. M., Ying K., Fu Y., Ji T., Yeh C. T., et al. , 2009.  Maize inbreds exhibit high levels of copy number variation (CNV) and presence/absence variation (PAV) in genome content. PLoS Genet. 5: e1000734. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Swanson-Wagner R. A., Eichten S. R., Kumari S., Tiffin P., Stein J. C., et al. , 2010.  Pervasive gene content variation and copy number variation in maize and its undomesticated progenitor. Genome Res. 20: 1689–1699 [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Tian F., Bradbury P. J., Brown P. J., Hung H., Sun Q., et al. , 2011.  Genome-wide association study of leaf architecture in the maize nested association mapping population. Nat. Genet. 43: 159–162 [DOI] [PubMed] [Google Scholar]
  65. Turner T. L., Stewart A. D., Fields A. T., Rice W. R., Tarone A. M., 2011.  Population-based resequencing of experimentally evolved populations reveals the genetic basis of body size variation in Drosophila melanogaster. PLoS Genet. 7: e1001336. [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Venkatraman E. S., Olshen A. B., 2007.  A faster circular binary segmentation algorithm for the analysis of array CGH data. Bioinformatics 23: 657–663 [DOI] [PubMed] [Google Scholar]
  67. Waples R. S., Do C., 2008.  ldne: a program for estimating effective population size from data on linkage disequilibrium. Mol. Ecol. Resour. 8: 753–756 [DOI] [PubMed] [Google Scholar]
  68. Weir B. S., Cockerham C. C., 1984.  Estimating F-statistics for the analysis of population structure. Evolution 38: 1358–1370 [DOI] [PubMed] [Google Scholar]
  69. Wisser R. J., Murray S. C., Kolkman J. M., Ceballos H., Nelson R. J., 2008.  Selection mapping of loci for quantitative disease resistance in a diverse maize population. Genetics 180: 583–599 [DOI] [PMC free article] [PubMed] [Google Scholar]
  70. Wright S., 1951.  The genetical structure of populations. Ann. Eugen. 15: 323–354 [DOI] [PubMed] [Google Scholar]
  71. Yang Z., van Oosterom E. J., Jordan D. R., Doherty A., Hammer G. L., 2010.  Genetic variation in potential kernel size affects kernel growth and yield of sorghum Crop Sci. 50: 685–695 [Google Scholar]
  72. Yu J., Holland J. B., McMullen M. D., Buckler E. S., 2008.  Genetic design and statistical power of nested association mapping in maize. Genetics 178: 539–551 [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information
supp_198_1_409__index.html (5.4KB, html)
11a4b2116de7253e784ccd24499ab898_genetics.114.167155-1.pdf (993.3KB, pdf)
c6c7be43ea1c4699481b9bb16f97ff78_genetics.114.167155-9.pdf (91.7KB, pdf)
ceba1284dccb4a14338e008579777a15_genetics.114.167155-6.pdf (577.9KB, pdf)
f3c57e7d05fac19d7f482a387ab9bd7d_genetics.114.167155-5.pdf (88.4KB, pdf)
b2316452e529353760b7424677e8e9c3_genetics.114.167155-2.pdf (97.6KB, pdf)
3fb9d4dce4c8d7170f7427ea09050d1d_genetics.114.167155-8.pdf (96KB, pdf)
596f58a0ce8a2636a8e606ca5e8225ea_genetics.114.167155-7.pdf (93.8KB, pdf)
cd76dc13e377b1c289a8ddd453c3f060_genetics.114.167155-4.pdf (121.4KB, pdf)
0cd65d81ea1c5c72b361f2e7da6a0e13_genetics.114.167155-10.pdf (87.7KB, pdf)
668fd6040e57cb84c295739bb8d0a066_genetics.114.167155-3.pdf (81.5KB, pdf)
bfbe0b15e6503dbd7e3e2c9304d85285_genetics.114.167155-11.pdf (65.4KB, pdf)
d1c42789a0db2e5aa8de6bbe5ce791ac_genetics.114.167155-18.pdf (61.5KB, pdf)
2938b7fc454e94f5497304f01570be15_genetics.114.167155-15.pdf (64.6KB, pdf)
9bac2a57259d7ca158e554260772f844_genetics.114.167155-14.pdf (72.1KB, pdf)
0580dbd4a5a95796357cff5795611532_genetics.114.167155-12.xls (2.2MB, xls)
c24a9ab7aca8a152c4ef6c27e0b7fac5_genetics.114.167155-17.xls (167.5KB, xls)
3898e9652aceaa5098590b6e16ed033b_genetics.114.167155-16.pdf (64.5KB, pdf)
66c3f4edb317acd0a03d7925c1d375ad_genetics.114.167155-13.pdf (78.8KB, pdf)

Articles from Genetics are provided here courtesy of Oxford University Press

RESOURCES