Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2014 Aug 26;118(38):11028–11036. doi: 10.1021/jp502233u

Role of Microscopic Flexibility in Tightly Curved DNA

Maryna Taranova †, Andrew D Hirsh ‡, Noel C Perkins ‡, Ioan Andricioaei †,*
PMCID: PMC4174995  PMID: 25155114

Abstract

graphic file with name jp-2014-02233u_0004.jpg

The genetic material in living cells is organized into complex structures in which DNA is subjected to substantial contortions. Here we investigate the difference in structure, dynamics, and flexibility between two topological states of a short (107 base pair) DNA sequence in a linear form and a covalently closed, tightly curved circular DNA form. By employing a combination of all-atom molecular dynamics (MD) simulations and elastic rod modeling of DNA, which allows capturing microscopic details while monitoring the global dynamics, we demonstrate that in the highly curved regime the microscopic flexibility of the DNA drastically increases due to the local mobility of the duplex. By analyzing vibrational entropy and Lipari–Szabo NMR order parameters from the simulation data, we propose a novel model for the thermodynamic stability of high-curvature DNA states based on vibrational untightening of the duplex. This novel view of DNA bending provides a fundamental explanation that bridges the gap between classical models of DNA and experimental studies on DNA cyclization, which so far have been in substantial disagreement.

Introduction

Growing interest in the microscopic flexibility of double-stranded DNA is continuously stimulated by the discovery of new protein–DNA complex structures in which DNA has a significantly curved helical axis or is distorted. Because many of the proteins that sharply bend DNA play a crucial role in gene expression and regulation, flexibility of DNA is believed to contribute importantly to several biological functions. Some examples of regulatory proteins that introduce localized bents in DNA are the T7-RNA polymerase, the lac repressor, the TATA box binding protein (TBP), and the catabolite activator protein (CAP) protein.1 It is also being increasingly recognized that, in instances involving contorted DNA structures, the view that the protein drives the DNA protein interactions needs to be revised; the protein-centric view takes second place to the observation that DNA has the capability to be an active participant in its transactions. In such instances, DNA topology can induce structural changes in the duplex structure, and that it turn can strongly influence the DNA–protein interactions;2 examples are topoisomerase type II enzymes that bind preferentially to the apexes of DNA plectonemes.3

A variety of theoretical models and several physicochemical techniques4−7 have been developed to study DNA conformational properties, and significant advances in our understanding of the DNA flexibility and bendability have been recently made.8−12 However, many aspects of DNA mechanics and their possible effect on the protein binding machinery are still open questions. A particularly intriguing question is whether DNA bending can occur spontaneously or if a bound protein has to exert a strong force on DNA to overwhelm the intrinsic rigidity of the DNA duplex. While various theoretical and experimental approaches have been implemented to characterize the intrinsic bendability of the DNA and to estimate the probability of spontaneous DNA cyclization, there is still ongoing controversy in the field regarding this question.13,14

A classical continuum worm-like chain (WLC) model,15,16 in which the inherent flexibility of DNA is characterized by its persistence length, has been widely used to predict DNA topology. The model has accurately reproduced experimental data for DNA motifs larger than the persistence length of DNA.17−19 Cloutier and Widom20 recently questioned the validity of the WLC description for DNA shorter than the persistence length. They developed ligase-catalyzed DNA cyclization assays to measure the probability of ring closure, that is, the so-called j factor. Measured j factors for 94-base-pair (bp) DNAs were several magnitudes greater than the theoretical predictions. The authors claim that none of the existing DNA looping models accurately describes high-curvature mechanics of DNA and insist on the redevelopment of the formalism.

The study by Cloutier and Widom motivated the development of kinkable21 and meltable22,23 DNA models. The kinkable and the meltable DNA models are extensions of the classical WLC approach, in which DNA was parametrized to account for an enhanced local flexibility of DNA due to the presence of sharp kinks or melted bubbles.

Vologodskii and coworkers have revised the experimental procedure used by Cloutier and Widom and argued that the study was not sufficient to conclude the enhanced DNA flexibility in a highly bent regime. According to Vologodskii et al.,24 the high cyclization efficiency observed in the Cloutier and Widom study is the result of a nonadequate concentration of ligase used in the experiment. Vologodskii and coworkers have developed improved ligase-catalyzed DNA cyclization assays, and the data from their measurements are in a good agreement with the WLC model. However, the validity of the classical WLC model has been recently questioned again. This time, Vafabakhsh and Ha25 have reported high cyclization rates for short DNA motifs (67 to 106 bp) observed in the protein-free fluorescence-based DNA cyclization assays. The results of this study have yet again been challenged by Vologodskii et al.,13 who doubted the accuracy of the j-factor determination and the quality of the DNA duplex used in the Vafabakhsh and Ha experiment. These controversies and mutually exclusive data indicate that there is no agreement on whether sharp localized bending can affect DNA flexibility. Furthermore, the kinkable and the meltable DNA models, the only models that accurately predict high DNA cyclization rates, implicate distortions of the double helix. Several recent studies have demonstrated localized DNA “softening’’ in the absence of kinks and melted regions, modulated by the salt effects.26,27 However, none of the studies has investigated the intrinsic flexibility of the DNA duplex in a highly bent regime.

In the current study, we examine the microscopic structure and flexibility of short DNA (107 bp) via a multiscale modeling approach. The modeling technique involves an interplay between atomistic simulations and continuum representation of DNA and has previously provided insightful results from simulation of complex nucleic acid assemblies.11,12,28 We uncover a significant increase in local flexibility of DNA upon duplex bending by comparing the bond vector dynamics and configurational entropy between linear and circular DNA states. On the basis of simulation data, we propose a model for high-curvature DNA mechanics that involves vibrational untightening of the DNA duplex upon its bending. Our new model of DNA bending posits that “softening’’ of DNA in a highly bent regime is an inherent property of DNA and does not necessarily require kinking or melting of the double helix. The model has several important implications for protein–nucleic acid interaction: it suggests the existence of possible DNA site-recognition mechanism that can take advantage of the shape-specific local mobility of the duplex and provides evidence that DNA bending could be a driving force in protein–DNA complex formation. Calculation of the bond-order parameters from the simulation leads to testable hypotheses via nuclear magnetic resonance (NMR) experiments.

Methods

Setup and Dynamics of the Atomistic Model of DNA

We have set up two identical 107-bp DNA duplexes with a sequence presented in Table 1.

Table 1. Sequence of the 107-bp DNA Duplex.

5′-AGATCGCTGAGGATGACATCGGGGGGCCGTGCGCA
TTCGCCGTGTGGAGCCTGTCAGGTGGTGGTTGTGGTC
TCCCTATAGTGAGTCGTATTAGGATCCG ATGCTTC-3′
Open in a new tab

Each DNA double helix has 10.7 bp per helical turn, which induces a slightly negative twist on DNA. One of the two DNA duplexes was uniformly bent to form a planar circle. The 3′ and 5′ ends of the bent DNA were patched to create a continuous DNA minicircle. Building of atomic coordinates as well as DNA bending and twisting procedures were performed by means of the DNA structure modeling server, 3D-DART.29 Patching of the circular DNA was accomplished in the CHARMM molecular modeling package.30 Initial structures were then subject to energy minimization and all-atom MD simulation in implicit solvent. The system was energy-minimized for 1000 steps and then gradually heated to 300 K with 50 K increments each 200 ps. The heating stage was followed by constant temperature equilibration. The average temperature of the system was maintained at 300 K via a Langevin thermostat with coupling coefficient of 5 ps–1. Vibrations of covalent bonds to hydrogen atoms were harmonically restrained, which allowed 2 fs integration time steps during the MD runs. MD trajectories were obtained with the NAMD package31 using the CHARMM27 force field.32 The solvation effects were simulated with the generalized Born implicit solvent model33 with a cutoff of 16 Å for calculating the Born radius. The long-range interactions were truncated at 18 Å, and the salt concentration was set to 0.2 M. Because the study employs a short linear DNA fragment to mimic the behavior of the long continuous DNA molecule, the ends of the linear DNA motif were restrained from fraying. A root-mean-square displacement of heavy atoms on all four terminal bases was harmonically restrained to an initial structure with a force constant of 1000 kcal/mol/Å2 to preserve the DNA duplex structure on the terminal DNA bases in the linear DNA. Three independent 50 ns long trajectories for each of the DNA systems (linear and circular) were generated from different Maxwell–Boltzman distributed initial conditions. Atomic coordinates were saved every picosecond.

Elastic Rod Model of DNA

We approximate DNA as a homogeneous, isotropic, linear elastic rod with uniform circular cross section.11,34 Specifically, we assume a slender rod undergoing small deflections in which shear deformation and rotary inertia can be neglected (except in the torsional modes). The bending and torsional stiffnesses of the rod are based on the DNA bending and torsional persistence lengths of 50 and 75 nm, respectively.35,36 Following classical Euler–Bernoulli beam theory (see, for example, ref (37)), the equation governing the flexural vibrations of the rod is

graphic file with name jp-2014-02233u_m001.jpg 1

where w(x,t) is the lateral deflection of the rod, A is the bending stiffness, and the linear DNA density ρL is assumed to be equal to 3.32 × 10–15 kg/m. The equation governing the torsional vibration of the rod is

graphic file with name jp-2014-02233u_m002.jpg 2

where θ(x,t) is the angular deflection of the rod, C is the torsional stiffness, ρ is the mass density, and Izz is the polar area moment of inertia equal to πd4/32, where d is the 2 nm diameter of DNA. The DNA length (L) is equal to 107 bp, and thus the radius of the minicircle (R) is equal to 2π/L.

Entropy Calculations from the Atomistic Simulations of DNA

Quasiharmonic frequency analysis was used to calculate the configurational entropy of DNA from MD simulations. The approach is based on estimation of the mass-weighed covariance matrix of the atomic fluctuations obtained from MD trajectory. The matrix is then diagnolized, and the matrix eigenvalues λi are used to compute the quasiharmonic frequencies of bond vibrations: ωi = (kBT/λi)1/2. Configurational entropy is then estimated via formula for the quantum mechanical vibrations in the rigid-rotor harmonic oscillator model38

graphic file with name jp-2014-02233u_m003.jpg 3

where the summation occurs over 3N – 6 vibrational frequencies, where N is the number of heavy atoms in the corresponding DNA system.

The quasiharmonic approach has been implemented to estimate the configurational entropies of circular and linear DNA fragments from the three independent production-run simulations (last 45 ns of a total of 50 ns simulation time). Using eq 3, the time-dependent entropies S(t) were calculated from increasingly long trajectory windows of duration t = 1, 3, 5, 10, 15, 20, ..., 45 ns. Following refs (39 and 40), the entropy at infinite simulation time S∞, that is, at convergence, was extrapolated from the data by fitting the time-dependent entropy points with a function

graphic file with name jp-2014-02233u_m004.jpg 4

where α and γ are the fitting constants.

Entropy Calculations from the Elastic Rod Model of DNA

Following the formalism in ref (41), we compute the natural vibrational frequencies (ωn) of the elastic rod in two conformations, linear and circular. In both cases, we ignore extensional deformations and rigid body modes. In the linear case, we consider a rod with free boundary conditions subject to torsional deformations about the helical axis and bending deformations in the two orthogonal directions. The bending modes for linear DNA are given by

graphic file with name jp-2014-02233u_m005.jpg 5

where x{1–5} = {4.73, 7.85, 11.00, 14.14, 17.28} and π/2(2n + 1) for n > 5. The torsional modes for linear DNA have eigenfrequencies

graphic file with name jp-2014-02233u_m006.jpg 6

In the minicircle case, we consider torsional and in- and out-of-plane bending deformations. The eigenfrequencies for the modes of a DNA ring are41

graphic file with name jp-2014-02233u_m007.jpg 7
graphic file with name jp-2014-02233u_m008.jpg 8
graphic file with name jp-2014-02233u_m009.jpg 9

The vibrational entropy of the elastic rod is then estimated with eq 3 with the summation over the rod natural frequencies (ωn). Upon computing the natural frequencies, we rank the associated wavelengths (1/ωn) in straight and minicircle cases without regard to the type of deformation. As the mode number increases, the difference between the straight and minicircle wavelengths vanishes on account of the wavelength becoming small relative to the diameter of the minicircle. At ∼30 modes, the difference between straight and minicircle conformations drops to 1% of the initial difference, and thus it is unnecessary to consider higher modes. Thus, only the lowest 30 modes are required in the summation in eq 3 to discriminate between linear and minicircle DNA conformations.

Calculation of S2 NMR Order Parameter from the Atomistic Trajectories

To be able to make connections to future NMR measurements, we characterized the local motion in linear and circular DNA fragments by S2 NMR order parameters for deoxyribose H1′–C1′ bond and base C6–H6/C8–H8 bond vectors. The Lipari–Szabo model-free approach42 allows calculation of S2 as well as corresponding correlation time (τ) through the parametrization of the bond–bond auto correlation function with a sum two exponentials

graphic file with name jp-2014-02233u_m010.jpg 10

Here subscripts f and s denote fast and slow motions, respectively, and S2 = Sf2Ss is the plateau of the time autocorrelation function. It is assumed that fast and slow motions are not correlated. Values of S2 close to zero correspond to increased bond mobility, while values of S2 close to 1 correspond to “frozen’’ motion. S2 values for corresponding bond vectors were calculated from the last 40 ns of simulation time. All frames in the trajectory were aligned by least-squares superposition of heavy atoms to remove overall rotation and translation of the system. The bond–bond autocorrelation functions for H1′–C1′, C6–H6, and C8–H8 bond vectors were computed from four trajectory windows, each of duration 10 ns. Plateau values at 1 ns were determined by averaging the tail values of the autocorrelation function. The results were averaged across 12 ensembles.

Results and Discussion

We combined all-atom molecular dynamics simulations and the elastic rod approximation of DNA to determine the difference in structure, dynamics, and flexibility between circular and linear DNA of the same length and superhelical density (see Figure 1). The atomistic simulations reveal spontaneous transitions of DNA double helix into short-lived states characterized by strand stretch and shear, base flips, and local melting. To gain further insight into the dynamics of these transitions, the time evolution of the distances between hydrogen-bond donor (D) and acceptor (A) atoms in the Watson–Crick base pairs (the W&C D–H–A distances) has been analyzed and visualized via the W&C D–H–A distance matrix (see Figure 2a–f). The plots illustrate numerous instances of the W&C D–H–A distances higher than 3.4 Å (regions colored in red and blue), which denote DNA conformations deviated from the canonical B form. It is evident from Figure 2a–f that the deviations of the DNA duplex from the canonical form appear to have stochastic nature and to be sequence-independent. Also, the helical distortions observed in the simulations are reversible within several nanoseconds, with the only exception of a local strand separation in the linear duplex that lasted ∼30 ns and did not reverse within the simulation time (see Figure 2a).

Figure 1.

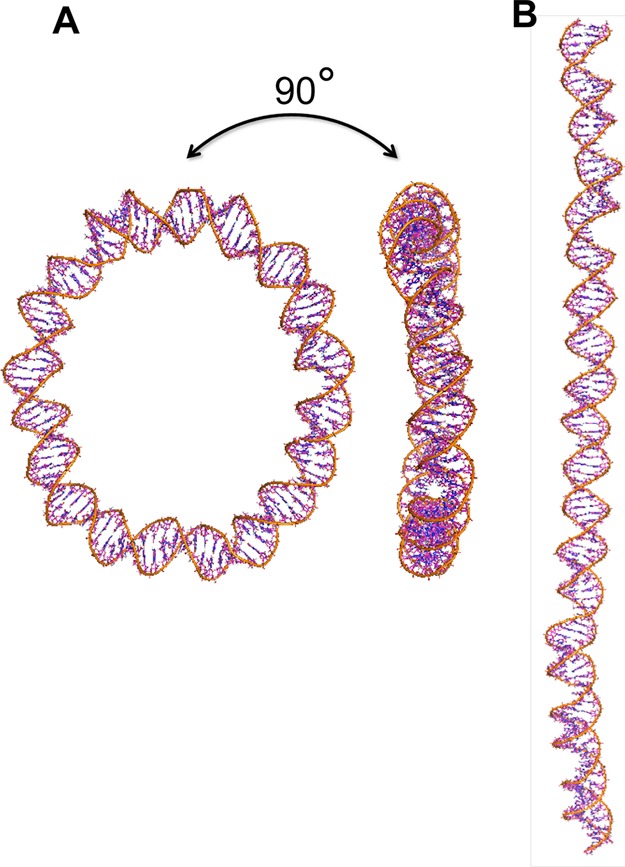
Figure 1

Open in a new tab

Snapshots of the 107-bp DNA minicircle (A) and the 107-bp linear DNA (B) obtained from the atomistic simulations.

Figure 2.

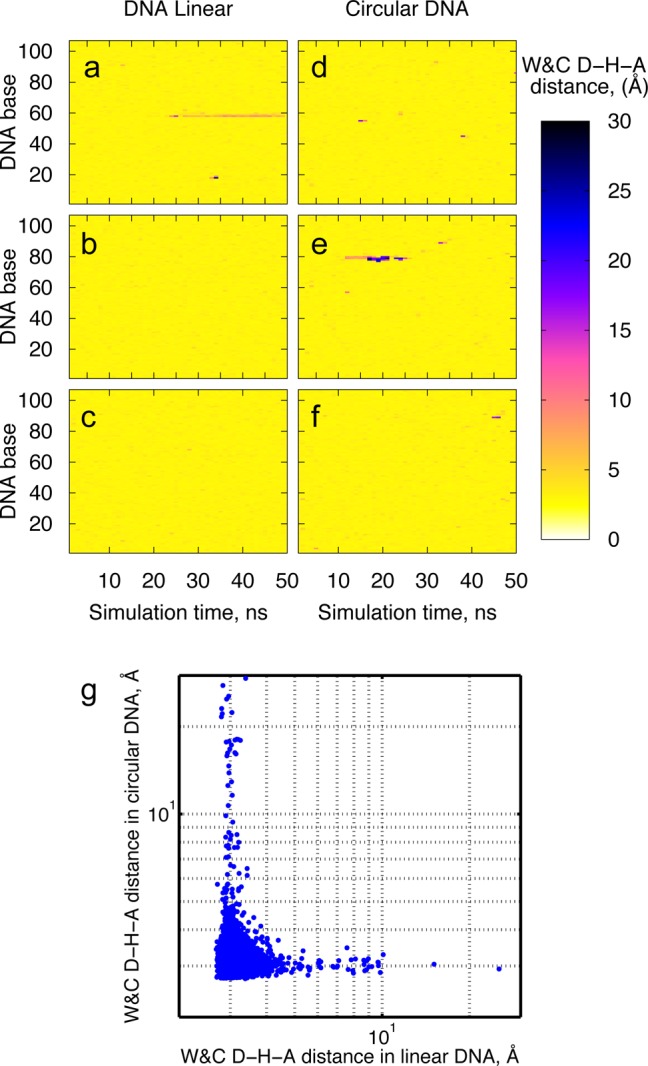
Figure 2

Open in a new tab

W&C D–H–A distance matrix for the linear and circular DNA: Panels a–c present results from the three independent simulation runs of the 107-bp linear DNA, and panels d–f represent the three independent simulation runs of the 107-bp circular DNA. Panel g shows the scatter plot of all instantaneous W&C D–H–A distances in the linear and circular duplexes sampled during the simulation.

While observed for both DNA states, linear and circular, an abundant local dynamics within the duplex is more profound for DNA minicircles: helix disruptions are greater and occur more frequently in the circular DNA as compared with its linear counterpart. This becomes even more evident from the analysis of the scatter plot of the W&C D–H–A distances (see Figure 2g), which illustrates the spread of all instantaneous W&C D–H–A distances sampled during the simulation runs. The plot points out that while the majority of the sampled distances segregate between 2 and 5 Å, large distances (>5 Å) frequently occur in both duplexes during the simulation. It further indicates that circular DNA encounters more instances of hydrogen-bonding distortion during the simulation in contrast with linear duplex and that the overall magnitude of the helical distortions is larger in circular than in linear DNA.

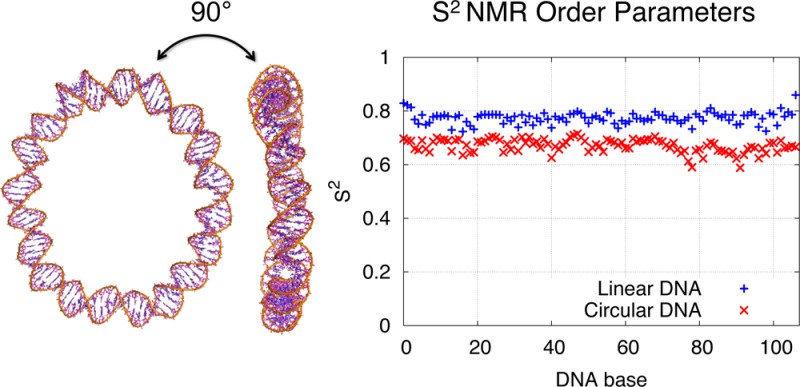
Local motions within linear and circular DNA duplexes were further characterized by NMR order parameter S2. S2 designates an amplitude of the bond–bond autocorrelation function and is often used to describe the bond vector dynamics. We have chosen to examine the behavior of the following DNA bond vectors: the deoxyribose bond vector C1′–H1′ and nucleobase bond vectors C8–H8 (in pyrimidine bases) or C6–H6 (in purine bases). These bond vectors not only provide a sufficient microscopic description of the base and sugar-backbone flexibility but also are easily measurable with NMR carbon spin-relaxation experiments.43,44

Estimated S2 values in linear DNA are in a good agreement with ones measured previously by NMR techniques44−46 or calculated in previous MD experiments.44 In accord with previous study,44 our calculations reveal slightly higher S2 values for C–H bond vectors in the base than in the ribose (see Table 2). The terminal fraying effect was not readily evident in our simulation due to the strong harmonic restrains applied on the terminal bases (see Methods section). The order parameters in linear DNA have been averaged over the nonterminal residues to exclude the contribution of the harmonic force applied to the terminal residues of the linear DNA (see Table 2). Similarly to the linear DNA, circular DNA also demonstrates a slight drop in S2 values (increase in internal motion) from the base to the ribose (see Table 2). The distribution of S2 along the DNA sequence is merely uniform in both linear and circular states, and no significant sequence-dependent mobility variation was noticed. While sequence-dependence effects are expected to exist (for example, when the DNA sequence involves adenosine tracts43), such effects may be masked in our simulation model by the mixed sequence used and may need a larger sampling of sequence space to be observed.

Table 2. S2 Order Parameters for the Ribose and the Base Sites in Linear and Circular DNA Averaged over the Sequence Residues.

  Slin2 Scir2 Δ = Slin2 – Scir
deoxyribose C1′–H1′ bond vector 0.773 ± 0.020 0.670 ± 0.025 0.103 ± 0.032
base C6/8–H6/8 bond vector 0.791 ± 0.026 0.689 ± 0.030 0.102 ± 0.040
Open in a new tab

An important trend is observed when examining the relaxation dynamics of the bond vectors. In the circular DNA, the nucleobase and sugar sites span a narrow S2 range of approximately 0.65 to 0.7 units, which is systematically ∼0.1 units lower than values from the corresponding sites on the linear DNA (see Table 2 and Figure 3). Low S2 values unambiguously characterize enhanced local mobility of sugar-backbone and nucleobases in circular DNA relative to its linear counterpart.

Figure 3.

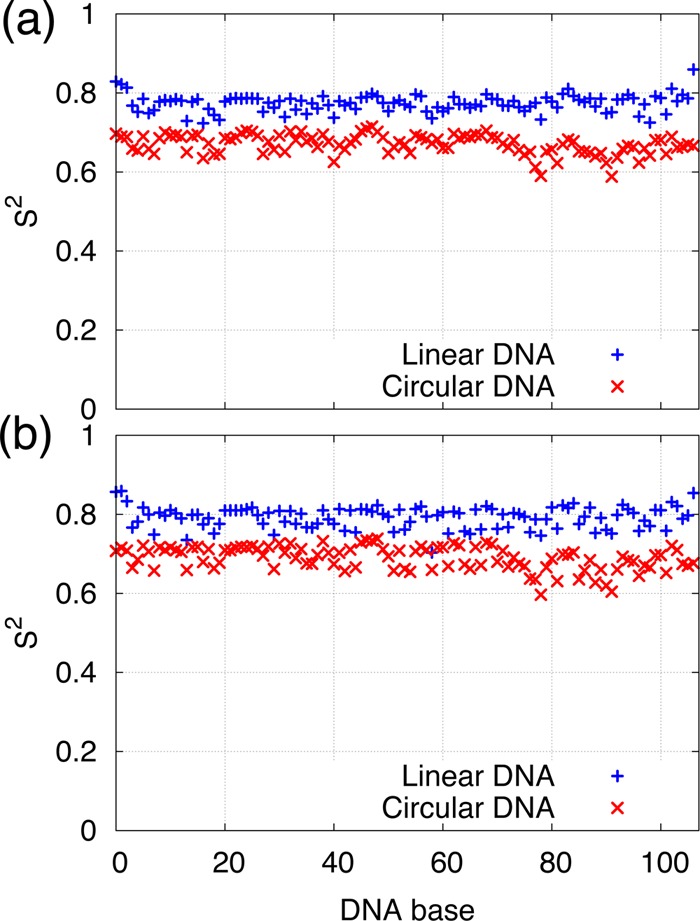
Figure 3

Open in a new tab

S2-NMR order parameters in linear and circular DNA for the deoxyribose H1′-C1′ bond vectors (a) and for the base bond vectors H8–C8/H6-C6 (b).

The Lipari–Szabo model-free approach assumes that the internal and the overall motions are not correlated, and thus because overall motion was eliminated in postprocessing the trajectories (as described in section Methods), the reported S2 parameters describe the internal motion of the DNA duplex and characterize an intrinsic flexibility of the DNA. Complete opening events, while they do occur, are not the main contributors to this intrinsically increased mobility. Compare, for example, Figure 2a–f and Figure 3. Figure 2a–f shows the magnitude and the location of the opening events observed in the simulation, while Figure 3 gives us the S2 parameter for a given location (base). From Figure 2e, one sees that in the circular DNA, the 80–90 bp region has the largest opening events. However, in Figure 3, the S2 values for this region are just slightly lower than the mean S2 value. The large openings around 60 bp in linear DNA are not even evident in the S2 plot for linear DNA.

Instances of unusually low S2 values in nucleic sequences have been reported previously. For example, it has been shown that order parameters can drastically drop by about 0.2 units for nucleic residues flanking A-tracts43 or located on the RNA hairpin loop,47 at the DNA–protein interface,45,48 or at DNA damage49 sites. Our current study uncovers large-amplitude motion in tightly looped DNA duplex. This finding indicates that a new motional model of DNA has to be developed to explain the steady and systematic mobility increase in sharply bent DNA.

Calculation of vibrational entropies provides further insight into the microscopic behavior of tightly looped DNA minicircles and allows us to propose a new model of DNA bending. Various polymer models have been widely used to characterize the behavior of DNA loops.34,50−52 In the realm of the polymer theory, DNA ring closure is an entropically unfavorable process. The loss of entropy is associated with the restricted conformational space available to a polymer chain when its ends are tied together.51 However, the polymer models do not account for the microscopic structure of DNA and hence fail to include entropic contributions from the internal vibrations within the DNA duplex. Conversely, the MD simulations provide an excellent microscopic description of local, that is, bond-level dynamics, but do not capture the large-scale, long-time dynamics (because of the short time scale of the atomistic trajectories). Our study implements the elastic rod representation of DNA, in which the vibrational motion of DNA is approximated as the vibrational motion of a homogeneous elastic rod, together with the atomistic simulations that provide the information on the internal (local) vibrations within the DNA duplex. Merging the two representations of DNA, atomistic and continuum, allows us to estimate entropic costs of DNA cyclization due to both large-scale and internal vibrational fluctuations of the DNA double helix. Computationally, our study is important because large-scale dynamics at the atomic level is impossible to simulate given the prohibitively large simulation time required, while large-scale continuum models (capable of capturing such large-scale motions) lack atomistic resolution.

Vibrational analysis of the continuum model suggests that the cyclization of the 107-bp DNA, which is shorter than the persistence length of the DNA double helix (∼150 bp), occurs with a loss of vibrational entropy −TΔS = 21 kcal·mol–1 (see Table 3). This estimate is comparable to the entropy loss upon cyclization of large polymer chains that has been predicted with the WLC model to be ≃3–5 kcal·mol–1.51,53 The atomistic quasiharmonic analysis reveals that the entropic contribution from the internal motion of the duplex is quite large, and, in contrast with the vibrational entropy of the rod, favors tight DNA looping. The configurational entropy values estimated from the six independent simulation runs (see Table 4) are consistently higher in the circular DNA as opposed to the linear DNA. The calculation suggests that for 107-bp DNA the entropy gain from the internal vibration of the duplex upon its cyclization TΔS accounts to 805 or 7.5 kcal·mol–1 on average per bp (see Table 3). Thus, for sharply bent circular DNA motifs, the entropy gain from the vibrational untightening is at least an order of magnitude greater than the entropy loss from the polymer ring closure. This also implies that for short DNA duplexes, ∼100 bp, the cyclization is an entropically favorable process.

Table 3. Vibrational Entropy Change upon Looping of 107-bp DNA Duplex T(Scir–Slin) at T = 300 K in Units of kcal·mol–1.

  total average per bp
continuum model estimate –21 –0.20
atomistic model estimate 805 ± 445 7.50 ± 4.15
Open in a new tab

Table 4. Calculated DNA Configurational Entropy Values in Units of kcal·mol–1·K–1.

  linear DNA circular DNA
simulation 1 25.857 27.089
simulation 2 24.573 29.281
simulation 3 24.810 26.927
average 25.080 ± 0.683 27.766 ± 1.315
Open in a new tab

It is noteworthy that the change in vibrational entropy of a DNA duplex upon looping of a short duplex is greater than that upon undergoing the B- to Z-DNA transition (∼2 to 3 kcal·mol–1 per bp54) or upon drug intercalation into a DNA dodecamer (∼5 kcal·mol–1 per bp55).

One could argue that the harmonic restraints applied to the terminal base pairs of the linear DNA would restrict the conformational space available to the system and thus would lower the overall configurational entropy of the linear DNA molecule. The simulation data indicate that the mean configurational entropy of a base pair in the linear DNA indeed drops down when bases with harmonic restrains are included in the calculation. However, the drop accounts only to 0.5%. Although the total configurational entropy is estimated from the covariance matrix of collective atomic fluctuations of the entire DNA and not as the summation over individual residues, the underestimate of the total configurational entropy in the linear DNA due to the harmonic restrains should not exceed 0.5%.

On the basis of our calculation of the NMR order parameters and configurational entropy, we propose a new model of DNA bending that comprises a uniform sequence-independent “softening” of the double helix due to the vibrational loosening of the bent duplex. Our model also indicates that the driving force for a DNA high-curvature conformation is the favorable entropic contribution from the vibrational untightening that largely overwhelms the unfavorable entropy loss from the polymer ring closure.

Vibrational loosening and enhanced local flexibility imply a higher probability for a bent DNA duplex to transition into short-lived alternative DNA conformations, which has been observed in our atomistic simulation (see Figure 2). Enhanced local mobility in sharply bent DNA also implicates a higher probability for spontaneous kinking or melting of “soft” regions. This microscopic signature can further refine the kinkable and the meltable statistical models proposed previously.

Structural analysis of the linear and circular duplexes suggests that mechanical stress (in particular, bending) induces a change in hydrogen-bonding formation in DNA duplex. Thus, the W&C D–H–A distances in circular DNA are on average slightly larger than in its linear counterpart (see Table 5). Also, the linear duplex forms more hydrogen bonds than the circular one (see Table 5). On the basis of these observations, we speculate that vibrational untightening and significant increase in internal motion upon DNA looping arise most likely from the distortion of hydrogen bonding and destabilization of the π–π base stacking interaction caused by bending of the DNA double helix. However, a more detailed experimental study is required to elucidate the details of this phenomenon.

Table 5. Hydrogen-Bond Signature Pattern in the Initial (Before Dynamics) Energy-Minimized Linear and Circular Duplex Conformations.

  linear circular
number of hydrogen bondsa 260 224
average D–H–A distance, Å 3.066 ± 0.118 3.083 ± 0.121
Open in a new tab
a

Formation of a hydrogen bond is assumed when the D–H–A distance is <3 Å and the D–H–A angle is <20°.

Interestingly, the atomistic simulations indicate that the formation of a DNA minicircle is also driven by a favorable enthalpic contribution (see Table 6), albeit less favorable than the entropic one (68 vs 805 kcal·mol–1, respectively). Calculation of molecular interaction energies within linear and circular DNA states from the atomistic trajectories reveals an intriguing feature: although the bonded energy (i.e., bond, angle, dihedral, and improper potential energy terms) of DNA duplex grows upon DNA cyclization (by 47 kcal·mol–1), the electrostatic and van der Waals (nonbonded) forces drive the circular duplex into an energetically favorable basin (see Table 6). We assume that the drop of nonbonded interactions is caused by destabilization of the π–π base stacking and distortion of hydrogen bonding in bent DNA. Our observation is in good qualitative agreement with a recently published electrostatic energy landscape for DNA helix bending, which suggests that slightly bent DNA is electrostatically favorable.56 However, the exact value of the enthalpic contribution calculated in our simulation should be interpreted with caution. The implicit solvent model implemented in the simulation accounts only for partial screening of Coulombic repulsion/attraction forces between two strands that are brought together. In real systems, positively charged ions could reside in the DNA grooves or bind to the strand phosphates. Ion binding and correlation between ions would induce additional attraction between DNA strands and thus further facilitate DNA bending.26,27

Table 6. Interaction Energy Change upon DNA looping (Ucir–Ulin) in Units of kcal·mol–1.

bonded energy 47 ± 1
nonbonded energy –115 ± 4
total –68 ± 4
Open in a new tab

The relaxed bond distance interaction observed in the DNA minicircle implies a spontaneous curvature of the DNA duplex that is independent of the sequence, which, in turn, suggests that thermal fluctuations could drive the DNA interconversion between the linear and circular states. However, a (slow) kinetics of the interconversion between two states is defined by a (large) potential barrier that separates the two stable minima on the energetic hyper surface. Because of the slow kinetics of the process, the interconversion of the linear and circular DNA forms occurs on a time scale exceeding the simulation time of the current study and therefore is not evident in the current atomistic simulations.

In contrast with explicit representation of solvent molecules, a less accurate generalized Born implicit solvent (GBIS) model allows a much more efficient sampling of conformational space and hence a better estimate of configurational entropy. Given the large size of the DNA models in the current simulation study, we choose to sacrifice atomic solvent details for computational efficiency and therefore use the GBIS. However, one may argue that some of the observed flexibility in a bent DNA duplex could be an artifact caused by the approximations in the implicit solvent model. Several previous studies examined the effect of the GBIS model on linear DNA57−59 and on small DNA minicircles.57,60,61 They show that the average structure of the linear DNA oligomers modeled with the GBIS is in a good agreement with the results of explicitly solvated calculations, although a slight increase in flexibility is observed for the GBIS. Less agreement between the implicit and the explicit solvation models was reported for the circular DNA. A study by Mitchell and Harris reveals that the structural form of helix disruptions differs between the two solvent models.57 However, the authors insist that the GBIS is a legitimate approximation if one aims to estimate the overall shape and the amount of DNA denaturation but not the specific structure of the helix disruptions.57 Provided that we aim to examine the overall local flexibility of the duplex but not the specific structure of the helix disruptions, we are confident that the GBIS is a good choice. Previously, the GBIS was successfully implemented to model DNA minicircles of ∼100 base pairs and provided results that were in a good agreement with explicit calculation10,57,60,61 Furthermore, it was demonstrated57 that the local DNA flexibility increases with the torsional load on the circular DNA duplex (either positive or negative) in both solvation models but is less evident in the implicit calculations.57 This observation implies that the local flexibility and the destruction of the hydrogen bonding observed in the slightly underwound DNA minicircles of our simulation study would only increase in explicit solvent calculations, which in turn would increase the difference between the circular and linear DNA and thus reinforce the present simulation results.

Conclusions

New aspects of DNA cyclization are revealed in the current study. Our simulations suggest a local, bp-level vibrational loosening of DNA upon duplex bending, which results in an enhanced microscopic flexibility in bent and looped DNA motifs. Here we discuss a physiological relevance of this finding and propose an experimental study that could investigate this new view in greater detail.

The inclusion of local motional in loosening of DNA during bending provides an explanation for spontaneous cyclization of DNA duplex observed in ligase-catalyzed and fluorescence-based DNA cyclization assays (see the discussion in the Introduction). We can justify the discrepancy between the experimental data and the classical WLC model predictions by the localized “softening’’ of bent DNA regions, which the WLC approach or any continuum representation of DNA does not account for. We demonstrate that the gain in inherent microscopic flexibility of the DNA duplex upon bending is substantial and hence should be incorporated into the existing models of DNA looping.

A significant entropy gain upon sharp DNA bending might be an important factor in the choice of a thermodynamic strategy for protein–DNA complex formation. The binding entropy has been largely attributed to the conformational rearrangements within the DNA and the protein at the interaction interface and the displacement of water molecules from the binding site.62,63 However, a recent study has uncovered an intriguing systemic relationship between structural properties of the complex and the thermodynamics of binding. Its authors argue that there is a positive correlation between the extent of DNA bending/distortion in protein–DNA complexes and the entropic contribution to the binding free energy.64 Our model for DNA bending speaks in favor of this notion. The model also suggests that favorable entropic contribution from the vibrational loosening of bent DNA might be the driving force in formation of such complexes. An average DNA binding site is ∼4–6 bp long. According to our model, the entropy gain upon bending of binding sequence of this length should vary in the range of ∼30 to 45 kcal·mol–1. Provided that the binding entropy does not exceed 30 kcal·mol–1,64 it is very likely that the entropy gain upon helix bending contributes the most to the free entropy of binding.

Many proteins recognize and bind to a specific DNA sequence. These proteins are called site-specific and bind to their target sequence with affinities much higher in comparison with random sequences. A sequence recognition mechanism has been studied rigorously, and two strategies for sequence readout (direct an indirect) have been proposed. The direct readout implies that protein amino acid side chains directly examine a hydrogen-bonding pattern between the four bases along the DNA. The mechanism of indirect readout relies on examining the overall structure generated by the sequence, for example, by recognizing the sequence-dependent mechanical properties of the duplex, structural inhomogeneities, differences in stacking and twisting parameters, and sequence-dependent flexibility and bendability of the DNA.

It has also been demonstrated that regulatory proteins exhibit unusually high affinities when they bind to prebent DNA binding sites,65−70 indicating that “learning” DNA shape is an important component of site-specific recognition. However, the exact molecular mechanism of DNA shape readout has not been uncovered. The new model of DNA bending allows us to propose a new strategy for DNA shape recognition that takes advantage of the conformation-specific local mobility of the DNA duplex. According to our model, local bond dynamics in prebent unbound DNA depends on the extent of vibrational untightening, which is dictated by the intrinsic curvature of the duplex. The model suggests that protein can recognize the shape of the DNA by probing the internal motion of the duplex. We propose that the DNA shape recognition, based on “censoring’’ the local details of the mobility of the duplex, could be an effective search strategy for bent DNA regions.

Furthermore, we argue that enhanced local mobility of the prebent DNA region would allow a more sufficient sampling of conformational space of DNA binding site, optimizing a search for the best fit DNA conformation. The best fit of the DNA binding site assures a tighter protein binding, which results in higher binding affinity. Similar mobility considerations have been recently proposed for the existence of a “second-tier” genetic code involving motions in “excited” DNA Hoogsteen states.9

High-curvature DNA mechanics might also alter interconversion pathways between alternative DNA conformations, such as A, B, Z, and S, and affect the mechanism of ligand intercalation into the DNA. It has been demonstrated in previous studies that inclusion of a ligand in between base pairs of DNA requires local vibrational untightening of the duplex around the binding site55 and might cause duplex bending. The vibrational entropy loss due to the ligand intercalation is ∼5 kcal·mol–1 per bp.55 Thus, vibrational loosening of the duplex upon bending implies facilitated ligand insertion into high-curvature DNA regions. Transitions of DNA into alternative forms occur on a complicated free-energy landscape and often involve the formation of noncanonical intermediate conformers.71 Curved DNA regions with inherently high entropy could drive the structural transition along a pathway that is different from the one for linear molecule to accommodate vibrational freedom of the duplex.

Vibrational loosening of bent DNA duplex could similarly be a key mechanism underlying allosteric properties of DNA. A recent study of allostery through DNA72 has demonstrated that protein binding affinity to DNA is highly correlated with another binding event through the separation distance between the two sites. The authors also provide evidence that the degree of correlation between the two events largely depends on the mechanical properties of the linker DNA. We further argue that the two sequential binding events are most likely to be modulated throughout the vibrational loosening of the DNA duplex caused by the first event.

In summary, we have proposed a new model of DNA bending based on vibrational loosening of bent duplex and characterized by an enhanced local dynamics of sharply bent regions. Bond dynamics in DNA minicircles can be probed by NMR experiments. In particular, S2 values for C–H bonds can be measured with NMR carbon relaxation techniques and compared with the order parameters calculated in the current study.

The presence of an enhanced microscopic flexibility in a bent DNA brings us one step closer to understanding of the structural and energetic principles of DNA architecture. The proposed model of DNA bending suggests new mechanisms for protein–DNA and drug–DNA interaction and complex formation. The knowledge of the microscopic flexibility of the DNA obtained from this study can be beneficial for future design, engineering, and manipulation of various nucleic-acid-based nanomaterials.

Acknowledgments

We acknowledge funding from NIH grant 5R01GM089846 and thank the National Energy Research Scientific Computing Center and TeraGrid/XSEDE for supercomputing allocation awards.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States

References

  1. Williams M. C.; Maher L. J.. Biophysics of DNA-Protein Interactions; Springer Science+Business Media: New York, 2010. [Google Scholar]
  2. Fogg J. M.; Randall G. L.; Pettitt B. M.; Sumners D. W. L.; Harris S. A.; Zechiedrich L. Bullied No More: When and How DNA Shoves Proteins Around. Q. Rev. Biophys. 2012, 45, 257–299. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Vologodskii A. V.; Zhang W.; Rybenkov V. V.; Podtelezhnikov A. A.; Subramanian D.; Griffith J. D.; Cozzarelli N. R. Mechanism of Topology Simplification by Type II DNA Topoisomerases. Proc. Natl. Acad. Sci. U.S.A. 2001, 98, 3045–3049. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Robinson B. H.; Drobny G. P. Site-Specific Dynamics in DNA: Theory and Experiment. Methods Enzymol. 1995, 261, 451–509. [DOI] [PubMed] [Google Scholar]
  5. Millar D. P. Fluorescence Studies of DNA and RNA Structure and Dynamics. Curr. Opin. Struct. Biol. 1996, 6, 322–326. [DOI] [PubMed] [Google Scholar]
  6. Cohen A. E.; Moerner W. E. Principal-Components Analysis of Shape Fluctuations of Single DNA Molecules. Proc. Natl. Acad. Sci. U.S.A. 2007, 104, 12622–12627. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Cohen A. E.; Moerner W. E. Internal Mechanical Response of a Polymer in Solution. Phys. Rev. Lett. 2007, 98, 116001–116004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Matsumoto A.; Tobias I.; Olson W. K. Normal-Mode Analysis of Circular DNA at the Base-Pair Level. 1. Comparison of Computed Motions with the Predicted Behavior of an Ideal Elastic Rod. J. Chem. Theory Comput. 2005, 1, 117–129. [DOI] [PubMed] [Google Scholar]
  9. Nikolova E. N.; Kim E.; Wise A. A.; O’Brien P. J.; Andricioaei I.; Al-Hashimi H. M. Transient Hoogsteen Base Pairs in Canonical Duplex DNA. Nature 2011, 470, 498–502. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Bomble Y. J.; Case D. A. Multiscale Modeling of Nucleic Acids: Insights into DNA Flexibility. Biopolymers 2008, 89, 722–731. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Hirsh A. D.; Lillian T. D.; Lionberger T. A.; Taranova M.; Andricioaei I.; Perkins N. C. A Model for Highly Strained DNA Compressed Inside a Protein Cavity. J. Comput. Nonlinear Dyn. 2013, 8, 031001–031008. [Google Scholar]
  12. Hirsh A. D.; Taranova M.; Lionberger T. A.; Lillian T. D.; Andricioaei I.; Perkins N. C. Structural Ensemble and Dynamics of Toroidal-like DNA Shapes in Bacteriophage ϕ29 Exit Cavity. Biophys. J. 2013, 104, 2058–2067. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Vologodskii A.; Du Q.; Frank-Kamenetskii M. D. Bending of Short DNA Helices. Artif. DNA: PNA XNA 2013, 4, 1–3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Vologodskii A.; Frank-Kamenetskii M. D. Strong Bending of the DNA Double Helix. Nucleic Acids Res. 2013, 14, 6785–6792. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Doi M.The Theory of Polymer Dynamics; Oxford University Press: New York, 1988. [Google Scholar]
  16. Rubinstein M.; Colby R. H.. Polymer Physics; Oxford University Press: New York, 2003. [Google Scholar]
  17. Shaw S. Y.; Wang J. C. Knotting of a DNA Chain During Ring Closure. Science 1993, 260, 533–536. [DOI] [PubMed] [Google Scholar]
  18. Klenin K. V.; Vologodskii A. V.; Anshelevich V. V.; Dykhne A. M.; Frank-Kamenetskii M. D. Effect of Excluded Volume on Topological Properties of Circular DNA. J. Biomol. Struct. Dyn. 1988, 5, 1173–1185. [DOI] [PubMed] [Google Scholar]
  19. Rybenkov V. V.; Vologodskii A. V.; Cozzarelli N. R. The Effect of Ionic Conditions on the Conformations of Supercoiled DNA. II. Equilibrium Catenation. J. Mol. Biol. 1997, 267, 312–323. [DOI] [PubMed] [Google Scholar]
  20. Cloutier T. E.; Widom J. Spontaneous Sharp Bending of Double-Stranded DNA. Mol. Cell 2004, 14, 355–362. [DOI] [PubMed] [Google Scholar]
  21. Wiggins P. A.; Phillips R.; Nelson P. C. Exact Theory of Kinkable Elastic Polymers. Phys. Rev. E 2005, 71, 0219091–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Sivak D. A.; Geissler P. L. Consequences of Local Inter-Strand Dehybridization for Large-Amplitude Bending Fluctuations of Double-Stranded DNA. J. Chem. Phys. 2012, 136, 0451021–11. [DOI] [PubMed] [Google Scholar]
  23. Forties R. A.; Bundschuh R.; Poirier M. G. The Flexibility of Locally Melted DNA. Nucleic Acids Res. 2009, 37, 4580–4586. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Du Q.; Smith C.; Shiffeldrim N.; Vologodskaia M.; Vologodskii A. Cyclization of Short DNA Fragments and Bending Fluctuations of the Double Helix. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 5397–5402. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Vafabakhsh R.; Ha T. Extreme Bendability of DNA Less than 100 Base Pairs Long Revealed by Single-Molecule Cyclization. Science 2012, 337, 1097–1101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Spiriti J.; Kamberaj H.; de Graff A. M. R.; Thorpe M. F.; van der Vaart A. DNA Bending through Large Angles Is Aided by Ionic Screening. J. Chem. Theory Comput. 2012, 8, 2145–2156. [DOI] [PubMed] [Google Scholar]
  27. Manning G. S. The Contribution of Transient Counterion Imbalances to DNA Bending Fluctuations. Biophys. J. 2006, 90, 3208–3215. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Lillian T. D.; Taranova M.; Wereszczynski J.; Andricioaei I.; Perkins N. C. A Multiscale Dynamic Model of DNA Supercoil Relaxation by Topoisomerase IB. Biophys. J. 2011, 100, 2016–2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. van Dijk M.; Bonvin A. M. J. J. 3D-DART: a DNA Structure Modelling Server. Nucleic Acids Res. 2009, 37, W235–W239. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Brooks B. R.; Bruccoleri R. E.; Olafson B. D.; States D. J.; Swaminathan S.; Karplus M. CHARMM: A Program for Macromolecular Energy, Minimization, and Dynamics Calculations. J. Comput. Chem. 1983, 4, 187–217. [Google Scholar]
  31. Phillips J. C.; Braun R.; Wang W.; Gumbart J.; Tajkhorshid E.; Villa E.; Chipot C.; Skeel R. D.; Kale L.; Schulten K. Scalable Molecular Dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. MacKerell A. D.; Banavali N.; Foloppe N. Development and Current Status of the CHARMM Force Field for Nucleic Acids. Biopolymers 2000, 56, 257–265. [DOI] [PubMed] [Google Scholar]
  33. Onufriev A.; Bashford D.; Case D. A. Modification of the Generalized Born Model Suitable for Macromolecules. J. Phys. Chem. 2000, 104, 3712–3720. [Google Scholar]
  34. Hirsh A. D.; Lillian T. D.; Lionberger T. A.; Perkins N. C. DNA Modeling Reveals an Extended Lac Repressor Conformation in Classic in Vitro Binding Assays. Biophys. J. 2011, 101, 718–726. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Hagerman P. J. Flexibility of DNA. Annu. Rev. Biophys. Chem. 1988, 17, 265–86. [DOI] [PubMed] [Google Scholar]
  36. Schlick T. Modeling superhelical DNA: Recent Analytical and Dynamic Approaches. Curr. Opin. Struct. Biol. 1995, 5, 245–262. [DOI] [PubMed] [Google Scholar]
  37. Inman D. J.Engineering Vibrations; Prentice Hall: Upper Saddle River, NJ, 2001. [Google Scholar]
  38. Andricioaei I.; Karplus M. On the Calculation of Entropy from Covariance Matrices of the Atomic Fluctuations. J. Chem. Phys. 2001, 115, 6289–6292. [Google Scholar]
  39. Harris S. A.; Gavathiotis E.; Searle M. S.; Orozco M.; Laughton C. A. Cooperativity in Drug-DNA Recognition: a Molecular Dynamics Study. J. Am. Chem. Soc. 2001, 123, 12658–12663. [DOI] [PubMed] [Google Scholar]
  40. Harris S. A.; Laughton C. A. A Simple Physical Description of DNA Dynamics: Quasi-harmonic Analysis as a Route to the Configurational Entropy. J. Phys.: Condens. Matter 2007, 19, 076103–076114. [DOI] [PubMed] [Google Scholar]
  41. Blevins R. D.Formulas for Natural Frequency and Mode Shape; Van Nostrand Reinhold Company; New York, 1979. [Google Scholar]
  42. Lipari G.; Szabo A. Model-Free Approach to the Interpretation of Nuclear Magnetic-Resonance Relaxation in Macromolecules 0.1. Theory and Range of Validity. J. Am. Chem. Soc. 1982, 104, 4546–4559. [Google Scholar]
  43. Nikolova E. N.; Bascom G. D.; Andricioaei I.; Al-Hashimi H. M. Probing Sequence-Specific DNA Flexibility in A-tracts and Pyrimidine-Purine Steps by Nuclear Magnetic Resonance 13C Relaxation and Molecular Dynamics Simulations. Biochemistry 2012, 51, 8654–8664. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Duchardt E.; Nilsson L.; Schleucher J. Cytosine Ribose Flexibility in DNA: a Combined NMR 13C Spin Relaxation and Molecular Dynamics Simulation Study. Nucleic Acids Res. 2008, 36, 4211–4219. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Shajani Z.; Varani G. 13C Relaxation Studies of the DNA Target Sequence for Hhai Methyltransferase Reveal Unique Motional Properties. Biochemistry 2008, 47, 7617–7625. [DOI] [PubMed] [Google Scholar]
  46. Kojima C. C.; Ono A. A.; Kainosho M. M.; James T. L. DNA Duplex Dynamics: NMR Relaxation Studies of a Decamer with Uniformly 13C-Labeled Purine Nucleotides. J. Magn. Reson. 1998, 135, 310–333. [DOI] [PubMed] [Google Scholar]
  47. Hall K. B.; Tang C. 13C Relaxation and Dynamics of the Purine Bases in the Iron Responsive Element RNA Hairpin. Biochemistry 1998, 37, 9323–9332. [DOI] [PubMed] [Google Scholar]
  48. Khandelwal P.; Panchal S. C.; Radha P. K.; Hosur R. V. Solution Structure and Dynamics of GCN4 Cognate DNA: NMR Investigations. Nucleic Acids Res. 2001, 29, 499–505. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Spielmann H. P. Dynamics in Psoralen-Damaged DNA by 1H-Detected Natural Abundance 13C NMR Spectroscopy. Biochemistry 1998, 37, 5426–5438. [DOI] [PubMed] [Google Scholar]
  50. Lillian T. D.; Goyal S.; Kahn J. D.; Meyhöfer E.; Perkins N. C. Computational Analysis of Looping of a Large Family of Highly Bent DNA by LacI. Biophys. J. 2008, 95, 5832–5842. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Hanke A.; Metzler R. Entropy Loss in Long-Distance DNA Looping. Biophys. J. 2003, 85, 167–173. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Duplantier B. Statistical Mechanics of Polymer Networks of any Topology. J. Stat. Phys. 1989, 54, 581–680. [Google Scholar]
  53. Allemand J. F.; Cocco S. S.; Douarche N. N.; Lia G. G. Loops in DNA: an Overview of Experimental and Theoretical Approaches. Eur. Phys. J. E 2006, 19, 293–302. [DOI] [PubMed] [Google Scholar]
  54. Wereszczynski J.; Andricioaei I. Conformational and Solvent Entropy Contributions to the Thermal Response of Nucleic Acid-Based Nanothermometers. J. Phys. Chem. B 2010, 114, 2076–2082. [DOI] [PubMed] [Google Scholar]
  55. Kolář M.; Kubař T.; Hobza P. Sequence-Dependent Configurational Entropy Change of DNA upon Intercalation. J. Phys. Chem. 2010, 114, 13446–13454. [DOI] [PubMed] [Google Scholar]
  56. Tan Z. J.; Chen S. J. Electrostatic Free Energy Landscapes for DNA Helix Bending. Biophys. J. 2008, 94, 3137–3149. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Mitchell J.; Harris S. Testing the Use of Implicit Solvent in the Molecular Dynamics Modelling of DNA Flexibility. Prog. Theor. Phys. Suppl. 2011, 191, 96–108. [Google Scholar]
  58. Tsui V. V.; Case D. A. Theory and Applications of the Generalized Born Solvation Model in Macromolecular Simulations. Biopolymers 2000, 56, 275–291. [DOI] [PubMed] [Google Scholar]
  59. Sands Z. A.; Laughton C. A. Molecular Dynamics Simulations of DNA Using the Generalized Born Solvation Model: Quantitative Comparisons with Explicit Solvation Results. J. Phys. Chem. B 2004, 108, 10113–10119. [Google Scholar]
  60. Harris S. A.; Laughton C. A.; Liverpool T. B. Mapping the Phase Diagram of the Writhe of DNA Nanocircles Using Atomistic Molecular Dynamics Simulations. Nucleic Acids Res. 2008, 36, 21–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Ruscio J. Z.; Onufriev A. A computational Study of Nucleosomal DNA Flexibility. Biophys. J. 2006, 91, 4121–4132. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Baldwin R. L. Temperature Dependence of the Hydrophobic Interaction in Protein Folding. Proc. Natl. Acad. Sci. U.S.A. 1986, 83, 8069–8072. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Spolar R. S.; Record M. T. J. Coupling of Local Folding to Site-Specific Binding of Proteins to DNA. Science 1994, 263, 777–784. [DOI] [PubMed] [Google Scholar]
  64. Jen-Jacobson L. L.; Engler L. E.; Jacobson L. A. Structural and Thermodynamic Strategies for Site-Specific DNA Binding Proteins. Structure 2000, 8, 1015–1023. [DOI] [PubMed] [Google Scholar]
  65. Parvin J. D.; McCormick R. J.; Sharp P. A.; Fisher D. E. Pre-Bending of a Promoter Sequence Enhances affinity for the TATA-Binding Factor. Nature 1995, 373, 724–727. [DOI] [PubMed] [Google Scholar]
  66. Starr D. B.; Hoopes B. C.; Hawley D. K. DNA Bending is an Important Component of Site-Specific Recognition by the TATA Binding protein. J. Mol. Biol. 1995, 250, 434–446. [DOI] [PubMed] [Google Scholar]
  67. Kahn J. D.; Crothers D. M. Protein-Induced Bending and DNA Cyclization. Proc. Natl. Acad. Sci. U.S.A. 1992, 89, 6343–6347. [DOI] [PMC free article] [PubMed] [Google Scholar]
  68. Zhang Y.; Xi Z.; Hegde R. S.; Shakked Z.; Crothers D. M. Predicting Indirect Readout Effects in Protein-DNA Interactions. Proc. Natl. Acad. Sci. U.S.A. 2004, 101, 8337–8341. [DOI] [PMC free article] [PubMed] [Google Scholar]
  69. Kahn J. D.; Yun E.; Crothers D. M. Detection of Localized DNA Flexibility. Nature 1994, 368, 163–166. [DOI] [PubMed] [Google Scholar]
  70. van den Broek B.; Lomholt M. A.; Kalisch S.-M. J.; Metzler R.; Wuite G. J. L. How DNA Coiling Enhances Target Localization by Proteins. Proc. Natl. Acad. Sci. U.S.A. 2008, 105, 15738–15742. [DOI] [PMC free article] [PubMed] [Google Scholar]
  71. Moradi M.; Babin V.; Roland C.; Sagui C. Reaction Path Ensemble of the B-Z-DNA Transition: a Comprehensive Atomistic Study. Nucleic Acids Res. 2013, 41, 33–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
  72. Kim S.; et al. Probing Allostery Through DNA. Science 2013, 339, 816–819. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES