Disease mapping

14.1 Background

The mapping of disease incidence and prevalence has long been a part of public health, epidemiology, and the study of disease in human populations (Koch, 2005). In this chapter, we focus on the challenge of obtaining reliable statistical estimates of local disease risk based on counts of observed cases within small administrative districts or regions coupled with potentially relevant background information (e.g., the number of individuals at risk and, possibly, covariate information, such as the regional age distribution, measures of socioeconomic status, or ambient levels of pollution). Our goals are twofold: we want statistically precise (i.e., low variance) local estimates of disease risk for each region, and we also want the regions to be “small” in order to maintain geographic resolution (i.e., we want the map to show local detail as well as broad trends). The fundamental problem in meeting both goals is that they are directly at odds with one another: the areas are not only “small” in geographic area (relative to the area of the full spatial domain of interest) resulting in a detailed map, but also “small” in terms of local sample size, resulting in deteriorated local statistical precision.

Classical design-based solutions to this problem are often infeasible since the local sample sizes within each region required for desired levels of statistical precision are often unavailable or unattainable. For example, large national or state health surveys in the United States such as the National Health Interview Survey, the National Health and Nutrition Examination Survey, or the Behavioral Risk Factor Surveillance System provide design-based estimates of aggregate or average values at the national or possibly the state level. But, even as large as they are, such surveys often do not include sufficient sample sizes at smaller geographic levels to allow accurate, local, design-based estimation everywhere (Schlaible, 1996).

In contrast, model-based approaches offer a mechanism to “borrow strength” across small areas to improve local estimates, resulting in the smoothing of extreme rates based on small local sample sizes. Such approaches often are expressed as mixed effects models and trace back to the work of Fay and Herriot (1979), who proposed the use of random intercepts to pool information and provide subgroup-level estimated rates. Their model forms the basis of a considerable literature in small area estimation (Ghosh and Rao, 1994; Ghosh et al. 1998, Rao, 2003) which sees wide application in the analysis of statistical surveys, including the aforementioned health surveys (Raghunathan et al., 2007).

While addressing the fundamental problem of analyzing data from subsets with small sample sizes, most traditional approaches to small area estimation are non-spatial; the methods essentially borrow information equally across all small areas without regard to their relative spatial locations and smoothing estimates toward a global mean. In the statistical literature, “disease mapping” refers to a collection of methods extending small area estimation to directly utilize the spatial setting and assumed positive spatial correlation between observations, essentially borrowing more information from neighboring areas than from areas far away and smoothing local rates toward local, neighboring values. The term “disease mapping” itself derives from Clayton and Kaldor (1987), who defined empirical Bayesian methods building from Poisson regression with random intercepts defined with spatial correlation. This hierarchical approach provides a convenient conceptual framework wherein one induces (positive) spatial correlation across the estimated local disease rates via a conditionally autoregressive (CAR; Besag, 1974 and Chapter 13, this volume) random effects distribution assigned to the area-specific intercepts. The models were extended to a fully Bayesian setting by Besag, York, and Mollié (1991) and are readily implemented via Markov chain Monte Carlo (MCMC) algorithms (Chapter 13, this volume). The framework is inherently hierarchical and almost custom-made for MCMC, allowing straightforward extensions to allow for model-based estimation of covariate effects (in spatially correlated outcomes), prediction of missing data (e.g., if a county neglects to report the number of new cases for a particular month when reports are available for neighboring counties), and spatio-temporal covariance structures.

In both the non-spatial and spatial settings, the amount of smoothing is determined by the data and the formulation of the model. This smoothing permits easy visualization of the underlying geographic pattern of disease. We remark, however, that such smoothing may not be appropriate if the goal is instead to identify boundaries or regions of rapid change in the response surface, since smoothing is antithetic to this purpose. For more on this area, called boundary analysis or wombling, see Banerjee and Gelfand (2006), Ma et al. (2009), and Banerjee (Chapter 30, this volume).

In the sections below, we describe in detail the basic model structure of the CAR models typically used in disease mapping, their implementation via MCMC, and various extensions to handle more complex data structures (e.g., spatiotemporal data, multiple diseases, etc.). We also illustrate the methods using real-data examples, and comment on related issues in software availability and usage.

14.2 Hierarchical Models for Disease Mapping

In this section, we outline the essential elements and structure of the CAR-based family of hierarchical disease mapping models. Additional detailed development and further illustrations of the models appear in several texts and book chapters, including Mollié (1996), Best et al. (1999), Lawson (2001), Wakefield et al. (2000), Banerjee et al. (2004, Sec. 5.4), Waller and Gotway (2004, Sec. 9.5), Waller (2005), Carlin and Louis (2009, Sec. 7.7.2).

14.2.1 The generalized linear model

To begin, suppose we observe counts of disease cases Y_i for a set of regions i = 1,…,I partitioning our study domain 𝒟. We model the counts as either Poisson or binomial random variables in generalized linear models, using a log or logit link function, respectively. In some cases we may also have observed values of region-specific covariates x_i with associated parameters β. Other data often include either the local number of individuals at risk n_i or a local number of cases “expected” under some null model of disease transmission (e.g., constant risk for all individuals), denoted E_i. We assume the n_i (alternatively, the E_i) values are fixed and known.

We typically justify the use of a Poisson model as an approximation to a binomial model when the disease is rare (i.e., the binomial probability is small). We focus on Poisson models here, based on the relative rarity of the diseases in our examples, and refer readers to Wakefield (2001, 2003, 2004, Chapter 29, this volume) for a full discussion of the binomial approach, as well as related concerns about the ecological fallacy, i.e., the tendency of correlations obtained from fitting at an aggregate (say, regional) level to overstate those that would be obtained if the data allowed fitting of models based on individual levels of risk.

Our Poisson model in its most basic, fixed effects-only form is

$$Y_i|{\zeta }_i\stackrel{\mathit{\text{ind}}}{~}\text{\hspace{1em}Poisson}(E_i\text{exp}({\mathit{x}}_i^{\prime }\mathit{\beta })),\text{for}i=1,\dots ,I.$$

Here we define the expected number of events in the absence of covariate effects as E_i. This expected number is often expressed as the number of cases defined by an epidemiologic “null model” of incidence, i.e., the product of n_i, the number of individuals at risk in region i, and r, a constant “baseline” risk per individual. This individual-level risk is often estimated from the aggregate population data via $\widehat{r}={\displaystyle {\sum }_{i=1}^n{Y}_i}/{\displaystyle {\sum }_{i=1}^n{n}_i}$, the global observed disease rate. The resulting Poisson GLM models the natural logarithm of the mean count as

$$\text{log}[E(Y_i)]=\text{log}(E_i)+{\mathit{x}}_i^{\prime }\mathit{\beta },$$

with an offset E_i and multiplicative impacts on the model-based expected observation counts for each covariate, resulting in a region-specific relative risk of $\left({\mathit{x}}_i^{\prime }\mathit{\beta }\right)$.

Some discussion of the expected counts E_i, i = 1,…,I is in order. The estimated baseline risk defined above, known as internal standardization, is a bit of a “cheat” since we continue to think of the E_i as known, even though they now depend on our estimate of r. But since the impact of this choice fades within increasing numbers of regions I, and noting that our definition of r serves only to set the relatively uninteresting grand intercept β₀, this seems a minor concern. In addition, one may wish to further standardize the risks and expectations to account for spatial variation in the distribution of known risk factors (such as age), rather than adjust for such risk factors in the region-specific covariates. Waller and Gotway (2004, Chapter 2) provide an overview of the mechanisms of and arguments for and against standardization in spatial epidemiology.

14.2.2 Exchangeable random effects

In order to borrow information across regions, we next define the random effects version of the model, but for the moment we describe the model without covariates for simplicity. In other words, consider an intercept-only GLM with offset E_i, but allow a random intercept υ_i associated with each region, i.e.,

$$\begin{array}{ccc}\hfill Y_i|{\upsilon }_i& \stackrel{\mathit{\text{ind}}}{~}\hfill & \text{Poisson}(E_i\text{exp}[{\beta }_0+{\upsilon }_i]),\hfill \\ \hfill \text{where}{\upsilon }_i& \stackrel{\mathit{\text{ind}}}{~}\hfill & N(0,{\sigma }_{\upsilon }^2),\text{for}i=1,\dots ,I.\hfill \end{array}$$

The hierarchical structure allows us to build the overall (marginal) distribution of the Y_i in two stages. At the first stage, observations Y_i are conditionally independent given the values of the random effects, υ_i. The second stage (the distribution of the random effects) allows a mechanism for inducing extra-Poisson variability in the marginal distribution of the Y_is. Other options exist for introducing different types of excess variability or overdispersion into generalized linear models of counts (e.g., McCullagh and Nelder 1989, Gelfand and Dalal 1990). Here, we focus on the exchangeable random intercept approach due to its similarity to the approach proposed for spatial random effects in the sections below.

From a Bayesian perspective, the first stage of the model defines the likelihood and the second stage a set of exchangeable prior distributions for the random effects, which are estimable provided ${\sigma }_{\upsilon }^2$ is known or is assigned a proper hyperprior. To complete the model specification, we assign a vague (perhaps even improper uniform, or “flat”) prior to the “fixed” effect β₀, which is well identified by the likelihood.

The hierarchical structure allows a wide variety of options for shaping the random effects and resulting marginal correlations among the Y_is. This feature of maintaining a conditionally independent framework for observations given the random effects and defining a second-stage distribution for the random effects represents one of the primary advantages of hierarchical models, and has led to their widespread use in statistical analyses with complex correlation patterns (e.g., spatial, temporal, longitudinal, repeated measures, and so on), particularly for non-Gaussian data such as our small area counts.

The addition of the random effects addresses the small area estimation problem by inducing a connection among the local relative risks (the ζ_is) through the random effects distribution, and transforming the estimation of I local relative risks to the estimation of only two parameters: the overall mean effect β₀, and the random effects variance ${\sigma }_{\upsilon }^2$. The approach provides a local estimate defined by a weighted average of the observed data in location i and the global overall mean. Clayton and Kaldor (1987), Marshall (1991), and Waller and Gotway (2004, Section 4.4.3) provide details of an empirical Bayes approach using data-based estimates of β₀ and ${\sigma }_{\upsilon }^2$. In a fully Bayesian approach we assign a hyperprior distribution to ${\sigma }_{\upsilon }^2$ (e.g., a conjugate inverse gamma distribution) and summarize the full posterior distribution for statistical inference.

Extending the model to include region-specific fixed-effect covariates simply involves replacing β₀ above by ${\mathit{x}}_i^{\prime }\mathit{\beta }$ (including the fixed intercept β₀ within β) and assigning vague priors to the elements of β. As with β₀ above, the fixed-effect parameters are well-identified by the likelihood and provide baseline (pre-smoothing) estimates of each local relative risk ζ_i.

14.2.3 Spatial random effects

To this point, the model induces some correlation, but does not specifically induce spatial correlation among the observations. All local estimates are compromises between the local data and a global weighted average based on all of the data, with weights based on the relative variances observed in the local and global estimates. Clayton and Kaldor (1987) introduced the idea of replacing the set of exchangeable priors at the second stage with a spatially structured prior distribution, leading to empirical Bayes estimates wherein local estimates are a weighted average of the regional data value and an average of observations in nearby or neighboring regions. This approach borrows strength locally, rather than globally. Besag et al. (1991) extended the approach to a fully Bayesian formulation, clarified some technical points regarding the spatial prior distribution, and proposed the use of MCMC algorithms for fitting such models.

In this vein, suppose we modify the model to

$$\begin{array}{ccc}\hfill Y_i|u_i& \stackrel{\mathit{\text{ind}}}{~}\hfill & \text{Poisson}(E_i\text{exp}[{\beta }_0+u_i]),\hfill \\ \hfill \text{where}\mathbf{u}& ~\hfill & \mathit{\text{MVN}}(\mathbf{0},{\sum }_u).\hfill \end{array}$$

Here, ∑_u denotes a spatial covariance matrix and we distinguish between the exchangeable random effects υ_i above and a vector u = (u₁,…,u_I) of spatially correlated random effects. Fixed effect covariates may be added in the same manner as before. In practice, the spatial covariance matrix typically consists of parametric functions defining covariance as a function of the relative locations of any pair of observations (e.g., geostatistical covariance functions and variograms). Cressie (1993, Sections 2.3–2.6) and Waller and Gotway (2004, Section 8.2) provide introductions to such covariance functions, and Diggle et al. (1998), Banerjee et al. (2004, Sec. 2.1) and Diggle and Ribeiro (2007) illustrate their use within hierarchical models such as that above.

The model based on a multivariate Gaussian random effects distribution represents a relatively minor conceptual change from the small area estimation literature, and ties the field to parametric covariance models from geostatistics (Matheron, 1963, Cressie, 1993, Chapter 3, Waller and Gotway, Chapter 8). However, the goals of disease mapping (statistically stable local estimation) and geostatistics (statistical prediction at locations with no observations) differ and such models currently represent a relatively small fraction of the disease mapping literature. An alternative formulation built from Clayton and Kaldor’s (1987) CAR formulation sees much broader application in the spatial analysis of regional disease rates, largely thanks to the computational advantages it offers over the multivariate Gaussian model. But since the spatial structure induced by the CAR model is less immediately apparent, we now consider it in some detail.

Specifically, the CAR formulation replaces the multivariate Gaussian second stage above with a collection of conditional Gaussian priors for each u_i wherein the prior mean is a weighted average of the other u_j, j ≠ i,

$$u_i|u_{j\ne i}~N\left(\frac{{\displaystyle {\sum }_{j\ne i}{c}_{\mathit{\text{ij}}}{u}_j}}{{\displaystyle {\sum }_{j\ne i}{c}_{\mathit{\text{ij}}}}},\frac{1}{{\tau }_{\mathit{\text{CAR}}}{\displaystyle {\sum }_{j\ne i}{c}_{\mathit{\text{ij}}}}}\right),i=1,\dots ,I.$$ (14.1)

Here, the c_ijs are user-defined spatial dependence parameters defining which regions j are “neighbors” to region i, or more generally weights defining the influence of region u_j on the prior mean of u_i. The parameter τ_CAR denotes a hyperparameter related to the conditional variance of u_i given the values of the other elements of u. By convention, one sets c_ii = 0 for all i, so no region is its own neighbor. Many applications consider adjacency-based weights, where c_ij = 1 if region j is adjacent to region i, and c_ij = 0 otherwise. Other weighting options also are available (e.g., Best et al., 1999) but are much less widely applied. Weights are typically assumed to be fixed, but see Lu, Reilly, Banerjee, and Carlin (2007) for a spatial boundary analysis application where the weights are estimated from the data.

To define the connection between the autoregressive spatial dependence parameters {c_ij} and the joint spatial covariance matrix ∑_u, Besag and Kooperberg (1995) note that, if u follows a multivariate Gaussian distribution with covariance ∑_u, then the density, f(u), takes the form

$$f(\mathbf{u})\propto \text{exp}\left(-\frac{1}{2}\mathbf{u}\prime {\displaystyle {\sum }_u^{-1}\mathbf{u}}\right).$$ (14.2)

Standard multivariate Gaussian theory defines the associated conditional distributions as

$$u_i|u_{j\ne i}~N\left({\displaystyle \sum _{j\ne i}\left(\frac{-{\displaystyle {\sum }_{u,\mathit{\text{ij}}}^{-1}}}{{\displaystyle {\sum }_{u,\mathit{\text{ii}}}^{-1}}}\right)}{u}_j,\frac{1}{\left({\displaystyle {\sum }_{u,\mathit{\text{ii}}}^{-1}}\right)}\right),$$ (14.3)

where ${\sum }_{u,\mathit{\text{ij}}}^{-1}$ denotes the (i, j)th element of the precision matrix ${\sum }_u^{-1}$. Note the conditional mean for u_i is a weighted sum of u_j, j ≠ i, and the conditional variance is inversely proportional to the diagonal of the inverse of ∑_u, just as it is in the CAR specification above.

Reversing direction and going from a set of conditional Gaussian distributions to the associated joint distribution is more involved, requiring constraints on the {c_ij} to ensure, first, a Gaussian joint distribution and, second, a symmetric and valid covariance matrix ∑_u (c.f. Besag, 1974; Besag and Kooperberg, 1995; Arnold et al., 1999). Results in Besag (1974) indicate the set of CAR priors defined in equation (14.1) uniquely defines a corresponding multivariate normal joint distribution with mean zero, ${\displaystyle {\sum }_{u,\mathit{\text{ii}}}^{-1}=}{\displaystyle {\sum }_j{c}_{\mathit{\text{ij}}}}$, and ${\displaystyle {\sum }_{u,\mathit{\text{ij}}}^{-1}=-c_{\mathit{\text{ij}}}}$. However, for symmetric c_ijs, the sum of any row of the matrix ${\sum }_u^{-1}$ is zero, indicating ${\sum }_u^{-1}$ is singular, and the corresponding covariance matrix ∑_u is not well-defined. This holds for any symmetric set of spatial dependence parameters c_ij (including the adjacency-based c_ijs appearing in many applications). Remarkably, the singular covariance does not preclude application of the model with such weight matrices, since pairwise contrasts u_i − u_j are well-identified even though the individual u_is are not (Besag et al., 1995). These distributions are improper priors since they define contrasts between pairs of values u_i − u_j, j ≠ i, but they do not identify an overall mean value for the elements of u (since such distributions define the value of each u_i relative to the values of the others). In this case, any likelihood function based on data allowing estimation of an overall mean also allows the class of improper pairwise difference priors to generate proper posterior distributions. In practice, one often assures this by the ad-hoc addition of the constraint

$${\displaystyle \sum _{i=1}^I{u}_i=0.}$$ (14.4)

While the addition of the constraint slightly complicates formal implementation of equation (14.1), Gelfand and Sahu (1999) note that the constraint can be imposed “on the fly” within an MCMC algorithm simply by replacing u_i by u_i − ū for all i following each MCMC iteration. These authors also provide additional theoretical justification, and note that the constraint maintains attractive full conditional distributions for most CAR models in the literature while avoiding awkward reduction to (I − 1)-dimensional space. In contrast, Rue and Held (2005, Section 2.3.3) avoid the constraint altogether through block updates of the entire set of random effects. See also Richardson et al. (2004), Knorr-Held and Rue (2002), and Chapter 13 (this volume) for important algorithmic advances related to this model.

As a computational aside, note that both the conditional mean and the conditional variance in equation (14.3) depend on elements of the inverse of the covariance matrix ∑_u. As a result, MCMC algorithms applied to the joint specification based on straightforward updates from full conditional distributions will involve some sort of matrix inversion at each update of the covariance parameters. This reveals a computational advantage of the CAR prior formulation: it effectively limits modeling to the elements of ${\sum }_u^{-1}$, avoiding inversion and we focus attention on CAR models in the remainder of this chapter. We note, however, that computational convenience carries considerable conceptual cost (parameterizing ${\sum }_u^{-1}$ rather than ∑_u). Recent algorithmic developments seek to ease this computational/conceptual trade-off by using structured covariance matrices to reduce the computational burden of directly modeling the joint distribution, an issue discussed in more detail in Chapter 13 (this volume).

In addition to its (indirectly) defining the covariance structure of our model, the choice of c_ijs also has direct impact on the posterior variances. In the usual case where τ_CAR is unknown, it is conventionally assigned a conjugate gamma hyperprior distribution (see e.g. Carlin and Louis, 2009, p.424), since this leads to a closed form for the τ_CAR full conditional distribution needed by the MCMC algorithm. However, even here there is some controversy, since the impropriety of the standard CAR means that, despite our use of the proportionality sign in (14.2), the joint distribution of the u_is really has no normalizing constant. Knorr-Held (2002) advocated k = (n − 1)/2 for Gaussian Markov random fields (a set containing the CAR-specified model above) based on the rank of the resulting precision matrix. Hodges et al. (2003) argue that the most sensible joint density to use in this case is

$$f(\mathbf{u})\propto {\tau }_{\mathit{\text{CAR}}}^{(I-k)/2}\text{exp}\left(-\frac{{\tau }_{\mathit{\text{CAR}}}}{2}\mathbf{u}\prime Q\mathbf{u}\right),$$ (14.5)

where Q is I × I with non-diagonal entries q_ij = − 1 if i ~ j and 0 otherwise, and diagonal entries q_ii equal to the number of region i’s neighbors, and k is the number of disconnected “islands” in the spatial structure. Thus in the usual case where every county is connected to every other by some chain of neighbors, the exponent on τ_CAR is (I − 1)/2, as advocated earlier by Knorr-Held (2002), and not I/2, as originally suggested by Besag et al. (1991). In the case of multiple islands in the spatial map, this exponent drops further (reflecting the greater rank deficiency in Q), and the sum-to-zero constraint (14.4) must be applied to each island separately. See Lu, Hodges and Carlin (2007) for extensions of these ideas that enable “counting” degrees of freedom in spatial models that are distinct from but related to those given by Spiegelhalter et al. (2002).

14.2.4 Convolution priors

Further extending disease mapping models, Besag et al. (1991) point out that we could include both global and local borrowing of information within the same model via a convolution prior including both exchangeable and CAR random effects for each region, as follows:

$$\begin{array}{ccc}\hfill Y_i|u_i& \stackrel{\mathit{\text{ind}}}{~}\hfill & \text{Poisson}(E_i\text{exp}[{\beta }_0+u_i+{\upsilon }_i]),\hfill \\ \hfill \text{where}{u}_i|u_{j\ne i}& ~\hfill & N\left(\frac{{\displaystyle {\sum }_{j\ne i}{c}_{\mathit{\text{ij}}}{u}_j}}{{\displaystyle {\sum }_{j\ne i}{c}_{\mathit{\text{ij}}}}},\frac{1}{{\tau }_{\mathit{\text{CAR}}}{\displaystyle {\sum }_{j\ne i}{c}_{\mathit{\text{ij}}}}}\right),\hfill \\ \hfill \text{and}{\upsilon }_i& \stackrel{\mathit{\text{ind}}}{~}\hfill & N(0,{\sigma }_{\upsilon }^2),\text{for}i=1,\dots ,I.\hfill \end{array}$$

To complete the model, we assign hyperpriors to the hyperparameters τ_CAR and ${\tau }_{\upsilon }\equiv {\sigma }_{\upsilon }^2$. Again, fixed-effect covariates may be added if desired. As mentioned above, typical applications define conjugate gamma hyperpriors, and Ghosh et al. (1999) and Sun et al. (1999) define conditions on these distributions necessary to ensure proper posterior distributions. When we include both u and v in the model some care is required to avoid assigning “unfair” excess prior weight to either global or local smoothing, since τ_CAR is related to the conditional variance of u_i|u_j≠_i but τ_υ is related to the marginal variance of each υ_i. This issue is explored by Bernardinelli et al. (1995a), who, based on their empirical example, suggest taking the prior marginal standard deviation of υ_i to be roughly equal to the conditional standard deviation of u_i|u_j≠_i divided by 0.7. We stress that this is only a “rule of thumb” and merits closer scrutiny (Eberly and Carlin, 2000; Banerjee et al., 2004, p.164). In any given application, a simple yet “fair” approach might be to first run the MCMC algorithm without including the data (e.g., by commenting the Poisson likelihood terms out of the WinBUGS code), and then choose hyperpriors that produce no-data “posteriors” for τ_CAR and τ_υ that are roughly equal. Another approach based on marginal variances induced by the CAR prior appears in Rue and Held (2005, pp. 103–105). In any case, note that we cannot take both of these hyperpriors to be noninformative, because then only the sum of the random effects (u_i + υ_i), and not their individual values, will be identified.

14.2.5 Alternative formulations

It is important to note that, while arguably the most popular, the formulation proposed by Besag et al. (1991) is not the only mechanism for including both spatial and non-spatial variance components within a single hierarchical disease mapping model. For example, Leroux et al. (1999) and MacNab and Dean (2000) define spatially structured and unstructured variation built on additive components of the precision matrix of a single random intercept rather than via the sum of two additive random intercepts. To contrast the approaches briefly, the Besag et al. (1991) formulation above defines a random intercept consisting of the sum of two parameters (u_i and υ_i) for each region, resulting in a variance-covariance matrix for the multivariate normal sum u + v defined by

$${\displaystyle {\sum }_{u+\upsilon }={\sigma }_u^2{Q}^{-1}}+{\sigma }_{\upsilon }^2\mathit{I}$$

where I denotes the I-dimensional identity matrix and Q contains the number of neighbors for each region along the diagonal, q_ij = − 1 if i ~ j, and 0 otherwise as in equation (14.5) above. The Leroux et al. (1999) formulation defines a single random intercept w_i for each region where

$$\begin{array}{ccc}\hfill Y_i|w_i& \stackrel{\mathit{\text{ind}}}{~}\hfill & \text{Poisson}(E_i\text{exp}[{\beta }_0+w_i]),\hfill \\ \hfill \mathit{w}& ~\hfill & \mathit{\text{MVN}}(\mathbf{0},{\sum }_w),\text{and}\hfill \\ \hfill {\sum }_w& =\hfill & {\sigma }^2{D}^{-1}.\hfill \end{array}$$

Here, σ² defines an overall dispersion parameter, and

$$D=\lambda Q+(1-\lambda )\mathit{I},$$

with 0 ≤ λ ≤ 1 denoting a spatial dependence parameter where λ = 0 defines a non-spatial model and the level of spatial dependence increases with λ. By defining the spatial and non-spatial components for the inverse (or generalized inverse) of ∑_w, Leroux et al. allow ready definition of the conditional mean and variance for the random effects in terms of parameters λ and σ², i.e.,

$$\begin{array}{cc}\hfill E(w_i|w_{j\ne i})& =\frac{\lambda }{1-\lambda +\lambda q_{\mathit{\text{ii}}}},\text{and}\hfill \\ \hfill \text{Var}(w_i|w_{j\ne i})& =\frac{{\sigma }^2}{1-\lambda +\lambda q_{\mathit{\text{ii}}}},\hfill \end{array}$$

recalling q_ii denotes the number of neighbors for region i, i = 1,…,I. Leroux et al.’s formulation also allows parameter estimation via penalized quasi-likelihood in the manner of Breslow and Clayton (1993).

Another set of alternative approaches seeks to identify potential discontinuities in the risk surface by loosening the rather strong amount of spatial smoothing often induced by the Besag et al. (1991) general CAR formulation above. Besag et al. (1991) propose replacing the squared pairwise differences, (u_i − u_j)², inherent in the Gaussian CAR formulation, with the L1-norm-based pairwise differences, |u_i − u_j|, resulting in shrinkage toward neighborhood median rather than mean values, hence yielding relatively weaker amounts of smoothing between neighboring values as illustrated in simulation studies by Best et al. (1999).

Green and Richardson (2002) take a different approach based on a hidden Markov field, thereby deferring spatial correlation to an additional, latent layer in the hierarchical model. Their formulation draws from a spatial type of cluster analysis where each region belongs to one of several classes and class assignments are allowed to be spatially correlated (Knorr-Held and Rasser 2000, Denison and Holmes 2001). The number of classes and the regional class assignments are unobserved, requiring careful MCMC implementation within the variable dimensional parameter space. The approach allows for discontinuities between latent class assignments and for spatially-varying amounts of spatial correlation (i.e., stronger correlation for some classes, weaker for others). The approach is not a direct extension of the CAR models above, but rather utilizes a Potts model from statistical image analysis and statistical physics to model spatial association in the regional labels. This increased flexibility (at an increased computational cost) provides inference for both group membership as well as very general types of spatial correlation. However, the advantages of the added flexibility increase with the number of regions and the complexity of subgrouping within the data. As a result, applications of the Green and Richardson (2002) approach appear more often in the analysis of high-dimensional biomedical imaging and genetic expression data than in disease mapping.

Simulation studies in Leroux et al. (1999), MacNab and Dean (2000), and Green and Richardson (2002) identify the types of situations where these alternative model formulations gain advantage over the CAR formulation. For example, the Leroux et al. (1999) model shows gains in performance over the CAR model as spatial correlation decreases to zero, and the Green and Richardson (2002) approach improves several measures of model fit from those observed in CAR formulations, particularly in cases with strong underlying discontinuities in risk. However, the near custom-fit between the Besag et al. (1991) formulation and fairly standard MCMC implementation continues to fuel its popularity in general disease mapping applications. As such, we focus on this model and its extensions below.

14.2.6 Additional considerations

The WinBUGS software package (www.mrc-bsu.cam.ac.uk/bugs/welcome.shtml) permits ready fitting of the disease mapping models defined above with exchangeable, CAR, or convolution prior distributions on the random intercepts. WinBUGS also allows mapping of the fitted spatial residuals E(u_i|y) or the fitted region-specific relative risks, E(e^{β₀+u_i+υ_i}|y), local estimates of the relative risk of being in region i compared to what was expected.

While hierarchical models with CAR and/or convolution priors see broad application for parameter estimation and associated small area estimation for regional data, they certainly are not the only models for such data, nor necessarily optimal in any particular way. In addition, CAR-based hierarchical models are defined only for the given set of regions and do not aggregate or disaggregate sensibly into CAR models on larger or smaller regions, respectively. Furthermore, regions on the edges of the study domain often have fewer neighbors and hence less information to draw from for borrowing strength locally than interior regions resulting in “edge effects” of reduced performance. The dependence on the given set of regions also implies that adjacency-based neighborhoods can correspond to very different ranges of spatial similarity around geographically large regions than around geographically small regions. For these reasons, the CAR prior cannot be viewed as a simple “discretized” version of some latent, smooth random process; see e.g. Banerjee et al. (2004, Sec. 5.6). However, Besag and Mondal (2005) provide some connections between CAR-based models and latent de Wijs processes on smaller scales that may allow rescaling of distance-based correlation structures across zonal systems.

Finally, it is important to keep in mind that the CAR structure is applied to the random effects at the second stage of the hierarchy, not directly to the observed data themselves. Generally speaking, this ensures a proper posterior distribution for the random effects for a broad variety of likelihood structures. In applications where one assumes a Gaussian first stage, CAR random effects are especially attractive with closed form full conditional distributions. In a generalized linear model setting (as in most disease mapping applications), the hierarchical structure allows us to maintain use of Gaussian CAR random variables within the link function, rather than attempting to work with Poisson (or binomial) CAR distributions for the counts themselves. For Poisson outcomes, the Gaussian-CAR-within-the-link-function structure avoids extreme and unfortunate restrictions (e.g., negative spatial correlation and normalizing constants defined by awkward functions of model parameters) imposed by CAR-based “autoPoisson” models (Besag, 1974). The hierarchical modeling approaches based on the CAR and convolution priors described above allow us to incorporate spatial correlation into generalized linear models of local disease rates, as well as conveniently defer such correlation to the second level of the model. That is, the formulation avoids analytical complications inherent in modeling spatial correlation within non-Gaussian distributions with inter-related mean and variance structures.

14.3 Example: Sasquatch Reports in Oregon and Washington

To illustrate the disease mapping models above, we consider an admittedly unconventional (and a bit whimsical) data set, namely the number of reported encounters with the legendary North American creature Sasquatch (Bigfoot) for each county in the U.S. states of Washington and Oregon. These data were obtained in May 2008 from the website of the Bigfoot Field Research Organization, www.bfro.net. For those unfamiliar with the story, Sasquatch is said to be a large, bipedal hominoid primarily purported to reside in remote areas in the Pacific Northwest. While reported encounters do not reflect a “disease” per se and we do not necessarily expect all individuals residing in a given county to experience the same “risk” of reporting an encounter, cryptozoologists and Sasquatch enthusiasts alike may be interested in identifying areas with higher-than expected local per-person rates of reported encounters. For our purposes, the data serve as a general example of the type we have described; namely, regional counts of a (thankfully) rare event standardized by the local population size and with associated regional covariates. The models above allow us to explore region-specific relative risks of reporting in order to explore any underlying geographic patterns and identify where reports are higher or lower than expected if every individual were equally likely to file a report. While the null model of equal per-person risk of reporting is unlikely to be true, it nevertheless forms a point of reference for our region-to-region comparisons. As we shall see, the data also offer an opportunity to explore in some detail the behavior of the methods in the presence of a single, large outlying observation. While the data provide a template for illustrating the models, readers in search of more traditional applications of CAR-based disease mapping models may find detailed examples in Mollié (1996), Best et al. (1999), Wakefield et al. (2000), Banerjee et al. (2004), and Waller and Gotway (2004, Chapter 9).

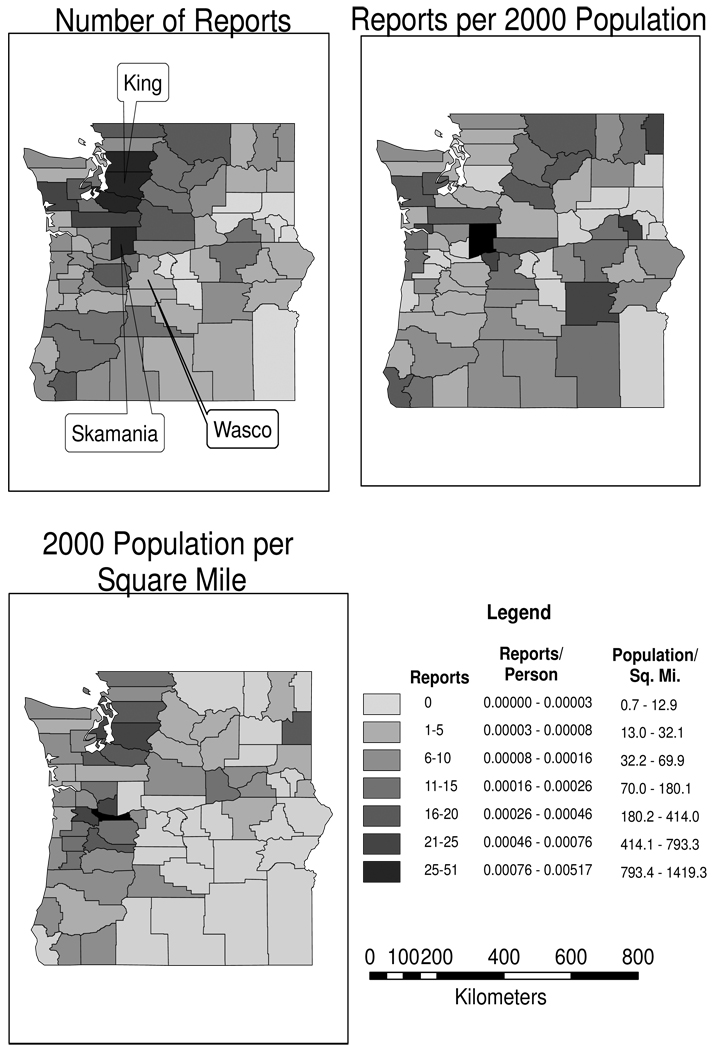
Figure 14.1, created by linking our data to maps of U.S. county boundaries using ArcGIS (ESRI, Redlands, CA), displays the data. The map in the upper left shows the number of reports per county ranging from zero (light grey) to a high of 51 in Skamania County in Washington, on the border with Oregon. The map in the upper right displays the local “rate” of reporting defined as the number of reports divided by the county population as reported by the 2000 U.S. Census, displayed in intervals defined by Jenks’ “natural breaks” method (Jenks, 1977; MacEachren, 1995, Chapter 4). The population adjustment is somewhat contrived as some reports in the data set can date back to the 1970s and a few back to the 1950s, but the 2000 population counts offer a crude form of standardization. The adjustment from counts to rates is most dramatic in the counties surrounding Puget Sound, revealing that the numbers of reports in this area are quite small when computed on a roughly per-person basis. The shift is particularly striking in King County, home to much of the Seattle metropolitan area. In contrast, Skamania County is extreme for both counts and rates and clearly of interest as our analysis continues. Finally, the lower left map shows the geographic distribution of a potential covariate, the population density based on the number of residents per square mile (again, from the 2000 Census and classified by Jenks’ natural breaks method). We note that rural Skamania County, while high in both number and rate of reporting, is in the lowest category of (log) population density.

Figure 14.1.

Maps of the number of reported encounters with Sasquatch (Bigfoot) by county (upper left), the “rate” of reports by county (upper right), and the population density per county reported as the number of residents per square mile (2000 U.S. Census).

Our model begins with the simple Poisson regression,

$$Y_i|\mathit{\beta }\stackrel{\mathit{\text{ind}}}{~}\text{Poission}(E_i\text{exp}({\beta }_0+{\beta }_1{x}_i)),\text{for}i=1,\dots ,I,$$

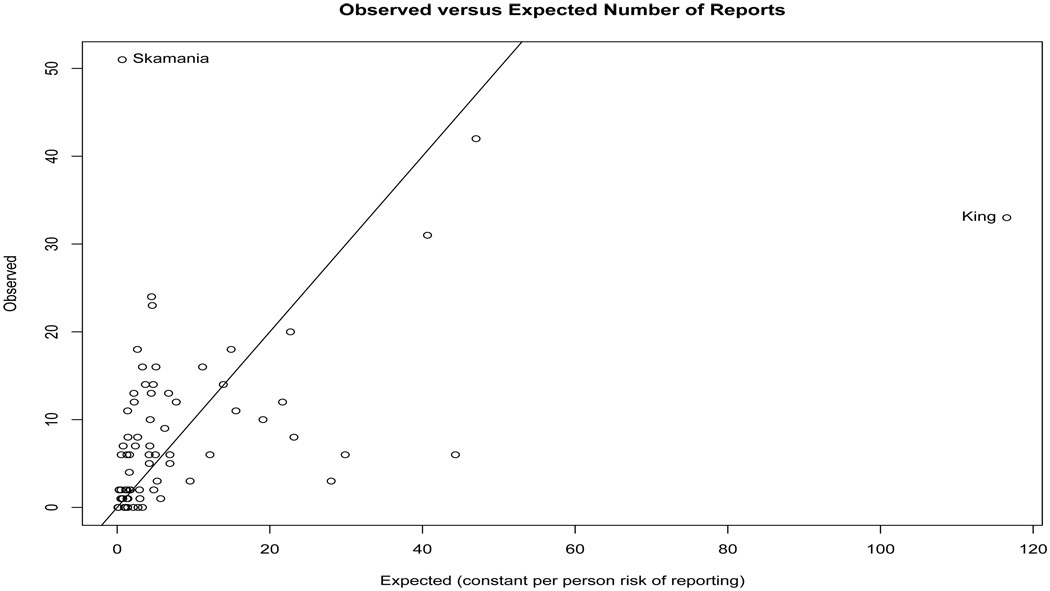
with x_i denoting the natural logarithm of population density and E_i the internally standardized expected count n_i(∑_i Y_i/∑_i n_i), i.e., the number of reports expected if each resident is equally likely to file a report. Figure 14.2 shows a scatterplot of the observed and expected counts, revealing (not surprisingly) a great deal of heterogeneity about the line of equality, with Skamania and King counties again standing out for reporting considerably more and less than expected, respectively.

Figure 14.2.

Observed number of Sasquatch reports per county compared to the number expected under a constant per-person probability of filing a report.

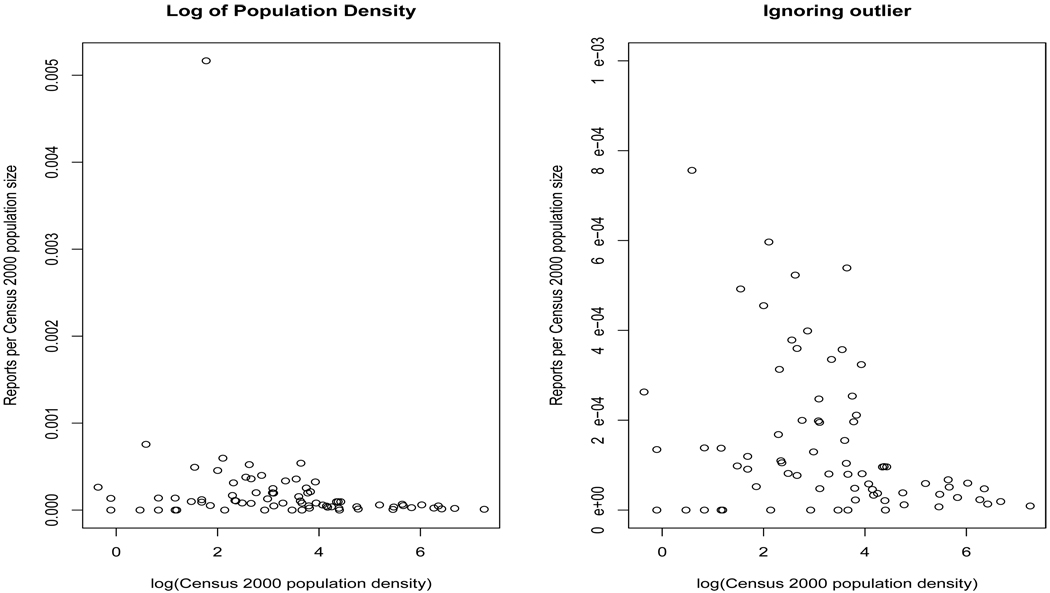
Figure 14.3 motivates our choice of covariate by illustrating how the county-specific rate of reporting decreases with increasing population density, with Skamania county remaining a obvious outlier. The extreme variation displayed suggests potential local instability in rates and suggests the use of random effects to adjust for the excess heterogeneity present in the data. However, we note that in most disease mapping applications unstable high local rates are often due to very low expected numbers of cases (e.g., E_i << 1) and a single observed case, while here the high rate in Skamania is apparently due to an extremely high number of local reports (51).

Figure 14.3.

Scatterplots of the county-specific reporting rates versus the natural logarithm of population density with (left) and without (right) Skamania County.

We fit four models to the data, first a simple fixed effect model, then models with random intercepts following exchangeable (non-spatial), CAR (spatial), and convolution (both) priors. We used the program maps2WinBUGS (sourceforge.net/projects/maps2winbugs) to transfer the map data from ArcGIS format to WinBUGS format, then used GeoBUGS (the spatial analysis and mapping tool within WinBUGS) define our adjacency matrix. We note that the adjacency matrix defines c_ij = 1 for any regions i and j sharing a common boundary, but also includes some counties falling very close to one another; for example, Wasco County is included among the neighbors of Skamania County. Each model was fit using MCMC within WinBUGS using 100,000 iterations. To reduce correlation between parameters β₀ and β₁, we centered our covariate by subtracting the overall mean (log) population density from each value. Our MCMC samples provide posterior inference for model parameters and for county-specific relative risks (e.g., RR_i = exp(β₀+β₁x_i+u_i+υ_i) for the convolution model).

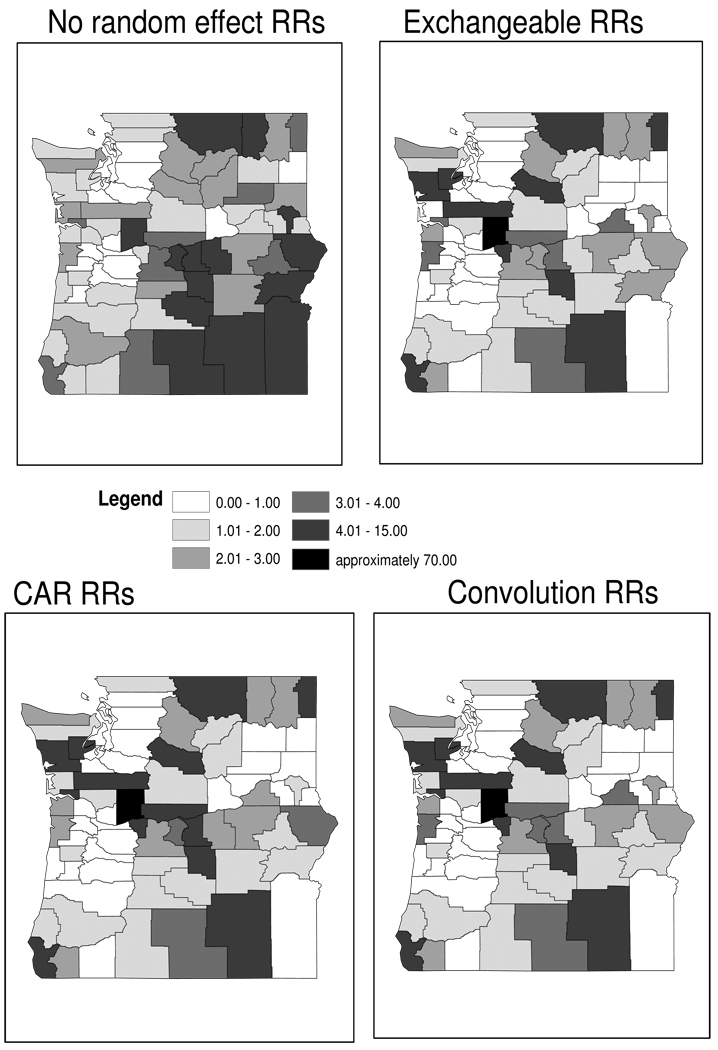
In all four models, the estimated effect of population density (β₁) was negative and significantly different from 0; in the convolution model we obtained a 95% equal-tail credible interval of (−0.68, −0.35). Thus Bigfoot sightings are significantly more likely to arise in more thinly populated counties. One might speculate that this is due to Bigfoot’s preference for habitats with fewer humans per unit area, or simply a tendency of Bigfoot afficionados to live and work in such regions. Effective model size (p_D) and DIC scores (Spiegelhalter et al., 2002) do not differ appreciably across the 3 random effects models. This is confirmed by Figure 14.4, which shows the local relative risk (RR_i) for each county based on the maps. Counties are shaded by the same intervals to ease comparisons between maps. We note that the model with no random effects (top left) does a very poor job of predicting the local high rate in Skamania County, and that relative risks are exaggerated in the low population density counties along Oregon’s southern border. The maps of relative risks based on the three random effects models are similar in general, with some subtle differences. All three are able to capture the excess variability observed in the data, especially the extreme value in Skamania County. We note that the interval containing the largest estimated relative risks covers a very large range of values, with the darkest counties in the fixed effect model representing local relative risks less than 20, but the other three maps all assigning Skamania County a relative risk near 70. The convolution prior appears to offer something of a compromise between the nonspatial exchangeable model and the spatial CAR model, particularly along the eastern border of our study area. This is sensible, since with both types of random effects in our model, we would expect the fitted values to exhibit both spatial and nonspatial heterogeneity.

Figure 14.4.

Maps of county-specific relative risk of reporting sitings. Each map has counties shaded by the intervals reported in the legend.

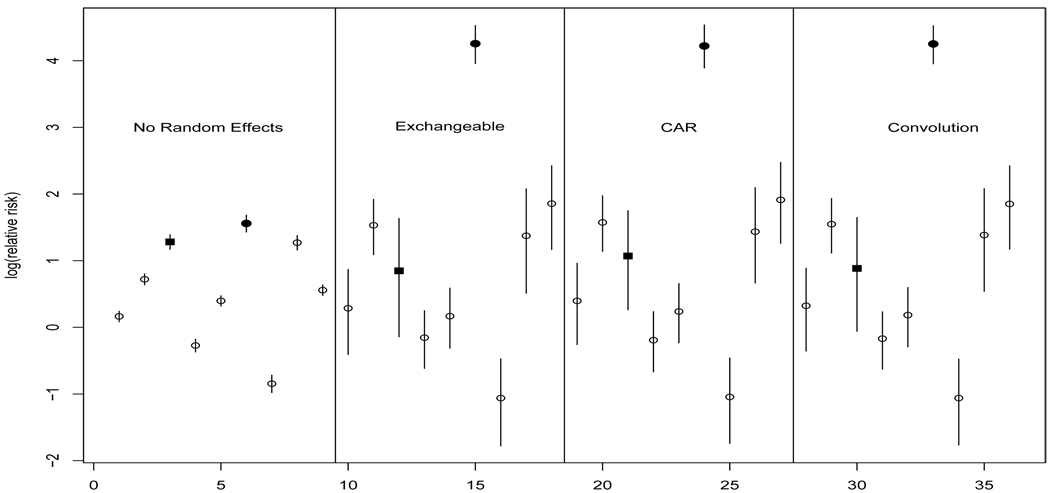
This compromise is seen more clearly in Figure 14.5, which shows the posterior median and 95% credible sets for the log relative risks associated with Skamania County and its neighbors for each of the four models. As noted above, for Skamania County the neighborhood includes seven adjacent counties and one nearby county, namely Wasco County to the southeast (labeled in Figure 14.1). Figure 14.5 reveals that the model with no random effects generates deceptively tight credible sets (ignoring the substantial extra-Poisson variation in the data set) and clearly misses the increased risk of reporting observed in Skamania County (indicated by a filled circle), well above that expected based on the offset (population size) and the covariate (population density). The three random effect models are quite similar for our data, and all three capture the increased risk of reporting in Skamania County.

Figure 14.5.

Posterior median and 95% credible sets for local relative risks associated with Skamania County (filled circles) and its neighboring counties. Wasco County is of interest and is labeled by a filled square.

A closer look at the posterior distribution for Wasco County (indicated by a filled square) in Figure 14.5 highlights the subtle differences between models in our data. Note that Wasco County has a wide credible set, suggesting a locally imprecise estimate in need of input from other regions. In the CAR model, the posterior distribution of the relative risk of reporting in Wasco County is pulled (slightly) upward toward that of its neighbor Skamania when compared to the posterior distribution for Wasco County in the exchangeable model. As suggested by the maps, the convolution model represents a compromise between the posterior distributions of relative risks from the spatial CAR model and the non-spatial exchangeable model. We remark that the WinBUGS code for the full model (given in the Appendix) uses a relatively vague Gamma(0.1, 0.1) hyperprior for τ_CAR; a hyperprior centered more tightly on smaller values (or even a fixed, larger value of τ_CAR) would further smooth Wasco toward Skamania.

Our example illustrates several features of disease mapping models. First, there is often a concern that disease mapping models may oversmooth extreme rates, particularly observations that are very unlike their neighbors. Our data provide an extreme example of this with a single outlier, well identified by the model which does not overly influence its neighboring estimates. As noted in Figure 14.5 there is some impact on the most variable neighboring estimates (e.g., that from Wasco County) but this is very slight and unlikely to strongly influence conclusions. In addition, the example reveals that all three random effects models fit the data approximately equally well, suggesting a clear need for borrowing strength from other regions, but does not suggest a clear preference for global versus local assistance. Further analyses might check the robustness of the Bayesian model choice decision (via DIC or some other method) to deleting Skamania from the dataset and recomputing the posterior.

14.4 Extending the Basic Model

14.4.1 Zero-inflated Poisson models

Many spatial datasets feature a large number of zeros (areas with no reported disease cases) that may stretch the credibility of our Poisson likelihood. As such, a zero-inflated Poisson (ZIP) model may offer a sensible alternative. Lambert (1992) implemented such a model in a manufacturing-related regression context using the EM algorithm; Agarwal et al. (2002) offer a fully Bayes-MCMC version for spatial count data.

In our context, suppose we model the disease count in region i as a mixture of a Poisson(λ_i) distribution and a point mass at 0. That is, when there are no cases observed in region i, we assume that such zero counts arise as Poisson variates with probability (1 − ω_i), and as “structural zeros” with probability ω_i. More formally, we can write the regression model as

$$\mathit{\text{Pr}}(Y_i=y|{\omega }_i,{\lambda }_i)=\{\begin{array}{cc}{\omega }_i+(1-{\omega }_i)\text{exp}(-{\lambda }_i)\hfill & \text{for}y=0,\hfill \\ (1-{\omega }_i)\text{exp}(-{\lambda }_i){\lambda }_i^y/y!\hfill & \text{for}y>0,\hfill \end{array}$$

where $\text{log}({\lambda }_i)=\text{log}(E_i)+{\mathit{x}}_i^{\prime }\mathit{\beta }+u_i\text{\hspace{1em}and\hspace{1em}logit}({\omega }_i)={\mathit{z}}_i^{\prime }\mathit{\gamma }+w_i$, and x_i and z_i are covariate vectors which may or may not coincide. More parsimonious models are often used to preserve parameter identifiability, or to allow the λ_i and ω_i to be related in some way. Agarwal et al. (2002) set x_i = z_i and eliminate the w_i random effects; a follow-up paper by Agarwal (2006) retains both the u_i and w_i, but assigns them independent proper CAR priors. Another possibility is to replace ${\mathbf{z}}_i^{\prime }\mathbf{\gamma }+w_i$ with $\nu \left({\mathit{x}}_i^{\prime }\mathit{\beta }+u_i\right)$ in the expression for logit(ω_i) (Lambert, 1992); note that ν < 0 will often be necessary to reverse the directionality of x_i’s relationship when switching responses from λ_i to ω_i.

To complete the Bayesian model, we assign vague normal priors to β and γ, and CAR or exchangeable priors to the u_i and w_i. Disease mapping can now proceed as usual, with the advantage of now being able to use the posterior means of the ω_i as the probability that region i is a structural zero in the spatial domain.

We remark that this model may be sensible for the data in the previous section, since 10 of the 75 counties had no reported Sasquatch sightings. In the interest of brevity, however, we leave this investigation (in WinBUGS or some other language) to the interested reader.

14.4.2 Spatiotemporal models

Many spatially-referenced disease count datasets are collected over time, necessitating an extension of our Section 14.2 models to the spatiotemporal case. This is straightforward if time and space are both discretely indexed – say, with space indexed by county and time indexed by year. In fact, the data may have still more discrete indexes, as when disease counts are additionally broken out by race, gender, or other sociodemographic categories.

To explicate the spatiotemporal extension as concretely as possible, we develop spatiotemporal extensions in the context of a particular dataset originally analyzed by Devine (1992, Chapter 4). Here, Y_ijkt is the number of lung cancer deaths in county i during year t for gender j and race k in the U.S. state of Ohio, and n_ijkt is the corresponding exposed population count. These data were originally taken from a public use data tape (Centers for Disease Control, 1988), and are now available online at www.biostat.umn.edu/~brad/data2.html. The subset of lung cancer data we consider here are recorded for J = 2 genders (male and female) and K = 2 races (white and nonwhite) for each of the I = 88 Ohio counties over an observation period of T = 21 years, namely 1968–1988 inclusive, yielding a total of 7392 observations.

We begin our modeling by extending our Section 14.2 Poisson likelihood to

$$Y_{\mathit{\text{ijkt}}}\stackrel{\mathit{\text{ind}}}{~}\text{Poisson}(E_{\mathit{\text{ijkt}}}\text{exp}({\mu }_{\mathit{\text{ijkt}}})).$$

We obtain internally standardized expected death counts as E_ijkt = n_ijktr̂, where r̂ = ȳ = ∑_ijkt y_ijkt=∑_ijkt n_ijkt, the average statewide death rate over the entire observation period. The temporal component is of interest to explore changes in rates over a relatively long period of time. Demographic issues are of interest because of possible variation in residential exposures for various population subgroups. In addition, the demographic profile of the counties most likely evolved over the time period of interest.

Devine (1992) and Devine, Louis, and Halloran (1994) applied Gaussian spatial models employing a distance matrix to the average lung cancer rates for white males over the 21-year period. Waller et al. (1997) explored a full spatiotemporal CAR-based model, adopting the mean structure

$${\mu }_{\mathit{\text{ijkt}}}=s_j\alpha +r_k\beta +s_j{r}_k\xi +u_i^{(t)}+{\upsilon }_i^{(t)},$$ (14.6)

where s_j and r_k are the gender and race scores

$$s_j=\{\begin{array}{cc}0\hfill & \text{if male}\hfill \\ 1\hfill & \text{if female}\hfill \end{array}\text{\hspace{1em}and\hspace{1em}}{r}_k=\{\begin{array}{cc}0\hfill & \text{if white}\hfill \\ 1\hfill & \text{if nonwhite}\hfill \end{array}.$$

Letting ${\mathbf{u}}^{(t)}=\left(u_1^{(t)},\dots ,u_I^{(t)}\right)\prime ,{\mathbf{v}}^{(t)}=\left({\upsilon }_1^{(t)},\dots ,{\upsilon }_I^{(t)}\right)\prime$, and denoting the I-dimensional identity matrix by I, we adopt the prior structure

$${\mathbf{u}}^{(t)}|{\lambda }_t\stackrel{\mathit{\text{ind}}}{~}\mathit{\text{CAR}}({\lambda }_t)\text{\hspace{1em}and\hspace{1em}}{\mathbf{v}}^{(t)}|{\tau }_t\stackrel{\mathit{\text{ind}}}{~}N(\mathbf{0},\frac{1}{{\tau }_t}\mathbf{I}),t=1,\dots ,T,$$ (14.7)

so that heterogeneity and clustering may vary over time. Note that the socio-demographic covariates (gender and race) do not interact with time or location.

To complete the model specification, we require prior distributions for α, β, ξ, the τ_t and the λ_t. Since α, β, and ξ will be identified by the likelihood, we may employ a flat prior on these three parameters. Next, for the priors on the τ_t and λ_t we employed conjugate, conditionally i.i.d. Gamma(a, b) and Gamma(c, d) priors, respectively. As mentioned earlier, some precision is required to facilitate implementation of an MCMC algorithm in this setting. On the other hand, too much precision risks likelihood-prior disagreement. To help settle this matter, we fit a spatial-only (reduced) version of model (14.6) to the data from the middle year in our set (1978, t = 11), using vague priors for λ and τ having both mean and standard deviation equal to 100 (a = c = 1, b = d = 100). The resulting posterior 0.025, 0.50, and 0.975 quantiles for λ and τ were (4.0, 7.4, 13.9) and (46.8, 107.4, 313.8), respectively. As such, in fitting our full spatio-temporal model (14.6), we retain a = 1, b = 100 for the prior on τ, but reset c = 1, d = 7 (i.e., prior mean and standard deviation equal to 7). While these priors are still quite vague, the fact that we have used a small portion of our data to help determine them does give our approach a slight empirical Bayes flavor. Still, our specification is consistent with the aforementioned advice of Bernardinelli et al. (1995a). Specifically, recasting their advice in terms of prior precisions and the adjacency structure or our CAR prior for the $u_i^{(t)}$, we have λ ≈ τ/(2 m̃), where m̃ is the average number of counties adjacent to a randomly selected county (about 5–6 for Ohio).

Model fitting is readily accomplished in WinBUGS using an assortment of univariate Gibbs and Metropolis steps. Convergence was diagnosed by graphical monitoring of the chains for a representative subset of the parameters, along with sample autocorrelations and Gelman and Rubin (1992) diagnostics. The 95% posterior credible sets (−1.10, −1.06), (0.00, 0.05), and (−0.27, −0.17) were obtained for α, β, and ξ, respectively. The corresponding point estimates are translated into the fitted relative risks for the four subgroups in Table 14.1. It is interesting that the fitted sex-race interaction ξ reverses the slight advantage white men hold over nonwhite men, making nonwhite females the healthiest subgroup, with a relative risk nearly four times smaller than either of the male groups. Many Ohio counties have very small nonwhite populations, so this result could be partly the result of our failure to model covariate-region interactions. Replacing the raw death counts Y_ijkt by age-standardized counts also serves to eliminate the nonwhite females’ apparent advantage, since nonwhites die from lung cancer at slightly younger ages in our dataset; see Xia and Carlin (1998).

Table 14.1.

Fitted relative risks for the four socio-demographic subgroups in the Ohio lung cancer data.

demographic subgroup	contribution to εjk	fitted log- relative risk	fitted relative risk
white males	0	0	1
white females	α	−1.08	0.34
nonwhite males	β	0.02	1.02
nonwhite females	α + β + ξ	−1.28	0.28

Turning to the spatio-temporal parameters, histograms of the sampled values (not shown) showed ${\upsilon }_i^{(t)}$ distributions centered near 0 in most cases, but $u_i^{(t)}$ distributions typically removed from 0. This suggests some degree of clustering in the data, but no significant additional heterogeneity beyond that explained by the CAR prior. Use of the DIC statistic (Spiegelhalter et al., 2002) or some other Bayesian model choice statistic confirms that the nonspatial ${\upsilon }_i^{(t)}$ terms may be sensibly deleted from the model.

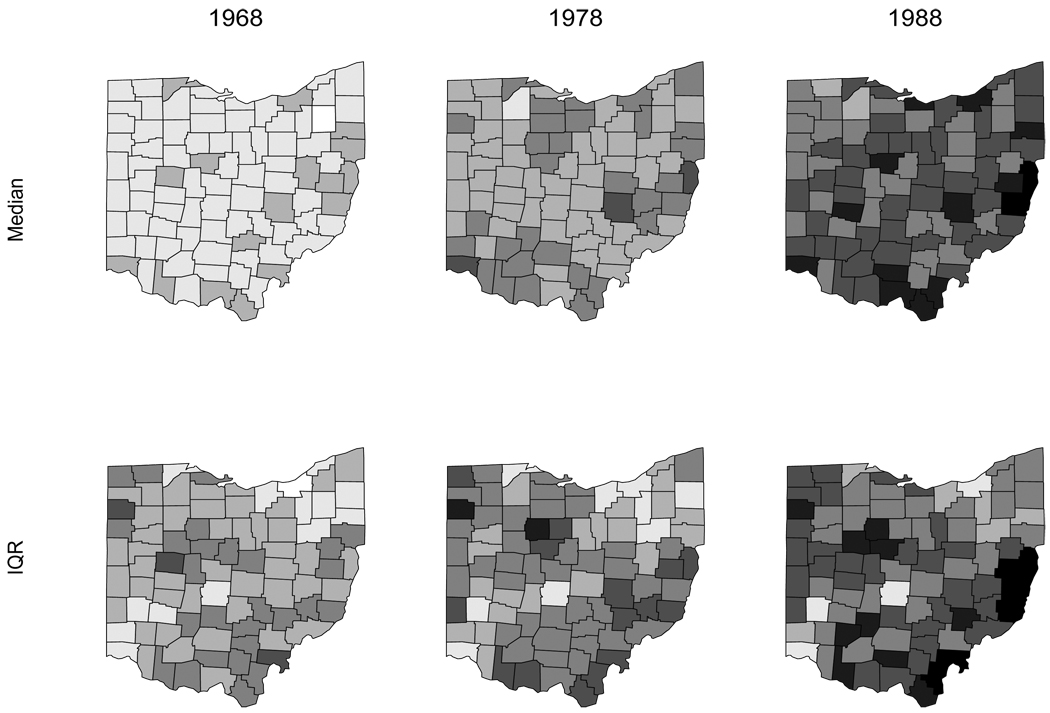
Since under our model the expected number of deaths for a given subgroup in county i during year t is E_ijkt exp(μ_ijkt), we have that the (internally standardized) expected death rate per thousand is 1000ȳ exp(μ_ijkt). The first row of Figure 14.6 maps point estimates of these fitted rates for nonwhite females during the first (1968), middle (1978), and last (1988) years in our dataset. These estimates are obtained by plugging in the estimated posterior medians for the μ_ijkt parameters calculated from the output of the Gibbs sampler. The rates are greyscale-coded from lowest (white) to highest (black) into seven intervals: less than 0.08, 0.08 to 0.13, 0.13 to 0.18, 0.18 to 0.23, 0.23 to 0.28, 0.28 to 0.33, and greater than 0.33. The second row of the figure shows estimates of the variability in these rates (as measured by the interquartile range) for the same subgroup during these three years. These rates are also greyscale-coded into seven intervals: less than 0.01, 0.01 to 0.02, 0.02 to 0.03, 0.03 to 0.04, 0.04 to 0.05, 0.05 to 0.06, and greater than 0.06.

Figure 14.6.

Posterior median and interquartile range (IQR) by county and year, nonwhite female lung cancer death rate per 1000 population (see text for greyscale key).

Figure 14.6 reveals several interesting trends. Lung cancer death rates are increasing over time, as indicated by the gradual darkening of the counties in the figure’s first row. But their variability is also increasing somewhat, as we would expect given our Poisson likelihood. This variability is smallest for high-population counties, such as those containing the cities of Cleveland (northern border, third from the right), Toledo (northern border, third from the left), and Cincinnati (southwestern corner). Lung cancer rates are high in these industrialized areas, but there is also a pattern of generally increasing rates as we move from west to east across the state for a given year. One possible explanation for this is a lower level of smoking among persons living in the predominantly agricultural west, as compared to those in the more mining and manufacturing-oriented east. Finally, we see increasing evidence of clustering among the high rate counties, but with the higher rates increasing and the lower rates remaining low (i.e., increasing heterogeneity statewide). The higher rates tend to emerge in the poorer, more mountainous eastern counties, suggesting we might try adding a socioeconomic status fixed effect to the model.

Interested readers can find other variants of CAR-based spatio-temporal disease mapping models in the literature including those proposed by Bernardinelli et al. (1995b), Knorr-Held and Besag (1998), and Knorr-Held (2000). Further extensions include spatial age-period-cohort models (Lagazio et al., 2003; Schmid and Held, 2004; Congdon, 2006) which incorporate temporal effects through time-varying risk and through birth-cohort-specific risks. In addition, MacNab and Dean (2001) extend the alternate formulation for convolution priors proposed by Leroux et al. (1999) (and described in Section 14.2.4) to the spatio-temporal setting through the addition of smoothing splines to model temporal and spatio-temporal trends in mortality rates.

14.4.3 Multivariate CAR (MCAR) models

The methods illustrated so far apply to the modeling of regional counts of a single disease. However, it will often be the case that we have counts of multiple diseases over the same regional grid. This type of analysis has been examined in different ways (Held et al., 2005; Knorr-Held and Best, 2001), but can be considered within a multivariate extension of the CAR models above. To adapt our notation to this case, suppose we let Y_ij be the observed number of cases of disease j in region i, i = 1,…,I, j = 1,…,p, and let E_ij be the expected number of cases for the same disease in this same region. As in Section 14.2, the Y_ij are thought of as random variables, while the E_ij are thought of as fixed and known. For the first level of the hierarchical model, conditional on the random effects u_ij, we assume the Y_ij are independent of each other such that

$$Y_{\mathit{\text{ij}}}\stackrel{\text{ind}}{~}\text{Poission}(E_{\mathit{\text{ij}}}\text{exp}({\mathit{x}}_{\mathit{\text{ij}}}^{\prime }{\mathit{\beta }}_j+u_{\mathit{\text{ij}}})),i=1,\dots ,I,j=1,\dots ,p,$$ (14.8)

where the x_ij are explanatory, region-level spatial covariates for disease j having (possibly region-specific) parameter coefficients β_j.

Carlin and Banerjee (2003) and Gelfand and Vounatsou (2003) generalized the univariate CAR (14.2) to a joint model for the random effects u_ij under a separability assumption, which permits modeling of correlation among the p diseases while maintaining spatial dependence. Separability assumes that the association structure separates into a non-spatial and spatial component. More precisely, the joint distribution of u is assumed to be

$$\mathbf{u}~N_{\mathit{\text{np}}}(0,{[\mathrm{\Lambda }\otimes (D-\alpha W)]}^{-1}),$$ (14.9)

where $\mathbf{u}=\left({\mathbf{u}}_1^{\prime },\dots ,{\mathbf{u}}_p^{\prime }\right)\prime ,{\mathbf{u}}_j=(u_{1j},\dots ,u_{\mathit{\text{Ij}}})\prime$, Λ is a p × p positive definite matrix that is interpreted as the non-spatial precision (inverse dispersion) matrix between diseases, and ⊗ denotes the Kronecker product. Also, α ∈ [0, 1] is a spatial autocorrelation parameter that ensures the propriety of the joint distribution; α = 1 returns us to the improper CAR case, while α = 0 delivers an independence model. We denote the distribution in (14.9) by MCAR(α, Λ). The improper MCAR(1, Λ) model is sometimes referred to as a multivariate intrinsic autoregression, or MIAR model.

The MCAR(α, Λ) can be further generalized by allowing different smoothing parameters for each disease, i.e.,

$$\mathbf{u}~N_{\mathit{\text{np}}}(\mathbf{0},{[\mathit{\text{Diag}}(R_1,\dots ,R_p)(\mathrm{\Lambda }\otimes I_{n\times n})\mathit{\text{Diag}}(R_1,\dots ,R_p)\prime ]}^{-1}),$$ (14.10)

where $R_j{R}_j^{\prime }=D-{\alpha }_{j}W,j=1,\dots ,p$. The the distribution in (14.10) is sometimes denoted by MCAR(α₁,…,α_p, Λ). Note that the off-diagonal block matrices (the R_i’s) in the precision matrix in (14.10) are completely determined by the diagonal blocks. Thus, the spatial precision matrices for each disease induce the cross-covariance structure in (14.10).

Jin et al. (2005) developed a more flexible generalized multivariate CAR (GMCAR) model for the random effects u. For example, in the bivariate case (p = 2), they specify the conditional distribution u₁|u₂ as N ((η₀I + η₁W)u₂, [τ₁(D − α₁W)]⁻¹), and the marginal distribution of u₂ as N (0, [τ₂(D − α₂W)]^{− 1}), both of which are univariate CAR. This formulation yields the models of Kim et al. (2001) as a special case and recognizes explicit smoothing parameters (η₀ and η₁) for the cross-covariances, unlike the MCAR models in (14.10) where the cross-covariances are not smoothed explicitly. However, it also requires the user to specify the order in which the variables (for us, diseases) are modeled, since different conditioning orders will result in different marginal distributions for u₁ and u₂ and, hence, different joint distributions for u. This may be natural when one disease is a precursor to another, but in general may be an awkward limitation of the GMCAR. To overcome this, Jin et al. (2007) developed an order-free MCAR that uses a linear model of coregionalization (Wackernagel, 2003; Gelfand et al., 2004) to develop richer spatial association models using linear transformations of much simpler spatial distributions. While computationally and conceptually more challenging, Jin et al. (2007) do illustrate the strengths of this approach over previous methods via simulation, and also offer a real-data application involving annual lung, larynx, and esophageal cancer death rates in Minnesota counties between 1990 and 2000. For more on MCAR models and underlying theory, the reader is referred to the textbooks by Banerjee et al. (2004, Sec. 7.4) and Rue and Held (2005).

Regarding computer package implementations of MCAR, WinBUGS offers an implementation of the MIAR case in a function called mv.car. While this is the only MCAR model that is built into the software itself, other more general MCAR models can be added fairly easily. For example, WinBUGS code to implement the GMCAR is available online at www.biostat.umn.edu/~brad/software/GMCAR.txt.

14.4.4 Recent developments

The field of disease mapping and areal data modeling more generally continues to generate research interest, building on the basic models outlined and illustrated in the sections above. As elsewhere in statistics, many of these new developments have been motivated by special features of particular spatially-referenced datasets. For instance, Reich et al. (2007) develop a 2NRCAR model that can accommodate two different classes of neighbor relations, as would be needed if spatial similarity among regions that neighbor in an east-west direction is known to be different from that between north-south neighbors. The authors actually illustrate in a periodontal data setting, where many observations are taken on each tooth, and the first neighbor relation corresponds to measurements that neighbor as we go around the jaw while the second corresponds to neighbors across each tooth (i.e., from the cheek to the tongue side).

Another important area of recent application is spatially varying coefficient models. Here the basic idea is to place a CAR (or other areal) prior on a collection of regional regression coefficients in a model, rather than simply on regional intercepts, thereby allowing the associations between outcomes and covariates to vary by location. So for example assuming a univariate covariate x_ij in (14.8), a CAR model would go directly onto the collection of region-specific coefficients β_j = (β_1j,…,β_Ij)′ for each disease j. The spatial residuals u_ij might revert to an exchangeable formulation, or be deleted entirely. Such models require some care in implementation due to an increased potential for multicollinearity among the varying coefficients. However, the hierarchical approach provides a sounder, model-based inferential basis for statistical inference than more algorithmic competitors (Waller et al., 2007; Wheeler and Calder, 2007).

14.5 Summary

The disease mapping models described and illustrated above provide a rich framework for the definition and application of hierarchical spatial models for areal data that simultaneously address our twin (but competing) goals of accurate small area estimation and fine-scale geographic resolution. As noted, the models retain some rough edges in terms of scalability and generalization of underlying continuous phenomenon. Nevertheless, the CAR-based structure within a hierarchical generalized linear model offers a robust, flexible, and enormously popular class of models for the exploration and analysis of small area rates. Basic and even relatively advanced variations of such models are readily fit using commonly available GIS (e.g. ArcGIS) and Bayesian (e.g. WinBUGS) software tools. The coming years will no doubt bring further expansion of the hierarchial spatial modeling and software toolkits.

Appendix

WinBUGS code for fitting the convolution model to the Sasquatch report data.

model
{
  for (i in 1 : N) {
      O[i] ~ dpois(mu[i])
      log(mu[i]) <- log(E[i]) + alpha0 + alpha1 * (X[i]-mean(X[])) +
                    c[i] + h[i]
      SMR[i] <- exp(alpha0 + alpha1 * (X[i]-mean(X[])) + c[i] + h[i])
      h[i] ~ dnorm(0,tau.h)
  }
  c[1:N] ~ car.normal(adj[], weights[], num[], tau.h)
  for(k in 1:sumNumNeigh) {
      weights[k] <- 1
  }

  alpha0 ~ dflat()
  alpha1 ~ dnorm(0.0, 1.0E-5)
  tau.c ~ dgamma(0.1, 0.1)
  tau.h ~ dgamma(0.01, 0.01)
  sigma.h <- sqrt(1/tau.h)
  sigma.c <- sqrt(1/tau.c)
  sd.c <- sd(c[])
  sd.h <- sd(h[])
  psi <- sd.c / (sd.c + sd.h) # proportion excess variation that is spatial
}

DATA:

list(N = 75,
O = c(12, 13, 6, 1, 3, 5, 6, 8, 16, 0, 14, 9, 6, 10, 2,
      11, 16, 24, 1, 2, 7, 2, 6, 1, 1, 8, 18, 7, 23, 4,
      20, 6, 0, 18, 0, 14, 1, 2, 6, 3, 51, 8, 6, 0, 0,
      11, 13, 31, 2, 13, 33, 12, 42, 3, 1, 0, 0, 2, 14,
      0, 1, 16, 6, 10, 5, 6, 0, 2, 7, 1, 0, 2, 1, 12, 2),
E=c(21.66807,6.736003,4.18522,2.9842,5.243467,
    4.21199,12.16176,1.418131,5.080634,0.9444588,
    13.91193,6.236098,1.627794,4.329133,1.741247,
    15.56334,3.314697,4.508202,1.407866,0.2565611,
    2.3905,2.922542,29.87904,5.702312,0.4870904,
    2.688122,2.654441,0.7871273,4.602534,1.596194,
    22.70344,5.011663,2.733342,14.93348,3.310806,
    4.73323,0.7376802,1.645775,44.31355,9.55898,
    0.6623355,23.16282,1.285556,0.1284818,0.1297566,
    1.369422,4.469423,40.65957,4.800993,2.187411,
    116.5417,2.238335,47.01965,28.04050,0.6832684,
    1.102193,0.1608203,0.2726633,3.702155,1.378815,
    0.4848092,11.19194,6.909102,19.11018,6.91514,
    0.5323777,2.121124,0.5105056,4.278814,0.4979593,
    0.1037918,1.275358,1.286965,7.740242,1.123193),
X=c(4.247066,2.985682,4.428433,3.811097,4.745801,
    3.663562,4.169761,2.557227,3.830813,4.403054,
    5.640843,4.37827,3.091042,3.600048,2.660260,
    6.352978,3.927896,3.549617,3.109061,2.624669,
    3.777348,4.146304,6.419832,4.772378,1.163151,
    2.76001,2.00148,2.104134,3.339322,2.292535,
    5.193512,3.288402,2.928524,3.943522,3.663562,
    3.08191,1.686399,2.484907,7.257919,4.393214,
    1.774952,6.265301,2.312535,0.4700036,0.8329091,
    3.642836,3.104587,5.661223,5.82482,2.867899,
    6.676201,2.660260,6.025866,5.458308,1.481605,
    2.140066,1.193922,1.547563,3.749504,3.468856,
    0.8329091,4.345103,4.07244,5.47395,3.797734,
    0.5877867,1.163151,−0.3566749,2.341806,−0.1053605,
    −0.1053605,2.360854,1.856298,3.632309,1.686399),
num = c(6, 6, 6, 5, 5, 3, 3, 3, 4, 0,
        4, 5, 6, 1, 5, 6, 5, 5, 4, 5,
        5, 7, 8, 6, 3, 4, 7, 2, 8, 9,
        7, 9, 8, 8, 6, 7, 6, 4, 6, 8,
        8, 5, 8, 6, 4, 5, 8, 5, 4, 5,
        6, 6, 7, 4, 8, 5, 4, 6, 6, 3,
        7, 3, 5, 8, 6, 9, 3, 5, 5, 4,
        7, 7, 6, 7, 4),
adj = c(74, 69, 65, 5, 4, 2,
        69, 9, 8, 7, 6, 1,
        65, 64, 24, 13, 5, 4,
        24, 13, 5, 3, 1,
        65, 64, 4, 3, 1,
        9, 8, 2,
        69, 9, 2,
        9, 6, 2,
        8, 7, 6, 2,
        53, 29, 18, 17,
        42, 41, 29, 22, 20,
        24, 23, 22, 21, 4, 3,
        15,
        49, 18, 17, 16, 14,
        53, 51, 49, 48, 17, 15,
        53, 18, 16, 15, 11,
        29, 19, 17, 15, 11,
        29, 21, 20, 18,
        29, 22, 21, 19, 12,
        23, 22, 20, 19, 13,
        42, 39, 23, 21, 20, 13, 12,
        64, 42, 39, 31, 24, 22, 21, 13,
        64, 31, 23, 13, 4, 3,
        55, 27, 26,
        55, 54, 28, 25,
        63, 62, 55, 50, 47, 32, 25,
        54, 26,
        53, 41, 34, 20, 19, 18, 12, 11,
        72, 71, 64, 46, 45, 44, 43, 41, 31,
        72, 64, 46, 39, 30, 24, 23,
        56, 55, 52, 50, 47, 40, 35, 34, 27,
        60, 59, 58, 57, 56, 55, 54, 35,
        53, 52, 51, 43, 41, 40, 32, 29,
        59, 58, 56, 40, 33, 32,
        66, 61, 59, 58, 40, 38, 37,
        71, 66, 44, 43, 40, 36,
        75, 66, 61, 36,
        46, 42, 41, 31, 23, 22,
        59, 56, 43, 37, 36, 35, 34, 32,
        46, 43, 42, 39, 34, 30, 29, 12,
        41, 39, 23, 22, 12,
        46, 45, 44, 41, 40, 37, 34, 30,
        71, 66, 45, 43, 37, 30,
        71, 44, 43, 30,
        43, 41, 39, 31, 30,
        63, 62, 52, 51, 50, 48, 32, 27,
        63, 51, 49, 47, 16,
        63, 48, 16, 15,
        55, 52, 47, 32, 27,
        53, 52, 48, 47, 34, 16,
        53, 51, 50, 47, 34, 32,
        52, 51, 34, 29, 17, 16, 11,
        55, 33, 28, 26,
        56, 54, 50, 33, 32, 27, 26, 25,
        55, 40, 35, 33, 32,
        61, 60, 58, 33,
        61, 59, 57, 36, 35, 33,
        61, 58, 40, 36, 35, 33,
        61, 57, 33,
        75, 60, 59, 58, 57, 38, 36,
        63, 47, 27,
        62, 49, 48, 47, 27,
        72, 65, 31, 30, 24, 23, 5, 3,
        74, 72, 64, 5, 3, 1,
        75, 73, 71, 68, 67, 44, 38, 37, 36,
        75, 68, 66,
        74, 73, 70, 67, 66,
        74, 70, 7, 2, 1,
        74, 73, 69, 68,
        73, 72, 66, 45, 44, 37, 30,
        74, 73, 71, 65, 64, 31, 30,
        74, 72, 71, 70, 68, 66,
        73, 72, 70, 69, 68, 65, 1,
        67, 66, 61, 38),
sumNumNeigh = 414)

INITIAL VALUES:

list(tau.c = 1, tau.h=1, alpha0 = 0, alpha1 = 0,
c=c(0,0,0,0,0,0,0,0,0,0,
       0,0,0,0,0,0,0,0,0,0,
       0,0,0,0,0,0,0,0,0,0,
       0,0,0,0,0,0,0,0,0,0,
       0,0,0,0,0,0,0,0,0,0,
       0,0,0,0,0,0,0,0,0,0,
       0,0,0,0,0,0,0,0,0,0,
       0,0,0,0,0),
h=c(0,0,0,0,0,0,0,0,0,0,
       0,0,0,0,0,0,0,0,0,0,
       0,0,0,0,0,0,0,0,0,0,
       0,0,0,0,0,0,0,0,0,0,
       0,0,0,0,0,0,0,0,0,0,
       0,0,0,0,0,0,0,0,0,0,
       0,0,0,0,0,0,0,0,0,0,
       0,0,0,0,0))