Equilibrium simulations of proteins using molecular fragment replacement and NMR chemical shifts

Significance

Chemical shifts are the most fundamental parameters measured in nuclear magnetic resonance spectroscopy. Since these parameters are exquisitely sensitive to the local atomic environment, they can provide detailed information about the three-dimensional structures of proteins. It has recently been shown that using such information directly as input in molecular simulations based on the molecular fragment replacement strategy can help the process of protein structure determination. Here, we show how to implement this strategy to determine not only the structures of proteins but also their thermal fluctuations, thereby broadening the scope of chemical shifts in structural biology.

Abstract

Methods of protein structure determination based on NMR chemical shifts are becoming increasingly common. The most widely used approaches adopt the molecular fragment replacement strategy, in which structural fragments are repeatedly reassembled into different complete conformations in molecular simulations. Although these approaches are effective in generating individual structures consistent with the chemical shift data, they do not enable the sampling of the conformational space of proteins with correct statistical weights. Here, we present a method of molecular fragment replacement that makes it possible to perform equilibrium simulations of proteins, and hence to determine their free energy landscapes. This strategy is based on the encoding of the chemical shift information in a probabilistic model in Markov chain Monte Carlo simulations. First, we demonstrate that with this approach it is possible to fold proteins to their native states starting from extended structures. Second, we show that the method satisfies the detailed balance condition and hence it can be used to carry out an equilibrium sampling from the Boltzmann distribution corresponding to the force field used in the simulations. Third, by comparing the results of simulations carried out with and without chemical shift restraints we describe quantitatively the effects that these restraints have on the free energy landscapes of proteins. Taken together, these results demonstrate that the molecular fragment replacement strategy can be used in combination with chemical shift information to characterize not only the native structures of proteins but also their conformational fluctuations.

Despite significant advances in the development of accurate force fields for protein simulations (1), it frequently remains a challenge to obtain the level of agreement between simulation and experiment necessary to draw biologically relevant conclusions. As a consequence, it is becoming increasingly common to use experimental data as restraints in molecular simulations to modify the force fields in a system-dependent manner to obtain descriptions consistent with the experimental data themselves. These developments have generated an interest in developing new methods to make optimal use of the available experimental data. From the initial emphasis on the determination of the native structures of proteins, the focus is increasingly shifting toward generating conformational ensembles representing their conformational fluctuations (2–4). In this context, problems with overfitting are systematically addressed (5), and in general efforts are made to implement the structural restraints as conservatively as possible, for instance by using the maximum entropy principle (6–9). The field is also seeing increasingly sophisticated modeling approaches, often based on Bayesian statistics, for dealing rigorously with the problem of updating prior information (e.g., the force field) in the light of observed data (10–12).

Although there are substantial differences between these methods, they share the same basic approach of applying a perturbation to the force field. There is an alternative approach, however, which is applicable in cases where the experimental data provide information primarily about local structural properties of a molecule. In such cases, without modifying the force field, the data can be integrated directly in the sampling procedure, which can dramatically increase the efficiency of the simulations. For instance, local structural information can be integrated into the simulations through the use of molecular fragments, which serve as building blocks during the conformational sampling (13–16). The molecular fragments are selected according to the degree to which they match the experimental data, and during the simulations these fragments are continuously reassembled to form new candidate structures. Simulated molecular structures are thus ensured to retain local structural properties consistent with the experimental data, which reduces the size of the conformational search space substantially.

NMR chemical shifts (CS) are an example of such data. These parameters are those most readily and accurately measurable in NMR spectroscopy, and are highly sensitive to the local structure of proteins. This information has been used to characterize protein secondary structures (17, 18) and to determine the allowed ranges of dihedral angles (19). More recently it has been demonstrated that by encoding the chemical shift information into molecular fragments it is possible to accurately determine the structures of small- to medium-sized globular proteins (14–16, 20–23).

The fragment replacement approach has thus proven to be an extremely powerful method for rapid exploration of conformational space. This success builds on two main factors: (i) an efficient sampling of the conformational space, and (ii) a system-specific perturbation to the force field, which is implicitly introduced by using fragment replacement to navigate the conformational space. Given the complexity of their interplay, however, it has been difficult to assess which of these contributions plays the dominant role. Because of the implicit nature of the bias, it also remains challenging to ascertain whether simulations based on fragment replacement reach the global free energy minimum in the conformational space of a protein. The bias is difficult to quantify, as it depends on the specific library of fragments used and on the statistical weights by which fragments are selected. It is therefore generally not possible to satisfy the detailed balance condition, which is a central requirement to ensure that simulations sample the Boltzmann distribution of a force field. A further problem is that the discrete fragment libraries may not necessarily cover the entire relevant space of protein conformations. Although fragment replacement methods are thus efficient in finding a structure compatible with the available data, it is not straightforward to demonstrate that such a structure actually represents the native state, even if, for practical purposes, it does so in most cases (22). Likewise, it is difficult to use fragment-based approaches to generate alternative conformers that represent the less densely populated regions of the native free energy landscape.

For chemical shifts, efforts have been made to avoid these problems by integrating the data into the simulations in the traditional way, using an explicit perturbation of the force field to penalize any deviations between calculated and experimental chemical shifts. Approaches of this kind have been successful in providing information about the properties of native ensembles and alternative conformers (24, 25). Because of their computational requirements, however, these methods have not been used so far to find the native states of proteins starting from fully unfolded states, suggesting that the performance gains obtained through fragment replacement are necessary to obtain convergence.

In this paper, we present the CS-TORUS method, a probabilistic model that uses chemical shift information for the efficient sampling of the conformational space of proteins. CS-TORUS quantifies the information encoded in the available chemical shifts, and makes it possible to use this information either as a specific modification to the force field, or strictly as a guide for more efficient sampling, while maintaining the original Boltzmann distribution. This method thus combines the strength of the two approaches described above: Similar to traditional fragment replacement, CS-TORUS generates candidate structures consistent with the available chemical shifts, but because these correspond to samples from a well-defined probability distribution, the introduced bias is quantified, allowing the original statistical weights to be restored.

We first demonstrate that CS-TORUS results are consistent with those of other methods when used in a corresponding setting. We show with two examples that CS-TORUS, when combined with a simple force field, allows proteins to be folded from their unfolded state to their native structures. We then proceed by illustrating the advantages that a probabilistic model provides. First, we quantify the extent to which the experimental restraints modify the free energy landscape of proteins in a setting where chemical shifts are used to bias molecular simulations. Second, we provide an example where chemical shift data are used solely to enhance sampling from an unbiased Boltzmann distribution.

Results and Discussion

Definition and Parameterization of the CS-TORUS Model.

The probabilistic model used in this study is a dynamic Bayesian network (26), which simultaneously captures dihedral angle, amino acid, secondary structure, and chemical shift information. The sequential dependencies along a protein chain are modeled using a matrix of transition probabilities between so-called hidden states. At any given time in a simulation, each residue is associated with a hidden value (H), which is dependent on neighboring hidden values through this transition probability matrix. Each hidden node value is associated with a particular conditional distribution over all output nodes: dihedral angles (D), amino acid type (A), secondary structure (S), cis/trans state of the peptide bond (T), and distributions over backbone chemical shift values (C_Cα, C_Cβ, C_C, C_N, C_Hα, and C_H). This design is an extension of an earlier model of protein local structure (27). A graphical illustration of the model (Fig. 1) shows explicitly the assumed independence relationships in the model, allowing us to readily write up the corresponding probability distribution

$$\begin{array}{l}P\left(\overline{D},\overline{T},\overline{S},\overline{A},{\overline{C}}_{\text{C}\alpha }\dots {\overline{C}}_{\text{H}}\right)={\displaystyle \sum _{\overline{H}}P\left(\overline{D},\overline{T},\overline{S},\overline{A},{\overline{C}}_{\text{C}\alpha }\dots {\overline{C}}_{\text{H}},\overline{H}\right)}\\ ={\displaystyle \sum }_{\overline{H}}P\left(D_1|H_1\right)\cdots P\left(C_{\text{C}\alpha ,1}|H_1\right)\cdots P\left(C_{\text{H},1}|H_1\right)P\left(H_1\right)\\ {\displaystyle \prod _{i=2}^{N}P\left(D_i|H_i\right)\cdots P\left(C_{\text{C}\alpha ,i}|H_i\right)\cdots P\left(C_{\text{H},i}|H_i\right)P\left(H_i|H_{i-1}\right)},\end{array}$$ [1]

where i is the index in the sequence and N refers to the total number of residues in the chain. The sum runs over all possible sequences of hidden nodes, a calculation that can be done efficiently using dynamic programming (27). Although the model is Markovian, it will capture longer range effects up to six residues along the protein chain through allocated paths in the transition matrix (27), and thus contains similar information as that encoded in fragment libraries (SI Appendix).

Fig. 1.

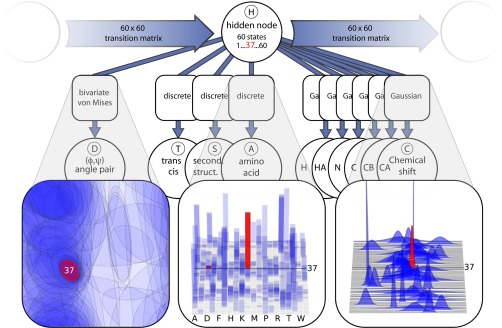
Schematic illustration of the CS-TORUS model. Circular nodes represent stochastic variables; the type of distribution is specified in square boxes. The graph structure encodes the conditional independence relations among the variables. The model is a variant of a hidden Markov model: a Markov chain of hidden nodes (H) captures the sequential dependencies along the peptide chain, and each hidden node corresponds to a particular emission distribution over backbone (ϕ, ψ) dihedral angle pairs (D), amino acid types (A), secondary structure labels (S), labels for the cis/trans conformation of the peptide bond (T), and six chemical shift observables (C): H, HA, N, C, CB, CA. We highlight a single hidden node (red) as an example of how the choice of hidden node dictates which mixture component is used. See SI Appendix, Fig. S3 for details.

The symmetry among the output nodes in this type of model provides a convenient flexibility: dihedral angles can be sampled conditionally on an input of amino acid and chemical shift information, but it is also possible to sample chemical shift values or even amino acid types compatible to a given protein structure. Any input that is not available, such as unassigned chemical shifts, can be integrated out by simply omitting the value during the calculation. Indeed, this is the reason that the chemical shifts are modeled as conditionally independent Gaussians, rather than a single multivariate distribution: the current design facilitates use of the model when only some of the chemical shifts have been observed (see SI Appendix, Fig. S2 for the impact of the different CS nuclei). Likewise, the model automatically handles stretches of amino acids with unobserved chemical shifts, simply reverting to the general Ramachandran-like statistics applicable for the given amino acid type. As described in Materials and Methods, the parameters of CS-TORUS were estimated using a set of 1,349 protein structures with known experimental chemical shifts.

Monte Carlo Simulations with the CS-TORUS Model.

The CS-TORUS model generates dihedral angles compatible with the preferences inherent both to the amino acid sequence and with experimentally determined chemical shifts. For individual positions, this is done directly by drawing samples from d_i ∼ P(D_i|H_i−1, H_i+1, A_i, C_Cα,i … C_H,i), but it is also possible to sample entire subsequences from the model using the forward–backtrack algorithm (27). Random stretches of dihedral angles can thereby be repeatedly replaced to construct new candidate structures, thus mimicking the traditional fragment replacement strategy, but avoiding the boundary issues associated with the discrete fragments.

The probabilistic nature of the CS-TORUS model makes it particularly suitable for Markov chain Monte Carlo simulations. In this approach, the simulation proceeds by accepting or rejecting a move according to an acceptance criterion that ensures detailed balance and thereby correct sampling from the equilibrium distribution of a system. In the CS-TORUS model, by manipulating the detailed balance equation for a transition from a sequence of dihedral angles $\overline{D}$ to a new sequence ${\overline{D}}^{\prime }$ (for simplicity omitting the variables we condition on), a standard Metropolis–Hastings acceptance criterion can be written as

$$\alpha \left(\overline{D}\to {\overline{D}}^{\prime }\right)=\text{min}\left(1,\frac{\pi \left({\overline{D}}^{\prime }\right)P_p\left({\overline{D}}^{\prime }\to \overline{D}\right)}{\pi \left(\overline{D}\right)P_p\left(\overline{D}\to {\overline{D}}^{\prime }\right)}\right),$$ [2]

where π is the target distribution for the Markov chain (e.g., the Boltzmann distribution corresponding to the applied force field), P_p is the CS-TORUS proposal probability, and α is the acceptance probability.

Eq. 2 implies that to sample from the original Boltzmann distribution π, the proposal probability P_p corresponding to the chemical shift bias should be taken into account each time a new structure is evaluated. Conversely, the expression also explicitly states the consequence of not compensating for this bias. In effect, this scenario corresponds to sampling from a modified target distribution

$$P_e\left(\overline{D}\right)=\pi \left(\overline{D}\right)P_p\left(\overline{D}\right)=\exp \left(-\beta E\left(\overline{D}\right)+\log \left(P_p\left(\overline{D}\right)\right)\right).$$ [3]

This translation to energies demonstrates that an uncompensated proposal in the simulation corresponds to adding an implicit energy term to the force field. We will refer to this as biased sampling. The traditional fragment replacement strategy for protein structure determination can be seen as an example of this approach—although in this case it is not possible to calculate the value of the energetic bias that is introduced, because $P_p\left(\overline{D}\right)$ cannot explicitly be calculated. Also, depending on the scheme used, it is not always trivial to demonstrate that traditional fragment replacement approaches correspond to a well-defined probability distribution, because the assembly process may introduce angles that are not part of the library itself.

Using Chemical Shifts to Bias the Sampling by Changing the Force Field.

Chemical shifts have in recent years been successfully integrated into molecular simulations, modifying force fields to produce protein structures that are consistent with the measurements. Whether the modification is made explicitly to the force field (24, 25), or through selection of compatible fragments from the Protein Data Bank (PDB) (14, 15, 16, 20, 21), the result is an effective force field that is modified to increase the agreement with the experimental data.

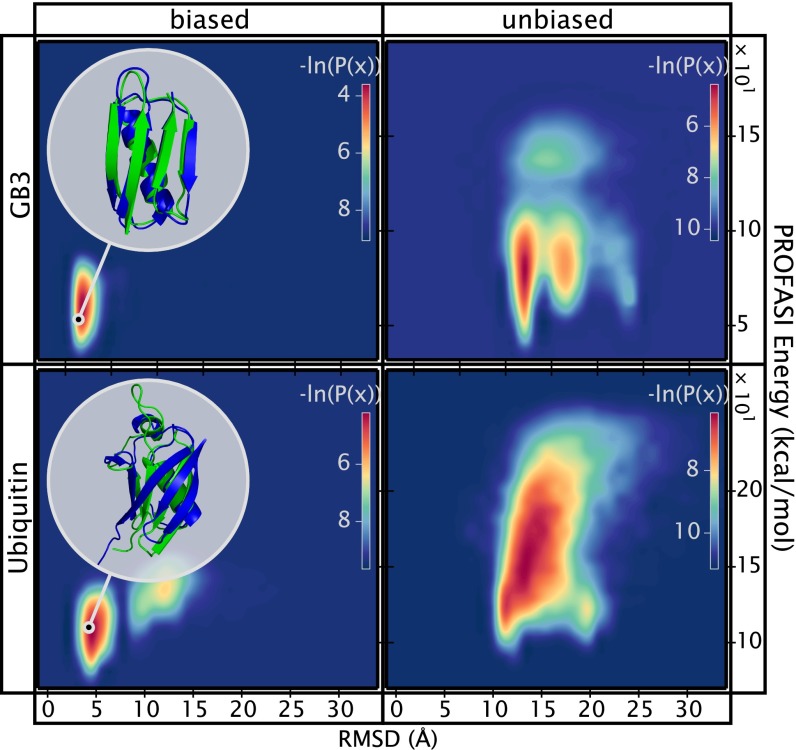
As an initial test of the model, we examined whether CS-TORUS could be used in a similar way to determine protein structures using chemical shift input. For all simulations in this paper we used the PROFASI force field, which has been shown to enable the reversible folding of peptides and small proteins (28). We selected two proteins, Ubiquitin and GB3, that do not fold using the force field alone, due to limitations in PROFASI. The task was therefore to investigate whether the perturbation of the force field through biased sampling with our model was sufficient to fold these proteins.

We sampled conformations of ubiquitin and GB3 both directly from PROFASI and from a biased simulation that also included the experimental chemical shifts, and calculated the corresponding free energy surfaces (Fig. 2). As expected, simulations with PROFASI alone do not result in native-like structures. In contrast, in the CS-TORUS simulations we obtain a clear free energy minimum around the correct native structure of these two proteins. It thus appears that CS-TORUS can be applied in traditional structure determination settings, similar to existing methods. Having established this equivalence, the remainder of the paper will focus on the simulation features made possible by the unique features of probabilistic models.

Fig. 2.

Examples of the effect of the CS-TORUS chemical shift bias on two systems that do not fold with the PROFASI force field alone. (Right) Unbiased simulation using only the PROFASI force field. (Left) Biased simulation using the CS-TORUS pivot move, highlighting the minimum energy (PROFASI+CS-TORUS) structure obtained. Both types of simulations were conducted using a multicanonical (flat histogram) ensemble, which was then reweighted to the desired temperature (300 K for GB3; 315 K for Ubiquitin).

Using Chemical Shifts to Bias the Sampling.

The results presented in the previous section are similar in spirit to those obtainable using fragment-assembly–based methods like CHESHIRE (14) and CS-ROSETTA (16). However, the probabilistic nature of the CS-TORUS method allows us to address several questions that are not accessible by these established methods.

In general, one can use the chemical shift information to modify: (i) the force field used in the simulations; and/or (ii) the manner in which the conformational space is sampled. Existing methods differ in these respects. For example, CHESHIRE and CS-ROSETTA do both i and ii, while the replica-averaged molecular dynamics simulation method (29) does i. A recent method based on the use of chemical shifts as collective variables in metadynamics simulations (30) also does i, but enables the correct statistical weights to be obtained at the end of the simulations. In contrast to previous methods, the CS-TORUS naturally covers any combination of these scenarios, by allowing us to obtain the same bias either through sampling or by evaluation of the likelihood of the model and adding it as part of the energy function.

We illustrate this point by comparing the folding free energy landscapes in the presence and absence of experimental restraints, focusing on four protein and peptide systems that are known to fold correctly in the unperturbed PROFASI force field: Trp-Cage, the GB1-hairpin, Beta3s, and the C-terminal fragment of the Top7 protein (Top7-Cfr), each with different levels of chemical shift coverage (SI Appendix, Table S1). This analysis allows us to quantify the potential increase in computational efficiency compared with a folding simulation with an unperturbed force field, and to evaluate the effect that experimental restraints have on the computational free energy surface.

The free energy landscapes obtained in the PROFASI force field for all four proteins show multiple minima, which for three of four proteins include both the native state, unfolded state, and various near-native conformations (Fig. 3A). The inclusion of the experimental restraints, either in the form of biased moves or energies (Fig. 3 B and C, respectively), shows clearly that the experimental data generally works by selecting the native basin from the multiple basins in the unperturbed force field.

Fig. 3.

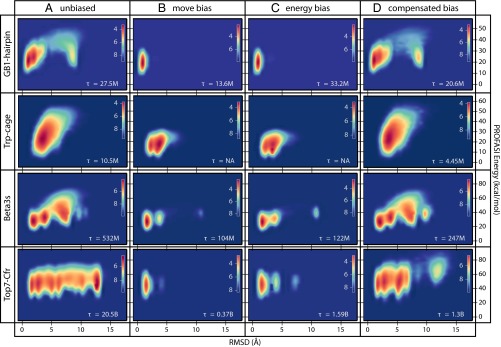
Comparison of the free energy landscapes of four proteins using different Monte Carlo sampling strategies made possible by CS-TORUS. Each plot shows a 2D free energy profile using RMSD and PROFASI energies as reaction coordinates, and with the color code providing the free energy scale. The simulations sample a multicanonical (flat histogram) ensemble, which is subsequently reweighted to a Boltzmann distribution at a specific temperature (279 K for GB1-hairpin, Beta3s, and Top7-Cfr; 300 K for Trp-Cage). All simulations use uniform sidechain steps and biased Gaussian steps (31), but differ in the choice of pivot move. (A) Unbiased sampling using simple pivot moves; (B) biased sampling using CS-TORUS–driven pivot moves; and (C) simple pivot moves, including the bias as a term in the energy function. (D) Like B but including the bias with negative weight in the energy function, thus canceling out the chemical shift bias at the specified temperature. The τ values refer to the round trip time measured in Monte Carlo steps (SI Appendix). In the two cases with τ = NA, no unfolding events were observed (SI Appendix, Fig. S5). The simulations on the different proteins have different CS data to their disposal: GB1-hairpin lacks hydrogen chemical shifts, Trp-cage only has hydrogen chemical shifts, Beta3s has CA and hydrogen chemical shifts, and Top7-Cfr has all six backbone chemical shifts observed (SI Appendix, Table S1).

To examine the effect of the experimental restraints on the time it takes to reach the native state we also calculated the “round trip” times (the time it takes to transition reversibly from the unfolded state to the folded state and back) for these simulations (Fig. 3 A–C; see SI Appendix, Fig. S5 for the full trajectories). We obtained a consistent and considerable speedup as a consequence of the chemical shift bias implemented in CS-TORUS. For complex systems with many competing minima, such as Top7-Cfr, the speedup can be quite substantial (∼13×). Also, as expected, the bias induced by sampling (Fig. 3B) is the same as that obtained by enforcing it through a perturbation of the force field (Fig. 3C), but the former is clearly seen to be more efficient.

Bias through Sampling or Force Field Perturbation.

Recent work has demonstrated that experimental data can be integrated into simulation in a minimally biased way by using the maximum entropy principle (6–9). The fragment-based approaches and the CS-TORUS simulations described above generally violate this principle and introduce such a strong bias that it potentially disrupts key features of the original force field. It is therefore interesting to investigate whether it is possible to use the bias from chemical shifts in a less intrusive manner, and still maintain the improvements in sampling efficiency described above.

The dual nature of our model allows us to evaluate the bias we introduce in a simulation and to compensate for this effect to recover the Boltzmann distribution of the force field in the absence of the experimental restraints. The simplest way to achieve this result follows directly from Eq. 3: in each iteration, we add a negative energy contribution corresponding to the bias induced through sampling (SI Appendix). This technique allows us to conduct simulations where the chemical shift signal is used mainly to reduce the conformational space in the unfolded state, and we maintain the ability to obtain unbiased statistics (in this case of the PROFASI force field) at a specified temperature of interest.

We therefore repeated the simulations of the four proteins in the previous section with this setup (Fig. 3D). The first three systems clearly demonstrate the expected behavior: the free energy profiles obtained with the compensated bias approach are very similar to those obtained using unbiased Monte Carlo sampling with the PROFASI force field (Fig. 3A); because these two different kinds of simulations sample from the same distribution, any minor differences can be ascribed to lack of full convergence. Although the same distributions are reproduced, we find substantially reduced round-trip times, demonstrating how CS-TORUS makes it possible to use the experimental data to enhance simulation efficiencies without perturbing the free energy landscape.

For Top7-Cfr, the free energy landscape differs notably from the unbiased case. The primary difference is missing peaks at high RMSD. A closer inspection (SI Appendix, Fig. S6) reveals that these peaks correspond to structures where the helix has been replaced by beta structure. This is likely an artifact of the force field, and because this type of structure is at odds with the available chemical shifts, structures in this part of phase space will never be proposed by the model. This example thus illustrates the origin of the speedup obtained using biased sampling: greater emphasis is placed on important parts of the conformational space, and unrealistic conformations are excluded from the sampling. Note, however, that the low-RMSD peaks, for which the model and force field are not in conflict, are correctly recovered. The free energy landscape of Top7-Cfr is known to be extremely challenging to estimate (28), and minor differences in the low-RMSD region are not surprising, but an analysis of the progression of convergence of this system strongly suggests that completely identical peaks would eventually be obtained (SI Appendix, Fig. S6B).

In practice, the compensated bias approach can thus serve as an efficient means to explore those regions of the free energy landscape of a force field that are compatible with the provided chemical shift signal. The method will faithfully reproduce any competing minima for which the local structures are reasonable, while excluding force field artifacts that are inconsistent with the chemical shifts.

Overall, these results demonstrate the flexibility of a model like CS-TORUS in a Monte Carlo framework. The two central columns in Fig. 3 correspond to the two approaches that have previously been used to incorporate chemical shift data into molecular simulations: a biased sampling technique (fragment replacement) and an energy perturbation approach. With the probabilistic method developed here, these approaches emerge as merely two different applications of the same model, with identical outcomes. Our results thus allow us to quantify how fragment-based chemical shift biases affect the folding free energy landscape. The dual nature of the model, allowing for both sampling and evaluation, also provides the possibility for other applications. We give one such example (Fig. 3D) by demonstrating that the bias introduced through sampling can be compensated for so that the chemical shift signal is used only to improve sampling efficiency, without affecting the produced ensemble.

It has recently been suggested (30) that using chemical shift data as collective variables in a metadynamics simulations might provide substantial gains in the exploration efficiency of free energy landscapes. The biased sampling approach presented here (Fig. 3D) offers a new perspective on this approach, where the bias is introduced directly through sampling. Metadynamics is often conducted using molecular dynamics frameworks, where the move set is given. The results above suggest that there might be benefits to looking at a Monte Carlo based metadynamics approach, where the bias is included directly through the move set.

Conclusions

The molecular fragment replacement approach is highly effective in incorporating local structural information into molecular simulations of complex biomolecular systems. This method plays a central role in the success of protein structure prediction methods (13) and in the recent developments in the ability to perform protein structure determination using only NMR residual dipolar couplings and chemical shifts (14, 15, 16, 20, 21).

In this work we have presented a probabilistic model, CS-TORUS, to extend the molecular fragment-replacement approach from the energy minimization needed for structure determination to the equilibrium sampling required for the determination of the free energy landscapes of proteins. At variance with existing molecular fragment replacement approaches, the probabilistic nature of CS-TORUS makes it possible to quantify the bias introduced through the fragment assembly process—and to compensate for it if so desired. This feature makes the method well-suited for general Markov chain Monte Carlo simulations, and, as we have illustrated in this work with several examples, introduces the possibility for novel simulation approaches. The flexibility provided by this probabilistic approach thus expands the scope of molecular fragment replacement, and provides new opportunities for the efficient characterization of the structure and dynamics of proteins.

Materials and Methods

Model Training.

The model parameters were estimated using the RefDB dataset (April 2011), containing PDB structures with rereferenced chemical shifts (32). Proteins from this set were excluded if they belonged to the same superfamily as any of the proteins used for our simulations (SI Appendix). This left 1,349 PDB structures (SI Appendix, Fig. S4), for which ϕ, ψ angles, amino acid labels, secondary structure, peptide bond cis/trans information, and CA, CB, C, N, HA, and H chemical shift information was extracted. The model was trained using the stochastic EM algorithm in the Mocapy++ software package (33). The hidden node size was estimated by training models with varying number of hidden node components, and using the Bayesian information criterion for model selection (SI Appendix, Fig. S1). See SI Appendix for details.

Simulations.

A standard set of Monte Carlo moves was used for the simulations (34). Sidechain χ angles were sampled uniformly, while backbone dihedrals were sampled using biased Gaussian steps (31) and either standard or CS-TORUS pivot moves, altering a single (ϕ, ψ) pair. When using the latter, the CS-TORUS bias was included in the acceptance criterion of the biased Gaussian step, to ensure that both moves sample from the same distribution (SI Appendix). Simulations were conducted using the PHAISTOS software package (35), except for the unbiased simulation of Top7-Cfr, for which we used the PROFASI software package (34) (with identical settings). All simulations were conducted using generalized ensembles in the MUNINN software library (36). See SI Appendix for details.

Availability.

The CS-TORUS model is implemented as part of the PHAISTOS simulation framework, which is freely available at http://sourceforge.net/projects/phaistos/.