Neural mechanism of optimal limb coordination in crustacean swimming

Significance

Despite the general belief that neural circuits have evolved to optimize behavior, few studies have clearly identified the neural mechanisms underlying optimal behavior. The distinct limb coordination in crustacean swimming and the relative simplicity of the neural coordinating circuit have allowed us to show that the interlimb coordination in crustacean swimming is biomechanically optimal and how the structure of underlying neural circuit robustly gives rise to this coordination. Thus, we provide a concrete example of how an optimal behavior arises from the anatomical structure of a neural circuit. Furthermore, our results suggest that the connectivity of the neural circuit underlying limb coordination during crustacean swimming may be a consequence of natural selection in favor of more effective and efficient swimming.

Abstract

A fundamental challenge in neuroscience is to understand how biologically salient motor behaviors emerge from properties of the underlying neural circuits. Crayfish, krill, prawns, lobsters, and other long-tailed crustaceans swim by rhythmically moving limbs called swimmerets. Over the entire biological range of animal size and paddling frequency, movements of adjacent swimmerets maintain an approximate quarter-period phase difference with the more posterior limbs leading the cycle. We use a computational fluid dynamics model to show that this frequency-invariant stroke pattern is the most effective and mechanically efficient paddling rhythm across the full range of biologically relevant Reynolds numbers in crustacean swimming. We then show that the organization of the neural circuit underlying swimmeret coordination provides a robust mechanism for generating this stroke pattern. Specifically, the wave-like limb coordination emerges robustly from a combination of the half-center structure of the local central pattern generating circuits (CPGs) that drive the movements of each limb, the asymmetric network topology of the connections between local CPGs, and the phase response properties of the local CPGs, which we measure experimentally. Thus, the crustacean swimmeret system serves as a concrete example in which the architecture of a neural circuit leads to optimal behavior in a robust manner. Furthermore, we consider all possible connection topologies between local CPGs and show that the natural connectivity pattern generates the biomechanically optimal stroke pattern most robustly. Given the high metabolic cost of crustacean swimming, our results suggest that natural selection has pushed the swimmeret neural circuit toward a connection topology that produces optimal behavior.

It is widely believed that neural circuits have evolved to optimize behavior that increases reproductive fitness. Despite this belief, few studies have clearly identified the neural mechanisms producing optimal behaviors. The complexity of behaviors generally makes it difficult to assess their optimality, and neural circuits are often too complicated to concretely link neural mechanisms to the overt behavior. Energy-intensive locomotion such as steady swimming, walking, and flying provides important model systems for studying optimality because the goal of the behavior is clear and it is likely to have been optimized for efficiency (1). For example, the kinematics of locomotion has been shown to be optimal in the cases of the undulatory motion of the sandfish lizard and the lamprey (2, 3). On the other hand, the neural circuits underlying locomotion in most organisms are not sufficiently characterized to understand how they give rise to the optimal motor behavior. Because of the distinct frequency-invariant stroke pattern and the relative simplicity of the neuronal circuit, limb coordination of long-tailed crustaceans during steady swimming provides an ideal model system for examining the optimality of motor behavior and its neural underpinnings.

During forward swimming, long-tailed crustaceans, like crayfish, krill, shrimp, and lobsters, propel themselves through the water using four or five pairs of abdominal limbs called swimmerets that move rhythmically through cycles of power strokes (PSs) and return strokes (RSs). Although these animals vary in size from 0.5 cm to over 40 cm and beat their swimmerets with frequencies ranging from about 1 to 10 Hz (4, 5), the stroke pattern is invariant: limbs on neighboring abdominal segments always maintain an approximate quarter-period (0.25) phase difference in a tail-to-head metachronal wave (Fig. 1). This phenomenon is known as phase constancy. Measurements of the metabolic cost of krill swimming show that up to 73% of their daily energy expenditure is devoted to paddling (6). This and the facts that the distinct limb coordination is the only stroke pattern that these crustaceans exhibit when the swimmeret system is active and that this limb coordination is conserved across many species suggest that the stroke pattern is biomechanically optimized for swimming. This in turn suggests that evolution has pushed the properties of the underlying neural circuit to produce the distinct phase constant limb coordination.

Fig. 1.

Forward swimming of a crustacean. Cycles of power strokes (PSs) and return strokes (RSs) of the swimmerets provide the thrust for forward swimming. Movement of neighboring swimmerets maintains a quarter-period phase difference with the more posterior swimmeret leading the cycle. Image courtesy of Wikimedia Commons/Øystein Paulsen.

Metachronal waves of motor activity during locomotion are observed in many animals, and the underlying neural circuits have been shown to consist of chains of local pattern-generating microcircuits [i.e., local central pattern generators (CPGs)] (7–10). This is the case for the neural circuits that control the undulatory motion of bony fish, amphibians, and lamprey during swimming (9–12) and the movements of swimmerets in crayfish (Pacifastacus leniusculus) (13). By modeling the neural circuit of the crayfish swimmeret system as a chain of generic phase oscillators, previous theoretical studies (14–16) showed that the tail-to-head 0.25 phase constant stroke pattern could be achieved if the phase response properties of the local CPGs to inputs from ascending and descending inter-CPG connections satisfy two different constraints. Similar results were obtained for the lamprey swimming neural circuit (11, 17). Many studies (e.g., refs. 14, 16, and 18) have addressed aspects of how these two constraints are satisfied, but it remains unclear how they are achieved and maintained over a wide range of frequencies. Recent experimental work has elucidated the cellular composition of the local swimmeret CPGs and the synaptic organization of the circuit that connects them in the crayfish swimmeret system (13, 19, 20), allowing these issues to be directly addressed.

In this article, we first use computational fluid dynamics simulations to show that the metachronal multilimb stroke pattern with ∼0.25 intersegmental phase differences is the most effective and efficient metachronal stroke pattern across the entire biologically relevant range of body sizes and stroke frequencies in crustacean swimming. We then show that the half-center structure of the local-CPG circuits (21–23) and the topology of the inter-CPG connections in the crayfish swimmeret circuit (19, 20) provide a robust neural mechanism for producing the 0.25 phase-locked metachronal wave. This reduces the previously determined constraints on the phase response properties of the CPGs to a single condition. Furthermore, we experimentally measure the phase response properties of the crayfish swimmeret CPG circuit and show that this single condition holds. Finally, we consider all possible topologies for connections between the local CPGs and show that the network topology present in the crayfish swimmeret circuit generates the biomechanically optimal stoke pattern most robustly.

The Mechanical Advantage of the Tail-to-Head Metachronal Wave of Swimmeret Coordination

Metachronal waves of ciliary beating in microorganisms are the subject of intense recent study (24–27). These previous works found that metachronal waves may allow cilia to propel cells forward with higher propulsion velocity and efficiency. However, metachronal waves in ciliary beating differ from the metachronal paddling rhythm in crustacean swimming in many ways: (i) Swimmerets are plate-like paddles, whereas cilia are hair-like appendages. (ii) The limb angle of swimmerets changes smoothly through the cycle with a duty cycle of approximately one-half, whereas cilia use a fast power stroke and a slow sweeping recovery stroke. (iii) Although both swimmerets and cilia beat in a back-to-front metachronal wave, the phase difference between neighboring swimmerets is ∼25%, whereas the phase difference between appendages varies from ∼1% to ∼10% depending on the organism and location of the cilia on the organism. (iv) Evidence suggests that phase locking of cilia occurs through hydrodynamic forces, whereas neural activity is the primary determinant of phase locking of crustacean swimmerets. (v) The fluid dynamics resulting from cellular level metachronal waves are characterized by Reynolds numbers (Re) close to 0. The Re characterizes the relative importance of inertial forces to viscous forces in the flow. For Re ≈ 0, viscous forces dominate and inertial forces can be neglected. The Re increases with the size of the animal (characteristic length scale) and decreases with the stroke period (characteristic time scale). The natural variation in a crustacean’s size and stroke frequency leads to Re ranging from about 10 to 1,000 (SI Text, section 1.1), under which both viscous and inertial effects are relevant. Hence, the fluid dynamics of cilia beating are significantly different from the fluid dynamics of crustacean swimming. Relatively few studies have examined metachronal limb paddling for the range of Re under which crustaceans operate (28–30). Recently, a model based on drag forces alone predicted a slight mechanical advantage of metachronal wave in krill swimming (31). However, this model does not capture the nonlinear interactions of the forces generated by the multiple limbs arising from the local flow, which have a significant effect on swimming when limbs are close to each other. To capture this essential effect, we build a computational fluid dynamics model and numerically compute the flow field produced by crayfish’s tail-to-head metachronal limb stroke pattern and other hypothetical patterns.

Our fluid dynamics model consists of four rigid paddles as limbs moving with prescribed motion attached to a fixed wall immersed in a two-dimensional fluid. To approximate the fact that swimmerets are straight and fanned-out during PS and are curled and folded during RS, we treat swimmerets as impermeable during PS and permeable during RS (see Materials and Methods, SI Text, section 1, and Figs. S1–S6 for details).

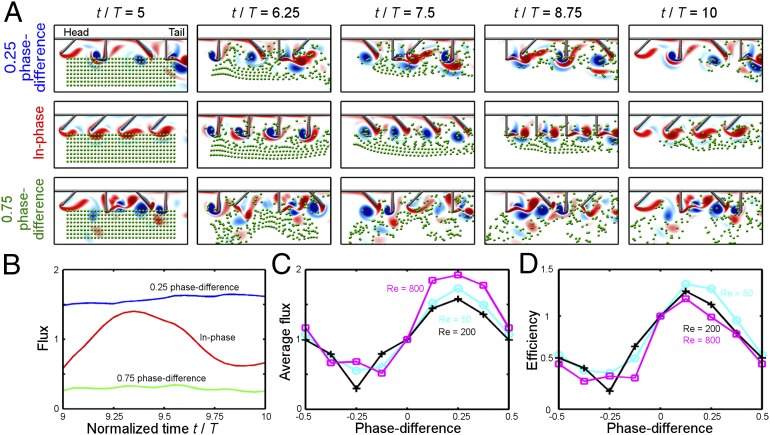
We compute the flux of the fluid moving in the tail direction and take its time average as a measure of the effectiveness of the swimmeret stroke pattern. Fig. 2B depicts the flux of three different stroke patterns (the natural tail-to-head metachronal wave with 0.25 intersegmental phase differences, the in-phase rhythm, and the head-to-tail metachronal wave with 0.75 intersegmental phase differences) at an intermediate Reynolds number (Re = 200). Both metachronal stroke patterns produce smoother temporal variation in flux compared to the in-phase rhythm because PS and RS are evenly distributed in time among the four limbs. A remarkable observation is that the natural tail-to-head metachronal wave produces a 60% increase in average flux over that of the in-phase rhythm and a 500% increase over that of the head-to-tail metachronal wave.

Fig. 2.

Computational fluid dynamics model of crayfish swimmeret paddling. (A) Snapshots of the flow field at Reynolds number 200 under the natural tail-to-head metachrony with 0.25 phase difference, the hypothetical in-phase rhythm, and the hypothetical head-to-tail metachrony with 0.75 phase difference. Free-flowing tracers are shown as green dots; red denotes positive vorticity; and blue denotes negative vorticity. (B) Flux vs. normalized time for flows in A. (C) Average flux vs. phase difference. (D) Efficiency vs. phase difference. For B–D, the curves are normalized by the time-averaged flux or efficiency of the in-phase rhythm. For C and D, results for three Reynolds numbers are provided: 50 (cyan curve with “O”), 200 (black curve with “+”), and 800 (magenta curve with “☐”).

To illustrate this increased effectiveness of the natural tail-to-head metachronal wave over other stroke patterns, we put in free-flowing tracers in the flow and observe how different stroke patterns lead to different tracer displacement. To allow the initial transient effect to disappear, we first let the swimmerets beat for five periods. At the end of the fifth period, we put in the passive tracers uniformly underneath the body. We observe how the passive tracers move as the swimmerets undergo another five periods of strokes under the three different stroke patterns (Fig. 2A and Movies S1–S3). Fig. 2A illustrates that, with the natural 0.25 phase-locked tail-to-head metachrony, the majority of the tracers are propelled toward the tail direction. The in-phase rhythm is less effective in driving the tracers toward the tail direction compared to the natural tail-to-head metachrony. With the 0.75 phase-locked head-to-tail metachrony, it is not clear whether the tracers are flowing in any particular direction. Overall, among the three stroke patterns, the natural tail-to-head metachronal wave of swimmeret coordination is the most effective stroke pattern in maximizing flux.

The above results are based on simulations for an intermediate Reynolds number (Re = 200). As the $\mathrm{Re}$ changes, the flow characteristics change significantly (Movies S1–S3). Nevertheless, the relative advantage of the tail-to-head metachronal wave over other metachronies is preserved across biologically relevant Reynolds numbers. Fig. 2C shows that the natural tail-to-head metachronal wave of swimmeret coordination with 0.25 intersegmental phase differences produces the largest average flux among all metachronal waves for $\mathrm{Re}=50$, 200, and 800.

As a measure of the efficiency of the stroke pattern, we normalize the average flux by the average power consumption per stroke period (SI Text, section 1.3). The natural tail-to-head metachronal wave of swimmeret coordination achieves close-to-maximal efficiency among all metachronies over a wide range of biologically relevant Reynolds numbers. Fig. 2D shows that the efficiency peaks at 0.125 phase difference closely followed by the 0.25 phase difference. Across Reynolds numbers from 50 to 800, the natural tail-to-head metachronal wave is up to 30% more efficient than the in-phase rhythm and 300% to 550% more efficient than the head-to-tail metachronal wave.

Overall, the above results show that the natural 0.25 phase-locked metachrony leads to near-maximal effectiveness and efficiency over the full span of biologically relevant Reynolds numbers in crustacean swimming, i.e., a significant biomechanical advantage is preserved despite the large variation in crustaceans’ size and swimmeret stroke frequency. The biomechanical optimality of the tail-to-head metachronal wave with approximate 0.25 intersegmental phase differences that is independent of swimmeret beat frequencies raises the question: What are the neural mechanisms that maintain this limb coordination in such a robust manner?

A Robust Neural Mechanism Producing Phase Constancy

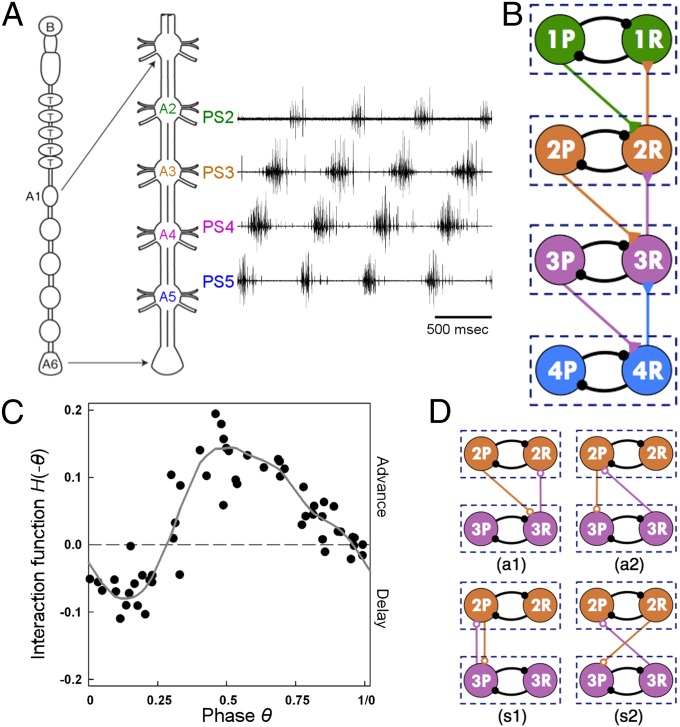
The isolated neural ventral cord of the crayfish, which contains the neural circuit driving the movement of the swimmerets, displays fictive locomotion (Fig. 3A). That is, it expresses rhythmic neural activity that is analogous to the distinct stroke pattern observed behaviorally (13, 32). This centrally generated rhythm is the primary determinant of the swimmeret coordination (SI Text, sections 1.2, 2.1, and 3). Experiments on the crayfish neural ventral cord indicate that (i) each swimmeret is innervated by an anatomically separate and functionally independent CPG (22, 33), and (ii) these CPGs are connected through ascending and descending coordinating neurons (19). Thus, the neural circuit driving metachronal swimmeret movements can be considered as a chain of four pairs of neuronal oscillators.

Fig. 3.

Neuronal circuitry underlying the crayfish swimmeret system. (A) The neural circuit underlying the crayfish swimmeret system consists of a chain of four CPGs located in the abdominal ganglion A2–A5. Each CPG innervates motor neurons that drive the power strokes (PSs) and return strokes (RSs) of a swimmeret. The dissected neural cord in isolation can generate the tail-to-head metachronal wave of neuronal activity as seen in the simultaneous extracellular recordings from the four PS motor nerves, PS2–PS5. (B) Schematic diagram of the neural circuit composed of a chain of four coupled CPGs. Each CPG is modeled as an HCO consisting of two mutually inhibited cells (large circles in diagram) that oscillate in antiphase. Cells in HCOs denoted by iP drive PS motor neurons, and cells denoted by iR drive RS motor neurons (i = 1, 2, 3, and 4). The small solid black circles symbolize inhibitory connections, the small solid triangles symbolize excitatory connections, and the colors indicate the origin of each intersegmental connection. (C) Experimentally measured interaction function H for a crayfish swimmeret CPG. (D) The natural network topology (a1) in the crayfish swimmeret neural circuit and three hypothetical network topologies, (a2), (s1), and (s2), in a chain of four HCOs with nearest-neighbor coupling. Only the middle two HCOs are shown. The small open circles symbolize either excitatory or inhibitory connections.

A useful mathematical framework for studying dynamics of interconnected CPGs is the coupled phase model (17, 34), where the state of each CPG is described completely by its phase. If the ith CPG is isolated, then its phase ${\theta }_i$ ($0\le {\theta }_i<1$) will evolve at its intrinsic frequency $\omega$, i.e., ${\theta }_i=\left(\omega t+{\varphi }_i^0\right)\mathrm{mod}\hspace{0.17em}1$, where ${\varphi }_i^0$ is the initial phase of the CPG. If the ith CPG is coupled with the jth CPG, then the rate of change of phase will be sped up or slowed down due to input from this intersegmental coupling. The magnitude of the acceleration or deceleration of phase depends on the timing and structure of the input from the jth CPG and the state-dependent response of the ith CPG. This effect is quantified by the “interaction function,” which is a function of the phase difference between the two coupled CPGs (18, 35) and is related to the phase response curve (SI Text, section 2.2).

Previously, Skinner et al. (15) used the phase model framework to describe the neural circuit of the crayfish swimmeret system as a chain of four generic oscillators with nearest-neighbor coupling:

$$\{\begin{array}{l}\frac{d{\theta }_1}{dt}=\omega +H_{\text{asc}}\left({\theta }_2-{\theta }_1\right),\\ \frac{d{\theta }_i}{dt}=\omega +H_{\text{asc}}\left({\theta }_{i+1}-{\theta }_i\right)+H_{\text{dsc}}\left({\theta }_{i-1}-{\theta }_i\right),\hspace{1em}\\ \frac{d{\theta }_4}{dt}=\omega +H_{\text{dsc}}\left({\theta }_3-{\theta }_4\right),\end{array}\begin{array}{cc}i=2\text{\hspace{0.17em}and\hspace{0.17em}}3,& \end{array}$$ [1]

where H_asc and H_dsc are the interaction functions for ascending and descending connections, respectively. Because the interaction functions are functions of the phase difference between the CPGs, they are 1-periodic functions. Phase-locked rhythms correspond to states in which the intersegmental phase differences $\mathrm{\Delta }{\theta }_i={\theta }_{i+1}-{\theta }_i$ are constant, i.e., $\left(d\mathrm{\Delta }{\theta }_i\right)/dt=0$ for $i\mathrm{=}1,2,\mathrm{and}3$. Metachronal waves correspond to phase-locked states where $\mathrm{\Delta }{\theta }_i$ are equal. Note that the tail-to-head 0.25 phase-locked state requires both $H_{\text{asc}}\left(0.25\right)=0$ and $H_{\text{dsc}}\left(-0.25\right)=0$. The question remains as to how the structure of the crayfish neural circuit maintains these two constraints on the interaction functions, and therefore maintains the optimal stroke pattern, over a broad range of stroke frequencies. However, recent experimental findings elucidating the structure of the crayfish swimmeret neural circuit allow this question to be addressed.

Accumulated anatomical and physiological results on the local and intersegmental circuitry of the crayfish swimmeret system (13, 19, 20, 23, 36) have revealed the following circuit architecture (for a more detailed description of the circuit, see SI Text, section 2.1 and Fig. S7): Each local CPG is composed of a half-center oscillator (HCO) that consists of two mutually inhibited neurons, a P cell and an R cell, that oscillate in antiphase. The P cell drives the PS motor neurons, and the R cell drives the RS motor neurons. Each local HCO has the same frequency and is effectively coupled with its nearest neighbor(s) through intersegmental connections diagramed in Fig. 3B. The descending connection is effectively excitatory and goes from the P cell of an HCO to the R cell of its more posterior neighbor HCO. The ascending connection is effectively excitatory and goes from the R cell in an HCO to the R cell of its more anterior neighbor HCO. The ascending and the descending intersegmental connections between nearest neighbors have similar strength and dynamics. We will show that the CPGs' half-center structure and the asymmetric intersegmental connectivity described above provide a robust mechanism for generating the 0.25 phase constancy independent of the intrinsic properties of the CPGs and details of the intersegmental coupling.

A Phase Model for Two Coupled HCOs.

It is instructive to first consider a subnetwork of two coupled HCOs in which each HCO has only one incoming connection and one outgoing connection. Because (i) the ascending connection between the HCOs is between R cells, (ii) the descending connection links a P cell to an R cell, and (iii) the P and R cells in each HCO are in antiphase, the descending output is effectively phase delayed by a half-period with respect to the ascending output. In the phase model, the entire local module is considered to be an oscillatory unit, whose state is described by its phase ${\theta }_i$ alone, but the ascending and descending outputs are in antiphase, i.e., ${\theta }_i$ and ${\theta }_i+0.5$, respectively. Hence, by defining $H\left({\theta }_2-{\theta }_1\right)=H_{\text{asc}}\left({\theta }_2-{\theta }_1\right)$, the interaction function for the descending connection can be rewritten as $H_{\text{dsc}}\left({\theta }_1-{\theta }_2\right)=H\left({\theta }_1-{\theta }_2+0.5\right)$. Therefore, the dynamics of the two HCOs is described by a system of two differential equations:

$$\{\begin{array}{l}\frac{d{\theta }_1}{dt}=\omega +H_{\text{asc}}\left({\theta }_2-{\theta }_1\right)=\omega +H\left({\theta }_2-{\theta }_1\right),\\ \frac{d{\theta }_2}{dt}=\omega +H_{\text{dsc}}\left({\theta }_1-{\theta }_2\right)=\omega +H\left({\theta }_1-{\theta }_2+0.5\right).\end{array}$$ [2]

It follows that the phase difference $\mathrm{\Delta }\theta ={\theta }_2-{\theta }_1$ between the HCOs is given by a single differential equation:

$$\frac{d\mathrm{\Delta }\theta }{dt}=H\left(-\mathrm{\Delta }\theta +0.5\right)-H\left(\mathrm{\Delta }\theta \right).$$ [3]

Because H has a period of 1, Eq. 3 reveals that $\mathrm{\Delta }\theta$ = 0.25 and 0.75 are always phase-locked states. We stress that this result is independent of the frequency of the oscillator and does not rely on tuning any specific biophysical parameters. This implies that the phase constancy of the 0.25 phase-locked state arises robustly from the organization of the neuronal circuitry (37).

The invariance of the phase-locked state with the 0.25 phase difference can be understood by considering the timing of the output from the half-center oscillators relative to the phase at which the oscillators receive the input. Suppose that HCO-2 is phase advanced by 0.25 relative to HCO-1. The R cell of HCO-1 receives input from the R cell of HCO-2 that is phase advanced by 0.25. On the other hand, the R cell of HCO-2 receives input from the P cell of HCO-1, which is a half-period out of phase with the R cell of HCO-1. Thus, the R cell of HCO-2 receives input that is effectively phase advanced by 0.25 (i.e., $-0.25+0.5$). This implies that both oscillators receive input at the exact same phases in their cycles. Therefore, they adjust their instantaneous frequencies in the exact same way, and HCO-2 remains phase advanced by 0.25 relative to HCO-1.

The Full Circuit of Four Coupled HCOs.

Although the crayfish’s four-HCO neural circuit is not a trivial generalization of the two-HCO circuit, the half-center structure of the CPG and the asymmetric intersegmental connectivity are still the key organizational features of the four-HCO neural circuit that gives rise to an approximate 0.25 phase constancy. From Eq. 1, the dynamics of the phase differences between each neighboring HCO $\left[\right(\mathrm{\Delta }{\theta }_1,\mathrm{\Delta }{\theta }_2,\mathrm{\Delta }{\theta }_3)$, where $\mathrm{\Delta }{\theta }_i={\theta }_{i+1}-{\theta }_i]$ are described by:

$$\{\begin{array}{l}\frac{d\mathrm{\Delta }{\theta }_1}{dt}=H_{\text{asc}}\left(\mathrm{\Delta }{\theta }_2\right)+H_{\text{dsc}}\left(-\mathrm{\Delta }{\theta }_1\right)-H_{\text{asc}}\left(\mathrm{\Delta }{\theta }_1\right),\\ \frac{d\mathrm{\Delta }{\theta }_2}{dt}=H_{\text{asc}}\left(\mathrm{\Delta }{\theta }_3\right)+H_{\text{dsc}}\left(-\mathrm{\Delta }{\theta }_2\right)-H_{\text{asc}}\left(\mathrm{\Delta }{\theta }_2\right)-H_{\text{dsc}}\left(-\mathrm{\Delta }{\theta }_1\right),\\ \frac{d\mathrm{\Delta }{\theta }_3}{dt}=H_{\text{dsc}}\left(-\mathrm{\Delta }{\theta }_3\right)-H_{\text{asc}}\left(\mathrm{\Delta }{\theta }_3\right)-H_{\text{dsc}}\left(-\mathrm{\Delta }{\theta }_2\right).\end{array}$$ [4]

As mentioned earlier, $\left(\mathrm{\Delta }{\theta }_1,\mathrm{\Delta }{\theta }_2,\mathrm{\Delta }{\theta }_3\right)=\left(0.25,0.25,0.25\right)$ is a phase-locked state if and only if both $H_{\text{asc}}\left(0.25\right)=0$ and $H_{\text{dsc}}\left(-0.25\right)=0$. Note that these are two independent conditions that the crayfish swimmeret neural circuit needs to satisfy. However, because of the half-center structure of the CPGs and the intersegmental connectivity (Fig. 3B), one of the above two conditions is eliminated. Recall that the descending outputs are effectively phase delayed by a half-period with respect to the ascending outputs, i.e., $H_{\text{asc}}\left({\theta }_2-{\theta }_1\right)=$$H\left({\theta }_2-{\theta }_1\right)$ and $H_{\text{dsc}}\left({\theta }_1-{\theta }_2\right)=$$H\left({\theta }_1-{\theta }_2+0.5\right)$. By substituting these expressions into Eq. 4, we find that $\left(\mathrm{\Delta }{\theta }_1,\mathrm{\Delta }{\theta }_2,\mathrm{\Delta }{\theta }_3\right)=$$\left(0.25,0.25,0.25\right)$ is a phase-locked state if and only if $H\left(0.25\right)=0$. That is, because of the special organization of the four-HCO neural circuit, the crayfish swimmeret neural circuit only needs to meet one condition to produce the tail-to-head 0.25 phase locking.

Furthermore, the condition $H\left(0.25\right)=0$ can be relaxed if we allow a small deviation from the exact 0.25 phase locking, i.e., if we consider an approximate 0.25 phase-locked solution $\left(\mathrm{\Delta }{\theta }_1,\mathrm{\Delta }{\theta }_2,\mathrm{\Delta }{\theta }_3\right)=\left(0.25+\epsilon ,0.25,0.25-\epsilon \right)$ for some small $\epsilon$. From Eq. 4, an approximate 0.25 phase locking exists if and only if $H\left(0.25\right)+H\left(0.25-\epsilon \right)-H\left(0.25+\epsilon \right)=0$. This condition is equivalent to the condition that $\epsilon \approx H\left(0.25\right)/2H\prime \left(0.25\right)$ is small. For example, if the ratio $\left|H\left(0.25\right)/H\prime \left(0.25\right)\right|$ is less than 20%, the resulting phase differences will be between 0.15 and 0.35 approximately. In addition, one can show that the tail-to-head 0.25 phase locking is stable if $H$ has a positive slope at 0.25, i.e., $H^{\prime }\left(0.25\right)>0$ (SI Text, section 2.3 and Tables S1 and S2). Note that, in the above analysis, we have assumed identical strength for ascending and descending connections because experimental results have shown that they are similar in strength and dynamics. In SI Text, section 2.4, we further show that this equal strength minimizes the deviation of the phase-locked state from 0.25.

Experimentally Measured Interaction Function.

Our analysis shows that if each crayfish swimmeret local CPG (the kernel of which is a HCO) satisfies the condition that $\epsilon =H\left(0.25\right)/2H\prime \left(0.25\right)$ is small, then the swimmeret neuronal circuitry gives rise to the robust 0.25 phase locking. Indeed, Fig. 3C shows that the experimentally measured interaction function $H\left(\theta \right)$ is relatively small at 0.25, and has a relatively steep positive slope at this point, giving rise to $\epsilon \approx H\left(0.25\right)/2H\prime \left(0.25\right)=0.06$. Therefore, both the existence condition ($\epsilon$ is small) and the stability condition [$H^{\prime }\left(0.25\right)>0$] predicted by our mathematical model are satisfied. It can be further shown that these conditions on the interaction function arise from the generic phase response properties of HCOs (SI Text, section 2.6).

Discussion

Our results demonstrate that the distinct limb coordination in crustacean swimming provides the biomechanically optimal stroke pattern over a wide range of biologically relevant paddling frequencies and animal sizes, i.e., Reynolds numbers (Re). Furthermore, the relative simplicity of the crustacean nervous system and recent advances in the knowledge of the crayfish swimmeret neuronal circuit allow us to identify how the structure of the circuit robustly gives rise to this stroke pattern. Thus, the swimmeret system of long-tailed crustaceans serves as a concrete example of how the architecture of a neural circuit gives rise to optimal locomotor behavior.

Our computational fluid dynamics simulations show that the flow characteristics are substantially different as the Re changes from 50 to 800 (Movies S1–S3). Despite these differences, the distinct tail-to-head metachronal stroke pattern maintains a significant advantage over other stroke patterns. Furthermore, the relative advantage of this limb coordination persists over the natural variation of limb spacing (SI Text, section 1.3, and Fig. S6). This suggests that the primary mechanism that gives the distinct tail-to-head metachronal stroke pattern a significant advantage over other stroke patterns does not involve careful timing of limb movements to exploit subtle fluid–structure interactions. Instead, we conjecture that the advantage arises from a simple, robust geometric mechanism based on the asymmetric arrangement of the neighboring limbs during PSs and RSs. Because PS generates positive flux whereas RS counteracts the flux generation, an efficient stroke pattern should maximize the effect of PS while minimizing the effect of RS. As illustrated in Fig. 4, under the natural tail-to-head metachrony with 0.25 phase difference, the volume of fluid enclosed by the neighboring limbs during PS is much larger than that during RS. This significant asymmetry in the volume of fluid enclosed by the PS and the RS leads to a very effective mechanism for generating positive flux. Therefore, a significantly larger average flux is generated under the natural 0.25 phase-locked rhythm compared to the case with the in-phase rhythm, under which the PS and the RS enclose the same volume of fluid. Similar to the reasoning above, under the hypothetical 0.75 phase-locked head-to-tail metachrony, the PS encloses a much smaller volume of fluid than the RS does. Hence, the head-to-tail metachrony is an ineffective stroke pattern for generating positive flux.

Fig. 4.

Position of neighboring limbs in the middle of the PS and the RS, respectively, in the natural 0.25 phase-locked rhythm.

Experimental results show that the timing of the swimmeret movements is strongly correlated with the timing of the bursts of muscle activity caused by motor neuron input (38). Furthermore, long-tailed crustaceans exhibit the distinct tail-to-head stroke pattern in a variety of swimming modes, including forward swimming and hovering, in which the limbs experience different hydrodynamic forces (29). These observations suggest that the intersegmental phase differences between swimmerets result primarily from neural input to the muscles rather than from the interaction between hydrodynamic forces and passive body mechanics. Neural input to the muscles is shaped by the rhythm intrinsically generated in the central nervous system and sensory feedback. However, while proprioceptive reflexes appear to be able to increase the PS motor drive to compensate for changes in load on the swimmerets (39, 40), extensive experimental evidence suggests that proprioceptive feedback has little effect on interlimb coordination (41–43). Thus, sensory feedback, hydrodynamic forces, and limb mechanics are likely to influence the stroke kinematics of an individual limb and the animal’s overall swimming performance, but the feedforward drive from the central nervous system is the primary determinant of coordination between limbs. (See SI Text, section 1.2 and section 3, for details.)

The key organizational features of the crayfish neural circuit for producing the phase constancy with 0.25 intersegmental phase differences are the internal half-center structure of the local CPG and the topology of the ascending and descending connections between the local CPGs. To highlight this fact, let us consider other hypothetical patterns of intersegmental connection in a chain of four HCO-based CPGs. Fig. 3D shows the four fundamentally different connectivity patterns that can occur between HCOs with only one ascending and one descending connection. Connection scheme (a1) is the connectivity that is present in the crayfish swimmeret neural circuit, and (a2), (s1), and (s2) are three hypothetical network topologies. Depending on whether the coupling is between a P cell and an R cell or between the same cell type, the overall network topology can be asymmetric or symmetric. It can be shown (SI Text, section 2.3) that a symmetric network topology (s1) or (s2) can robustly produce the in-phase rhythm and the antiphase rhythm (0.5 phase difference); however, they do not robustly produce the natural tail-to-head metachronal wave (0.25 phase difference). Furthermore, given the response properties of the crayfish swimmeret local CPGs (as in Fig. 3C), the asymmetric topology (a2) can robustly produce the head-to-tail metachronal wave (0.75 phase difference) but not the natural tail-to-head metachronal wave (0.25 phase difference).

The results discussed above can be extended beyond circuits with single ascending and descending connections between neighboring modules and equal connection strengths. In fact, it can be shown that, in the chain of four HCOs, equal ascending and descending connection strengths minimize the deviation of the intersegmental phase difference from 0.25 (SI Text, section 2.4). Furthermore, if multiple ascending or descending connections between neighboring HCOs are permitted, then circuit topologies other than (a1) can produce robust phase locking with phase lags of 0.25, but these connectivity schemes must have an analogous structure to the (a1) connection scheme. That is, descending connections must link P and R cells, whereas ascending connections must link R cells to R cells and/or P cells to P cells, and the connection strengths must be appropriately balanced (SI Text, section 2.5). Although it is possible that other connectivity schemes could support the 0.25 tail-to-head metachronal limb coordination, well-tuned compensatory mechanisms would be required to maintain this coordination over a wide range of paddling frequencies. Thus, the natural asymmetric circuit topology (a1) appears to generate this stroke pattern with the maximal robustness and minimal requirements.

HCOs are general, primitive motifs in locomotor CPGs and often serve as building blocks for networks of CPGs (44, 45). This fact and our finding that the natural asymmetric network topology in the crayfish swimmeret neural circuit is superior to all other intersegmental connectivity schemes in a chain of HCOs in robustly producing the biomechanically optimal tail-to-head metachronal stroke pattern suggest that similar neural circuits drive coordinated swimmeret movement in all long-tailed crustaceans. Furthermore, given the large metabolic cost of crustacean swimming (6, 46), our results suggest that the asymmetric network topology is the result of natural selection in favor of more effective and efficient swimming.

Materials and Methods

In our fluid model of the swimmeret system, the motion of the limbs drives the motion of the surrounding fluid. The equations that determine the motion of the fluid are Navier–Stokes equations. We use the immersed boundary method, in which structures (limbs and body) are represented in a moving, Lagrangian coordinate system, whereas fluid variables are represented in a fixed, Eulerian coordinated system (47). Because the limbs during PSs and the body are impermeable, the fluid is forced to move with the prescribed velocity on these structures. When the limbs become permeable during RSs, the fluid will permeate through the orthogonal direction of the limb with a slip velocity. SI Text, section 1, provides a detailed description of our fluid model, the biomechanics of the swimmerets, and the numerical method for the fluid model.

To experimentally measure the interaction function H of a crayfish swimmeret local CPG, we effectively isolate local CPGs in the isolated neural ventral cord preparation and subject them to input that mimics the input from neighboring CPGs (19, 20). By varying the phase of the input within the local CPG’s cycle and plotting changes in cycle period as a function of phase, we construct the interaction function H plotted in Fig. 3C (SI Text, section 2.2; see also figure 2 in ref. 20) (48).