Abstract
The mechanism of the Wittig reaction of anisaldehyde with a stabilized ylide was studied by a combination of 13C kinetic isotope effects, conventional calculations, and molecular dynamics calculations in a cluster of 53 THF molecules. The isotope effects support a cycloaddition mechanism involving two sequential transition states associated with separate C–C and P–O bond formations. However, the betaine structure in between the two transition states is bypassed as an equilibrated intermediate in most trajectories. The role of the dynamics of solvent equilibration in the nature of mechanistic intermediates is discussed.
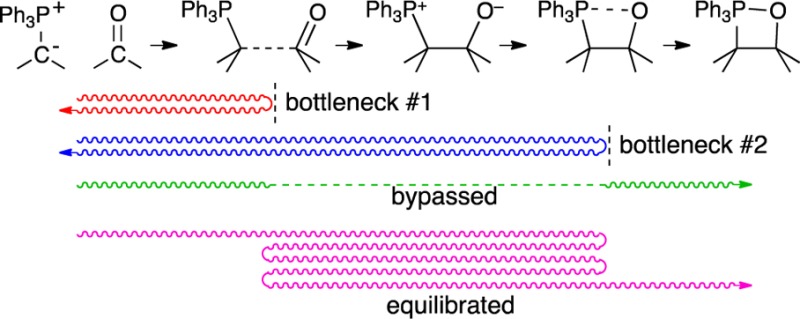
A long-standing textbook mechanism
of the Wittig reaction involved a two-step formation of the observable
oxaphosphetane species via a betaine intermediate.
For Wittig reactions under salt-free conditions, this “betaine
mechanism” has been largely dismissed in the recent literature.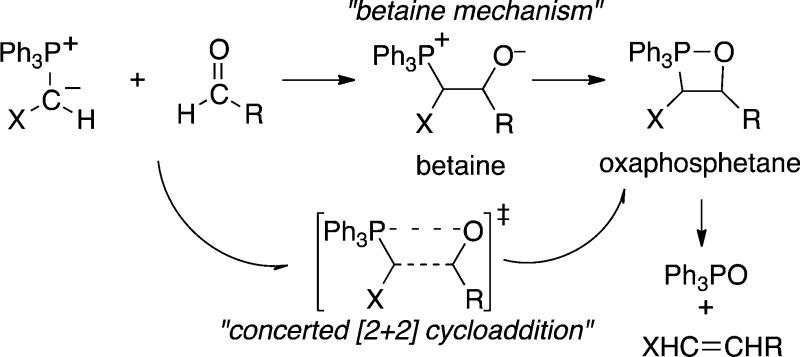
An elegant stereochemical experiment by Vedejs and Marth
provided key evidence in its observation of differing oxaphosphetane
mixtures from the Wittig reaction versus independently generated betaine.1 In place of the betaine mechanism, Vedejs proposed
that the phosphonium ylide and carbonyl compound undergo an asynchronous
[2+2] cycloaddition to afford the oxaphosphetane. Diverse experimental
observations and computational studies have supported a concerted
cycloaddition mechanism.2−5 The evidence against the intermediacy of betaines
has been described as overwhelming.3,4,6
The older support for the betaine mechanism had largely consisted of rationalizations of Wittig stereoselectivity in terms of the reversibility of adduct formation, and in retrospect these arguments were flawed.4 However, the evidence for a concerted cycloaddition to afford the oxaphosphetane is itself less than conclusive. As recognized by Vedejs, the stereochemical evidence for a concerted cycloaddition is subject to the same limitation as all such evidence: it can only show that the lifetime of any intermediate is insufficient for stereochemical equilibration. The computational studies are naturally subject to the usual concerns over the accuracy of the calculated energy surface, but they are also subject to other subtler if potentially substantial defects. We have previously shown that statistical or nonstatistical dynamics can complicate the understanding of reactions that appear concerted in simplistic calculations, for example by leading to kinetically important intermediates that are not observable on the potential energy surface.7 Here, a combined experimental, computational, and dynamic trajectory study provides evidence for a betaine intermediate in the cycloaddition, but we then see how dynamics complicates the nature of that intermediate. Our results highlight the inadequacy of the conventional mechanistic paradigm for subtle mechanistic questions in complex solution reactions.
The role of dynamics in the Wittig reaction was initially of interest because of the exceptional asynchronicity of the putative cycloadditions, exhibiting P–O interatomic distances of up to 4.4 Å in calculated structures.5 We have observed that asynchronous cycloadditions can be subject to substantial transition-state recrossing, and we had found that kinetic isotope effects (KIEs) can be used to probe this otherwise hidden phenomenon.7b,8 We therefore sought to examine the Wittig reaction using KIEs and trajectory calculations.
The reaction of anisaldehyde (1)
with the stabilized
ylide 2 was chosen for study. The 13C KIEs
for this clean homogeneous reaction were determined at natural abundance
by NMR methodology. For reactions of 1 at 67 °C
taken to 69 ± 2% and 73 ± 2% conversion, the reisolated
unreacted 1 was analyzed by 13C NMR in comparison
with samples of 1 that had not been subjected to the
reaction conditions. 
For the ylide carbon of 2,
the 13C KIE was measured by analysis of samples of 3 from
reactions in which 2 was taken to 20% conversion versus
samples of 3 obtained from complete conversion of 2 using excess 1. In the analyses, the carbons
meta to the aldehyde of 1 and in the ketonic methyl group
of 3 were used as internal standards with the assumption
that their isotopic fractionation is negligible. From the changes
in the relative isotopic composition in the various positions, the 13C KIEs were calculated in standard ways.
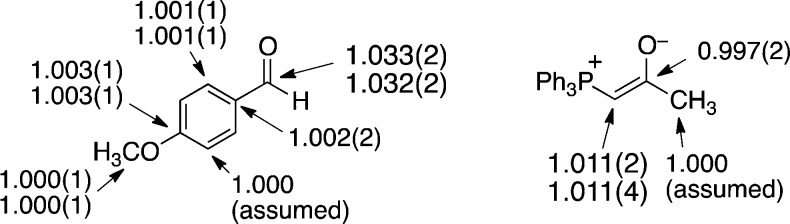
The results are summarized in Figure 1. The carbonyl carbon of 1 exhibits a substantial 13C KIE, while the ylide carbon of 2 exhibits a modest but still significant KIE. These KIEs indicate that carbon–carbon bond formation is either fully or at least partially rate limiting. Qualitatively, this does not distinguish between stepwise and concerted formation of the expected oxaphosphetane intermediate.
Figure 1.
13C KIEs (k12/k13, 67 °C) for the reaction of 1 with 2.
Computations were used for a quantitative interpretation. Diverse DFT methods were explored versus G3B3 calculations for the model reaction of Me3PCHCHO with formaldehyde [see the Supporting Information (SI)]. Previously employed B3LYP calculations fared poorly, having average absolute errors versus G3B3 of 4.2–6.2 kcal/mol. The lowest average errors, only 1.0–1.3 kcal/mol, were seen in M06-2X, B3P86, and lc-wPBE calculations with large basis sets (e.g., aug-cc-pvtz), but these were impractical for full-system optimizations. Calculations with 6-31G* and 6-31+G** basis sets showed average errors of 1.3– 2.6 kcal/mol and had relative energies for the key transition states and intermediate (see below) that matched closely with the large-basis results. We opted to use these basis sets for geometry optimizations and dynamics, augmented by 6-31+G(2df,p) single-point energies (average error 1.1 kcal/mol). These calculations in combination with a PCM implicit solvent model for THF were applied to the complete mechanism for the full experimental system. An alternative solvent model (SMD) and alternative solvation parameters were also explored, with no qualitative difference in the results (see the SI).
The three “benchmarked” DFT methods each predict a different mechanism. The M06-2X calculations nominally predict a stepwise mechanism with competitive rate-limiting steps (Figure 2). In this mechanism, 1 and 2 react via the potential-energy saddle point 4⧧ to afford the potential-energy minimum betaine 5. The formation of the oxaphosphetane 7 is completed by P–O bond formation via saddle point 6⧧. The lc-wPBE mechanism is concerted, with an asynchronous transition state resembling 4⧧ (see the SI). The B3P86 mechanism is stepwise but with the second step, P–O bond formation, being rate limiting.
Figure 2.
Calculated pathway for the reaction of 1 with 2. Relative potential energies are given in kcal/mol, with harmonic free energies in parentheses.
To distinguish these mechanisms, 13C KIEs were predicted for each by conventional transition-state theory including a one-dimensional tunneling correction.9 Such predictions have been found to be highly accurate for diverse reactions, provided that the mechanisms and calculated transition states are accurate.10 Table 1 summarizes the results. Whether stepwise or concerted, C–C bond formation entails large motions of the carbonyl and ylide carbons in the transition vector and larger KIEs than observed. With rate-limiting P–O bond formation, the 13C KIE would be smaller for the carbonyl carbon and inverse for the ylide carbon. Only the M06-2X mechanism with competitively rate-limiting 4⧧ and 6⧧ agrees reasonably with experiment.11
Table 1. Predicted versus Experimental 13C KIEs.
|
13C KIEa |
||
|---|---|---|
| mechanism/method | ArCHO | Ph3PCHCOMe |
| concerted (lc-wPBE) | 1.043 | 1.024 |
| 2nd step RLS (B3P86) | 1.017 | 0.998 |
| 4⧧ (M06-2X) | 1.043 | 1.022 |
| 6⧧ (M06-2X) | 1.015 | 0.994 |
| 4⧧/6⧧ weightedb | 1.028 | 1.008 |
| 4⧧/6⧧ weightedc | 1.033 | 1.012 |
| experimental | 1.032–1.033 | 1.011 |
k12C/k13C at 67 °C
Weighted by the difference in harmonic free energies at 67 °C in M06-2X/6-31+G(2df,p)//M06-2X/6-31+G** calculations.
Weighted from recrossings in trajectories.
So the KIEs strongly support a stepwise mechanism through a betaine intermediate, but what does that mean? The complexity of this question can be recognized by noting that the betaine is predicted to be >1 kcal/mol higher in free energy than either of the flanking transition states. (For the purpose of comparison with classical trajectories below, it should be noted that the same unusual order of relative free energies is obtained using fully classical enthalpy/entropy calculations.) The energy surface is extraordinarily flat over the broad range encompassing 4⧧, 5, and 6⧧, varying by only 1.4 kcal/mol in potential energy. Frequency calculations along the minimum-energy path between 4⧧ and 6⧧ (projecting out the transition vector) suggest that there is a minimum in the free energy within the harmonic approximation, but the limitations of frequency calculations and the harmonic approximation with a large system on a small energy scale would make a detailed interpretation dubious. A more subtle concern was that continuum solvent models implicitly assume equilibrium solvation. The dipole moment increases rapidly with C–C bond formation, reaches a maximum of 10 D at 5, and then falls to <5 D at 7. The time scale of trajectories was expected to be faster than solvent can reorganize to maintain equilibrium solvation. The same problem would apply to approaches mapping the potential of mean force.
To learn about the nature of this “stepwise” mechanism and the betaine with minimal assumptions, we carried out molecular trajectory calculations in a cluster of 53 THF molecules in a 20.4 Å cubic box (density 0.84). In a series of independent trajectories, the carbonyl atoms of 1 and the ylide carbon and phosphorus atoms of 2 were constrained in the area of 4⧧ while the full system was subjected first to an extended equilibration in PM3 calculations and then to a 1.25 ps equilibration at 67 °C in ONIOM calculations, using M06-2X/6-31G* for all atoms of 4⧧ and using PM3 for the THF molecules. The series of constrained ONIOM equilibrations was then continued for 10 ps each. At 250 fs intervals, structures and velocities were extracted, and the constrained atoms were given independent Boltzmann-random velocities. The resulting unconstrained trajectories were integrated forward and backward in time using direct dynamics until either 7 was formed or 1 + 2 were re-formed.
A total of 302 trajectories were obtained, and Figure 3 illustrates representative examples. Descriptively, the trajectories that result may be grouped into four categories:
-
(1)
“productive trajectories” proceeding from 1 + 2 to 7 (B, D, G, I, and M in Figure 3, observed in 128 cases)
-
(2)
“deep recrossings” that fully form the C–C bond but subsequently re-form 1 + 2 (A, F, K, and N in Figure 3, 76 cases)
-
(3)
“immediate recrossings” that re-form 1 + 2 (C, H, and L in Figure 3, 82 cases)
-
(4)
trajectories passing from 7 to the area of 4⧧ and then re-forming 7 (E and J in Figure 3, 16 cases)
By the nature of the simulation, it can only observe trajectories traversing the area of 4⧧.
Figure 3.
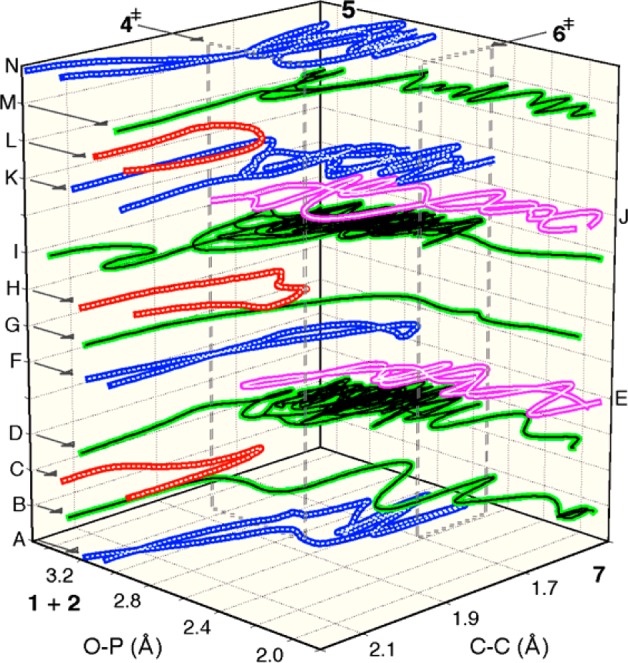
Stacked plot of the paths for C–C and P–O bond formation in representative trajectories. See the SI for a movie and additional plots.
A first item of note is that the trajectories predict that the cycloaddition is subject to two dynamical bottlenecks, one involving C–C bond formation and resembling 4⧧, and a second involving P–O bond formation and resembling 6⧧. The presence of such bottlenecks is most readily recognized by the paths of long trajectories such as D, I, and K in Figure 3 that traverse the area between bottlenecks many times before crossing one threshold or the other and proceeding to 7 or 1 + 2. A second item of note is the agreement of the trajectories with experimental observations. That is, the proportion of trajectories that fully form the C–C bond and then recross (i.e., with reversible betaine formation) versus those that form 7 (76:128) can be used to weight the expected contributions of 6⧧ versus 4⧧, respectively, to the overall observed KIE. (This assumes that the KIEs predicted for the PCM structures are reasonably representative of those for the solution bottlenecks.) When this is done, the overall KIEs (Table 1) are in striking agreement with experiment.
The trajectories themselves then tell an even more interesting story. Many of the productive trajectories pass directly through the area of 5 in the manner of B and G in Figure 3. Such trajectories are indistinguishable from those of many asynchronous concerted cycloadditions.7b,12 Nearly 30% traverse the area between 4⧧ and 6⧧ within 100 fs and 50% within 150 fs. Put another way, once the betaine is formed (defined by a C–C distance <1.65 Å), its half-life is 90 fs, less than two vibrations of the weak C–C bond. But the trajectories are bimodal: At longer times, the betaine persists longer than would be expected from the earlier decay (see the SI), and 5% last 1–2 ps. On a shorter time scale, bimodal decay can arise simply from the confounding effect of orthogonal vibrational motions on bond formation,12b but the times here are more suggestive of a competition between concerted and stepwise pathways.
To gain insight into the bimodal behavior, we carried out a series of trajectories in which the system was now equilibrated in the area of 5, instead of 4⧧. The productive trajectories resulting from this initialization in explicit THF now require a median of 600 fs to traverse the area between 4⧧ and 6⧧, and they bear no resemblance to concerted cycloadditions. The half-life of the equilibrated betaine is now 260 fs.
Our interpretation of these results is that, in trajectories started from 4⧧, the “full intermediacy” of a betaine is bypassed.13 Trajectories certainly pass through the area of 5, but few linger. They either rapidly pass through 6⧧ or are rapidly reflected by the bottleneck of 6⧧. Why? The equilibrium stability of an intermediate by definition reflects the complete ensemble of accessible molecular and solvent structures, but most trajectories here do not have time to representatively explore this ensemble. When 5 is formed from 4⧧, neither the atomic motions nor the solvation is initially equilibrated. The effect of the former can be discerned in the shortest 10–20% of trajectories through the area of 5; they lead to product or starting-material channels by a direct continuation or reflection of atomic motions along the path taken from 4⧧ (see trajectories F and G in Figure 3, and see the SI for additional trajectory plots). This is a form of dynamic matching,12c,14 in which the path taken through an initial transition state dictates the subsequent outcome of trajectories. Most trajectories, however, lack discernible dynamic matching but still finish much faster than those from equilibrated 5. Our hypothesis is that this is an effect of the time required for solvent reorganization. Optimal solvent stabilization of 5 simply takes longer than its lifetime without such stabilization. The solvent dynamics must compete with the molecular reaction dynamics, and the latter are faster. For a portion of trajectories started from 4⧧, however, the solvation either is better by chance to start with or catches up when the completion of the trajectory is delayed, leading to the bimodal behavior reflecting the longer lifetime of an equilibrium-solvated intermediate.
The failure of the conventional paradigm dividing reactions into concerted versus two-step processes should no longer be surprising.7 Here, the experimental observations would characterize a two-step mechanism with an intermediate, while many of the productive trajectories are indistinguishable from those of an ordinary concerted cycloaddition. The most disconcerting aspect of our results, in our view, is the suggested role of solvent dynamics in the nature of mechanistic intermediates. That is, a putative intermediate may only become an intermediate in a clear sense when the solvent fully stabilizes it, and this takes time. Because of the role of dynamics in this process, even energetically perfect calculations employing any of the standard equilibrium methods cannot unambiguously assign mechanisms.
Acknowledgments
We thank the NIH (Grant GM-45617) for financial support.
Supporting Information Available
Complete descriptions of experimental procedures, calculations, and structures, additional trajectory plots, and a movie of Figure 3. This material is available free of charge via the Internet at http://pubs.acs.org.
The authors declare no competing financial interest.
Funding Statement
National Institutes of Health, United States
Supplementary Material
References
- Vedejs E.; Marth C. F. J. Am. Chem. Soc. 1990, 112, 3905–3909. [Google Scholar]
- a Vedejs E.; Fleck T. J. J. Am. Chem. Soc. 1989, 111, 5861–5871. [Google Scholar]; b Vedejs E.; Meier G. P.; Snoble K. A. J. J. Am. Chem. Soc. 1981, 103, 2823–2831. [Google Scholar]; c Appel R.; Loos R.; Mayr H. J. Am. Chem. Soc. 2009, 131, 704–714. [DOI] [PubMed] [Google Scholar]
- Byrne P. A.; Gilheany D. G. J. Am. Chem. Soc. 2012, 134, 9225–9239. [DOI] [PubMed] [Google Scholar]
- Byrne P. A.; Gilheany D. G. Chem. Soc. Rev. 2013, 42, 6670–6696. [DOI] [PubMed] [Google Scholar]
- Robiette R.; Richardson J.; Aggarwal V. K.; Harvey J. N. J. Am. Chem. Soc. 2006, 128, 2394–2409. [DOI] [PubMed] [Google Scholar]
- For a thiobetaine, see:Puke C.; Erker G.; Wibbeling B.; Frohlich R. Eur. J. Org. Chem. 1999, 1831–1841. [Google Scholar]
- a Bekele T.; Lipton M. A.; Singleton D. A.; Christian C. F. J. Am. Chem. Soc. 2005, 127, 9216–9223. [DOI] [PMC free article] [PubMed] [Google Scholar]; b Gonzalez-James O. M.; Kwan E. E.; Singleton D. A. J. Am. Chem. Soc. 2012, 134, 1914–1917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ussing B. R.; Hang C.; Singleton D. A. J. Am. Chem. Soc. 2006, 128, 7594–7607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- a Bigeleisen J. J. Chem. Phys. 1949, 17, 675–678. [Google Scholar]; b Bell R. P.The Tunnel Effect in Chemistry; Chapman & Hall: London, 1980; pp 60–63. [Google Scholar]
- a Beno B. R.; Houk K. N.; Singleton D. A. J. Am. Chem. Soc. 1996, 118, 9984–9985. [Google Scholar]; b Meyer M. P.; DelMonte A. J.; Singleton D. A. J. Am. Chem. Soc. 1999, 121, 10865–10874. [Google Scholar]; c Hirschi J. S.; Takeya T.; Hang C.; Singleton D. A. J. Am. Chem. Soc. 2009, 131, 2397–2403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The first step should become more rate limiting with more reactive ylides or aldehydes and less rate limiting with less reactive addends. This leads to the testable prediction that 13C KIEs will increase in the former case and decrease in the latter case.
- a Thomas J. R.; Waas J. R.; Harmata M.; Singleton D. A. J. Am. Chem. Soc. 2008, 130, 14544–14555. [DOI] [PMC free article] [PubMed] [Google Scholar]; b Xu L.; Doubleday C. E.; Houk K. N. J. Am. Chem. Soc. 2011, 133, 17848–17854. [DOI] [PubMed] [Google Scholar]; c Wang Z.; Hirschi J. S.; Singleton D. A. Angew. Chem., Int. Ed. 2009, 48, 9156–9159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- For related phenomena, see:; a Hu X.; Hase W. L. J. Phys. Chem. 1992, 96, 7535–7546. [Google Scholar]; b Nummela J. A.; Carpenter B. K. J. Am. Chem. Soc. 2002, 124, 8512–8513. [DOI] [PubMed] [Google Scholar]; c Debbert S. L.; Carpenter B. K.; Hrovat D. A.; Borden W. T. J. Am. Chem. Soc. 2002, 124, 7896–7897. [DOI] [PubMed] [Google Scholar]; d Costentin C.; Robert M.; Saveant J. M. J. Am. Chem. Soc. 2004, 126, 16834–16840. [DOI] [PubMed] [Google Scholar]; e Lopez J. G.; Vayner G.; Lourderaj U.; Addepalli S. V.; Kato S.; DeJong W. A.; Windus T. L.; Hase W. L. J. Am. Chem. Soc. 2007, 129, 9976–9985. [DOI] [PubMed] [Google Scholar]; f Sun L.; Song K.; Hase W. L. Science 2002, 296, 875–878. [DOI] [PubMed] [Google Scholar]; g Ammal S. C.; Yamataka H.; Aida M.; Dupuis M. Science 2003, 299, 1555–1557. [DOI] [PubMed] [Google Scholar]
- Carpenter B. K. J. Am. Chem. Soc. 1995, 117, 6336–6344. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.