Prevalence estimation subject to misclassification: the mis-substitution bias and some remedies

Abstract

We consider the problem of estimating the prevalence of a disease under a group testing framework. Because assays are usually imperfect, misclassification of disease status is a major challenge in prevalence estimation. To account for possible misclassification, it is usually assumed that the sensitivity and specificity of the assay are known and independent of the group size. This assumption is often questionable, and substitution of incorrect values of an assay’s sensitivity and specificity can result in a large bias in the prevalence estimate, which we refer to as the mis-substitution bias. In this article, we propose simple designs and methods for prevalence estimation that do not require known values of assay sensitivity and specificity. If a gold standard test is available, it can be applied to a validation subsample to yield information on the imperfect assay’s sensitivity and specificity. When a gold standard is unavailable, it is possible to estimate assay sensitivity and specificity, either as unknown constants or as specified functions of the group size, from group testing data with varying group size. We develop methods for estimating parameters and for finding or approximating optimal designs, and perform extensive simulation experiments to evaluate and compare the different designs. An example concerning human immunodeficiency virus infection is used to illustrate the validation subsample design.

1. Introduction

Estimating the prevalence of a disease is a common objective in epidemiologic research. For a rare disease such as human immunodeficiency virus (HIV) infection, prevalence estimation can be performed under a group testing (also known as pooled testing) approach, where individual specimens (e.g., blood) are physically combined and the pooled samples are tested for the presence of the disease. Since its introduction by Dorfman [1] as a cost-efficient way of screening for syphilis, the group testing approach has been applied to many different areas of biomedical research including HIV [2, 3, 4, 5], hepatitis [6], influenza [7], genetics [8], and drug development [9]. Following decades of research, a variety of statistical methods are now available for disease screening [1, 10, 11, 12, 13, 14, 15], prevalence estimation [16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26], and regression models where group testing may be performed on the response variable (e.g., disease) [27, 28, 29, 30] or on a covariate such as exposure to an environmental hazard or presence of some genotype [31, 32]. This article is concerned with prevalence estimation under the group testing framework, which includes individual testing as a special case. For prevalence estimation, group testing is not only cost-efficient but also can have a statistical efficiency advantage over individual testing when the diagnostic test is imperfect, giving rise to possible misclassification [21, 22, 26].

Misclassification is a major challenge in prevalence estimation because assays are usually imperfect. For example, Petricciani [33] reports 93–99% sensitivity and > 99% specificity for detecting HIV infection with an enzyme-linked immunosorbent assay (ELISA). These results may be seen as indicative of good accuracy, but the reported error rates can be rather large in comparison to the true prevalence of HIV, which is estimated to be 2.4% among black men and 0.4% among white men in the United States [34]. Without appropriate adjustment, misclassification could introduce a substantial amount of error into prevalence estimation [21]. To account for misclassification, it is usually assumed that the sensitivity and specificity of the assay are known and independent of the group size. This is a strong assumption because available estimates of these accuracy measures are themselves error-prone and sometimes vary across studies due to differences in laboratory techniques, individual characteristics and other aspects of study design and implementation. The latter observation is particularly troubling as it casts doubt on the applicability of historical estimates of accuracy measures to the current prevalence study. A sensitivity analysis may be performed to account for the uncertainty about the sensitivity and specificity estimates [35], although the interpretation of a sensitivity analysis can be arbitrary. Hwang [11] and MaMahan et al. [30] consider models that allow the sensitivity and specificity of an assay to depend on the group size. The model of MaMahan et al. [30] is based on realistic assumptions about bioassays and may be appropriate in many epidemiologic studies; however, application of their model requires a large amount of information, including the distributions of the continuous biomarker on which the assay is based among diseased and non-diseased subjects, as well as the conditional distribution of the measured concentration given the true concentration of the biomarker. Such information may not be readily available in a typical prevalence study.

The objective of this article is to develop simple designs and methods for prevalence estimation that do not require known values of assay sensitivity and specificity. In the next section, we describe the group testing framework and demonstrate that misspecified values of accuracy measures can result in a large bias in the prevalence estimate, which we refer to as the mis-substitution bias. In this article, we are primarily concerned with asymptotic bias, which is separate from the finite-sample bias of a consistent estimator [36, 37]. For a rare disease in a large population, even a slight bias in the prevalence estimate can have a large adverse impact on public health research and decision making. If a gold standard (i.e., a perfectly accurate assay) is available (though perhaps too expensive to use widely), it can be applied to a validation subsample (VS) to yield information on the imperfect assay’s sensitivity and specificity. For example, the Western blot (WB) test, which is more accurate and more expensive than ELISA, is sometimes considered a gold standard for HIV testing [21]. This VS design is similar to the designs proposed by Gastwirth and colleagues [18, 13, 38], which involve re-testing positive groups with a gold standard assay in one or two stages of group testing. The difference is that the VS design requires re-testing both positive and negative groups, which allows us to identify all relevant parameters without assuming (partial) knowledge of assay sensitivity and specificity. The VS design and the associated estimation problem are studied in Section 3. For situations where a gold standard is unavailable, we propose in Section 4 to estimate assay sensitivity and specificity, either as unknown constants or as specified functions of the group size, from group testing data with varying group size (VGS). This VGS design has been considered before, either as a given reality that poses an analytical challenge [39, 40, 19, 41] or as a result of adjusting the group size adaptively to improve efficiency [20, 42, 23]. To our best knowledge, the utility of the VGS design in dealing with the misclassification problem has not been discussed. It is easy to see that a VGS design with three different group sizes is able to identify the prevalence together with the unknown sensitivity and specificity of the assay, assuming that the sensitivity and specificity are independent of the group size. The latter assumption may be reasonable in ELISA-based HIV testing, for which published data suggest that there is little loss in sensitivity when pooling sera from up to 15 (and possibly more) subjects [2, 3, 4, 5]. When this assumption is in doubt, a dilution effect can be accommodated by a parsimonious model allowing the sensitivity (and specificity, if necessary) to depend on the group size. The article ends with a discussion in Section 5.

2. Group Testing and the Mis-Substitution Bias

Our objective is to estimate the prevalence of a disease, denoted by π. Let D* indicate the presence of the disease in a generic subject, so D* = 1 if the subject is diseased and 0 otherwise. Then π = P(D* = 1) if a subject is chosen randomly from the target population. When k subjects (with disease status $D_1^{\ast },\dots ,D_k^{\ast }$, say) are grouped for testing, the disease status for the group is given by $D=max\{D_1^{\ast },\dots ,D_k^{\ast }\}$; that is, a group is considered diseased if one or more subjects in the group are diseased. If the subjects in the group are chosen randomly and independently from the population, then P(D = 1) = 1 − (1 − π)^k. Suppose an imperfect assay is performed on the pooled specimens, with test result T (1 if positive; 0 if negative). Writing Se = P(T = 1|D = 1) and Sp = P(T = 0|D = 0) for the assay’s sensitivity and specificity, respectively, we then have

$$p_k:=\mathrm{P}(T=1)=\text{Se}\mathrm{P}(D=1)+(1-\text{Sp})\mathrm{P}(D=0)=\text{Se}-(\text{Se}+\text{Sp}-1){(1-\pi )}^k,$$ (1)

by the law of total probability.

In a study where subjects are grouped randomly into pools of size k, the data are directly informative about p_k, from which π can be identified as

$$\pi =1-{\left(\frac{\text{Se}-p_k}{\text{Se}+\text{Sp}-1}\right)}^{1/k},$$ (2)

if the values of (Se, Sp) are known. Let T_i (i = 1, … , n) denote the test result for the ith group. A natural estimator of p_k is then given by $\overline{T}=n^{-1}{\sum }_{i=1}^n{T}_i$, and the corresponding estimator of π is

$${\widehat{\pi }}_{\text{sbt}}=1-{\left(\frac{\text{Se}-\overline{T}}{\text{Se}+\text{Sp}-1}\right)}^{1/k},$$

where the subscript sbt is short for substitution. This estimator may be undefined or out of range for some combinations of (Se, Sp, T̄), in which case ad hoc adjustments can be made. For large n, the estimator π̂_sbt is approximately normally distributed with mean π and variance

$$var({\widehat{\pi }}_{\text{sbt}})\approx \frac{p_k(1-p_k)}{{nk}^2{(\text{Se}+\text{Sp}-1)}^2{(1-\pi )}^{2k-2}}.$$ (3)

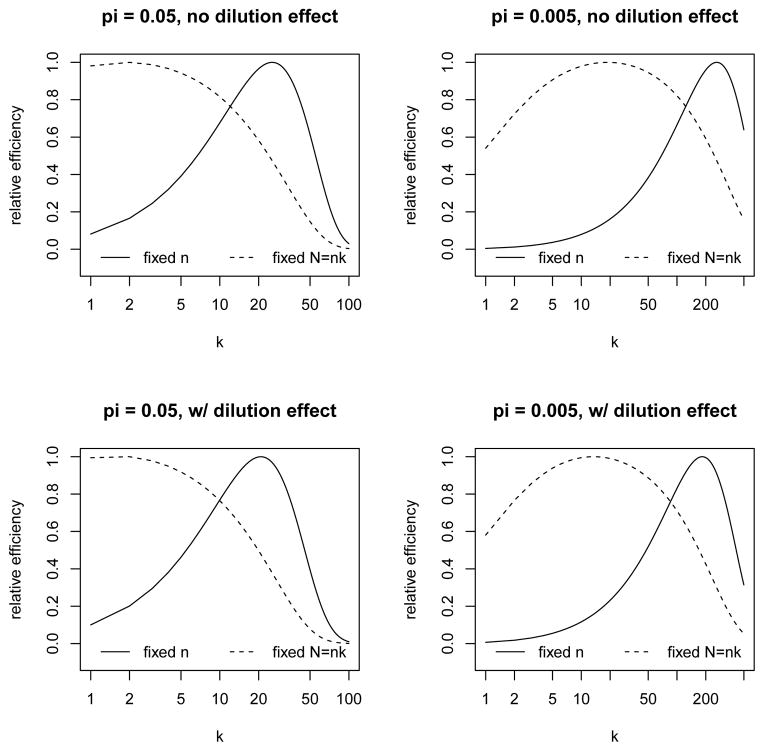
Based on conjectured values of (π, Se, Sp), the group size k may be chosen by minimizing expression (3) for a fixed n (and the optimal k will not depend on n) or for a fixed N = nk (total number of subjects), in which case n in (3) will be replaced by N/k. Some examples of such optimization are given in Figure 1, which shows the relative efficiency (to the optimal design) as a function of k in several scenarios. For a given scenario and a given k, the relative efficiency is obtained as the ratio of the minimum variance (over all k-values in the same scenario) to expression (3). In Figure 1 and the subsequent numerical studies, we consider π = 0.05, 0.005 and Sp = 0.995, and either fix Se = 0.95 or allow Se to decrease with k, which may happen because of a dilution effect [11, 30]. In the latter case, we work with the model

Figure 1.

Design considerations under the standard group testing approach: relative efficiency as a function of k, for fixed n versus fixed N = nk, with π = 0.05, 0.005 and Sp = 0.995, with and without a dilution effect (see Section 2 for details).

$$\text{Se}(k;\mathit{\alpha })=\text{expit}({\alpha }_0+{\alpha }_{1}logk),$$ (4)

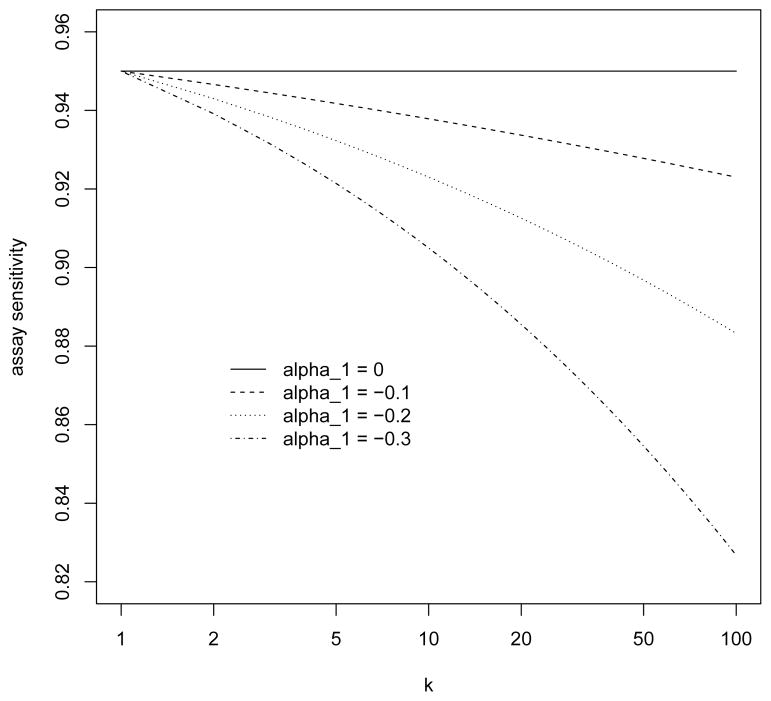
where α = (α₀, α₁) and expit(u) = exp(u)/{1 + exp(u)}. Some examples of this model are shown in Figure 2, where we fix Se(1; α) = expit(α₀) = 0.95 and let α₁ range from 0 to −0.3. Figure 1 and all subsequent numerical studies involving a dilution effect are based on the lowest curve in Figure 2 corresponding to α₁ = −0.3. In contrast, the case where Se is fixed at 0.95 (regardless of k) will be referred to as the case of no dilution effect.

Figure 2.

The dilution effect under the logistic model (4).

Because π̂_sbt depends on specified values of (Se, Sp), the estimator is generally biased when the values of (Se, Sp) are misspecified. This remains true if k = 1, which corresponds to the traditional individual testing approach. So the mis-substitution bias is not caused by group testing; rather, it is caused by an imperfect assay with unknown sensitivity and specificity. Table 1 shows the limit of the mis-substitution bias (as n → ∞) when either or both of Se = 0.95 and Sp = 0.995 are misspecified. Although Table 1 does not explicitly include a dilution effect, it does examine the consequences of misspecifying Se. The k-values in Table 1 are chosen to cover a range of possible scenarios (to be considered later). In Table 1, the mis-substitution bias is evaluated in terms of the relative bias for π and the absolute bias for λ = logit(π) (for later comparisons). Because π is usually small, it seems more sensible to consider the relative bias for π than the absolute bias for π. It is clear in Table 1 that a substantial bias can result from misspecification of Se and/or Sp. Note that equation (1) implies that 1 − Sp < p_k < Se. When either inequality is violated by the specified values of (Se, Sp), the standard procedure fails to produce a meaningful prevalence estimate asymptotically. This occurs several times in Table 1, as indicated by the “NA” entries. Specifically, we have p_k ≈ 0.0097 < 0.01 = 1 − Sp* when π = 0.005, k = 1 and Sp* = 0.99, and p_k ≈ 0.9496 > 0.9 = Se* when π = 0.05, k = 150 and Se* = 0.9, where Sp* and Se* are misspecified values.

Table 1.

The mis-substitution bias: relative bias for π and absolute bias for λ = logit(π) due to misspecifying one or both of (Se = 0.95, Sp = 0.995), evaluated for the limiting case that n → ∞ (see Section 2 for details). “NA” indicates that the limit of π̂_sbt is undefined or out of range.

Prevalence (π)	Group Size (k)	Specified Values of (Se, Sp)
		(0.95, 1)	(0.95, 0.99)	(1, 0.995)	(0.9, 0.995)	(1, 1)	(0.9, 0.99)
relative bias for π
0.05	1	0.10	−0.10	−0.05	0.06	0.05	−0.05
	5	0.02	−0.02	−0.06	0.06	−0.04	0.04
	15	0.01	−0.01	−0.07	0.08	−0.07	0.08
	50	0.00	0.00	−0.18	0.42	−0.18	0.41
	150	0.00	0.00	−0.61	NA	−0.61	NA
0.005	1	1.05	NA	−0.05	0.06	0.95	NA
	5	0.21	−0.21	−0.05	0.06	0.15	−0.17
	15	0.07	−0.07	−0.05	0.06	0.01	−0.02
	50	0.02	−0.02	−0.06	0.06	−0.04	0.04
	150	0.01	−0.01	−0.07	0.09	−0.07	0.08
bias for λ = logit(π)
0.05	1	0.10	−0.11	−0.05	0.06	0.05	−0.05
	5	0.02	−0.02	−0.06	0.06	−0.04	0.04
	15	0.01	−0.01	−0.08	0.09	−0.07	0.08
	50	0.00	0.00	−0.21	0.37	−0.21	0.37
	150	0.00	0.00	−0.96	NA	−0.96	NA
0.005	1	0.72	NA	−0.05	0.05	0.67	NA
	5	0.19	−0.24	−0.05	0.06	0.14	−0.18
	15	0.07	−0.07	−0.05	0.06	0.01	−0.02
	50	0.02	−0.02	−0.06	0.06	−0.04	0.04
	150	0.01	−0.01	−0.08	0.08	−0.07	0.08

3. The VS Design (With a Gold Standard Available)

3.1. Basics

Suppose a gold standard test is available but too expensive to apply to the entire sample. We propose to apply the gold standard to a subsample of pooled specimens, selected in a manner that may depend on the test results (T_i) for the imperfect assay but is otherwise random. Let V_i = 1 if the ith group is included in the VS, and 0 otherwise. Note that V_i = 1 implies that D_i is observed. The assumed sampling mechanism for the VS implies that the positive and negative predictive values can now be identified as

$$\begin{array}{l}\text{PPV}=\mathrm{P}(D_i=1\mid T_i=1)=\mathrm{P}(D_i=1\mid T_i=1,V_i=1),\\ \text{NPV}=\mathrm{P}(D_i=0\mid T_i=0)=\mathrm{P}(D_i=0\mid T_i=0,V_i=1),\end{array}$$

respectively, provided that the T_i are not identically 0 or 1 in the VS. Because the probability p_k = P(T_i = 1) is trivially identifiable, we can now identify the joint distribution of (T_i, D_i) and hence

$$\begin{array}{l}\text{Se}=\frac{p_k\text{PPV}}{p_k\text{PPV}+(1-p_k)(1-\text{NPV})},\\ \text{Sp}=\frac{(1-p_k)\text{NPV}}{p_k(1-\text{PPV})+(1-p_k)\text{NPV}}.\end{array}$$

The foregoing discussion motivates the following estimates:

$$\begin{array}{l}{\widehat{\text{Se}}}_{\text{vs}}=\frac{\overline{T}\widehat{\text{PPV}}}{\overline{T}\widehat{\text{PPV}}+(1-\overline{T})(1-\widehat{\text{NPV}})},\\ {\widehat{\text{Sp}}}_{\text{vs}}=\frac{(1-\overline{T})\widehat{\text{NPV}}}{\overline{T}(1-\widehat{\text{PPV}})+(1-\overline{T})\widehat{\text{NPV}}},\end{array}$$

where the subscript vs indicates the VS design, T̄ is defined in Section 2, and

$$\begin{array}{l}\widehat{\text{PPV}}=\frac{{\sum }_{i=1}^n{V}_i{T}_i{D}_i}{{\sum }_{i=1}^n{V}_i{T}_i},\\ \widehat{\text{NPV}}=\frac{{\sum }_{i=1}^n{V}_i(1-T_i)(1-D_i)}{{\sum }_{i=1}^n{V}_i(1-T_i)}.\end{array}$$

Substituting these estimates into equation (2) yields

$${\widehat{\pi }}_{\text{vs}}=1-{\left(\frac{{\widehat{\text{Se}}}_{\text{vs}}-\overline{T}}{{\widehat{\text{Se}}}_{\text{vs}}+{\widehat{\text{Sp}}}_{\text{vs}}-1}\right)}^{1/k}.$$

Note that (π_vs, ${\widehat{\text{Se}}}_{\text{vs}},{\widehat{\text{Sp}}}_{\text{vs}}$) can be seen as the maximum likelihood estimate (MLE) based on the following log-likelihood:

$$l_{\text{vs}}(\pi ,\text{Se},\text{Sp})=\sum _{i=1}^n[(1-V_i)logP(T_i;\pi ,\text{Se},\text{Sp})+V_i\{logP(D_i;\pi )+D_{i}logP(T_i\mid D_i=1;\text{Se})+(1-D_i)log\mathrm{P}(T_i\mid D_i=0;\text{Sp})\}].$$

As such, $\sqrt{n}({\widehat{\pi }}_{\text{vs}}-\pi ,{\widehat{\text{Se}}}_{\text{vs}}-\text{Se},{\widehat{\text{Sp}}}_{\text{vs}}-\text{Sp})$ converges, as n → ∞, to a normal distribution with mean 0 and variance ${\mathbf{I}}_{\text{vs}}^{-1}$ , where I_vs is the Fisher information for (π, Se, Sp) in a single group of size k (see Web Appendix A for explicit expressions). In particular, π̂_vs is, for large n, approximately normally distributed with mean π and variance

$$var({\widehat{\pi }}_{\text{vs}})\approx n^{-1}{\mathbf{I}}_{\text{vs}}^{-1}[1,1],$$ (5)

where [1, 1] denotes the first diagonal element of a matrix. If $0<{\widehat{\pi }}_{\text{vs}},{\widehat{\text{Se}}}_{\text{vs}},{\widehat{\text{Sp}}}_{\text{vs}}<1$, these estimates can be substituted into I_vs to obtain variance estimates, and standard techniques such as Wald confidence intervals (CIs) can be used for inference. Alternatively, inference can be based on nonparametric bootstrap CIs (described in Web Appendix B).

3.2. Optimal Design

We now consider how to optimize the VS design with respect to k and the VS sampling mechanism, as characterized by γ_t = P(V = 1|T = t) (t = 0, 1), for given values of (π, Se, Sp). This will be done for a fixed number of validated groups (i.e., $m={\sum }_{i=1}^n{V}_i$) together with (i) fixed n or (ii) fixed N = nk. The first constraint (fixed m) arises from the expectation that the gold standard test is very expensive, and the second constraint (fixed n or N) reflects the relative cost of performing an imperfect assay versus enrolling a subject. A fixed N would be appropriate if the cost of the imperfect assay is negligible in comparison to the cost of enrolling a subject, while a fixed n would be appropriate in the opposite situation.

We start by considering case (i), where m and n are fixed and N is free. In light of (5), we seek to minimize I_vs(k, γ) ⁻¹[1, 1], where we emphasize the dependence on k and γ = (γ₀, γ₁), subject to the constraint

$$p_k{\gamma }_1+(1-p_k){\gamma }_0=m/n=:v.$$ (6)

Let us fix k for the moment and consider how to minimize I_vs(k, γ)⁻¹[1, 1] with respect to γ subject to the above constraint. To this end, we note that γ can be expressed as

$$\begin{array}{l}{\gamma }_1=p_{k(V)}v/p_k,\\ {\gamma }_0=(1-p_{k(V)})v/(1-p_k),\end{array}$$ (7)

where p_k(V) = P(T = 1|V = 1) is the proportion of T-positive groups in the VS. This expression for γ satisfies the constraint (6), although p_k(V) itself is constrained as follows:

$$p_{k(V)}^{min}:=max\{0,v-(1-p_k)\}/v\le p_{k(V)}\le min\{p_k,v\}/v=:p_{k(V)}^{max}.$$

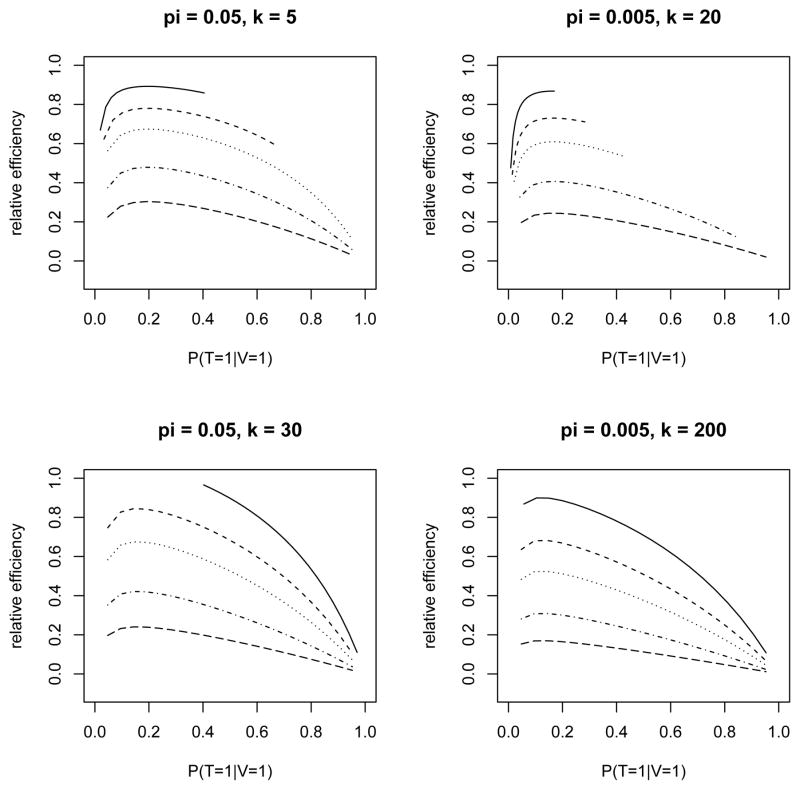
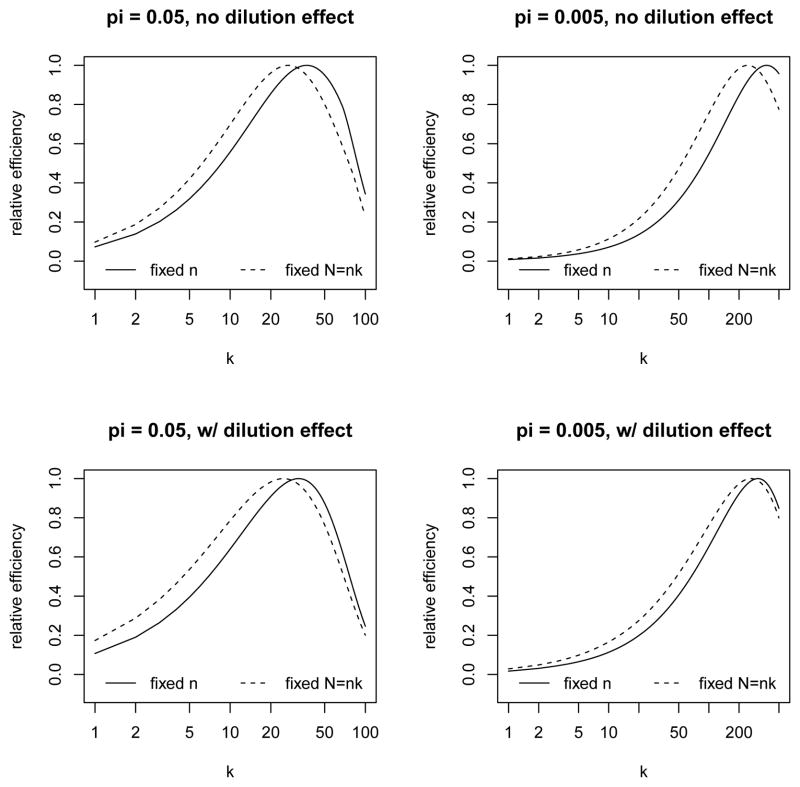
The lower bound acknowledges the fact that if υ > 1 − p_k then some T -positive groups have to be included in the VS, and the upper bound addresses the opposite situation. Figure 3 shows the range and impact of p_k(V) in a variety of situations with different values of π, k and υ (and fixed Se = 0.95, Sp = 0.995) in the presence of a dilution effect. The analogous plots without a dilution effect are shown in Web Figure 1. Within each panel of Figure 3 (with π and k fixed), the relative efficiency of π̂_vs is plotted as a function of p_k(V) (over the range of feasible values) for each of several values of υ. The range for p_k(V) is generally wider for smaller values of υ. Within each panel, the relative efficiency is defined as the variance of π̂_vs at υ = 1 (i.e., m = n, which implies that γ₁ = γ₀ = 1) divided by that for specified values of υand p_k(V). Each curve in Figure 3 attains its maximum at some p_k(V) ∈ (0, 1), which represents the optimal allocation of the VS between test-positive and test-negative groups for estimating π. The optimal value of p_k(V) can be found through a grid search in practice. The corresponding value of γ, denoted by ${\mathit{\gamma }}_{\text{opt}}^{(i)}(k)$, can be substituted into the objective function to yield ${\mathbf{I}}_{\text{vs}}{(k,{\mathit{\gamma }}_{\text{opt}}^{(i)}(k))}^{-1}[1,1]$, which can then be minimized over k. Some examples of this are shown as solid lines in Figure 4 for υ = 0.1 and π = 0.05, 0.005, with and without a dilution effect. For each curve in Figure 4, the relative efficiency is calculated as the ratio of the minimum variance over all k to that for a given k (similarly to previous graphs). In Figure 4 (and similar figures not shown in the article), neither the dilution effect nor the value of υ seems to have much impact on the optimal k, but a lower prevalence does clearly favor larger values of k, as one might expect from Figure 1.

Figure 3.

Allocation of the VS between T-positive and T-negative groups in the presence of a dilution effect: relative efficiency as a function of p_k(V) = P(T = 1|V = 1), the proportion of T-positive groups in the VS, for selected values of π, k, and the sampling fraction υ = P(V = 1) ∈ {0.5, 0.3, 0.2, 0.1, 0.05} (from top curve to bottom curve within each panel).

Figure 4.

Design considerations under the VS approach: relative efficiency as a function of k, for fixed n versus fixed N = nk, with π = 0.05, 0.005 and Sp = 0.995, with and without a dilution effect (see Section 3.2 for details). In the case of fixed n, we set υ = m/n = 0.1. In the case of fixed N, we set m/N = 0.001 for π = 0.05 and 0.0002 for π = 0.005.

Let us now consider case (ii), where m and N are fixed and n is free. After replacing n in (5) with N/k, we seek to minimize kI_vs(k, γ)⁻¹[1, 1] subject to the constraint (6). Note that υ = m/n = km/N is now dependent on k. For each fixed k, the approach described in the preceding paragraph can again be used to find the optimal γ, keeping in mind that υ is now a function of k. Let ${\mathit{\gamma }}_{\text{opt}}^{(ii)}(k)$ denote the resulting value of γ; then the objective function becomes $k\mapsto k{\mathbf{I}}_{\text{vs}}{(k,{\mathit{\gamma }}_{\text{opt}}^{(\text{ii})}(k))}^{-1}[1,1]$, which is shown as dashed lines in Figure 4, where m/N is set to be 0.001 for π = 0.05 and 0.0002 for π = 0.005. As in case (i), the dilution effect appears to have little impact and the optimal k increases with decreasing prevalence.

In practice, it may be necessary to consider all costs (the imperfect assay, the gold standard, subject enrollment, and other expenses) simultaneously. When concrete information is available regarding the various costs, a constrained optimization may be performed to minimize (5) subject to a fixed total cost. Some of the reasoning for cases (i) and (ii) may prove helpful in this general case, though the computation will necessarily be more complicated.

When an optimal VS design is obtained, it is important to verify that the resulting n is large enough for the asymptotic approximation (5) to be valid. This can be a problem when, for example, the optimization is for a fixed N and the optimal design suggests a relatively large k. In any case, it is advisable to conduct a simulation study to examine the accuracy of the asymptotic variance and the performance of the estimation and inference procedures, as we will do in the next subsection.

3.3. Simulation

A simulation study is conducted to evaluate the finite-sample performance of (π̂_vs, ${\widehat{\text{Se}}}_{\text{vs}},{\widehat{\text{Sp}}}_{\text{vs}}$) and the associated CIs. The study is based on n = 10000, k ∈ {1, 5, 30, 60} for π = 0.05, and k ∈ {1, 20, 100, 200} for π = 0.005. Motivated by Figure 4 (and additional ones not shown), the chosen k-values include those that are nearly optimal in terms of efficiency as well as smaller and larger values which may be preferred for practical reasons. For each π = 0.05, 0.005 and each chosen value of k, we conduct a series of experiments with υ ∈ {1, 0.5, 0.2, 0.1, 0.05}. In each scenario, 10000 replicate samples are generated and analyzed.

Table 2 presents the simulation results for the case where a dilution effect is present. The results include empirical relative bias and standard deviation for the point estimates (π̂_vs, ${\widehat{\text{Se}}}_{\text{vs}},{\widehat{\text{Sp}}}_{\text{vs}}$). These estimates are always available, but they may lie on the boundary of the parameter space; for example, ${\widehat{\text{Sp}}}_{\text{vs}}$ is frequently equal to 1 when υ is small. In that case, the observed information matrix cannot be used to construct Wald CIs. Table 2 reports the proportion of replicate samples in which closed-form standard errors are available (SEA) from the observed information matrix, and the coverage probabilities (nominal level 0.95) for (π, Se, Sp) among the SEA samples. Bootstrap CIs could be obtained for the non-SEA sampls, but they are too time-consuming to be included in this simulation study. For the SEA samples, Wald CIs are first constructed for (λ = logit(π), α = logit(Se), β = logit(Sp)) and then transformed to the original scale. The results in Table 2 show that the point estimates are nearly unbiased. Comparing the bias results in Table 2 with those in Table 1 demonstrates the effectiveness of the VS design for dealing with the mis-substitution bias. For each fixed υ, the best efficiency for π is attained by k = 30 for π = 0.05 and by k = 200 for π = 0.005, consistent with theoretical predictions based on Figure 4 and similar figures. It should be noted that high efficiency does not necessarily correspond to a large proportion of SEA samples. In this simulation study, the proportion of SEA samples is maximized at k = 5 for π = 0.05 and at k = 20 for π = 0.005. Regardless of the proportion of SEA samples, the Wald CIs do appear to provide good coverage (for π, at least) whenever they are available.

Table 2.

Simulation results for the VS design with a dilution effect: empirical relative bias and standard deviation (SD), proportion of replicate samples in which closed-form standard errors are available (SEA) from the observed information matrix, and coverage probability for (π, Se, Sp) among the SEA samples, under different combinations of π, k and the sampling fraction υ = P(V = 1) (see Section 3.3 for details).

k	υ	Relative Bias			SD (10−2)			P(SEA)	P(Coverage|SEA)
		π	Se	Sp	π	Se	Sp		π	Se	Sp
π = 0.05
1	1	0.000	0.000	0.000	0.22	0.98	0.07	1.00	0.95	0.95	0.95
	0.5	−0.001	0.000	0.000	0.22	1.40	0.07	1.00	0.95	0.95	0.95
	0.2	0.000	0.000	0.000	0.24	2.37	0.08	0.98	0.95	0.96	0.95
	0.1	0.000	0.001	0.000	0.28	3.25	0.11	0.87	0.97	0.96	0.95
	0.05	0.001	0.002	0.000	0.35	4.58	0.15	0.64	0.98	0.94	0.96
5	1	0.000	0.000	0.000	0.10	0.57	0.08	1.00	0.95	0.95	0.95
	0.5	0.000	0.000	0.000	0.11	0.78	0.12	1.00	0.95	0.95	0.95
	0.2	0.000	0.000	0.000	0.13	1.19	0.19	1.00	0.95	0.95	0.97
	0.1	0.000	0.000	0.000	0.15	1.69	0.26	0.97	0.95	0.95	0.97
	0.05	0.000	0.000	0.000	0.19	2.39	0.37	0.83	0.95	0.96	0.96
30	1	0.000	0.000	0.000	0.06	0.38	0.15	1.00	0.95	0.95	0.95
	0.5	0.000	0.000	0.000	0.06	0.38	0.28	0.96	0.95	0.95	0.96
	0.2	0.000	0.000	0.000	0.07	0.45	0.73	0.35	0.96	0.95	0.81
	0.1	0.000	0.000	0.000	0.09	0.60	1.01	0.20	0.97	0.96	0.90
	0.05	0.000	0.000	0.000	0.12	0.83	1.46	0.11	0.97	0.95	0.01
60	1	0.000	0.000	0.000	0.07	0.37	0.33	0.90	0.95	0.95	0.97
	0.5	0.000	0.000	0.000	0.07	0.37	0.51	0.60	0.95	0.95	0.91
	0.2	0.000	0.000	0.000	0.08	0.37	1.70	0.08	0.96	0.94	0.00
	0.1	0.001	0.000	0.001	0.11	0.41	2.22	0.04	0.99	0.93	0.00
	0.05	0.001	0.000	0.001	0.15	0.48	2.78	0.02	0.99	0.93	0.00
π = 0.005
1	1	0.000	0.000	0.000	0.07	3.12	0.07	0.92	0.94	0.96	0.95
	0.5	0.002	0.001	0.000	0.07	4.27	0.07	0.71	0.95	0.95	0.95
	0.2	−0.001	0.004	0.000	0.08	6.56	0.07	0.38	0.96	0.86	0.96
	0.1	−0.003	0.010	0.000	0.09	8.40	0.07	0.20	0.96	0.89	0.95
	0.05	0.001	0.016	0.000	0.10	10.60	0.07	0.10	0.98	0.01	0.95
20	1	0.000	0.000	0.000	0.02	1.04	0.07	1.00	0.95	0.95	0.95
	0.5	−0.001	0.000	0.000	0.02	1.46	0.08	1.00	0.95	0.95	0.95
	0.2	0.000	0.001	0.000	0.02	2.29	0.12	1.00	0.95	0.95	0.95
	0.1	0.001	0.001	0.000	0.03	3.20	0.17	1.00	0.95	0.96	0.96
	0.05	0.000	0.002	0.000	0.03	4.42	0.26	0.97	0.95	0.97	0.96
100	1	0.000	0.000	0.000	0.01	0.61	0.09	1.00	0.95	0.95	0.95
	0.5	0.000	0.000	0.000	0.01	0.71	0.21	1.00	0.95	0.95	0.97
	0.2	0.000	0.000	0.000	0.01	1.08	0.31	0.93	0.95	0.95	0.96
	0.1	0.000	0.000	0.000	0.01	1.51	0.43	0.73	0.95	0.95	0.94
	0.05	0.000	0.001	0.000	0.02	2.07	0.61	0.48	0.96	0.95	0.94
200	1	0.000	0.000	0.000	0.01	0.51	0.12	1.00	0.95	0.95	0.95
	0.5	0.000	0.000	0.000	0.01	0.53	0.35	0.85	0.95	0.95	0.95
	0.2	0.000	0.000	0.000	0.01	0.74	0.49	0.64	0.95	0.95	0.95
	0.1	0.000	0.000	0.000	0.01	1.00	0.69	0.40	0.96	0.95	0.90
	0.05	0.001	0.000	0.000	0.02	1.38	0.96	0.22	0.95	0.95	0.87

The simulation study also includes the case where a dilution effect is absent, and the results, shown in Web Table 1, are similar to those in Table 2.

3.4. Example

We now apply the methodology for the VS design to a study concerning Canadian blood donors [43, 18]. The study was designed to evaluate the effectiveness of a confidential self-administered questionnaire for excluding HIV-infected blood donors. The questionnaire describes high risk behaviors for HIV infection and asks donors to designate their blood for either laboratory use or transfusion based on the perceived risk level. Each subject in the lab group is matched with a control subject from the transfusion group based on age, sex and clinic. All subjects had their blood samples assayed for HIV antibodies using ELISA. In addition, the WB test (considered the gold standard) was performed on all subjects in the lab and control groups, as well as all subjects in the transfusion group with positive ELISA results. Although this study was not designed as a prevalence study, we will use it as an illustrative example for the VS design, and our interest is in estimating the HIV prevalence in the transfusion group (including the control subjects), for which the relevant data are summarized in Table 3.

Table 3.

Summary of the Canadian blood donor data (the transfusion group, including the control subjects), with ELISA as the imperfect assay and WB as the gold standard (see Section 3.4 for details).

	V = 1		V = 0	Row Total
	D = 0	D = 1
T = 0	622	0	94091	94713
T = 1	393	15	0	408
Column Total	1015	15	94091	95121

The estimation method in Section 3.1 allows k = 1 and therefore can be applied to the individual-level test data from the Canadian blood donor study. There is a complication, however, due to the fact that the control subjects were chosen to match the subjects in the lab group. This sampling mechanism may not satisfy the assumption that V is conditionally independent of D given T, depending on how strongly the matching variables are related to disease status. This assumption could be relaxed by including the matching variables as conditioning variables, and a simple extension of the estimation method in Section 3.1 (to a regression model that relates disease status to matching variables) could be applied if subject-level data were available on the matching variables. Without access to such data, we shall proceed under the conditional independence assumption, which would be appropriate if the matching variables are weakly related to disease status. Our analysis yields an estimated prevalence of 158 per million (95% CI: 84–252 per million) and an estimated specificity of 99.59% (95% CI: 99.55–99.62%). Because no false negatives have been found in the transfusion group, the estimated sensitivity is 1 and the associate CI is concentrated at 1. These CIs are obtained using a nonparametric bootstrap percentile method (based on 1000 bootstrap samples) because the estimated sensitivity lies on the boundary of the parameter space.

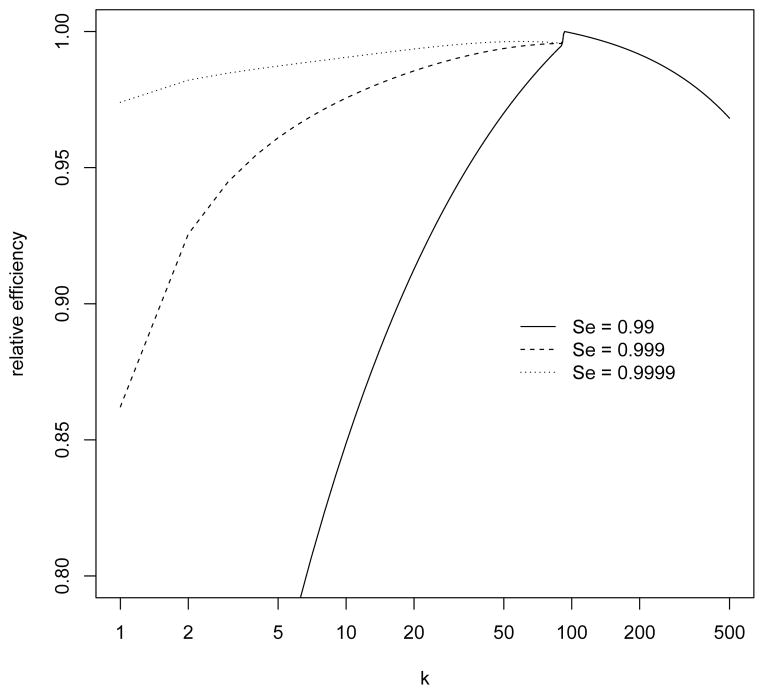
Our main objective here is to improve the study design retrospectively. Specifically, we consider how to choose the group size so as to achieve better efficiency for estimating the HIV prevalence in the transfusion group. This will be done while fixing the total number of subjects (N = 95121) and the total number of WB tests (m = 1030) as in the original study. It seems sensible to base new designs on the estimates from our analysis, with the possible exception of sensitivity. There actually is a false negative in the lab group, so the sensitivity cannot be 1. To account for this fact, we consider a range of values (99%, 99.9% and 99.99%) for the sensitivity in our search for optimal designs. In addition, we consider a possible dilution effect (described in Section 2). For each combination, we compute the relative efficiency as a function of the group size k using the methodology of Section 3.2. The results are shown in Figure 5 (with a dilution effect) and Web Figure 2 (without a dilution effect). The curves in both figures indicate that the optimal choice of k is 93, which is the smallest group size for which all groups are included in the VS. Decreasing k from 93 to 92 means that some groups cannot be included in the VS, which results in an immediate drop in efficiency. Increasing k from 93 means that some of the available WB tests are not used, which results in a steady decline in efficiency.

Figure 5.

Design considerations for the Canadian blood donor study: relative efficiency as a function of k, for fixed m and N with a dilution effect (see Section 3.4 for details).

Table 4 presents the simulation results for the 6 scenarios just described. The results show that π̂_vs is nearly unbiased in all cases and its precision is insensitive to the value of Se and the presence of a dilution effect. In the present setting, with a very low prevalence, Wald CIs are frequently unavailable. When they are available, Table 4 shows that they can still provide good coverage for π and Sp in some scenarios. (The poor coverage for Se is probably due to the low prevalence, which results in a small denominator in ${\widehat{\text{Se}}}_{\text{vs}}$ and hence a large departure of ${\widehat{\text{Se}}}_{\text{vs}}$ from Se when ${\widehat{\text{Se}}}_{\text{vs}}<1$.) If Wald CIs are not available, a bootstrap method can be used to obtain CIs, as in our analysis of the original data.

Table 4.

Simulation results for the Canadian blood donor study: empirical relative bias and standard deviation (SD), proportion of replicate samples in which closed-form standard errors are available (SEA) from the observed information matrix, and coverage probability for (π, Se, Sp) among the SEA samples, for k = 93 and Se ∈ {0.99, 0.999, 0.9999}, with and without a dilution effect (see Section 3.4 for details).

Se	Dilution Effect?	Relative Bias			SD			P(SEA)	P(Coverage|SEA)
		π	Se	Sp	π (10−5)	Se (10−2)	Sp (10−3)		π	Se	Sp
0.99	no	−0.001	0.001	0.000	4.08	2.59	2.01	0.13	0.95	0.68	0.98
	yes	0.000	−0.001	0.000	4.13	5.26	2.03	0.43	0.94	0.90	0.97
0.999	no	−0.002	0.000	0.000	4.09	0.84	2.02	0.02	0.97	0.00	0.98
	yes	0.000	0.000	0.000	4.08	1.57	1.99	0.05	0.94	0.00	0.97
0.9999	no	−0.001	0.000	0.000	4.08	0.19	2.00	0.00	0.67	0.00	1.00
	yes	0.000	0.000	0.000	4.06	0.51	2.00	0.01	0.96	0.00	0.96

4. The VGS Design (Without a Gold Standard)

4.1. Basics

Suppose a gold standard test is unavailable. Because equation (2) involves (Se, Sp), the fixed-k design is unable to identify π when the values of (Se, Sp) are unknown; this is analogous to solving for three unknowns with one equation. Here we propose a partial solution to the identification problem: a VGS design with varying k. Let denote the support of k and | 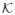| the size of 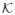. If | 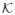| ≥ 3, the VGS design is able to identify all three parameters (π, Se, Sp) under the following assumption:

Assumption (constancy). Se and Sp do not depend on the group size k.

To solve for three unknowns generally requires three equations, so the condition that | 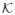| ≥ 3 is clearly necessary for the identification of (π, Se, Sp). In Web Appendix C, we show that the condition is also sufficient by ruling out the existence of multiple roots.

When | 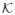| > 3, the parameters (π, Se, Sp) are over-identified, which allows us to examine the constancy assumption and possibly replace it with weaker assumptions. As noted in Section 1, the constancy assumption may be reasonable in some situations such as ELISA-based HIV testing with k ≤ 15. When this assumption is in doubt, Se and Sp can be allowed to depend on k in a parsimonious way. To emphasize this dependence, we now write Se(k; α) and Sp(k; β), where α and β are unknown parameters. A simple example for Se(k; α) is the logistic regression model given by (4), where α₀ determines the sensitivity of the assay when applied to an individual subject, and a negative α₁ indicates a dilution effect that is commonly suspected in group testing. The linear term log k in model (4) seems natural but is not essential; it could be replaced or augmented with other terms such as (log k)², k and $\sqrt{k}$ if necessary. A possible dilution effect, which causes the sensitivity to decrease with k, is probably the most common reason to question the constancy assumption, but [30] point out that the specificity may change with k as well, which can be accommodated by specifying a model for Sp(k; β). It seems reasonable to expect the parameters to be identifiable if | 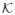| ≥ dim(α) + dim(β) + 1, although a rigorous proof will likely depend on the specification of the models Se(k; α) and Sp(k; β).

We now consider estimation of θ = (λ, α, β) under appropriate models Se(k; α) and Sp(k; β) that ensure parameter identification. One or both of these models may be trivial; for example, we could have Sp(k; β) = expit(β) if Sp is assumed constant over k. Even if both models are trivial, it is still computationally convenient to work with transformed parameters (e.g., λ instead of π) that are free-ranging. Let k_i and T_i (i = 1, … , n) denote the size and the test result, respectively, of the ith group. Based on these data, the log-likelihood for θ is given by

$$l_{\text{vgs}}(\mathit{\theta })=\sum _{i=1}^n[T_{i}log{p}_{k_i}(\mathit{\theta })+(1-T_i)log\{1-p_{k_i}(\mathit{\theta })\}],$$

where the subscript vgs indicates the VGS design and p_k(θ) denotes the far right side of (1) with (Se, Sp) replaced by the models. The above log-likelihood may be maximized using a quasi-Newton algorithm (available in R as the optim function). Denote by θ̂_vgs = (λ̂_vgs, α̂_vgs, β̂_vgs) the MLE of θ. We conceptualize the k_i as a random sample from some discrete distribution supported by 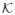, so that $n^{-1}{\sum }_{i=1}^{n}I(k_i=k)$, where I(·) is the indicator function, converges to some τ_k almost surely for each k ∈ 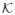. Then it follows from standard asymptotic theory that $\sqrt{n}({\widehat{\mathit{\theta }}}_{\text{vgs}}-\mathit{\theta })\to N(\mathbf{0},{\mathbf{I}}_{\text{vgs}}^{-1})$), where I_vgs is the Fisher information for θ in a single group of random size. In particular, the variance of π̂_vgs = expit(λ̂_vgs) in large samples is given by

$$var({\widehat{\pi }}_{\text{vgs}})\approx {\pi }^2{(1-\pi )}^{2}var({\widehat{\lambda }}_{\text{vgs}})\approx n^{-1}{\pi }^2{(1-\pi )}^2{\mathbf{I}}_{\text{vgs}}^{-1}[1,1].$$ (8)

By conditioning on the group size, we can write I_vgs = Σ_k∈ 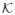τ_kI_vgs,_k, where I_vgs,k is the information for θ in a group of size k. It follows from simple algebra that

$${\mathbf{I}}_{\text{vgs},k}=\frac{\{\partial p_k(\mathit{\theta })/\partial \mathit{\theta }\}{\{\partial p_k(\mathit{\theta })/\partial \mathit{\theta }\}}^{\mathrm{T}}}{p_k(\mathit{\theta })\{1-p_k(\mathit{\theta })\}},$$

with explicit expressions given in Web Appendix A. Each I_vgs;k is necessarily singular, but I_vgs is non-singular if 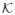is sufficiently large. A consistent variance estimate for θ̂_vgs can be obtained by replacing τ_k with $n^{-1}{\sum }_{i=1}^{n}I(k_i=k)$ and θ with θ̂_vgs in the above expressions. Alternatively, if the quasi-Newton algorithm is used to find θ̂_vgs, then a numerically differentiated Hessian matrix of the log-likelihood is readily available. Furthermore, one could always use a bootstrap procedure to obtain standard errors and confidence intervals.

4.2. Optimal Design

An important practical question is how to optimize the VGS design, as characterized by τ = (τ_k)_k∈ 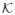, with respect to the precision for estimating π, the parameter of interest. We consider three scenarios for this optimization problem. In the first scenario, var(π̂_vgs) is to be minimized for a fixed number of groups (n); this may be appropriate when a large number of subjects are readily available and the cost of the study is driven by an expensive assay. In this scenario, expression (8) suggests that we should search for τ that minimizes

$${\left(\sum _{k\in \mathcal{K}}{\tau }_k{\mathbf{I}}_{\text{vgs},k}\right)}^{-1}[1,1].$$ (9)

In the second scenario, the total number of subjects, $N={\sum }_{i=1}^n{k}_i$, is fixed, which may be realistic when the cost of the assay is negligible in comparison to the cost of a subject. In this scenario, we approximate n by N/E(k) = N/Σ_k∈ 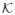τ_kk and substitute this into (8), and the goal is then to find τ that minimizes

$$\left(\sum _{k\in \mathcal{K}}{\tau }_{k}k\right){\left(\sum _{k\in \mathcal{K}}{\tau }_k{\mathbf{I}}_{\text{vgs},k}\right)}^{-1}[1,1].$$ (10)

It is arguably more likely that both the assay and a study subject incur a considerable cost, and we therefore consider a third scenario where the study is constrained by the total cost, which may be expressed as N + ρn with ρ being a given cost ratio (assay to subject). Because N ≈ n E(k) = nΣ_k∈ 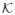τ_kk, the total cost constraint implies that n is inversely proportional to ρ + Σ_k∈ 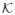τ_kk, and the goal is now to find τ that minimizes

$$\left(\rho +\sum _{k\in \mathcal{K}}{\tau }_{k}k\right){\left(\sum _{k\in \mathcal{K}}{\tau }_k{\mathbf{I}}_{\text{vgs},k}\right)}^{-1}[1,1].$$ (11)

This scenario includes the second one as a special case (ρ = 0) and the first one as a limiting case (ρ → ∞). In each scenario, the optimal τ depends on the true value of θ (and ρ in the third scenario) but not on the actual value of the constraint (n, N or N + ρn), provided that the optimal design does not invalidate the approximation (8) on which it is based. Consequently, an optimal VGS design can be applicable to a class of studies with the same cost considerations, even though the actual size (n or N) and costs may vary across studies.

Although all three criteria, (9)–(11), are closed-form functions of τ, it seems difficult to find the optimal τ analytically, a major complication being matrix inversion. One can certainly evaluate the criteria numerically for given values of τ and θ. However, because 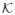is required to contain at least three values, the brute force approach to finding the optimal τ can easily become infeasible in practice. Suppose 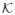= {1, … , K} for some integer K ≥ dim(α) + dim(β) + 1. If we rely on the constancy assumption, K may be chosen to be the largest group size for which the constancy assumption is plausible (for example, one might take K = 15 in ELISA-based HIV testing). Without assuming constancy, the choice of K will be driven by other practical considerations such as assay sensitivity and feasibility. For K ≤ 15, the optimization can be done using a quasi-Newton algorithm with {log(τ_j/τ₁) : j = 2, … , K} as independent variables; this will be referred to as the unrestricted approach. As a general approach, we propose to optimize τ within a parametric family of distributions. A parametric model for τ may be obtained by discretizing a parametric family of continuous distributions. Let F(·; ν) denote a cumulative distribution function with parameter ν; then a parametric model for τ may be obtained as

$${\tau }_k(\mathit{\nu })=F(x_k;\mathit{\nu })-F(x_{k-1};\mathit{\nu }),k=1,\dots ,K,$$

where the x_k (k = 0, … , K) are a user-specified monotone sequence with F (x₀; ν) = 0 and F (x_K; ν) = 1, and the quasi-Newton algorithm can again be used for optimization. An obvious candidate for F is the beta family, for which we set x_k = k/K, k = 0, … , K. Although the beta family includes a variety of shapes, our numerical experience suggests that it is worthwhile to seek extra flexibility in a parametric family that includes multimodal distributions. For this purpose, we consider a family of normal mixture distributions with a specified number of components and unspecified weights and mean and variance parameters for the individual components. For this choice of F, we let x_k (k = 1, … , K − 1) be the k/K-quantile of the standard normal distribution, and set x₀ = −∞ and x_K = ∞. Our experience also suggests that the number of normal components in the mixture family can be set equal to dim(α) + dim(β) + 1, the number of parameters to estimate, and that having more than the suggested number of components is not beneficial. In fact, there are strong indications that the optimal τ is concentrated on exactly dim(α) + dim(β) + 1 points, including 1 and K, in 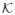= {1, … , K}. This conjecture motivates yet another approach, which seeks to optimize τ within the conjectured family and which will be referred to as the conjecture-based approach. In searching for the optimal design in a given situation characterized by θ and K, we employ all applicable approaches (conjecture-based, normal mixture, beta and, if K ≤ 15, unrestricted) and use the specified objective function to choose the best design among those suggested by the various approaches. The chosen design will be referred to as the top candidate design because it is not guaranteed to be truly optimal in all cases.

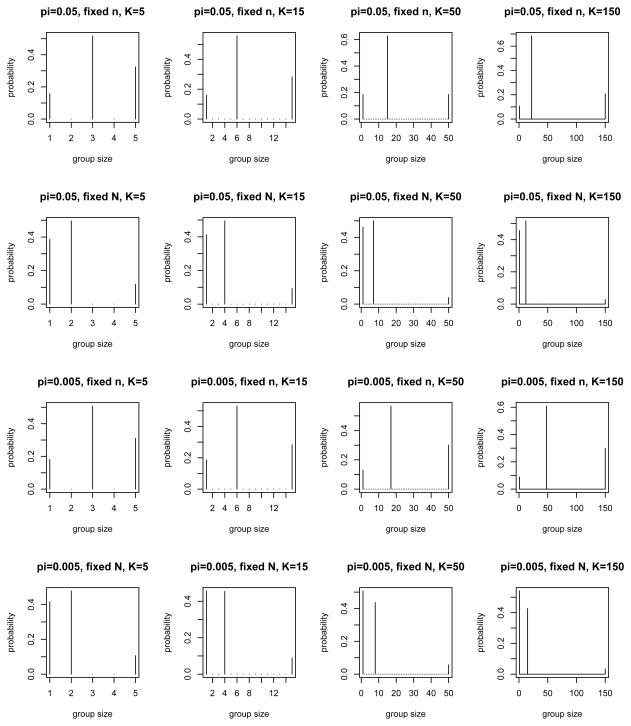
For the case of no dilution effect (Se = 0.95 and Sp = 0.995, regardless of k), Figure 6 shows top candidate designs for fixed n or N with π = 0.05, 0.005 and K = 5, 15, 50, 150, obtained using the approaches just described. Interestingly, it turns out that all top candidate designs in Figure 6 are supported by 3 points: 1, K and an intermediate value. (The exact k-values are given in Web Table 2.) Compared with the fixed-n constraint, the fixed-N constraint tends to shift the probability masses in τ to lower values of k, as predicted by theory (the term Σ_k∈ 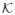τ_kk in (10) can be seen as a penalty on large k). Decreasing π from 0.05 to 0.005, on the other hand, tends to shift the intermediate value of k (other than 1 and K) upward.

Figure 6.

Top candidate VGS designs for fixed n versus fixed N = nk, with &pi; = 0.05, 0.005, Se = 0.95, Sp = 0.995 and K = 5, 15, 50, 150, without a dilution effect (see Section 4.2 for details).

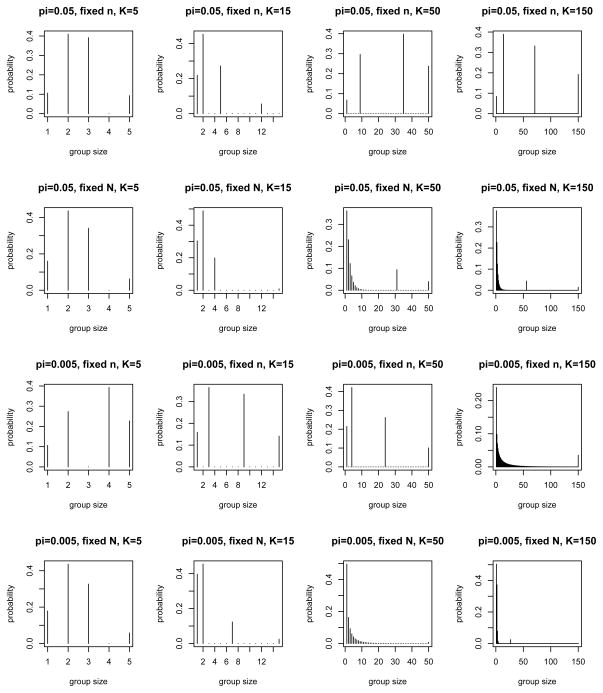
Figure 7 shows the analogous results for the case where a dilution effect is present and accounted for by model (4). Most designs in Figure 7 are supported by 4 points, consistent with the fact that there are now 4 parameters to estimate. The few designs that do not follow this pattern tend to correlate with numerical difficulties in matrix inversion.

Figure 7.

Top candidate VGS designs for fixed n versus fixed N = nk, with π = 0.05, 0.005, Sp = 0.995 and K = 5, 15, 50, 150, in the presence of a dilution effect (see Section 4.2 for details).

4.3. Simulation

Table 5 presents the simulation results (based on 1000 replicates) for the fixed-n designs in Figure 7 (with a dilution effect). The results include empirical bias (relative for π, absolute for the other parameters) and standard deviation for the point estimates. The point estimates are almost always (> 99%) available, as in previous simulation studies, but the observed information matrix is sometimes numerically singular. As a result, Table 5 also presents the proportion of SEA samples and the coverage probability (nominal level 0.95) among SEA samples, separately for each parameter. The primary objective here is to assess the feasibility of the VGS method for estimating π or, equivalently, λ = logit(π). For a fixed π, parameter estimation is generally easier with larger K and n. For π = 0.05 and K = 150, it seems that n = 1000 suffices for coverage, although there is some bias for π and λ, which becomes smaller with increasing n. (The bias problem can be worse for the other parameters, but this is a secondary concern for us.) When K is smaller, the proportion of SEA samples becomes smaller and good coverage becomes difficult to achieve (even for SEA samples). For π = 0.05 and K = 50, 15, good coverage requires n = 10⁵. For π = 0.05 and K = 5, even n = 10⁵ is not enough for good coverage. Table 5 shows clearly that π = 0.005 is more difficult to estimate than π = 0.05, with higher requirements on n for each K. Otherwise the results for π = 0.005 follow the same patterns as those for π = 0.05. A notable advantage of the VGS design is the possibility of detecting and estimating a dilution effect, as characterized by α₁. Table 5 shows that this is indeed possible, although it requires large K and n (e.g., K = 150, n = 10000 for π = 0.05).

Table 5.

Simulation results for the VGS design with a dilution effect: empirical bias (relative for π, absolute for the other parameters) and standard deviation (SD), proportion of replicate samples in which closed-form standard errors are available (SEA) from the observed information matrix, and coverage probability for (λ = logit(π), α₀, α₁, β = logit(Sp)) among the SEA samples, under different combinations of π, K and n (see Section 4.3 for details).

K	n	Bias					SD				P(SEA)				P(Coverage|SEA)
		π	λ	α0	α1	β	λ	α0	α1	β	λ	α0	α1	β	λ	α0	α1	β
π = 0.05
150	1000	0.09	0.05	0.19	−0.03	0.88	0.27	2.20	0.46	2.58	1.00	1.00	1.00	0.91	0.96	0.88	0.89	0.81
	5000	0.03	0.03	−0.06	0.01	7.47	0.09	0.89	0.19	1.99	1.00	1.00	1.00	0.42	0.96	0.95	0.95	0.98
	10000	0.00	0.00	0.04	−0.01	0.97	0.06	0.67	0.14	2.18	1.00	1.00	1.00	0.96	0.96	0.95	0.95	0.88
50	10000	−0.02	−0.03	1.25	−0.31	0.60	0.12	2.41	0.58	2.03	0.95	0.96	0.96	0.96	0.83	0.93	0.94	0.85
	100000	0.02	0.03	−0.11	0.02	19.20	0.03	0.53	0.13	1.05	0.97	0.97	0.97	0.51	0.97	0.96	0.96	1.00
15	100000	−0.02	−0.02	0.93	−0.28	0.05	0.08	3.81	1.51	0.85	0.61	0.62	0.63	0.87	0.93	0.97	0.97	0.94
5	100000	−0.02	−0.02	0.60	−0.19	0.29	0.06	2.73	1.67	1.69	0.56	0.55	0.71	0.81	0.90	0.89	0.96	0.91
π = 0.005
150	5000	0.09	0.03	2.42	−0.20	0.19	0.28	10.27	3.11	1.14	0.83	0.81	0.84	0.96	0.89	0.94	0.94	0.89
	10000	0.02	−0.01	2.65	−0.37	0.03	0.20	8.66	2.36	0.59	0.83	0.83	0.84	0.96	0.92	0.96	0.96	0.91
50	10000	0.05	0.03	0.81	−0.04	0.17	0.19	6.06	1.81	1.15	0.87	0.86	0.91	0.93	0.87	0.95	0.98	0.84
	100000	−0.02	−0.03	1.81	−0.37	−0.03	0.10	3.98	1.02	0.17	0.83	0.84	0.84	0.95	0.92	0.99	1.00	0.96
15	100000	0.02	0.01	0.35	−0.05	−0.05	0.14	4.32	1.74	0.35	0.82	0.80	0.87	0.92	0.94	0.92	0.99	0.88
5	100000	0.20	0.13	−0.27	−0.18	0.09	0.30	4.90	3.17	0.78	0.73	0.67	0.82	0.83	0.93	0.83	0.99	0.82

Web Table 3 presents the analogous results for the fixed-n designs in Figure 6 (without a dilution effect). With only 3 parameters to estimate, the results in Web Table 3 are somewhat better in the sense of lower requirements on (K, n), but otherwise follow the same patterns as those in Table 5.

5. Discussion

In this article, we draw attention to the mis-substitution bias and propose ways to deal with it. The proposed designs allow the sensitivity and specificity of an imperfect assay to be estimated from data (together with the prevalence of interest), and eliminate the need to rely on known values of these accuracy measures. Although such designs may have been used in practice for various reasons, their utilities in dealing with the mis-substitution bias do not appear to have been discussed before. For example, when a gold standard is available, it is sometimes applied to the test-positives (for the imperfect assay) as a confirmatory test. This practice does not allow the prevalence to be estimated without assuming known values of the accuracy measures. For the latter purpose, our findings suggest that the gold standard should be applied to some test-negatives as well and that one should strive for an optimal allocation between test-positives and test-negatives in the VS. Our consideration of the VGS design, which also has been used before, reveals a new advantage (i.e., improved identifiability) of the group testing approach over the traditional individual testing approach, in addition to its well-known advantages in cost-effectiveness and statistical efficiency. Although the VGS design requires assumptions (constancy or a model for Se), those assumptions are certainly weaker than assuming constant and known values of sensitivity and specificity. The VGS design may also require very large n and K, depending on the true parameter values, and therefore should be used carefully (e.g., with a simulation study to verify its performance in a given situation).

The VS design is similar to the approach of McMahan et al. [30] in that both approaches require that a gold standard assay be available and applied to a training sample. In the VS design, the training sample is an internal validation subsample. In the approach of McMahan et al., the training sample may be internal or external, and its purpose is to provide biomarker information that can be used to estimate Se and Sp as functions of k. By taking advantage of biomarker information, the approach of McMahan et al. can be expected to be more efficient for estimating Se, Sp and a possible dilution effect. On the other hand, the VS design remains feasible in the absence of biomarker information. When the training sample in McMahan et al. happens to be an internal subsample, it may be possible to combine the two approaches into a unified analysis, which is an area for future research.

We have not considered a Bayesian approach to the misclassification problem. Instead of treating an assay’s accuracy measures as known or unknown, one could use a prior distribution to represent the relevant information from one or more studies. Such a prior distribution could be used to choose a study design that is optimal with respect to the prior (as opposed to a single set of parameter values) and to analyze the resulting data in a Bayesian fashion. It will be of interest to explore this approach in the context of a suitable application.