Biased Gene Conversion Skews Allele Frequencies in Human Populations, Increasing the Disease Burden of Recessive Alleles

Abstract

Gene conversion results in the nonreciprocal transfer of genetic information between two recombining sequences, and there is evidence that this process is biased toward G and C alleles. However, the strength of GC-biased gene conversion (gBGC) in human populations and its effects on hereditary disease have yet to be assessed on a genomic scale. Using high-coverage whole-genome sequences of African hunter-gatherers, agricultural populations, and primate outgroups, we quantified the effects of GC-biased gene conversion on population genomic data sets. We find that genetic distances (F_ST and population branch statistics) are modified by gBGC. In addition, the site frequency spectrum is left-shifted when ancestral alleles are favored by gBGC and right-shifted when derived alleles are favored by gBGC. Allele frequency shifts due to gBGC mimic the effects of natural selection. As expected, these effects are strongest in high-recombination regions of the human genome. By comparing the relative rates of fixation of unbiased and biased sites, the strength of gene conversion was estimated to be on the order of Nb ≈ 0.05 to 0.09. We also find that derived alleles favored by gBGC are much more likely to be homozygous than derived alleles at unbiased SNPs (+42.2% to 62.8%). This results in a curse of the converted, whereby gBGC causes substantial increases in hereditary disease risks. Taken together, our findings reveal that GC-biased gene conversion has important population genetic and public health implications.

Introduction

Meiotic recombination results in either crossover or noncrossover events, and gene conversion can occur in either case.¹ In humans the mean tract length of these gene conversion events is approximately 500 base pairs.² Gene conversion is defined here as the nonreciprocal exchange of genetic information between homologous sequences, and two kinds of gene conversion exist: conversion between two alleles of the same gene (allelic gene conversion) and conversion between paralogs (interlocus gene conversion).^1,3 In humans there is evidence that allelic gene conversion has affected the fast-evolving ADCYAP1 gene⁴ (MIM 102980), and interlocus gene conversion has shaped the evolution of genes that encode erythrocyte glycoproteins in malaria-endemic African populations.⁵ In this paper, we focus on the population genetic and public health implications of allelic gene conversion.

Recombination results in the formation of heteroduplex DNA, and mispairing due to differences in parental alleles is corrected by the mismatch repair machinery.¹ However, mismatch repair preferentially retains guanine (G) and cytosine (C) over adenine (A) and thymine (T) alleles.⁶ This causes gene conversion to be biased toward G or C alleles. GC-biased gene conversion (gBGC) likely evolved as a response to high mutation rates caused by the deamination of methylated cytosine.^1,7 Strong (G or C) alleles are represented by the IUPAC code S, and weak (A or T) alleles are represented by the IUPAC code W. Listing the ancestral allele first and derived allele second, pairs of IUPAC codes can be used to describe different types of SNPs (Figure 1). For example, a SNP with an ancestral A allele and derived G allele is labeled WS. One implication of gBGC is that when an individual is heterozygous for a strong (G or C) and weak (A or T) allele, the strong allele is more likely to be passed on to their offspring. Because equal segregation does not occur, gene conversion results in non-Mendelian inheritance. WW and SS SNPs are unbiased, SW SNPs have ancestral alleles that are favored by gBGC, and WS SNPs have derived alleles that are favored by gBGC.

Figure 1.

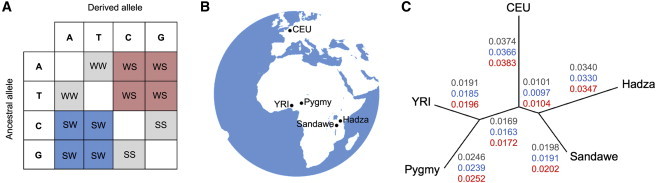
Biased Gene Conversion, Study Populations, and Genetic Distances

(A) Depending on ancestral and derived states, SNPs can be classified as WW or SS (gray), SW (blue), and WS (red). Weak (A or T) alleles are represented by W and strong (G or C) alleles are represented by S.

(B) Study populations: Pygmy, YRI (Yoruba), Sandawe, Hadza, and CEU (Northern and Western European ancestry). Five high-coverage whole genomes were analyzed for each population.

(C) Genetic distances using population branch statistics. Mean values are shown for thee different types of SNPS: WW or SS (gray), SW (blue), and WS (red). Branch lengths depicted are for WW or SS SNPs.

There is increasing evidence that gene conversion is an important evolutionary phenomenon. Gene conversion influences GC content^8–10 and decreases linkage disequilibrium over small scales.^11,12 Haplotypes containing variants that increase recombination rates are more likely to be converted, and this leads to what has been called the “recombination hotspot paradox.”^13,14 Alleles favored by gBGC are evolutionarily (and mathematically) equivalent to semidominant mutations under positive selection.^1,15 Because of this, gene conversion results in shifts in site frequency spectra. Low-coverage whole-genome sequences from the 1000 Genomes Project reveal that these allele frequency shifts are stronger in high-recombination regions of the human genome,¹⁶ and gBGC modifies the allele frequencies of nonsynoymous SNPs that are likely to contribute to hereditary disease.¹⁷ Comparisons with other primate genomes have identified human accelerated regions (HARs), and these genomic regions are enriched for WS substitutions, a pattern that is consistent with gene conversion.^18,19 However, substitutions caused by gBGC can be nonadaptive and these substitutions may be “the Achilles’ heel of our genome.”²⁰ Indeed, gBGC modifies d_N/d_S ratios and has contributed to the fixation of deleterious mutations in primate lineages.²¹

At present there is a lack of studies that analyze the effects of GC-biased gene conversion using high-coverage whole-genome sequence data from diverse global populations. It also is unknown how gBGC affects genetic distances between human populations, and there is a need to estimate the strength of gBGC from genomic data that are free from ascertainment bias. In addition, the effects of gBGC-induced allele frequency shifts on hereditary disease risks are yet to be quantified. GC-biased gene conversion results in the following predictions: (1) increased genetic distances and modified evolutionary rates for variants favored by gene conversion, (2) detectable shifts in allele frequency distributions, (3) greater effects in high-recombination regions of the human genome, and (4) effects of gBGC observable in every population.

In this study we use high-coverage whole-genome sequences from five global populations to test each of the above predictions. We determine how much gBGC perturbs population genetics statistics that are commonly used for demographic inference and scans of selection. We then use relative rates of fixation of biased and unbiased SNPs to infer the strength of gene conversion. Finally, because allele frequency shifts modify allele frequencies and the chance of observing recessive homozygotes, we quantify the effects of gBGC on the risk of hereditary disease.

Material and Methods

Whole-Genome Sequences

A total of 25 high-coverage (∼60×) genomes sequenced by Complete Genomics²² were analyzed in this study. Error rates for these genomes are on the order of 1 per 100,000 base pairs.^22–24 The standard Complete Genomics bioinformatics pipeline was used for sequence alignment, read mapping, assembly, and SNP calling (Assembly Pipeline v.1.10 and CGA Tools 1.4). Five genomes were analyzed per population, and the geographic locations of study populations are shown in Figure 1B. Populations sampled include Pygmies from Cameroon (Baka, Bakola, and Bedzan), Yoruba from Nigeria (YRI), Sandawe from Tanzania, Hadza from Tanzania, and individuals with Northern and Western European ancestry (CEU). Pygmy, Sandawe, and Hadza genomes were previously analyzed in a recent study of African hunter-gatherers,²³ and YRI and CEU genomes were obtained from the Complete Genomics public data release. Prior to collection of Pygmy, Hadza, and Sandawe samples, informed consent was obtained from all research participants. Permits were received from the Ministry of Health and National Committee of Ethics in Cameroon and from COSTECH and NIMR in Dar es Salaam, Tanzania. In addition, appropriate IRB approval was obtained from both the University of Maryland and the University of Pennsylvania.

Data Processing

After merging genomes using CGA Tools, we selected sites that were polymorphic in at least one study population. We then filtered out sex-linked and mitochondrial variants and required that sites be fully called in all 25 genomes. For each autosomal locus, this gives a sample size of n = 10 per population. As per a previous study, derived and ancestral states of SNPs were found via maximum likelihood using chimpanzee, orangutan, and rhesus macaque genomes as outgroups.²³ A total of 10,770,084 SNPs remained after obtaining derived allele frequencies of fully called autosomal SNPs.

Hypermutable CpG dinucleotides can cause derived allele frequencies to be misestimated.²⁵ To correct for this, base pairs flanking each SNP were identified and variants were flagged if they belong to a CpG dinucleotide in either humans or chimpanzees. Flagged variants were then excluded from subsequent polymorphism analyses, resulting in a total of 7,539,623 non-CpG SNPs. GC-biased gene conversion favors strong alleles (G or C, denoted by the IUPAC code S) over weak alleles (A or T, denoted by the IUPAC code W). Because of this, we binned SNPs into three broad categories (Figure 1A): SNPs unaffected by gBGC (WW or SS SNPs), SNPs where the ancestral allele is favored by gBGC (SW), and SNPs where the derived allele is favored by gBGC (WS).

To generate 95% confidence intervals of genetic distances and population genetics statistics (see below), we bootstrapped whole-genome data sets for five different populations and four different types of data: WW or SS, SW, WS, and all non-CpG SNPs. For each combination of population and SNP type, we bootstrapped whole-genome data sets 1,000 times, generating 10,000 unlinked SNPs per bootstrap run. Mann-Whitney U tests were used to compare bootstrapped values of population genetics statistics and to generate two-tailed p values. For recombination rate tests, bootstrapped statistics for SNPs in the lowest quintile (0%–20%) were compared to SNPs with recombination rates in the highest quintile (80%–100%) using Mann-Whitney U tests. Because 10,000 SNPs were analyzed for each bootstrap run, even small effect sizes resulted in low p values.

Calculating Genetic Distances

Pairwise F_ST statistics were used to estimate genetic distances between populations and population branch statistics (PBS) were used to estimate relative rates of evolution. To correct for small sample size, F_ST was calculated using Weir and Cockerham’s method.²⁶ PBS statistics measure the amount of sequence change along branches of a population tree.^27,28 These statistics have also been called locus-specific branch length²⁹ and relative rate statistics.³⁰ Whenever four or more populations are analyzed, such as in this present study, PBS statistics require a known topology, and we used a neighbor joining tree generated from whole-genome sequencing data:²³ (Pygmy, (YRI, ((Hadza, Sandawe), CEU))). An unrooted version of this tree is shown in Figure 1C. PBS for all internal and external branches of the population tree were calculated using pairwise F_ST statistics and Equations A1–A7 in Appendix A. Negative values of F_ST and PBS statistics were treated as 0. To assess the effects of gBGC on genetic distances, mean values of PBS statistics were calculated for WW or SS SNPs, SW SNPs, and WS SNPs using the R programming language.³¹

Allele Frequency Distributions and Summary Statistics

Normalized site frequency spectra (SFS) were obtained for each population and type of SNP (WW or SS, SW, and WS). For each pooled set of SNPs (i.e., population and type of SNP), we calculated Tajima’s D,³² normalized Fay and Wu’s H,^33,34 and mean derived allele frequency (DAF). We also calculated a summary statistic that compares WS and SW DAF spectra (W→S DAF skew). This statistic involves performing a Mann-Whitney U test and then normalizing by the maximum possible value of the test.¹⁶ To test whether the effects of gBGC are stronger in regions of high recombination, we obtained recombination rates from the deCODE 2010 data set,³⁵ averaged over 100 kb intervals, and annotated each SNP. SNPs were then binned into five different recombination rate fractions, and population genetics statistics (Tajima’s D, Fay and Wu’s H, mean DAF, and W→S DAF skew) were calculated for sets of pooled SNPs for each recombination rate quintile (20% bin).

Estimating the Strength of GC Bias

Relative rates of fixation were used to estimate the strength of GC-biased gene conversion (b). We define r as the relative rate of fixation of biased WS or SW substitutions compared to unbiased WW or SS substitutions. Accelerated evolution yields r > 1 and decelerated evolution yields r < 1. Alleles favored by gBGC are evolutionarily equivalent to semidominant mutations under selection.^1,15 Because of this, the mathematics of natural selection can be repurposed to estimate the strength of GC bias. Here, gBGC coefficients (b) are used instead of selection coefficients. Note that the frequency of G or C alleles among gametes produced by WS or SW heterozygotes is equal to (1+b)/2.¹ The probability of fixation of selected (or biased) substitutions follows from Kimura’s diffusion approximation³⁶ and the probability of fixation of neutral (or unbiased) substitutions is equal to 1/2N, where N is the population size. The ratio of these two expressions yields equations for the relative rate of fixation at biased sites compared to unbiased sites. For small values of b:

$$r_{WS}=\frac{4Nb}{1-e^{-4Nb}}$$ (Equation 1)

$$r_{SW}=\frac{4Nb}{e^{4Nb}-1}$$ (Equation 2)

Empirical estimates of r can be calculated from the number of substitutions per site (D) and mutation rates (μ). Ancestral states were inferred at a total of 2.58 × 10⁹ autosomal sites. The ancestral allele was A or T at 1.52 × 10⁹ sites and G or C at 1.06 × 10⁹ sites. We observed a total of 6.85 × 10⁶ WS substitutions, 7.65 × 10⁶ SW substitutions, and 2.68 × 10⁶ WW or SS substitutions. Mutation rates were obtained from the Kong et al.³⁵ (μ_WS = 6.89 × 10⁻⁹, μ_SW = 1.48 × 10⁻⁸, and μ_WWorSS = 1.91 × 10⁻⁹). For WS and SW sites:

$$r_{WS}=\frac{D_{WS}/{\mu }_{WS}}{D_{WWorSS}/{\mu }_{WWorSS}}$$ (Equation 3)

$$r_{SW}=\frac{D_{SW}/{\mu }_{SW}}{D_{WWorSS}/{\mu }_{WWorSS}}$$ (Equation 4)

By combining Equations 1, 2, 3, and 4, we were able to numerically estimate the population-scaled strength of gBGC (Nb) from accelerated evolutionary rates at WS sites and decelerated evolutionary rates at SW sites. These estimates were made for the full set of autosomal sites and for each recombination rate quintile.

$$\frac{4Nb}{1-e^{-4Nb}}=\frac{D_{WS}/{\mu }_{WS}}{D_{WWorSS}/{\mu }_{WWorSS}}$$ (Equation 5)

$$\frac{4Nb}{e^{4Nb}-1}=\frac{D_{SW}/{\mu }_{SW}}{D_{WWorSS}/{\mu }_{WWorSS}}$$ (Equation 6)

Estimating Disease Burden from Site Frequency Spectra

We used SFS shifts to determine the extent that gBGC influences the burden of hereditary disease. Predicted disease burden (β) is influenced by penetrance (π), derived allele frequency (p), the probability that disease alleles are derived alleles (d), the inbreeding coefficient (F), and the dominance coefficient (h). For a set of j SNPs, the mean disease burden can be found by averaging across allele frequencies and weighting by the probability that pathogenic alleles are derived as opposed to ancestral (see Appendix A for additional equations).

$$\overline{\beta }=\sum _{i=1}^j{\pi }_i\left[\left(d_i{p}_i^2+\left(1-d_i\right){\left(1-p_i\right)}^2+p_i\left(1-p_i\right)F\right)+\left(2p_i\left(1-p_i\right)\left(1-F\right)\right)h_i\right]/j$$ (Equation 7)

Because small sample sizes bias SFS toward intermediate frequency alleles,³⁷ we corrected the empirical SFS from whole-genome sequencing using trueFS.³⁸ Sites included in this analysis were required to be polymorphic in at least one population.

To determine whether β statistics are reasonable proxies of actual disease risk, we examined whether the effects of inbreeding on Equation 7 are comparable to increases in hereditary disease risk from clinical data. For each population, we used the corrected SFS of all non-CpG SNPs and assumed that disease alleles were derived and recessive. By setting F = 0 we inferred the predicted disease burden under random mating. We then simulated the effects of first-cousin mating by setting F = 0.0625. The ratio of β_first-cousin / β_random was then calculated for each population. These values were then compared to clinical estimates of increased risks of hereditary disease due to inbreeding obtained from a global panel of 69 populations.³⁹

Using corrected SFS and Equation 7, the predicted disease burden was obtained for unbiased WW or SS SNPs, SW SNPs, WS SNPs, and all non-CpG SNPs. We then compared the relative disease burden of each type of SNP (Equations A15, A16, and A17) and used Student’s t tests to determine statistical significance. We also assessed whether the effects of gBGC are stronger for recessive alleles, for alleles with intermediate dominance, or for dominant alleles (Equations A10, A11, and A12), and how the proportion of disease alleles that are derived or ancestral influences disease burden (Equation A13). The relative disease burden of different populations was compared using Equations A18, A19, A20, and A21.

Because the SFS of disease alleles can be affected by natural selection, we used theoretical population genetics to examine genetic systems where there is a balance between mutation, selection, and gene conversion. Here, wild-type alleles can mutate to disease alleles. These recessive disease alleles are favored by gBGC when heterozygous and selected against when homozygous. Equilibrium allele frequency ($\hat{p}$) is affected by the strength of biased gene conversion (b), the strength of selection against recessive alleles (s), and the per generation rate of mutation (μ). Using Equation 4d from Glémin:⁴⁰

$$\hat{p}=\frac{b+\sqrt{b^2+4\mu \left(b+s\right)}}{2\left(b+s\right)}$$ (Equation 8)

Values of μ were obtained from the from the Kong et al., 2012 deCODE data set,³⁵ and values of b were estimated from relative rates of fixation of biased and unbiased sites.

Results

Genetic Distances and Rates of Evolution Are Modified by gBGC

GC-biased gene conversion results in slower rates of evolution for sites where ancestral alleles are favored (SW SNPs) and faster rates of evolution for sites where derived alleles are favored (WS SNPs). We calculated genetic distances for all ten population pairs using F_ST statistics, finding that WS SNPs result in mean values of F_ST that are 0.1% to 0.8% greater than WW or SS SNPs and 0.9% to 1.7% greater than SW SNPs. Bootstrapping 10,000 SNPs of each type from each population 1,000 times reveals that although the genome-wide effect of gBGC on F_ST is small, differences between types of SNPs are highly significant (p value < 10⁻¹⁵ for all comparisons using Mann-Whitney U tests).

Population branch statistics (PBS) indicate that GC-biased gene conversion modifies evolutionary rates across all branches of a human evolutionary tree (Figure 1). When comparisons are made between different types of SNPs, we find the same rank order for each internal and external branch: SW SNPs have the smallest PBS, WW or SS SNPs have intermediate PBS, and WS SNPs have the largest PBS (p value < 10⁻¹⁵ for all comparisons using Mann-Whitney U tests). PBS differences between different types of SNP are modest for each branch (WS SNPs have PBS statistics that are 1.9% to 3.1% greater than WW or SS SNPs and 4.5% to 6.6% greater than SW SNPs). However, values shown in Figure 1C are genome-wide estimates, and they include SNPs in recombination hotspots and coldspots. Furthermore, we find that PBS outliers (defined as the top 1% sites) are enriched for WS SNPs (p value < 0.0001 for all branches, two proportion Z-test). Comparing PBS statistics for different branches of the tree in Figure 1, we find that the largest branch lengths are for CEU and Hadza populations and WS SNPs. Note that PBS statistics reflect both divergence times and the amount of genetic drift that occurs along each branch of an evolution tree.

gBGC Leads to Shifts in the SFS

The site frequency spectrum is left-shifted when ancestral alleles are favored by GC-biased gene conversion and right-shifted when derived alleles are favored by GC-biased gene conversion. This pattern occurs for all five global populations (Figure 2). Note that SW SNPs (blue) are enriched for low-frequency (DAF = 0.1) alleles and WS SNPs (red) are enriched for high-frequency (DAF > 0.5) alleles. When these allele frequency shifts are quantified by population genetics statistics, we find that SNPs favored by gBGC tend to result in an excess of intermediate-frequency derived alleles. Tajima’s D, which is positive when there is an excess of intermediate-frequency alleles, is significantly higher for WS SNPs than SW and unbiased WW or SS SNPs (Table 1, p value < 10⁻¹⁵ for all populations using Mann-Whitney U tests). Similarly, Fay and Wu’s H, which is negative when there is a lack of rare alleles, is significantly lower for WS than SW and unbiased WW or SS SNPs (p value < 10⁻¹⁵ for all populations using Mann-Whitney U tests). The mean frequency of derived alleles also differs for different types of SNPs (p value < 10⁻¹⁵ for all populations using Mann-Whitney U tests), with SW SNPs having the lowest derived allele frequencies and WS SNPs having the highest derived allele frequencies. We also note that Hadza and CEU populations have significantly higher values of Tajima’s D and lower values of Fay and Wu’s H than Pygmy, YRI, and Sandawe populations (Table 1 and Figure 3, p value < 10⁻¹⁵ for all comparisons using Mann-Whitney U tests). This pattern is consistent with population growth for each of the latter three populations.

Figure 2.

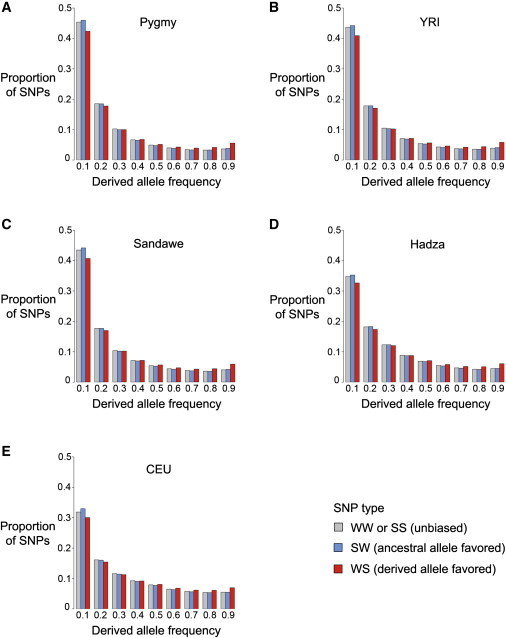
GC-Biased Gene Conversion Modifies the Site Frequency Spectra of Diverse Human Populations

Pygmy (A), YRI (B), and Sandawe (C) populations have an excess of low-frequency derived alleles relative to Hadza (D) and CEU (E) populations. Probability distributions sum to one for each type of SNP: WW or SS (gray), WS (blue), and WS (red). Site frequency spectra of SW SNPs are left-shifted and site frequency spectra of WS SNPs are right-shifted.

Table 1.

Biased Gene Conversion Modifies Summary Statistics of the Site Frequency Spectrum

Population	Type of SNP	Tajima’s D (95% CI)	Fay and Wu’s H (95% CI)	Mean DAF (95% CI)
Pygmy	WW or SS	−0.430 (−0.479 to −0.383)	0.264 (0.192 to 0.332)	0.271 (0.265 to 0.277)
	SW	−0.465 (−0.515 to −0.415)	0.248 (0.186 to 0.317)	0.270 (0.264 to 0.276)
	WS	−0.385 (−0.438 to −0.334)	−0.048 (−0.125 to −0.031)	0.297 (0.291 to 0.304)
YRI	WW or SS	−0.357 (−0.411 to −0.300)	0.182 (0.106 to 0.255)	0.282 (0.275 to 0.288)
	SW	−0.389 (−0.444 to −0.333)	0.172 (0.099 to 0.243)	0.281 (0.274 to 0.287)
	WS	−0.319 (−0.374 to −0.268)	−0.123 (−0.206 to −0.041)	0.307 (0.300 to 0.315)
Sandawe	WW or SS	−0.349 (−0.401 to −0.294)	0.159 (0.080 to 0.231)	0.284 (0.278 to 0.291)
	SW	−0.386 (−0.441 to −0.333)	0.152 (0.075 to 0.225)	0.282 (0.276 to 0.289)
	WS	−0.311 (−0.365 to −0.257)	−0.139 (−0.227 to −0.050)	0.309 (0.302 to 0.316)
Hadza	WW or SS	−0.011 (−0.072 to 0.046)	−0.013 (−0.109 to 0.075)	0.319 (0.311 to 0.326)
	SW	−0.036 (−0.094 to 0.022)	−0.003 (−0.087 to 0.081)	0.316 (0.309 to 0.323)
	WS	0.015 (−0.050 to 0.073)	−0.280 (−0.378 to −0.188)	0.340 (0.332 to 0.348)
CEU	WW or SS	0.102 (0.038 to 0.168)	−0.310 (−0.415 to −0.208)	0.348 (0.340 to 0.357)
	SW	0.057 (−0.011 to 0.123)	−0.291 (−0.393 to −0.191)	0.344 (0.336 to 0.352)
	WS	0.120 (0.051 to 0.189)	−0.550 (−0.657 to −0.445)	0.367 (0.358 to 0.376)

SNPs analyzed here are autosomal and non-CpG (a total of 7.54 million fully called SNPs). Values of Fay and Wu’s H were normalized as per Zeng et al.³⁴ 95% confidence intervals of each statistic were found by bootstrapping 10,000 random SNPs a total of 1,000 times.

Figure 3.

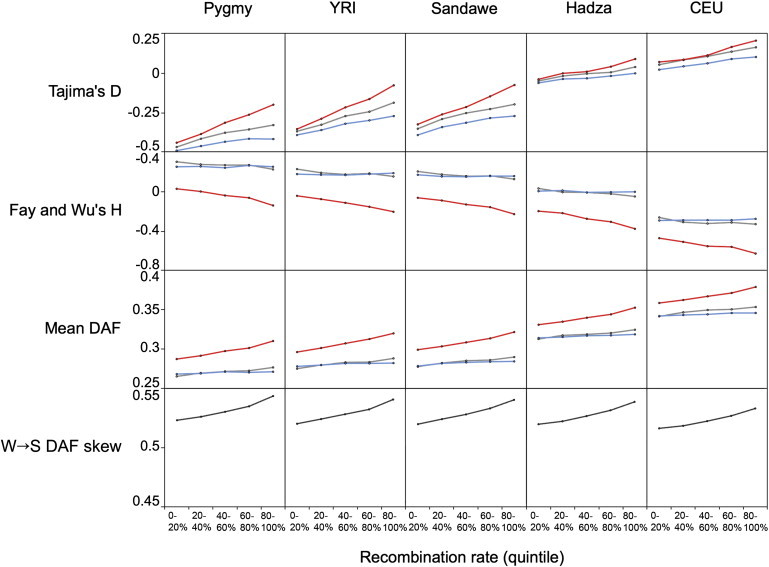
The Effects of Biased Gene Conversion Are Stronger in High-Recombination Regions of the Genome

SNPs were divided into quintile (20%) bins based on recombination rates from the 2010 deCODE data set. Four population genetic statistics were calculated for each population and recombination bin: Tajima’s D, Fay and Wu’s H, mean derived allele frequency (DAF), and a measure of W→S DAF skew. For the first three of these statistics, values were calculated separately for WW or SS (gray), SW (blue), and WS (red) SNPs.

Effects of gBGC Are Stronger in Regions of High Recombination

Allele frequency shifts for WS SNPs are magnified in high-recombination regions of the genome, a pattern that is consistent with GC-biased gene conversion (Figure 3). The effects of recombination and gBGC on the SFS were quantified using multiple summary statistics: Tajima’s D, Fay and Wu’s H, mean DAF, and W→S DAF skew. We find that values of Tajima’s D are higher for high-recombination regions of the genome for all three types of SNPs (p value < 10⁻¹⁵ for Mann-Whitney U tests comparing bottom and top quintile data for all types of SNPs). This effect arises because Tajima’s D is defined as the ratio of two random variables that are functions of the number of segregating sites in a sample.⁴¹ Values of Fay and Wu’s H are strikingly different for WS SNPs, and we find that values of H are lower in high-recombination regions of the genome (p value < 10⁻¹⁵ for Mann-Whitney U tests comparing bottom and top quintile data for WS SNPs). Fay and Wu’s H indicate that derived alleles are more likely to be found at intermediate and high frequencies for WS SNPs in high-recombination regions of the genome. On a related note, WS SNPs in high-recombination regions of the genome have a higher mean DAF than WS SNPs in low-recombination regions (p value < 10⁻¹⁵ for Mann-Whitney U tests comparing bottom and top quintile data for WS SNPs). Finally, relative amounts of allele frequency skew for different types of SNPs were quantified using a W→S DAF skew statistic. This statistic compares the derived allele frequencies of WS and SW SNPs and is higher than 0.5 when G or C alleles are found at higher frequencies than A or T alleles.¹⁶ We found similar patterns for each population: WS SNPs have a SFS that is skewed more toward high-frequency derived alleles than the SFS of SW SNPs, and this effect is greater in regions of high recombination (Figure 3). Although the deCODE recombination map uses data from Icelandic individuals, recombination rates had similar effects on European and African samples. This pattern probably arises because we used recombination rates averaged over 100 kb intervals and large-scale recombination rates are known to be similar for different populations.⁴²

Recombination rates also influence genetic distances and rates of fixation. In the top recombination quintile, PBS statistics for WS SNPs are 4.6% greater than WW or SS SNPs and 9.7% greater than SW SNPs. By contrast, in the lowest recombination quintile, PBS statistics for WS SNPs are 0.6% greater than WW or SS SNPs and 2.4% greater than SW SNPs. Similarly, the strength of gBGC (as inferred by relative rates of fixation) is greater in high-recombination regions of the genome (Figure 4B).

Figure 4.

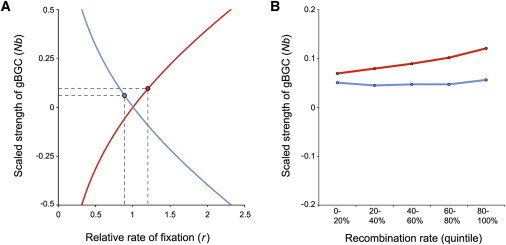
Estimated Strength of Biased Gene Conversion

After correcting for mutation rate differences, relative rates of fixation were used to estimate the population-scaled strength of gBGC.

(A) Curves describe the mathematical relationship between Nb and r for WS sites (red, Equation 5) and SW sites (blue, Equation 6). Circles denote genome-wide estimates of Nb from empirical data (0.0934 for WS sites and 0.0523 for SW sites).

(B) Effects of different recombination rate quintiles on the population-scaled strength of gBGC.

Strength of gBGC

Using relative rates of fixation, we inferred that the strength of GC-biased gene conversion is akin to weak selection. Per base pair rates of substitution are greater for WS (4.50 × 10⁻³) and SW (7.25 × 10⁻³) sites compared to WW or SS sites (1.04 × 10⁻³). However, mutation rates for WS sites are 3.61 times that of WW or SS sites and mutation rates for SW sites are 7.75 times that of WW or SS sites.³⁶ After correcting for mutation rate differences, r_WS = 1.198 and r_SW = 0.899. This indicates that evolutionary rates are accelerated at WS sites where derived alleles are favored by gene conversion and decelerated at SW sites where ancestral alleles are favored by gene conversion. Using population genetics theory, we inferred the mathematical relationship between rates of fixation and the population-scaled strength of gBGC (Equations 5 and 6), and the mapping of r to Nb is shown in Figure 4A. Nb was estimated to be 0.0934 for WS sites and 0.0523 for SW sites. These scaled gBGC coefficients are comparable to weak, nearly neutral selection (|Ns| < 1). Assuming N = 10,000, values of b range from 5.23 × 10⁻⁶ to 9.34 × 10⁻⁶.

Predicted Disease Burden

β statistics calculated from SFS data (Equation 7) can be used as a proxy of hereditary disease risk. To test the validity of Equation 7, we estimated how inbreeding would increase the probability of observing a homozygote and compared this to known values of increased disease burden from the clinical literature. Using the corrected SFS for all non-CpG SNPs and comparing the relative homozygosity that would arise from first-cousin mating as opposed to random mating, we find that the predicted increase in homozygosity due to first-cousin mating ranges between 2.3% (CEU) and 3.8% (YRI). These values are comparable to clinical estimates of 3.5% excess mortality in the progeny of first cousins.³⁹ This suggests that it is reasonable to use corrected SFS and Equation 7 to infer how gBGC affects disease burden.

Allele frequency changes due to gBGC have a secondary effect of increasing the risk of hereditary disease. Because most deleterious mutations are recessive^43–46 and derived alleles are more likely to be pathogenic than ancestral alleles^47–49 (but see Di Rienzo and Hudson⁵⁰), we focus on the disease burden of recessive derived alleles. Subsequently, this restriction is relaxed. After correcting for ascertainment bias due to small sample sizes, we weighted SNPs by the probability of observing a homozygote to obtain the mean recessive disease burden for unbiased and biased SNPs. The probability of observing derived homozygotes is similar for biased SW SNPs and unbiased WW or SS SNPs where the ancestral is favored by gene conversion (${\overline{\beta }}_{SW}/{\overline{\beta }}_{WW\text{or}SS}\approx 1$, p value > 0.3 using a two-tailed Student’s t test). These similarities may arise because higher mutation rates for SW SNPs may balance out the effects of gBGC, or because small sample sizes limit our ability to distinguish between allele frequency shifts at the rare end of the SFS. However, SNPs where the derived allele is favored by gene conversion exhibited a strikingly different pattern (Figure 5). In all five populations, WS SNPs have a significantly higher probability of being homozygous than WW or SS SNPs (${\overline{\beta }}_{WS}/{\overline{\beta }}_{WW\text{or}SS}>>1$, p value < 1 × 10⁻⁶ using a one-tailed Student’s t test). This increased homozygosity translates to a 42.2% (Hadza) to 62.8% (Pygmy) increase in the predicted risk of recessive diseases. Because only a subset of all SNPs are WS SNPs, we also quantified the overall effect of gBGC on recessive disease burden by calculating the relative homozygosity of all non-CpG SNPs compared to unbiased SNPs (i.e., ${\overline{\beta }}_{\text{All non CpG}}/{\overline{\beta }}_{WW\text{or}SS}$). Within each population, the overall predicted increase in disease burden due to gBGC ranges from 17.9% to 27.8% (Figure 5A). The probability of observing homozygous derived alleles also varies by population. Comparing different populations, we find that the predicted disease burden of recessive alleles is lowest for YRI genomes and highest for Hadza and CEU genomes (Figure 5B). This pattern is consistent with the ancestors of modern-day Hadza and Europeans having a lower effective population size due to population bottlenecks, reducing the efficacy of natural selection to eliminate deleterious mutations in each of these populations.

Figure 5.

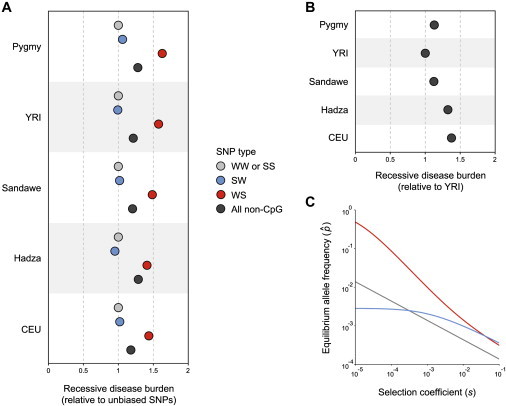
Predicted Disease Burden of Recessive Alleles and Mutation-Selection-Conversion Balance

(A) After correcting for small sample sizes using trueFS, the disease burden of recessive alleles was estimated from the corrected site frequency spectrum and the probability of observing homozygous individuals. Values for each population are normalized relative to unbiased WW or SS SNPs. The overall effect of gBGC (dark gray) was found by weighting the probability of observing WW or SS, SW, or WS SNPs.

(B) Relative disease burden of recessive alleles compared across different populations. Values shown are for all non-CpG SNPs and are normalized relative to YRI.

(C) The joint effects of mutation, selection, and GC-biased gene conversion on equilibrium allele frequencies. Equation 8 was used to generate equilibrium allele frequencies ($\hat{p}$) for deleterious recessive alleles at WS (red), SW (blue), and WW or SS SNPs (gray). Parameter values used: b_WS = 9.34 × 10⁻⁶, b_SW = −5.23 × 10⁻⁶ (negative because gBGC favors S alleles), b_WWorSS = 0, μ_WS = 6.89 × 10⁻⁹, μ_SW = 1.48 × 10⁻⁸, and μ_WWorSS = 1.91 × 10⁻⁹.

We relax the assumption that disease alleles are recessive and derived and find that predicted disease burden is still increased by gBGC, albeit to a lesser extent. The effects of gBGC on disease burden are strongest for recessive disease alleles and weakest for dominant alleles (Table 2). This occurs because the SFS is weighted toward rare alleles and small increases in the frequency of derived alleles lead to relatively large homozygosity increases. We also find that the effects of gBGC are stronger if 100% of disease alleles are derived as opposed to 90% derived and 10% ancestral (Table 2). It is likely that the effects of gBGC in different populations are modulated by demographic phenomena like population bottlenecks, admixture, and the explosive growth of modern human populations.⁵¹

Table 2.

Relative Disease Burden of Biased WS SNPs Compared to Unbiased WW or SS SNPs

Scenario	Pygmy	YRI	Sandawe	Hadza	CEU
Recessive alleles (π = 1, h = 0, d = 1, F = 0)	1.628	1.576	1.485	1.422	1.436
Alleles with intermediate dominance (π = 1, h = 0.5, d = 1, F = 0)	1.390	1.357	1.307	1.268	1.315
Dominant alleles (π = 1, h = 1, d = 1, F = 0)	1.294	1.268	1.229	1.198	1.251
Recessive alleles, 90% derived, 10% ancestral (π = 1, h = 0, d = 0.9, F = 0)	1.206	1.180	1.166	1.157	1.170

Corrected SFS and Equations A10, A11, A12, A13, A14, and A15 were used to obtain the relative disease burden (${\overline{\beta }}_{WS}/{\overline{\beta }}_{WW\text{or}SS}$) for each scenario. Parameters: π (penetrance), h (dominance coefficient), d (proportion of disease alleles that are derived), and F (inbreeding coefficient).

Because selection against deleterious alleles can also modify the SFS and affect the risk of hereditary disease, we calculated the effects of gBGC for genetic systems that include mutation, selection, and gene conversion. Here, recessive disease alleles are removed by natural selection when homozygous and favored by gBGC when heterozygous, leading to a form of balancing selection. Using gBGC coefficients from Figure 4A and mutation rates from the 2012 deCODE data set,³⁵ we calculated equilibrium allele frequencies for a theoretical model of mutation-selection-conversion balance. Figure 5 shows equilibrium allele frequencies for biased WS SNPs (red), biased SW SNPs (blue). and unbiased WW or SS SNPs (gray). Due to elevated mutation rates, equilibrium allele frequencies for WS and SW SNPs are higher than unbiased WW or SS SNPs (Figure 5C). When selection is weak, equilibrium allele frequencies are driven by a balance between gBGC and mutation, and when selection is strong, equilibrium allele frequencies are driven by a balance between selection and mutation. Because otherwise deleterious alleles can be pushed to intermediate frequencies by biased gene conversion, recessive disease alleles are more likely to be homozygous at WS SNPs. This increased hereditary disease burden is magnified when selection is weak.

Discussion

The Population Genetic Effects of gBGC in Humans

Using high-coverage whole-genome sequencing data from multiple populations, we have demonstrated that GC-biased gene conversion modifies evolutionary distances and confirmed that allele frequency shifts are greater in high-recombination regions of the human genome. High-coverage sequence data minimizes the confounding effects of genotyping error, and by studying multiple populations we were able to show that the population genetics effects of gBGC are robust to demographic history. Statistical differences between different types of SNPs in a single population are comparable to statistical differences for the same type of SNP in different populations (Table 1). Because allele frequency distributions and population genetics statistics differ for variants that are favored or unfavored by gBGC, demographic inference is likely to be inaccurate if biased SNPs are analyzed. For example, computational tools like δaδi⁵² rely on accurate SFS to infer demographic history. Modified values of F_ST can also lead to misestimates of population split times. Inclusion of WS SNPs results in lower values of Fay and Wu’s H, and this can be misinterpreted as evidence of a recent population bottleneck (Table 1 and Figure 3). We also find that gBGC behaves like natural selection: the SFS of SW SNPs is left-shifted, a pattern that mimics negative selection, and the SFS of WS SNPs is right-shifted, a pattern that mimics positive selection (Figure 2). Because of this, studies that ignore gBGC may overestimate the effects of selection. Similarly, phylogenetic data from multiple primates indicate that gBGC results in elevated d_N/d_S ratios, a pattern that can be misinterpreted as selection.⁴ gBGC decreases the allele frequencies of derived A or T alleles and increases the allele frequencies of derived G or C alleles. Furthermore, because A/T and G/C alleles differ in their chance of being passed to the next generation, the effects of gBGC are similar to meiotic drive. Classical population genetics theory does not focus on the molecular nature of alleles (i.e., whether variants involve adenine, thymine, guanine, or cytosine). Instead, it traditionally describes populations in terms of allele frequencies.^53,54 Our findings underscore the need for theoretical population genetics to include molecular phenomena such as biased gene conversion.

gBGC Is a Weak, but Important, Evolutionary Force

Comparisons between the relative rates of fixation of biased and unbiased sites reveal that the population-scaled strength of gBGC is on the order of Nb ≈ 0.0523 to 0.0934 (Figure 4A). This indicates that gene conversion is a relatively weak force on a genomic scale—comparable to a nearly neutral allele under weak selection. Assuming an effective population size of 10,000 individuals, gBGC coefficients range between 5.23 × 10⁻⁶ and 9.34 × 10⁻⁶. This means that WS or SW heterozygotes have a 50.000364% chance of passing on a G or C allele to their offspring, and gBGC results in non-Mendelian inheritance. As a point of comparison, gBGC coefficients are approximately 600 times greater than the genome-wide mutation rate parameter.³⁵ Even a modest amount of bias can have a noticeable effect on the genetics of populations because the effects of gBGC are compounded over evolutionary time. For example, we find that F_ST and PBS statistics are greater for SNPs favored by gBGC. We also note that Nb is greater in high-recombination regions of the genome (Figure 4B) and that the strength of gene conversion is known to be greater in recombination hotspots.⁴⁰

This present study marks the first time that the evolutionary strength of gBGC in humans has been quantified using high-coverage whole-genome sequencing data. Our estimates of Nb for the top recombination quintile (0.056 for SW sites and 0.121 for WS sites) are roughly comparable to prior estimates that use data from chromosome 20 (0.325).^9,17 Aside from methodological differences, we note that estimates from prior studies are complicated by the use of SFS data from admixed African American samples. Our genome-wide estimates of Nb were also smaller than a previous study that focused on GC-rich coding regions²¹ and a pair of studies that used phylogenetic methods to estimate the strength of gBGC.^55,56 Minor differences in the estimated strength of gBGC at WS and SW sites in Figure 4 may be due to ancestral state misidentification. Consider the situation where cytosine in a hypermutable CpG dinucleotide mutates to thymine and reaches fixation in chimpanzee and orangutan lineages, causing an ancestral C to be misinferred as T. If this site remains unchanged in the human lineage, it will incorrectly appear to be a WS substitution, and if this site also fixes in the human lineage it will incorrectly appear to be unchanged as opposed to a SW substitution. Taken together, these two scenarios suggest that the ancestral state misidentification may cause the strength of gBGC to be overestimated at WS sites and underestimated at SW sites. We also note that the effects of recombination rate on Nb appear to be greater for WS sites than SW sites. This pattern can arise if mutation rates for different types of sites are not independent of recombination rates. We anticipate that estimates of Nb in future studies will benefit from higher-resolution recombination maps (including maps of actual gene conversion events⁵⁷) and more accurate mutation rates.

GC-biased gene conversion can be an important mechanism for loss of genetic variation and divergence of isolated populations, and it is known that small biases in gene conversion can dramatically affect fixation probabilities and segregation times.¹⁵ Indeed, human accelerated regions of the genome are enriched for the signatures of biased gene conversion.¹⁸ In contrast to selection, gBGC is sequence dependent and it can act genome-wide, while only a small fraction of base pairs are likely to actually be under selection. One key difference between gBGC and selection is that gene conversion tracts are on the order of a few hundred base pairs,² while genetic hitchhiking can influence linked variation up to 1 Mb away if selection is strong (s > 0.01).⁵⁸

The Curse of the Converted

What sort of processes can cause disease alleles to be common? Our results indicate that biased gene conversion should be added to the list more familiar causes (population bottlenecks, evolutionary tradeoffs, and recessivity). We find that hereditary disease burden can be reasonably captured by the SFS and Equation 7. Allele frequency shifts due to gBGC result in a curse of the converted, whereby WS SNPs are more likely to result in genetic diseases. The increase in predicted disease burden can be substantial (+42.2% to 62.8% for recessive derived alleles). To our knowledge, this marks the first time that relative increases in hereditary disease risks due to gBGC have been quantified for human populations. The increased disease risk due to allelic gene conversion found here parallels the increased disease risk that arises from interlocus gene conversion between paralogs.⁵⁹ Similarly, gBGC tracts identified using a phylogenetic hidden Markov model (HMM) appear to be enriched for disease-associated polymorphisms.⁶⁰

The curse of the converted is stronger for recessive disease alleles. We find that biased WS SNPs are more likely to be homozygous than biased SW or unbiased WW or SS SNPs, and this leads to an increased recessive disease burden (Figure 5). Increases in allele frequency at WS SNPS will have a disproportionate effect compared to decreases in allele frequency at SW SNPs because the probability of observing a recessive homozygote is a function of the square of allele frequency. The overall effect of gBGC is to increase the homozygosity of derived alleles (and consequently increase the disease burden of recessive alleles). This is shown in Figure 5, as the set of all non-CpG SNPs has an increased recessive disease burden compared to unbiased WW or SS SNPs. The effects of gBGC on hereditary disease risk also apply to scenarios where disease alleles are not recessive, albeit to a lesser degree (Table 2). Intermediate dominance (h = 0.5) yields increases in risk that are two-thirds that of recessive alleles, and complete dominance yields increases in risk that are half that of recessive alleles. Similarly, the effects of gBGC on hereditary disease risk are reduced if a fraction of disease-causing alleles are ancestral.

The predicted disease burden also varies for different global populations. Specifically, genomes from bottlenecked Hadza and CEU populations are more likely to be homozygous for derived alleles than genomes from Pygmy, YRI, and Sandawe populations (Figure 5). This result is consistent with a previous study that used high-coverage whole-genome sequences to find that non-African genomes contain more damaging homozygous alleles than African genomes.⁴⁹ Similarly, a smaller proportion of genetic variation found in African and African American genomes involves deleterious nonsynonymous mutations.^23,61 By contrast, data from the 1000 Genomes Project suggest that non-African individuals do not have an excess of loss-of-function mutations.⁶²

A general pattern is that the effects of gBGC are dampened by selection against disease alleles. Genetic systems where selection against recessive alleles is balanced by gene conversion and mutation have equilibrium allele frequencies that are substantially different than genetic systems with just selection and mutation (Figure 5C). The effects of gBGC on hereditary disease risk are robust to weak selection. These effects are greater for recessive alleles that are nearly neutral, and if selection is sufficiently weak, gBGC can result in the fixation of deleterious G or C alleles.¹⁵ However, if selection is sufficiently strong (s > 0.01), the effects of gBGC on disease burden are likely to be minimal.

In conclusion, GC-biased gene conversion shapes patterns of diversity in human genomes, and it contributes to substantially increased risks of hereditary disease. These effects are stronger in high-recombination regions of the genomes and are observed in multiple populations. Genetic data obtained from high-coverage whole-genome sequencing suggest that realistic models of evolution should incorporate the details of molecular genetic phenomena like gene conversion.

Appendix A

Population Branch Statistics

Equations for population branch statistics (PBS) were obtained using pairwise genetic distances between populations (as quantified by F_ST) and the topology in Figure 1.

$$PB{S}_{Pygmy}=\frac{F_{ST\left(Pygmy,YRI\right)}+F_{ST\left(Pygmy,CEU\right)}-F_{ST\left(YRI,CEU\right)}}{2}$$ (Equation A1)

$$PB{S}_{YRI}=\frac{F_{ST\left(Pygmy,YRI\right)}+F_{ST\left(YRI,CEU\right)}-F_{ST\left(Pygmy,CEU\right)}}{2}$$ (Equation A2)

$$PB{S}_{\left(\left(YRI,Pygmy\right),\left(CEU,\left(Hadza,Sandawe\right)\right)\right)}=\frac{2F_{ST\left(Pygmy,CEU\right)}+F_{ST\left(YRI,Hadza\right)}+F_{ST\left(YRI,Sandawe\right)}}{4}-\frac{2F_{\left(Pygmy,YRI\right)}+F_{ST\left(CEU,Hadza\right)}+F_{ST\left(CEU,Sandawe\right)}}{4}$$ (Equation A3)

$$PB{S}_{CEU}=\frac{2F_{ST\left(YRI,CEU\right)}+F_{ST\left(CEU,Hadza\right)}+F_{ST\left(CEU,Sandawe\right)}}{4}-\frac{F_{ST\left(YRI,Hadza\right)}+F_{ST\left(YRI,Sandawe\right)}}{4}$$ (Equation A4)

$$PB{S}_{\left(\left(\left(YRI,Pygmy\right),CEU\right),\left(Hadza,Sandawe\right)\right)}=\frac{2F_{ST\left(CEU,Sandawe\right)}+F_{ST\left(Pygmy,Hadza\right)}+F_{ST\left(YRI,Hadza\right)}}{4}-\frac{2F_{\left(Sandawe,Hadza\right)}+F_{ST\left(Pygmy,CEU\right)}+F_{ST\left(YRI,CEU\right)}}{4}$$ (Equation A5)

$$PB{S}_{Hadza}=\frac{F_{ST\left(CEU,Hadza\right)}+F_{ST\left(Hadza,Sandawe\right)}-F_{ST\left(CEU,Sandawe\right)}}{2}$$ (Equation A6)

$$PB{S}_{Sandawe}=\frac{F_{ST\left(CEU,Sandawe\right)}+F_{ST\left(Hadza,Sandawe\right)}-F_{ST\left(CEU,Hadza\right)}}{2}$$ (Equation A7)

Disease Burden of Ancestral and Derived SNPs

Disease burden (β) is influenced by penetrance (π), derived allele frequency (p), the probability that disease alleles are derived alleles (d), the inbreeding coefficient (F), and the dominance coefficient (h). When ancestral alleles are pathogenic:

$${\beta }_{d=0}=\pi \left[\left({\left(1-p\right)}^2+p\left(1-p\right)F\right)+\left(2p\left(1-p\right)\left(1-F\right)\right)h\right].$$ (Equation A8)

When derived alleles are pathogenic:

$${\beta }_{d=1}=\pi \left[\left(p^2+p\left(1-p\right)F\right)+\left(2p\left(1-p\right)\left(1-F\right)\right)h\right].$$ (Equation A9)

Mean Disease Burden in Special Cases

Simplified equations for the mean disease burden per SNP can be found by considering special cases of Equation 7. Unless otherwise specified, these equations assume penetrance to be complete, derived alleles to be pathogenic, and populations to be outbred. Mean disease burden per SNP when disease alleles are recessive:

$${\overline{\beta }}_{h=0,d=1,F=0}=\sum _{i=1}^j\left[p_i^2\right]/j.$$ (Equation A10)

Mean disease burden per SNP when disease alleles have intermediate dominance:

$${\overline{\beta }}_{h=0.5,d=1,F=0}=\sum _{i=1}^j\left[p_i\right]/j.$$ (Equation A11)

Mean disease burden per SNP when disease alleles are dominant:

$${\overline{\beta }}_{h=1,d=1,F=0}=\sum _{i=1}^j\left[p_i\left(2-p_i\right)\right]/j.$$ (Equation A12)

Mean disease burden per SNP when disease alleles are recessive (90% of pathogenic alleles derived and 10% of pathogenic alleles ancestral):

$${\overline{\beta }}_{h=0,d=0.9,F=0}=\sum _{i=1}^j\left[0.9p_i^2+0.1{\left(1-p_i\right)}^2\right]/j.$$ (Equation A13)

Mean disease burden per SNP when disease alleles are recessive and there is first-cousin mating:

$${\overline{\beta }}_{h=0,d=1,F=0.0625}=\sum _{i=1}^j\left[p_i^2+0.0625p_i\left(1-p_i\right)\right]/j.$$ (Equation A14)

Relative Disease Burden

The relative disease burden of different types of SNPs can be obtained by dividing the mean disease burden of a particular type of SNP by the mean disease burden of unbiased WW or SS SNPs.

$$\text{Relative disease burden of}WS\text{SNPs}={\overline{\beta }}_{WS}/{\overline{\beta }}_{WW\text{or}SS}$$ (Equation A15)

$$\text{Relative disease burden of}SW\text{SNPs}={\overline{\beta }}_{SW}/{\overline{\beta }}_{WW\text{or}SS}$$ (Equation A16)

$$\text{Overall effect of gBGC on disease burden}={\overline{\beta }}_{\text{All non-CpG}}/{\overline{\beta }}_{WW\text{or}SS}$$ (Equation A17)

Similarly, the relative disease burden of different populations can be compared:

$$\text{Pygmy disease burden relative to YRI}={\overline{\beta }}_{\text{All non-CpG, Pygmy}}/{\overline{\beta }}_{\text{All non-CpG, YRI}}$$ (Equation A18)

$$\text{Sandawe disease burden relative to YRI}={\overline{\beta }}_{\text{All non-CpG, Sandawe}}/{\overline{\beta }}_{\text{All non-CpG, YRI}}$$ (Equation A19)

$$\text{Hadza disease burden relative to YRI}={\overline{\beta }}_{\text{All non-CpG, Hadza}}/{\overline{\beta }}_{\text{All non-CpG, YRI}}$$ (Equation A20)

$$\text{CEU disease burden relative to YRI}={\overline{\beta }}_{\text{All non-CpG, CEU}}/{\overline{\beta }}_{\text{All non-CpG, YRI}}$$ (Equation A21)