Brain Imaging Analysis

Abstract

The increasing availability of brain imaging technologies has led to intense neuroscientific inquiry into the human brain. Studies often investigate brain function related to emotion, cognition, language, memory, and numerous other externally induced stimuli as well as resting-state brain function. Studies also use brain imaging in an attempt to determine the functional or structural basis for psychiatric or neurological disorders and, with respect to brain function, to further examine the responses of these disorders to treatment. Neuroimaging is a highly interdisciplinary field, and statistics plays a critical role in establishing rigorous methods to extract information and to quantify evidence for formal inferences. Neuroimaging data present numerous challenges for statistical analysis, including the vast amounts of data collected from each individual and the complex temporal and spatial dependence present. We briefly provide background on various types of neuroimaging data and analysis objectives that are commonly targeted in the field. We present a survey of existing methods targeting these objectives and identify particular areas offering opportunities for future statistical contribution.

1 Introduction

Neuroimaging utilizes powerful noninvasive techniques to capture properties of the human brain in vivo. Imaging studies reveal insights about normal brain function and structure, neural processing and neuroanatomic manifestations of psychiatric and neurological disorders, and neural processing alterations associated with treatment response. There are several widely used imaging modalities, including magnetic resonance imaging (MRI), functional MRI, diffusion tensor imaging (DTI), positron emission tomography (PET), electroencephalography (EEG), and magnetoencephalography (MEG), among others. These modalities leverage different physiological characteristics to reflect properties of either brain structure or function. This review will largely focus on the commonly used fMRI, which captures correlates of neural activity, but some of the ideas presented incorporate or extend to other modalities.

1.1 Imaging Modalities

Functional MRI quantifies brain activity by measuring correlates of blood flow and metabolism. A fundamental concept behind fMRI is that neural activity is associated with localized changes in metabolism. As a brain area becomes more active, for example to perform a memory task, there is an associated localized increase in oxygen consumption. To meet this increased demand, there is an increase in oxygen-rich blood flow to the active brain area. There is a relative increase in oxyhemogloblin and decrease in deoxyhemoglobin in activated brain areas, since the increased supply of oxygen outpaces the increased demand.

The most common form of fMRI works by leveraging magnetic susceptibility properties of hemoglobin in capillary red blood cells, which delivers oxygen to neurons. Hemoglobin is diamagnetic when oxygenated and paramagnetic when deoxygenated. The MR scanner produces blood oxygenated level dependent (BOLD) signals that vary according to the degree of oxygenation. Thus, fMRI can be used to produce distributed maps of localized brain activity (see Figure 1(a)). It is important to keep in mind that although we use the phrase brain activity, what we actually measure with BOLD fMRI is several steps removed from the actual neuronal activity. MRI works in a conceptually similar manner except that the MR signal varies according to tissue type, enabling the production of structural (anatomical) images that distinguish gray matter, white matter, and cerebral spinal fluid (see Figure 1(b)).

Figure 1.

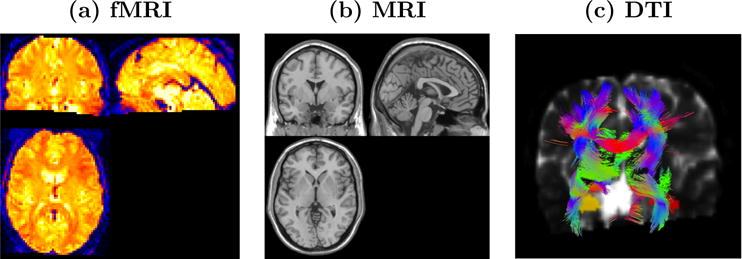
Images of (a) distributed patterns of brain activity based on a BOLD fMRI scan, (b) an anatomical scan revealing gray matter, white matter, and cerebral spinal fluid, and (c) likely white-matter tracts based on a tractography algorithm.

DTI is an MRI technique that provides information regarding the white matter structure in the brain. Neurons are the basic unit of the brain, and humans amazingly have an approximate 86 billion neurons (Suzana Herculano-Houzel, 2012), with longstanding estimates reaching up to 100 billion (Society for Neuroscience, 2008). Axons are neuron fibers that serve as lines of transmission in the nervous system, and they form (millions of) bundles of textured fibers in the white-matter of the brain. This extensive system of white-matter bundles directly links some brain structures, with association bundles joining cortical areas within the same hemisphere, commissural bundles linking cortical areas in separate hemispheres, and projection fibers uniting areas in the cerebral cortex to subcortical structures (Hendelman, 2005). DTI non-invasively maps the diffusion of water molecules, which reveals the presence, integrity, and direction of white-matter fibers since water molecules are more likely to diffuse in the direction of white-matter fibers than perpendicular to these fibers. Further, white-matter fiber tracking techniques portray axonal fibers and structural brain connectivity (see Figure 1(c)) (Behrens et al., 2003 and 2007). There is widespread interest in mapping the structural and functional connectivity of the human brain as evidenced by the National Institutes of Health’s (NIH’s) Human Connectome Project (NIH).

1.2 Common Analysis Objectives

Targeting insights about normal brain function and structure, neural manifestations of mental and neurological disorders, and neural plasticity associated with treatment response, statistical analyses often center on objectives targeting localization, brain connectivity, and prediction/classification. Localization is predicated on the theory of functional specialization – that is, the notion that different areas in the brain are specialized for different functions. From properly designed studies, one can perform statistical analyses to identify localized changes in the brain that correspond to changes in tasks performed in the scanner. These analyses produce images highlighting statistically significant (or highly probable) task-related changes in neural activity as illustrated in Figure 2(a). Localization studies, also referred to here as activation (or neuroactivation) studies, can be extended to identify localized differences in brain function between groups of subjects, for example schizophrenia patients and healthy controls, and differences between scanning sessions, which may reflect treatment-related alterations. For example, Figure 2(a) highlights brain regions exhibiting high probabilities of increased inhibitory control related neural activity from a baseline to a post-treatment period for cocaine addicts relative to corresponding changes in control subjects. The brain regions include the middle frontal gyrus and left and right thalamus.

Figure 2.

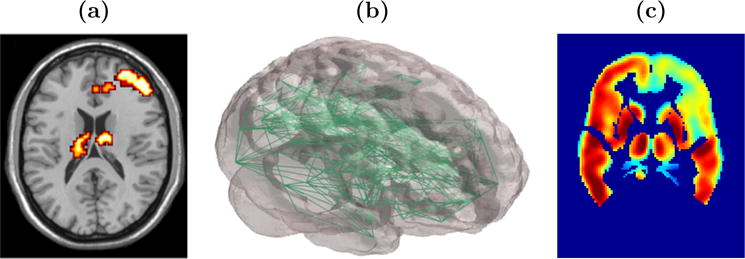
Images displaying results from (a) a localization or neuroactivation study; highlights brain regions exhibiting increased neural activity from baseline to a post-treatment scanning session for cocaine addicts relative to control subjects, (b) a complex network analysis reflecting whole-brain functional connectivity (Simpson et al., 2011), and (c) a model yielding predicted maps of post-baseline neural activity, shown here as predicted regional glucose uptake at 6-months post-baseline for an Alzheimer’s disease patient (Derado et al., 2012).

Functional connectivity studies seek to determine multiple brain areas that exhibit similar temporal activity profiles, either task-related or at resting state. These studies may determine links to selected seed brain regions, dissociate particular brain networks, or generate whole brain complex brain networks (see Figure 2(b)). Functional connectivity properties may be compared between subgroups of subjects and between different scanning sessions. Whereas functional connectivity merely targets associations in brain activity between distinct brain regions, effective connectivity seeks to establish a stronger relationship reflecting the influence that one brain region exerts on another.

Prediction or classification analyses stand to have a significant translational impact. For example, one can use baseline imaging and clinical data to generate maps forecasting metabolic activity in the brain of an Alzheimer’s disease patient at a six month follow up visit (see Figure 2(c)). Another example involves the use of imaging and other clinical or biologic data to blindly classify individuals into one or more groups, for instance as either a treatment responder on non-responder. Such models would have important clinical applications to aid in treatment decisions, predict disease progression, and as a diagnostic tool when costs are not prohibitive.

Numerous statistical tools have been developed to address these common objectives in brain imaging studies. We provide an overview of select approaches. This review is not intended to offer a complete description of existing approaches in the field, but rather it will provide the reader with select methods that are used to address central substantive issues, highlight analytic challenges that statisticians face in applying existing methods and in developing new ones, and discuss important areas for future research that will benefit from statistical thinking. We begin by describing the data collected in fMRI studies and highlighting attributes that are important for statistical modeling.

2 Data Descriptions, Analytic Challenges, and Preprocessing

Functional MRI yields dynamic three-dimensional (3-D) maps giving second to second depictions of distributed brain activity patterns. Studies commonly acquire scans every two to three seconds and may yield hundreds of scans in a single session, but the acquisition speed and duration varies according to study objectives. At the time of statistical analysis, each scan is often arranged in a 91×109×91 array, with each volume element (or voxel) in the array containing a localized measure of neural activity. Figure 2(c) displays a 91×109 array for a selected axial slice across the z-dimension. The temporal evolution of brain activity at a single location (voxel), denoted Y_i(v) (S × 1), forms a time series as illustrated for two distinct locations in Figure 3. Thus, we may regard fMRI data as either a collection of hundreds of thousands of time series arising from spatially distinct sources or alternatively as a movie of dynamic 3-D brain maps. Either of these perspectives reveals the massive amount of data produced in an imaging study with tens of millions of spatio-temporal neural activity measures for each subject and billions of measures across all subjects for many studies. The enormity of the data poses challenges for statistical modeling and computation.

Figure 3.

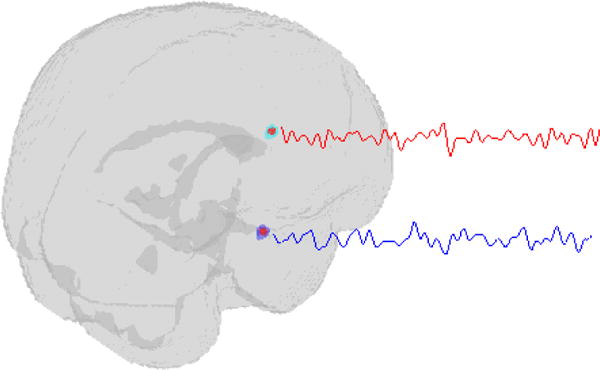
fMRI scans for a single individual may be regarded as tens or hundreds of thousands of time series, two of which are illustrated here, with each time series representing the evolution of measured brain activity at a particular brain location.

Incorporating known biologic information into statistical models is often beneficial, but the mere complexity of the brain presents challenges. One challenge stems from the voluminous and intricate systems of networks in the brain, which render correlations that do not necessarily decay with increasing distance. Figure 4(a) shows correlations between the fMRI profile for the selected voxel (at the cross hair) and the profiles from all other voxels in the image. Note that high correlations exist between the selected voxel and many neighboring voxels, bilaterally in the opposite hemisphere, and in some distant areas. There are obvious departures from an assumption that the strengths of associations decrease with increasing distances (see Figure 4(b)), which poses a major challenge for modeling spatial dependence. Another analytic challenge arising from the ultra high dimensionality is that many objectives seek to make inferences at each voxel. One has to cope with multiplicity issues, since this often amounts to tens or hundreds of thousands of statistical tests.

Figure 4.

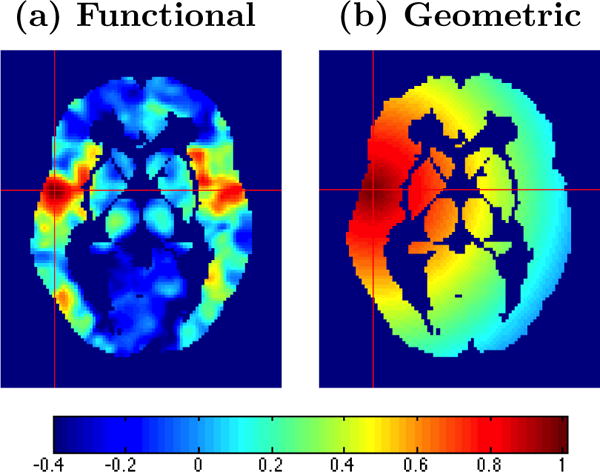
Images displaying (a) spatial patterns reflecting correlations between the BOLD signal from the selected voxel and all other voxels in the image and (b) hypothetical correlation model in which correlations decrease with increasing distance from the selected voxel. The figure reveals that a covariance function specified based on Euclidean distances may be inappropriate for the data.

The data proceed through a series of steps from the time that they are retrieved from the scanner to the time of statistical analysis, and we generally refer to these steps as the preprocessing pipeline. Detailed coverage of preprocessing is beyond the scope of this review; however, it is important for the reader to have knowledge of these steps as they may substantially impact subsequent statistical analysis. Our brief remarks omit data processing that occurs prior to retrieving data from the scanner. Typical preprocessing steps include motion correction to adjust for head movement, slice timing correction because each 3-D scan representing a single time point actually consists of several 2-D slices acquired at slightly different times, registration of the fMRI scans to an anatomical MRI scan, normalization to warp each individual’s set of scans to a standard space for group analysis, temporal filtering to address temporal correlations and to remove non-physiologic trends such as scanner drift, and spatial smoothing, e.g. using convolution with a Gaussian kernel, to adjust for residual between-subject neuroanatomic differences that persist following normalization. Another source of motivation for spatial smoothing is that it helps to support the assumptions underlying random field theory (discussed later), which is a popular technique to address multiple testing. These preprocessing steps are covered in more detail by Strother (2006), and they are implemented in several neuroimaging software packages, some of which are freely available (82).

3 Survey of Existing Methods

3.1 Methods for Localization

3.1.1 THE GENERAL LINEAR MODEL

The general linear model (GLM) has been a cornerstone of neuroimaging analyses targeting localization (40). A linear mixed model is conceptually very well suited for neuroactivation analyses to incorporate subject-specific effects, group-level parameters, and correlations between repeated measures obtained from each individual. The massive amount of data, however, precludes routine use of the mixed model due to heavy computational demands. As an alternative, a two-stage modeling approach is employed, with the first stage single-subject GLM given by

$${\mathbf{Y}}_i(v)={\mathbf{X}}_{\mathit{iv}}{\beta }_i(v)+{\mathbf{H}}_{\mathit{iv}}{\gamma }_i(v)+{\epsilon }_i(v),$$ (1)

where Y_i(v) (S × 1) is a vector of S serial brain activity (BOLD) measures for subject i at voxel v, X_iv (S × q) is the design matrix containing q independent variables, β_i(v) (q × 1) represents the parameter vector linking experimental tasks to the fMRI responses, H_iv (S × m) contains m additional covariates that are not of substantive interest (e.g. high-pass filtering to remove low-frequency signal drift), and ε_i(v) (S × 1) is random error about the ith subject’s mean (93). We assume ${\epsilon }_i(v)~\text{Normal}(\mathbf{0},{\tau }_v^2\mathbf{V})$, where ${\tau }_v^2$ is unknown, and V reflects the correlations between serial BOLD measures.

The BOLD response to neuronal activity is governed by properties of a hemodynamic response function (HRF) (see Figure 5). Following a stimulus evoking a neuronal response, there is a period of increased blood flow and oxygenation, which peaks after roughly 5 or 6 seconds, and then falls back toward baseline. There is often a transient dip below baseline characterizing the post-stimulus undershoot. To accommodate the HR properties, it is standard to convolve the design matrix with the HRF using $(h\ast x)(s)={{\displaystyle \int }}_{-\infty }^{\infty }h(\tau )x(s-\tau )\mathit{d\tau }$. Often a single HRF model is specified for all voxel locations, but some methods more flexibly allow for spatially varying HRFs across voxels (88).

Figure 5.

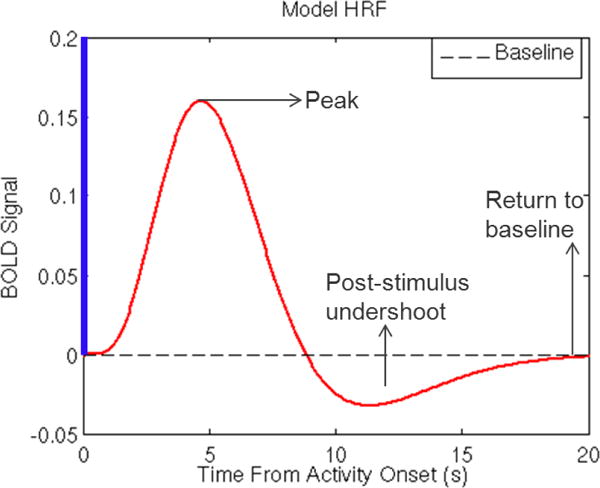
The hemodynamic response function (HRF). Following a stimulus evoking a neuronal response, there is a period of increased blood flow and oxygenation, which peaks after roughly 5 or 6 seconds, which then falls back toward and temporarily below baseline characterized by the post-stimulus undershoot.

Next, one models the individualized experimental effects in terms of group-level parameters using a second-stage GLM:

$${\beta }_i(v)=\mathit{\mu }(v)+{\mathbf{d}}_i(v),$$ (2)

where β_i(v) contains regression coefficients from (1), μ(v) is the group-level mean vector, d_j(v) contains random errors, and ${\mathbf{d}}_j(v)~\text{Normal}(\mathbf{0},{\omega }_v^2\mathbf{R})$. One often considers linear contrasts Cβ_i(v), rather than modeling the entire vector. It is straightforward to show that this two-stage procedure implies the following linear mixed model

$${\mathbf{Y}}_i(v)={\mathbf{X}}_{\mathit{iv}}\mathit{\mu }(v)+{\mathbf{X}}_{\mathit{iv}}{\mathbf{d}}_i(v)+{\mathbf{H}}_{\mathit{iv}}{\gamma }_i(v)+{\epsilon }_i(v),$$ (3)

with fixed effects X_ivμ(v), random subject-specific effects X_ivd_i(v), and random error introduced by ε_i(v). The two-stage approach substantially reduces the computational burden, since estimation in both GLMs uses least-squares and avoids use of the Newton Raphson procedure or alternative iterative algorithms required for (3). In practice, one replaces β_i(v) with estimates, say ${\widehat{\beta }}_i(v)$, which sacrifices some efficiency relative to fitting the linear mixed model (3) directly.

The matrix V incorporating covariances between serial BOLD responses is rarely known in practice, and two strategies are used to address it. Prewhitening obtains an initial estimate of the temporal autocorrelation from the data and subsequently transforms Y_i(v) to remove this correlation (87). Precoloring, on the other hand, introduces known autocorrelations through a linear transformation or temporal filtering, say WY_i(v) (87,40,92,16,69). Temporal filtering introduces autocorrelations, which are deemed to dominate the existing correlations in V so that the resulting covariance structure $\mathrm{Var}({\mathbf{WY}}_i(v))={\tau }_v^2\mathbf{WVW}\prime$ is well approximated by ${\tau }_v^2\mathbf{WW}\prime$, and estimation proceeds using weighted least-squares.

3.1.2 SPATIAL MODELING

One apparent limitation of the GLM framework is that the models are estimated separately for each of the v = 1,…, V voxels, which assumes independence between voxels. Several approaches have been developed that incorporate spatial correlations between neural activity arising from different voxels. The most conceptually straightforward approaches incorporate correlations between a voxel and its contiguous first-order neighbors. Penny et al. (2005) incorporate correlations between in-plane neighboring voxels in a Bayesian model with priors for regression parameters relying on a user specified spatial kernel matrix. Their approach assumes that BOLD responses are spatially homogeneous and locally contiguous within each slice of an image. Katanoda et al. (2002) addressed spatial correlations by including data (for a given voxel) from the six physically contiguous voxels in three orthogonal directions (53). Woolrich et al. (2004) propose a spatio-temporal Bayesian framework that uses simultaneous autoregressive models for neighboring voxels allowing both separable and nonseparable models (89).

As illustrated in Figure 4, spatial correlations extend beyond first order neighbors, may not decrease with increasing distances, and often include select long-range associations. Bowman (2007) proposed a linear mixed model, an extended version of 3, which incorporates temporal (repeated measures) correlations using random effects and captures spatial correlations between voxels with the strengths of these correlations depending on a measure of functional distance d_ij between the neural activity in voxels i and j (11). Specifically, the model is given by

$${\mathbf{Y}}_i={\mathbf{X}}_i\mathit{\mu }+{\mathbf{Z}}_i{\alpha }_i+{\epsilon }_i,$$ (4)

where Y_i = [Y_i(1)′,…, Y_i(V)]′, with Y_i(V) as in (1), and Z_i = (I_V ⊗ 1_S). The model decomposes the measured BOLD signal into localized mean components X_iβ, individualized mean-zero random deviations α_i that induce temporal correlations between scans, and random errors that exhibit functionally based spatial correlations. The model simultaneously incorporates temporal and spatial correlations via Var(Y_i) = (Φ_i + I_S) + σ_t(I_V ⊗ J_S), where J_S denotes a unit matrix, and Φ_i handles parametric covariance structures of the form (Φ)_ij = σ²f(d_ij). Despite its flexibility, this model was proposed for region of interest (ROI) studies, which focus on particular neuroanatomic structures, and intensive computations may limit applicability to whole-brain studies.

Other methods offer broader spatial coverage for correlations by linking parameters both within and between defined brain regions. Bowman (2005) uses a simultaneous autoregressive model to capture exchangeable spatial correlations between all pairs of voxels within functionally defined networks. Using a known parcellation of the brain (see Figure 6), Derado et al. (2010) extend this autoregressive model to additionally incorporate repeated measures associations between multiple scanning sessions, e.g. before and after treatment (10, 29). Bowman et al. (2008) also leverage the neuroanatomic parcellation to establish a Bayesian framework for incorporating shorter and longer range correlations by pooling the jth effect from model (2) across all voxels in brain region g (14). The second-stage likelihood function for β_igj = (β_igj(1),…, β_igj(V_g))′ follows from

$${\beta }_{\mathit{igj}}|{\mu }_{\mathit{gj}},{\alpha }_{\mathit{igj}},{\sigma }_{\mathit{gj}}^2~\text{Normal}({\mathit{\mu }}_{\mathit{gj}}+\mathbf{1}{\alpha }_{\mathit{igj}}+{\mathbf{X}}_i{\mathit{\eta }}_{\mathit{gj}},{\sigma }_{\mathit{gj}}^2\mathbf{I}),$$ (5)

where μ_gj = (μ_gj1,…, μ_gjV_g)′. Spatial correlations are introduced by modeling the random effects α_igj collectively for all G brain regions, α_ij = (α_i1j,…, α_iGj)′, through the following prior probability distributions:

$$\begin{array}{l}{\alpha }_{\mathit{ij}}|{\mathbf{\Gamma }}_j~\text{Normal}(\mathbf{0},{\mathbf{\Gamma }}_j)\\ {\mathbf{\Gamma }}_j^{-1}~\text{Wishart}\{{(h_0{\mathbf{H}}_{0j})}^{-1},h_0\}.\end{array}$$ (6)

Similar to (10,29), this model includes exchangeable correlations between voxels within a neuroanatomic region, and Γ_i incorporates between region correlations. The model provides an excellent compromise between the necessary sophistication to address several aspects of spatial and temporal correlations present in the data and simplicity to facilitate computational demands as it can be readily implemented with user-friendly software making use of the Gibbs sampler (95). The model does not, however, account for dependence between different scanning sessions or multiple effects obtained on each individual and includes a relatively simple intra-regional correlation model. To overcome these shortcomings, Derado et al. (2012) propose an approach that augments model (5). Their model has useful predictive capabilities, and we discuss the approach in section 3.4.

Figure 6.

Brodmann areas. Alternative parcellations, such as automatic anatomical labeling (AAL), also exist.

Xu et al. (2009) present an alternative spatial modeling framework, where the goal is to address variability in activation locations across individuals (94). Collectively, all of the aforementioned spatial modeling extensions offer clear advantages over the standard two-stage GLM. Notable advantages are that the modeling assumptions are better suited to the properties of the data and underlying neurophysiology, increased precision for estimation, increased statistical power, and expanded interpretations concerning the associations, hence interplay, between different brain regions. Spatial smoothing of the data, performed prior to statistical analysis, is a standard preprocessing step for fMRI data. The analyst should carefully consider the influence of spatial smoothing, and we recommend either forgoing spatial smoothing during preprocessing or performing very focal spatial smoothing to limit the impact on subsequent spatial modeling and estimation. Despite the substantial progress in spatial modeling, this remains an important area for involvement by statisticians. Some potential areas of future development include the development of unified (one-stage) spatio-temporal modeling, perhaps with non-separable covariance models and multimodal modeling, integrating supplementary information from other imaging modalities, e.g. regarding the underlying structural connectivity. Note that our use of the term multimodal is consistent with the neuroimaging literature and describes data from two or more imaging techniques that are combined for analysis, rather than the conventional use of the term in statistics to describe multiple modes of a distribution.

3.1.3 UNSPECIFIED ONSETS OF STIMULI

Occasionally studies are designed with unspecified onset times of stimuli to prompt changes in neural activity. For example, if subjects trained in Zen meditation are instructed to focus their awareness by concentrating on breathing while in the scanner, the time at which a subject achieves a deep meditative state may be unknown (66). Robinson et al. (2010) present a model to identify unknown change points in the data (72). Their work estimates the onset distributions evoking a change in neural activity from baseline and present a hidden Markov random field model to cluster voxels based on characteristics of their onset, duration, and anatomical location. Independent component analysis (ICA) is another approach that does require a design matrix a priori, and we discuss ICA in section 3.3.

3.1.4 SPECTRAL MODELING

There are alternatives to modeling fMRI data in the time domain, which may be based on Fourier or wavelet transformations of the data. A primary benefit of performing such transformations is that it simplifies analyses in the transformed space, e.g. because Fourier coefficients are approximately uncorrelated across frequencies, and similarly wavelets have decorrelating properties. The previously discussed approach by Katanoda et al. (2002) conducts a Fourier domain analysis for their model that captures spatial correlations between six nearest neighbor voxels (53). Ombao et al. (2008) present a spatio-spectral model to account for spatial and temporal correlations using spatially varying temporal spectra to characterize the underlying spatiotemporal processes (65).

Kang et al. (2012) proposed a spatio-spectral mixed-effects model that is conceptually similar to the model in equations (5) and (6) (51). The linear mixed effects model is specified for a given frequency band ${\mathbf{\Omega }}_{\mathcal{l}}$ as follows:

$${\mathbf{Y}}_{\mathit{gv}}({\mathbf{\Omega }}_{\mathcal{l}})=\mathbf{X}({\mathbf{\Omega }}_{\mathcal{l}})[{\mathit{\mu }}_g+{\mathbf{b}}_{\mathit{gv}}]+{\mathbf{d}}_g({\mathbf{\Omega }}_{\mathcal{l}})+{\epsilon }_{\mathit{gv}}({\mathbf{\Omega }}_{\mathcal{l}}),$$ (7)

where g = 1,…, G represents ROIs, v = 1,…, V_g indexes voxels in ROI g, and b_gv, ${\mathbf{d}}_g({\mathbf{\Omega }}_{\mathcal{l}})$, and ${\epsilon }_{\mathit{gv}}({\mathbf{\Omega }}_{\mathcal{l}}$ are mutually independent and normally distributed. With analysis performed in the frequency domain, there are associated components for real and imaginary parts, indexed by j ∈ {R, I}. Correspondingly, ${\mathbf{d}}_g({\mathbf{\Omega }}_{\mathcal{l}})={\mathbf{d}}_g^R({\mathbf{\Omega }}_{\mathcal{l}})+i{\mathbf{d}}_g^I({\mathbf{\Omega }}_{\mathcal{l}})$, with $(d_1^j({\mathbf{\Omega }}_{\mathcal{l}}),\dots ,d_G^j({\mathbf{\Omega }}_{\mathcal{l}}))\prime ~\text{Normal}(\mathbf{0},{\mathbf{\sum }}_d^j)$; $(b_{g1}^p,\dots ,b_{g{V}_g}^p)\prime ~\text{Normal}(\mathbf{0},{\mathbf{\sum }}_{\mathit{bg}}^p)$ for stimulus p; and $\epsilon ({\mathbf{\Omega }}_{\mathcal{l}})={\epsilon }^R({\mathbf{\Omega }}_{\mathcal{l}})+i{\epsilon }^I({\mathbf{\Omega }}_{\mathcal{l}})$, with ${\epsilon }^j({\mathbf{\Omega }}_{\mathcal{l}})~\text{Normal}(\mathbf{0},0.5f({\mathbf{\Omega }}_{\mathcal{l}})\mathbf{I})$, where $f({\mathbf{\Omega }}_{\mathcal{l}})$ is the spectrum at frequency band ${\mathbf{\Omega }}_{\mathcal{l}}$. The matrix ${\mathbf{\sum }}_{\mathit{bg}}^p$ introduces correlations between the V_g voxels within ROI g and assumes that the covariance elements are determined as a function the Euclidean distances between the corresponding voxels within the ROI, ${\mathbf{\sum }}_d^j$ models correlations between the G ROIs, and the simplified covariance structure resulting from the frequency domain model are reflected by $\mathrm{Var}({\epsilon }^j({\mathbf{\Omega }}_{\mathcal{l}}))$.

Rowe (2005) presents a model for complex fMRI data that describes both the magnitude and phase and can be used to test for task related changes in the magnitude, the phase, or both the magnitude and phase (74). Zhu et al. (2009) also present a Rician regression model to characterize noise contributions in fMRI along with associated estimation and diagnostic procedures (96).

3.2 Statistical Inferences

Statistical inferences in neuroactivation studies seek to identify localized task related alterations in brain activity, localized differences in neural activity between groups of subjects, and treatment (or other session) related changes in localized activity. One may target these objectives via a set of null hypotheses H₀ = {H₀₁,… ,H_0V}, addressed by linear combinations of group-level effects, e.g. C_μ. For frequentist approaches, one proceeds by calculating an appropriate test statistic at each voxel, T_v, often a t-statistic or an F-statistic based on the underlying modeling assumptions. One may also consider nonparametric alternatives such as permutation testing for localized inferences (64). The goal for any of these approaches, whether frequentist or Bayesian, is to produce activation maps as shown in Figure 2(a), which reveal locations exhibiting significant or highly probable changes (or differences) in neural activity. Given the massive number of tests performed, typically hundreds of thousands, it is desirable to establish some control over the collective testing errors.

For a given search region $\mathcal{R}$, controlling familywise error at a significance level α involves selecting a threshold t_α such that $\mathrm{Pr}[\underset{v=1}{\overset{V}{{\displaystyle \cup }}}(T_v\ge t_{\alpha })|H_0,\mathcal{R}]\le \alpha$. Common methods for addressing multiplicity in neuroimaging include uncorrected approaches that specify an arbitrarily small significance level such as α = 0.005, Bonferroni-type procedures, random field theory, permutation testing, and false discovery rate (FDR). Of these, the Bonferroni, random field theory, and permutation testing control familywise error.

The widely used Bonferroni approach selects a threshold t_α such that for each voxel $\mathrm{Pr}[T_v\ge t_{\alpha }|H_0,v\in \mathcal{R}]\le \alpha /V$, which by Boole’s inequality ensures that the familywise error control is achieved. The number of voxels V is extremely larger for whole-brain studies and the test statistics at each voxel are not statistically independent, making the Bonferroni procedure highly conservative. This approach would rarely yield statistical significance, and in practice, Bonferroni corrections are often adapted to consider the size of an activated cluster.

Random field theory is a mathematically elegant approach that regards a map of localized test statistics as a continuous random field, e.g. Gaussian, t, F, or χ². Any threshold t_α applied to the test statistic map has an associated excursion set containing the voxels where the localized statistic exceeds the threshold. Random field theory uses a topological property called the Euler characteristic to summarize this set, which Worsley et al. (1992) heuristically describe as follows: “the number of isolated parts of the excursion set, irrespective of their shape, minus the number of ’holes’ (91),” although the formal definition involves the curvature of the boundary of the excursion set at tangent planes (1). As simple examples, the Euler characteristic is 1 for a solid ball and 0 for a doughnut. If no holes are present, then it counts the number of isolated regions of activation in an image above the threshold. Figure (7) illustrates the appearance of both isolated regions and holes for lower thresholds applied to the t-statistic map (see (a)) and only isolated regions remaining for higher thresholds.

Figure 7.

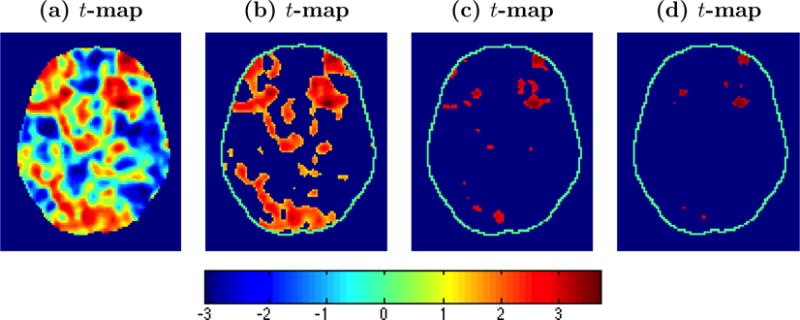
t-statistic maps with various levels of thresholding applied. The maps reflect working memory related differences among individuals with schizophrenia. One notes that features of the Euler characteristic, blobs and holes appear in (b), with only blobs remaining as the threshold increases.

Under the null hypothesis for a given search region $\mathcal{R}$, the critical value t_α satisfies $\mathrm{Pr}[T_{\max }>t_{\alpha }|\mathcal{R}]\le \alpha$. If t_α is large, then the exceedence probability for the maximum is approximated by the expected value of the Euler characteristic, E(χ_tα), and is given by

$$\begin{array}{l}\mathrm{Pr}[T_{\max }>t_{\alpha }|\mathcal{R}]\approx \mathrm{E}({\chi }_{t_{\alpha }})\\ \approx V{|\mathbf{\Lambda }|}^{1/2}{(2\pi )}^{-2}(t_{\alpha }^2-1)e^{-t_{\alpha }^2/2}\\ \approx R{(4{\log }_{e}2)}^{3/2}{(2\pi )}^{-2}(t_{\alpha }^2-1)e^{-t_{\alpha }^2/2},\end{array}$$ (8)

where Λ is a matrix of partial derivatives of the random field with respect to the dimensions x, y, and z, which (under a set of assumptions) can be approximated as |Λ|^1/2 = (FWHM_x × FWHM_y × FWHM_z)⁻¹(4 log_e 2)^3/2 using the full widths at half maximum (FWHM) of the Gaussian smoothing kernel, and R = V/(FWHM_x × FWHM_y × FWHM_z) is a measure of the number of resolution elements (resels) in the search volume (91).

The random field theory approach is widely used in the neuroimaging community and is easily implemented using available software packages. Criticisms largely target the required assumptions, which are clearly delineated by Nichols and Hayasaka (2003) (63). Considering the Gaussian case, one assumes that under the null hypothesis, the test statistic image can be modeled by a smooth, homogeneous, mean-zero, unit variance Gaussian random field. The level of smoothness should be sufficient to reflect properties of a continuous random field. The random field theory approach works well with extensive smoothing, for example 10 voxels FWHM, but low smoothness may yield conservative results. The spatial autocorrelation function (ACF) must be twice differentiable at the origin. The random field theory approach assumes that the data are stationary or are stationary after a deformation of space (90). Also, the roughness/smoothness is assumed to be known without appreciable error. Random field theory becomes more conservative with decreasing sample sizes and was shown to yield thresholds comparable to the Bonferroni procedure for data analyses with low degrees of freedom (63).

Resampling testing procedures have been proposed as alternatives for statistical inferences for neuroimaging data, including wavelet-based procedures and traditional permutation testing (19,17,18,64). Nichols and Holmes (2001) use permutation testing to construct an empirical distribution for the maximum statistic T_max. Implementation for fMRI group-level analyses involves permuting labels across individuals defining contrasts or subgroups, computing the voxel test statistics, and determining $T_{\max }^b$ for each permutation sample b = 1,…, B, which yields the permutation distribution $T_{\max }^{(1)}\le T_{\max }^{(2)}\le \cdots \le T_{\max }^{(B)}$ for the maximum statistic. At significance level α, the critical value is determined from this empirical distribution by the smallest b* such that (1 − b*/B) ≤ α, and any voxel with $T_v>T_{\max }^{(b^{\ast })}$ is declared statistically significant, and exact p-values may be determined directly from this distribution. A key advantage of permutation testing is that it does not require strong assumptions about the distribution of the data, in contrast to the random field theory approach. Nichols and Holmes (2002) showed that permutation tests may yield increases in power with small sample sizes over other testing procedures.

FDR has received attention in several large-scale data areas. In contrast to familywise error control, FDR protects against the expected rate of false discoveries (or false positives) among the significant tests (9,43) and is defined to be 0 when no tests are rejected. FDR offers control according to the following: E(FDR) ≤ π₀ω, where π₀ is the unknown proportion of null hypotheses that are true and ω is the user-specified level of control. In many neuroimaging applications, π₀ ≈ 1 since there will be no effect in the vast majority of voxels. So setting π₀ = 1 is often reasonable, yet it may be conservative when π₀ is substantially smaller than 1. Adaptive FDR procedures seek less conservative approaches by estimating the unknown quantity π₀. Reiss et al. (2012) reveal vulnerabilities with adaptive FDR, including astonishing paradoxical cases where adaptive FDR yields more liberal results than not making any correction for multiplicity (70). FDR is easily implemented, for a specified rate ω, by first ordering the p-values p₍₁₎ ≤ p₍₂₎ ≤ … ≤ p(V) for the V voxels and then determining the largest i, say i*, such that

$$p_{(i^{\ast })}\le \frac{i^{\ast }\omega }{V[{\displaystyle \sum }_{i=1}^V(1/i)]}.$$ (9)

The procedure declares voxels corresponding to p₍₁₎,…, p_(i*) as significant.

FDR is a flexible approach for addressing multiplicity, since it is implemented using p-values, which can be produced by a range of models and testing frame-works. FDR does not require smoothed data and, in fact, is more powerful for unsmoothed data. This is a relative strength compared to random field theory, which often requires aggressive smoothing for good performance. Some view FDR as a technique that is best suited for applications targeting preliminary discovery, where one seeks to control the number of discoveries that prove to be false at a subsequent validation phase. In neuroimaging, however, activation results from whole-brain analyses tend to be the final goal and are not routinely designed with plans for subsequent validation analyses on discovered findings.

3.3 Connectivity

3.3.1 FUNCTIONAL CONNECTIVITY

Functional connectivity refers to the temporal coherence in neural activity between spatially remote brain regions (39). It is examined using various undirected measures of association including Pearson’s correlation coefficient, partial correlation, mutual information, and spectral coherence, among others. Seed-based methods represent one simple approach to determine functional connectivity. Seed-based techniques simply identify a select number of brain regions, usually via hypothesis driven selection, and calculate the associations between these seeds and every other brain region considered, producing correlation images such as that depicted in Figure 4(a). To mitigate the impact of varying hemodynamics for different brain regions, one may accommodate time lags between brain regions i and j, e.g. using the following:

$${\rho }_{\mathit{ij}}=\underset{u\in U}{\max }\left\{\frac{{\displaystyle \sum }_{t=1}^{T-u}[y_i(t+u)-{\overline{y}}_i][y_j(t)-{\overline{y}}_j]}{{\widehat{\sigma }}_i{\widehat{\sigma }}_j}\right\}.$$ (10)

An area of growing interest for seed-based (and other) connectivity approaches concerns the potential dynamic nature of functional associations or networks, whereby connectivity patterns change dynamically over time. Seed-based procedures remain popular due to their simplicity in implementation and interpretation. A major drawback is that they may miss important findings since they are inherently limited in scope by considering a small number of seed regions. These methods are typically hypothesis driven, but the exact seed locations may heavily influence the findings.

A related approach to determine connectivity is to select a set of brain regions to serve as nodes and then calculate associations between all nodal pairs. The nodes may target hypothesis driven brain regions, such as the putative depression-related regions in Figure 8(a), or may represent subregions drawn from an exhaustive parcellation of the brain, with an example shown in Figure 8(b). In either case, associations are computed between every pair of nodes, which produces a complete functional connectivity matrix. The connectivity matrix in Figure 8(c) corresponds to the 90 whole-brain ROIs shown in Figure 8(b). Depending on the objectives, one may scale up to include a larger number of regions to generate whole-brain connectivity networks (see Figure 2(b)). As the ultimate goal, functional connectivity studies often seek to determine group or treatment related differences in connectivity patterns.

Figure 8.

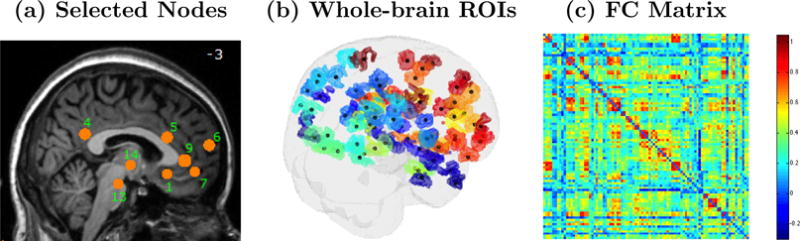
(a) Subregions that are thought to be associated with depression, (b) subregions representing larger regions from an exhaustive brain parcellation, and (c) a matrix of correlations between each pair of regions in (b), where the correlations reflect associations between resting-state brain activity profiles (time series) from pairs of distinct brain regions.

Partitioning approaches organize the brain into collections of voxels that have shared properties, with larger differences between groupings. Two such procedures are independent component analysis (ICA) and cluster analysis. ICA is often motivated by the classical cocktail party problem, in which a group of people are talking simultaneously in a room, and one is interested in isolating one of the voices (or discussions). The human brain is quite adept at handling such tasks. Signal processing approaches regard the problem as one of blind source separation, in which the goal is to dissociate the mixture of signals into the originating sources without a priori information about the sources or the mixing process, while assuming that the sources are statistically independent.

Letting Y(T × V) represent an individual’s fMRI data from T scans, ICA decomposes the data into linear combinations of spatio-temporal source signals:

$$\mathbf{Y}=\mathbf{MS}+\mathbf{E},$$ (11)

where M(T × q) is the nonsingular mixing matrix whose columns contain latent time series for each of the q independent components, S(q × V) has rows containing statistically independent spatial signals, with columns assumed to be non-Gaussian, and E(T × V) contains noise or variability not explained by the independent components, with each column assumed to follow a multivariate normal distribution (5, 56). Noise free ICA omits the error term E (56). From the noise free formulation, S = M⁻¹Y, which clearly reveals that M⁻¹ operates as an unmixing matrix yielding statistically independent signals from the fMRI data. ICA has been extended for group analyses, with approaches developed by Calhoun et al. (2001), Beckmann and Smith (2005), Guo and Pagnoni (2008), Guo (2011), and Eloyan et al. (2013) (6, 21, 34, 48, 47).

ICA decomposes observed fMRI data into spatially independent sources, with each component having an associated latent time series. Putative attributions about the nature of the components may be made, for example, consistently task-related, transiently task-related, and other physiologic and non physiologic sources. These task-related attributions stem from relating the latent time series to the stimuli, but the interpretation of many components is often challenging and can not be established with certainty. One noted advantage of ICA relative to modeling approaches such as the GLM is that it does not require specification of a design matrix. Yet one can still determine brain regions that are associated with the experimental stimuli. ICA does not, however, provide a comprehensive framework for inferences concerning the relationship between the experimental stimuli and the BOLD response. Another advantage of ICA is that noise related signals revealed by the procedure can be removed from the BOLD response prior to subsequent analyses.

Cluster analysis is another set of techniques for partitioning the brain into networks of voxels or regions that exhibit similar temporal or task-related dynamics. There are well established methods in the statistical literature for performing cluster analysis. These data-driven methods have been successfully applied in brain imaging, including K-means (2, 44, 45), fuzzy clustering (3, 35, 36, 80), hierarchical clustering methods (45, 12, 13, 26, 81), a hybrid hierarchical K-means approach (37), and dynamical cluster analysis (DCA) (4), among others. Hierarchical clustering generally begins with each brain region (or node) as a single cluster, calculates functional distances between all pairs of brain regions, e.g. f_ij = 1 − ρ_ij, where ρ_ij is the partial correlation between regions i and j, and iteratively joins the most similar regions or clusters (recalculating the functional distances at each step), with the process ceasing when only a single cluster remains. The procedures then examine each stage of the resulting clustering tree to determine the optimal number of clusters, often based on criteria assessing both within and between cluster variability. Bowman et al. (2012) present a multimodal approach that combines fMRI with structural connectivity information derived from DTI to determine functional connectivity via cluster analysis (15). They defined a distance measure

$$d_{\mathit{ij}}=(1-\frac{{\pi }_{\mathit{ij}}}{\lambda })f_{\mathit{ij}}$$ (12)

where π_ij ∈ [0,1) is the probability of structural connectivity between brain regions i and j determined from the DTI and λ ∈ [0, ∞) is an attenuation parameter that is optimized empirically. This distance incorporates structural connectivity, but still permits clustering of regions (or clusters) based on f_ij in the absence of structural connectivity, i.e. when π_ij → 0. This method generally improves network coherence, particularly with increased noise in the fMRI signal.

There has been a recent emergence of complex functional brain network analyses, borrowing from other applications of network science. Such methods work in conjunction with approaches that specify a set of brain regions to serve as nodes and then quantify associations between the temporal fMRI profiles for every pair of regions. One may view the resulting map of associations as a system of interacting regions, for instance shown in Figure 2(b). Network analyses attempt to summarize various characteristics of these whole-brain networks and then to conduct hypothesis testing about these properties. Typical summaries include graph metrics to reflect communication ability (either local or global), such as clustering coefficient, path length, and efficiency; centrality metrics such as degree, betweenness, closeness, eigenvector centrality; and community structure including whole-brain topological properties such as small-worldness (76).

Most methods address undirected networks and thus convey information on whole-brain functional connectivity. There are current needs for statistical input for proper inference based on network metrics. For example, the metrics are estimated and have associated sampling distributions, but most approaches do not take this variability into account. Comparing brain network properties between groups of subjects also requires statistical thinking for formal inferences.

Simpson et al. (2011) develop a multivariate approach that applies exponential random graph models (ERGMs) to functional brain networks (75). The approach represents global network structure by locally specified explanatory metrics. Let W(G × G) denote a random, symmetric, connectivity matrix with the (i, j)th element W_ij = 1 if regions i and j pass a minimum connection threshold, resulting in a connecting edge in the graphic representation, and W_ij = 0 otherwise, where i = 1,…, G and j = 1,…, G. ERGMs specify

$$\mathrm{Pr}(\mathbf{W}=\mathbf{w}|\mathbf{X},\mathit{\theta })=\kappa {(\mathit{\theta })}^{-1}\exp \{\mathit{\theta }\prime h(\mathbf{w},\mathbf{X})\}$$ (13)

where h(w, X) is a pre-specified network feature, possibly consisting of covariates that are functions of the network (e.g., number of paths of specified length) and nodal covariates X (e.g. location of the node), θ is a parameter vector linking the network feature to the connectivity matrix after accounting for the contribution of other network features in the model, and κ(θ) is a normalizing constant. The model yields inferences about whether certain local network properties are observed more than would be expected by chance.

3.3.2 EFFECTIVE CONNECTIVITY

Some neuroimaging analyses seek to determine stronger relationships than the undirected associations describing functional connectivity. As an example, effective connectivity targets the influence that one region exerts on another (39). Patel et al. (2006) present an approach that uses a Bayesian model to quantify functional connectivity based on the relative difference between the marginal probability that a voxel, v₁, is active and the probability that v₁ is active conditional on elevated activity in voxel v₂. Larger differences between these conditional and marginal probabilities reflect voxel pairs exhibiting stronger functional connections (67). Their approach then investigates the existence of a stronger hierarchical relationship between each pair of functionally connected voxels using a measure called ascendancy. v₁ is ascendant to v₂ when the marginal activation probability of v₁ is larger than that of v₂. The model yields measures of the degree of functional connectivity between a voxel pair and the degree of ascendancy of one voxel relative to the other.

Structural equation models (SEM) have been applied to fMRI and PET to determine causal associations between brain regions. SEM focuses on the covariance structure that reflects associations between the variables. Parameter estimation in SEM minimizes differences between the observed covariances and those implied by a user-defined path (or structural) model. The parameters of the SEM represent the connection strengths between the brain activity measurements in different regions and correspond with measures of effective connectivity.

Dynamic causal modeling (DCM) regards the brain as a deterministic nonlinear dynamic system that receives inputs and produces outputs and uses a Bayesian modeling framework to estimate effective connectivity (41, 42). DCM seeks to estimate parameters at the neuronal level so that the modeled BOLD signals are maximally similar to the observed BOLD signals. The approach parameterizes effective connectivity in terms of coupling, representing the influence of one brain region on another (42).

Granger causality (GC) has recently gained attention in the neuroimaging literature as a method to establish directional relationships between the neural activity from two spatially distinct regions. Let Y_v = {Y_v(t), t = 1,…, T} denote a stationary time series reflecting the measured brain activity in voxel v. Consider the model

$$\left[\begin{array}{c}{Y}_{v_1}(t)\\ Y_{v_2}(t)\end{array}\right]={\displaystyle \sum }_{j=1}^p{\mathbf{\Lambda }}_j\left[\begin{array}{c}{Y}_{v_1}(t-j)\\ Y_{v_2}(t-j)\end{array}\right]+\left[\begin{array}{c}{\epsilon }_{v_1}(t)\\ {\epsilon }_{v_2}(t)\end{array}\right],$$ (14)

where Λ_j(2 × 2) is a matrix of unknown coefficients and ε_v represents model error. This model regresses the current value of a time series for one voxel, say v₁, on the history of both v₁ and v₂. Additionally consider the model

$$Y_{v_1}(t)={\displaystyle \sum }_{j=1}^p{\gamma }_j{Y}_{v_1}(t-j)+e(t),$$ (15)

where γ_j is an unknown scalar coefficient relating the current neural activity in voxel v₁ to its own history. GC is defined as

$$C_{v_1\to v_2}=\ln \left[\frac{\mathrm{Var}(e)}{\mathrm{Var}({\epsilon }_{v_1})}\right],$$ (16)

which gives a measure of the extent to which the past values from v₁ and v₂ assist in predicting the current value of v₁ over and above the extent to which the past values of v₁ predict the current value of v₁ (46). Causality is inferred if there is a significant improvement in model fit by including the cross-autoregressive terms.

Critics of GC have raised issues about its utility in practice for functional neuroimaging (38, 84, 85, 86, 60, 62). Questions center on whether there is sufficient temporal resolution in fMRI data, with repetition times often two seconds or more, to ascertain causality from the lagged association models. Solo (2011) notes that GC found on a slow time-scale, e.g. based on fMRI, does not necessarily hold on a faster time-scale (79). He suggests that ms time-scale measurements, e.g. MEG/EEG, are necessary to pursue dynamic causality. This critique is of course applicable to other effective connectivity approaches based on fMRI data. Also, haemodynamic variations across the brain are likely to swamp any causal lag in the underlying neural time series (38, 73). Measurement noise can reverse the estimation of GC direction, and temporal smoothing can induce causal relationships (77). Smith et al. (2011) empirically evaluated the performances of several functional connectivity approaches as well as directional measures. They observed that GC and other lagged methods generally performed poorly, but the approach by Patel et al. (2006) performs reasonably well.

3.4 Prediction

There are an increasing number of neuroimaging analyses targeting prediction and classification. This area has perhaps the greatest potential for translational impact for functional neuroimaging. There have been a range of prediction objectives targeted. We consider methods that involve the use of neuroimaging data, perhaps coupled with other data, to either forecast future neural activity or to predict or blindly classify a clinical outcome or behavioral response. For example, prediction and classification methodology could potentially be used to define imaging markers of depression subtypes, to identify neural patterns of individuals in an undifferentiated aging population who have a high probability of developing Parkinson’s disease, and to determine distinct neural profiles of patients who respond to a particular therapeutic treatment.

We begin with methods aimed at forecasting future neural activity. Guo et al. (2008) developed a Bayesian model that uses a patient’s pretreatment scans, along with relevant characteristics, to predict the patient’s brain activity after a specified treatment regimen (49). The predicted post-treatment neural activity maps provide objective and clinically relevant information that may be incorporated into the treatment selection process. Let Y_i1(v)(S₁ × 1) denote the vector of baseline scans for subject i corresponding to voxel v, Y_i2(v) (S₂ × 1) represent scans from a post-baseline follow-up period, and Y_i(v) = (Y_i1(v), Y_i2(v))′. Guo et al. fit a GLM for Y_i(v) (S × 1) analogous to that specified in (1), but extended by assuming a linear covariance structure for the error term of the second stage model (analogous to (2)) to capture the correlations between pre- and post-baseline neuroimaging data. Prediction proceeds using the conditional distribution of [β_i2(v) | β_i1, μ(v)]. They demonstrated that their prediction framework accurately forecasted post-treatment neural processing in both a PET study of working memory among individuals with schizophrenia and an fMRI study of inhibitory control among cocaine-dependent subjects.

Derado et al. (2012) developed an extended Bayesian spatial hierarchical framework for predicting follow-up neural activity based on an individual’s baseline functional neuroimaging data (30). Their approach increases precision by borrowing strength from the spatial correlations present in the data, while handling temporal correlations between different scanning sessions. Let β_ig(v) = (β_ig1(v), β_ig2(v)) represent parameters for both sessions one and two from a first stage GLM. Extending models (2) and (5), Derado et al. (2012) propose

$${\beta }_{\mathit{ig}}(v)|{\mathit{\mu }}_g,{\varphi }_g,{\mathit{\alpha }}_{\mathit{ig}},{\mathit{\gamma }}_{\mathit{gv}},{\mathbf{\Psi }}_g~\text{Normal}({\mathit{\mu }}_g(v)+{\varphi }_g(v)+{\mathit{\alpha }}_{\mathit{ig}}+{\mathbf{X}}_{\mathit{ig}}{\gamma }_g,{\mathbf{\Psi }}_g)$$ (17)

where ϕ_g(v) is a spatial dependence parameter for local correlations, α_ig is a random effects vector, and Ψ_g is a variance-covariance matrix associated with the repeated scanning sessions. Figure 9 depicts the framework for temporal and local spatial correlations. Priors addressing spatio-temporal correlations include

$$\begin{array}{l}\varphi (v)|\varphi (v\prime ),v\ne v\prime ,\mathbf{\sum },v=1\dots ,V~\text{Normal}(\rho {\displaystyle \sum }_{v\prime }\frac{w_{\mathit{vv}\prime }}{w_{v+}}\varphi (v\prime ),\frac{1}{w_{v+}}\mathbf{\sum })(\text{MCAR}(\rho ,\mathbf{\sum }))\\ {\mathbf{\sum }}^{-1}~\text{Wishart}({(c_2{\mathbf{\Omega }}_2)}^{-1},c_2)\\ {\mathit{\alpha }}_i^{(j)}|{\mathbf{\Gamma }}_j~\text{Normal}(\mathbf{0},{\mathbf{\Gamma }}_j)({\mathit{\alpha }}_i^{(j)}=({\mathit{\alpha }}_{i1j},\dots ,{\mathit{\alpha }}_{\mathit{iGj}})\prime )\\ {({\mathbf{\Gamma }}_j)}^{-1}~\text{Wishart}\{{(h_j{H}_j)}^{-1},h_j\}j=1,2.\end{array}$$ (18)

Hence, their approach addresses spatial correlations between defined neuroanatomical regions via Γ_j using an unstructured model, between all voxel pairs within each of the defined brain region using an exchangeable covariance structure, and via a multivariate conditional autoregressive model for the immediate 26 neighbors of each brain voxel (see Figure 9). Correlations due to repeated scanning sessions are captured by the variance-covariance matrix Ψ_g. They demonstrated good performance using PET data from a study of Alzheimer’s disease to predict disease progression, and the method is also applicable to fMRI data.

Figure 9.

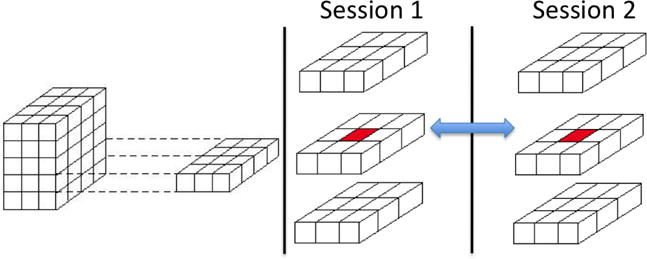
Depiction of temporal correlations between repeated measures at a particular voxel location and local spatial correlations between 26 third-order neighbors within each scanning session.

An increasingly common goal is to use neuroimaging data to predict a behavioral or clinical response. One begins with training data D = {X, y}, where X(n × p) is a matrix of p image-derived independent variables (also called features), and y is a response vector, with y_i ∈ {+1, −1} for binary prediction and $y_i\in \mathbb{R}$ for regression. One uses the training data to develop a model that yields accurate prediction of a separate sample y* from input variables x*. We consider the binary case for simplicity, and we include both settings in which observation of y* follows that of x* (prediction) and those in which a temporal sequence cannot be established but one seeks to blindly distinguish subgroups $y_i^{\ast }$ (classification). Prediction and classification are often based on $\mathrm{Pr}(y_i^{\ast }=1|{\mathbf{x}}_i^{\ast },\mathbf{D})$. These studies face challenges due to the commonly described curse of dimensionality caused by having substantially greater number of measures p on each subject (possibly hundreds of thousands) than the number subjects (n ≤ 50, in many cases).

Support vector machines (SVM) or support vector classifiers (SVC) have perhaps been the most popular tool for prediction or classification in neuroimaging analyses (22, 27, 31, 32, 54, 59). In its simplest form, the SVC determines linear boundaries in the feature space to distinguish two classes. This framework can be extended to identify nonlinear boundaries and extended to multi-class or regression settings for continuous outcomes. SVM methods do not perform variable selection, but they are able to cope with high-dimensional neuroimaging data structures. The existing literature, coupled with our experiences applying SVM, suggests that these techniques usually exhibit good performance in practice. Chen et al. (2011) developed methodology to apply SVM techniques to longitudinal neuroimaging data, where prediction is based on linear combinations of features from different scanning sessions (24).

Related methods for prediction and classification have been proposed, which incorporate a loss function and a penalty term on the model complexity, e.g. penalized least-squares. Chu et al. (2011) apply two kernel regression techniques, specifically kernel ridge regression (KRR) and relevance vector regression (RVR) (25). The KRR method implements the dual formulation of ridge regression to facilitate computations, and RVR considers a set of linear basis functions as the kernel and uses sparse Bayesian methods for estimation. Michel et al. (2011a) also present a sparse Bayesian regression approach for multiclass prediction, which initially groups features into several classes and then applies class-specific regularization, attempting to adapt the amount of regularization to the available data (57). Michel et al (2011b) apply an ${\mathcal{l}}_1$ norm of the image gradient, also called the total variation (TV), as regularization (58). Their method tends to determine block structure, assuming that the spatial layout of the neural processing is sparse and spatially structured in groups of connected voxels. Bunea et al. (2011) apply the widely used LASSO and elastic net procedures to neuroimaging data for prediction and implement a bootstrap based extension to aid parsimony of variable selection (20). Marquand et al. (2010) present a prediction model that uses Gaussian processes to forecast pain intensity from whole-brain fMRI data (55).

Despite the number of studies pursuing prediction and classification, there is a need for more principled applications of statistical methods and for the development of new methods. Examples of more principled use of existing techniques include assessments of the sensitivity of various approaches to tuning parameters, evaluating variability involved in assessing generalization accuracy, and incorporating precision into variable selection techniques, among others. In addition, there are opportunities to apply or possibly develop techniques to leverage the vast and complicated structure present in imaging-derived variables and to incorporate known structure from auxiliary information. Statistics may also play a role in encouraging biologic plausibility in the variable selection process.

3.5 Software

There are several software that are available for neuroimaging analysis, reflecting a major strength in the field. Many of these software packages are freely accessible and serve as major assets to applied researchers. Several packages are fairly comprehensive, implementing various preprocessing steps, statistical analyses, and advanced visualization techniques. Numerous specialized software packages are also available. We list some popular software tools to aid readers, but we do not attempt to give a comprehensive summary of available packages.

FMRIB Software Library (FSL), developed by is a comprehensive library of tools for fMRI, MRI and DTI. Statistical Parametric Mapping (SPM) is a collection of MATLAB functions equipped with a graphical user interface, which offers broad preprocessing and analysis capabilities for fMRI and MRI data. Similarly, AFNI (often interpreted as an acronym for Analysis of Functional NeuroImages) is a set of C programs for processing, analyzing, and displaying fMRI data. Brain Voyager is a commercial package containing tools for the analysis of fMRI, DTI, EEG, MEG and Transcranial magnetic stimulation (TMS) data. Beyond these comprehensive packages, numerous software tools are available to implement specialized analytic methods or analyses of data from a particular modality. Examples of such tools include Bayesian Spatial Model for Activation and Connectivity (BSMac), DTI Studio, Meta-analysis Toolbox, Brain Connectivity Toolbox (BCT), Connectome Workbench, and medInria.

4 Discussion

Neuroimaging is an exciting and rapidly expanding field that is advancing our understanding of the brain, impacting neuroscience, psychology, psychiatry, and neurology. This paper provides a survey of major substantive objectives and existing analytic methods, but by no means is our summary comprehensive. Brain imaging research is inherently interdisciplinary, and the role of statistics is critical as it contributes to defining rigorous methodology for extracting information and for quantifying statistical evidence.

One area of growing interest is multimodal imaging, which has the potential to incorporate imaging modalities reflecting physiologically distinct, yet complementary, information, for instance related to brain function, localized properties of tissue density, local diffusion properties, structural connections between regions, and electrophysiological measures of neural activity. These multimodal imaging data may lead to more accurate and reliable analytic approaches than considering data from a single modality and also may expand the information content and possible interpretations. Multimodal analyses also have the benefit of more complete information by pooling data with physiologically similar objectives, such as brain function, but with distinct bases for measurement such as blood oxygenation, blood flow, metabolism, and electrical activity. Moreover, various imaging modalities incorporates information across different temporal and spatial scales. Despite the many potential advantages, multimodal data present challenges for statistical analysis. The dimensionality may become unwieldy. Alignment of information across different temporal scales, say milliseconds to seconds, may cause analytic and interpretative issues. Similarly, integrating information across spatial scales may prove difficult. Adding to the potential sources of information, multimodal data may include non-imaging data such as genomic, clinical, demographic, and biologic information, which also exacerbates some the aforementioned challenges.

A second area for statistical contribution involves developing methodology that is able to incorporate biologic information. Given the rapid expansion and intense interest in neuroimaging research, more information will become available to incorporate in future modeling efforts. To give examples, the Human Connectome Project, funded by the National Institutes of Health, is an enormous initiative aimed at advancing our knowledge about the human brain and its functional and structural connectivity properties. Also, United States President Barack Obama announced plans for the Brain Research through Advancing Innovative Neurotechnologies (BRAIN) initiative, which promises to be another substantial national investment to aid our understanding of the brain. As these large-scale initiatives, combined with the rapid expansion of the field more broadly, provide insights about the brain, statisticians will have an opportunity to develop more functionally and structurally informed models, e.g. via Bayesian modeling frameworks through incorporation of physiologically-based prior distributions.

Many imaging datasets have both nested spatial and temporal structures, which make Bayesian methodology appealing. Bayesian modeling has proven to be beneficial for neuroimaging data by distributing the overall complexities of the data across various hierarchical levels and enabling flexible posterior inferences. The models, however, often involve a very large number of parameters, which may bring about computational issues related to Markov chain Monte Carlo methods for posterior simulations and concerning assessments of properties of simulations such as convergence and dependence of posterior draws for model parameters. Carefully constructed models, for example those enabling the use of Gibbs sampler, facilitate computations and are often reasonable to implement in practice. For additional modeling flexibility, there may be a need to consider the use of alternative posterior approximation strategies such as variational Bayes to reduce the computational demands.

Some neuroimaging studies are moving from traditional cross-sectional designs to longitudinal designs. The growing number of longitudinal studies and the acquisition of multimodal images raises the issue of missing data. Subjects may have data missing from a single measurement occasion or from a single modality, so the common practice of discarding all data from subjects who have any missing data is inefficient. Some immediate gains may be made by applying existing methods in the statistical literature for handling missing data to neuroimaging, but the enormity and complexity of imaging data prompts the need for additional methodological development.

There is substantial variability in fMRI data, both within and between subjects, and group studies are often based on limited sample sizes, prompting the need to consider analytic techniques and study design considerations that lead to reliable findings. As one strategy, meta-analyses are important to determine both the consistency in task-related changes in brain activity across studies and the consistency of simultaneously activated pairs or networks of brain regions (23, 33, 52, 72). Conducting studies with larger sample sizes would also help to yield more precise estimates and more powerful tests of statistical hypotheses, and such larger studies including hundreds or even thousands of subjects are beginning to emerge in the field. In summary, neuroimaging is an exciting and rapidly expanding field, which presents numerous challenges for quantifying evidence, and statistics should play a critical role in the growth of this interdisciplinary field.