Structure-Function Relations and Rigidity Percolation in the Shear Properties of Articular Cartilage

Abstract

Among mammalian soft tissues, articular cartilage is particularly interesting because it can endure a lifetime of daily mechanical loading despite having minimal regenerative capacity. This remarkable resilience may be due to the depth-dependent mechanical properties, which have been shown to localize strain and energy dissipation. This paradigm proposes that these properties arise from the depth-dependent collagen fiber orientation. Nevertheless, this structure-function relationship has not yet been quantified. Here, we use confocal elastography, quantitative polarized light microscopy, and Fourier-transform infrared imaging to make same-sample measurements of the depth-dependent shear modulus, collagen fiber organization, and extracellular matrix concentration in neonatal bovine articular cartilage. We find weak correlations between the shear modulus |G^∗| and both the collagen fiber orientation and polarization. We find a much stronger correlation between |G^∗| and the concentration of collagen fibers. Interestingly, very small changes in collagen volume fraction v_c lead to orders-of-magnitude changes in the modulus with |G^∗| scaling as (v_c – v₀)^ξ. Such dependencies are observed in the rheology of other biopolymer networks whose structure exhibits rigidity percolation phase transitions. Along these lines, we propose that the collagen network in articular cartilage is near a percolation threshold that gives rise to these large mechanical variations and localization of strain at the tissue’s surface.

Introduction

Healthy mammalian long bones are protected by a living tissue known as articular cartilage (AC). Recognized for its role in facilitating normal joint functioning, AC has a unique combination of material properties (1). For example, it is entirely self-assembled (2,3) and can endure 60+ years of daily loading despite an inability to regenerate normal tissue when injured (4). These characteristics are highly desirable for tissue engineering (5) and soft robotics (6) applications; however, the relevant design principles remain largely unknown. Although ongoing studies continue to make progress toward understanding AC’s microscopic structure (7–11), recent advances in experimental techniques have enabled higher resolution measurements of the spatial heterogeneity in AC’s mechanical properties. For example, confocal rheology techniques have combined high-resolution optical and force data to quantify depth-dependent variations in the shear properties (12,13). With this technique, a spatially localized region was found near the tissue surface with a shear modulus up to 100 times smaller than the typical 1 MPa bulk-averaged value (12–18). This region was also found to dissipate ≈90% of the energy imparted during shear, suggesting a specialized function as a biological shock absorber (18,19). The combination of structural data and improved measurements of local mechanical properties opens the door to studies that correlate microscopic structure with mechanical function in AC.

Broadly, healthy AC is a fluid-filled porous medium composed primarily of water (60–85% wet weight), type II collagen (15–22%), and the large aggregating proteoglycan called aggrecan (4–7%) (1). A significant development in the understanding of AC came when poroelasticity was first used to model its multicomponent architecture with a continuum description (20–22). This theoretical framework, which remains a cornerstone of the cartilage mechanics literature, enabled the interpretation of bulk-averaged compressive mechanical properties in terms of the underlying biopolymer network and interstitial fluid flow.

Here, we ask: what are the design principles underlying AC’s depth-dependent shear properties? The current paradigm attributes the mechanical data to depth-dependent variations in collagen fiber organization (Fig. 1). Specifically, in the tangential, mid, and deep zones, collagen fibers are respectively aligned parallel, random, and perpendicular to the articular surface (1,23–29). Although the exact details vary with animal, age, and location within the joint, the general schematic is largely conserved and superficially appears to correlate with mechanical data. Here, we control for the effect of fiber alignment by studying neonatal bovine tissue, which is known to have less fiber organization relative to adult tissue, allowing us to deconvolve structural and compositional contributions to shear properties. Using natural biological variation as a means to vary material properties, we test this fiber-reinforced hypothesis with same-sample mechanical, structural, and compositional measurements. For small strains, we surprisingly find the shear modulus does not correlate with fiber organization, but rather, these large variations in the shear modulus (≈100-fold) instead correlate with small variations in matrix concentration (≈twofold). Similar behavior has been previously seen in reconstituted biopolymer networks and is a hallmark of a mechanical phase transition known as rigidity percolation (30–37). We adapt this class of models to account for the multicomponent nature of AC, and show it can reproduce the empirical trends observed in our data.

Figure 1.

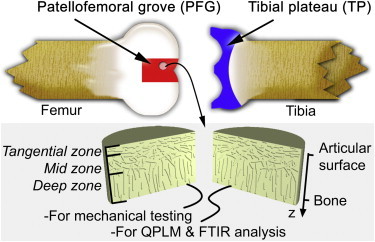
Schematic diagram of a bovine knee joint indicating sample harvesting sites. Cylindrical plugs of AC were removed from the joint, halved, and separated out for mechanical testing or biochemical analysis. AC is known to have three zones distinguished by collagen fiber orientation as indicated. The coordinate system is also shown, where the depthwise direction z is 0 at the surface of the tissue, and increases toward the bone. To see this figure in color, go online.

Materials and Methods

Sample preparation

One-to-three-day-old neonatal bovine knee joints were acquired from a local abattoir (Gold Medal Packing, Rome, NY). Cylindrical explants 3.5 mm in thickness and 6 mm in diameter were dissected from the patellofemoral grove (PFG) and tibial plateau (TP). Each sample was cut into two equal semicylindrical portions, one half being fixed in 10% PBS-buffered formalin for biochemical analysis, the other stored in 100% PBS (Life Technologies, Grand Island, NY) for mechanical testing. In total, n = 8 samples were collected: four PFG samples and four TP samples from two knees. In the analysis presented below, we measure multiple distinct quantities from each sample and compare these quantities on a same-sample basis. Thus, for statistical purposes, the data can be considered as independently acquired, despite coming from two knees. Moreover, all mechanical and structural measurements were similar to previously reported data indicating that these joints were in no way atypical.

Confocal elastography

Before shear testing, each semicylindrical sample was soaked for 3 h in PBS with 7 mg/mL 5-DTAF (5-dichlorotriazinylaminofluorescein) (Life Technologies, Carlsbad, CA), an all-protein stain. Samples were rinsed in PBS for 1 h to remove excess dye, and then loaded into a Tissue Deformation Imaging Stage (Harrick Scientific, Pleasantville, NY). In this apparatus, two plates grip a sample, one of which applies shearing strains, whereas the other measures shearing stresses (Fig. 1, and see the Supporting Material) (16,19). Samples were loaded so that displacements were applied to the articular surface, whereas stress measurements were recorded in the deep zone. Every sample was held with a 7.5 ± 0.5% depthwise compression along z and given 1 h to come to mechanical equilibrium. This time was chosen to be greater than the poroelastic relaxation time, which for our samples is ≈20 min (1). Friction was sufficiently high at the articular surface to prevent slippage during shear. At the deepest portion of the tissue near the cartilage-bone interface, a small bit of cyanoacrylate glue was used to enhance contact with the stress measurement plate. Samples were immersed in PBS to maintain tissue hydration during testing.

The Tissue Deformation Imaging Stage (Harrick Scientific) was mounted onto a LSM 510 confocal microscope (Carl Zeiss, Jena, Germany), where a line was photobleached onto the rectangular surface of the semicylinder parallel to the z axis. This line caused no damage to the tissue and was used to facilitate automated computer tracking of the strain with a depthwise resolution of 10.4 μm. Imaging of 1 Hz oscillatory shear at 1% peak amplitude was carried out with a 10× objective, and movies were acquired at 20 FPS throughout the entire depth of the tissue (16,19). All mechanical testing was performed within 24 h of tissue harvesting, bypassing the necessity for antibiotics or protease inhibitors.

To obtain same-sample, depth-dependent comparisons between mechanical and structural properties, measurements of the local compression profile were made before and after compression. Depthwise measurements of axial compression were acquired by photobleaching a series of lines spaced 23 ± 1 μm apart parallel to the direction of shear. Images were acquired in the uncompressed state, and again in the equilibrated compressed state. Custom MATLAB software (The MathWorks, Natick, MA) quantified the change in line spacing and produced a local depth-dependent axial strain ε_zz(z) that was used to facilitate comparisons between mechanical (compressed) and structural (uncompressed) data.

Quantitative polarized light microscopy

Half of each cylindrical explant was designated for shear testing, whereas the other half was fixed in formalin, embedded in paraffin wax, and sectioned into 4-μm-thick slices. Sections for quantitative polarized light microscopy (QPLM) were placed on glass slides, dewaxed in three xylene baths for 2 min each, rehydrated in three baths of ethyl alcohol (100, 95, and 70% ethanol, appropriately diluted with distilled water) for 2 min each, and dyed with Picrosirius red for 1 h. Sections were then dunked three times each in two acetic water baths (5 mL glacial acetic acid to 1 L distilled water), soaked for 2 min each in three baths of ethyl alcohol (70, 95, and 100%), and laid out to dry in a fume hood. This histochemical staining selectively binds to fibrillar collagen, enhancing tissue birefringence (38). Staining was carried out on all samples simultaneously to ensure dye uniformity.

Once prepared, samples were placed on a bright-field microscope with a 4× objective and two independently rotating linear polarizers set 90° apart (Bruker, Billerica, MA). Incident light was polarized, passed through the sample, and then passed through a second polarizer, producing a map of the local birefringence. By rotating the polarizers through an angle θ from 0 to 90° with respect to the tissue sample and recording images every 6°, we were able to quantify the local light intensity variations. Fitting each pixel intensity I(θ) to the function A₀ + A₁cos²(2θ – ϕ), we measured the local polarization index (PI), PI = A₁/(A₁ + A₀) and the local fiber orientation ϕ, which corresponds to the direction that maximizes I(θ) (23,24). Light intensity was adjusted to prevent pixel saturation, and all samples were imaged under identical lighting conditions. In our measurements, ϕ = 90° is parallel to the articular surface, whereas ϕ = 0° ≡ 180° is perpendicular.

Fourier transform infrared imaging

Sections, 4 μm thick from each tissue sample, were placed on 2-mm-thick mid-infrared (IR) transparent BaF₂ disks that were 25 mm in diameter (Spectral Systems, Hopewell Junction, NY). Although the sectioning plane was fixed, the section cutting direction was randomized to prevent systematic biases in section thickness due to cutting. Sections were dewaxed and rehydrated as described above.

Samples were loaded into a Hyperion 2000 Fourier transform infrared imaging (FTIR-I) microscope (Bruker, Billerica, MA) in transmission mode set to acquire data on wavenumbers between 600 and 4000 cm⁻¹ with a resolution of 4 cm⁻¹. A 15× objective was used with a slit aperture configured to acquire spectra over a rectangular region 25 × 200 μm², where the long dimension was parallel to the articular surface. Fifteen background-corrected scans were repeated at a given measurement point and averaged to generate a single IR spectra. The acquisition window was translated along the tissue sample’s z direction by a computer-controlled stage to acquire measurements at 80 points spaced 25 μm apart.

Beer’s law states that IR absorbance is proportional to molecular concentration, and as a corollary, two mixed species of molecules have additive contributions. Across all samples and spectra, we found the maximum IR absorbance did not exceed 0.3, demonstrating that samples were thin enough to prevent deviations from Beer’s law via molecular shadowing. At physiological concentrations, the spatial proximity of each molecule is sufficiently large that intermolecular interactions do not cause significant deviations from pure-compound spectra acquired at lower concentrations. Although such deviations may be important for precision FTIR-I spectroscopy experiments, our analysis is insensitive to these subtle effects (see the Supporting Material).

The two primary solid-matrix contributions to AC come from type II collagen and aggrecan. Hence, we used previously published pure-compound spectra where both compounds were extracted from bovine AC femoral condyles (39). Each AC spectra was fit to a linear combination of a type II collagen spectrum, an aggrecan spectrum, and a linear baseline over the spectral window from 900 to 1725 cm⁻¹ (see the Supporting Material) (40,41). This procedure has four fitting parameters for each measured spectra. The spectra comprises 147 data points in total, with one multiplicative coefficient for each pure-compound spectra, and two coefficients for the baseline. The pure-compound fitting coefficients, which are proportional to the molecular concentration, were scaled to wet volume fractions by a multiplicative prefactor chosen to reproduce literature values for the bulk averages of 0.35 for collagen and 0.15 for aggrecan (42–45). The inclusion of a linear baseline correction accounts for instrument-specific deviations and drift that can occur in different labs with different environmental conditions (46). Additionally, the absorbance peaks dominating the fitting process are much larger than the spectral resolution of either the published spectra or the spectra acquired here. Thus, any differences in resolution are inherently negligible. Because AC contains type IX collagen, type XI collagen, elastin, small nonaggregating proteoglycans, and other matrix macromolecules in trace amounts, their IR signatures, which are proportional to concentration, are negligible and were not included in the spectral fits.

We note the analysis used here is inherently coarse: there is a dimensional reduction of the data by the fitting process from 147 to 4, which adds a high degree of robustness to our results. For example, we find that peak integration and Gaussian decomposition analysis methods provide qualitatively similar results supporting our main conclusions from the FTIR-I data (see the Supporting Material). The sum-of-spectra results are presented here because they are the least sensitive to baseline techniques, which, in the worst case, can have a nonlinear effect on measurements of the solid matrix volume fraction.

Experimental Results and Discussion

Depth-dependent shear properties of AC

To study spatially localized variations in the shear properties of AC, the PFG (n = 4) and TP (n = 4) of neonatal bovine knee joints (Fig. 1) were selected as sites of interest because of the following:

• 1.They are the most distinct in terms of their local shear properties;
• 2.They offer two decades in variation of the shear modulus; and
• 3.They are transversely isotropic, which greatly simplifies the handling of tissue specimens due to in-plane orientational symmetry (18).

Defining the tissue’s articulating surface to be z = 0, where increasing z moves toward the bone (Fig. 1), we treat the depth-dependent complex shear modulus G^∗(z) as a macroscopic tissue property. For small amplitude oscillatory shear, G^∗(z) is primarily elastic (18) (i.e., tan⁻¹ [Im G^∗/Re G^∗] ≲ 10°). Plotting |G^∗(z)| for all eight samples, we observed a compliant region near the articular surface where 0 ≤ z ≤ 100 μm (Fig. 2, gray highlight). The numerical value of |G^∗(z)| in this region was typically 10 times less than the region where z > 400 μm for PFG samples, and 100 times less for TP samples.

Figure 2.

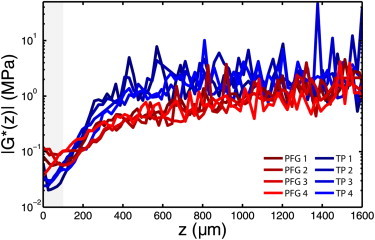
The measured shear modulus for all eight samples is plotted on a log scale as a function of depth. (Red curves) Patellofemoral grove (PFG); (blue curves) tibial plateau (TP). The surface region (highlighted in gray) is found to be 10–100 times more compliant than the tissue at greater depths, and when compared to fiber organization data, corresponds to AC’s tangential zone. To see this figure in color, go online.

To ensure no-slip contact during shear testing, samples were initially compressed before mechanical testing and allowed to come to mechanical equilibrium. Structural measurements, however, were performed on uncompressed samples. To relate these data, we use the measured local axial strain field, ε_zz(z). The compression data showed deviations from uniformity that were well fit by ε_zz(z) = ε₀ – ε₁exp(−z/ℓ), where ε₀ = 0.075 was the target strain, while ε₁ = 0.028, ℓ = 680 μm for PFG, and ε₁ = 0.038, ℓ = 350 μm for TP (1). Although an overall small correction, this scaling of z was used to adjust QPLM and FTIR-I measurements so data at a given depth could be directly compared to |G^∗(z)|. For each sample, this led to 80 measurements along the z axis, with an average spacing of 22 ± 2 μm, although specific spacing values varied according to ε_zz(z).

Depth-dependent collagen fiber organization

QPLM enabled measurements of structural variation with a resolution of 29 μm²/pixel in the shear plane. These birefringence data produced spatial maps of two order parameters that quantify the degree of collagen fiber alignment and their preferred orientation (23,24) (Fig. 3, A and B, inset). The polarization index takes values from 0 to 1, where PI = 0 corresponds to isotropically distributed fiber orientations, and PI = 1 corresponds to perfectly aligned fibers. We note, The fiber orientation angle ϕ only takes values from 0 to 180° due to rotational symmetry.

Figure 3.

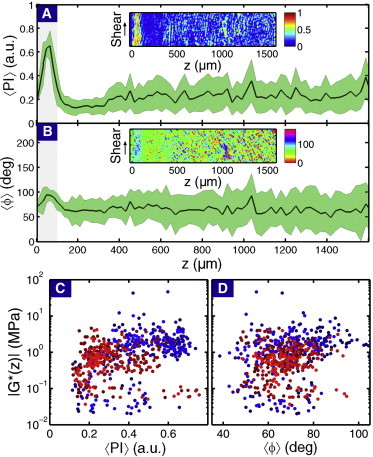
Example of (A) 〈PI(z)〉 and (B) 〈ϕ (z)〉 for sample PFG 1 illustrating typical depth-dependent structural variations. (Green shaded bands) Correspondence to ±1 standard deviation from the mean. (Insets) Two-dimensional maps of each order parameter before being averaged along the shear direction. (Gray-shaded region) Tangential zone for comparison with the shear modulus data. We also note, ϕ = 0° runs parallel to the z axis, whereas ϕ = 90° runs parallel to the articular surface. Comparing (C) 〈PI(z)〉 and (D) 〈ϕ (z)〉 to |G^∗(z)| for all eight samples reveals weak correlations. (The red and blue coloring is coordinated to match Fig. 2.) To see this figure in color, go online.

Averaging along the shear direction produced plots of the depth-dependent parameters 〈PI(z)〉 and 〈ϕ(z)〉 (Fig. 3, A and B). Consistent with the known depth-dependent variations in collagen fiber organization, we found that fibers in the tangential zone, where z < 100 μm, were more ordered and were aligned more nearly parallel to the surface in comparison to fibers deeper in the tissue (z > 100 μm). Although schematics of the depth-dependent collagen fiber network (Fig. 1) have similarities to the profile of |G^∗(z)|, these data reveal the depth-dependent fiber organization is qualitatively uncorrelated with the shear modulus (gray-shaded region in Figs. 2 and 3). Specifically, the QPLM data exhibit wide variations in the tangential zone, whereas the shear modulus data is essentially flat. To quantitatively test for structure-function correlations, we plot both order parameters against |G^∗(z)| (Fig. 3, C and D). Linear regression analysis comparing log|G^∗(z)| to 〈PI(z)〉 (R = 0.28, p < 0.01) and 〈ϕ(z)〉 (R = 0.20, p < 0.01) confirmed the depth-dependent collagen fiber organization weakly varies with the depth-dependent shear modulus.

Depth-dependent matrix density

To quantify matrix constituents, we used FTIR-I to generate spatially resolved IR spectral maps that were decomposed into the sum of spectra from pure type II collagen and pure aggrecan (Fig. 4 A) (26–29,47–49). The pure compound spectra were converted to the depth-dependent wet aggrecan volume fraction v_a(z), and the depth-dependent wet collagen volume fraction v_c(z) (see Materials and Methods). These data show a decrease in matrix concentration near the articular surface where z < 100 μm, and an essentially constant concentration for z > 400 μm (Fig. 4 B and see the Supporting Material). Visually comparing to depth-dependent mechanical data, we see qualitative correlations suggesting potential structure-function relationships (Fig. 2 and Fig. 4 B).

Figure 4.

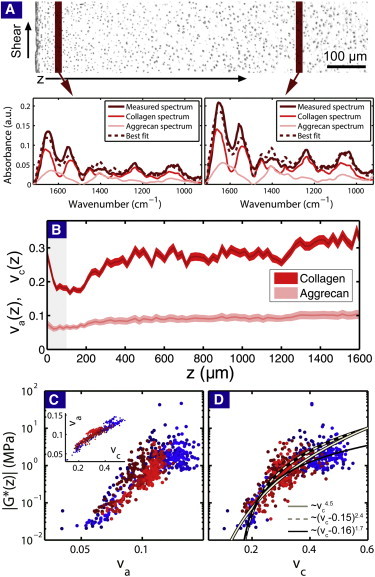
(A) An AC micrograph of sample PFG 1 illustrating two regions where FTIR-I measurements were performed. The two example spectra have been decomposed to a linear combination of a pure type II collagen spectrum and pure aggrecan spectrum. (B) Plotting the wet volume fraction of aggrecan v_a(z) and type II collagen v_c(z) reveals depth-dependent variations reminiscent of those in the shear modulus (as can be seen by directly comparing the gray-shaded region). Error estimates in the fitting parameters are represented here by the thickness of the band, which is the 95% confidence interval. Plotting |G^∗(z)| against (C) v_a(z) and (D) v_c(z) for all same-sample measurements reveals a correlation between matrix density and mechanical function. (C, inset) Linear relationship between v_a and v_c. (D, gray lines) Best fits to the critical scaling function with the two extreme values of the threshold volume fraction, v₀ = 0.0 (solid) and v₀ = 0.15 (dashed). (Solid black line) Fit captures qualitative trends in the data automated fitting routines may miss. (The red and blue coloring in panels C and D is coordinated to match Fig. 2.) To see this figure in color, go online.

To quantitatively test these observations, we compare same-sample measurements of both v_a(z) and v_c(z) with log|G^∗(z)| (Fig. 4, C and D).

Linear regression analysis confirms a high degree of correlation in both cases (R = 0.82, p < 0.01 for v_a(z) and R = 0.79, p < 0.01 for v_c(z)). The aggrecan matrix alone is insufficient to account for the depth-dependent mechanics, because previous rheological studies of aggrecan gels at shear rates comparable to those used here have reported shear moduli in the 0.1–100 Pa range (50). Collagen fibers, however, are known to have Young’s moduli in the GPa range, making it likely that their contribution dominates the overall AC shear mechanics. The apparent correlation between v_a(z) and |G^∗(z)| can then be interpreted as a biproduct of the empirically linear relationship between v_a(z) and v_c(z), i.e., v_a = (0.205 ± 0.0006)v_c + (0.035 ± 0.002) (R² = 0.87; see Fig. 4 C, inset). The wider biophysical context therefore suggests the correlation between v_c(z) and |G^∗(z)| may be causal, and hence collagen volume fraction drives AC’s small-amplitude shear properties.

A remarkable feature of this data is the small (twofold) change in collagen volume fraction coinciding with a very large (100-fold) change in shear modulus. From the view of theoretical mechanics (51,52), simple composites and continuum approximations for entropic spring networks follow |G^∗(v_c)| ∼ v_c. Conversely, work on reconstituted biopolymer networks has found a critical scaling relation where the functional form for the modulus follows a power-law relation that depends on a threshold volume fraction v₀ below which the network loses integrity (30–37). Here, we take an agnostic approach and fit the data to the functional form

$$\left|G^{\ast }\left(v_c\right)\right|\sim {\left(v_c-v_0\right)}^{\xi },$$

where |G^∗(v_c < v₀)| = 0, and v₀ is varied from 0.0 to 0.2 (Fig. 4 D, gray lines; and see the Supporting Material). For 0 ≤ v₀ ≤ 0.15, we find the fits for ξ have essentially indistinguishable residuals (R² ≈ 0.69), with power-law exponents ranging from ξ = 4.5 ± 0.1 when v₀ = 0, to ξ = 2.4 ± 0.1 when v₀ = 0.15 (errors correspond to 95% confidence interval).

Although these fits minimize residuals for a given v₀, they tend to miss qualitative features such as the “knee” at v_c ≈ 0.3. Choosing v₀ = 0.16 and ξ = 1.7 yields a curve that better captures these qualitative trends in the data, indicating the functional form is sufficiently robust to capture such features (Fig. 4 D, black line, R² = 0.68). We find that for v₀ = 0 corresponding to a pure power-law, the exponent is too large to be consistent with a simple continuum model. An alternative explanation is that v₀ is finite and that the system is described by a critical scaling function similar to those found in reconstituted biopolymer networks. In this interpretation, for small strains, the subset of collagen fibers that transmit stresses behaves like a network of elastic fibers near the rigidity percolation phase transition. Reanalyzing the raw FTIR-I data using the total integrated absorbance, individual integrated peaks, and Gaussian decomposition of the spectra provided three confirmations of this result, which are found independent of the pure compound spectra (see the Supporting Material). To further explore the empirical structure-function relation and the implications of these fits, we adapt a percolating fiber model for AC to study the volume fraction dependence of the shear modulus.

Rigidity Percolation Model

We consider a biopolymer rheology model that is known to produce large variations in the shear modulus with small variations in fiber content (30–37,53–55). This scaling arises from a second-order mechanical phase transition known as rigidity percolation, and with some minor modifications, the generic model can be made to reflect the basic character of AC. The model makes the following assumptions:

• 1.The cross-linked collagen network is approximated by a kagome lattice (35–37) (Fig. 5 A), where every node is a freely rotating cross-link (56), every continuous series of colinear bonds constitute a fiber, and disorder is introduced by randomly removing bonds between nodes with probability 1 – p, where 0 ≤ p ≤ 1. The removal of bonds produces a broad distribution of fiber lengths, consistent with qualitative observations of AC. The fiber cross-linking occurs at lattice nodes homogeneously spaced by a minimum distance ℓ_c, but is assumed to have a concentration proportional to fiber density. Although the cross-linker distribution was not quantified here, these assumptions are consistent with previous work (57–59). The kagome lattice was chosen over square and triangular lattices because its mechanical properties are independent of orientation, and each node connects only two fibers as is known to be the case for collagen cross-links.
• 2.Collagen fibers are modeled as linearly elastic rods with constant stretching modulus α and bending modulus κ. This simplification treats simulated fibers as having uniform radii (60), whereas real collagen fibers are known to vary in thickness (1,57).
• 3.The hydrated aggrecan matrix is modeled as a simple elastic medium with shear modulus μ₀, that elastically resists transverse displacement of individual fibers at the microscale and undergoes deformation in parallel with the fiber network at the macroscale. This assumption neglects viscous effects on the grounds that |G^∗(z)| is predominantly elastic. It also neglects poroelastic fluid-flow effects and depth-dependencies in water content, consistent with the fact that small amplitude shear preserves volume, and hence does not induce fluid flows.
• 4.As an explicitly simplified model, all other compositional and structural elements in AC are neglected. This assumption is consistent with the lack of correlation between |G^∗(z)| and QPLM measurements (Fig. 3, C and D), as well as data showing additional AC matrix proteins are only present in trace amounts (1,57).

Figure 5.

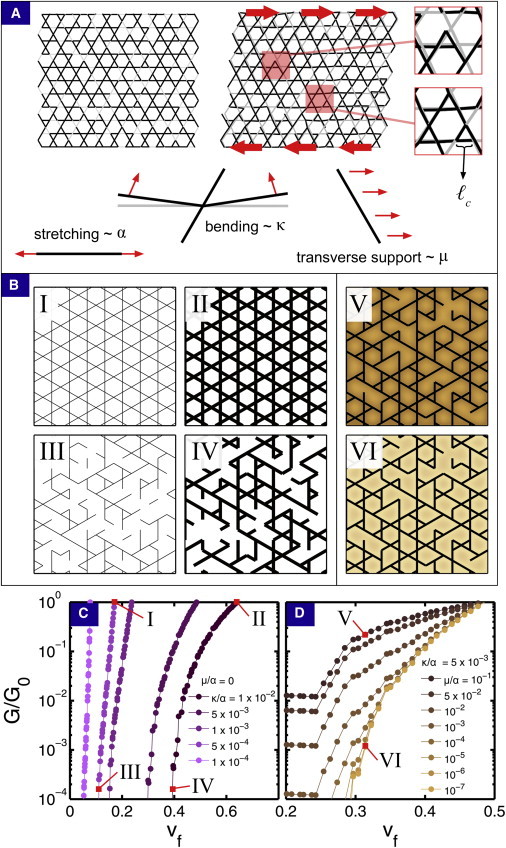
(A) A section of kagome lattice before and after shear illustrates local affine and nonaffine deformations. Continuous black lines represent fibers and light gray lines represent missing bonds. Zooming in on the sheared lattice, we find affine deformations where light- and dark-colored bonds overlap, and nonaffine deformations where they do not. Schematic diagrams illustrate the various energetic contributions included in the model described by Eq. 1. (B) In the absence of a reinforcing medium (μ/α = 0), four distinct regimes of the model corresponding to the four points labeled I–IV in panel C are schematically illustrated. In the presence of a reinforcing medium, such as shown by points V and VI in panel D, the strength of μ/α can be schematically illustrated by shading the background. (C) Exploring the model’s dependence on the fiber bending/stretching ratio κ/α in the absence of a supporting medium (μ/α = 0) reveals a rigidity percolation phase transition as a function of v_f. (D) In the presence of a supporting medium (μ/α > 0), the phase transition is broadened, and G(v_f) becomes dominated at low v_f by the modulus of the reinforcing medium. All modulus curves are normalized by G₀ = G[v_f(p =1)]. To see this figure in color, go online.

Simulations of the reinforced percolating fiber model utilized FORTRAN 90 and MATLAB to determine the linear response under 1% shear at zero temperature. For each set of parameters, 10 kagome networks containing ∼10⁵ nodes were randomly generated with a fraction of bonds 1 – p missing and the results averaged. Defining ${\hat{\mathbf{r}}}_{ij}$ to be the unit vector along bond ij, u_i as the displacement of the ith lattice site, and u_ij = u_i – u_j as the displacement field, the deformation energy given by (30–37,53,54,61)

$$E=\frac{\alpha }{2}\sum _{\langle ij\rangle }{p}_{ij}{\left({\mathbf{u}}_{ij}\cdot {\hat{\mathbf{r}}}_{ij}\right)}^2+\frac{\kappa }{2}\sum _{\langle ijk\rangle }{p}_{ij}{p}_{jk}{\left[\left({\mathbf{u}}_{ji}+{\mathbf{u}}_{jk}\right)\times {\hat{\mathbf{r}}}_{ji}\right]}^2+\frac{\mu }{2}\sum _{\langle ij\rangle }{p}_{ij}\left[{\mathbf{u}}_{ij}^2-{\left({\mathbf{u}}_{ij}\cdot {\hat{\mathbf{r}}}_{ij}\right)}^2\right]$$ (1)

was minimized for the macroscopic shear strain applied on the boundary. Here, p_ij is 1 if bond ij is occupied and 0 otherwise, ${\sum }_{\langle ij\rangle }$ represents sum over all bonds, and ${\sum }_{\langle ijk\rangle }$ represents the sum over pairs of colinear bonds sharing a node. The first term is the cost of bond extension or compression, and is proportional to the fiber-stretching modulus α. In terms of the Young’s modulus Y, radius r, and cross-linking length l_c, we have α ∼ Yr²/ℓ_c. The second term arises from bending about the node connecting colinear bonds ij and jk, and is proportional to the scaled bending rigidity κ ∼ Yr⁴/ℓ_c³. The third term represents elastic deformations of the reinforcing medium in the direction perpendicular to ${\hat{\mathbf{r}}}_{ij}$, which is proportional to the effective gel modulus experienced by a one-dimensional fiber μ ∼ μ₀ℓ_c/2π, where μ₀ is the gel shear modulus (54,62).

In simulations, the shear modulus G(v_f) was measured as a function of fiber volume fraction

$$v_f=8p{\left(\kappa /\alpha \right)}^{1/2}\left[1-2{\left(\kappa /\alpha \right)}^{1/2}\right],$$

where κ/α ∼ (r/ℓ_c)², and p is the fraction of occupied bonds. This expression is found by calculating the dependence of v_f on r for a unit cell. In the context of this work, v_f corresponds to the experimentally measured collagen volume fraction v_c; however, its meaning is more general. For example, in another experimental system, it may quantify the volume fraction of some other noncollagenous fibers. In each simulation run, p is systematically varied, the curve G(v_f) is determined, and the results normalized by G₀ = G[v_f(p = 1)] ∼ α/ℓ_c. As a simplification for quoting numeric values in the simulation results, we nondimensionalize and rescale all lengths by setting ℓ_c ≡ 1.

Simulations of network mechanics

We first simulated isotropic fiber networks without any reinforcing medium, i.e., a bare collagen network without aggrecan or depthwise variations. Here, percolation is purely a function of the network geometry and is controlled by p. Consistent with simple rigidity percolation on kagome lattices, we find that for p ≤ p₀ ≈ 0.6, too many bonds were missing to maintain a spanning-connected network. The elastic properties of the fibers in the network are governed by the fiber bending to stretching ratio κ/α, where physiological evidence suggests 10⁻⁴ ≤ κ/α ≤ 10⁻² (1). Therefore, we plot the dimensionless modulus G/G₀ versus v_f for this range of κ/α (Fig. 5, B and C).

The network mechanics are controlled by the balance of fiber stretching and bending. In all cases, response to shear is predominately bending-dominated near the percolation transition. At larger volume fractions, the behavior depends on the specific value of κ/α (Fig. 5 C). In the stiff limit where κ/α ∼ 10⁻², deformations are largely uniform at all length scales >ℓ_c. Here, G(v_f) changes relatively slowly with v_f and is governed by stretching elasticity. When κ/α ∼ 10⁻⁴, the filaments are floppier, deformations are nonaffine (63), and the macroscopic mechanics are set by the spatially localized interplay between stretching and bending. Correspondingly, we find that the curves for G/G₀ are relatively steeper in this limit.

To the bare fiber network, we added a reinforcing medium characterized by elastic modulus μ, and investigated the parameter range 10⁻⁷ ≤ μ/α ≤ 10⁻¹ (Fig. 5, B and D). The lower bound is an estimate based on rheology experiments of pure aggrecan gels (50), whereas the upper bound is a coarse approximation for the effective modulus when it contains fragmented nonpercolating fibers, i.e., it acts as fiber-reinforced composite. The underlying assumption for this bound is that the shear modulus of the supporting medium is dominated by the rheology of the nonpercolating fibers, and hence can be related to the stretching modulus α by setting μ₀ to the maximum possible value G₀. At the microscale, the reinforcing medium interacts with the fiber network by elastically resisting transverse deformations. At the macroscale, global deformations of the fiber network occur in parallel to the reinforcing gel, such that the macroscopic modulus is the sum of two contributions:

$$G\left(v_f\right)=G_{\text{fiber}}\left(v_f,\mu /\alpha \right)+{\mu }_0\left(1-v_f\right).$$

The first term is the supported fiber network, which explicitly depends on μ; and the second is the gel shear modulus multiplied by its volume fraction 1 − v_f.

In simulations, we found the reinforcing medium can significantly enhance G(v_f) by suppressing nonaffine deformations of the fiber network, especially near the percolation transition (Fig. 5 D). Below the percolation transition, the modulus is dominated by the properties of the reinforcing medium. Collectively, the reinforcing medium sets a lower bound for the shear modulus while still allowing for orders-of-magnitude variation in G(v_f) above the percolation threshold (Fig. 5 D). Although these results were obtained with fixed κ/α = 5 × 10⁻³, qualitatively similar trends were found at other values tested.

To illustrate how the simulation relates back to depth-dependent mechanical measurements, we replaced the isotropic random lattices with lattices that have depthwise variations. Spatial heterogeneity was introduced using the experimentally measured v_c(z) from sample PFG 1 in place of the otherwise uniform v_f (Fig. 6 A). Model parameters, which were optimized using a Newton iteration procedure to best match the empirical structure-function relationship, were set to κ/α = 4 × 10⁻³ and μ/α = 10⁻¹ (Fig. 6 B, R² = 0.59). As a check of the simulation, we set G₀ = 1 MPa, r = 1 μm (1), and redimensionalize the model parameters to find the Young’s modulus of the fiber Y ∼ 1 GPa, the fiber cross-linking length ℓ_c ∼ 10 μm, and the reinforcing medium shear modulus μ₀ ∼ 100 kPa. The values for Y and ℓ_c are consistent with experiments that have measured the modulus (64), and transmission electron microscopy studies that have imaged individual collagen fibers (58). The value for μ₀ indicates the modulus of the supporting medium is much higher than that of pure aggrecan gels, suggesting it is strongly reinforced with nonpercolating fibers. Thus, we generated a G/G₀-versus-z curve with depthwise variations in the collagen volume fraction (Fig. 6 C, red line, R² = 0.58). As expected, this reproduced all of the salient features associated with the experimental measurements of the depth-dependent shear modulus.

Figure 6.

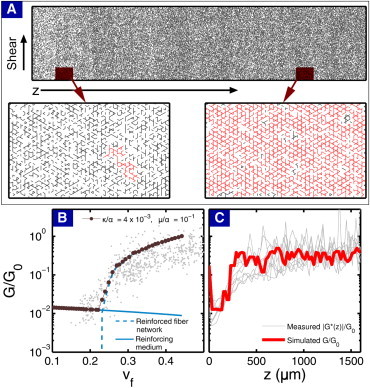
(A) Using wet volume fraction data from sample PFG 1, we generated a kagome lattice that is random and isotropic along the direction of shear, but has a varying density of bonds along the z axis. (Zoomed insets) The region near the articular surface is below the percolation threshold; the region at greater z is better connected. (Insets) (Red) Largest percolating cluster in the zoomed in section of the network; (black) remaining network. In regions below the percolation threshold, stresses are transmitted by the supporting background medium. (B) For specific model parameters, a comparison between experiment (light gray points) and simulation (dark gray points) show reasonable agreement. The shear modulus is decomposed into contributions from the reinforced fiber network G_fiber(v_f,μ/α), dashed blue) and the reinforcing medium (μ₀(1 – v_f), solid blue). For low v_f, the fiber network does not percolate across the system and the reinforcing medium dominates. At a critical connectivity threshold, the fiber network forms a spanning cluster and stresses can be transmitted across the system. This effect rapidly dominates with increasing v_f, but becomes less sensitive at higher volume fractions. (C) The spatially homogeneous v_f is replaced with experimentally measured v_c(z) from PFG 1 to generate a depth-dependent G(z) profile (red), which, when superimposed on experimental data (light gray lines), shows qualitatively similar behavior. To see this figure in color, go online.

Conclusions

In this work, we distilled neonatal bovine AC microstructure into three basic elements: collagen fiber alignment, collagen content, and aggrecan content. Neonatal bovine tissue was used in this study for two reasons: First, similar depth-dependent shear modulus profiles have been reported in both young bovine and adult human tissue (12,13,16–18), suggesting the phenomenon is quite robust and arises independent of age; and second, young tissue generally has less collagen fiber organization, which helps deconvolve this factor from the shear properties, effectively reducing the chance of a false-positive. Our empirical observations demonstrate that fiber alignment cannot fully account for this tissue’s small amplitude shear properties. Moreover, we find that very small differences in the collagen content correlate with large changes in the shear modulus. As illustrated with the rigidity percolation model, this sensitivity can be explained by viewing the collagen fibers as a percolating network near its rigidity threshold. With respect to design principles, this shift of emphasis away from fiber alignment is conceptually important because it elevates the role of network connectivity, which tends to be lost in continuum elasticity. The implications for tissue engineering are highly suggestive, because it indicates that increasing cross-linking and fiber rigidity may be more effective than increasing fiber density when culturing cartilaginous tissues intended to mimic AC’s material properties.

Beyond the small strain measurements described here, large strain experiments present further challenges to understanding AC, where, for example, strain stiffening has been previously reported (13,61,65,66). Within the context of the percolating fiber network model, this behavior can arise from buckled fibers that experience no tension at small strain, and hence act as nonpercolating elements. At large strain, these buckled fibers can straighten out, mediate stresses, and contribute to the mechanical response. This point is important, inasmuch as it is not included in the proposed model and changes the interpretation of the rigidity percolation threshold as being strain-dependent. From this perspective, simulations that cross below the percolation threshold are still percolating from the connectivity point of view, but nonpercolating in the sense that they do not mediate stresses. Experimental measurements of the relative fiber motion looking for bending, stretching, or sliding behavior would provide significant insights on this question. Clearly, progress exploring such ideas requires more detailed simulations coupled with higher-resolution confocal elastography studies that further investigate the microscopic details of AC shear mechanics.