Summary
In epidemiologic studies of time to an event, mean lifetime is often of direct interest. We propose methods to estimate group- (e.g., treatment-) specific differences in restricted mean lifetime for studies where treatment is not randomized and lifetimes are subject to both dependent and independent censoring. The proposed methods may be viewed as a hybrid of two general approaches to accounting for confounders. Specifically, treatment-specific proportional hazards models are employed to account for baseline covariates, while inverse probability of censoring weighting is used to accommodate time-dependent predictors of censoring. The average causal effect is then obtained by averaging over differences in fitted values based on the proportional hazards models. Large-sample properties of the proposed estimators are derived and simulation studies are conducted to assess their finite-sample applicability. We apply the proposed methods to liver wait list mortality data from the Scientific Registry of Transplant Recipients.
Keywords: Counterfactual, Cumulative treatment effect, Inverse weighting, Proportional hazards model
1. Introduction
Often in clinical and epidemiologic studies, groups of subjects are compared with respect to their survival times. Since any study is of finite duration, the time until the event of interest may be censored. Typically in observational studies, the factor of interest is not randomized (e.g., method of treatment) and may not even be assigned (e.g., race, gender, diagnosis), necessitating some form of covariate adjustment, such as that obtained through regression modeling. Since its development, the proportional hazards model (Cox, 1972) has dominated the biomedical literature as the method of choice for the regression modeling of censored data.
The popularity of the Cox model among practitioners and, by now, clinical investigators makes it an attractive means of comparing groups in observational studies. In Cox regression, the impact of each covariate is usually summarized by its effect on the hazard function. However, when comparing groups of subjects, investigators are often more interested in differences in mean lifetime than ratios of hazard functions. The survival time distribution may be heavily right skewed. Moreover, for semi- or non-parametric modeling, the mean is not well estimated; e.g., the estimated survival function need not drop td alternative is the restricted mean lifetime; i.e., for fixed L > 0, if T denotes survival time, then the restricted mean lifetime is defined as E{min(T, L)}. Restricted mean lifetime can also be expressed as , the area under the survival curve over (0, L], a quantity easily understood by clinical investigators. For example, if L =5 years, one could interpret E{min(T, L)} as the average number of years lived out of the next 5. Restricted mean lifetime is typically of greater interest to clinicians than the usual Cox metric, the hazard ratio. In fact, in certain settings E{min(T, L)} may be of more interest than E(T) itself. For example, in the context of pediatric liver transplantation, it is almost always that case that a child receiving a liver transplant will need a second liver transplant in the next 10 years. Hence, using T to represent post-transplant survival time, survival after the first 10 years of post-transplant follow-up could not be realistically assumed to be due to the initial liver transplant; making E{min(T, 10)} of greater relevance than E(T).
This article is motivated by the desire to compare wait list survival among end-stage liver disease (ESLD) patients listed for liver transplantation. A frequent cause of chronic liver disease is Hepatitis C virus (HCV), the primary diagnosis for approximately 40% of ESLD cases. Liver transplantation is the preferred treatment for ESLD, but there are far more patients awaiting transplantation than there are available donor organs. The principle underlying the current system for allocating deceased-donor livers in the U.S. is that priority for transplantation should be based on a patients's death rate in the absence of liver transplantation. Specifically, the patients most likely to die on the wait list should get top priority for transplantation. Currently, patients on the liver transplant wait list are sequenced in decreasing order of Model of End Stage Liver Disease (MELD) score (Weisner et al, 2001). The MELD score is a function of three laboratory measures indicative of liver function, but does not consider underlying liver disease. It is suspected that HCV+ patients have lower wait list survival than HCV- patients. However, few studies have directly compared mean wait list survival time by diagnosis group. To our knowledge, no published analysis has compared mean wait list survival times (i.e., survival, in the absence of liver transplantation) between HCV+ and HCV- patients. Therefore, our objective is to estimate the difference between wait list lifetime between HCV+ and HCV- patients, adjusting for baseline (i.e., time 0) characteristics (e.g., age, gender, race, MELD score).
Comparison of liver wait list survival times is complicated by the potential for dependent censoring. Specifically, death on the liver wait list is censored by the receipt of a liver transplant, and such censoring is not independent of the survival time that would have been observed on the wait list, even conditional on the baseline adjustment covariates. A given patient's MELD score typically changes over time. The updating of MELD scores is mandatory, meaning that a longitudinal sequence of MELD scores is observed for each patient. As discussed by several previous authors in the context of causal inference (e.g., Robins, 2000; Hernan et al 2000, 2001), a comparison of survival time by HCV status should not adjust for internal time-dependent covariates, as defined by Kalbfleisch and Prentice (2002). The fact that time-dependent MELD strongly affects both wait list mortality and censoring (liver transplantation) means that lack of its adjustment (i.e., by adjusting for baseline values only) will result in the dependent censoring of wait list death time via liver transplantation.
Various authors have proposed methods for comparing restricted mean survival time in the context of Cox regression (e.g., Karrison, 1987; Zucker, 1998; Chen and Tsiatis, 2001). For example, the method of Chen and Tsiatis (2001) proposes fitting separate group-specific Cox models, then averaging over the fitted restricted mean lifetimes, with the averaging being with respect to the covariate distribution of the entire study sample. These approaches have several nice properties. First, it is not required that treatment-specific hazards be proportional. Second, an ‘overall’ treatment effect estimator is obtained, without assuming that treatment-specific adjustment covariate effects are equal. Third, the target treatment effect is interpretable as an average over a well-defined covariate distribution. However, each of the afore-listed methods assumes that censoring conditionally independent of the survival time, conditional on baseline adjustment covariates.
We propose methods for estimating group-specific differences in restricted mean lifetime, for the setting in which survival time is dependently censored. The structure of the hazard model we assume is very flexible, allowing for group-specific baseline hazards and regression coefficients. In its most general form, this amounts to fitting separate models for each treatment group. The dependent censoring is overcome through the well-established inverse probability of censoring weighting (IPCW); see Robins and Rotnitzky (1992), Robins (1993); Robins and Finkelstein (2000).
The remainder of this article is organized as follows. In Section 2 we set up the notation and formalize the problem of interest. The proposed methods are described in Section 3. Asymptotic properties are listed in Section 4, with corresponding proofs given in the Web Appendix. In Section 5, a simulation study is presented. The proposed methods are applied to national liver wait list data in Section 6. The article concludes with a discussion in Section 7.
2. Notation and Data Structure
Suppose we are interested in comparing two groups (A = 0, 1), which are not randomized, in terms of restricted mean lifetime up to time L. We denote the survival time by T. As in almost all studies involving time to an event, the event time T may be censored due to various reasons. Two types of censoring are considered in the following development. We let C1 denote censoring which is independent conditional on baseline covariates, Z, and group indicator, A; e.g., censoring due to the end of study. We let C2 denote dependent censoring; i.e., censoring which is not independent of T given (Z, A). For example, in the context of the data which motivated our work, a patient's wait-list mortality is censored if and when the patient receives a liver transplant and the transplant hazard and wait list mortality hazards may be correlated, even conditional on (Z, A), through mutual dependence on time-dependent covariates (e.g., MELD score). In notation, we assume that C1╨T|Z, A, where ╨ denotes “independent of ”; while C2 is not assumed to satisfy this condition. In practice, one observes the minimum of the survival time and time to censoring. We therefore let U = T ∧ C1 ∧ C2 represent the observation time and define indicators for observing the failure time and dependent censoring times: Δ1 = I(T ≤ C1 ∧ C2) and Δ2 = I(C2 ≤ T ∧ C1), respectively. We let X†(t) represent the time-dependent covariate at time t. Note that X†(0) would include the elements of Z and potentially other factors predictive of C2. We let X̃(t) = {X†(u); u ∈ [0, t)} denote the history of all baseline and time-dependent covariates up to just before time t. The observed data may be summarized as Oi = {Ai, Ui, Δ1i, Δ2i, Zi, X̃i(Ui)}, with the Oi assumed to be independent and identically distributed (iid) across i = 1,…, n. Note that the set of observed variates is redundant, in the sense that X̃(t) includes all baseline covariates Z; however, this representation is convenient for presentation purposes.
To define the parameter of interest, we follow the potential outcome framework studied by Rubin (1974 Rubin (1978) and adopted by Chen and Tsiatis (2001). Let T0 denote the potential (or counterfactual) lifetime for a randomly selected subject from the population if, possibly contrary to the fact, s/he were in group 0, and similarly T1 the potential random variable corresponding to group 1. In reality, T0 and T1 are never observed simultaneously for a subject and the (possibly) observed survival time T relates the two-dimensional potential outcomes (T0, T1) through T = I(A = 0)T0 + I(A = 1)T1. The group-specific difference in restricted mean lifetime is defined as
| (1) |
Under the assumption that(T0, T1)╨A|Z, it follows that P(T > t|A = j, Z) = P(Tj > t|A = j, Z) for j = 0, 1. Although defined through potential outcomes, the parameter of interest, δ, can then be expressed in terms of observable variates as
| (2) |
where the expectation EZ is taken respect to the marginal distribution of Z. When A is an indicator of treatment, δ has the interpretation of average causal treatment effect. We set Sj(t|Z) = P(T > t|A = j, Z) and Sj(t) = EZ{Sj(t|Z)} for j = 0, 1.
Estimators for δ are proposed by Chen and Tsiatis (2001) under the assumption of independent censoring. That is, in our notation, it was assumed that censoring C2 does not exist. Using sample averages to estimate expectations, if one can obtain estimators for S0(t|Z) andS1(t|Z), say, Ŝ0(t|Z) and Ŝ1(t|Z) respectively, then a natural estimator for δ is given by
| (3) |
3. Methods
As argued in the previous section, we wish to model the conditional survival function of T given baseline covariates and group indicator, Sj(t|Z), j = 0, 1. Because of its flexibility and popularity in practice, we adopt the Cox's proportional hazards model (Cox, 1972, 1975) and, in the following development, we work with the more general model where both baseline hazards functions and regression coefficients of Z are allowed to vary by group. Specifically, it is assumed that
| (4) |
where λ(t|Zi, Ai = j) denotes the conditional hazard function given baseline covariates Zi and membership in group Ai = j, while λ0j(t) is the unspecified baseline hazard function for group A = j.
We now describe how to estimate parameters for model (4). To begin, suppose that C2i was not dependent censoring, but was instead another form of censoring that was conditionally independent of T given (Z, A). In this case, βj could be consistently estimated by the maximum partial likelihood estimator, , which could be computed as the root of the estimating equation,
| (5) |
where τ satisfies P(U ⩾ τ) > 0 and, in practice, can be set to the maximum observation time in the study; Nij(t) = I(Ai = j)I(Ui ≤ t,Δ1 i = 1); and Yij(t) = I(Ai = j)I(Ui ⩾ t). Additionally, could be consistently estimated by the Breslow estimator,
| (6) |
From a different perspective, and are the solutions to the following estimating equations,
| (7) |
| (8) |
respectively, where dMij(t;β,Λ) = dNij(t) − Yij(t)eβT ZidΛ(t) and dMij(t) ≡ dMij(t;βj, Λ0 j). Under the assumption that (C1 i, C2 i)╨Ti|(Ai, Zi), we have E{dMij(u)|Zi, Ai} = 0 and E{Zi dMij(u)|Zi, Ai} = 0 such that (7) and (8) have mean zero at the true parameter values.
However, as stated previously, although C1i ╨Ti |(Ai, Zi), it is not the case that C2i╨Ti|(Ai, Zi). As a result, neither (7) nor (8) have mean zero at the truth, meaning that consistent estimators of βj and Λ0j(t) cannot be obtained from (5) and (6) respectively. We assume that the dependence of C2i and Ti occurs through (and only through) the time-dependent process, X̃i(Ui); i.e., observed data. That is, we assume that C2i is conditionally independent of Ti given {Zi, Ai, X̃i(Ui)}; a condition we can express formally as follows,
| (9) |
Assumption (9) is the critical “no unmeasured confounders” (Rubin, 1977; Robins, 1993) for censoring assumption. In our setting, the assumption essentially states that the hazard of being censored by C2 at time t depends only on observed data up to time t and not additionally on future possibly unobserved data. We define the hazard function for the dependent censoring time, C2i for a subject in group j as
then set .
We return now to the issue of estimating the parameters in (4). Reconsidering (7) and (8), although E{dMij(t)|Zi, Ai} ≠ 0, under (9), it can be shown that (Robins and Finkelstein, 2000) and, after iterating the expectation, that . More generally, it can be shown that E{Wij(t)dMij(t)|Zi, Ai} = 0, where , where the function κ(t;Zi, Ai) acts as a stabilization factor. Similarly, it can be shown that E{Wij(t)Zi dMij(t)|Zi, Ai} = 0. Combining these zero-mean properties suggests the following set of inverse probability of censoring weighted (IPCW) estimating equations,
| (10) |
| (11) |
Substituting the solution to (10) into (11) then re-organizing algebraically suggests that βj be estimated by the solution to
| (12) |
and that the weighted Breslow estimator,
| (13) |
be used to estimate Λ0j(t) for j = 0, 1.
The estimators in (12) and (13) are Inverse Probability of Censoring Weighting (IPCW) estimators (Robins and Rotnitzky, 1992; Robins, 1993; Robins and Finkelstein, 2000). The quantity can be thought of heuristically as the inverse of the probability of not having been dependently censored as of time t. Note that X̃i(t) is an internal time-dependent covariate (Kalbfleisch & Prentice, 2002); i.e., a process generated by subject i (as opposed to an external time-dependent covariate such as temperature or air quality). Therefore, is not actually a probability, per se, but a product of conditional probabilities. Nonetheless, using Robins' Fundamental Identities (Robins & Rotnitzky, 1992; Robins and Finkelstein, 2000), it can be shown that the estimating function in (12) can be expressed as a (dependent censoring process) Martingale integral and hence has mean 0; a proof for which is outlined in Section 2 of the Web Appendix. The function κ(t; Ai, Zi) can be any function of Zi and Ai (since these are conditioned upon by model (4) anyway) and is intended to stabilize the weighted estimators. In particular, could be quite large towards the tail of the observation time distribution, which would result in weights which are quite large. One choice of κ which has been suggested (e.g., Robins and Finkelstein, 2000; Hernán, Brumback, and Robins, 2000) is . While would be based on a time-to-censoring model which used X̃i(t−) as covariates, would only use the baseline values. If censoring was in fact independent, then Wij(t) would tend towards 1. κ(t; Ai, Zi) = 1, which may be appropriate if censoring is light or moderate, in which case Wij(t) does not get unduly large. Hereafter, we refer to κ(t; Ai, Zi) = 1 as the ‘unstabilized’ estimator. Stabilized estimators are intended to be more efficient than the unstabilized version, at the expense of additional modeling effort.
In practice, in the weight function is unknown to us and therefore has to be modeled and estimated. To fit models for the dependent censoring time C2 i, one uses Ui as the censored time variable but use Δ2i as the indicator for observing C2i. Again, due to its flexibility, the proportional hazards model is a natural choice for the dependent censoring time, C2i, with the model being conditional on the group indicator and both baseline and time-dependent covariates. To allow for more flexibility in modeling and hence robustness in estimating the weight, one could fit group-specific Cox models,
where , j = 0, 1, are unspecified group-specific baseline hazard functions for C2i and Xi(t) is a function of X̃i(t) determined empirically (e.g., using standard model selection techniques, such as stepwise regression) to satisfy . Based on the fitted model, one can estimate by , which can then be used to compute the estimated weight function, Ŵij(t).
Having estimated βj and Λ0 j(t), one can correspondingly estimate Sij(t) ≡ Sj(t|Zi) by
| (14) |
Finally, the proposed estimat or for difference in restricted mean lifetime δ is then given by
| (15) |
where for j = 0, 1.
The key step in implementing the proposed method is to solve the weighted estimating equation (12), for which existing software may be exploited. For example, one can use proc phreg (SAS Institute; Cary, NC) with the counting process input format and the weight option. Correspondingly, Λ̂0 j(t) and Ŝij(t) can be easily obtained. Estimating the variance is more involved, requiring additional programming (e.g., SAS's proc iml). For illustrative purpose, a SAS macro implementing the proposed methods is available at http://www.sph.umich.edu/mzhangst/.
4. Asymptotic Properties
In this section, we derive the asymptotic properties of the proposed estimators given by (15). To begin, we specify the regularity conditions, assumed to hold for i = 1,…, n and j = 0, 1.
{Ai, Zi, Ui, Δ1i, Δ2 i, X̃i(Ui)} are independent and identically distributed.
P(Ui ⩾ τ) > 0.
|Zik| < bz and , where bz < ∞ and bX < ∞, and k denotes the kth element.
Λ0j(τ) < ∞; .
-
For d = 0, 1, 2,
where we define
with z⊗0 = 1, z⊗1 = z and z⊗2 = zzT.
-
The matrices Ωj(βj) and are assumed to be positive-definite, where
with and .
-
P(Ai = j|Zi) ∈ (0, 1).
Variations on Condition (a) are possible, although at the expense of additional technical (e.g., Lindeberg-type) conditions. Condition (b) is a standard identifiability criterion. The boundedness implied by Condition (c) helps ensure the convergence of the several stochastic integrals used in the proofs; the same can be said for Condition (d). The second-derivative matrices in condition (f) are at least non-negative definite and will be positive-definite under any sensible specification of the covariate vectors. Condition (g) is the well-known positivity requirement from the causal inference literature. If it fails, δ fails to have a causal interpretation.
We describe the primary asymptotic result for our proposed unstabilized group effect estimator in the following theorem.
Theorem 1: Under conditions (a) ‒ (g), as n → ∞, δ̂ converges in probability to δ, and for the unstabilized estimator, n1/2(δ̂ ‒ δ) converges to a zero-mean Normal with variance E{(ϕi1 − ϕi0)2}, where
where and with Φij(t) and Uij(βj) defined in the Web Appendix.
The variance can be consistently estimated by , where ϕ̂ij is obtained by replacing limiting values in ϕij with their empirical counterparts. However, as shown in the Web Appendix, the computation of ϕ̂ij is quite complicated owing to the complexity of Ûij(β̂j) and Φ̂ij(t). As a result, estimating the variance through ϕ̂ij is very inconvenient computationally. A computationally attractive alternative is to estimate Var(δ̂) by , where is obtained by replacing Ûij(β̂j) and Φ̂ij(t) with and , respectively, where
The key difference between ϕ̂ij and
is that the former accounts for the fact that Ŵij(t) is estimated, while is derived with Ŵij(t) treated as fixed.
We refer to (ϕi1 − ϕi0) in Theorem 1 as the influence function of δ̂, which satisfies . The asymptotic results stated in Theorem 1 are for the unstabilized estimator with the stabilization factor κ(t; Ai, Zi) = 1. As equations (12) and (13) are unbiased estimating equations for general κ(t; Ai, Zi), by similar argument, it can be shown that consistency and asymptotic normality hold for estimators with κ(t; Ai, Zi) ≠ 1 but the form of influence function will be different and even more complicated. Therefore, treating the weights as fixed would be a practical way to estimate the variance of the proposed estimators. As demonstrated in the Web Appendix, for general κ(t;| Ai, Zi), Var(δ̂) can still be estimated by with specified previously. According to Tsiatis (2006) Chapter 9.1, the influence function of δ̂, if the weight is estimated, is the projection of the influence function when weight is known and fixed onto the orthogonal complement of the nuisance tangent space; e.g., the spaces associated with the nuisance baseline hazard function and nuisance parameter θj in the model for C2. As the true influence function is a projection, its variance is smaller than the influence function if weight is fixed and therefore the proposed variance estimator will be conservative in estimating the variance of δ̂ where weight is actually estimated. This point is discussed by several previous authors (Hernán et al. 2000 and 2001; Pan and Schaubel, 2008). The effect of estimating the weight is slight, as will be demonstrated empirically in the next section.
5. Simulation Study
We report on simulations to evaluate performance of the proposed methods. Results of two other methods are also reported: a naive method, which estimates δ by taking difference in areas under group-specific Kaplan-Meier curves from time 0 to L and consequently ignores all possible confounding, and the method proposed by Chen and Tsiatis (2001), which adjusts for baseline covariates but not time-dependent confounders for censoring.
Data were generated under three scenarios, corresponding to different confounding mechanisms and, in each scenario, two different percentages of censoring were considered, referred to as light censoring or heavy censoring cases. Specifically, in each scenario, for the light censoring case, about 20% subjects are censored by C2 and about 5% are censored by C1, and for the heavy censoring case, about 30% subjects are censored by C2 and about 10% are censored by C1. All reported results are based on 2000 Monte Carlo datasets, and L is chosen to be 15.
In the first scenario, data were generated such that both baseline and time-dependent confounders exist. For each Monte Carlo dataset, a single baseline confounder Z was generated as a truncated standard normal, truncated at -4 and 4 on each side, and group indicator A as Bernoulli with parameter exp(−0.6Z)/{1 + exp(−0.6Z)}. Survival time T was generated by transforming ε1 ∼ Uniform (0, 1) using the inverse of the cumulative distribution function (cdf) of a Weibull distribution with shape parameter 1.25 and scale parameter exp(−0.3Z− 3.3) for group A = 1 or exp(−0.4Z−3) for A = 0. We then generated dependent censoring C2 such that it depends both on baseline and time-dependent covariates as follows. In order for a time-dependent covariate to be a confounder, it should be correlated both with T and C2 conditioning on (A, Z). To achieve this, we first generated Xt such that Xt = −5log{Aε1 + (1 − A)(1 − ε1)} + ε2, where ε2 ∼ Uniform(0, 1), independent of all other variables, and then let X(t) = I(Xt ⩾ t). Consequently, the time-dependent covariate X(t) is correlated with survival time T through their mutual relationships with ε1 and such correlation exits even conditioning on (A, Z). Next, we generated dependent censoring time C2 using a proportional hazards model with hazard rate exp{γ1 + 0.2A + 0.2Z+γ2X(t)}. This procedure ensures that X(t) is a time-dependent confounder and C2 follows a proportional hazards model with Z and X(t) as our model assumes. Finally, censoring time C1 was generated as Weibull with shape and scale parameters 3 and exp(γ3) respectively. The coefficients (γ1, γ2, γ3) are set to (-5.1, 1.5, -11) for light censoring case and to (-4.45, 1.5,-9.7) for heavy censoring case.
In the second scenario, data were generated such that, conditioning on (A, Z), timedependent covariate X(t) correlates only with survival time T but not with censoring time C2 and therefore it is not a confounder if (A, Z) is properly adjusted for. We compare the proposed methods with the Chen and Tsiatis (2001) method, which should be consistent and asymptotically normal under this scenario. Data are generated similarly as before except for that γ2 was set to 0, ensuring that X(t) does not affect C2. Specifically, we chose (γ1, γ2, γ3) equal to (-4, 0, -11) for light censoring case and equal to (-3.4, 0, -9.7) for heavy censoring case.
In the third scenario, we let the time-dependent covariateX(t) be conditionally independent of survival time T but still correlated with censoring time C2 and, consequently, is not a confounder either. Data were generated the same as in scenario one except for that Xt = —51og{Aε3 + (1 — A)(1 — ε3)} + ε2, where ε3 ∼ Uniform(0, 1), independent of all other variables. We evaluate how the proposed methods compare with those of Chen and Tsiatis (2001), which should be unbiased under this scenario. All coefficients are set equal to those used in scenario 1.
Tables 1 and 2 list the results of our simulation study. The proposed estimators (unstabilized or stabilized) are consistent for the true parameter under all scenarios, whereas the Chen and Tsiatis (2001) method leads to biased estimators under scenario 1, where a time-dependent confounder exists. The naive estimator is biased under all three scenarios, where baseline or/and time-dependent confounders exist. Although the variance is estimated by treating the estimated weight as fixed, coverage probabilities of the proposed estimators achieve the nominal level. On the other hand, due to the non-ignorable bias, coverage probabilities of the other two estimators are very low, illustrating that the impact of confounders can be severe if they are not properly accounted for in the analysis.
Table 1.
Estimators for difference in restricted mean lifetime under scenario 1-3, light censoring case (2000 Monte-Carlo datasets; sample size: 1000; True is the true value of parameter; MC Bias is the Monte Carlo Bias; MC SD is the Monte Carlo standard deviation of estimates; Ave. SE is the Monte Carlo average of estimated standard errors; CP is the coverage probability of nominal 95% Wald confidence intervals.)
| Method | True | MC Bias | MC SD | Ave. SE | CP |
|---|---|---|---|---|---|
| Light Censoring, Scenario 1 | |||||
| Unstabilized Inverse Weighting | 1.172 | 0.021 | 0.319 | 0.327 | 0.950 |
| Stabilized Inverse Weighting | 1.172 | 0.015 | 0.317 | 0.327 | 0.952 |
| Chen & Tsiatis' Method | 1.172 | 0.316 | 0.321 | 0.324 | 0.840 |
| Naive | 1.172 | -0.429 | 0.325 | 0.332 | 0.755 |
| Light Censoring, Scenario 2 | |||||
| Unstabilized Inverse Weighting | 1.172 | 0.005 | 0.321 | 0.330 | 0.954 |
| Stabilized Inverse Weighting | 1.172 | 0.002 | 0.321 | 0.330 | 0.953 |
| Chen & Tsiatis' Method | 1.172 | 0.005 | 0.323 | 0.329 | 0.953 |
| Naive | 1.172 | -0.729 | 0.326 | 0.336 | 0.422 |
| Light Censoring, Scenario 3 | |||||
| Unstabilized Inverse Weighting | 1.172 | -0.013 | 0.337 | 0.328 | 0.939 |
| Stabilized Inverse Weighting | 1.172 | -0.016 | 0.337 | 0.327 | 0.936 |
| Chen & Tsiatis' Method | 1.172 | -0.017 | 0.336 | 0.326 | 0.934 |
| Naive | 1.172 | -0.746 | 0.341 | 0.332 | 0.392 |
Table 2. Estimators for difference in restricted mean lifetime under Scenario 1-3, heavy censoring case (entries are as in Table 1).
| Method | True | MC Bias | MC SD | Ave. SE | CP |
|---|---|---|---|---|---|
| Heavy Censoring, Scenario 1 | |||||
| Unstabilized Inverse Weighting | 1.172 | 0.040 | 0.331 | 0.342 | 0.948 |
| Stabilized Inverse Weighting | 1.172 | 0.050 | 0.334 | 0.344 | 0.947 |
| Chen & Tsiatis' Method | 1.172 | 0.593 | 0.334 | 0.337 | 0.584 |
| Naive | 1.172 | -0.157 | 0.339 | 0.344 | 0.926 |
| Heavy Censoring, Scenario 2 | |||||
| Unstabilized Inverse Weighting | 1.172 | 0.006 | 0.329 | 0.329 | 0.959 |
| Stabilized Inverse Weighting | 1.172 | 0.003 | 0.328 | 0.346 | 0.960 |
| Chen & Tsiatis' Method | 1.172 | 0.004 | 0.334 | 0.345 | 0.956 |
| Naive | 1.172 | -0.725 | 0.344 | 0.350 | 0.455 |
| Heavy Censoring, Scenario 3 | |||||
| Unstabilized Inverse Weighting | 1.172 | -0.009 | 0.350 | 0.345 | 0.936 |
| Stabilized Inverse Weighting | 1.172 | -0.014 | 0.348 | 0.343 | 0.941 |
| Chen & Tsiatis' Method | 1.172 | -0.015 | 0.345 | 0.340 | 0.940 |
| Naive | 1.172 | -0.743 | 0.348 | 0.344 | 0.424 |
Under scenarios 2 and 3, where there are no time-dependent confounders, the usual partial likelihood estimator is semiparametric efficient in estimating coefficients of a Cox proportional hazards model. Therefore, the Chen and Tsiatis (2001) method can be used as a benchmark to evaluate the loss of efficiency of the proposed methods due to inverse probability weighting. Our results demonstrate that stabilized version of the proposed estimator behaves very similarly to the estimator of Chen and Tsiatis (2001). This would be expected since the weights would tend towards 1 in this scenario, such that the loss of efficiency (corresponding to the unstabilized weighting) is only mild. In addition, simulation results suggest that the effect of the stabilization factor, κ(t; Z, A), on the efficiency is more pronounced for estimators of the Cox regression parameter, compared to the estimators of δ. Results in Table 3 show that, at least under the simulated scenarios, stabilization results in considerable efficiency gains for β̂j but only mild increases in precision for δ̂.
Table 3.
Comparing efficiency of the unstabilized and stabilized inverse weighting methods in estimating δ in (1) and coefficients of Cox's proportional hazards models in (4) (δ̂ is weighted estimator for δ; β̂j is weighted estimator for βj in (4), j = 0, 1; RE is the relative efficiency compared to the unstabilized inverse weighting method, calculated as the square of the ratio of the Monte Carlo standard deviation for the unstabilized inverse weighting estimator over that for the indicated estimator)
| Method | β̂1 | β̂0 | δ̂ | |||
|---|---|---|---|---|---|---|
| MC SD | RE | MC SD | RE | MC SD | RE | |
| Light censoring, Scenario 1 | ||||||
| Unstabilized Inverse Weighting | 0.059 | 1 | 0.058 | 1 | 0.319 | 1 |
| Stabilized Inverse Weighting | 0.057 | 1.085 | 0.055 | 1.114 | 0.317 | 1.011 |
| Light censoring, Scenario 2 | ||||||
| Unstabilized Inverse Weighting | 0.058 | 1 | 0.058 | 1 | 0.321 | 1 |
| Stabilized Inverse Weighting | 0.057 | 1.035 | 0.057 | 1.060 | 0.320 | 1.004 |
| Light censoring, Scenario 3 | ||||||
| Unstabilized Inverse Weighting | 0.060 | 1 | 0.060 | 1 | 0.337 | 1 |
| Stabilized Inverse Weighting | 0.057 | 1.094 | 0.056 | 1.143 | 0.337 | 0.999 |
| Heavy censoring, Scenario 1 | ||||||
| Unstabilized Inverse Weighting | 0.069 | 1 | 0.066 | 1 | 0.334 | 1 |
| Stabilized Inverse Weighting | 0.063 | 1.195 | 0.059 | 1.250 | 0.331 | 1.016 |
| Heavy censoring, Scenario 2 | ||||||
| Unstabilized Inverse Weighting | 0.064 | 1 | 0.066 | 1 | 0.329 | 1 |
| Stabilized Inverse Weighting | 0.062 | 1.070 | 0.062 | 1.110 | 0.328 | 1.006 |
| Heavy censoring, Scenario 3 | ||||||
| Unstabilized Inverse Weighting | 0.069 | 1 | 0.072 | 1 | 0.350 | 1 |
| Stabilized Inverse Weighting | 0.062 | 1.217 | 0.063 | 1.320 | 0.348 | 1.024 |
6. Application
Data were obtained from the Scientific Registry of Transplant Recipients (SRTR). The study population (n = 6, 371) included all chronic liver disease patients initially wait listed for deceased-donor liver transplantation in the U.S. at age ⩾ 18 between March 1, 2002 and February 28, 2003. For each patient, the time origin (t = 0) was the date of wait listing. Patients were followed from that date until the earliest of death, receipt of a liver transplant, loss to follow-up and the end of the observation period: December 31, 2008.
The event of interest was wait list mortality. Independent censoring consisted of random loss to follow-up and administrative censoring at the end of the observation period. Dependent censoring occurred through liver transplantation which, although not preventing the observation of death, does preclude wait list death.
The objective of the analysis was to compare 5-year mean wait list survival time between Hepatitis C positive (HCV+) versus HCV- patients. HCV is a leading cause of chronic liver disease. Baseline adjustment covariates included the following factors, as measured at the time of wait initial listing: age, gender, race, region, Model for End-stage Liver Disease (MELD) score, serum albumin, sodium, bodymass index, diabetes, hospitalization status, ascites, dialysis and encephalopathy. The MELD score is a log linear combination of serum creatinine, bilirubin and international normalized ratio for prothrombin time. MELD has been shown to be a very strong predictor of wait list mortality. Currently, patients are ordered on the wait list in decreasing order of MELD score, such that the higher the MELD score, the greater the liver transplant hazard.
MELD is time-dependent, since a patient's score will be updated regularly. Other time-dependent covariates include dialysis, serum albumin, sodium and active and removal status. In the time-until-transplant model, each of these factors was represented in the time-dependent covariate vector. The Cox model for transplant was given by
| (16) |
where Ii(t) is an indicator for being inactivated from the wait and Ri(t) is an indicator for being removed from the wait list at time t. It is not possible for a patient to receive a transplant while they are inactivated (usually temporary) or removed (typically permanent). To fit model (16), we deleted patient subintervals where either Ii(t) = 1 or Ri(t) = 1. After model (16) was fitted, the IPCW weight was then computed using , such that the transplant hazard increment was set to 0 for each subinterval where the patient was either inactivated or removed.
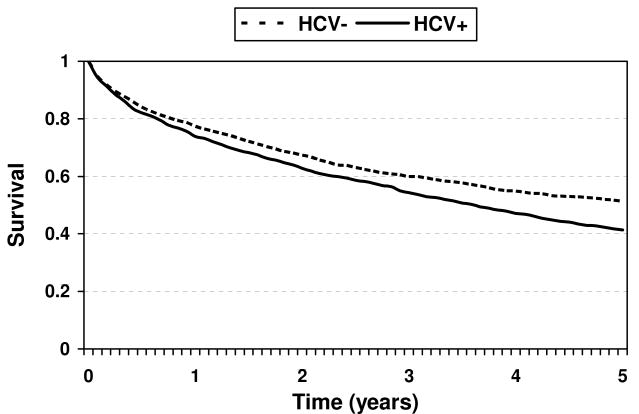
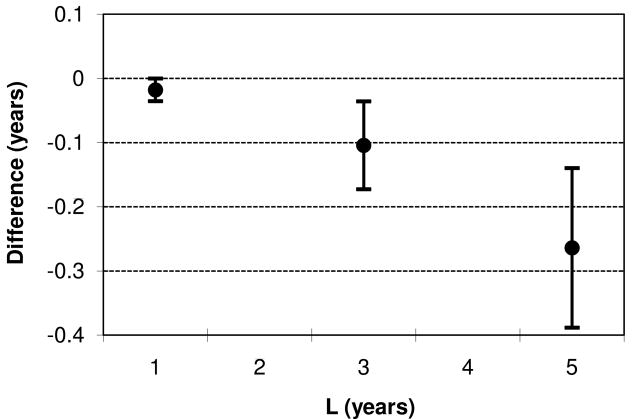
The study population consisted of 2,754 HCV+ (j=1) and 3,617 HCV- (j=0) patients. There were a total of 1,849 wait list deaths; 3,194 liver transplants and 1,328 independently censored subjects. Average survival curves are presented in Figure 1. Average wait list survival probability was 51% for HCV- patients at 5 years, compared to 41% for HCV+ patients. In Table 4, we compute 1-, 3- and 5-year average restricted mean wait list lifetime for HCV+ and HCV- patients. For each of L = 1, L = 3 and L = 5 years, average restricted mean lifetime is significantly greater for HCV- compared to HCV+ patients. In Figure 2, we plot the point estimates and 95% confidence intervals for δ.
Figure 1.
Average wait list survival probability for HCV- and HCV + patients at 5 years.
Table 4.
Average restricted mean wait list lifetime for HCV+ and HCV- patients restricted to L = 1, L = 3 and L = 5 years.
| L | μ̂1 | μ̂0 | δ̂ | SE (δ̂) | p |
|---|---|---|---|---|---|
| 1 | 0.83 | 0.85 | -0.02 | 0.01 | 0.047 |
| 3 | 2.10 | 2.21 | -0.11 | 0.03 | 0.002 |
| 5 | 3.04 | 3.31 | -0.26 | 0.06 | <0.0001 |
Figure 2.
Point estimates and 95% confidence intervals for differences in average restricted mean wait list lifetime between HCV+ and HCV- patients.
7. Discussion
In this article, we have proposed methods for estimating differences in restricted mean survival time between groups where group assignment is not randomized and, conditional on baseline covariates and group assignment, censoring may still be correlated with survival time. Differences in restricted mean lifetime may be of direct interest, and could also serve as a cumulative effect measure in settings where group-specific hazards are non-proportional. To be general, in our formulation, we considered that both conditionally independent and dependent censoring exist, which is often the case in practice; this formulation includes as a special case when only one type of censoring exits. The proposed methods employ two general approaches to account for two types of confounders. The proposed methods combine inverse probability of censoring weighting (e.g., Robins & Rotnitzky, 1992) and the procedure of explicitly averaging over the marginal covariate distribution (e.g., Chen & Tsiatis, 2001).
In our proposed procedure, computation is simplified by treating the IPCW weights as fixed. Since the inverse weights are actually estimated using the data, treating them as fixed should result in conservative confidence intervals and hypothesis tests, as reported by several previous authors (e.g., Pan & Schaubel, 2008; Hernán et al. 2000 and 2001). Our simulation results reveal the proposed standard error estimators and corresponding confidence intervals are quite accurate. An alternative to treating the weights as fixed would be to use the bootstrap, but this is much less convenient computationally.
The methods we propose require that the IPCW weight be correctly specified. The degree of bias introduced by misspecifying the Cox model for censoring would be expected to increase with increasing proportion of dependent (relative to independent) censoring; increasing strength of association (i) between the death hazard and time-dependent confounders and (ii) between the dependent censoring hazard and time-dependent confounders; and of course degree to which the IPCW model is misspecified. Fortunately, one can readily evaluate the fit of the proportional hazards model through well-established techniques and using standard software.
There are several alternatives to our proposed approach, one being joint modeling. For example, one could combine a mixed model for the longitudinal measurements with a hazard model which uses time-dependent covariates (e.g., Proust-Lima & Taylor, 2009). Or, one could also model mean residual survival time directly using pseudo-observations (Andersen, Hansen, and Klein, 2004). It could well be the case that the preferred method is a function of the data configuration. A detailed comparison of the three types of approaches would be very useful to practitioners.
Supplementary Material
Acknowledgments
This research was supported in part by National Institutes of Health grant R01 DK-70869 (DES). The authors thank the Scientific Registry for Transplant Recipients (SRTR) and Organ Procurement and Transplantation Network (OPTN) for access to the organ failure database.The SRTR is funded by a contract from the Health Resources and Services Administration (HRSA), U.S. Department of Health and Human Services.
Footnotes
Supplementary Materials Web Appendices, referenced in Section 4 are available under the Paper Information link at the Biometrics website http://www.biometrics.tibs.org.
References
- Andersen PK, Hansen MG, Klein JP. Regression Analysis of Restricted Mean Survival Time Based on Pseudo-Observations. Lifetime Data Analysis. 2004;10:335–350. doi: 10.1007/s10985-004-4771-0. [DOI] [PubMed] [Google Scholar]
- Chen P, Tsiatis AA. Causal inference on the difference of the restricted mean life between two groups. Biometrics. 2001;57:1030–1038. doi: 10.1111/j.0006-341x.2001.01030.x. [DOI] [PubMed] [Google Scholar]
- Cox DR. Regression models and life tables (with Discussion) Journal of the Royal Statistical Society, Series B. 1972;34:187–200. [Google Scholar]
- Cox DR. Partial likelihood. Biometrika. 1975;62:269–275. [Google Scholar]
- Hernán MA, Brumback B, Robins JM. Marginal structural models to estimate the causal effect on the survival of HIV-positive men. Epidemiology. 2000;11:561–570. doi: 10.1097/00001648-200009000-00012. [DOI] [PubMed] [Google Scholar]
- Hernán MA, Brumback B, Robins JM. Marginal structural models to estimate the joint causal effect of nonrandomized treatments. Journal of the American Statistical Association – Applications and Case Studies. 2001;96:440–448. [Google Scholar]
- Kalbfleisch JD, Prentice RL. The Statistical Analysis of Failure Time Data, 2nd Edition. New York: Wiley; 2002. [Google Scholar]
- Karrison T. Restricted mean life with adjustment for covariates. Journal of the American Statistical Association. 1987;18:151–167. [Google Scholar]
- Pan Q, Schaubel DE. Proportional hazards regression based on biased samples and estimated selection probabilities. Canadian Journal of Statistics. 2008;36:111–127. [Google Scholar]
- Proust-Lima C, Taylor JM. Development and validation of a dynamic prognostic tool for prostate cancer recurrence using repeated measures of posttreatment PSA: a joint modeling approach. Biostatistics. 2009;10:535–549. doi: 10.1093/biostatistics/kxp009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robins JM. Proceedings of the Biopharmaceutical Section, American Statistical Assocation. Alexander, Virginia: American Statistical Association; 1993. Information recovery and bias adjustment in proportional hazards regression analysis of randomized trials using surrogate markers; pp. 24–23. [Google Scholar]
- Robins JM. Robust estimation in sequentially ignorable missing data and causal inference models. Proceedings of the American Statistical Association Section on Bayesian Statistical Science. 2000;1999:6–10. [Google Scholar]
- Robins JM, Finkelstein D. Correcting for Non-compliance and Dependent Censoring in an AIDS Clinical Trial with Inverse Probability of Censoring Weighted (IPCW) Log-rank Tests. Biometrics. 2000;56:779–788. doi: 10.1111/j.0006-341x.2000.00779.x. [DOI] [PubMed] [Google Scholar]
- Robins JM, Rotnitzky A. AIDS Epidemiology - Methodological Issues. Birkhäuser; Boston: 1992. Recovery of information and adjustment for dependent censoring using surrogate markers; pp. 297–331. [Google Scholar]
- Rubin DB. Estimating causal effects of treatments in randomized and nonrandomized studies. Journal of Educational Psychology. 1974;66:688–701. [Google Scholar]
- Rubin DB. Inference and missing data. Biometrika. 1977;63:581–592. [Google Scholar]
- Rubin DB. Bayesian inference for causal effects: The role of randomization. Annals of Statistics. 1978;6:34–58. [Google Scholar]
- SAS Institute Inc. SAS Online Doc 9.1.3.Cary. North Carolina: SAS Institute, Inc; 2006. [Google Scholar]
- Tsiatis AA. Semiparametric Theory and Missing Data. New York: Springer; 2006. [Google Scholar]
- Wiesner RH, McDiarmid SV, Kamath PS, Edwards EB, Malinchoc M, Kremers WK, Krom RA, Kim WR. MELD and PELD: Application of survival models to liver allocation. Liver Transplantation. 2001;7:567–580. doi: 10.1053/jlts.2001.25879. [DOI] [PubMed] [Google Scholar]
- Zucker DM. Restricted mean life with covariates: modification and extension of a useful survival analysis method. Journal of the American Statistical Association. 1998;93:702–709. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.