Hv1 Proton Channel Opening Is Preceded by a Voltage-independent Transition

Abstract

The voltage sensing domain (VSD) of the voltage-gated proton channel Hv1 mediates a H⁺-selective conductance that is coordinately controlled by the membrane potential (V) and the transmembrane pH gradient (ΔpH). Allosteric control of Hv1 channel opening by ΔpH (V-ΔpH coupling) is manifested by a characteristic shift of approximately 40 mV per ΔpH unit in the activation. To further understand the mechanism for V-ΔpH coupling in Hv1, H⁺ current kinetics of activation and deactivation in excised membrane patches were analyzed as a function of the membrane potential and the pH in the intracellular side of the membrane (pH_I). In this study, it is shown for the first time to our knowledge that the opening of Hv1 is preceded by a voltage-independent transition. A similar process has been proposed to constitute the step involving coupling between the voltage-sensing and pore domains in tetrameric voltage-gated channels. However, for Hv1, the VSD functions as both the voltage sensor and the conduction pathway, suggesting that the voltage independent transition is intrinsic to the voltage-sensing domain. Therefore, this article proposes that the underlying mechanism for the activation of Hv1 involves a process similar to VSD relaxation, a process previously described for voltage-gated channels and voltage-controlled enzymes. Finally, deactivation seemingly occurs as a strictly voltage dependent process, implying that the kinetic event leading to opening of the proton conductance are different than those involved in the closing. Thus, from this work it is proposed that Hv1 activity displays hysteresis.

Introduction

The proton channel known as Hv1 mediates a voltage-dependent H⁺ conductance (G_vH⁺) that was first measured in molluscan neurons and subsequently shown to be prominently expressed in alveolar epithelial cells and phagocytic leukocytes of the innate immune system (1). A variety of other cells, ranging from mammalian microglia, skeletal muscle, and B-cells to a unicellular dinoflagellate, are known to express Hv1 or G_vH⁺ (2–13). Studies in knockout mice demonstrate that Hv1 channels are required for high-level superoxide production and efficient bacterial clearance in granulocytes and neutrophils (10,13,14) and superoxide-dependent B-cell receptor signaling (3). Also, Hv1 contributes to microglial ROS-dependent neuronal damage (15).

A biophysical signature of both native G_vH⁺ and expressed Hv1 channels is that its voltage dependence shifts as a function of the difference in pH between the extracellular (pH_O) and intracellular (pH_I) sides of the membrane, also known as the transmembrane pH gradient (ΔpH = pH_I – pH_O) (4,9,11,16–18). In general, the voltage dependence of Hv1 shifts ∼ 40 mV per ΔpH unit over a wide range of absolute pH_I or pH_O, displaying activation of the conductance at potentials above the reversal potential for protons (1,16). For instance, for a ΔpH = 0, Hv1 opens at positive potential; for intracellular acidification (ΔpH < 0), as is physiologically the case, Hv1 opens at more negative potentials. Consequently, voltage-gated H⁺ channels normally mediate only steady-state proton efflux from cells (1).

Control over the direction of H⁺ flow through H⁺ channels and concomitant changes in pH_I are likely to have important consequences for signaling and metabolic cascades in cells that express Hv1 (1). Therefore, identifying the mechanism by which changes in pH modulate voltage-dependent gating in Hv1 is essential for understanding how H⁺ channels contribute to cellular pH homeostasis. In spite of advances in structural and functional insights of proton channels, the mechanism of coupling between ΔpH-sensing and voltage-sensing machineries (V-ΔpH coupling) remains unknown. In the late 1990s, it was postulated that sensitivity to changes in ΔpH results from H⁺ binding to a channel-associated site in the membrane electric field (16). However, failure to identify a H⁺ regulatory site using mutagenesis strategies has cast doubt on the validity of this postulate (18,19). In addition, V-ΔpH coupling is also unaffected by mutations that impair H⁺ selectivity for ion permeation in Hv1 (19). Furthermore, the available data are consistent with the hypothesis that protein-associated water molecules that reside in the putative central crevice within the structure of Hv1 are required for a Grotthuss-type H⁺ transfer in an aqueous “water-wire” (18). Depending on proton concentration, changes in the structure of the water network associated to the channels may also be transduced into VSD conformational changes altering voltage-dependent gating (18). In addition, these channels form dimers displaying activation that is tuned by cooperativity (20–22). Allosteric modulation in H⁺ channels has been shown to be intimately related to a coil-coil interaction between the C terminus of each subunit (21,23). Thus, it is conceivable that changes in ΔpH may induce conformational transitions in the resting state of the channels that, following activation, may result in shifting voltage dependence. Consequently, one possible outcome would be that the activation of Hv1 involves both voltage-dependent and voltage-independent transitions. In this study, kinetic evidence are provided to demonstrate that these two types of transitions operate during the Hv1 activation and deactivation and are likely to determine V-ΔpH coupling in Hv1 channels.

Material and Methods

Electrophysiology

Defolliculated Xenopus laevis oocytes were injected with in vitro-transcribed cRNA (Life Technology, Carlsbad, CA, Ambion mMessage mMachine) produced from NotI-linearized N-terminal GFP-Homo sapiens Hv1 (NM_032369) (Ramsey et al., 2006 (6); Murata et al., 2005 (24)) in the vector pBSTA. Proton currents were recorded from excised membrane patches in the inside-out configuration using a patch clamp amplifier (model 2400, A-M Systems, Carlsborg, WA) with pipette filled with a pH 6.5-solution (see below) and the indicated pH_I. Recording solutions contained (in mM): 100 pH buffer (used near its respective pK_a: pH 4.5 and 5.5, MES; pH 6.5, Bis-Tris; pH 7.5, HEPES), 60 to 80 tetramethylammonium (TMA⁺)-methanesulfonate (MeSO₃^-), 4 HCl, 2 CaCl₂, 1 EGTA. pH (at 22°C) was adjusted using TMA-OH (25% w/v) and methanesulfonic acid (>99%) solutions as necessary to achieve a final osmolality of 310 to 320 mOsm; the final TMA⁺ and MeSO₃^– concentrations are therefore slightly different in solutions of various pH. For measurement of Hv1 activation, test pulses ranging from -80mV to +150 mV were applied for 1200 ms from a holding potential of -60 mV at 0.1 Hz. For deactivation, channels were opened by a 1200 ms pre-pulse to +80 mV from a holding potential of -60 mV and 1000 ms test pulses from +50 mV to -160 mV were applied at 0.1 Hz. Bath was grounded using a Ag/AgCl. There was no leakage currents subtraction.

Electrophysiological data were filtered at 100 kHz, digitized at 250 to 1000 kHz, and oversampled for storage and analysis at 5 to 20 kHz. A custom LabVIEW-based package was used to control a USB-6221 or USB-6251 (National Instruments, Austin, TX) for voltage commanding and current acquisition (C. A. Villalba-Galea, unpublished). Data were analyzed using a custom Java-based software (C. A. Villalba-Galea, unpublished,) and OriginPro9.0 (OriginLab, Northampton, MA).

Kinetic analysis

Current recordings were fitted to a first-order ordinary differential equation system representing the following four-state sequential model using MatLab.

$${\text{C}}_1\underset{{\text{β}}_1}{\overset{{\text{α}}_1}{\rightleftarrows }}{\text{C}}_2\underset{{\text{β}}_2}{\overset{{\text{α}}_2}{\rightleftarrows }}{\text{C}}_3\underset{{\text{β}}_3}{\overset{{\text{α}}_3}{\rightleftarrows }}\text{O}$$

The transition rates of the sequential four-state model were considered to exponentially depend on the membrane potential (see Supporting Material for details). For this type of systems, it can be demonstrated that the general analytical solution has the following form:

$$\overrightarrow{S}\left(t\right)=\sum _{i=1}^n{c}_i{\overrightarrow{\eta }}_i{e}^{{\lambda }_{i}t},$$

where $\overrightarrow{S}\left(t\right)$ is a vector with elements representing the fraction population of each state; n is the number of states; c_i is the i-th integration constant; and ${\lambda }_i$ is the i-th eigenvector of the matrix with element representing the transitions rate constants (see Supporting Material for details) and ${\overrightarrow{\eta }}_i$ is its corresponding eigenvalue. To calculate the integration constant c_i, $\overrightarrow{S}\left(t\right)$ was evaluated at time zero, making the exponential term equal to 1. Thus,

$$\overrightarrow{S}\left(0\right)=\sum _{i=1}^n{c}_i{\overrightarrow{\eta }}_i$$

Then, replacing the calculated c_i in $\overrightarrow{S}\left(t\right)$ gives an expression that yields the fractional population of each state as a function of time. Finally, having found $\overrightarrow{S}\left(t\right)$ and the fraction of open channels (O(t)) that is the last element of the vector $\overrightarrow{S}\left(t\right)$, current can be calculated using the following expression:

$$I\left(t\right)=O\left(t\right)G_{MAX}\left(V-V_{H^{+}}\right),$$

where $G_{MAX}$ is the maximum conductance for protons, $V$ is the membrane potential, and $V_{H^{+}}$ is the reversal potential for protons.

Using this model, individual set of recordings were fitted using Simplex (25) as implemented in MatLab. Leak currents were subtracted for the fittings. A built-in Simplex minimization algorithm was set to 50 cycles of 500 iterations (25,000 iterations totals) for each set of currents. The α₀ and β₀ parameters were constrained to ± 25% of their running values; and the z_α and z_β values were constrained to ± 2.5% of their running values. These constrains were updated every cycle. After all the minimizations were finished, the parameters obtained from fitting each data set were averaged and the resulting mean values used as “seed” values for a new round (50 cycles × 500 iterations) of minimization. This procedure was repeated until the standard deviations of all parameters were smaller than their correspondent mean. For each pH_I, the number of round of minimization was over 25 sessions, totaling more than 625,000 iterations per data set.

Exponential fits and weighted average time constant

Activating currents were fitted to a two-exponential function defined as follows:

$$I_{ACT}\left(t\right)=I_{MAX}(1-f_1{e}^{\raisebox{1ex}{$-t$}\!\left/ \!\raisebox{-1ex}{${\tau }_1$}\right.}-f_2{e}^{-\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{${\tau }_2$}\right.}),$$

where f₁ and f₂ are the fraction of the currents in each of the components (f₁ + f₂ = 1) and τ₁ and τ₂ are the corresponding time constants. For deactivation, the two-exponential function was defined as follows:

$$I_{DEACT}\left(t\right)=I_{MAX}(f_{FAST}{e}^{\raisebox{1ex}{$-t$}\!\left/ \!\raisebox{-1ex}{${\tau }_{FAST}$}\right.}+f_{SLOW}{e}^{-\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{${\tau }_{SLOW}$}\right.})$$

Whereas, for deactivation, the weighted average time constant was calculated using the following equation:

$${\tau }_{AVE}=f_{FAST}{\tau }_{FAST}+f_{SLOW}{\tau }_{SLOW},$$

where τ_FAST, τ_SLOW, f_FAST, and f_SLOW are equivalent to τ₁, τ₂, f₁, and f₂, respectively.

Single Boltzmann equation

The curves of open probability (Po) as a function of the membrane potential (Po-V curves) were fitted to a single (two-state) Boltzmann equation (26) defined as follows:

$$Po\left(V\right)=\frac{P{o}_{MAX}}{1+e^{\raisebox{1ex}{$z\left(V-V_{1/2}\right)$}\!\left/ \!\raisebox{-1ex}{$kT$}\right.}},$$

where, as before, V is the membrane potential, z the apparent sensing charge, Po_MAX is the maximum open probability, V_1/2 is the potential of half-maximum activation, k is the Boltzmann constant, and T is the absolute temperature.

Results

Initial assessment of the Hv1 activation kinetics

Recording of H⁺-currents were performed in 15 to 20 μm inside-out (macro-)patches of the plasma membrane from Xenopus oocytes expressing human Hv1. To obtain fast activating H⁺-conductance, currents were recorded in ΔpH = -2 (pH_O/pH_I = 6.5/4.5) at potentials ranging between -80 mV and +80 mV from a holding potential (H.P.) of -60 mV (Fig. 1 A). The recorded currents displayed at least two temporal components. As shown before, a two-exponential function was used to quantify the activation kinetics of the H⁺-conductance (22,27). Plotting the fitted time constants as a function of the membrane potential (τ_ACT-V curve) revealed that both components were associated to voltage-dependent transitions because both time constants decreased at higher potentials (Fig. 1 B). To estimate the apparent charge associated with these components, the time constants were assumed to be described by the following expression:

$${\text{τ}}_{\text{ACT}}={\text{τ}}_{\text{ACT},0}{e}^{-zV/kT},$$ (1)

where τ_ACT,0 is the time constant in the absence of an electric field (at 0 mV), z is the apparent charge modulating this rate, V is the membrane potential, k is the Boltzmann constant, and T is the absolute temperature. Fitting the τ_ACT-V curve to Eq. 1 showed that both temporal components of the activation were voltage dependent with z values of 3 ± 6 and 3 ± 9 (n = 6; fitted values ± fitting error) for the fast and slow component, respectively. This observation seemingly indicated that the activation of Hv1 involved only voltage-dependent transitions. However, the high error in the fits indicates that assuming the existence of only two transitions was insufficient to describe the activation of Hv1. Further, the fit with two-exponentials ignores the sigmoidal onset of the conductance, indicating that additional components are needed to fit the activation of Hv1. Furthermore, using the sum of exponentials to fit the current traces yields parameters (amplitudes and time constants) that cannot always be directly assigned to specific transitions in the activation of these channels. To overcome these problems, it was sought to describe the activation of Hv1 using a system of first-order linear differential equations that define the sequential four-state model depicted in Fig. 2 A.

Figure 1.

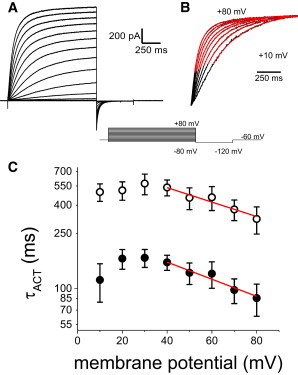
Initial characterization of the Hv1 activation kinetics. (A) Inside-out, patch-clamp current recordings of Hv1 expressed in Xenopus oocytes. The patches were 15 to 20 μm in diam. and currents were recorded in the presence of a pH gradient (ΔpH, pH_O/pH_I) of 6.5/4.5. From a holding potential of -60 mV, currents were evoked with pulses ranging from -80 mV to +80 mV and deactivated at -120 mV. (B) The timing of the currents was estimated by fitting the sum of two exponentials (black versus red traces) to those currents recorded at potentials of +10 mV and above and the lag-phase of traces was ignored. The currents were normalized to the maximum values recorded at each potential for visual comparison. (C) The time constants yielded by the fits were plotted against the membrane potential (τ_ACT-V curves) and the resulting plots show that both exponential components display voltage sensitivity. To estimate the apparent gating charge associated with this components, the high-voltage end of the τ_ACT-V curves was fitted to Eq. 1. The fits (red lines) show that the apparent gating charges for these components were 3 ± 6 e^- and 3 ± 9 e^- (fitted values ± fitting error), for the fast and slow components, respectively. To see this figure in color, go online.

Figure 2.

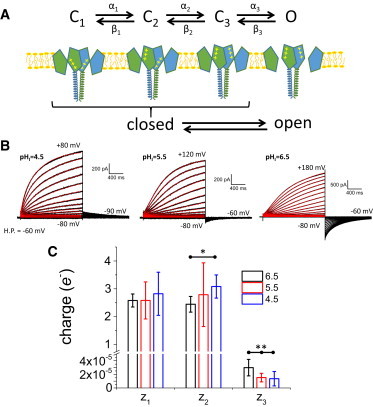
Sensitivity of the electrical component in Hv1 gating to changes in pH_I. (A) A four-state sequential model was used to fit the activation kinetics of Hv1, where the first three states of the model are nonconductive (closed, C1-C3), whereas the last one was the conductive state (open, O). All forward (α_i) and backward (β_i) transition rates were considered to be voltage-sensitive (Eqs. 1 and 2). (B) Examples set of proton currents recorded at three different pH_I, while keeping pH_O at 6.5. All currents (black traces) were recorded from a H.P. of -60 mV, pulsing from -80 mV to +80 mV, +120 mV and +180 mV (left to right), at pH_I of 4.5, 5.5, and 6.5, respectively. The four-state model was used to simultaneously fit the activation of the currents evoked at potentials +40 mV and above in each condition (red traces). (C) Average gating charge (z_i = z_α,i + z_β,i) associated with each transition were calculated from the values obtained from the fit of individual experiments. The charge associated with the first and second transition (z₁ and z₂, respectively) average ∼ 2.5 e^-, suggesting that they emerged from the gating of each one of the voltage sensors. These charge values were not statistically different, except for z₂ that was 3.0 ± 0.4 (n = 8) at pH_I 4.5 and 2.4 ± 0.3 (n = 5) at pH_I 6.5 (^∗; p > 0.05). For the third transition, the values of z₃ were not different (p < 0.05) at pH_I 4.5 (1 × 10⁻⁵ ± 1 × 10⁻⁵) and 5.5 (1.5 × 10⁻⁵ ± 6 × 10⁻⁶), but there was a statistically significant increase (^∗∗; p < 0.05) at pH_I 6.5 (2.6 × 10⁻⁵ ± 1.6 × 10⁻⁶). To see this figure in color, go online.

Kinetic characterization of the Hv1 activation using a multistep process

The model shown in Fig. 2 A consists of three sequential transitions connecting four states. As shown in Fig. 1, two exponentials were able to fit the late phase of the proton currents, but were not sufficient to describe the initial lag phase of the activation. To make up for this deficiency, a third component—or transition—was required to fit the activation of the proton conductance. Consequently, a minimal model comprised of four sequential states linked by three voltage-dependent transitions was used to fit the protons currents. For this model, all the transitions were considered to be voltage dependent, with a forward and a backward rate, each one defined by two to-be-fitted parameters (see Methods for details). For transitions leading to the open state (forward transitions), the parameters α_0,i and z_α,i corresponded to the transition rate of the i-th transition in the absence of an electric field and the charge associated with the transition, respectively. Likewise, β_0,i and z_β,i were corresponding parameters for the transitions leading in the opposite direction (backward transitions). The forward and backward rates were functions of the membrane potential and were defined as follows:

$${\alpha }_i\left(V\right)={\alpha }_{0,i}{e}^{z_{\alpha ,i}V/kT},$$ (2)

$${\beta }_i\left(V\right)={\beta }_{0,i}{e}^{-z_{\beta ,i}V\text{/}kT},$$ (3)

where, as before, k and T are the Boltzmann constant and the absolute temperature, respectively.

For these fits, it was assumed that both voltage sensors in the dimer must be activated to open the conductive pathway (Fig. 2 A). Thus, consistent with a recent report (28), only the last state (O) will be conductive. Also, the total gating charge was constrained between 5 and 6 e^- as per recent determination of minimum gating charge by “limiting slope” measurements (22).

From a H.P. of -60 mV, proton currents were evoked by pulses from -80 mV to + 80 mV and typical activation of Hv1 mediated currents were observed. Then, those currents recorded above -50 mV were taken for fitting to the four-state model (Fig. S1 A in the Supporting Material). All the traces were simultaneously fitted to the model, thus the calculated traces (Fig. S1 A, red traces) reflect the best global reproduction of the data that the model can produce. As expected, the activation of the proton current was voltage dependent. Consistent with the two-exponential fits shown above, the total charge associated with the first and second transition, z₁ = z_α,1 + z_β,1 and z₂ = z_α,2 + z_β,2, respectively, in the particular instance shown in Supporting Material. Fig. 1 B were 2.4 e^- and 2.8 e^-, respectively. This observation indicated that these transitions were sensitive to membrane potential changes. However, the present analysis also revealed that the charge associated with the last transition (z₃ = z_α,3 + z_β,3) was 2 × 10⁻⁵ e^-, implying that the transition leading to the opening of the proton conductance was practically voltage-independent. Therefore, it seemed that the transition preceding the opening of the conductance is rate limiting for the activation of Hv1.

To further explore the voltage-dependence of Hv1 activation, it was sought to determine how ΔpH modulates activation in terms of the four-state model. To do this, the kinetic analysis was extended to proton currents recorded at other pH_I values, while keeping pH_O at 6.5. From a H.P. of -60 mV, currents were recorded at potentials ranging from -80 mV to +80, +120 mV and +180 mV for pH_I of 4.5, 5.5, and 6.5, respectively. Individual sets of currents were fitted to the four-state model (fitted values in Table S1). From these fits, it was observed that the average gating charge associated with the first and second transitions were not statistically different at any pH (n = 6 to 8; p > 0.05), except for the charge for the second transition at pH_I 6.5 with respect to pH_I 4.5 (Fig. 2 C). Likewise, the average charge associated with the last transition was in the order of 2 × 10⁻⁵ at all the pH_I tested (Fig. 2 C). This observation indicated that the third transition was practically insensitive to membrane potential changes.

From the fits, it was found that all of the rate coefficients were sensitive to changes in pH_I (Fig. 3). In general, the forward rates decreased as a function of the pH_I, whereas the backward rates increased as a function of the pH_I. This observation suggested that the kinetic analysis shown in this study produced parameters that were able to reproduce the voltage-dependent activity of Hv1. To show this further, curves of open probability (Po) as a function of the membrane potential (Po-V curves) were generated and, as expected, found that voltage-dependence shifted toward positive potentials as the pH_I increased (Fig. 4 A, open symbols). For simplicity, the Po-V curves were fitted to a single Boltzmann equation (Fig. 4 A, lines). The values for the half-maximum activation, V_1/2, were plotted against pH_I (Fig. 4 B). A linear regression of the plots revealed that the voltage dependence shifted ∼ 39 mV per unit of pH_I, indicating that the parameters obtained from the kinetic analysis shown here could also reproduce steady-state features of the activity of Hv1. Similar to what was reported for H⁺-currents in eosinophils (29), decreasing pH_I seems to increases the Po_MAX. It cannot be ruled out that is the change in the gradient, rather than the absolute value of pH_I, is what modulates Po_MAX. Nevertheless, as shown in Figure Fig. 4 C, the Po_MAX values calculated from the fits to the Boltzmann equation increases from 0.80 to 0.95 when pH_I changes from 6.5 to 4.5. Further, this increased activity of the channels seems to be determined by the last transition. Because the first and second transitions have voltage-dependent transition rates, their backward rates tend to go to zero at positive potentials, whereas their forward rates become very large. In contrast, the rates for the last transition remain virtually unchanged. Following this idea, Po_MAX was approximated using the following equation:

$$P{o}_{MAX}=\frac{{\alpha }_{\mathrm{0,3}}}{{\alpha }_{\mathrm{0,3}}+{\beta }_{\mathrm{0,3}}}$$ (4)

As shown in Fig. 4 C, the values of Po_MAX calculated from the rate constants coincided with the values obtained from the fits to the Boltzmann equation. This observation suggested that the last transition has an important contribution to the pH sensitivity of the activity of Hv1.

Figure 3.

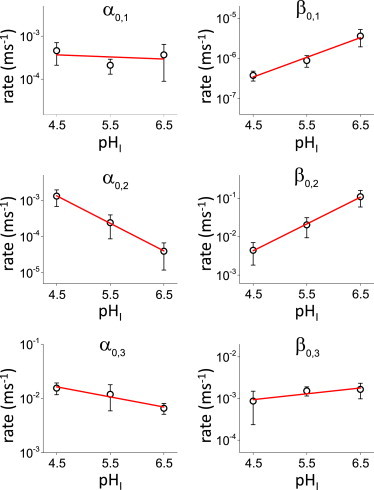
pH_I-dependence of the transition rates at 0 mV. The parameters α₀ and β₀ (Eqs. 1 and 2 ) were obtained from fitting proton currents to the four-state model. These coefficients are the rate constant of the reaction in the absence of any electrical field, thus they correspond to the chemical component of the reaction. All coefficient were sensitive to pH_I, where the forward rates increased as the intracellular side was acidified, whereas the backward rate increased when the intracellular side was alkalinized. The red lines correspond to the fit of the logarithm of the rates as a function of pH_I. The slope of this traces constitute a measure of pH_I-dependence of these rate coefficients, so that increasing the steepness of the slope indicates higher pH_I sensitivity (see Fig. 5). To see this figure in color, go online.

Figure 4.

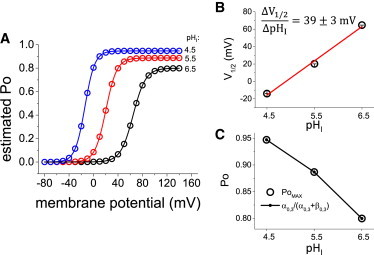
Predicted open probability for Hv1. (A) The open probability (P_O) of Hv1 was estimated as a function of the potential (P_O-V curve) and pH_I using both the rate coefficient at 0 mV and the sensing charge values obtained from the fits. The calculated P_O-V curves were fitted to a single Boltzmann equation (lines). (B) From the fit to the Boltzmann equations, the half-maximum potential (V_1/2) shifted to more negative potentials as pH_I was lower. Linear regression of the V_1/2-vs-pH_I plot showed a shift of ∼ 39 mV per unit of pH_I in the value of V_1/2. (C) The P_O-V curves also predicted a decrease in the maximum Po (P_O,MAX) for Hv1. P_O,MAX seems to be determine by the last transition as the fitted P_O,MAX and the one calculated from the rates coincide in the graph. To see this figure in color, go online.

All transitions display pH_I dependency

Next, the pH_I dependence of the remaining transitions was determined using the plots of the average α_0,i and β_0,i with respect to pH_I (Fig. 3) to quantitatively assess pH_I sensitivity. To do this, the quantities pα_0,i and pβ_0,i were defined as the logarithm of the rate constant of the i-th transition at 0 mV and a linear regression was calculated with respect to pH_I (Fig. 3, red traces). Using the slope of the fitted linear equation as a measure of pH_I sensitivity, Δpα_0,i/ΔpH_I and Δpβ_0,i/ΔpH_I for the forward and backward transitions, respectively, it was found that the second transition rates displayed the highest pH_I sensitivity, reaching almost an order of magnitude change per unit of pH_I (Fig. 5). In the case of the first transition, the forward rate seemed to be pH_I-independent. Yet, the backward transition rate displayed over a half-order magnitude change when comparing pH_I 4.5 with 6.5 (Fig. 5). Finally, the last transition rates displayed a modest pH_I-dependence changing lesser than 0.2 logarithmic units per unit of pH_I (Fig. 5). These combined observations indicated that the intermediate steps in the activation of Hv1 are those displaying higher sensitivity to pH_I.

Figure 5.

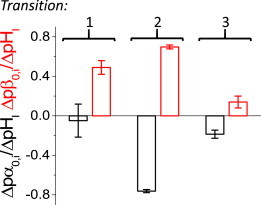
Rate coefficient pH_I-dependence. To access pH_I-dependence of the rate coefficients, a linear regression (Fig. 4, red lines) of the log10 of α_0,i and β_0,i values (pα_0,i and pβ_0,i, respectively) as a function of the pH_I was calculated and the slope of the regression (Δpα_0,i/ΔpH_I and Δpβ_0,i/ΔpH_I, respectively) were taken as indices of pH_I-sensitivity. In this figure the average values for slope are plotted for each forward and backward transition. All values were statistically different (p < 0.05). To see this figure in color, go online.

Closing of Hv1 does not show a discernible voltage-independent transition

Thus far, it has been shown that all transitions leading to the opening of the proton conductance are sensitive to pH_I and that the last transition is voltage-independent. Next, the voltage-sensitivity of the closing was kinetically quantified from the deactivation kinetics of Hv1 as a function of membrane potential. To do this, proton currents were activated with a pulse to a fixed positive potential followed by deactivation of the current with a second pulse to voltages ranging from -150 mV to -40 mV. For instance, as illustrated on Fig. 6 A, for pH_I 6.5, a depolarizing 1500 ms-pulse to +80 mV was applied to activate Hv1 to later deactivate the current with a 1200 ms-pulse to negative potentials. The deactivating currents were then fitted to a two exponential function to quantify the time course of this process. In contrast to activation, the deactivation of the proton current was well-fitted by this function (Fig. 6 B) and, therefore, this analytical approach was considered sufficient to kinetically characterize the deactivation of the currents. As shown in Figs. 6 C and D, plotting the both time constants as a function of the membrane potential during deactivation (τ_DEACT-V plot) showed that both, the fast and slow, components were voltage dependent, such that the deactivation became faster as the membrane potential was more negative.

Figure 6.

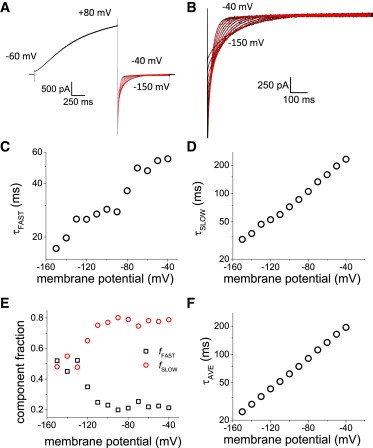
Proton current deactivation kinetics. (A) Proton currents (black traces) were evoked with a 1500 ms-pulse to +80 mV and deactivated at potentials ranging from -150 mV to -40 mV. (B) The entire time course of the deactivating currents (black traces) were well-fitted by a two-exponential function (red traces). (C,D) The time constants of the two temporal components observed during deactivation were plotted against the membrane potential (τ_DEACT-V curves). Both components showed shorter time constant as the membrane potential was more negative. (E) The relative amplitude of the “slow” component dominated the deactivation kinetics. However, the fast components equalized its contribution at more negative potentials. (D) The overall deactivation kinetics were voltage dependent as shown by the plot of the weighted average time constants (τ_AVE) with respect to membrane potential. To see this figure in color, go online.

To quantify the voltage-dependence of deactivation of Hv1, the τ_DEACT-V plots were fitted to the following equation:

$${\text{τ}}_{\text{DEACT}}={\text{τ}}_{\text{DEACT},0}{e}^{zV/kT},$$ (5)

where, analogously to Eq. 1, τ_DEACT,0 is the time constant in the absence of an electric field (at 0 mV); z is the apparent sensing charge. As before, the z values will be an indication of the voltage-dependency of the process. Fitting Eq. 5 to the more negative range of potential (Fig. 7, red line), revealed that the gating charge associated with both components of the proton conductance closing (Fig. 8) were, at least, one order of magnitude smaller than the total charge associated with the opening, and four orders of magnitude higher than the charge associated with the last activating transition. These observations strongly suggest that the closing of the proton conductance involves transitions that are not observed during activation. In other words, the pathways of activation may differ from the deactivation pathway.

Figure 7.

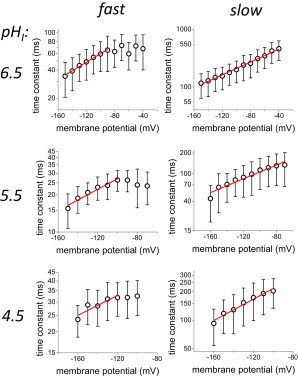
Voltage-dependence of the proton current deactivation. The mean time constant for deactivation (τ_DEACT) for both, fast and slow, components were plotted against potential (τ_DEACT-V curve). Both components (left and right) were unambiguously voltage sensitive at the three pH_I conditions evaluated here (top to bottom) (n = 3 to 6). Voltage sensitivity was determined by fitting to Eq. 5 (red trace). To see this figure in color, go online.

Figure 8.

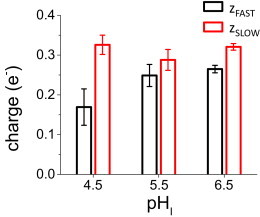
Apparent gating charge associated to closing. From the fit of the τ_DEACT-V curves, each component seemed to have between 0.15 and 0.35 gating charges driving these transitions, indicating that deactivation was a voltage-dependent process. To see this figure in color, go online.

Discussion

Exponential and powered-exponential functions have been used to characterize the time-course and pH dependence of native proton conductance (22,27,30). More recently, multistate kinetic analysis has been used to describe the activity of channels in an attempt to gain insightful information about the mechanism governing their activity. For instance, in the case of the proton channels isolated from Ciona intestinalis (Ci-Hv1), a three-state model was sufficient to describe the activation kinetics of the conductance (31). Using a similar approach in this study, discrete gating steps have been identified in the activation kinetics of Hv1 and characterized their sensitivity to membrane potential and pH_I. In this case, a four-state model was found to be sufficient to describe the activation kinetics of the human Hv1 expressed in Xenopus oocytes. The analysis presented in this article has provided important insights into the mechanism of Hv1 gating that are consistent with previous reports using exponential fits of the H⁺ current activation (1,16,32,33). Particularly, the findings show that 1), Hv1 activation gating proceeds in distinct steps, at least one of which is voltage-independent, whereas the channel closing rate is voltage-dependent; 2), pH_I differentially affects each of the steps in the Hv1 activation pathway; 3), the V-ΔpH relation in Hv1 is a composite response that requires contributions from both electrical and nonelectrical (i.e., voltage-independent) transitions.

The present analysis also indicates that the activation of Hv1 requires the total movement of 5.4 ± 0.9 (n = 18) net gating charges for activation, which is similar to what has been reported for the Ci-Hv1 using “limiting-slope” measurements (31). These observations suggest that, as for tetrameric voltage-gated channels (tVGC), the activation of the conductance occurs after a large fraction of the total gating charge has been mobilized. In Hv1, a similar situation seems to be at play, where sensing charges move leading to the opening of the conductance. Here, however, it was observed that a voltage-independent step is directly linked to the open state, suggesting that the electrically sensitive components of the activation lead the channels to an activated, but not conductive conformation.

In the case of deactivation, the present work shows that this process is voltage dependent, involving nearly 0.5e^- net charges. This seems to be inconsistent with the sequential model used for activation, in which the last transition to the open state is essentially voltage independent. Thus, it is hereby proposed that the return to the resting states occurs through a different pathway than the one leading to the open state (Fig. 9). A direct implication to this idea is that Hv1 may display hysteresis. Specifically, by imposing an activating potential, the VSDs of Hv1 go through voltage-driven conformational changes from the resting (Fig. 9, “C₁”) to the activated state (Fig. 9, “C₃”). At this point, the protein has gained energy from the work done by the electrical field on the gating charges and this energy drives a new transition that leads the channel to the open state (Fig. 9, “O”). While the channel opens, a fraction of the energy gained during the gating charge movement is transformed and is not “stored” in the VSD any longer.

Figure 9.

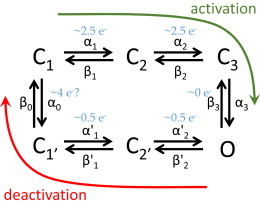
Proposed scheme for activation and deactivation of Hv1. The activation pathway involves four sequential states, C₁ to C₃ and O, whereas the deactivation goes from states C₂’ to C₁’. The return to the resting state, C₁, is mediated by a hypothetical step driven by four gating charge. However, it is possible that this transition occurs in several steps. To see this figure in color, go online.

This type of behavior has been seen in tVGC (34–40) and voltage-sensitive phosphatases (VSP) (41–43), in which prolonged imposition of an activating potential leads the VSD, through a voltage-independent transition, into a new state known as the “relaxed” state (36). In tVGC and VSP, VSD relaxation occurs after prolonged activation of the VSD (36,43,44). In the case of Hv1, the analysis shown here suggests that the open state is equivalent to the “relaxed” state observed in tVGC and VSPs. Testing this idea would imply recording gating currents or taking any other approach that can reliably report conformational changes in the VSD that are strictly related to activation. To the author’s knowledge however, attempts from many research labs, including this, to record gating currents from Hv1 have failed. Therefore, direct proof of this idea remains to be provided.

Regarding the fitting procedure implemented for this project and in light of the elegant work recently published by Hines, Middendorf, and Aldrich (45), it is important to make some considerations on the uniqueness of the fitted parameters reported in this article. In general, when fitting individual sets of experimental data to a given model, a parameter-searching algorithm would render parameters for each set of data. Ideally, these sets of parameters would be very similar to each other. However, it is also possible that these sets of parameters may display a large variability. This variability may be due to noise in the measurement and also to heterogeneities in the data emerging from the intrinsic fluctuations of the system under study. Variability in the fitted parameters may arise from technical issues such as how the searching algorithm is initialized, constrained or tuned. Nevertheless, regardless of the nature of the variability, the important point to be highlighted is that fitting the same type of data to a given model may yield multiple distinct solutions. This idea is also applicable to the present work. Thus, the question to be asked is which the “actual” solution is. To address this issue is important to focus on the nature of the problem at hand. Arguably, a fundamental difference between the examples provided by Aldrich and colleagues and those in this work is that the sets of data fitted here involved multiple conditions as the recordings within a single set were performed at multiple membrane potentials. Thus, for a single set of currents, the same set of parameters (α_0,i, β_0,i, z_α,i, and z_βi) was simultaneously fitted, so not only the timing of the currents, but also the voltage dependences of the rates were evaluated. As Aldrich and colleagues point out, one way to increase reliability of the fitted parameters is by collecting other types of data using existing approaches. The approach taken for this work seems to comply with this requirement since the data provided not only information as a function of the time, but also as a function of voltage.

Finally, the data reported in this study raise intriguing questions about the pH sensitivity of VSD-containing proteins. In Hv1, a network of water molecules in the crevice of the VSD that is hypothesized to mediate Grotthuss H⁺ transfer may also be required for ΔpH sensing (18). An intriguing possibility is that proton occupancy of a centrally located water network within the VSD crevice catalyzes hydrogen bond reorganization and thereby influences the voltage-independent conformational transition that the presented finding is rate-limiting for channel opening when pH_I ≤ pH_O. However the precise molecular mechanisms underlying pH-dependent and voltage-independent transitions in distinct VSD proteins remains unknown and merits further investigation.