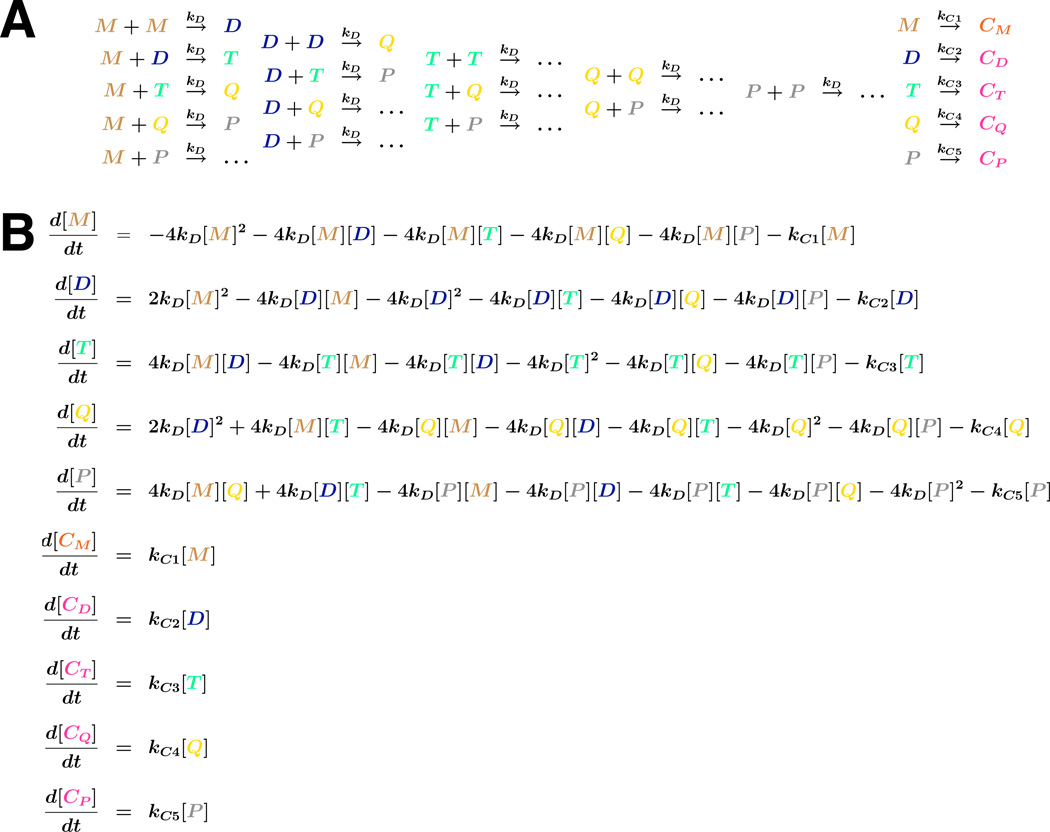Quantitative methods for measuring DNA flexibility in vitro and in vivo

Abstract

The double-helical DNA biopolymer is particularly resistant to bending and twisting deformations. This property has important implications for DNA folding in vitro and for the packaging and function of DNA in living cells. Among the outstanding questions in the field of DNA biophysics are the underlying origin of DNA stiffness, and the mechanisms by which DNA stiffness is overcome within cells. Exploring these questions requires experimental methods to quantitatively measure DNA bending and twisting stiffness both in vitro and in vivo. Here we discuss two classical approaches, T4 DNA ligase-mediated DNA cyclization kinetics, and lac repressor-mediated DNA looping in E. coli. We review the theoretical basis for these techniques and how each can be applied to quantitate biophysical parameters that describe the DNA polymer. We then show how we have modified these methods and applied them to quantitate how apparent DNA physical properties are altered in vitro and in vivo by sequence non-specific architectural DNA binding proteins such as the E. coli HU protein and eukaryotic HMGB proteins.

Introduction

The biophysics of DNA have been studied for more than half a century with the goals of understanding and predicting the behavior of the polymer chain. This work is applicable to the understanding of DNA packaging and gene expression in vitro and in vivo, and for design and implementation of DNA as a nanomaterial. Much progress has been made toward understanding the properties of purified DNA in vitro, but interpretation of even these relatively simple experiments can be controversial. What is the origin of the remarkable inflexibility of double-stranded DNA? To what extent do base pair stacking and electrostatics contribute? Over what length scales do simple polymer models apply? Beyond these questions, it remains of great interest to better understand the physical properties (e.g. bend and twist flexibility) of the double-stranded DNA polymer in the presence of proteins, in chromatin, and ultimately, in living cells.

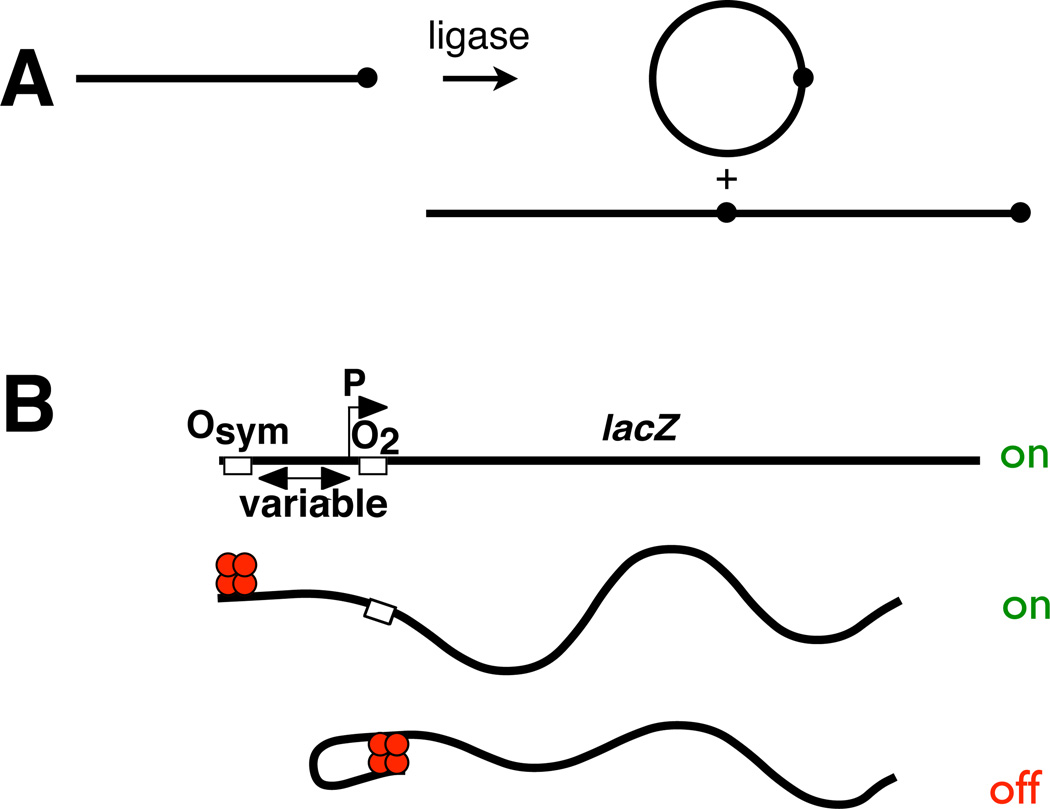
Here we focus on our recent implementations and revisions of two classical methods to quantitate DNA flexibility (Fig 1). The first method involves ligase-catalyzed DNA cyclization kinetics in vitro (Fig. 1A). The second method involves analysis of DNA repression looping in living bacteria (Fig. 1B). We sketch the theory underlying each classic method, and then show how we have updated the procedures and extended them to increasingly complex systems.

Figure 1.

Analysis methods described in this work. A. Classic in vitro assay of DNA j-factor by T4 DNA ligase-catalyzed cyclization kinetics. Linear radiolabeled DNA molecules of known concentration carry cohesive termini. Dot emphasizes monomer unit. Ligation gives rise to cyclic and linear products (two examples shown). Rates of accumulation of monomeric circles vs. all other species are analyzed quantitatively by native polyacrylamide gel electrophoresis and fit to rate equations to estimate the j-factor. Determination of j-factor as a function of length allows estimation of persistence length (WLC model), helical repeat and twist constant. B. Classic in vivo assay of DNA looping mediated by lac repressor tetramer binding simultaneously to pairs of operators (O_sym, O₂) flanking a test promoter (P). Operator spacing is varied to monitor the length dependence of repression, allowing fitting to a thermodynamic model that links promoter repression to DNA looping.

DNA polymer theory

Worm-like Chain (WLC) model

The mechanical properties of double-stranded DNA have been classically treated by the worm-like (WLC) model of DNA flexibility (Kratky and Porod, 1949; Rippe et al., 1995; Shimada and Yamakawa, 1984). This model applies particularly well to polymers intermediate in behavior between a rigid rod and a random coil. The WLC model invokes a single variable, the persistence length, to account for both the local stiffness and the long-range bend flexibility of double-stranded DNA. The WLC model was derived by sequential imposition of constraints on chain geometry starting from a random flight chain. Limiting such a chain to segments of equal non-zero length yields a freely jointed chain. For such a chain with n segments of length a, the contour length of the chain is na. Constraining the valence (included) angle between segments to the value θ (but not constraining the torsion angles between segments) in this chain results in a freely rotating chain, with free rotation permitted for every segment. The first segment r₁ may be considered to be along the z-axis. If e_z is a unit vector along the z-axis, the average z component of the end-to-end vector R for the chain is:

$$\langle \mathbf{R}·{\mathbf{e}}_z\rangle =(\sum _{i=1}^n\langle {\mathbf{r}}_i\rangle )•\frac{{\mathbf{r}}_1}{a}=\frac{1}{a}\sum _{i=1}^n\langle {\mathbf{r}}_1·{\mathbf{r}}_i\rangle$$ (1)

The terms in the sum can be evaluated analytically. 〈r₁·r₂〉, the scalar projection of r₂ onto r₁, is given by:

$$\langle {\mathbf{r}}_1·{\mathbf{r}}_2\rangle =a^2(-\text{cos}\theta )$$ (2)

because the angle between r₁ and r₂ is π−θ and cos(π−θ)=−cosθ. The value of 〈r₁·r₃〉 is found by projecting r₃ onto r₂ and then projecting the result onto r₁. Upon repeating scalar projections, the scalar products r₁·r_i are given by:

$$\langle {\mathbf{r}}_1·{\mathbf{r}}_i\rangle =a^2{(-\text{cos}\theta )}^{i-1}$$ (3)

and the sum is a geometric series a+a(−cosθ)+a(−cosθ)²+…+a(−cosθ)ⁿ⁻¹. The sum of the first n terms in this series is:

$$\langle \mathbf{R}·{\mathbf{e}}_z\rangle =a\frac{1-{(-\text{cos}\theta )}^n}{1-(-\text{cos}\theta )}$$ (4)

In the limit n − ∞

$$\underset{n\to \infty }{\text{lim}}\langle \mathbf{R}·{\mathbf{e}}_z\rangle =\frac{a}{1+\text{cos}\theta }\equiv P$$ (5)

where the length P is defined as the persistence length of the chain. P conveys the length over which the chain’s “memory” of its initial direction persists.

The Kratky-Porod worm-like chain (WLC) is derived from the freely-rotating chain by letting n→∞, a→0, and θ→π under the constraint that both na≡l (the chain contour length) and a/(1+cosθ) (the chain persistence length) remain constant. The WLC model can be used to express the mean-squared distance, R, between ends of (or points along) a DNA chain in terms of the persistence length, P, and the contour length, l, separating the points:

$$\langle R^2\rangle =2Pl[1-\frac{P}{l}(1-e^{-\frac{l}{P}}\left)\right]$$ (6)

Under physiological conditions, conventional values for P are near 50 nm (~150 bp). For contour lengths l ≤ P, DNA behaves as a rod with elastic resilience. For contour lengths l >> P, DNA behaves as a flexible polymer for which chain entropy dominates over bending energy, and <R²> = 2Pl, so that the RMS end-to-end distance scales with the square root of the number of segments as for any random walk.

The j-factor

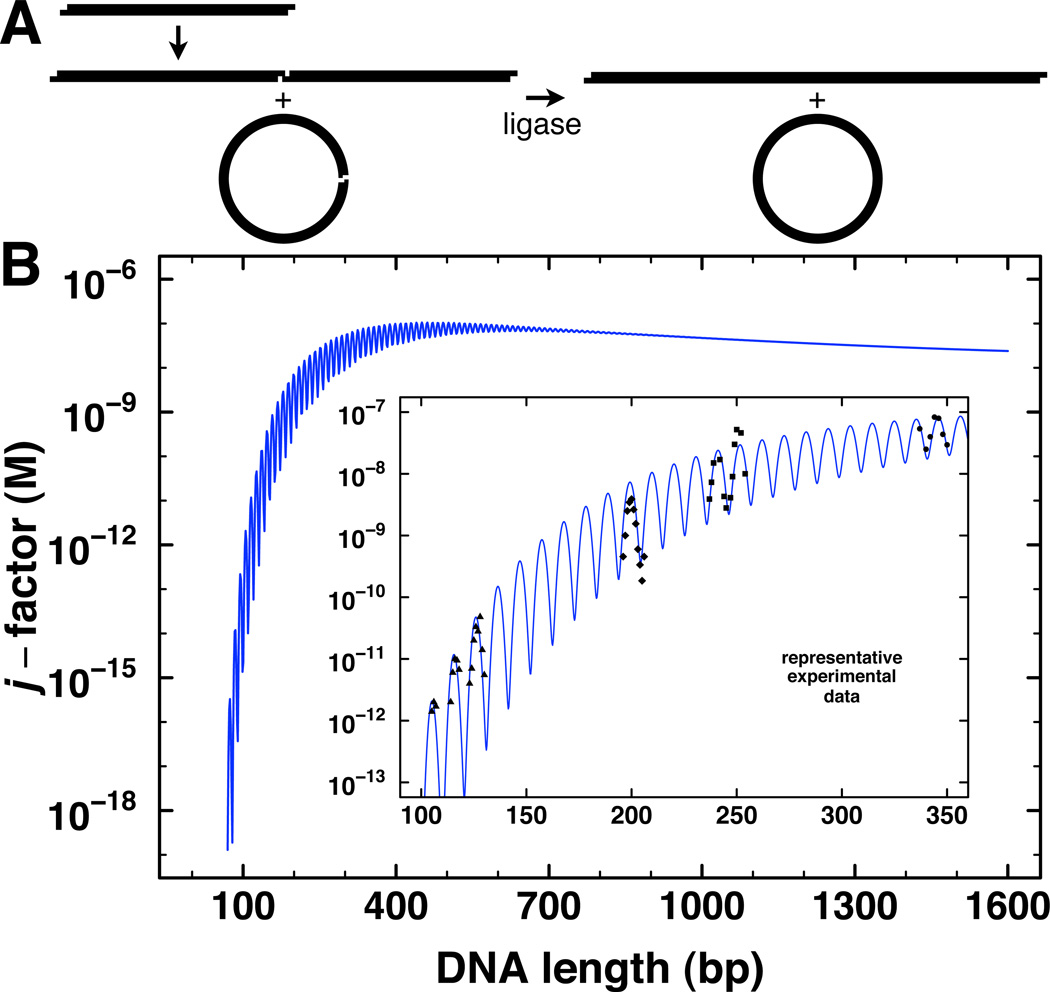
The effective concentration of one site along the DNA contour in the neighborhood of another is an extremely useful measure of DNA stiffness. This parameter can be expressed by the experimental j-factor, most often obtained from the ring-closure probability for DNA fragments with cohesive termini in the presence of DNA ligase (Fig. 2A). DNA flexibility described by the WLC model predicts two global regimes that appear in plots of the j-factor as a function of the length of the intervening DNA tether (Fig. 2B). For DNA tether lengths less than ~400 bp, the j-factor increases dramatically with length, reflecting rod-like behavior: the energetic cost of bending a rod into a circle decreases rapidly as length increases. Beyond ~400 bp the plot drops gradually with DNA length, reflecting dilution of DNA sites and more random coil-like behavior.

Figure 2.

Theoretical and experimental j-factor determination by DNA cyclization kinetics in vitro. A. Schematic depiction of the formation of transient circles and multimers by DNA terminal interactions, which are then captured by DNA ligation. B. Predicted dependence of j-factor on DNA length for a persistence length of 46.5 nm, torsion constant of 2.4 × 10⁻¹⁹ erg-cm, and helical repeat of 10.48 bp. Inset: expanded trace of predicted j-factor with representative experimental data from multiple laboratories for purified DNA in vitro.

For DNA ligation, the requirement for 5’-3’ alignment of the helical ends demands consideration of DNA torsional flexibility. Typical values for the twist constant of DNA in vitro yield predictions shown in Fig. 2B, with the j-factor oscillating through maxima and minima for every ~10.5 bp (one helical turn) of increased length. Experimental estimates of the j-factor in vitro have been most commonly made using ligase-dependent DNA cyclization assays (Fig. 2B, inset) as a function of DNA length. Related processes, such as the formation of protein-DNA loops, can depend on the same physical properties that determine the j-factor, but the results of such experiments will depend upon the nature of the site-site interactions in question. For example, protein-DNA looping can be modeled using the same methods used for cyclization by simply changing the boundary conditions for end-joining (Levene and Crothers, 1986; Lillian et al., 2008; Swigon et al., 2006). In practice, contact through a bound protein has usually been found to be a much less stringent constraint than covalent ligation of the termini (Allemand et al., 2006; Peters and Maher, 2010; Rippe, 2001; Rippe et al., 1995).

A. Ligase-catalyzed DNA cyclization kinetics in vitro

DNA cyclization kinetics theory

Ligase-catalyzed DNA cyclization is a powerful classic approach that has received widespread theoretical and experimental consideration (Crothers et al., 1992; Du et al., 2005; Hagerman and Ramadevi, 1990; Kahn and Crothers, 1992; Peters and Maher, 2010; Podtelezhnikov et al., 2000; Shore et al., 1981; Taylor and Hagerman, 1990; Vologodskaia and Vologodskii, 2002; Zhang and Crothers, 2003). Details of experimental conditions and key assumptions can be crucial to the validity of the results (Davis et al., 1999; Du et al., 2005). We have recently reviewed the theoretical derivation underlying analysis of ligase-catalyzed DNA cyclization kinetics (Peters and Maher, 2010) as originally described by Shore and Baldwin (Shore and Baldwin, 1983; Shore et al., 1981). In brief, cyclization converts a linear DNA molecule (L) with cohesive termini into a circular substrate (S_c) for DNA ligase (E). The ligation reaction produces a covalently closed DNA circle as product (P_c).

Cyclization is proposed to proceed through the following kinetic mechanism:

$$L\underset{k_{\mathit{21}}}{\overset{k_{\mathit{12}}}{\rightleftarrows }}Sc+E\underset{k_{\mathit{32}}}{\overset{k_{\mathit{23}}}{\rightleftarrows }}ESc\stackrel{k_{\mathit{34}}}{\to }E+Pc$$ (7)

The subscripts on the rate constants indicate which sets of species are being converted.

Ligation kinetics experiments should be performed under conditions where the dissociation of cohesive ends is fast compared to ligase-catalyzed ring closure, so that there exists a rapid pre-equilibrium between L and S_c. In this case the formation of ES_c, which involves the bimolecular formation of an enzyme-substrate complex (ES_c), is slow relative to end dissociation, and the rate of ligase-catalyzed covalent ring closure (k_C) is directly proportional to the equilibrium fraction of cyclized molecules (f_Sc) given by:

$$f_{S_c}=\frac{[S_c]}{[L]+[S_c]}=\frac{k_{12}}{k_{12}+k_{21}}$$ (8)

This condition can be assured by using a sufficiently small concentration of enzyme E. If in addition the concentrations of S_c is sufficiently small relative to L, then the rate constants k_C and k_D for the ligation of both circular and biomolecular substrates can be expressed in terms of the equilibrium constants for transient end-joining by applying the steady-state approximation to the kinetic mechanism given in equation 7, along the lines of Michaelis-Menten kinetics. The full derivation (Peters and Maher, 2010) yields:

$$j\equiv \frac{K_{a,\mathit{\text{circular}}}}{K_{a,\mathit{\text{bimolecular}}}}\approx \frac{k_C}{k_D}$$ (9)

where K_a values are equilibrium constants and k_C and k_D are the rate constants for ligase-catalyzed intramolecular cyclization and intermolecular dimerization, respectively. Equation 9 shows that, subject to the rapid pre-equilibrium conditions, the j-factor (defined as a ratio of equilibrium constants) can be obtained from the ratio of two experimentally measurable rate constants. These constants (k_C and k_D) are both dependent on DNA length and on temperature. However, for DNA lengths 126–4361 bp, k_D has been shown to be essentially independent of DNA length (Shore et al., 1981). The length dependence of j therefore reflects primarily changes in k_C, which Fig. 2B shows to be much more dramatic. As above, the dominant determinants of k_C for small DNA molecules are the energy required for bending DNA into a small circle and the energy required for twisting the DNA for alignment of termini.

The conditions that are required for the validity of equation 9 have been a matter of concern in the field. Rapid pre-equilibria among species requires that the K_m of ligase for substrate is in excess of the substrate concentration, and the connection between kinetics and thermodynamics requires that the fraction of substrate must be small for each substrate type. Thus, in practice the rate of product formation must be directly proportional to the ligase concentration. The requirement that K_m >>[substrate] must be met for both circular and bimolecular substrates (which are likely to be at very different concentrations) so that the relative equilibrium populations of each are faithfully reported. Fundamentally, the j-factor estimate should not be dependent on experimental DNA or ligase concentrations, and this must be tested over a range of concentrations of each. This can be challenging because if the j-factor is too small or the DNA concentration is too large then the amount of cyclized product is very small relative to bimolecular products, and if the j-factor is large then the bimolecular product can be completely suppressed.

Careful cyclization experiments require substrates of higher purity than typical molecular biology applications such as cloning, mobility shift experiments, or even many types of footprinting. This is because cyclization requires that both DNA termini be fully active, with the correct sequence overhangs and phosphorylation states. DNA with only one active terminus can still undergo bimolecular ligation, and the appearance of low levels of bimolecular products from DNA that is incapable of cyclization can lead to underestimation of the j-factor, especially for molecules with large j-factors. On the other hand, it can be difficult to measure the true cyclization-competent concentration (the endpoint of the cyclization reaction) because partially melted molecules or molecules with defective termini can still be ligated, albeit slowly, and ligation of a small population of aberrant molecules can lead to overestimation of the j-factor, especially for molecules with low j-factors. These issues have been discussed (Davis et al., 1999), but because of the inhomogeneity of the problematic DNA molecules, to date there is no satisfactory way to consider them quantitatively in the analysis of ligation data.

Representative protocols for DNA probe design, preparation, labeling, and quantitation

Several methods have been described for preparing DNA probes for j-factor determination and for carrying out the ligation experiments (Shore et al., 1981; Vologodskaia and Vologodskii, 2002; Zhang and Crothers, 2003). We have found the approach described below to be relatively simple and to give consistent experimental results. The approach provides stronger signals than analyses requiring limited reaction progress with little depletion of starting material, and thus any problems with non-uniform reactivity of the probe are more readily apparent. We routinely use this procedure to measure the effect of high mobility group B (HMGB) proteins or DNA base modifications on the j-factor. Comparisons are facilitated because the effects of nonspecific DNA binding proteins or the differential effects of base modifications can be examined using a uniform set of starting DNA constructs. These are provided by plasmid pUC19-based constructs pJ823, pJ825, pJ827, pJ829, pJ831, and pJ833, which contain intrinsically straight ~200 bp sequences (Vologodskaia and Vologodskii, 2002). The sequences were created using unique 5-bp direct repeats to eliminate long-range sequence-directed curvature.

Polymerase chain reaction (PCR) products containing these intrinsically-straight subsequences, flanked by HindIII sites, are amplified using primers LJM-3222 (5′-G₃TA₂CGC₂AG₃T₄) and LJM-3223 (5′-TGTGAGT₂AGCTCACTCAT₂AG₂) to give ~400 bp products. PCR reactions (300 µL) include 24 ng plasmid template, 0.4 µM each forward and reverse primers, 100 µg/mL bovine serum albumin (BSA), Taq DNA polymerase buffer (Invitrogen), 4 mM MgCl₂, 0.2 mM each dNTP (exact concentrations confirmed spectrophotometrically at pH 7.0: dATP, λ_{max 259 nm} 15.2×10³ M⁻¹cm⁻¹; dCTP, λ_{max 271 nm} 9.1×10³ M⁻¹cm⁻¹; dGTP, λ_{max 253 nm} 13.7×10³ M⁻¹cm⁻¹; dTTP, λ_{max 267 nm} 9.6×10³ M⁻¹cm⁻¹), 60 µCi [α-³²P]dATP (typically 3000 Ci/mmol stock specific activity, but any specific activity can be used as long as the chemical concentration of the label is << 0.2 mM), and 12 U Taq DNA polymerase (Invitrogen). Cycle conditions are initial denaturation at 98°C for 3 min, 30 cycles of 94°C (30 s), 55°C (30 s), 72°C (45 s), and a final extension at 72°C for 5 min. The reaction is then adjusted to 5 mM EDTA, 10 mM Tris-HCl (pH 8.0), and 0.5% SDS, and treated with 50 ng/µL proteinase K at 37°C for 1 h.

Radioactivity in a defined fraction of the total PCR mixture is measured by scintillation counting. Reactions are extracted with an equal volume of phenol:chloroform (1:1) and the DNA is precipitated from ethanol before overnight digestion with HindIII under conditions recommended by the supplier (New England Biolabs). We recommend using the smallest amount of restriction enzyme that is sufficient for a nearly complete digest, as this minimizes the fraction of damaged termini arising from star activity or from contaminating nucleases or phosphatases. The digest is loaded onto a 5% native polyacrylamide gel (29:1 acrylamide:bisacrylamide) and visualized by exposure to BioMAX XR film. The ~400-bp PCR product is cleaved by HindIII digestion into three easily distinguishable products, allowing facile purification of the ~200 bp probe species without any uncut DNA, and with the added advantage that no synthetic DNA remains in the final product. If an inactive DNA problem is encountered, purification on a higher-percentage 40 cm gel and allowing the desired probe to migrate at least 30 cm may help separate the desired product from possible exonuclease/phosphatase products. The gel slice including the probe is cut out, crushed, and eluted overnight at 22°C in 50 mM NaOAc, pH 7.0. The eluted DNA is precipitated with ethanol. The final concentration of probe DNA is calculated by determining the fraction of original radioactivity incorporated, multiplying this result by the unlabeled dNTP concentration in the PCR reaction, and dividing by the number of dA residues per duplex DNA probe. For example, typically 1 µL of the original 300 µL PCR reaction is diluted 1:100 and the radioactivity in 2 µL of this diluted sample is compared with the radioactivity in 2 µL of purified DNA probe. That fraction (corrected for dilution) determines the fraction of the 60 nmol dATP (the amount in the original PCR reaction) that is present in the purified DNA probe, giving the number of moles of A residues in the purified product.

Purification of HMGB proteins

The S. cerevisiae Nhp6A coding region is cloned between the NcoI and BamHI sites of bacterial expression vector pET-15b (Novagen). The resulting plasmid (pJ1400) encodes untagged Nhp6A protein (molecular weight 10,801) with the following amino acid sequence:

• MVTPREPK₂RT₂RK₃DPNAPKRALSAYMF₂ANENRDIVRSENPDITFGQVGK₂LGE-KWKALTPE₂KQPYEAKAQADK₂RYESEKELYNATLA

A 6-mL overnight LB culture of E. coli strain BL21(DE3) containing carbenicillin (Cb) (50 µg/mL) is grown from a single colony, pelleted by centrifugation, washed with 1 mL fresh LB medium to remove secreted β-lactamase, and resuspended in 1 ml of medium. A 250 µL aliquot is used to inoculate a 250 mL LB-Cb culture. Cells are grown with shaking (250 rpm) at 37°C until an OD₆₀₀ of 0.600 is achieved. IPTG is added to a final concentration of 1 mM and cells are grown at 37 °C for a further 3 h with continued shaking. The culture is then subjected to centrifugation at 6000 g for 15 min at 4° C to pellet cells. The pellet is resuspended in 6 mL lysis buffer (50 mM Na₂HPO₄/NaH₂PO₄, 100 mM NaCl, 1 mM EDTA, pH 7.0), sonicated three times with 15 s pulses separated by 1-min intervals on ice. Lysate is clarified by centrifugation at 20,000 g for 45 min at 4 °C. The soluble fraction is retained and heated at 70 °C in a water bath for 10 min to irreversibly denature host proteins. The resulting opaque suspension is cooled at room temperature for 30 min, clarified by centrifugation at 20,000 g for 45 min (4 °C), and the supernatant retained. A 1:40 dilution of 3 % polyethyleneimine (PEI) is added to the supernatant with gentle agitation for 20 min at 4 °C. Nucleic acids are then removed by centrifugation at 5000 g for 10 min at 4°C, and the clear supernatant, containing the Nhp6a protein, is recovered. The protein is concentrated using Vivaspin spin columns (Vivascience; 5,000 molecular weight cutoff) and purified by reverse phase-HPLC on a Jupiter C₁₈ column (250 × 21.2 mm, 15 µm; Phenomenex, Torrance, CA) in 0.1 % trifluoroacetic acid (TFA)/water with a 50 min gradient from 10–70% B, where B is 80 % acetonitrile/0.1 % TFA. Protein concentrations are estimated by Bradford assay (BioRad, Hercules, CA).

Plasmid pJ1192 encodes rat HMGB1 (boxes A+B, with an internal NdeI site removed by silent site-directed mutagenesis) subcloned between the NdeI and XhoI sites of expression vector pET-15b. The encoded HMGB1(A+B) protein (molecular weight 23,321) lacks the acidic C-terminal tail and has the amino acid sequence shown below (affinity tag in lower case), HMG boxes A and B underlined:

• mgs₂h₆s₂glvprgshMGKGDPK₂PRGKMS₂YAF₂VQTCRE₂HK₃HPDASVNFSEFSK₂CSE RWKTMSAKEKGKFEDMAKADKARYEREMKTYIP₂KGETK₃FKDPNAPKRP₂SAF₂ LFCSEYRPKIKGEHPGLSIGDVAK₂LGEMWN₂TA₂D₂KQPYEK₂A₂KLKEKYEKDIA ₂YRAKGKPDA₂K₂GV₂KAEKSK₄

This plasmid is transformed into bacterial strain BL21 Gold (Stratagene) and a single bacterial colony is used to inoculate a 6-mL overnight LB-Cb culture. Cells are then pelleted, washed with 1 mL fresh LB medium to remove excess β-lactamase, and 250 µL is used to inoculate a 250 mL culture that is then grown as described above. Cells are pelleted by centrifugation at 6000 g and stored at −80 °C. The cell pellet is resuspended in 10 mL 1 X Nickel binding buffer (Novagen) and sonicated as described above. The lysate is clarified by centrifugation at 15000 g for 20 min (4°C). Protein is purified from the lysate using Nickel chelate chromatography on a Novagen "Quick 900" cartridge with buffers provided by the manufacturer. Eluted fractions are concentrated to ~2 mL using Vivaspin spin columns (Vivascience). Purified protein is dialyzed overnight against 1L storage buffer (20 mM HEPES pH 7.5, 100 mM KCl, 1 mM EDTA) in 3500 MWCO Slide-a-Lyzer dialysis cassettes (Pierce) at 4°C, and then dialyzed a second time, overnight against storage buffer containing 5% glycerol. Protein is further purified by size exclusion chromatography with a Superdex 75 10/30 column and dialyzed into storage buffer containing glycerol.

DNA ligation kinetics

T4 DNA ligase-catalyzed cyclization reactions (50 µL) are performed at 22°C with 30 nM DNA restriction fragment (with or without various concentrations of added HMGB protein), ligation buffer (20 mM Tris-HCl, pH 8.0, 30 mM KCl, 100 µg/mL BSA, 1.8 mM ATP, 10 mM MgCl₂), and T4 DNA ligase [final concentrations of 50 U/mL (DNA alone) or 20 U/mL (DNA and HMGB protein), with ligase units as defined by New England Biolabs]. Ligase concentrations must be varied empirically depending on the j-factor and the stability of cohesive end hybridization. If a wide range of ligase concentrations is to be used, it is necessary to use siliconized tubes and to add NP40 detergent (Igepal) to the ligase buffer prevent loss of ligase upon serial dilution. As described below, we test ligase concentrations to demonstrate that they do not influence j-factor estimates for ~200-bp probes, and a similar conclusion was previously reached for DNA probes as short as 100 bp (Du et al., 2005). Aliquots (10 µL) are removed at various times and quenched by addition of EDTA to 20 mM. In cases where high concentrations of HMGB proteins were present, protein is purified away from DNA using Qiagen QIAQuick PCR Clean Up columns and DNA recovered in 30 µL elution buffer.

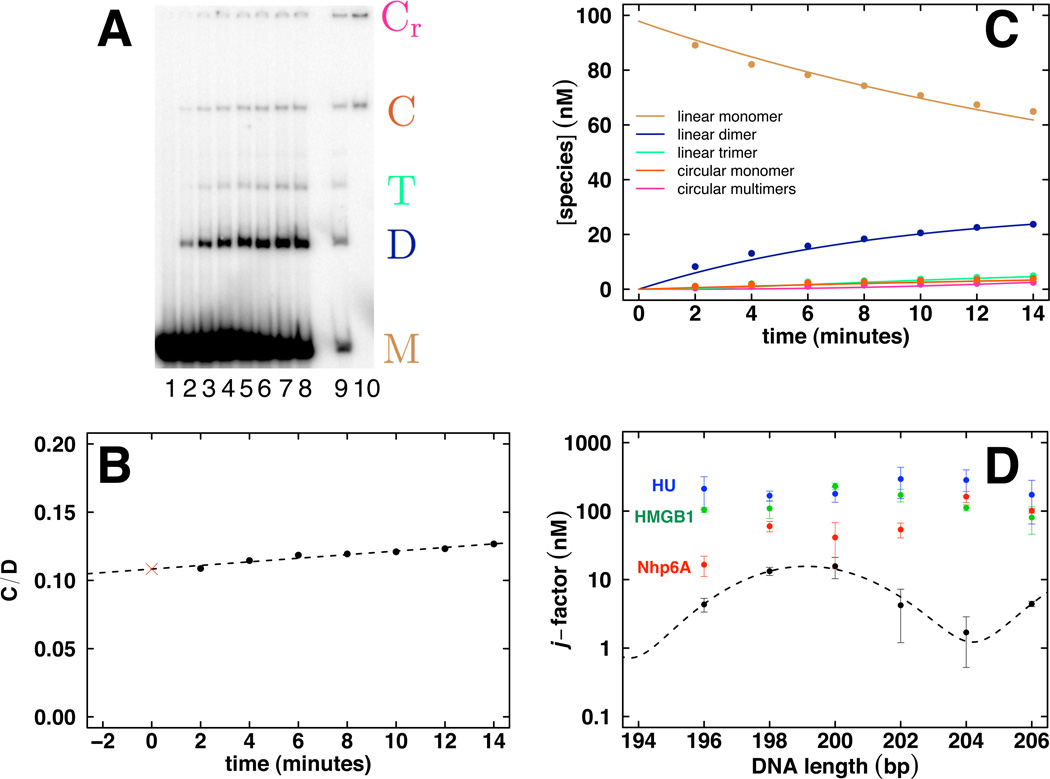
Ligation reaction aliquots are analyzed (Fig. 3) by electrophoresis through 5% native polyacrylamide gels (29:1 acrylamide:bisacrylamide) in 0.5 X TBE buffer, drying, and storage phosphor imaging (Fig. 3A). Gel imaging is done with STORM Scan software, and quantitation is performed with NIH ImageJ software for Macintosh. After correction for background, signal intensities for individual species are measured and normalized to the total signal for each gel lane. The resulting values are multiplied by the original DNA concentration to estimate the concentration of each species (Fig. 3C).

Figure 3.

Cyclization kinetics data analysis to estimate j-factor in vitro. A. Imaged native polyacrylamide gel. Lane 1 contains monomer (M) alone and lanes 2–8 are increasing 2 min time points showing the evolution of linear monomer (M), dimer (D), and trimer (T) as well as circular monomer (C) and circular dimer and trimer (collectively C_r). Lanes 9 and 10 are control treatment and Bal31 exonuclease treatment, respectively, of the final time point. Bal31 treatment (lane 10) provides verification of circular species. B. Extrapolation method based on the ratio (C/D) of monomer circle products (C = C) to the sum of all other ligation products (D = D + T + C_r) under conditions that limit extent of ligation reaction. The j-factor estimate is given by twice the initial probe DNA concentration multiplied by the y-intercept value (red cross). C. Kinetic analysis applicable to full time course of ligation reactions with multiple products and depletion of starting material. D. Example of cyclization data published for intrinsically straight DNA (Vologodskaia and Vologodskii, 2002) and measured in our laboratory for either free DNA (black) or in the presence of 40 nM Nhp6A (red), 40 nM HMGB1 (green) or 10 nM HU (blue).

Experiments done at varying DNA concentration can determine which products are linear vs. circular: circular products are relatively more abundant at lower DNA concentrations. In addition, results may be verified using treatment with Bal31 exonuclease as follows. Aliquots (~10 µL) of the final time point (prior to EDTA addition) are diluted in Bal31 reaction buffer (New England BioLabs) and brought to a final volume of 20 µL with addition of 1 U of Bal31 exonuclease. Reactions are incubated at 30°C for 30 minutes. The Bal31 reactions can then be analyzed by electrophoresis with the other reactions. The circular products will be the only remaining labeled species (Fig. 3A, c.f. lanes 9 and 10). Very small DNA circles (<80 bp) or supercoiled minicircle DNA may also be digested.

Data fitting and ODE approach

Ligation kinetics results in which only one circular product is formed can be fit to analytical expressions described in our early work (Davis et al., 1999; Kahn and Crothers, 1992). Systems in which multimer cyclization is considered require numerical simulation. Our current method of j-factor analysis is based on modeling cyclization kinetics with a reasonable reaction model derived from principles of mass action (Fig. 4A) and a corresponding system of ordinary differential equations (ODEs; Fig. 4B). Rate constants are determined by least-squares fitting to the experimental data. This approach can be applied throughout the course of the reaction. In contrast, analysis based on linear extrapolation methods requires limited reaction progress. When applied to DNA concentrations where the production of pentameric (and larger) products is negligible, all possible interactions of linear species up to pentamer are modeled, i.e. linear monomer (M), dimer (D), trimer (T), tetramer (Q), and pentamer (P). Each of these linear species can also cyclize. The ODE system expresses rates of change of concentration for each species. This system is integrated numerically by R software (Version 2.8.1) using the ODE solver package deSolve. The theoretically predicted values of concentrations are used for non-linear least-squares refinement of rate constants to fit the measured experimental data. R scripts and related files containing the code to solve the ODE system, perform the optimization, and generate plots of the results (e.g. Fig. 3C) are provided in Appendices 1 and 3. From the fit, optimized values for the rates of intramolecular (k_Ci) and intermolecular (k_D) collisions are used to determine the desired j-factor, where:

$$j_i=k_{Ci}/k_D$$ (10)

and i is taken to be 1 for monomer cyclization. Alternatively, using the substitution k_D = k_C1/j₁, the j-factor of interest can be directly obtained from the curve fitting routine. If topoisomers are formed from a given linear molecule, each topoisomer has an independent j-factor.

Figure 4.

Kinetic scheme for analysis of DNA cyclization kinetics. A. Left: Intermolecular ligation reactions giving rise to linear products. Right, intramolecular cyclization reactions giving rise to cyclic (C) products. Monomer, dimer, trimer, tetramer, and pentamer are indicated by M, D, T, Q, and P, respectively. Rate constants are indicated, assumed equal for all intermolecular ligations. B. System of ordinary differential equations describing accumulation of species up to and including pentamers. When it occurs, the statistical factor of 4 accounts for the inability to distinguish between identical DNA termini in intermolecular ligation of linear species.

Fig. 3 shows an example of cyclization kinetics analysis. A method based on linear extrapolation of the ratio of monomer circle (C) to all forms of intermolecular products [D; (Vologodskaia and Vologodskii, 2002; Vologodskii et al., 2001)] can be effective early in the reaction when DNA monomer is not significantly depleted (Fig. 3B). The more general fitting approach advocated here is shown in Fig. 3C.

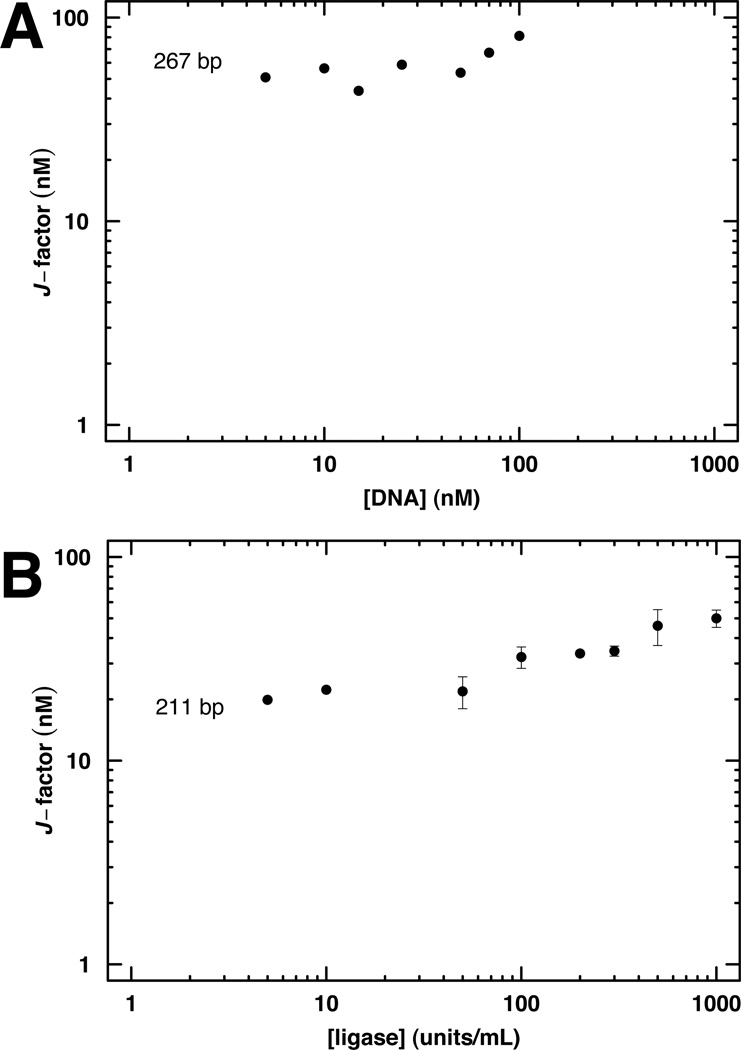
Our fitting method is based on the standard assumptions about ligation reaction kinetics described above. The validity of these assumptions is subject to verification. Importantly, the experimental j-factor should not be dependent on the concentration of either ligase or DNA. Example analyses of these assumptions are shown in Fig. 5. In contrast to the analytical solutions or low-conversion approximation, the ODE method can be extended to consider different populations of linear substrates, such as mixtures of bound vs. free DNA or populations with inactive DNA ends; accurate determination of more rate or equilibrium constants will require correspondingly comprehensive experimental data.

Figure 5.

Control experiments to ensure validity of experimental DNA cyclization kinetics. The experimental j-factor should be estimated under conditions where the apparent j-factor is independent of DNA concentration (A) and ligase concentration (B).

Example data

Fig. 3D shows examples of data obtained by this method. The experimental j-factor was determined for labeled DNA probes of the indicated lengths, either as free DNA or in the presence of the indicated concentrations of sequence-nonspecific HMGB proteins known to enhance the apparent flexibility of DNA. Data from our laboratory for purified DNA (Fig. 3D, black) are similar to those previously published (Vologodskaia and Vologodskii, 2002). The yeast (Nhp6A), mammalian (HMGB1), and bacterial (HU) architectural proteins dramatically increase apparent DNA flexibility as measured by the j-factor (Fig. 3D, red, green, blue, respectively). These results emphasize how the profound ability of HMGB and related architectural proteins to enhance the apparent flexibility of DNA can be quantitated by experimental measurement of the j-factor. The proteins add random kink sites, increasing the experimental j-factor by multiple orders of magnitude, and serving to facilitate DNA transactions requiring small loops.

It should also be noted that there are a number of approaches to the quantitative prediction of j-factors from DNA sequence and structural models, but these are beyond the scope of this article.

B. In vivo analysis of E. coli lac repression loops

Concept

Certain in vivo assays provide the unusual opportunity to measure processes that depend upon DNA flexibility and looping in living cells. Assays based on components of the E. coli lac operon depend upon DNA flexibility through cooperativity at a distance (Fig. 1B;Becker et al., 2005; Becker et al., 2007; Becker et al., 2008; Bellomy et al., 1988; Kramer et al., 1987; Law et al., 1993; Mossing and Record, 1986; Muller et al., 1996; Oehler et al., 1990; Peters and Maher, 2010). Here one operator (O₂) overlaps with the promoter of the lacZ reporter gene and serves as a very weak lac repressor binding site. The lacZ gene is only weakly repressed when this operator is present in isolation. Repression is strongly enhanced by placement of a high-affinity operator (O_sym) upstream of the promoter. The bidentate lac repressor tetramer bound at O_sym site has the potential to increase the local repressor concentration at O₂ by virtue of DNA looping (Mossing and Record, 1986; Oehler and Müller-Hill, 2009). Such looping requires different degrees of DNA (and repressor) distortion as a function of inter-operator spacing and any intrinsic curvature or unusual flexibility in the loop DNA. The requirement for DNA twisting when the operators are out-of-phase with the DNA helical repeat makes looping less energetically favorable in these cases. Analysis of lacZ repression as a function of operator spacing has been shown to provide a sensitive assay of the bending and twisting flexibility of the DNA/lac repressor complex in vivo (Becker et al., 2005; Becker et al., 2007; Becker et al., 2008; Bellomy et al., 1988; Garcia et al., 2007; Zhang et al., 2006a; Zhang et al., 2006b).

The E. coli lac looping system permits quantitative analysis of DNA looping by measurement of β-galactosidase (the lacZ gene product) activity extracted from living cells. Analysis is performed in the absence (uninduced) or presence (induced) of IPTG, an allolactose analog that reduces lac repressor affinity for DNA. Thermodynamic modeling allows for identification of subtle trends in the data (Becker et al., 2005; Becker et al., 2007; Becker et al., 2008; Bellomy et al., 1988; Law et al., 1993; Zhang et al., 2006a; Zhang et al., 2006b). Although the present analysis is limited to in vivo DNA looping using components of the E. coli lac operon, other analyses have been performed in eukaryotic cells, as recently reviewed (Peters and Maher, 2010).

The goals of the in vivo work include assessing how the results differ from the in vitro WLC model. The bending and flexibility of DNA in vivo may be influenced by supercoiling, DNA binding proteins, and ionic and osmotic conditions. Eventually, for quantitative modeling of gene regulation it will be necessary to understand the in vivo physical chemistry of DNA in as much detail as we now have for DNA in vitro.

Experimental design

The thermodynamic model described here is based on the pioneering work of Record and co-workers (Bellomy et al., 1988; Law et al., 1993). Analysis is based on the premise that promoter repression is determined by the degree of occupancy of the proximal lac operator (O₂ in our system) at equilibrium; we do not consider possible effects of looping per se. A variety of related models have been developed that differ in their descriptions of the effects of length variation (Bintu et al., 2005; Zhang et al., 2006a; Zhang et al., 2006b).

In our model, the extent of promoter repression is calculated by evaluating the distribution of possible states of the proximal lac operator. The promoter is repressed whenever the weak proximal O₂ operator is bound by lac repressor. This condition is most likely to arise from singly bound repressor at O₂ (“single bound”) or from repressor bound to the proximal operator by virtue of DNA looping from the strong distal O_sym operator (a phase-dependent “specific loop”). Even the minimal observed repression looping (for out-of-phase operator separations) provides stronger repression than is observed when either of the operators is deleted. Other possible repressed states include repressor delivered to O₂ by non-phase-dependent transfer mechanisms (e.g. sliding or hopping) from the distal operator, or repressor delivered by looping to pseudooperator sites overlapping O₂. Such states are considered together in our model as nonspecific loops (“NS loop”).

A partition function for the system expresses the sum of possible states of the O₂ operator:

$$[\mathit{\text{Free}}]+[\mathit{\text{Specific Loop}}]+[NS\mathit{\text{Loop}}]+[\mathit{\text{Single bound}}]=[O2]$$ (11)

This expression can be cast in terms of the equilibrium constants for the different states:

$$[\mathit{\text{Free}}](1+K_{SL}+K_{NSL}+K_{O2})=[O2]\text{where}{K}_{SL}=\frac{[\mathit{\text{Specific Loop}}]}{[\mathit{\text{Free}}]},K_{NSL}=\frac{[NS\mathit{\text{Loop}}]}{[\mathit{\text{Free}}]},\text{and}{K}_{O2}=\frac{[\mathit{\text{Single bound}}]}{[\mathit{\text{Free}}]}.$$ (12)

The constant cellular concentration of lac repressor has been absorbed into each of the equilibrium constants; we assume one or low copy number DNA template so there is no interaction between separate DNA molecules and no depletion of LacI.

The fraction of bound (repressed) O₂ operators is given by the sum of the statistical weights of the bound forms divided by the total partition function:

$$f_{\mathit{\text{bound}}}=([\mathit{\text{Specific Loop}}]+[NS\mathit{\text{Loop}}]+[\mathit{\text{Single bound}}])/[O2]=([O2]-[\mathit{\text{Free}}])/[O2]=(K_{SL}+K_{NSL}+K_{O2})/(1+K_{SL}+K_{NSL}+K_{O2})$$ (13)

Experimentally, the fraction bound is given by:

$$f_{\mathit{\text{bound}}}=\frac{\text{max induced activity}-\text{observed activity}}{\text{max induced activity}}$$ (14)

where the maximum induced activity is potentially different for each E. coli strain background. Control experiments (performed under both repressing and inducing conditions) with an isolated O₂ operator are used to determine K_O2 for each strain background. Based on the results of initial experiments these values were fixed at 1 and 0 for repressing and inducing conditions, respectively.

Torsional flexibility of the repression loop is modeled by formulating a helical-phasing dependent equilibrium constant for specific loop formation, K_SL. A sum of Gaussians expresses the total probability of twist deformations needed to bring the two operators into phase.

$$K_{SL}=\sum _{i=-5}^5{K}_{\text{max}}{e}^{-{(sp-s{p}_{\mathit{\text{optimal}}}+i·hr)}^2/2{{\sigma }_{Tw}}^2}$$ (15)

The parameter sp gives the actual spacing (bp) between operator centers for a given construct, sp_optimal is the spacing (bp) for optimal repression, K_max is the equilibrium constant for DNA loop formation when operators are perfectly phased, and σ_Tw is the standard deviation of the torsion angle between operators, given thermal fluctuations. Summation over the integer i captures all possible overtwisting or undertwisting needed to give the helical phasing required for optimal loop formation. Finally, σ_Tw is calculated from the torsional flexibility per base pair:

$${{\sigma }_{Tw}}^2=sp·{{\sigma }_{bp}}^2$$ (16)

where σ_bp is the standard deviation of twist (per bp) given by:

$${\sigma }_{bp}=\sqrt{\frac{\ell kT}{C_{\mathit{\text{app}}}}}\text{radians}•\frac{1\text{turn}}{2\pi \text{radians}}•\frac{hr\mathrm{b}\mathrm{p}}{\text{turn}}=\frac{hr}{2\pi }\sqrt{\frac{\ell kT}{C_{\mathit{\text{app}}}}}$$ (17)

in units of bp twist increments. Here ℓ is the average bp separation (3.4 Å), k is Boltzmann’s constant, T is the absolute temperature, C_app is the apparent torsional modulus for the DNA in the loop, and hr is the DNA helical repeat. Variability in the possible torsion angles permitted in a protein-DNA loop reduces the apparent torsional modulus, C_app, increasing the apparent σ_Tw.

In principle, additional K_SL terms could be included to consider different loop geometries: “open-form” vs. V-shaped Lac repressor might well have different optimal spacing and K_max values. However, the data we have to date have not required consideration of multiple loop shapes for uninduced loops: complex repression efficiency curves derive instead from the relationship between induced and uninduced activities.

Surprisingly, our experimental data typically show no dependence of K_SL on operator spacing except through the effect of spacing on torsion: the apparent persistence length is effectively small enough that the loop free energy does not change markedly with distance. Since fitting the data did not require consideration of persistence length, our initial approach (Becker et al., 2005; Becker et al., 2007) did not consider DNA length per se: f_bound was modeled as a function of DNA length (sp), with five adjustable parameters hr, C_app, K_max, K_NSL, and sp_optimal. Predicted absolute activities were calculated using f_bound and the measured maximal induced activity, and repression ratios were calculated from the ratios of these computed absolute activities.

A more general version of this model was subsequently developed for the analysis of data on the effects of eukaryotic HMGB proteins expressed in E. coli, which did exhibit twist-independent length dependence (Becker et al., 2008). The experimental fraction of O₂ bound by repressor (f_bound) is now modeled as a function of DNA spacer length (sp) with six adjustable parameters. Three parameters reflect properties of the repressor-DNA complex. These are the optimal operator spacing in bp as above (sp_optimal), the equilibrium constant for specific O_sym-O₂ loop formation when operators are perfectly phased (K´_max, replacing the previous K_max, see below), and the equilibrium constant for all forms of O_sym-dependent enhanced binding to O₂ other than the specific loop as above (K_NSL). Three fitting parameters focus on properties of the looped DNA. The first two are the helical repeat (hr) and the apparent torsional modulus of the DNA loop (C_app) as above. The length dependence that is observed in the data is addressed by the third empirical fitting parameter, P_app, which reflects the expected decrease in DNA bending free energy as operator spacing sp increases:

$$\mathrm{\Delta }{G}_{\mathit{\text{bend}}}=\frac{PRT}{2·sp}{(\mathrm{\Delta }\mathrm{\Theta })}^2=P_{\mathit{\text{app}}}/sp$$ (18)

The DNA persistence length P, the thermal energy RT, and the extent of bending (Δ Θ) have been included into a single constant P_app with units of bp × energy in increments of RT. Assuming a constant Δ Θ is equivalent to a simplifying assumption of constant loop geometry for all sp; as above, alternative loops would have different P_app values. The bending energy above contributes an e^−P_app/sp factor to the looping equilibrium constant K_max. Therefore, normalization of the length dependence is accomplished by replacing K_max in the fitting routines with:

$$K_{\mathit{\text{max}}}^{\prime }=K_{\mathit{\text{max}}}\text{exp}\left[P_{\mathit{\text{app}}}\right(\frac{1}{s{p}_{\mathit{\text{avg}}}}-\frac{1}{sp}\left)\right]$$ (19)

where sp_avg is the mean spacing over the data set. K_max (the value of K´_max at sp = sp_avg) can be compared directly to the K_max obtained using the prior fitting procedure (Becker et al., 2005). An in vivo DNA persistence length can be recovered from P_app if Δ Θ is known, but it is complicated because Δ Θ may not be constant. The fact that the amount of actual DNA curvature in the loop likely changes with operator spacing is considered in P_app. We view the P_app parameter as a physically reasonable way to address cases where increased repression is observed with increasing operator spacing.

Finally, the latest implementation of the model takes into account the distinct values of K_O2 for each strain background, as determined from control experiments with an isolated O₂ operator and the maximal induced activity for the given strain. Consequently, comparison of the equilibrium constants requires normalization to K_O2. Thus, we define K°_max = K_max /K_O2 and K°_NSL = K_NSL /K_O2; in our early work K_O2 was found to be ~1 and the normalization was implicit, but in general this is not the case.

Data handling and curve fitting

The experimental data comprise β-galactosidase activities (E) in the presence and absence of inducer and the conventional repression ratio (RR), defined as the reporter gene activity in the presence of IPTG (inducing conditions) divided by the activity in the absence of inducer (repressing conditions):

$$RR=\frac{E_{+IPTG}}{E_{-IPTG}}$$ (20)

Treating the quotients of activities as independent data points in addition to the activities themselves recognizes that changes in absolute E values due to small changes in promoter strength or day-to-day variations tend to compensate, so repression ratios show fewer outliers.

Curve fitting is performed in two steps. First, a global non-linear least-squares refinement to each set of E values (repressed and induced) is performed with the six adjustable parameters for each data set. This first fitting is followed by a global non-linear least-squares refinement to E (repressed and induced) and RR simultaneously, with K_max, K_NSL, and P_app estimates held fixed from the first fitting routine. Values and ranges for hr, C_app, and sp_optimal are reported from this second fitting. Matlab was used initially, but recently the open source R environment (version 2.8.1) has been used for all data analysis and fitting. R scripts and related files containing this code appear in Appendices 2 and 3.

Normalized reporter expression (E’) is plotted to allow for comparisons among experiments. E’ are obtained by dividing the observed β-galactosidase activity (E_OsymO2) by the activity observed in a bacterial strain lacking an upstream O_sym operator, (E_O2), under either repressing or inducing conditions:

$$E\prime =\frac{E_{O_2{O}_{\mathit{\text{sym}}}}}{E_{O_2}}$$ (21)

Additionally, as mentioned above K_max and K_NSL are normalized to K_O2 to allow for comparisons among strains.

Reporter constructs for DNA looping in bacteria

Our DNA looping constructs are typically single-copy genes inserted into the F128 episome by way of the plasmid pJ992, which was created by modification of pFW11-null (Whipple, 1998). The wild type lacZ O₂ at +401 (underlined below) was inactivated by site directed mutagenesis (bold, QuikChange, Stratagene: La Jolla, CA). Upper and lower mutagenic primers are LJM-1921 5’-CG₂AGA₂TC₂GACGGGGTGCTATTCATTAACTTTCA₂TGT₂GATG and LJM-1922 5’-CATCA₂CAT₂GAAAGTTAATGAATAGCACCCCGTCG₂AT₂CTC₂G. Primers LJM-1930 (5’-CGTCGT₄ACA₂CGTCG) and LJM-1931 (5’-CAT₂GA₃GT₂A₂TGA₂TAGCAC) are used to monitor and confirm the lacZ mutations by PCR amplification. A 362-bp PCR product is amplified only when the mutagenized O₂ is present. A UV5 promoter was then installed between BamHI and SalI sites in pFW11-null. A new O₂ sequence (5’- A₃TGTGAGCGAGTA₂CA₂C₂) was cloned immediately downstream of the transcription start site between SalI and PstI sites. This step also installs a NotI site downstream of O₂. Additional spacing constructs are created by ligation of different operator inserts between SalI and NotI sites of pJ992 with the upstream O_sym operator at spacings ranging from 49.5 bp to 90.5 bp (distances measured between operator centers). Constructs with a single upstream O_sym in the absence of a downstream O₂ are created by insertion of an inactive O₂ sequence (5’-GA₃GT₂A₂TGA₂TAGCAC₃) between the SalI and NotI sites of pJ992.

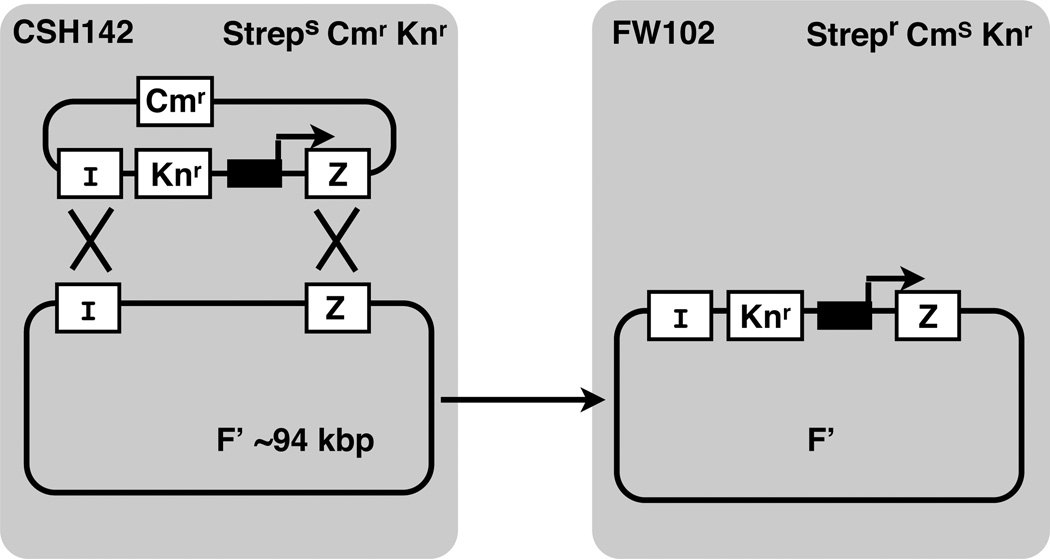
LacZ looping constructs are moved from the plasmid onto the large single copy F128 episome by homologous recombination. F128 encodes the lacI gene producing wild type levels of lac repressor. Bacterial conjugation and selection for the desired recombinants (Fig. 6) is carried out as described (Whipple, 1998). Correct recombinants are confirmed by PCR amplification to detect the inactivated internal lacZ O₂ sequence using primers LJM-1930 and LJM-1931.

Figure 6.

Bacterial recombination system (Whipple, 1998) used to move engineered lac promoter/operator constructs (black box and broken arrow) from small recombinant plasmids to the large F’ episome of E. coli in strain CSH142 (wild type levels of lac repressor), followed by conjugative transfer to FW102 cells. LacI and lacZ genes, sites of homologous recombination, and antibiotic resistance markers (Strep, streptomycin; Cm, chloramphenicol; Kn, kanamycin) are indicated.

Disruption of hupA and hupB genes

For investigation of the effects of exogenous DNA binding proteins, the endogenous hupA and hupB genes encoding HU protein (and genes encoding other nucleoid proteins) are disrupted in E. coli strain FW102 as described (Datsenko and Wanner, 2000). Gene disruption reagents are obtained from the E. coli Genetic Stock Center (New Haven, CT). The entire hupA coding sequence is first replaced by recombination with a selectable marker (complementary sequence in bold) amplified with primer pair LJM-2201 5’-GAT₃A₂CGC₂TGAT₃GTCGTAC₂TG₂AGTCT₂C₃T₃CGC₃GTGTAG₂CTG₂AGCTGC₂C and LJM-2202 5’-G₃C₂AC₄T₂CGT₂A₄CTGT₂CACTGC₂ACGCA₂TCT₂ACAT₂C₂G₄ATC₂GTCGAC₂. This is followed by replacement of hupB with a selectable marker amplified with primer pair LJM-2203 5’-CTGATATA₂CTGCTGCGCGT₂CGTAC₂T₂GA₂G₂AT₂CA₂GTGCGGTGTAG₂CTG₂AGCTGCT₂C and LJM-2204 5’-GCAGA₃GTCAC₂GA₂TACA₃TA₆GGCACATCAGTAGATGAT₂C₂G₄ATC₂GTCGAC₂. In each case, the selectable marker is then removed in a second step (Datsenko and Wanner, 2000). Deletions are confirmed by PCR amplification. For example, primers flanking hupA, LJM-2243 (5’-GCA₂TAT₂G₂TATA₂TTTTTC) and LJM-2244 (5’-GA₂GTGA₂GAGT₂ATGACTACAG), amplify a 612-bp product from strain FW102 and a 297-bp product when hupA is deleted. Similarly, primers flanking hupB, LJM-2245 (5’-C₂T₇GTCTCGCTA₂G) and LJM-2246 (5’-G₂C₂TAT₂GTGACA₂GA₃C), amplify a 550-bp product from strain FW102 and a 294-bp product when hupB is deleted. Genotypes of all ΔHU strains containing looping episomes are confirmed by PCR amplification with the same primer sets following conjugation and selection, and the presence of the looping episome is confirmed by PCR as above.

Protein expression

It is sometimes of interest to monitor repression looping in vivo after expression of E. coli proteins or heterologous proteins. Protein expression plasmids are created using a modified version of pXL20 (Whipple, 1998). The EcoRI to XbaI segment was removed. To create pJ1035, this region is replaced with the complementary oligonucleotide pair LJM-2085 (5’-A₂T₂CTC₂TCT₂AG₂CAC₄AGGCT₃ACACT₃ATGCT₂C₂G₂CTCGTATA₂TGTGTG₂GA₂CTACATC₂TC₂GCTAG₂T₂CACACAG₂A₃T) and LJM-2086 (5’- CTAGAT₃C₂TGTGTGA₂C₂TAGCG₂AG₂ATGTAGT₂C₃ACACAT₂ATACGAGC₂G₂A₂GCATA₃GTGTA₃GC₂TG4TGC₂TA₂GAG₂AG), creating an E. coli promoter of moderate strength (underlined). As an example, protein expression plasmid pJ1043 is created by PCR amplification of rat HMGB1. Primers LJM-2092 (5’-GCTCTAGA₂TG₃CA₃G₂AGATC₂TA₂G) and LJM-2093 (5’-CG₃ATC₂T₂ACT₂CT₅CT₂GCTCT₂CTC) amplify the coding region from met-1 to lys-185, including both HMG boxes. Upper primer LJM-2092 installs a XbaI site and lower primer LJM-2093 installs both a TAA stop codon and BamHI site for cloning into pJ1035. To recover HU expression in cells disrupted for HU expression, a hupA/hupB co-cistronic gene expression plasmid was created. Primers LJM-2361 (5’-GCTCTAGA₂TGA₂CA₂GACTCA₂CTGAT₂G) and LJM-2362 (5’-CGC₂ATG₂CGCAGT₂ACT₂A₂CTGCGTCT₃CAG) amplify hupA from FW102 genomic DNA. Primers LJM-2361 and LJM-2362 introduce terminal XbaI and NcoI sites. The hupA PCR product is cloned between XbaI and NcoI sites of pJ1035. To create the co-cistronic hupA/hupB gene product, hupB is amplified from FW102 genomic DNA using primers LJM-2363 (5’-GC₂ATG₂CAG₂A₂GAGA₂GA₂TGA₂TA₃TCTCA₂T₂G; introduces a NcoI restriction site and a Shine/Delgarno sequence prior to first ATG of hupB) and LJM-2364 (5’-GCGGATC₂T₂AGT₃ACCGCGTCT₃CAG; introduces a BamHI site for cloning). The hupB PCR product is then cloned between the NcoI and BamHI sites of pJ1035 to produce a co-cistronic hupA/hupB construct.

E. coli β-galactosidase reporter assays

Reagents are purchased from Sigma (St. Louis, MO). LacZ expression is measured using a liquid β-galactosidase colorimetric enzyme assay (Miller, 1992). Duplicate 2 mL subcultures of LB medium in 96-well boxes are inoculated with 100 µL of saturated overnight culture in the presence of either 0 or 2 mM IPTG. Results of preliminary experiments showed 2 mM IPTG to be saturating: higher levels of IPTG did not induce increased levels of β-galactosidase. Subcultures are grown at 37°C until OD₆₀₀ reaches ~0.3. For samples with low β-galactosidase activity, 1 mL of bacterial culture is assayed after centrifugation and resuspension in 1 mL Z-buffer (60 mM Na₂HPO₄, 40 mM NaH₂PO₄, 10 mM KCl, 1 mM MgSO₄, 50 mM β-mercaptoethanol). For samples with high levels of β-galactosidase activity, 100 µL of bacterial culture is first diluted with 900 µL Z-buffer. Cells are lysed by addition of 50 µL chloroform and 25 µL 0.1% SDS, followed by vortex agitation for 10 s. Samples are then equilibrated at 30° C for 5 min, followed by the addition of 200 µL O-nitrophenylpyranogalactoside solution (ONPG; 4 mg/mL) in Z-buffer. Incubation is continued at 30° C with accurate timing until OD₄₂₀ reaches ~ 0.5. Reactions are terminated with 500 µL 1 M Na₂CO₃ and the reaction time recorded. Cell debris is removed by centrifugation for 3 min at 15000 × g. Sample absorbance is measured on a Molecular Devices SpectraMax 340 microtiter plate reader. β-galactosidase activity (E) is calculated according to:

$$E=1000\frac{[O{D}_{420}-1.75(O{D}_{550})]}{t•\nu •O{D}_{600}}$$ (22)

where OD_x is the optical density at wavelength x, t indicates reaction time (min), and v indicates assay culture volume (mL). Assays are performed for a total of four colonies using two independent strains repeated on two days. Assays with ΔHU cells and different protein expression plasmids are typically performed with a total of 6 colonies repeated on two days. Repression due to specific DNA looping is expressed in terms of the normalized expression parameter E’ as described in equation 21 (above).

Example data and analysis

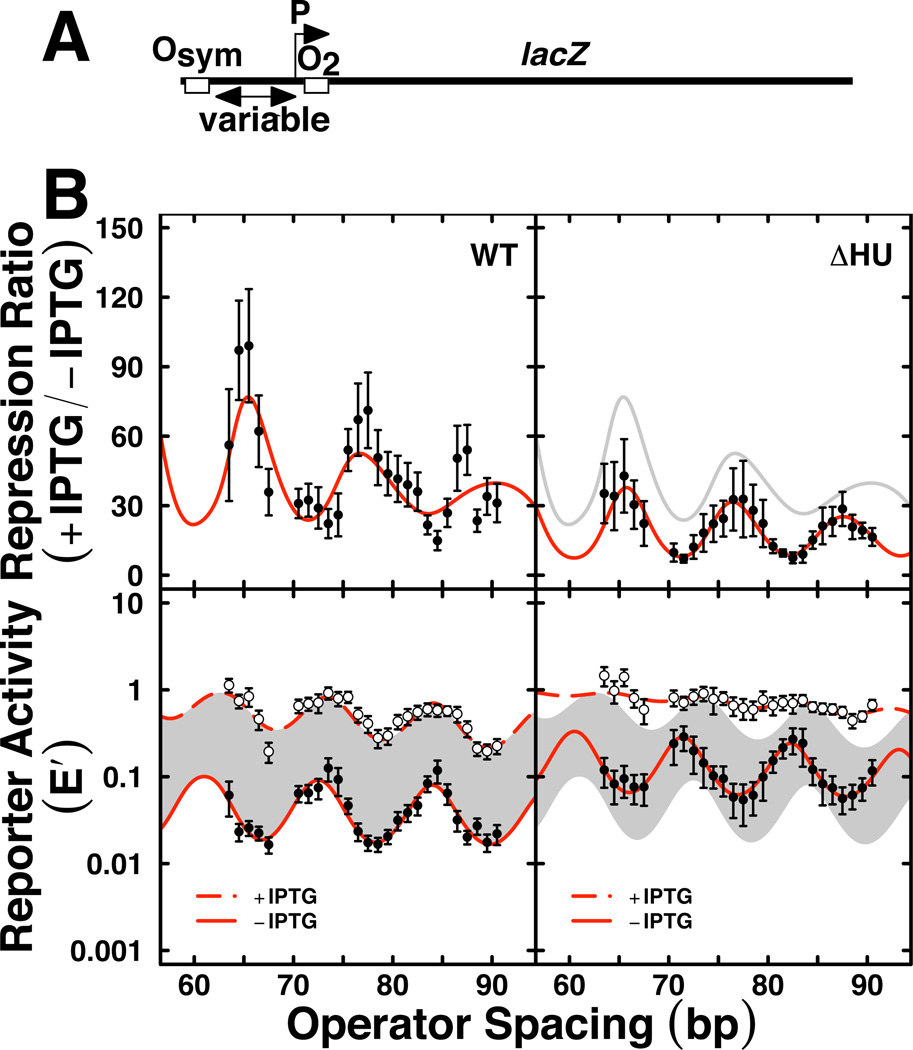
We have applied the experimental system (Fig. 7A) to study the properties of lac repression loops in vivo for E. coli cells altered in nucleoid proteins (Becker et al., 2005; Becker et al., 2007; Becker et al., 2008; Sebastian et al., 2009). Examples of data and fits are presented in Fig. 7B and Table 1. The data for lac repression looping in wild type (WT) E. coli cells (Fig. 7B, left) are presented as the repression ratio (upper) and E’ reporter gene expression values in the absence (closed circles) and presence (open circles) of IPTG inducer (lower). Fits to the thermodynamic model are shown as smooth red lines, with best fit values in Table 1. The right panels of Fig. 7B show corresponding data for E. coli cells lacking the HU protein. These data revealed several important insights that have been discussed (Becker et al., 2005). Wild type cells show repression that oscillates with loop length (bottom). Surprisingly, an oscillating pattern (with slightly different phasing) is observed even in the presence of IPTG inducer, indicating residual weak DNA looping. The dephasing of these two traces gives rise to an irregular pattern in the repression ratio (Fig. 7B, top). Loss of HU protein disables lac repression looping (Fig. 7B, ΔHU).

Figure 7.

Example of quantitative in vivo lac repression analysis. A. Experimental design with variable operator spacing to measure occupancy of O₂ as a function of increased local lac repressor concentration due to DNA looping-dependent collisions with bidentate lac repressor tetramer bound at the strong O_sym operator. B. Experimental data (mean and standard deviation) with best least-squares fits to thermodynamic model for repression ratio (top) and normalized reporter activity (E’, bottom; lower and upper E’ curves are uninduced and induced, respectively). Left and right panels compare length-dependent DNA looping in wild type E. coli cells (WT) vs. cells deleted for both hupA and hupB genes encoding nucleoid heat unstable protein HU [ΔHU; (Becker et al., 2005)].

Table 1.

Example lac repressor looping fit parameters in vivo¹

parameter	WT fit value		ΔHU fit value
	−IPTG	+IPTG	−IPTG	+IPTG
hr (bp)	11.1±0.2	10.7±0.7	11.3±0.2	10.5±2.5
Capp (× 10−19 erg cm)	0.97±0.03	1.65±1.14	1.10±0.13	0.35±0.13
spoptimal (bp)	79.2±0.1	80.2±1.0	78.5±0.3	79.6±1.5
KO2	4.9	0.6	10.8	0.7
K°max	62±15	0.9±0.6	14±3	0.1±0.1
K°NSL	0±1	0±0.1	0±1	0±0.1
Papp (bp)	0±71	0±390	0±68	382±500

¹Parameters not well determined by fitting are in italics

Examination of best fit values in Table 1 is interesting. The helical repeat in vivo is generally higher than observed for relaxed DNA in vitro, consistent with the sites being in a plectonemic superhelix. The DNA twist constant is well below the accepted range of 2–4 × 10⁻¹⁹ erg cm for pure DNA in vitro, suggesting that the flexibility of lac repressor (and/or other proteins) enhances the expected torsional inflexibility of DNA. The looping equilibrium constant, K_max, is dramatically weakened by IPTG induction, as expected, and is more than two-fold lower in cells lacking HU protein. Finally, the fit value for the apparent persistence length of the lac repressor loop (including potential contributions from both protein and DNA) is less than 25% of the typical in vitro value for DNA. These fit values exemplify the complexity of understanding the mechanics of the protein/DNA loop when loop geometry is unknown. The work suggests a strong effect of HU on looping, but the thermodynamic model does not reveal the mechanism of this effect. Others have concluded that HU affects the overall apparent flexibility of the repression loop DNA (Zhang et al., 2006a).

Concluding comments

The methods presented here are firmly rooted in classic experiments in DNA biophysics. The approaches take advantage of two particularly tractable model systems: in vitro DNA cyclization kinetics and in vivo repression looping in bacteria. Though established through biophysical approaches more than 20 years ago, the latter gene regulatory system is still inadequately understood. Both systems offer the opportunity to quantitatively measure DNA physical properties, and to assess how these properties are changed as the systems are perturbed by proteins. Here we have shown adaptations that update the execution and interpretation of these experiments.