Molecular Dynamics Simulations of Galectin-1-oligosaccharide Complexes Reveal the Molecular Basis for Ligand Diversity

Abstract

Galectin-1 is a member of a protein family historically characterized by its ability to bind carbohydrates containing a terminal galactosyl residue. Galectin-1 is found in a variety of mammalian tissues as a homodimer of 14.5-kDa subunits. A number of developmental and regulatory processes have been attributed to the ability of galectin-1 to bind a variety of oligosaccharides containing the Gal-β-(1,4)-GlcNAc (LacNAc_II) sequence. To probe the origin of this permissive binding, solvated molecular dynamics (MD) simulations of several representative galectin-1-ligand complexes have been performed. Simulations of structurally defined complexes have validated the computational approach and expanded upon data obtained from X-ray crystallography and surface plasmon resonance measurements. The MD results indicate that a set of anchoring interactions between the galectin-1 carbohydrate recognition domain (CRD) and the LacNAc core are maintained for a diverse set of ligands and that substituents at the nonreducing terminus of the oligosaccharide extend into the remainder of a characteristic surface groove. The anionic nature of ligands exhibiting relatively high affinities for galectin-1 implicates electrostatic interactions in ligand selectivity, which is confirmed by a generalized Born analysis of the complexes. The results suggest that the search for a single endogenous ligand or function for this lectin may be inappropriate and instead support a more general role for galectin-1, in which the lectin is able to crosslink heterogeneous oligosaccharides displayed on a variety of cell surfaces. Such binding promiscuity provides an explanation for the variety of adhesion phenomena mediated by galectin-1.

INTRODUCTION

Galectin-1 is one of a family of 11 β-galactoside binding vertebrate lectins.¹ As an S-type lectin, it contains free sulfhydryl groups that must be maintained in a reduced state for full binding activity, but does not require the presence of Ca²⁺ for activity. Galectin-1, expressed as a homodimer of 14.5-kDa subunits, is found in a wide range of tissue types and has been shown to play a part in the regulation of cellular growth and differentiation² as well as the immune response.³

Glycoproteins, such as laminin,⁴ fibronectin,⁵ ${\text{CD}}_{45}^6$ LAMP I and II, α₇β₁ integrin,⁷ and the glycolipid ${\mathrm{G}}_{\mathrm{M}1}^8$ have been proposed as in vivo ligands for galectin-1. Gal-β-(1,4)-GlcNAc (LacNAc_II) (1) disaccharide units are found in each of the N-, O-, and ceramide-linked glycans found in these molecules. The various in vitro effects exhibited by this lectin have been attributed to the ability of dimeric galectin-1 to crosslink these oligosaccharides.^9,10 A number of crystal structures of galectins with bound oligosaccharide ligands have been determined,^10–14 including the strucure of bovine galectin-1 with LacNAc_II from Liao et al.¹⁵ The ligands in each of the reported structures have a β-linked galactosyl residue at the nonreducing terminus. The carbohydrate recognition domain (CRD) consists of a deep channel, formed by an antiparallel β-sandwich, which spans the entire length of the monomeric subunit. The structure of galectin-1 with LacNAc bound in the CRD highlights several important protein-carbohydrate interactions. The interactions between Arg-48 and His-44, with the 4-hydroxyl group of the galactosyl residue provide the binding specificity for galactose, are conserved throughout the entire galectin family.^16,17

Galectin-1 can be considered to contain a CRD that is characteristic for the galectin family. The β-sheet motif, which comprises the galectin-1 CRD, shares a high level of structural homology with other galectins,¹⁸ especially with galectin-2 and galectin-3. Structural homology with the galectin-1 CRD extends not only to the CRDs of other galectin family members, but also to mammalian pentraxins, such as serum amyloid protein and legume lectins. This homology highlights the conservation of this structural motif throughout a number of different lectins.

The energetics of the binding of Gal-terminating and non-Gal-terminating ligands with galectin-1 have been well characterized.^19–22 However, the mechanism by which galectin-1 accommodates non-Gal-terminating ligands as well as those containing multiple LacNAc units remains undetermined. Early results from ELISA experiments by Zhou and Cummings²³ on polylactosamines from CHO cells, suggested that up to four LacNAc units could be accommodated by the galectin-1 CRD and that these longer ligands did not require a terminal galactosyl residue for binding. In addition, it has been proposed that galectin-1 binds to the Type II polylactosamine chains found on laminin or fibronectin through interactions with the LacNAc repeat unit.²⁴ No X-ray structural data have been reported for complexes between galectin-1 and any non-Gal-terminating ligands.

We have performed solvated MD simulations on a number of biologically relevant galectin-1-ligand complexes using the AMBER force field, augmented with the GLYCAM²⁵ parameters for carbohydrates. Explicitly solvated MD simulations have been shown to reproduce the experimental structures of lectin-carbohydrate^26,27 and antibody-carbohydrate^28,29 complexes. Nevertheless, to establish the accuracy of the theoretical methods in the case of galectin-1, preliminary simulations were performed on the X-ray structure of the galectin-1-LacNAc complex.¹⁵ The simulations were then extended to novel, but related, galectin-1-ligand complexes. To ensure that the calculations were able to reproduce the specificity of galectin-1 binding, we have included simulations of two complexes involving ligands, which show no measurable binding affinity in vitro.¹⁹ The inclusion of negative controls in MD simulations is rare, but here is found to be a useful technique to assess the sensitivity of the simulation to changes in ligand structure.

From the MD data, it is possible to analyze the contributions from key structural properties, such as the hydrogen bonding and van der Waals and electrostatic forces, as well to determine the presence of additional contacts made by the larger ligands. Analysis of snapshots taken from the molecular trajectories allow for estimates of the energetic components responsible for ligand binding. This analysis facilitated the development of a model for the mechanism of galectin-1-ligand binding, which explains both the diversity and relative affinities of the carbohydrate ligands.

MATERIALS AND METHODS

Molecular Modeling and Dynamics

Coordinates for the galectin-1-LacNAc complex¹⁵ were retrieved from the Protein Data Bank³⁰ (pdb: 1slt). A single monomer of the dimeric complex was used in the simulations. Hydrogen atoms were added to the X-ray coordinates, and the system was solvated with the EDIT module of AMBER. All histidine residues were assumed to be neutral and were protonated at the Nε position. For the water droplet, a sphere of TIP3P waters³¹ with a radius of 26 Å was centered at the ligand center of mass. Diffusion of waters out of this droplet was prevented through the use of a half-harmonic potential applied at the droplet surface. For periodic boundary condition (PBC) simulations, the protein-ligand complex was placed within a theoretical box of TIP3P water with approximate dimensions of 45 × 55 × 60 Å. In all cases the CRD was defined with a residue-based cutoff, consisted of all amino acids containing any atom within 12 Å of any atom in LacNAc_II, and was allowed complete motional freedom. This 39-residue subset included most of the front β-sheet and the loops that interact with the ligand (residues 27–32, 40–72, 107, and 110). The remainder of the protein was either restrained in its experimentally determined position or allowed motional freedom, as described in the text. The simulations were performed with the all-atom AMBER force field³² using the PARM94 parameters for proteins,³³ augmented with GLYCAM parameters²⁵ (version 99d) for oligosaccharides. Partial atomic charges for the ligands were computed from quantum mechanical molecular electrostatic potentials as reported.³⁴ The initial unfavorable contacts made by the solvent were removed by 1500 cycles of energy minimization; 10 cycles of steepest descent were followed by 1490 steps of conjugate gradient. The energy of the solvent molecules and binding site residues was then minimized further for 1500 steps. Energy minimization was followed by a 150-ps period of simulated annealing, during which the temperature was raised from 5 to 300 K over 50 ps, maintained at 300 K for 50 ps, and then cooled to 5 K over 50 ps. The energy of the whole system was then minimized, followed by heating from 5 K to 300 K over 50 ps, with initial velocities assigned from a Maxwellian distribution at 5 K.

For the simulations utilizing the droplet and PBC solvation methods, an 8 Å cutoff was used for calculating nonbonded interactions. One to four electrostatics and nonbonded interactions were scaled by the default values of 1/1.2 and 1/2.0, respectively. Production dynamics were performed at 300 K using a 2-fs time-step, with the SHAKE algorithm applied to all hydrogen-containing bonds. For the Particle Mesh Ewald (PME) simulation,³⁵ a 1 Å grid spacing was used to calculate the electrostatic energies, with a fourth-order spline used for interpolation.

The energetic analysis of the galectin-1-ligand trajectories was undertaken using the MM-PBSA module of AMBER 7.³⁶ For the 2-ns trajectories, snapshots of the coordinates were taken every 10 ps. The resulting 200 snapshots were analyzed with the modified generalized Born solvation model, modified for use with PARM 94³⁶ to obtain the energetic contributions from solvation. Average molecular mechanical energies were also computed from the same set of 200 snapshots. The normal mode analysis³² was performed on 10 snapshots, corresponding to 200-ps intervals. The energies of the structures used in the normal mode analysis were minimized to within a cutoff of 10⁻⁴ kcal/(mol · Å). No distance cutoff was applied to nonbonded interactions. The resulting enthalpic and entropic terms were combined to give estimates of the binding free energies.

Ligand Docking

The oligosaccharide ligands were docked in the binding site by superimposing the LacNAc component with the equivalent residues observed in the crystal structure of the galectin-1-LacNAc_II complex.¹⁵ Initial alignment of the remaining residues was achieved by evaluating the steric fit as a function of the glycosidic torsion angles. In the case of Neu5Ac-α-(2-3)-LacNAc, each of the three low energy rotamers for the α-(2,3) linkage (ϕ = +60°, −60° and 180° with ψ = 0°) was initially examined. Analysis of these three complexes showed that the −60° structure made steric clashes with the protein and was eliminated from further study. Both the +60° and 180° structures were able to fit and were subjected to preliminary MD refinement, during which the +60° rotamer spontaneously interconverted to the 180° structure (data not shown). All subsequent studies were performed with the 180° Neu5Ac-α-(2-3)-LacNAc structure. LacNAc_I, in which the β-(1,4) glycosidic linkage is replaced by a β-(1,3) linkage, was overlaid with the heavy atoms of the sugar rings of LacNAc_II. This change in conformation resulted in a conformation in which the N-acetyl group was positioned 180° away from its position in the crystal structure. For (LacNAc)₂, the disaccharide containing the reducing terminus was superimposed with the LacNAc disaccharide from the crystal structure. The glycosidic torsion angles associated with distal LacNAc were varied so as to minimize steric clashes with the protein. The resultant orientation (ϕ_1-4 = 56.3° ψ_1-4 = −4.6° ϕ_1-3 = 41.1° ψ_1-3 = −15.4°) was consistent with expectations base on the exo-anomeric effect.³⁷ Neu5Ac-α-(2,3)-LacNAc was neutralized with a Na⁺ counterion placed 2.5 Å away from the carbon of the carboxylic acid, along the bisector of the O—C—O angle. 3′-OSO₃-LacNAc was treated in a similar manner, with the counterion placed 2.5 Å away from the sulfur atom, along the trisector of the SO₃ angle.

RESULTS

Galectin-1 Affinity for Oligosaccharide Ligands

The relative binding affinities for galectin-1 with a number of carbohydrates that contain a LacNAc core are presented in Table I. The binding data in Table I clearly illustrate the remarkable ability of the galectin-1 CRD to bind a variety of glycans (see Scheme 1). The similar affinities of oligosaccharides containing LacNAc_II (Gal-β-(1,4)-GlcNAc) (1) and LacNAc_I (Gal-β-(1,3)-GlcNAc) (2) highlight the fact that the change in linkage has little effect on overall molecular shape, a fact that was first observed for disaccharide components of Lewis blood group antigens.⁴⁰ The affinities for anionic ligands implicate electrostatic interactions in ligand binding. The attachment of an anionic moiety at the 3′-position of LacNAc can considerably enhance ligand affinity (see Table I). One such oligosaccharide, Neu5Ac-α-(2,3)-LacNAc (4), is a potentially important biological ligand, because of its prevalence in mammalian N-linked glycans. Further, 3′-O-sulfation of LacNAc increases affinity sixfold relative to LacNAc. 3′-OSO₃-LacNAc (3) has been shown to be an important component of glycolipids from brain, kidney, spleen, granulocytes, stomach, and intestine.^41,42 The lower affinity seen for the 6′-O-sulfated oligosaccharide relative to the 3′-O analog further suggests that the electrostatic interactions are specific. Elucidating the role of charge-charge interactions in stabilizing galectin-ligand complexes has therefore become critical to understanding the ligand affinities.

TABLE I.

Relative Affinities of Galectin-1 Ligands^†

Ligand	Kaa SPR38	Kab ITC22	Activityc ELISA39
Lactose (Gal-β-(1,4)-Glc)	1.0	1.0	1.0
1 LacNAcII (Gal-β-(1,4)-GlcNAc)	2.4	5.5	5.5
2 LacNAcI (Gal-β-(1,4)-GlcNAc)	2.4	5.5	5.5
3 3′-SO3-Gal-β-(1,4)-GlcNAc		4.0
4 Neu5Ac-α-(2,3)-Gal-β-(1,4)-GlcNAc	3.3
5 (LacNAc)2 (Gal-β-(1,4)-GlcNAc-β-(1,3)-Gal-β-(1,4)-GlcNAc)
6 GlcNAc
7 Glc-β-(1,4)-GlcNAc

^†Affinities are relative to Gal-β-(1,4)-Glc-β-OR. For SPR studies, sugar is linked to Biacore chip via spacer, which is β-linked to the reducing termini of sugar ligands; other studies use the free saccharide.

^aChinese hamster galectin-1 (C2S mutant).

^bBovine spleen galectin-1.

^cAlkylated human galectin-1.

Scheme 1.

Selected ligands of galectin-1. (1) Glu-71 Oε2–GlcNAc-O3; (2) Arg-73 Nη2–GlcNAc-O3; (3) Arg-48 Nη1–GlcNAc-O5; (4) Arg-48 Nη2–GlcNAc-O4; (5) Arg-48 Nη2–GlcO5; (6) His-44 Nε–Glc-O4; (7) Asn-61 Nδ2–Glc-O6.

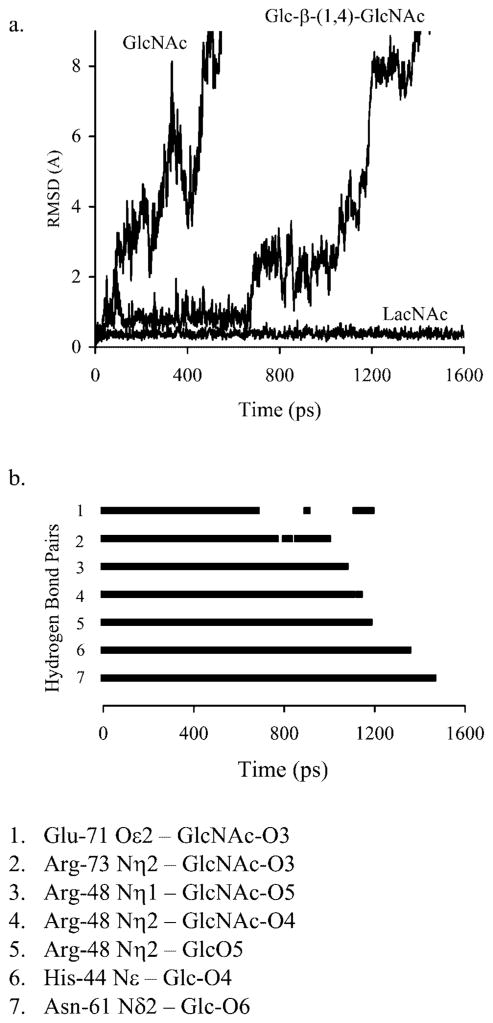
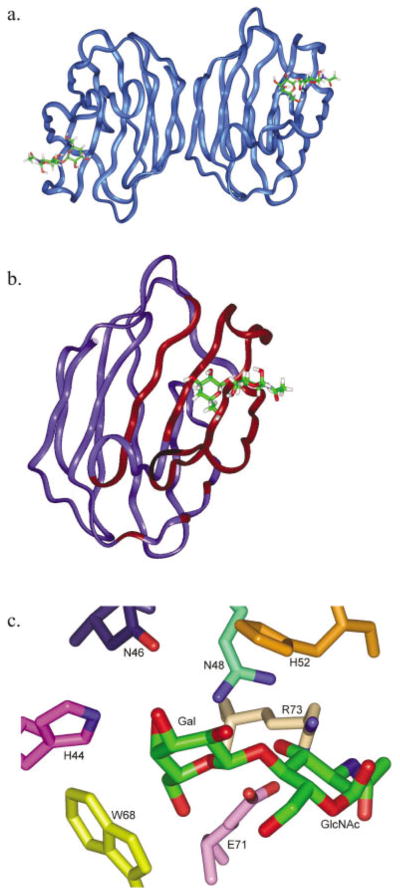
A crystal structure of the galectin-1-LacNAc complex served the basis for the MD simulations.¹⁵ The X-ray structure showed the presence of several hydrogen bonds, which contribute to ligand affinity. Seven amino acid residues, which interact directly with the LacNAc functional groups, are highly conserved within the galectin family.¹⁶ The hydrogen bonding network between hydroxyl groups of Gal and binding site residues His-44, Asn-46, and Trp-68 is responsible for galactose binding specificity. Glu-71 and Arg-48 make contacts with both sugars of the disaccharide, whereas His-52, Asp-54 and Arg-73 form contacts with the GlcNAc moiety. The relevant structural details of this complex are shown in Figure 1. Utilizing this crystal structure, oligosaccharides 2, 3, 4, and 5 were modeled into the galectin-1 binding site, as described in Material and Methods, and are shown in Figure 2.

Fig. 1.

X-ray structure of the galectin-1 complex with 1 (Liao et al.¹⁵). (a) Dimer structure showing the pseudo-symmetric dimer of galectin-1 (ribbon) with bound LacNAc (stick). (b) Galectin-1 monomer as employed in the MD simulations. Binding site residues allowed motional freedom during restrained simulations are depicted with red ribbon. (c) Detail of CRD showing conserved amino acids important in LacNAc binding.

Fig. 2.

Modeled structures of galectin-1-ligand complexes with (a) 2_, (b) 4, and (c) 5.

MD Simulation of Galectin-1-oligosaccharide Complexes

The stability and dynamics of proteins in MD simulations depends greatly on the treatment of solvation and electrostatic forces. In order to achieve a correct balance between intra- and intermolecular forces, we believe it is necessary to employ an explicit solvation model. To determine a computational protocol that could achieve a high degree of accuracy within a reasonable simulation timeframe, three different treatments of explicit solvation and long-range electrostatics were examined. Our initial approach was to surround the binding site with a droplet of water and define a subset of crucial binding-site residues. This protein subset, along with the ligand and surrounding water molecules, was allowed complete motional freedom, whereas the remainder of the protein was kept frozen in its crystallographic conformation. In these droplet simulations, the water was prevented from diffusing away from the complex by applying a restraint potential. Possible artifacts, arising from the use of a partially restrained water droplet, were addressed by a second simulation, in which the protein-ligand complex was fully solvated within a box of TIP3P water molecules. These simulations used the same protein restraints and 8 Å nonbonded cutoff as in the droplet simulations, but were performed under periodic boundary conditions (PBC). The PBC treatment enabled the simulation to be performed at room temperature and pressure.

The third computational approach employed the use of a fully unrestrained PBC simulation using the Particle Mesh Ewald (PME)³⁵ method to treat long-range electrostatic forces. The PME method includes electrostatic effects that are omitted by the use of a cutoff in standard PBC simulations. The more complete treatment of interatomic forces, as computed using PME, allowed the removal of all restraints on the protein and therefore enabled an estimation of the influence of the restraints used in the droplet and PBC (non-PME) simulations. A comparison of the droplet solvation approach with both the PBC and PBC/PME methods indicated that the droplet simulation gave results comparable to both of the more sophisticated treatments, while taking approximately one-third the CPU time of the PBC simulation. An analysis of hydrogen-bond distances in the galectin-1-ligand complexes is shown in Table II.

TABLE II.

Hydrogen Bond Distances, Ligand RMS Values, and Simulation Parameters for Three Treatments of Solvation and Electrostatics for the Complex with 1^†

Residue	Protein atom	Carbohydrate atom	X-raya	Droplet	PBC	PBC PME
His-44	Nε	Gal-O4	2.8	3.0 (0.2)b	3.0 (0.2)	3.4 (0.4)
Asn-46	Oδ1	Gal-O4	3.4	3.4 (0.3)	3.4 (0.3)	3.4 (0.3)
Arg-48	Nη2	Gal-O4	3.0	2.9 (0.2)	2.9 (0.2)	3.0 (0.2)
Arg-48	Nη2	Gal-O4	3.0	2.9 (0.2)	2.9 (0.1)	3.0 (0.2)
Asn-61	Nδ2	Gal-O6	2.7	3.0 (0.2)	2.9 (0.1)	3.0 (0.2)
Glu-71	Oε1	Gal-O6	4.7	4.3 (0.6)	3.8 (0.9)	4.6 (0.2)
Glu-71	Oε2	Gal-O6	2.8	2.9 (0.6)	3.5 (0.9)	2.7 (0.1)
Arg-48	Nη1	GlcNAc-O3	2.8	2.9 (0.1)	2.9 (0.1)	2.8 (0.1)
Arg-48	Nη2	GlcNAc-O3	3.2	3.3 (0.3)	3.4 (0.3)	3.3 (0.2)
Arg-48	Nη1	GlcNAc-O4	4.2	4.1 (0.3)	4.1 (0.3)	4.3 (0.3)
Arg-48	Nη2	GlcNAc-O4	3.6	3.6 (0.3)	3.5 (0.2)	3.5 (0.3)
Glu-71	Oε1	GlcNAc-N	4.0	3.8 (0.5)	4.0 (0.6)	3.5 (0.2)
Glu-71	Oε1	GlcNAc-O3	3.3	2.9 (0.3)	2.9 (0.4)	3.0 (0.2)
Glu-71	Oε2	GlcNAc-O3	2.4	3.2 (0.5)	3.0 (0.4)	2.8 (0.2)
Arg-73	Nη1	GlcNAc-C=O	4.5	4.1 (0.6)	4.3 (0.5)	4.5 (0.6)
Arg-73	Nη2	GlcNAc-C=O	3.3	4.5 (0.4)	4.5 (0.4)	4.6 (0.4)
Arg-73	Nη1	GlcNAc-O3	4.7	4.1 (0.5)	4.5 (0.4)	4.6 (0.4)
Arg-73	Nη2	GlcNAc-O3	3.3	3.1 (0.3)	3.3 (0.3)	3.4 (0.4)
Binding site RMSD
All atoms				1.1 (0.4)	1.0 (0.1)	1.2 (0.2)
Backbone only				0.7 (0.3)	0.7 (0.1)	0.9 (0.2)
LacNAc ring atoms only				0.9 (0.3)	0.7 (0.2)	1.1 (0.4)
No. of particles				7278	16056	16056
Simulation time (h)				168	436	604

^†Distances are in Ångstroms, and root-mean-squared deviation (Å) in the nonhydrogen atomic positions, relative to the X-ray structure.

^aLiao et al.¹⁵

^bStandard deviations in parentheses.

Hydrogen Bonding

The most notable feature of the data in Table II is the high level of agreement between the values of the interatomic distances seen in the crystal structure with those seen in all of the solvated MD simulations. Nearly all of the hydrogen bonding distances between LacNAc functional groups and the side chains of binding site residues are within 0.5 Å of the experimental distances, with small standard deviations. Specifically, the key interactions between Gal-O4 and His-44 Nε, Asn-46 Oδ1 and Arg-48 Nη2 are noteworthy for their relatively short distances and low standard deviations, suggesting that they are very strong hydrogen bonds. The interactions of Gal-O6 (with Asn-61 Nδ2 and Glu-71 Oε2) and GlcNAc-O3 (with Arg-48 Nε1 and Glu71 Oε1) also show values indicative of a relatively strong hydrogen bonding network.

The interatomic distances of hydrogen bonded atoms are the most commonly used structural measure of the strength of hydrogen bonds. Nonetheless, the standard deviations obtained from the MD data also help to rank the relative strengths. For example, the standard deviations observed for the interatomic distances between the Gal-O4 and both His-44 Nε and Arg-48 Nη are lower than those observed for the Gal-O6 interaction with the carboxylate oxygens of Glu-71, suggesting that the former are stronger hydrogen bonds. Nonetheless, the overall agreement with experiment was satisfactory and based on these preliminary studies, all subsequent simulations were performed with the droplet solvation model.

For all complexes with extended ligands (3, 4, and 5), the core LacNAc residues show an overall conservation of hydrogen bonding geometry (Table III). Interactions involving the Gal-O4 (with His-44 Nε, Asn-46 Oδ1, and Arg-48 Nε2), Gal-O6 (with Asn-61 Nδ2 and Glu-71-Oε2), and GlcNAc-O3 (with Arg-48 Nη1 and Glu-71 Oε1) were maintained for all of the ligands. Even in the case of 2, which contains a Gal-β-(1,3)-GlcNAc linkage, many of the LacNA-c_II-core interactions were maintained, particularly those between Gal-O4 and His-44 and between Gal-O6 and Asn-61. The loss of the contacts between galectin-1 and the GlcNAc in 2 is due to the change in linkage position, which results in a 180° rotation of the GlcNAc ring relative to its orientation in 1. This conformation has previously been proposed from an analysis of the X-ray structure of galectin-1 bound to a complex biantennary oligosaccharide.¹⁰ Notably, this conformational change appears to result in a slight decrease in the relative affinity of 2 (see Table I).

TABLE III.

Ligand-Galectin-1 Heavy Atom Distances and Ligand RMS Values as a Function of Simulational Protocol for 2 ns Simulations

Residue	Protein atom	Carbohydrate atom	Ligand
			1 (X-raya)	2	3	4	5
His-44	Nε	Gal-O4	2.8	3.2 (0.5)	3.0 (0.2)	3.1 (0.2)	2.9 (0.1)
Asn-46	Oδ1	Gal-O4	3.4	3.9 (1.0)	3.7 (0.5)	3.3 (0.2)	3.5 (0.2)
Arg-48	Nη2	Gal-O4	3.0	3.8 (1.1)	3.2 (0.4)	2.9 (0.1)	2.9 (0.1)
Arg-48	Nη2	Gal-O5	2.9	3.5 (0.8)	3.0 (0.2)	2.9 (0.1)	3.1 (0.2)
Asn-61	Nδ2	Gal-O6	2.7	3.0 (0.2)	3.0 (0.2)	2.9 (0.1)	3.0 (0.1)
Glu-71	Oε1	Gal-O6	4.7	5.3 (1.4)	3.9 (0.8)	4.8 (0.2)	5.3 (0.1)
Glu-71	Oε2	Gal-O6	2.8	5.1 (0.8)	4.3 (0.7)	2.9 (0.1)	2.8 (0.1)
Arg-48	Nη1	GlcNAc-O3	2.8	4.1 (1.2)	3.0 (0.2)	3.7 (0.2)	3.1 (0.1)
Arg-48	Nη2	GlcNAc-O3	3.2	3.8 (0.8)	3.5 (0.3)	5.0 (0.2)	4.5 (0.2)
Arg-48	Nη1	GlcNAc-O4	4.2	3.6 (0.6)	3.9 (0.3)	3.7 (0.2)	3.6 (0.2)
Arg-48	Nη2	GlcNAc-O4	3.6	3.2 (0.4)	3.5 (0.3)	3.4 (0.2)	3.3 (0.2)
Glu-71	Oε1	GlcNAc-N	4.0	—	4.0 (0.5)	2.9 (0.2)	3.0 (0.1)
Glu-71	Oε1	GlcNAc-O3	3.3	—	2.9 (0.5)	2.7 (0.1)	2.7 (0.1)
Glu-71	Oε2	GlcNAc-O3	2.4	—	3.9 (0.7)	5.1 (0.6)	6.6 (0.2)
Arg-73	Nη1	GlcNAc-C=O	4.5	—	4.0 (0.5)	4.7 (0.4)	7.7 (0.2)
Arg-73	Nη2	GlcNAc-C=O	3.3	—	4.4 (0.4)	4.5 (0.3)	2.8 (0.1)
Arg-73	Nη1	GlcNAc-O3	4.7	—	3.7 (0.3)	3.3 (0.3)	3.1 (0.1)
Arg-73	Nη2	GlcNAc-O3	3.3	—	3.0 (0.1)	2.9 (0.1)	2.8 (0.1)
RMSD
CRD All atoms				1.2 (0.2)	1.2 (0.5)	1.4 (0.3)	0.8 (0.1)
CRD Backbone				0.9 (0.2)	0.7 (0.3)	0.9 (0.3)	0.5 (0.1)
LacNAc ring atoms				1.5 (0.5)	1.4 (1.2)	1.4 (0.4)	1.2 (0.5)

^aLiao et al.¹⁵

Hydrogen bonds between the extended portions of the non-Gal-terminating ligands and the CRD are presented in Table IV. For the complex with 4, the interactions between His-52, and the carboxylic acid of Neu5Ac as well as those between Trp-68 and the glyceryl side chain of Neu5Ac are the primary interactions between the CRD and the sialic acid. In the terminal LacNAc unit of 5, the strongest hydrogen bonds were observed between Asp38 and Gal₂-O3, as well as between Asp38 and the amide proton of the N-acetyl group in GlcNAc_2. The binding of 1 to the CRD, and the interactions between the extended portions of 4 and 5 are similar, in that the protein-carbohydrate interactions seen are confined to one face of each oligosaccharide. In addition, both interactions have at most only one or two strong hydrogen bonds between the CRD and extended sugars.

TABLE IV.

Predicted Hydrogen Bond Distances between Extended Ligands and the Galectin-1 CRD

Ligand	Carbohydrate atom	CRD residue	Protein atom	Distance
4	Neu5Ac-O9	Asn-33	Nδ2	4.7 (1.4)
	Neu5Ac-O1Aa	His-52	Nε	4.4 (0.5)
	Neu5Ac-O1B	His-52	Nε	3.1 (0.5)
	Neu5Ac-O7	Trp-68	Nε1	3.3 (0.4)
5	Gal2-O3b	Asp-38	Oδ2	3.8 (0.8)

^aO1A and O1B are the carboxylate oxygens in Neu5Ac, with O1A being more deeply buried in the protein binding site.

^bGal₂ is the galactose of the non-core LacNAc in 5.

Aromatic Ring Stacking

In addition to hydrogen bonding between the protein and oligosaccharide ligands, hydrophobic interactions between sugar rings and aromatic amino acid side chains in the CRDs of lectins and anticarbohydrate antibodies are commonly observed.^18,43 The geometries of the aromatic stacking interactions, between the conserved Trp-68 and the galactosyl ring in each complex, are presented in Table V. We have characterized this interaction by the angle (θ) between the normals to the planes defining the galactosyl ring and the six membered ring of tryptophan. For a perfectly parallel stacking arrangement θ would have a value of 180°. In the simulations, each ligand formed a stacking interaction with Trp-68, with an overall average θ value of 139°, which compares favorably with the X-ray value of 142°. Further characterization of these interactions may be obtained by measuring the distance R between the geometric centroids of the pyranosyl and aromatic rings. The average value of R for each ligand was 5.7 Å; slightly longer than that present in the X-ray structure (5.1 Å), presumably reflecting the influence of internal motions.

TABLE V.

Ring Stacking between Trp-68 and the Galactose Ring of Core LacNAc

	X-ray	1	2	3	4	5
θa	142	131.0 (10.0)	133.2 (21.8)	131.7 (10.3)	144.0 (3.8)	157.8 (4.0)
Rb	5.1	6.0 (0.3)	5.6 (.9)	5.4 (0.4)	5.8 (0.2)	5.5 (0.1)

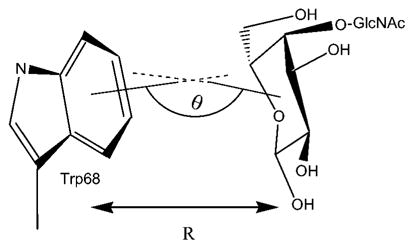
^aThe angle is degrees between the surface normals to the plane of the ring of Trp-68 and galactose. For a perfectly planar system the angle would be 180°. Standard deviations shown in parentheses.

^bDistance in Ångstroms between the geometric centroids.

Structural Analysis of Bound and free Galectin-1 Ligands

The average values for the glycosidic torsion angles of each ligand, for both the protein-bound and free states, are presented in Table VI. As is typical for oligosaccharide-protein complexes,^44,45 the glycosidic linkages of the free oligosaccharides exhibited greater ranges of motion than when bound to galectin-1. The φ and ψ torsion angles of the β-(1,4) linkage of the LacNAc_II core remained within 15° of the crystal values of 52° and 13°, respectively, for all ligand complexes. The solution and bound conformation of the LacNAc core showed little variation in φ, adopting the conformation preferred on the basis of the exo-anomeric effect.³⁷ The ψ angle, however, consistently displayed a modest distortion from the crystal structure geometry of approximately 15°. The large standard deviations seen in the β-(1,3) linkage of 5 reflect a highly flexible linkage, consistent with predictions based on gas-phase energy calculations for this linkage.⁴⁶

TABLE VI.

Average Glycosidic Torsion Angles for Ligands in the Protein-bound and Free States

Ligand	Linkage	Torsion angle
			Bound	Free
1	β-(1,4)1	φa	45.9 (9.3)	46.6 (11.2)
		ψ	15.7 (8.5)	0.6 (12.8)
3	β-(1,4)1	φ	38.9 (11.4)	47.7 (11.8)
		ψ	17.6 (9.7)	−6.2 (13.2)
4	α-(2,3)2	φb	158.8 (12.9)	−169.7 (12.4)
		ψ	8.1 (11.5)	−13.8 (11.9)
	β-(1,4)1	φ	45.1 (10.3)	45.1 (11.9)
		ψ	14.2 (9.5)	−6.3 (12.5)
5	β-(1,4)3	φ	51.1 (11.9)	40.8 (14.7)
		ψ	13.1 (15.3)	−5.4 (15.7)
	β-(1,3)2	φ	68.6 (14.9)	41.7 (13.8)
		ψ	29.2 (19.1)	11.8 (45.2)
	β-(1,4)1	φ	55.0 (9.0)	46.9 (12.1)
		ψ	4.0 (7.8)	−3.3 (12.3)

^aφ and ψ values for β-(1,3) and (1,4) linkages defined as: H1-C1-Ox-Cx and C1-Ox-Cx-Hx, respectively.

^bφ and ψ values for α-(2,3) linkage defined as C1-C2-O3-C3 and C2-O3-C3-H3, respectively.

Negative Controls

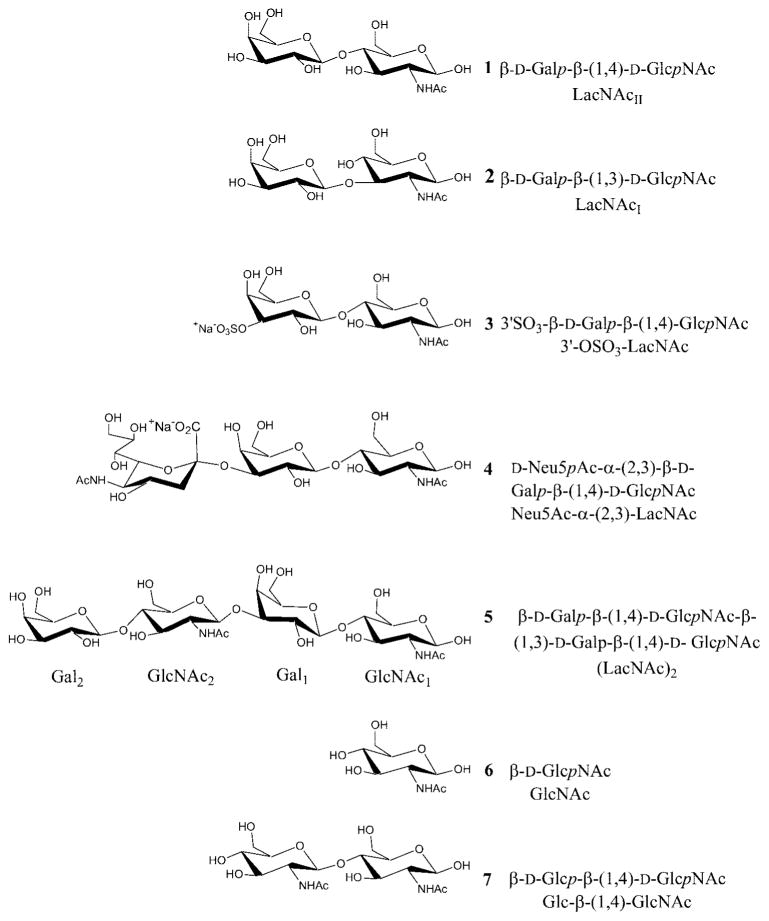
In order to determine the extent to which the simulations were able to discriminate between high and very low affinity ligands,¹⁹ galectin-1 complexes with a monosaccharide, GlcNAc (6) and the 4′-epimer of LacNAc, Glc-β-(1,4)-GlcNAc or N-acetylmaltosamine (7) were examined. Over the course of the simulations, both negative controls diffused out of the binding site within 1500 ps, reaching positional RMSD values of 9 Å relative to their initial positions, in 680 and 1403 ps, respectively [Fig. 3(a)]. The diffusion may be characterized in terms of the specific sequence of hydrogen bond breakage, and in the case of 7, began with the disruption of hydrogen bonds between GlcNAc-O3 and both Glu-71-Oε2 and Arg73-Nη2, at ~680 ps. This was followed by the loss of three hydrogen bonds between Arg-48 and ligand atoms GlcNAc-O3, GlcNAc-O4, and Glc-O5 between 1075 and 1112 ps. Hydrogen bonding pairs His-44 Nε–Glc-O4 and Asn-61 Nδ2–Glc-O6 persisted until 1348 and 1457 ps, respectively [see Fig. 3(b)]. In contrast to the case of the disaccharide, 6 alone did not show any persistent hydrogen bonds prior to diffusing out of the CRD.

Fig. 3.

Diffusion of negative controls from the galectin-1 CRD. (a) Relative RMSD of the glycan center of mass. (b) Persistence of hydrogen bonds (r_H-bond < 4.0 Å) during the diffusion of Glc-β-(1,4)-GlcNAc from the CRD.

Electrostatic Interactions in Galectin-1 Complexes

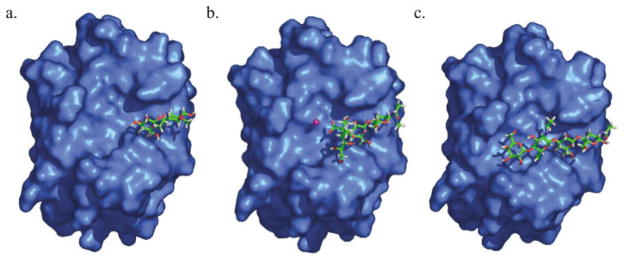
Electrostatic potential mapping of the galectin-1 surface shows a large positively charged region at the entrance to the binding channel, shown in Figure 4. This observation, suggests the manner in which electrostatic complementarity plays a role in the binding of the anionic carbohydrates. The positive electrostatic potential observed in the galectin-1 CRD arises from several positively charged residues (Lys-28, Lys-63, Arg-48, and Arg-73) located within the CRD. Both Arg-48 and Arg-73 make direct contacts with the LacNAc_II core, whereas Lys-28 and Lys-63 are located in the binding site near the 3′-OSO₃-moiety in 3.

Fig. 4.

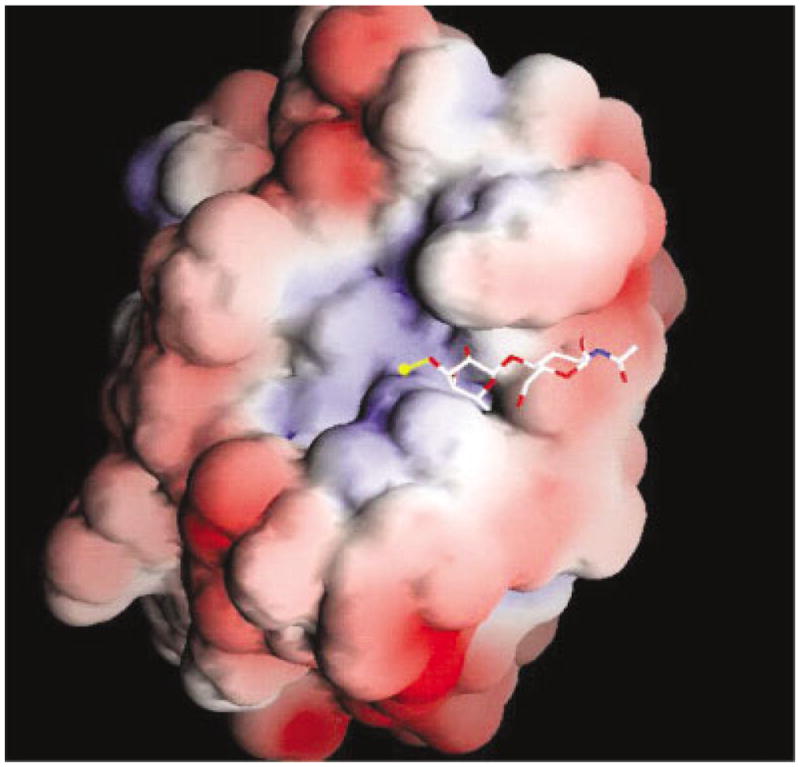
GRASP representation of the electrostatic potential of galectin-1 mapped onto the solvent accessible surface. Regions of positive potential are shown in blue, and negative potential is shown in red. The values set for the coloring scale are −3.6 and +3.7 k_bT, respectively. LacNAc is shown in stick form. The sulfate, found at the nonreducing terminus, is shown in yellow.

Binding Free Energy Estimates from MD Trajectories

Employing the trajectories from each of the droplet simulations, it was possible to compute estimates of the free energies of binding for each complex. This was performed in three stages. First, the water molecules were removed from the trajectories and the molecular mechanical energies computed for the complex, the unliganded receptor and for each ligand. These calculations were performed for each snapshot while maintaining the molecules in their bound conformations. Next, estimates of the solvation free energies were made for each component using a generalized Born solvation model optimized for use with AMBER, and consistent with our choice of partial atomic charges in the carbohydrate ligands.³⁶ Lastly, estimates of the entropy changes during complex formation were generated from a normal mode analysis of the energy-minimized structures. Recently, this combined protocol has been used successfully to examine the stabilities of antibody-hapten complexes,⁴⁷ as well as to estimate the relative stabilities of oligonucleotides,⁴⁸ and oligonucleotide complexes.^49,50 The accuracy of this approach is enhanced when there is negligible difference between the bound and free conformations for the ligand, as is the case in general here. The overestimation of the absolute binding free energies is due primarily to the use of a vacuum dielectric constant when computing the interior electrostatic interactions (ε_int = 1). In calculations employing non-polarizable force fields, or in cases where the protein is not given complete conformational freedom, larger interior dielectric values have been shown to perform well.⁵¹ Further, it should be recalled that the simulations employ the monomer subunit, whereas the experimental data are for binding to the dimer. Presented in Table VII are component energies for each ligand computed with ε_int = 1, as well as total binding energies computed with ε_int = 4. ⁵²

TABLE VII.

Energy Component Analysis of MD Trajectories^†

	1	2	3	4	5
<Δ Eelec>	−67.5 (5.7)	−30.8 (11.2)	−59.9 (9.7)	−53.2 (8.3)	−103.0 (15.0)
<Δ Evdw>	−17.5 (3.8)	−17.0 (3.4)	−23.9 (3.2)	−24.4 (3.6)	−37.9 (4.1)
<Δ EMM>	−84.9 (5.9)	−47.9 (12.7)	−83.8 (9.5)	−77.6 (9.7)	−141.0 (15.4)
<Δ Gnp>	−3.7 (0.3)	−2.7 (0.7)	−4.2 (0.2)	−4.7 (0.3)	−6.4 (0.5)
<Δ Gpol>	15.4 (4.4)	6.5 (8.5)	1.2 (6.8)	6.0 (10.3)	23.9 (12.5)
<Δ Gsolv>	11.7 (4.5)	3.8 (8.7)	−3.0 (6.8)	1.4 (10.2)	17.5 (12.4)
<Δ Gelec,tot>	−52.2 (6.9)	−24.3 (12.7)	−58.7 (8.3)	−47.1 (10.7)	−79.1 (13.7)
<Δ Gtot>	−73.3 (7.3)	−44.1 (14.9)	−86.7 (7.8)	−76.2 (11.8)	−123.5 (13.8)
<− TΔS>	18.3 (3.7)	18.2 (4.0)	22.5 (4.3)	30.1 (5.4)	31.6 (2.5)
ΔGbinding
(εint = 1)††	−55.0 (8.3)	−25.9 (7.2)	−64.2 (9.0)	−46.1 (7.7)	−91.9 (8.8)
(εint = 4)	−16.0 (2.6)	−7.7 (1.7)	−20.2 (2.7)	−11.0 (1.6)	−32.8 (2.6)

^†Values are expressed in kcal/mol, with standard deviations in parentheses.

<ΔE_elec>, electrostatic molecular mechanical energy; <ΔE_vdw>, van der Waals molecular mechanical energy; <ΔE_MM> = <E_elec> + <E_vdw>, total molecular mechanical energy; <ΔG_np>, non-polar contribution to the solvation energy; <ΔG_pol>, polar contribution to the solvation energy; <ΔG_solv> = <ΔG_np> + <ΔG_pol>, total solvation energy; <ΔG_elec,tot> = <E_elec> + <G_pol>, total electrostatic energy; <ΔG_tot>, total energy (without entropic contribution); <−TΔS> = −T (temperature) * ΔS (sum of rotational, translational and vibrational entropies); ΔG_bind, total binding energy of the system.

^††〈 Δ E_elec 〉 and 〈 Δ G_pol 〉 respond inversely to the dielectric constant.

Several features are evident from the energetic analysis. The binding free energies correctly rank the affinities of the ligands, with the exception that ligand 4 is predicted to bind more weakly to galectin-1 than 1. There are however, significant standard deviations on all of the binding free energies. Nevertheless, 3 is clearly predicted to bind better to galectin-1 than 1, whereas 2 is correctly predicted to be the poorest ligand. It is impossible to discriminate between ligands 1, 3, and 4 on the basis of net molecular mechanical energies 〈 Δ E_MM 〉 alone, with values being indistinguishable within error limits. Instead, distinguishing the relative affinities of these ligands also requires the consideration of estimated solvation free energies 〈 Δ G_solv 〉 and entropic contributions 〈 TΔS 〉. For example, the enhanced affinity of the sulfated ligand does not arise only from direct electrostatic interactions 〈 Δ E_elec 〉 with the receptor. A complete picture of the overall electrostatic contribution 〈 Δ G_elec,tot 〉 requires that the interaction energies associated with solvation 〈 Δ G_solv 〉 be included. Both LacNAc ligands (1 and 2), display essentially identical favorable net van der Waals interactions 〈 Δ E_vdw 〉 and net entropic penalties 〈 −TΔS 〉. The weaker interaction with 2 appears to arise primarily from poor intermolecular and solvation electrostatic energies 〈 Δ G_elec,tot 〉.

The much higher affinity predicted for 5 is the result of an interplay of electrostatics, in which a much more favorable intermolecular electrostatic term 〈 ΔE_elec 〉 over-comes a less favorable contribution from the polar component of solvation energy 〈 Δ G_pol 〉. The predicted increase in affinity with increasing level of LacNAc polymerization is consistent with previous observations of galectin-1 binding, which suggested that an increase in polylactosamine chain length, leads to an increase in binding affinity.²⁴ In addition, recent measurements of galectin-1 affinities⁵³ show a threefold increase in binding affinity for Gal-β-(1,4)-GlcNAc-β-(1,3)-Gal-β-(1,4)-Glc, relative to lactose.

DISCUSSION

The tests of simulation protocols indicated that a relatively simple model, consisting of a partially restrained protein, a dynamic ligand and binding site with droplet solvation, performed as well as the more sophisticated PBC and PBC/PME simulations. The savings in computational time afforded by the use of the droplet model allowed the simulation of a number of biologically relevant galectin-1 complexes. These substituted lactosamines maintained a set of key LacNAc-CRD interactions, indicating that the differences in affinities observed for these ligands arise from the chemical properties of the substituents themselves and not from induced changes in the protein. Hydrogen bonds are also observed for the extended portions of the substituted lactosamines (4 and 5), between hydroxyl groups on one face of the oligosaccharide and the binding groove of the CRD. The relative weakness of these interactions indicates that factors other than hydrogen bonds must contribute to the range of observed affinities.

Coulombic interactions between the positive electrostatic potential of the galectin-1 CRD and anionic ligands serve to modulate their affinities. In the case of 3, the sixfold increase in affinity can be ascribed to charge complimentarity. 6′-O-sulfation leads to very little change in affinity, relative to LacNAc, presumably because favorable electrostatics are offset by the disruption of interaction between the Gal-O6 and galectin-1 CRD. The electrostatic complimentarity between galectin-1 and 3 exists in the absence of any direct salt bridges between the sulfate group and amino acid residues within the CRD. This stands in contrast to the case of sulfate binding protein, in which the binding of HOSO₃ occurs via an extensive hydrogen bonding network.⁵⁴ The fact that the affinities of 1 and 4 are nearly equal, results from entropic penalties in the larger oligosaccharide, off-setting the favorable electrostatic interactions between the carboxylate of Neu5Ac and the positive electrostatic potential of the galectin-1 CRD (Table VII).

The analysis of the electrostatic properties of the solvated protein-ligand complexes gives another important clue to the factors responsible for carbohydrate binding by galectin-1. For ligands 1, 3, and 4, differences in binding affinities are markedly dependent on solvation effects, as calculated from the generalized Born implicit solvation model. Details of the water structure as well as the role of water in mediating the binding affinities in these complexes are the subject of ongoing study.

Analysis of the structure of the oligosaccharide ligands of galectin-1, both in the protein-bound and free states shows an expected difference in the structure and flexibility of the glycosidic linkages. Although the free ligands, on the whole, exhibit greater flexibility about the glycosidic bonds, the average angles are in good agreement with the lowest energy conformations of disaccharide fragments.⁵⁵ This indicates that these ligands are bound in low energy conformations, with the largest effect being a decrease in the deviations from these averages. The normal mode analyses show that each ligand pays an entropic penalty upon binding, which is roughly proportional to the number of atoms in the ligand.

It should be remembered that, in vivo, these ligands do not occur as free oligosaccharides. The reducing termini of 1, 3, and 4 would be linked to larger glycans, whereas 5 would be incorporated within polylactosamine. These structural differences may have an effect on the conformational behavior of these oligosaccharides, which may influence their in vivo affinities. Further, affinities in vivo may result from avidity effects in longer oligosaccharides, such as (LacNAc)₄.²³

CONCLUSIONS

The overall picture that emerges from these data is one in which a set of key LacNAc-CRD hydrogen bonding and ring stacking interactions tolerate a number of substitutions at the nonreducing terminus as well as differences in internal glycosidic linkages (1 and 2). The idea that galectin-1 is specific for Gal-terminating oligosaccharides is slightly inaccurate, and instead the protein can be thought to bind galactose in the context of lactose and lactosamine units occurring in a variety of positions in an oligosaccharide. The simulations of 4 and 5, bound in the galectin-1 CRD, show that the binding groove of the protein can accommodate much longer oligosaccharide chains, without requiring significant conformational changes in the CRD. Because of the highly polar nature of the ligands, the binding free energies depend on the balance between electrostatic interactions in the complex and in solution. This is a challenge for any implicit solvation model; however, the generalized Born approach used here was able to qualitatively rank the ligands, in agreement with the experimental data. A more detailed study of the effects of implicit solvation model on computed binding free energies for carbohydrate-protein interactions is currently underway.

The differences in affinities exhibited by galectin-1 ligands implicate differential carbohydrate modification as a factor in galectin-1 function. The promotion or inhibition of cell growth and metastasis, for example, is likely the result of the interaction of galectin-1 with differentially expressed cell-surface carbohydrates. Although crosslinking between heterotypic glycoprotein ligands has been proposed earlier,^9,10 we have provided a detailed structural mechanism, by which galectin-1 can accommodate a variety of ligands in the same CRD.

Abbreviations

AMBER

Assisted Model Building and Energy Refinement

CHO

chinese hamster ovary

CD

cluster of differentiation

CRD

carbohydrate recognition domain

MD

molecular dynamics

PBC

periodic boundary conditions

GLYCAM

Glycosides and Glycoproteins with AMBER

LacNAc

N-acetyllactosamine (Gal-β-GlcNAc)

LAMP

lysosome associated membrane protein