Mechanobiological stability: a new paradigm to understand the enlargement of aneurysms?

Abstract

Static and dynamic mechanical instabilities were previously suggested, and then rejected, as mediators of aneurysmal development, which leaves open the question of the underlying mechanism. In this paper, we suggest as a new paradigm the interpretation of aneurysms as mechanobiological instabilities. For illustrative purposes, we compare analytical calculations with computational simulations of the growth and remodelling of idealized fusiform abdominal aortic aneurysms and experimental and clinical findings. We show that the concept of mechanobiological stability is consistent with the impact of risk factors such as age, smoking or diabetes on the initiation and enlargement of these lesions as well as adaptive processes in the healthy abdominal aorta such as dilatation during ageing or in hypertension. In general, high stiffness, an increased capacity for stress-mediated matrix production, and slow matrix turnover all improve the mechanobiological stability of blood vessels. This theoretical understanding may help guide prognosis and the development of future therapies for aneurysms as it enables systematic ways to attenuate enlargement.

1. Introduction

Aneurysms are local dilatations of the arterial wall that typically evolve over years; rupture of these lesions results in significant morbidity and mortality. Despite advances in cell biology, genetics, medical imaging and surgical techniques, the natural history of aneurysms, especially their initiation, remains poorly understood. Blowout instabilities were discussed as a potential initiation mechanism for cerebral aneurysms [1–3], but rejected because of the highly nonlinear strain energy function for arteries [3–5]. Similarly, dynamic instabilities [6,7] were debated, but ultimately considered unlikely due to the viscous dissipation in the system [8,9]. Besides the mechanical mechanisms of initiation, factors governing aneurysmal enlargement similarly remain unclear. Whereas recent numerical studies provide insights into some parameters that affect the initiation and enlargement of aortic aneurysms [10,11], there remains a need for a unifying theory to understand experimental and clinical observations. Towards this end, we generalized in [12], on the basis of Lyapunov's stability theory, concepts of statics and stability for mechanobiology. We also suggested mechanobiological instability as a potential initiating mechanism for aneurysms and presented mathematical statements regarding the possible impact of various parameters on their development.

In this paper, we use illustrative examples for the abdominal aorta and abdominal aortic aneurysms (AAAs) to show that this mechanobiological stability theory provides a simple and yet powerful analytical framework to understand diverse aspects of the natural history of aneurysms as well as prior findings arising from related computational models. We thus suggest a change of paradigm: using the theory of mechanobiological stability as a unifying framework, future risk analyses of aneurysms should not focus solely on diameter or wall stress, but also consider measures of mechanobiological stability.

2. Mathematical model of growth and remodelling

The following section summarizes the mechanobiological stability theory presented in [12], to which the reader is referred for details. Regarding the notation, vectors and higher order tensors and also linear operators, which are equivalent to such in finite dimensional systems, are written in bold print, and single contraction products, such as vector–vector or matrix–vector products, without operator.

2.1. Mechanics and mechanobiology

As a first approximation, we model the macroscopic behaviour of blood vessels as membranes subject to an internal mean pressure p. They consist of n incompressible material species, which allows the effective mechanical behaviour to be modelled using a rule of constrained mixtures, that is, each species may possess unique material properties and reference configurations but must deform with the tissue as a whole. In practice, the primary species are elastin, circumferentially oriented smooth muscle, and multiple families of parallel collagen fibres. Let x(X, t) be the spatial position of each material point X of the membrane at time t and Mⁱ(x, t) the (reference) areal mass density of the ith species there. In general, an upper index i will denote quantities referring to the ith species. The areal mass densities of all species are gathered in the vector M having elements Mⁱ, which allows characterization of the state of the membrane by

2.1

Vascular growth and remodelling (G&R) typically occurs on the time scale of weeks to years. Inertia and viscosity are negligible on this time scale, on which we focus. Therefore, according to eqns (2.15) and (2.16) in [13], quasi-static mechanical equilibrium requires at each point in the interior of the domain

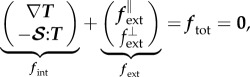2.2

where f_int, f_ext and f_tot are internal, external and total loads, respectively, T is the Cauchy membrane stress tensor (units of N m⁻¹), ∇T its divergence and 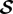the shape tensor (or second fundamental tensor) for the curved surface representing the membrane. The external in-plane 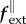and out-of-plane 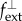loads may represent, for example, wall shear stress and blood pressure p, respectively. With J the Jacobi determinant of the deformation gradient between reference and current configurations and 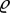the volumetric mass density, the membrane stress can be related to the mean Cauchy stress σⁱ of each species (averaged across the mass of this species and having units of N m⁻²) by

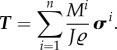2.3

It is well known that G&R of blood vessels is governed in large part by mechanical stimuli. We thus follow the general modelling approach outlined in [14], as adopted in [12], and assume that extant collagen and smooth muscle degrade at the rate 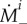while new material is deposited at the rate 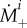with a prestress 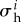. The total rate of change of mass density is 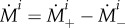. Assuming degradation according to a Poisson process (i.e. an exponential survival function of existing material), we have

2.4

where τⁱ is the turnover time constant, and

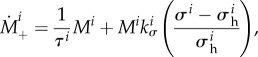2.5

where σ ⁱ is the magnitude of the Cauchy stress of the ith species in its respective fibre direction—note that turnover is considered only for collagen and smooth muscle, which are modelled by uniaxial fibre families—and 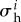is a scalar homeostatic value of stress at which mass deposition and degradation balance. The gain factor 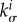weights effects of deviations from the homeostatic stress state on the mass production, which will vary point-wise in general. Higher values of 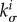yield higher mass productions if the current stress exceeds the homeostatic value.

For mathematical convenience, we assume that collagen and smooth muscle exhibit the same turnover time constant τ and that 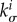and τ are uniform throughout the domain. This is not to say that these constituents necessarily change at the same rate, but rather that rates of change in their natural configurations could be similar. This assumption is consistent with the possibility that the turnover of collagen causes integrin or cadherin re-engagement and thus changes in the natural configuration of the smooth muscle, particularly given the general loss of elastin in aneurysms. Finally, we disregard elastin production consistent with the common assumption that functional, load-bearing elastin is not produced in maturity. Degradation of elastin (during ageing, by localized insults, or also by pathologic proteolytic activity especially in aneurysms) is modelled not by (2.5) but separately by time-dependent mass perturbations (cf. (3.3) and (3.7)).

2.2. Mechanobiological equilibrium, stability and adaptivity

2.2.1. Theory

In classical solid mechanics, statics simply requires 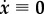. Hence, a natural generalization of this notion to mechanobiology is (cf. [12])

Definition 2.1. —

A state is said to be mechanobiologically static, or equivalently to be in mechanobiological equilibrium, if and only if

2.6

and, additionally, for all species subject to G&R (i.e. with finite τⁱ) the Cauchy stress in any of its mass increments at a given point is the same (i.e. equals the average value σⁱ(t, X) at this point).

That is, both the geometric configuration and mass remain constant over time (thus, the mass of a species at a given point exhibits the same Cauchy stress because all of it was deposited in this persistent configuration). Stability can be generalized for mechanobiology on the basis of Lyapunov's stability theory by

Definition 2.2. —

A mechanobiologically static state of a system is called mechanobiologically stable if and only if for each there exists an so that for all t ≥ 0 we have

2.7

In other words, mechanobiological stability requires that small perturbations of a mechanobiologically static state remain forever small or decay to zero. In nonlinear systems, Lyapunov stability can often be checked by a linearization around the equilibrium state of interest and a subsequent eigenvalue analysis of the linear operators governing the dynamics in this neighbourhood (Lyapunov's first method). In the following, all quantities referring to the mechanobiologically static state of interest will be denoted by an upper bar and deviations from this state by a prefixed variation δ. For species subjected to G&R (e.g. collagen and smooth muscle), the displacement part δx of the perturbation δy can be decomposed into

2.8

where 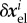captures any elastic deformation relative to 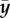and 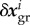any inelastic deformation due to changes in the stress-free reference configuration by mass turnover. Neglecting the first-order small term due to stress-mediated growth in (2.5), mass turnover replaces per unit time the mass fraction Mⁱ/τⁱ at the current stress σⁱ by the same amount of mass at the prestress 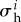and releases this way per unit time the fraction 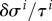of the difference between the average current stress σ ⁱ of the ith species and its homeostatic stress. As δσ ⁱ is in the linear regime of small perturbations directly proportional to the elastic deformation 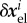, and the rate of change of 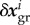equals the release of elastic deformation per unit time, we have, assuming the same τ ⁱ = τ for all species subject to G&R (i.e. collagen and smooth muscle herein)

2.9

Immediately after the perturbation, no inelastic deformation by G&R has yet occurred so that 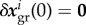for all species. Using (2.9) with this identical initial value for all species in (2.8) reveals that all 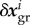are identical at each time so that we can omit the upper index, rewriting (2.8) as

2.10

On the time scale of G&R, mechanical equilibrium (2.2) is satisfied at each time after an initial perturbation. In the linear regime, which we consider herein, this can be expressed as

2.11

where linear operators 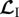, 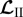and 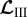represent derivatives of 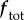with respect to variations δx_el, δx and δM, respectively. Because we assume that mass production depends only on the elastic Cauchy stress

2.12

for linear operator 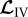. Using (2.12), (2.10) and (2.9) in the time derivative of (2.11) and defining

2.13

with 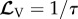yields

2.14

Thus

2.15

From (2.8), (2.12), (2.9) and (2.15), we conclude that the system is mechanobiologically stable if and only if the real parts of all eigenvalues of the linear operator are strictly positive. Then the elastic deformation δx_el will decay to zero after a perturbation (i.e. the homeostatic stress will be restored). Owing to (2.12) and (2.9), this will also stop any further G&R dynamics, that is, the system will again be in a mechanobiologically static state. Hence, the necessary and sufficient condition for mechanobiological stability is

2.16

where the so-called stability margin 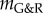is the smallest real part of any eigenvalue of 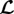. Note that we focus herein on uniform pressure loads with Dirichlet or periodic boundary conditions, which ensures that 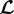is symmetric and has only real eigenvalues [12]. In (2.15), 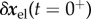can be computed from (2.10) and (2.11), and recalling that 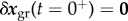, so that

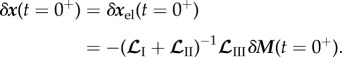2.17

In a stable system 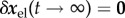. From (2.9) and (2.10), however, we see that each perturbation will leave some inelastic residual displacement perturbation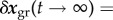 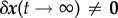. That is, the system is only neutrally, not asymptotically, stable. This neutral stability can be characterized by the so-called mechanobiological adaptivity

2.18

which is shown in [12] to satisfy

2.19

for 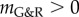. That is, the residual displacement perturbation is inversely proportional to the stability margin .

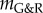The total tangent stiffness of the system is

2.20

which can be split into a geometric part K_geo that describes the change of internal and external loads assuming that the strain energy remains constant, and its complement, the elastic stiffness

2.21

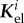denotes the contribution of the ith species to 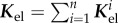and the so-called G&R stiffness

2.22

will be used below to characterize mechanobiological stability. With the additional stiffness-like operators

2.23

which characterize the change of internal forces under variations of the areal mass densities, it was shown in [12] that

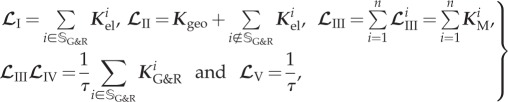2.24

and

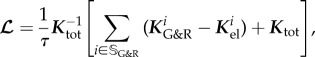2.25

where 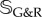is the set of all indices of species subject to G&R, that is, collagen fibre families and smooth muscle. In the following, we assume mechanical stability (i.e. strictly positive real parts of the eigenvalues of K_tot) as the vessel could otherwise not maintain its geometry in the long term. As 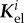, and thus 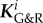, is typically positive definite, we expect from (2.25) that the stability margin increases with the gain factor 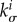. Noting that in (2.25) 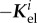cancels out with a term of the opposite sign in K_tot, we also expect from (2.22) that the eigenvalues of 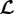, and thus the stability margin, will increase with the elastic stiffness. As a prefactor in (2.25), τ defines the natural time scale of G&R dynamics in (2.15); it also appears in (2.22) in a product with 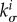and thus should stabilize the system on the normalized time scale t/τ. These rules about parameter impacts on mechanobiological stability were proven generally in [12].

2.2.2. Example: uniform vessel dilation

An instructive special case is that of a circular cylindrical vessel of length L and radius R under internal blood pressure p while axially fixed at its ends such that the in vivo stretch is maintained. Consider a uniform change δR along the axis, which consists of elastic and inelastic parts δR_el and δR_gr as in (2.10). In this case, (2.2) reduces to the scalar equilibrium relationship between blood pressure p and the circumferential membrane stress T_θθ (Laplace's equation) and with (2.3) becomes

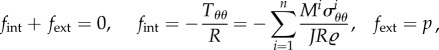2.26

where we denote by the scalar loads f_int and f_ext, in the context of a uniform distension, the radial components of f_int and f_ext (i.e. we disregard axial components in this discussion due to the Dirichlet boundary conditions in axial direction). The radial components of second-order tensors are treated below in the same way (e.g. K_tot for the radial component of K_tot). In this special case, all relevant quantities can be calculated analytically (cf. appendix A). For example, (2.17) and (2.15) yield

2.27

and

2.28

with 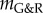from (A 9) in appendix A. By (2.9), (2.10) and (2.24), the total radial deformation

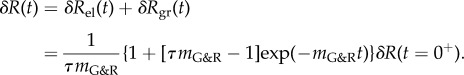2.29

As a result, δR(t) starts at the initial value δR(t = 0⁺) and evolves exponentially towards the limit 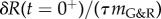in accordance with (2.19).

It is instructive to note that (2.29) mathematically characterizes motions following a uniform perturbation in either mass or blood pressure. In the latter case,

2.30

To see this, we note that δR(t = 0⁺) in (2.30) can be understood as the deformation of a hypothetical vessel with reference radius 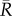, blood pressure 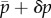, and some areal mass densities 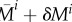directly after a uniform mass perturbation 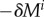. The reference configuration of this hypothetical vessel differs from the original only by infinitesimal variations δp and δMⁱ. Thus, its linearized dynamics following the perturbation −δMⁱ is described by the same operators (neglecting higher order terms) and (2.29) is applicable with δR(t = 0⁺) from (2.30). The phase space of this system is illustrated in figure 1 around a mechanobiologically static state for positive and negative 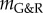. After an initial uniform perturbation of the homeostatic stress by a loss of mass or increase in blood pressure, the stress level is restored in stable systems with positive 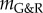leaving, however, a residual deformation δR_gr > 0 due to the adaptivity of the system. By contrast, in an unstable system with negative 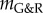an initial small perturbation results in continuing enlargement.

Figure 1.

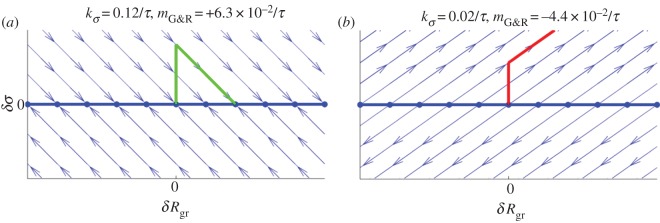
Phase spaces around a mechanobiologically static state of a stable (a) and unstable (b) cylindrical vessel for uniform deformations: trajectories (thin lines with arrowheads indicating direction of system evolution), set of stationary points (thick horizontal line), trajectory for evolution after one specific perturbation (thick kinked line originating from centre). (Online version in colour.)

3. Mechanobiological stability and clinical observations

3.1. General

Mechanobiologically stable vessels compensate for sufficiently small perturbations in wall mass or blood pressure by protective G&R and return close to their initial state soon thereafter (cf. (2.29) and figure 1). Such stability is a necessary requirement to maintain the geometry and properties of the vasculature nearly the same over decades as observed in healthy individuals. Conversely, in mechanobiologically unstable vessels even small perturbations initiate potentially progressive changes. In certain cases, the vessels may restabilize in another homeostatic equilibrium state after a period of finite G&R. Otherwise, as can be seen from (2.15), wall stress and diameter could keep increasing until failure. Herein, we hypothesize as a possible initiation mechanism of aneurysms a change in wall parameters by which the positive stability margin in the initially healthy vessel drops close to or below zero, thus giving rise to large or even unbounded changes in geometry subsequent to perturbations in mass turnover or blood pressure as is common in the vasculature.

To test this hypothesis, we first demonstrate in §§3.2 and 3.3 that the response of healthy vessels to perturbations, such as an increased blood pressure or slow uniform degradation of elastin during ageing, can be understood via the adaptivity of mechanobiologically stable vessels. Subsequently, we show in §3.4 that clinically observed positive risk factors for aneurysms correspond to parameter changes that decrease the stability margin, which supports the idea that aneurysms are a consequence of failed mechanobiological stability.

In the following, consider an idealized axisymmetric segment of human aorta of length 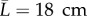(to lessen end effects) with initial radius 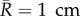, blood pressure p = 100 mm Hg, and parameters for mass fractions, half-life times, constitutive functions, deposition stretch and mass density as listed in §2(c) and table 1 of Wilson et al. [11] (unless otherwise specified). Collagen is modelled by four fibre families in axial, circumferential and symmetric diagonal (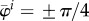) directions, while smooth muscle is modelled as a single fibre family in the circumferential direction and elastin as a homogenized isotropic two-dimensional sheet. Periodic boundary conditions are employed in §§3.2 and 3.3, and Dirichlet boundary conditions in axial and radial directions in §§3.4.1 and 3.4.3. Wall properties are modelled according to Wilson et al. [11], that is, elastin is modelled as a relatively compliant, isotropic material having a nearly linear stress response and thus characterized by a neo-Hookean strain energy function

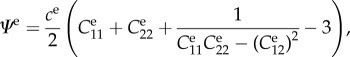3.1

where 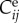are the elements of the in-plane right Cauchy–Green tensor and c^e is a material parameter. Superscript e denotes elastin rather than a summation index. To capture the significant strain-stiffening in collagen and, though less marked, passive smooth muscle, we model both with Fung exponential functions

3.2

with stretch λ and unique material parameters c₁ and c₂ for each type of constituent. For simplicity, we assume the same gain factor k_σ for smooth muscle and collagen.

3.2. Age-related dilatation

Production of functional elastin nearly ceases after early childhood [15] and thereafter it degrades slowly with a half-life time of approximately 74 years [16]. This continuous degradation can be modelled as a monotonically decreasing perturbation in elastin mass 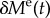with 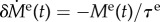and mean lifetime τ^e = 74 years/ln (2). With 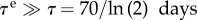[17], the mean lifetime of collagen, the vessel will slowly evolve its homeostatic state, responding to the loss 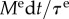during each short time interval dt within a few τ. According to (2.17)–(2.19) and (2.24), the residual radial dilatation is

3.3

where the uniformity of the elastin degradation allows us to use equations from §2.2.2. Using (A 9) and dividing (3.3) by dt leads to an expansion rate

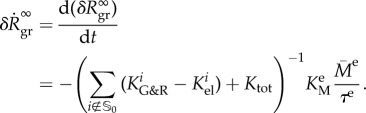3.4

With (A 6)–(A 8), the dilatation rate 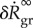in (3.4) depends on the gain factor 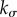, which is the only parameter in this equation that cannot be determined by independent experiments unrelated to G&R (such as biaxial mechanical testing of tissue patches). In figure 2a, 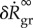is plotted versus k_σ. Age-related dilatation of elastic arteries is well known. Averaging data from [18–20], one can estimate an expansion rate of 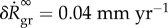for the radius of the adult abdominal aorta, which according to (3.4) is equivalent to k_σ = 0.12/τ as seen in figure 2a. Thus via (3.4), the mechanobiological stability theory can not only be used to understand age-related vessel dilatation in general (hypothesizing it to be primarily a consequence of slow elastin degradation and adaptivity), it can also estimate for the first time a realistic value for k_σ in healthy individuals.

Figure 2.

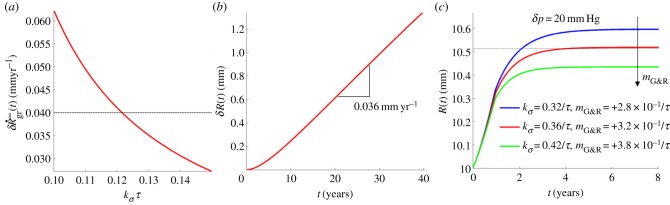
(a) Abdominal aortic expansion rate according to (3.4) as a function of gain factor k_σ compared with the clinically observed value of 0.04 mm yr⁻¹ (horizontal line); hence a value of k_σ = 0.12/τ appears clinically relevant. (b) Nonlinear finite-element simulation of aortic expansion due to elastin degradation with k_σ = 0.12/τ. (c) Aortic expansion after a pressure increase of δp = 20 mm Hg over 1 year revealed a predominantly elastic dilatation during the phase of pressure increase followed by a longer period of G&R resulting in a residual dilatation according to the principle of adaptivity; residual dilatation expected from experiments [22] represented as a horizontal line. (Online version in colour.)

Since (3.4) is but a linear approximation, a fully nonlinear finite-element simulation with time-step size Δt = 5d and k_σ = 0.12/τ was performed to confirm the result. Assuming the system to be homeostatic at t = 0, the first 10–15 years were dominated by transient effects governing the transition to a steady state of continued elastin degradation and compensatory collagen production and can thus be considered a numerical artefact due to the initial conditions. During the final 25 years, an expansion rate of approximately 0.036 mm yr⁻¹ was observed (cf. figure 2b), which agreed well with the 0.04 mm yr⁻¹ expected from the linearized calculation (3.4).

Patients with AAAs exhibit, on average, a 30% larger thoracic aortic diameter distant from the aneurysm when compared with healthy matched controls [21]. Moreover, the diameter of the descending thoracic aorta generally correlates positively with well-known risk factors for aortic aneurysms such as smoking, male gender and age. Although the precise mechanisms underlying this observation remain unclear, it is interesting that the theory of mechanobiological stability predicts by (3.3) an increased age-related dilatation for a lower mechanobiological stability margin, which could also increase the risk of aneurysmal formation.

In summary, the stability theory introduced in [12] may provide a theoretical basis to understand not only age-related vessel dilatation in general, but even its positive correlation with the appearance of aneurysms. The comparison between clinically observed dilatation rates on the one hand and analytical calculations based on the stability theory on the other hand suggests k_σ = 0.12/τ as a physiologically reasonable value for the gain parameter in our G&R model in healthy patients. Note that using another value τ* as a mean lifetime instead of the above τ = 70/ln (2) days, all results reported herein still hold except that the time axes in figures 2c, 3 and 4 have to be rescaled by τ*/τ.

Figure 3.

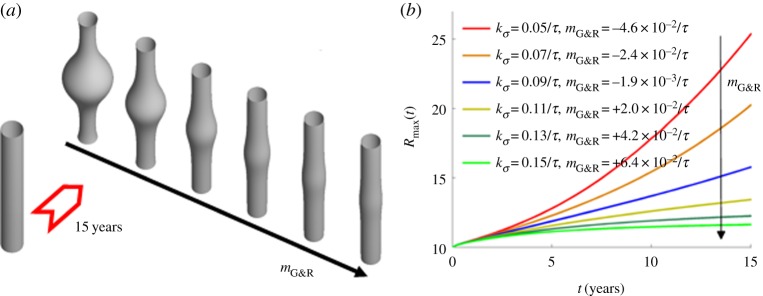
Expansion of an idealized human AAA over 15 years following a focal insult to elastin for different stability margins 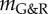obtained for different gain factors k_σ (using τ = 70 days for the half-life of collagen and remaining smooth muscle): (a) initial geometry versus geometry after 15 years for increasing values of ; (b) increase in maximal radius over time. (Online version in colour.)

Figure 4.

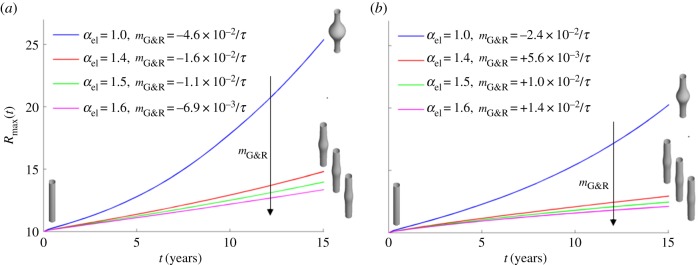
Maximal radius of an idealized fusiform AAA over 15 years after focal insult to elastin for k_σ = 0.05 (a) and k_σ = 0.07 (b) if wall stiffness is increased by factor α_el. Insets show initial and final vessel geometries. (Online version in colour.)

3.3. Dilatation of elastic arteries under hypertension

Arteries respond to increased blood pressure by thickening their walls, presumably to maintain/restore a homeostatic level of circumferential Cauchy stress [22]. In elastic arteries, this thickening is typically accompanied by a minor nearly uniform dilatation of the whole vessel, which can be understood as a natural consequence of the immediate distension due to the increased pressure described in (2.30) and a subsequent G&R process resulting in a residual dilatation due to adaptivity (cf. (2.18) and (2.19)). The residual dilation after a (small) pressure increase δp is

3.5

For rat aortas, for example, it has been reported (fig. 2 in [22]) that 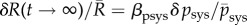with 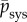the systolic blood pressure and parameter 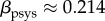. Assuming the same β_psys in human aortas and considering for simplicity a change in mean blood pressure, not pulse pressure, so that δp_sys = δp, we infer for 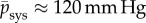, 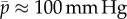and 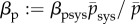from (3.5)

3.6

where 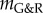was converted into an equivalent k_σ using (A 9) and (A 7).

Figure 2c shows results of finite-element simulations for an initially normotensive aorta subjected to an increase in blood pressure δp = 20 mm Hg over 1 year. An initially predominantly elastic distension resulted in a residual G&R-induced dilatation according to adaptivity. During the simulation, elastin mass was assumed constant to eliminate confounding factors and make the results comparable with the study of Matsumoto & Hayashi [22]. In addition, we compared the (modest) pressure jump over 1 year with one over 36 days and another one over 4 years and found a difference in residual dilatation (and wall thickening) of less than 1%, which suggests a negligible influence of the rate by which a certain level of hypertension is built up (provided the vessel is mechanobiologically stable). This result agrees well with previous numerical studies (cf. fig. 10 in [23]). Owing to the nonlinear response to the imposed (finite) change in pressure, the dilatation expected from the data in [22] was not observed exactly at k_σ = 0.42/τ as predicted in (3.6), but rather at k_σ = 0.36/τ. The difference compared to the value of k_σ = 0.12/τ determined from the age-related dilatation in §3.2 may be explained by several simplifications in our model and calculations. For example, the age-related increase in blood pressure of approximately 0.34 mm Hg yr⁻¹ [24] was neglected in §3.2 and would, according to (3.5), make up for about 20% of the age-related dilatation and would thus increase k_σ by about this factor if incorporated. Moreover, we simply applied rat data [22] to enable a calculation for humans, and finally simple relation (2.5) may be considered but a linear approximation to vascular G&R.

That two different clinical observations can be understood and reproduced with fairly similar values for k_σ is a promising result both for the G&R model from Figueroa et al. [14] in general and for the stability theory from Cyron & Humphrey [12] in particular. This finding emphasizes its applicability to age-related vessel dilatation and changing pressures and suggests that a gain parameter 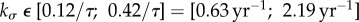, assuming τ = 70 days, is a reasonable choice for collagen production in healthy individuals.

3.4. Mechanobiological stability and aneurysms

Although §§3.2 and 3.3 considered adaptations after a uniform perturbation of pressure or loss of elastin, we now consider a focal loss of elastin as often associated with the formation of aneurysms. For large positive values of 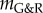, we expect this perturbation to be compensated by protective G&R of collagen and smooth muscle. As 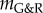becomes smaller, however, we expect an increasing residual dilatation. For 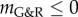, we expect unbounded expansion of the vessel. According to Cyron & Humphrey [12], the stability margin should increase with an increasing gain factor k_σ, which means that an increase in k_σ should attenuate aneurysmal progression after focal damage to the elastin layer.

To test these expectations, we subjected our model aorta to a focal loss of elastin according to the damage function (cf. [11])

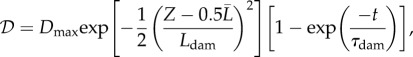3.7

where 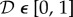is the fraction of initial elastin mass degraded by an insult at time t at the axial reference coordinate 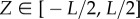. D_max = 0.7, L_dam = 1 cm and τ_dam = 40 days allowed the time-dependent part in (3.7) to saturate within around 120 days, resulting in a Gaussian damage distribution with a peak of D_max = 70% in the centre and a spread of L_dam = 1 cm.

In a parametric study, we examined the impact of different values on G&R after the elastin damage according to (3.7) at time t = 0. To this end, we performed nonlinear finite-element simulations similar to Wilson et al. [11] (and with consistent results) with 180 axisymmetric membrane elements along the Z-axis of the domain over a period of 15 years. The same discretization was used to compute a finite dimensional approximation of 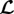and by an eigenvalue analysis the respective stability margin .

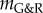3.4.1. Gain factor

Varying k_σ confirmed its inverse relationship with aneurysmal expansion rate, as reported in [11]. Figure 3 confirms the proportionality between the gain factor and stability margin predicted in [12]. For negative 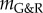(i.e. small k_σ), an unstable exponential dilatation of the vessel ensued, whereas for positive 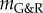(i.e. large k_σ) the vessel stabilized after an initial period of enlargement in a slightly dilated geometry, which further confirms the concept of adaptivity, namely, even mechanobiologically stable vessels will not restore their initial configuration after a perturbation; rather, they stabilize in a nearby configuration. For stability margins close to zero, such as 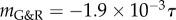in figure 3, we expected from (2.14) a nearly constant supra-homeostatic wall stress after the initial lesion and thus a dilatation at a nearly constant rate, which was observed. Although 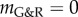mathematically marks the threshold between stable and unstable G&R, it is emphasized that as 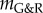approaches zero, the adaptivity approaches infinity so that for positive but very small 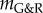a perturbation can still result in dilatation large enough to be considered an aneurysm (i.e. greater than or equal to 50% increase in diameter). Conversely, even for slightly negative 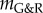a significant dilatation may occur only after a period too long to be relevant for aged patients. Although 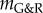correlates with expansion rate in general, clinical decisions should therefore not be made only on the basis of the sign of .

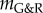The mechanobiological stability theory provides a theoretical basis not only to understand outcomes of nonlinear finite-element simulations based on the same G&R model but also a number of experimental and clinical observations. In [25], the microRNA miR-29 was shown to decrease the production of extracellular matrix, particularly collagen, which in aneurysms, where typically 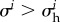, is equivalent to a drop of k_σ and thus the stability margin 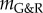in our model. Increased miR-29 levels have been found in human thoracic aneurysms. Moreover, enlargement of AAAs in mouse models is promoted by increased miR-29 levels [25] and attenuated by inhibition of miR-29 [26]. Age and smoking are important risk factors for aneurysms, and elevated miR-29 levels are observed in older individuals [27–29] and after exposure to nicotine [30]. These observations can be understood from the negative impact of a reduced capacity for stress-mediated collagen production (i.e. reduced k_σ) on the stability margin. By contrast, increasing extracellular matrix production in aneurysms can, in the spirit of Cyron & Humphrey [12], be understood as strengthening neighbouring Lyapunov attractors, which helps drive vessels with pathological G&R processes into nearby homeostatic equilibrium states.

3.4.2. Turnover time

Given (2.25), the turnover time τ affects the system dynamics via the prefactor 1/τ in 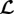by setting a characteristic time scale for G&R that allows the definition of a non-dimensional time t/τ. On this non-dimensionalized time scale, τ affects G&R via 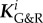exactly as does 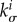since 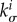appears in only via 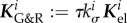. As normalization of time does not change the mechanobiological stability properties, but only defines the time scale on which the system evolves, the general statements about the impact of k_σ on the mechanobiological stability in §3.4.1 hold equally for τ, namely, a longer turnover time always stabilizes the system. An increased concentration of type I collagen carboxyterminal telopeptide fragments (a collagen I degradation product) [31] and of PIIINP (a propeptide indicative of increased collagen III turnover) [32] has been reported for AAAs. This suggests either a generally accelerated turnover of collagen or at least an increased degradation rate that correspond in our model to a smaller τ or k_σ and thus to a decreased mechanobiological stability.

3.4.3. Elastic stiffness

It was shown mathematically in [12] that a sufficient increase in wall stiffness can always ensure a positive-definite operator 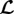in (2.25) and thus stabilize the system. The plausibility of this statement is clear from (2.25) given an infinite elastic stiffness. In this limit, K_tot equals the sum of all elastic stiffnesses and is thus positive definite. The term in the brackets equals the sum over all 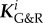for collagen and smooth muscle plus the elastic stiffness of elastin, which is for k_σ > 0 also positive definite. Therefore, 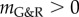and the system is mechanobiologically stable.

In relation to the expansion of aneurysms, this prediction was evaluated parametrically by varying c₁ and c₂ in the strain energy function of collagen (3.2) such that prestrain and prestress were kept constant in the initial homeostatic state while the stiffness was changed by a factor 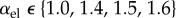. As illustrated in figure 4, the stability margin 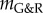increased as expected with increased elastic stiffness (i.e. α_el). For clearly negative 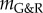, the vessel enlarged exponentially, while for clearly positive 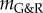the vessel stabilized after a period of protective G&R with a slightly increased diameter. Nearly linear expansion occurred in between these extremes (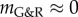). Again, the stability margin from the linear mechanobiological stability theory [12] allows reasonable quantitative estimates when unstable responses are expected even for significant deformations (such as a circumferential stretch of up to approx. 1.4 as in figure 4 for 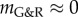). This robustness against nonlinear effects is an important quality for the practical application of the concept of mechanobiological stability.

It is well known that diabetes decreases the prevalence or severity of thoracic and AAAs [33,34]. Increased cross-linking and the resulting higher stiffness of the collagenous tissue observed in diabetic patients have been proposed as a possible reason. Pulse wave velocity increases by approximately 20% in diabetic patients [35], which corresponds to an increase in wall stiffness by a factor of α_el ≈ 1.45. This value is in good accordance with [36] and an increase in stiffness of 60% found in diabetic rats [37]. The parameter study presented in this section confirms that the mechanobiological stability theory [12] captures the significant stabilizing effect on aneurysms due to increased wall stiffness, as in diabetic patients. Moreover, this theory explains the decreased diameter of the descending thoracic aorta found diabetic patients [38] via the inverse relationship between the stability margin and adaptivity as well as the above discussion of age-related vessel dilatation (cf. §3.2).

Note that the stabilizing effects of collagen production capacity, half-life and stiffness shown mathematically in [12], and related herein to computational as well as clinical and experimental findings, agree qualitatively with results reported in [39] for a simple scalar arterial model with a goal-function based G&R. However, the theory of mechanobiological stability pursued herein is applicable to arbitrary vascular geometries and material compositions and does not experience the probably unphysiological oscillatory G&R observed partially in [39].

3.4.4. Blood pressure

For vessels with k_σ ∈ {0.32/τ, 0.36/τ, 0.42/τ} studied in §3.3, we observed a change of the stability margin between the homeostatic states before and in hypertension by less than 5%. For smaller values of k_σ, down to 0.05/τ, which may be relevant for aneurysms in practice (cf. §3.4.1), the decay of the stability margin introduced by hypertension was slightly higher, but still not dramatic. It thus appears that mechanical effects due to increased blood pressure do not alone render healthy (mechanobiologically stable) vessels susceptible to aneurysms because in healthy vessels increased blood pressure is compensated by increased wall thickness. The situation is different, however, if hypertension begins in an already mechanobiologically unstable vessel. From (2.27) and (2.30), we infer that a change in blood pressure has practically the same effect as a perturbation of areal mass density with opposite sign. For example, with the parameters of our aortic model, an increase in blood pressure by 26 mm Hg excites G&R as strong as the loss of all vascular elastin. In a mechanobiologically unstable vessel that cannot compensate for such a perturbation by protective G&R, this excitation is expected to cause a dramatic unstable expansion. In this sense, the temporal order of the occurrence of hypertension and mechanobiological instability (e.g. aneurysm) may play a crucial role.

Indeed, decreasing blood pressure after the initiation of an aneurysm (that is, in potentially mechanobiologically unstable vessels) has been seen experimentally to attenuate their enlargement [40]. Yet, the question of whether hypertension is in general a risk factor for aneurysms remains controversial despite a large number of studies [41]. Our mechanobiological stability theory suggests that paying more attention to the temporal order of the occurrence of aneurysm and hypertension, not just the absolute blood pressure, might help resolve this controversy. Moreover, as suggested in [42,43], and supported by Shiraya et al. [44], hypertension may be responsible for other effects that reduce effective extracellular matrix production (and thus lower both k_σ and 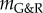) in addition to its purely mechanical effect (increased load and thicker walls). These complexities and their effects on aneurysmal progression require further investigation to understand relationships between hypertension and aneurysms. Nevertheless, the mechanobiological stability theory provides a useful platform to explore hypotheses and guide future experiments.

4. Conclusion

As introduced in [12], mechanobiological stability can be understood as the property of a blood vessel to return to a state close to its initial one following a perturbation, and mechanobiological adaptivity is a measure of the residual change in configuration. In this paper, we demonstrated that these concepts provide a simple conceptual framework to help understand clinically relevant G&R processes such as age-related dilatation, adaptations in hypertension and the development of aneurysms.

We illustrated how this framework can be used to estimate, from experimental and clinical data on age-related dilatation and hypertensive G&R, the interval [0.63 yr^–1; 2.19 yr^–1] as a reasonable choice in healthy vessels for the gain parameter k_σ in [14]. Moreover, we used the inverse relationship between mechanobiological stability and adaptivity to explain the clinically observed correlation between age-related vessel dilatation and susceptibility for AAAs. As a change of paradigm, we suggested that aneurysms be interpreted as a form of mechanobiological instability while purely mechanical instabilities probably play little to no role. This interpretation was supported by comparisons of mathematical statements from Cyron & Humphrey [12], computational parametric studies similar to ones in [11], and clinical and experimental observations. These comparisons suggested that common risk factors for AAAs (such as smoking and age) and mitigating factors (such as diabetes) can be understood from their (patho)physiological impact on the stability margin 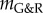, a simple scalar measure of mechanobiological stability. We emphasize that the discussion of the relationship between different physiological conditions and mechanobiological stability in this paper is meant to be more illustrative than comprehensive, and that more detailed studies (e.g. considering also other microRNAs than only miR-29 as herein) remain a promising avenue of future research. Finally, the discussion in this paper focused mainly on AAAs. To examine the applicability of the concept of mechanobiological stability to other types of aneurysms will require further study.

We hope that the concepts of mechanobiological stability and adaptivity can help promote an increasingly rigorous mathematical understanding of vascular G&R in general and aneurysms in particular. We also hope that this framework may drive improved methods of computational prognosis for aneurysms, taking into account not only the maximal diameter or wall stress, but also growth and remodelling dynamics. Finally, it may help in the development of new therapies. The theory of mechanobiological stability suggests that increases in stress-mediated collagen production capacity, constituent half-life, and wall stiffness can attenuate (and potentially reverse) the enlargement of aneurysms. Some of these factors can, in principle, be controlled by appropriate drugs, which may be optimized on the basis of more comprehensive versions of the theory introduced in Cyron & Humphrey [12].

Appendix A

For uniaxial (fibre-like) species such as smooth muscle and collagen fibres, which are assumed to be aligned at one angle φⁱ relative to the circumferential direction and to carry only the stress 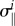in this direction, the contribution to the (radial component of the) internal loads is

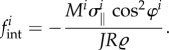A1

In general, the circumferential engineering strain, relative to the initial radius ,

A2

Around the initial configuration with and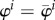

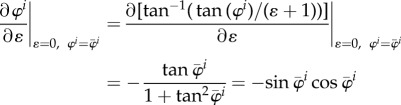A3

and

A4

This leads to the geometric stiffness

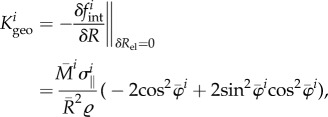A5

where, due to the constraint 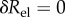, only φⁱ, J and R depend on δR during the differentiation whereas 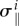is considered constant. The elastic stiffness

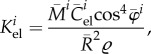A6

where 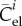is the elastic modulus in direction 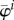in the sense of the theory of small on large [45] and 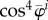follows from the usual transformation rules (cf. [46], eqns (6.31)–(6.33)) for tensors. With (2.22) and (A 6)

A7

and with (2.23) and (A 1)

A8

Since δR_el is a scalar, also is and then so that with (2.25)

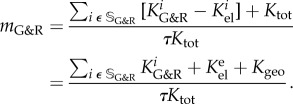A9

Funding statement

This work was supported by a Fellowship within the Postdoc-Program of the German Academic Exchange Service (DAAD) to C.J.C., an AHA Predoctoral Fellowship Award 13PRE14130007 to J.S.W. and NIH grant nos. RO1 HL086418, R01 HL105297 and UO1 HL116323 to J.D.H.