Simple and accurate methods for quantifying deformation, disruption, and development in biological tissues

Abstract

When mechanical factors underlie growth, development, disease or healing, they often function through local regions of tissue where deformation is highly concentrated. Current optical techniques to estimate deformation can lack precision and accuracy in such regions due to challenges in distinguishing a region of concentrated deformation from an error in displacement tracking. Here, we present a simple and general technique for improving the accuracy and precision of strain estimation and an associated technique for distinguishing a concentrated deformation from a tracking error. The strain estimation technique improves accuracy relative to other state-of-the-art algorithms by directly estimating strain fields without first estimating displacements, resulting in a very simple method and low computational cost. The technique for identifying local elevation of strain enables for the first time the successful identification of the onset and consequences of local strain concentrating features such as cracks and tears in a highly strained tissue. We apply these new techniques to demonstrate a novel hypothesis in prenatal wound healing. More generally, the analytical methods we have developed provide a simple tool for quantifying the appearance and magnitude of localized deformation from a series of digital images across a broad range of disciplines.

1. Introduction

Analysis of images to detect and quantify spatial variations in deformation is critical for understanding morphogenesis [1], wound healing [2], tissue mechanics [3–5] and structural mechanics [6]. A standard approach for such analysis involves estimating displacement fields inferred by comparing images of the same system taken at different times or under different conditions [7,8]. The most broadly used technique involves matching image intensities over a grid of regions of a sample before and after the sample is deformed [8,9], then differentiating the resulting displacement fields numerically to estimate the tensor of strains that describes the spatial distribution of deformation. Displacement field estimation can be improved dramatically for large deformations through the Lucas–Kanade (LK) algorithm that applies and optimizes a ‘warping function’ to the undeformed image before matching it to an undeformed image [7,10–12]. Strain fields estimated through these approaches underlie much of cell mechanics [13–16], using a technique that compares images of a deformable medium contracted by cells to images of the same medium after deactivation or removal of the cells. The framework is fast and well established for most mechanical loads that isolated cells apply to their surroundings [17], and similar approaches have been used to study collective cell motion [18], tissue morphogenesis [1] and tissue mechanics [3–5].

However, these methods are subject to large errors when strain is high or localized. Specifically, small inaccuracies in displacement estimation become amplified through the numerical differentiation needed to estimate strain fields [7–9]. Minor mistracking of a single displacement can lead to an artefact that is typically indistinguishable from a region of concentrated strain. Although accuracy can be improved by incorporating a mathematical model that describes how a specific tissue deforms into the image matching [19,20], such techniques cannot be applied to a tissue whose properties are not known a priori.

We therefore developed a simple ‘Direct Deformation Estimation’ algorithm (DDE) that circumvents the need to estimate displacement fields before estimating strain fields, and thus avoids the inaccuracies associated with displacement mapping artefacts. We also developed an associated metric that distinguishes local concentration of strain from errors in the calculation of deformation. We call this method the ‘Strain Inference with Measures of Probable Local Elevation’ (SIMPLE) algorithm.

The DDE algorithm improves the accuracy of local strain estimates by three orders of magnitude compared with standard cross-correlation techniques and by up to an order of magnitude over prior techniques based upon the LK algorithm. This is achieved by directly incorporating the calculation of deformation into the warping function used in the algorithm, a powerful simplification that has not previously been implemented. By examining how the output of the DDE algorithm differs from the output of the LK algorithm, the SIMPLE algorithm provides a measure that is remarkably sensitive to strain localization. To illustrate the potential impact of the DDE and SIMPLE algorithms, we validate them using model problems. We then demonstrate them on four problems that pose a challenge to existing methods: (i) detection of spatially varying modulus in a polydimethylsiloxane (PDMS) scaffold with a spatial gradient in cross-linking density, (ii) detection of spatially varying modulus in a collagen scaffold with a spatial gradient in mineral content, (iii) prediction of crack formation prior to appearance of a visible crack in a vinylidene chloride sheet in tension, and (iv) confirmation of a long-standing hypothesis about the balance between active and passive contraction during the healing of embryonic wounds.

2. Results

2.1. Optical strain estimation is simpler, more precise and more accurate when numerical derivatives are avoided

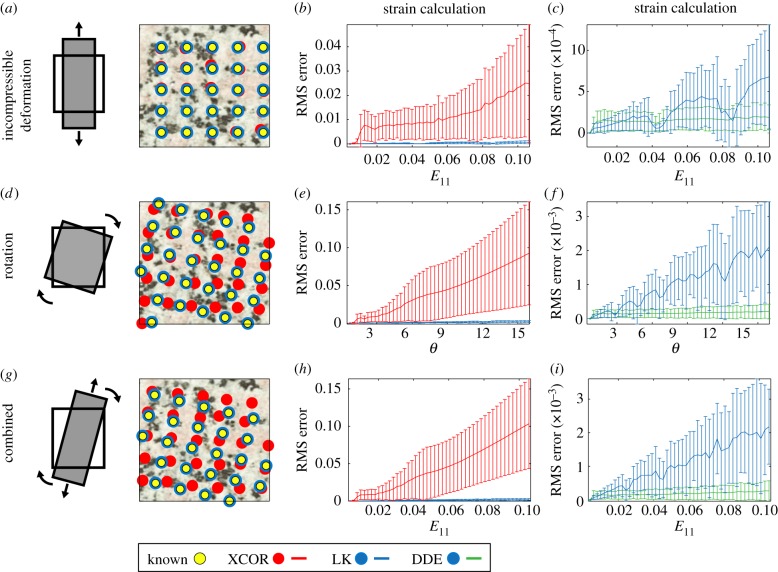
Optical strain measurements use texture matching to estimate deformation. The basic texture-matching algorithm divides an initial reference image into several regions and finds the best-matching region in a deformed image. The most widely implemented class of algorithms, termed standard cross correlation (XCOR), search for matching regions without considering how the shape of the individual undeformed texture regions change (figure 1a,b) [21]. Strain fields can be estimated from the displacements of the midpoints of each region, often through calculation of a deformation gradient tensor that can be used to relate the spatial gradient of displacement fields to the strain fields (figure 1b).

Figure 1.

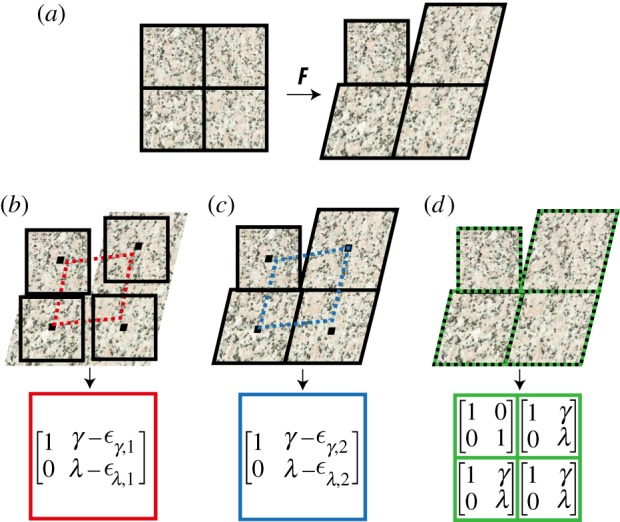
Schematic of how XCOR, LK and DDE calculate two-dimensional deformation gradient tensors. (a) Original test image (left) and warped image (right). (b) Rigid registration yields errors due to a parallelogram fit of the midpoints of a minimum of four regions (red boxes). (c) The LK method improves on this, but errors and reduced precision remain due to the parallelogram fit of the midpoints to calculate F (blue boxes). (d) DDE accurately calculates the deformation of all four regions independently (green boxes). Black borders: matched regions; dotted borders: calculated deformations for XCOR (red), LK (blue) and DDE (green). F, deformation gradient tensor; γ, shear strain; λ, stretch ratio in y direction; ε_α,x, error in α strain.

Although not widely used in the biomedical and engineering communities, the LK method is broadly applied in computer vision to improve region-matching (figure 1a,c) [7,8,10,11]. Rather than matching regions of identical size and shape, the LK method optimizes a warping function for each region to improve the matching. Displacements of the midpoints of each region are then used to estimate the deformation gradient tensor and strain fields with a least-squares fit (LSF) [8]. This can reduce errors in strain estimation in cases of large deformations by two orders of magnitude (figure 2b,e,h). Alternate deformable image registration techniques have been developed and used in biomedical applications which improve upon LK displacement estimation, however all of these alternative techniques require a LSF of the displacement field [22,23].

Figure 2.

The DDE method was superior to all previously used methods for calculating strains in a deforming sample. In simulations where strains and rotations were known a priori, the DDE algorithm (green lines) calculated strains with higher precision and accuracy than XCOR (red lines) and LK (blue lines) algorithms. LK and DDE methods produced lower errors than XCOR at all strain levels. DDE methods produced lower errors than LK, with differences becoming more apparent with increasing strain levels. (a–c) The first simulation consisted of an increasing tensile incompressible deformation to a final strain of E₁₁ = 0.1. XCOR produced errors on the order of 0.03 strain for a strain level of 0.1. By contrast, the LK and DDE strain calculations introduced errors on the order of 0.0005 strain. (d–f) The second simulation consisted of a pure rotation to θ = 15° in the absence of strain. XCOR was unable to accurately track displacements in this simulation, leading to large errors in the strain calculations. For this simulation, errors in strain calculation for the LK method were on the order of 0.002 strain, whereas errors for the DDE method were on the order of 0.0001 strain. (g–i) The third simulation consisted of incompressible deformation (E₁₁ = 0.1) combined with rotation θ = 15°. XCOR once again failed to track deformation, leading to large errors in strain calculations. The errors associated with the LK and DDE algorithms were similar to those for pure rotation, with the DDE algorithm about an order of magnitude better than the LK algorithm. E₁₁, strain in 11 direction; θ, rotation.

We found that errors could be reduced another order of magnitude by incorporating continuum mechanics directly into the LK algorithm. During the Newtonian optimization performed to solve for the LK method, a warping function must be defined to describe the change from an undeformed to a deformed image and is usually chosen for efficiency and accuracy in estimation of displacement fields [8]. We defined a warping function that could be directly related to the deformation gradient tensor (see the electronic supplementary material for details). Using this approach, referred to as DDE, the deformation gradient tensor is intrinsically calculated as part of the region-matching algorithm, without the need to take numerical derivatives (figure 1a,d).

When tested against idealized images with deformation fields known a priori, the DDE approach out-performed LK and XCOR approaches substantially in pure incompressible deformation (figure 2a), pure rotation with no deformation (figure 2d) and incompressible deformation with rotation (figure 2g). Three advantages of the DDE approach are: (i) improved accuracy due to a unique deformation gradient tensor associated with each region (figures 1 and 2), (ii) increased precision due to circumvention of a least-squares estimation of the deformation gradient tensor (figures 1 and 2), and (iii) improved simplicity because least-squares estimation based on image motion is eliminated.

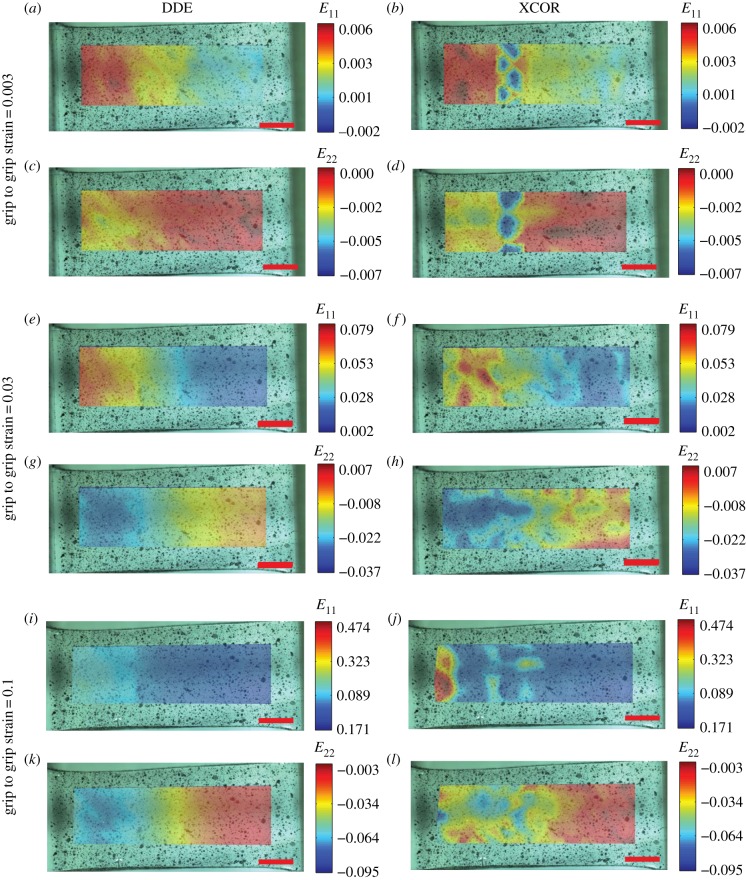
To demonstrate the utility of the increased accuracy and precision, we analysed deformation of PDMS samples fabricated with gradients in cross-linking and hence gradients of material stiffness, followed by coating with a speckle pattern to track deformations. Using videos taken as specimens were cyclically strained between 0 and 10% grip-to-grip strain, the DDE algorithm detected smooth spatial gradients of both axial strain and lateral contraction along the sample, corresponding to the expected stiffness gradient at a grip-to-grip strain of only 0.003 (figure 3a,c; electronic supplementary material, video 1). These patterns were evident long before detection using XCOR (figure 3b,d). Both methods detected strain gradients at a grip-to-grip strain of 0.03, but the strain fields predicted by XCOR were irregular, with regions of high strain seen next to regions of low strain (figure 3f). At higher strain levels, the XCOR methods failed to capture a meaningful strain field, whereas the DDE algorithm continued to identify the smooth gradient, even with peak strains over 0.2 (figure 3i–l). Similar results were seen using collagen scaffolds with gradients in mineral content (electronic supplementary material, figure S2 and video 2).

Figure 3.

The advantages of the increased precision and accuracy of DDE over XCOR were demonstrated by cyclically stretching a PDMS sheet with a spatial gradient in stiffness. (a–d) At a low grip-to-grip strain of 0.003, DDE was able to detect a gradient in stiffness, as evidenced by gradients in the first and second principal strains, whereas XCOR failed to detect gradients in strain above noise. (e–h) At a grip-to-grip strain of 0.03, DDE revealed a smooth gradient in first and second principle strains. XCORR also detected the spatial gradients in strain, however the detected strains were irregular and noisy. (i–l) At a large grip-to-grip strain of 0.1, DDE detected a smooth strain gradient, with local strains greater than 0.2. By contrast, XCOR failed to detect a smooth strain gradient, demonstrating its limitations at high strains. Scale bar, 2 mm. E₁₁, strain in 11 direction.

Many algorithms exist for improving the smoothing and improving the accuracy of displacement fields [24]. As these were not applied in this example, the example does not represent the limitations of XCOR. However, it does represent the strength and simplicity of DDE strain tracking which is inherently sensitive, does not require smoothing/averaging, has higher resolution and tracks to much higher strain levels.

2.2. The strain inference with measures of probable local elevation algorithm identifies strain localizations and predicts crack formation

The irregular strain pattern in figure 3f,h represents a well-known challenge with XCOR methods. Slight mistracking of a texture region leads to zones of over-estimated strain abutting zones of underestimated strain. If strain fields are known to be smooth, this can be fixed by simply averaging over several regions. However, in the absence of such information, a strain field such as that in figure 3f,h might lead to the erroneous conclusion that strain concentrations existed in these regions and that the material did not have a smooth stiffness gradient. Although the DDE method is able to reveal the smooth material gradient, detection of strain concentrations remains difficult because strain concentration detection methods must rely on post processing filtering techniques to detect local features.

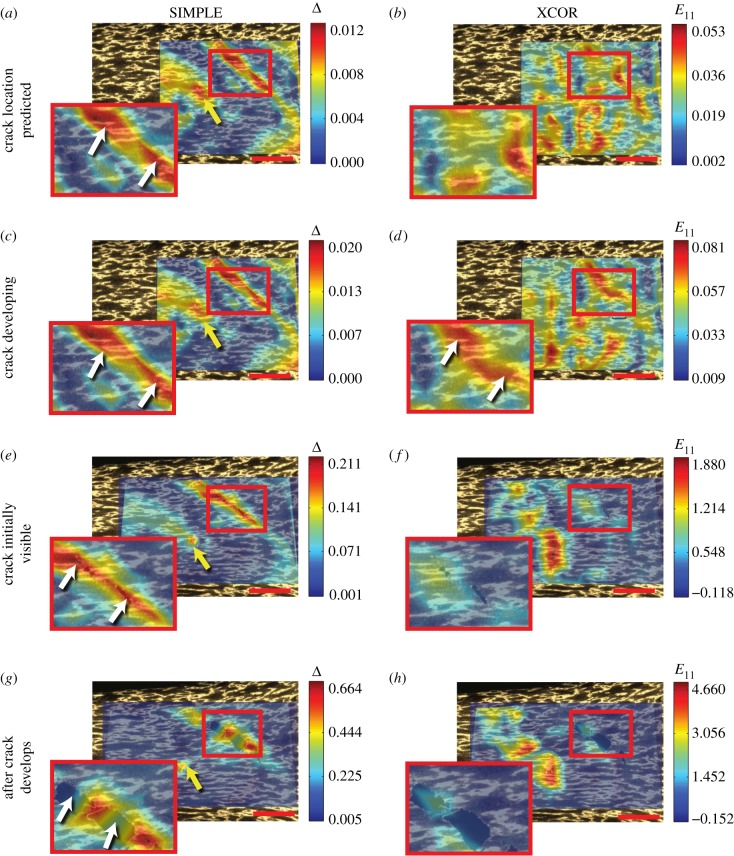
The SIMPLE algorithm achieved robust prediction of strain localization and crack formation through a metric based upon differences between predictions of the DDE and LK methods (figure 4a,b; details in the electronic supplementary material, Methods). The output of this algorithm is a tensor Δ whose principal components reveal strain concentrations. As a demonstration, a vinylidene chloride sheet with a speckle pattern on its surface was pulled to failure. The peak principal value of Δ, termed the strain concentration detector, Δ_I, identified strain localizations leading to cracks earlier and with more certainty than XCOR (figure 5a,b, white arrow; electronic supplementary material, video 3). As the primary region of strain localization inferred using Δ_I cracked, Δ_I continued to increase over the uncracked ligaments (figure 5c). Further, as the crack developed, neighbouring strain concentrations halted their development and unloaded, demonstrating transfer of stress to the propagating crack (figure 5, yellow arrows). By contrast, the strain concentration was difficult to identify above noise using XCOR methods (figure 5d, white arrow), XCOR returned unreasonable strains of 200% while cracks were propagating (figure 5f), and the XCOR method failed to track deformations after the crack had formed (figure 5f,h).

Figure 4.

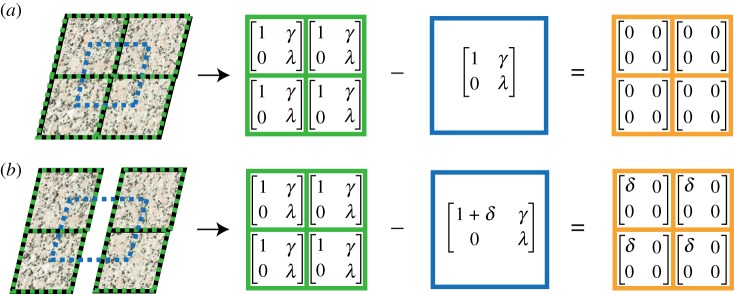
The SIMPLE method uses the difference between the two-dimensional deformations calculated by DDE (green boxes) and the LK method (blue boxes) to determine an outcome we refer to as the strain concentration detector (orange boxes). (a) When deformations are continuous and have no local discontinuities, the DDE and LK methods agree and their difference is exactly 0. (b) If there is a local discontinuity in the data, the DDE and LK methods disagree and their difference is non-zero. γ, shear strain; λ, stretch ratio in y direction; δ difference in calculation between methods.

Figure 5.

The SIMPLE method accurately detected strain concentrations predictive of crack initiation formation and was able to track crack propagation. (a,b) The SIMPLE algorithm detected two developing strain concentrations (white and yellow arrows) at a low grip-to-grip strain (E₁₁ = 0.26). By contrast, noise in the XCOR calculation resulted in significant uncertainty for determining the location of the strain concentrations. (c,d) At higher levels of grip-to-grip strain (E₁₁ = 1.16), both algorithms were able to detect the developing crack, however, the strain concentration remained partially obscured by noise for the XCOR method. (e) The strain concentration predicted by the SIMPLE algorithm can be visualized as a crack in the material (white arrows). (e–h) As the crack formed and propagated (E₁₁ = 1.56), the XCOR algorithm failed, whereas the SIMPLE algorithm continued to track the crack in the material (white arrows in g). Furthermore, the second strain concentration (yellow arrow) stopped developing, suggesting that the material failure at the crack (white arrows) resulted in unloading of the second concentration. Scale bar, 1 mm. E₁₁, strain in 11 direction; Δ, SIMPLE difference. Strains are shown relative to an initial grip-to-grip strain of E₁₁ = 1.2, at which the optical analysis was started.

SIMPLE identifies when the strain field arising from the best estimates for displacements differ significantly from the piecewise constant DDE strain field that best represents how a defined portion of an image has deformed. Estimating displacements based upon the DDE strain fields, as is required for the former, has the advantage of providing a compatible strain field, meaning that it corresponds to a unique displacement field [25]. However, imposing compatibility is not in general appropriate for piecewise constant averaged strain fields (electronic supplementary material, §2).

2.3. Direct deformation estimation and strain inference with measures of probable local elevation algorithms reveal previously ambiguous mechanisms of embryonic wound healing

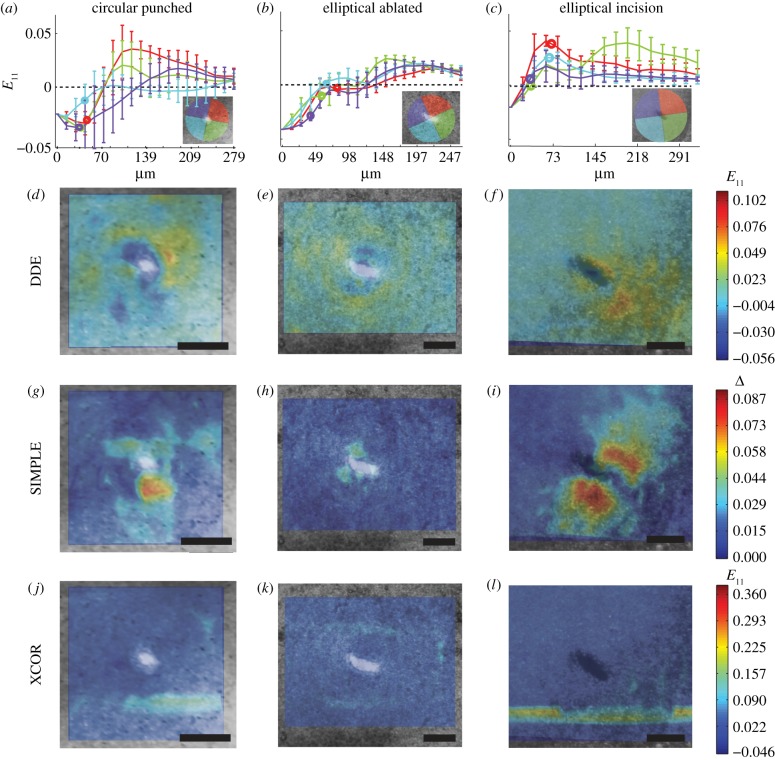
Embryonic wounds can heal without scarring and therefore serve as model systems for regenerative healing strategies and fetal surgery [26]. Central unresolved issues surround identification of the contractile field around a wound perimeter shortly after wounding and of how surgical technique affects this behaviour [2]. The dominant model suggests that a local ring contracts isotropically [2], but the strain fields needed to support this model have never before been imaged successfully. We therefore studied differences between three wound types in early stage chick embryos: (i) circular wounds created with a punch [2], (ii) elliptical wounds created by ablation (electronic supplementary material, Methods Section), and (iii) elliptical wounds created by incision with a micro-scalpel [2]. We sought to delineate three sources of tissue strain in vicinity of the wound: (i) isotropic contraction of the wound, (ii) passive elastic recovery of tissue distal to the wound, and (iii) stretching introduced during wound creation (electronic supplementary material, figure S3).

The DDE method succeeded in identifying the time course of straining, whereas XCOR revealed only noise (figure 6). For the circular punched wound, the first principal strain showed a contractile ring around the wound border, consistent with the isotropic contraction model [2] (figure 6a,d; electronic supplementary material, video 4). The SIMPLE algorithm detected a strain concentration around the wound consistent with localized isotropic contraction [2] (figure 6g and the electronic supplementary material, video 4).

Figure 6.

The DDE and SIMPLE algorithms described the spatial and temporal patterns of embryonic wound closure, whereas the XCOR algorithm revealed only noise. (a–c) First principle strains in the radial direction away from the wound centre for 90° bins around the wound (inset) with wound border marked by a circle. (a,d,g) For the circular punched wound, the first principal strain determined by DDE demonstrated an isotopic contractile ring around the wound border. A strain concentration was identified around the wound by the SIMPLE algorithm, consistent the presence on a localized isotropic contraction. (b,e,h) For the elliptical ablated wound, DDE demonstrated a localized ring of isotropic contraction and tension distal to the wound. A strain concentration was identified around the wound by the SIMPLE algorithm. (c,f,i) For the elliptical incision wound, DDE identified high tensile strain was at the leading edge of the incision and low strain in the wake of the incision. SIMPLE detected strain concentrations along the flanks of the wound. (j,k,l) XCOR failed to identify any patterns of strain at or near the wound sites. Scale bars, 200 μm. E₁₁, strain in 11 direction; Δ, SIMPLE difference.

For the elliptical ablated wound, a localized isotropic contractile ring again formed, and small amounts of tension distal to the wound were evident (figure 6b,e; electronic supplementary material, video 5). The SIMPLE algorithm again detected a strain concentration around the wound (figure 6h and the electronic supplementary material, video 5).

By contrast, the micro-scalpel incision showed elevated tensile strain at the leading edge of the incision, and very low strain in the wake of the incision (figure 6c,f; electronic supplementary material, video 6). Strain concentrations were detected along the flanks of the wound, and subsequent analysis revealed these to arise from shearing of the wound flanks (figure 6i and the electronic supplementary material, video 6).

Results suggest that the mode of incision, rather than the shape of the wound, dictated where strains were localized during closure/contracture. As discussed below, this supports predictions of the isotropic contraction model and sheds light on some basic mechanisms of fetal wound healing.

3. Discussion

The DDE and SIMPLE methods can identify strain concentrations that are very difficult to detect with any previously published method and are appealing due to the simplicity of their implementation. The SIMPLE method detected strain concentrations on the order of 0.005, long before they were evident using XCOR (figure 5a). Strain localizations were predictive of crack initiation and are therefore useful for applications ranging across biomaterial design and structural engineering. We are unaware of any other techniques to detect strain concentrations as robustly or predict the onset of fracture with this precision and accuracy.

DDE and SIMPLE quantified features of embryonic wound healing that were previously undetectable and in addition enabled a qualitative picture of the effect of wound type. The interplay of isotropic constriction, passive elastic recovery and stretching introduced during wound creation became apparent, providing insight into wound healing mechanisms and fetal surgery [2,27,28]. The strain fields associated with circular and elliptical ablated wounds exhibited a trade-off between localized isotropic contraction and distal tissue tension, with no additional effects of the wounding process (figure 6 and electronic supplementary material, figure S3). The scalpel incision, however, left tension in the wake of the wound, compression ahead of the wound and shear abutting the flanks. Cells surrounding the wound reacted to reach a homeostatic state, which combined with the effects of the localized isotropic contraction to induce wound closure (figure 6). Results suggest that ablating and punching are less disruptive to embryonic wounds than scalpel incisions and show that the method of wounding has a strong effect on the initial stages of the wound-healing response.

The DDE method showed improvement in accuracy, precision and resolution over previously employed techniques and maintained this through high strains. This renders the method particularly suitable for biologic systems, which often endure large and inhomogeneous strains [1–5]. DDE also demonstrated sensitivity sufficient to differences in strain as small as 0.001 (figure 3). The method is insensitive to movements and rotations of a specimen and is relatively robust against image noise. The method is therefore suitable for analysis of low-resolution/noisy images (e.g. from magnetic resonance imaging). Other methods for deformable image registration employ more flexibility than the simple affine transformation used here [10]; however, the DDE method is the first to take into account the formulations of mechanics directly into the image correlation algorithm, and thus delivers improved accuracy. Importantly, as with other texture-based methods including XCOR and LK, DDE is limited by image resolution and the size of the smallest image feature: the region size cannot be known a priori and must be adjusted for each sample based on the image resolution and the size of the smallest texture feature.

The techniques described are useful outside of biology as well. Glacial rifts and fronts of earthquakes begin as strain localizations before failure [29,30], and estimates of strain concentrations at these fronts might prove useful. Further, the method would be useful in monitoring of civil structures. We are hopeful that the simplicity of DDE and SIMPLE will enable easy strain estimation and strain concentration detection across many fields.

Funding statement

This work was funded by the National Institutes of Health (NIH) (AR060820 and HL109505), the National Science Foundation (NSF) (CAREER 844607) and the NIH and NSF jointly (U01EB016422).