Abstract
Very little is known about the mechanism of antifreeze action of antifreeze glycoproteins (AFGPs) present in Antarctic teleost fish. Recent NMR and CD studies assisted with total synthesis of synthetic AFGP variants have provided insight into the structure of short AFGP glycopeptides, though the observations did not yield information on the antifreeze mechanism of action. In this study, we use Hamiltonian replica exchange (HREX) molecular dynamics simulations to probe the structure and surrounding aqueous environments of both the natural (AFGP8) and synthetic (s-AFGP4) AFGPs. AFGPs can adopt both amphiphilic and pseudoamphiphilic conformations, the preference of which is related to the proline content of the peptide. The arrangement of carbohydrates allows the hydroxyl groups on terminal galactose units to form stable water bridges which in turn influence the hydrogen-bond network, structure, and dynamics of the surrounding solvent. Interestingly, these local effects lead to the perturbation of the tetrahedral environment for water molecules in hydration layers far (10.0–12.0 Å) from the AFGPs. This structure-induced alteration of long-range hydration dynamics is proposed to be the major contributor to antifreeze activity, a conclusion that is in line with terahertz spectroscopy experiments. The detailed structure–mechanism correlation provided in this study could lead to the design of better synthetic AFGP variants.
Antifreeze glycoproteins (AFGPs) are present in the blood serum of deep sea teleost fish found in the Arctic and Antarctica. These glycoproteins enable the survival of the fish by preventing the growth of ice crystals, hence protecting the fish against cryoinjury.1−3 Structurally, AFGPs are polymeric mucin type glycopeptides, consisting of repeating tripeptide units (Ala-Thr-Ala)n with a disaccharide moiety (Galβ1–3GalNAcα1−) attached to each Thr residue.4,5 In addition to Ala and Thr, AFGP also contains Pro residues, the significance of which is still unclear. Due to their polymeric nature, AFGPs range in molecular weights from approximately 2.6 kDa (4 repeat units) to 33.7 kDa (50 repeat units).
Very little is known about the underlying mechanism of the antifreeze activity of AFGP.1−3 This generally stems from the lack of secondary structure information for AFGP. Attempts to crystallize AFGP have been unsuccessful due to challenges in isolation and purification of AFGP from natural sources.6 Additionally, there has been little success with expression and post-translational modification of AFGP in cell lines. The challenges in crystallization have also been ascribed to the flexible nature of AFGP in solution, which is also found to affect structural characterizations using NMR and CD experiments.7,8
In general, an adsorption-inhibition process is hypothesized as the proposed mechanism for antifreeze action, wherein AFGP is proposed to irreversibly bind to the surface of ice crystals, resulting in the lowering of the observed freezing point, thereby creating a hysteresis on the order of 1–2 °C between the equilibrium melting point and the observed freezing point.3 This mechanism however has been challenged by tetrahertz adsorption spectroscopy experiments, which observed signatures of retarded water dynamics around AFGP.9,10 It has also been argued that the relatively low physiological concentrations and noncolligative action of AFGP cannot be explained by the adsorption-inhibition mechanism, which was initially proposed for antifreeze proteins (AFPs), molecules that present a well-characterized and well-defined structural ice binding face contrary to the highly flexible AFGP.11
Chemical synthesis and controlled polymerization have allowed researchers to synthesize synthetic AFGP (s-AFGP) containing native and non-native glycans.12−16 The access to s-AFGP led to the establishment of structure–activity relationships using biophysical characterizations like thermal hysteresis and ice crystal morphologies.12 It was found that both the geometry and composition of AFGP were important for antifreeze activity. Three structural features were found to be critical for antifreeze activity, namely, (i) an N-acetyl group in galactosamine, (ii) an α-glycosidic linkage, and (iii) the Thr γ-methyl group.12
CD studies of AFGPs have not been conclusive, with reported structural characteristics varying from random-coil structures and β-sheet geometries to PPII-helix conformations for both native AFGP8 (antifreeze glycoprotein fraction 8) and s-AFGPs.7,12,13,17 Temperature dependent (−5 to 85 °C) CD studies reported PPII helical structures for s-AFGP at low temperatures with the structural features diminishing with increasing temperatures.13 NMR studies of AFGPs have been limited by the polymeric nature of AFGP (repeating ATA units) which introduces NMR spectral overcrowding.7,8,12,18 To date, NMR structural determination using distance and dihedral based restraints has been limited to s-AFGP3 (AT*AAT*AAT*A, where T* denotes glycosylated Thr).12
While these studies alluded to the mechanism of antifreeze activity, there is still a lack of a detailed structural mechanism of these antifreeze glycopeptides. Questions remain as to how the three critical structural features correlate to antifreeze activity. Additionally, the current structural models, like the NMR restrained structures, arrived at in the absence of explicit water, do not account for experimental results such as the observation of hydrated forms of s-AFGP3 in cold-spray ionization time-of-flight mass spectroscopy experiments or the suppression of antifreeze activity upon the addition of sodium borate.9,10,19
In this study, we use Hamiltonian replica exchange (HREX) molecular dynamics (MD) simulations supplemented with standard MD simulations to probe the structural features of AFGPs in explicit water. By including explicit water, we also investigate the influence of carbohydrates on the structure and dynamics of the surrounding solvent. Two AFGP systems were chosen for the present study, the naturally occurring AFGP8 (AAT*AAT*PAT*AAT*PA) and the synthetic derivative: s-AFGP4 (AT*AAT*AAT*AAT*A). The synthetic derivative was chosen to maintain an identical number of O–Thr linkages to compare with AFGP8.
The restraint independent HREX MD conformational sampling protocol has been successfully tested earlier for studying model O-linkage systems and antiproliferative glycopeptides in solution.20,21 Excellent agreement was obtained with NMR observables (J-coupling data and NOE distances) which instilled confidence in the use of the protocol to study AFGP. The starting conformations for the HREX MD simulations were generated in accordance with the available NMR data for both AFGP8 and s-AFGP3.8,12 Water was treated in the simulations using both the TIP5P and TIP4P-2005 water models, which accurately capture the temperature–density anomaly of water.22,23 In addition to the glycopeptide systems, simulations were performed for the underlying peptide sequences AATAATPATAATPA and ATAATAATAATA to delineate the structural influence of carbohydrates with respect to protein.
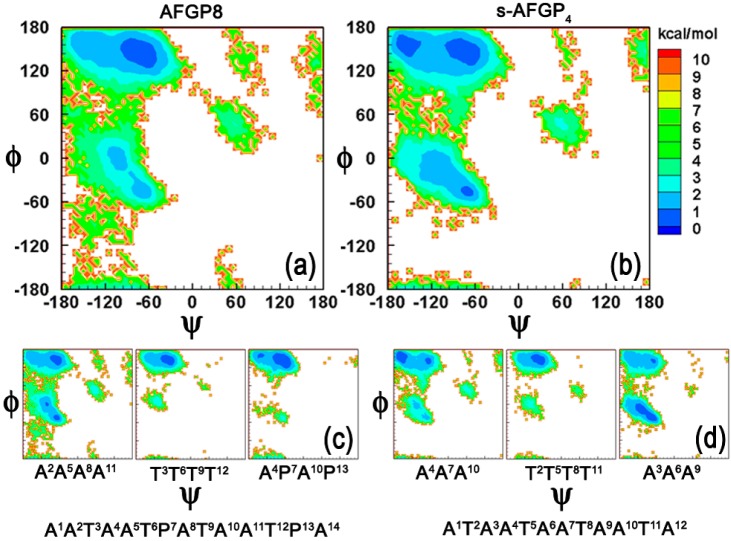
In Figure 1, we present ϕ/ψ analysis for both AFGP8 and s-AFGP4 obtained from the 300 K simulations. The Boltzmann inverted ϕ/ψ distribution obtained from all the ϕ/ψ pairs in AFGP8 and s-AFGP4 is presented in parts a and b of Figure 1, respectively. AFGP8 generally samples conformations belonging to the PPII region of ϕ/ψ space, while s-AFGP4 samples PPII, β-sheet, and α-helical regions. This correlates with the experimental findings which predict PPII conformations for AFGP8,7,8,17 while evidence of all three conformations has been observed for (ATA)n polymers.12,13 To gain insight into the shift toward PPII conformations for AFGP8, we partition the ϕ/ψ distribution into three distinct categories on the basis of the location of the amino acid with respect to the Thr residues, such that i corresponds to the position of Thr with the distributions i – 1 and i + 1 indicating the residues preceding and following Thr, respectively. All the Thr residues (middle panel in Figure 1c and d) sample the extended PPII conformation irrespective of the system type (AFGP8 or s-AFGP4). The major difference between the two systems is observed for the ϕ/ψ distribution around the i + 1 amino acids (right panel in Figure 1c and d). For AFGP8, the amino acids (A4P7A10P13) sample the PPII region, while, for s-AFGP4, a significant sampling corresponding to the α-helical region is observed. This shift in the distribution is largely due to the introduction of Pro at P7 and P13, which imparts rigidity and lends a structural bias to the system toward PPII conformations.
Figure 1.
Boltzmann inverted ϕ/ψ distributions obtained from all dihedral pairs for (a) AFGP8 and (b) s-AFGP4. Boltzmann inverted ϕ/ψ distributions obtained from i – 1 (left panel), i (middle panel), and i + 1 (right panel) dihedral pairs, where i corresponds to the position of Thr for (c) AFGP8 and (d) s-AFGP4. The relative free energies are given in kcal/mol.
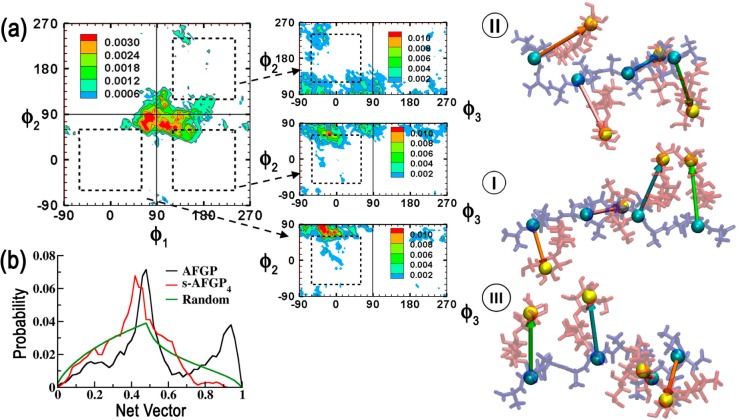
The spatial arrangement of the carbohydrates with respect to the peptide backbone was next characterized. For this, pseudodihedrals (ϕ1, ϕ2, ϕ3) between the centers of geometry of β-Gal and AT(A/P) units were evaluated (pseudodihedrals illustrated in the representative structure in Figure 2). For each pseudodihedral pair, ϕ1/ϕ2 and ϕ3/ϕ2, the 2D probability distribution was analyzed from −90 to 270° to classify the pseudodihedral space into four quadrants:
-
1:
ϕ1 (−90 to 90°, eclipsed) and ϕ2 (−90 to 90°, eclipsed)
-
2:
ϕ1 (90 to 270°, trans) and ϕ2 (−90 to 90°, eclipsed)
-
3:
ϕ1 (90 to 270°, trans) and ϕ2 (90 to 270°, trans)
-
4:
ϕ1 (−90 to 90°, eclipsed) and ϕ2 (90 to 270°, trans)
Figure 2.
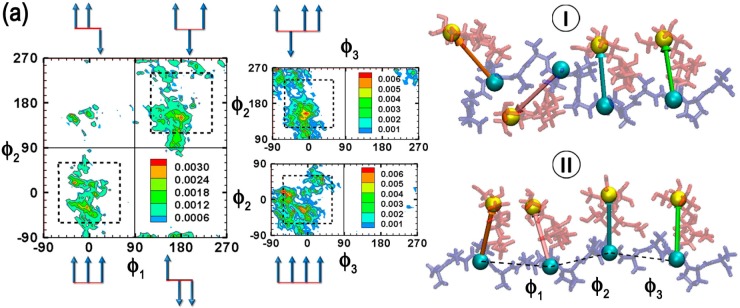
ϕ1/ϕ2 probability distributions for AFGP8. The four quadrants are demarcated by solid lines. Dotted lines are used to differentiate the intermediate regions. ϕ3/ϕ2 distributions corresponding to the populated quadrants in the ϕ1/ϕ2 distribution are also presented. Representative structures belonging to each quadrant obtained from clustering analysis are presented to the right of the distributions. Cluster numbers are presented in roman numerals. Pictorial vector representations are used to illustrate the relative orientations of the carbohydrates in the representative structures. The pseudodihedral angles are calculated between the centers of geometry illustrated by VDW spheres in the representative structure. The peptide backbone is presented in blue, while the carbohydrates are presented in red.
AFGP8 populates the all eclipsed 1 (31%) and all trans 3 (48%) regions of the ϕ1/ϕ2 distribution (Figure 2). On analyzing the ϕ3/ϕ2 distributions corresponding to these two regions, it is found that ϕ3 generally samples the pseudodihedral space corresponding to the eclipsed conformation (−90 to 90°). In Figure 2, we also present the representative structures of the top two clusters obtained by clustering the trajectories using the peptide ϕ/ψ dihedrals. For the largest cluster, the ϕ1/ϕ2/ϕ3 conformation corresponds to a trans/trans/eclipsed alignment of the carbohydrates, while, for the second largest cluster, this corresponds to an eclipsed/eclipsed/eclipsed alignment. It is to be noted that the latter alignment of the carbohydrates corresponds to an amphipathic structure in which predominantly all the alcohol groups on the carbohydrates are aligned onto one face of the glycopeptide, a conformation that has been previously hypothesized for AFGP.12
For s-AFGP4, the loss of peptide rigidity (Figure 1b) is reflected in the spatial arrangement of the carbohydrates. The conformations populate three regions of the ϕ1/ϕ2 distribution, 1 (20%), 2 (37%), and 3 (33%) (Figure 3a). In contrast to AFGP8, the additional peptide flexibility leads to the carbohydrates populating intermediate ϕ1/ϕ2 regions (regions outside the dotted areas in Figure 3a). Even ϕ3 corresponding to each ϕ1/ϕ2 distribution predominantly samples the intermediate conformations (Figure 3a). Clustering of the trajectories yielded three significant clusters corresponding to regions 1, 2, and 3 of the ϕ1/ϕ2 distributions (Figure 3a). While a truly amphipathic arrangement of carbohydrates akin to the second largest cluster for AFGP8 does not occur in s-AFGP4, pseudoamphipathic arrangements of the carbohydrate alcohol groups even in s-AFGP4 are sampled. These observations further highlight the importance of select prolines in AFGP8.
Figure 3.
(a) ϕ1/ϕ2 probability distributions for s-AFGP4. Corresponding ϕ3/ϕ2 distributions, representative structures, and pictorial vector representations are also presented (see Figure 2 legend). (b) Analysis of the magnitude of the resultant net vector, s, obtained from component vector addition. The peptide backbone is presented in blue, while the carbohydrates are presented in red.
In addition to the above analysis, we also calculate a net resultant vector by component vector addition using unit vectors along the centers of geometry of β-Gal and AT(A/P) (Figures 2 and 3). By assuming that the first vector is aligned with the origin (θ1 = 0), we use ϕ1, ϕ2, and ϕ3 (angles between the vectors) to calculate the components and obtain the net resultant vector, s, using the following equations:
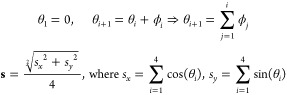 |
The distributions of the resultant net vectors are presented in Figure 3b. For AFGP8, two peaks occur around 0.95 and 0.48 that correspond to the alignment of all the vectors (0.95) and where one of the vectors points in the opposite direction (0.48). Note that the profile differs strongly from the baseline for random arrangement of the vectors and that both of the aforementioned peaks are significantly higher. For s-AFGP4, only one clear peak occurs around 0.42 and the profile differs from the random baseline mainly in a sharply decreased sampling of the fully aligned conformation (with correspondingly higher populations elsewhere). This analysis reinforces the fact that, while both AFGP8 and s-AFGP4 sample pseudoamphipathic structures, AFGP8 has a bias toward a truly amphipathic structure, while the same structure is virtually inaccessible to s-AFGP4.
Analysis of the trajectories also revealed persistent hydrogen bonds (H-bond) between the N-acetyl hydrogens (−NHCOCH3) on GalNAc units and the carbonyl oxygens of Thr. The occupancies corresponding to these H-bonds have been tabulated in Table 1. This H-bond locks the conformation of the carbohydrate with respect to the peptide backbone and also influences the ϕ/ψ distribution of the underlying peptide. Its presence has been observed earlier in mucin type architectures involving Thr O–GalNAc linkages.20,21,24−26 It has also been reported that this H-bond is lost on substituting Thr with Ser or upon changing the linkage geometry from α- to β-linkage.20,21,24−26 Thus, both the N-acetyl group and the α-linkage are required to maintain the orientation of the carbohydrate with respect to the underlying peptide, which is also found to influence the antifreeze activity of AFGP.
Table 1. Significant Hydrogen Bond and Bridge Water Occupancies from 300 K Simulations of AFGP8 and s-AFGP4.
| AFGP8 | s-AFGP4 | ||||
|---|---|---|---|---|---|
| Hydrogen Bonds | |||||
| Thr 3 (O) | GalNAc 15 (NH) | 0.56 | Thr 2 (O) | GalNAc 13 (NH) | 0.58 |
| Thr 6 (O) | GalNAc 17 (NH) | 0.76 | Thr 5 (O) | GalNAc 15 (NH) | 0.75 |
| Thr 9 (O) | GalNAc 19 (NH) | 0.65 | Thr 8 (O) | GalNAc 17 (NH) | 0.60 |
| Thr 12 (O) | GalNAc 21 (NH) | 0.62 | Thr 11 (O) | GalNAc 19 (NH) | 0.35 |
| Average | 0.65 | 0.57 | |||
| Carbohydrate–H2O–Protein Bridges | |||||
| Thr 3 (NH) | GalNAc 15 (NH/O) | 0.46 | Thr 2 (NH) | GalNAc 13 (NH/O) | 0.33 |
| Thr 6 (NH) | GalNAc 17 (NH/O) | 0.27 | Thr 5 (NH) | GalNAc 15 (NH/O) | 0.31 |
| Thr 9 (NH) | GalNAc 19 (NH/O) | 0.35 | Thr 8 (NH) | GalNAc 17 (NH/O) | 0.49 |
| Thr 12 (NH) | GalNAc 21 (NH/O) | 0.51 | Thr 11 (NH) | GalNAc 19 (NH/O) | 0.62 |
| Average | 0.40 | 0.44 | |||
| Carbohydrate–H2O–Carbohydrate Bridges | |||||
| Gal 16 (O5) | GalNAc 15 (O4/HO4) | 0.23 | Gal 14 (O5) | GalNAc 13 (O4/HO4) | 0.24 |
| Gal 18 (O5) | GalNAc 17 (O4/HO4) | 0.18 | Gal 16 (O5) | GalNAc 15 (O4/HO4) | 0.23 |
| Gal 20 (O5) | GalNAc 19 (O4/HO4) | 0.23 | Gal 18 (O5) | GalNAc 17 (O4/HO4) | 0.23 |
| Gal 22 (O5) | GalNAc 21 (O4/HO4) | 0.18 | Gal 20 (O5) | GalNAc 19 (O4/HO4) | 0.19 |
| Average | 0.21 | 0.22 | |||
| Gal 16 (O2/HO2) | GalNAc 15 (O) | 0.13 | Gal 14 (O2/HO2) | GalNAc 13 (O) | 0.13 |
| Gal 18 (O2/HO2) | GalNAc 17 (O) | 0.21 | Gal 16 (O2/HO2) | GalNAc 15 (O) | 0.16 |
| Gal 20 (O2/HO2) | GalNAc 19 (O) | 0.16 | Gal 18 (O2/HO2) | GalNAc 17 (O) | 0.15 |
| Gal 22 (O2/HO2) | GalNAc 21 (O) | 0.20 | Gal 20 (O2/HO2) | GalNAc 19 (O) | 0.17 |
| Average | 0.18 | 0.15 | |||
| Gal 16 (O4/HO4) | Gal 16 (O5) | 0.17 | Gal 14 (O4/HO4) | Gal 14 (O5) | 0.17 |
| Gal 18 (O4/HO4) | Gal 18 (O5) | 0.17 | Gal 16 (O4/HO4) | Gal 16 (O5) | 0.16 |
| Gal 20 (O4/HO4) | Gal 20 (O5) | 0.19 | Gal 18 (O4/HO4) | Gal 18 (O5) | 0.17 |
| Gal 22 (O4/HO4) | Gal 22 (O5) | 0.17 | Gal 20 (O4/HO4) | Gal 20 (O5) | 0.17 |
| Average | 0.18 | 0.17 | |||
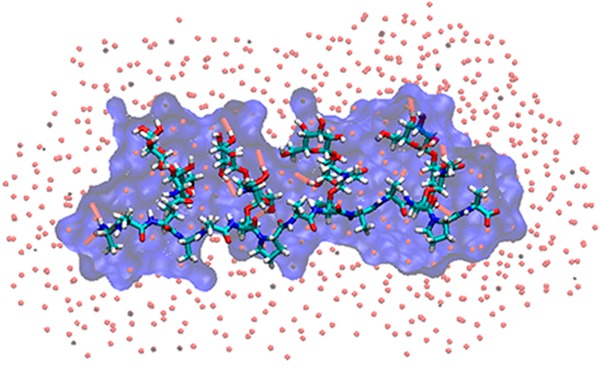
The presence of hydrogen bonding alcohol groups in close proximity to each other allows carbohydrates to form stable water bridges.19,21,25−27 Analysis of the trajectories revealed both carbohydrate–protein and carbohydrate–carbohydrate water bridges (Table 1). A significant water bridge occurred between the amide hydrogen of Thr and the N-acetyl side chain of GalNAc, wherein the water molecule could form hydrogen bonds with both the amide hydrogen and oxygen of GalNAc, i.e., GalNAc(HN)–H2O–Thr(HN) and GalNAc(O)–H2O–Thr(HN). The 3D probability distributions of the bridged water oxygen constructed from the 300 K simulation trajectories for both AFGP8 and s-AFGP4 are presented in parts a and b of Figure 4, respectively, along with a representative snapshot of the glycopeptide for visualization. The presence of one bridged water molecule per Thr–O–GalNAc linkage is in agreement with the experimental finding of three D2O water molecules complexed with s-AFGP3 from cold-spray ionization time-of-flight mass spectroscopy experiments.19 While similar water bridges between the amide hydrogen of Thr and the N-acetyl side chain of GalNAc have been observed in earlier MD studies of Thr O–GalNAc dipeptide systems,21,26 to the best of our knowledge, this is the first report of the presence of multiple water bridges in AGFP using MD simulations. Note that the formation of the strong intramolecular H-bond between GalNAc and Thr (NH···O) brings about the proximity of H-bond donors and acceptors involved in the stable water bridge. Earlier studies on O-linked dipeptides have reported that the water bridge is lost upon substituting Thr with Ser.21,26 The loss of the water bridge was a direct consequence of the weakening of the H-bond (NH···O) between GalNAc and Ser, which is due to the loss of the steric strain on the N–Cα–Cβ–O dihedral due to the absence of the Thr γ-methyl group in Ser. It is also of importance to note that a loss of antifreeze activity was also observed on substituting Thr by allo-Thr and d-Thr,14−16 modifications that affect the conformations at Thr Cα and Cβ. Thus, the results indicate the importance of three structural features—(i) an N-acetyl group in galactosamine, (ii) an α-glycosidic linkage, and (iii) the Thr γ-methyl group—in restricting the conformational space accessible to AFGP. However, it is not clear how the three key structural features directly contribute to the antifreeze activity, which highlights the importance of analyzing the solvent structure around the glycopeptides in closer detail.
Figure 4.
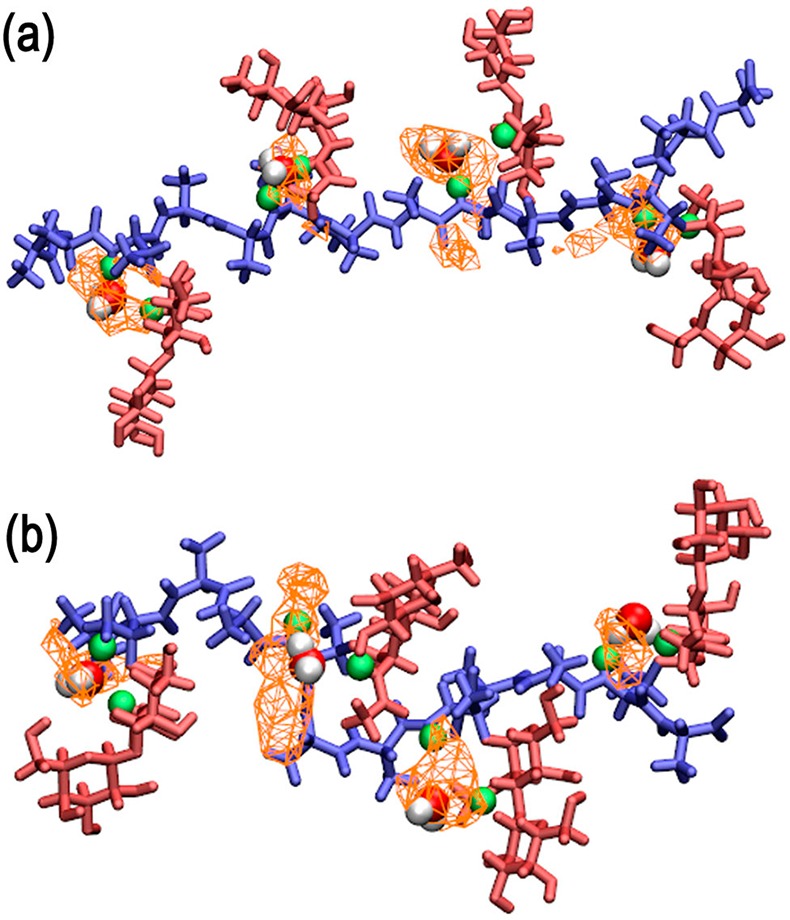
3D probability distributions of the bridged water oxygen’s involved in the GalNAc(HN)–H2O–Thr(HN) water bridge from the 300 K simulation trajectories along with representative snapshots of (a) AFGP8 and (b) s-AFGP4 glycopeptides. Color code: probability distribution, orange (wireframe); peptide backbone, blue; carbohydrate, red; bridging hydrogen atoms, green.
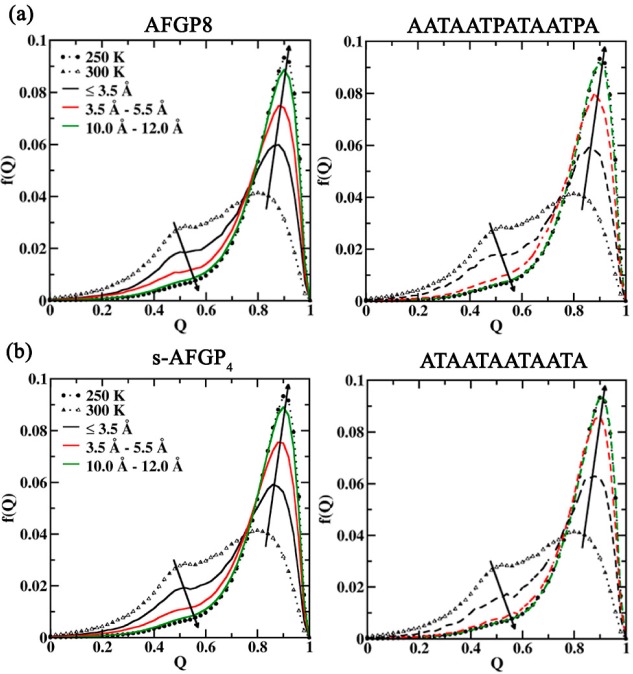
In addition to the significant carbohydrate–protein water bridge, three less populated carbohydrate–carbohydrate water bridges occurred in both AFGP8 and s-AFGP4. Two water bridges were present between Gal and GalNAc, Gal(O5)–H2O–GalNAc(O4/HO4) and Gal(O2/HO2)–H2O–GalNAc(O). A third water bridge occurred in Gal between the hydroxyl group at C4 and the endocyclic oxygen, Gal(O4/HO4)–H2O–Gal(O5). It is interesting that the hydroxyl groups at C6 are not involved in any water bridges. To gain insight into the influence of these water bridges on the distribution of water molecules around the carbohydrates, the radial distributions g(r) of water oxygens around the hydroxyl oxygens of both Gal and GalNAc were calculated. The g(r) values obtained from 300 K simulations of AFGP8 and s-AFGP4 are presented in Figure 5a and b, with the corresponding data from the 250 K simulations presented in Figure S1a and b of the Supporting Information. The g(r) values obtained from 250 K simulations using the TIP4P-2005 water model are presented in Figure S2a and b of the Supporting Information. The differences in the radial distribution functions (Δ = g(r)water – g(r)oxygen) with respect to pure water radial distributions are also presented in the respective figures. First, a reduction in the amplitude of the first peak at 2.75 Å as compared to water occurs in all of the distributions due to the expected reduction in the number of water molecules in the first solvation shell owing to the presence of the carbohydrate. On comparing the g(r) around the second peak at 4.5 Å, for all the hydroxyls not involved in water bridges (O6 and O3), the g(r) is similar to the pure water distribution. However, for hydroxyls involved in water bridges (O2 and O4), there is a significant lowering in the peak amplitude. Additionally, the g(r) around O4 of Gal also exhibits a different profile when compared to the other hydroxyls with a peak around 6.00 Å in the distribution when compared to the peak around 6.75 Å observed in the pure water distribution and g(r) for other hydroxyls. These differences are more pronounced on comparing the difference distributions (Δ).
Figure 5.
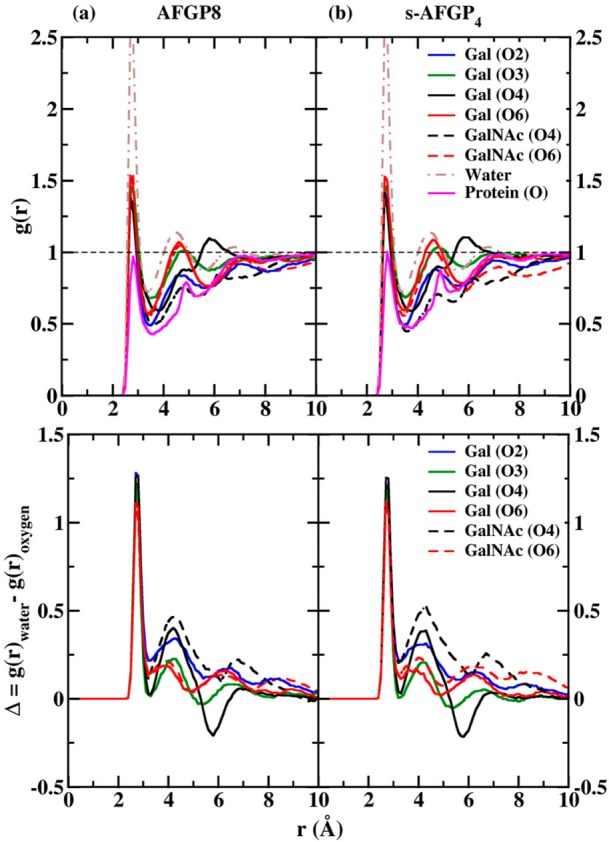
Upper panel: Selected oxygen (carbohydrate)–oxygen (water) radial distribution functions, g(r), from 300 K simulations of (a) AFGP8 and (b) s-AFGP4. The g(r) for pure water under the same simulation conditions is also presented for comparison. Lower panel: Difference (Δ) between the radial distribution functions. Δ is calculated as the difference between g(r) of pure water and g(r) of select oxygen (carbohydrate)–oxygen (water) radial distribution functions from 300 K simulations of (a) AFGP8 and (b) s-AFGP4.
On the basis of these observations, we evaluate the effect of the glycopeptide on the structural order of proximal water molecules. For this, the local tetrahedral order parameter Qk was calculated, which is a measure of a particular water molecule and its four neighbors adopting a tetrahedral arrangement, to quantify the local degree of tetrahedrality.28
where φikj is the angle formed by the molecule k and its nearest neighbors i and j. Especially for waters close to the glycopeptide, the nearest neighbors can be either the water oxygen or glycopeptide/protein oxygen or nitrogen atoms. For a perfect tetrahedral arrangement, Qk is equal to 1. On the basis of the g(r) analysis, Qk was evaluated for water molecules within three spatial regions, namely, (a) less than 3.5 Å, (b) between 3.5 and 5.5 Å, and (c) between 10.0 and 12.0 Å from the respective atom selections. Since our interest is in the antifreeze properties of AFGPs, the Qk distributions were analyzed for the 250 K simulations to capture differences in local tetrahedral character at a subfreezing temperature when compared to pure water Qk distributions at 250 K. The Qk distributions were evaluated for water molecules around Gal, GalNAc, and the peptide regions in glycopeptide simulations and around the peptide regions from peptide only simulations. In Figure 6, we present the Qk distributions obtained from both glycopeptide and peptide only simulations using the TIP5P water model. The Qk distributions obtained from simulations using the TIP4P-2005 water model are presented in Figure S3 of the Supporting Information file. The Qk distributions obtained from 250 and 300 K pure water simulations of both the TIP5P and TIP4P-2005 water models are also presented for comparison in the respective figures.
Figure 6.
Q distributions for water molecules around Gal (left panels) from 250 K simulations of (a) AFGP8 and (b) s-AFGP4. The Q distributions for water molecules around protein (right panels) from 250 K protein-only simulations of (a) AATAATPATAATPA and (b) ATAATAATAATA are also presented. The distributions were evaluated for water molecules less than 3.5 Å, between 3.5 and 5.5 Å, and between 10.0 and 12.0 Å from the selection (Gal or protein). The Q distributions for pure water at 250 K (dotted line with filled circles) and 300 K (dotted line with open triangles) are also presented. The distributions are evaluated from simulations using the TIP5P water model.
The presence of glycopeptides or peptides leads to a loss in the tetrahedral arrangement for water molecules within 3.5 Å of glycopeptides or peptides. This is evident by the lowering of the high Qk peak (around 0.82) (Figure 6 and Figure S3, Supporting Information). Note that this loss in tetrahedrality mimics the effect of a temperature increase as observed on comparing the 250 and 300 K distributions from the pure water simulations. However, the direct effect of the presence of sugar, especially Gal, is reflected on comparing the Qk distributions for water molecules in the regions 3.5–5.5 and 10.0–12.0 Å. For these two distributions, it is observed that the water molecules around the glycopeptides are less structured (solid lines) when compared to the water molecules around the peptides (dashed lines). Notice that for water molecules 10.0–12.0 Å from the peptides the distribution overlaps with the pure water distribution at 250 K. However, a lowering of the peak amplitude is observed for water molecules around Gal even at these long distances for the TIP5P water model. It is interesting to note that the same effect is more pronounced in the region 3.5–5.5 Å with the TIP4P-2005 water model. Thus, the presence of Gal causes a significant decrease in the tetrahedral arrangement for water even at large distances, a phenomenon which is partially dependent on the water model chosen in the simulation due to the variations in the water density for each water model.23 It is this long-range perturbation of the water structure that we propose as an explanation of the antifreeze properties of glycopeptides and the lack of such properties in the peptides.
Additionally, Qk was evaluated for water molecules around Gal and the backbone peptide in finer increments of 0.2 Å shells in the glycopeptide and peptide simulations, respectively. The distributions are presented in Figure S4 (Supporting Information) for simulations using the TIP5P water model. The trace of the highest Qk peak from all of these profiles is also presented in Figure S4e (Supporting Information). The profiles clearly show a lowering of the high Qk peak in the region around 3.5 Å which then gradually increases and converges for distances >10.0 Å. Notably, the Qk values around Gal remain lower than the pure water Qk value, while the Qk profile for water molecules around the peptide parts reaches the pure water Qk value at distances >10.0 Å. This clearly indicates long-range effects in AFGPs.
The observed long-range impact of the AFGPs on the water structure is in line with results obtained from terahertz spectroscopy studies. From the experimental studies, it was observed that AFGPs perturb the aqueous solvent over long distances with the observation of long-range temperature dependent retardation of water dynamics in water shells as far as 20 Å from AFGP.9,10 At 20 °C, the terahertz excess was found to be 6 cm–1 with a maximum at AFGP concentrations of 12 mg/mL, while, at 5 °C, the terahertz excess was even more pronounced (10 cm–1) and peaked at lower AFGP concentrations of 4 mg.9,10 Our simulations at 250 and 300 K accurately capture the temperature dependent phenomenon, which is critical to the antifreeze activity. Additionally, it was observed that the addition of sodium borate resulted in the suppression of the antifreeze activity with the hydration dynamics shifting more toward bulk-like features. Other studies have indicated that borate can form complexes with the proximal free hydroxyl groups on Gal (HO3 and HO4) or GalNAc (HO4 and HO6).29,30 These results, combined with a report that acetylation or oxidation of HO6 does not affect antifreeze activity,30−32 suggest that the HO3 and HO4 hydroxyls on Gal contribute to the antifreeze activity. From our simulations, we find that the O4 hydroxyls on Gal are involved in the formation of water bridges, which directly affect the resulting distribution of the water molecules with an additional peak around 6.0 Å in the radial distribution g(r) (Figure 5). At lower temperatures, this additional modification of the tetrahedral environment around bridged water molecules propagates to hydration shells removed from AFGPs that affect the freezing behavior of water.
To further quantify the effect of glycopeptide on water–water dynamics, we analyzed the H-bond autocorrelation functions.33 The H-bond autocorrelation function was calculated as
where h(t) is a binary H-bond operator that takes the value of 1 if a H-bond between a tagged pair of oxygen atoms that belong to different molecules (at t = 0) exists after time t and 0 otherwise. The bracket represents an average over all possible pairs of oxygen atoms and different time origins. A hydrogen bond exists between two molecules if the oxygen–oxygen distance is less than 3.5 Å and the angle between the O–O axis and one of the O–H bonds is less than 30°. Note that the correlation is independent of intermediate H-bond breaking. These calculations were performed on continuous MD simulations as described in the Methods.
In Figure 7, the results of the CHB(t) analysis are presented for both AFGP8 and s-AFGP4 from simulations using the TIP5P water model. The corresponding results using the TIP4P-2005 water model are presented in Figure S5 of the Supporting Information. CHB(t) profiles were analyzed in two spatial regions, less than 3.5 Å and between 10.0 and 12.0 Å, from the Gal residues, similar to the Qk analysis. For the 300 K simulations, it can be seen that CHB(t) for water molecules close to the glycopeptides (<3.5 Å) decays slower when compared to the bulk water. Also, the CHB(t) for water molecules remote from the glycopeptides (10.0–12.0 Å) overlaps with the bulk CHB(t). This indicates that at 300 K the formation of carbohydrate–water H-bonds only influences the water–water H-bond dynamics in the first solvation shell. This is an observation that occurs with both water models used in the simulation.
Figure 7.
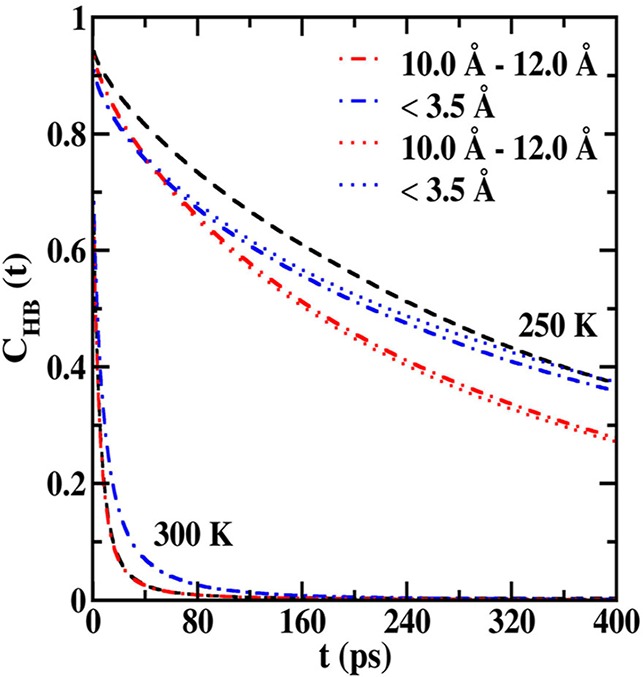
Water–water H-bond autocorrelation functions from 250 and 300 K simulations of AFGP8 (dot-dashed lines) and s-AFGP4 (dotted lines). The autocorrelation functions were evaluated for water molecules within two spatial regions, less than 3.5 Å (blue lines) and 10.0–12.0 Å (red lines) from the glycopeptides. Autocorrelation functions evaluated from 250 and 300 K pure water simulations (dashed black line) are also presented for comparison. The distributions are evaluated from simulations using the TIP5P water model.
The scenario at 250 K is markedly different from that at 300 K. Water at 250 K forms a well-defined H-bonding network with each water molecule present in a tetrahedral environment (Figure 6). This arrangement leads to a significantly longer CHB(t) decay time for bulk water. For the TIP5P simulations, the water in the first solvation shell around the glycopeptides exhibits CHB(t) decay times lower than the bulk water initially, while tending toward the bulk value at longer time scales. Interestingly, for the TIP4P-2005 water model, the CHB(t) decay times are slower than the bulk water throughout the simulation. These effects are a direct influence of the formation of strong carbohydrate–water H-bonds that lead to a loss in the tetrahedral environment (Figure 7) and result in the observed water dynamics.
Remarkably, the influence on H-bond dynamics is more pronounced for solvation shells far from the glycopeptide. Concurrent with the lower Qk for water molecules in this region, 10.0–12.0 Å (Figure 6), faster decays occur for CHB(t) versus the bulk, indicating that the water molecules are less ordered in these regions when compared to bulk water at 250 K. This disorder in bulk regions, wherein the water has more liquid-like properties, is proposed to inhibit the freezing of water, thereby explaining the antifreeze properties of these glycopeptides even at very low concentrations. Here it is important to note that this behavior is observed with both water models with the effect being more pronounced in the TIP5P water model, which is in line with the results obtained from the Qk analysis.
Conclusion
In summary, our investigations reveal a close interplay between the glycopeptide geometry and the antifreeze properties of AFGP. Both AFGP8 and s-AFGP4 can adopt amphipathic structures wherein the alignment of the carbohydrates onto one face is governed by the proline content, which imparts rigidity to the AFGP template and enhances the PPII helical content. This is important, as recent studies on larger AFGP synthetic derivatives revealed lower thermal hysteresis gaps in AFGP lacking prolines, which may be due to folded structures in these larger systems.13 The three key structural elements identified by synthetic and mutation studies—(i) an N-acetyl group in galactosamine, (ii) an α-glycosidic linkage, and (iii) the Thr γ-methyl group—mainly restrict the conformational space available to the glycopeptide. In fact, the presence of the N-acetyl group in galactosamine locks the conformation of the sugar relative to the peptide bond via strong H-bonds and bridge waters, as observed in cold-spray ionization time-of-flight mass spectroscopy experiments.19
The antifreeze activity of AFGP however is closely related to the modulation of the surrounding solvent H-bond network due to the glycopeptides. Radial distribution functions, tetrahedral order parameters, and water–water H-bond autocorrelation functions reveal the importance of free hydroxyl groups on Gal modulating the water H-bond network. The formation of water bridges on the surface of the glycopeptide by Gal affects the local tetrahedral order of the water molecules in the first solvation shell. This effect causes disorder in the H-bond network, which propagates to the remaining solvation shells at low temperatures, as evidenced by the water dynamics in 10.0–12.0 Å water shells around both AFGP8 and s-AFGP4. This observation is in accordance with both the suppression of antifreeze activity on the addition of borate and retardation of long-range hydration dynamics observed in terahertz spectroscopy experiments. It must also be noted that upon the removal of terminal Gal monosaccharide AFGPs exhibit very weak antifreeze activity, which agrees with our observation of the importance of Gal in restructuring the surrounding solvent.9,15,19 The direct dependence of the antifreeze activity on the solvent restructuring by Gal also addresses the observance of similar antifreeze activity for AFGP8 and s-AFGP4 even though the latter glycopeptide exibits enhanced conformational flexibility upon the loss of proline rigidity.
Interestingly, the proposed long-range effect on water dynamics at 250 K does not occur at 300 K. This suggests that the long-range “disordering” effect only manifests itself in the more ordered water environment at lower temperature, again in agreement with terahertz studies. Such increased order is proposed to allow the local perturbation of water structure in the first hydration layer of the glycopeptide to be communicated to regions 10 Å or more from the solute, thereby leading to the antifreeze activity.
The detailed structure–mechanism correlation provided in this study could lead to the design of better synthetic AFGP variants. On the basis of these results, it would be worthwhile to investigate modifications of the carbohydrate that facilitate the formation of bridged waters, thereby modulating H-bond dynamics and affecting the overall antifreeze activity. One such modification could be the incorporation of 1,2,3,4,5,6-cyclohexanehexol derivatives in place of the terminal Gal monosaccharide. Since the synthetic variants utilize chemical polymerization for the synthesis of oligomeric AFGP, it might be difficult to incorporate proline residues at select locations. However, attempts could be made to increase the hydrophobic content of the amino acids, i.e., AT*V or VT*V, which may impart rigidity to AFGP akin to the presence of proline. Additionally, these results can be used to describe the antifreeze activity of the C-linked AFGPs and other synthetic variants like the AFGP diastereomers.14−16,18,34,35
Methods
MD simulations were performed with the CHARMM program.36 The CHARMM22 protein force field37 with CMAP (dihedral correction map),38 the CHARMM carbohydrate force field,39−45 and the modified TIP5P or TIP4P-2005 water models22,23 were used to represent the AFGP systems in solution. The initial geometries of AFGPs were constructed in accordance with the available NMR data.7,8,12 For the carbohydrates, the H–N–C2–H2 dihedral in the N-acetyl side chain in GalNAc was set to the anti (180°) configuration, while the O1–Cβ–Cα–N dihedral in the O-linkage was set to the gauche+ (60°) configuration. For the peptides, the ψ dihedral was set to 150° for all the amino acids, while the ϕ dihedral was set to −145° for Thr and −75° for the remaining amino acids. The rest of the geometry was constructed from the topology information present in the force field. These initial geometries were subjected to a 1000-step steepest descent (SD) minimization followed by an adopted basis Newton–Raphson (ABNR) minimization to a force gradient tolerance of 10–6 kcal/mol/Å.46 The minimized geometries were then immersed in a pre-equilibrated cubic water box of size 65 Å × 65 Å × 65 Å. The size of the water box was selected on the basis of the condition that it extended at least 15 Å beyond the non-hydrogen atoms of AFGP. Water molecules with the oxygen overlapping with the non-hydrogen solute atoms within a distance of 2.8 Å were deleted. For all of the subsequent minimizations and MD simulations, periodic boundary conditions were employed using the CRYSTAL module implemented in the CHARMM program.
System equilibration was initiated with a 50-step SD and 50-step ABNR minimization followed by a 100 ps simulation in the NVT ensemble at 300 K during which mass-weighted harmonic restraints of 1.0 kcal/mol/Å were applied on the non-hydrogen atoms of AFGP. A 200 ps NPT simulation at 1 atm and 300 K followed the NVT simulation, wherein all the previous restraints were removed. In the NPT simulation, the center of mass of the AFGP was restrained near the origin by applying a harmonic restraint of 1.0 kcal/mol/Å using the MMFP module in CHARMM. The long-range electrostatic interactions were treated via the particle mesh Ewald method with a real-space cutoff of 12 Å, a kappa value of 0.34 Å–1, and a sixth-order spline.47Nonbond interaction lists were updated heuristically out to 16 Å with a force switch smoothing function from 10 to 12 Å used for the Lennard-Jones interactions.48 The Leapfrog integrator employing an integration time step of 1 fs was used in conjunction with the SHAKE algorithm to constrain all covalent bonds involving hydrogen atoms.49 The temperature was maintained at 300 K by a Nosé–Hoover heat bath with a thermal piston parameter of 2000 kcal mol–1 ps2.50 A constant pressure of 1 atm was controlled using the Langevin piston with a mass calculated using the equation Pmass = integer(system mass/50.0).51
HREX MD production simulations were performed using the REPDSTR module of a modified version of CHARMM c36a2.52 The HREX simulations were started from the equilibrated coordinates obtained after the 200 ps unbiased NPT simulation at 1 atm and 300 K. The same harmonic restraints used in the NPT runs were utilized in the HREX runs to constrain the AFGP at the center of the simulation box. An exchange between neighboring replicas was attempted every 1000 MD steps, and the coordinates were saved every 1 ps. Each replica was simulated for 10.5 ns, thereby amounting to a cumulative simulation time of 84.0 ns (10.5 ns × 8), and the trajectories from the first replica (unbiased, ground state replica) were used for subsequent analysis.
A combination of the two-dimensional (2D) dihedral grid-based energy correction map (CMAP) extension of the CHARMM force field and a Saxon–Woods potential was used as the biasing potential across the different replicas. Two CMAP biasing potentials were used, corresponding to the sugar ϕs/ψs and protein ϕ/ψ dihedral pairs to sample the conformational space of AFGP. Additionally, the Saxon–Woods potential was used to enhance the conformational sampling about the sugar χs dihedral in the Thr side chain.
where h = (n × −0.75) kcal/mol, with n going from 0 to 7 for replicas 1–8, p1 = 0.1, p2 = 0.3, and θref = 90°. The biasing potential CMAPs were obtained using an established protocol for glycopeptide O-linkages that has been reported in detail earlier and successfully applied in studying O-linked glycopeptides.20,21
To study the influence of AFGP on the structure of the surrounding solvent at a subfreezing temperature, additional HREX simulations were performed at 250 K using both the TIP5P and TIP4P-2005 water models.22,23 These simulations were initiated from representative structures from the largest clusters obtained by clustering the 10.5 ns unbiased 300 K HREX simulation trajectory using the peptide ϕ/ψ dihedrals. The same protocol described for the 300 K simulations was used to set up and run the 250 K simulations. The major differences were that the representative structures from the 300 K simulation selected on the basis of RMSD clustering (see Figures 2 and 3) were immersed in a water box (either TIP5P or TIP4P-2005 water model) pre-equilibrated at 250 K and the temperature in the remainder of the simulations was maintained at 250 K. For AFGP8, two HREX simulations were performed for 3 ns each amounting to a cumulative simulation time of 48.0 ns (3.0 ns × 2 × 8), while, for s-AFGP4, three HREX simulations were performed for 3 ns each amounting to a cumulative simulation time of 72 ns (3.0 ns × 3 × 8). The use of multiple simulations allows the solvent to reorganize around the different conformations of the glycopeptides, as initial calculations at 250 K showed the glycopeptides to maintain their starting conformations. The representative structures were also used to initiate 4 ns MD simulations at 250 and 300 K (two simulations for AFGP8 and three simulations for s-AFGP4 for both water models), which were used to calculate the H-bond autocorrelation function in Figure 7 and Figure S5 (Supporting Information) and the diffusion coefficient (Table S1, Supporting Information).
To delineate the influence of carbohydrates with respect to protein, HREX simulations at 300 and 250 K were also performed on the two peptides: AATAATPATAATPA and ATAATAATAATA. The protocol described to set up the 300 K AFGP simulations was used to set up the 300 K protein simulations. This included retaining the restraints on the protein ϕ/ψ to set up the initial protein geometry. Following equilibration, HREX MD simulations were performed for 2.0 ns, a cumulative sampling time of 16.0 ns (2.0 ns × 8) at 300 K. The 250 K HREX simulations (using both the TIP5P and TIP4P-2005 water models) were set up using the top representative structure obtained by clustering the first 1.0 ns of the 300 K unbiased replica simulation trajectory using the ϕ/ψ dihedrals. Simulations at 250 K were run for 1.0 ns, leading to a cumulative sampling time of 8.0 ns (1.0 ns × 8).
3D probability distributions of the selected bridge water oxygens (Figure 4) were constructed from snapshots output every 20 ps from the 300 K HREX trajectory of the unbiased ground state replica. These coordinates were binned into 1 Å × 1 Å × 1 Å cubic volume elements (voxels) of a grid spanning the entire system.
Acknowledgments
Financial support from the NIH (GM070855) is acknowledged. We thank Dr. E. Prabhu Raman, Dr. Jing Huang, and Dr. Dhilon Patel for helpful discussions.
Supporting Information Available
Figures showing selected radial distribution functions g(r) using the TIP5P and TIP4P-2005 water models, tetrahedral order parameter Qk from 250 K simulations using the TIP5P and TIP4P-2005 water models, and water–water H-bond autocorrelation functions from simulations using the TIP4P-2005 water model. Table showing diffusion coefficients. This material is available free of charge via the Internet at http://pubs.acs.org.
The authors declare no competing financial interest.
Funding Statement
National Institutes of Health, United States
Supplementary Material
References
- Garner J.; Harding M. M. Design and Synthesis of Antifreeze Glycoproteins and Mimics. ChemBioChem 2010, 11, 2489–2498. [DOI] [PubMed] [Google Scholar]
- Harding M. M.; Anderberg P. I.; Haymet A. D. ’Antifreeze’ Glycoproteins from Polar Fish. Eur. J. Biochem. 2003, 270, 1381–1392. [DOI] [PubMed] [Google Scholar]
- Yeh Y.; Feeney R. E. Antifreeze Proteins: Structures and Mechanisms of Function. Chem. Rev. 1996, 96, 601–618. [DOI] [PubMed] [Google Scholar]
- DeVries A. L.; Komatsu S. K.; Feeney R. E. Chemical and Physical Properties of Freezing Point-Depressing Glycoproteins from Antarctic Fishes. J. Biol. Chem. 1970, 245, 2901–2908. [PubMed] [Google Scholar]
- Komatsu S.; DeVries A. L.; Feeney R. E. Studies of the Structure of Freezing Point-Depressing Glycoproteins from an Antarctic Fish. J. Biol. Chem. 1970, 245, 2909–2913. [PubMed] [Google Scholar]
- Wu Y.; Banoub J.; Goddard S. V.; Kao M. H.; Fletcher G. L. Antifreeze Glycoproteins: Relationship between Molecular Weight, Thermal Hysteresis and the Inhibition of Leakage from Liposomes During Thermotropic Phase Transition. Comp. Biochem. Physiol., Part B: Biochem. Mol. Biol. 2001, 128, 265–273. [DOI] [PubMed] [Google Scholar]
- Lane A. N.; Hays L. M.; Feeney R. E.; Crowe L. M.; Crowe J. H. Conformational and Dynamic Properties of a 14 Residue Antifreeze Glycopeptide from Antarctic Cod. Protein Sci. 1998, 7, 1555–1563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lane A. N.; Hays L. M.; Tsvetkova N.; Feeney R. E.; Crowe L. M.; Crowe J. H. Comparison of the Solution Conformation and Dynamics of Antifreeze Glycoproteins from Antarctic Fish. Biophys. J. 2000, 78, 3195–3207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ebbinghaus S.; Meister K.; Born B.; DeVries A. L.; Gruebele M.; Havenith M. Antifreeze Glycoprotein Activity Correlates with Long-Range Protein-Water Dynamics. J. Am. Chem. Soc. 2010, 132, 12210–12211. [DOI] [PubMed] [Google Scholar]
- Meister K.; Ebbinghaus S.; Xu Y.; Duman J. G.; DeVries A.; Gruebele M.; Leitner D. M.; Havenith M. Long-Range Protein-Water Dynamics in Hyperactive Insect Antifreeze Proteins. Proc. Natl. Acad. Sci. U. S. A. 2013, 110, 1617–1622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nutt D. R.; Smith J. C. Dual Function of the Hydration Layer around an Antifreeze Protein Revealed by Atomistic Molecular Dynamics Simulations. J. Am. Chem. Soc. 2008, 130, 13066–13073. [DOI] [PubMed] [Google Scholar]
- Tachibana Y.; Fletcher G. L.; Fujitani N.; Tsuda S.; Monde K.; Nishimura S. Antifreeze Glycoproteins: Elucidation of the Structural Motifs That Are Essential for Antifreeze Activity. Angew. Chem., Int. Ed. Engl. 2004, 43, 856–862. [DOI] [PubMed] [Google Scholar]
- Wilkinson B. L.; Stone R. S.; Capicciotti C. J.; Thaysen-Andersen M.; Matthews J. M.; Packer N. H.; Ben R. N.; Payne R. J. Total Synthesis of Homogeneous Antifreeze Glycopeptides and Glycoproteins. Angew. Chem., Int. Ed. Engl. 2012, 51, 3606–3610. [DOI] [PubMed] [Google Scholar]
- Nagel L.; Budke C.; Dreyer A.; Koop T.; Sewald N. Antifreeze Glycopeptide Diastereomers. Beilstein J. Org. Chem. 2012, 8, 1657–1667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagel L.; Budke C.; Erdmann R. S.; Dreyer A.; Wennemers H.; Koop T.; Sewald N. Influence of Sequential Modifications and Carbohydrate Variations in Synthetic Afgp Analogues on Conformation and Antifreeze Activity. Chem.—Eur. J. 2012, 18, 12783–12793. [DOI] [PubMed] [Google Scholar]
- Nagel L.; Plattner C.; Budke C.; Majer Z.; DeVries A.; Berkemeier T.; Koop T.; Sewald N. Synthesis and Characterization of Natural and Modified Antifreeze Glycopeptides: Glycosylated Foldamers. Amino Acids 2011, 41, 719–732. [DOI] [PubMed] [Google Scholar]
- Bouvet V. R.; Lorello G. R.; Ben R. N. Aggregation of Antifreeze Glycoprotein Fraction 8 and Its Effect on Antifreeze Activity. Biomacromolecules 2006, 7, 565–571. [DOI] [PubMed] [Google Scholar]
- Tam R. Y.; Rowley C. N.; Petrov I.; Zhang T.; Afagh N. A.; Woo T. K.; Ben R. N. Solution Conformation of C-Linked Antifreeze Glycoprotein Analogues and Modulation of Ice Recrystallization. J. Am. Chem. Soc. 2009, 131, 15745–15753. [DOI] [PubMed] [Google Scholar]
- Nishimura S.; Nagahori N.; Takaya K.; Tachibana Y.; Miura N.; Monde K. Direct Observation of Sugar-Protein, Sugar-Sugar, and Sugar-Water Complexes by Cold-Spray Ionization Time-of-Flight Mass Spectrometry. Angew. Chem., Int. Ed. Engl. 2005, 44, 571–575. [DOI] [PubMed] [Google Scholar]
- Mallajosyula S. S.; Adams K. M.; Barchi J. J.; MacKerell A. D. Jr. Conformational Determinants of the Activity of Antiproliferative Factor Glycopeptide. J. Chem. Inf. Model. 2013, 53, 1127–1137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mallajosyula S. S.; MacKerell A. D. Jr. Influence of Solvent and Intramolecular Hydrogen Bonding on the Conformational Properties of O-Linked Glycopeptides. J. Phys. Chem. B 2011, 115, 11215–11229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahoney M. W.; Jorgensen W. L. A Five-Site Model for Liquid Water and the Reproduction of the Density Anomaly by Rigid, Nonpolarizable Potential Functions. J. Chem. Phys. 2000, 112, 8910–8922. [Google Scholar]
- Abascal J. L. F.; Vega C. A General Purpose Model for the Condensed Phases of Water: Tip4p/2005. J. Chem. Phys. 2005, 123, 234505-1–234505-12. [DOI] [PubMed] [Google Scholar]
- Coltart D. M.; Royyuru A. K.; Williams L. J.; Glunz P. W.; Sames D.; Kuduk S. D.; Schwarz J. B.; Chen X. T.; Danishefsky S. J.; Live D. H. Principles of Mucin Architecture: Structural Studies on Synthetic Glycopeptides Bearing Clustered Mono-, Di-, Tri-, and Hexasaccharide Glycodomains. J. Am. Chem. Soc. 2002, 124, 9833–9844. [DOI] [PubMed] [Google Scholar]
- Corzana F.; Busto J. H.; Jimenez-Oses G.; Asensio J. L.; Jimenez-Barbero J.; Peregrina J. M.; Avenoza A. New Insights into Alpha-Galnac-Ser Motif: Influence of Hydrogen Bonding Versus Solvent Interactions on the Preferred Conformation. J. Am. Chem. Soc. 2006, 128, 14640–14648. [DOI] [PubMed] [Google Scholar]
- Corzana F.; Busto J. H.; Jimenez-Oses G.; Garcia de Luis M.; Asensio J. L.; Jimenez-Barbero J.; Peregrina J. M.; Avenoza A. Serine Versus Threonine Glycosylation: The Methyl Group Causes a Drastic Alteration on the Carbohydrate Orientation and on the Surrounding Water Shell. J. Am. Chem. Soc. 2007, 129, 9458–9467. [DOI] [PubMed] [Google Scholar]
- Lee S. L.; Debenedetti P. G.; Errington J. R. A Computational Study of Hydration, Solution Structure, and Dynamics in Dilute Carbohydrate Solutions. J. Chem. Phys. 2005, 122, 204511-1–204511-10. [DOI] [PubMed] [Google Scholar]
- Errington J. R.; Debenedetti P. G. Relationship between Structural Order and the Anomalies of Liquid Water. Nature 2001, 409, 318–321. [DOI] [PubMed] [Google Scholar]
- Ahmed A. I.; Yeh Y.; Osuga Y. Y.; Feeney R. E. Antifreeze Glycoproteins from Antarctic Fish. Inactivation by Borate. J. Biol. Chem. 1976, 251, 3033–3036. [PubMed] [Google Scholar]
- Feeney R. E.; Burcham T. S.; Yeh Y. Antifreeze Glycoproteins from Polar Fish Blood. Annu. Rev. Biophys. Biophys. Chem. 1986, 15, 59–78. [DOI] [PubMed] [Google Scholar]
- Ahmed A. I.; Osuga D. T.; Feeney R. E. Antifreeze Glycoprotein from an Antarctic Fish. Effects of Chemical Modifications of Carbohydrate Residues on Antifreeze and Antilectin Activities. J. Biol. Chem. 1973, 248, 8524–8527. [PubMed] [Google Scholar]
- Geoghegan K. F.; Osuga D. T.; Ahmed A. I.; Yeh Y.; Feeney R. E. Antifreeze Glycoproteins from Polar Fish. Structural Requirements for Function of Glycopeptide 8. J. Biol. Chem. 1980, 255, 663–667. [PubMed] [Google Scholar]
- Luzar A.; Chandler D. Hydrogen-Bond Kinetics in Liquid Water. Nature 1996, 359, 55–57. [Google Scholar]
- Liu S.; Ben R. N. C-Linked Galactosyl Serine Afgp Analogues as Potent Recrystallization Inhibitors. Org. Lett. 2005, 7, 2385–2388. [DOI] [PubMed] [Google Scholar]
- Czechura P.; Tam R. Y.; Dimitrijevic E.; Murphy A. V.; Ben R. N. The Importance of Hydration for Inhibiting Ice Recrystallization with C-Linked Antifreeze Glycoproteins. J. Am. Chem. Soc. 2008, 130, 2928–2929. [DOI] [PubMed] [Google Scholar]
- Brooks B. R.; Brooks C. L. 3rd; MacKerell A. D. Jr.; Nilsson L.; Petrella R. J.; Roux B.; Won Y.; Archontis G.; Bartels C.; Boresch S.; et al. Charmm: The Biomolecular Simulation Program. J. Comput. Chem. 2009, 30, 1545–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKerell A. D. Jr.; Bashford D.; Bellott; Dunbrack R. L.; Evanseck J. D.; Field M. J.; Fischer S.; Gao J.; Guo H.; Ha S.; et al. All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [DOI] [PubMed] [Google Scholar]
- MacKerell A. D. Jr.; Feig M.; Brooks C. L. 3rd. Extending the Treatment of Backbone Energetics in Protein Force Fields: Limitations of Gas-Phase Quantum Mechanics in Reproducing Protein Conformational Distributions in Molecular Dynamics Simulations. J. Comput. Chem. 2004, 25, 1400–1415. [DOI] [PubMed] [Google Scholar]
- Guvench O.; Greene S. N.; Kamath G.; Brady J. W.; Venable R. M.; Pastor R. W.; MacKerell A. D. Jr. Additive Empirical Force Field for Hexopyranose Monosaccharides. J. Comput. Chem. 2008, 29, 2543–2564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guvench O.; Hatcher E. R.; Venable R. M.; Pastor R. W.; MacKerell A. D. Jr. Charmm Additive All-Atom Force Field for Glycosidic Linkages between Hexopyranoses. J. Chem. Theory Comput. 2009, 5, 2353–2370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hatcher E.; Guvench O.; MacKerell A. D. Jr. Charmm Additive All-Atom Force Field for Aldopentofuranoses, Methyl-Aldopentofuranosides, and Fructofuranose. J. Phys. Chem. B 2009, 113, 12466–12476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hatcher E.; Guvench O.; MacKerell A. D. Jr. Charmm Additive All-Atom Force Field for Acyclic Polyalcohols, Acyclic Carbohydrates and Inositol. J. Chem. Theory Comput. 2009, 5, 1315–1327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raman E. P.; Guvench O.; MacKerell A. D. Jr. Charmm Additive All-Atom Force Field for Glycosidic Linkages in Carbohydrates Involving Furanoses. J. Phys. Chem. B 2010, 114, 12981–12994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guvench O.; Mallajosyula S. S.; Raman E. P.; Hatcher E.; Vanommeslaeghe K.; Foster T. J.; Jamison F. W. 2nd; MacKerell A. D. Jr. Charmm Additive All-Atom Force Field for Carbohydrate Derivatives and Its Utility in Polysaccharide and Carbohydrate-Protein Modeling. J. Chem. Theory Comput. 2011, 7, 3162–3180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mallajosyula S. S.; Guvench O.; Hatcher E.; MacKerell A. D. Jr. Charmm Additive All-Atom Force Field for Phosphate and Sulfate Linked to Carbohydrates. J. Chem. Theory Comput. 2012, 8, 759–776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Becker O. M., MacKerell A. D. Jr., Roux B., Watanabe M., Eds. Computational Biochemistry and Biophysics; Marcel-Dekker, Inc.: New York, 2001. [Google Scholar]
- Darden T.; York D.; Pedersen L. Particle Mesh Ewald: An N-Log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar]
- Steinbach P. J.; Brooks B. R. New Spherical-Cutoff Methods for Long-Range Forces in Macromolecular Simulation. J. Comput. Chem. 1994, 15, 667–683. [Google Scholar]
- Ryckaert J.-P.; Ciccotti G.; Berendsen H. J. C. Numerical Integration of the Cartesian Equations of Motion of a System with Constraints: Molecular Dynamics of N-Alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar]
- Nose S. A Unified Formulation of the Constant Temperature Molecular Dynamics Methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar]
- Feller S. E.; Zhang Y.; Pastor R. W.; Brooks B. R. Constant Pressure Molecular Dynamics Simulation: The Langevin Piston Method. J. Chem. Phys. 1995, 103, 4613–4621. [Google Scholar]
- Woodcock H. L.; Hodošček M.; Gilbert A. T. B.; Gill P. M. W.; Schaefer H. F.; Brooks B. R. Interfacing Q-Chem and Charmm to Perform QM/MM Reaction Path Calculations. J. Comput. Chem. 2007, 28, 1485–1502. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.