Giant and switchable surface activity of liquid metal via surface oxidation

Significance

We present a method to control the interfacial energy of a liquid metal via electrochemical deposition (or removal) of an oxide layer on its surface. Unlike conventional surfactants, this approach can tune the interfacial tension of a metal significantly (from ∼7× that of water to near zero), rapidly, and reversibly using only modest voltages. These properties can be harnessed to induce previously unidentified electrohydrodynamic phenomena for manipulating liquid metal alloys based on gallium, which may enable shape-reconfigurable metallic components in electronic, electromagnetic, and microfluidic devices without the use of toxic mercury. The results also suggest that oxides—which are ubiquitous on most metals and semiconductors—may be harnessed to lower interfacial energy between dissimilar materials.

Abstract

We present a method to control the interfacial tension of a liquid alloy of gallium via electrochemical deposition (or removal) of the oxide layer on its surface. In sharp contrast with conventional surfactants, this method provides unprecedented lowering of surface tension (∼500 mJ/m² to near zero) using very low voltage, and the change is completely reversible. This dramatic change in the interfacial tension enables a variety of electrohydrodynamic phenomena. The ability to manipulate the interfacial properties of the metal promises rich opportunities in shape-reconfigurable metallic components in electronic, electromagnetic, and microfluidic devices without the use of toxic mercury. This work suggests that the wetting properties of surface oxides—which are ubiquitous on most metals and semiconductors—are intrinsic “surfactants.” The inherent asymmetric nature of the surface coupled with the ability to actively manipulate its energetics is expected to have important applications in electrohydrodynamics, composites, and melt processing of oxide-forming materials.

The ability to control interfacial energy is an effective approach for manipulating fluids at submillimeter length scales due to the dominance of these forces at these small length scales and can be accomplished using a wide variety of methods including temperature (1, 2), light (3), surface chemistry (4–6), or electrostatics (7). These techniques are effective for many organic and aqueous solutions, but they have limited utility for manipulating high interfacial tension liquids, such as liquid metals. Liquid metals offer new opportunities for soft, stretchable, and shape-reconfigurable electronic and electromagnetic components (8–12). Although it is possible to mechanically manipulate these fluids at submillimeter length scales (13), electrical methods (14, 15) are preferable due to the ease of miniaturization, control, and integration. Existing electrohydrodynamic techniques can modestly tune the interfacial tension of metals but either limit the shape of liquid metals to plugs (e.g., continuous electrowetting) (16) or necessitate excessive potentials to achieve actuation on a limited scale (e.g., electrowetting) (17). Here, we demonstrate that the surface oxide on a liquid metal can be formed or removed in situ using low voltages (<1 V) and behaves like a surfactant that can significantly lower its interfacial tension from ∼500 mJ/m² to near zero. In contrast, conventional molecular surfactants effect only modest changes in interfacial tension (changes of ∼20–50 mJ/m²) and are difficult to remove rapidly on demand (18). Our approach relies on the electrical control of surface oxidation, which is simple, requires minimal energy, and provides rapid and reversible control of interfacial tension over an enormous range, independent of the properties of the substrate upon which it rests. Furthermore, this method avoids the use of toxic mercury and the ensuing modulation of surface tension is compatible with microfluidics.

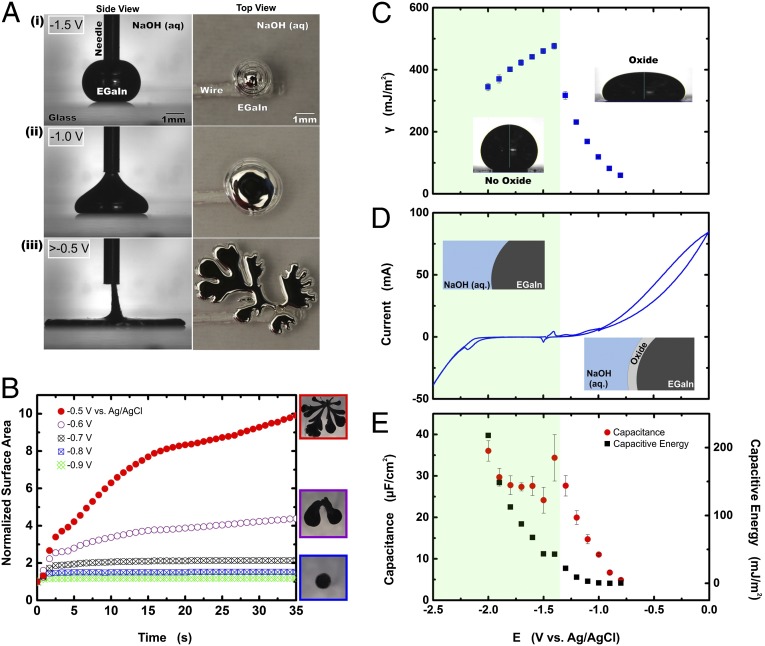
Fig. 1A contains a series of images that illustrate how liquid metal alloys of gallium [here, eutectic gallium indium (EGaIn), 75 wt % Ga, 25 wt % In (19)] spread dramatically in electrolyte in response to modest voltages (Movies S1 and S2). Fig. 1 reports the potentials relative to a saturated Ag–AgCl reference electrode in which the open-circuit potential is approximately −1.5 V. Spreading occurs in a variety of electrolytes, over a wide range of pH (over all pH attempted from 0 to 14), with and without dissolved oxygen, over a range of electrolyte concentrations, and on a wide variety of substrates including glass, Teflon, polystyrene, and tungsten. The spreading observed here has been reported previously in the literature, but was attributed to electrocapillarity (20). We show here that the mechanism goes beyond electrocapillarity and the electrochemical formation of the surface oxide plays an essential role.

Fig. 1.

Spreading enabled by a surface oxide. (A) Oxidative spreading of a bead of liquid metal in 1 M NaOH solution. (Left) A needle serves as a top electrical contact to the droplet. (Right) A wire serves as a bottom electrical contact to the droplet (see Fig. S2 for details). (A, i) The drop assumes a spherical shape initially due to its large surface tension; (A, ii) upon application of an oxidative potential, the metal assumes a new equilibrium shape; (A, iii) above a critical potential, the metal flattens and spreads without bound and ultimately forms fingering patterns that further increase its surface area and destabilize the metal. (B–D) The unshaded region denotes oxidative potentials. (B) The areal footprint of a drop of EGaIn as a function of time and potential identifies the critical potential above which spreading occurs without bound (solid circles) and below which the droplet adopts equilibrium shapes (hashed symbols). (C) An electrocapillary curve of EGaIn measured by sessile drop profile in 1 M NaOH. (D) A cyclic voltammogram of EGaIn. (E) The measured capacitance and calculated capacitive energy of EGaIn from impedance spectroscopy.

Fig. 1B plots the areal footprint of a spreading EGaIn drop as a function of time and potential (for example, see Fig. S1). The shape of the metal represents a balance between the interfacial tension and gravity. Lower interfacial tensions therefore correspond to an increased areal footprint. Above a critical potential (∼−0.6 V relative to a saturated Ag–AgCl reference electrode), the metal spreads initially as a disk that eventually breaks into a fingering morphology (Fig. 1 A, iii) that continues to increase in area with respect to time until it becomes unstable and separates from the electrode entirely. Below this critical potential (i.e., at potentials that are less oxidative), the drop adopts equilibrium shapes, as indicated by the plateaus in the normalized area in Fig. 1B.

The change in surface tension of a liquid drop with respect to potential—that is, electrocapillarity—has been used previously to alter the shape of liquid metals (21), albeit less dramatically than that seen in Fig. 1A. Electrocapillarity lowers the interfacial tension of the metal γ from its maximum value γ₀ due to capacitive effects arising from the potential E as shown in Eq. 1 (22),

$$\gamma ={\gamma }_0-\frac{1}{2}C{(E-E_{PZC})}^2,$$ [1]

where C is the capacitance per unit area and E_PZC is the potential of zero charge (PZC). The PZC is the potential at which the excess surface charge is zero and the surface tension is at its maximum value. One implication of Eq. 1 is that any change in potential from the E_PZC, whether positive or negative, will result in a symmetric decrease in the surface tension. In contrast, the spreading in Fig. 1A only occurs at oxidative potentials. Normally, undesirable electrochemical reactions, such as electrolysis, limit electrocapillarity to a small range of potentials (E) and thus a modest range of interfacial tension, whereas here the electrochemical reactions further lower the interfacial tension.

Fig. 1C plots the interfacial tension of the metal measured by analyzing the shape of multiple sessile droplets (viewed from the side) versus potential. Between −2 and −1.4 V, in the absence of the oxide or electrochemical reactions, a droplet of EGaIn behaves in a manner that is consistent with classic electrocapillarity. Fitting this portion of the curve yields a maximum surface tension of 509 mJ/m² and an E_PZC of −0.91 V, consistent with previous electrocapillary measurements (23). At potentials more oxidative than −1.4 V, the oxide layer begins to form on the surface (24), as confirmed by the cyclic voltammogram in Fig. 1D. This oxidation causes a sudden and substantial drop in the surface tension, despite the decrease of measured capacitance and calculated capacitive energy over this potential range, as shown in Fig. 1E.

The remarkable implication of the data summarized in Fig. 1 is that the oxide layer acts like a surfactant on the surface of the metal. In the absence of the oxide, the interfacial tension is large, as expected for a metal in contact with electrolyte. When the oxide forms, it replaces this high-energy interface with two new interfaces: metal–metal oxide and metal oxide–electrolyte. Most oxides, including gallium oxide, form hydroxyl groups on their exterior surface, rendering them hydrophilic (confirmed by a near-zero contact angle of water on the oxide surface). The interior surface of gallium oxide, however, consists of Ga atoms (25). The absence of any notable change in contact angle between the droplet and substrate during spreading and the independence of spreading relative to substrate composition further suggests spreading is due primarily to liquid metal–oxide–electrolyte interactions.

Oxygen adsorption is known to lower the interfacial tension of molten metals as a function of the partial pressure of oxygen (26). At partial pressures in which the oxide forms fully, the interfacial tension of the metal becomes challenging to measure because it is encased in an oxide with mechanical properties that prevent the liquid from adopting an equilibrium shape. Alloys of gallium are no exception; the oxide can stabilize the metal in nonequilibrium shapes (27) despite being quite thin [∼1 nm in dry air (25, 28, 29)]. To achieve spreading, an electrochemical driving force is necessary. Although it is conceivable that spreading could be due to mechanical stresses arising from oxide growth, the ability of the drop to return to equilibrium shapes after physical perturbation at subcritical potentials (Movie S3), the lack of hysteresis in the “electrocapillary” curve, and the retardation of spreading by the formation of thicker oxides in pH neutral electrolytes (Movie S4), suggest otherwise. In NaOH(aq.), dissolution of the oxide (30) competes with the electrochemical formation of the oxide (31), which likely allows the metal to behave as a fluid with minimal mechanical hindrance.

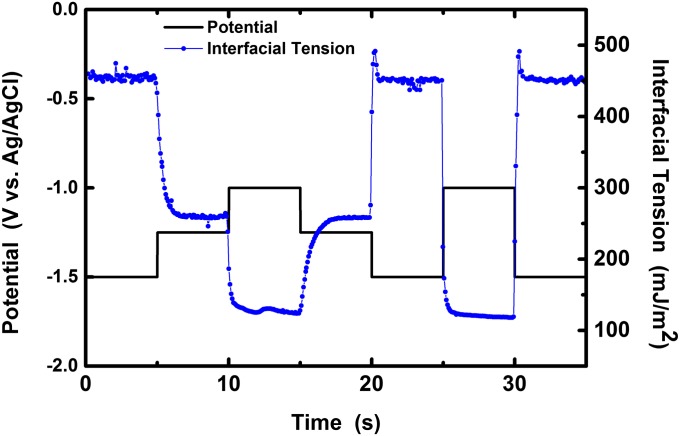
The change in surface tension in response to potential is completely reversible, with limited hysteretic effects. Fig. 2 demonstrates the ability to reversibly and rapidly switch the interfacial tension over a large range by only varying the potential modestly in steps of 0.25 or 0.5 V. In each case, the drop returns to the expected interfacial tension in <1 s, despite the kinetics of oxide growth and dissolution.

Fig. 2.

Interfacial tension of the metal may be tuned dramatically, rapidly, and reversibly in response to small changes in potential, as shown using multistep chronoamperometry of a sessile EGaIn drop in 1 M NaOH. Increasing the electrochemical potential results in a corresponding decrease of the interfacial tension, consistent with the values in Fig. 1C.

The interfacial tension undergoes a large step change when the oxide forms at −1.4 V, but continues to decrease with increased potential according to Fig. 1C. The dynamic interfacial behavior in this regime is difficult to analyze, but the decrease in the measured capacitance values from −1.4 to −0.7 V suggests that (i) electrocapillary behavior cannot solely explain the decrease in interfacial tension with respect to potential and (ii) the effectiveness of the oxide for separating the electrolyte from the metal likely improves with respect to potential.

At potentials above the critical voltage (−0.6 V), two self-consistent observations suggest behavior resembling that of very low surface tension: (i) the area increases without bound until it becomes unstable, and (ii) the interfacial tension projects toward zero at this critical voltage (compare Fig. 1C). It is difficult to measure the interfacial tension beyond −0.6 V because the metal spreads without ever reaching an equilibrium shape and sessile drop analysis fails. To approximate the interfacial tension at potentials greater than −0.6 V, we use a scaling analysis based on the capillary length because the shape of the metal represents a balance between gravity and interfacial tension. Comparing the critical dimension (height) during spreading to the critical dimension at voltages of known tension provides an estimate, as described in SI Materials and Methods. First, comparing the capillary length of the oxide-coated metal when it is nearly spherical (−1.3 V) to when it spreads critically (−0.6 V) suggests the interfacial tension is ∼2 mN/m at −0.6 V. Likewise, comparing the capillary length of the oxide-coated metal at the last measurable point in Fig. 1C (i.e., −0.7 V) to the critical voltage (−0.6 V) also suggests the interfacial tension is ∼2 mN/m at −0.6 V. Although these two values are above zero, we refer to them as “near zero” because (i) the values are only estimates and are remarkably low considering the enormous tension of the bare metal, (ii) the metal never reaches an equilibrium shape at this potential, and (iii) the oxide may provide some minor mechanical impediment to spreading, in which case the liquid tension would be even lower.

The spreading of EGaIn at oxidative potentials can be exploited to manipulate the shape of the metal in both closed and open systems. For example, oxidative potentials can induce the metal to flow uphill into capillaries containing electrolyte, as shown in Fig. 3A (Movie S5). Removal of the oxide chemically or electrochemically reverses the direction of flow, making it possible to impart reversible flow. Likewise, the position of a counterelectrode in electrolyte directs the movement of the metal in an open channel, as shown in Fig. 3B (Movie S6), because the spreading metal moves preferentially toward the counterelectrode. Oxidative potentials can also cause the metal to form metastable fibers as it extrudes from a syringe, as shown in Fig. 3D (Movie S7). In the absence of applied potential, metal pumped out of the end of a capillary forms beads that fall periodically due to the force of gravity, as shown in Fig. 3C.

Fig. 3.

(A) Inducing liquid metal into an upward-tilted capillary channel (∼0.9 mm i.d.) by application of a voltage in the presence of 1 M NaOH. (B) Controlling the shape and direction of a metal drop into an open T-shaped Plexiglas channel submerged in 1 M NaOH solution using only voltage. Switching the position of the counterelectrode at different points (B, ii-iv), guides the direction of the metal droplet. (C) Side view of a small droplet of EGaIn pumped out of a 0.5-mm-i.d. polymer tube at 20-mL/h in 1 M NaOH. The metal forms droplets in the absence of potential. (D) Formation of an oxide-coated liquid metal fiber coming out of the tube at 5 V.

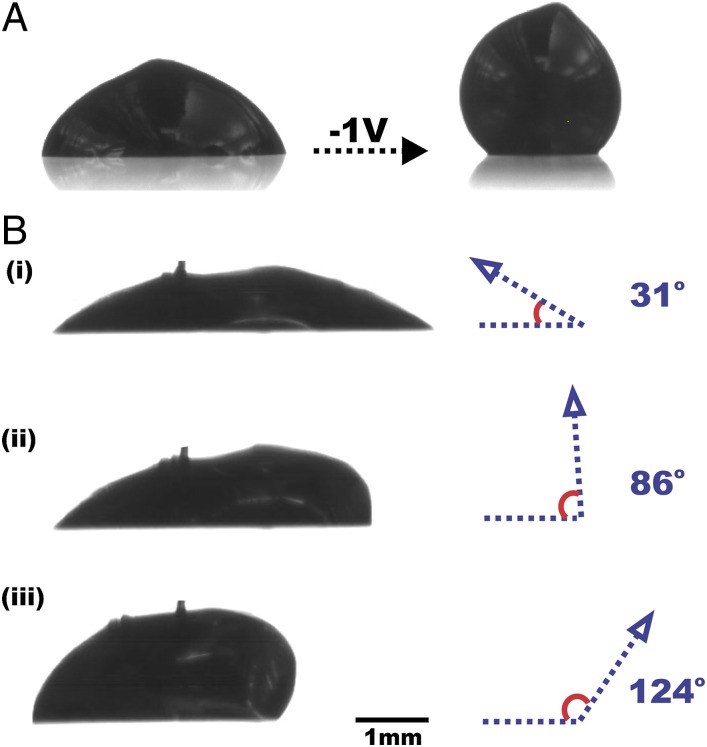
It is also possible to remove the oxide skin using modest reductive potentials (e.g., −1 V applied) to return the metal to a state of large interfacial tension, induce capillary behavior, change the contact angle, and alter the rheological properties on demand; we call this behavior “recapillarity” (reductive capillarity). Before reduction, the oxide layer stabilizes the metal droplet in a nonequilibrium shape in pH-neutral electrolytes and gives it non-Newtonian rheological properties (32). In the absence of the stabilizing skin, the metal becomes Newtonian, decreases its footprint, and increases its contact angle (Fig. 4A). The experiments reported in Fig. 4 began by placing a droplet of the metal on a dry glass substrate before submerging the substrate in pH-neutral electrolyte. The presence of the oxide pins the drop to the dry substrate and allows the drop to be physically manipulated to a low initial contact angle before applying potential. The ability to mechanically manipulate the contact angle is indicative of the hysteretic nature of the wetting of the oxide-coated metal on dry surfaces (33). Removing the oxide allows the metal to dewet the substrate and return to an equilibrium contact angle. Recapillarity can turn this dewetting process on or off by electrochemically removing the oxide in pH-neutral solutions. Dewetting can occur asymmetrically by removing oxide preferentially from one side of the drop. Fig. 4B shows sequential images of a drop of metal in which the contact angle changes asymmetrically from 31° to 86° to 124° incrementally by inducing recapillarity in discrete steps on one side of the drop (Movie S8). The contact angle on the other side of the drop increases due to the combination of conservation of mass in the drop and the ability of the underlying oxide to pin the drop to the substrate.

Fig. 4.

Recapillarity can manipulate the shape and local contact angle of droplets placed on dry substrates. (A) A droplet of liquid metal with a surface oxide (Left) supported by a glass slide. Electrochemical reduction of the oxide causes the metal to bead up (Right). Removal of the electrode before imaging creates the lobe on the top of the drop. (B) Three sequential side views (B, i–iii) of an EGaIn drop that asymmetrically dewets a glass slide in deionized water upon application of reductive potentials relative to a counterelectrode placed on the right side of the drop. Recapillarity causes the metal to move away from the anode, which is outside the frame of the image. The cathode gently touches the top of the drop to minimize perturbation of the shape of the metal.

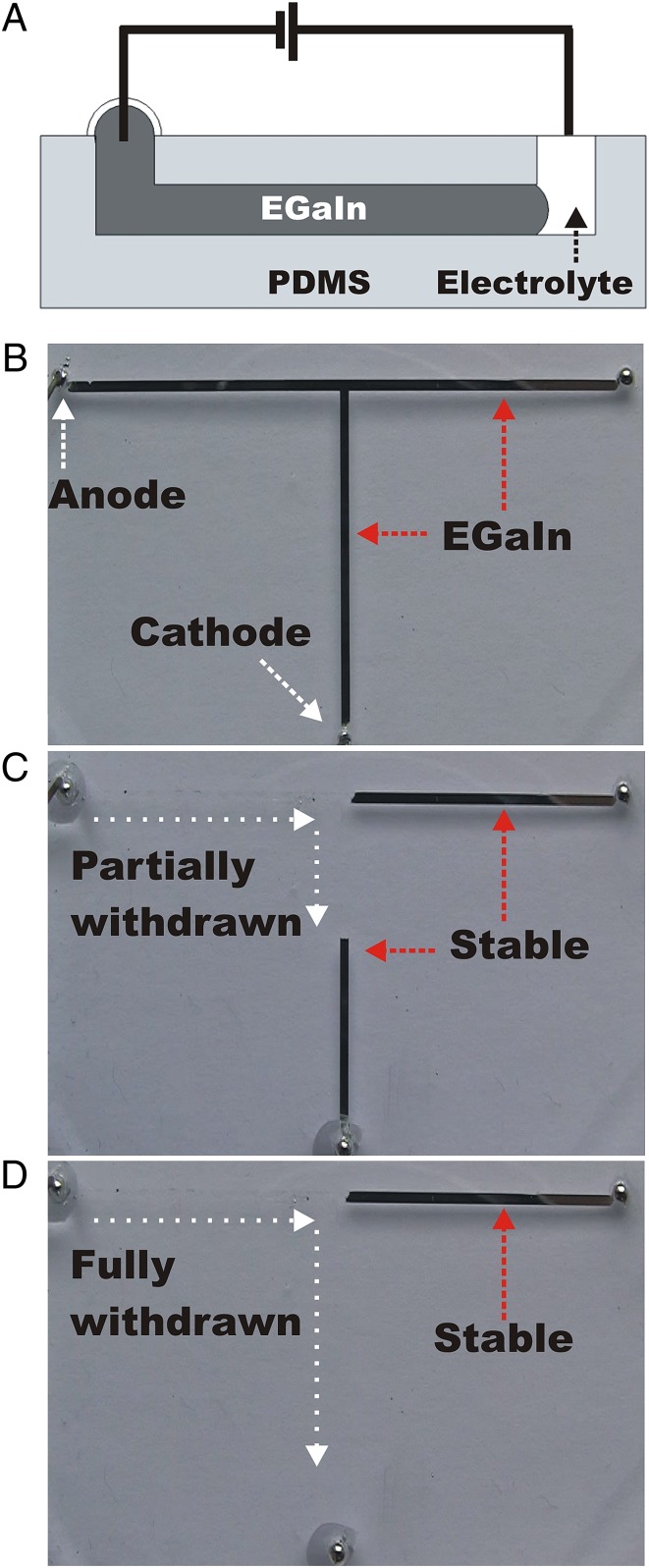
In the absence of potential, the oxide mechanically stabilizes the metal in microchannels (Fig. 5B). The adhesion of the oxide to the walls of dry channels makes it difficult to remove the metal by pressure differentials without leaving residue (34). In contrast, recapillarity induces liquid metal to withdraw controllably, smoothly, and rapidly (up to 20 cm/s) from microchannels via capillary action without leaving metal and oxide residue (Fig. 5 and Movie S9). The use of a pH-neutral electrolyte (NaF) ensures that segments of the metal that are not in the electrical path remain stable because of the presence of oxide skin (Fig. 5C).

Fig. 5.

Recapillarity-induced withdrawal of liquid metal from microchannels. (A) The electrochemical reduction of gallium oxide in pH-neutral electrolyte induces retreat of the metal from the channel by applying a reductive potential. (B) Top-down photograph of a T-shaped microfluidic channel (1 mm wide, 100 µm tall, 65 mm long horizontally). The surface oxide stabilizes the liquid metal in the channel. (C) A reductive bias (−1 V) applied to the metal relative to a drop of electrolyte (0.01 M NaF) at the anode removes the oxide and the liquid metal retreats toward the cathode. (D) The metal continues to withdraw until the applied voltage ceases. Metal that is not in the electrical pathway remains stable.

This paper demonstrates that surface oxides behave as excellent surfactants for metals and may be removed or deposited to rapidly and reversibly tune the interfacial tension of a low-toxicity liquid metal from ∼500 mJ/m² to near zero using modest voltages. This capability enables previously unidentified types of electrohydrodynamic phenomena to manipulate the shape of metal, which is attractive for a wide range of applications including microelectromechanical systems (MEMS) switches and conductive microcomponents (35), microactuators and pumps (36), adaptive electronic skins (37), tunable antennas and apertures (38, 39), fluidic optical components and displays (40, 41), field-programmable circuits (42), and metamaterials with reversible cloaking. The necessity of electrolyte and the reliance on electrochemical reactions may present some practical limitations for long-term switchability, although batteries operate with similar restrictions. The spreading behavior induced by a surface oxide provides the most significant evidence to date that buried oxide interfaces—which exist ubiquitously on most metals and semiconductors, yet are difficult to probe—lower interfacial energy of the underlying substrate significantly. The ability to rapidly remove and deposit oxides on a wide range of materials may enable new methods to control interfacial phenomena on both liquids and solids.

Materials and Methods

Additional details may be found in SI Materials and Methods.

Cyclic Voltammetry.

Electrochemical measurements (i.e., cyclic voltammetry and electrochemical impedance spectroscopy) were made using a Bio-Logic SP-200 potentiostat. A saturated Ag–AgCl reference electrode and a platinum mesh counterelectrode were used in all of the experiments, with copper acting as the connection to the EGaIn working electrode. Unless otherwise stated, all experiments took place in 1 M NaOH.

Spreading Area.

EGaIn drops of ∼30 μL were placed in a plastic Petri dish filled with 1 M NaOH. A copper wire was connected to the top of the drop, and a video camera was placed underneath the transparent Petri dish. Oxidative potentials were applied from −1.4 to −0.5 V vs. the reference electrode, in 100-mV increments.

Interfacial Tension.

The interfacial tension was determined as a function of potential by using the potentiostat in conjunction with a goniometer (First Ten Angstroms 1000B). At potentials more positive than −0.7 V, the shape of the EGaIn drop flattened to such an extent that interfacial tension could no longer be estimated using the goniometer, although the metal did continue to spread until it disconnected from the electrode.

Capacitance.

The capacitance was measured by electrochemical impedance spectroscopy (EIS). An EIS scan was performed at each potential used in the interfacial tension measurements, from 200 kHz to 1 Hz. Fitting software determined the double-layer capacitance from the resulting Nyquist plots (examples of which can be seen in Fig. S3).