Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2014 Sep 9;136(40):14215–14222. doi: 10.1021/ja507809w

Heterodimetallic [LnLn′] Lanthanide Complexes: Toward a Chemical Design of Two-Qubit Molecular Spin Quantum Gates

David Aguilà †, Leoní A Barrios †, Verónica Velasco †, Olivier Roubeau ‡, Ana Repollés ‡, Pablo J Alonso ‡, Javier Sesé §, Simon J Teat ∥, Fernando Luis ‡,*, Guillem Aromí †,*
PMCID: PMC4195387  PMID: 25203521

Abstract

graphic file with name ja-2014-07809w_0007.jpg

A major challenge for realizing quantum computation is finding suitable systems to embody quantum bits (qubits) and quantum gates (qugates) in a robust and scalable architecture. An emerging bottom-up approach uses the electronic spins of lanthanides. Universal qugates may then be engineered by arranging in a molecule two interacting and different lanthanide ions. Preparing heterometallic lanthanide species is, however, extremely challenging. We have discovered a method to obtain [LnLn′] complexes with the appropriate requirements. Compound [CeEr] is deemed to represent an ideal situation. Both ions have a doubly degenerate magnetic ground state and can be addressed individually. Their isotopes have mainly zero nuclear spin, which enhances the electronic spin coherence. The analogues [Ce2], [Er2], [CeY], and [LaEr] have also been prepared to assist in showing that [CeEr] meets the qugate requirements, as revealed through magnetic susceptibility, specific heat, and EPR. Molecules could now be used for quantum information processing.

Introduction

Processing information with quantum states is expected to outperform current computation technologies in some specific tasks.1 The main challenge continues to be finding suitable, robust, and scalable physical systems for its implementation. Individual spins are natural candidates to realize the basic information units of a quantum computer, that is, the qubits.1 Molecules carrying several, individually addressable, spin qubits can perform as quantum sensors,2 with sensitivities exceeding those of most powerful classical devices, or even as quantum processors, able to implement simple quantum algorithms. The first “quantum calculation” was, in fact, carried out using the 13C and 1H nuclear spins of chloroform (CHCl3).3 Because nuclear spins are, however, very difficult to initialize, such computations are performed on distributions of thermally populated nuclear spin states (NMR quantum computation is, for this reason, often termed “ensemble quantum computation”) rather than on individual quantum states, which obscures their interpretation and limits their usefulness. Electron spins can, by contrast, be efficiently initialized by the application of sufficiently strong magnetic fields at low temperatures.4 For this reason, a lanthanide ion with a doubly degenerate magnetic ground state appears as a convenient realization of a spin qubit.5

Within this framework, a promising approach toward realizing multiqubit logic gates, such as the paradigmatic universal CNOT gate (see Scheme 1), is by chemically engineering molecules holding and weakly coupling selected lanthanide atoms. Coordination chemistry offers the possibility of designing multimetallic molecular architectures with predetermined structures.6 However, given the very close chemical reactivities of all lanthanide metals, it is extremely challenging to selectively position different 4f metals on intended locations within the same molecule.7 Most of the scarce existing examples of heterometallic complexes have been prepared through stepwise procedures.8−10 Otherwise, such species have been prepared and studied as part of statistical mixtures, containing the corresponding fractions of the homometallic analogues.11 Given the well-known lanthanide contraction along the series,12 no lanthanide ion is equal in size to any other. Attempts of preparing 4f–4f′ molecules under thermodynamic control exploiting this property have been made using ligand systems that generate disparate coordination sites. However, only deviations from the expected statistical distributions have been achieved at most.13−15 Here, we report a reaction system involving an asymmetric bridging ligand, which leads to the direct formation of pure homo- or heterometallic dinuclear complexes of lanthanide(III) ions sitting at intended positions solely determined by their size differences. The synthetic method reported here enables then the preparation of molecules containing a large number of combination of two 4f metals. Sufficient differences in ionic radii have thus allowed the production of many [LnLn′] molecules with a high degree of purity, quasi-on-demand, thus opening the possibility of exploring such architectures as prototypes of two-qubit “molecular quantum processors”. The [CeEr] species was chosen as a close to ideal candidate to test this idea. Ce(III) and Er(III) exhibit very different magnetic configurations: according to Hund’s rules, Ce(III) is characterized by a net angular momentum J = 5/2 and a gyromagnetic ratio gJ = 6/7, whereas Er(III) has J = 15/2 and gJ = 6/5. In addition, both are Kramer’s ions, thus meaning that the crystal field interaction leads to a doubly degenerate ground state, i.e., to a proper definition of qubit states. And, finally, all stable Ce isotopes have nonmagnetic nuclei, while only 22.9% of the stable isotopes of Er carry a nuclear spin. This contributes to reduce the decoherence caused by hyperfine interactions.16 We experimentally show that this molecule fulfills the necessary requirements to carry out universal quantum logic operations, such as the CNOT quantum gate.

Scheme 1. Schematic Representation of the Operation of a Universal CNOT Quantum Logic Gate Acting on a Pair of Coupled Qubits.

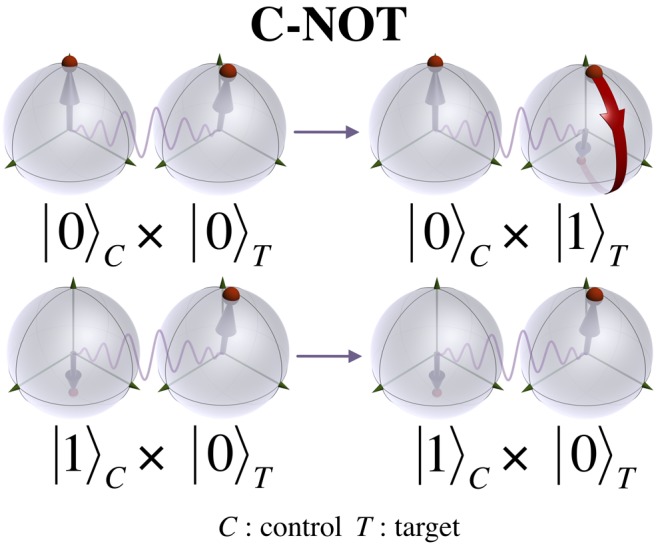
Scheme 1

Open in a new tab

The CNOT switches a target bit if and only if a control bit is in a particular state (here defined as state |0⟩). Each qubit state is typically represented by a point on the surface of a Bloch sphere, describing a quantum superposition of states. The quantum gate operation is depicted, for simplicity, on a target qubit in state |0⟩.

Experimental Section

Synthesis

All reactions were performed under aerobic conditions. Reagents were used as received unless otherwise indicated. The ligand 6-(3-oxo-3-(2-hydroxyphenyl)propionyl)pyridine-2-carboxylic acid (H3L) was prepared according to a previously published procedure.17

[CeEr(HL)2(H2L)(NO3)(py)(H2O)] (1)

A yellow solution of H3L (30.0 mg, 0.105 mmol) in pyridine (10 mL) was added into a colorless solution of Ce(NO3)3·6H2O (15.2 mg, 0.035 mmol) and Er(NO3)3·5H2O (15.5 mg, 0.035 mmol) in pyridine (10 mL). The mixture was stirred for 2 h, and the resulting orange solution was layered with Et2O. After 2 weeks, the complex was obtained as orange crystals in 61% yield. Anal. calcd (found) for 1·1.3H2O·1.7py: C 47.63 (47.58), H 3.15 (3.04), N 6.36 (6.46). Metal composition calcd (found) for 1·1.3H2O·1.7py: Ce 9.50 (9.37), Er 11.4 (10.9). ESI MS: m/z = 1057.99 [CeEr(HL)2(H2L)]+. IR (KBr pellet, cm–1): 3403 mb, 1618 s, 1584 s, 1558 m, 1528 s, 1463 m, 1401 s, 1384 s, 1324 m, 1299 m, 1240 w, 1201 w, 1147 w, 1120 w, 1060 w, 951 w, 890 w, 763 w, 706 w, 664 w, 635 w, 569 w.

[LaEr(HL)2(H2L)(NO3)(py)(H2O)] (4)

A yellow solution of H3L (30.0 mg, 0.105 mmol) in pyridine (10 mL) was added into a colorless solution of La(NO3)3·6H2O (15.2 mg, 0.035 mmol) and Er(NO3)3·5H2O (15.5 mg, 0.035 mmol) in pyridine (10 mL). The mixture was stirred for 2 h, and the resulting orange solution was layered with Et2O. After 2 weeks, the complex was obtained as yellow crystals in 69% yield. Anal. calcd (found) for 4·1.7H2O·1.2py: C 46.66 (46.59), H 3.10 (2.98), N 6.02 (6.12). Metal composition calcd (found) for 4·1.7H2O·1.2py: La 9.64 (9.23), Er 11.6 (11.2). ESI MS: m/z = 1156.99 [LaEr(HL)2(H2L)]+. IR (KBr pellet, cm–1): 3447 mb, 1617 s, 1584 s, 1559 m, 1533 s, 1464 m, 1399 s, 1384 s, 1323 m, 1298 m, 1239 w, 1198 w, 1148 w, 1120 w, 1060 w, 951 w, 890 w, 764 w, 706 w, 668 w, 635 w, 568 w.

[CeY(HL)2(H2L)(NO3)(py)(H2O)] (5)

A yellow solution of H3L (30.0 mg, 0.105 mmol) in pyridine (10 mL) was added into a colorless solution of Ce(NO3)3·6H2O (15.2 mg, 0.035 mmol) and Y(NO3)3·6H2O (13.4 mg, 0.035 mmol) in pyridine (10 mL). The mixture was stirred for 2 h, and the resulting orange solution was layered with Et2O. After 2 weeks, orange crystals of 5 were obtained in 70% yield. Anal. calcd (found) for 5·1.8py: C 51.30 (51.13), H 3.21 (3.22), N 6.90 (7.09). Metal composition calcd (found) for 5·1.8py: Ce 10.1 (10.3), Y 6.44 (6.24). ESI MS: m/z = 1078.97 [CeY(HL)2(H2L)]+. IR (KBr pellet, cm–1): 3446 mb, 1617 s, 1584 s, 1559 m, 1533 s, 1464 m, 1399 s, 1384 s, 1323 m, 1298 m, 1239 w, 1200 w, 1147 w, 1120 w, 1060 w, 951 w, 891 w, 763 w, 706 w, 664 w, 635 w, 569 w.

[CeY(HL)2(H2L)(NO3)(py)(H2O)]0.7[Y2(HL)2(H2L)(NO3)(py)(H2O)]0.3 (6)

A yellow solution of H3L (30.0 mg, 0.105 mmol) in pyridine (10 mL) was added into a colorless solution of Ce(NO3)3·6H2O (7.6 mg, 0.018 mmol) and Y(NO3)3·6H2O (20.1 mg, 0.053 mmol) in pyridine (10 mL). The mixture was stirred for 2 h, and the resulting orange solution was layered with Et2O. After 2 weeks, orange crystals of 6 were obtained in 41% yield. Anal. calcd (found) for 6·0.5H2O·1.3py: C 50.81 (50.68), H 3.21 (3.33), N 6.61 (6.99). ESI MS: m/z = 1078.95 [CeY(HL)2(H2L)]+ and 1027.95 [Y2(HL)2(H2L)]+. IR (KBr pellet, cm–1): 3400 mb, 1618 s, 1584 s, 1558 m, 1529 s, 1464 m, 1404 s, 1384 s, 1325 m, 1299 m, 1240 w, 1206 w, 1148 w, 1121 w, 1059 w, 951 w, 891 w, 755 w, 707 w, 665 w, 636 w, 569 w.

[LaY(HL)2(H2L)(NO3)(py)(H2O)] (7)

A yellow solution of H3L (30.0 mg, 0.105 mmol) in pyridine (10 mL) was added into a colorless solution of La(NO3)3·6H2O (15.2 mg, 0.035 mmol) and Y(NO3)3·6H2O (13.4 mg, 0.035 mmol) in pyridine (10 mL). The mixture was stirred for 2 h, and the resulting yellow solution was layered with Et2O. After 2 weeks, the complex was obtained as yellow crystals in 40% yield. Anal. calcd (found) for 7·3.9H2O: C 45.92 (45.51), H 3.30 (2.87), N 5.35 (5.52). ESI MS: m/z = 1077.96 [LaY(HL)2(H2L)]+. IR (KBr pellet, cm–1): 3445 mb, 1618 s, 1583 s, 1557 m, 1530 s, 1463 m, 1402 s, 1382 s, 1325 m, 1299 m, 1239 w, 1202 w, 1148 w, 1120 w, 1060 w, 951 w, 891 w, 762 w, 707 w, 664 w, 635 w, 569 w.

X-ray Crystallography

Crystals systematically suffer from deterioration of crystallinity once out of their mother liquor, likely due to lattice solvent loss. Single crystals were therefore selected and mounted directly from their mother liquor using the oil-drop method and mounted as fast as possible into the cold N2 stream on the goniometer. Data for compounds 1·5py, 6·5py, and 7·3py were collected using Mo Kα radiation (λ = 0.710 73 Å) at 150 K with an Oxford Diffraction Excalibur diffractometer with enhanced Mo Kα radiation (λ = 0.710 73 Å) at the X-ray Diffraction and Fluorescence Analysis Service of the Servicio General de Apoyo a la Investigación-SAI, Universidad de Zaragoza. Cell refinement, data reduction, and absorption corrections were performed with the CrysAlisPro suite.18 Data for compounds 4·5.5py and 5·5py were collected at 100 K with a Bruker APEX II CCD diffractometer on the Advanced Light Source beamline 11.3.1 at Lawrence Berkeley National Laboratory, from a silicon 111 monochromator (λ = 0.7749 Å). Data reduction and absorption corrections were performed with SAINT and SADABS.19 Structures were solved with either SIR9720 or SHELXS21,22 and refined on F2 with the SHELXTL suite.21,22 All non-hydrogens were refined anisotropically. Hydrogens were placed geometrically on their carrier atom and refined with a riding model. In all cases displacement parameters restraints were used to refine some of the lattice solvent molecules as well as a few atoms of the main residue. For 1·5py, 6·5py, and 7·3py, void space with only diffuse electron density remaining at the end of the refinement was analyzed and taken into account with SQUEEZE as implemented in the PLATON package.23,24 The heterometallic composition and the relative position of the two metal ions were confirmed by much poorer final agreement factors as well as worse or even unreasonable relative displacement parameters in any of the other possibilities (inverted positions or homometallic composition). Crystallographic and refinement parameters are summarized in Table S1 (Supporting Information, SI). Selected bond distances and angles are given in Table S2 (SI). All details can be found in the supplementary crystallographic data for this paper in CIF format with CCDC numbers 973881, 973882, 973883, 973884, and 973885 for compounds 1, 4, 5, 6, and 7, respectively. These data can be obtained free of charge from The Cambridge Crystallographic Data Centre via www.ccdc.cam.ac.uk/data_request/cif.

Physical Measurements

Magnetic susceptibility χ data were measured, between 2 and 300 K, with a commercial magnetometer equipped with a SQUID sensor and a commercial Physical Properties Measurement System (PPMS), both hosted by the Physical Measurements Unit of the Servicio General de Apoyo a la Investigación-SAI, Universidad de Zaragoza. The diamagnetic contributions to the susceptibility were corrected using Pascal’s constant tables. Direct current (dc) data were collected between 2 and 300 K with an applied field of 1000 Oe. Alternating current (ac) data were collected in the range 2–100 K with an applied field of 4 Oe oscillating at different frequencies in the range 0.1 ≤ ν ≤ 10 000 Hz. Ac susceptibility measurements were extended to the region of very low temperatures using an integrated micro-SQUID susceptometer, recently developed by some of us,100 which works in the temperature region from 13 mK up to 3 K and for frequencies from 0.03 Hz up to 200 kHz. The excitation field amplitude of the microSQUID susceptometer is 0.01 Oe. For sufficiently low frequencies (typically, ν < 5 Hz), the susceptibility becomes independent of ν at any temperature. This limit is taken as the equilibrium linear susceptibility. Continuous wave EPR measurements were taken in a Bruker ELEXYS 580 spectrometer operating in X- and Q-band. The same spectrometer working in X-band was used to obtain echo-induced EPR and echo decay measurements. The length of the π/2 and π pulses was 16 and 32 ns, respectively, and the sampling time was 4 ns. Finally, heat capacity data were also measured between 350 mK and 300 K on compact pellet samples using a commercial PPMS. Positive-ion ESI mass spectrometry experiments were performed using a LC/MSD-TOF (Agilent Technologies) with a dual source equipped with a lock spray for internal reference introduction at the Unitat d'Espectrometria de Masses (SSR) of the University of Barcelona.

Results and Discussion

Synthesis

The ligand H3L (Figure 1) features three different coordination pockets arranged in a completely asymmetric manner. We previously showed that three (partially) deprotonated H3L ligands bridge two Ln(III) ions to form a quasi-isostructural series of asymmetric dimers, with formula [Ln2(HL)2(H2L)(NO3)(py)(H2O)] (Ln = La, Ce, Pr, Nd, Sm, Eu, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu, and also Y).25 The two metal centers within each complex then necessarily have markedly different environments. Inspection of the molecular structures revealed that one of the metal sites (site 1) of the assembly offers a cavity that is systematically smaller than the other one (site 2, Figure S1, SI). This can be visualized by comparing the Ln–O distances of both sites. There is an average distance difference, ΔO, between both sites of 0.03–0.05 Å (for homogeneous comparison, only donor atoms of HL2– and H2L– are included). It was thought that this property could be advantageously exploited in order to face one of the current challenges in synthetic coordination chemistry: the controlled preparation of heterometallic 4f–4f′ complexes, here embodied as a series of dinuclear molecules with formulas [LnLn′(HL)2(H2L)(NO3)(py)(H2O)] (abbreviated [LnLn′]). In considering the best candidates to fabricate a molecular quantum processor, the ideal properties of the Ce(III)/Er(III) combination rendered it a highly desired one. A solution with equimolar amounts of Ce(NO3)3 and Er(NO3)3 in pyridine produces, in the presence of H3L and after layering with Et2O, a homogeneous phase of yellow crystals that was found to consist of pure [CeEr(HL)2(H2L)(NO3)(py)(H2O)] (1, Figure 1).

Figure 1.

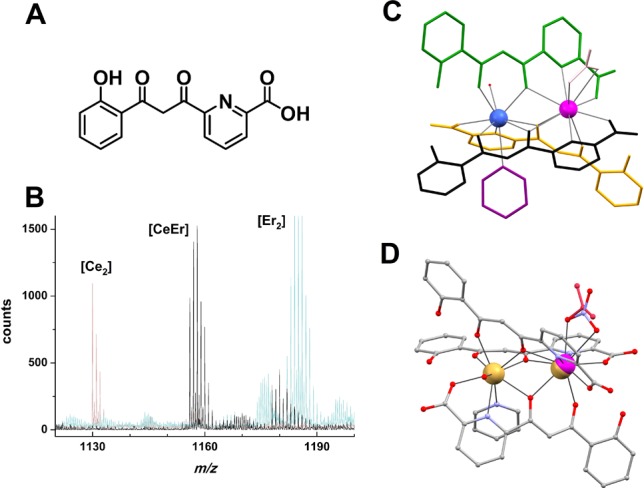
Figure 1

Open in a new tab

Heterometallic [LnLn′] Complexes. (A) Representation of ligand 6-(3-oxo-3-(2-hydroxyphenyl)propionyl)pyridine-2-carboxylic acid (H3L). (B) Superposition of a selected area of the mass spectrograms of complexes [CeEr(HL)2(H2L)(NO3)(py)(H2O)] (1), [Ce2(HL)2(H2L)(NO3)(py)(H2O)] (2), and [Er2(HL)2(H2L)(NO3)(py)(H2O)] (3), emphasizing the absence of any trace of homometallic species on the diagram from heterometallic [CeEr]. (C) Molecular structure of [CeEr(HL)2(H2L)(NO3)(py)(H2O)] (1) showing each ligand in a different color (black, green, or yellow), pyridine in purple, Ce(III) in pink, Er(III) in blue, water in red, and nitrate in pink. H atoms are not shown. (D) Molecular representation of [(Ce0.7Y0.3)Y(HL)2(H2L)(NO3)(py)(H2O)] (6), showing the occupancy of Ce(III) (pink) and Y(III) (yellow), consistent with the composition as well as the ratio of mono- and didentate NO3–. C is in gray, O in red, and N in violet; H atoms not shown.

The heterometallic nature of 1 was established by single-crystal X-ray crystallography (see below), which shows that the cation of smaller size, Er(III),12 occupies site 1, as expected, whereas the larger cation, Ce(III),12 goes to the position favoring larger Ln–O/N bonds (site 2). The 1:1 metal composition of 1 was confirmed by ICP-AES spectroscopy (see above), whereas conclusive evidence for its formulation came from mass spectrometry (MS, Figures 1 and S2 and S3, SI), which produced only signals of heterodimetallic fragments. The availability of the homometallic derivatives [Ce2(HL)2(H2L)(NO3)(py)(H2O)] (2) and [Er2(HL)2(H2L)(NO3)(py)(H2O)] (3)25 was important to corroborate the purity of 1 in the bulk, as this conclusion follows from the absence of any detectable amount of homodimetallic fragments in the mass spectrogram of the latter (Figure 1). The successful preparation of 1 suggests that this coordination system constitutes a host–guest assembly, capable of discriminating between two different lanthanides by their size, by selectively distributing them over two different locations. Site selectivity between different lanthanides is extremely difficult to achieve, given the chemical similarity that exists among them.7 In the present case, the system is in addition adaptive; when only one type of metal is present, it is hosted in both sites.25

In order to evaluate the metals in 1 as suitable qubits, their study in their respective environments, without the magnetic influence of the other, was necessary. The plasticity of this coordination architecture enables the design and preparation of the analogues [LaEr] and [CeY], where Er and Ce occupy the same position they hold in 1 but are now accompanied by a diamagnetic cation [La(III) and Y(III), respectively]. For these pairs, the differences in ionic radii are Δr = 0.21 Å (LaEr) and 0.15 (CeY), respectively.12,26 The same synthetic procedure described above was carried out using Er(NO3)3 or Ce(NO3)3, in combination with La(NO3)3 and Y(NO3)3, respectively, producing successfully pure [LaEr(HL)2(H2L)(NO3)(py)(H2O)] (4) and [CeY(HL)2(H2L)(NO3)(py)(H2O)] (5). The results from single crystal X-ray crystallography are consistent with the identity of both complexes (see below) as well as metal analysis (confirming equimolar contents of both metals in each case). Mass spectrometry measurements (SI) convincingly evidence that crystals of 4 and 5 are only made of heterometallic molecules (Figures S4–S7, SI), while the magnetic properties of both compounds also support the formulated composition (see below). The need to investigate the possible effects of dipolar interactions between the spin magnetic moments of Er(III) or Ce(III) in the bulk of [LaEr] (4) or [CeY] (5) (see below) prompted attempts to dilute these molecules within an isostructural diamagnetic lattice. The synthetic work described above suggests that a mixture of Ce(NO3)3 and Y(NO3)3 (1:3 molar ratio) in a pyridine solution of H3L should lead to an equimolar mixture of [CeY(HL)2(H2L)(NO3)(py)(H2O)] and [Y2(HL)2(H2L)(NO3)(py)(H2O)]. X-ray diffraction studies performed on a single crystal from this reaction system indicate that both complexes are present within a homogeneous solid solution (see below), randomly distributed in a 70:30 molar ratio: [CeY(HL)2(H2L)(NO3)(py)(H2O)]0.7[Y2(HL)2(H2L)(NO3)(py)(H2O)]0.3 or [(Ce0.7Y0.3)Y(HL)2(H2L)(NO3)(py)(H2O)] (6). Very low temperature heat capacity experiments (Figure S8, SI) were conclusive with regard to the successful dilution of [CeY] molecules within this single phase. Mass spectrometry of these crystals shows the existence of heterometallic [CeY] and homometallic [Y2] fragments, but no trace of [Ce2] moieties (Figure S9, SI).

The complex [LaY(HL)2(H2L)(NO3)(py)(H2O)] (7) was also obtained using the same synthetic procedure, with the aim of measuring the nonmagnetic energy contributions to the specific heat in these compounds. The identity and purity of 7 was established by single-crystal X-ray diffraction, IR spectroscopy, mass spectrometry (Figure S10, SI), and microanalysis.

The above experiments confirm a new method for locking a large number of combinations of two lanthanide ions within a well-defined molecular entity (Figure 1). This represents a huge step toward the goal of obtaining pure heterometallic 4f–4f′ complexes from one-pot reactions.

Molecular Structures

The single-crystal structures of compounds 1 and 4–7 were determined by X-ray diffraction (SI). The neutral complex [CeEr(HL)2(H2L)(NO3)(py)(H2O)] (1, Figures 1 and S11, SI) is chiral, with both enantiomers present in the crystal lattice. The unit cell belongs to the monoclinic space group P21/c and contains four asymmetric units (Table S1, SI). Each of the latter comprises one dinuclear [CeEr] complex and five molecules of pyridine. The complex exhibits a Ce(III) ion and an Er(III) center surrounded by three partially deprotonated H3L ligands (two as HL2– and one as H2L–) in the same way as its homometallic congeners.25 Each ligand chelates both metals through two distinct coordination pockets, a β-diketonate and a dipicolinate-like cavity, both sharing a common central O donor which participates in a Ce–O–Er bridge. Two of the ligands lie in a mutual head-to-head configuration, while the third one points in the opposite direction. An important consequence is that the metals, which lie 3.851 Å apart, are in different coordination environments; Ce(III) is located within two tridentate (O, N, O) pockets and one β-diketonate (O, O) one, whereas Er(III) is bound to one (O, N, O) and two (O, O) donor groups, respectively (Table S2, SI). A 9-fold coordination around the latter metal is completed by one molecule of pyridine and one of water, whereas Ce(III) exhibits 10-fold coordination, with the concurrence of a η2-NO3– ligand. This anion provides the one negative charge necessary for the complex to be electrically neutral. The nature of the metal on each position could be unambiguously established from the refinement of the diffraction data, yielding unreasonable displacement parameters or agreement factors whenever any other metal distribution was considered. It might then be concluded that the metal ion with the smallest radius (Er) goes to the site with the shortest coordination distances (site 1), while Ce accommodates into the other site (site 2). A further consequence is that, in the present (heterometallic) complex, the difference ΔO = 0.17 Å between the average Ln–O distances in both sites is larger than those observed for any of the analogous homometallic complexes studied previously.17,25 The four ionizable protons remaining on the ligands have all been identified crystallographically and are located on the phenol groups and on one carboxylic moiety. A pyridine solvate molecule is forming a strong hydrogen bond to the latter (Figure S12, SI).

Complexes [LaEr(HL)2(H2L)(NO3)(py)(H2O)] (4, Figure S13, SI) and [CeY(HL)2(H2L)(NO3)(py)(H2O)] (5, Figure S14, SI) are analogous to the heterometallic complex 1. The empirical differences in ionic radii12,26 (Δr) of both metals in each complex are 0.21 Å (La > Er) and 0.15 Å (Ce > Y). Accordingly, Er(III) and Y(III) occupy site 1 of 4 and 5, respectively, whereas La(III) and Ce(III) are in site 2. Larger disparities in ionic radii within one complex also enhance differences between sites 1 and 2. Therefore, this difference is slightly larger in 4 than in 5, namely ΔO = 0.18 and 0.15 Å for [LaEr] and [CeY], respectively (Table S2, SI). The metal–metal separations are 3.857 Å (La···Er) and 3.851 Å (Ce···Y).

Compound [CeY(HL)2(H2L)(NO3)(py)(H2O)]0.7[Y2(HL)2(H2L)(NO3)(py)(H2O)]0.3 (6, Figures 1 and S15, SI) constitutes a solid solution containing 70% of the heterometallic complex [CeY] and 30% of the diamagnetic [Y2] species, both molecules occupying the same space of the unit cell. In fact, the positions of all atoms from both species coincide, except for the metal on site 2 (Ce or Y) and three atoms of the NO3– ligand. Each of these four atoms is disordered over two locations with 0.7:0.3 occupancy ratios. Therefore, two metal···metal separations have been resolved (3.695 and 3.880 Å for Y···Y and Ce···Y, respectively) as well as two coordination modes of NO3– (mono- and didentate for coordination to Y and Ce, respectively). The only nondisordered atom of NO3– is the oxygen atom with the shortest distance to the metal. In addition to the disordered [LnY] molecule, the asymmetric unit of the structure contains five molecules of pyridine.

The heterometallic complex [LaY(HL)2(H2L)(NO3)(py)(H2O)] (7, Figure S16, SI) is isostructural to 1 with three pyridine molecules in the asymmetric unit (instead of five). The value of Δr for La(III) and Y(III) is 0.18 Å,12,26 which leads to ΔO = 0.18 Å and a La···Y distance of 3.869(1) Å. As expected, the La(III) center exhibits 10-fold coordination, with the nitrate ligand in the terminal η2-NO3– coordination mode.

Thermal and Magnetic Study

The synthetic tool reported here allows choosing almost any desired pair of lanthanide ions for the fabrication of a molecular qugate. In order to build a molecular CNOT gate, the combination of Ce(III) with Er(III) was deemed to be most appropriate. This heteronuclear combination minimizes the amount of nuclear spins located at the lanthanide sites [none for Ce(III) and only 22.9% of the 167Er isotope with I = 7/2 for Er(III)], thus contributing to reduce decoherence. It should be noted, however, that nuclear spins strongly coupled to the electronic ones might enhance the computational space of each qubit27,28 or act in situ as quantum memories.29 Such additional possibilities are, of course, compatible with the same chemical structures reported here, which can be realized with lanthanide ions having nonzero I [such as e.g. Pr(III), Tb(III), or Ho(III)]. The present physical characterization, which is described in the following, aims to show that 1 fulfills the following conditions: (i) each lanthanide behaves, at sufficiently low temperatures, as an effective spin-1/2, thus providing a good realization of spin qubits, and (ii) these spin qubits are magnetically nonequivalent and (iii) weakly coupled, thereby enabling the realization of “single shot” quantum gate operations.30

Qubit Characterization

Complexes [LaEr] (4) and [CeY] (5) were prepared and studied to characterize each of the two lanthanide ions of [CeEr] (1) in their respective local coordination environments, isolated from the influence of the other magnetic center. In 4 and 5, Er(III) and Ce(III) metals occupy the same positions they take in 1, being accompanied by the diamagnetic ions La(III) and Y(III), respectively. According to Hund’s rules, free Er(III) and Ce(III) ions are characterized by J = 15/2 with gJ = 6/5 and J = 5/2 with gJ = 6/7, respectively. In a material, these multiplets are split into Kramers doublets by the interaction of 4f electrons with the crystal field (magnetic anisotropy). Information on the magnetic energy level structure and the nature of the ground state doublet, which forms the computational qubit basis, can be obtained from linear magnetic susceptibility χ and electron paramagnetic resonance (EPR) experiments. Results of experiments performed on powder samples of 4 and 5 are shown in Figure 2. The plateau in the χT product observed at sufficiently low T (T ≤ 3 K for [LaEr] and T ≤ 7 K for [CeY]) reflects the magnetic behavior of the ground-state doublet. In this temperature region, each lanthanide effectively behaves as a two-level system and can therefore be described by a simple effective spin-1/2 Hamiltonian31

graphic file with name ja-2014-07809w_m001.jpg 1

where ĝi is the effective gyromagnetic tensor of spin i [i = 1, 2 refer to Er(III) and Ce(III) ions, respectively], with principal values gxi, gyi, and gzi. These values have been determined by fitting EPR spectra measured at a frequency ν = 9.8 GHz (X-band) on complexes 4 and 5, as shown in Figure 2. The low-T limit of χT is then (χT)T→0 = (NAμB2/4kB)⟨gi2⟩, where ⟨gi2⟩ = (gxi2 + gyi2 + gzi2)/3 which, using the EPR values, amounts to 0.35 and 3.70 emu K/mol Oe for CeY and LaEr, respectively, in good agreement with the results of magnetic measurements. It is worth mentioning that the principal axes of sites 1 and 2 need not be collinear to each other.

Figure 2.

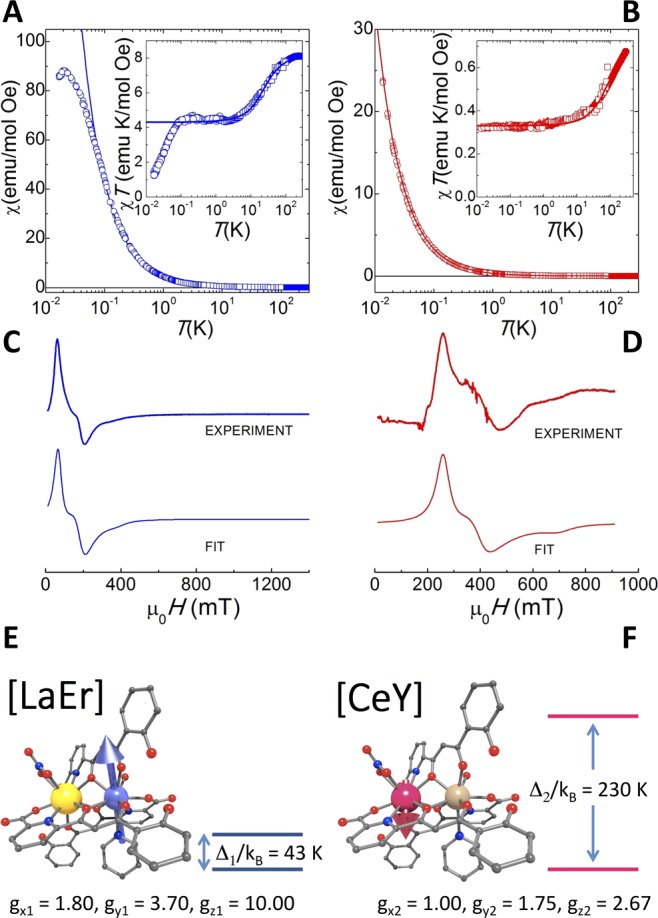
Figure 2

Open in a new tab

Individual lanthanide spin qubits. (A and B) Temperature dependence of the equilibrium magnetic susceptibility of, respectively, [LaEr] (4) and [CeY] (5) molecular complexes. Open symbols represent zero-field ac susceptibility data recorded, at 1.5 Hz, with a microSQUID susceptometer (circles, ac field amplitude 0.01 Oe) and a commercial SQUID magnetometer (squares, ac field amplitude 4 Oe). Solid symbols are dc susceptibility data measured under a 1000 Oe applied magnetic field. The agreement between data measured by different techniques shows that they correspond to the linear response, i.e., to the zero-field susceptibility. The insets show the χT products. The solid lines are least-squares fits based on eq 2. (C and D) X-band continuous wave EPR spectra of 4 and 5, respectively. The fits are based on a spin-1/2 Hamiltonian (eq 1) describing the magnetic properties of the ground-state doublet, which defines each qubit basis. Panels E and F show both complexes and their low-energy magnetic level structures.

At finite temperatures, χT increases, showing the gradual population of excited Kramers doublets. This behavior can be described using Van Vleck’s general formalism for the susceptibility of anisotropic spins.32,33 For temperatures where only the populations of the ground and first excited doublets, separated by an energy gap Δ, are significant, Van Vleck’s expression reduces to the following34

graphic file with name ja-2014-07809w_m002.jpg 2

where C0, C1, and C2 are numerical coefficients that depend on the electronic structure of each doublet. It can be seen in Figure 2A,B that eq 2 accurately describes the temperature dependence of the susceptibility and, therefore, that it enables an accurate determination of Δ. The lowest lying magnetic energy level structures of complexes 4 and 5 are shown in Figure 2. Both lanthanide ions have a ground-state doublet that is energetically isolated from all excited levels, therefore providing a proper definition of qubit states. Below T = 0.1 K, the susceptibility of [LaEr] deviates from the pure paramagnetic behavior and shows a peak that can be associated with the onset of magnetic order likely induced by dipolar interactions between spins in different molecules. In [CeY], such interactions are even weaker, in agreement with the smaller magnetic moment of this ion, and no significant deviation from paramagnetism is observed. Heat capacity experiments (Figure S8, SI) confirm these conclusions. In fact, the extent of the dipolar intermolecular interactions was corroborated by comparing the specific heat of the [CeY] complex with that of the magnetically dilute analog [(Ce0.7Y0.3)(Y)] system (Figure S8, SI).

These results also imply that, for almost any given magnetic field intensity and orientation, the Zeeman splitting of the two qubit levels of 4 is different from that of 5, i.e., that these qubits are magnetically inequivalent and therefore separately addressable by either changing frequency or magnetic field. A further salient feature is that gxi and gyi are on the same order as gzi. This result is in striking contrast with values reported for other lanthanide spin qubits, for which the ratios gx/gz and gy/gz are typically on the order of 10–3 or even less. It probably results from the low symmetry of the local coordination of Er(III) and Ce(III) and has important implications for the coherent control of these spins. The gyromagnetic ratios determine the Rabi frequencies ΩR of transitions between qubit states induced by radiofrequency (rf) electromagnetic fields.35 Therefore, we expect that 4 and 5 show very high ΩR values for almost any orientation of the external dc and rf magnetic fields.

Interqubit Coupling

With the information obtained already on both lanthanide ions separately, it is straightforward to test the magnetic coupling between them. For this, we compare in Figure 3 the magnetic susceptibility of the double qubit system [CeEr] (1) to those measured on the single qubit molecules [LaEr] (4) and [CeY] (5). Above approximately 0.2 K, the χ of this compound almost coincides with the sum of the susceptibilities of [CeY] (4) and [LaEr] (5). Interqubit coupling effects become visible only below this temperature, where χ of [CeEr] clearly drops below the value expected for the two uncoupled spins. This effect shows that the coupling is weak and likely antiferromagnetic. The existence of a finite intramolecular coupling is confirmed by the results of EPR experiments. The X-band spectrum of 1 at 5 K is clearly not a simple superposition of the spectra of 4 and 5. Furthermore, spectra measured on 1 at different frequencies do not scale when they are plotted against the ratio H/ν, as they should if the spins of Ce(III) and Er(III) were uncoupled and simply described by eq 1.

Figure 3.

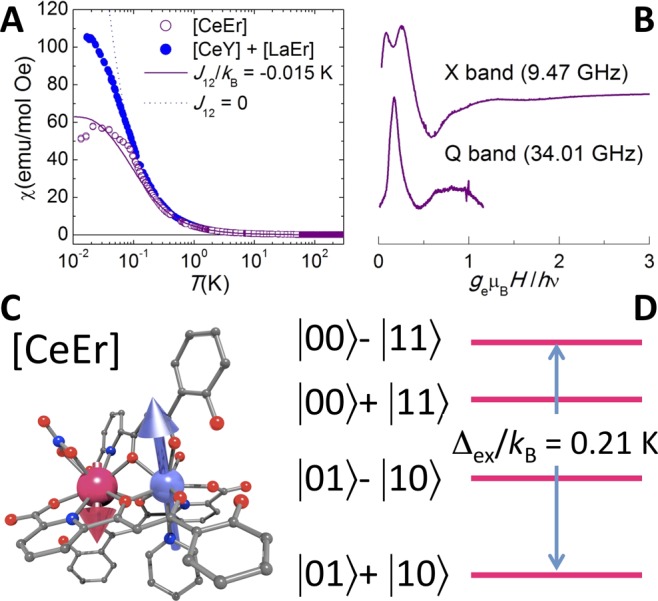
Figure 3

Open in a new tab

Coupled lanthanide spin qubits. (A) Temperature dependence of the equilibrium magnetic susceptibility (open circles, zero-field ac susceptibility data at 1.5 Hz; open squares, dc susceptibility under a 1000 Oe applied field) of [CeEr] (1), compared to the sum of susceptibilities of [LaEr] and [CeY] (solid symbols). The blue dotted and purple solid lines show, respectively, the susceptibilities of two uncoupled and two coupled effective spin-1/2 moments with noncollinear ĝi tensors (eq 3; see the text). (B) EPR spectra of 1 measured at 5 K and two different frequencies. Panel C shows the [CeEr] complex and panel D a scheme of its low-energy magnetic level structure.

The same conclusions can be drawn from specific heat data (Figure S17, SI). The specific heat of 1 deviates from that expected for molecules consisting of two noninteracting spins only at very low temperatures. This effect becomes clear from measurements performed on 1 at zero field, which below 1 K exceed the sum of the specific heats of 4 and 5. This extra heat capacity reflects the splitting in energy of different ferro- and antiferromagnetic configurations of the two spin qubits, confirming the latter as the ground state. It gradually vanishes with increasing magnetic field, thus suggesting that the differences observed at zero field are due to the presence, in complex 1, of a finite exchange interaction between Ce(III) and Er(III).

Energy Level Structure and Operation as a Molecular Spin Quantum Gate

From the above discussion, it follows that [CeEr] behaves, at sufficiently low temperatures, as a system of two anisotropic and weakly coupled effective S-1/2 spins. The underlying physics and its operation as a quantum gate can be described with the following effective Hamiltonian, which is derived in the SI:

graphic file with name ja-2014-07809w_m003.jpg 3

where J12 is an exchange constant describing the coupling between the angular momenta of Ce(III) and Er(III) ions in 1. It follows from eq 3 that χ drops below the paramagnetic response for J12 < 0. However, no accurate fit can be achieved if the local principal axes of the two spins are collinear to each other. This situation obviously arises from the strong asymmetry of the molecule and was already observed in homonuclear compounds of the same family.30 The results are compatible with a tilt of one of the local easy magnetization axes, say z2, with respect to the other, z1, of about 70° with respect to each other. Results for χ calculated in a particular situation, where y2 and z2 have been rotated along x2 = x1, account reasonably well for the data measured on [CeEr], as shown in Figure 3. Although the fit does not univocally fix the relative orientations of the ĝ1 and ĝ2 tensors, thus other solutions giving similar results, the structure of magnetic energy levels, shown in Figure 4 as a function of Hz1, remains qualitatively the same.

Figure 4.

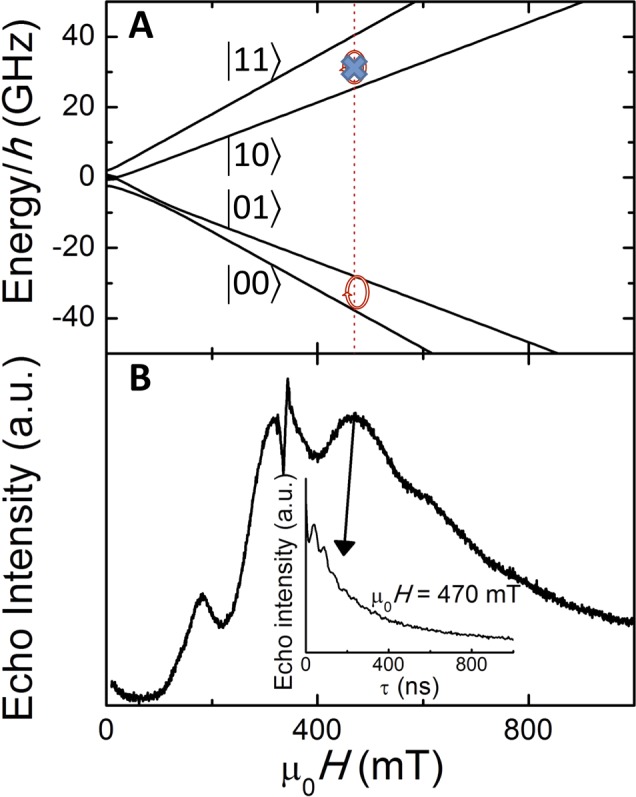
Figure 4

Open in a new tab

Quantum gate operation. (A) Magnetic field dependence of the four lowest-lying energy levels of 1 calculated with the effective spin Hamiltonian eq 3 for J12/kB = −0.015 K and a magnetic field parallel to the z1 axis [easy magnetization axis of Er(III)]. At μ0Hz1 = 470 mT, X-band photons (9.5 GHz) are only resonant with the |00⟩ → |01⟩ transition, thus providing realization of a single-shot CNOT gate. (B) Echo-detected EPR spectrum of a MeOH/EtOH frozen solution of 1 measured at a fixed separation τ between the π/2 and π pulses of 140 ns. The inset shows the decay with τ of the spin-echo measured at a magnetic field μ0H = 470 mT. An exponential fit gives a decoherence time T2 = 410 ns.

At any magnetic field, the four lowest-lying levels of 1 are unequally separated, meaning that there are no degenerate transitions. This is a consequence of the very different magnetic properties of Er(III) and Ce(III) and their weak coupling. The four-dimensional Hilbert space defined by the energy eigenstates (hereafter labeled simply as {|00⟩, |10⟩, |01⟩, |11⟩}) provides then a suitable computational basis for a molecular spin quantum gate. For instance, if we set μ0Hz1 = 470 mT (Figure 4), only the |00⟩ → |01⟩ transition is resonant with X-band photons; i.e., under these conditions the interaction with the radiation field flips qubit 2 if, and only if, qubit 1 is in state “0”; thus, it provides a simple realization of a single-shot CNOT gate (Scheme 1). Notice that, because of the low symmetry of the two lanthanide sites, the wave functions are not simple products of states of each lanthanide ion. An important consequence is that all possible transitions, and sequences of them, can be induced by electromagnetic radiation of the appropriate frequency. This ensures the feasibility of any operation linking any two states of the Hilbert space defined by the computational basis. Therefore, this molecule can operate as a universal two-qubit spin quantum processor, controlled by either electromagnetic frequency or magnetic field.

A further crucial step for ascertaining the suitability of 1 for quantum information processing is to evaluate the coherence times associated with these transitions. A convenient method to examine this is time-domain EPR spectroscopy. Experiments were performed on this complex dissolved in MeOH/EtOH, which unveiled that indeed coherent spin dynamics can be generated from the molecule through radiofrequency pulses (Figure 4). An echo signal was detected for μ0H = 0.47 T, which approximately corresponds to the |01⟩ ↔ |00⟩ transition, associated with a CNOT gate operation where the first qubit acts as control (Figure 4). While these experiments do not represent a full realization of the quantum gate operation, or quantum tomography, they evidence that such coherent manipulations are feasible and provide the first evaluation of the decoherence time scales on a two-qubit molecular spin quantum gate. The estimated decoherence time T2 of this resonance, approximately 410 ns, is still short as compared to values obtained for other physical realizations.1,36 Further experiments will serve to identify the main sources of decoherence and to engineer adequate methods to reduce its effects.

Conclusion

Small differences in the ionic radius of Ln(III) atoms can be exploited with the ligand H3L for the preparation of pure heterodimetallic [LnLn′] complexes for a large number of combinations, opening a very important synthetic pathway for many applications. Here, this potential has been used to prepare an optimal molecular assembly to act as a two-qubit spin quantum processor, the complex [CeEr(HL)2(H2L)(NO3)(py)(H2O)] (1). To assist in the qubit and qugate characterization, the analogues [CeY], [LaEr], [LaY] and the diluted [(Ce0.7Y0.30)Y] where also prepared and studied. EPR, ultralow temperature micro-SQUID, and heat capacity measurements and analysis have served to demonstrate that the individual qubits in 1 feature the appropriate computational qubit basis and the properties to exhibit large Rabi oscillation frequencies between qubit state transitions, as required. In addition, the energy eigenstates of the two qubits coupled within the [CeEr] molecule form a four-dimensional Hilbert space suited for the realization of universal two-qubit logic operations. Time-resolved EPR experiments show that this molecule exhibits coherent spin dynamics, from where a decoherence time T2 of about 400 ns has been extracted. These molecules could now be coupled to quantum devices in a significant step forward toward the goal of realizing quantum information processing.

Acknowledgments

The authors thank the European Research Council for Starting Grant ERC-2010-StG-258060 (G.A., L.A.B., V.V.); Spanish MINECO for projects CTQ2009-06959 (G.A., D.A.), CTQ2012-32247 (G.A., D.A.), MAT2012-38318-C03 (A.R., J.S., F.L.), MAT2011-23861 (P.J.A.), and MAT2011-24284 (O.R.); the Generalitat de Catalunya for the ICREA Academia price 2008 and 2013 (G.A.); and Gobierno de Aragón for grants E98-“MOLCHIP” (A.R., J.S., F.L., O.R.) and E33 (P.J.A.). The Advanced Light Source (S.J.T.) is supported by the Director, Office of Science, Office of Basic Energy Sciences of the U.S. Department of Energy under Contract DE-AC02-05CH11231.

Supporting Information Available

Derivation of the Hamiltonian in equation 3; X-ray crystallographic data, CIF files, positive-ion ESI mass spectrograms, and structures for 1 and 4–7; and heat capacity data. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Present Address

⊥ CNRS, CRPP, UPR 8641, Pessac, F-33600, France, and University of Bordeaux, CRPP, UPR 8641, Pessac, F-33600, France

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States

Supplementary Material

ja507809w_si_001.pdf (2.7MB, pdf)
ja507809w_si_002.cif (38.8KB, cif)
ja507809w_si_003.cif (43.1KB, cif)
ja507809w_si_004.cif (46.9KB, cif)
ja507809w_si_005.cif (41.9KB, cif)
ja507809w_si_006.cif (37KB, cif)

References

  1. Ladd T. D.; Jelezko F.; Laflamme R.; Nakamura Y.; Monroe C.; O’Brien J. L. Nature 2010, 464, 45–53. [DOI] [PubMed] [Google Scholar]
  2. Jones J. A.; Karlen S. D.; Fitzsimons J.; Ardavan A.; Benjamin S. C.; Briggs G. A. D.; Morton J. J. L. Science 2009, 324, 1166–1168. [DOI] [PubMed] [Google Scholar]
  3. Chuang I. L.; Vandersypen L. M. K.; Zhou X.; Leung D. W.; Lloyd S. Nature 1998, 393, 143–146. [Google Scholar]
  4. Simmons S.; Brown R. M.; Riemann H.; Abrosimov N. V.; Becker P.; Pohl H.-J.; Thewalt M. L. W.; Itoh K. M.; Morton J. J. L. Nature 2011, 470, 69–72. [DOI] [PubMed] [Google Scholar]
  5. Martínez-Pérez M. J.; Cardona-Serra S.; Schlegel C.; Moro F.; Alonso P. J.; Prima-García H.; Clemente-Juan J. M.; Evangelisti M.; Gaita-Ariño A.; Sesé J.; van Slageren J.; Coronado E.; Luis F. Phys. Rev. Lett. 2012, 108, 247213. [DOI] [PubMed] [Google Scholar]
  6. Aromí G.; Aguilà D.; Gamez P.; Luis F.; Roubeau O. Chem. Soc. Rev. 2012, 41, 537–546. [DOI] [PubMed] [Google Scholar]
  7. Dalla-Favera N.; Hamacek J.; Borkovec M.; Jeannerat D.; Ercolani G.; Piguet C. Inorg. Chem. 2007, 46, 9312–9322. [DOI] [PubMed] [Google Scholar]
  8. Ishikawa N.; Iino T.; Kaizu Y. J. Am. Chem. Soc. 2002, 124, 11440–11447. [DOI] [PubMed] [Google Scholar]
  9. Costes J. P.; Dahan F.; Nicodème F. Inorg. Chem. 2003, 42, 6556–6563. [DOI] [PubMed] [Google Scholar]
  10. Chen X.-Y.; Bretonnière Y.; Pécaut J.; Imbert D.; Bünzli J.-C.; Mazzanti M. Inorg. Chem. 2007, 46, 625–637. [DOI] [PubMed] [Google Scholar]
  11. Bunzli J. C. G.; Froidevaux P.; Harrowfield J. M. Inorg. Chem. 1993, 32, 3306–3311. [Google Scholar]
  12. D’Angelo P.; Zitolo A.; Migliorati V.; Chillemi G.; Duvail M.; Vitorge P.; Abadie S.; Spezia R. Inorg. Chem. 2011, 50, 4572–4579. [DOI] [PubMed] [Google Scholar]
  13. Floquet S.; Borkovec M.; Bernardinelli G.; Pinto A.; Leuthold L.-A.; Hopfgartner G.; Imbert D.; Bünzli J.-C. G.; Piguet C. Chem., Eur. J. 2004, 10, 1091–1105. [DOI] [PubMed] [Google Scholar]
  14. Andre N.; Scopelliti R.; Hopfgartner G.; Piguet C.; Bunzli J.-C. G. Chem. Commun. 2002, 214–215. [DOI] [PubMed] [Google Scholar]
  15. Dalla-Favera N.; Hamacek J.; Borkovec M.; Jeannerat D.; Ercolani G.; Piguet C. Inorg. Chem. 2007, 46, 9312–9322. [DOI] [PubMed] [Google Scholar]
  16. Wedge C. J.; Timco G. A.; Spielberg E. T.; George R. E.; Tuna F.; Rigby S.; McInnes E. J. L.; Winpenny R. E. P.; Blundell S. J.; Ardavan A. Phys. Rev. Lett. 2012, 108, 107204. [DOI] [PubMed] [Google Scholar]
  17. Aguilà D.; Barrios L. A.; Luis F.; Repollés A.; Roubeau O.; Teat S. J.; Aromí G. Inorg. Chem. 2010, 49, 6784–6786. [DOI] [PubMed] [Google Scholar]
  18. CrysAlis PRO; Agilent Technologies, Yarnton, UK, 2012. [Google Scholar]
  19. SAINT and SADABS; Bruker AXS Inc., Madison, WI, 2007. [Google Scholar]
  20. Altomare A.; Burla M. C.; Camalli M.; Cascarano G. L.; Giacovazzo C.; Guagliardi A.; Moliterni A. G. G.; Polidori G.; Spagna R. J. Appl. Crystallogr. 1999, 32, 115–119. [Google Scholar]
  21. Sheldrick G. M. Acta Crystallogr., Sect. A 2008, 64, 112–122. [DOI] [PubMed] [Google Scholar]
  22. Sheldrick G. M.SHELXTL; Bruker AXS Inc., Madison, WI. [Google Scholar]
  23. Spek A. L.PLATON, A Multipurpose Crystallographic Tool; Utrecht University, Utrecht, The Netherlands, 2008. [Google Scholar]
  24. Spek A. L. J. Appl. Crystallogr. 2003, 36, 7–13. [Google Scholar]
  25. Martínez-Pérez M. J.; Sesé J.; Luis F.; Drung D.; Schurig T. Rev. Sci. Instrum. 2010, 81, 016108. [DOI] [PubMed] [Google Scholar]
  26. Aguilà D.; Barrios L. A.; Velasco V.; Arnedo L.; Aliaga-Alcalde N.; Menelaou M.; Teat S. J.; Roubeau O.; Luis F.; Aromí G. Chem., Eur. J. 2013, 19, 5881–5891. [DOI] [PubMed] [Google Scholar]
  27. Shannon R. D. Acta Crystallogr., Sect. A 1976, 32, 751–767. [Google Scholar]
  28. Bertaina S.; Gambarelli S.; Tkachuk A.; Kurkin I. N.; Malkin B.; Stepanov A.; Barbara B. Nat. Nanotechnol. 2007, 2, 39–42. [DOI] [PubMed] [Google Scholar]
  29. van der Sar T.; Wang Z. H.; Blok M. S.; Bernien H.; Taminiau T. H.; Toyli D. M.; Lidar D. A.; Awschalom D. D.; Hanson R.; Dobrovitski V. V. Nature 2012, 484, 82–86. [DOI] [PubMed] [Google Scholar]
  30. Fuchs G. D.; Burkard G.; Klimov P. V.; Awschalom D. D. Nat. Phys. 2011, 7, 789–793. [Google Scholar]
  31. Luis F.; Repollés A.; Martínez-Pérez M. J.; Aguilà D.; Roubeau O.; Zueco D.; Alonso P. J.; Evangelisti M.; Camón A.; Sesé J.; Barrios L. A.; Aromí G. Phys. Rev. Lett. 2011, 107, 117203. [DOI] [PubMed] [Google Scholar]
  32. Abragam A.; Bleaney B.. Electron Paramagnetic Resonance of Transition Ions; Clarendon Press: Oxford, 1970. [Google Scholar]
  33. García-Palacios J. L.; Gong J. B.; Luis F. J. Phys.: Condens. Matter 2009, 21, 456006. [DOI] [PubMed] [Google Scholar]
  34. Carlin R. L. In Magnetochemistry; Springer: Berlin, 1986; p 21. [Google Scholar]
  35. Bartolomé E.; Alonso P. J.; Arauzo A.; Luzón J.; Bartolomé J.; Racles C.; Turta C. Dalton Trans. 2012, 41, 10382–10389. [DOI] [PubMed] [Google Scholar]
  36. Jenkins M.; Hümmer T.; Martínez-Pérez M. J.; García-Ripoll J.; Zueco D.; Luis F. New J. Phys. 2013, 15, 095007. [Google Scholar]
  37. Plantenberg J. H.; de Groot P. C.; Harmans C.; Mooij J. E. Nature 2007, 447, 836–839. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja507809w_si_001.pdf (2.7MB, pdf)
ja507809w_si_002.cif (38.8KB, cif)
ja507809w_si_003.cif (43.1KB, cif)
ja507809w_si_004.cif (46.9KB, cif)
ja507809w_si_005.cif (41.9KB, cif)
ja507809w_si_006.cif (37KB, cif)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES