Φ-Value analysis and the nature of protein-folding transition states

Abstract

Φ values are used to map structures of protein-folding transition states from changes in free energies of denaturation (ΔΔG_D-N) and activation on mutation. A recent reappraisal proposed that Φ values for ΔΔG_D-N < 1.7 kcal/mol are artifactual. On discarding such derived Φ values from published studies, the authors concluded that there are no high Φ values in diffuse transition states, which are consequently uniformly diffuse with no evidence for nucleation. However, values of ΔΔG_D-N > 1.7 kcal/mol are often found for large side chains that make dispersed tertiary interactions, especially in hydrophobic cores that are in the process of being formed in the transition state. Conversely, specific local interactions that probe secondary structure tend to have ΔΔG_D-N ≈ 0.5–2 kcal/mol. Discarding Φ values from lower-energy changes discards the crucial information about local interactions and makes transition states appear uniformly diffuse by overemphasizing the dispersed tertiary interactions. The evidence for the 1.7 kcal/mol cutoff was based on mutations that had been deliberately designed to be unsuitable for Φ-value analysis because they are structurally disruptive. We confirm that reliable Φ values can be derived from the recommended mutations in suitable proteins with 0.6 < ΔΔG_D-N < 1.7 kcal/mol, and there are many reliable high Φ values. Transition states vary from being rather diffuse to being well formed with islands of near-complete secondary structure. We also confirm that the structures of transition-state ensembles can be perturbed by mutations with ΔΔG_D-N » 2 kcal/mol and that protein-folding transition states do move on the energy surface on mutation.

The Φ-value analysis is a particular set of protein-engineering methods that is used to map the structures of transition states and intermediates in protein-folding, catalysis, binding, and conformational transitions of proteins at the level of individual residues (1–5). Φ is the ratio of change of free energy of activation for folding, ΔΔG_‡-D, to the equilibrium free energy of folding, ΔΔG_N-D,† and scores the extent of formation of structure on a scale of 0 to 1 at the level of individual residues. Φ is similar but not identical to the constants α or β of classical rate-equilibrium-free-energy relationships (REFERs) of covalent-bond chemistry. Linear free-energy relationships are the classical means of analyzing the structures of transition states. The structure of a reagent is subtly altered by small changes, and the consequent perturbations of the kinetics and equilibrium of the reaction are measured. Under certain circumstances, which often rely on the chemist's judgement in making sensible structural changes, there can be a linear relationship between ΔG^‡, the change in activation energy, and ΔG⁰, the change in equilibrium free energy; i.e., (∂ΔG^‡/∂structure)/(∂ΔG⁰/∂structure) = α in an REFER (6) (or = β in the earlier Brønsted plots for catalysis). The α (or β) value is a measure of extent of covalent-bond making or breaking in the reaction, with α = 0 implying no bond making (or breaking) and α = 1 implying complete making (or breaking). Intermediate values of α imply partial bond making or breaking. Protein engineering allowed the equivalent of REFERs to be applied to changes in noncovalent interactions of protein side chains as true multipoint plots and as a collection of two-point Φ values (1, 2). In general, protein engineering gives two-point, mutationally specific plots, and the existence of multipoint plots is a bonus when all mutations respond with the same α or β (2)

There are important differences between Φ and α or β. Many chemical processes respond smoothly to changes in structure that are remote from the seat of reaction, but Φ can depend on the specific interactions that are mutated and the change in energetics of the denatured state, including its solvation energy, on mutation (3, 4, 7). These energies affect the interpretation of Φ and require that Φ-value analysis is best applied to certain types of mutation, interpreted within various constraints, and can be difficult for fractional values of Φ. In the purest form of Φ-value analysis, mutations are made that delete interactions that stabilize the native state of the protein without disrupting the structure of the protein, introducing new interactions or changing stereochemistry: “nondisruptive deletion mutations” (2), preferably of hydrophobic moieties, although more radical mutations of surface residues are permitted (4).

Φ-value analysis should be applied with the following caveats. (i) In general, fractional values of Φ are not linear with the extent of bond formation, and only the extreme values of 0 and 1 are fully interpretable per se as being completely denatured-like and completely native-like, respectively [the term “denatured” is used because denatured states can have residual structure, and thus changes are measured relative to the residual structure (8)]. (ii) However, Φ for nondisruptive deletion mutations of hydrophobic side chains is approximately linear with the extent of formation of the bonds between denatured and native conformations, and thus fractional values are a good indicator of the extent of noncovalent-bond formation. (iii) Deletion of large side chains can alter many interactions between different substructures and thus give an average value of Φ for all of those interactions [a fine structure analysis is required to dissect the different components (9)]. (iv) Deletion of large side chains may also move the transition state by Hammond and anti-Hammond effects (10–12). (v) Because of the uncertainties in interpretation of Φ, as many Φ values as possible should be made and the results divided into classes of “weak,” “medium,” and “strong” (as with nuclear Overhauser effects in NMR spectroscopy) for purposes of combining with simulation to obtain atomic-level resolution of transition states (13).

Φ values per se can give extensive atomic-level information on structures of transition states. For example, Φ-value analysis on chymotrypsin-inhibitor 2 (CI2) provided the experimental evidence for the nucleation–condensation mechanism of folding in which secondary and tertiary interactions form together in the transition state, which appears to form around an extended nucleus that has moderate Φ values, with Φ falling off with distance from the nucleus (5, 14, 15). In general, Φ values are the experimental data for benchmarking simulation and for reconstructing protein-folding transition states and pathways at atomic resolution by combining experiment and simulation, and Φ-value analysis is at its most powerful when in combination with simulation (16–21). The theoretical studies use a global analysis of the Φ values, not just a selected few.

A recent appraisal of the results of Φ-value analysis concluded that measurements should be restricted to those for ΔΔG_D-N values >1.7 kcal/mol (7 kJ/mol) (22). It also was concluded that most high values of Φ were artifacts of ΔΔG_D-N being <7kJ/mol. On discarding the “artifactually” high Φ values, it was concluded that “diffuse” protein-folding transition states are uniformly diffuse, which is counter to much of theory, experiment, and simulation (16, 23–27). The authors' reasoning was based on the premise that Φ should be the same for all mutations at the same site, and thus deviations from this will show which Φ values are inaccurate (22). They tested the linearity hypothesis on a data set (28), which appeared to give the 1.7 kcal/mol cutoff point. However, in many cases, Φ is mutation-specific, because each mutation removes different interactions and has different effects on the denatured state (3, 4) and the data set used to calibrate Φ values had been deliberately designed by Davidson and coworkers (28) to be unsuitable for Φ-value analysis.

We formally demonstrate the flaws in the Φ-value reappraisal and confirm from experimental data that Φ values from non-disruptive mutations can be adequately reliable down to a ΔΔG_D-N value of ≈0.6 kcal/mol (2.5 kJ/mol) for suitable proteins. We show how the crucial probes for the formation of local secondary structure tend to have ΔΔG_D-N values of ≈0.6–2 kcal/mol (2.5–8 kJ/mol), and thus discarding their values discards the evidence for nucleation sites. We also refute the proposal (22, 29) that structures of transition-state ensembles are not affected by mutation. We use the REFER methods that supposedly indicated the 1.7 kcal/mol cutoff point to show that the cutoff is closer to 0.6 kcal/mol for suitable proteins.

Formal Analysis of Φ Values.

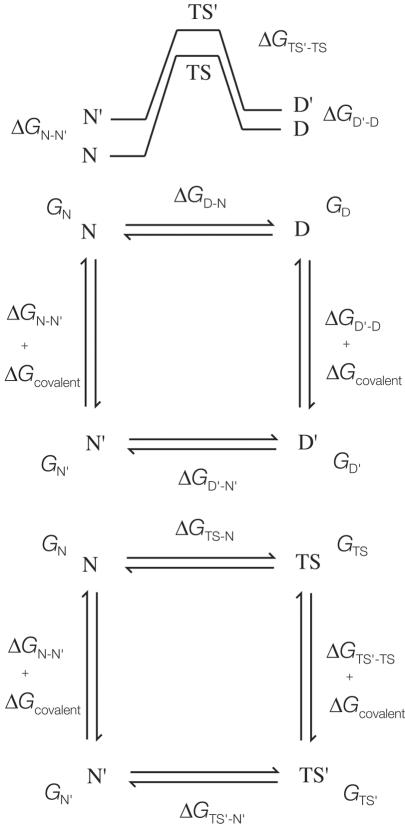
Relationship Between Φ and α. The premise of Sanchez and Kiefhaber (22) is that Φ is identical to the Leffler α and that all mutations at a particular position should give the same value of Φ. However, there is a crucial difference between the Leffler α and Φ, which may be shown formally. Let the free energy of the native state N be G_N, that of the denatured state be G_D, that of the transition state be G_TS, and mutant states be denoted by a prime (Fig. 1). The free energy of denaturation ΔG_D-N = G_D – G_N; the free energy of folding ΔG_N-D = G_N – G_D; the activation energy of unfolding ΔG_TS-N = G_TS – G_N; and the activation energy of folding ΔG_TS-D = G_TS – G_D. Abbreviating structure to “S”:

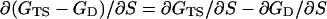[1]

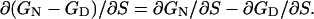[2]

Thus,

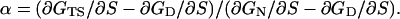[3]

The change in free energy of the denatured state with mutation, ∂G_D/∂S, is an important component of α. It was the essential difference between the classical Leffler α or Brønsted β that led us to give the free-energy constant a new name, Φ (3).

Fig. 1.

Schematics of thermodynamic cycles and free-energy profiles.

The experimentally accessible quantities used in Φ-value analysis are equilibrium and kinetic data of denaturation measured on wild-type and mutant proteins separately, ΔG_D-N, ΔG_D′-N′, ΔG_TS-N, ΔG_TS′-N′, ΔG_TS-D, and ΔG_TS′-D′ (Fig. 1). The observed difference in free energy of denaturation of wild-type protein and that of a mutant (denoted by ′) ΔΔG_D-N = ΔG_D′-N′ – ΔG_D-N. The difference in free energy of activation of unfolding ΔΔG_TS-N = ΔG_TS′-N′ – ΔG_TS-N. The difference in free energy of activation of folding ΔΔG_TS-D = ΔG_TS′-D′ – ΔG_TS-N, which for two-state kinetics has the same transition state. The observed experimental quantities are related to the changes in the individual states on mutation for virtual thermodynamic cycles based on Fig. 1 (3, §): ΔΔG_D-N = ΔG_D′-D – ΔG_N′-N; ΔΔG_TS-N = ΔG_TS′-TS – ΔG_N′-N; and ΔΔG_TS-D = ΔG_TS′-TS – ΔG_D′-D.

The experimentally determined Φ value for folding, Φ_F,¶ is defined by

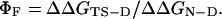[4]

In terms of the other changes in the cycle,

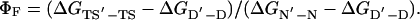[5]

Eq. 5 is the two-point version of Eq. 3 for a finite change in structure.

The change in free energy on mutating N to N′, ΔG_N′-N, can be split up into notional components: the change in energy of the covalent bond that is mutated, ΔG_cov, the change in noncovalent interactions at the site of mutation, ΔG_noncov (without any reorganization of the structure of the protein on mutation), plus any additional changes because of the reorganization of the protein, ΔG_reorg, and the change in solvation energy, ΔG_solv (4, 7). ΔG_cov is the same for all states and drops out of the equations.

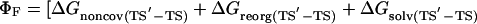[6]

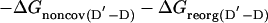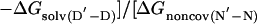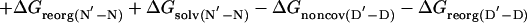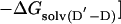The presence of the ΔG_D′-D term in Eq. 5 [= ΔG_{reorg(D′-D)} + ΔG_solv(D′-D) in Eq. 6] can lead to Φ being uninterpretable, and the ΔG_noncov terms can be mutation-specific (2, 3, 7).

Φ is identical to the classical α or β under two extreme circumstances. (i) The target region is as unstructured in the transition state as in the denatured state. Under these circumstances, all the ΔG terms in TS′-TS are the same as those of D′-D, and Eqs. 5 and 6 reduce to Φ_F = 0 (and for two-state folding, Φ for unfolding, Φ_U, = 1). (ii) The target region is as structured in the transition state as in the native state. Under these circumstances; all the ΔG terms in TS′-TS are the same as those of N′-N, and Eqs. 5 and 6 reduce to Φ_F = 1 (and for two-state folding, Φ_U = 1). The extreme values of 0 and 1 should be interpretable, therefore, for all mutations.

Fractional values of Φ are readily interpretable for the chemically sensible nondisruptive deletion mutations, especially of hydrophobic side chains, because the ΔG_reorg terms are minimized (2, 4) as are also the ΔG_solv for aliphatic to aliphatic mutations. For example, mutations of Ile → Ala and Val have values of ΔG_solv in water for fully exposed side chains of only –0.21 and –0.16 kcal/mol, respectively (31). Thus, when ΔΔG_D-N is significant and ΔG_reorg and ΔG_solv are low, Φ_U = [ΔG_{noncov(TS′-TS)} – ΔG_{noncov(N′-N)}]/[ΔG_{noncov(D′-D)} – ΔG_{noncov(N′-N)}], which is analogous to α. Additionally, the energetics for deletion of hydrophobic elements of side chains is dominated by van der Waals' interactions, which are approximately additive, as is found experimentally (32). Thus, for nondisruptive deletions of hydrophobic side chains, Φ_F ≈ (n_TS – n_D)/(n_N – n_D), where n_TS is the number of van der Waals' interactions made by the target portion of the side chain in the transition state, n_N is in the native state, and n_D in the denatured state. For two-state kinetics, Φ_U ≈ (n_TS – n_N)/(n_D – n_N). Importantly, Φ reports back on the interactions made in the native protein.

Fractional values can arise from either genuinely weakened interactions in a single transition-state ensemble or from a mixture of states in parallel pathways. The folding of the barley CI2, for example, has predominantly fractional values of Φ (14, 33). The conforming to an REFER shows that there are not parallel pathways (34).

Fractional values may also arise if a side chain makes interactions with multiple elements of substructures that have varying degrees of structure formation. The overall Φ value is then the weighted mean value of all the interactions. This possibility was noted for barnase and CI2, and a fine structure analysis was performed by making systematic mutations in the side chains concerned: e.g., Ile → Val → Ala → Gly, which gave the individual Φ values (9, 32, 35).

Accordingly, our preferred strategy for Φ-value analysis is to (i) mutate buried hydrophobic moieties by nondisruptive deletions (preferably Ile → Val → Ala → Gly; Leu → Ala → Gly; Thr → Ser; and Phe → Ala → Gly, avoiding Phe → Leu because of the change in stereochemistry); (ii) make a wider range of surface mutations, because larger side chains may be acceptable; (iii) use double-mutant cycles in which changes in solvation and reorganization energies tend to cancel out (4); and (iv) mutate Ala → Gly at solvent-exposed positions in secondary structural regions (“Ala → Gly scanning”), especially in α-helices, because they provide an exquisite probe of secondary structure (12). (v) Perform additional fine structure analyses by deleting different parts of larger side chains.

The magnitude of ΔΔG_D-N on mutation is a compromise: small values represent the smallest perturbation to the structure but have more attendant errors; larger values can be measured more accurately but often involve large changes that have more artifacts from reorganization energy changes on mutation and removing dispersed interactions. Our lower limit of acceptability for ΔΔG_D-N has generally been ≈0.6 kcal/mol (2.5 kJ/mol) for small, nondisruptive deletions (9, 14, 36).

Experimental Evidence for Lower Limit of ΔΔG_D-N for Φ Values. Comparing individual Φ values for mutations at a particular site with a multipoint Leffler plot would be a good means of detecting deviations for particular mutations (22), but for the problem of the ΔG_solv terms involved in ΔG_D′-D and ΔG_reorg in the native state, unless carefully chosen, the different mutants will have different values of ΔG_solv and could have very different values of ΔG_reorg in the native and transition-state structures. Additionally, there must also be a relatively linear function of ΔG_noncov with formation of structure over the range of structural transition.

An earlier attempt to calibrate two-point Φ plots against a multipoint Leffler plot (37) used mutations that are specifically not recommended, with only 5 of 47 being nondisruptive hydrophobic deletions: Ser → Asp, Glu; Ile → Thr, Tyr; Val → Ala, Lys; Leu → Ala, Thr, Ile; Ala → Cys, Pro, Ser, Gly, Thr, Leu, Asn; Gln → Ala, Leu, Ser, Thr, Lys; Ser → Ala, Gly, Trp, Cys, Thr, Ile, Tyr, Val, Asn, Gln, Lys; Val → Ala, Cys, Leu, Thr; Leu → Ser, Gln, Pro, Phe, Asn, Glu, Tyr; Leu → Ala, Ser; and Ser → Ala, Leu. Sanchez and Kiefhaber (22) showed that two-point Φ values deviated from a multipoint Leffler plot for ΔΔG_D-N < 1.7 kcal/mol by using data from a study by Davidson and coworkers (28). However, the title of that study was “Protein Folding Kinetics Beyond the Φ-Value: Using Multiple Amino Acid Substitutions to Investigate the Structure of the SH3 Domain Folding Transition State,” and the rationale was described by the authors in the abstract as: “In contrast to most other folding kinetic studies which have focused primarily on nondisruptive substitutions with Ala or Gly, here we have examined the effects of substitutions with diverse amino acid residues.” They mutated Glu → Asp, Gln, His, Lys, Ala, Ser, Val, Pro, Gly, Arg, Ile, Leu, and Ser → Lys, Arg, Leu, Ala, His, Val, Ile, Asn, Asp, Gly, Phe, Tyr, which are virtually all disruptive mutations of a mainly buried hydrogen bond. These mutations are by intent and definition unsuitable for calibrating Φ-value analysis (28).

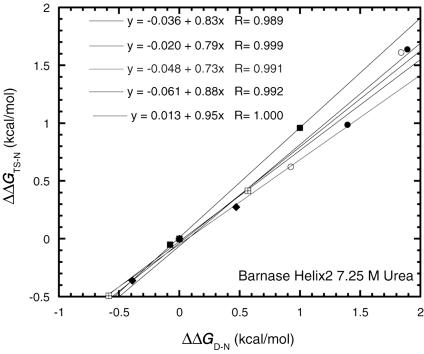
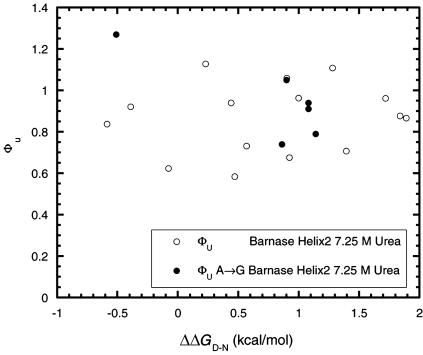
Leffler Plots and Ala → Gly Scanning for Exposed Surface Regions. The Davidson and coworkers (28) mutations are not suitable, because the side chains are buried, which complicates both the specific interactions involved for each chain as well as the changes in solvation on mutation. In contrast, surface-exposed residues, especially of α-helices, provide an opportunity for testing REFERS of more than two points. If the solvent-exposed end of the residue in the N state does not make any specific interactions with the rest of the protein, then it should make similar interactions with solvent in the TS and D states. Thus, the energetics of solvation of polar moieties of common surface residues such as Arg, Lys, Glu, Asp, Gln, and Asn, for example, will cancel out in the equations defining Φ. We have accumulated data for several helices in which surface-exposed residues are mutated to Ala and Gly. Helix 2 of barnase provides a good test for three-point Leffler plots, because the two-point Φ values show that the helix becomes highly unfolded in the transition state for unfolding (9) and thus the whole of the helix could constitute a multipoint REFER. Indeed, the energetics of mutation of Thr-26 → Ala → Gly, Lys-27 → Ala → Gly, Ser-28 → Ala → Gly, Glu-29 → Ala → Gly, and Gln-31 → Ala → Gly (Fig. 2) fit a good linear plot, with each three-point plot for an individual position having a correlation coefficient (R) between 0.99 and 1.0 and the slopes varying between 0.73 and 0.95 (mean = 0.84 ± 0.04 standard error). Individual values of Φ for all mutants (relative to wild type; Fig. 3) give a mean value of Φ of 0.86 ± 0.04 in a spread of 0.6 to 1.1. Ala → Gly scanning at each position gives a mean of 0.95 ± 0.08. The Φ values were derived from values of ΔΔG_D-N that have a standard error of ± 0.06 kcal/mol and values of ΔΔG_TS-N at 7.25 M urea that have a standard error of ±0.01–0.03 kcal/mol (12). Even with a ΔΔG_D-N value of 0.6 kcal/mol, the expected error in Φ should be only ≈10%. The linear plots in Fig. 2 and the values of Φ (Fig. 3) are nearly all obtained from values of ΔΔG_D-N below the 1.7 kcal/mol (7 kJ/mol) cutoff proposed by Sanchez and Kiefhaber (22).

Fig. 2.

Three-point Leffler plots for the unfolding of barnase. Mutations are as follows: Thr-26 → Ala → Gly, Lys-27 → Ala → Gly, Ser-28 → Ala → Gly, Glu-29 → Ala → Gly, and Gln-31 → Ala → Gly in helix 2.

Fig. 3.

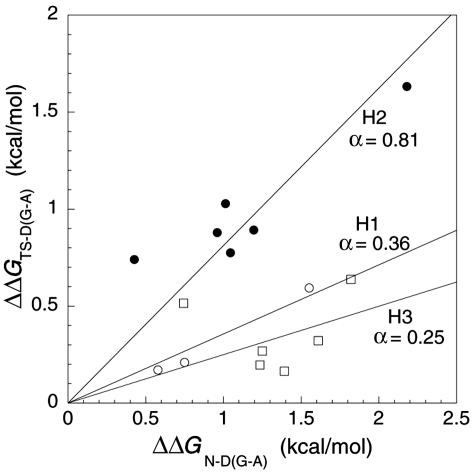
Plot of Φ_U versus ΔΔG_D-N for mutations in helices 1 and 3 of barnase.

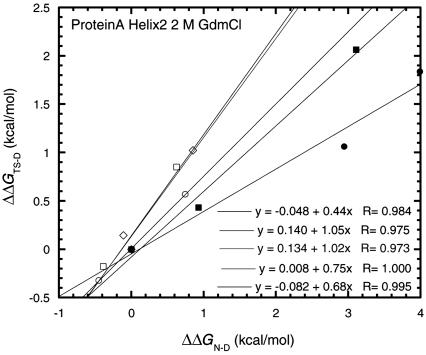
Another suitable protein for testing the accuracy of values of Φ derived from low ΔΔG_D-N values is the B-domain of protein A from Staphylococcus aureus, a three-helix bundle protein. The data are slightly less accurate (ΔΔG_D-N ± 0.1 and ΔΔG_TS-N ± 0.08 kcal/mol), so that Φ for ΔΔG_D-N = 0.6 kcal/mol should have an error of ±20%, dropping to ±10% at ΔΔG_D-N = 1.2 kcal/mol (36). Individual Φ values show that the first and third helices are in the process of being formed in the transition state, whereas the second is nearly fully formed. There are good three-point REFERs (Fig. 4) for the mutations in helix 2 of Gln-27 → Ala → Gly, Arg-28 → Ala → Gly, Asn-29 → Ala → Gly, Gln-33 → Ala → Gly, and Ser-34 → Ala → Gly. The only low value of the slope is for Gln-27 → Ala → Gly, which results from specific interactions. Gln-27 makes a hydrogen bond with Asn-24, and there are large changes of ΔΔG_D-N (3 and 4 kcal/mol) on its mutation. REFERs for the energetics of Ala → Gly scanning (Fig. 5) show that helix 2 is ≈80% formed in the transition state, whereas the other two are not. The data for Ala → Gly scanning are clearly acceptable down to a ΔΔG_D-N value of ≈0.6 kcal/mol.

Fig. 4.

Three-point Leffler plots for the following mutations of helix 2 of the B-domain of protein A: Gln-27 → Ala → Gly, Arg-28 → Ala → Gly, Asn-29 → Ala → Gly, Gln-33 → Ala → Gly, and Ser-34 → Ala → Gly.

Fig. 5.

Leffler plots of Ala → Gly scanning mutations in the three helices of the B-domain of protein A.

Schmid and coworkers (38), in a careful study of the folding of CspB protein, independently used a ΔΔG_D-N value of ≈0.6 kcal/mol as the lower limit for Φ-value analysis and also divided their results into weak, medium, and strong values. Radford and coworkers (25) used a cutoff of 0.7 kcal/mol for analyzing the folding of the immunity proteins Im7 and Im9, with satisfactory agreement. [Sanchez and Kiefhaber (22) recalculated Φ values from ref. 25, but the data were incomplete; several values from larger destabilizing mutations, some of which result in Φ values >0.3, are omitted, and other values are shown that were not calculated in ref. 25 because the ΔΔG_D-N was below the cut off of 3 kJ/mol (0.7 kcal/mol) used (S. E. Radford, personal communication)].

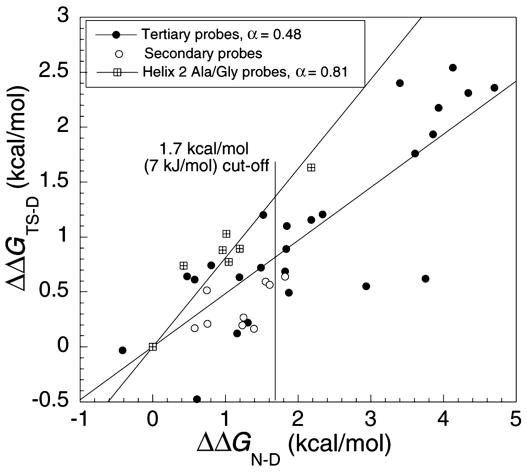
Values of ΔΔG_D-N for Secondary and Tertiary Structure Probes. The fine structure probes that test specific interactions tend to be those that delete a small interaction; e.g., that of a single methylene group, or a single hydrogen bond, which both typically have ΔΔG_D-N values in the range of 1.5 ± 0.5 kcal/mol (39–41). Large changes of ΔΔG_D-N tend to be associated with the deletion of large side chains, especially in the hydrophobic core, or the disruption of buried salt bridges (32), as shown in Fig. 6 for the B-domain of protein A. By discarding the Φ values derived from a ΔΔG_D-N value of <1.7 kcal/mol, Sanchez and Kiefhaber (22) discarded most of the secondary structure probes and thus constructed REFER plots of mainly tertiary interactions, especially in the hydrophobic core. The formation of the core is always part of the rate-determining process and has fractional Φ values (3, 27, 36, 42, 43). Thus, by concentrating on such data, they concluded incorrectly that transition states are uniformly diffuse.

Fig. 6.

Leffler plot for all mutations in the B-domain of protein A. Filled circles are used for the tertiary probes, and open circles are used for secondary structural probes.

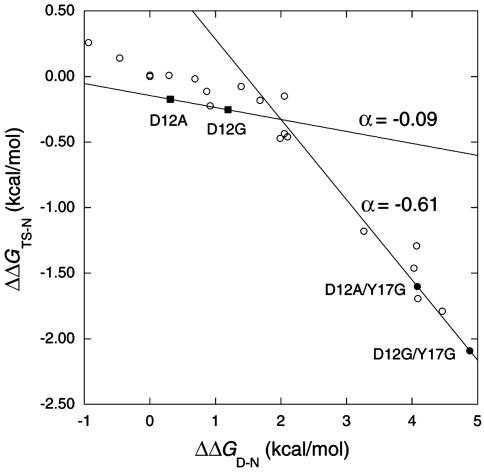
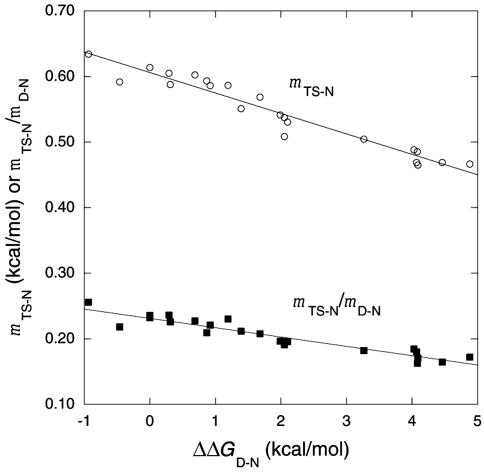
Movement of Transition-State Structure on Mutation. Sanchez and Kiefhaber (22, 29) claim that the structures of transition states do not change on mutation. They suggest that the observed movements of transition states along a reaction coordinate (10–12) are not a consequence of a change in transition-state structure via a Hammond effect but instead result from (partial) changes in rate-determining steps between formation and breakdown of intermediates or have complications from effects of mutation on the denatured state (44). It is very difficult to distinguish between true Hammond behavior and changes in the rate-determining step. However, there are well documented examples of anti-Hammond behavior (movement perpendicular to the reaction coordinate) that cannot be accounted for by changes in the rate-determining step along a reaction coordinate (12). A Leffler plot of successive mutations in helix 1 of barnase (Fig. 7) has a slope for unfolding of –0.09 for mutations with ΔΔG_D-N < 2 kcal/mol, showing that it is ≈90% folded in the transition state, but for ΔΔG_D-N > 3 kcal/mol, the slope gets steeper at –0.61, indicating it is only 40% folded and follows anti-Hammond behavior (12). The slopes are measured by Ala → Gly scanning at position 12 in wild-type protein and the same position in the mutant Tyr-17 → Gly, which is destabilized by 4.1 kcal/mol (12). Whereas the helix becomes less folded in the transition state on destabilization, the overall transition state follows Hammond and becomes more folded, with its relative surface exposure decreasing from 55% to 37% over a change of 5 kcal/mol in ΔΔG_D-N (Fig. 8). The data are for unfolding and are independent of mutations on the denatured state. The anti-Hammond behavior can be explained by either a gradual movement of the transition state or by a switch between parallel pathways (12). Simulation favors the gradual movement (45).

Fig. 7.

Leffler plots for single, double, and triple mutations in helix 1 of barnase plus Ala → Gly scanning at position 12 in the mutant Tyr-17 → Gly. The mutants are as follows: Asp-8 → Ala, Asp-12 → Gly, Asp-12 → Ala, Tyr-13 → Ala, Tyr-13 → Ala/Thr-16 → Ser, Tyr-13 → Ala/Tyr-17 → Ala, Tyr-13 → Ala/Thr-16 → Ser/Tyr-17 → Ala, Gln-15 → Ile, Thr-16 → Ala, Thr-16 → Gly, Thr-16 → Ser, Thr-16 → Ser/Tyr-17 → Ala, Thr-16 → Arg, Tyr-17 → Ala, His-18 → Lys, His-18 → Gln, Tyr-17 → Ala, Tyr-17 → Gly, His-18 → Ala, His-18 → Gly, Asp-12 → Ala/Tyr-17 → Gly, and Asp-12 → Gly/Tyr-17 → Gly.

Fig. 8.

Plots of data relating surface exposure on denaturation kinetics of barnase. m_TS-N is the slope of the plot of ΔG_TS-N versus [urea], and m_D-N is the slope of the plot of ΔG_D-N versus [urea]. m_TS-N is the value at 7.25 M urea, measured for unfolding data acquired between 6 and 8.5 M urea, and it is accurate to ±2%. The ratio of m_TS-N/m_D-N is a measure of the relative solvent exposure of the transition state to the denatured state. The value of m_TS-N is a function of just the difference in solvent-accessible surface area of TS and N and does not depend on the properties of the denatured state.

Sanchez and Kiefhaber propose that the larger the value of ΔΔG_D-N, the better for Φ-value analysis (22). However, Fig. 7 shows clearly that large changes of ΔΔG_D-N can lead to radical changes in structure in transition states. In general, the fine structural information requires specific probes, with energies of 0.6–2 kcal/mol. The more energy-disruptive probes can perturb the transition-state structure, which complicates a simple Φ-value analysis but can give information about the energy surface around the transition state.

Nature of Folding Transition States. Sanchez and Kiefhaber (22) use the classification of transition states being either diffuse, whereby most of the Φ values are fractional and polarized where there are regions that are fully formed or fully denatured. They suggest that there are never regions of high Φ value in the diffuse states, and thus all transition states are similar to that found for CI2. However, the transition state for the folding of the B-domain of protein A is not polarized, and there are regions, especially involving helix 2, that have Φ values approaching 1 (36). The Φ analyses of the Engrailed homeodomain family, although not extensive, show transition states that are basically structured all over and with regions of Φ values of 1 (27, 43). Transition states have a spectrum of structures, varying from the diffuse of pure nucleation–condensation to the more compact that approach the classical framework mechanism of folding, in which the repeating secondary structure is nearly fully formed and the core is in the process of consolidation (23–25, 38, 44–50).

In any case, it is not possible to divine from the transition-state structure per se whether there are nucleation sites, because the structure does not reveal per se the starting point of folding or the route by which the structure is formed (51). The experimental evidence for nucleation in CI2 folding, for example, came from ancillary studies that examined the denatured state of the protein and its fragments (52), and the evidence for framework for Engrailed homeodomain came from analyzing the structures of ground states as well as simulation (43). Additionally, high Φ values need not be associated with a nucleus, and low Φ values can be found in nuclei (19).

Conclusions

There are strong analogies between the determination of solution structures of proteins by NMR combined with simulated annealing and the determination of structures of transition states by Φ values and simulation. Just as there are nuclear Overhauser effects in NMR spectra of spurious intensity, there are undoubtedly some misleading Φ values, especially when ΔΔG_D-N is small. However, provided mutations are made within the prescribed rules and that a sufficient number are analyzed, then reliable results will be obtained down to changes in ΔΔG_D-N of ≈0.6 kcal/mol under optimal conditions. Higher values of ΔΔG_D-N do give statistically more precise data, but much larger values of ΔΔG_D-N may give less precise information, because they arise from dispersed interactions and may have higher contributions from perturbations of structure. Just as special methods are continually introduced to refine NMR methods, so ancillary methods such as Ala → Gly scanning are required for refining by Φ-value analysis.